The Partial Derivative Method for Dynamic Stiffness and Damping Coefficients of Supercritical CO₂ Foil Bearings

Abstract

Supercritical CO₂ foil bearings are promising bearing technology for supercritical CO₂ high-speed turbomachinery. The partial derivative method including complete variable perturbation of the compressible turbulent lubrication Reynolds equation is effective to predict the frequency dependent dynamic stiffness and damping coefficients of supercritical CO₂ bearings. In this research, the structural perturbation of foil dynamic model was introduced into this method and then the dynamic coefficients of supercritical CO₂ foil bearings were calculated. The results of parametric analysis show that the structural loss factor has little influence on the trend of dynamic coefficients changing with the dimensionless support stiffness but mainly affects the value of stiffness coefficients as well as damping coefficients. Due to the turbulence effect, the bearing number is not able to directly determine the characteristics of supercritical CO₂ foil bearings, which is different from air bearings. Compared to the bearing number, the influence of the average Reynolds number on the change of dynamic coefficients with dimensionless support stiffness is more obvious.

1. Introduction

The supercritical carbon dioxide closed-loop Brayton cycle is a promising power generation system due to compact structure and high efficiency [1,2,3]. The characters of high parameters and high efficiency of supercritical CO₂ turbomachinery require the rotor with high speed, which makes the bearing technology attract a lot of attentions [4,5]. Supercritical CO₂ lubricated bearings can simplify the rotor structure to improve its dynamics as well as eliminate the pollution of lubricant oil completely [6,7,8]. The compliant foil gas bearing technology from Capstone was used in the tests of supercritical CO₂ power system in Sandia, which is one of the key technologies of turbo-alternator-compressor configuration [9]. Some of other successful supercritical CO₂ turbomachinery test projects also used the foil bearings [1,10].

At present, there are many research studies on the air foil bearing were published, including both mechanism analysis [11,12,13] and prototype test [14,15]. Although the foil bearings lubricated by both supercritical CO₂ and air belong to compressible fluid lubrication, their lubricating mechanisms are essentially different because the compressive behavior of supercritical CO₂ shows a real gas effect and the turbulence exists in the supercritical CO₂ bearing clearances [16]. Conboy developed a model for supercritical CO₂ foil thrust bearing based on Reynolds equation considering turbulence and real gas effect [17]. Munroe used COMSOL for the multiphysics field analysis of supercritical CO₂ foil thrust bearings [18]. Kim proposed an analysis tool for three-dimensional thermal fluid analysis of radial foil bearings with turbulence and real gas effects [19]. These studies mentioned above only related to the static characteristics of supercritical CO₂ foil bearings.

However, the theoretical calculation and design approach to supercritical CO₂ foil bearings are still deficient because the dynamic characteristics of bearings are the only basis in the simulation on dynamics of rotor-bearing system [20,21]. For the bearings lubricated with compressible fluid, their dynamic stiffness and damping coefficients change with the perturbation frequency [22]. Chapman recognized the importance of subsynchronous perturbation and derived subsynchronous dynamic coefficients of supercritical CO₂ hydrostatic foil bearings by CFD [23]. However, the CFD-based method makes it difficult to consider the dynamical structural deformation of foil. Bi presented the partial derivative method embracing dynamical variations of complete variables in the Reynolds equation for solving the dynamic coefficients of supercritical CO₂ rigid cylindrical bearings under different perturbation frequencies [24].

In this paper, the complete variables perturbed partial derivative method given in Ref. [24] is furthered by introducing the structural perturbation theory for the dynamic model of foil. Then, the method is able to calculate the frequency dependent dynamic stiffness and damping coefficients of supercritical CO₂ foil bearings with consideration of dynamical deformation of the foil. The calculation model for foil bearing in this study was verified by comparing with the experimental and numerical results in the literature. Under different perturbation frequencies, the influences of foil support stiffness, structural loss factor, bearing number, and average Reynolds number on the dynamic coefficients of supercritical CO₂ foil bearing are investigated in detail.

2. Mathematics for Dynamic Coefficients of Supercritical CO₂ Foil Bearings

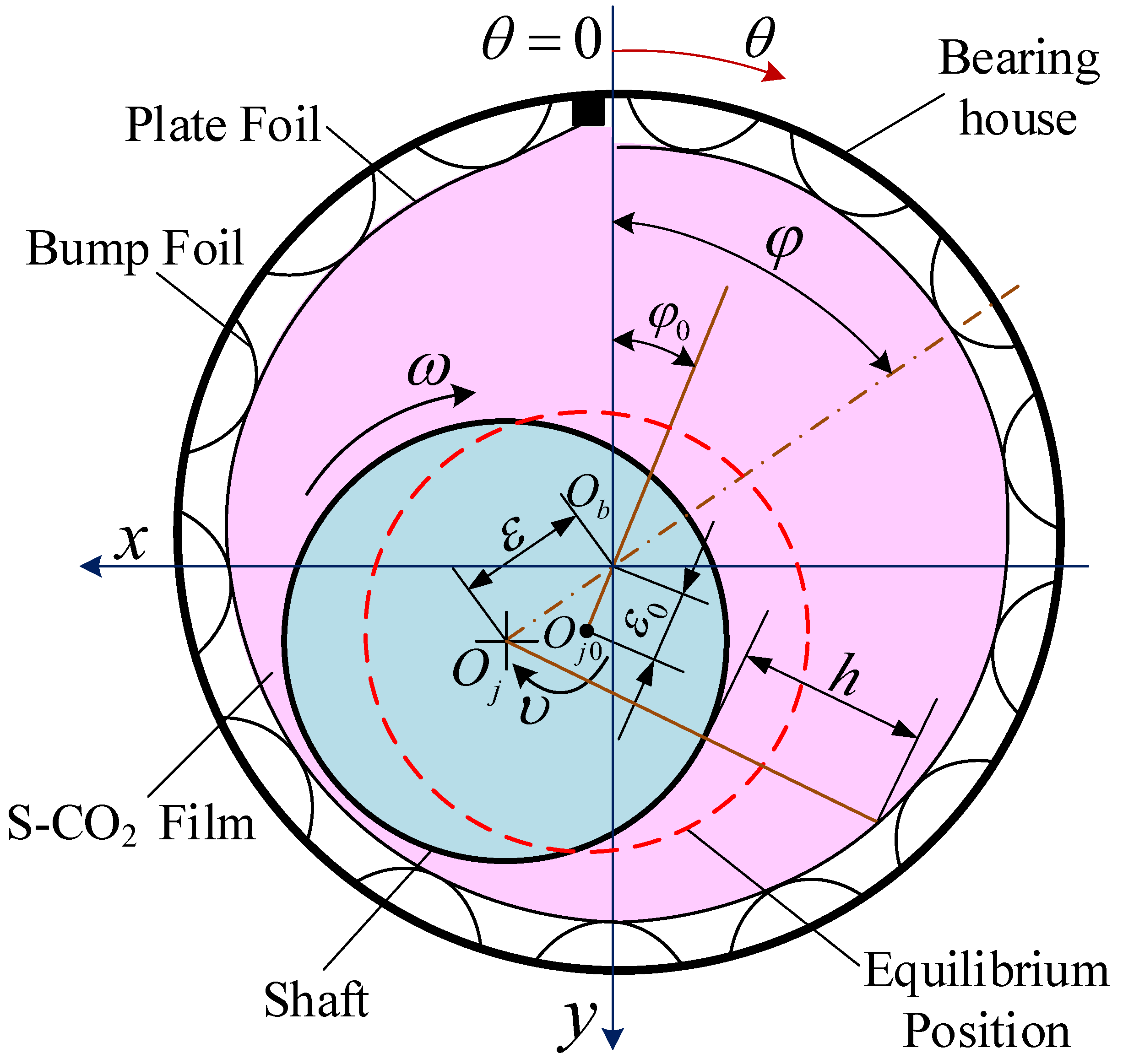
2.1. Supercritical CO₂ Lubricated Foil Bearing

The schematic diagram of supercritical CO₂ foil bearing studied in this paper is shown in Figure 1. The foil bearing is composed of plate foil, bump foil, and bearing house. In circumferential direction, one end of the two kinds of foil is fixed on the bearing house and the other end is free.

The shaft rotate with angular velocity ω in the foil bearing from free end to fixed end at its equilibrium position described by eccentricity ratio ε₀ and attitude angle φ₀. The thickness of lubricating film h is the distance between the shaft surface and the inner surface of the plate foil, under the perturbation in the small neighborhood of equilibrium position; its dimensionless form is composed of the static film thickness ${\overline{h}}_0$ and the perturbed one ${\tilde{h}}_d$.

$$\overline{h}={\overline{h}}_0+{\tilde{h}}_d{e}^{i\mathsf{\Omega }\overline{t}}$$

(1)

where Ω is dimensionless perturbation frequency, which equals the ratio of the perturbation circular frequency υ to the rotating circular frequency ω of the shaft. The ${\overline{h}}_0$ and ${\tilde{h}}_d$ of the fixed pad bearing with rigid surface can be determined directly by the geometric and kinematic relationship between the shaft and pad. However, the ${\overline{h}}_0$ and ${\tilde{h}}_d$ of the foil bearings need to be determined by introducing the structural perturbation (see Section 2.2.1) which reflects the relation between the dynamical deformation and pressure.

2.1.1. The Compressible Turbulence Reynolds Equation and Its Boundary Conditions

The dimensionless compressible turbulent lubrication Reynolds equations including real gas effect for supercritical CO₂ bearings were obtained by the partial derivative method in [24] and are shown as follows.

$$\frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^3}{{\overline{\mu }}_0}{G}_x\frac{\partial {\overline{p}}_0}{\partial \theta }\right)+\frac{\partial }{\partial \lambda }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^3}{{\overline{\mu }}_0}{G}_z\frac{\partial {\overline{p}}_0}{\partial \lambda }\right)=\mathsf{\Lambda }\frac{\partial \left({\overline{\rho }}_0{\overline{h}}_0\right)}{\partial \theta }$$

(2)

$$\begin{array}{cc}\hfill \frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^3}{{\overline{\mu }}_0}{G}_x\frac{\partial {\tilde{p}}_d}{\partial \theta }\right)& +\frac{\partial }{\partial \lambda }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^3}{{\overline{\mu }}_0}{G}_z\frac{\partial {\tilde{p}}_d}{\partial \lambda }\right)\hfill \\ \hfill & +\left(1-{\beta }_1\right)\frac{\partial }{\partial \theta }\left[\left({\overline{\partial }}_p\rho \left(p_0,T\right)-\frac{{\overline{\rho }}_0}{{\overline{\mu }}_0}{\overline{\partial }}_p\mu \left(p_0,T\right)\right)\frac{{\overline{h}}_0^3}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \theta }{G}_x{\tilde{p}}_d\right]\hfill \\ \hfill & +\left(1-{\beta }_2\right)\frac{\partial }{\partial \lambda }\left[\left({\overline{\partial }}_p\rho \left(p_0,T\right)-\frac{{\overline{\rho }}_0}{{\overline{\mu }}_0}{\overline{\partial }}_p\mu \left(p_0,T\right)\right)\frac{{\overline{h}}_0^3}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \lambda }{G}_z{\tilde{p}}_d\right]\hfill \\ \hfill & =\left({\beta }_1-3\right)\frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \theta }{G}_x{\tilde{h}}_d\right)+\left({\beta }_2-3\right)\frac{\partial }{\partial \lambda }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \lambda }{G}_z{\tilde{h}}_d\right)\hfill \\ \hfill & +\Lambda \frac{\partial }{\partial \theta }\left({\overline{h}}_0{\overline{\partial }}_p\rho \left(p_0,T\right){\tilde{p}}_d+{\overline{\rho }}_0{\tilde{h}}_d\right)+2i\Omega \Lambda \left({\overline{h}}_0{\overline{\partial }}_p\rho \left(p_0,T\right){\tilde{p}}_d+{\overline{\rho }}_0{\tilde{h}}_d\right)\hfill \end{array}$$

(3)

The static Equation (2) is for static pressure distribution ${\overline{p}}_0$ and the perturbed Equation (3), which involves the dynamical variations of density, viscosity and the turbulence, governs the perturbed pressure ${\tilde{p}}_d$ for obtaining the dynamic coefficients. For the foil bearings, the structural perturbation reflects the relation between the ${\tilde{p}}_d$ and ${\tilde{h}}_d$.

In the Equations (2) and (3), the dimensionless turbulent lubrication coefficients G_x and G_z are shown below.

$$\begin{gathered} G_x={\left(1+{\alpha }_1/12R{e}^{{\beta }_1}\right)}^{-1}={\left(1+0.0136/12R{e}^{0.9}\right)}^{-1} \\ {G}_z={\left(1+{\alpha }_2/12R{e}^{{\beta }_2}\right)}^{-1}={\left(1+0.0043/12R{e}^{0.96}\right)}^{-1} \end{gathered}$$

(4)

The values of the constants α₁, α₂, β₁, and β₂ in the Equation (4) are given by the Ng-Pan turbulence model, which is reasonable for supercritical CO₂ bearings [25].

The boundary conditions for the supercritical CO₂ foil bearings are absolutely same to the ones which are appropriate for the air foil bearings. The boundary conditions for Equations (2) and (3) are shown below.

$$\begin{gathered} {\overline{p}}_0\left(\theta ,\lambda =\pm L/D\right)={\overline{p}}_0\left(\theta =0,\lambda \right)=1 \\ {\tilde{p}}_d\left(\theta ,\lambda =\pm L/D\right)={\tilde{p}}_d\left(\theta =0,\lambda \right)=0 \end{gathered}$$

(5)

Due to large flexibility, the plate foil is not able to bear the pressure lower than ambient pressure. The Reynolds boundary condition Equation (6), governing the separation of the plate foil from the bump foil, should be supplied to the simulation of the foil bearings.

$$if {\overline{ p}}_{0\_trend}\left(\theta ,\lambda \right)<1\{\begin{array}{c}{\overline{p}}_0\left(\theta ,\lambda \right)=1, \frac{\partial {\overline{p}}_0}{\partial \theta }=0\\ {\tilde{p}}_d\left(\theta ,\lambda \right)=0, \frac{\partial {\tilde{p}}_d}{\partial \theta }=0\end{array}$$

(6)

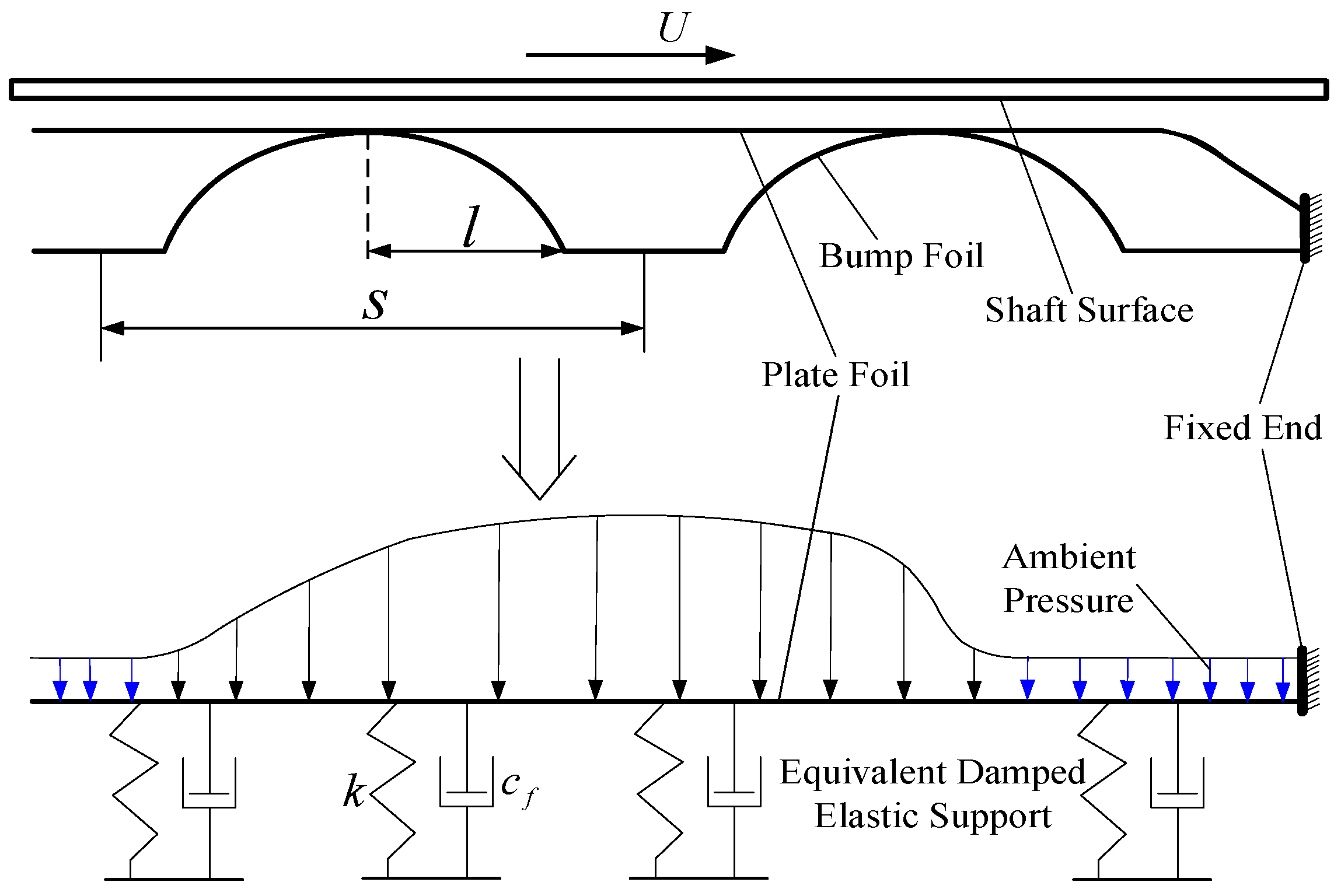
2.1.2. The Damped Elastic Support Comprehensive Dynamic Model for Foil System

The hydrodynamic lubricating film is generated by relative motion of the shaft and the inner surface of the plate foil. As shown in Figure 2, the foil system can be modeled as the acting surface of hydrodynamic lubrication with damped elastic support.

The comprehensive foil model containing elastic support and structure damping is given below.

$$p-p_a=k{w}_t+c_f\frac{\partial w_t}{\partial t}$$

(7)

where the w_t is the displacement of plate foil. The p-p_a is the force onto the foil, which is generated by the pressure difference between the hydrodynamic pressure of the lubricating film and the ambient pressure. The k and c_f are the support stiffness and structure damping of the damped elastic support system equivalent to the foil.

Taking the dimensionless pressure $\overline{p}=p/p_a$, dimensionless plate foil displacement ${\overline{w}}_t=w_t/C_0$ and dimensionless time $\overline{t}=\omega t$ into Equation (7), the dimensionless dynamic equation for the foil system can be obtained.

$$\overline{p}-1=\overline{k}{\overline{w}}_t+{\overline{c}}_f\frac{\partial {\overline{w}}_t}{\partial \overline{t}}$$

(8)

where the dimensionless support stiffness $\overline{k}$ and dimensionless structure damping ${\overline{c}}_f$ are as follows.

$$\begin{gathered} \overline{k}=\frac{C_0}{p_a}k \\ {\overline{c}}_f=\frac{\omega C_0}{p_a}{c}_f \end{gathered}$$

(9)

The structure damping $c_f$ depends on the interaction among the plate foil, bump foil and bearing house, which can be described by the structural loss factor $\gamma$ based on its relationship with the excitation frequency ${\upsilon }_f$ and the support stiffness k. The structure loss factor $\gamma$ can be determined by energy dissipation extracted from the dynamical loaded test; its value range is between 0.2 and 0.4 in [26] while Rubio [27] measured values between 0.06 and 0.21.

$$\gamma =\frac{c_f}{k}{\upsilon }_f=\frac{{\overline{c}}_f}{\overline{k}}\frac{{\upsilon }_f}{\omega }$$

(10)

Pronobis pointed out that the excitation frequency ${\upsilon }_f$ should be equal to the shaft rotation frequency ω rather than the shaft perturbation frequency $\upsilon$, because the deformation speed of the foil under the instability critical state is equal to the rotation speed of the shaft [28]. The instability rotation speed calculated by the eigenvalue method is consistent with the transient dynamic calculation as long as the ${\upsilon }_f/\omega =1$ is satisfied. Taking Equation (10) into Equation (8), the dimensionless foil dynamic equation can be obtained as follow.

$$\frac{\overline{p}-1}{\overline{k}}={\overline{w}}_t+\gamma \frac{\partial {\overline{w}}_t}{\partial \overline{t}}$$

(11)

2.2. The Structural Perturbation Theory of Foil Bearings

2.2.1. The Relation between the Perturbation of Foil Displacement and Perturbed Pressure

The dynamical variation of the displacement of plate foil ${\overline{w}}_t$ is expressed as the superposition of the static displacement ${\overline{w}}_{t0}$ and the perturbed displacement ${\tilde{w}}_t$.

$${\overline{w}}_t={\overline{w}}_{t0}+{\tilde{w}}_t{e}^{i\mathsf{\Omega }\overline{t}}$$

(12)

Considering the dynamical displacement of plate foil, the static film thickness ${\overline{h}}_0$ and the perturbed film thickness ${\tilde{h}}_d$ are shown as follows.

$${\overline{h}}_0={\overline{h}}_{J_0}+{\overline{w}}_{t0}=1+{\epsilon }_0\cos \left(\theta -{\phi }_0\right)+{\overline{w}}_{t0}$$

(13)

$${\tilde{h}}_d={\tilde{h}}_{J_d}+{\tilde{w}}_t={\tilde{\epsilon }}_d\cos \left(\theta -{\phi }_0\right)+{\epsilon }_0{\tilde{\phi }}_d\sin \left(\theta -{\phi }_0\right)+{\tilde{w}}_t$$

(14)

The expressions of ${\overline{w}}_{t0}$ and ${\tilde{w}}_t$ require to be obtained by perturbing the damped elastic support model of the foil system. Taking the perturbation expansions of foil displacement Equation (12) and pressure ($\overline{p}={\overline{p}}_0+{\tilde{p}}_d{e}^{i\mathsf{\Omega }\overline{t}}$) into the dimensionless foil dynamic Equation (11), the zero order and first order terms are separated and then the structural perturbation of foil bearings is obtained below.

$${\overline{w}}_{t0}=\frac{{\overline{p}}_0-1}{\overline{k}}$$

(15)

$${\tilde{w}}_t=\frac{{\tilde{p}}_d}{\overline{k}\left(1+i\mathsf{\Omega }\gamma \right)}$$

(16)

Equation (15) is the relation between the static plate foil displacement ${\overline{w}}_{t0}$ and static pressure ${\overline{p}}_0$, while Equation (16) is the relation between the perturbed foil displacement ${\tilde{w}}_t$ and perturbed pressure ${\tilde{p}}_d$. The damped elastic support foil dynamic model was modeled as dynamical complex stiffness $\overline{k}\left(1+i\mathsf{\Omega }\gamma \right)$, which expresses the elastic support and structure damping together by the superposition of the static support stiffness (real part) and perturbed stiffness (imaginary part).

2.2.2. The Partial Differential Equations for Complex Perturbed Pressure

Taking Equation (16) into Equation (14), the expression of perturbed film thickness ${\tilde{h}}_d$ can be obtained below.

$${\tilde{h}}_d={\tilde{\epsilon }}_d\cos \left(\theta -{\phi }_0\right)+{\epsilon }_0{\tilde{\phi }}_d\sin \left(\theta -{\phi }_0\right)+\frac{{\tilde{p}}_d}{\overline{k}\left(1+i\mathsf{\Omega }\gamma \right)}$$

(17)

Two perturbation variables ${\tilde{\epsilon }}_d$ and ${\tilde{\phi }}_d$ are involved in Equation (17). Let P_ε=$\partial {\tilde{p}}_d/\partial {\tilde{\epsilon }}_d$, P_φ = (1/ε₀)$\left(\partial {\tilde{p}}_d/\partial {\tilde{\phi }}_d\right)$, and taking partial derivative of ${\tilde{h}}_d$ to ${\tilde{\epsilon }}_d$ and ${\epsilon }_0{\tilde{\phi }}_d$, the H_ε and H_φ are defined as Equation (18).

$$\begin{gathered} H_{\epsilon }=\frac{\partial {\tilde{h}}_d}{\partial {\tilde{\epsilon }}_d}=\cos \left(\theta -{\phi }_0\right)+\frac{P_{\epsilon }}{\overline{k}\left(1+i\mathsf{\Omega }\gamma \right)} \\ {H}_{\phi }=\frac{1}{{\epsilon }_0}\frac{\partial {\tilde{h}}_d}{\partial {\tilde{\phi }}_d}=\sin \left(\theta -{\phi }_0\right)+\frac{P_{\phi }}{\overline{k}\left(1+i\mathsf{\Omega }\gamma \right)} \end{gathered}$$

(18)

In Equation (3), replacing the ${\tilde{p}}_d$ by P_ε, P_φ and the ${\tilde{h}}_d$ by H_ε, H_φ, respectively, yields two partial differential equations for P_ε and P_φ, shown as Equations (19) and (20).

$$\begin{array}{cc}\hfill \frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^3}{{\overline{\mu }}_0}{G}_x\frac{\partial P_{\epsilon }}{\partial \theta }\right)& +\frac{\partial }{\partial \lambda }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^3}{{\overline{\mu }}_0}{G}_z\frac{\partial P_{\epsilon }}{\partial \lambda }\right)+\left(3-{\beta }_1\right)\frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \theta }\frac{G_x{P}_{\epsilon }}{\overline{k}(1+i\Omega \gamma )}\right)\hfill \\ \hfill & +\left(1-{\beta }_1\right)\frac{\partial }{\partial \theta }\left[\left({\overline{\partial }}_p\rho \left(p_0,T\right)-\frac{{\overline{\rho }}_0}{{\overline{\mu }}_0}{\overline{\partial }}_p\mu \left(p_0,T\right)\right)\frac{{\overline{h}}_0^3}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \theta }{G}_x{P}_{\epsilon }\right]\hfill \\ \hfill & +\left(1-{\beta }_2\right)\frac{\partial }{\partial \lambda }\left[\left({\overline{\partial }}_p\rho \left(p_0,T\right)-\frac{{\overline{\rho }}_0}{{\overline{\mu }}_0}{\overline{\partial }}_p\mu \left(p_0,T\right)\right)\frac{{\overline{h}}_0^3}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \lambda }{G}_z{P}_{\epsilon }\right]\hfill \\ \hfill & +\left(3-{\beta }_2\right)\frac{\partial }{\partial \lambda }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \lambda }\frac{G_z{P}_{\epsilon }}{\overline{k}(1+i\Omega \gamma )}\right)\hfill \\ \hfill & =\left({\beta }_1-3\right)\frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \theta }{G}_{x}cos\left(\theta -{\phi }_0\right)\right)\hfill \\ \hfill & +\left({\beta }_2-3\right)\frac{\partial }{\partial \lambda }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \lambda }{G}_{z}cos\left(\theta -{\phi }_0\right)\right)+\Lambda \frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{P}_{\epsilon }}{\overline{k}(1+i\Omega \gamma )}\right)\hfill \\ \hfill & +\frac{2i\Omega \Lambda {\overline{\rho }}_0{P}_{\epsilon }}{\overline{k}(1+i\Omega \gamma )}+\Lambda \left(\frac{\partial }{\partial \theta }+2i\Omega \right)\left({\overline{h}}_0{\overline{\partial }}_p\rho \left(p_0,T\right)P_{\epsilon }+{\overline{\rho }}_{0}cos\left(\theta -{\phi }_0\right)\right)\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^3}{{\overline{\mu }}_0}{G}_x\frac{\partial P_{\phi }}{\partial \theta }\right)& +\frac{\partial }{\partial \lambda }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^3}{{\overline{\mu }}_0}{G}_z\frac{\partial P_{\phi }}{\partial \lambda }\right)+\left(3-{\beta }_1\right)\frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \theta }\frac{G_x{P}_{\phi }}{\overline{k}(1+i\Omega \gamma )}\right)\hfill \\ \hfill & +\left(1-{\beta }_1\right)\frac{\partial }{\partial \theta }\left[\left({\overline{\partial }}_p\rho \left(p_0,T\right)-\frac{{\overline{\rho }}_0}{{\overline{\mu }}_0}{\overline{\partial }}_p\mu \left(p_0,T\right)\right)\frac{{\overline{h}}_0^3}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \theta }{G}_x{P}_{\phi }\right]\hfill \\ \hfill & +\left(1-{\beta }_2\right)\frac{\partial }{\partial \lambda }\left[\left({\overline{\partial }}_p\rho \left(p_0,T\right)-\frac{{\overline{\rho }}_0}{{\overline{\mu }}_0}{\overline{\partial }}_p\mu \left(p_0,T\right)\right)\frac{{\overline{h}}_0^3}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \lambda }{G}_z{P}_{\phi }\right]\hfill \\ \hfill & +\left(3-{\beta }_2\right)\frac{\partial }{\partial \lambda }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \lambda }\frac{G_z{P}_{\phi }}{\overline{k}(1+i\Omega \gamma )}\right)\hfill \\ \hfill & =\left({\beta }_1-3\right)\frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \theta }{G}_{x}sin\left(\theta -{\phi }_0\right)\right)\hfill \\ \hfill & +\left({\beta }_2-3\right)\frac{\partial }{\partial \lambda }\left(\frac{{\overline{\rho }}_0{\overline{h}}_0^2}{{\overline{\mu }}_0}\frac{\partial {\overline{p}}_0}{\partial \lambda }{G}_{z}sin\left(\theta -{\phi }_0\right)\right)+\Lambda \frac{\partial }{\partial \theta }\left(\frac{{\overline{\rho }}_0{P}_{\phi }}{\overline{k}(1+i\Omega \gamma )}\right)\hfill \\ \hfill & +\frac{2i\Omega \Lambda {\overline{\rho }}_0{P}_{\phi }}{\overline{k}(1+i\Omega \gamma )}+\Lambda \left(\frac{\partial }{\partial \theta }+2i\Omega \right)\left({\overline{h}}_0{\overline{\partial }}_p\rho \left(p_0,T\right)P_{\phi }+{\overline{\rho }}_{0}sin\left(\theta -{\phi }_0\right)\right)\hfill \end{array}$$

(20)

The dynamic coefficients of the supercritical CO₂ foil bearing based on the equations above include the coupling perturbations of the complete variables in the compressible turbulent lubrication Reynolds equation and the dynamic model of foil.

The complex pressure distributions P_ε and P_φ were solved numerically by finite difference method. Then, the dynamic coefficients in the coupled coordinate system of x-y and ε-φ are obtained by numerical integration below.

$$\begin{gathered} -\frac{R}{L}{{\displaystyle \int }}_{-\frac{L}{2R}}^{\frac{L}{2R}}{{\displaystyle \int }}_0^{2\pi }{P}_{\epsilon }\sin \theta d\theta d\lambda =k_{x\epsilon }+i\mathsf{\Omega }{c}_{x\epsilon } \\ -\frac{R}{L}{{\displaystyle \int }}_{-\frac{L}{2R}}^{\frac{L}{2R}}{{\displaystyle \int }}_0^{2\pi }{P}_{\epsilon }\cos \theta d\theta d\lambda =k_{y\epsilon }+i\mathsf{\Omega }{c}_{y\epsilon } \\ -\frac{R}{L}{{\displaystyle \int }}_{-\frac{L}{2R}}^{\frac{L}{2R}}{{\displaystyle \int }}_0^{2\pi }{P}_{\phi }\sin \theta d\theta d\lambda =k_{x\phi }+i\mathsf{\Omega }{c}_{x\phi } \\ -\frac{R}{L}{{\displaystyle \int }}_{-\frac{L}{2R}}^{\frac{L}{2R}}{{\displaystyle \int }}_0^{2\pi }{P}_{\phi }\cos \theta d\theta d\lambda =k_{y\phi }+i\mathsf{\Omega }{c}_{y\phi } \end{gathered}$$

(21)

The dynamic coefficients in the x-y Cartesian coordinate system shown in Figure 1 can be obtained by the transformation below.

$$\begin{gathered} \left[\begin{array}{c}{k}_{xx}\\ k_{xy}\end{array}\right]=\left[A\right]\left[\begin{array}{c}{k}_{x\epsilon }\\ k_{x\phi }\end{array}\right]=\left[\begin{array}{cc}\sin {\phi }_0& \cos {\phi }_0\\ \cos {\phi }_0& -\sin {\phi }_0\end{array}\right]\left[\begin{array}{c}{k}_{x\epsilon }\\ k_{x\phi }\end{array}\right] \\ \left[\begin{array}{c}{k}_{yx}\\ k_{yy}\end{array}\right]=\left[A\right]\left[\begin{array}{c}{k}_{y\epsilon }\\ k_{y\phi }\end{array}\right];\left[\begin{array}{c}{c}_{xx}\\ c_{xy}\end{array}\right]=\left[A\right]\left[\begin{array}{c}{c}_{x\epsilon }\\ c_{x\phi }\end{array}\right];\left[\begin{array}{c}{c}_{yx}\\ c_{yy}\end{array}\right]=\left[A\right]\left[\begin{array}{c}{c}_{y\epsilon }\\ c_{y\phi }\end{array}\right] \end{gathered}$$

(22)

where the $\left[A\right]$ is rotation matrix.

3. Numerical Results and Discussion

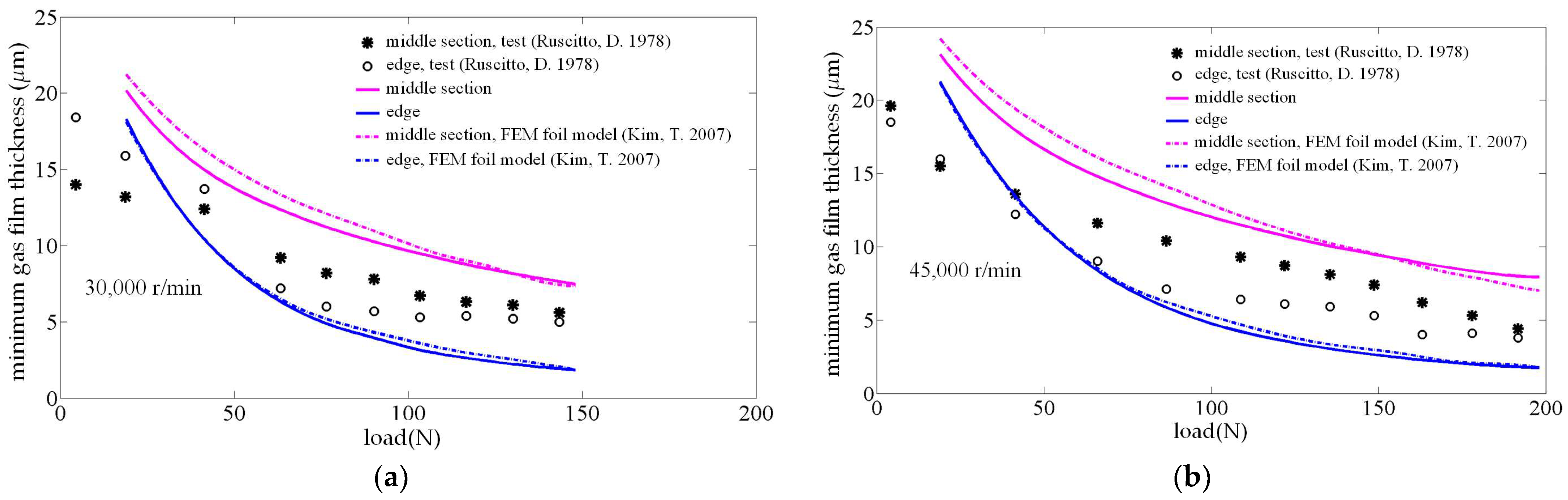
3.1. Program Verification

In order to verify the calculation program in this paper, the Reynolds equation for the supercritical carbon dioxide lubricating film was regressed and then used for air foil bearing. The calculation results of the minimum air film thickness are compared with the experimental results published in [29] and the numerical results with FEM foil model [30]. The structure and material parameters of the foil bearing corresponding to the experimental data in the literature are listed in

Table 1. Structure and material parameters of the foil bearing corresponding to the test data.

Parameters	Value	Unit
Bearing length L	38.1	mm
Bearing radius R = D/2	19.05	mm
Circumferential length of top foil lx	120	mm
Radius Clearance C0	31.8	μm
Top foil thickness tt	101.6	μm
Bump foil thickness tb	101.6	μm
Bump foil pitch S	4.572	mm
Half bump length l	1.778	mm
Bump height hb	0.508	mm
Number of bumps	26	/
Young’s modulus of elasticity Eb	214	GPa
Poisson’s ratio νb	0.29	/

. Based on these parameters, the Iordanoff formula [31] is used to calculate the support stiffness (per unit area) of the uniform linear spring, the value of which is 1.04 × 10¹⁰ N/m³.

Figure 3a,b show the comparison of the minimum gas film thickness of the two-dimensional uniform spring model with the results of experiments [29] and simulations [30] at rotating speeds of 30,000 r/min and 45,000 r/min, respectively. The calculation results of the minimum gas film thickness obtained by the program in this paper decrease with the increase of the load, and the variation trend is consistent with the test results. It can be seen that whether it is 30,000 r/min or 45,000 r/min, the calculated result of the minimum air film thickness at the axial middle section of the foil bearing is larger than the experimental result, while the results at the edge are in contrary. This shows that the calculated difference between the midsection and the edge is larger than the test result. The reason is that the support stiffness is evenly distributed along the axial direction during the calculation, and the three-dimensional bending of the bump foil along the axial direction can resist deformation when there is a pressure difference along the axial direction. The discontinuous distribution of bump foil support stiffness is taken into account by Kim TH [30], in which the top foil needs to be modeled by 2D plate elements.

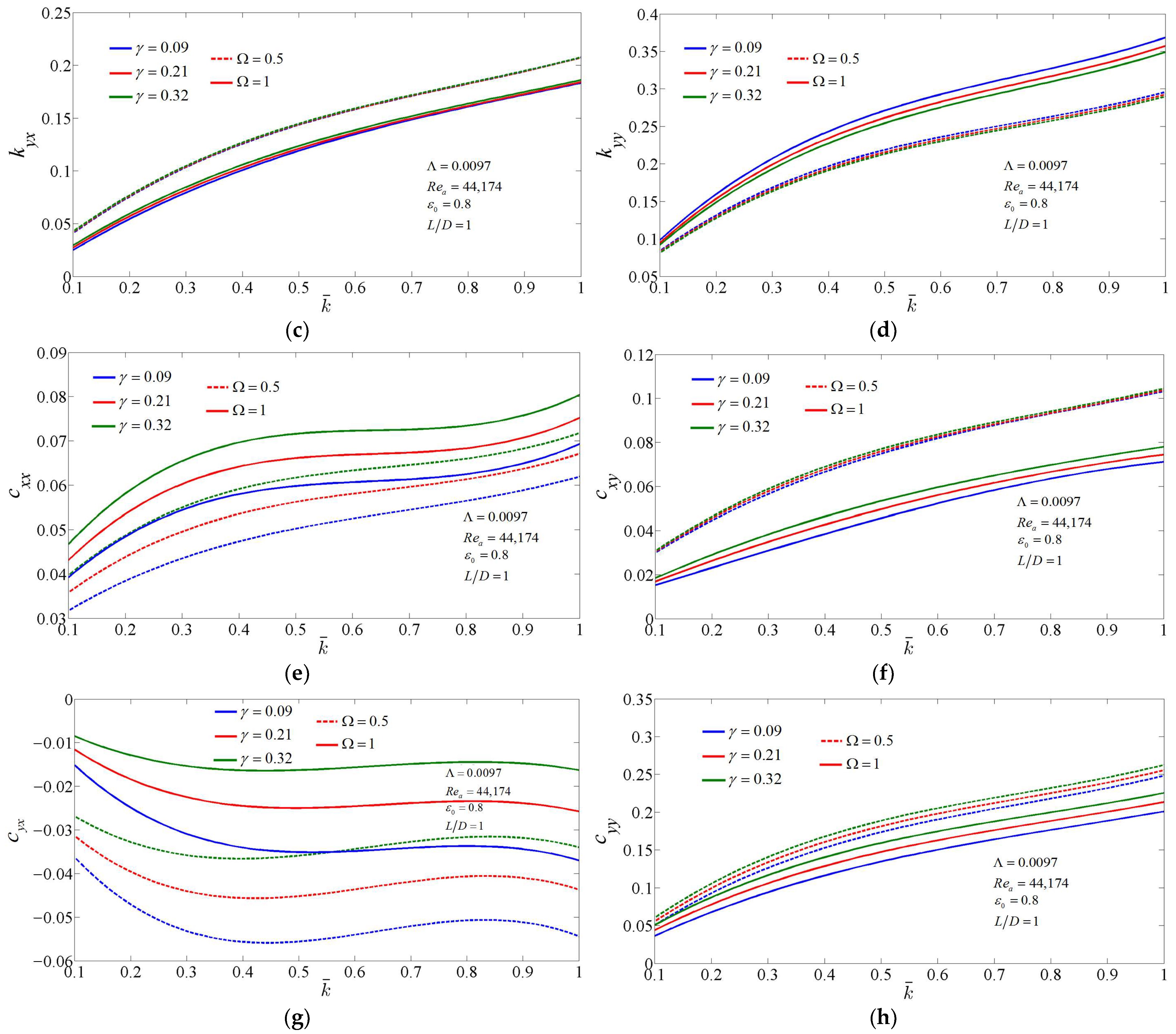
3.2. The Influence of Structural Loss Factor on the Dynamic Coefficients of Supercritical CO₂ Foil Bearing

In this Section, and the following Section 3.3 and Section 3.4, the fluid in the lubricating thin film of foil bearing is supercritical CO₂. Both the ambient pressure and ambient temperature (p_a, T_a) of bearings are higher than and not extremely close to the critical point. The input parameters of foil bearing in this paper are dimensionless, which, related to ambient parameters, includes the bearing number Λ = 6μ_aω/p_a(R/C₀)² and the average Reynolds number Re_a = ρ_aωRC₀/μ_a.

The variations of dynamic stiffness and damping coefficients of supercritical CO₂ foil bearing are shown in Figure 4, when eccentricity ε₀ is 0.8, bearing number Λ is 0.0097, average Reynolds number Re_a is 44,174 and length-to-diameter ratio L/D is 1, respectively. In Figure 4, the structural loss coefficients are 0.09, 0.21, and 0.32, respectively, and the dimensionless perturbation frequencies are 0.5 and 1, respectively.

As $\overline{k}$ varies from 0.1 to 1 in Figure 4, dynamic stiffness coefficients increase with the dimensionless bearing stiffness $\overline{k}$. Whether the dimensionless perturbation frequency Ω is 1 or 0.5, the difference among the direct stiffness coefficients k_xx under different structural loss factors are small. The direct stiffness coefficients k_xx are nearly the same under the dimensionless perturbation frequencies Ω = 1 and 0.5. Whether the dimensionless perturbation frequency Ω is 1 or 0.5, the larger the structural loss factor γ, the smaller the cross-coupling stiffness coefficient k_xy. The difference of the cross-coupling stiffness coefficients k_xy under different structural loss factors γ varies with the dimensionless support stiffness $\overline{k}$, and the difference increases first and then remains unchanged. When the dimensionless perturbation frequency Ω is 1, the cross-coupling stiffness coefficient k_xy is larger than that under the dimensionless perturbation frequency Ω = 0.5. The difference among the cross-coupling stiffness coefficients k_xy under different structural loss factors is also in the same regulation. When the dimensionless perturbation frequency Ω is 0.5, the cross-coupling stiffness coefficients k_yx under different structural loss factors γ are equal. When the dimensionless perturbation frequency Ω is 1, the difference among the cross-coupling stiffness coefficients k_yx under different structural loss factors γ is also small, and the larger the structural loss factor γ, the larger the cross-coupling stiffness coefficient k_yx.

For different structural loss factors γ and dimensionless perturbation frequencies Ω in Figure 4, the variation of the direct stiffness coefficient k_yy with the dimensionless support stiffness $\overline{k}$ is highly similar to the cross-coupling stiffness coefficient k_xy, but the difference among the results of the direct stiffness coefficients k_yy under different parameters is smaller. Whether the dimensionless perturbation frequency is 1 or 0.5, the larger the structural loss factor γ, the larger the values of the four dynamic damping coefficients. Under the same structural loss factor γ, for the direct damping coefficient c_xx and the cross-coupling damping coefficient c_yx, the results under dimensionless perturbation frequency Ω = 1 are larger than that under Ω = 0.5. The results of the direct damping coefficient c_yy and the cross-coupling damping coefficient c_xy when the dimensionless perturbation frequency Ω is 1 are smaller than those when the dimensionless perturbation frequency Ω is 0.5. The effect of the structural loss factor γ on the c_xx and c_yx is more pronounced than that of the structural loss factor γ on c_xy and c_yy.

It can be seen that the structural loss factor has influence on the stiffness coefficients as well as the damping coefficients of foil bearing. Such reason is that the dynamic coefficients are determined by the dynamical stiffness of foil support system, which is a complex number, and the structural loss factor is contained in the imaginary part.

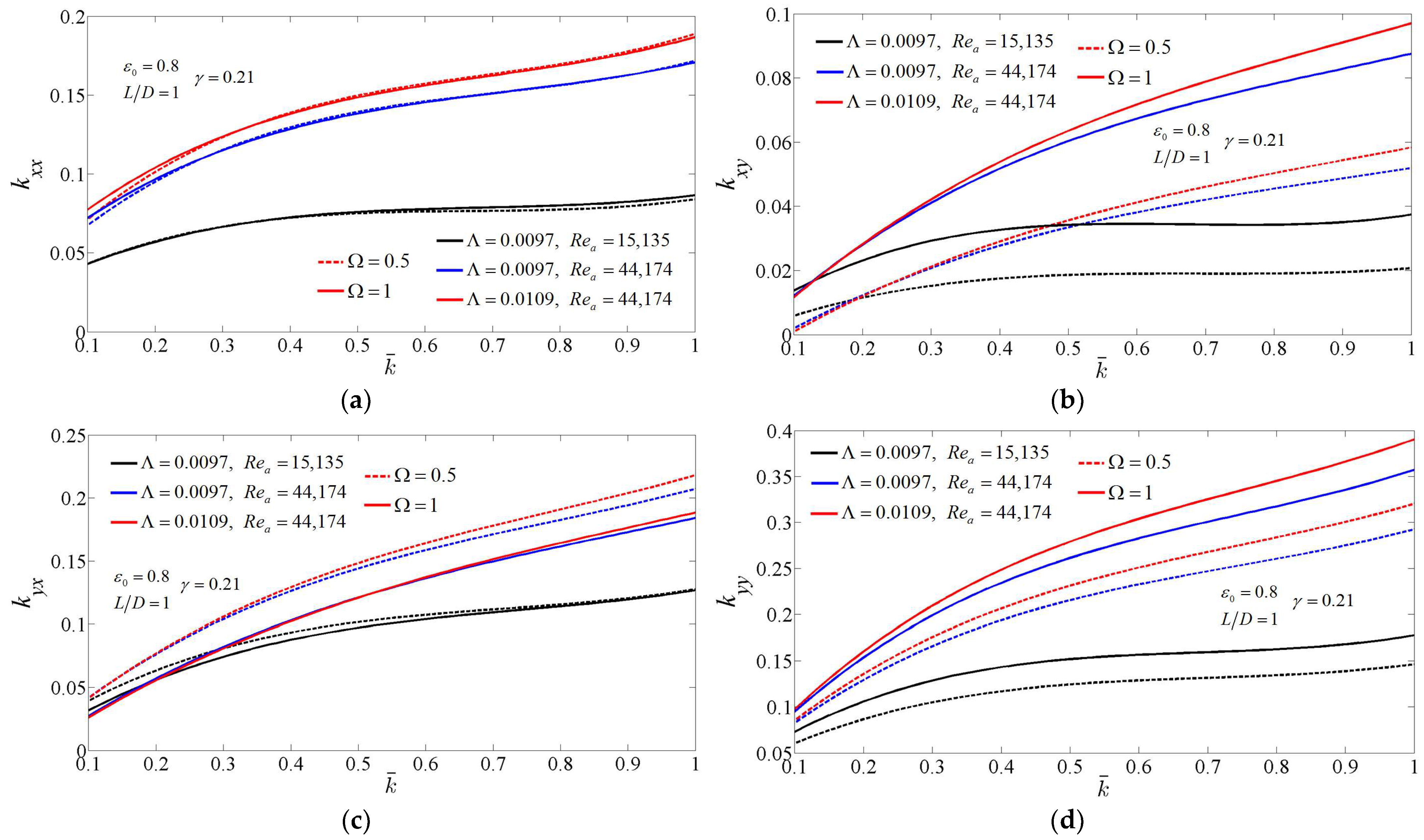
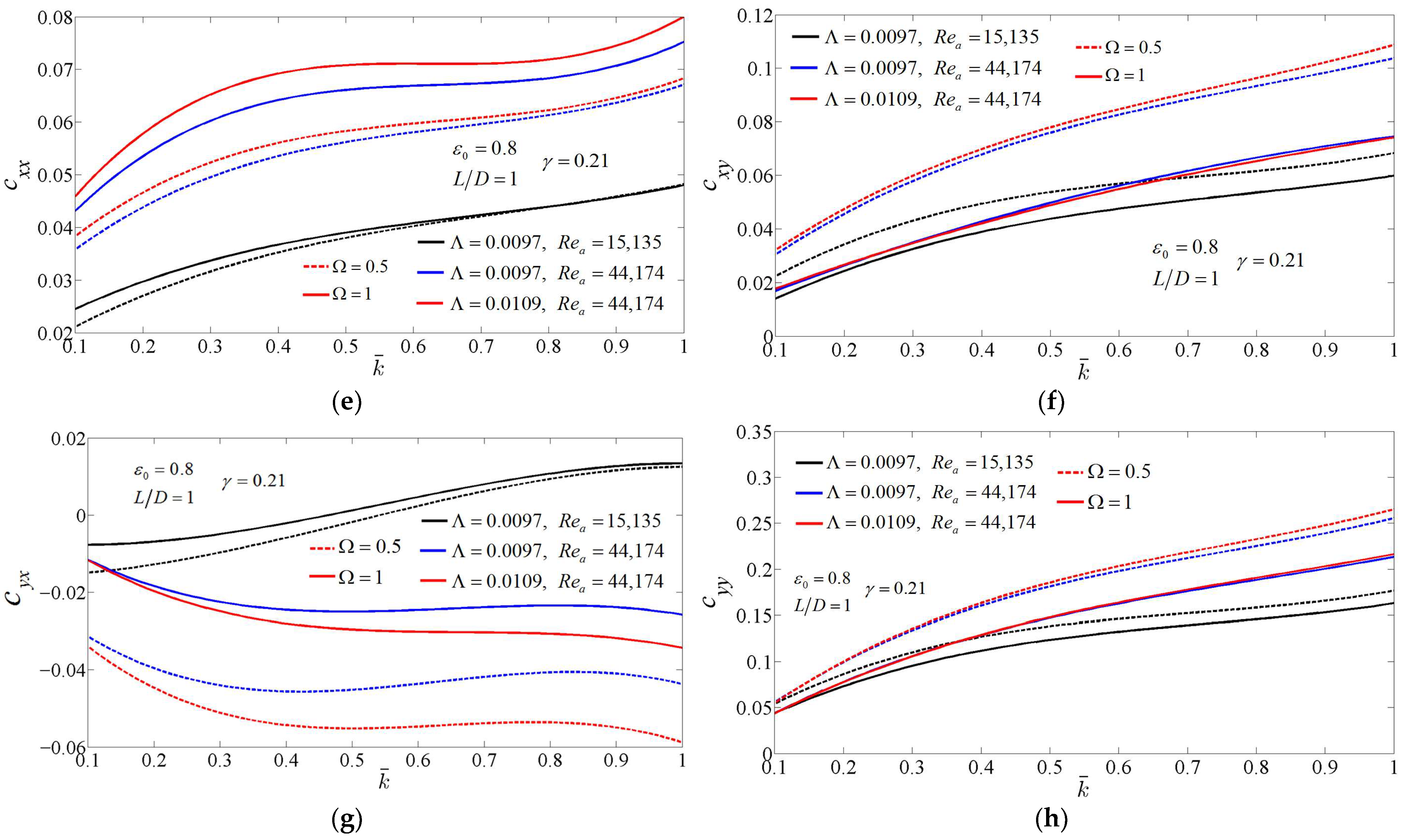
3.3. The Influence of Bearing Number and Average Reynolds Number on the Dynamic Coefficients of Supercritical CO₂ Foil Bearing

Dynamic stiffness and damping coefficients of the supercritical CO₂ foil bearing are shown in Figure 5 with different bearing numbers Λ and average Reynolds number Re_a, when the structural loss factor γ is 0.21, the eccentricity ε₀ is 0.8 and the length-to-diameter ratio L/D is 1, and the dimensionless perturbation frequency Ω is 0.5 or 1, respectively, where the results for the blue lines are the same as the input parameters when the structural loss factor γ is 0.21 in Figure 4.

By comparing the results of the red lines and the blue lines, it can be seen that for the same average Reynolds number Re_a, the variation of the direct stiffness coefficients with the dimensionless support stiffness $\overline{k}$ is nearly the same under different bearing numbers Λ and different dimensionless perturbation frequencies Ω. Similar results are obtained for other stiffness and damping coefficients. Under the same average Reynolds number Re_a and dimensionless perturbation frequency Ω, the direct stiffness coefficients k_xx and direct damping coefficients c_xx at the Λ = 0.0109 are larger than the results at the Λ = 0.0097. However, the cross-coupling damping coefficient c_yx at the Λ = 0.0109 is smaller than the results at the Λ = 0.0097. For the cross-coupling stiffness coefficient k_xy with dimensionless support stiffness $\overline{k}$ < 0.3 and the direct stiffness coefficients k_yy with dimensionless support stiffness $\overline{k}$ = 0.1, the results at the Λ = 0.0109 are equal to that at the Λ = 0.0097. The results of k_xy and k_yy under the other dimensionless support stiffness $\overline{k}$ and the Λ = 0.0109 are larger than that at the Λ = 0.0097. Under the same average Reynolds number Re_a, the dimensionless perturbation frequency Ω = 1 and the dimensionless support stiffness $\overline{k}$ < 0.73, the cross-coupling stiffness coefficients k_yx at the Λ = 0.0109 are equal to that at the Λ = 0.0097. The cross-coupling stiffness coefficients k_yx under the other dimensionless support stiffness $\overline{k}$ at the bearing number Λ = 0.0109 is slightly larger than the results at the bearing number Λ = 0.0097. The stiffness coefficients under dimensionless perturbation frequency Ω = 0.5 are similar to those under dimensionless perturbation frequency Ω = 1. Under the same average Reynolds number Re_a, when the dimensionless perturbation frequency Ω is 1, the cross-coupling damping coefficient c_xy at the bearing number Λ = 0.0109 is nearly the same as the results at the bearing number Λ = 0.0097. When the dimensionless perturbation frequency is 0.5 and the bearing number Λ is 0.0109, the results are slightly larger than those when the bearing number is 0.0097. The variation of the direct damping coefficient c_yy with the dimensionless support stiffness $\overline{k}$ is similar to that of the cross-coupling damping coefficient c_xy.

However, comparing the results of the black lines and the blue lines, at the same bearing number, the variation of bearing stiffness and damping coefficients with the dimensionless support stiffness $\overline{k}$ under different average Reynolds numbers Re_a and different dimensionless perturbation frequencies Ω have nearly no similarity. Such reason is that both the compressibility and the turbulence effect are included in the average Reynolds number, while the bearing number reflects the compressibility only. Because of the turbulence effect, the bearing number is not able to directly determine the characteris-tics of supercritical CO₂ foil bearings, which is different from air bearings.

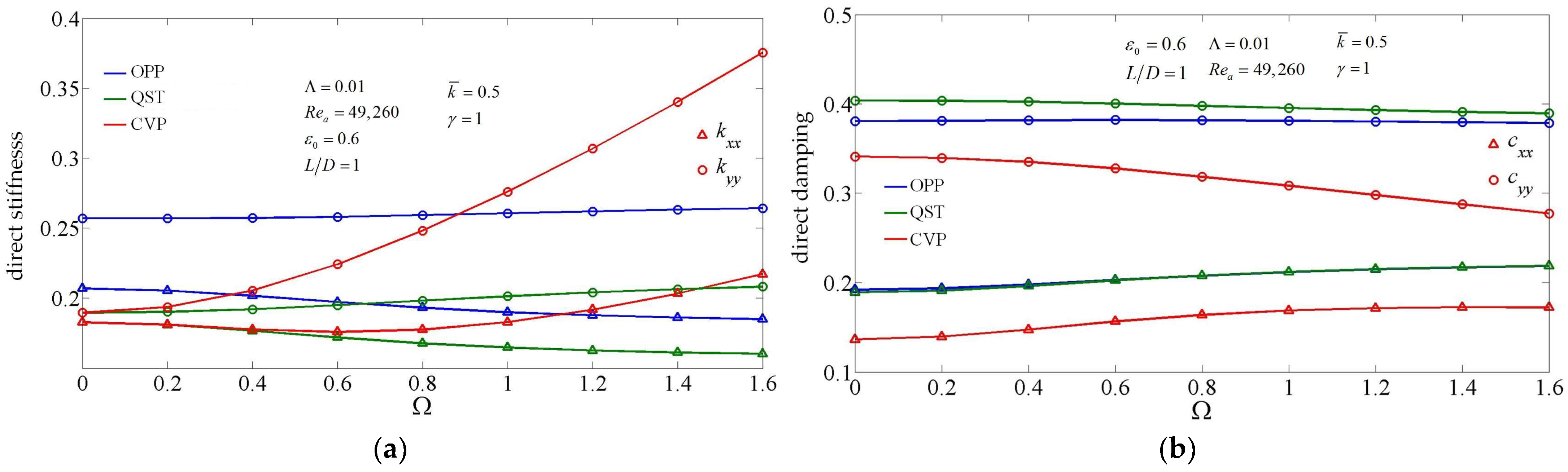
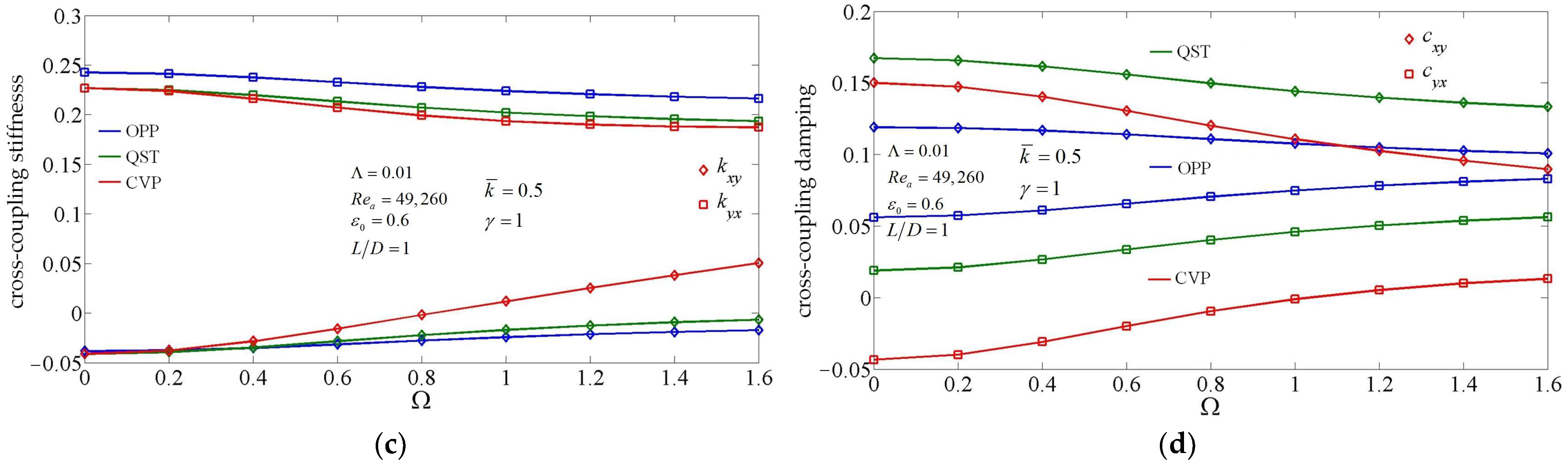
3.4. The Influence of Compressibility of Supercritical CO₂ on the Dynamic Coefficients

The variation of the dynamic stiffness and damping coefficients of supercritical CO₂ foil bearing with dimensionless perturbation frequency Ω are shown in Figure 6, when the eccentricity ε₀ is 0.6, bearing number Λ is 0.01, average Reynolds number Re_a is 49,260, and L/D is 1. The results by the partial derivative method at different conditions of perturbation are shown by different colors in each subplot, with the red lines (CVP) considering the complete variables perturbations, the green lines (QST) and blue lines (OPP) considering quasistatic treatment (without ∂ρ/∂t) and only perturbed pressure, respectively.

The blue line shows that the conventional perturbation method for air bearings indiscriminately applied to supercritical CO₂ bearings. The difference between the blue lines and the red lines reflects the perturbation effects of density, viscosity, and Reynolds number. The difference between the green lines and red lines reflects the effect of partial density over partial time (The hysteresis of lubricating film to perturbation caused by compressibility of lubricant).

When the dimensionless perturbation frequency Ω tends to 0⁺, all the stiffness coefficients of the foil bearing considering the complete variable perturbation are identical to the results of the quasi-static treatment. Because the foil deformation is a static process independent of time under infinitely slow small displacements of the shaft. As the dimensionless perturbation frequency Ω increases, for the direct stiffness coefficient k_xx, when Ω is less than 0.4, the results considering the complete variable perturbation are equal to the quasi-static treatment, and decrease with Ω. However, when Ω > 0.4, the results by complete variable perturbation begin to increase while the results by the quasi-static treatment continue to decrease. The direct stiffness coefficient k_yy by complete variable perturbation increases significantly with Ω.

In the range of perturbation frequencies Ω in Figure 6, the cross-coupling stiffness k_xy by the complete variable perturbation is larger than that by the two degenerate conditions, while the k_yx by complete variable perturbation is the smallest. The direct damping c_xx by quasi-static treatment is nearly equal to that by only perturbed pressure. The direct damping coefficients and the cross-coupling damping coefficient c_yx obtained by complete variable perturbation are significantly smaller than those by the two degenerate conditions. For the cross-coupling damping coefficient c_xy, the results by complete variable perturbation are between the two degradation conditions when dimensionless perturbation frequencies Ω is less than 1.1, and less than the two degradation conditions when Ω > 1.1.

Although the time lag effect of the compressible lubrication ∂ρ/∂t can be reflected only by the partial derivative method including complete variable perturbation, all the dynamic coefficients obtained by the two degradation conditions in Figure 6 also vary with the dimensionless perturbation frequency Ω, which is brought about by the structural perturbation of the foil bearing through the ∂h/∂t term. Such indicates that the frequency effect of the dynamic coefficients of compressible lubricated foil bearings is the result of both the properties of lubricant and the dynamical deformation of the foil.

4. Conclusions

In this paper, both the damped elastic support foil model and the compressible turbulent lubrication Reynolds equation were perturbed by the partial derivative method with dynamical variations of complete variables. Then the partial derivative method can be used to solve the stiffness and damping coefficients of supercritical CO₂ foil bearings under different perturbation frequencies. The main conclusions are as follows:

• The results of minimum film thickness of an air foil bearing were calculated by the program of the method of this research (through a simple change) and compared with the test and calculation data in the literature. It is verified that the two-dimensional uniform spring model for support stiffness is reasonable for foil bearings.
• The partial derivative method is able to take into account the influence of structural loss factor as well as perturbation frequency on the dynamic coefficients of foil bearings. The structural loss factor has influence on the stiffness coefficients as well as the damping coefficients. Thus, for compressible lubricated bearings, the static stiffness and damping coefficients (obtained under perturbation frequency infinitely close to zero) are not the dynamic coefficients required for rotor dynamics analysis. The structural loss factor has little influence on the trend of dynamic coefficients changing with the dimensionless support stiffness, but mainly affects their value.
• Due to the turbulence effect, the bearing number is not able to directly determine the characteristics of supercritical CO₂ foil bearings, which is different from air bearings. For the same average Reynolds number, the trends of stiffness and damping coefficients changing with the dimensionless support stiffness are similar, and the bearing number only affects the value of dynamic coefficients. The average Reynolds number not only affects the values of the dynamic coefficients but also has influence on their variations with the dimensionless support stiffness.