Dynamics of Magnetized and Magnetically Charged Particles around Regular Nonminimal Magnetic Black Holes
Abstract
1. Introduction
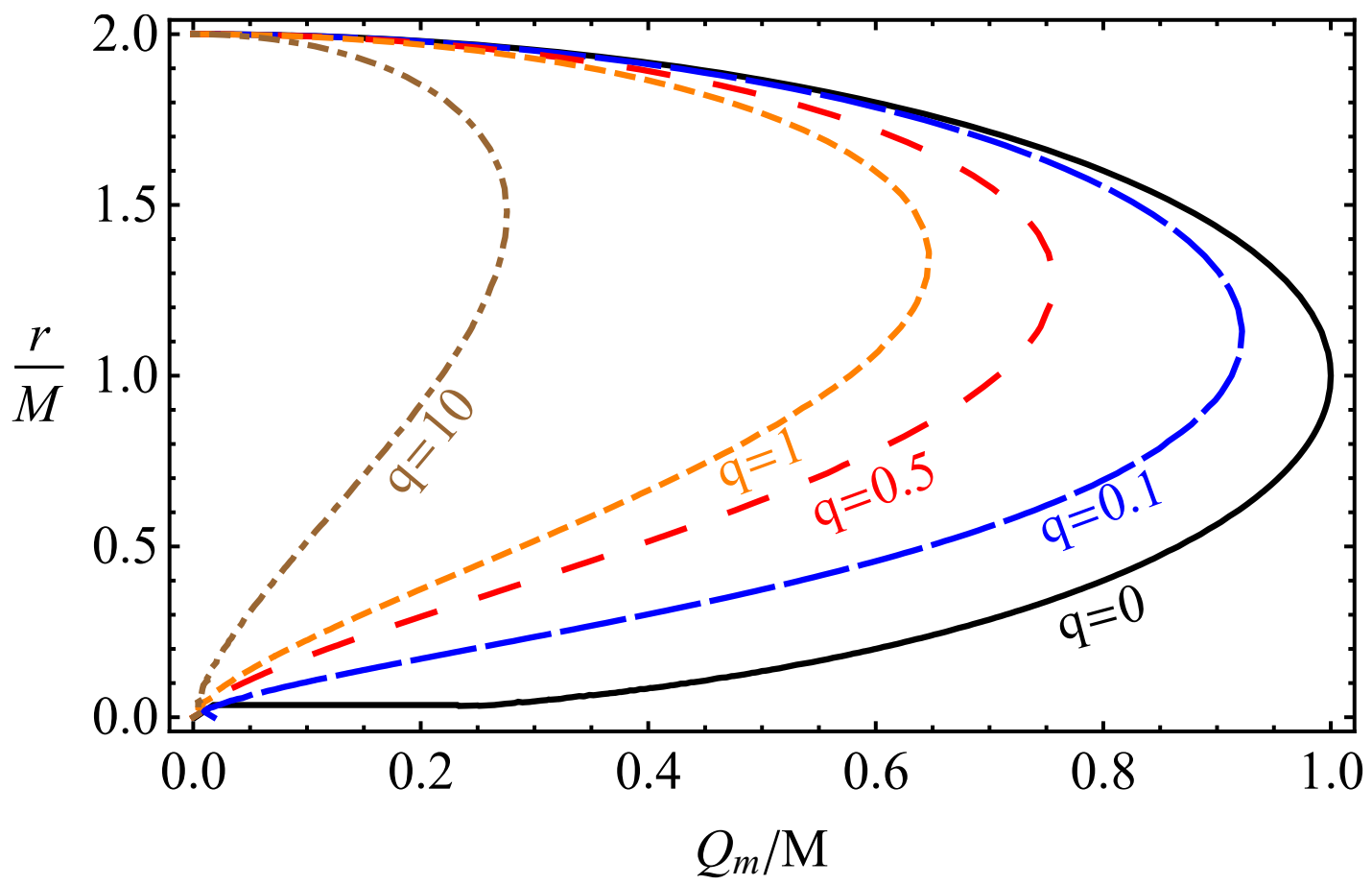
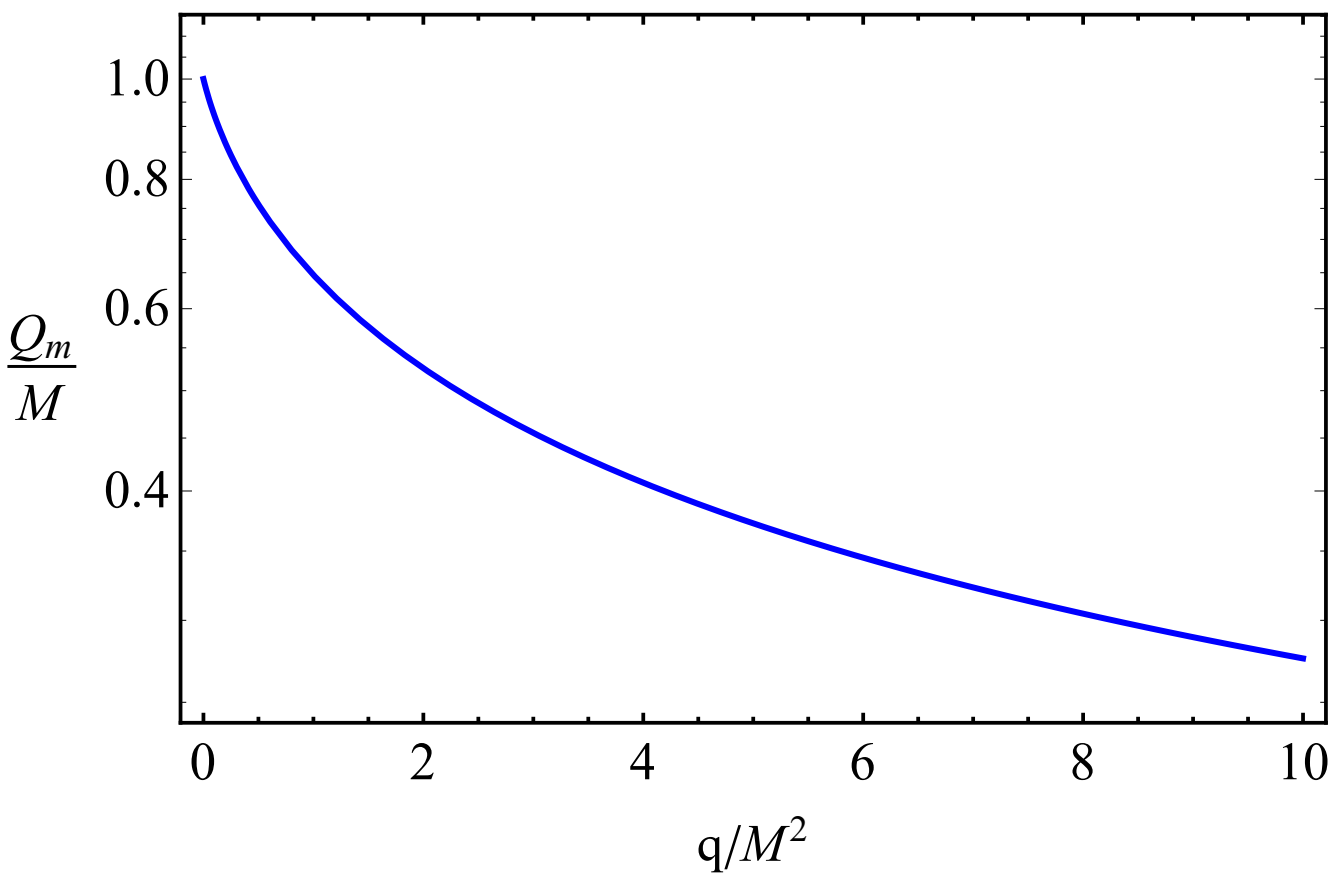
2. The Spacetime Properties
3. Magnetized Particles Motion
3.1. Magnetic Interaction
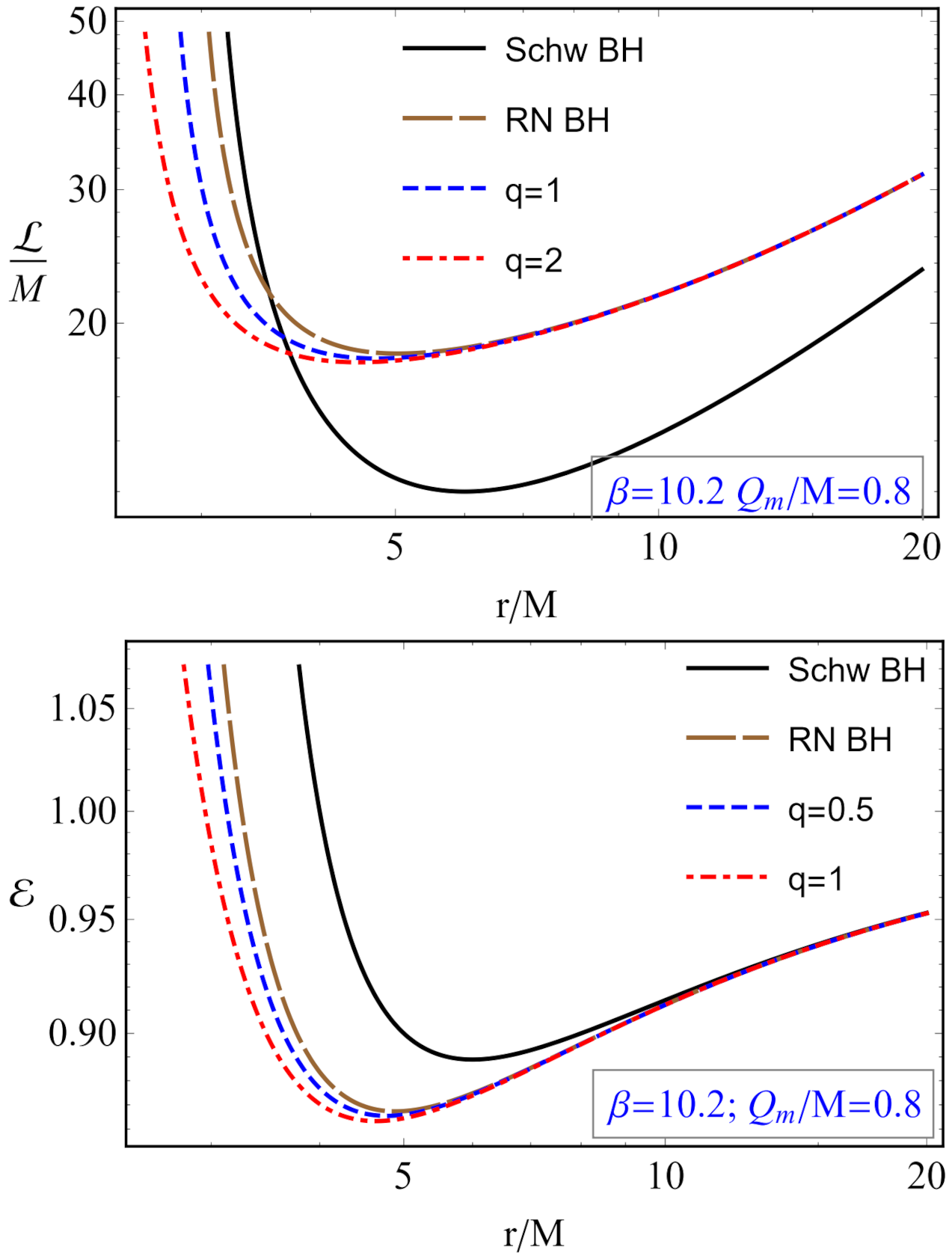
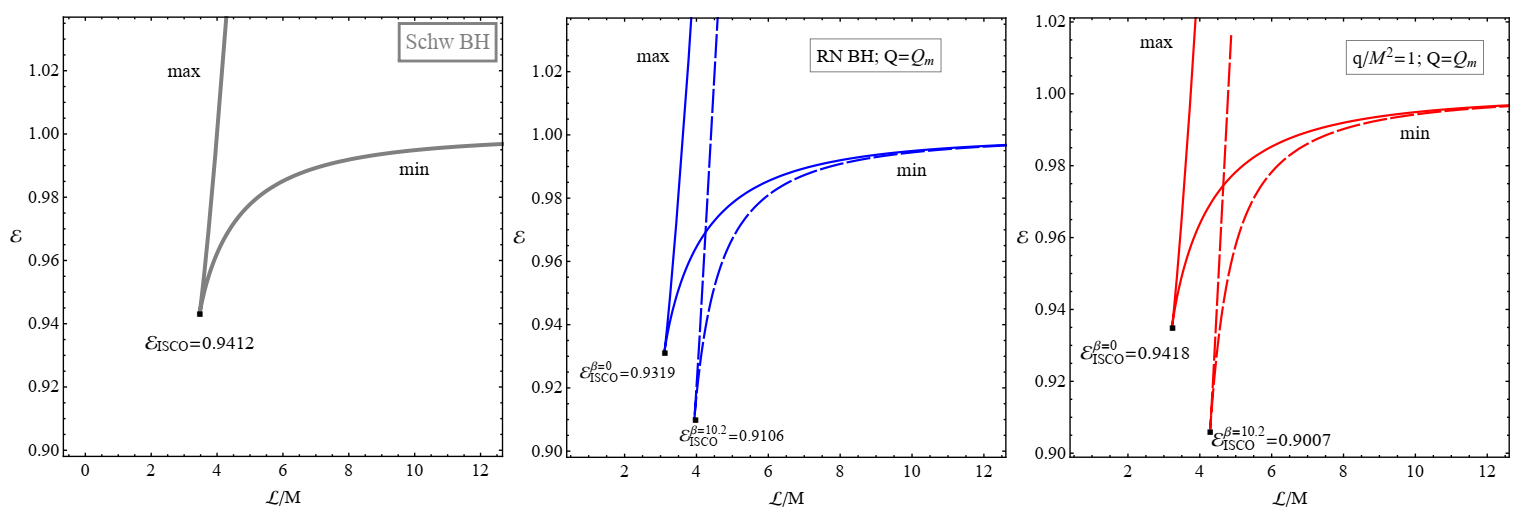
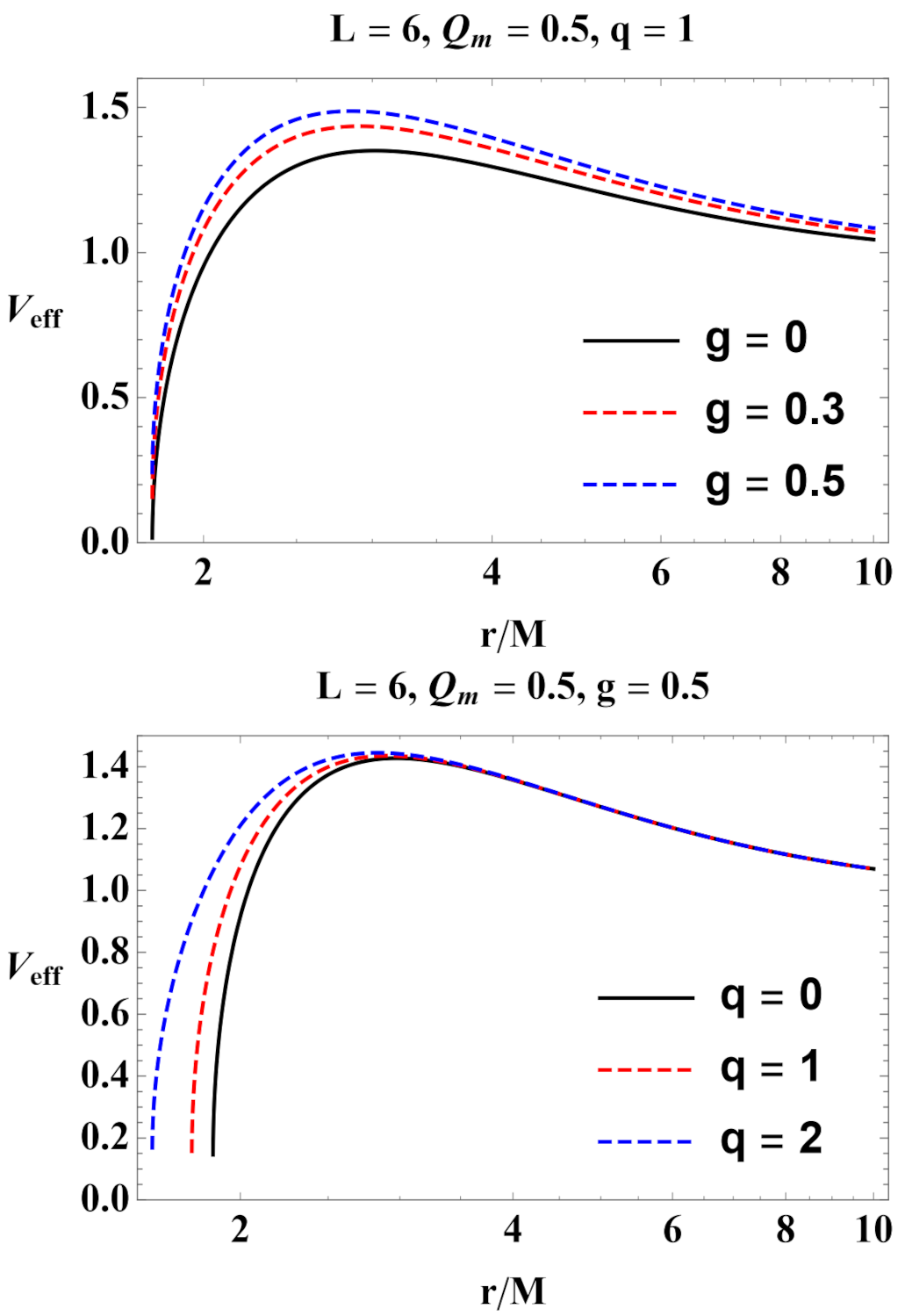
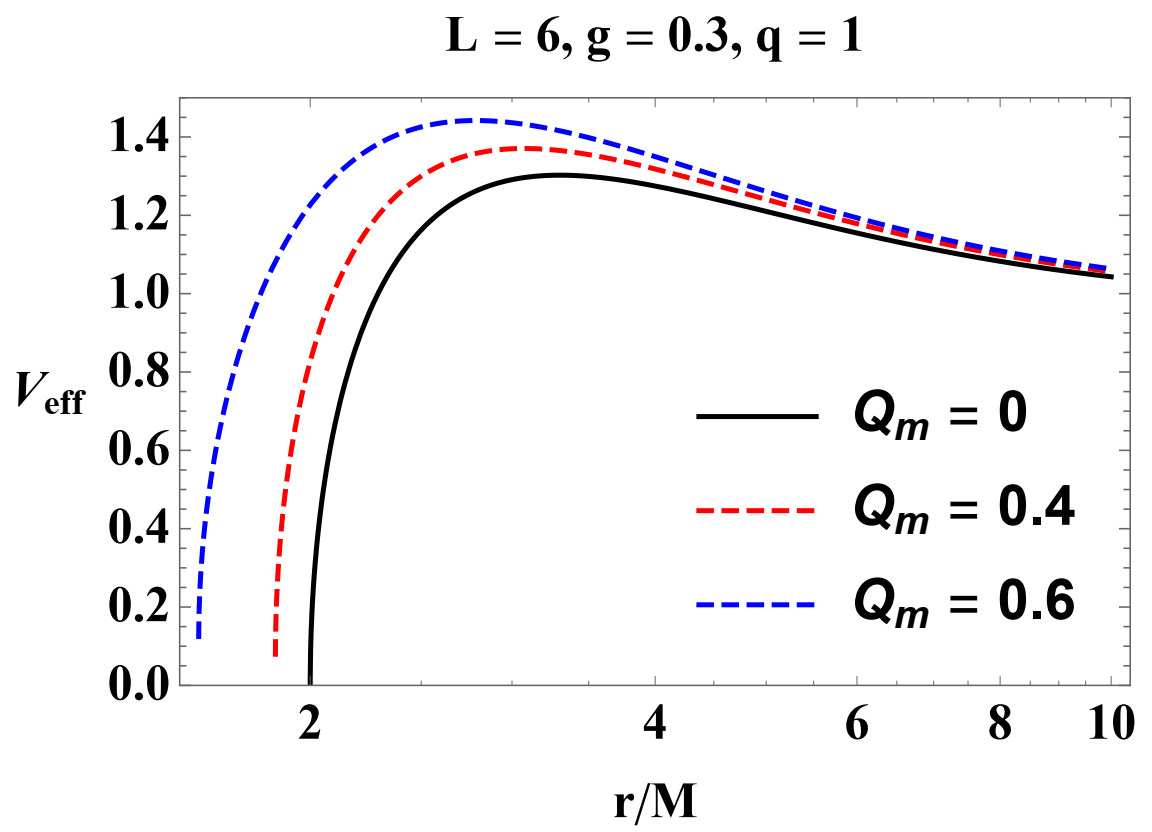
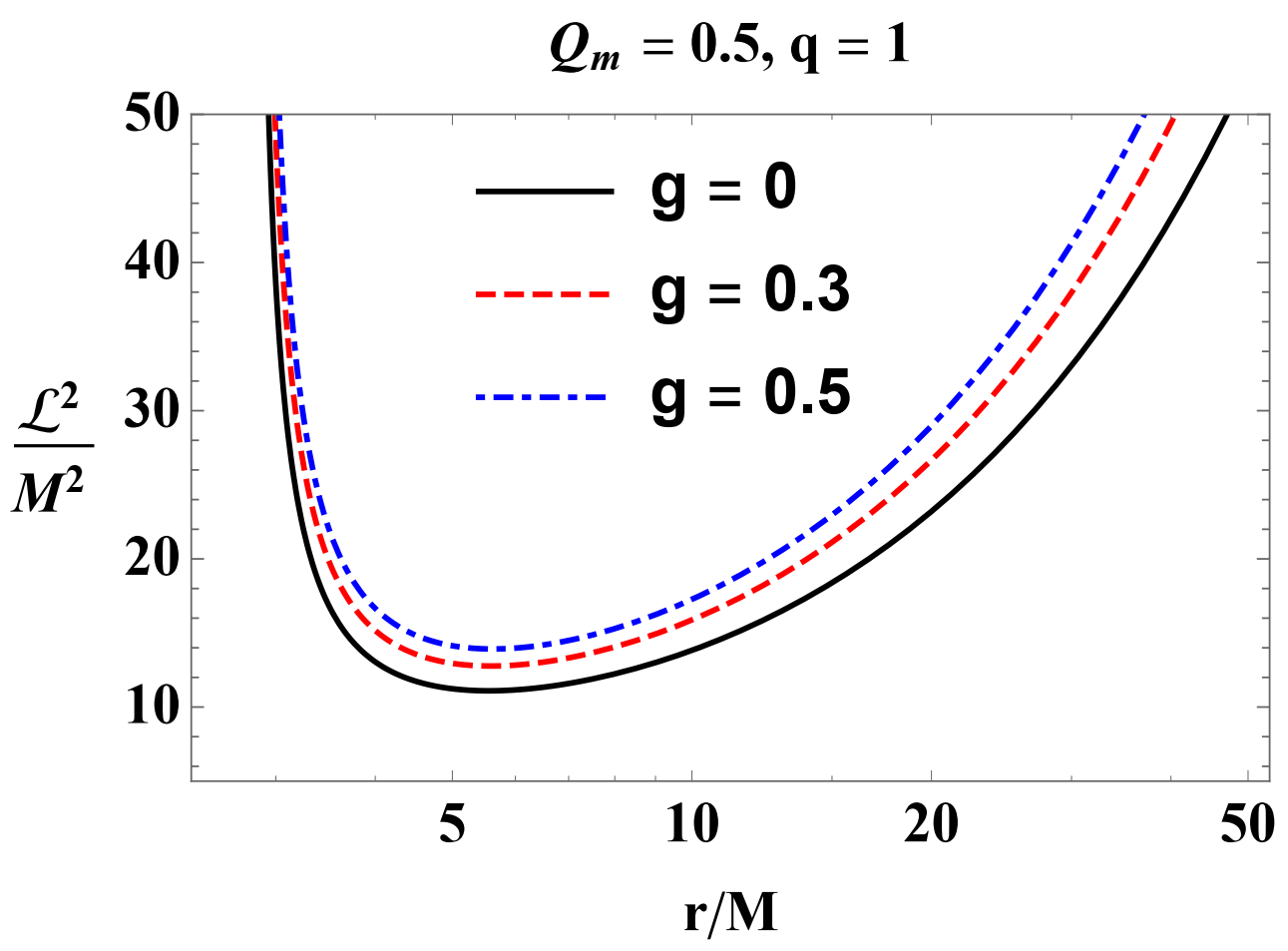
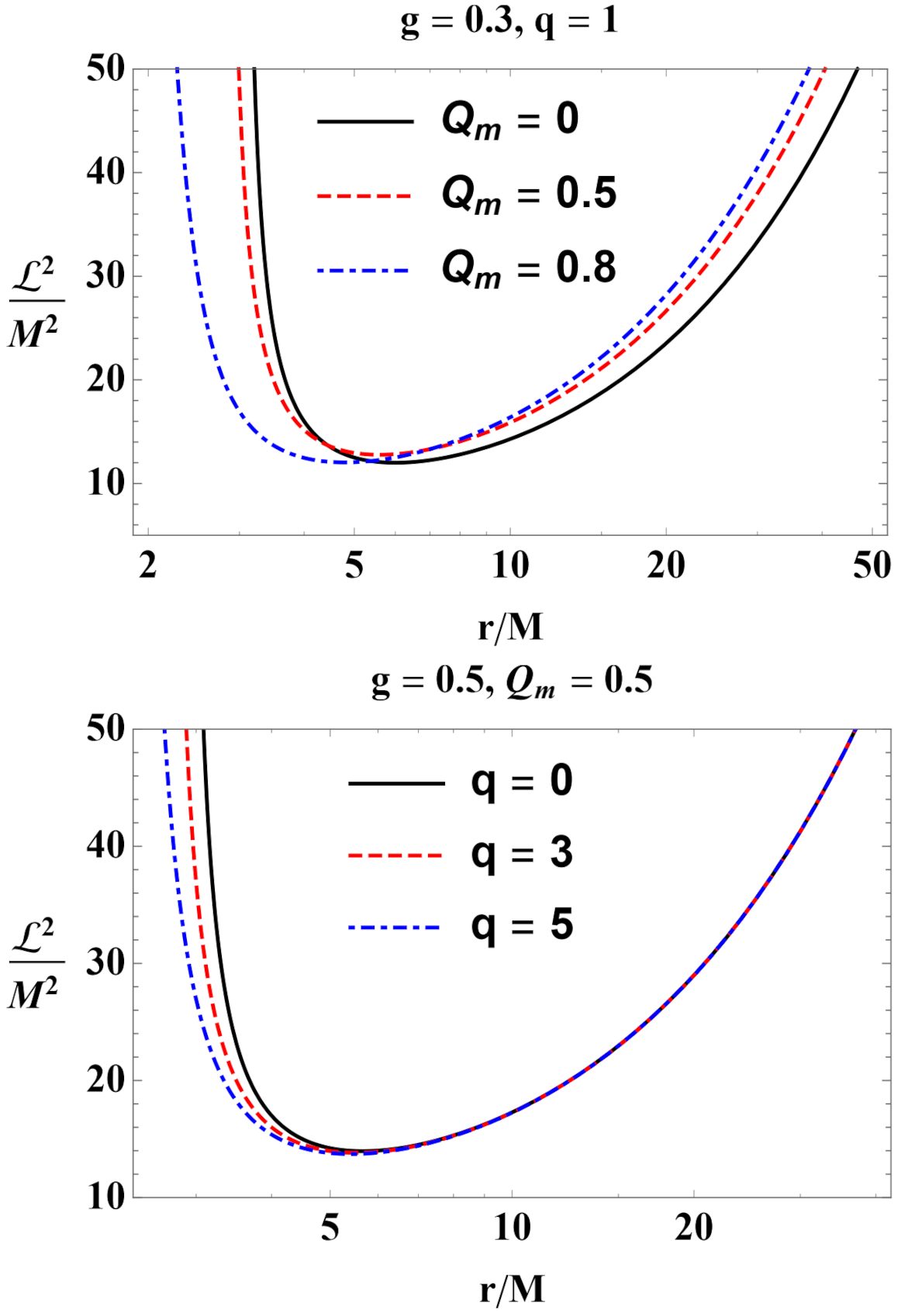
3.2. Stable Circular Orbits
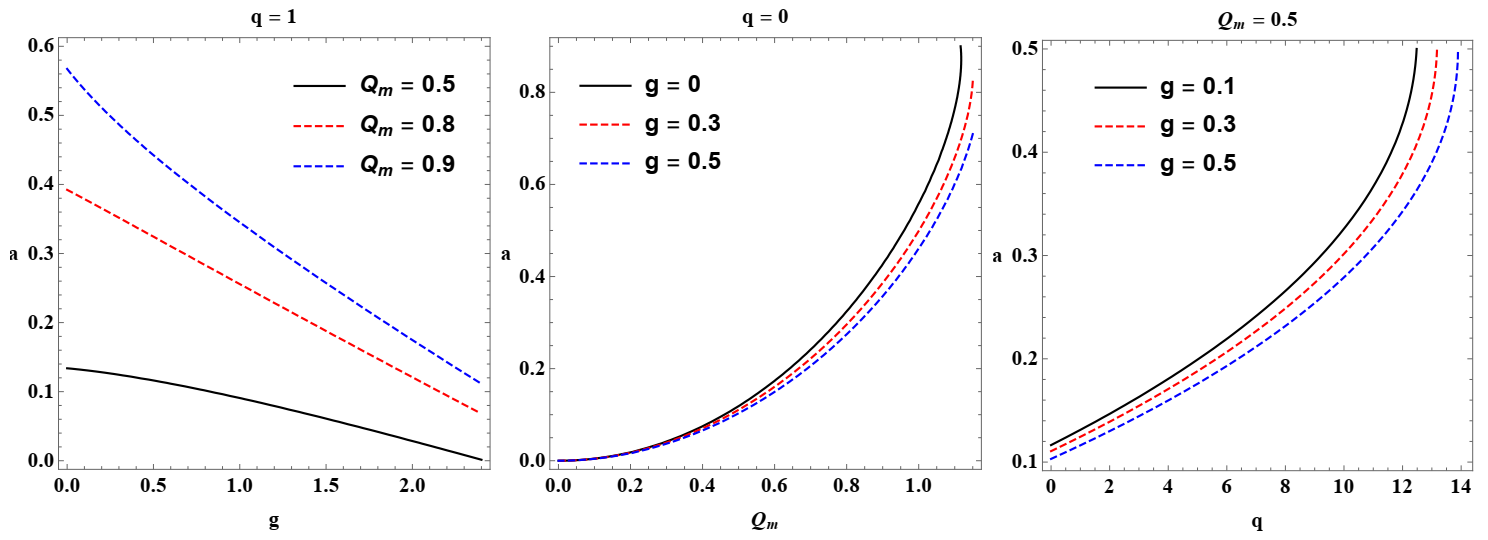
3.3. Kerr BH versus Regular Nonminimal Magnetic BH
3.4. Instability of Circular Orbit
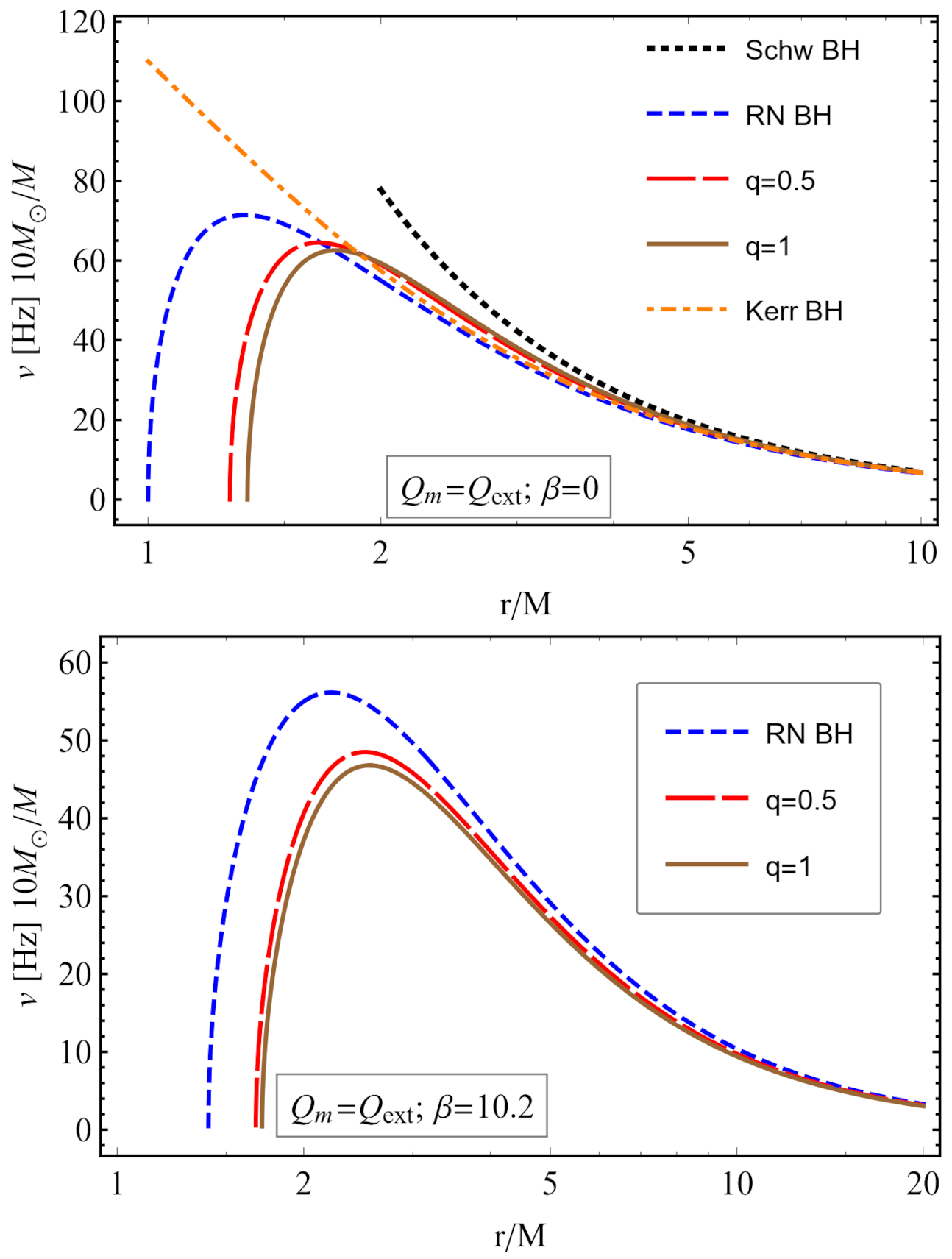
3.5. Keplerian Frequency
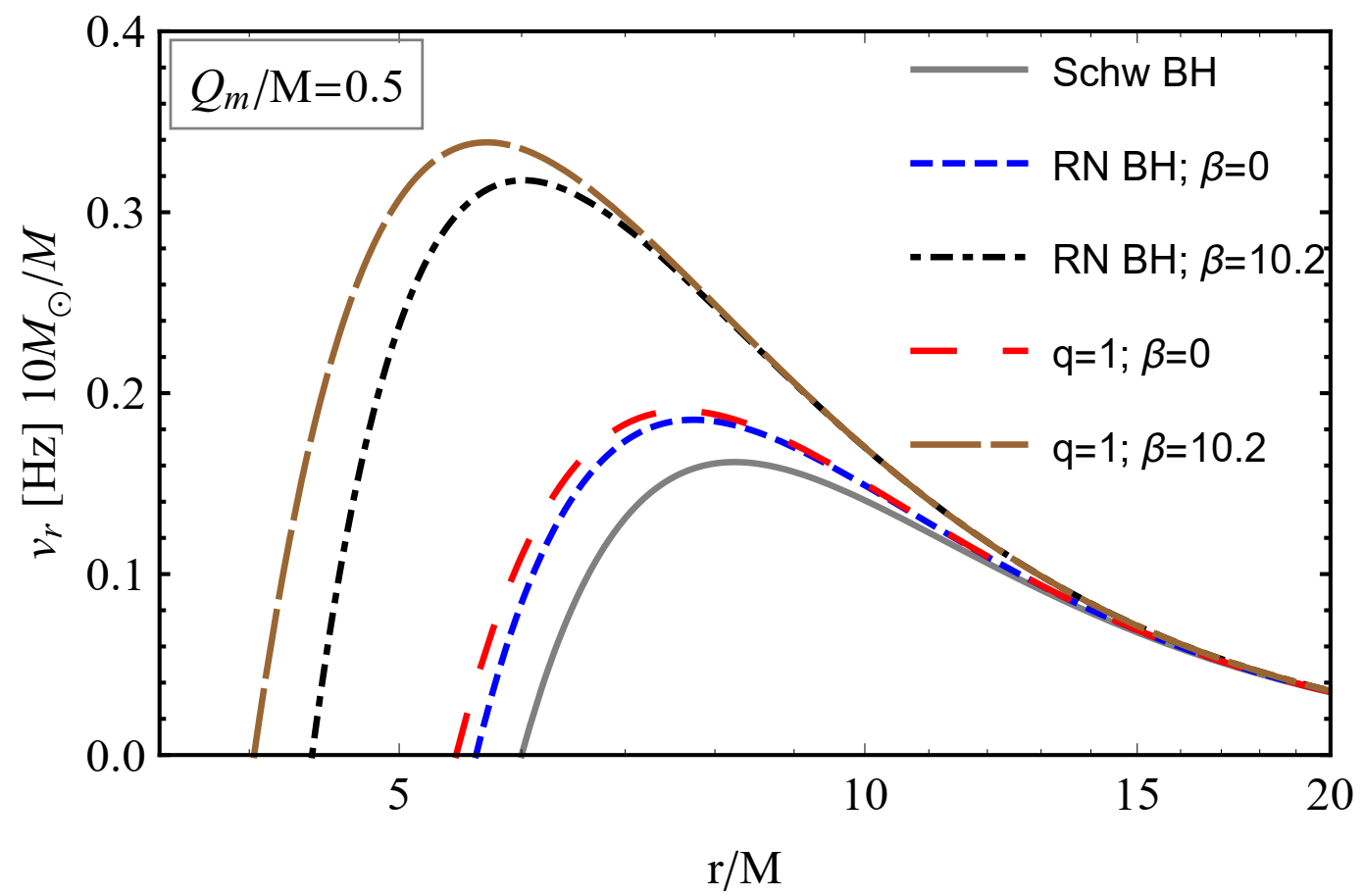
3.6. Epicyclic Motion of Test Magnetized Particles
4. Magnetically Charged Particle Motion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bambi, C. Black Holes: A Laboratory for Testing Strong Gravity; Springer: Singapore, 2017. [Google Scholar]
- Johannsen, T.; Psaltis, D. Metric for rapidly spinning black holes suitable for strong-field tests of the no-hair theorem. Phys. Rev. D 2011, 83, 124015. [Google Scholar] [CrossRef]
- Konoplya, R.; Rezzolla, L.; Zhidenko, A. General parametrization of axisymmetric black holes in metric theories of gravity. Phys. Rev. D 2016, 93, 064015. [Google Scholar] [CrossRef]
- Scherrer, W. Zur Theorie der Elementarteilchen. Verhandlungen Schweiz. Naturforschenden Ges. 1941, 121, 86. [Google Scholar]
- Jordan, P. Zur projektiven Relativitätstheorie. Nachr. Akad. Wiss. Gott. II Math.-Phys. Kl. 1945, 1945, 39. [Google Scholar]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Goenner, H. Some remarks on the genesis of scalar-tensor theories. Gen. Relativ. Gravit. 2012, 44, 2077–2097. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Coleman, S.; Jackiw, R. A new improved energy-momentum tensor. Ann. Phys. 1970, 59, 42–73. [Google Scholar] [CrossRef]
- Faraoni, V.; Gunzig, E.; Nardone, P. Conformal transformations in classical gravitational theories and in cosmology. Fundam. Cosm. Phys. 1999, 20, 121–175. [Google Scholar]
- Prasanna, A.R. A new invariant for electromagnetic fields in curved space-time. Phys. Lett. A 1971, 37, 331–332. [Google Scholar] [CrossRef]
- Drummond, I.T.; Hathrell, S.J. QED vacuum polarization in a background gravitational field and its effect on the velocity of photons. Phys. Rev. D 1980, 22, 343–355. [Google Scholar] [CrossRef]
- Hehl, F.W.; Obukhov, Y.N. How Does the Electromagnetic Field Couple to Gravity, in Particular to Metric, Nonmetricity, Torsion, and Curvature? In Gyros, Clocks, Interferometers...: Testing Relativistic Gravity in Space; Lämmerzahl, C., Everitt, C.W.F., Hehl, F.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 562, p. 479. [Google Scholar] [CrossRef]
- Balakin, A.B.; Lemos, J.P.S. Non-minimal coupling for the gravitational and electromagnetic fields: A general system of equations. Class. Quantum Gravity 2005, 22, 1867–1880. [Google Scholar] [CrossRef]
- Horndeski, G.W. Conservation of charge and second-order gauge-tensor field theories. Arch. Ration. Mech. Anal. 1981, 75, 229–249. [Google Scholar] [CrossRef]
- Balakin, A.B.; Dehnen, H.; Zayats, A.E. Nonminimal Einstein–Yang-Mills-Higgs theory: Associated, color, and color-acoustic metrics for the Wu-Yang monopole model. Phys. Rev. D 2007, 76, 124011. [Google Scholar] [CrossRef]
- Balakin, A.B.; Dehnen, H.; Zayats, A.E. Nonminimal Isotropic Cosmological Model with Yang-Mills and Higgs Fields. Int. J. Mod. Phys. D 2008, 17, 1255–1269. [Google Scholar] [CrossRef]
- Balakin, A.B.; Ni, W.T. Non-minimal coupling of photons and axions. Class. Quantum Gravity 2010, 27, 055003. [Google Scholar] [CrossRef]
- Horndeski, G.W. Static spherically symmetric solutions to a system of generalized Einstein–Maxwell field equations. Phys. Rev. D 1978, 17, 391–395. [Google Scholar] [CrossRef]
- Muller-Hoissen, F.; Sippel, R. Spherically symmetric solutions of the non-minimally coupled Einstein–Maxwell equations. Class. Quantum Gravity 1988, 5, 1473–1488. [Google Scholar] [CrossRef]
- Balakin, A.B.; Sushkov, S.V.; Zayats, A.E. Nonminimal Wu-Yang wormhole. Phys. Rev. D 2007, 75, 084042. [Google Scholar] [CrossRef]
- Balakin, A.B.; Lemos, J.P.S.; Zayats, A.E. Nonminimal coupling for the gravitational and electromagnetic fields: Traversable electric wormholes. Phys. Rev. D 2010, 81, 084015. [Google Scholar] [CrossRef]
- Balakin, A.B.; Zayats, A.E. Dark energy fingerprints in the nonminimal Wu-Yang wormhole structure. Phys. Rev. D 2014, 90, 044049. [Google Scholar] [CrossRef]
- Balakin, A.B.; Bochkarev, V.V.; Lemos, J.P.S. Nonminimal coupling for the gravitational and electromagnetic fields: Black hole solutions and solitons. Phys. Rev. D 2008, 77, 084013. [Google Scholar] [CrossRef]
- Balakin, A.B.; Zayats, A.E. Nonminimal black holes with regular electric field. Int. J. Mod. Phys. D 2015, 24, 1542009. [Google Scholar] [CrossRef]
- Balakin, A.B.; Zayats, A.E. Non-minimal Wu Yang monopole. Phys. Lett. B 2007, 644, 294–298. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Abdujabbarov, A.; Wen-Biao, H. Regular nonminimal magnetic black hole as a source of quasiperiodic oscillations. Phys. Rev. D 2021, 103, 104070. [Google Scholar] [CrossRef]
- Smoller, J.A.; Wasserman, A.G.; Yau, S.T. Existence of black hole solutions for the Einstein–Yang/Mills equations. Commun. Math. Phys. 1993, 154, 377–401. [Google Scholar] [CrossRef]
- Volkov, M.S.; Straumann, N. Slowly Rotating Non-Abelian Black Holes. Phys. Rev. Lett. 1997, 79, 1428–1431. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J. Rotating Hairy Black Holes. Phys. Rev. Lett. 2001, 86, 3704–3707. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Navarro-Lérida, F. Rotating Einstein–Yang-Mills black holes. Phys. Rev. D 2002, 66, 104001. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Dadhich, N. Radiating black holes in Einstein–Yang-Mills theory and cosmic censorship. Phys. Rev. D. 2010, 82, 044038. [Google Scholar] [CrossRef]
- Moon, T.; Myung, Y.S.; Son, E.J. f (R) black holes. Gen. Relativ. Gravit. 2011, 43, 3079–3098. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; Valcarcel, J.G. Einstein–Yang-Mills-Lorentz black holes. Eur. Phys. J. C 2017, 77, 853. [Google Scholar] [CrossRef]
- Protter, M.; DeBenedictis, A. Loop quantum corrected Einstein Yang-Mills black holes. Phys. Rev. D 2018, 97, 106009. [Google Scholar] [CrossRef]
- Balakin, A.B.; Lemos, J.P.S.; Zayats, A.E. Regular nonminimal magnetic black holes in spacetimes with a cosmological constant. Phys. Rev. D 2016, 93, 024008. [Google Scholar] [CrossRef]
- Jusufi, K.; Azreg-Aïnou, M.; Jamil, M.; Wei, S.W.; Wu, Q.; Wang, A. Quasinormal modes, quasiperiodic oscillations, and the shadow of rotating regular black holes in nonminimally coupled Einstein–Yang-Mills theory. Phys. Rev. D 2021, 103, 024013. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D. 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Chen, S.; Wang, M.; Jing, J. Chaotic motion of particles in the accelerating and rotating black holes spacetime. J. High Energy Phys. 2016, 2016, 82. [Google Scholar] [CrossRef]
- Hashimoto, K.; Tanahashi, N. Universality in chaos of particle motion near black hole horizon. Phys. Rev. D 2017, 95, 024007. [Google Scholar] [CrossRef]
- Dalui, S.; Majhi, B.R.; Mishra, P. Presence of horizon makes particle motion chaotic. Phys. Lett. B 2019, 788, 486–493. [Google Scholar] [CrossRef]
- Han, W. Chaos and dynamics of spinning particles in Kerr spacetime. Gen. Relativ. Gravit. 2008, 40, 1831–1847. [Google Scholar] [CrossRef][Green Version]
- de Moura, A.P.S.; Letelier, P.S. Chaos and fractals in geodesic motions around a nonrotating black hole with halos. Phys. Rev. E 2000, 61, 6506–6516. [Google Scholar] [CrossRef]
- Morozova, V.S.; Rezzolla, L.; Ahmedov, B.J. Nonsingular electrodynamics of a rotating black hole moving in an asymptotically uniform magnetic test field. Phys. Rev. D 2014, 89, 104030. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- Jawad, A.; Ali, F.; Jamil, M.; Debnath, U. Dynamics of Particles Around a Regular Black Hole with Nonlinear Electrodynamics. Commun. Theor. Phys. 2016, 66, 509. [Google Scholar] [CrossRef]
- Hussain, S.; Jamil, M. Timelike geodesics of a modified gravity black hole immersed in an axially symmetric magnetic field. Phys. Rev. D 2015, 92, 043008. [Google Scholar] [CrossRef]
- Jamil, M.; Hussain, S.; Majeed, B. Dynamics of particles around a Schwarzschild-like black hole in the presence of quintessence and magnetic field. Eur. Phys. J. C 2015, 75, 24. [Google Scholar] [CrossRef]
- Hussain, S.; Hussain, I.; Jamil, M. Dynamics of a charged particle around a slowly rotating Kerr black hole immersed in magnetic field. Eur. Phys. J. C 2014, 74, 210. [Google Scholar] [CrossRef]
- Babar, G.Z.; Jamil, M.; Lim, Y.K. Dynamics of a charged particle around a weakly magnetized naked singularity. Int. J. Mod. Phys. D 2016, 25, 1650024. [Google Scholar] [CrossRef]
- Bañados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef]
- Majeed, B.; Jamil, M. Dynamics and center of mass energy of colliding particles around black hole in f(R) gravity. Int. J. Mod. Phys. D 2017, 26, 1741017. [Google Scholar] [CrossRef]
- Zakria, A.; Jamil, M. Center of mass energy of the collision for two general geodesic particles around a Kerr–Newman-Taub-NUT black hole. J. High Energy Phys. 2015, 2015, 147. [Google Scholar] [CrossRef]
- Brevik, I.; Jamil, M. Black holes in the turbulence phase of viscous rip cosmology. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950030. [Google Scholar] [CrossRef]
- De Laurentis, M.; Younsi, Z.; Porth, O.; Mizuno, Y.; Rezzolla, L. Test-particle dynamics in general spherically symmetric black hole spacetimes. Phys. Rev. D 2018, 97, 104024. [Google Scholar] [CrossRef]
- Shaymatov, S.R.; Ahmedov, B.J.; Abdujabbarov, A.A. Particle acceleration near a rotating black hole in a Randall-Sundrum brane with a cosmological constant. Phys. Rev. D 2013, 88, 024016. [Google Scholar] [CrossRef]
- Atamurotov, F.; Ahmedov, B.; Shaymatov, S. Formation of black holes through BSW effect and black hole-black hole collisions. Astrophys. Space Sci. 2013, 347, 277–281. [Google Scholar] [CrossRef]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Possible signature of magnetic fields related to quasi-periodic oscillation observed in microquasars. Eur. Phys. J. C 2017, 77, 860. [Google Scholar] [CrossRef]
- Kovář, J.; Kopáček, O.; Karas, V.; Stuchlík, Z. Off-equatorial orbits in strong gravitational fields near compact objects II: Halo motion around magnetic compact stars and magnetized black holes. Class. Quantum Gravity 2010, 27, 135006. [Google Scholar] [CrossRef]
- Kovář, J.; Slaný, P.; Cremaschini, C.; Stuchlík, Z.; Karas, V.; Trova, A. Electrically charged matter in rigid rotation around magnetized black hole. Phys. Rev. D 2014, 90, 044029. [Google Scholar] [CrossRef]
- Aliev, A.N.; Gal’tsov, D.V. Reviews of Topical Problems: “Magnetized” black holes. Sov. Phys. Uspekhi 1989, 32, 75–92. [Google Scholar] [CrossRef]
- Aliev, A.N.; Özdemir, N. Motion of charged particles around a rotating black hole in a magnetic field. Mon. Not. R. Astron. Soc. 2002, 336, 241–248. [Google Scholar] [CrossRef]
- Aliev, A.N.; Galtsov, D.V.; Petukhov, V.I. Negative absorption near a magnetized black hole—Black hole masers. Astrophys. Space Sci. 1986, 124, 137–157. [Google Scholar] [CrossRef]
- Frolov, V.P.; Krtouš, P. Charged particle in higher dimensional weakly charged rotating black hole spacetime. Phys. Rev. D 2011, 83, 024016. [Google Scholar] [CrossRef]
- Frolov, V.P. Weakly magnetized black holes as particle accelerators. Phys. Rev. D. 2012, 85, 024020. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J.; Abdujabbarov, A. Ultra-high-energy collisions of particles in the field of near-extreme Kehagias-Sfetsos naked singularities and their appearance to distant observers. Phys. Rev. D 2014, 89, 104048. [Google Scholar] [CrossRef]
- Shaymatov, S.; Atamurotov, F.; Ahmedov, B. Isofrequency pairing of circular orbits in Schwarzschild spacetime in the presence of magnetic field. Astrophys. Space Sci. 2014, 350, 413–419. [Google Scholar] [CrossRef]
- Hakimov, A.; Abdujabbarov, A.; Narzilloev, B. Quantum interference effects in conformal Weyl gravity. Int. J. Mod. Phys. A 2017, 32, 1750116. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B. Test particle motion around a black hole in a braneworld. Phys. Rev. D 2010, 81, 044022. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B.; Hakimov, A. Particle motion around black hole in Hořava-Lifshitz gravity. Phys. Rev. D 2011, 83, 044053. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Shaymatov, S.R.; Rakhmatov, A.S. Penrose process in Kerr-Taub-NUT spacetime. Astrophys. Space Sci. 2011, 334, 237–241. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Kagramanova, V.G. Particle motion and electromagnetic fields of rotating compact gravitating objects with gravitomagnetic charge. Gen. Relativ. Gravit. 2008, 40, 2515–2532. [Google Scholar] [CrossRef]
- Karas, V.; Kovar, J.; Kopacek, O.; Kojima, Y.; Slany, P.; Stuchlik, Z. Regular and Chaotic Motion in General Relativity. Case of Magnetized Black Hole and a Massive Magnetic Dipole. In American Astronomical Society Meeting Abstracts #220; The SAO/NASA Astrophysics Data System: Washington, DC, USA, 2012; Volume 220, p. 430-07. [Google Scholar]
- Shaymatov, S.; Patil, M.; Ahmedov, B.; Joshi, P.S. Destroying a near-extremal Kerr black hole with a charged particle: Can a test magnetic field serve as a cosmic censor? Phys. Rev. D 2015, 91, 064025. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Turimov, B.; Marcos, F.; Palvanov, S.; Rakhmatov, A. Particle acceleration and electromagnetic field of deformed neutron stars. Mod. Phys. Lett. A 2020, 35, 2050056. [Google Scholar] [CrossRef]
- Turimov, B.; Ahmedov, B.; Abdujabbarov, A.; Bambi, C. Electromagnetic fields of slowly rotating magnetized compact stars in conformal gravity. Phys. Rev. D 2018, 97, 124005. [Google Scholar] [CrossRef]
- Turimov, B.V.; Ahmedov, B.J.; Hakimov, A.A. Stationary electromagnetic fields of slowly rotating relativistic magnetized star in the braneworld. Phys. Rev. D 2017, 96, 104001. [Google Scholar] [CrossRef]
- Shaymatov, S.; Vrba, J.; Malafarina, D.; Ahmedov, B.; Stuchlík, Z. Charged particle and epicyclic motions around 4D Einstein–Gauss–Bonnet black hole immersed in an external magnetic field. Phys. Dark Universe 2020, 30, 100648. [Google Scholar] [CrossRef]
- Rayimbaev, J.R.; Ahmedov, B.J.; Juraeva, N.B.; Rakhmatov, A.S. Plasma magnetosphere of deformed magnetized neutron star. Astrophys. Space Sci. 2015, 356, 301–308. [Google Scholar] [CrossRef]
- Shaymatov, S. Magnetized Reissner–Nordström black hole restores cosmic censorship conjecture. Int. J. Mod. Phys. Conf. Ser. 2019, 49, 1960020. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Turimov, B.; Ahmedov, B. Braneworld effects in plasma magnetosphere of a slowly rotating magnetized neutron star. Int. J. Mod. Phys. D 2019, 28, 1950128–1950209. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Tadjimuratov, P. Can modified gravity silence radio-loud pulsars? Phys. Rev. D 2020, 102, 024019. [Google Scholar] [CrossRef]
- Shaymatov, S.; Malafarina, D.; Ahmedov, B. Effect of perfect fluid dark matter on particle motion around a static black hole immersed in an external magnetic field. arXiv 2020, arXiv:2004.06811. [Google Scholar]
- Narzilloev, B.; Abdujabbarov, A.; Bambi, C.; Ahmedov, B. Charged particle motion around a quasi-Kerr compact object immersed in an external magnetic field. Phys. Rev. D 2019, 99, 104009. [Google Scholar] [CrossRef]
- Narzilloev, B.; Malafarina, D.; Abdujabbarov, A.; Bambi, C. On the properties of a deformed extension of the NUT space-time. Eur. Phys. J. C 2020, 80, 784. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Abdujabbarov, A.; Bambi, C. Charged particle motion around non-singular black holes in conformal gravity in the presence of external magnetic field. Eur. Phys. J. C 2020, 80, 1074. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Shaymatov, S.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Can the dynamics of test particles around charged stringy black holes mimic the spin of Kerr black holes? Phys. Rev. D 2020, 102, 044013. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Shaymatov, S.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Dynamics of test particles around a Bardeen black hole surrounded by perfect fluid dark matter. Phys. Rev. D 2020, 102, 104062. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Dynamics of charged particles and magnetic dipoles around magnetized quasi-Schwarzschild black holes. Eur. Phys. J. C 2021, 81, 269. [Google Scholar] [CrossRef]
- Shaymatov, S.; Narzilloev, B.; Abdujabbarov, A.; Bambi, C. Charged particle motion around a magnetized Reissner-Nordström black hole. Phys. Rev. D 2021, 103, 124066. [Google Scholar] [CrossRef]
- Narzilloev, B.; Malafarina, D.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Particle motion around a static axially symmetric wormhole. Phys. Rev. D 2021, 104, 064016. [Google Scholar] [CrossRef]
- Narzilloev, B.; Shaymatov, S.; Hussain, I.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Motion of Particles and Gravitational Lensing Around (2+1)-dimensional BTZ black holes in Gauss-Bonnet Gravity. Eur. Phys. J. C 2021, 81, 849. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B. Regular Bardeen Black Holes in Anti-de Sitter Spacetime versus Kerr Black Holes through Particle Dynamics. Galaxies 2021, 9, 63. [Google Scholar] [CrossRef]
- de Felice, F.; Sorge, F. Magnetized orbits around a Schwarzschild black hole. Class. Quantum Gravity 2003, 20, 469–481. [Google Scholar] [CrossRef]
- de Felice, F.; Sorge, F.; Zilio, S. Magnetized orbits around a Kerr black hole. Class. Quantum Gravity 2004, 21, 961–973. [Google Scholar] [CrossRef]
- Rayimbaev, J.R. Magnetized particle motion around non-Schwarzschild black hole immersed in an external uniform magnetic field. Astrophys. Space Sci. 2016, 361, 288. [Google Scholar] [CrossRef]
- Oteev, T.; Abdujabbarov, A.; Stuchlík, Z.; Ahmedov, B. Energy extraction and particle acceleration around a rotating black hole in quintessence. Astrophys. Space Sci. 2016, 361, 269. [Google Scholar] [CrossRef]
- Toshmatov, B.; Abdujabbarov, A.; Ahmedov, B.; Stuchlík, Z. Motion and high energy collision of magnetized particles around a Hořava-Lifshitz black hole. Astrophys. Space Sci. 2015, 360, 19. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B.; Rahimov, O.; Salikhbaev, U. Magnetized particle motion and acceleration around a Schwarzschild black hole in a magnetic field. Phys. Scr. 2014, 89, 084008. [Google Scholar] [CrossRef]
- Rahimov, O.G.; Abdujabbarov, A.A.; Ahmedov, B.J. Magnetized particle capture cross section for braneworld black hole. Astrophys. Space Sci. 2011, 335, 499–504. [Google Scholar] [CrossRef][Green Version]
- Rahimov, O.G. Magnetized Particle Motion around Black Hole in Braneworld. Mod. Phys. Lett. A 2011, 26, 399–408. [Google Scholar] [CrossRef]
- Haydarov, K.; Abdujabbarov, A.; Rayimbaev, J.; Ahmedov, B. Magnetized Particle Motion around Black Holes in Conformal Gravity: Can Magnetic Interaction Mimic Spin of Black Holes? Universe 2020, 6, 44. [Google Scholar] [CrossRef]
- Haydarov, K.; Rayimbaev, J.; Abdujabbarov, A.; Palvanov, S.; Begmatova, D. Magnetized particle motion around magnetized Schwarzschild-MOG black hole. Eur. Phys. J. C 2020, 80, 399. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Abdujabbarov, A.; Jamil, M.; Ahmedov, B.; Han, W.B. Dynamics of test particles around renormalization group improved Schwarzschild black holes. Phys. Rev. D 2020, 102, 084016. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Figueroa, M.; Stuchlík, Z.; Juraev, B. Test particle orbits around regular black holes in general relativity combined with nonlinear electrodynamics. Phys. Rev. D 2020, 101, 104045. [Google Scholar] [CrossRef]
- Vrba, J.; Abdujabbarov, A.; Kološ, M.; Ahmedov, B.; Stuchlík, Z.; Rayimbaev, J. Charged and magnetized particles motion in the field of generic singular black holes governed by general relativity coupled to nonlinear electrodynamics. Phys. Rev. D 2020, 101, 124039. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Rayimbaev, J.; Turimov, B.; Atamurotov, F. Dynamics of magnetized particles around 4-D Einstein Gauss–Bonnet black hole. Phys. Dark Universe 2020, 30, 100715. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Rayimbaev, J.; Atamurotov, F.; Ahmedov, B. Magnetized Particle Motion in γ-Spacetime in a Magnetic Field. Galaxies 2020, 8, 76. [Google Scholar] [CrossRef]
- Turimov, B.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B.; Stuchlík, Z.C.V. Test particle motion around a black hole in Einstein–Maxwell-scalar theory. Phys. Rev. D 2020, 102, 064052. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Rayimbaev, J.; Ahmedov, B. Test particles dynamics around deformed Reissner-Nordström black hole. Phys. Rev. D 2020, 102, 124078. [Google Scholar] [CrossRef]
- Juraeva, N.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B.; Palvanov, S. Distinguishing magnetically and electrically charged Reissner–Nordström black holes by magnetized particle motion. Eur. Phys. J. C 2021, 81, 124078. [Google Scholar] [CrossRef]
- Mori, K.; Gotthelf, E.V.; Zhang, S.; An, H.; Baganoff, F.K.; Barrière, N.M.; Beloborodov, A.M.; Boggs, S.E.; Christensen, F.E.; Craig, W.W.; et al. NuSTAR Discovery of a 3.76 s Transient Magnetar Near Sagittarius A*. Astron. J. Lett. 2013, 770, L23. [Google Scholar] [CrossRef]
- Mondal, M.; Rahaman, F.; Singh, K.N. Lyapunov exponent, ISCO and Kolmogorov-Senai entropy for Kerr-Kiselev black hole. Eur. Phys. J. C 2021, 81, 84. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Shaymatov, S.; Jamil, M. Dynamics and epicyclic motions of particles around the Schwarzschild-de Sitter black hole in perfect fluid dark matter. Eur. Phys. J. C 2021, 81, 699. [Google Scholar] [CrossRef]
- Tursunov, A.; Stuchlík, Z.; Kološ, M. Circular orbits and related quasiharmonic oscillatory motion of charged particles around weakly magnetized rotating black holes. Phys. Rev. D 2016, 93, 084012. [Google Scholar] [CrossRef]



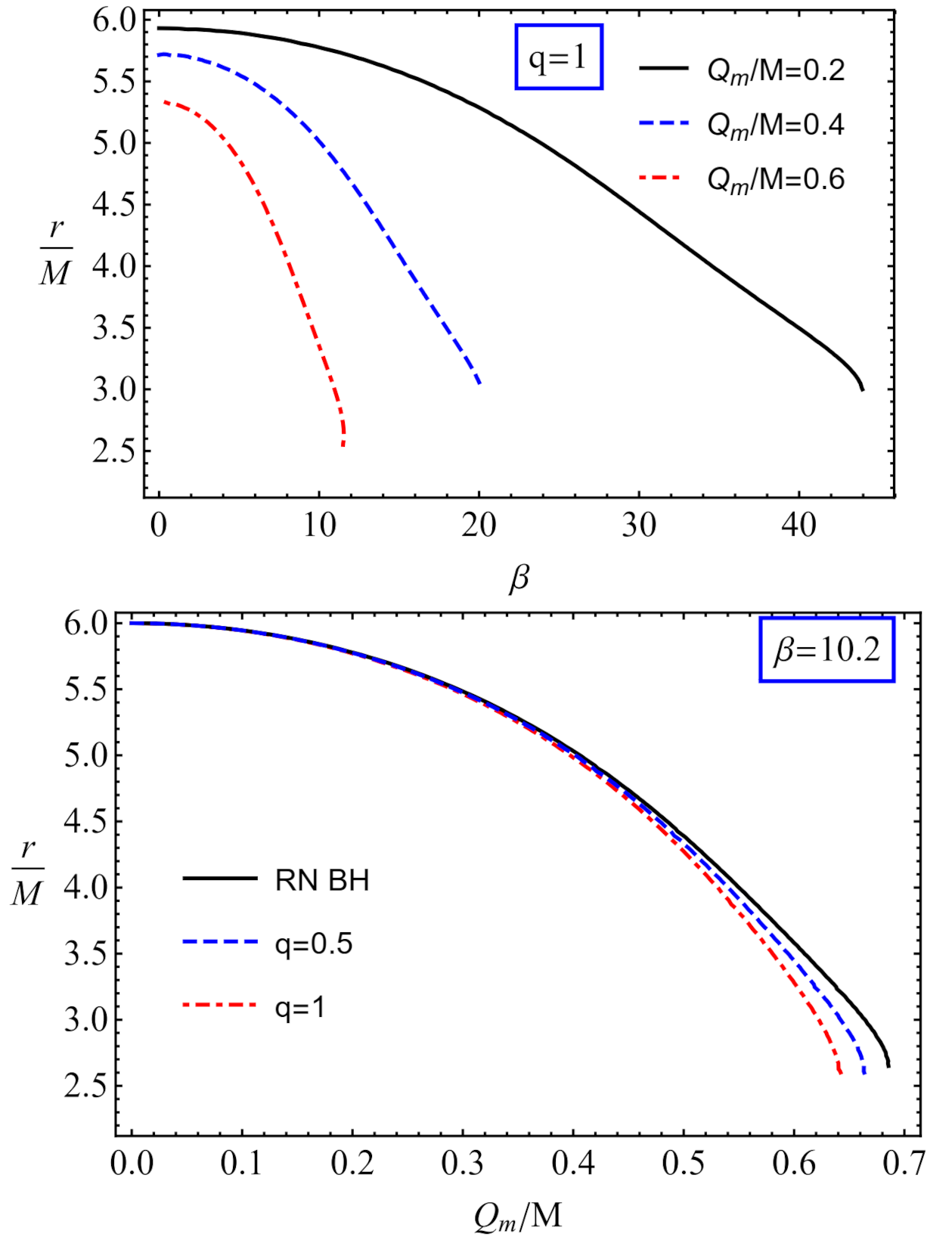
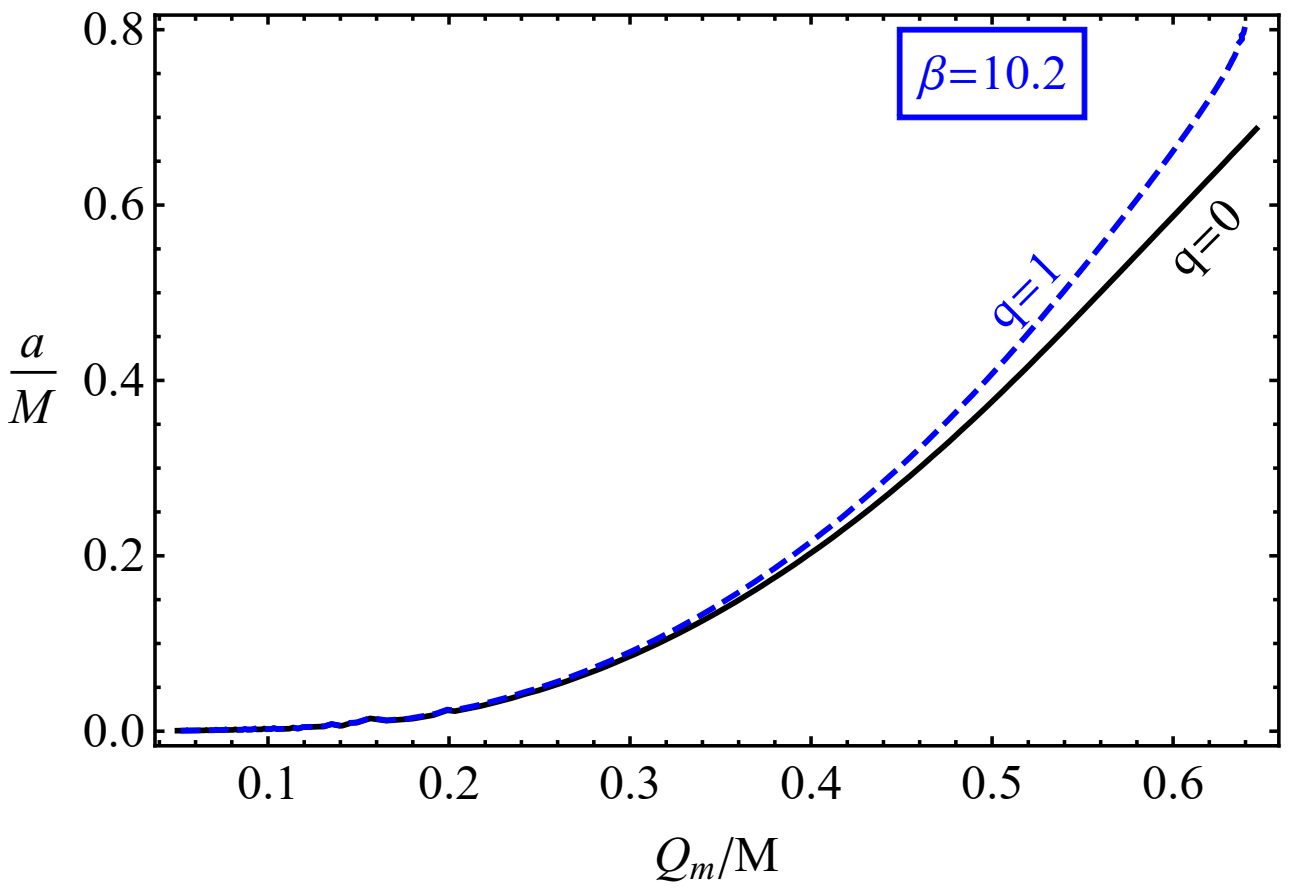

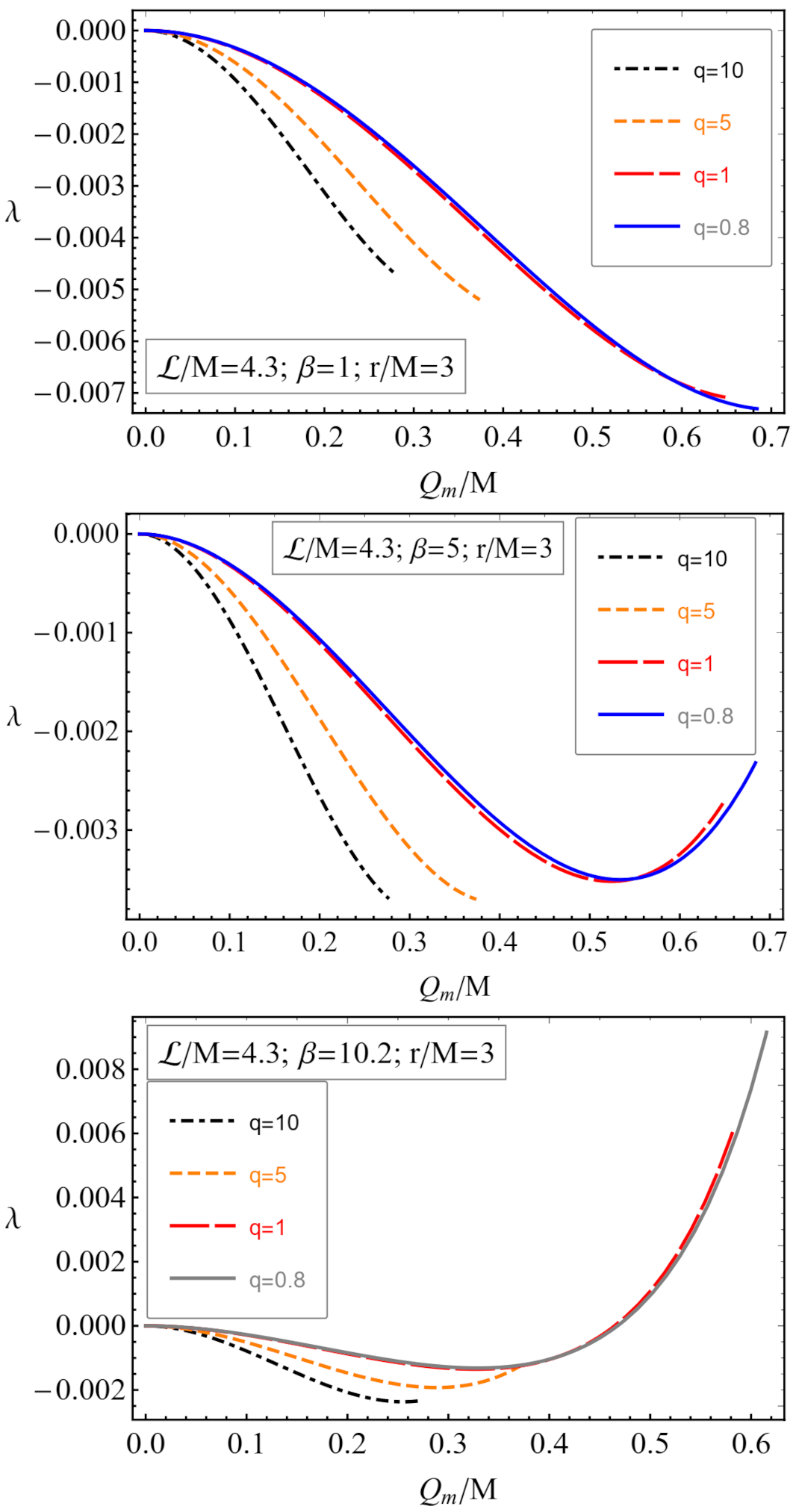
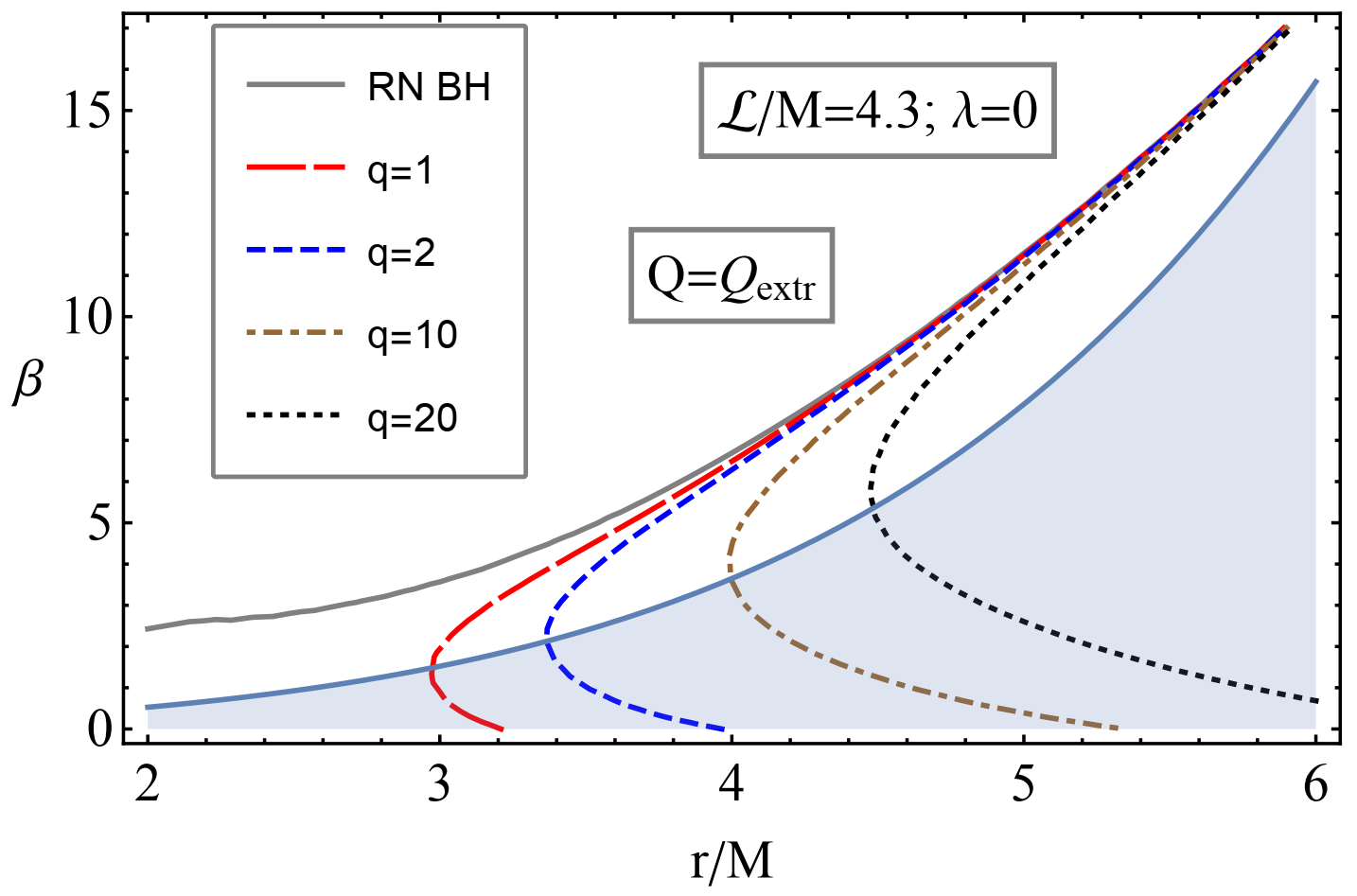

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rayimbaev, J.; Narzilloev, B.; Abdujabbarov, A.; Ahmedov, B. Dynamics of Magnetized and Magnetically Charged Particles around Regular Nonminimal Magnetic Black Holes. Galaxies 2021, 9, 71. https://doi.org/10.3390/galaxies9040071
Rayimbaev J, Narzilloev B, Abdujabbarov A, Ahmedov B. Dynamics of Magnetized and Magnetically Charged Particles around Regular Nonminimal Magnetic Black Holes. Galaxies. 2021; 9(4):71. https://doi.org/10.3390/galaxies9040071
Chicago/Turabian StyleRayimbaev, Javlon, Bakhtiyor Narzilloev, Ahmadjon Abdujabbarov, and Bobomurat Ahmedov. 2021. "Dynamics of Magnetized and Magnetically Charged Particles around Regular Nonminimal Magnetic Black Holes" Galaxies 9, no. 4: 71. https://doi.org/10.3390/galaxies9040071
APA StyleRayimbaev, J., Narzilloev, B., Abdujabbarov, A., & Ahmedov, B. (2021). Dynamics of Magnetized and Magnetically Charged Particles around Regular Nonminimal Magnetic Black Holes. Galaxies, 9(4), 71. https://doi.org/10.3390/galaxies9040071







