Stable Up-Down Quark Matter Nuggets, Quark Star Crusts, and a New Family of White Dwarfs
Abstract
1. Introduction
2. Equivparticle Model
3. QM Nuggets
4. QM Star
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Witten, E. Cosmic separation of phases. Phys. Rev. 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Bodmer, A.R. Collapsed Nuclei. Phys. Rev. 1971, 4, 1601–1606. [Google Scholar] [CrossRef]
- Terazawa, H. Super-Hypernuclei in the Quark-Shell Model. J. Phys. Soc. Jpn. 1989, 58, 3555–3563. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R.L. Strange matter. Phys. Rev. 1984, 30, 2379–2390. [Google Scholar] [CrossRef]
- Berger, M.S.; Jaffe, R.L. Radioactivity in strange quark matter. Phys. Rev. 1987, 35, 213–225. [Google Scholar] [CrossRef]
- Gilson, E.P.; Jaffe, R.L. Stability of very small strangelets. Phys. Rev. Lett. 1993, 71, 332–335. [Google Scholar] [CrossRef]
- Peng, G.X.; Wen, X.J.; Chen, Y.D. New solutions for the color-flavor locked strangelets. Phys. Lett. 2006, 633, 314–318. [Google Scholar] [CrossRef]
- Rújula, A.D.; Glashow, S.L. Nuclearites–a novel form of cosmic radiation. Nature 1984, 312, 734. [Google Scholar] [CrossRef]
- Lowder, D.M. Experimental searches for strange quark matter in cosmic rays. Nucl. Phys. (Proc. Suppl.) 1991, 24, 177–183. [Google Scholar] [CrossRef]
- Rafelski, J.; Labun, L.; Birrell, J. Compact Ultradense Matter Impactors. Phys. Rev. Lett. 2013, 110, 111102. [Google Scholar] [CrossRef]
- Itoh, N. Hydrostatic Equilibrium of Hypothetical Quark Stars. Prog. Theor. Phys. 1970, 44, 291–292. [Google Scholar] [CrossRef]
- Alcock, C.; Farhi, E.; Olinto, A. Strange stars. Astrophys. J. 1986, 310, 261–272. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L.; Schaeffer, R. Strange quark stars. Astron. Astrophys. 1986, 160, 121–128. [Google Scholar]
- Buballa, M.; Oertel, M. Strange quark matter with dynamically generated quark masses. Phys. Lett. 1999, 457, 261–267. [Google Scholar] [CrossRef]
- Klähn, T.; Fischer, T. Vector Interaction Enhanced Bag Model for Astrophysical Applications. Astrophys. J. 2015, 810, 134. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Maruyama, T.; Chiba, S.; Schulze, H.J.; Tatsumi, T. Hadron-quark mixed phase in hyperon stars. Phys. Rev. 2007, 76, 123015. [Google Scholar] [CrossRef]
- Peng, G.X.; Li, A.; Lombardo, U. Deconfinement phase transition in hybrid neutron stars from the Brueckner theory with three-body forces and a quark model with chiral mass scaling. Phys. Rev. 2008, 77, 065807. [Google Scholar] [CrossRef]
- Shao, G.Y.; Colonna, M.; Di Toro, M.; Liu, Y.X.; Liu, B. Isoscalar-vector interaction and hybrid quark core in massive neutron stars. Phys. Rev. 2013, 87, 096012. [Google Scholar] [CrossRef]
- Klähn, T.; Łastowiecki, R.; Blaschke, D. Implications of the measurement of pulsars with two solar masses for quark matter in compact stars and heavy-ion collisions: A Nambu-Jona-Lasinio model case study. Phys. Rev. 2013, 88, 085001. [Google Scholar] [CrossRef]
- Zhao, T.; Xu, S.S.; Yan, Y.; Luo, X.L.; Liu, X.J.; Zong, H.S. Studies of two-solar-mass hybrid stars within the framework of Dyson-Schwinger equations. Phys. Rev. 2015, 92, 054012. [Google Scholar] [CrossRef]
- Li, A.; Zuo, W.; Peng, G.X. Massive hybrid stars with a first-order phase transition. Phys. Rev. 2015, 91, 035803. [Google Scholar] [CrossRef]
- Greiner, C.; Koch, P.; Stöcker, H. Separation of strangeness from antistrangeness in the phase transition from quark to hadron matter: Possible formation of strange quark matter in heavy-ion collisions. Phys. Rev. Lett. 1987, 58, 1825–1828. [Google Scholar] [CrossRef]
- Greiner, C.; Stöcker, H. Distillation and survival of strange-quark-matter droplets in ultrarelativistic heavy-ion collisions. Phys. Rev. 1991, 44, 3517–3529. [Google Scholar] [CrossRef]
- Holdom, B.; Ren, J.; Zhang, C. Quark Matter May Not Be Strange. Phys. Rev. Lett. 2018, 120, 222001. [Google Scholar] [CrossRef]
- Xia, C.J.; Xue, S.S.; Xu, R.X.; Zhou, S.G. Supercritically charged objects and electron-positron pair creation. Phys. Rev. 2020, 101, 103031. [Google Scholar] [CrossRef]
- Zhao, T.; Zheng, W.; Wang, F.; Li, C.M.; Yan, Y.; Huang, Y.F.; Zong, H.S. Do current astronomical observations exclude the existence of nonstrange quark stars? Phys. Rev. 2019, 100, 043018. [Google Scholar] [CrossRef]
- Zhang, C. Probing up-down quark matter via gravitational waves. Phys. Rev. 2020, 101, 043003. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, L.W.; Chu, P.C.; Zhou, Y. GW190814: Circumstantial Evidence for Up-Down Quark Star. arXiv 2020, arXiv:2009.00942. [Google Scholar]
- Zhang, C.; Mann, R.B. Unified interacting quark matter and its astrophysical implications. Phys. Rev. 2021, 103, 063018. [Google Scholar]
- Lugones, G. From quark drops to quark stars. Eur. Phys. J. A 2016, 52, 53. [Google Scholar] [CrossRef]
- Xia, C.J. Interface effects of strange quark matter. AIP Conf. Proc. 2019, 2127, 020029. [Google Scholar]
- Oertel, M.; Urban, M. Surface effects in color superconducting strange-quark matter. Phys. Rev. 2008, 77, 074015. [Google Scholar] [CrossRef]
- Palhares, L.F.; Fraga, E.S. Droplets in the cold and dense linear sigma model with quarks. Phys. Rev. 2010, 82, 125018. [Google Scholar] [CrossRef]
- Pinto, M.B.; Koch, V.; Randrup, J. Surface tension of quark matter in a geometrical approach. Phys. Rev. 2012, 86, 025203. [Google Scholar] [CrossRef]
- Kroff, D.; Fraga, E.S. Nucleating quark droplets in the core of magnetars. Phys. Rev. 2015, 91, 025017. [Google Scholar] [CrossRef]
- Garcia, A.F.; Pinto, M.B. Surface tension of magnetized quark matter. Phys. Rev. 2013, 88, 025207. [Google Scholar] [CrossRef]
- Ke, W.Y.; Liu, Y.X. Interface tension and interface entropy in the 2+1 flavor Nambu-Jona-Lasinio model. Phys. Rev. 2014, 89, 074041. [Google Scholar]
- Mintz, B.W.; Stiele, R.; Ramos, R.O.; Schaffner-Bielich, J. Phase diagram and surface tension in the three-flavor Polyakov-quark-meson model. Phys. Rev. 2013, 87, 036004. [Google Scholar] [CrossRef]
- Gao, F.; Liu, Y.X. Interface effect in QCD phase transitions via Dyson-Schwinger equation approach. Phys. Rev. 2016, 94, 094030. [Google Scholar] [CrossRef]
- Xia, C.J.; Peng, G.X.; Sun, T.T.; Guo, W.L.; Lu, D.H.; Jaikumar, P. Interface effects of strange quark matter with density dependent quark masses. Phys. Rev. 2018, 98, 034031. [Google Scholar] [CrossRef]
- Fraga, E.S.; Hippert, M.; Schmitt, A. Surface tension of dense matter at the chiral phase transition. Phys. Rev. 2019, 99, 014046. [Google Scholar] [CrossRef]
- Lugones, G.; Grunfeld, A.G. Surface tension of hot and dense quark matter under strong magnetic fields. Phys. Rev. 2019, 99, 035804. [Google Scholar] [CrossRef]
- Lugones, G.; Grunfeld, A.G. Surface tension of highly magnetized degenerate quark matter. Phys. Rev. 2017, 95, 015804. [Google Scholar] [CrossRef]
- Wen, X.J.; Li, J.Y.; Liang, J.Q.; Peng, G.X. Medium effects on the surface tension of strangelets in the extended quasiparticle model. Phys. Rev. 2010, 82, 025809. [Google Scholar] [CrossRef]
- Lugones, G.; Grunfeld, A.; Ajmi, M.A. Surface tension and curvature energy of quark matter in the Nambu-Jona-Lasinio model. Phys. Rev. 2013, 88, 045803. [Google Scholar] [CrossRef]
- Alford, M.; Rajagopal, K.; Reddy, S.; Wilczek, F. Minimal color-flavor-locked-nuclear interface. Phys. Rev. 2001, 64, 074017. [Google Scholar] [CrossRef]
- Berger, M.S. Surface tension of strange-quark matter in the early Universe. Phys. Rev. 1989, 40, 2128–2130. [Google Scholar] [CrossRef] [PubMed]
- Heiselberg, H. Screening in quark droplets. Phys. Rev. 1993, 48, 1418–1423. [Google Scholar] [CrossRef] [PubMed]
- Alford, M.G.; Rajagopal, K.; Reddy, S.; Steiner, A.W. Stability of strange star crusts and strangelets. Phys. Rev. 2006, 73, 114016. [Google Scholar] [CrossRef]
- Jaikumar, P.; Reddy, S.; Steiner, A.W. Strange Star Surface: A Crust with Nuggets. Phys. Rev. Lett. 2006, 96, 041101. [Google Scholar] [CrossRef]
- Alford, M.; Eby, D. Thickness of the strangelet-crystal crust of a strange star. Phys. Rev. 2008, 78, 045802. [Google Scholar] [CrossRef]
- Chu, P.C.; Chen, L.W. Quark Matter Symmetry Energy and Quark Stars. Astrophys. J. 2014, 780, 135. [Google Scholar] [CrossRef]
- Jeong, K.S.; Lee, S.H. Symmetry energy in cold dense matter. Nucl. Phys. 2016, 945, 21–41. [Google Scholar] [CrossRef]
- Chen, L.W. The symmetry energy in nucleon and quark matter. Nucl. Phys. Rev. 2017, 34, 20–28. [Google Scholar]
- Chu, P.C.; Zhou, Y.; Qi, X.; Li, X.H.; Zhang, Z.; Zhou, Y. Isospin properties in quark matter and quark stars within isospin-dependent quark mass models. Phys. Rev. 2019, 99, 035802. [Google Scholar] [CrossRef]
- Wu, X.; Ohnishi, A.; Shen, H. Quark matter symmetry energy effect on equation of state for neutron stars. AIP Conf. Proc. 2019, 2127, 020032. [Google Scholar]
- Xia, C.J.; Peng, G.X.; Zhao, E.G.; Zhou, S.G. From strangelets to strange stars: A unified description. Sci. Bull. 2016, 61, 172–177. [Google Scholar] [CrossRef]
- Xia, C.J. Strange quark matter: From strangelets to strange stars (in Chinese). Sci. Sin. Phys. Mech. Astron. 2016, 46, 012021. [Google Scholar] [CrossRef]
- Xia, C.J.; Peng, G.X.; Zhao, E.G.; Zhou, S.G. Properties of strange quark matter objects with two types of surface treatments. Phys. Rev. 2016, 93, 085025. [Google Scholar] [CrossRef]
- Xia, C.J.; Zhou, S.G. Stable strange quark matter objects with running masses and coupling constant. Nucl. Phys. B 2017, 916, 669–687. [Google Scholar] [CrossRef]
- Peng, G.X.; Chiang, H.C.; Zou, B.S.; Ning, P.Z.; Luo, S.J. Thermodynamics, strange quark matter, and strange stars. Phys. Rev. 2000, 62, 025801. [Google Scholar] [CrossRef]
- Wen, X.J.; Zhong, X.H.; Peng, G.X.; Shen, P.N.; Ning, P.Z. Thermodynamics with density and temperature dependent particle masses and properties of bulk strange quark matter and strangelets. Phys. Rev. 2005, 72, 015204. [Google Scholar] [CrossRef]
- Wen, X.J.; Peng, G.X.; Chen, Y.D. Charge, strangeness and radius of strangelets. J. Phys. 2007, 34, 1697. [Google Scholar] [CrossRef][Green Version]
- Xia, C.J.; Chen, S.W.; Peng, G.X. Properties of strangelets in a new quark mass confinement model with one-gluon-exchange interaction. Sci. China Phys. Mech. Astron. 2014, 57, 1304. [Google Scholar] [CrossRef]
- Chen, S.W.; Gao, L.; Peng, G.X. One-gluon-exchange effect on the properties of quark matter and strange stars. Chin. Phys. 2012, 36, 947. [Google Scholar] [CrossRef]
- Chang, Q.; Chen, S.W.; Peng, G.X.; Xu, J.F. Properties of color-flavor locked strange quark matter and strange stars in a new quark mass scaling. Sci. China Phys. Mech. Astron. 2013, 56, 1730. [Google Scholar] [CrossRef]
- Xia, C.J.; Peng, G.X.; Chen, S.W.; Lu, Z.Y.; Xu, J.F. Thermodynamic consistency, quark mass scaling, and properties of strange matter. Phys. Rev. 2014, 89, 105027. [Google Scholar] [CrossRef]
- Hou, J.X.; Peng, G.X.; Xia, C.J.; Xu, J.F. Magnetized strange quark matter in a mass-density-dependent model. Chin. Phys. 2015, 39, 015101. [Google Scholar] [CrossRef][Green Version]
- Peng, C.; Peng, G.X.; Xia, C.J.; Xu, J.F.; Zhang, S.P. Magnetized strange quark matter in the equivparticle model with both confinement and perturbative interactions. Nucl. Sci. Tech. 2016, 27, 98. [Google Scholar] [CrossRef]
- Chu, P.C.; Chen, L.W. Isovector properties of quark matter and quark stars in an isospin-dependent confining model. Phys. Rev. 2017, 96, 083019. [Google Scholar] [CrossRef]
- Particle Data Group. Review of Particle Physics. Chin. Phys. 2016, 40, 100001. [Google Scholar] [CrossRef]
- Fowler, G.N.; Raha, S.; Weiner, R.M. Confinement and phase transitions. Z. Phys. C 1981, 9, 271–273. [Google Scholar] [CrossRef]
- Peng, G.X.; Chiang, H.C.; Yang, J.J.; Li, L.; Liu, B. Mass formulas and thermodynamic treatment in the mass-density-dependent model of strange quark matter. Phys. Rev. 1999, 61, 015201. [Google Scholar] [CrossRef]
- Audi, G.; Kondev, F.G.; Wang, M.; Huang, W.; Naimi, S. The NUBASE2016 evaluation of nuclear properties. Chin. Phys. 2017, 41, 030001. [Google Scholar] [CrossRef]
- Huang, W.; Audi, G.; Wang, M.; Kondev, F.G.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (I). Evaluation of input data; and adjustment procedures. Chin. Phys. 2017, 41, 030002. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. 2017, 41, 030003. [Google Scholar] [CrossRef]
- Xia, C.J. A unified description for strange quark matter objects. J. Phys: Conf. Ser. 2017, 861, 012022. [Google Scholar]
- Brown, G.E.; Rho, M. Scaling effective Lagrangians in a dense medium. Phys. Rev. Lett. 1991, 66, 2720–2723. [Google Scholar] [CrossRef]
- Wang, P. Strange matter in a self-consistent quark mass-density-dependent model. Phys. Rev. 2000, 62, 015204. [Google Scholar] [CrossRef]
- Torres, J.R.; Menezes, D.P. Quark matter equation of state and stellar properties. Europhys. Lett. 2013, 101, 42003. [Google Scholar] [CrossRef]
- Dexheimer, V.; Torres, J.; Menezes, D. Stability windows for proto-quark stars. Eur. Phys. J. C 2013, 73, 2569. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. 2009, 80, 084035. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. 2010, 81, 123016. [Google Scholar] [CrossRef]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love numbers of neutron and self-bound quark stars. Phys. Rev. 2010, 82, 024016. [Google Scholar] [CrossRef]
- Zhou, E.P.; Zhou, X.; Li, A. Constraints on interquark interaction parameters with GW170817 in a binary strange star scenario. Phys. Rev. 2018, 97, 083015. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- LIGO Scientific and Virgo Collaborations. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Sakai, T.; Mori, J.; Buchmann, A.; Shimizu, K.; Yazaki, K. The interaction between H-dibaryons. Nucl. Phys. 1997, 625, 192–206. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Schaffner-Bielich, J. Neutron star constraints on the H dibaryon. Phys. Rev. 1998, 58, 1298–1305. [Google Scholar] [CrossRef]
- Lai, X.Y.; Gao, C.Y.; Xu, R.X. H-cluster stars. Mon. Not. R. Astron. Soc. 2013, 431, 3282–3290. [Google Scholar] [CrossRef]
- Xu, R.X. Solid Quark Stars? Astrophys. J. 2003, 596, L59. [Google Scholar] [CrossRef]
- Wang, W.; Lu, J.; Tong, H.; Ge, M.; Li, Z.; Men, Y.; Xu, R. The Optical/UV Excess of X-Ray-dim Isolated Neutron Stars. I. Bremsstrahlung Emission from a Strangeon Star Atmosphere. Astrophys. J. 2017, 837, 81. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Blaschke, D.; Typel, S. Mixed phase within the multi-polytrope approach to high-mass twins. Astron. Nachr. 2017, 338, 1048. [Google Scholar] [CrossRef]
- Xia, C.-J.; Maruyama, T.; Yasutake, N.; Tatsumi, T.; Shen, H.; Togashi, H. Systematic study on the quark-hadron mixed phase in compact stars. Phys. Rev. 2020, 102, 023031. [Google Scholar] [CrossRef]
- Alford, M.G.; Han, S.; Reddy, S. Strangelet dwarfs. J. Phys. 2012, 39, 065201. [Google Scholar] [CrossRef]
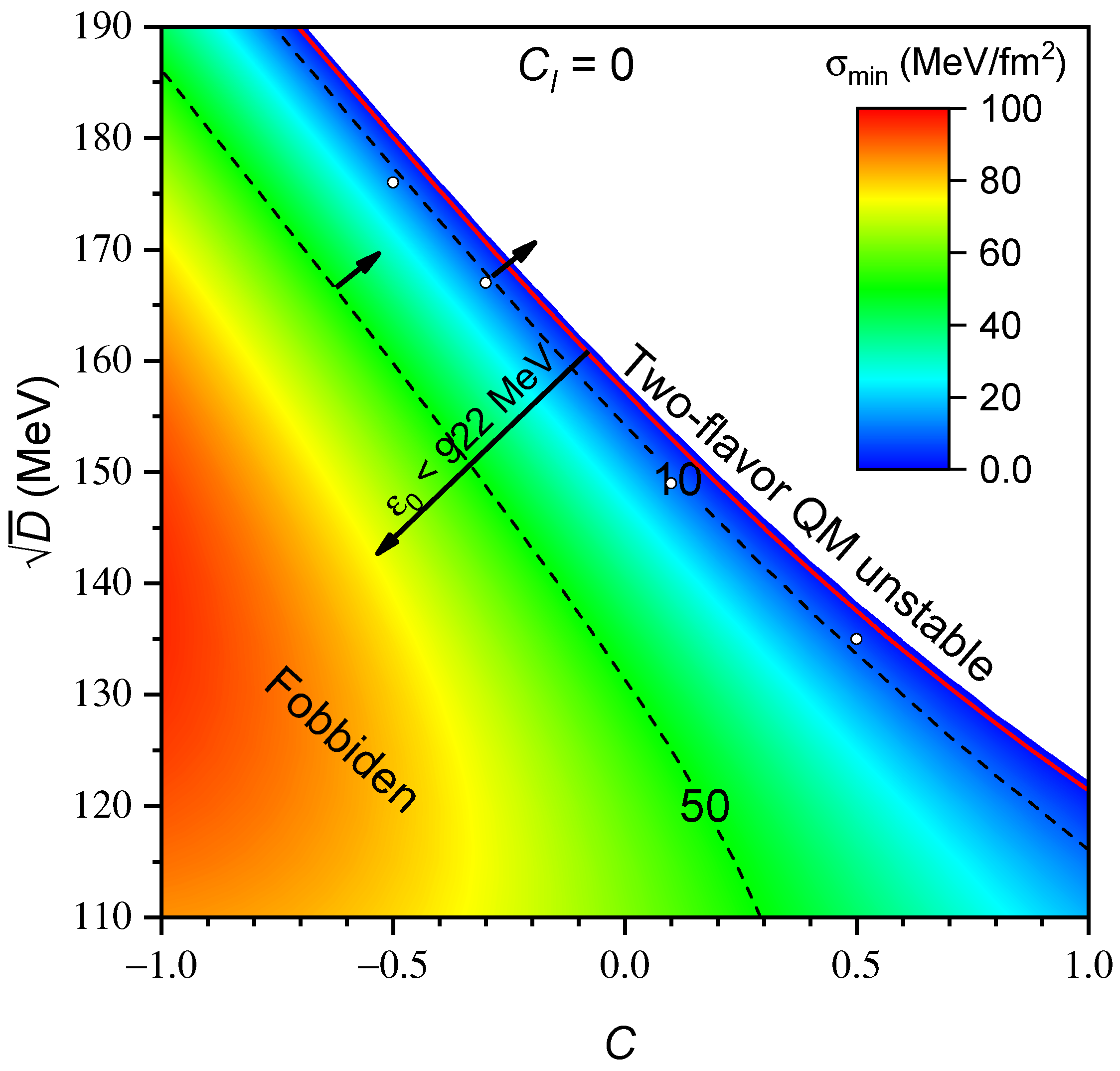
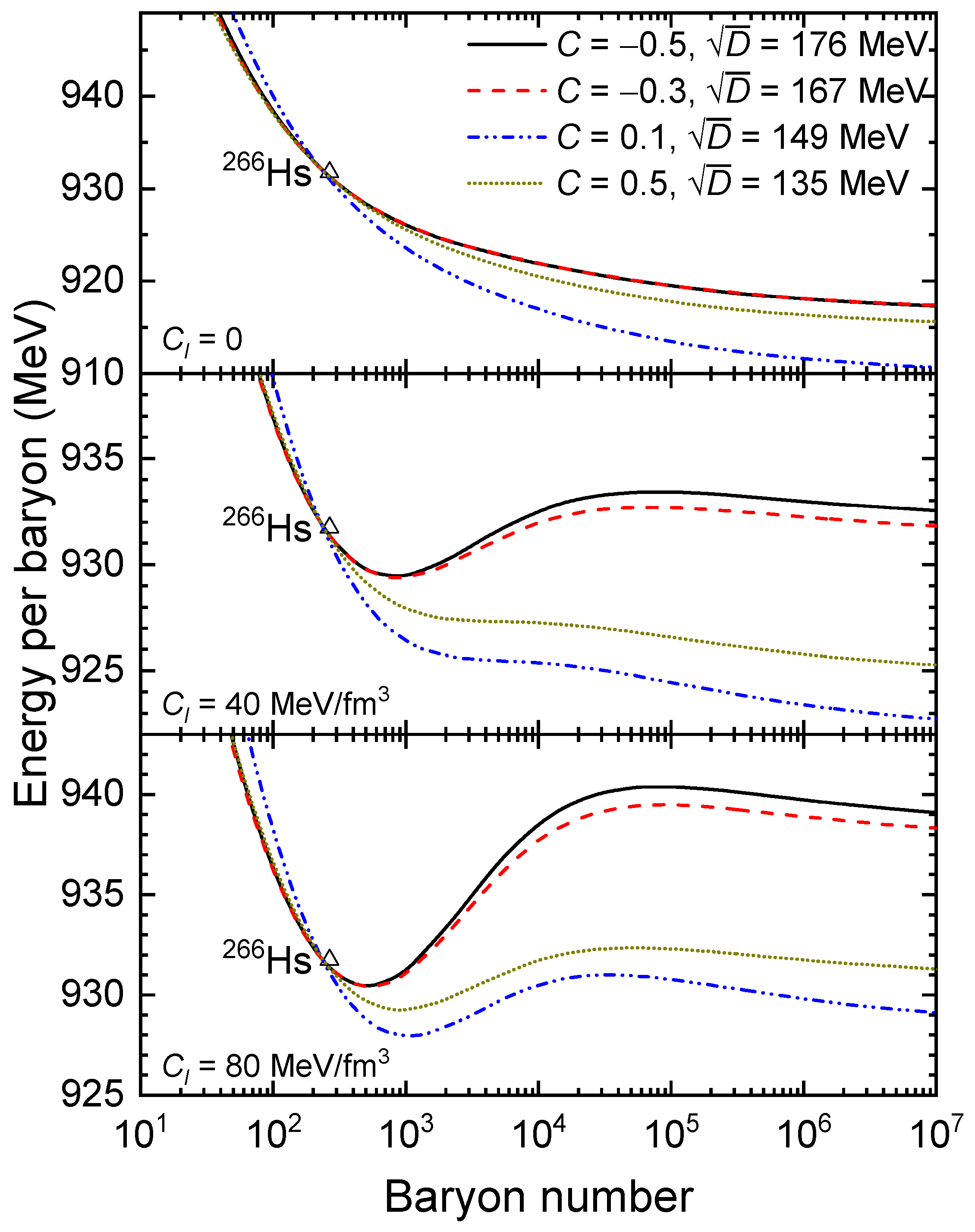
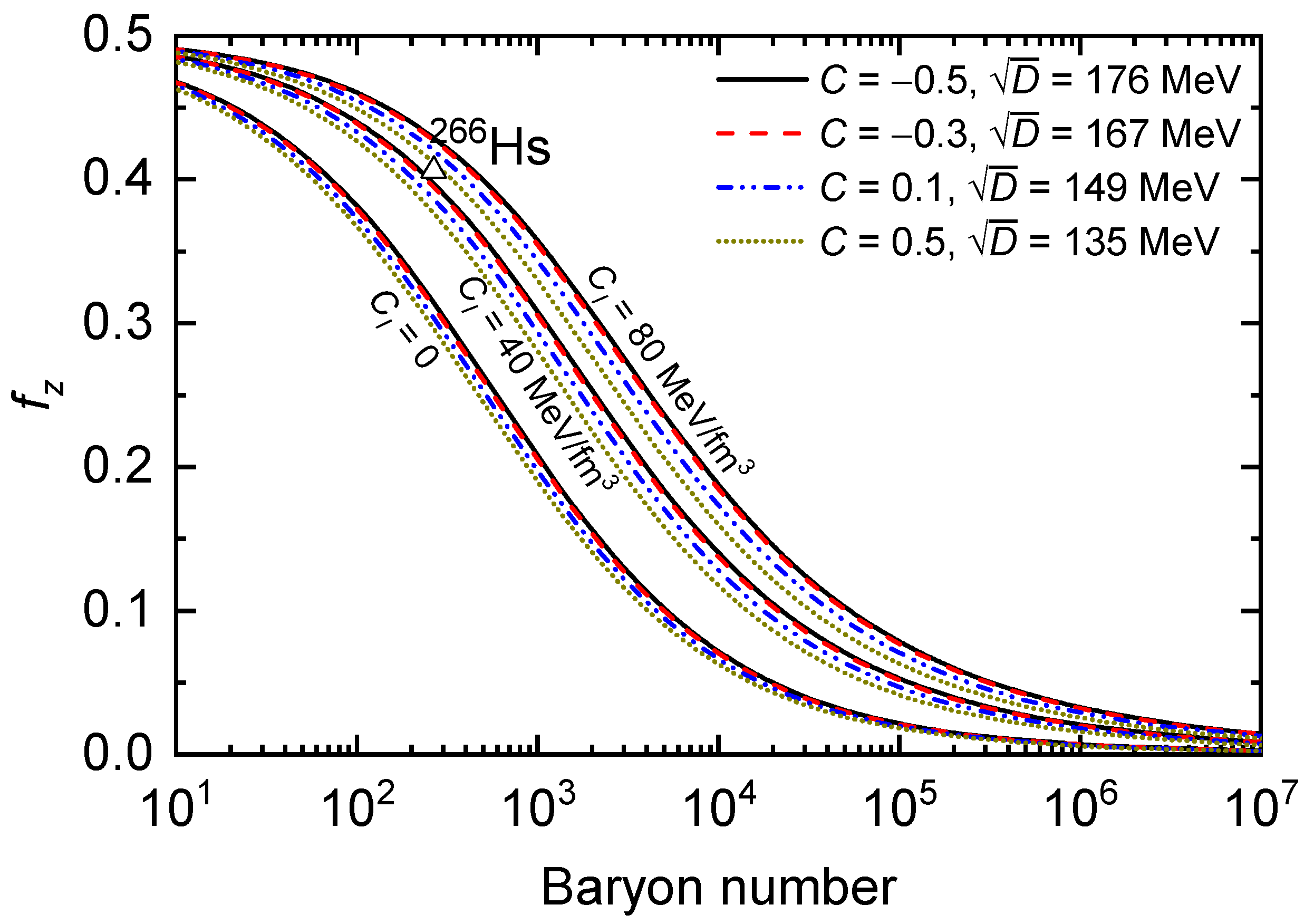
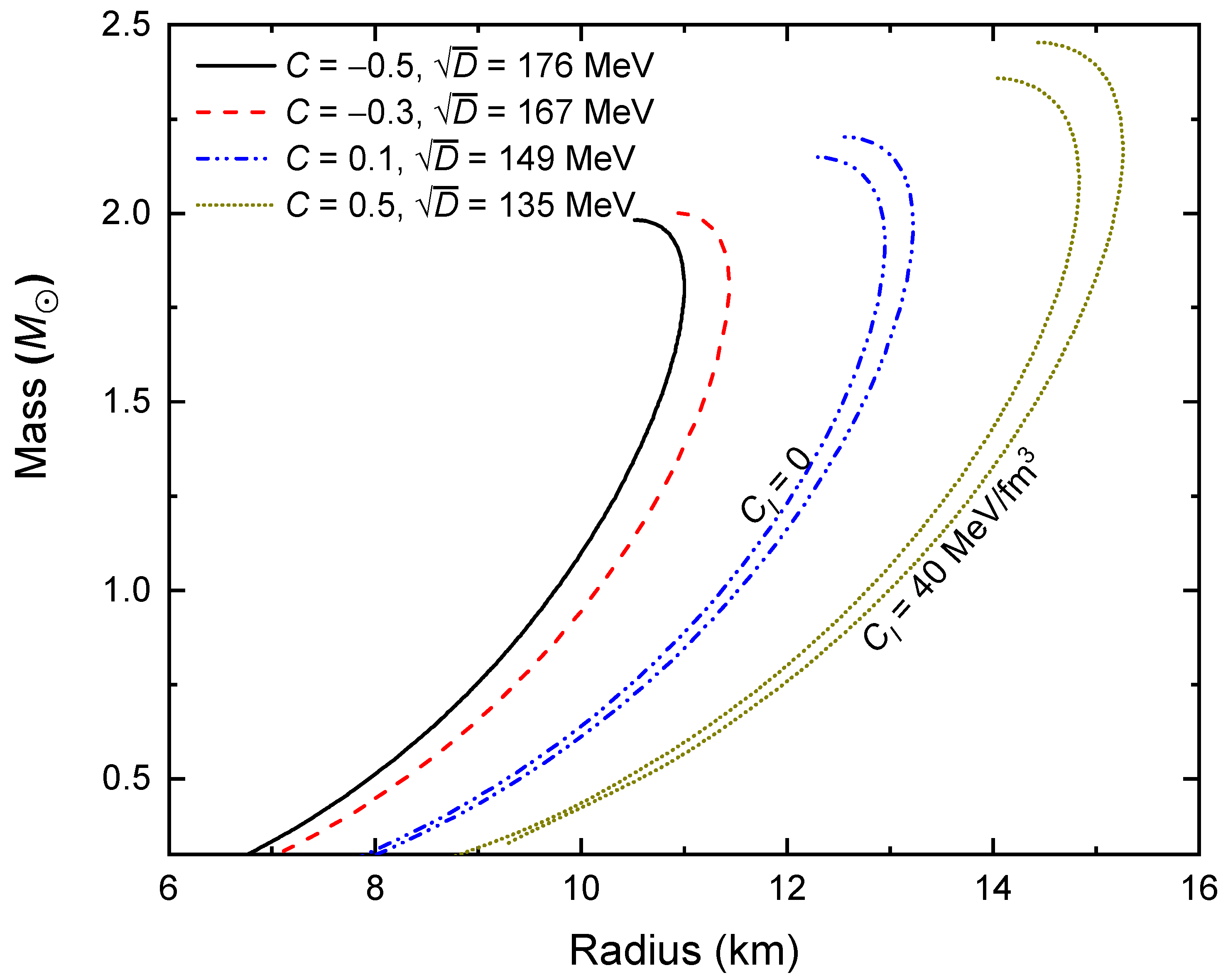
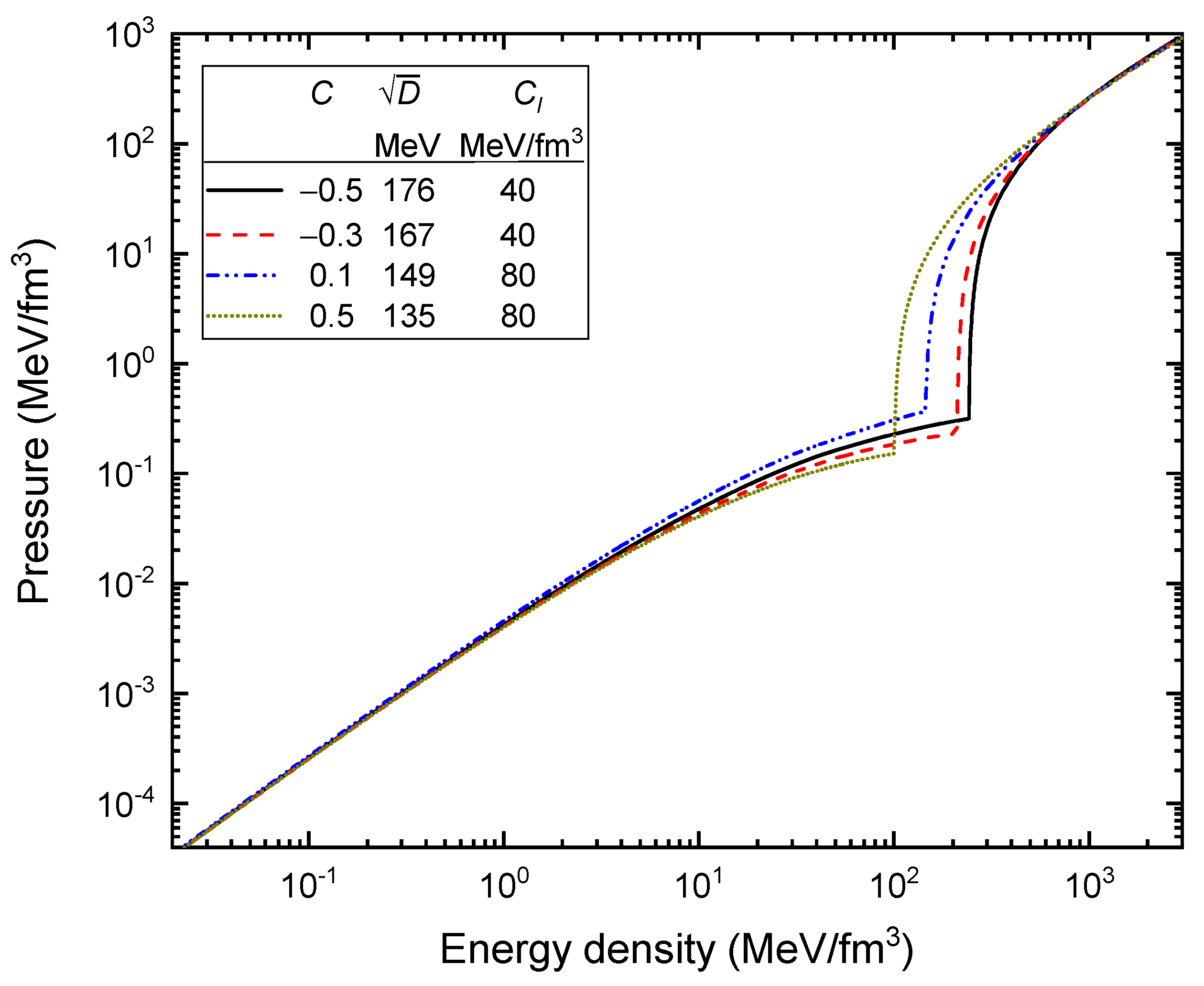
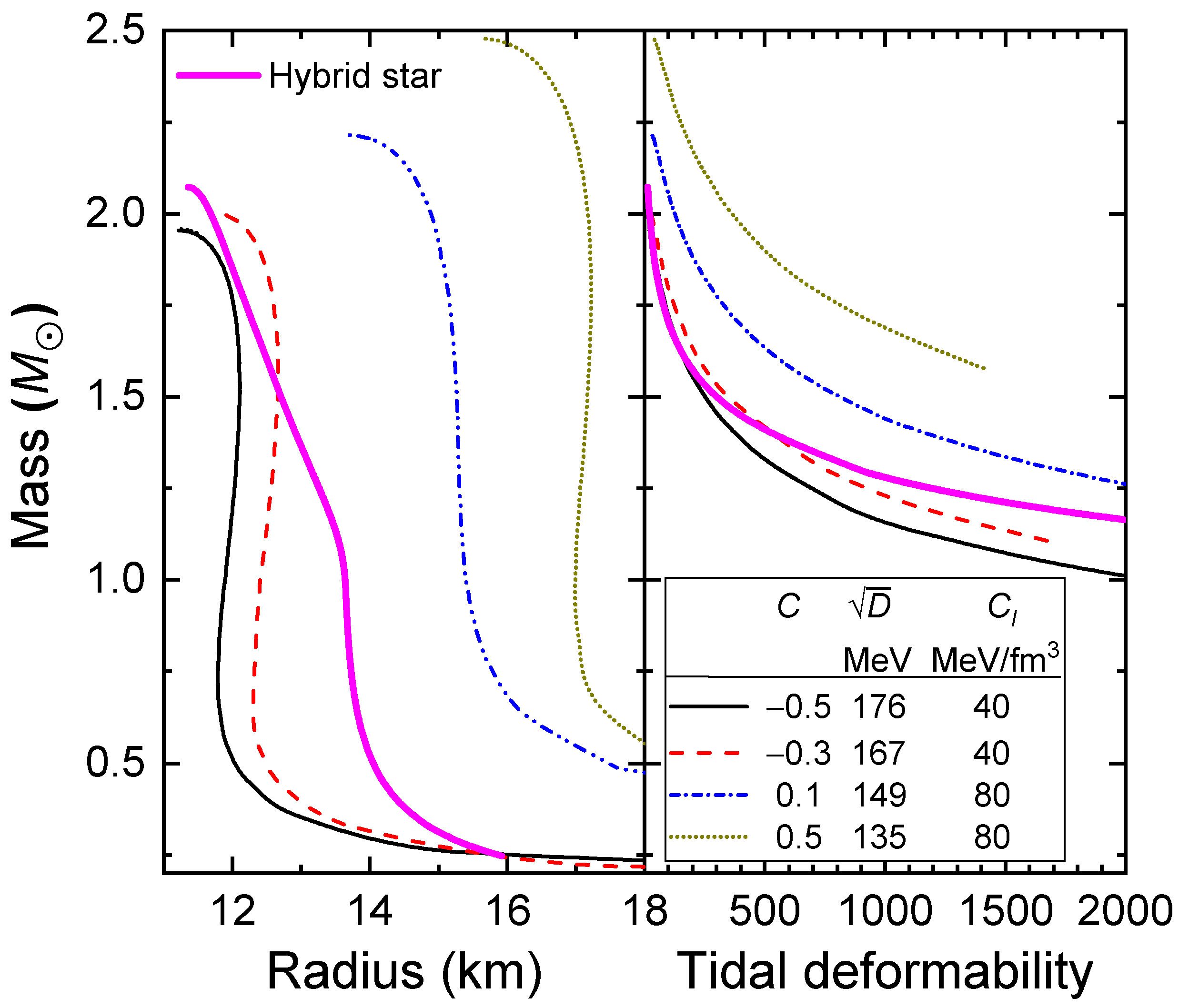
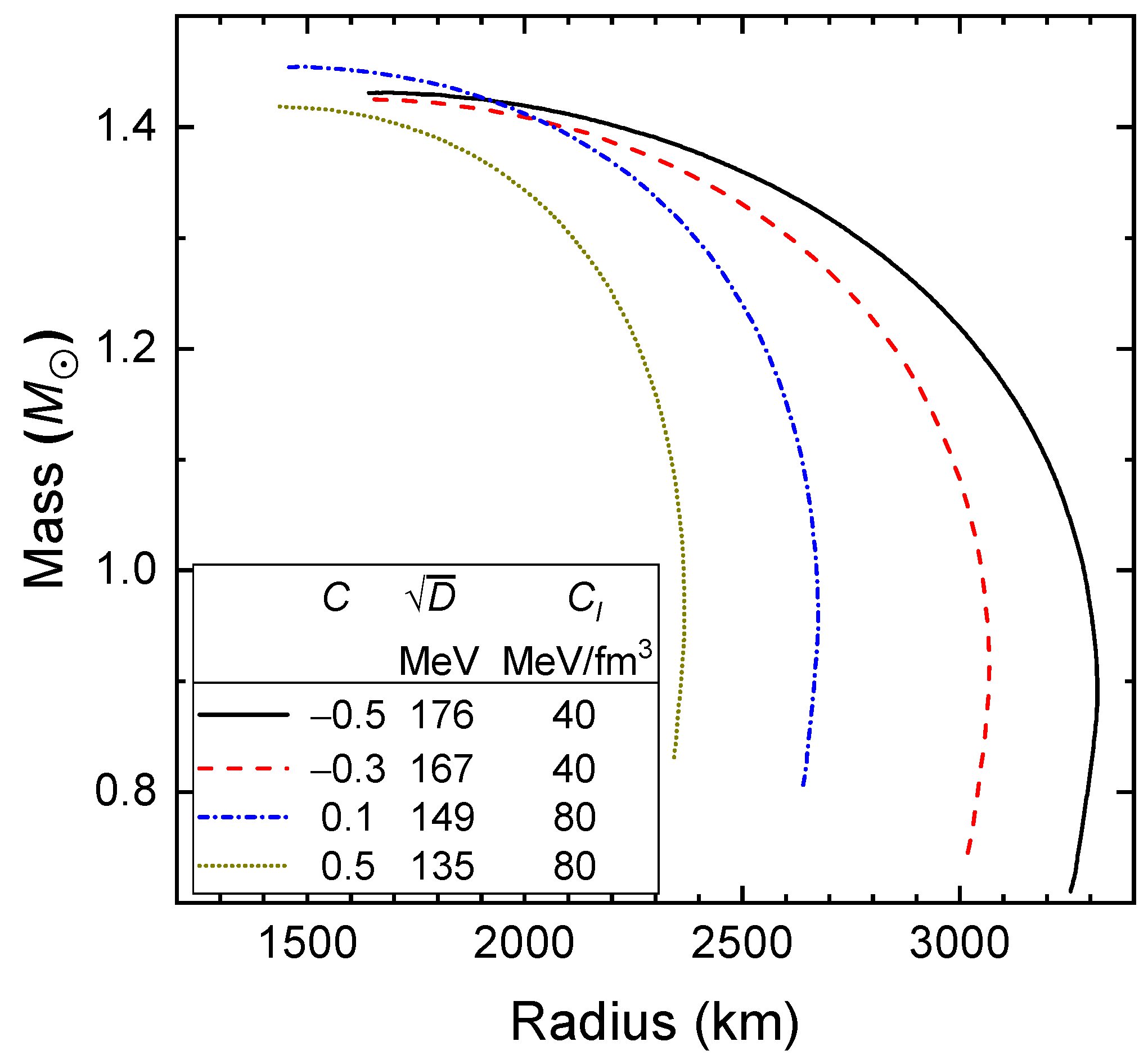
| C | ||||||||
|---|---|---|---|---|---|---|---|---|
| MeV | MeV/fm | fm | MeV | MeV | MeV | MeV/fm | MeV/fm | |
| 176 | 0 | 0.275 | 900.9 | 2571.5 | 16.0 | 14.0 | 5.03 | |
| 40 | 36.5 | 13.1 | 14.5 | |||||
| 80 | 57.5 | 12.8 | 24.2 | |||||
| 167 | 0 | 0.241 | 902.0 | 2306.4 | 15.0 | 12.4 | 4.24 | |
| 40 | 34.1 | 11.7 | 12.1 | |||||
| 80 | 53.5 | 11.4 | 20.1 | |||||
| 0.1 | 149 | 0 | 0.172 | 897.4 | 1942.0 | 12.6 | 12.1 | 2.77 |
| 40 | 27.8 | 11.6 | 7.58 | |||||
| 80 | 43.1 | 11.4 | 12.5 | |||||
| 0.5 | 135 | 0 | 0.120 | 904.6 | 1786.3 | 10.4 | 7.40 | 1.77 |
| 40 | 22.0 | 7.03 | 4.65 | |||||
| 80 | 33.5 | 6.87 | 7.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Hu, J.; Xia, C.-J.; Xu, J.-F.; Peng, G.-X.; Xu, R.-X. Stable Up-Down Quark Matter Nuggets, Quark Star Crusts, and a New Family of White Dwarfs. Galaxies 2021, 9, 70. https://doi.org/10.3390/galaxies9040070
Wang L, Hu J, Xia C-J, Xu J-F, Peng G-X, Xu R-X. Stable Up-Down Quark Matter Nuggets, Quark Star Crusts, and a New Family of White Dwarfs. Galaxies. 2021; 9(4):70. https://doi.org/10.3390/galaxies9040070
Chicago/Turabian StyleWang, Lang, Jian Hu, Cheng-Jun Xia, Jian-Feng Xu, Guang-Xiong Peng, and Ren-Xin Xu. 2021. "Stable Up-Down Quark Matter Nuggets, Quark Star Crusts, and a New Family of White Dwarfs" Galaxies 9, no. 4: 70. https://doi.org/10.3390/galaxies9040070
APA StyleWang, L., Hu, J., Xia, C.-J., Xu, J.-F., Peng, G.-X., & Xu, R.-X. (2021). Stable Up-Down Quark Matter Nuggets, Quark Star Crusts, and a New Family of White Dwarfs. Galaxies, 9(4), 70. https://doi.org/10.3390/galaxies9040070






