Abstract
Gamma-ray bursts (GRBs) are the most luminous explosions in the Universe and are powered by ultra-relativistic jets. Their prompt -ray emission briefly outshines the rest of the -ray sky, making them detectable from cosmological distances. A burst is followed by, and sometimes partially overlaps with, a similarly energetic but very broadband and longer-lasting afterglow emission. While most GRBs are detected below a few MeV, over 100 have been detected at high (≳0.1 GeV) energies, and several have now been observed up to tens of GeV with the Fermi Large Area Telescope (LAT). A new electromagnetic window in the very-high-energy (VHE) domain (≳0.1 TeV) was recently opened with the detection of an afterglow emission in the –TeV energy band by ground-based imaging atmospheric Cherenkov telescopes. The emission mechanism for the VHE spectral component is not fully understood, and its detection offers important constraints for GRB physics. This review provides a brief overview of the different leptonic and hadronic mechanisms capable of producing a VHE emission in GRBs. The same mechanisms possibly give rise to the high-energy spectral component seen during the prompt emission of many Fermi-LAT GRBs. Possible origins of its delayed onset and long duration well into the afterglow phase, with implications for the emission region and relativistic collisionless shock physics, are discussed. Key results for using GRBs as ideal probes for constraining models of extra-galactic background light and intergalactic magnetic fields, as well as for testing Lorentz invariance violation, are presented.
1. Introduction
Gamma-ray bursts (GRBs) are cataclysmic events that occur at cosmological distances. (See, e.g., [1,2,3,4] for a comprehensive review.) They are the most electromagnetically luminous transient phenomena in the Universe. GRBs involve the explosive release of energy over a short timescale, producing a burst of -rays with isotropic-equivalent luminosity of ∼10–10 . Their emission is powered by ultrarelativistic (with bulk Lorentz factors ) bipolar collimated outflows driven by a compact object central engine. The identity of the central engine, which could be either a black hole (BH) or a millisecond magnetar, is not entirely clear as the highly variable emission is produced far away from it at a radial distance of – cm. The most luminous phase of the burst, referred to as the “prompt” phase, is short-lived with a bimodal duration distribution separated at s, where the short and long GRBs have typical observed durations of s and s, respectively [5]. These two classes of GRBs are also distinct spectrally, with the short GRBs being spectrally harder compared to the long GRBs that produce softer -rays. The long-soft GRBs are associated with the core collapse of massive (≳(20–30)) Wolf–Rayet stars [6,7], whereas (at least some) short-hard GRBs originate in compact object mergers of two neutron stars (NSs) or a NS-BH binary [8,9]. The first-ever detection of a short GRB coincident with gravitational waves (GWs) from the merger of two NSs came from GW 170817/GRB 170817A [10,11].
Many details of the prompt GRB emission, in particular, the energy dissipation process, the exact radiation mechanism, and the transfer of radiation in the highly dynamical flow remain poorly understood. All of these different processes combine to produce a non-thermal spectrum that is often well-described by the Band-function [12], an empirical fit to the spectrum featuring a smoothly broken power law. This break manifests as a peak in the spectrum, at a mean photon energy keV, with the asymptotic power-law photon indices below and above the peak energy having mean values of and , respectively [13,14].
While most of the energy in the prompt GRB comes out at , the featureless power-law spectrum above this energy extends beyond MeV in most GRBs detected by the Fermi-Large Area Telescope (LAT) [15], with a high-energy spectral cutoff seen in only about 20% of the cases, e.g., [16], which are most likely caused by intrinsic opacity to pair production [16,17]. In rare cases, the prompt GRB spectrum shows an additional hard spectral component that extends beyond ∼10 GeV, as seen by the Fermi-LAT, and well into very high energies (≳0.1 TeV), as seen by ground-based atmospheric Cherenkov telescopes, e.g., MAGIC and H.E.S.S. (See, e.g., [18,19] for a review.) This high-energy (HE; ≳100 MeV) emission overlaps with the sub-MeV prompt GRB, and both the HE and very- high-energy (VHE) emissions persist throughout the afterglow phase—the much longer-lasting and broadband (X-rays/Optical/Radio) emission that follows the short-lived prompt phase. The spectral and temporal properties of the HE emission provide a glimpse into the global energetics of the bursts as well as yield important constraints on GRB physics that cannot be obtained from the sub-MeV emission alone.
The main objective of this review is to provide a concise summary of the widely discussed radiation mechanisms that may explain the spectral and temporal properties of the VHE and/or HE emission in GRBs. We first discuss several HE/VHE radiation mechanisms in Section 2 and provide some of the fundamental quantities that can be calculated and compared to observations. This is followed by a discussion of the delayed HE emission, additional prompt GRB spectral component at high energies, and long-lived HE emission seen by Fermi-LAT as well as popular theoretical explanations offered for it, along with implications for the bulk Lorentz factor , in Section 3. Next, Section 4 presents an overview of the HE afterglow seen in the exceptionally bright GRB 130427A, along with several important implications for the radiation mechanism and relativistic shock acceleration physics. The recent detection of a ∼TeV afterglow emission by MAGIC and H.E.S.S in only a few GRBs and key implications of such a detection for GRB physics are discussed in Section 5. The use of HE photons from distant GRBs as a probe of extra-galactic background light (EBL), inter-galactic magnetic field, and Lorentz invariance violation are the topics of discussion in Section 6. Finally, in Section 7, we end this review with important outstanding questions in GRB physics and present closing remarks in Section 8.
2. Relevant High-Energy or Very-High-Energy Emission Mechanisms
There are several HE/VHE -ray emission mechanisms that operate wherever particles (leptons and hadrons) are accelerated to or generated with high Lorentz factors (LFs). In GRBs, the emission regions can be either internal to the relativistic outflow, e.g., at internal shocks or magnetic reconnection sites, or external to it, e.g., in the shocked external medium behind the external forward (afterglow) shock, or even at larger distances from the outflow. Below, we review some of the widely discussed processes that are capable of producing HE to VHE -ray photons. Other more detailed reviews on this topic are [4,20].
2.1. Electron Synchrotron Emission
Relativistic electrons with LFs cool by emitting synchrotron photons when gyrating around magnetic field lines with comoving magnetic field strength (all primed quantities are in the comoving/fluid rest frame). At collisionless shocks (internal or external), a fraction of the electrons are accelerated into a non-thermal power-law energy distribution, for and , that holds a fraction of the post-shock internal energy density, and arises due to Fermi acceleration [21,22,23]. The minimal LF of this distribution is
where is the relative LF between the regions upstream and downstream of the shock front. The resulting (observed) optically thin synchrotron spectrum in this case comprises multiple power-law segments joined smoothly at characteristic break energies [24,25] (shown here for fiducial parameters relevant for prompt emission for which and ),
where with h being the Planck’s constant, is the Thomson cross section, e is the elementary charge, is the electron rest mass, and c is the speed of light. The energy corresponds to the characteristic synchrotron frequency () of minimal energy electrons with LF , and the cooling break energy corresponds to the cooling frequency () of electrons with LF that are cooling at the dynamical time, such that their synchrotron cooling time, , equals the dynamical time, . For some model parameters, , which is obviously unphysical, but instead represents very rapid cooling of particles to non-relativistic velocities in less than the dynamical time [26]. As a result, relativistically hot particles only occupy a thin layer behind the shock which is a fraction of the comoving width of the ejecta shell, where the electrons are cold in the remaining majority of the shell. In the above equations, we have expressed the comoving magnetic field in terms of the more useful quantities, using the fact that the total isotropic-equivalent power of the outflow can be written in terms of and , the kinetic energy and magnetic field powers, respectively. So that,
, where is the fraction of total power carried by the magnetic field with being the outflow magnetization, and is the isotropic-equivalent -ray luminosity which is a fraction of the total power. This yields the comoving B-field strength G with for an ultra-relativistic flow. The ordering of the break energies depends on whether the electrons are in the fast cooling regime, for which , or the slow cooling regime, with . This relative ordering also decides the values of the spectral indices of the flux density for the different power law segments,
The emission in the power-law segment above the spectral peak energy () can only extend up to the maximum synchrotron energy . This energy depends on the efficiency of the acceleration process while the charged particles (electrons or protons) lose energy to synchrotron cooling. The typical timescale over which particles, say the electrons with LF , are accelerated as they are scattered across the relativistic shock is at best the Larmor time , i.e., . Their radiative cooling timescale is at most as any additional radiative cooling besides synchrotron (e.g., inverse-Compton) would only shorten , i.e., with . Equating the acceleration and radiative cooling timescales, , yields the maximum LF attained by the electrons, where . These electrons then radiate at the characteristic synchrotron energy, e.g., [27,28,29,30,31]
where is the fine structure constant, and is a factor expected to be of order unity that depends mainly on the details of particle acceleration and diffusion in the shock downstream and upstream.
It is therefore challenging to explain VHE photons as arising from synchrotron emission by electrons. In addition, depending on the compactness of the emission region, emission can be suppressed due to -pair production via -annihilation (, e.g., [32,33,34,35,36,37]. This poses more of a problem for the prompt emission and less so for the afterglow. Alternatively, the VHE photons can be explained by proton synchrotron emission (see Section 2.2) or synchrotron self-compton (SSC; see Section 2.3) emission by the same electron population that produced the seed synchrotron radiation.
2.2. Proton Synchrotron Emission
High-energy protons that are accelerated at shocks (like the electrons) to LFs can also cool by emitting synchrotron photons in magnetized regions [38,39]. However, the emitted power per particle ( for ) is much smaller where it is suppressed by a factor with respect to that for electrons when (and suppressed by the square of this factor for ) since the Thomson scattering cross section for protons is much smaller, , than that of electrons. To compensate for this suppression, the magnetic field in the emission region must be larger than that obtained in a leptonic synchrotron scenario, so much so that the magnetic field energy would hold a good fraction of the total energy [40]. The characteristic synchrotron energy of minimal energy protons is (assuming the electrons and protons hold fractions and of the post-shock internal energy, and that fractions and of the electrons and protons, respectively, form a power-law energy distribution), and the cooling break energy is , with the corresponding LF . As a result, the maximum LF of protons accelerated at the same shock as electrons is , which yields TeV, e.g., [39].
Recent suggestions replacing electron with proton synchrotron emisson have been made to explain the apparent low-energy (below the spectral peak) spectral breaks that are difficult to explain with electron synchrotron emission, e.g., [41]. However, knowing that protons are inefficient at radiating away their internal (or random-motion) energy as compared to electrons, the significant reduction in radiative efficiency must be compensated by having a much larger total energy budget, a requirement that may be too demanding, e.g., [42,43]. Moreover, in such a scenario it would also be very difficult to suppress the much more efficient radiation from the electrons for it to not over-power that from the protons.
2.3. Synchrotron Self-Compton (SSC)
A distribution of relativistic electrons can inverse-Compton scatter some of the same synchrotron photons that it produced, leading to a synchrotron self-Compton emission. When the energy of the incoming synchrotron photon in the rest frame of the scattering electron is much smaller than the electron’s rest energy, , then the scattering occurs in the Thomson regime (where the electron’s recoil can be neglected) and is called elastic or coherent. The scattered photon emerges with an energy of . The additional cooling of particles due to inverse-Compton scattering introduces a factor of in the cooling time, such that . Here is the Compton-y parameter given by the ratio of the power radiated in the IC component to that in the synchrotron component.
In the Thomson regime, for isotropic emission, which yields (where ) that is independent of , where is the energy density of the seed synchrotron emission that is IC scattered by the electrons. If this seed radiation arises from shock-heated electrons, , e.g., [44], where is the fraction of electron energy radiated away in synchrotron and IC photons, and is the downstream velocity relative to the shock front (and is order unity for a relativistic shock). With and , where and are the fractions of the total internal energy behind the shock () that goes into accelerating electrons and generating the magnetic fields, the expression for Y simplifies to, e.g., [26,44,45,46,47],
When , then , and Compton cooling is negligible. Otherwise, the extra cooling also means that the maximum particle LF is reduced, , and likewise . The characteristic spectral break energies of the SSC spectrum corresponding to that of the synchrotron spectrum are
where , and . The maximum energy of an inverse-Compton scattered photon is , and since for a power-law electron distribution,
When the energy of the incoming photon in the rest frame of the scattering electron exceeds the rest mass energy of the electron, , the recoil suffered by the electron can no longer be ignored, and quantum corrections need to be taken into account. The scattering no longer occurs in the Thomson regime, and the correct scattering cross section in this case is the Klien–Nishina cross section (), which depends on the energy of the incoming photon [48]. For incoming photon energy , the scattering cross section is highly suppressed, with . Moreover, the electron recoil implies that in this limit. Therefore, IC scattering can efficiently cool an electron with LF only for seed synchrotron photons with energies . Thus, accounting of Klein–Nishina effects causes the Compton-Y parameter of each electron to depend on its LF, . This may cause interesting modifications of the spectrum (in both the synchrotron and SSC components) when [47]. Notice that since may vary between different electrons, it is natural to define the global Compton-Y parameter by , which is the mean value of weighted by the synchrotron emissivity. Therefore, the SSC flux is suppressed above the photon energy
where ( are the energies where the synchrotron spectrum peaks in the fast (slow) cooling scenario. Likewise, the spectral peak of the SSC spectrum occurs at in the fast (slow) cooling case. The ratio of the spectral peak flux is given by . If , second order SSC scatterings also occur in the Thomson regime, and if is not much smaller than unity, a third spectral peak can appear, e.g., [49,50].
2.4. External Inverse-Compton
External inverse-Compton emission (EIC) arises when the softer seed photons are inverse-Compton scattered to high energies by relativistic electrons in a location physically distinct from where the seed photons were produced. This can occur in several different ways, e.g., (i) seed photons produced in internal dissipation and upscattered by forward-shock or reverse-shock-heated electrons [51,52,53,54,55,56,57,58], (ii) seed photons produced in the reverse shock and upscattered by forward shock-heated-electrons [59,60], (iii) seed photons produced in the forward shock and upscattered by reverse shock-heated electrons [59,60], (iv) externally produced ambient seed photons, e.g., from the accretion disk [61] or the massive star progenitor’s envelope [62], are upscattered by cold electrons in the relativistic outflow in a process also referred to as bulk Compton scattering or Compton drag, (v) photospheric seed photons in the relativistic baryon-poor jet upscattered by the shocked electrons in the shock transition layer between the baryon-poor jet and baryon-loaded envelope [63], and (vi) seed photons provided by the cocoon [64], after it breaks out of the dynamical ejecta in a NS-NS merger, or that from the AGN disk [65], if the merger occurs inside the disk of an AGN, that are IC upscattered to VHE -rays by electrons energized in the dissipation of prolonged jets powered by late-time central engine activity. As an illustrative example, below we summarize the important points for the simplest case in scenario (i) and provide estimates of the maximum photon energy obtained in this process when the X-ray flare emission overlaps with the external forward shock electrons [53].
IC Scattering of X-ray Flare Photons by External Forward Shock Electrons
As the relativistic ejecta plows through the circumburst medium (CBM), with density where R is the radial distance from the central engine, it is slowed down. In the process, two shocks are formed where the shocked regions are separated by a contact discontinuity that has a bulk LF . The forward shock runs ahead of the contact discontinuity with bulk LF , sweeping up the CBM and shock-heating it. The reverse shock moves backward (in the rest frame of the contact discontinuity) into the ejecta, decelerating and shock-heating it. In the following, we adopt the thin-shell case for which the reverse shock is Newtonian (or mildly relativistic). Alternatively, the reverse shock becomes relativistic before crossing the ejecta shell in the thick-shell case, which we will not discuss here (but see Sari and Piran [66]). Most of the isotropic-equivalent kinetic energy of the ejecta () is transferred to the kinetic and internal energy of the shock-heated swept up CBM behind the forward shock at the deceleration radius,
where for (ISM) and for (wind medium; corresponds to a mass loss rate of with a wind speed of ), and is the initial LF of the relativistic ejecta at which it coasts for . For , the blast wave dynamics become self-similar, and the bulk LF of the shocked material decays as a power law in R [67]. The transition for from the coasting to the self-similar power-law phase is smooth in general, but here we use the broken power-law approximation in Equation (11) for simplicity.
The LF of minimal energy power-law electrons accelerated at collisionless shocks is given by in Equation (1). For electrons accelerated at the forward shock , in which case the minimal particle LF for is given by (for )
at the apparent time s. Here the factor represents a one-zone approximation and is taken here to be , which is appropriate along the LoS (corresponding to the radial time ) if is taken to be that of the shock front, . If instead, it is taken to be that of the matter just behind the shock, then along the LoS. Since there is significant contribution to the observed flux up to angles from the LoS, one should also account for the angular time along the equal arrival time surface from the shock front. Finally, the exact value of also depends on the effective thickness of the radiating shell [24,68,69] and any value is only as good as the one-zone approximation it represents.
If the spectral peak (of ) energy of the X-ray flare is in the observer frame, its energy in the comoving frame of the blast wave is for X-ray flare photons that are tightly beamed in the radial direction and catch up with the electrons behind the shock with (almost) radial velocity vectors. When the forward-shock electrons are in the fast cooling regime, the peak of the IC spectral component corresponds (without accounting for Klein–Nishina effects) to upscattering of ∼ seed photons (flare photons considered monoenergetic here for simplicity) by electrons, e.g., [53],
The spectrum of this GeV flash is expected to have power-law spectral indices of approximately and below and above the energy . Klein–Nishina effects start to become important for electrons with LF () and (), corresponding to , and depending on the ratio of electron LFs,
the Klein–Nishina suppression of the IC scattered spectrum can occur at energies below or above for or , respectively.
2.5. Pair Echoes
High-energy photons from cosmological sources are absorbed en route by their interaction with the much softer diffuse extragalactic background light (EBL), producing -pairs via -annihilation [70,71,72,73,74,75,76]. The cross section () for the annihilation of two photons [77,78], with energies and colliding with a mutual angle of between their momentum vectors, depends on the (non-dimensional) interaction energy which must be larger than unity. For photons traversing through an isotropic radiation bath for head-on collisions with , the cross section attains its peak value of slightly above threshold at .
VHE primary -ray photons with energy E from GRBs dominantly annihilate with the much softer EBL photons having energy
over the mean free path length of
The produced and will share the energy of the primary -ray photon equally and have a typical LF . These pairs will then IC scatter the more numerous and softer CMB photons, with temperature K and mean energy eV, to observed energies
This secondary HE emission is dubbed “Pair Echoes”, and it arrives with a characteristic time delay with respect to the primary HE emission due to the pairs being deflected by the weak intergalactic magnetic field (IGMF) present in cosmic voids that are much less dense in comparison to filaments and clusters (much higher and highly structured magnetic fields are expected in cosmic filaments (– G [79]) and galaxy clusters (– G [80]), where the secondary pairs are expected to produce synchrotron pair echoes [81] with .). The pairs IC cool over a characteristic distance
where is the CMB radiation energy density, and a is the radiation constant. Assuming that the pair front expands spherically over a distance with particles at a typical LF , the radial delay suffered by the secondary HE emission with respect to the primary one is of the order for when . The pair echo will also be temporally smeared out but over a much larger angular time , where and , due to light travel time effects over the angular size of the emission region centered at the observer’s line-of-sight. Another angular delay is caused by the deflections of the pairs in the intergalactic magnetic field IGMF; ref. [82]. If the coherence length scale of the IGMF is , then the root mean square angular deflection is , where is an order unity factor that depends on the spectrum of the magnetic field as a function of the coherence length [74,75], and is the Larmor radius. The corresponding angular time over which the pair echo will be smeared is . For extremely energetic pairs with , the two timescales, and , can become smaller than , the duration of the primary VHE emission (which could be either prompt and/or afterglow). In addition, for the mean free path for VHE -ray photons () can become smaller than the cooling distance () of the produced pairs, in which case and . Therefore, the correct timescale over which the pair echo signal will be smeared out is . In the top panel of Figure 1, we show the different timescales as a function of the particle Lorentz factor . Only at very large does the timescale dominate due to a sharp decline in caused by the sharp rise in the number density of target CMB photons for -rays with TeV.
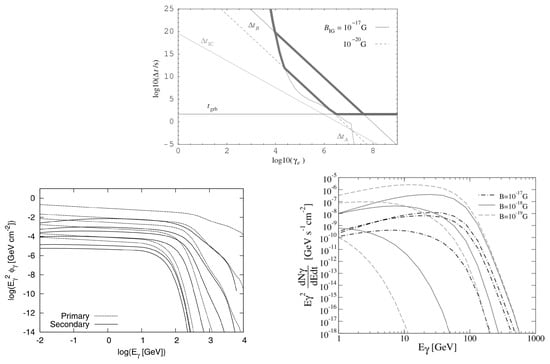
Figure 1.
(Top) Different timescales (thin solid lines) over which the pair echo signal can be temporally smeared, shown for VHE -ray photons produced during the prompt emission over a duration . Other timescales are the angular time due to IC cooling ( and deflection of the produced pairs by the IGMF (; shown for two different IGMF magnetic field strengths) and the angular time associated to the mean free path over which the VHE -ray photons produce pairs (). The thick solid line highlights the dominant timescale for a given particle Lorentz factor GeV. Figure from [71] (©AAS. Reproduced with permission.). (Bottom-left) The (observed) model primary and secondary (pair-echo) VHE -ray spectral fluences (, for flux density ) from GRBs at different redshifts (top to bottom): . The intrinsic primary spectrum is assumed to be a broken power-law: for and for , where is the synchrotron self-absorption break energy, is the peak photon energy and is the intrinsic high-energy cutoff. The intrinsic spectrum in the figure assumes , , keV, and TeV. Figure from [73] (©AAS. Reproduced with permission.). (Bottom-right) The observed pair-echo spectrum shown for different IGMF strengths (with coherence length scale pc) and at different times () for a source at a fixed redshift of . The primary prompt emission spectrum is assumed to be a power-law with photon index above the peak energy keV with a cut-off energy of TeV, where the prompt GRB has a duration of s and luminosity . Figure from [74] (©AAS. Reproduced with permission.).
In the bottom-left panel of Figure 1, we show example model fluence spectra of the primary and secondary (pair-echo) spectra that can be observed from GRBs at different redshifts. The maximum energy of the intrinsic GRB spectrum is assumed to be TeV; therefore, the maximum energy of the produced pairs is ∼5 TeV. As a result, the energies of IC scattered CMB photons can reach ∼100 GeV, but these photons may also get absorbed en route to us. Above ∼100 GeV, the contribution from IC upscatted CIB photons becomes important, producing an additional bump in the spectrum. The bottom-right panel shows the pair-echo spectrum at different apparent times and for different IGMF strengths from a source at a fixed redshift . For a given IGMF, the flux at high energies decays much more rapidly with time compared to the hard power-law at low energies. This is a result of shorter IC cooling times and shorter delay times for pairs with larger . Since weaker IGMFs have shorter times, the flux is higher initially but decays much faster in comparison to stronger fields that have longer times [74].
One of the main advantages (see Section 6 for pair echoes as probes of the IGMF) of detecting pair echoes is that it offers the only way to reconstruct the primary VHE emission from GRBs which would otherwise be attenuated due to VHE photons pair producing on EBL photons.
2.6. High-Energy -Rays from Pion Decay
Two HE photons are produced directly in the decay of a neutral pion , in which each photon escapes with an energy MeV in the rest frame of the pion that is moving with LF in the fluid frame. These photons are then detected with energy GeV. Neutral pions can be produced via the following collisional processes between protons (p), neutrons (n), and photons ():
The most important of the above hadronic energy-loss mechanisms is the photohadronic process, where a photon interacts with a proton, at a threshold photon energy of MeV in the rest frame of the proton, to produce a pion, e.g., [83]. When a typical -ray photon with energy interacts with a proton in the flow having LF , the scattering cross section for the resonance peaks when the energy of the photon in the proton’s rest frame is GeV [84], where and . This is equivalent to the proton having energy . If , it would yield a VHE -ray photon of energy
The above three collisional processes also produce charged pions ( and ), which then decay to muons that further decay to produce electrons and positrons that can then produce HE synchrotron photons. The most important for producing HE photons is again the resonance that also yields
where is the anti-muon and and are its neutrino and anti-neutrino, and is the electron neutrino. Approximately 20% of the proton’s energy goes into , which is further equally distributed between the pion’s decay products [85]. This produces a high-energy positron with LF that produces HE synchrotron photons of energy
The photo-hadronic process, if operating in GRBs, opens up prospects for detecting high-energy ( eV) neutrinos by km-scale ground-based detectors [85], e.g., IceCube [86]. The intrinsic ratio between muon and electron neutrinos at the source is expected to be 2:1 (with no neutrinos), but vacuum oscillations between the three neutrino flavors () may yield equal distributions at Earth. The intrinsic ratio at the source can be different from 1:2:0 when the neutrinos are produced inside a star, e.g., a jet that propagates inside a blue supergiant. In this case, resonant flavor oscillations in matter due to the Mikheyev–Smirnov–Wolfenstein effect will alter the intrinsic ratios at the source [87]; therefore, after vacuum oscillations, the ratios observed at Earth will also be different from 1:1:1. The intrinsic flavor ratios can further be modified at high energies due to electromagnetic and adiabatic energy losses of muons and pions [88] as well as due to matter oscillations [87,89] at the source. This would lead to energy-dependent, unequal flavor ratios measured at Earth.
Detection of neutrinos from GRBs can only happen for very bright GRBs with -ray fluences [90,91,92]. Thus, far neutrino searches by IceCube have come out empty, even in the case of very bright GRBs, e.g., 130427A [93], and deeper upper limits have offered strong constraints on GRB physics and neutrino production therein [94,95].
Apart from the -pairs produced in the photo-hadronic cascades, additional secondary -pairs result from that can have important effects on both the low and high-energy parts of the spectrum [96,97]. Such pair cascades can also be important in other hadronic scenarios, namely proton synchrotron emission as discussed in Section 2.2. The injected pair spectrum in this case has which yields a relatively flat synchrotron spectrum. At low energies, i.e., below the peak of the sub-MeV Band component, the synchrotron emission from secondary pairs might dominate and make the spectrum too soft when compared with observations (see bottom-left panel of Figure 4). However, if the secondary pairs are stochastically accelerated (or heated) by MHD/plasma turbulence, then a low-energy photon index of that matches observations can be produced [98]. Above the Band-component peak energy, the spectrum is modified due to IC scattered emission by the secondary pairs.
2.7. High-Energy -Rays from the Bethe–Heitler Process
The Bethe–Heitler process is a photo-hadronic interaction in which the -pairs are produced directly,
The differential cross section for this process [99,100] strongly depends on the angle between the incoming photon and the outgoing in the proton’s rest frame. It peaks sharply near , where ( is the LF of the electron (positron) in the proton’s rest frame. When the proton’s LF in the jet comoving frame, , is much larger than that of the produced pairs in the proton’s rest frame, with , then the pairs are produced with LF in the jet comoving frame of , where on average [101]. For typical prompt emission spectral peak energies of , the Bethe–Heitler process is less efficient (by a factor of ) in producing pairs compared to the resonance when the LF of produced pairs is . However, for , it can be much more efficient, while for its efficiency depends on the spectral index of the prompt emission [101]. The high-energy pairs produced in the process can then give rise to HE to VHE photons via synchrotron or IC emission.
3. GRB Prompt HE Emission—Observations vs. Theory
HE emission in the energy range of (0.1–100) GeV has been detected by the Fermi-LAT in more than 170 GRBs [15]. Prior to Fermi, emission in this energy range (but below ∼20 GeV) was also detected by the Energetic Gamma Ray Experiment Telescope (EGRET) aboard the now defunct Compton Gamma-Ray Observatory (CGRO) from a handful of GRBs [102,103,104,105]. In most of the Fermi-LAT GRBs and that detected by EGRET, the broadband prompt emission spectrum is described by a single Band-like spectral component, generally peaking in the (0.1–1) MeV range and also extending to high energies. In rare cases, it shows a clear spectral cutoff in the (20–350) MeV energy range that is interpreted as a result of the opacity of HE photons to -annihilation within the source [17,106]. This may be intrinsically more common, the low observed fraction being a matter of sensitivity, as such a cutoff appears in 20% out of a sample of bright Fermi Gamma-ray Burst Monitor (GBM) bursts when performing a joint GBM-LAT spectral fit [16]. Moreover, many of the bright Fermi-LAT GRBs show a second spectral component, in addition to the softer Band-like component, that dominates the HE emission [107,108,109], typically well fit by a power law and sometimes showing a cutoff (also likely due to intrinsic -opacity). A similar HE spectral component was also seen by EGRET [105]. Overall, the HE emission seen by the Fermi-LAT shows three remarkable features [15]:
- Extra HE spectral component: An extra power-law spectral component that extends to high energies and which is distinct from the typical sub-MeV Band component appears in several bright LAT detected GRBs.
- Delayed onset: The onset of this HE emission is delayed relative to the softer -rays near the spectral peak, with typical delays of a few to several seconds (s) for long-soft GRBs and a few tenths of a second (s) for short-hard GRBs.
- Long duration: It is systematically longer-lasting (ks) with its flux decaying smoothly as a power law in time (see Figure 2) having [110].
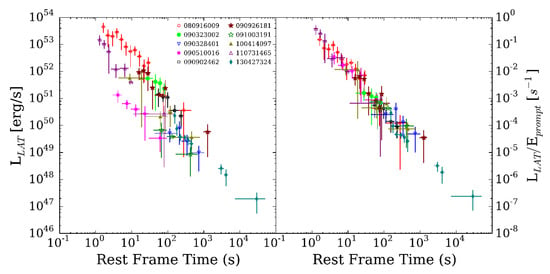 Figure 2. (Left): Fermi-LAT GRB lightcurves; (Right): The same as the left-panel but normalized by the energy released during the prompt emission. Figure from Nava et al. [111] (also see [112]).
Figure 2. (Left): Fermi-LAT GRB lightcurves; (Right): The same as the left-panel but normalized by the energy released during the prompt emission. Figure from Nava et al. [111] (also see [112]).
In the following, we discuss possible origins of the HE spectral component and its delayed onset with respect to the sub-MeV emission (also see, e.g., [113] for a review).
There are two main emission regions from where the HE spectral component can be produced. The first is internal to the outflow in which the emission arises due to dissipation of kinetic energy, e.g., via internal shocks, or magnetic energy, e.g., due to magnetic reconnection, and it occurs at smaller radii before the outflow is significantly slowed down by its interaction with the circumburst medium. In this case, the emission is expected to be highly variable, with where is the variability timescale, and correlated with the sub-MeV prompt emission, which is seen in all cases (as in this case, the two arise from the same outflow, albeit possibly at different radii). The second region is the external forward (afterglow) shock in which case the emission is produced by shock-heated swept-up circumburst medium. In contrast to the prompt emission, the lightcurve is expected to be much smoother, with , and decaying after its peaks at . Such behavior was also observed in many cases. In many LAT GRBs, there is initially a variable GeV emission followed by a smooth tail with a spectral change in the transition, suggesting a transition between prompt and afterglow GeV emission. Furthermore, upon closer inspection, in many cases the delayed onset is caused by the fact that the first spike in the prompt GRB lightcurve is missing at GeV energies, and only subsequent spikes appear in GeV and coincide with those at sub-MeV energies.
3.1. Delayed Onset of the Fermi-LAT HE Emission
In both the long-soft and short-hard GRBs detected by Fermi-LAT, the HE emission is generally delayed by (0.1–40) s in the former and (0.05–1) s in the latter. While formally reaches values as high as ≲ s in rare cases of both populations [15], these are mostly cases where the GRB was outside the LAT FoV at the time of the GRB trigger and likely do not have a similar physical origin. In the majority of GRBs, the onset of LAT HE emission occurs before the softer prompt -ray emission recorded by Fermi-GBM is over. A number of different scenarios have been proposed to explain the delayed onset, which we briefly discuss below.
3.1.1. Forward External Shock Emission
The shock-heated electrons behind the forward shock radiate synchrotron photons that produce the broadband afterglow emission, whose lightcurve peaks at the apparent time (assuming a thin-shell case, for which )
In this scenario [112,114,115,116,117], is the relevant timescale to explain . Furthermore, for , the proper velocity of the blast wave starts to decline as as more mass is swept up, and the dynamical evolution of the blast wave becomes self-similar [67]. For an adiabatic (constant energy with negligible radiative losses) relativistic spherical blast wave, the flux density for , the frequency regime relevant for HE afterglow emission, scales as for [24,25]. If the blast wave is radiative (a short-lived early phase where its energy decreases over time due to radiative losses), the flux density has the scaling [24]. (Even for fast cooling only a fraction of the internal energy generated at the afterglow shock is radiated away, and a similar fraction of the total energy is radiated over each dynamical time, so the blast wave may be far from being fully radiative as assumed in this scaling.) Evidently, the forward shock emission generally obeys a closure relation, whereby the temporal and spectral indices are coupled by virtue of their dependence on the electron energy distribution power-law index p. Kumar and Barniol Duran [115], Kumar and Barniol Duran [116] showed that three Fermi-LAT GRBs obeyed this closure relation of an adiabatic blast wave, with (GRB 080916C) and (GRB 090510, 090902B), that yielded consistent with the observed value to within 1- uncertainty. An additional argument in favor of this scenario is that the LAT emission lightcurve shows a very smooth decay, which is expected for afterglow emission. A caveat here is that this applies mainly to the long-lived LAT emission at , whereas the variable GeV emission seen at in bright LAT GRBs cannot be afterglow emission and is most likely prompt emission (especially when it is temporally correlated with MeV spikes in the prompt GRB lightcurve, e.g., [107,108,109,118,119])
The temporal evolution of the observed (isotropic-equivalent) luminosity is another useful probe for the origin of the HE emission. From energy conservation, , and with where , the time evolution of the isotropic-equivalent energy can be obtained, [120]. For an adiabatic () blast wave, , as it should be, and for radiative () blast wave . The observed luminosity then follows with , which yields for the adiabatic case and for the radiative case. The left panel of Figure 3 shows the radiative afterglow model fit to the LAT lightcurve of GRB 080916C [112]. This agreement presents a strong argument in favor of the synchrotron afterglow origin of the late-time LAT HE emission. However, the main LAT peak is too sharp to arise from the afterglow onset corresponding to the outflow deceleration time, and instead matches the second MeV peak, so it is more likely associated with the prompt GRB emission, while the temporally smoother afterglow GeV emission likely starts dominating later, after a few tens of seconds, with a rather shallow decay slope ().
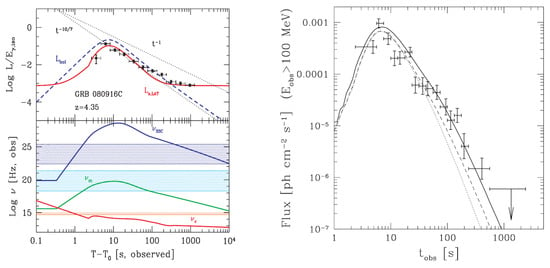
Figure 3.
(Left) Radiative afterglow with enrichment model fit to the lightcurve of GRB 080916C [112]. In the top-panel, the red curve shows the Fermi-LAT luminosity, the dashed blue curve is the expected bolometric luminosity, and the two dotted black curves show the expected temporal slopes of the afterglow luminosity when the blast wave is adiabatic () or radiative () for a uniform circumburst medium. The bottom panel shows the temporal evolution of the characteristic frequencies of synchrotron and SSC emission. The shaded regions show the energy ranges of the LAT [() GeV] and GBM [() keV] instruments, as well as the optical energy range (U and R filters). Right: Pre-accelerated and pair-loaded CBM afterglow model fit to the Fermi-LAT lightcurve of GRB 080916C [56] (©AAS. Reprodued with permission.).
There are two major hurdles for this scenario. First, many LAT GRBs show a peak in the GeV emission while the prompt emission is still active, which is difficult to explain with synchrotron emisson from the external forward shock. In the thin-shell afterglow shock scenario [66], the peak of the HE emission will occur at which is always larger than the duration of the prompt GRB emission, , given by the shell crossing time of the ejecta shell of initial thickness . Alternatively, in the thick-shell case, . Second, this model cannot explain the detection of VHE photons at late times when where the detected photons have energies much larger than [121]. Both of these arguments suggest that yet another mechanism might be responsible for the LAT emission.
3.1.2. Inverse-Compton GeV Flash
The shock-heated electrons behind the forward shock at radius R can be Compton-cooled by prompt emission MeV photons emitted at a smaller radius as the radiation front overlaps with the blast wave [51,52,56]. When the prompt emission photons travel ahead of the blast wave, a small fraction is scattered by the yet unshocked electrons in the CBM at large angles from the radial direction. The scattered photons then produce -pairs via -annihilaton on the radially expanding (collimated) prompt emission radiation front. The created pairs further scatter the prompt photons, causing exponential pair-creation and the resultant high multiplicity (with ) pair-loading of the CBM ahead of the forward shock [122,123,124,125,126]. Scattering of the prompt radiation by the pair-loaded CBM also imparts momentum to the pairs and pre-accelerates them to a typical LF , where is the bulk LF of the blast wave, i.e., material just behind the forward shock. As the blast wave sweeps up the pair-loaded CBM, with a relative LF , the shock-heated pairs are thermalized with when . This model assumes that only a small number of particles are accelerated into a power-law energy distribution and most of the energy resides with the quasi-thermal pairs. The radiative efficiency of the shock-heated pairs is almost 100% during the GeV flash; therefore, the blast wave does not start to evolve adiabatically until all the prompt emission photons have overtaken it.
In this scenario, the peak of the LAT emission occurs at where cm (in the case of GRB 080916C) is the radius where the LF of the electrons behind the forward shock is
so that the IC scattered emission peaks in the GeV energy range. At , the contrast between and is small and therefore . This contrast grows over larger radii and at , and for , the contrast is much larger which yields and produces VHE emission at ≳TeV energies. The right panel of Figure 3 shows the model fit to the LAT lightcurve of 080916C from Beloborodov et al. [56].
3.1.3. Synchrotron Emission from Protons Accelerated at the External Forward Shock
In the hadronic scenario, a proton-synchrotron emission model with a strong comoving B-field () can explain the delayed onset of the LAT emission [40,127,128]. Just like electrons, protons are also accelerated at the external blast wave to energies where they can radiate GeV to TeV synchrotron radiation. This radiation is further processed into -pairs via -annihilation where the produced pairs then radiate sub-GeV synchrotron photons. The onset of HE emission is delayed due to two effects. First, protons are accelerated over the Larmor time to achieve a maximum LF (see Section 2.2 for definition), which causes a delay of at least
This should also be a lower limit on the variability time, as the local emission cannot turn on or off faster than this. Second, as shown in the model put forth by Razzaque et al. [40], it takes a finite amount of time for the peak of the proton synchrotron radiation spectrum, which peaks at higher energies at early times, to move into the LAT energy range.
This scenario requires a strong magnetization of the shocked material downstream of the blast wave to explain the delays in the LAT emission onset. A major weakness of this model is that it is radiatively inefficient and therefore requires a large amount of energy in accelerated protons that must be injected with minimum LF of [42,101]. Furthermore, as the proton synchrotron cooling break sweeps across the observed energy band, the spectral index should change from to , where p is the power-law index of the proton energy distribution, for . However, no such spectral change has been observed in the delayed LAT emission. Although it is possible that this spectral component has only been observed at energies above the cooling break due to the limiting sensitivity of the Fermi-LAT at high energies, it would be too much of a coincidence to have happened in all LAT bursts that show delayed emission.
3.1.4. SSC Emission
The delay time of the LAT emission in the SSC scenario depends on the time it takes for the IC-scattered radiation field to build up in the LAT energy band. That depends on the temporal evolution of the Compton-y parameter which must become larger than unity for IC scattering to become the dominant particle cooling mechanism. Detailed one-zone numerical simulations [128,129,130] of prompt GRB emission show that under certain conditions SSC emission in the LAT energy range can be delayed with respect to the sub-MeV synchrotron component due to the time it takes to build up the seed synchrotron photon field in the emitting region (of the order of its light crossing time). However, in many cases, the temporal delay is insufficient to explain the observed ones and remains limited to , where is the variability timescale. This effect would also lead to a systematic delay of the GeV emission w.r.t the sub-MeV emission for each spike in the prompt lightcurve. In practice, the observed delay typically reflects the first spike being absent in the GeV, with subsequent spikes coinciding in MeV and GeV.
3.2. Distinct HE Spectral Component
Many bright Fermi-LAT GRBs show a distinct HE spectral component in addition to the Band-like spectrum, where the latter represents the canonical prompt emission spectrum peaking in the ∼(0.1–1) MeV energy range. This additional component has been modeled as a power-law, sometimes with a high-energy cutoff, in addition to the Band component. Such a component was required by the data in GRB 090227B [131], GRB 090228 [131], GRB 090510 [108], GRB 090902B [107], GRB 090926A [109], GRB 110731A [110], GRB 130427A [121], GRB 141207A [132], GRB 190114C [133]. The first such detection of an additional component, however, was made by EGRET in GRB 941017 [105]. In most cases, the additional power-law component extends to low energies (few keV) and exceeds the Band component below a few tens of keV, forming a low-energy excess. At high energies, this power-law component is detected up to – GeV with photon index to . In some cases (e.g., GRB 090926A and GRB 190114C), however, this component shows a high-energy turnover at early times before becoming a strict power-law as the spectral break moves above the LAT energy window. Example time-integrated and time-resolved spectra for the short-hard GRB 090510 [108] and long-soft GRB 090926A [109] are shown in Figure 4.
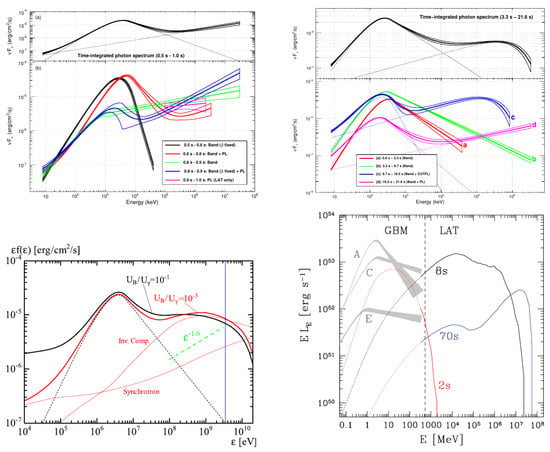
Figure 4.
Top: Time-integrated and time-resolved prompt emission spectra of short-hard GRB 090510 (left; [108], ©AAS. Reproduced with permission.) and long-soft GRB 090926A (right; [109], ©AAS. Reproduced with permission.). In both cases, the spectrum shows a low- and high-energy excess which is fit by a power-law or cutoff power-law component that has a distinct origin from the main Band component. Bottom: Theoretical modeling of the spectrum of GRB 090510 using a hadronic scenario with photo-hadronic cascades (left; [97], ©AAS. Reproduced with permission) and that of GRB 080916C using the pre-accelerated and pair-loaded ISM in the afterglow model (right; [56], ©AAS. Reproduced with permission.).
The low-energy excess presents a challenge for leptonic scenarios, e.g., SSC, that can only explain the excess emission above the peak of the sub-MeV emission and remain subdominant to the main synchrotron (Band) component at low energies. Such an excess can be produced in hadronic models featuring direct proton synchrotron emission [40] or photohadronic cascades [96]. Theoretical modeling of the prompt spectrum of GRB 090510 using the latter model is shown in the bottom-left panel of Figure 4 for two different ratios of , where is the energy density of the comoving B-field, and is the energy density of the Band component (shown with a black dashed curve; not produced by the same secondary pairs that IC scatter the Band component). In this case, the low- and high-energy excesses are given by synchrotron and inverse-Compton emissions from the secondary -pair cascades (shown by thin red curves without absorption). The peak around GeV arises from absorption due to -annihilation.
Alternatively, models that attribute the origin of the additional power-law component to afterglow emission also find it challenging to explain the low-energy excess. As mentioned earlier, in simple external forward shock models, e.g., [115,116], the dominant contribution from the afterglow occurs at ; therefore, these models cannot explain the origin of the additional power-law component in the prompt emission spectrum. In the model put forth by Beloborodov et al. [56], the inverse-Compton emission (as shown in the bottom-right panel of Figure 4) from shock-heated electrons behind the forward shock that sweeps up pre-accelerated and pair-loaded ISM remains sub-dominant at low-energies and therefore cannot explain the low-energy excess.
The low-energy excess is not always modeled as a low-energy extension of the power-law component that dominates at high energies above the Band component. In some cases, it has been interpreted as a combination of a Band plus photospheric (quasi-thermal) components that jointly produce this excess, e.g., [134,135,136]. This degeneracy produced by different spectral models describing the same data equally well further adds to the complexity of the underlying emission mechanism.
3.3. Long-Lived HE Emission
At an early time, when the sub-MeV prompt emission is still active, the HE emission detected by the Fermi-LAT shows significant temporal variability, which in many cases, e.g., [118] is correlated with the sub-MeV emission. This can be attributed to the HE emission having originated in the same spatial region as the sub-MeV component. After the prompt emission ceases and the afterglow commences, the HE emission shows a temporally smooth and long-lasting decay with and a standard deviation of 0.8 (in some cases a broken power-law fit to the lightcurve is statistically preferred) [15]. This is often referred to as the LAT extended emission (see Figure 2 and left panel of Figure 5). Since it lacks the short timescale variability and lasts much longer, it is naturally interpreted as the HE tail of the afterglow emission from the external forward shock.
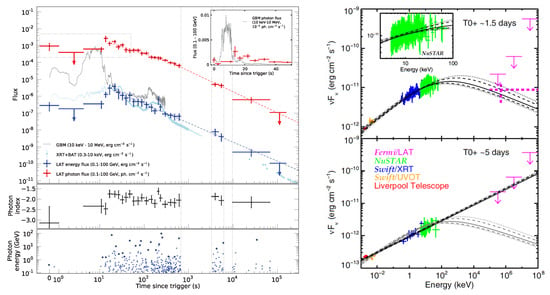
Figure 5.
Left: Temporally extended Fermi-LAT emission (from [121], Reprinted with permission from AAAS). Top: LAT energy flux (blue) and photon flux (red) light curves. The photon flux light curve shows a significant break at a few hundred seconds (red dashed line), whereas the energy flux light curve is well described by a single power law (blue dashed line). The 10 keV to 10 MeV (GBM, gray) and 0.3 to 10 keV (XRT + BAT, light blue) energy flux light curves are overplotted. Middle: LAT photon index. Bottom: Energies of all the photons with probabilities >90% of being associated with the GRB. Solid circles correspond to the photon with the highest energy for each time interval. The vertical gray lines indicate the first two time intervals during which the burst was occulted by Earth. Right: A smoothly broken power-law synchrotron afterglow model [25] fit to the optical to GeV spectrum of GRB 130427A (from [137], ©AAS. Reproduced with permission). Broadband SEDs are shown during the first (top panel) and the second (bottom panel) NuSTAR epochs. The Fermi LAT upper limits are shown as arrows, and the extrapolation of the LAT flux light curve is shown as a dashed magenta cross (only during the first epoch). The second epoch (bottom panel) is fit with a power law (black line); the fit to the first epoch is scaled down and superposed on the second epoch data for comparison (in gray).
As discussed in Section 3.1, synchrotron afterglow emission from an adiabatic [115,116] (or possibly in some cases from a radiative [112]) blast wave can very well explain the temporal decay index of the LAT extended emission. The agreement with multi-wavelength observations (see, e.g., [116]) suggests that it certainly is a strong candidate for the late-time extended emission, even though this model may not be the correct description for the early time (with its delayed onset and low-energy spectral excess if produced by the same non-thermal component) LAT emission.
The one problem this scenario faces is the detection of (V)HE photons at late times. In several GRBs, HE photons with observed energy GeV arrive at – s, much after the cessation of the prompt GRB emission [15]. The origin of such photons using the standard leptonic synchrotron afterglow scenario is difficult to explain as they violate . According to this limit, to produce photons with energy GeV in the cosmological rest-frame of the source would require bulk at late times, which is nearly impossible. Therefore, our assumptions regarding particle acceleration at shock fronts must be revised (see further discussion in Section 4 below). The alternative is SSC emission which would manifest as an additional spectral component in the LAT energy band and would also be detected at very high energies.
3.4. Constraints on Bulk
Since GRBs are extremely luminous sources, a typical photon near the peak with energy would see a large optical depth to pair production () [138]. For a Newtonian source, this would imply a huge compactness (Thomson optical depth of pairs if all photons pair produce), where is the radiation field energy density, which would result in a nearly blackbody spectrum, in stark contrast with the observed prompt GRB non-thermal spectrum. The solution to this so-called compactness problem, is that the emission region must be moving towards us at ultra-relativistic speeds with bulk LF [139,140,141]. The observed energy where the prompt GRB spectrum would display a cutoff due to -annihilation is sensitive to ; therefore, an observation of such a cutoff yields a direct estimate of , which is difficult to obtain otherwise. Spectral cutoffs have only been observed in a handful of GRBs, e.g., [17,106,109], and in most cases, the spectrum above the peak is a featureless power law extending to some , the maximum photon energy detected by the instrument. In such cases, only lower limits can be placed on the bulk LF with . The maximum possible bulk LF for a given is given by , and the true bulk LF is , e.g., [37].
In several bright GRBs detected by Fermi-LAT, estimates of have been obtained for a given using a simple one-zone analytic formalism, e.g., [33,34,35], with for GRB 080916C [119], for GRB 090510 [108], and for GRB 090902B [107]. When a more sophisticated formalism [36,142,143] that includes temporal, spatial, and angular dependence of the radiation field, and which is verified by numerical simulations [37], is applied, it yields a estimate smaller by a factor of ∼2–3 (similar results were obtained by [144,145]). In GRBs that show a high-energy spectral cutoff, bulk LF of 100–400 have been obtained using detailed numerical models [17].
4. High-Energy (GeV) Afterglow and GRB 130427A
GRB 130427A was an exceptionally bright GRB [121,146,147] that occurred at a relatively small redshift of [148]. Besides being observed by the Fermi-GBM [149] and LAT [121], its extremely intense emission was also detected by other satellites (AGILE [150], Konus-Wind [151], RHESSI [152], Swift [153]), which enabled multiple ground- and space-based follow-up observations. GRB 130427A was a unique event in that it had the largest fluence (), highest-energy photon at the time (95GeV), longest -ray duration (20 hours in the GeV energy range), and one of the largest isotropic energy releases (erg) ever observed from a GRB.
In addition to its phenomenal prompt emission, the afterglow emission GRB 130427A provided extremely interesting physical insights. In particular, as described below, its temporal and spectral analyses challenge the most widely accepted model for the afterglow phase of GRBs. Its prompt emission lasted about s (at 15–150 keV; [147]), and after it subsided, the observed emission was clearly dominated by the afterglow [137,147,154], showing a smooth power-law flux decay as well as a typical afterglow-like spectrum (see Figure 5). Moreover, while the reverse shock emission appears to dominate at early times at low frequencies, it does not dominate beyond the optical (even at early times), where the observed emission is dominated by the forward shock all along [154]. The values of the temporal and spectral indices in the power-law segment (PLS G from [25]), , imply an external density profile with [137], suggesting that the GRB progenitor star’s wind mass loss rate to velocity ratio ( or where is the wind ejection time prior to the stellar explosion leading to the GRB) slightly decreased towards the end of its life.
Most importantly, the high-energy emission from the afterglow of GRB 130427A was not only detected by the Fermi-LAT for 20 h (see top-left panel of Figure 5), but also included multiple high-energy photons up to very late times (see bottom-left panel of Figure 5) that were clearly in excess of the maximum synchrotron photon energy, . This upper limit on the energy of synchrotron photons is derived by equating the electron acceleration and synchrotron radiative cooling timescales, assuming a single acceleration and emission region [27,29,155,156]. While there was some evidence of violation in previous Fermi-LAT GRBs (e.g., [29,119]), in those cases on the one hand the violation was weaker (by a smaller factor and with fewer photons of less statistical significance), and on the other hand a different emission mechanism was a viable alternative explanation. In GRB 130427A, the long-lasting (∼1 day) Fermi-LAT afterglow included a 32 GeV photon after 34 ks, and altogether five >30 GeV photons after >200 s (with probability > 99.9% of being associated with GRB 130427A). All five significantly exceed , by factors of at least 6.25 for and 9.20 for (using Equation (4) of [29]).
This has led to suggestions that the Fermi-LAT high-energy photons were not synchrotron radiation, but instead arose from a distinct high-energy spectral component [121,157]. All such options require that the high-energy part of the Fermi-LAT detected energy range (above a few to several GeV, depending on the exact time) should be dominated by a distinct spectral component, while lower energies are dominated by the usual afterglow synchrotron spectral component. Such an option was considered by [137], who fit the SED from optical to GeV at two epochs (∼1.5 an 5 days) where observations were also performed by the Nuclear Spectroscopic Telescope ARray (NuSTAR) in the 3–79 keV energy range (see right panels of Figure 5). The spectrum was fit to a detailed synchrotron afterglow model [25], which provided a good fit at both epochs. Moreover, at the first and more constraining epoch (∼1.5 days), the Fermi-LAT flux that is extrapolated by a factor of ≲2 in time agrees very well with this synchrotron afterglow model. Furthermore, both this, as well as the simultaneous upper limit by the Fermi-LAT [121,137], and more importantly the nearly simultaneous VHE upper limit by the Very Energetic Radiation Imaging Telescope Array System (VERITAS) [158], hardly leaves any room for a distinct high-energy spectral component.
Therefore, this strongly suggests that the late-time Fermi LAT high-energy photons in GRB 130427A are indeed afterglow synchrotron radiation. This provides the strongest direct observational support for a genuine violation of by synchrotron photons. As the latter arise from the afterglow forward shock, this challenges our understanding of particle acceleration and magnetic field amplification in relativistic collisionless shocks. In particular, at least one of the assumptions in the derivation of must be incorrect, requiring a modification of our understanding of afterglow shock physics.
While this potential problem was known before, these results from GRB 130427A [137] have made it much harder to circumvent (and the VHE upper limit by VERITAS played an important role). A possible solution to this problem may lie in modifying the assumption of a single uniform region where both the acceleration of electrons and radiation from them occurs. Instead, one can allow for a lower magnetic field acceleration region and a higher magnetic field synchrotron radiation region (e.g., [30,159]). Such a situation may arise for diffusive shock acceleration (Fermi Type I) if the tangled shock-amplified magnetic field decays on a short length scale behind the shock front. In this case, most of the high-energy radiation is emitted just behind the shock from where the magnetic field has not decayed significantly, while the highest-energy electrons are accelerated further downstream where the magnetic field is lower [30]. This puzzle is still far from being resolved and poses a serious challenge to our understanding of relativistic collisionless shock physics.
5. Very-High-Energy (TeV) Afterglow
The detection by EGRET of MeV-GeV photons over ∼90 min from GRB 940217 [103], as well as the hard additional spectral component in the prompt emission of GRB 941017 [105], led to the consideration of SSC prompt [129,160,161,162,163] and afterglow radiation [44,45,46,59,164] and searches for VHE TeV photons by ground-based detectors. TeV emission is expected to be observed only from relatively nearby GRBs due to absorption of VHE -rays by -annihilation on EBL photons from the more distant sources. The Universe starts to become opaque to VHE photons with TeV for redshifts [165]. Early efforts at detecting VHE radiation from GRBs were made by the Milagro instrument, an extended air shower detector, and hints of VHE photon () detection from GRB 970417A were found by Milagrito [166] (see [167] for prompt TeV -ray emission model for this detection), the smaller and less sensitive prototype detector. Over the last two decades, imaging atmospheric Cherenkov telescopes (IACTs), namely the Very Energetic Radiation Imaging Telescope Array System (VERITAS; [168]), the Major Atmospheric Gamma Imaging Cherenkov (MAGIC; [169]), and the high-energy Stereoscopic System (H.E.S.S; [170]) have been routinely monitoring for VHE radiation from GRBs.
These efforts bore fruit in January of 2019 when MAGIC announced the (≳50) detection of VHE (∼0.2–1 TeV) photons from GRB 190114C [171]. Figure 6 shows the multi-wavelength lightcurve and broadband afterglow spectrum of this burst. GRB 190114C had a redshift of , and its prompt emission was detected by several space-based -ray instruments [133,172] that measured an isotropic-equivalent (keV to GeV) energy release of erg over a duration of ∼25 s (shown by the dashed vertical line in Figure 6). MAGIC detected afterglow VHE -ray photons from ∼60 s to ∼2400 s and measured an erg, which is only a lower limit due to the late start of observations and could be as high as ∼10% of the energy released in softer -rays. This was the first time that time-resolved afterglow spectra all the way up to TeV energies were obtained in any GRB observed to date. This naturally has important implications for GRB afterglow physics and overall energetics of the system.
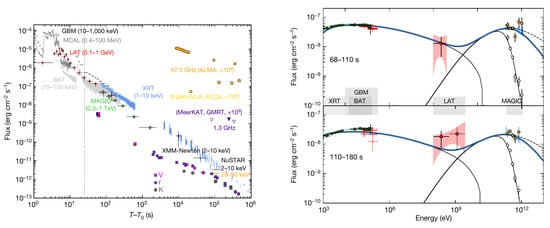
Figure 6.
Left: Multi-wavelength (Radio to TeV -rays) lightcurve of GRB 190114C. The dashed verticle line indicates the time when the highly variable prompt emission ended. Right: Broadband high-energy spectrum of GRB 190114C at different time intervals along with the synchrotron + SSC model fits. The shaded contours shown in different colors indicate the uncertainties on the model fit to the data. MAGIC data points shown in yellow have been corrected for the EBL absorption, whereas the open white circles are the actual observations. The black dashed curve shows the SSC spectral component without attenuation from internal and EBL absorption. Figures from [173] (Reprinted by permission from Springer Nature Customer Service Center GmbH: Springer Nature, Observation of inverse Compton emission from a long -ray burst, MAGIC Collaboration, ©2019).
After GRB 190114C, a few other GRBs (160821B [174] with a low detection significance of ∼3, 180720B [175], 190829A [176], 201216C [177]) were reported to have been detected at sub-TeV to TeV energies by both H.E.S.S and MAGIC (see the reviews by Nava [18], Noda and Parsons [19] for more details).
5.1. Key Results Implications
In the following, we briefly discuss the most important implications for GRB physics from the detection and theoretical modeling of ∼ TeV afterglow emission.
5.1.1. IC Emission Is Needed to Explain the VHE -Rays
As shown in the right panel of Figure 6, the hardening of the MAGIC-detected VHE spectrum with respect to the LAT detected HE spectrum in GRB 190114C indicates the presence of an additional spectral component. It simply cannot be explained with synchrotron emission from the external forward shock alone. Several works that use analytical/semi-analytical [178,179,180,181,182] and numerical models [183,184] have now been devoted to explaining the TeV emission as SSC or a combination of EIC and SSC [185]. Significant differences between the (semi-)analytical and numerical models arise due to inclusion and more accurate handling of some of the non-linear processes, such as pair cascades due to internal absorption and KN effects. In the end, the obtained shock microphysical parameters indicate that these bursts are not very different from the ones that are not detected with a VHE component, which may suggest that SSC afterglow emission is rather common. In that case, it becomes important to take into account the energy radiated in the SSC component to understand the global energetics of the bursts. For example, the energy in the SSC component was ∼40% of that radiated in the main synchrotron afterglow component for GRB 190114C [171]. Similar inferences regarding the total energy budget were also drawn before and around the first GeV detections from GRBs by the Fermi-LAT. It was later shown that on average , and at best the two become comparable for rare individual LAT GRBs. In GRB 190114C the detected TeV emission is from the afterglow. Therefore, it does not affect the prompt GRB energy budget.
An alternative to IC emission that can explain the VHE TeV -rays is photohadronic emission, as demonstrated by Sahu and Fortín [186], Sahu et al. [187]. In their model, VHE -ray photons are produced via the process, which then produces neutral pions that decay into -ray photons (see Section 2.6). The seed photons that interact with the protons can be of synchrotron or SSC origin as produced in the afterglow forward shock.
5.1.2. Constraints on Shock Microphysical Parameters
When fitting afterglow observations, the parameter space is usually degenerate, and unique values of the shock microphysical parameters cannot be obtained. The parameter space consists of , the isotropic-equivalent total kinetic energy of the flow, n, the number density of the ISM or its normalization () for a wind circumburst medium, and the shock microphysical parameters , , and . The power-law index p of the particle energy distribution is uniquely determined from the broadband spectrum. It is generally assumed that , in which case the remaining four afterglow model parameters can be uniquely determined using , leaving the degeneracy due to [188] where all values of fit the data equally well for any . This degeneracy may possibly be broken when accounting for the emission, absorption, or propagation effects of the thermal electrons [189,190,191,192,193]. In addition to these parameters, multi-wavelength modeling of TeV afterglows can potentially be used to constrain and in turn the acceleration efficiency () of relativistic collisionless shocks. Such constraints can then be used for comparison with first principles PIC simulations of Weibel-mediated collisonless shocks that do predict the value of .
In Table 1, we list the afterglow fit parameters of GRBs that were detected at very high energies. In all cases, the energy deposited in power-law electrons is much larger than that in the shock-generated B-field, i.e., . Consequently, this yields the Compton-y parameter larger than unity which results in producing a bright SSC component detected by MAGIC and H.E.S.S. In most works, the afterglow shock microphysical parameters are taken to be constant throughout the afterglow evolution; however, Misra et al. [194] report the possibility of evolving microphysical parameters to explain the long-term radio/mm afterglow of GRB 190114C.

Table 1.
Afterglow fit parameters for GRBs with VHE emission. Shows parameter for a wind environment.
5.1.3. VHE -Rays as Electromagnetic Counterparts of Binary NS Mergers
The detection of afterglow TeV -rays in long-soft GRBs has opened up the prospect of also detecting VHE emission in short-hard GRBs. Electromagnetic emission coincident with GWs was first detected from the binary NS merger in GW 170817/GRB 170817A. An impressive multiwavelength follow-up by a number of ground- and space-based observatories tracked its peculiar afterglow emission. No ∼TeV -rays were detected [196,198,199] for this relatively nearby (∼40 Mpc) event as the relativistic jet was observed off-axis, and none have been detected from other short-hard GRBs. Short-hard GRBs are detected more numerously at redshifts with a mean redshift of in comparison to for the long-soft GRBs. Therefore, attenuation of VHE -rays by the EBL is not as extreme for the short-hard GRBs (e.g., MAGIC detected GRB 190114C had a redshift of ) as it is for the more distant long-soft GRBs. Catching the VHE emission in time from short-hard GRBs will require high sensitivity (due to lower fluences), shorter telescope slew times, as well as a large field-of-view (since catching the prompt emission would require the GRB to be in the field-of-view without slewing). Fast follow-ups of GW triggers by existing (MAGIC, H.E.S.S, VERITAS, HAWC) and upcoming observatories, namely the Cherenkov Telescope Array (CTA; [200]), will play a pivotal role in the next several years.
6. Studying Non-GRB Physics
Since GRBs are the most electromagnetically luminous events in the Universe, they are observed up to cosmological distances. They emit HE and VHE photons that travel over cosmological distances on the way from the source to us. This can naturally be used to probe various processes involving these photons that may occur along their way to our detectors, which provide unique and valuable information about cosmology or basic physics.
6.1. Constraining the Extragalactic Background Light Models with GRBs
The detection of HE photons from distant GRBs proves to be an excellent probe of the extragalactic background light (EBL) [165,201,202,203,204,205,206,207], which is the cumulative star light emitted in the UV/optical to infrared energy range, i.e., ∼10 eV to eV (∼0.1 m to 10m), by all the stars in the Universe. The EBL is difficult to constrain otherwise due to contamination by the zodiacal and Galactic foreground light [208]. After the cosmic microwave background, the EBL is the second dominant component that contributes to the diffuse radiation that pervades entire space. Star light with wavelength m is highly absorbed by dust in the host galaxy, with only a fraction that escapes and contributes to the EBL. On the other hand, the dust re-radiates the star light but adds to the EBL in the infrared. As discussed in Section 2.5, VHE -ray photons with TeV interact with the infrared background and produce -pairs, while lower energy photons typically interact with UV/optical/NIR photons emitted directly by stars. The attenuation of the HE spectra of TeV sources, including GRBs, caused by this effect can be used to constrain models of EBL, with the assumption that the intrinsic spectrum can be extrapolated to higher energies using the lower energy part of the spectrum that is not affected by such attenuation.
Before the MAGIC detection of TeV -rays in GRB 190114C, constraints on EBL models were placed using the observations of HE photons from only a few GRBs. For example, the fast evolution and baseline models of Stecker et al. [165] were disfavored at the >3 level by the detection of a GeV photon from GRB 090902B which was at a redshift of [107]. Observations of higher redshift GRBs at high energies offer a better chance of constraining EBL models. A GeV photon was detected from GRB 080916C having a redshift of . The opacity of the Universe to such a photon is shown in Figure 7 that compares different EBL models. The suppression of the TeV spectrum of a GRB due to the EBL was first clearly seen in GRB 190114C [171,173], as shown in Figure 6.
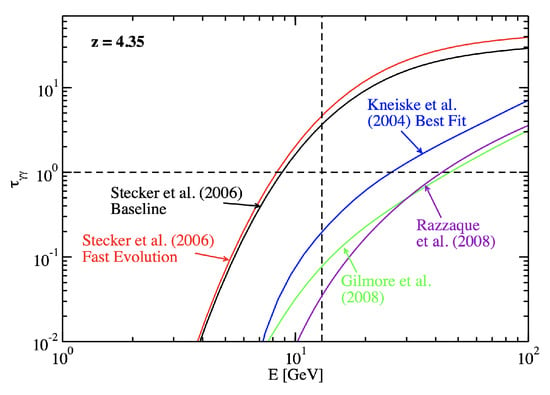
Figure 7.
Opacity of the Universe to HE photons, emitted at a redshift of , due to their interaction with EBL photons as calculated using different models. The vertical dashed line marks a GeV photon detected from GRB 080916C. Figure adapted from [119] (Reprinted with permission from AAAS).
6.2. Probing the Intergalactic Medium B-Field
The space between galaxies is expected to be permeated by a very weak (G) magnetic field [209,210,211,212], the origin, strength, and coherence length of which are poorly understood. This intergalactic magnetic field (IGMF) possibly acted as the seed magnetic field in galaxies and galaxy clusters, which was amplified to typical strengths of G by a dynamo mechanism as well as flux conserving collapse during their formation. Therefore, its origin predates structure formation in the Universe. Since such field amplification processes are absent in the voids between galaxies, which would have otherwise erased the initial magnetic field properties, study of the IGMF can provide important insights into the origin of the seed field in galaxies, and it can be used to constrain physical processes in the early Universe that may have generated it. Contamination of the primordial IGMF is possible via magnetized outflows from active galaxies and galactic winds driven by star formation.
One of the ways to study the IGMF, albeit indirectly, is by detecting GeV pair echos (see Section 2.5) created by the IC scattering of CMB photons by pairs that in turn are produced by ∼TeV -rays (from an astrophysical source) annihilating with EBL photons [82,213]. This causes several observable effects, e.g., time delays between the TeV and GeV signal [70,71,214] and extended -ray haloes [215], that can be used to constrain the properties of the IGMF. Non-observation of GeV -rays from persistent sources, e.g., TeV blazars, were used to derive a lower limit of G for a coherence length of 10 kpc to 1 Mpc [216,217]. The potential problem with persistent sources, when GeV radiation is observed, is that the pair echo photons can overlap with the intrinsic emission causing contamination. In that regard, GRBs serve as better probes since there could be a clear temporal separation between the short-lived prompt emission and the detection of the longer-lived GeV pair echo.
Before the detection of TeV -rays from GRB 190114C, constraints on the IGMF were obtained using GRB 130427A from (i) the VERITAS upper limits at 100 GeV at 0.82 days, (ii) Fermi-LAT detection of a 32 GeV photon at 34.4 ks post-trigger, that could not be explained as synchrotron afterglow radiation, and (iii) Fermi-LAT upper limits at GeV energies at late times [218]. From the non-detection of GeV emission in Fermi-LAT observations of the location of GRB 190114C over a period up to 3 months, Wang et al. [219] derive a lower limit of for the coherence length of Mpc. On the other hand, Dzhatdoev et al. [220] argued that the Fermi-LAT flux upper limits were insufficient in constraining the IGMF and that the results of Wang et al. [219] are in error due to overestimation of the pair echo intensity.
6.3. Lorentz Invariance Constraints
One of the tenets of the special theory of relativity is that the speed of light is a Lorentz invariant, i.e., it is the same in two Lorentz frames regardless of their relative motion. In particular, it is independent of the photon energy (or wavelength), which is frame-dependent. The underlying assumption is that this remains true at all length scales (or wavelengths) in nature, no matter how small. However, quantum effects are expected to strongly affect the nature of space-time at the Planck scale, corresponding to a length scale of cm, or equivalently at an energy scale of GeV. Such effects can possibly lead to Lorentz invariance violation (LIV) where the speed of light changes with photon energy [221,222,223]. In some theories of quantum gravity, this effect can lead to dispersion as the photon propagates in the vacuum of space, such that its speed varies as for , where is the photon energy, is the quantum gravity energy scale (expected to be ∼ ), and the sign ambiguity depends on the dynamical framework. Since is much larger than observed photon energies, the change in velocity is rather minute. However, this effect can accumulate over cosmological distance scales D, which makes GRBs ideal probes of LIV.
This LIV effect would manifest as an arrival time difference between photons having different energies, with and . Since GRBs show temporal variability as short as ms, their large distances cm can probe quantum gravity energy scales approaching the Planck scale using GeV photons, . This technique was employed in the case of short-hard GRB 090510 that emitted a 31 GeV photon 0.829 s after the burst onset and which coincided in time with the last of the seven pulses comprising the prompt emission [118]. By using an unbinned analysis, in both energy and time, testing different dispersion coefficients that would yield velocity differences of , and then maximizing so that it yields the sharpest lightcurve, Abdo et al. [118] obtained a lower limit of (at the 99% confidence level) or equivalently . Using the same data for the short-hard GRB 090510, this limit was somewhat improved using a more refined analysis [224], and a Planck-scale limit was also derived on space-time fuzziness and stochastic LIV [225], which are motivated by the notion of space-time foam.
7. Outstanding Questions
Even with only a handful of detections in the VHE domain, new questions have emerged. We briefly highlight some of the fundamental questions that may be resolved with future TeV detections as well as improved modeling of radiation processes.
- (a)
- What makes GRBs TeV bright?: All TeV bright GRBs are also very bright in prompt -rays as well as in their X-ray afterglow emission. In fact, apart from GRB 190829A, the rest of the TeV bright GRBs have high prompt -ray fluences that put them among the top 1%, see Figure 1 of [19], as is also evident from their high erg from Table 1. Although not all MeV-bright GRBs were observed at TeV energies, it begs the question why no TeV emission was detected from, e.g., 130427A (one of the most energetic GRBs with erg) by VERITAS and HAWC, and whether we would have seen TeV -rays from all such GRBs. The majority of the highly energetic GRBs are also more distant with see, e.g., Figure 3 of [19], which makes it challenging to detect their TeV emission due to suppression by -annihilation on EBL photons. Internal absorption due to -annihilation of IC photons (that produce the TeV component) on the seed synchrotron photons (that produce the X-ray afterglow) can also become important [184] and may perhaps be enough in some bursts to significantly suppress the VHE emission. Detailed semi-analytic numerical models including the effects of pair cascades and Klein–Nishina suppression that can explain the multi-wavelength spectral and temporal evolution may shed more light on the properties of the emission region.
- (b)
- What causes the delayed onset of the Fermi-LAT emission?: The delayed onset of the HE emission w.r.t the MeV prompt -rays as seen by the Fermi-LAT has been interpreted as the peak of the standard afterglow emission [115,116], IC GeV flash from the pre-accelerated pair-rich circumburst medium swept up by the external forward shock [52,56], acceleration time of protons in hadronic emission scenarios [40], and the timescale over which the SSC radiation field builds up [128]. The latter two scenarios have some difficulties with, respectively, the global energetics and limitation on the delay duration, and the former two struggle with producing the observed variability at early times (while the sub-MeV prompt emission is ongoing) as both invoke emission from the external forward shock. Future and more sensitive observations of such delayed emission will be important in distinguishing between the different models.
- (c)
- What mechanism produces the Fermi-LAT extended emission?: The smooth temporal decay of the GeV Fermi-LAT extended emission naturally favors its origin in emission arising from the external forward shock. The main question here is whether the emission is entirely synchrotron radiation from non-thermal shock-heated electrons [112,115,116], the standard scenario, or IC radiation from mostly quasi-thermal electrons as the blast wave encounters pair-rich and pre-accelerated circumburst medium [52,56]. The latter scenario can only operate as long as there are softer seed photons that can Compton cool the thermal electrons. At early times, they are the prompt sub-MeV photons that overlap the afterglow shock, and at later times softer photons can be of synchrotron origin [226]. Detailed numerical models of blast waves propagating into pair-enriched media and the comparison of afterglow lightcurves with observations over the entire duration of the LAT extended emission can shed more light on this issue.
- (d)
- What mechanism produces multi-GeV photons at late times?: The detection of ≳10 GeV photons in several GRBs at late times (– s) is puzzling. When their origin is interpreted as the standard afterglow synchrotron emission from shock-heated electrons, for which strong evidence came from the broad band (optical to GeV) SED fits of the afterglow of GRB 130427A [137], it challenges our understanding of particle acceleration at relativistic collisionless shocks since the photon energy clearly violates . The alternative is IC (either SSC or EIC) afterglow emission, which can produce HE photons at late times. A prime example is GRB 190114C from which HE and VHE photons were detected by the Fermi-LAT (s) and MAGIC (s), respectively, at late times. Future such events with multi-wavelength constraints, especially at VHEs, along with numerical simulations of particle acceleration at shock fronts will be able to shed more light on this issue.
To answer the above questions, both leptonic and hadronic models have been discussed. Important constraints on the latter scenario are offered by multi-messenger observations that include follow-up and monitoring of GRBs by neutrino detectors [227]. Even non-detections offer very useful information about the underlying radiation mechanism. However, the prospect of turning these non-detections into detections, or at least providing more stringent upper limits, is looking better with the installation of km-scaled neutrino detectors, namely Baikal-GVD [228] and KM3NeT [229], in the next few to several years.
8. Closing Remarks
The detection of afterglow TeV -rays in a few GRBs, first reported for GRB 190114C, has opened up a new window for understanding the properties of relativistic collisionless shocks and radiation processes that operate near the shock fronts. VHE emission was anticipated in GRBs for some time, but it remained undetected for decades, garnering only upper limits from ground-based imaging atmospheric Cherenkov detectors. Detailed spectral modeling of the afterglow TeV emission is now shedding new light on the global energetics of the system leading to better constraints on the prompt -ray emission efficiency. Moreover, detection of TeV emission during the prompt-GRB phase would help pin down its illusive emission mechanism(s). In most cases, one-zone SSC emission is the most favored radiation mechanism for producing afterglow TeV photons, however, with only a few sources the details of SSC emission from shock-heated relativistic electrons (or -pairs) are not entirely clear. Future, multi-messenger and perhaps more sensitive, observations from low redshift GRBs will offer better opportunities to constrain microphysical processes at shock fronts.
Author Contributions
Writing–original draft preparation–review and editing, R.G. and J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the ISF-NSFC joint research program under grant no. 3296/19 (J.G.).
Data Availability Statement
Not applicable.
Acknowledgments
We are grateful to Kohta Murase and Soebur Razzaque for their feedback and comments that improved the quality of this article. We also thank the anonymous referees for their comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Piran, T. The physics of gamma-ray bursts. Rev. Mod. Phys. 2004, 76, 1143–1210. [Google Scholar] [CrossRef]
- Zhang, B.; Mészáros, P. Gamma-Ray Bursts: Progress, problems & prospects. Int. J. Mod. Phys. A 2004, 19, 2385–2472. [Google Scholar] [CrossRef]
- Mészáros, P. Gamma-ray bursts. Rep. Prog. Phys. 2006, 69, 2259–2321. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts & relativistic jets. Phys. Rep. 2015, 561, 1–109. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of Two Classes of Gamma-Ray Bursts. Astrophys. J. 1993, 413, L101. [Google Scholar] [CrossRef]
- Woosley, S.E. Gamma-Ray Bursts from Stellar Mass Accretion Disks around Black Holes. Astrophys. J. 1993, 405, 273. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-Ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and gamma-rays from coalescing neutron stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Narayan, R.; Paczynski, B.; Piran, T. Gamma-ray bursts as the death throes of massive binary stars. Astrophys. J. 1992, 395, L83–L86. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- Band, D.; Matteson, J.; Ford, L.; Schaefer, B.; Palmer, D.; Teegarden, B.; Cline, T.; Briggs, M.; Paciesas, W.; Pendleton, G.; et al. BATSE Observations of Gamma-Ray Burst Spectra. I. Spectral Diversity. Astrophys. J. 1993, 413, 281. [Google Scholar] [CrossRef]
- Preece, R.D.; Briggs, M.S.; Mallozzi, R.S.; Pendleton, G.N.; Paciesas, W.S.; Band, D.L. The BATSE Gamma-Ray Burst Spectral Catalog. I. High Time Resolution Spectroscopy of Bright Bursts Using High Energy Resolution Data. Astrophys. J. Suppl. Ser. 2000, 126, 19–36. [Google Scholar] [CrossRef]
- Kaneko, Y.; Preece, R.D.; Briggs, M.S.; Paciesas, W.S.; Meegan, C.A.; Band, D.L. The Complete Spectral Catalog of Bright BATSE Gamma-Ray Bursts. Astrophys. J. Suppl. Ser. 2006, 166, 298–340. [Google Scholar] [CrossRef]
- Ajello, M.; Arimoto, M.; Axelsson, M.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bhat, P.N.; Bissaldi, E.; Blandford, R.D.; et al. A Decade of Gamma-Ray Bursts Observed by Fermi-LAT: The Second GRB Catalog. Astrophys. J. 2019, 878, 52. [Google Scholar] [CrossRef]
- Fermi Large Area Telescope Team; Ackermann, M.; Ajello, M.; Baldini, L.; Barbiellini, G.; Baring, M.G.; Bechtol, K.; Bellazzini, R.; Blandford, R.D.; Bloom, E.D.; et al. Constraining the High-energy Emission from Gamma-Ray Bursts with Fermi. Astrophys. J. 2012, 754, 121. [Google Scholar] [CrossRef]
- Vianello, G.; Gill, R.; Granot, J.; Omodei, N.; Cohen-Tanugi, J.; Longo, F. The Bright and the Slow—GRBs 100724B and 160509A with High-energy Cutoffs at ≲100 MeV. Astrophys. J. 2018, 864, 163. [Google Scholar] [CrossRef]
- Nava, L. Gamma-ray Bursts at the Highest Energies. Universe 2021, 7, 503. [Google Scholar] [CrossRef]
- Noda, K.; Parsons, R.D. Gamma-Ray Bursts at TeV Energies: Observational Status. Galaxies 2022, 10, 7. [Google Scholar] [CrossRef]
- Fan, Y.Z.; Piran, T. High-energy γ-ray emission from gamma-ray bursts—Before GLAST. Front. Phys. China 2008, 3, 306–330. [Google Scholar] [CrossRef][Green Version]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Axford, W.I.; Leer, E.; Skadron, G. The Acceleration of Cosmic Rays by Shock Waves. In Proceedings of the International Cosmic Ray Conference, International Cosmic Ray Conference, Plovdiv, Bulgaria, 13–26 August 1977; Volume 11, p. 132. [Google Scholar]
- Bell, A.R. The acceleration of cosmic rays in shock fronts—I. Mon. Not. R. Astron. Soc. 1978, 182, 147–156. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. 1998, 497, L17–L20. [Google Scholar] [CrossRef]
- Granot, J.; Sari, R. The Shape of Spectral Breaks in Gamma-Ray Burst Afterglows. Astrophys. J. 2002, 568, 820–829. [Google Scholar] [CrossRef]
- Guetta, D.; Granot, J. Observational implications of a plerionic environment for gamma-ray bursts. Mon. Not. R. Astron. Soc. 2003, 340, 115–138. [Google Scholar] [CrossRef]
- Guilbert, P.W.; Fabian, A.C.; Rees, M.J. Spectral and variability constraints on compact sources. Mon. Not. R. Astron. Soc. 1983, 205, 593–603. [Google Scholar] [CrossRef]
- de Jager, O.C.; Harding, A.K. The Expected High-Energy to Ultra–High-Energy Gamma-Ray Spectrum of the Crab Nebula. Astrophys. J. 1992, 396, 161. [Google Scholar] [CrossRef]
- Piran, T.; Nakar, E. On the External Shock Synchrotron Model for Gamma-ray Bursts’ GeV Emission. Astrophys. J. 2010, 718, L63–L67. [Google Scholar] [CrossRef][Green Version]
- Kumar, P.; Hernández, R.A.; Bošnjak, Ž.; Barniol Duran, R. Maximum synchrotron frequency for shock-accelerated particles. Mon. Not. R. Astron. Soc. 2012, 427, L40–L44. [Google Scholar] [CrossRef]
- Atwood, W.B.; Baldini, L.; Bregeon, J.; Bruel, P.; Chekhtman, A.; Cohen-Tanugi, J.; Drlica-Wagner, A.; Granot, J.; Longo, F.; Omodei, N.; et al. New Fermi-LAT Event Reconstruction Reveals More High-energy Gamma Rays from Gamma-Ray Bursts. Astrophys. J. 2013, 774, 76. [Google Scholar] [CrossRef]
- Fenimore, E.E.; Epstein, R.I.; Ho, C. The escape of 100 MeV photons from cosmological gamma-ray bursts. AASS 1993, 97, 59–62. [Google Scholar]
- Woods, E.; Loeb, A. Empirical Constraints on Source Properties and Host Galaxies of Cosmological Gamma-Ray Bursts. Astrophys. J. 1995, 453, 583. [Google Scholar] [CrossRef]
- Baring, M.G.; Harding, A.K. The Escape of High-Energy Photons from Gamma-Ray Bursts. Astrophys. J. 1997, 491, 663–686. [Google Scholar] [CrossRef]
- Lithwick, Y.; Sari, R. Lower Limits on Lorentz Factors in Gamma-Ray Bursts. Astrophys. J. 2001, 555, 540–545. [Google Scholar] [CrossRef]
- Granot, J.; Cohen-Tanugi, J.; Silva, E.D.C.E. Opacity Buildup in Impulsive Relativistic Sources. Astrophys. J. 2008, 677, 92–126. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J. The effect of pair cascades on the high-energy spectral cut-off in gamma-ray bursts. Mon. Not. R. Astron. Soc. 2018, 475, L1–L5. [Google Scholar] [CrossRef]
- Böttcher, M.; Dermer, C.D. High-energy Gamma Rays from Ultra-high-energy Cosmic-Ray Protons in Gamma-Ray Bursts. Astrophys. J. 1998, 499, L131–L134. [Google Scholar] [CrossRef]
- Totani, T. Very Strong TeV Emission as Gamma-Ray Burst Afterglows. Astrophys. J. 1998, 502, L13–L16. [Google Scholar] [CrossRef][Green Version]
- Razzaque, S.; Dermer, C.D.; Finke, J.D. Synchrotron Radiation from Ultra-High Energy Protons and the Fermi Observations of GRB 080916C. Open Astron. J. 2010, 3, 150–155. [Google Scholar] [CrossRef]
- Ghisellini, G.; Ghirlanda, G.; Oganesyan, G.; Ascenzi, S.; Nava, L.; Celotti, A.; Salafia, O.S.; Ravasio, E.M.; Ronchi, M. Proton-synchrotron as the radiation mechanism of the prompt emission of GRBs? arXiv 2019, arXiv:1912.02185. [Google Scholar]
- Wang, X.Y.; Li, Z.; Dai, Z.G.; Mészáros, P. GRB 080916C: On the Radiation Origin of the Prompt Emission from keV/MeV TO GeV. Astrophys. J. 2009, 698, L98–L102. [Google Scholar] [CrossRef][Green Version]
- Dermer, C.D. Sources of GeV Photons and the Fermi Results. Saas-Fee Adv. Course 2013, 40, 225. [Google Scholar] [CrossRef]
- Sari, R.; Esin, A.A. On the Synchrotron Self-Compton Emission from Relativistic Shocks and Its Implications for Gamma-Ray Burst Afterglows. Astrophys. J. 2001, 548, 787–799. [Google Scholar] [CrossRef]
- Panaitescu, A.; Kumar, P. Analytic Light Curves of Gamma-Ray Burst Afterglows: Homogeneous versus Wind External Media. Astrophys. J. 2000, 543, 66–76. [Google Scholar] [CrossRef]
- Zhang, B.; Mészáros, P. Gamma-Ray Burst Afterglow with Continuous Energy Injection: Signature of a Highly Magnetized Millisecond Pulsar. Astrophys. J. 2001, 552, L35–L38. [Google Scholar] [CrossRef]
- Nakar, E.; Ando, S.; Sari, R. Klein-Nishina Effects on Optically Thin Synchrotron and Synchrotron Self-Compton Spectrum. Astrophys. J. 2009, 703, 675–691. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; Wiley-VCH: Weinheim, Germany, 1979. [Google Scholar]
- Stern, B.E.; Poutanen, J. Gamma-ray bursts from synchrotron self-Compton emission. Mon. Not. R. Astron. Soc. 2004, 352, L35–L39. [Google Scholar] [CrossRef]
- Kobayashi, S.; Zhang, B.; Mészáros, P.; Burrows, D. Inverse Compton X-Ray Flare from Gamma-Ray Burst Reverse Shock. Astrophys. J. 2007, 655, 391–395. [Google Scholar] [CrossRef][Green Version]
- Beloborodov, A.M. Optical and GeV-TeV Flashes from Gamma-Ray Bursts. Astrophys. J. 2005, 618, L13–L16. [Google Scholar] [CrossRef][Green Version]
- Beloborodov, A.M. Afterglow Emission from Pair-loaded Blast Waves in Gamma-Ray Bursts. Astrophys. J. 2005, 627, 346–367. [Google Scholar] [CrossRef][Green Version]
- Wang, X.Y.; Li, Z.; Mészáros, P. GeV-TeV and X-Ray Flares from Gamma-Ray Bursts. Astrophys. J. 2006, 641, L89–L92. [Google Scholar] [CrossRef]
- Murase, K.; Toma, K.; Yamazaki, R.; Nagataki, S.; Ioka, K. High-energy emission as a test of the prior emission model for gamma-ray burst afterglows. Mon. Not. R. Astron. Soc. 2010, 402, L54–L58. [Google Scholar] [CrossRef]
- Murase, K.; Toma, K.; Yamazaki, R.; Mészáros, P. On the Implications of Late Internal Dissipation for Shallow-decay Afterglow Emission and Associated High-energy Gamma-ray Signals. Astrophys. J. 2011, 732, 77. [Google Scholar] [CrossRef]
- Beloborodov, A.M.; Hascoët, R.; Vurm, I. On the Origin of GeV Emission in Gamma-Ray Bursts. Astrophys. J. 2014, 788, 36. [Google Scholar] [CrossRef]
- Murase, K.; Toomey, M.W.; Fang, K.; Oikonomou, F.; Kimura, S.S.; Hotokezaka, K.; Kashiyama, K.; Ioka, K.; Mészáros, P. Double Neutron Star Mergers and Short Gamma-ray Bursts: Long-lasting High-energy Signatures and Remnant Dichotomy. Astrophys. J. 2018, 854, 60. [Google Scholar] [CrossRef]
- Zhang, B.T.; Murase, K.; Yuan, C.; Kimura, S.S.; Mészáros, P. External Inverse-Compton Emission Associated with Extended and Plateau Emission of Short Gamma-Ray Bursts: Application to GRB 160821B. Astrophys. J. 2021, 908, L36. [Google Scholar] [CrossRef]
- Panaitescu, A.; Mészáros, P. Radiative Regimes in Gamma-Ray Bursts and Afterglows. Astrophys. J. 1998, 501, 772–779. [Google Scholar] [CrossRef]
- Wang, X.Y.; Dai, Z.G.; Lu, T. The Inverse Compton Emission Spectra in the Very Early Afterglows of Gamma-Ray Bursts. Astrophys. J. 2001, 556, 1010–1016. [Google Scholar] [CrossRef]
- Shaviv, N.J.; Dar, A. Gamma-Ray Bursts from Minijets. Astrophys. J. 1995, 447, 863. [Google Scholar] [CrossRef]
- Lazzati, D.; Ghisellini, G.; Celotti, A.; Rees, M.J. Compton-dragged Gamma-Ray Bursts Associated with Supernovae. Astrophys. J. 2000, 529, L17–L20. [Google Scholar] [CrossRef][Green Version]
- Eichler, D.; Levinson, A. Polarization of Gamma-Ray Bursts via Scattering off a Relativistic Sheath. Astrophys. J. 2003, 596, L147–L150. [Google Scholar] [CrossRef]
- Kimura, S.S.; Murase, K.; Ioka, K.; Kisaka, S.; Fang, K.; Mészáros, P. Upscattered Cocoon Emission in Short Gamma-Ray Bursts as High-energy Gamma-Ray Counterparts to Gravitational Waves. Astrophys. J. 2019, 887, L16. [Google Scholar] [CrossRef]
- Yuan, C.; Murase, K.; Guetta, D.; Pe’er, A.; Bartos, I.; Mészáros, P. GeV Signature of Short Gamma-Ray Bursts in Active Galactic Nuclei. arXiv 2021, arXiv:2112.07653. [Google Scholar]
- Sari, R.; Piran, T. Hydrodynamic Timescales and Temporal Structure of Gamma-Ray Bursts. Astrophys. J. 1995, 455, L143. [Google Scholar] [CrossRef]
- Blandford, R.D.; McKee, C.F. Fluid dynamics of relativistic blast waves. Phys. Fluids 1976, 19, 1130–1138. [Google Scholar] [CrossRef]
- Waxman, E. Angular Size and Emission Timescales of Relativistic Fireballs. Astrophys. J. 1997, 491, L19–L22. [Google Scholar] [CrossRef]
- Panaitescu, A.; Mészáros, P. Rings in Fireball Afterglows. Astrophys. J. 1998, 493, L31–L34. [Google Scholar] [CrossRef][Green Version]
- Dai, Z.G.; Lu, T. Spectrum and Duration of Delayed MeV-GeV Emission of Gamma-Ray Bursts in Cosmic Background Radiation Fields. Astrophys. J. 2002, 580, 1013–1016. [Google Scholar] [CrossRef]
- Razzaque, S.; Mészáros, P.; Zhang, B. GeV and Higher Energy Photon Interactions in Gamma-Ray Burst Fireballs and Surroundings. Astrophys. J. 2004, 613, 1072–1078. [Google Scholar] [CrossRef]
- Wang, X.Y.; Cheng, K.S.; Dai, Z.G.; Lu, T. Constraining the Origin of TeV Photons from Gamma-Ray Bursts with Delayed MeV-GeV Emission Formed by Interaction with Cosmic Infrared/Microwave Background Photons. Astrophys. J. 2004, 604, 306–311. [Google Scholar] [CrossRef][Green Version]
- Murase, K.; Asano, K.; Nagataki, S. Effects of the Cosmic Infrared Background on Delayed High-Energy Emission from Gamma-Ray Bursts. Astrophys. J. 2007, 671, 1886–1895. [Google Scholar] [CrossRef]
- Ichiki, K.; Inoue, S.; Takahashi, K. Probing the Nature of the Weakest Intergalactic Magnetic Fields with the High-Energy Emission of Gamma-Ray Bursts. Astrophys. J. 2008, 682, 127–134. [Google Scholar] [CrossRef]
- Takahashi, K.; Murase, K.; Ichiki, K.; Inoue, S.; Nagataki, S. Detectability of Pair Echoes from Gamma-Ray Bursts and Intergalactic Magnetic Fields. Astrophys. J. 2008, 687, L5. [Google Scholar] [CrossRef]
- Murase, K.; Zhang, B.; Takahashi, K.; Nagataki, S. Possible effects of pair echoes on gamma-ray burst afterglow emission. Mon. Not. R. Astron. Soc. 2009, 396, 1825–1832. [Google Scholar] [CrossRef]
- Jauch, J.M.; Rohrlich, F. The Theory of Photons and Electrons; Addison-Wesley: Boston, MA, USA, 1959. [Google Scholar]
- Gould, R.J.; Schréder, G.P. Pair Production in Photon-Photon Collisions. Phys. Rev. 1967, 155, 1404–1407. [Google Scholar] [CrossRef]
- Ryu, D.; Kang, H.; Biermann, P.L. Cosmic magnetic fields in large scale filaments and sheets. AASS 1998, 335, 19–25. [Google Scholar]
- Kim, K.T.; Tribble, P.C.; Kronberg, P.P. Detection of Excess Rotation Measure Due to Intracluster Magnetic Fields in Clusters of Galaxies. Astrophys. J. 1991, 379, 80. [Google Scholar] [CrossRef]
- Oikonomou, F.; Murase, K.; Kotera, K. Synchrotron pair halo and echo emission from blazars in the cosmic web: Application to extreme TeV blazars. AASS 2014, 568, A110. [Google Scholar] [CrossRef]
- Plaga, R. Detecting intergalactic magnetic fields using time delays in pulses of γ-rays. Nature 1995, 374, 430–432. [Google Scholar] [CrossRef]
- Dermer, C.D.; Atoyan, A. Ultra-high energy cosmic rays, cascade gamma rays, and high-energy neutrinos from gamma-ray bursts. New J. Phys. 2006, 8, 122. [Google Scholar] [CrossRef]
- Mücke, A.; Rachen, J.P.; Engel, R.; Protheroe, R.J.; Stanev, T. Photohadronic Processes in Astrophysical Environments. PASA 1999, 16, 160–166. [Google Scholar] [CrossRef]
- Waxman, E.; Bahcall, J. High Energy Neutrinos from Cosmological Gamma-Ray Burst Fireballs. Phys. Rev. Lett. 1997, 78, 2292–2295. [Google Scholar] [CrossRef]
- Ahrens, J.; Bahcall, J.N.; Bai, X.; Bay, R.C.; Becka, T.; Becker, K.H.; Berley, D.; Bernardini, E.; Bertrand, D.; Besson, D.Z.; et al. Sensitivity of the IceCube detector to astrophysical sources of high energy muon neutrinos. Astropart. Phys. 2004, 20, 507–532. [Google Scholar] [CrossRef]
- Mena, O.; Mocioiu, I.; Razzaque, S. Oscillation effects on high-energy neutrino fluxes from astrophysical hidden sources. Phys. Rev. D 2007, 75, 063003. [Google Scholar] [CrossRef]
- Kashti, T.; Waxman, E. Astrophysical Neutrinos: Flavor Ratios Depend on Energy. Phys. Rev. Lett. 2005, 95, 181101. [Google Scholar] [CrossRef]
- Razzaque, S.; Smirnov, A.Y. Flavor conversion of cosmic neutrinos from hidden jets. J. High Energy Phys. 2010, 2010, 31. [Google Scholar] [CrossRef]
- Dermer, C.D.; Atoyan, A. High-Energy Neutrinos from Gamma Ray Bursts. Phys. Rev. Lett. 2003, 91, 071102. [Google Scholar] [CrossRef]
- Razzaque, S.; Mészáros, P.; Waxman, E. Neutrino signatures of the supernova: Gamma ray burst relationship. Phys. Rev. D 2004, 69, 023001. [Google Scholar] [CrossRef]
- Asano, K. Cooling of Accelerated Nucleons and Neutrino Emission in Gamma-Ray Bursts. Astrophys. J. 2005, 623, 967–972. [Google Scholar] [CrossRef][Green Version]
- Gao, S.; Kashiyama, K.; Mészáros, P. On the Neutrino Non-detection of GRB 130427A. Astrophys. J. 2013, 772, L4. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Samarai, I.A.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Extending the Search for Muon Neutrinos Coincident with Gamma-Ray Bursts in IceCube Data. Astrophys. J. 2017, 843, 112. [Google Scholar] [CrossRef]
- Albert, A.; André, M.; Anghinolfi, M.; Anton, G.; Ardid, M.; Aubert, J.J.; Aublin, J.; Baret, B.; Basa, S.; Belhorma, B.; et al. Constraining the contribution of Gamma-Ray Bursts to the high-energy diffuse neutrino flux with 10 yr of ANTARES data. Mon. Not. R. Astron. Soc. 2021, 500, 5614–5628. [Google Scholar] [CrossRef]
- Asano, K.; Inoue, S.; Mészáros, P. Prompt High-Energy Emission from Proton-Dominated Gamma-Ray Bursts. Astrophys. J. 2009, 699, 953–957. [Google Scholar] [CrossRef]
- Asano, K.; Guiriec, S.; Mészáros, P. Hadronic Models for the Extra Spectral Component in the Short GRB 090510. Astrophys. J. 2009, 705, L191–L194. [Google Scholar] [CrossRef]
- Murase, K.; Asano, K.; Terasawa, T.; Mészáros, P. The Role of Stochastic Acceleration in the Prompt Emission of Gamma-Ray Bursts: Application to Hadronic Injection. Astrophys. J. 2012, 746, 164. [Google Scholar] [CrossRef]
- Bethe, H.A.; Maximon, L.C. Theory of Bremsstrahlung and Pair Production. I. Differential Cross Section. Phys. Rev. 1954, 93, 768–784. [Google Scholar] [CrossRef]
- Chodorowski, M.J.; Zdziarski, A.A.; Sikora, M. Reaction Rate and Energy-Loss Rate for Photopair Production by Relativistic Nuclei. Astrophys. J. 1992, 400, 181. [Google Scholar] [CrossRef]
- Crumley, P.; Kumar, P. Hadronic models for Large Area Telescope prompt emission observed in Fermi gamma-ray bursts. Mon. Not. R. Astron. Soc. 2013, 429, 3238–3251. [Google Scholar] [CrossRef]
- Schneid, E.J.; Bertsch, D.L.; Fichtel, C.E.; Hartman, R.C.; Hunter, S.D.; Kanbach, G.; Kniffen, D.A.; Kwok, P.W.; Lin, Y.C.; Mattox, J.R.; et al. EGRET detection of high energy gamma rays from the gamma-ray burst of 3 May 1991. AASS 1992, 255, L13. [Google Scholar]
- Hurley, K.; Dingus, B.L.; Mukherjee, R.; Sreekumar, P.; Kouveliotou, C.; Meegan, C.; Fishman, G.J.; Band, D.; Ford, L.; Bertsch, D.; et al. Detection of a γ-ray burst of very long duration and very high energy. Nature 1994, 372, 652–654. [Google Scholar] [CrossRef]
- Dingus, B.L. Observations of the highest energy gamma-rays from gamma-ray bursts. In High Energy Gamma-Ray Astronomy: International Symposium; American Institute of Physics Conference Series; Aharonian, F.A., Völk, H.J., Eds.; American Institute of Physics: College Park, MD, USA, 2001; Volume 558, pp. 383–391. [Google Scholar] [CrossRef]
- González, M.M.; Dingus, B.L.; Kaneko, Y.; Preece, R.D.; Dermer, C.D.; Briggs, M.S. A γ-ray burst with a high-energy spectral component inconsistent with the synchrotron shock model. Nature 2003, 424, 749–751. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.W.; Peng, F.K.; Wang, X.Y.; Tam, P.H.T. Measuring the Bulk Lorentz Factors of Gamma-ray Bursts with Fermi. Astrophys. J. 2015, 806, 194. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; et al. Fermi Observations of GRB 090902B: A Distinct Spectral Component in the Prompt and Delayed Emission. Astrophys. J. 2009, 706, L138–L144. [Google Scholar] [CrossRef]
- Ackermann, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bechtol, K.; et al. Fermi Observations of GRB 090510: A Short-Hard Gamma-ray Burst with an Additional, Hard Power-law Component from 10 keV TO GeV Energies. Astrophys. J. 2010, 716, 1178–1190. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Asano, K.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bechtol, K.; et al. Detection of a Spectral Break in the Extra Hard Component of GRB 090926A. Astrophys. J. 2011, 729, 114. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Asano, K.; Baldini, L.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bellazzini, R.; Blandford, R.D.; Bonamente, E.; et al. Multiwavelength Observations of GRB 110731A: GeV Emission from Onset to Afterglow. Astrophys. J. 2013, 763, 71. [Google Scholar] [CrossRef]
- Nava, L.; Vianello, G.; Omodei, N.; Ghisellini, G.; Ghirlanda, G.; Celotti, A.; Longo, F.; Desiante, R.; Barniol Duran, R. Clustering of LAT light curves: A clue to the origin of high-energy emission in gamma-ray bursts. Mon. Not. R. Astron. Soc. 2014, 443, 3578–3585. [Google Scholar] [CrossRef]
- Ghisellini, G.; Ghirlanda, G.; Nava, L.; Celotti, A. GeV emission from gamma-ray bursts: A radiative fireball? Mon. Not. R. Astron. Soc. 2010, 403, 926–937. [Google Scholar] [CrossRef]
- Gehrels, N.; Razzaque, S. Gamma-ray bursts in the swift-Fermi era. Front. Phys. 2013, 8, 661–678. [Google Scholar] [CrossRef]
- Zou, Y.C.; Fan, Y.Z.; Piran, T. The possible high-energy emission from GRB 080319B and origins of the GeV emission of GRBs 080514B, 080916C and 081024B. Mon. Not. R. Astron. Soc. 2009, 396, 1163–1170. [Google Scholar] [CrossRef]
- Kumar, P.; Barniol Duran, R. On the generation of high-energy photons detected by the Fermi Satellite from gamma-ray bursts. Mon. Not. R. Astron. Soc. 2009, 400, L75–L79. [Google Scholar] [CrossRef]
- Kumar, P.; Barniol Duran, R. External forward shock origin of high-energy emission for three gamma-ray bursts detected by Fermi. Mon. Not. R. Astron. Soc. 2010, 409, 226–236. [Google Scholar] [CrossRef]
- Granot, J. Interaction of a highly magnetized impulsive relativistic flow with an external medium. Mon. Not. R. Astron. Soc. 2012, 421, 2442–2466. [Google Scholar] [CrossRef][Green Version]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; et al. A limit on the variation of the speed of light arising from quantum gravity effects. Nature 2009, 462, 331–334. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Arimoto, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. Fermi Observations of High-Energy Gamma-Ray Emission from GRB 080916C. Science 2009, 323, 1688. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J.; Wijers, R.A.M.J. Viewing Angle and Environment Effects in Gamma-Ray Bursts: Sources of Afterglow Diversity. Astrophys. J. 1998, 499, 301–308. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; et al. Fermi-LAT Observations of the Gamma-Ray Burst GRB 130427A. Science 2014, 343, 42–47. [Google Scholar] [CrossRef]
- Thompson, C.; Madau, P. Relativistic Winds from Compact Gamma-Ray Sources. II. Pair Loading and Radiative Acceleration in Gamma-Ray Bursts. Astrophys. J. 2000, 538, 105–114. [Google Scholar] [CrossRef]
- Mészáros, P.; Ramirez-Ruiz, E.; Rees, M.J. e+/- Pair Cascades and Precursors in Gamma-Ray Bursts. Astrophys. J. 2001, 554, 660–666. [Google Scholar] [CrossRef][Green Version]
- Beloborodov, A.M. Radiation Front Sweeping the Ambient Medium of Gamma-Ray Bursts. Astrophys. J. 2002, 565, 808–828. [Google Scholar] [CrossRef]
- Kumar, P.; Panaitescu, A. Creation of electron-positron wind in gamma-ray bursts and its effect on the early afterglow emission. Mon. Not. R. Astron. Soc. 2004, 354, 252–258. [Google Scholar] [CrossRef]
- Thompson, C. Deceleration of a Relativistic, Photon-rich Shell: End of Preacceleration, Damping of Magnetohydrodynamic Turbulence, and the Emission Mechanism of Gamma-Ray Bursts. Astrophys. J. 2006, 651, 333–365. [Google Scholar] [CrossRef][Green Version]
- Razzaque, S. A Leptonic-Hadronic Model for the Afterglow of Gamma-ray Burst 090510. Astrophys. J. 2010, 724, L109–L112. [Google Scholar] [CrossRef]
- Asano, K.; Mészáros, P. Delayed Onset of High-energy Emissions in Leptonic and Hadronic Models of Gamma-Ray Bursts. Astrophys. J. 2012, 757, 115. [Google Scholar] [CrossRef]
- Bošnjak, Ž.; Daigne, F.; Dubus, G. Prompt high-energy emission from gamma-ray bursts in the internal shock model. AASS 2009, 498, 677–703. [Google Scholar] [CrossRef]
- Asano, K.; Mészáros, P. Spectral-Temporal Simulations of Internal Dissipation Models of Gamma-Ray Bursts. Astrophys. J. 2011, 739, 103. [Google Scholar] [CrossRef]
- Guiriec, S.; Briggs, M.S.; Connaugthon, V.; Kara, E.; Daigne, F.; Kouveliotou, C.; van der Horst, A.J.; Paciesas, W.; Meegan, C.A.; Bhat, P.N.; et al. Time-resolved Spectroscopy of the Three Brightest and Hardest Short Gamma-ray Bursts Observed with the Fermi Gamma-ray Burst Monitor. Astrophys. J. 2010, 725, 225–241. [Google Scholar] [CrossRef]
- Arimoto, M.; Asano, K.; Ohno, M.; Veres, P.; Axelsson, M.; Bissaldi, E.; Tachibana, Y.; Kawai, N. High-energy Non-thermal and Thermal Emission from GRB 141207A Detected by Fermi. Astrophys. J. 2016, 833, 139. [Google Scholar] [CrossRef]
- Ajello, M.; Arimoto, M.; Axelsson, M.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Berretta, A.; Bissaldi, E.; Blandford, R.D.; et al. Fermi and Swift Observations of GRB 190114C: Tracing the Evolution of High-energy Emission from Prompt to Afterglow. Astrophys. J. 2020, 890, 9. [Google Scholar] [CrossRef]
- Guiriec, S.; Connaughton, V.; Briggs, M.S.; Burgess, M.; Ryde, F.; Daigne, F.; Mészáros, P.; Goldstein, A.; McEnery, J.; Omodei, N.; et al. Detection of a Thermal Spectral Component in the Prompt Emission of GRB 100724B. Astrophys. J. 2011, 727, L33. [Google Scholar] [CrossRef]
- Guiriec, S.; Kouveliotou, C.; Daigne, F.; Zhang, B.; Hascoët, R.; Nemmen, R.S.; Thompson, D.J.; Bhat, P.N.; Gehrels, N.; Gonzalez, M.M.; et al. Toward a Better Understanding of the GRB Phenomenon: A New Model for GRB Prompt Emission and its Effects on the New LiNT- Epeak,irest,NT Relation. Astrophys. J. 2015, 807, 148. [Google Scholar] [CrossRef]
- Guiriec, S.; Kouveliotou, C.; Hartmann, D.H.; Granot, J.; Asano, K.; Mészáros, P.; Gill, R.; Gehrels, N.; McEnery, J. A Unified Model for GRB Prompt Emission from Optical to γ-Rays: Exploring GRBs as Standard Candles. Astrophys. J. 2016, 831, L8. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Granot, J.; Racusin, J.L.; Bellm, E.; Vianello, G.; Oates, S.; Fryer, C.L.; Boggs, S.E.; Christensen, F.E.; Craig, W.W.; et al. NuSTAR Observations of GRB 130427A Establish a Single Component Synchrotron Afterglow Origin for the Late Optical to Multi-GeV Emission. Astrophys. J. 2013, 779, L1. [Google Scholar] [CrossRef]
- Piran, T. Gamma-ray bursts and the fireball model. Phys. Rep. 1999, 314, 575–667. [Google Scholar] [CrossRef]
- Goodman, J. Are gamma-ray bursts optically thick? Astrophys. J. 1986, 308, L47. [Google Scholar] [CrossRef]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. 1986, 308, L43–L46. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Relativistic fireballs—Energy conversion and time-scales. Mon. Not. R. Astron. Soc. 1992, 258, 41. [Google Scholar] [CrossRef]
- Zou, Y.C.; Fan, Y.Z.; Piran, T. A Revised Limit of the Lorentz Factors of Gamma-ray Bursts with Two Emitting Regions. Astrophys. J. 2011, 726, L2. [Google Scholar] [CrossRef]
- Hascoët, R.; Daigne, F.; Mochkovitch, R.; Vennin, V. Do Fermi Large Area Telescope observations imply very large Lorentz factors in gamma-ray burst outflows? Mon. Not. R. Astron. Soc. 2012, 421, 525–545. [Google Scholar] [CrossRef]
- Li, Z. Prompt GeV Emission from Residual Collisions in Gamma-Ray Burst Outflows: Evidence from Fermi Observations of Grb 080916c. Astrophys. J. 2010, 709, 525–534. [Google Scholar] [CrossRef]
- Aoi, J.; Murase, K.; Takahashi, K.; Ioka, K.; Nagataki, S. Can We Probe the Lorentz Factor of Gamma-ray Bursts from GeV-TeV Spectra Integrated Over Internal Shocks? Astrophys. J. 2010, 722, 440–451. [Google Scholar] [CrossRef]
- Preece, R.; Burgess, J.M.; von Kienlin, A.; Bhat, P.N.; Briggs, M.S.; Byrne, D.; Chaplin, V.; Cleveland, W.; Collazzi, A.C.; Connaughton, V.; et al. The First Pulse of the Extremely Bright GRB 130427A: A Test Lab for Synchrotron Shocks. Science 2014, 343, 51–54. [Google Scholar] [CrossRef] [PubMed]
- Maselli, A.; Melandri, A.; Nava, L.; Mundell, C.G.; Kawai, N.; Campana, S.; Covino, S.; Cummings, J.R.; Cusumano, G.; Evans, P.A.; et al. GRB 130427A: A Nearby Ordinary Monster. Science 2014, 343, 48–51. [Google Scholar] [CrossRef]
- Levan, A.J.; Cenko, S.B.; Perley, D.A.; Tanvir, N.R. GRB 130427A: Gemini-north redshift. GRB Coord. Netw. 2013, 14455, 1. [Google Scholar]
- von Kienlin, A. GRB 130427A: Fermi GBM observation. GRB Coord. Netw. 2013, 14473, 1. [Google Scholar]
- Verrecchia, F.; Pittori, C.; Giuliani, A.; Marisaldi, M.; Longo, F.; Lucarelli, F.; Del, M.E.; Lazzarotto, F.; Donnarumma, I.; Evangelista, Y.; et al. GRB 130427A: High energy gamma-ray detection by AGILE. GRB Coord. Netw. 2013, 14515, 1. [Google Scholar]
- Golenetskii, S.; Aptekar, R.; Frederiks, D.; Mazets, E.; Pal’Shin, V.; Oleynik, P.; Ulanov, M.; Svinkin, D.; Cline, T. Konus-wind observation of GRB 130427A. GRB Coord. Netw. 2013, 14487, 1. [Google Scholar]
- Smith, D.M.; Csillaghy, A.; Hurley, K.; Hudson, H.; Boggs, S.; Inglis, A. GRB 130427A: RHESSI observations. GRB Coord. Netw. 2013, 14590, 1. [Google Scholar]
- Maselli, A.; Beardmore, A.P.; Lien, A.Y.; Mangano, V.; Mountford, C.J.; Page, K.L.; Palmer, D.M.; Siegel, M.H. GRB 130427A: Swift detection of a very bright burst with a likely bright optical counterpart. GRB Coord. Netw. 2013, 14448, 1. [Google Scholar]
- Perley, D.A.; Cenko, S.B.; Corsi, A.; Tanvir, N.R.; Levan, A.J.; Kann, D.A.; Sonbas, E.; Wiersema, K.; Zheng, W.; Zhao, X.H.; et al. The Afterglow of GRB 130427A from 1 to 1016 GHz. Astrophys. J. 2014, 781, 37. [Google Scholar] [CrossRef]
- de Jager, O.C.; Harding, A.K.; Michelson, P.F.; Nel, H.I.; Nolan, P.L.; Sreekumar, P.; Thompson, D.J. Gamma-Ray Observations of the Crab Nebula: A Study of the Synchro-Compton Spectrum. Astrophys. J. 1996, 457, 253. [Google Scholar] [CrossRef]
- Kirk, J.G.; Reville, B. Radiative Signatures of Relativistic Shocks. Astrophys. J. 2010, 710, L16–L20. [Google Scholar] [CrossRef]
- Fan, Y.Z.; Tam, P.H.T.; Zhang, F.W.; Liang, Y.F.; He, H.N.; Zhou, B.; Yang, R.Z.; Jin, Z.P.; Wei, D.M. High-energy Emission of GRB 130427A: Evidence for Inverse Compton Radiation. Astrophys. J. 2013, 776, 95. [Google Scholar] [CrossRef][Green Version]
- Aliu, E.; Aune, T.; Barnacka, A.; Beilicke, M.; Benbow, W.; Berger, K.; Biteau, J.; Buckley, J.H.; Bugaev, V.; Byrum, K.; et al. Constraints on Very High Energy Emission from GRB 130427A. Astrophys. J. 2014, 795, L3. [Google Scholar] [CrossRef]
- Lyutikov, M. A high-sigma model of pulsar wind nebulae. Mon. Not. R. Astron. Soc. 2010, 405, 1809–1815. [Google Scholar] [CrossRef][Green Version]
- Guetta, D.; Granot, J. High-Energy Emission from the Prompt Gamma-Ray Burst. Astrophys. J. 2003, 585, 885–889. [Google Scholar] [CrossRef]
- Pe’er, A.; Waxman, E. Prompt Gamma-Ray Burst Spectra: Detailed Calculations and the Effect of Pair Production. Astrophys. J. 2004, 613, 448–459. [Google Scholar] [CrossRef]
- Gupta, N.; Zhang, B. Prompt emission of high-energy photons from gamma ray bursts. Mon. Not. R. Astron. Soc. 2007, 380, 78–92. [Google Scholar] [CrossRef]
- Pe’Er, A.; Zhang, B.B.; Ryde, F.; McGlynn, S.; Zhang, B.; Preece, R.D.; Kouveliotou, C. The connection between thermal and non-thermal emission in gamma-ray bursts: General considerations and GRB 090902B as a case study. Mon. Not. R. Astron. Soc. 2012, 420, 468–482. [Google Scholar] [CrossRef]
- Dermer, C.D.; Chiang, J.; Mitman, K.E. Beaming, Baryon Loading, and the Synchrotron Self-Compton Component in Gamma-Ray Bursts. Astrophys. J. 2000, 537, 785–795. [Google Scholar] [CrossRef]
- Stecker, F.W.; Malkan, M.A.; Scully, S.T. Intergalactic Photon Spectra from the Far-IR to the UV Lyman Limit for 0 < z < 6 and the Optical Depth of the Universe to High-Energy Gamma Rays. Astrophys. J. 2006, 648, 774–783. [Google Scholar] [CrossRef]
- Atkins, R.; Benbow, W.; Berley, D.; Chen, M.L.; Coyne, D.G.; Dingus, B.L.; Dorfan, D.E.; Ellsworth, R.W.; Evans, D.; Falcone, A.; et al. Evidence for TEV Emission from GRB 970417A. Astrophys. J. 2000, 533, L119–L122. [Google Scholar] [CrossRef] [PubMed]
- Razzaque, S.; Mena, O.; Dermer, C.D. Prompt TeV Emission from Cosmic Rays Accelerated by Gamma-Ray Bursts Interacting with a Surrounding Stellar Wind. Astrophys. J. 2009, 691, L37–L40. [Google Scholar] [CrossRef]
- Weekes, T.C.; Badran, H.; Biller, S.D.; Bond, I.; Bradbury, S.; Buckley, J.; Carter-Lewis, D.; Catanese, M.; Criswell, S.; Cui, W.; et al. VERITAS: The Very Energetic Radiation Imaging Telescope Array System. Astropart. Phys. 2002, 17, 221–243. [Google Scholar] [CrossRef]
- Ferenc, D.; MAGIC Collaboration. The MAGIC gamma-ray observatory. Nucl. Instrum. Methods Phys. Res. A 2005, 553, 274–281. [Google Scholar] [CrossRef]
- Hinton, J.A.; HESS Collaboration. The status of the HESS project. New Astron. Rev. 2004, 48, 331–337. [Google Scholar] [CrossRef]
- MAGIC Collaboration; Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; et al. Teraelectronvolt emission from the γ-ray burst GRB 190114C. Nature 2019, 575, 455–458. [Google Scholar] [CrossRef]
- Ursi, A.; Tavani, M.; Frederiks, D.D.; Romani, M.; Verrecchia, F.; Marisaldi, M.; Aptekar, R.L.; Antonelli, L.A.; Argan, A.; Bulgarelli, A.; et al. AGILE and Konus-Wind Observations of GRB 190114C: The Remarkable Prompt and Early Afterglow Phases. Astrophys. J. 2020, 904, 133. [Google Scholar] [CrossRef]
- MAGIC Collaboration; Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Engels, A.A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; et al. Observation of inverse Compton emission from a long γ-ray burst. Nature 2019, 575, 459–463. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Asano, K.; Baack, D.; Babić, A.; Baquero, A.; Barres de Almeida, U.; Barrio, J.A.; et al. MAGIC Observations of the Nearby Short Gamma-Ray Burst GRB 160821B. Astrophys. J. 2021, 908, 90. [Google Scholar] [CrossRef]
- Abdalla, H.; Adam, R.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arakawa, M.; Arcaro, C.; Armand, C.; Ashkar, H.; Backes, M.; et al. A very-high-energy component deep in the γ-ray burst afterglow. Nature 2019, 575, 464–467. [Google Scholar] [CrossRef] [PubMed]
- HSSS Collaboration; Abdalla, H.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arcaro, C.; Armand, C.; Armstrong, T.; Ashkar, H.; Backes, M.; et al. Revealing x-ray and gamma ray temporal and spectral similarities in the GRB 190829A afterglow. Science 2021, 372, 1081–1085. [Google Scholar] [CrossRef] [PubMed]
- Fukami, S.; Berti, A.; Loporchio, S.; Suda, Y.; Nava, L.; Noda, K.; Bošnjak, Z.; Asano, K.; Longo, F.; Acciari, V.A.; et al. Very-high-energy gamma-ray emission from GRB 201216C detected by MAGIC. PoS 2021, ICRC2021, 788. [Google Scholar] [CrossRef]
- Wang, X.Y.; Liu, R.Y.; Zhang, H.M.; Xi, S.Q.; Zhang, B. Synchrotron Self-Compton Emission from External Shocks as the Origin of the Sub-TeV Emission in GRB 180720B and GRB 190114C. Astrophys. J. 2019, 884, 117. [Google Scholar] [CrossRef]
- Zhang, H.; Christie, I.M.; Petropoulou, M.; Rueda-Becerril, J.M.; Giannios, D. Inverse Compton signatures of gamma-ray burst afterglows. Mon. Not. R. Astron. Soc. 2020, 496, 974–986. [Google Scholar] [CrossRef]
- Joshi, J.C.; Razzaque, S. Modelling synchrotron and synchrotron self-Compton emission of gamma-ray burst afterglows from radio to very-high energies. Mon. Not. R. Astron. Soc. 2021, 505, 1718–1729. [Google Scholar] [CrossRef]
- Yamasaki, S.; Piran, T. Analytic Modeling of Synchroton-Self-Compton Spectra: Application to GRB 190114C. arXiv 2021, arXiv:2112.06945. [Google Scholar]
- Jacovich, T.E.; Beniamini, P.; van der Horst, A.J. Modelling synchrotron self-Compton and Klein–Nishina effects in gamma-ray burst afterglows. Mon. Not. R. Astron. Soc. 2021, 504, 528–542. [Google Scholar] [CrossRef]
- Asano, K.; Murase, K.; Toma, K. Probing Particle Acceleration through Broadband Early Afterglow Emission of MAGIC Gamma-Ray Burst GRB 190114C. Astrophys. J. 2020, 905, 105. [Google Scholar] [CrossRef]
- Derishev, E.; Piran, T. GRB Afterglow Parameters in the Era of TeV Observations: The Case of GRB 190114C. Astrophys. J. 2021, 923, 135. [Google Scholar] [CrossRef]
- Zhang, B.T.; Murase, K.; Veres, P.; Mészáros, P. External Inverse-Compton Emission from Low-luminosity Gamma-Ray Bursts: Application to GRB 190829A. Astrophys. J. 2021, 920, 55. [Google Scholar] [CrossRef]
- Sahu, S.; Fortín, C.E.L. Origin of Sub-TeV Afterglow Emission from Gamma-Ray Bursts GRB 190114C and GRB 180720B. Astrophys. J. 2020, 895, L41. [Google Scholar] [CrossRef]
- Sahu, S.; Valadez Polanco, I.A.; Rajpoot, S. Very High-energy Afterglow Emission of GRB 190829A: Evidence for Its Hadronic Origin? Astrophys. J. 2022, 929, 70. [Google Scholar] [CrossRef]
- Eichler, D.; Waxman, E. The Efficiency of Electron Acceleration in Collisionless Shocks and Gamma-Ray Burst Energetics. Astrophys. J. 2005, 627, 861–867. [Google Scholar] [CrossRef]
- Sagiv, A.; Waxman, E.; Loeb, A. Probing the Magnetic Field Structure in Gamma-Ray Bursts through Dispersive Plasma Effects on the Afterglow Polarization. Astrophys. J. 2004, 615, 366–377. [Google Scholar] [CrossRef][Green Version]
- Toma, K.; Ioka, K.; Nakamura, T. Probing the Efficiency of Electron-Proton Coupling in Relativistic Collisionless Shocks through the Radio Polarimetry of Gamma-Ray Burst Afterglows. Astrophys. J. 2008, 673, L123. [Google Scholar] [CrossRef][Green Version]
- Giannios, D.; Spitkovsky, A. Signatures of a Maxwellian component in shock-accelerated electrons in GRBs. Mon. Not. R. Astron. Soc. 2009, 400, 330–336. [Google Scholar] [CrossRef]
- Ressler, S.M.; Laskar, T. Thermal Electrons in Gamma-Ray Burst Afterglows. Astrophys. J. 2017, 845, 150. [Google Scholar] [CrossRef]
- Warren, D.C.; Dainotti, M.; Barkov, M.V.; Ahlgren, B.; Ito, H.; Nagataki, S. A Semianalytic Afterglow with Thermal Electrons and Synchrotron Self-Compton Emission. Astrophys. J. 2022, 924, 40. [Google Scholar] [CrossRef]
- Misra, K.; Resmi, L.; Kann, D.A.; Marongiu, M.; Moin, A.; Klose, S.; Bernardi, G.; de Ugarte Postigo, A.; Jaiswal, V.K.; Schulze, S.; et al. Low frequency view of GRB 190114C reveals time varying shock micro-physics. Mon. Not. R. Astron. Soc. 2021, 504, 5685–5701. [Google Scholar] [CrossRef]
- Fraija, N.; Dichiara, S.; Pedreira, A.C.C.d.E.S.; Galvan-Gamez, A.; Becerra, R.L.; Montalvo, A.; Montero, J.; Betancourt Kamenetskaia, B.; Zhang, B.B. Modeling the Observations of GRB 180720B: From Radio to Sub-TeV Gamma-Rays. Astrophys. J. 2019, 885, 29. [Google Scholar] [CrossRef]
- Salafia, O.S.; Ravasio, M.E.; Yang, J.; An, T.; Orienti, M.; Ghirlanda, G.; Nava, L.; Giroletti, M.; Mohan, P.; Spinelli, R.; et al. Multi-wavelength view of the close-by GRB~190829A sheds light on gamma-ray burst physics. arXiv 2021, arXiv:2106.07169. [Google Scholar]
- Dichiara, S.; Troja, E.; Lipunov, V.; Ricci, R.; Oates, S.R.; Butler, N.R.; Liuzzo, E.; Ryan, G.; O’Connor, B.; Cenko, S.B.; et al. The early afterglow of GRB 190829A. arXiv 2021, arXiv:2111.14861. [Google Scholar] [CrossRef]
- Abdalla, H.; Abramowski, A.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arakawa, M.; Arrieta, M.; Aubert, P.; Backes, M.; Balzer, A.; et al. TeV Gamma-Ray Observations of the Binary Neutron Star Merger GW170817 with H.E.S.S. Astrophys. J. 2017, 850, L22. [Google Scholar] [CrossRef]
- Galván, A.; Fraija, N.; González, M.M. Search for very-high-energy emission with HAWC from GW170817 event. In Proceedings of the 36th International Cosmic Ray Conference (ICRC2019), Madison, WI, USA, 1 August 2019; Volume 36, p. 681. [Google Scholar]
- Acharya, B.S.; Actis, M.; Aghajani, T.; Agnetta, G.; Aguilar, J.; Aharonian, F.; Ajello, M.; Akhperjanian, A.; Alcubierre, M.; Aleksić, J.; et al. Introducing the CTA concept. Astropart. Phys. 2013, 43, 3–18. [Google Scholar] [CrossRef]
- Kneiske, T.M.; Bretz, T.; Mannheim, K.; Hartmann, D.H. Implications of cosmological gamma-ray absorption. II. Modification of gamma-ray spectra. AASS 2004, 413, 807–815. [Google Scholar] [CrossRef]
- Franceschini, A.; Rodighiero, G.; Vaccari, M. Extragalactic optical-infrared background radiation, its time evolution and the cosmic photon-photon opacity. AASS 2008, 487, 837–852. [Google Scholar] [CrossRef]
- Razzaque, S.; Dermer, C.D.; Finke, J.D. The Stellar Contribution to the Extragalactic Background Light and Absorption of High-Energy Gamma Rays. Astrophys. J. 2009, 697, 483–492. [Google Scholar] [CrossRef]
- Gilmore, R.C.; Madau, P.; Primack, J.R.; Somerville, R.S.; Haardt, F. GeV gamma-ray attenuation and the high-redshift UV background. Mon. Not. R. Astron. Soc. 2009, 399, 1694–1708. [Google Scholar] [CrossRef]
- Finke, J.D.; Razzaque, S.; Dermer, C.D. Modeling the Extragalactic Background Light from Stars and Dust. Astrophys. J. 2010, 712, 238–249. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; et al. Fermi Large Area Telescope Constraints on the Gamma-ray Opacity of the Universe. Astrophys. J. 2010, 723, 1082–1096. [Google Scholar] [CrossRef]
- Domínguez, A.; Primack, J.R.; Rosario, D.J.; Prada, F.; Gilmore, R.C.; Faber, S.M.; Koo, D.C.; Somerville, R.S.; Pérez-Torres, M.A.; Pérez-González, P.; et al. Extragalactic background light inferred from AEGIS galaxy-SED-type fractions. Mon. Not. R. Astron. Soc. 2011, 410, 2556–2578. [Google Scholar] [CrossRef]
- Hauser, M.G.; Dwek, E. The Cosmic Infrared Background: Measurements and Implications. Annu. Rev. Astron. Astrophys. 2001, 39, 249–307. [Google Scholar] [CrossRef]
- Kronberg, P.P. Extragalactic magnetic fields. Rep. Prog. Phys. 1994, 57, 325–382. [Google Scholar] [CrossRef]
- Grasso, D.; Rubinstein, H.R. Magnetic fields in the early Universe. Phys. Rep. 2001, 348, 163–266. [Google Scholar] [CrossRef]
- Widrow, L.M. Origin of galactic and extragalactic magnetic fields. Rev. Mod. Phys. 2002, 74, 775–823. [Google Scholar] [CrossRef]
- Kulsrud, R.M.; Zweibel, E.G. On the origin of cosmic magnetic fields. Rep. Prog. Phys. 2008, 71, 046901. [Google Scholar] [CrossRef]
- Tavecchio, F.; Ghisellini, G.; Foschini, L.; Bonnoli, G.; Ghirlanda, G.; Coppi, P. The intergalactic magnetic field constrained by Fermi/Large Area Telescope observations of the TeV blazar 1ES0229+200. Mon. Not. R. Astron. Soc. 2010, 406, L70–L74. [Google Scholar] [CrossRef]
- Murase, K.; Takahashi, K.; Inoue, S.; Ichiki, K.; Nagataki, S. Probing Intergalactic Magnetic Fields in the GLAST Era through Pair Echo Emission from TeV Blazars. Astrophys. J. 2008, 686, L67. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Coppi, P.S.; Voelk, H.J. Very High Energy Gamma Rays from Active Galactic Nuclei: Cascading on the Cosmic Background Radiation Fields and the Formation of Pair Halos. Astrophys. J. 1994, 423, L5. [Google Scholar] [CrossRef]
- Neronov, A.; Vovk, I. Evidence for Strong Extragalactic Magnetic Fields from Fermi Observations of TeV Blazars. Science 2010, 328, 73. [Google Scholar] [CrossRef] [PubMed]
- Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; Bloom, E.D.; et al. The Search for Spatial Extension in High-latitude Sources Detected by the Fermi Large Area Telescope. Astrophys. J. Suppl. Ser. 2018, 237, 32. [Google Scholar] [CrossRef]
- Veres, P.; Dermer, C.D.; Dhuga, K.S. Properties of the Intergalactic Magnetic Field Constrained by Gamma-Ray Observations of Gamma-Ray Bursts. Astrophys. J. 2017, 847, 39. [Google Scholar] [CrossRef]
- Wang, Z.R.; Xi, S.Q.; Liu, R.Y.; Xue, R.; Wang, X.Y. Constraints on the intergalactic magnetic field from γ -ray observations of GRB 190114C. Phys. Rev. D 2020, 101, 083004. [Google Scholar] [CrossRef]
- Dzhatdoev, T.A.; Podlesnyi, E.I.; Vaiman, I.A. Can we constrain the extragalactic magnetic field from very high energy observations of GRB 190114C? Phys. Rev. D 2020, 102, 123017. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Ellis, J.; Mavromatos, N.E.; Nanopoulos, D.V.; Sarkar, S. Tests of quantum gravity from observations of γ-ray bursts. Nature 1998, 393, 763–765. [Google Scholar] [CrossRef]
- Mattingly, D. Modern Tests of Lorentz Invariance. Living Rev. Relativ. 2005, 8, 5. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Astrophysical Tests of Lorentz and CPT Violation with Photons. Astrophys. J. 2008, 689, L1. [Google Scholar] [CrossRef]
- Vasileiou, V.; Jacholkowska, A.; Piron, F.; Bolmont, J.; Couturier, C.; Granot, J.; Stecker, F.W.; Cohen-Tanugi, J.; Longo, F. Constraints on Lorentz invariance violation from Fermi-Large Area Telescope observations of gamma-ray bursts. Phys. Rev. D 2013, 87, 122001. [Google Scholar] [CrossRef]
- Vasileiou, V.; Granot, J.; Piran, T.; Amelino-Camelia, G. A Planck-scale limit on spacetime fuzziness and stochastic Lorentz invariance violation. Nat. Phys. 2015, 11, 344–346. [Google Scholar] [CrossRef]
- Vurm, I.; Hascoët, R.; Beloborodov, A.M. Pair-dominated GeV-Optical Flash in GRB 130427A. Astrophys. J. 2014, 789, L37. [Google Scholar] [CrossRef]
- Dorner, D.; Mostafá, M.; Satalecka, K. High-Energy Alerts in the Multi-Messenger Era. Universe 2021, 7, 393. [Google Scholar] [CrossRef]
- Avrorin, A.D.; Avrorin, A.V.; Aynutdinov, V.M.; Bannash, R.; Belolaptikov, I.A.; Brudanin, V.B.; Budnev, N.M.; Domogatsky, G.V.; Doroshenko, A.A.; Dvornicky, R.; et al. Baikal-GVD: First results and prospects. Eur. Phys. J. Web Conf. 2019, 209, 01015. [Google Scholar] [CrossRef][Green Version]
- Adrián-Martínez, S.; Ageron, M.; Aharonian, F.; Aiello, S.; Albert, A.; Ameli, F.; Anassontzis, E.; Andre, M.; Androulakis, G.; Anghinolfi, M.; et al. Letter of intent for KM3NeT 2.0. J. Phys. G Nucl. Phys. 2016, 43, 084001. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).