Nomogram-Based Chronic Kidney Disease Prediction Model for Type 1 Diabetes Mellitus Patients Using Routine Pathological Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset Description
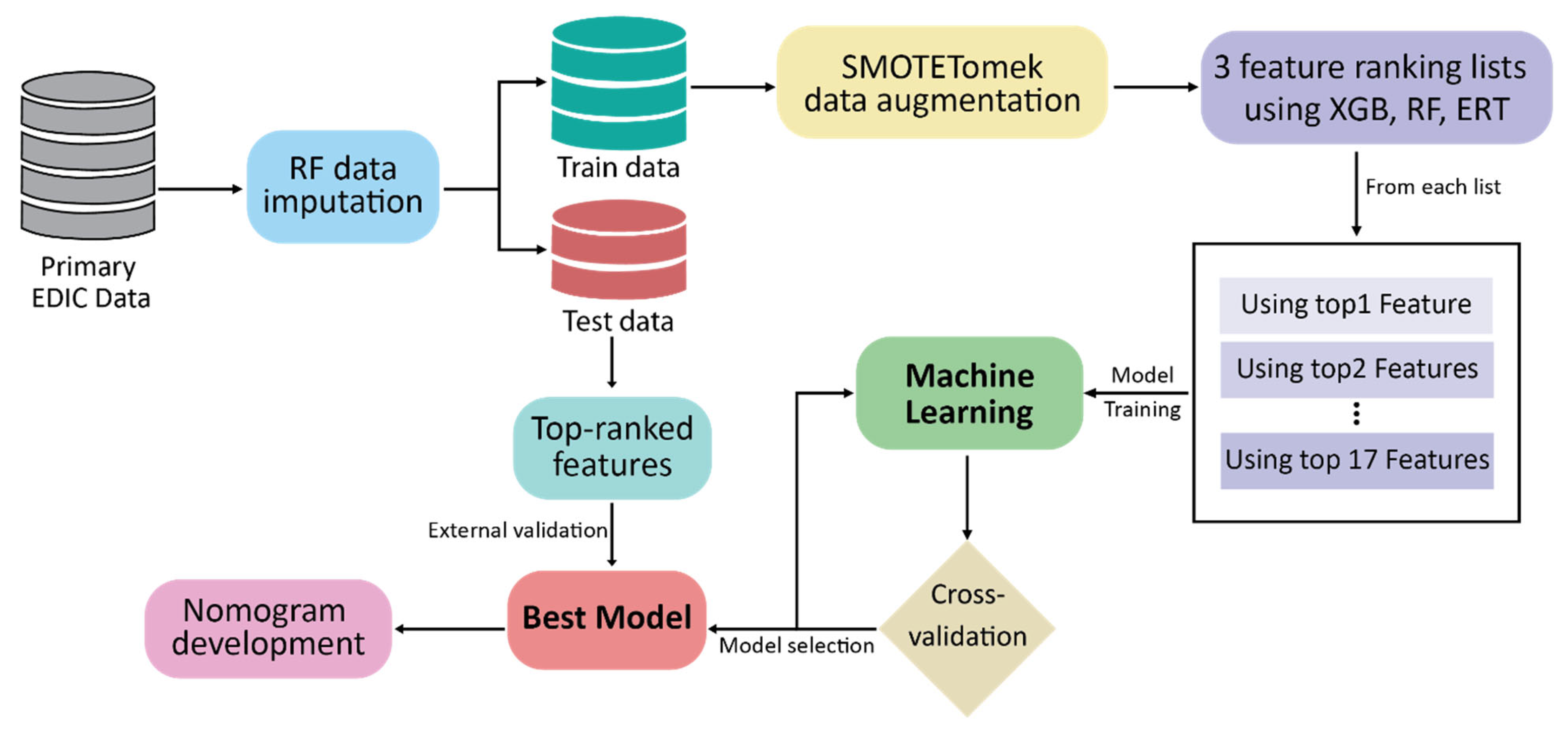
2.2. Data Preprocessing and Feature Ranking
2.3. Statistical Analyses
2.4. Development of Prediction Model
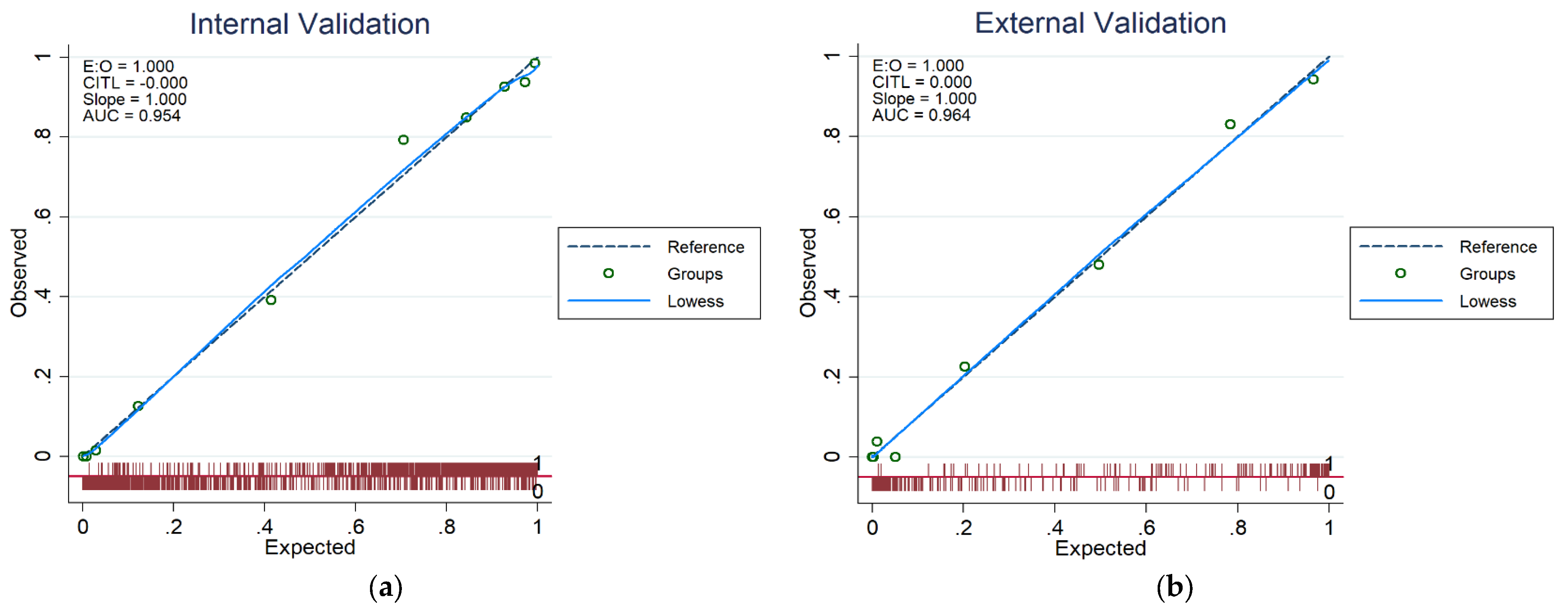
2.5. Validation of CKD Prediction Models
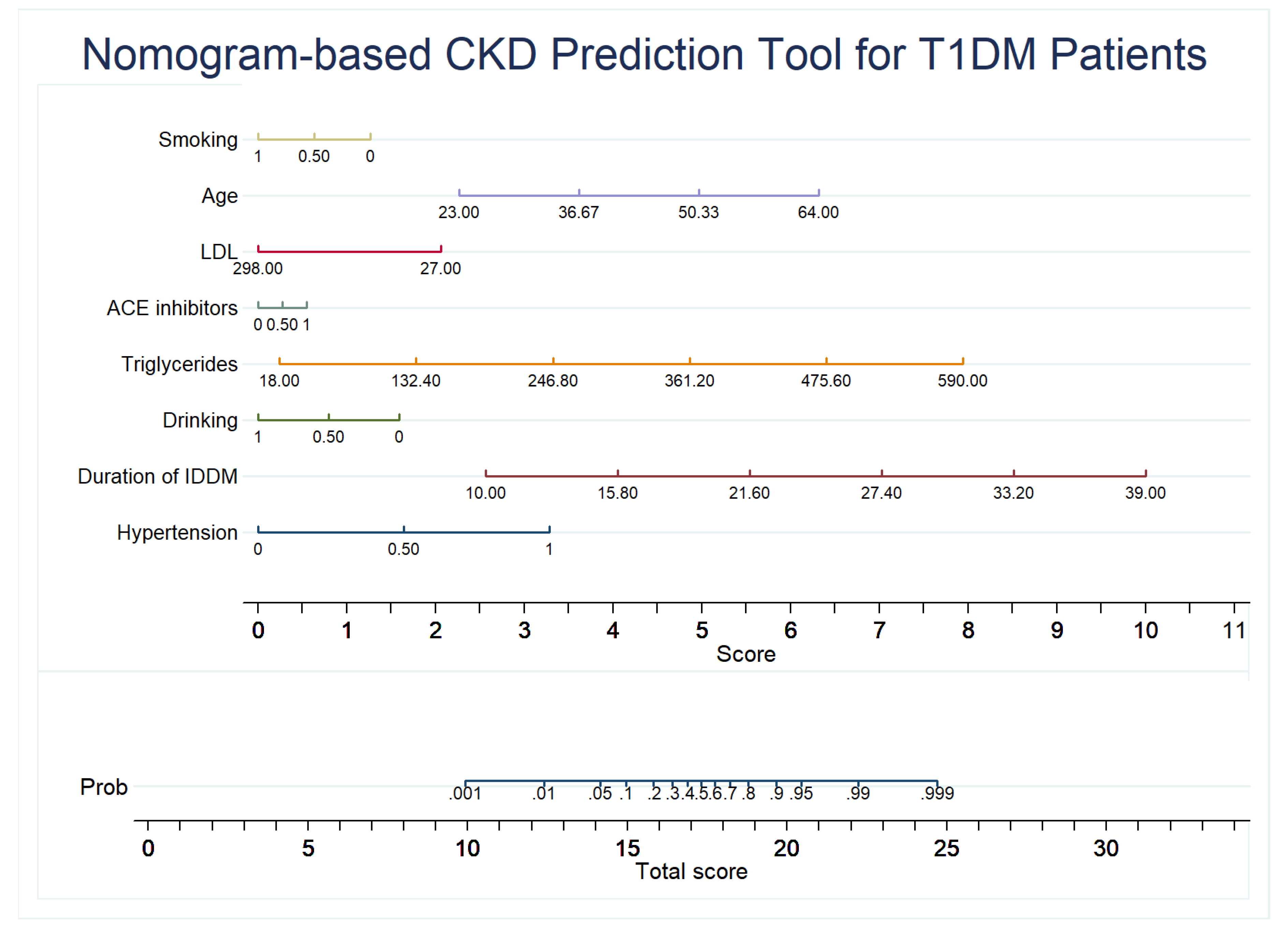
2.6. Development of the Nomogram
3. Results
3.1. Baseline Characteristics
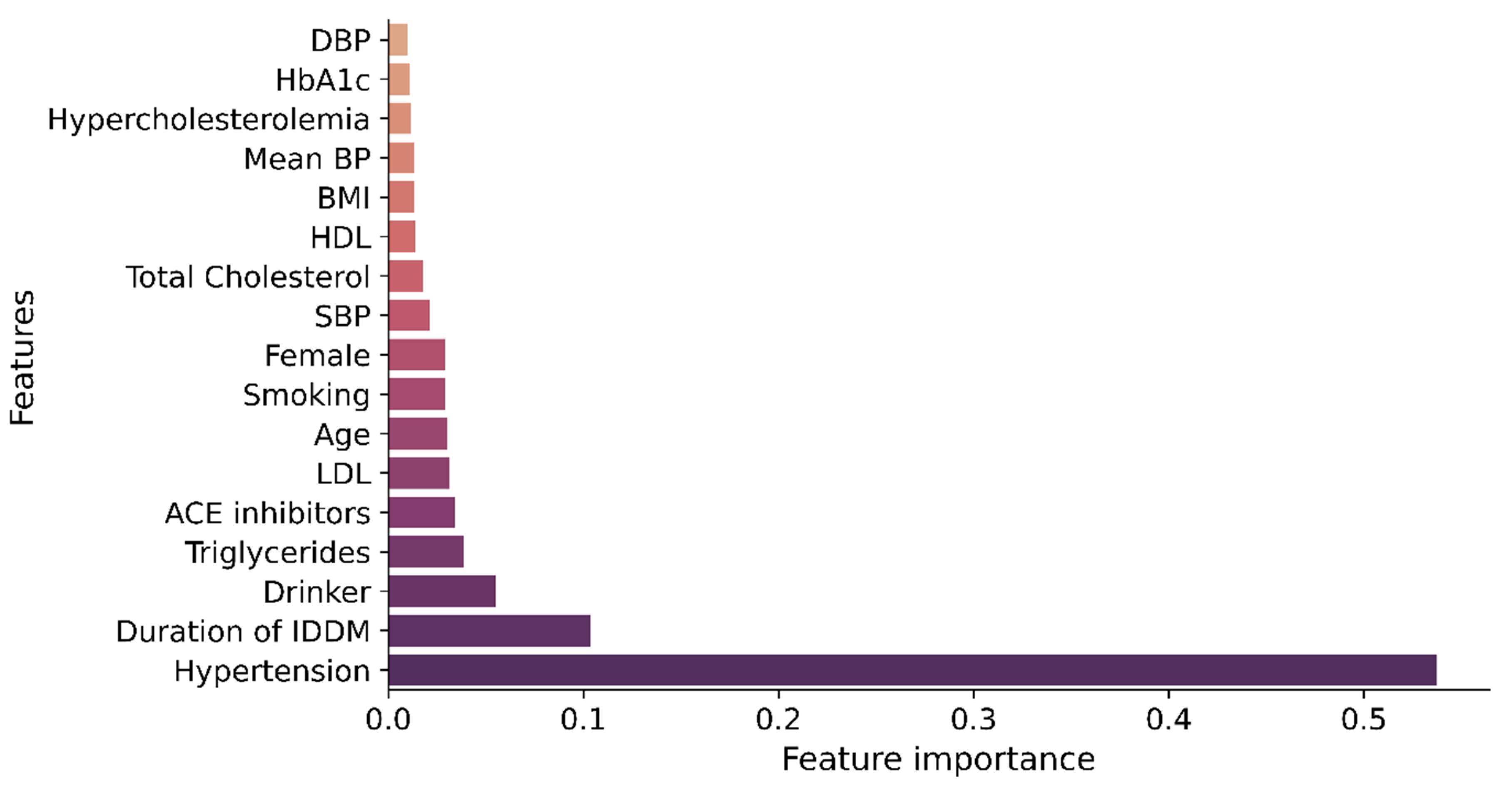
3.2. Performance Analysis of the Feature Ranking Techniques
3.3. CKD Prediction Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Internation Diabetes Federation Diabetes Atlas, 10th edition. 2021. Available online: https://diabetesatlas.org/atlas/tenth-edition/ (accessed on 23 October 2021).
- Costacou, T.; Orchard, T.J. Cumulative Kidney Complication Risk by 50 Years of Type 1 Diabetes: The Effects of Sex, Age, and Calendar Year at Onset. Diabetes Care 2017, 41, 426–433. [Google Scholar] [CrossRef] [PubMed]
- Saran, R.; Robinson, B.; Abbott, K.C.; Agodoa, L.Y.; Albertus, P.; Ayanian, J.; Balkrishnan, R.; Bragg-Gresham, J.; Cao, J.; Chen, J.L.T.; et al. US Renal Data System 2016 Annual Data Report: Epidemiology of Kidney Disease in the United States. Am. J. Kidney Dis. 2017, 69, 712. [Google Scholar] [CrossRef] [PubMed]
- Roggeri, A.; Roggeri, D.P.; Zocchetti, C.; Bersani, M.; Conte, F. Healthcare costs of the progression of chronic kidney disease and different dialysis techniques estimated through administrative database analysis. J. Nephrol. 2017, 30, 263–269. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. Chronic Kidney Disease in the United States, 2021; US Department of Health and Human Services, Centers for Disease Control and Prevention: Atlanta, GA, USA, 2021.
- The Kidney Disease: Improving Global Outcomes (KDIGO) 2012. CKD Evaluation and Management. Available online: https://kdigo.org/guidelines/ckd-evaluation-and-management/ (accessed on 25 October 2021).
- Segal, Z.; Kalifa, D.; Radinsky, K.; Ehrenberg, B.; Elad, G.; Maor, G.; Lewis, M.; Tibi, M.; Korn, L.; Koren, G. Machine learning algorithm for early detection of end-stage renal disease. BMC Nephrol. 2020, 21, 518. [Google Scholar] [CrossRef]
- Muskiet, M.H.A.; Tonneijck, L.; Smits, M.M.; Kramer, M.H.H.; Heerspink, H.J.L.; van Raalte, D.H. Pleiotropic effects of type 2 diabetes management strategies on renal risk factors. Lancet Diabetes Endocrinol. 2015, 3, 367–381. [Google Scholar] [CrossRef]
- Haque, F.; Reaz, M.B.I.; Chowdhury, M.; Srivastava, G.; Ali, S.H.; Bakar, A.; Bhuiyan, M. Performance Analysis of Conventional Machine Learning Algorithms for Diabetic Sensorimotor Polyneuropathy Severity Classification. Diagnostics 2021, 11, 801. [Google Scholar] [CrossRef]
- Khandakar, A.; Chowdhury, M.E.H.; Reaz, M.B.I.; Ali, S.H.; Abbas, T.O.; Alam, T.; Ayari, M.A.; Mahbub, Z.B.; Habib, R.; Rahman, T.; et al. Thermal Change Index-Based Diabetic Foot Thermogram Image Classification Using Machine Learning Techniques. Sensors 2022, 22, 1793. [Google Scholar] [CrossRef]
- Chowdhury, M.E.H.; Rahman, T.; Khandakar, A.; Mazhar, R.; Kadir, M.A.; Bin Mahbub, Z.; Islam, K.R.; Khan, M.S.; Iqbal, A.; Al Emadi, N.; et al. Can AI Help in Screening Viral and COVID-19 Pneumonia? IEEE Access 2020, 8, 132665–132676. [Google Scholar] [CrossRef]
- Haque, F.; Reaz, M.B.I.; Chowdhury, M.E.H.; Hashim, F.H.; Arsad, N.; Ali, S.H.M. Diabetic Sensorimotor Polyneuropathy Severity Classification Using Adaptive Neuro Fuzzy Inference System. IEEE Access 2021, 9, 7618–7631. [Google Scholar] [CrossRef]
- Thangarajoo, R.G.; Reaz, M.B.I.; Srivastava, G.; Haque, F.; Ali, S.H.; Bakar, A.A.A.; Bhuiyan, M.A.S. Machine Learning-Based Epileptic Seizure Detection Methods Using Wavelet and EMD-Based Decomposition Techniques: A Review. Sensors 2021, 21, 8485. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, X.; Ran, X.; Xu, Z.; Ji, L. Simple-to-use nomogram for evaluating the incident risk of moderate-to-severe LEAD in adults with type 2 diabetes: A cross-sectional study in a Chinese population. Sci. Rep. 2020, 10, 3182. [Google Scholar] [CrossRef]
- Lei, Z.; Liu, M.; Xu, X.; Yue, Q. A Data-experience intelligent model to integrate human judging behavior and statistics for predicting diabetes complications. Alex. Eng. J. 2022, 61, 8241–8248. [Google Scholar] [CrossRef]
- Thorsen-Meyer, H.-C.; Nielsen, A.B.; Nielsen, A.P.; Kaas-Hansen, B.S.; Toft, P.; Schierbeck, J.; Strøm, T.; Chmura, P.J.; Heimann, M.; Dybdahl, L.; et al. Dynamic and explainable machine learning prediction of mortality in patients in the intensive care unit: A retrospective study of high-frequency data in electronic patient records. Lancet Digit. Health 2020, 2, e179–e191. [Google Scholar] [CrossRef]
- Xiao, J.; Ding, R.; Xu, X.; Guan, H.; Feng, X.; Sun, T.; Zhu, S.; Ye, Z. Comparison and development of machine learning tools in the prediction of chronic kidney disease progression. J. Transl. Med. 2019, 17, 119. [Google Scholar] [CrossRef] [PubMed]
- Dunkler, D.; Gao, P.; Lee, S.F.; Heinze, G.; Clase, C.M.; Tobe, S.; Teo, K.; Gerstein, H.; Mann, J.F.; Oberbauer, R. Risk Prediction for Early CKD in Type 2 Diabetes. Clin. J. Am. Soc. Nephrol. 2015, 10, 1371–1379. [Google Scholar] [CrossRef] [PubMed]
- Low, S.; Lim, S.C.; Zhang, X.; Zhou, S.; Yeoh, L.Y.; Liu, Y.L.; Tavintharan, S.; Sum, C.F. Development and validation of a predictive model for Chronic Kidney Disease progression in Type 2 Diabetes Mellitus based on a 13-year study in Singapore. Diabetes Res. Clin. Pract. 2017, 123, 49–54. [Google Scholar] [CrossRef]
- Makino, M.; Ono, M.; Itoko, T.; Katsuki, T.; Koseki, A.; Kudo, M.; Haida, K.; Kuroda, J.; Yanagiya, R.; Suzuki, A. Artificial Intelligence Predicts Progress of Diabetic Kidney Disease-Novel Prediction Model Construction with Big Data Machine Learning. Diabetes 2018, 67 (Suppl. S1), 539. [Google Scholar] [CrossRef]
- Dagliati, A.; Marini, S.; Sacchi, L.; Cogni, G.; Teliti, M.; Tibollo, V.; De Cata, P.; Chiovato, L.; Bellazzi, R. Machine Learning Methods to Predict Diabetes Complications. J. Diabetes Sci. Technol. 2018, 12, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Wang, B.; Qiao, G.; Lou, H.; Xu, F.; Chen, Z.; Chen, S. Screening Tools Based on Nomogram for Diabetic Kidney Diseases in Chinese Type 2 Diabetes Mellitus Patients. Diabetes Metab. J. 2021, 45, 708–718. [Google Scholar] [CrossRef]
- Dong, W.; Wan, E.Y.F.; Fong, D.Y.T.; Kwok, R.L.P.; Chao, D.V.K.; Tan, K.C.B.; Hui, E.M.T.; Tsui, W.W.S.; Chan, K.H.; Fung, C.S.C.; et al. Prediction models and nomograms for 10-year risk of end-stage renal disease in Chinese type 2 diabetes mellitus patients in primary care. Diabetes Obes. Metab. 2021, 23, 897–909. [Google Scholar] [CrossRef]
- Aspriello, S.D.; Zizzi, A.; Tirabassi, G.; Buldreghini, E.; Biscotti, T.; Faloia, E.; Stramazzotti, D.; Boscaro, M.; Piemontese, M. Diabetes mellitus-associated periodontitis: Differences between type 1 and type 2 diabetes mellitus. J. Periodontal Res. 2011, 46, 164–169. [Google Scholar] [CrossRef] [PubMed]
- Diabetes UK. Differences between Type 1 and Type 2 Diabetes. Available online: https://www.diabetes.org.uk/diabetes-the-basics/differences-between-type-1-and-type-2-diabetes (accessed on 31 January 2022).
- Atkinson, M.A.; Eisenbarth, G.S.; Michels, A.W. Type 1 diabetes. Lancet 2014, 383, 69–82. [Google Scholar] [CrossRef]
- Sandholm, N.; Van Zuydam, N.; Ahlqvist, E.; Juliusdottir, T.; Deshmukh, H.A.; Rayner, N.W.; Di Camillo, B.; Forsblom, C.; Fadista, J.; Ziemek, D.; et al. The genetic landscape of renal complications in type 1 diabetes. J. Am. Soc. Nephrol. 2017, 28, 557–574. [Google Scholar] [CrossRef] [PubMed]
- Kristófi, R.; Bodegard, J.; Norhammar, A.; Thuresson, M.; Nathanson, D.; Nyström, T.; Birkeland, K.I.; Eriksson, J.W. Cardiovascular and Renal Disease Burden in Type 1 Compared with Type 2 Diabetes: A Two-Country Nationwide Observational Study. Diabetes Care 2021, 44, 1211–1218. [Google Scholar] [CrossRef]
- Vistisen, D.; Andersen, G.S.; Hulman, A.; McGurnaghan, S.J.; Colhoun, H.M.; Henriksen, J.E.; Thomsen, R.W.; Persson, F.; Rossing, P.; Jørgensen, M.E. A Validated Prediction Model for End-Stage Kidney Disease in Type 1 Diabetes. Diabetes Care 2021, 44, 901–907. [Google Scholar] [CrossRef]
- Colombo, M.; McGurnaghan, S.J.; Bell, S.; MacKenzie, F.; Patrick, A.W.; Petrie, J.R.; McKnight, J.A.; MacRury, S.; Traynor, J.; Metcalfe, W.; et al. Predicting renal disease progression in a large contemporary cohort with type 1 diabetes mellitus. Diabetologia 2020, 63, 636–647. [Google Scholar] [CrossRef]
- The DCCT/EDIC Research Group. Intensive Diabetes Therapy and Glomerular Filtration Rate in Type 1 Diabetes. N. Engl. J. Med. 2011, 365, 2366–2376. [Google Scholar] [CrossRef]
- American Diabetes Association. Epidemiology of Diabetes Interventions and Complications (EDIC). Long-term renal outcomes of patients with type 1 diabetes mellitus and microalbuminuria: An analysis of the Diabetes Control and Complications Trial/Epidemiology of Diabetes Interventions and Complications cohort. Diabetes Care 1999, 22, 99–111. [Google Scholar] [CrossRef]
- Perkins, B.A.; Bebu, I.; de Boer, I.H.; Molitch, M.; Tamborlane, W.; Lorenzi, G.; Herman, W.; White, N.H.; Pop-Busui, R.; Paterson, A.D.; et al. Risk Factors for Kidney Disease in Type 1 Diabetes. Diabetes Care 2019, 42, 883–890. [Google Scholar] [CrossRef]
- Papadopoulou-Marketou, N.; Chrousos, G.P.; Kanaka-Gantenbein, C. Diabetic nephropathy in type 1 diabetes: A review of early natural history, pathogenesis, and diagnosis. Diabetes/Metab. Res. Rev. 2017, 33, e2841. [Google Scholar] [CrossRef]
- Tangri, N.; Kitsios, G.D.; Inker, L.A.; Griffith, J.; Naimark, D.M.; Walker, S.; Rigatto, C.; Uhlig, K.; Kent, D.M.; Levey, A.S. Risk Prediction Models for Patients with Chronic Kidney Disease. Ann. Intern. Med. 2013, 158, 596. [Google Scholar] [CrossRef] [PubMed]
- Radcliffe, N.J.; Seah, J.-m.; Clarke, M.; MacIsaac, R.J.; Jerums, G.; Ekinci, E.I. Clinical predictive factors in diabetic kidney disease progression. J. Diabetes Investig. 2017, 8, 6–18. [Google Scholar] [CrossRef] [PubMed]
- Molitch, M.E.; Steffes, M.; Sun, W.; Rutledge, B.; Cleary, P.; de Boer, I.H.; Zinman, B.; Lachin, J.; for the Epidemiology of Diabetes Interventions and Complications (EDIC) Study Group. Development and Progression of Renal Insufficiency with and Without Albuminuria in Adults With Type 1 Diabetes in the Diabetes Control and Complications Trial and the Epidemiology of Diabetes Interventions and Complications Study. Diabetes Care 2010, 33, 1536–1543. [Google Scholar] [CrossRef]
- Silveiro, S.P.; Araújo, G.N.; Ferreira, M.N.; Souza, F.D.S.; Yamaguchi, H.M.; Camargo, E.G. Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) Equation Pronouncedly Underestimates Glomerular Filtration Rate in Type 2 Diabetes. Diabetes Care 2011, 34, 2353–2355. [Google Scholar] [CrossRef] [PubMed]
- Kokla, M.; Virtanen, J.; Kolehmainen, M.; Paananen, J.; Hanhineva, K. Random forest-based imputation outperforms other methods for imputing LC-MS metabolomics data: A comparative study. BMC Bioinform. 2019, 20, 492. [Google Scholar] [CrossRef] [PubMed]
- Zeng, M.; Zou, B.; Wei, F.; Liu, X.; Wang, L. Effective prediction of three common diseases by combining SMOTE with Tomek links technique for imbalanced medical data. In Proceedings of the 2016 IEEE International Conference of Online Analysis and Computing Science (ICOACS), Chongqing, China, 28–29 May 2016; pp. 225–228. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Tomek, I. Two Modifications of CNN. IEEE Trans. Syst. Man Cybern. 1976, SMC-6, 769–772. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Zlotnik, A.; Abraira, V. A General-purpose Nomogram Generator for Predictive Logistic Regression Models. Stata J. Promot. Commun. Stat. Stata 2015, 15, 537–546. [Google Scholar] [CrossRef] [Green Version]


| N = 1375 | Missing Values | Min | Max | Mean (±Sd) |
|---|---|---|---|---|
| Age (years) | 0 | 19.00 | 57.00 | 35.12 (±6.97) |
| Sex, n (%) | 0 | |||
| Male | 718 (52%) | |||
| Female | 657 (48%) | |||
| BMI (kg/m2) | 0 | 16.62 | 66.01 | 26.10 (±4.07) |
| Diabetic Duration (years) | 0 | 6.00 | 28.00 | 13.62 (±4.95) |
| ACE Inhibitors, n (%) | 0 | 91 (6%) | ||
| Hba1c (%) | 4 | 4.40 | 15.10 | 8.14 (±1.39) |
| HDL Cholesterol (mg/dL) | 25.00 | 103.00 | 52.54 (±13.10) | |
| LDL Cholesterol (mg/dL) | 0 | 26.00 | 310.00 | 113.94 (±30.57) |
| Total Cholesterol (mg/dL) | 0 | 85.00 | 444.00 | 183.59 (±35.97) |
| Hypertension, n (%) | 8 | 232 (16%) | ||
| Hypercholesterolemia, n (%) | 0 | 397 (28%) | ||
| Triglycerides (mg/dL) | 0 | 17.00 | 1110.00 | 86.44 (±64.43) |
| Systolic BP (mmHg) | 0 | 82.00 | 172.00 | 117.41 (±12.64) |
| Diastolic BP (mmHg) | 0 | 40.00 | 116.00 | 75.00 (±9.30) |
| Mean BP (mmHg) | 0 | 59.33 | 134.00 | 89.13 (±9.40) |
| Smoking, n (%) | 8 | 274 (19%) | ||
| Drinking, n (%) | 13 | 485 (35%) | ||
| Sensitivity | Specificity | Accuracy | Precision | Recall | F1 Score | Non-CKD | CKD | |||
|---|---|---|---|---|---|---|---|---|---|---|
| TN | FP | FN | TP | |||||||
| Top-1 Feature | 0.95 (±0.03) | 0.72 (±0.04) | 0.83 (±0.02) | 0.77 (±0.02) | 0.95 (±0.03) | 0.85 (±0.01) | 972 | 382 | 70 | 1291 |
| Top-2 Features | 0.92 (±0.04) | 0.84 (±0.04) | 0.88 (±0.03) | 0.85 (±0.03) | 0.92 (±0.04) | 0.88 (±0.03) | 1137 | 217 | 111 | 1250 |
| Top-3 Features | 0.91 (±0.06) | 0.85 (±0.02) | 0.88 (±0.03) | 0.86 (±0.02) | 0.91 (±0.06) | 0.89 (±0.03) | 1157 | 197 | 121 | 1240 |
| Top-4 Features | 0.92 (±0.06) | 0.86 (±0.03) | 0.89 (±0.03) | 0.87 (±0.03) | 0.92 (±0.06) | 0.89 (±0.03) | 1170 | 184 | 113 | 1248 |
| Top-5 Features | 0.93 (±0.05) | 0.86 (±0.02) | 0.89 (±0.03) | 0.87 (±0.02) | 0.93 (±0.05) | 0.90 (±0.03) | 1167 | 187 | 102 | 1259 |
| Top-6 Features | 0.92 (±0.06) | 0.86 (±0.03) | 0.89 (±0.03) | 0.87 (±0.02) | 0.92 (±0.06) | 0.89 (±0.04) | 1168 | 186 | 109 | 1252 |
| Top-7 Features | 0.93 (±0.04) | 0.86 (±0.02) | 0.89 (±0.02) | 0.87 (±0.01) | 0.93 (±0.04) | 0.90 (±0.02) | 1159 | 195 | 98 | 1263 |
| Top-8 Features | 0.92 (±0.07) | 0.87 (±0.04) | 0.90 (±0.04) | 0.88 (±0.03) | 0.92 (±0.07) | 0.90 (±0.04) | 1176 | 178 | 107 | 1254 |
| Top-9 Features | 0.91 (±0.06) | 0.84 (±0.03) | 0.88 (±0.03) | 0.85 (±0.03) | 0.91 (±0.06) | 0.88 (±0.03) | 1137 | 217 | 116 | 1245 |
| Top-10 Features | 0.92 (±0.08) | 0.86 (±0.03) | 0.89 (±0.04) | 0.87 (±0.03) | 0.92 (±0.08) | 0.89 (±0.04) | 1160 | 194 | 114 | 1247 |
| Top-11 Features | 0.90 (±0.07) | 0.85 (±0.04) | 0.88 (±0.03) | 0.86 (±0.03) | 0.90 (±0.07) | 0.88 (±0.03) | 1148 | 206 | 130 | 1231 |
| Top-12 Features | 0.91 (±0.06) | 0.85 (±0.03) | 0.88 (±0.02) | 0.86 (±0.02) | 0.91 (±0.06) | 0.88 (±0.02) | 1149 | 205 | 122 | 1239 |
| Top-13 Features | 0.92 (±0.04) | 0.85 (±0.03) | 0.88 (±0.01) | 0.86 (±0.02) | 0.92 (±0.04) | 0.89 (±0.01) | 1147 | 207 | 113 | 1248 |
| Top-14 Features | 0.91 (±0.05) | 0.86 (±0.03) | 0.89 (±0.03) | 0.87 (±0.02) | 0.91 (±0.05) | 0.89 (±0.03) | 1171 | 183 | 117 | 1244 |
| Top-15 Features | 0.91 (±0.03) | 0.86 (±0.02) | 0.88 (±0.02) | 0.87 (±0.02) | 0.91 (±0.03) | 0.89 (±0.02) | 1163 | 191 | 122 | 1239 |
| Top-16 Features | 0.90 (±0.07) | 0.85 (±0.05) | 0.87 (±0.05) | 0.86 (±0.05) | 0.90 (±0.07) | 0.88 (±0.05) | 1150 | 204 | 137 | 1224 |
| Top-17 Features | 0.91 (±0.04) | 0.86 (±0.04) | 0.89 (±0.04) | 0.87 (±0.03) | 0.91 (±0.04) | 0.89 (±0.04) | 1165 | 189 | 116 | 1245 |
| Features | Coef. | Std. Err. | z | p > z | (95% Conf. Interval) | |
|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | |||||
| Hypertension | 3.070858 | 0.1824329 | 16.83 | 0.000 | 2.713296 | 3.42842 |
| Duration of IDDM | 0.2398436 | 0.0162 | 14.81 | 0.000 | 0.2080922 | 0.271595 |
| Drinking | −1.486273 | 0.1685275 | −8.82 | 0.000 | −1.816581 | −1.155966 |
| Triglycerides | 0.0125956 | 0.0011376 | 11.07 | 0.000 | 0.0103659 | 0.0148252 |
| ACE inhibitors | 0.5133911 | 0.1522363 | 3.37 | 0.001 | 0.2150134 | 0.8117687 |
| LDL | −0.0071267 | 0.0018498 | −3.85 | 0.000 | −0.0107523 | −0.0035011 |
| Age | 0.0923286 | 0.0094812 | 9.74 | 0.000 | 0.0737458 | 0.1109114 |
| Smoking | −1.185757 | 0.2162176 | −5.48 | 0.000 | −1.609535 | −0.7619781 |
| _cons | −11.39143 | 0.633072 | −17.69 | 0.000 | −12.63223 | −10.15064 |
| Sensitivity (%) | Specificity (%) | Accuracy (%) | Precision (%) | F1 Score (%) | Confusion Matrix | ||||
|---|---|---|---|---|---|---|---|---|---|
| Non-CKD | CKD | ||||||||
| TN | FP | FN | TP | ||||||
| EDIC Train Set | 92.95 | 87.10 | 90.04 | 87.91 | 90.36 | 1175 | 174 | 96 | 1265 |
| EDIC Test Set | 91.67 | 87.56 | 88.59 | 71.18 | 80.13 | 345 | 49 | 11 | 121 |
| Train Dataset | Predicted Outcome (Train Dataset) | |||
|---|---|---|---|---|
| Non-CKD | CKD | Total | ||
| Actual Output | Non-CKD (1349) | 1175 (87.10%) | 174 (12.90%) | 1349 |
| CKD (1361) | 96 (7.05%) | 1265 (92.95%) | 1361 | |
| Total (2710) | 1271 | 1439 | 2710 | |
| Test dataset | Predicted Outcome (Test dataset) | |||
| Non-CKD | CKD | Total | ||
| Non-CKD (394) | 345 (87.56%) | 49 (12.44%) | 394 | |
| CKD (132) | 11 (8.33%) | 121 (91.67%) | 132 | |
| Total (526) | 356 | 170 | 526 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, N.H.; Reaz, M.B.I.; Ali, S.H.M.; Ahmad, S.; Crespo, M.L.; Cicuttin, A.; Haque, F.; Bakar, A.A.A.; Bhuiyan, M.A.S. Nomogram-Based Chronic Kidney Disease Prediction Model for Type 1 Diabetes Mellitus Patients Using Routine Pathological Data. J. Pers. Med. 2022, 12, 1507. https://doi.org/10.3390/jpm12091507
Chowdhury NH, Reaz MBI, Ali SHM, Ahmad S, Crespo ML, Cicuttin A, Haque F, Bakar AAA, Bhuiyan MAS. Nomogram-Based Chronic Kidney Disease Prediction Model for Type 1 Diabetes Mellitus Patients Using Routine Pathological Data. Journal of Personalized Medicine. 2022; 12(9):1507. https://doi.org/10.3390/jpm12091507
Chicago/Turabian StyleChowdhury, Nakib Hayat, Mamun Bin Ibne Reaz, Sawal Hamid Md Ali, Shamim Ahmad, María Liz Crespo, Andrés Cicuttin, Fahmida Haque, Ahmad Ashrif A. Bakar, and Mohammad Arif Sobhan Bhuiyan. 2022. "Nomogram-Based Chronic Kidney Disease Prediction Model for Type 1 Diabetes Mellitus Patients Using Routine Pathological Data" Journal of Personalized Medicine 12, no. 9: 1507. https://doi.org/10.3390/jpm12091507
APA StyleChowdhury, N. H., Reaz, M. B. I., Ali, S. H. M., Ahmad, S., Crespo, M. L., Cicuttin, A., Haque, F., Bakar, A. A. A., & Bhuiyan, M. A. S. (2022). Nomogram-Based Chronic Kidney Disease Prediction Model for Type 1 Diabetes Mellitus Patients Using Routine Pathological Data. Journal of Personalized Medicine, 12(9), 1507. https://doi.org/10.3390/jpm12091507








