Abstract
As an essential perceptual device, the tactile sensor can efficiently improve robot intelligence by providing contact force perception to develop algorithms based on contact force feedback. However, current tactile grasping technology lacks high-performance sensors and high-precision grasping prediction models, which limits its broad application. Herein, an intelligent robot grasping system that combines a highly sensitive tactile sensor array was constructed. A dataset that can reflect the grasping contact force of various objects was set up by multiple grasping operation feedback from a tactile sensor array. The stability state of each grasping operation was also recorded. On this basis, grasp stability prediction models with good performance in grasp state judgment were proposed. By feeding training data into different machine learning algorithms and comparing the judgment results, the best grasp prediction model for different scenes can be obtained. The model was validated to be efficient, and the judgment accuracy was over 98% in grasp stability prediction with limited training data. Further, experiments prove that the real-time contact force input based on the feedback of the tactile sensor array can periodically control robots to realize stable grasping according to the real-time grasping state of the prediction model.
1. Introduction
In recent years, machine learning put forward decades ago has been growing rapidly and has received substantial research interest with the popularity of artificial intelligence [1,2,3]. Currently, machine learning is widely used in computer vision [4], language processing [5,6,7], human-machine interfaces [8], and robots [9]. It is closely combined with sensors that serve as information collection terminals in applications, including pattern recognition [10,11] and wireless sensor networks [12]. However, machine learning methods based on tactile information are rarely applied to actual scenarios compared to visual and speech recognition. Tactile sensation is one of the major ways organisms perceive the external environment. By combining sensor components that mimic human touch, robots can acquire the ability of bionic grasping [13]. The perception of contact force is an indispensable element for achieving the flexible and stable grasping of objects. When picking up and moving target objects, especially fragile objects, sensitive contact force feedback can reduce the possibility of dilapidation caused by excessive force and rapid movement tendency of an object, such as a propensity toward sliding [14].
At present, the combination operation of grasp and touch of robot arm is still in in its immaturity, which is manifested in two aspect [15]. On the one hand, the combination of pressure sensors and mechanical prosthetic hands or clamps has a low sensitivity. It can only be used to grasp hard-to-break objects with a relatively large force to ensure the stable completion of the grasping task [16]. On the other hand, the robot hands or clamps used for grasping usually only consists of a tactile sensing section consisting of one or several large-volume pressure sensors [17,18]. A small contact area between the object and the sensor may cause an insufficient output value. Monolithic and low-density sensors struggle to clearly distinguish between the contact area and the shape between the robot hand and the object being clamped. Therefore, it increases the possibility of misjudgment in unconventional grasping conditions. G. D. Maria et al. proposed a tactile sensor prototype that can work as a torque sensor to estimate the geometry of the contact with a stiff external object for robotic applications [19]. However, the low sensitivity of this sensor does not allow it to sense contact with small mass or fragile objects, implying that the device is not suitable for applications where robots grasp soft or fragile objects. Pang et al. designed a three-dimensional flexible robot skin made from a piezoresistive nanocomposite to enhance the security performance of a collaborative robot [20]. The robot arm equipped with the robot skin can efficiently approach natural and secure human–robot interactions. However, the spatial resolution and the sensitivity of the sensor array are not enough to achieve effective collision detection for sharp objects. In our previous work [21], a flexible tactile electronic skin sensor with high precision and spatial resolution was presented for 3D contact force detection. Herein, we constructed a robot grasping system to achieve high accuracy grasping operation for multi-class objects.
Based on the analysis above, the effective combination of the robot arm and the high sensitivity and high spatial resolution of the tactile sensor is the hardware foundation for a flexible and precise grasping operation. Due to the low sensitivity and low spatial resolution of the touch sensor, current grasping systems judge the grasping in a simple manner. The next grasping operation step is determined by judging the relative relationship between the sensor output and the threshold, which is arbitrary and not reliable enough [22,23]. An efficient method can be devoted to intelligent and precise grasping state judgment via benefiting from the high precision and spatial resolution tactile sensor array. Some scholars divided the grasping state into three states: holding state, sliding state and rotation state. Heyneman [24] concentrated on the slip classification on eight kinds of texture plates by using tactile sensors and proposed a method that can accurately identify slip location. Su [25] also achieved slip detection using a tactile sensor when robot grasping. However, the slip and rotation states are two kinds of critical states between stable and unstable grasping. Both of these states are unstable and inevitably lead to unstable grasping. In general, only stability is concerned in the actual grip operation, not the instability of the grip operation. In addition, using a three-dimensional force perception tactile sensor array, the tangential force can be guaranteed to avoid object slip, and object rotation can be inhibited by choosing a proper contact center. Thus, the slip and rotation states are unnecessarily distinguished, especially when collecting grasping data to construct the dataset.
Meier [26] used convolutional networks to judge the grasping conditions for three kinds of objects to judge the grasping result based on grasping data. It is feasible for powerful GPU-supported and fewer kinds of objects judged.With the increase of the types of objects, the calculation will also increase greatly, and the application in embedded system cannot be guaranteed due to the limitation of GPU. In addition, high judgment accuracy requires a larger grasping dataset. Many limits prevent the convolutional networks from being applied for grasping operation prediction. Machine learning [27] that achieves pattern classification with higher efficiency and lower calculation costs can effectively compensate for the deficiency of a single threshold judgment and convolutional network judgment. The prediction model based on a machine learning algorithm can judge the actual grasping state by training the dataset to adjust the control parameters of the robot, achieving stable grasping operation.
Besides, many scholars have focused on robot grasping operations in other ways. They achieve grasping benefitted from the characteristics of a multi-fingered gripper. Yao [28] concentrates a on grasp configuration planning method based on a three-fingered robot hand, which depends on the grasping data described with the configuration of fingers and the attribute of the object. Kim [29] trained a deep neural network based on information of object and robot hand geometryand obtained the optimal grasping points between object and fingers. The geometry and attributes of objects and fingers are the key to achieve multi-fingered form-closure grasping on multiple kinds of objects, such as a polygon-type form-closure grasping achieved with a four-fingers parallel-jaw gripper [30]. What is more, a gecko-like robotic gripper, which is a kind of biomimetic multi-fingered structure, has been designed for grasping [31]. Furthermore, the haptic characteristics of objects have been identified with a three-fingered soft gripper [32]. The structure of a multi-fingered gripper makes it more efficient to achieve form-closure stable grasping for various objects. While the mechanical and control system is more complex compared with a two-finger gripper system. By the introduction of the tactile sensor array, it can also achieve stable grasping with a simple two-fingered gripper with high efficiency and reliability.
Herein, we construct an intelligent robot grasping system based on a highly sensitive tactile sensor array to achieve stable grasping. In this paper, the realization of stable grasping refers to finding an appropriate pressure distribution based on the tactile sensor array, which reflects the force situation of the contact area between the object and the clamp on the end-effector of the robot. The pressure distribution is not too large to break the objects but produces enough friction to prevent slip and rotation of the object.We set up a grasping dataset based on multiple groups of pressure distribution related to either stable grasping or unstable grasping, and trained grasp stability prediction models based on machine learning algorithms. With the grasp stability prediction models, the system realizes grasp state prediction on different kinds of objects. The prediction results of these models are compared by grasping success rate and standard deviation, then the best model is selected. The select model guarantees high precision and efficiency, and practically avoids redundant judgement on grasping state. It achieves judging grasping state periodically and adjusting the control force in actual grasping operations, based on the real-time feedback of the tactile sensor array.
2. Materials and Methods
2.1. Robot Grasping System Integrated with Flexible Tactile Sensor Array
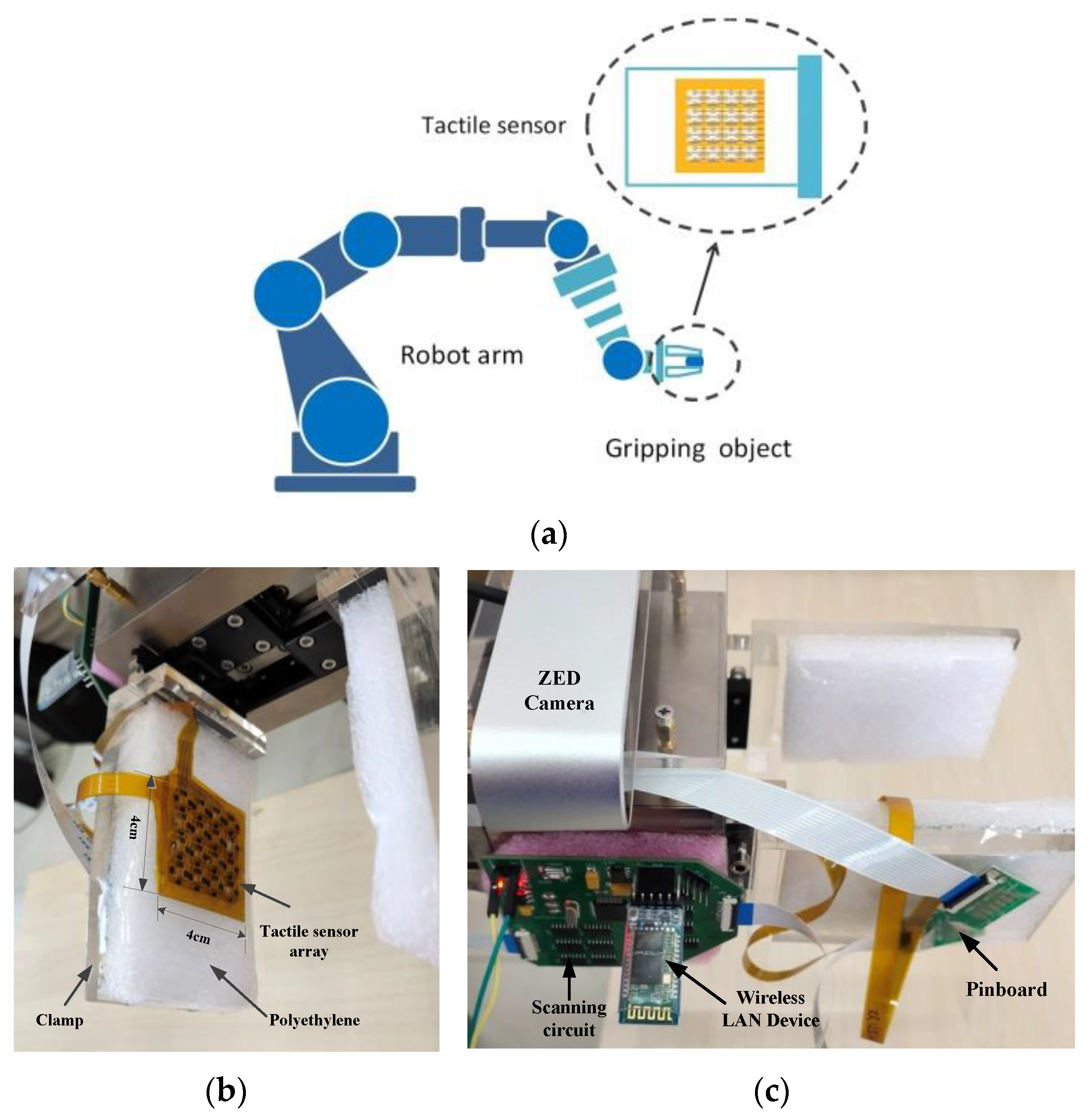
Figure 1a illustrates a robot grasping system based on a tactile sensor array. The behavior of an object holding mainly depends on the perception of tactile signals rather than vision. The tactile sensation plays a decisive role in stable object grasping operations. Similarly, the robot arm grasping system also requires the support of tactile sensors (shown in the dotted circle) to achieve the stable grasping of objects. In this work, a flexible piezoresistive sensor array with high sensitivity is assembled on the clamp of the manipulator arm, and the sensors can measure three-dimensional forces. The piezoresistive sensing material and the electrodes form a sandwich structure, and the electrodes are connected by electrical routings from different rows and columns. Figure 1b and c show the assembly details of the tactile sensor array on the finger of the robot. Generally, the robot grip is designed in a multi-fingered structure whose designing schemes have been discussed detailed in [33,34,35]. In this work, we propose a two-finger gripper-based grasping system, which has simple structures and achieves good performance on stable grasping benefitted from the tactile sensor array. A two-finger grip jaw is installed as the end-effector of the robot, and the tactile sensor array and data collection system are assembled on it. The tactile sensor array is designed in rectangular shape according to the regular and smooth surface of finger, which is attached on polyethylene and then installed on the finger of the grip jaw. This setup improves the contact performance between the object and the tactile array. Figure 1c shows the assembly details of the scanning circuit for the sampling of the tactile signals. A pin board is attached on the opposite side of the clamp, and the scanning circuit is installed on the clamp of the robot. The tactile signal is delivered through the pin board to the scanning circuit and then transmitted by the wireless LAN to the processor.
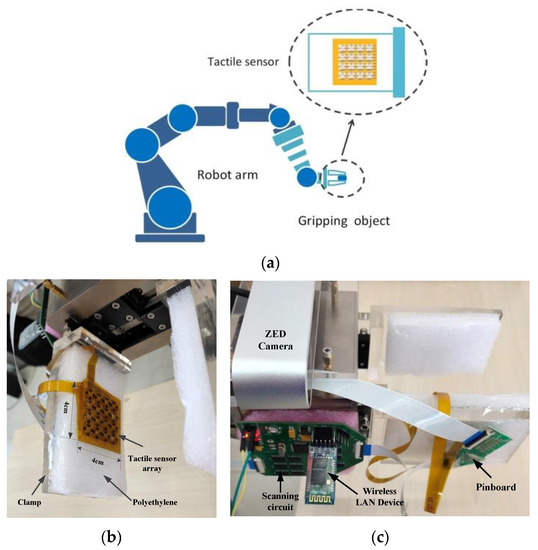
Figure 1.
Robot with flexible tactile sensor array. (a) Schematic diagram of grasping operation with tactile sensor. (b) Instalation of tactile sensor array at the clamp of robot. (c) The assembly of tactile data collecting system.
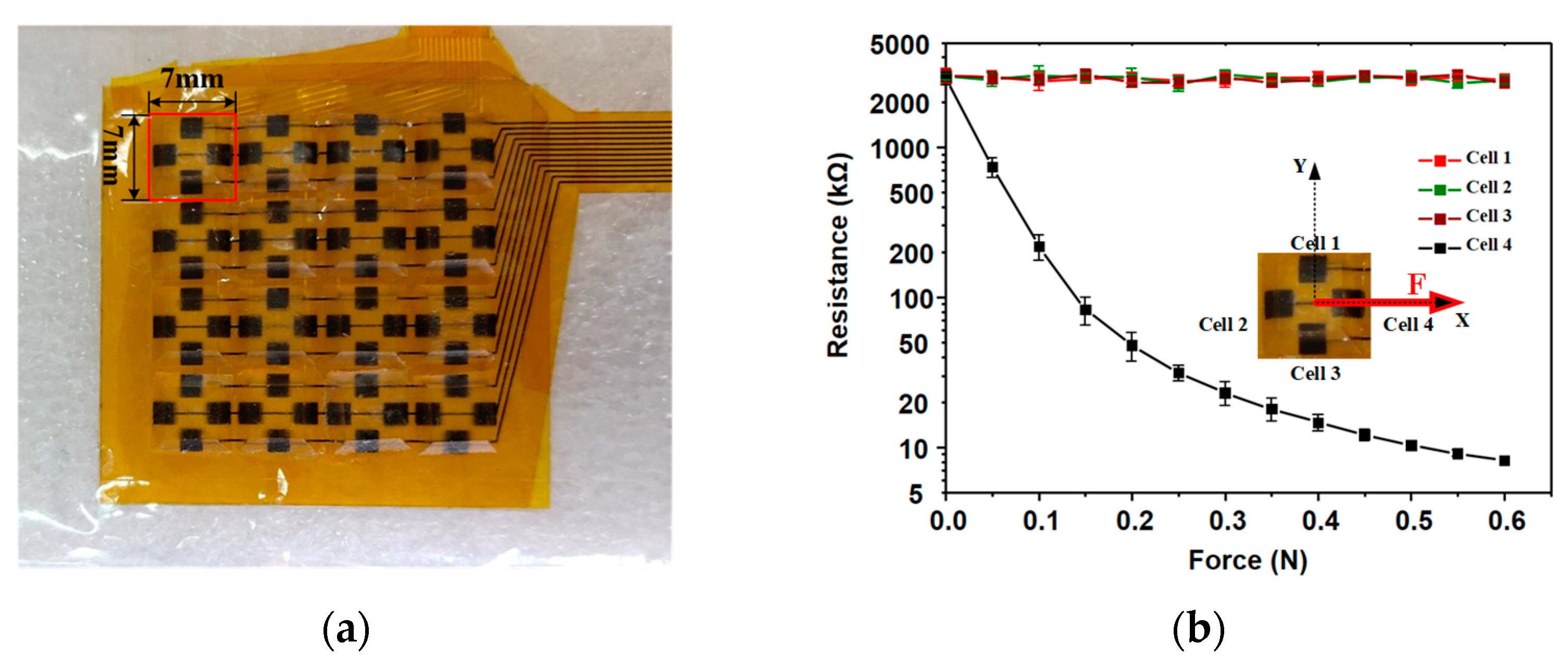
The overall appearance of the tactile sensor is shown in Figure 2a, which can sensitively achieve normal pressure perception, as well as the perception of tangential forces. The resistance variation under tangential force is displayed in Figure 2b. The thickness of the sensor is 2 mm, and the area of each three-dimensional force measurement unit is 7 × 7 mm2, which integrates four symmetrically distributed piezoresistive sensing cells, so the spatial resolution of the individual piezoresistive elements is 8/cm. The sensitivity of the tactile sensor reaches 20.8 kPa−1 in the range of <200 Pa, 12.1 kPa−1 in the range of <600 Pa and 0.68 kPa−1 in the range of 1–5 kPa [21]. In Figure 2b, a tangential force is implemented in x direction by a force gauge. The force is implemented by the interval of 0.05 N, and the output voltage is collected then transferred into resistances. As a result, the resistance responses and sensitivities of the four neighboring cells are shown. We can see that the sensitivity of the sensor can achieve 0.05 N when a transverse force is applied to the three-dimensional element, and the resistance of only one cell will produce obvious corresponding changes, while the resistance of the other three will remain basically unchanged. The curve in Figure 2b is measured three times, and the data are regressed to achieve the shown result, which provides a good basis for detecting the tangential contact force magnitude by using the difference.
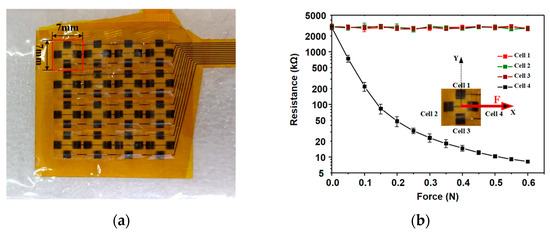
Figure 2.
The arrangement and piezoresistive curve of tactile sensor array. (a) Photo image of the applied tactile sensor array. (b) Piezoresistive curve of the tactile sensor under tangential force.
The arrangement of wires in the sensor array is simplified by connecting different cells in corresponding rows and columns. To eliminate the cross-talk between different sensor cells and improve the accuracy of information acquisition, a zero-potential method [36] that can efficiently achieve crosstalk elimination based on the row-column scanning circuit is adopted. The scanning circuit board is shown in Figure 3 and is composed of multiplexers, a microcontroller unit (MCU, STM32F103), an analog-to-digital converter (ADC, 12 bits and 0.806 mV resolution), reference resistances, and operational amplifiers. The measurement principle of the scanning circuit is that the row multiplexer is controlled by MCU to select one of the rows, and then the output of each column of the operational amplifiers is connected to the ADC through the column multiplexer. The output voltage of each cell can be scanned and converted to digital signals. The corresponding resistance value can be calculated by the product of the input voltage and reference resistance of each cell divided by the output voltage of each cell.

Figure 3.
PCB board of the sensor array scanning circuit.
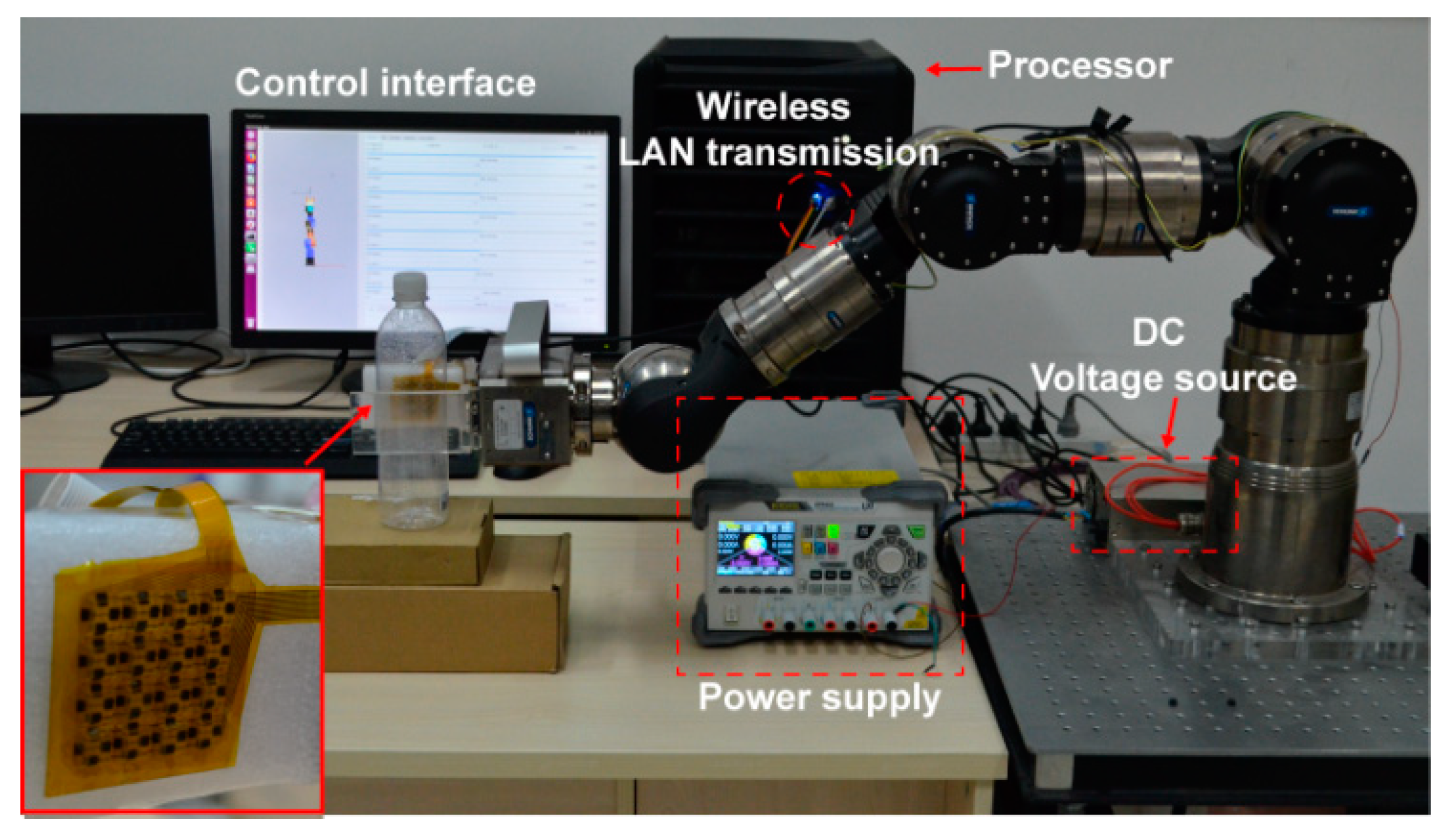
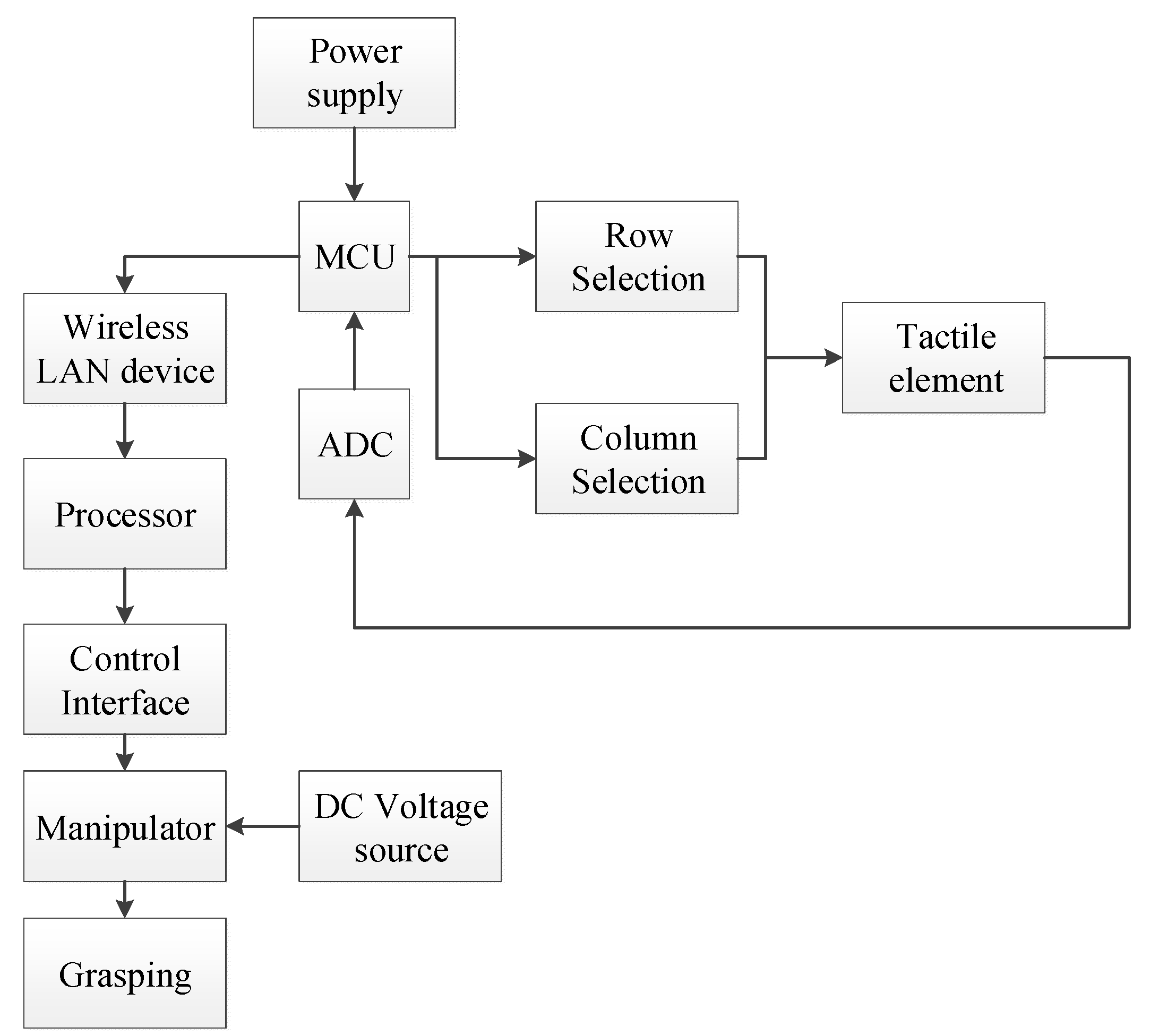
Figure 4 shows the entire robot grasping system with the control interface. The inset shows the flexible tactile sensor array attached to the robot clamp, which was fabricated with a transparent poly plate to clearly observe the deformation of objects in the process of clamping. To increase the buffer in the process of clamping objects, a 5-mm-thick polyethylene foam film (Young’s modulus is 0.172 GPa) was installed between the sensor array and the clamp. The seven-axis full-angle robotic arm is a product of the SCHUNK company (Lauffen, Germany), with a joint rotation resolution of 0.01°. A 24 V direct voltage power was used to supply energy for the manipulator, and a 5 V direct voltage was supplied to the sensor array scanning circuit. The scanning circuit transmits the collected array information to the PC processor through the wireless LAN for processing, storing and displaying. Figure 5 shows the working process of the sensor array scanning circuit and grasping system. By the power supply to the MCU, the rows and columns of the sensor array are selected by adjusting the electrical level. As a result, the tactile element for measuring is determined. The analog signal of the tactile element is collected and transferred into a digital signal by the ADC and then is then stored in the MCU. Via the wireless LAN device, the signal is delivered to the processor for grasp operations.
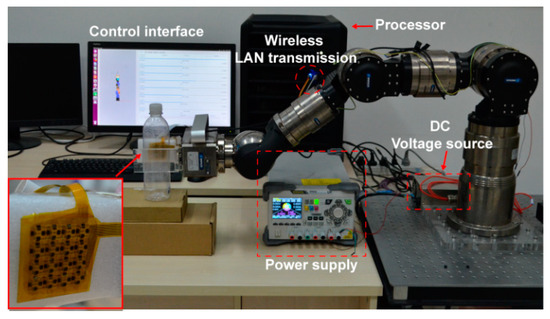
Figure 4.
The robot grasping system and control interface.
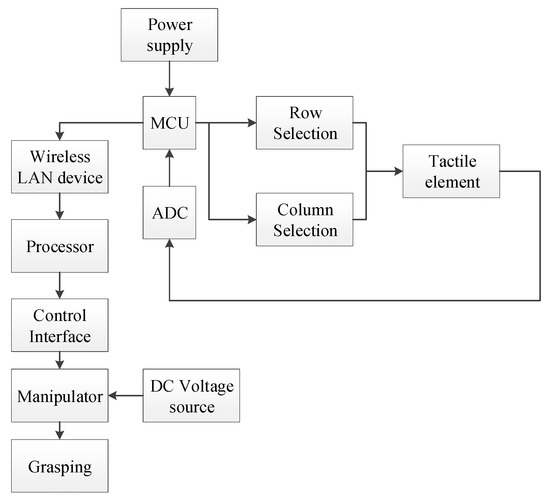
Figure 5.
Block diagram of sensor array scanning circuit and grasping system.
2.2. Grasp Stability Prediction Algorithm Based on Grasping Dataset
To achieve high accuracy and stable grasping, the grasp stability prediction model was constructed by training on a grasping dataset obtained from a tactile sensor array. The key of the stability prediction is to train the model to correctly predict the feasible and infeasible data for stable grasping. The model can be used to determine if the grasping operation is successful and stable based on real-time collected pressure distribution data. It can be treated as a binary classification problem for grasping stability prediction, where stable and unstable graspings are the two categories.
In this work, a grasping dataset was firstly built up for training the grasp stability prediction model. Several objects were applied for collecting data samples from the tactile sensor array for both stable and unstable grasping. The SVC (support vector classification) algorithm [37], the KNN (k-nearest neighbor) algorithm [38], and the LR (logical regression) algorithm [39] were introduced to train the prediction models. KNN is one of the simplest machine learning algorithms, while it has high computation cost, deep dependence on training data, and has poor fault tolerance on training data. SVC aims to obtain the optimal hyperplane in the feature space. The SVM learning can be expressed as a convex optimization problem, which is sure to achieve global optimum. However, it is hard to be implemented with large samples and on multi-category classification. LR uses the log function as its loss function, which should be implemented with large samples. In addition, it is sensitive to abnormal samples and needs a parametric model.
Anensemble learning algorithm is also discussed based on the SVC, KNN, and LR prediction models, which is achieved by adding a meta-classifier onto the predictions of the three models. Finally, comparing with the models according to the grasping success rate, the highest one was selected for judging grasping operation stable or not on real-time collected pressure distribution data.
(1) Grasping dataset
To train the prediction models, a grasping dataset of different objects was collected. Six kinds of objects (plastic bottle, pop-tip can, pear, orange, nectarine, and egg) are selected as test objects, which are shown in Figure 6. The hardness and volume of the test objects are different, which can fully reflect the scenarios encountered by the robot grasping system in grasping objects within the range of tactile sense. A total of five kinds of locations were set for grasping operations, and the grasp operation was carried out 10 times for each object at each location. As a result, 300 groups of grasping data were collected to form a dataset. Half of the data show a stable grasping operation, while the others were unstable. With this dataset, each algorithm of SVC, KNN, LR, and ensemble learning is respectively trained and the corresponding prediction model is obtained.

Figure 6.
Optical photographs of objects for grasping dataset.
To prevent the model from over-fitting and to obtain a better classifier, the original data were divided into three parts: training data, validation data, and test data at a certain proportion. The model is trained by these three parts. The training data was utilized to train the model, and the validation data is selected to make the model more effective. The test data was used to determine the accuracy of the model on unknown data, which can explain the generalization ability of the model to a certain extent.
(2) Grasp stability prediction models
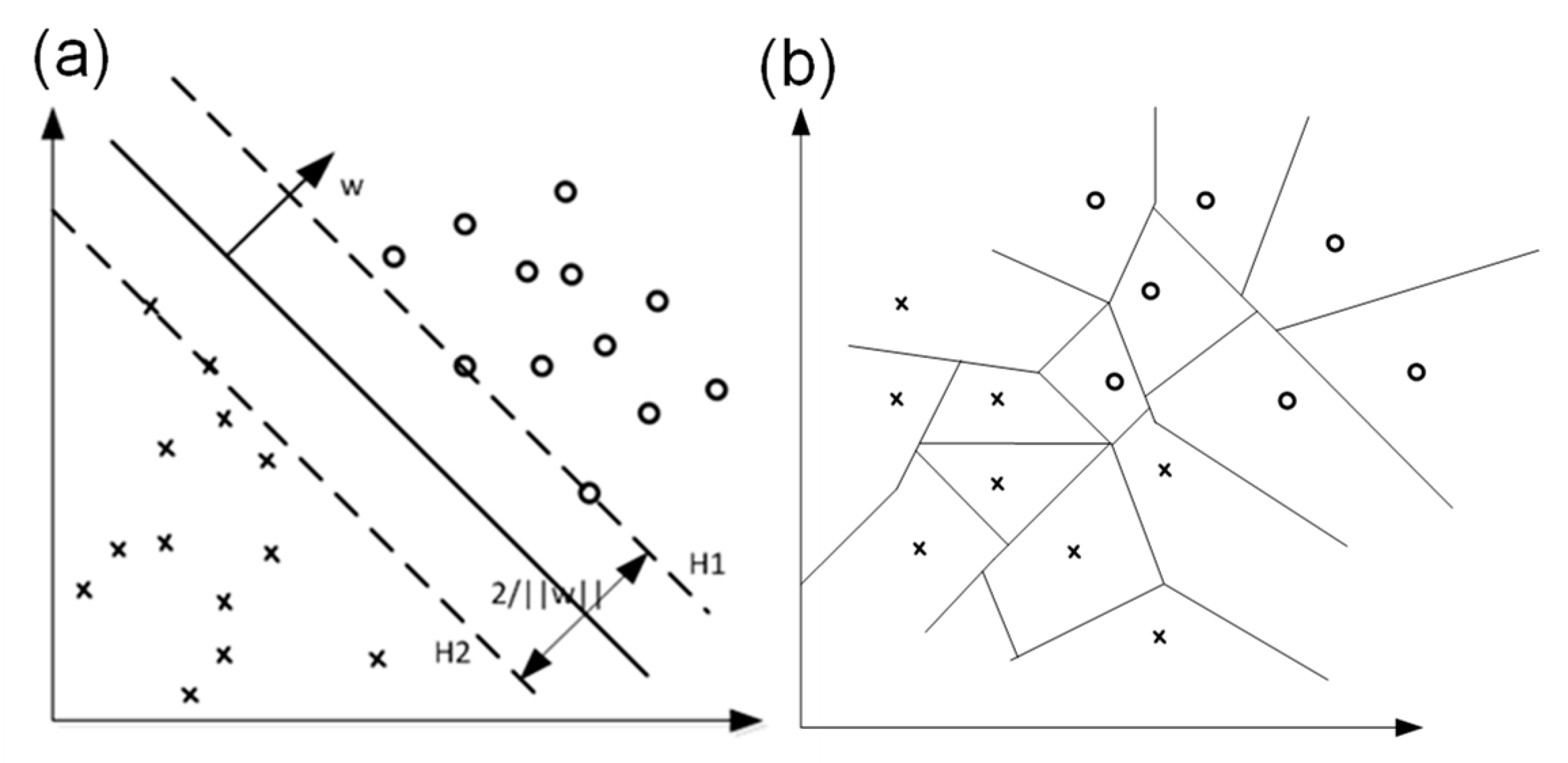
Figure 7a shows the schematic diagram of the SVC algorithm in a two-dimensional feature space. The hyperplane corresponding to boundary H1 is , and the hyperplane corresponding to boundary H2 is , where w is the normal vector. The instance points on H1 and H2 are the support vectors of the training data, and there are no instance points between lines H1 and H2. The width of the interval between two parallel dotted lines is 2/‖w‖, and the model trained by the SVC algorithm aims to maximize the interval.
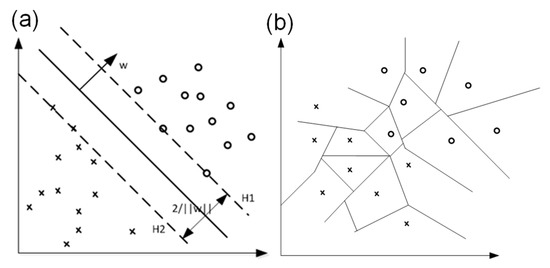
Figure 7.
Prediction principle of the SVC and KNN algorithm. (a) Schematic diagram of SVC for maximizing interval in two-dimensional feature space. (b) A division of two-dimensional feature space by KNN.
Figure 7b shows the schematic diagram of the KNN algorithm. The model trained by the KNN algorithm divides the feature space into some subspaces, and the classification can be determined according to the subspaces. In the model trained by the KNN algorithm, K is a hyper-parameter that needs to be set in advance, and the selection of the K value will affect the performance of the prediction model. If a smaller K value is chosen, the prediction result is determined by instance data in smaller neighborhoods, and the approximate error of learning is relatively decreased. However, if noise exists in the neighboring instances, the model is prone to overfitting, leading to an incorrect prediction result. If a larger K value is chosen, the prediction result is related to instance data in larger neighborhoods, which can reduce the estimation error of learning, but the approximation error will increase correspondingly. The choice of the K value determines the complexity of the model. The larger the K value, the simpler the overall model is; the smaller the K value, the more complex the model is.
The LR algorithm associates the characteristics of samples with the probability of the occurrence of the samples and categorizes samples through different probabilities of occurrence. For binary classification problems, the LR algorithm can be expressed as
where is the probability of sample occurrence, is the result of sample classification, is the extended sample feature, is the expanded weight vector, is the bias and represents the sigmoid function, of which the definition domain is and the range is (0,1). The function can be expressed as
where . By adjusting the extended weight vector w, the difference between the judgment value and the real value of the decision algorithm is minimized, and the model based on LR algorithm can be obtained.
Based on the models trained by SVC, KNN and LR algorithms, the ensemble learning model is constructed based on the framework of soft voting. The average probability of all model prediction results of each category is calculated respectively, and then the category with the highest average probability is voted as the final prediction result.
3. Results
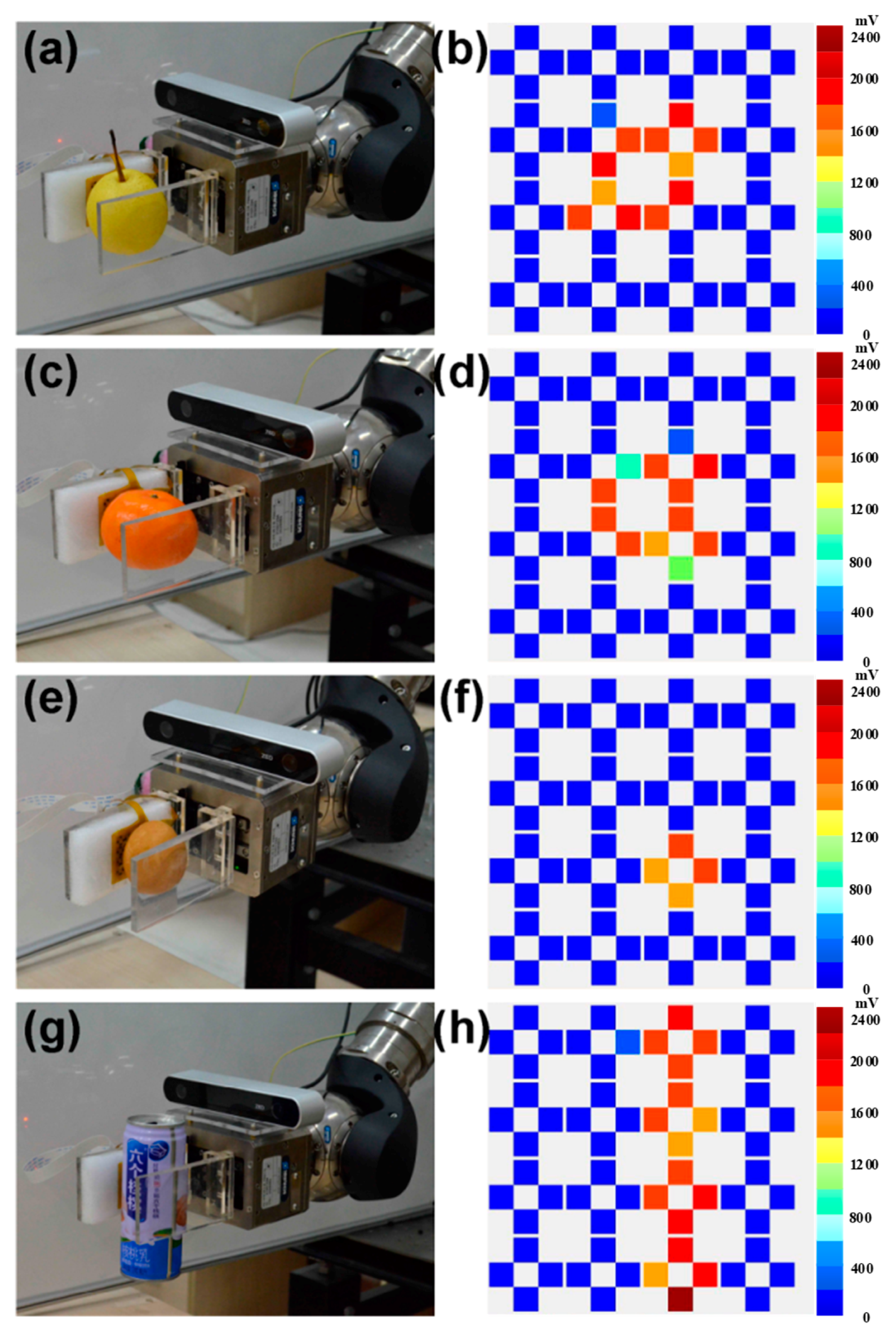
Figure 8 shows the state of different objects being stably grasped by clamps and the corresponding pressure distribution in the sensor array. Each color box represents a tactile sensor cell, and the value of the colors indicates the output voltage of each cell. At the beginning of the grasping operation, the two clamps move to each other, and the sensor array is unloaded. As the tactile sensor starts to contact the object, the output value of the corresponding sensing elementwill increase, and the real-time pressure data transmitted to the processor will be processed by the prediction algorithm to judge the state of grasping. If the model determines that the object is not being grasped, the clamps will continue to tighten up in case the object falls, and the grasping state of the object will continue to be judged circularly. When the grasping state changes from unstable to stable, the clamps of the manipulator driven by the motor will stop moving, and stable grasping operation is achieved. The pressure distribution in the tactile sensor array reflects the contact area and shape between the tactile sensor and the grasped object, which depends to some extent on the shape of the captured object.
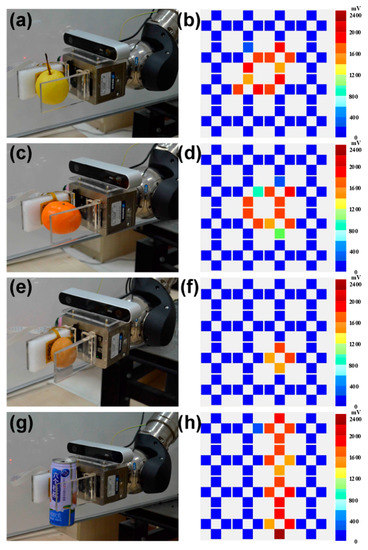
Figure 8.
Robot arm grasps different objects by clamps and corresponding pressure distribution diagram: (a,b) pear, (c,d) orange, (e,f) egg, (g,h) pop-top can.
A total of 300 groups of grasping data for each object are collected in random placement to form the dataset. All the grasping data of each object are divided randomly. A certain proportion of the data is used as training data, which is called the training ratio. The rest of the data are used for model validation and testing. Grasping data includes eigenvalues and label values. The eigenvalues are the pressure information of the 64 elements on the tactile pressure sensor array. The label value represents the grasping state, which is 1 for stable grasping and 0 for unstable grasping.
Based on the dataset, we implemented training on machine learning algorithms with Python on a Ubuntu operation system, using an open library “scikit-learn”, which is a powerful framework of machining learning, to obtain the prediction models. In the KNN model, the value of k is set as 1. The weight of the nearest neighbors of each sample is set as “distance”, which means the weight is inversely proportional to the distance among samples. The measure of distance is set as 1, namely the Manhattan distance. In the SVC model, Gaussian Kernel is used and the hyperparameter of penalty coefficient (a kind of soft margin classifier) is set to 0.03 to guarantee some tolerance of noise within the boundary. In the LR model, the regularization parameter is set as L2 and the coefficient of regularization is set 1, which can efficiently avoid overfitting. As a result, prediction models are trained at different training ratios. Evaluation is carried out with validation data to refresh the parameters of models. The judgement accuracy which represents the probability of correct judgment on the grasping state is tested on test data. The training process is iterated to achieve the best judgment accuracy of models on test data. So far, the complete grasping prediction models are obtained.
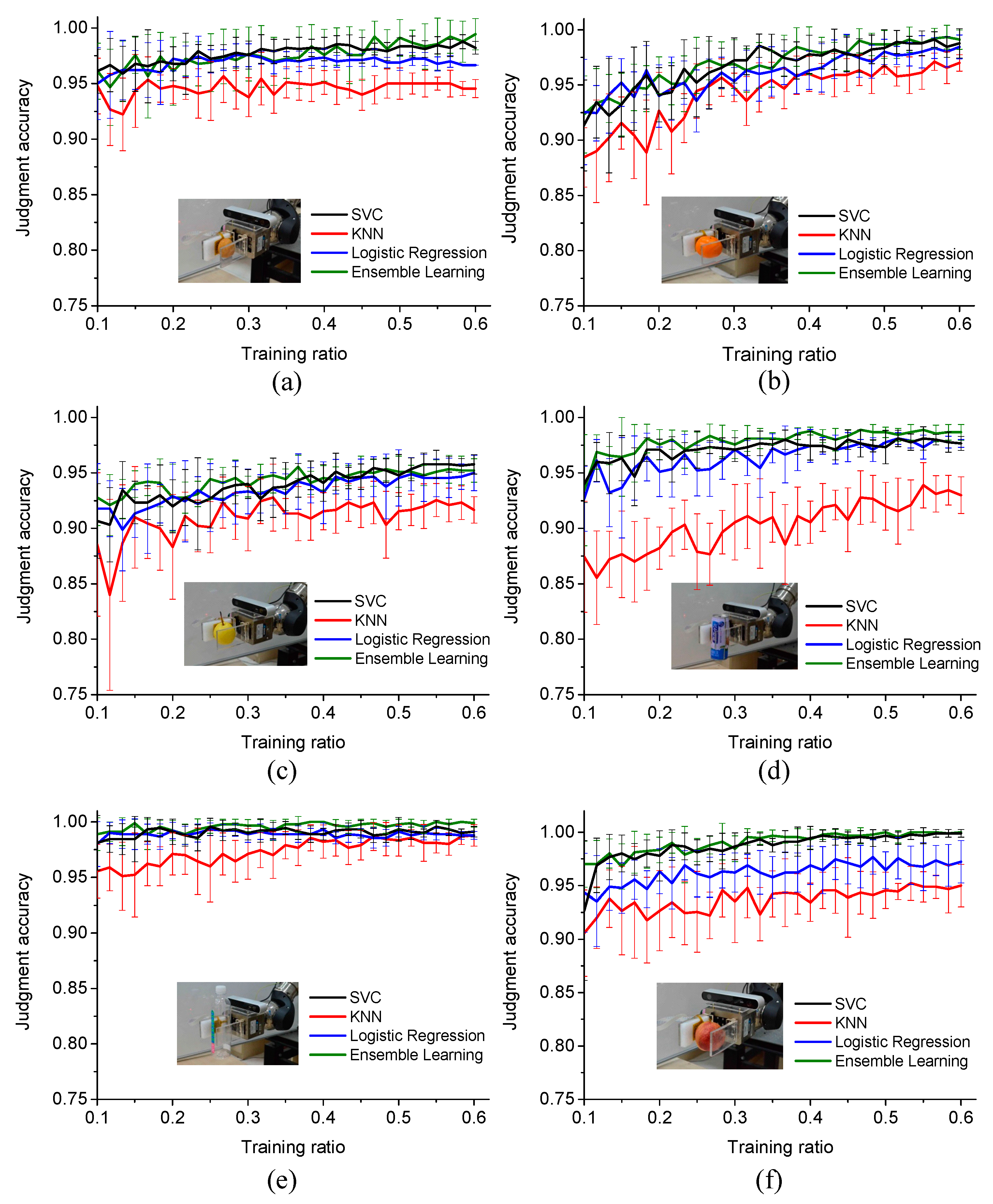
In the actual grasping operation, the prediction models work at each control cycle. When the clamp moves closer to the object, the tactile sensor array measures the pressure distribution, which is then immediately provides feedback to the prediction models to determine if the grasping is stable. If not, the clamp continuously moves closer to the object until the pressure distribution can be classified as stable. By this time, the object is grasped with the robot arm stably. Grasping operations are carried out with different prediction models, the judgment results are recorded in the processes. The judgment results curves at different training ratios when grasping different objects using the four types of prediction models are illustrated in Figure 9.
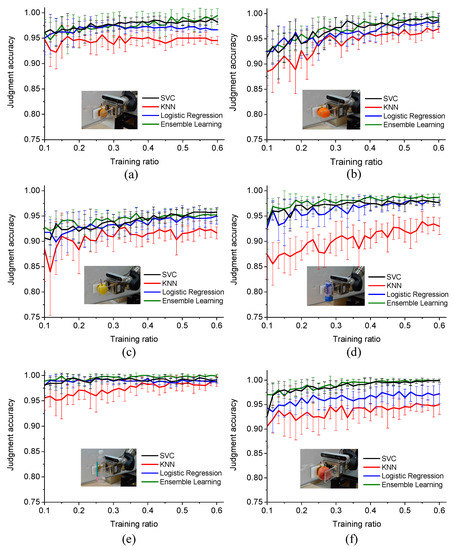
Figure 9.
The influence of the different proportions of training data on the judgment accuracy of different objects: (a) egg, (b) orange, (c) pear, (d) pop-top can, (e) plastic bottle, (f) nectarine and the error bar represents standard deviation.
As shown in Figure 9, for all the tested objects, the accuracy of each trained prediction model is relatively low, and the standard deviation is relatively large at a small proportion of training data. With the increase of the training ratio, the accuracy of each algorithm model increases, and the standard deviation decreases gradually. For example, the average grasping accuracy of the four prediction models on grasping plastic bottles is 98.67% at a training ratio of 0.2 and increases to 99.11% at a training ratio of 0.6. Correspondingly, the average standard deviation of the four prediction models on grasping plastic bottles is 1.18% at a training ratio of 0.2 and decreases to 0.54% at a training ratio of 0.6. Grasping experiment results on other objects have the same variation tendency. Thus, in order to achieve high judgement accuracy and low fluctuation, enough training data is necessary for prediction model training.
Table 1 shows the comparison of the judgment accuracy of the different models at a training ratio of 0.6. Among the four models adopted in this paper, the KNN model performs poorly except when grasping plastic bottles. Allfour of the models perform worse in judging grasping a pear, but perform much better in judging grasping a plastic bottle. The overall judgment accuracy of grasping stability for each object is greater than 95% at a training ratio of 0.6 for all the models. The overall judgment accuracy of each prediction model is also shown in Table 1.

Table 1.
Comparison of the judgment accuracy of different algorithms at a training ratio of 0.6.
Based on the analysis above, the model trained by the KNN algorithm possesses the lowest judgment accuracy for different training ratios, and the judgment accuracy of prediction models trained by various algorithms can be ranked: Ensemble learning SVC LR KNN. Since the ensemble learning model is integrated with other models, it inevitably has a more complex model frame and higher training cost than a single machine learning algorithm-based model. Therefore, for most application scenarios, the SVC algorithm can be qualitfied for the training prediction model that can provide high judgment accuracy for robot grasping stability prediction. As shown in Table 1, the judgment accuracy of the SVC model for the overall object exceeds 98% at a training ratio of 0.6.
Table 2 lists the differences among the judgment results of four prediction models trained by normalized data and unnormalized data at a training ratio of 0.5. Using the model fed by normalized training data, the judgment accuracy is improved for the LR model, SVC model, and ensemble learning model, but the judgment accuracy of the KNN model is affected little, which indicates that data normalization has a different influence on the judgment accuracy of the different models. From another point of view, when data for training is insufficient, in addition to the KNN model, data normalization is a feasible way to improve the judgment accuracy of the prediction model.

Table 2.
Effect of data normalization on the results of the different algorithm models.
In conclusion, the grasping prediction models are validated efficiently in judging the grasping state. The overall judgment accuracy of grasping state for each object is greater than 95% at a training ratio of 0.6 for all the models. The SVC algorithm-based prediction model, which achieves over 98% judgment accuracy for the overall objects, is proved to be the best cost-performance model because of the high prediction accuracy and low training resource cost. It guarantees grasping stability prediction of the robot system attached with tactile sensor array in most practical application scenarios. Since it is hard to gain abundant tactile data of robot grasping, the normalization of the training data is verified to be feasible in improving the prediction accuracy with lesser training data.
4. Conclusions
A robot grasping system that can grasp objects stably in a tactile sensing range by combining a highly sensitive tactile sensor array with a high motion resolution robot arm is proposed in this work. The prediction model trained by machine learning algorithm is used to judge the grasping state. The focus of this study is to find the appropriate pressure distribution to realize the stable grasping operation of a variety of objects. Different from the slip concern in other studies, we sought to find the most appropriate pressure distribution for grasping which guarantees it is neither too small to fail at grasping nor too large to cause damage to the object, toachieve a safe and strong grasping force for grasping operation. Benefitting from the sensitive tactile sensor array developed by our team, the pressure distribution of grasping operations can be collected and reflected in 64 cells, which can represent more details of contact.
Different prediction models have been compared in terms of judgment accuracy at different training ratios, the models trained by the SVC algorithm showed the best performance in actual grasping operations. The prediction model can achieve real-time judgment during each grasping control cycle (50 ms on average, with a minimum of 8 ms). In addition, it can work without a GPU environment and requires less training time than a CNN (convolutional neural networks) model. Moreover, the judgment accuracy can exceed 98% with the SVC algorithm-based model with limited training data.
Nowadays, the vision-based methods [40] have advantages in achieving force measurement for micro-object grasping, while for the daily objects grasping, pressure distribution feedback based on a tactile sensor array provides more force conditions of the contact area for precise force control. A stable prediction model based on machines learning algorithms is highly efficient in real-time grasping operations. The grasping system is adapted for further application scenes that are more complicated and high contact force-sensitive, such as man-machine interaction-based nursing and healthcare. Overall, the main contributions of this paper can be summarized in the following aspects:
- A highly sensitive tactile sensor array combined with a high motion resolution robot grasping system.
- A dataset of pressure distribution reflecting the contact force condition between objects and the end-effector of the robot.
- A high judgment accuracy grasping prediction model trained with the SVC algorithm on the dataset of pressure distribution.
- Real-time stable grasping prediction during actual robot grasping operation.
- Further application on high contact force sensitivity scenes such as man-machine interaction-based nursing and healthcare.
Author Contributions
Conceptualization, T.L. and N.X.; Investigation, X.S. (Xuguang Sun); Data curation, X.S. (Xin Shu); Methodology, T.L. and X.S. (Xin Shu); Software, C.W.; Visualization, Y.W.; Writing—original draft, X.S. (Xuguang Sun); Writing—review and editing, T.L.; Supervision, G.C.; Project administration, G.C. and N.X.; Funding acquisition, T.L. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by National Natural Science Foundation of China, grant number 61802363 and the Science and Technology Foundation of State Key Laboratory, grant number 19KY1213.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to intellectual property protection.
Acknowledgments
The authors give thanks to the State Key Laboratory of Transducer Technology, Aerospace Information Research Institute, Chinese Academy of Sciences for instrumentation and equipment support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Obermeyer, Z.; Emanuel, E.J. Predicting the Future—Big Data, Machine Learning, and Clinical Medicine. N. Engl. J. Med. 2016, 375, 1216–1219. [Google Scholar] [CrossRef] [PubMed]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef]
- Jean, N.; Burke, M.; Xie, M.; Davis, W.M.; Lobell, D.B.; Ermon, S. Combining satellite imagery and machine learning to predict poverty. Science 2016, 353, 790–794. [Google Scholar] [CrossRef]
- Stallkamp, J.; Schlipsing, M.; Salmen, J.; Igel, C. Man vs. computer: Benchmarking machine learning algorithms for traffic sign recognition. Neural Netw. 2012, 32, 323–332. [Google Scholar] [CrossRef]
- Young, T.; Cambria, E. Recent Trends in Deep Learning Based Natural Language Processing. IEEE Comput. Intell. Mag. 2018, 13, 55–75. [Google Scholar] [CrossRef]
- Weng, W.; Wagholikar, K.B.; Mccray, A.T.; Szolovits, P.; Chueh, H.C. Medical subdomain classification of clinical notes using a machine learning-based natural language processing approach. BMC Med. Inform. Decis. Mak. 2017, 17, 155. [Google Scholar] [CrossRef]
- Hirschberg, J.; Manning, C.D. Advances in natural language processing. Science 2015, 349, 261–266. [Google Scholar] [CrossRef] [PubMed]
- Martinsen, K.; Downey, J.; Baturynska, I. Human-Machine Interface for Artificial Neural Network based Machine Tool Process Monitoring. Procedia CIRP 2016, 41, 933–938. [Google Scholar] [CrossRef]
- Giusti, A.; Guzzi, J.; Cire, D.C.; He, F.; Rodríguez, J.P.; Fontana, F.; Faessler, M.; Forster, C.; Schmidhuber, J.; di Caro, G.; et al. A Machine Learning Approach to Visual Perception of Forest Trails for Mobile Robots. IEEE Robot. Autom. Lett. 2015, 1, 661–667. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Czejdo, B.; Perez, N. Gesture Classification with Machine Learning using Kinect Sensor Data. In Proceedings of the 2012 Third International Conference on Emerging Applications of Information Technology (EAIT), Kolkata, India, 30 November–1 December 2012; pp. 348–351. [Google Scholar]
- Jahangiri, A.; Rakha, H.A. Applying Machine Learning Techniques to Transportation Mode Recognition Using Mobile Phone Sensor Data. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2406–2417. [Google Scholar] [CrossRef]
- Alsheikh, M.A.; Lin, S.; Niyato, D.; Tan, H. Machine Learning in Wireless Sensor Networks: Algorithms, Strategies, and Applications. IEEE Commun. Surv. Tutor. 2014, 16, 1996–2018. [Google Scholar] [CrossRef]
- Kappassov, Z.; Corrales, J.; Systems, A.; Perdereau, V. Tactile sensing in dexterous robot hands—Review. Robot. Auton. Syst. 2015, 74, 195–220. [Google Scholar] [CrossRef]
- Romano, J.M.; Member, S.; Hsiao, K. Human-Inspired Robotic Grasp Control with Tactile Sensing. IEEE Trans. Robot. 2011, 27, 1067–1079. [Google Scholar] [CrossRef]
- Spiliotopoulos, J.; Michalos, G. A Reconfigurable Gripper for Dexterous Manipulation in Flexible Assembly. Inventions 2018, 3, 4. [Google Scholar] [CrossRef]
- Santos, A.; Pinela, N.; Alves, P.; Santos, R.; Farinha, R.; Fortunato, E.; Martins, R.; Hugo, Á.; Igreja, R. E-Skin Bimodal Sensors for Robotics and Prosthesis Using PDMS Molds Engraved by Laser. Sensors 2019, 19, 899. [Google Scholar] [CrossRef]
- Jelizaveta, S.; Agostino, K.; Kaspar, A. Fingertip Fiber Optical Tactile Array with Two-Level Spring Structure. Sensors 2017, 17, 2337. [Google Scholar]
- Costanzo, M.; de Maria, G.; Lettera, G.; Natale, C.; Pirozzi, S. Motion Planning and Reactive Control Algorithms for Object Manipulation in Uncertain Conditions. Robotics 2018, 7, 76. [Google Scholar] [CrossRef]
- De Maria, G.; Natale, C.; Pirozzi, S. Force/tactile sensor for robotic applications. Sens. Actuators A Phys. 2012, 175, 60–72. [Google Scholar] [CrossRef]
- Pang, G.; Deng, J.; Wang, F.; Zhang, J.; Pang, Z. Development of Flexible Robot Skin for Safe and Natural Human—Robot Collaboration. Micromachines 2018, 9, 576. [Google Scholar] [CrossRef]
- Sun, X.; Sun, J.; Li, T.; Zheng, S.; Wang, C.; Tan, W. Flexible Tactile Electronic Skin Sensor with 3D Force Detection Based on Porous CNTs/PDMS Nanocomposites. Nano-Micro Lett. 2019, 11, 57. [Google Scholar] [CrossRef]
- Úbeda, A.; Zapata-Impata, B.S.; Puente, S.T.; Gil, P.; Candelas, F.; Torres, F. A Vision-Driven Collaborative Robotic Grasping System Tele-Operated by Surface Electromyography. Sensors 2018, 18, 2366. [Google Scholar] [CrossRef]
- Sánchez-Durán, J.A.; Hidalgo-López, J.A.; Castellanos-Ramos, J.; Oballe-Peinado, Ó.; Vidal-Verdú, F. Influence of Errors in Tactile Sensors on Some High Level Parameters Used for Manipulation with Robotic Hands. Sensors 2015, 15, 20409–20435. [Google Scholar] [CrossRef]
- Heyneman, B.; Cutkosky, M.R. Slip classification for dynamic tactile array sensors. Int. J. Robot. Res. 2016, 35, 404–421. [Google Scholar] [CrossRef]
- Su, Z.; Hausman, K.; Chebotar, Y.; Molchanov, A.; Loeb, G.E.; Sukhatme, G.S.; Schaal, S. Force estimation and slip detection/classification for grip control using a biomimetic tactile sensor. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea, 3–5 November 2015; pp. 297–303. [Google Scholar] [CrossRef]
- Meier, M.; Patzelt, F.; Haschke, R.; Ritter, H.J. Tactile convolutional networks for online slip and rotation detection. In International Conference on Artificial Neural Networks; Springer: Cham, Sweden, 2016; pp. 12–19. [Google Scholar]
- Sundaram, S.; Kellnhofer, P.; Li, Y.; Zhu, J.Y.; Torralba, A.; Matusik, W. Learning the signatures of the human grasp using a scalable tactile glove. Nature 2019, 569, 698–702. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Ceccarelli, M.; Carbone, G.; Dong, Z. Grasp configuration planning for a low-cost and easy-operation underactuated three-fingered robot hand. Mech. Mach. Theory 2018, 129, 51–69. [Google Scholar] [CrossRef]
- Kim, D.; Li, A.; Lee, J. Stable Robotic Grasping of Multiple Objects using Deep Neural Networks. Robotica 2021, 39, 735–748. [Google Scholar] [CrossRef]
- Su, J.; Ou, Z.; Qiao, H. Form-closure caging grasps of polygons with a parallel-jaw gripper. Robotica 2015, 33, 1375–1392. [Google Scholar] [CrossRef]
- Modabberifar, M.; Spenko, M. Development of a gecko-like robotic gripper using scott–russell mechanisms. Robotica 2020, 38, 541–549. [Google Scholar] [CrossRef]
- Homberg, B.S.; Katzschmann, R.K.; Dogar, M.R.; Rus, D. Haptic identification of objects using a modular soft robotic gripper. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1698–1705. [Google Scholar] [CrossRef]
- Russo, M.; Ceccarelli, M.; Corves, B.; Hüsing, M.; Lorenz, M.; Cafolla, D.; Carbone, G. Design and test of a gripper prototype for horticulture products. Robot. Comput. Integr. Manuf. 2017, 44, 266–275. [Google Scholar] [CrossRef]
- Dimeas, F.; Sako, D.V.; Moulianitis, V.C.; Aspragathos, N.A. Design and fuzzy control of a robotic gripper for efficient strawberry harvesting. Robotica 2015, 33, 1085–1098. [Google Scholar] [CrossRef]
- Liu, C.H.; Chen-Hua, C.; Mao-Cheng, H.; Chen, Y.; Chiang, Y.P. Topology and size–shape optimization of an adaptive compliant gripper with high mechanical advantage for grasping irregular objects. Robotica 2019, 37, 1383–1400. [Google Scholar] [CrossRef]
- Vidal-Verdú, F.; Oballe-Peinado, Ó.; Sánchez-Durán, J.A.; Castellanos-Ramos, J.; Navas-González, R. Three realizations and comparison of hardware for piezoresistive tactile sensors. Sensors 2011, 11, 3249–3266. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Fukunaga, K.; Narendra, P.M. A branch and bound algorithm for computing k-nearest neighbors. IEEE Trans. Comput. 1975, 100, 750–753. [Google Scholar] [CrossRef]
- Ruczinski, I.; Kooperberg, C.; LeBlanc, M. Logic regression. J. Comput. Graph. Stat. 2003, 12, 475–511. [Google Scholar] [CrossRef]
- Riegel, L.; Hao, G.; Renaud, P. Vision-based micro-manipulations in simulation. Microsyst. Technol. 2020, 1–9. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).