Abstract
The rotational motion of the medium granules under the influence of an impeller installed in the bottom of a cylindrical reservoir is considered. The dependencies of the circulation velocity of the abrasive granules, as well as the dependence of the pressure in the circulation flow of the granules on the radius of the vibrating machine cylindrical reservoir for different speeds of the impeller rotation are obtained. Furthermore, the velocities of the abrasive granules at various distances from the center of the cylindrical reservoir of the vibrating machine have been determined. The amplitudes of the tangential and radial components of the velocity of movement of pseudo-gas from abrasive granules are obtained. The total pressure on the surface of the processed part and the average velocity of the abrasive granules colliding with it are determined. The graphical dependencies of the integral metal removal on the amplitude and frequency of oscillations of the walls of the vibrating machine reservoir are given for various values of the angular velocities of the impeller rotation.
1. Introduction
The improvement of vibration processing technologies and the expansion of their technological capabilities lead to the creation of new multi-energy technologies. The main prerequisite for their development is the principle of combining different processing schemes, as well as two or more types of energy action.
As methods and features for the development of multi-energy technologies, various energy levels can be used, causing changes in the state of the processed material. These include: low temperatures, high speeds and pressures, and application of oscillations of the infrasonic and ultrasonic ranges [1].
Among the number of above-mentioned features of multi-energy processing should be included a limited volume of the vibrating machine reservoir, in which the processing medium of the required characteristics and composition can be placed. The characteristics of the medium in terms of its physical, mechanical and physicochemical properties may be of a wide range [2,3,4]. These are solid, liquid, gaseous and combined, chemically active or inert media. Processing can be carried out under conditions of superposition of electric and magnetic fields on the reservoir. The processed parts can be supplied with additional types of energy by installing them on spindle devices and vibration manipulators [5].
By combining various combinations of the noted parameters, it is possible to significantly expand the area of effective use of vibration treatment, based on the creation of its multi-energy varieties. On this basis spindle, vibratory-abrasive electrochemical; magneto-vibratory-abrasive [6]; vibration mechanical-thermal; vibrating eccentric; vibration electrical-physical and others are developed.
The variety of new kinds of multi-energy vibration processing, presented in the article, led to the need to study the mechanisms of their work, which, in our case, are associated with mathematical simulation of the mechanism of action of the oscillatory and rotational motion of the working medium and parts on the processing.
The existing traditional technology of vibration treatment of parts is widely used in in numerous industrial fields [7,8], while it is also employed in the metalworking industry [9,10]. Vibration finishing and grinding processing is a method of group-agent processing of parts in an oscillating reservoir with a free abrasive or non-abrasive working medium in the presence of a chemically active solution [11,12]. The vibration processing method is used for grinding surfaces with removal of burrs and scale, rounding-off sharp edges, as well as for polishing to achieve high classes of surface cleanliness [13,14]. Cyclic motion is communicated to the reservoir to ensure the force interaction of the medium granules and the processed parts under their relative movement and mutual pressure [15,16].
Vibration modes during vibration treatment are subjected to variation, as well as other basic parameters of the technology. This makes it possible to expand the field of effective use of vibration processing based on the creation of its new varieties. For this purpose, dynamic models of the collision of the processed part with the working medium have been developed. Thus, it is possible to predict the rate and amount of metal removal during vibration treatment as well any changes in quality [17,18,19]. Additional kinds of oscillatory and rotary motion are communicated to the processed parts by installing them in manipulators and spindle devices.
Increasing the efficiency of the vibration treatment process involves the use of multi-energy technologies, consisting in additional energy action on the medium and the processed parts [20,21]. This refers to the simultaneous impact of two or more types of energies, for example, the energy of vibrational and centrifugal action. The physical and technological features of the schemes of energy which impact on the medium and the processed parts, are the structural characteristics of the vibrating machine reservoir, as well as the principle of placing the processed parts in the reservoir. A finely dispersed working medium is used as an abrasive, the granule size of which does not exceed 1–2 mm [22].
This article presents the mathematical modeling of the process of multi-energy vibration treatment, including the rotational motion of the medium granules created by an impeller installed in the lower part of the reservoir. The aim of the work is to consider the mechanism of the action of oscillating and rotational motion of the working medium and parts on the processing process.
2. General Approach
The diagram of the arrangement of the processed parts inside the reservoir of the vibrating machine is presented in Figure 1. The circle on the cylindrical wall of the reservoir shows the dynamics of any point on its surface. The circulation of the abrasive caused by the rotation of the impeller is shown with a curved arrow. The movement of the processed parts is shown by arrows outside small circles representing processed parts.
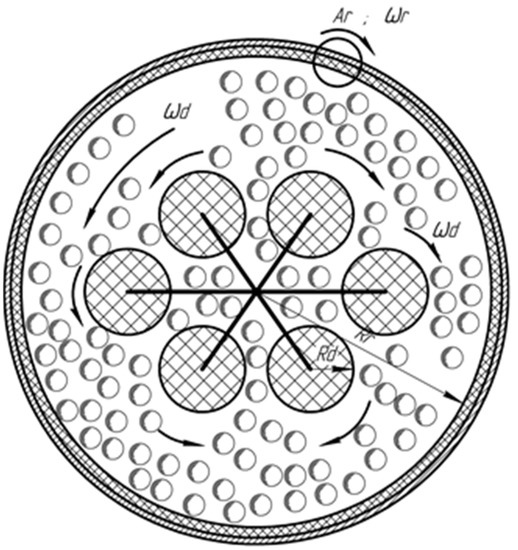
Figure 1.
The layout of parts in the vibration machine cylindrical reservoir.
Studies show that the energetic action of the impeller on pseudo-gas from abrasive granules significantly exceeds the effect of rotating parts on these granules, that makes it possible to divide the solution of the hydrodynamic problem of the rotation of pseudo-gas from abrasive granules inside the reservoir of a vibrating machine into two problems, consisting in the movement of an abrasive medium under the action of an impeller and flow around rotating parts with moving abrasive granules of the medium [23].
The circular motion of all points of the vibration machine reservoir surface can be decomposed into radial and tangential components. As shown in [23], both of these components create a wave-like motion in a pseudo-gas of abrasive granules without causing stationary radial and tangential flows. Such motion is described not by the classical solution of the wave equation of the form for a plane wave or in the case of a spherical wave [24], but is described by the product of the harmonic function of time and the radial component, which is determined by the Bessel equations [25]. In the case of the rotating impeller action, a tangential flow will occur. The solution of the problem of finding the dependence of the velocity field of an elementary volume of a pseudo-gas, its density and pressure on the coordinates and time should be sought using the Navier–Stokes equations, the continuity equations and the equations of gas state.
In this study, the change in density, gravitational influence and convective acceleration are neglected. All simplifications are consistent with experimental results on the study of vibration-processed parts. Thus, the following simplified Navier–Stokes equations can be written [26]:
where is the kinematic viscosity of a pseudo-gas of abrasive granules.
The value of is the force arising due to the effect of a rotating impeller on the pseudo-gas of abrasive granules. In polar coordinates, the Equation (1) for the tangential component of the velocity of movement of the abrasive granules will have the following form:
Solutions of Equation (2) are both time-dependent expressions [23] and the solution of the equation for steady-state motion is:
Since Equation (2) is linear, in our case its complete solution is the sum of solutions [23] and Equation (3). Based on the sticking hypothesis [27], it is assumed that the elementary volume of gas located on the inner wall of a cylinder-shaped reservoir has a velocity equal to the velocity of this wall.
Processing of parts with the abrasive granules occurs due to both the oscillations of the reservoir walls with modes and due to the circular movement of the granules caused by the movement of the impeller at a velocity of and its own rotation of parts with a radius of at a velocity of around its axis. The novelty in this article is the determination of the nature of the multi-energy impacts on the machined parts. Such an additional energy impact on the working medium and the parts makes it possible to increase the efficiency of vibration treatment.
3. The Circulating Movement of the Abrasive Medium Granules under the Action of a Rotating Impeller
In the previous section, it is shown that the oscillations of the cylindrical walls of the reservoir cause a movement in the medium of granules similar to an acoustic wave in a gas. In the next paragraphs, the effect of the rotation of the impeller on this medium is considered.
3.1. Equations of the Circulating Movement
The rotational movement of the abrasive granules in the vibrating machine reservoir occurs due to the impeller installed in the bottom of the cylindrical reservoir (see Figure 2). The impeller has a radius of and rotates at an angular velocity of . The height of the reservoir is equal to the height of the volume occupied by the pseudo-gas from the abrasive granules. and are the radii of the reservoir wall of the vibrating machine and impeller, respectively. is the angular velocity of rotation of the impeller.
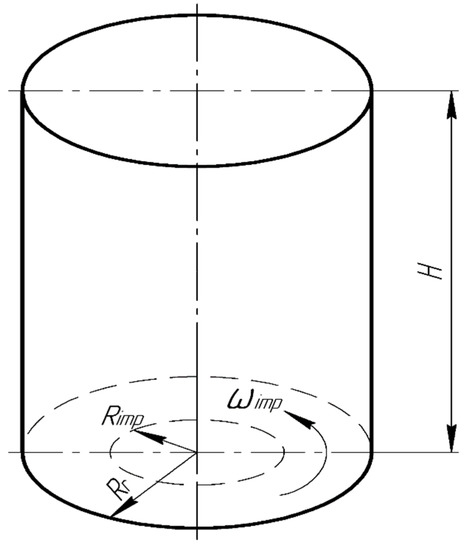
Figure 2.
The layout of the impeller inside the cylindrical reservoir.
To determine the characteristics of the circular motion of a pseudo-gas of abrasive granules, the following simplifications are considered:
- the equation for determining the circulation motion, neglecting changes in the motion parameters along the vertical axis, that is, the flow will be considered as flat;
- the gravitation is neglected;
- the flow will be considered as laminar;the action of the impeller on the abrasive medium granules is replaced by the distributed force acting per unit volume at any point of the pseudo-gas.
The laminar flow will be realistic if the Reynolds number for the pseudo-gas of abrasive granules is less than 1000 [28,29,30]. An estimation of this value can be obtained; for the pseudo-gas of abrasive granules, the Reynolds number can be written as [31]:
where is the tangential velocity of the circulating motion of the pseudo-gas, the average velocity of the chaotic motion of the granules m/s; is the radius of the cylindrical reservoir; is the average diameter of the abrasive granule; is the concentration of the granules in a pseudo-gas. The value of can be estimated by the velocity of the impeller; its angular velocity is rad/s. With an impeller disk radius of mm, the tangential velocity component will be m/s and the average diameter of the granules is mm. The concentration of the abrasive granules can be estimated from the ratio , where is the unit volume of the pseudo-gas. So m−3. Thus, and, therefore, the pseudo-gas motion is assumed as laminar.
Finding the gas flow field in a cylinder under the action of a rotating disk at the bottom of the cylinder is a complex three-dimensional problem that can be solved only numerically and, therefore, goes beyond the assumptions made in this work. However, the determination of the energy effect of the impeller on the pseudo-gas of abrasive granules is possible with the help of experimental data and approximate calculations [32]. That allows us to solve the task of analyzing the mechanism of action of circular motion of the working medium and parts on the processing of their surface.
By virtue of all of the above assumptions, to determine the flow field from abrasive granules in a cylindrical reservoir it is necessary to solve Equation (3), supplemented by the equation for pressure [33]:
In [26], it was shown that the force action of a disk (impeller) rotating in a liquid has a linear dependence on the radius. It is assumed that this dependence of the force action is maintained up to the reservoir wall of the vibrating machine. The more accurate this assumption is, the closer the impeller radius will be to the reservoir radius. In our case, the impeller radius is 200 mm, and the radius of the cylindrical surface of the reservoir walls is 300 mm. Thus, the following expression for the mass force is considered,
The solution of the second equation of the system (5) is as follows:
where and are needed constants. The distribution of pressure along a radius of the cylindrical reservoir can be calculated with the equation of the system (5), after determining the coefficients in expression (7).
3.2. Determination of Unknown Constants in the Expression of the Velocity of the Abrasive Medium Granules Moving under the Action of the Rotating Impeller
In Formula (6) there are two unknown constants, one of which can be determined from the equality to zero of the velocity of the reservoir cylindrical wall. To determine the second constant, it is necessary to identify the action of the impeller on the rotation of the pseudo-gas of abrasive medium granules. In [32], a solution is given that determines the moment of friction forces acting on a disk rotating in a cylinder. For small Reynolds numbers, this value is equal to the following:
where is the height of the abrasive granules above the impeller.
By determining the moment of friction forces acting on the impeller, the power consumed by the rotating impeller, and, consequently, the power transmitted by the impeller to the pseudo-gas can be found. According to the law of conservation of energy, this power is expended on work against the forces of internal friction, as well as on friction on the reservoir wall arising from the circulation movement of a pseudo-gas made up of abrasive granules. From the sticking hypothesis, the pseudo-gas velocity on the wall is zero, that is, the equality (8) leads to the emergence of steady-state motion in the vibrating machine reservoir. The equality to zero of the pseudo-gas velocity on the reservoir wall allows us to represent one of the constants in the expression for the velocity (7) as:
The power transmitted to the abrasive granules by the mass force must be equal to the power transmitted to the pseudo-gas by the impeller. It is presented in the form:
where , a certain diameter less than , a correction factor, taking into account the fact that the impeller has vertical ribs to increase the “grip” of the impeller with the abrasive granules. The value of the coefficient can be determined based on the engine power (3 kW), which rotates the impeller. To do this, at first the viscosity of a pseudo-gas from abrasive granules is estimated. According to [29] gas viscosity is determined by the following relationship:
where is the gas density, is the average velocity of the gas molecules, is the concentration of gas molecules, and is the effective diameter of the gas molecules. In the examined case, kg/m3, m/s, 1/m3. At the maximum angular frequency of rotation rad/s, the power transmitted to the pseudo-gas by the impeller, calculated by Formulas (9) and (10) (at ) will be equal to the expression:
Consequently . To find the constant A in Formula (7), it is necessary to equate the power dissipation of the energy of the circulating motion of a pseudo-gas from the abrasive granules and the power delivered to the abrasive granules by the impeller. According to [33,34], the power dissipation of the flow of a fluid or gas per unit volume in cylindrical coordinates is equal to:
where and are the tangential and parallel axes of rotation of the vertical velocity component. In this study, the change in velocity along the vertical axis is neglected and it is assumed that , which corresponds to a flat flow. In this case the expression (13) is simplified:
The expression (14) must be integrated over the volume occupied by the pseudo-gas and equate to the power transmitted to the abrasive granules by the impeller. Having carried out these actions, taking into account the Formulas (7), (9) and (10) and the numerical value of the correction factor (12), it is obtained:
From Equation (14) it follows that:
To obtain the relation connecting the unknown constant , it is necessary to substitute the expression (7) into the second equation of system (5). As a result, it can be written:
The dependence of the pressure inside the abrasive granules pseudo-gas on the impeller radius can be determined from the first equation of the system (5). Having performed the calculations and equating the pressure in the center of the cylindrical reservoir to zero, it is obtained:
The plots of dependencies of the circulation velocity of the abrasive granules and the pressure on the radius of the vibration machine cylindrical reservoir for various angular velocities of the impeller are presented in Figure 3 and Figure 4.
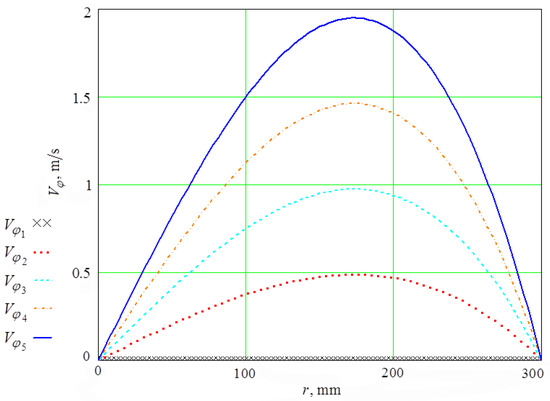
Figure 3.
Dependencies of the circulation velocity of the abrasive granules on the radius of the cylindrical reservoir for different impeller rotation frequencies (0; 0.5; 1; 1.5; 2 Hz).
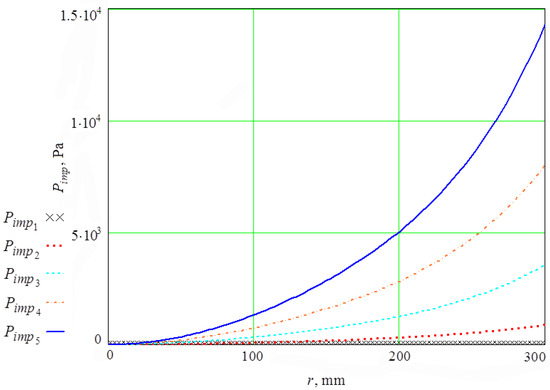
Figure 4.
Dependence of pressure in the circulation flow of the abrasive granules on the radius of the cylindrical reservoir for different impeller rotation velocities (0; 0.5; 1; 1.5; 2 Hz).
4. The Total Action on the Surface of the Processed Part
The action of all the above factors on the processed part is determined. When calculating the total pressure affecting the surface of the cylindrical parts, it is necessary to take into account the influence of the oscillating walls of the vibration machine reservoir, the impact of the impeller, and the action of the rotating part.
4.1. Pressure Created by the Oscillating Walls of the Vibration Machine
As mentioned, in [23], oscillations of the cylindrical walls of the reservoir propagate in abrasive granule pseudo-gas in the form of an acoustic wave. The pressure created by the acoustic wave is equal to the following relationship [35]:
In relation (19), it is taken into account that for a monatomic gas, the quantity .
When interacting with the surface of the processed part, an acoustic wave in a pseudo-gas from abrasive granules will be reflected. The pressure in this case depends on the reflection of the wave. The main role in the reflection coefficient is played by the ratio . Here is the density of pseudo-gas from abrasive granules, is the velocity of sound in a pseudo-gas, is the density of the material of the part, and is the velocity of sound in the material of the part. The smaller this ratio, the more accurately the incident wave is reflected [36]. For steel parts kg/m3, m/s [37]. For pseudo-gas kg/m3.
The velocity of sound in a pseudo-gas of abrasive granules must be determined. For an ideal gas, the velocity of sound is equal to the following:
where is the adiabatic index, which in the case of a monatomic pseudo-gas is , is the Boltzmann constant, is the pseudo-gas temperature, and is the mass of the granule (pseudo-gas atom). From the kinetic theory of gases [31] it is known that the average kinetic energy of an atom (granule) of a pseudo-gas is related to its temperature by the following relationship:
where is the root-mean-square (rms) velocity of the atom (granule). Thus, in order to determine the velocity of sound in a pseudo-gas from abrasive granules, it is necessary to determine the root-mean-square velocity of the abrasive granules.
As mentioned, the mass of the granules during operation of the vibration machine turns into a flow of separately moving granules due to the action of oscillations of the reservoir walls. The velocity of the particles of the abrasive is determined by the velocity of movement of the vibration machine walls. The velocities of the abrasive granules at different distances from the center of the vibration machine cylindrical reservoir are shown graphically (see Figure 5a,b). The dependencies of the radial component of the velocity of the abrasive particles at different distances from the center of the cylindrical reservoir are also presented in Figure 5a. The first curve corresponds to velocity directly near the wall , the second , the third , and the fourth .
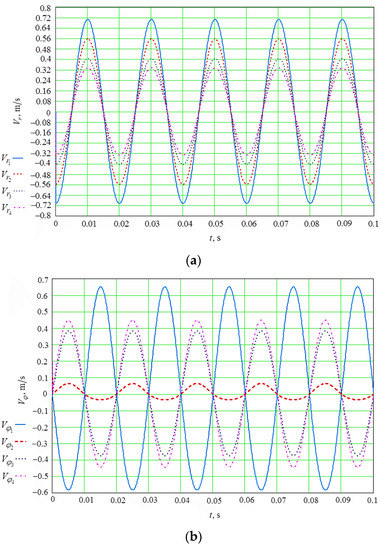
Figure 5.
The velocities of the abrasive granules at different distances from the center of the cylindrical reservoir, the oscillation frequency of the reservoir = 50 Hz, the amplitude = 2 mm. (a) radial component; (b) tangential component.
Dependencies of the tangential component of the velocity of the abrasive granules at various distances from the center of the cylindrical reservoir are also given in Figure 5b. The first curve corresponds to velocity directly near the wall m, the second , the third , and the fourth .
It is obvious from Figure 5a that the radial component of the velocity of the granules decreases monotonously with distance from the wall of the reservoir. The behavior of the curves in Figure 5b is different. That is, the tangential component of the velocity of the granules initially decreases with increasing distance from the reservoir wall, i.e., decreasing radius, and then increases. The behavior of the tangential component is presented in more detail in Figure 6 and is calculated. From the graphs (see Figure 6), it can be seen that the amplitude of the radial component monotonously decreases to zero with decreasing radius. And in this case, the amplitude of the tangential component changes sign as the radius changes.
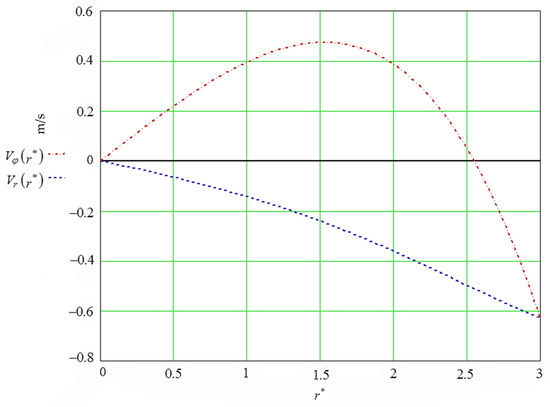
Figure 6.
Amplitudes of tangential— and radial— components of the velocity of motion of the abrasive granule pseudo-gas, depending on the relative radius .
Such behavior is similar to the behavior of the function describing the propagation of the wave motion of the abrasive medium inside the reservoir, along its radius. However, since is a solution of the Bessel equation, such a wave cannot be described by a simple dependence of the form . Function tends to this form only as [38]. The ratio of the modulus of the amplitudes of the radial component of the velocities is determined as , while for the tangential component a similar ratio is obtained: (Figure 5). Based on the above, it can be assumed that:
Substituting expressions (21) and (22) into Formula (20), the final expression for the velocity of sound in the pseudo-gas of abrasive granules near the surface of the rotating processed parts is obtained:
where and are the circular frequency and amplitude of oscillations of the walls of the vibration machine reservoir, respectively. For mm and Hz, m/s. Thus, ; therefore, the surface of the part represents an absolutely solid surface for the wave in an abrasive granule pseudo-gas, from which the wave is completely reflected. The wavelength of propagation of oscillations in a pseudo-gas, according to (23), is equal to:
With amplitude mm mm, which is much less than the diameter of the part (approximately equal to mm). That is, the incident wave will be reflected in the same phase and with the same amplitude. Consequently, the acoustic pressure on the surface of the processed part will be twice the value calculated by Formula (19). Taking into account the fact that and using Formulas (19) and (22), the expressions of pressure created by the vibrations of the reservoir walls of the vibration machine on the surface of the rotating processed part are finally:
4.2. Total Pressure on the Surface of the Processed Part and the Average Velocity of the Abrasive Granules Colliding with It
The total pressure on the surface of the rotating processed part, taking into account relation (25), is as follows:
According to the laws of the molecular theory of gases [31] the pressure and temperature of the gas are related as follows:
where and are the volume occupied by the pseudo-gas and the number of granules in this volume, respectively. Taking into account relation (21), the expression for the root-mean-square velocity of the chaotic movement of abrasive granules near the surface of the processed part depending on the pressure on its surface can be written as:
where, as in all the above ratios, is the pseudo-gas density of abrasive granules. To compare the magnitude of with the rotational velocities of the impeller, of the part and the oscillating reservoir wall, the graphs of the dependence of this quantity on the above parameters are presented in Figure 7.
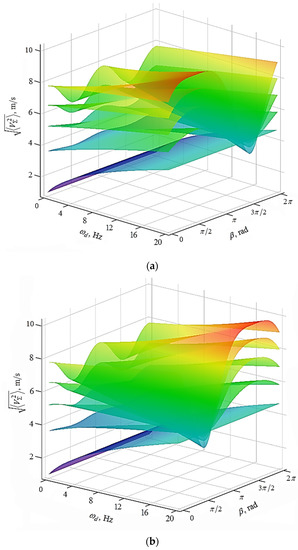
Figure 7.
Graphic dependencies of root-mean-square velocities of chaotic movement of abrasive granules near the surface of the processed part, depending on the angle β and the angular velocity of rotation of the part X for different values of the impeller angular velocity. Graphic dependencies (a) correspond to the rotation of the processed part and the impeller in the same direction, dependencies (b) correspond to the opposite direction of rotation of the processed part and the impeller.
From the dependencies (Figure 7) it follows that the rms velocity of the chaotic movement of abrasive granules is comparable to the velocity of a circular motion of the part surface (up to m/s). Therefore, to calculate the metal removal it is necessary to add with the velocity of the circular movement of the part surface.
The velocities of the abrasive granules approach to the surface of the part from different sides with the same probability (random motion). Therefore, it is necessary to average the magnitude of the velocity of the approximation of the granule over the angle between the radius of the part and the direction of movement of the granule (Figure 8).
Figure 8.
Scheme of averaging the velocities of the granules approaching to the surface of the part: velocity of approaching the granule to the part; radius of the part; angle between the radius-vector and the approaching velocity of the granule .
The average velocity of the granules approaching the surface of the part will be equal to:
The velocity will be directed along the radius-vector and perpendicular to the surface of the part. Thus, the mutual rate of approach of any point on the part surface and the granule approaching it will be equal to the following:
Graphic dependencies on the angle , the angular velocity of rotation of the processed part, are presented for several values of the angular velocity of rotation of the impeller in Figure 9. The graphic dependencies shown in Figure 7 and Figure 9 are visually similar, but differ numerically. It is the velocity that will be used in the future to determine the amount of metal removal using multi-energy technology, which consists of the joint action of vibrational and centrifugal forces on the working medium.
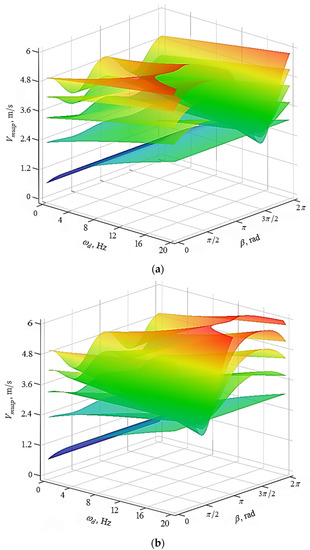
Figure 9.
Graphic dependencies on angle and the angular velocity of rotation of the part for different values of the angular velocity of the impeller. The graphical dependencies (a) correspond to the rotation of the processed part and the impeller in one direction, the dependencies (b) correspond to the opposite direction of rotation of the processed part and the impeller.
5. Removal of Metal Using Multi-Energy Technology
To determine the metal removal during multi-energy exposure of the joint action of vibratory and centrifugal forces on the working medium, Formula (39) is used:
where and are functions depending on the friction coefficient and the surface area of the processed part, respectively; is the combined constant determined by the mechanism of metal removal by a single granule of the medium from the surface of the processed part; and are coefficients which are corrections of velocity for the circulation movement of granules in terms of the frequency and amplitude parameters of the oscillations of the walls of the vibration machine cylindrical reservoir; s2/m2; is the average radius of the abrasive granule; and is the time of vibration treatment.
The function is determined by the following expression:
The function has been derived under the assumption that the reflection of the granule from the processed part surface, in the direction perpendicular to its surface, is absolutely elastic, that is, without loss of kinetic energy. Taking into account the reduction coefficient— [39], where is the coefficient of dry friction, (Figure 10).
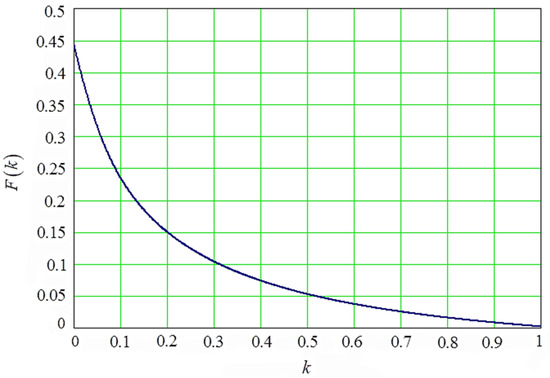
Figure 10.
Behavior of function depending on parameter .
Comparison of dependencies in Figure 11a,b shows that the difference in the direction of rotation of the impeller and the part does not greatly affect the removal of metal.
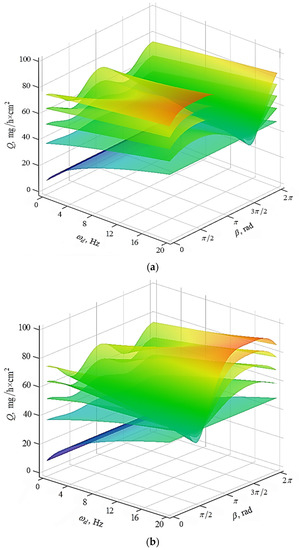
Figure 11.
Graphic dependencies of metal removal from a rotating part on angle β, angular velocity of rotation of the processed part for several values of the angular velocity of rotation of the impeller. The graphical dependencies (a) correspond to the rotation of the processed part and the impeller in the same direction, the dependencies (b) correspond to the opposite direction of rotation of the processed part and the impeller.
The surfaces (Figure 11) do not describe the integral of metal removal, but the removal of the part’s material at different points of the surface depending on the angle defining this point. Thus, the dependencies (Figure 11) allow the determination of the efficiency of multi-energy technology, which consists of the joint action of vibrational and centrifugal forces on the working medium at different points on the rotating surface of the processed part.
The integral metal removal is determined by averaging over the angle in expression (33). In this case, graphical dependencies of the integral metal removal rate on the part rotation frequency were obtained for different values of the angular velocity of the impeller rotation (Figure 12).
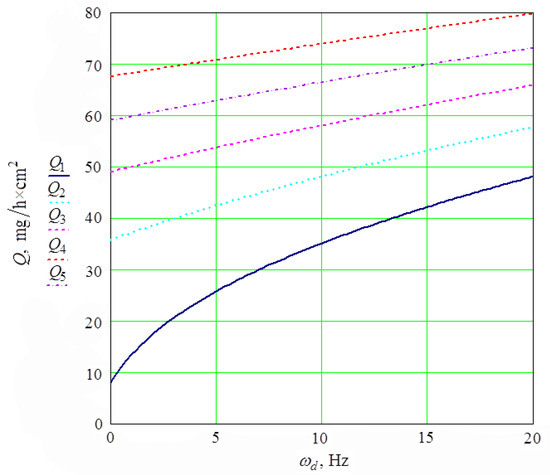
Figure 12.
Graphic dependencies of the integral metal removal on the frequency of the part rotation for different values of the angular velocity of rotation of the impeller: —angular velocity of rotation equal to 0; rad/s; rad/s; rad/s, rad/s.
It is obvious that the integral metal removal increases both with an increase in the velocity of the part rotation and with increasing the velocity of rotation of the impeller. The non-zero value of the metal removal at zero velocities of rotation of the part and impeller is explained by the action of vibrating reservoir walls oscillating with a frequency of 50 Hz and amplitude of 2.0 mm. The graphical dependencies of the integral metal removal on the amplitude and frequency of oscillation of the walls of the vibration machine reservoir are presented in Figure 13 for various values of the angular velocities of rotation of the impeller.
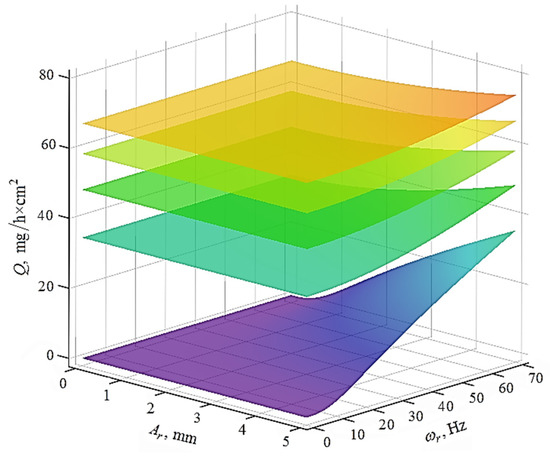
Figure 13.
Graphic dependencies of the integral metal removal rate on the amplitude and frequency of oscillation of the walls of the reservoir for various values of the angular velocities of rotation of the impeller.
The rotational velocity of the part . The lower surface corresponds to the angular velocity of the impeller rotation equal to 0, the second from the bottom is 3.14 rad/s, the third is 6.28 rad/s, the fourth is 9.42 rad/s, and the fifth is 12.56 rad/s. It is quite clear that the contribution of oscillations of the reservoir wall to metal removal rate decreases as the impeller velocity increases; when reaches 12.56 rad/s, the contribution of oscillations of the reservoir walls is almost zero (Figure 14).
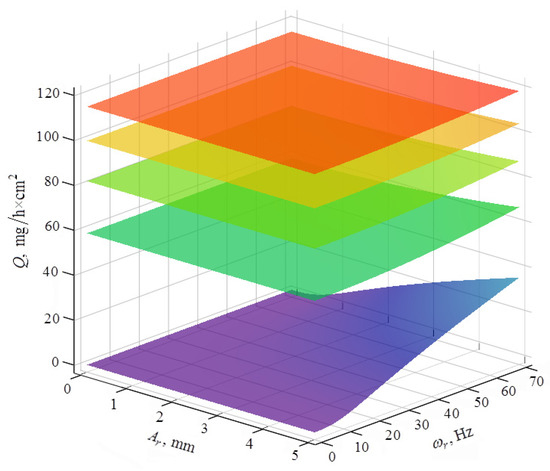
Figure 14.
Contribution of oscillations of the reservoir walls to the metal removal during the rotation of the part. Impeller rotation velocity .
The bottom surface corresponds to the angular velocity of the part rotation equal to 0, the second from the bottom —15.7 rad/s, the third —31.4 rad/s, the fourth —47.1 rad/s, and the fifth —62.8 rad/s. As in the previous case, the metal removal rate from the action of oscillating reservoir walls in the total metal removal decreases with increasing velocity of rotation of the part; when reaches 31.4 rad/s, while the contribution of the oscillations of the reservoir walls is almost zero.
For experimental verification of the effectiveness of the described method of finishing and grinding processing, a vibrating machine was developed (Figure 15). It consists of: V-belt gears—1, 13; bevel reduction gears—2, 14; flexible couplings—3, 16; oscillating system—4; elastic suspensions—6, 9; rigid supports—7, 10; vertical vibration exciters—11, 21; electric motors—12, 22; shafts—15, 17, 23, 24; impeller—18; reservoir—19; locating fingers—20; fastenings of the elastic suspension—8. In the reservoir 19 of the vibrating machine are loaded and the processed parts—5 and the working medium—25.
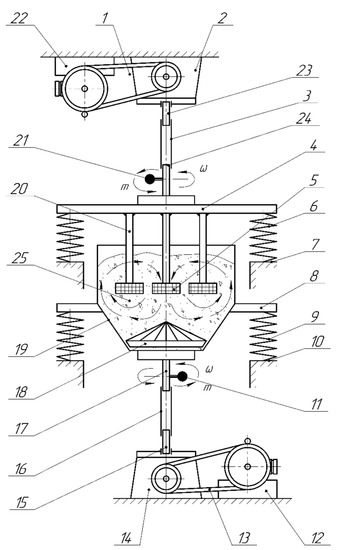
Figure 15.
Schematic diagram and general view of the components of a hybrid vibrating machine for the implementation of multi-energy technologies.
The proposed method is implemented as follows. The parts 5 to be machined are mounted on locating fingers 20 located along concentric circles using an elastic suspension 6 on a rigid support 7. First, the vertical vibration exciter 21 of the oscillating system 4 is turned on. The system is placed in the working area of the reservoir 19 together with the parts 5. The reservoir 19 is mounted on a rigid support 10 with the help of an elastic suspension 9 and is filled with a working medium 25. The medium 25 receives rotational motion from the impeller 18 and oscillatory motion from the vertical vibration exciter 11, rigidly mounted on the shaft 17 of the impeller 18 and kinematically connected to the reservoir 19.
The rotary motion from the electric motor 12 by the V-belt transmission 13 is transmitted to the bevel reduction gear 14, the shaft 15 of which, through a flexible coupling 16, communicates with the shaft 17 of the impeller 18. As a result of the use of the energy of vibrational and centrifugal forces that affect the working medium and processed parts in the vertical and horizontal planes, we carry out processing, remove the defective metal layer, and achieve the required surface roughness. Approbation of the described method and experimental confirmation of theoretical calculations, as well as their convergence was conducted during vibration finishing and grinding processing of complex-profile body specimens-parts after the previous operations of turning, milling and drilling. The material of the specimen-part is aluminum alloy AL7 DSTU 2839-94 (G-AlCu4Ti DIN 1725-2), and the technological method of producing the blanks is casting into a chill mold. The thickness of the burrs at the base did not exceed 0.2 mm, the initial surface roughness was μm.
The shape of the specimen-part is complex, obtained by conjugation of curved surfaces. The design of the specimen-part had blind and through holes of various diameters, as well as niches, pockets, and stepped transitions of surface elements. A through central hole was used when installing the specimen-part in the fixture. The dimensions of the specimen part are mm. Finishing and grinding processing was carried out in a vibrating machine reservoir, which made it possible to place simultaneously 16 parts. The porcelain spheres with a diameter of 2 mm were used as a working medium. The working medium and specimens-parts in the reservoir were moistened with a chemically active solution on an alkaline basis.
Processing modes are the following: impeller rotation speed—1440 rpm; the amplitude and frequency of the reservoir movement—1.3 to 1.5 mm, 50 Hz; amplitude and frequency of movement of the oscillating system of the device with parts—1 to 1.2 mm, 30 Hz, respectively. The machine processing time was about 30 min. As a result of processing, surface defects are completely removed, the required surface roughness is achieved with a natural shade of the metal. Sorting quality control of finishing and grinding processing did not establish the appearance of defects.
6. Conclusions
The paper presents the results of using the multi-energy technology of vibration finishing and grinding processing proposed by the authors. This technology is characterized by the combined effect of vibrational and centrifugal forces on the working medium and the processed parts. The study was carried out on the basis of a mathematical model, under the assumption that during vibration treatment the collective behavior of abrasive granules is similar to the behavior of gas molecules or atoms. Simulation of multi-energy impact processes is based on the application of the Navier–Stokes equations and the use of gas laws.
- It has been established that the circular motion of all points of the reservoir surface of the vibrating machine can be decomposed into radial and tangential components, which create wave motion in the granules of the working medium, without leading to the appearance of stationary radial and tangential flows. The dependencies of the radial and tangential components of the velocity of movement of the granules of the medium inside the oscillating cylindrical reservoir on its radius and period of oscillations are obtained.
- It has been found that when distributing the pressure of the working medium granules over the surface of the rotating processed part, it is necessary to take into account the force of the impeller and the pressure caused by the rotation of the processed part, as well as the friction force between the surface of the rotating processed part and the granules of the medium.
- Graphical dependencies of the speed of approach of any point of the surface of the part and the granule of the medium flying up to it on the angle of the ordinate axis and the angular velocity of rotation of the part for different values of the angular velocity of the impeller are obtained.
- It has been established that the integral metal removal increases with an increase in the rotation speeds of the processed part and the impeller. The presence of removal at these speeds equal to zero is explained by the action of the oscillating reservoir wall. The share of these influences in the resulting metal removal decreases as the speed of rotation of the impeller and part increases. When the rotation speeds reach for the impeller 12.56 rad/s and for the part 31.4 rad/s, respectively, this fraction is equal to zero.
Author Contributions
Conceptualization, J.K., A.V.M. and V.A.F.; Data curation, V.A.F.; Formal analysis, A.V.M.; Funding acquisition, V.A.F., A.P.M. and A.I.G.; Investigation, A.V.M.; Methodology, J.K. and A.V.M.; Project administration, J.K., V.A.F. and A.I.G.; Resources, V.A.F. and A.P.M.; Supervision, V.A.F., A.P.M. and A.I.G.; Validation, A.V.M. and A.P.M.; Visualization, A.I.G.; Writing—original draft, A.V.M. and V.A.F.; Writing—review & editing, J.K., A.P.M. and A.I.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, Z.; Zhu, L.; Zhang, G.; Ni, C.; Lin, B. Review of ultrasonic vibration-assisted machining in advanced materials. Int. J. Mach. Tools Manuf. 2020, 156, 103594. [Google Scholar] [CrossRef]
- Malkorra, I.; Souli, H.; Salvatore, F.; Arrazola, P.; Rech, J.; Cici, M.; Mathis, A.; Rolet, J. Modeling of drag finishing—Influence of abrasive media shape. J. Manuf. Mater. Process. 2021, 5, 41. [Google Scholar] [CrossRef]
- Stańczyk, M.; Figlus, T. The effect of selected parameters of vibro-abrasive processing on the surface quality of products made of 6082 aluminium alloy. Materials 2019, 12, 4117. [Google Scholar] [CrossRef]
- Alcaraz, J.Y., II; Ahluwalia, K.; Yeo, S.-H. Predictive models of double-vibropolishing in bowl system using artificial intelligence methods. J. Manuf. Mater. Process. 2019, 3, 27. [Google Scholar] [CrossRef]
- Kundrák, J.; Mitsyk, A.V.; Fedorovich, V.A.; Markopoulos, A.P.; Grabchenko, A.I. Modeling the energy action of vibration and centrifugal forces on the working medium and parts in a vibration machine oscillating reservoir with an impeller. Manuf. Technol. 2021, 21. [Google Scholar] [CrossRef]
- Xie, H.; Zou, Y. Investigation on finishing characteristics of magnetic abrasive finishing process using an alternating magnetic field. Machines 2020, 8, 75. [Google Scholar] [CrossRef]
- Królczyk, J.B. An attempt to predict quality changes in a ten-component granular system. Teh. Vjesnik-Tech. Gaz. 2014, 21, 255–261. [Google Scholar]
- Królczyk, J.B. Metrological changes in the surface morphology of cereal grains in the mixing process. Int. Agrophys. 2016, 30, 193–202. [Google Scholar] [CrossRef]
- Shengqiang, Y.; Wenhui, L. Surface Finishing Theory and New Technology; Springer: Berlin/Heidelberg, Germany, 2018; p. 497. [Google Scholar]
- Gillespie, L. Mass Finishing Handbook; SME Industrial Press Inc.: New York, NY, USA, 2007; p. 800. [Google Scholar]
- Davidson, D.A. Vibratory finishing: Versatile effective. and reliable. Metal Finish. 2008, 106, 30–34. [Google Scholar] [CrossRef]
- Holzknecht, E. Everything you need to know about mechanical / mass finishing. Metal Finish. 2009, 107, 27–31. [Google Scholar] [CrossRef]
- Pandiyan, V.; Castagne, S.; Subbiah, S. High frequency and amplitude effects in vibratory media finishing. Procedia Manuf. 2016, 5, 546–557. [Google Scholar] [CrossRef][Green Version]
- Domblesky, J.; Cariapa, V.; Evans, R. Investigation of vibratory bowl finishing. Int. J. Prod. Res. 2003, 41, 3943–3953. [Google Scholar] [CrossRef]
- Hashimoto, F.; Johnson, S.P. Modeling of vibratory finishing machines. CIRP Ann. 2015, 64, 345–348. [Google Scholar] [CrossRef]
- Hashimoto, F.; Johnson, S.P.; Chaudhari, R.G. Modeling of material removal mechanism in vibratory finishing process. CIRP Ann. 2016, 65, 325–328. [Google Scholar] [CrossRef]
- Królczyk, G.; Gajek, M.; Legutko, S. Predicting the tool life in the dry machining of duplex stainless steel. Eksploat. Niezawodn. 2013, 15, 62–65. [Google Scholar]
- Achiamah-Ampomah, N.; Cheng, K. Investigation on multi-physics simulation-based virtual machining system for vibratory finishing of integrally bladed rotors (IBRS). J. Multiscale Model. 2016, 7, 1640003. [Google Scholar] [CrossRef]
- Mullany, B.; Shahinian, H.; Navare, J.; Azimi, F.; Fleischhauer, E.; Tkacik, P.; Keanini, R. The application of computational fluid dynamics to vibratory finishing processes. CIRP Ann. 2017, 66, 309–312. [Google Scholar] [CrossRef]
- Kundrák, J.; Morgan, M.; Mitsyk, A.V.; Fedorovich, V.A. The effect of the shock wave of the oscillating working medium in a vibrating machine’s reservoir during a multi-energy finishing-grinding vibration processing. Int. J. Adv. Manuf. Technol. 2020, 106, 4339–4353. [Google Scholar] [CrossRef]
- Mamalis, A.; Kundrák, J.; Mitsyk, A.V.; Fedorovich, V.A. Development of modular machine design and technologies of dynamic action for finishing-grinding treatment by an oscillating abrasive medium. Mach. Form. Technol 2015, 7, 1–10. [Google Scholar]
- Mamalis, A.G.; Grabchenko, A.I.; Mitsyk, A.V.; Fedorovich, V.A.; Kundrák, J. Mathematical simulation of motion of working medium at finishing–grinding treatment in the oscillating reservoir. Int. J. Adv. Manuf. Technol. 2014, 70, 263–276. [Google Scholar] [CrossRef]
- Fedorovich, V.A.; Mitsyk, A.V. Mathematical simulation of kinematics of vibrating boiling granular medium at treatment in the oscillating reservoir. Key Eng. Mater. 2013, 581, 456–461. [Google Scholar] [CrossRef]
- Lyu, Y.; Jamil, M.; Ma, P.; He, N.; Gupta, M.K.; Khan, A.M.; Pimenov, D.Y. An ultrasonic-based detection of air-leakage for the unclosed components of aircraft. Aerospace 2021, 8, 55. [Google Scholar] [CrossRef]
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Cherny, G.G. Gas Dynamics; Nauka: Moscow, Russia, 1988. (In Russian) [Google Scholar]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Oxford Engineering Science Series; Clarendon Press: Oxford, UK, 1994; p. 458. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000; p. 631. [Google Scholar]
- Sokolov, V. Diffusion of circular source in the channels of ventilation systems. In Advances in Engineering Research and Application. ICERA 2018. Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2018; Volume 63, pp. 278–283. [Google Scholar] [CrossRef]
- Sokolov, V. Transfer functions for shearing stress in nonstationary fluid friction. In Proceedings of the 5th International Conference on Industrial Engineering (ICIE 2019). ICIE 2019. Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2019; pp. 707–715. [Google Scholar] [CrossRef]
- Sivukhin, D.V. General Course of Physics: Vol. 2. Thermodynamics and Molecular Physics; Fizmatlit: Moscow, Russia, 2019; p. 544. (In Russian) [Google Scholar]
- Prandtl, L.; Oswatitsch, K.; Wieghardt, K. Führer Durch Die Strömungslehre; Springer: Berlin/Heidelberg, Germany, 1990. (In German) [Google Scholar]
- Kochin, N.E.; Kibel, I.A.; Rose, N.V. Theoretical Hydromechanics; Fizmatlit: Moscow, Russia, 1963; Volume 2, p. 727. (In Russian) [Google Scholar]
- Vallander, S.V. Lectures in Hydroaeromechanics; Leningrad State University: Leningrad, Russia, 1978; p. 296. (In Russian) [Google Scholar]
- Strett, J.V.; Rayleigh, L. The Theory of Sound; Cambridge University Press: Cambridge, UK, 2011; Volume 2, p. 318. [Google Scholar]
- Rzhevkin, S.N. A Course of Lectures on the Theory of Sound; Pergamon Press: London, UK, 1963; p. 464. [Google Scholar]
- Babichev, A.P.; Babushkina, N.A.; Bratkovsky, A.M.; Grigorieva, I.S.; Meilikhov, E.Z. Physical Quantities: Handbook; Energoatomizdat: Moscow, Russia, 1991; p. 1232. (In Russian) [Google Scholar]
- Prokhorov, A.M. (Ed.) Physical Encyclopedia; Great Russian Encyclopedia: Moscow, Russia, 1998; Volume 5, p. 687. (In Russian) [Google Scholar]
- Mitsyk, A.V. Increase of the Effectiveness of Treatment of Large-Sized Planed Products by an Activation of Motion of the Working Medium in Vibrating «U»—Shaped Containers. Ph.D. Thesis, National Technical University «Kharkiv Polytechnic Institute», Kharkov, Ukraine, 2008; p. 331. (In Russian). [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).