Adaptive Obstacle Avoidance for a Class of Collaborative Robots
Abstract
1. Introduction
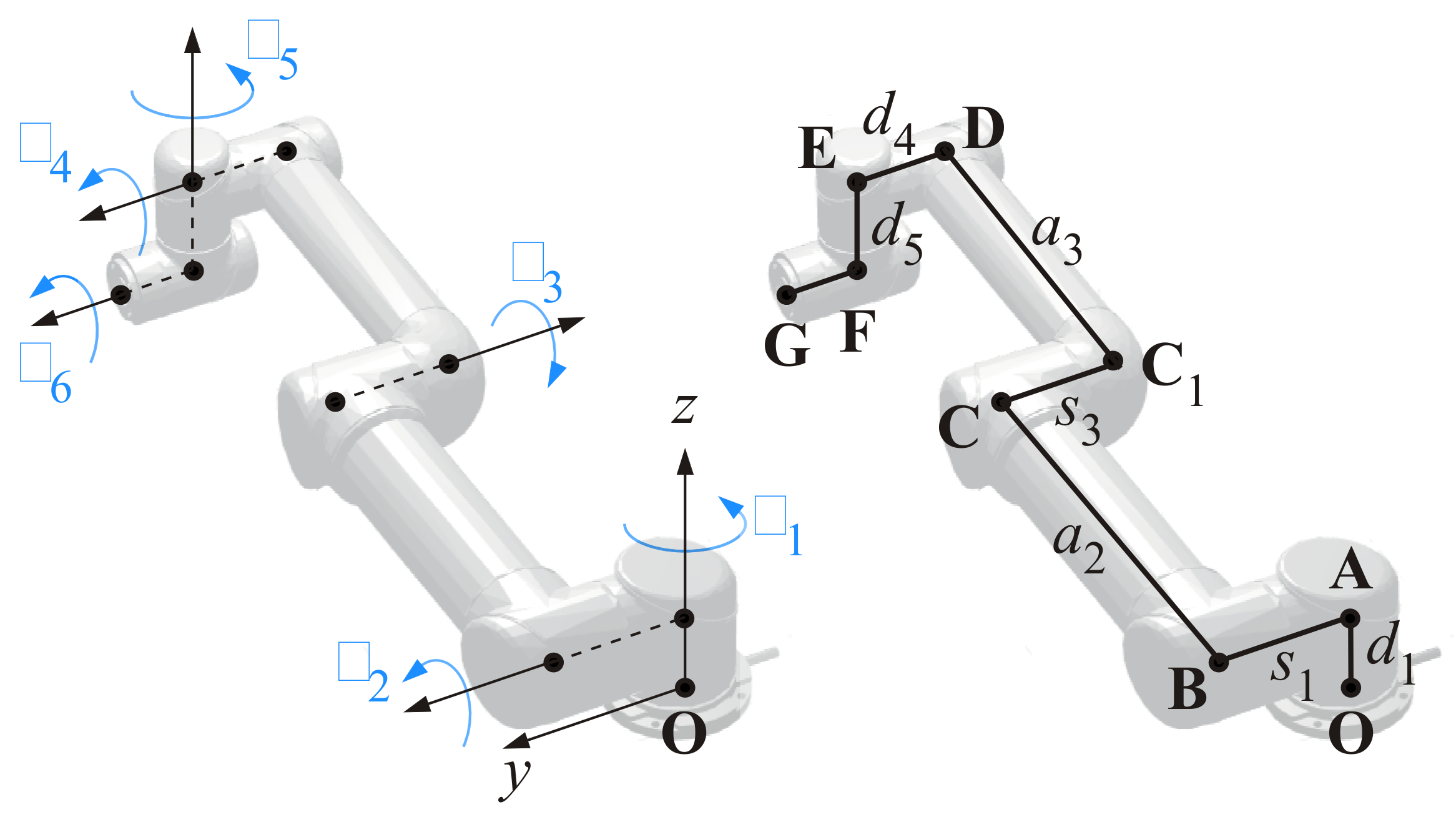
- While in previous works the safety regions enveloping the structure of the robot were defined as spheres centred on a series of control points equally spaced along the serial kinematic chain, a more efficient strategy is proposed here defining only one safety volume for each link; such volume is the combination of a cylinder, with a height equal to the length of the link, and two hemispheres at the extremities of the link.
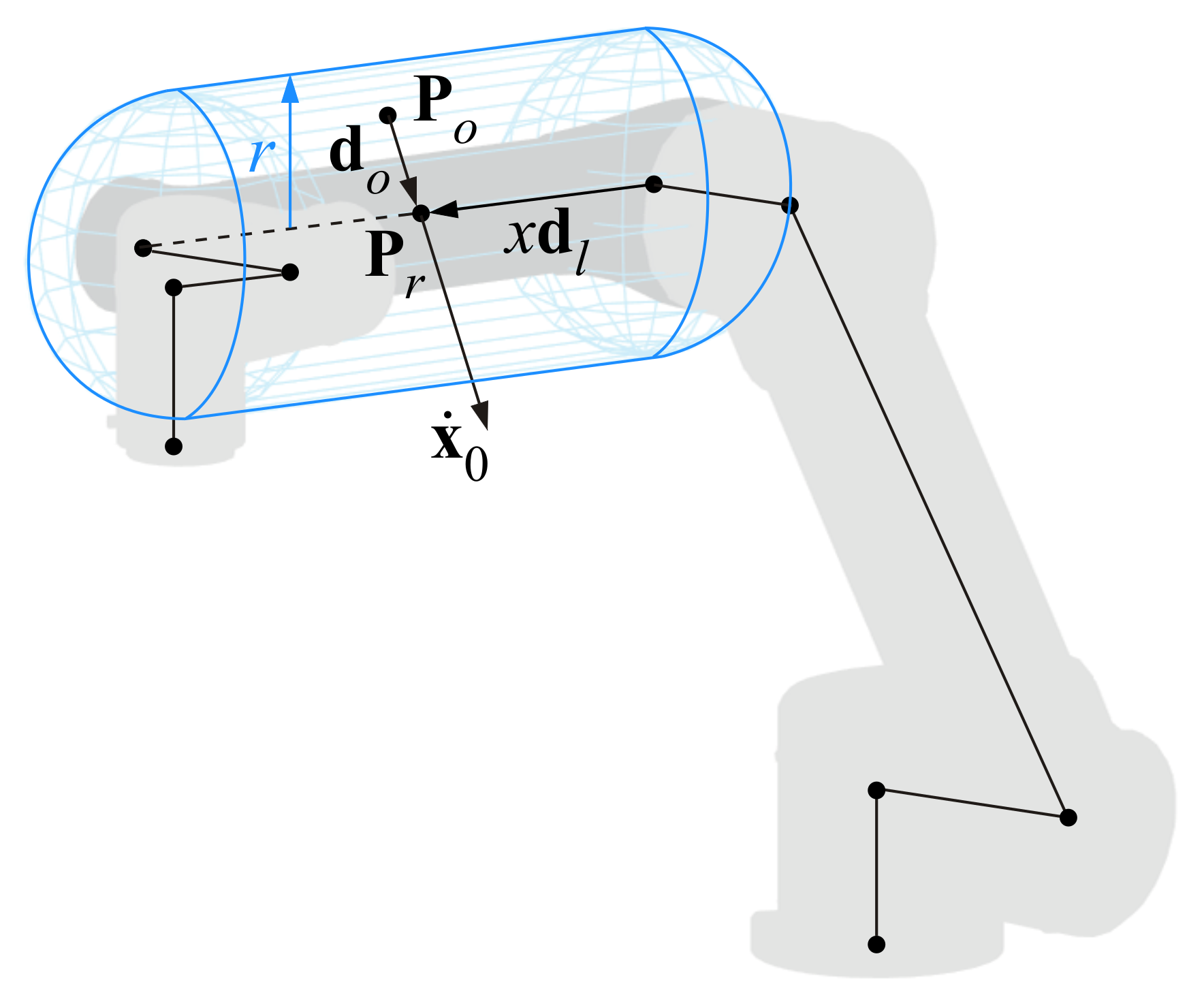
- In order to adapt the algorithm to different cases, with fixed or moving obstacles, the radius of the cylindrical/hemispherical safety volume of each link is variable, as a function of the obstacle velocity: a small radius is adopted for fixed obstacles, facilitating the mobility of the robot, whereas the radius increases with the speed of the obstacle, so that the risk of collision is reduced for the dynamic case.
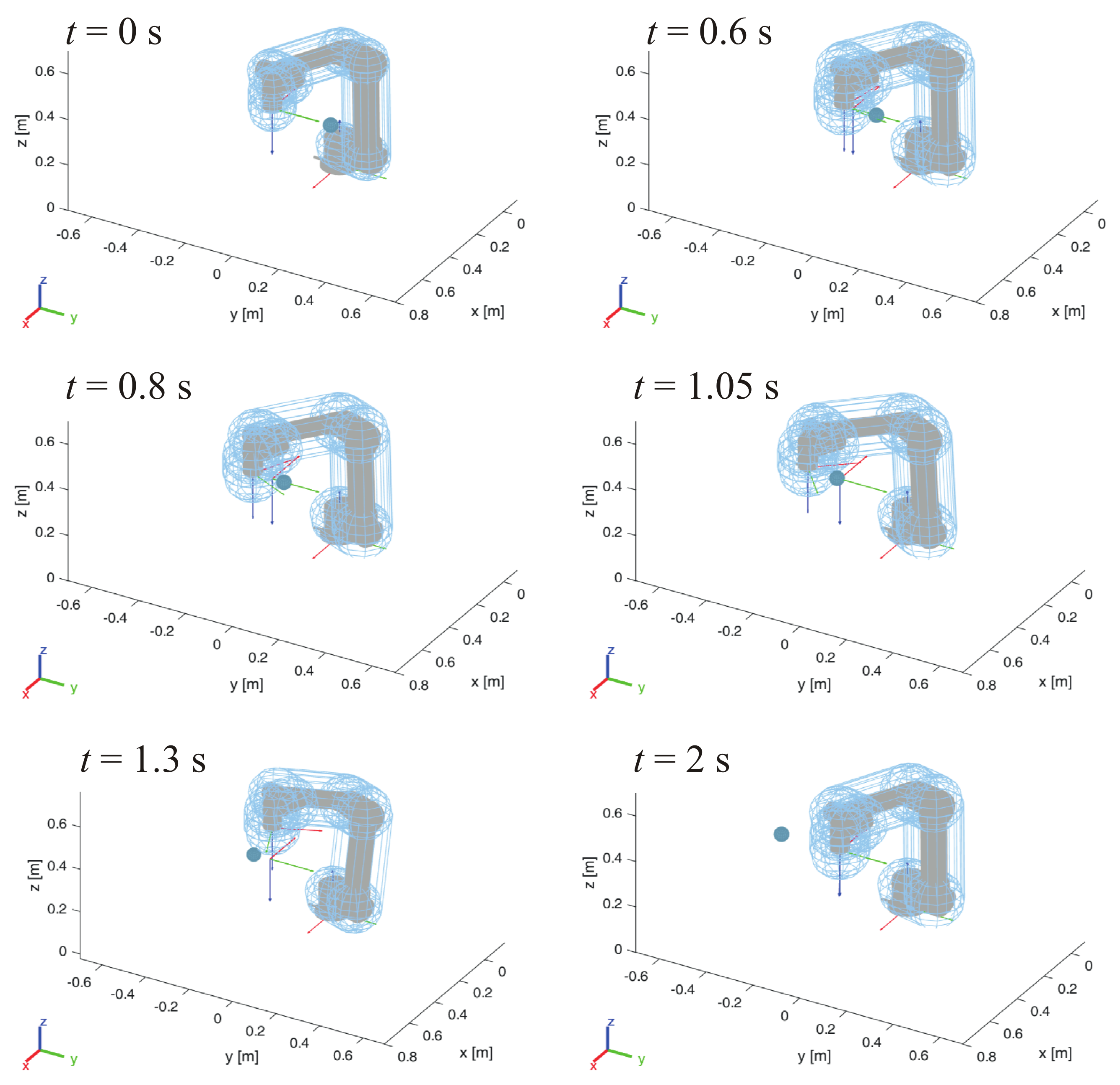
- Three different modalities for the collision avoidance control law are proposed, which differ in the type of motion admitted for the perturbation of the end-effector. The first mode, the most general, allows for a 6-DOF perturbation of the end-effector, whose pose may vary in position and orientation in order to avoid a collision. If such condition is not admissible due to the specific application, some restrictions can be imposed. As an example, in this paper, two additional modes characterized by a reduced mobility of the perturbation are proposed. The second mode allows for a 4-DOF Schoenflies-like perturbation, where all translations and the rotation about the vertical axis are admitted. If the last rotation is not admitted, the third mode can be used, where the orientation of the end-effector remains unchanged during the perturbation due to a collision avoidance.
2. Motion Control Law
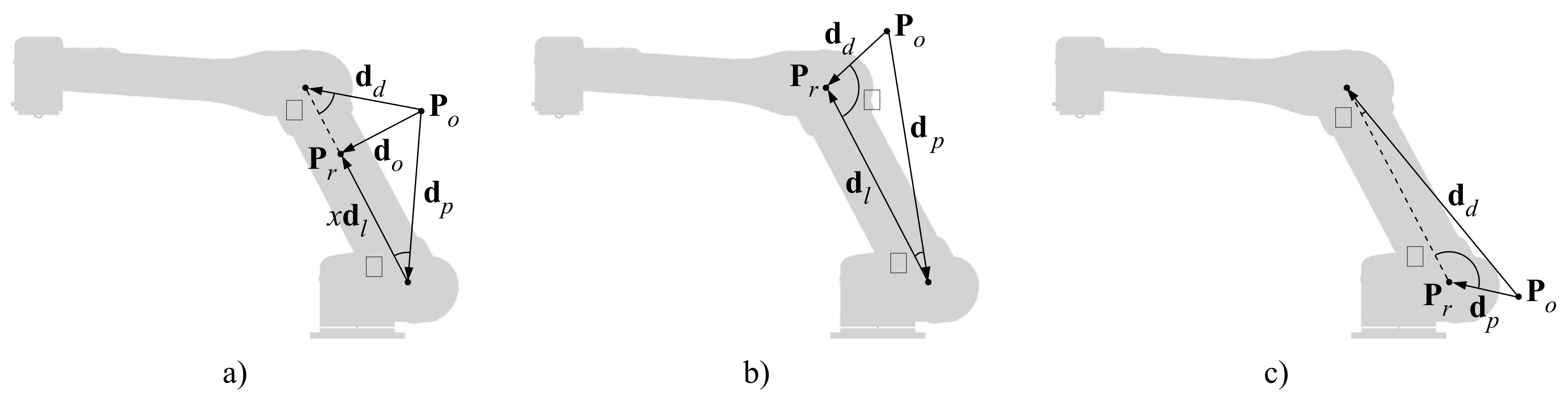
- (a)
- If and , then the distance is orthogonal to the link, and the position of along the link is defined by the scalar parameter x:
- (b)
- If , then the point is coincident with the distal extremity of the link, thus:
- (c)
- If , then the point is coincident with the proximal extremity of the link, thus:
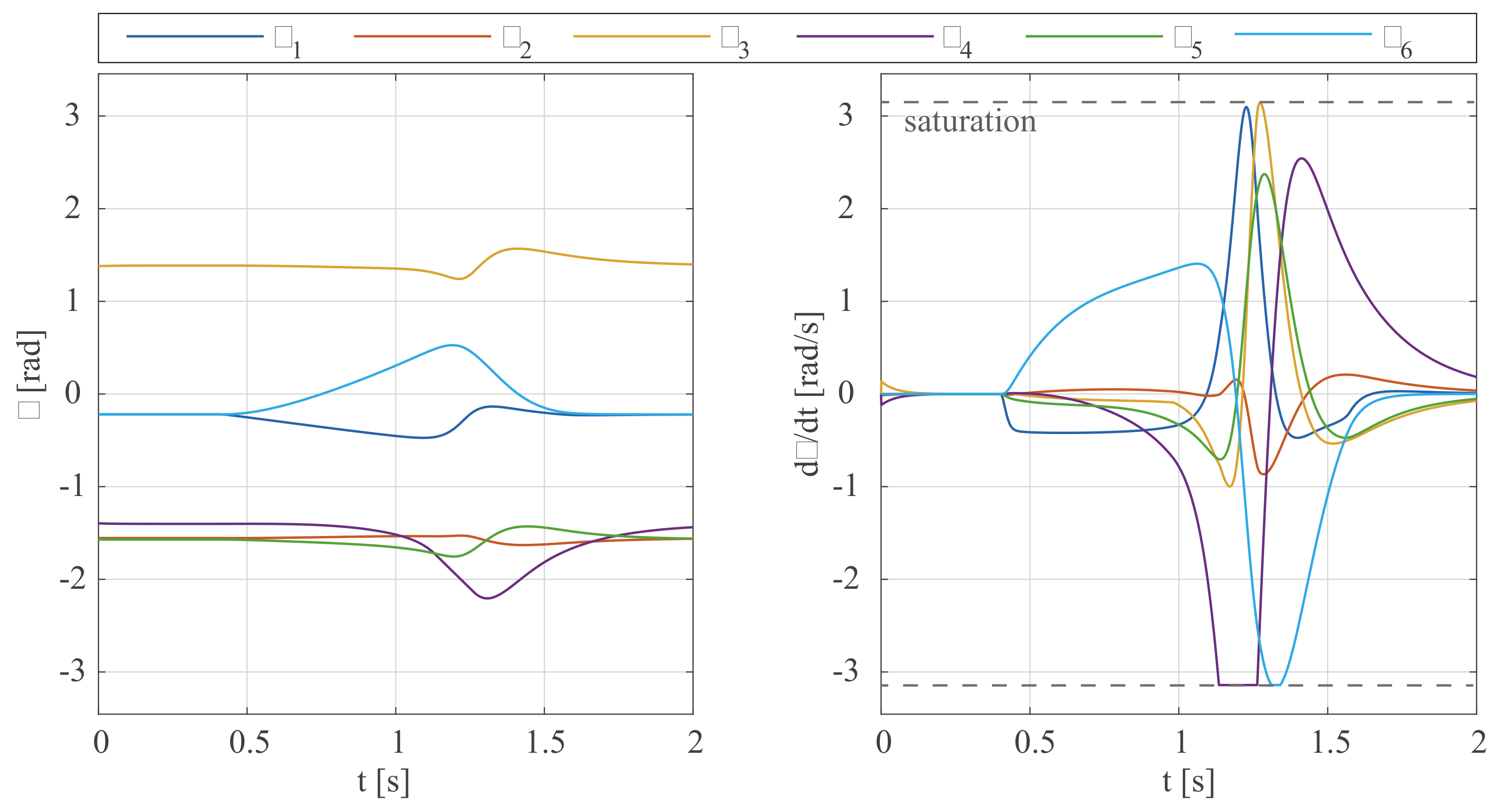
2.1. Mode I: 6-DOF Perturbation
- is a positive-defined gain matrix, for simplicity set as .
- The position error between the desired and actual position is defined as [30]:where is the translation error vector and is the orientation error vector; the position and orientation of the end-effector are, respectively, expressed by the vector and the rotation matrix , with being the unit vectors of the end-effector frame.
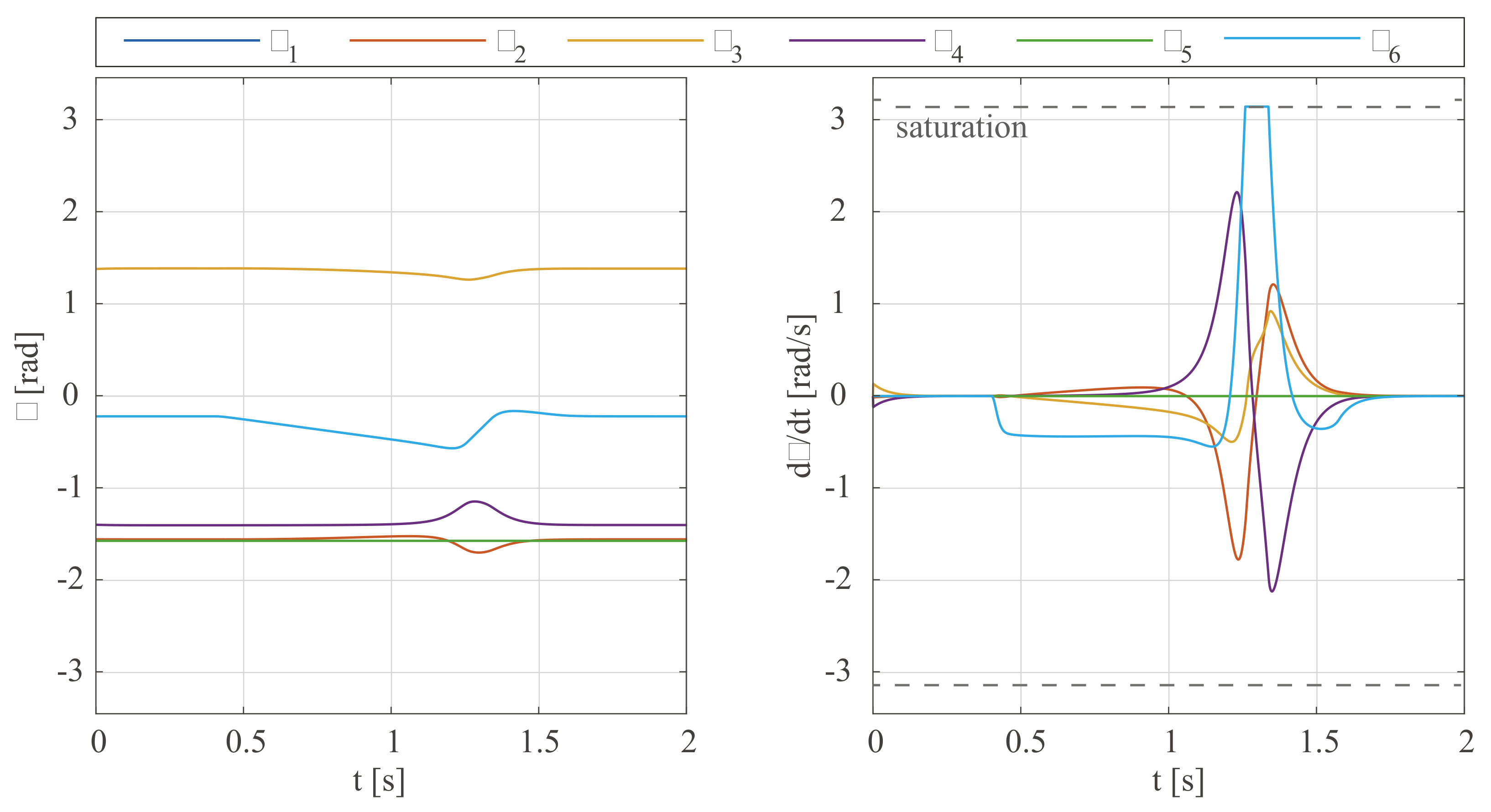
- The repulsive velocity is modulated as , where is a tunable magnitude and is an activation factor that is function of the distance (Figure 4b) according to
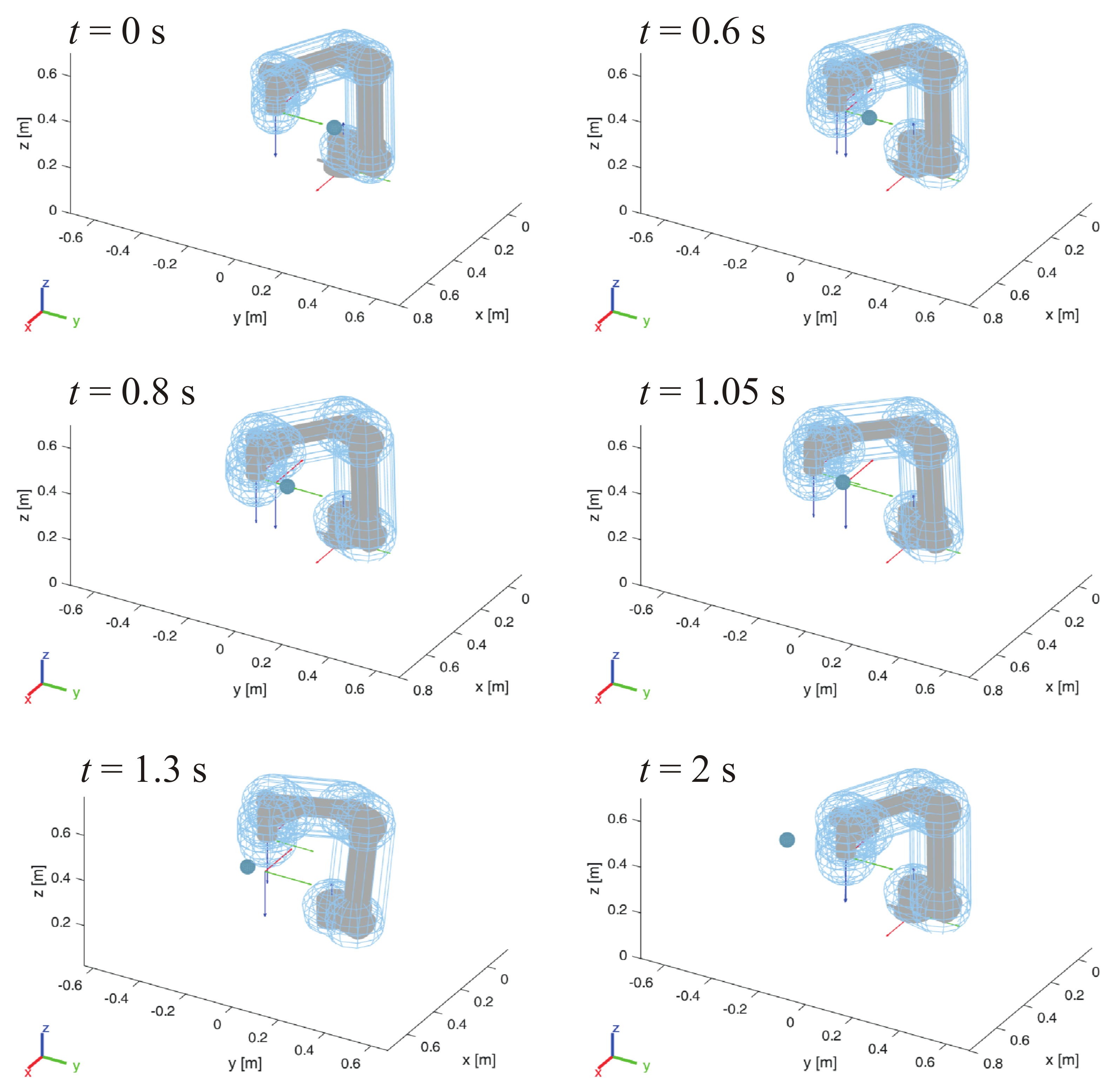
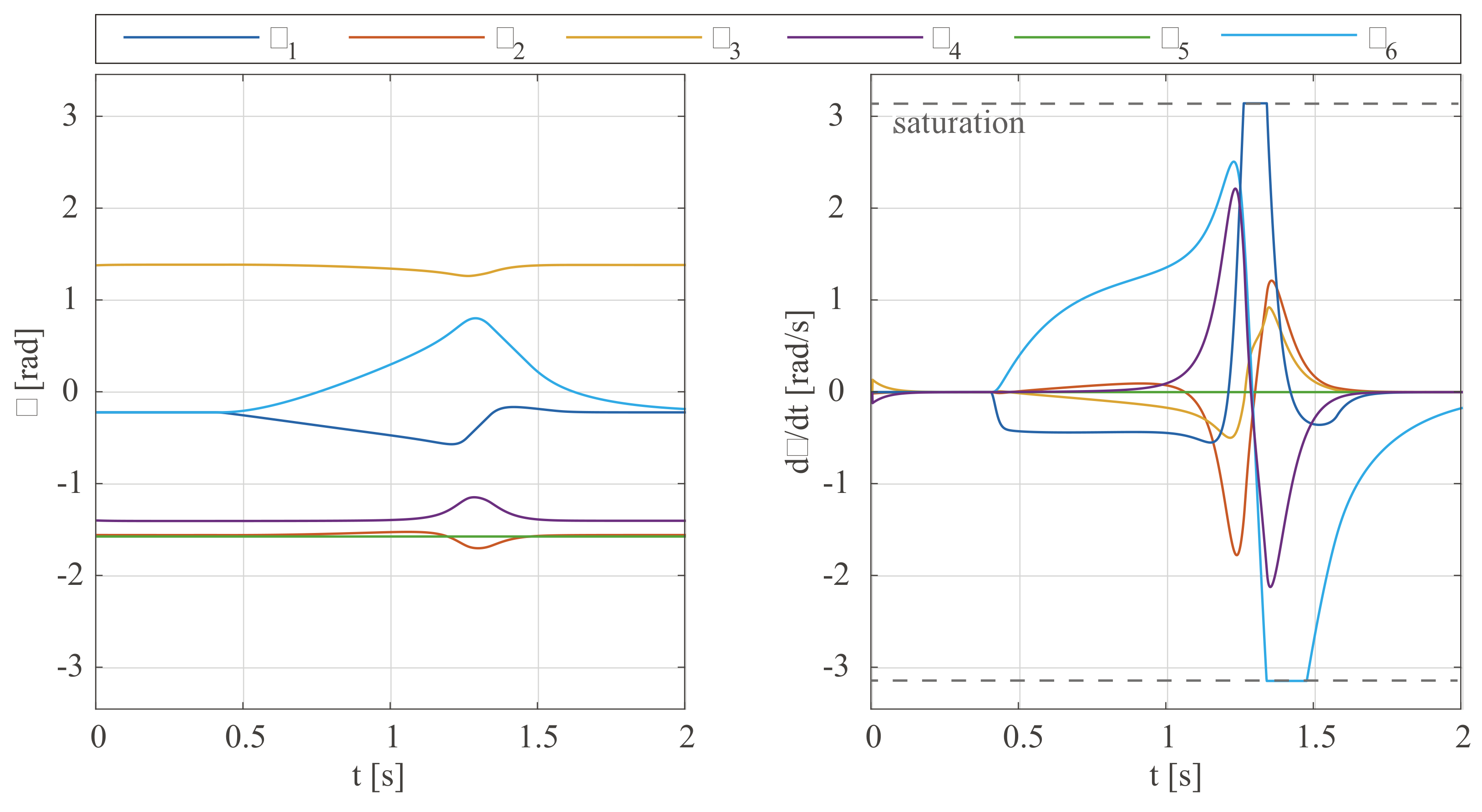
2.2. Mode II: 4-DOF Schoenflies Perturbation
2.3. Mode III: Perturbation with Fixed Orientation
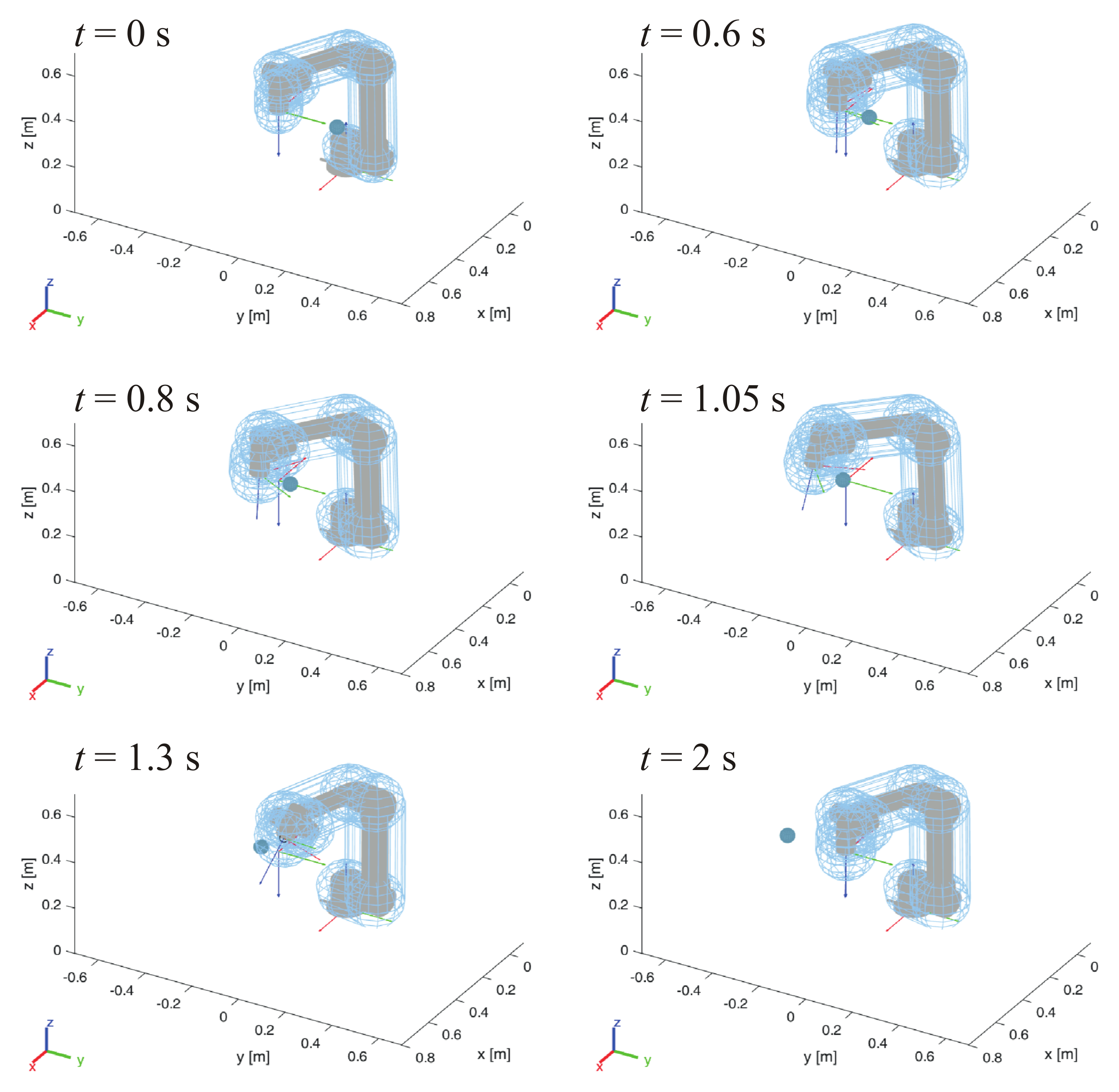
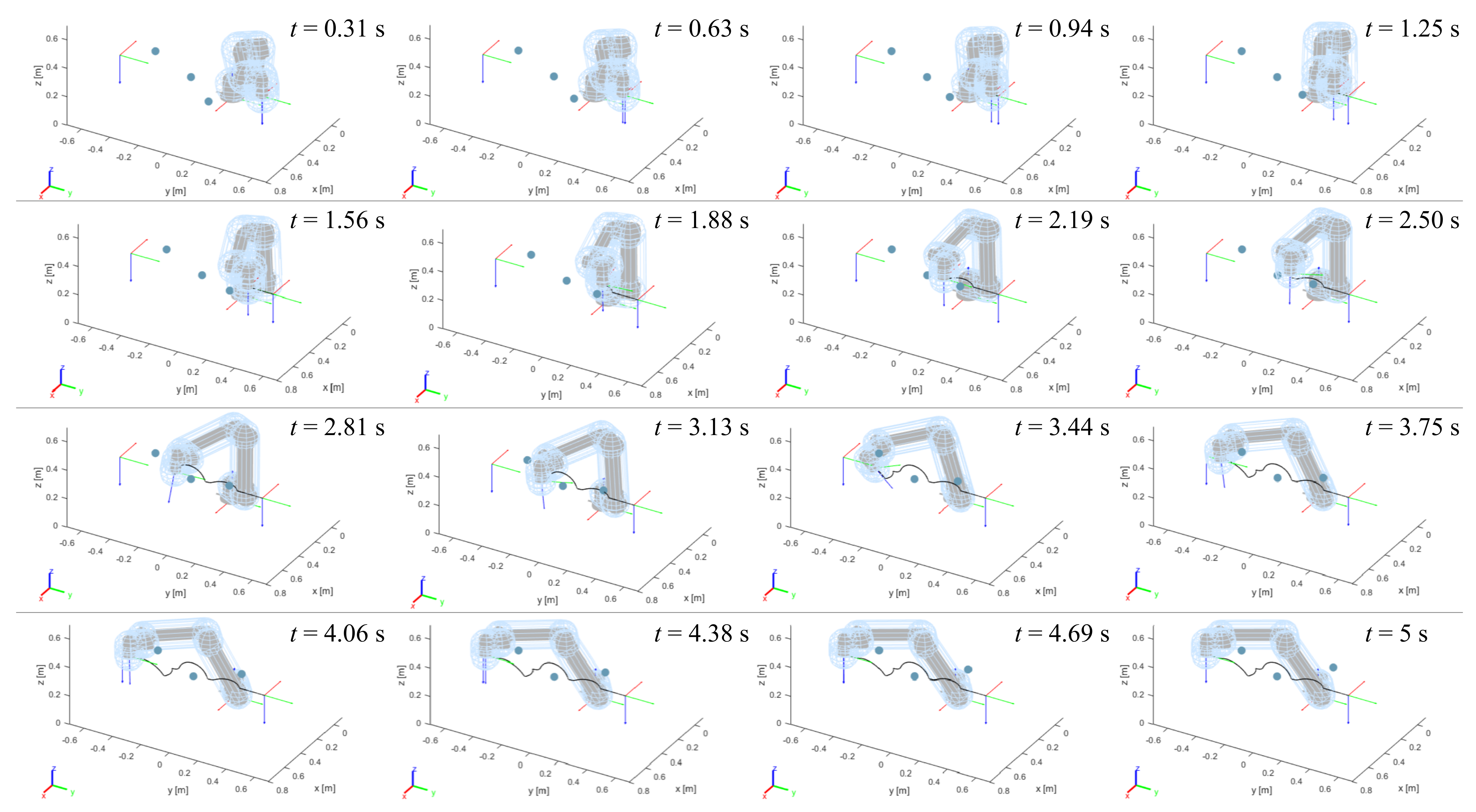
3. Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Vicentini, F. Collaborative robotics: A survey. J. Mech. Des. 2021, 143, 040802. [Google Scholar] [CrossRef]
- El Zaatari, S.; Marei, M.; Li, W.; Usman, Z. Cobot programming for collaborative industrial tasks: An overview. Robot. Auton. Syst. 2019, 116, 162–180. [Google Scholar] [CrossRef]
- Lasota, P.A.; Fong, T.; Shah, J.A. A Survey of Methods for Safe Human-Robot Interaction; Now Publishers: Hanover, MA, USA, 2017. [Google Scholar]
- Robla-Gómez, S.; Becerra, V.M.; Llata, J.R.; González-Sarabia, E.; Torre-Ferrero, C.; Pérez-Oria, J. Working Together: A Review on Safe Human-Robot Collaboration in Industrial Environments. IEEE Access 2017, 5, 26754–26773. [Google Scholar] [CrossRef]
- Valori, M.; Scibilia, A.; Fassi, I.; Saenz, J.; Behrens, R.; Herbster, S.; Bidard, C.; Lucet, E.; Magisson, A.; Schaake, L.; et al. Validating Safety in Human–Robot Collaboration: Standards and New Perspectives. Robotics 2021, 10, 65. [Google Scholar] [CrossRef]
- Morlock, M.; Bajrami, V.; Seifried, R. Trajectory tracking with collision avoidance for a parallel robot with flexible links. Control Eng. Pract. 2021, 111, 104788. [Google Scholar] [CrossRef]
- Dinh, K.H.; Oguz, O.; Huber, G.; Gabler, V.; Wollherr, D. An approach to integrate human motion prediction into local obstacle avoidance in close human-robot collaboration. In Proceedings of the 2015 IEEE International Workshop on Advanced Robotics and its Social Impacts (ARSO), Lyon, France, 30 June–2 July 2015; pp. 1–6. [Google Scholar]
- Pagani, R.; Nuzzi, C.; Ghidelli, M.; Borboni, A.; Lancini, M.; Legnani, G. Cobot User Frame Calibration: Evaluation and Comparison between Positioning Repeatability Performances Achieved by Traditional and Vision-Based Methods. Robotics 2021, 10, 45. [Google Scholar] [CrossRef]
- Flacco, F.; Kröger, T.; De Luca, A.; Khatib, O. A depth space approach to human-robot collision avoidance. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 338–345. [Google Scholar]
- Schmidt, B.; Wang, L. Depth camera based collision avoidance via active robot control. J. Manuf. Syst. 2014, 33, 711–718. [Google Scholar] [CrossRef]
- Mohammed, A.; Schmidt, B.; Wang, L. Active collision avoidance for human–robot collaboration driven by vision sensors. Int. J. Comput. Integr. Manuf. 2017, 30, 970–980. [Google Scholar] [CrossRef]
- Du, G.; Long, S.; Li, F.; Huang, X. Active Collision Avoidance for Human-Robot Interaction With UKF, Expert System, and Artificial Potential Field Method. Front. Robot. AI 2018, 5, 125. [Google Scholar] [CrossRef] [PubMed]
- Scimmi, L.S.; Melchiorre, M.; Troise, M.; Mauro, S.; Pastorelli, S. A Practical and Effective Layout for a Safe Human-Robot Collaborative Assembly Task. Appl. Sci. 2021, 11, 1763. [Google Scholar] [CrossRef]
- Scalera, L.; Seriani, S.; Gallina, P.; Lentini, M.; Gasparetto, A. Human–Robot Interaction through Eye Tracking for Artistic Drawing. Robotics 2021, 10, 54. [Google Scholar] [CrossRef]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Path planning and trajectory planning algorithms: A general overview. In Motion and Operation Planning of Robotic Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 3–27. [Google Scholar]
- Xu, X.; Hu, Y.; Zhai, J.; Li, L.; Guo, P. A novel non-collision trajectory planning algorithm based on velocity potential field for robotic manipulator. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418787075. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, M.; Wang, X.; He, S.; He, J.; Xu, Z. An improved artificial potential field method of trajectory planning and obstacle avoidance for redundant manipulators. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, H.; Liu, Z.; Liu, Y.; Zhu, Y.; Zhao, J. Real-time kinematic control for redundant manipulators in a time-varying environment: Multiple-dynamic obstacle avoidance and fast tracking of a moving object. IEEE Trans. Ind. Inform. 2019, 16, 28–41. [Google Scholar] [CrossRef]
- Safeea, M.; Neto, P.; Bearee, R. On-line collision avoidance for collaborative robot manipulators by adjusting off-line generated paths: An industrial use case. Robot. Auton. Syst. 2019, 119, 278–288. [Google Scholar] [CrossRef]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Maciejewski, A.A.; Klein, C.A. Obstacle Avoidance for Kinematically Redundant Manipulators in Dynamically Varying Environments. Int. J. Robot. Res. 1985, 4, 109–117. [Google Scholar] [CrossRef]
- Abhishek, T.S.; Schilberg, D.; Doss, A.S.A. Obstacle Avoidance Algorithms: A Review. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1012, p. 012052. [Google Scholar]
- Perdereau, V.; Passi, C.; Drouin, M. Real-time control of redundant robotic manipulators for mobile obstacle avoidance. Robot. Auton. Syst. 2002, 41, 41–59. [Google Scholar] [CrossRef]
- Moe, S.; Pettersen, K.Y.; Gravdahl, J.T. Set-based collision avoidance applications to robotic systems. Mechatronics 2020, 69, 102399. [Google Scholar] [CrossRef]
- Zhang, W.; Cheng, H.; Hao, L.; Li, X.; Liu, M.; Gao, X. An obstacle avoidance algorithm for robot manipulators based on decision-making force. Robot. Comput. Integr. Manuf. 2021, 71, 102114. [Google Scholar] [CrossRef]
- Scoccia, C.; Palmieri, G.; Palpacelli, M.C.; Callegari, M. A Collision Avoidance Strategy for Redundant Manipulators in Dynamically Variable Environments: On-Line Perturbations of Off-Line Generated Trajectories. Machines 2021, 9, 30. [Google Scholar] [CrossRef]
- Scoccia, C.; Palmieri, G.; Palpacelli, M.; Callegari, M. Real-Time Strategy for Obstacle Avoidance in Redundant Manipulators. Mech. Mach. Sci. 2021, 91, 278–285. [Google Scholar]
- Kebria, P.M.; Al-Wais, S.; Abdi, H.; Nahavandi, S. Kinematic and dynamic modelling of UR5 manipulator. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 004229–004234. [Google Scholar]
- Moe, S.; Antonelli, G.; Teel, A.R.; Pettersen, K.Y.; Schrimpf, J. Set-based tasks within the singularity-robust multiple task-priority inverse kinematics framework: General formulation, stability analysis, and experimental results. Front. Robot. AI 2016, 3, 16. [Google Scholar] [CrossRef]
- Chiaverini, S.; Siciliano, B.; Egeland, O. Review of the damped least-squares inverse kinematics with experiments on an industrial robot manipulator. IEEE Trans. Control Syst. Technol. 1994, 2, 123–134. [Google Scholar] [CrossRef]
- Corrales, J.; Candelas, F.; Torres, F. Safe human–robot interaction based on dynamic sphere-swept line bounding volumes. Robot. Comput. Integr. Manuf. 2011, 27, 177–185. [Google Scholar] [CrossRef]

| b | |||||||
|---|---|---|---|---|---|---|---|
| 0.09 | 0.14 | 0.42 | 0.12 | 0.39 | 0.11 | 0.09 | 0.05 |
| 0.09 | 0.15 | 0.1 | 0.5 | 20 | 2 |
| Mode | T | L | Avg. Comp. Time | ||
|---|---|---|---|---|---|
| (1 Cycle) [ms] | |||||
| I | 2 | 486 | 5.58 | 180.27 | 0.79 |
| II | 2 | 491 | 4.68 | 180.27 | 0.82 |
| II | 2 | 491 | 4.96 | 180.27 | 0.86 |
| Mode | T | L | Avg. Comp. Time | ||
|---|---|---|---|---|---|
| (1 Cycle) [ms] | |||||
| I | 2 | 1219 | 3.85 | 171.02 | 0.79 |
| II | 2 | 1176 | 3.30 | 171.02 | 0.82 |
| II | 2 | 1176 | 4.13 | 171.02 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiriatti, G.; Palmieri, G.; Scoccia, C.; Palpacelli, M.C.; Callegari, M. Adaptive Obstacle Avoidance for a Class of Collaborative Robots. Machines 2021, 9, 113. https://doi.org/10.3390/machines9060113
Chiriatti G, Palmieri G, Scoccia C, Palpacelli MC, Callegari M. Adaptive Obstacle Avoidance for a Class of Collaborative Robots. Machines. 2021; 9(6):113. https://doi.org/10.3390/machines9060113
Chicago/Turabian StyleChiriatti, Giorgia, Giacomo Palmieri, Cecilia Scoccia, Matteo Claudio Palpacelli, and Massimo Callegari. 2021. "Adaptive Obstacle Avoidance for a Class of Collaborative Robots" Machines 9, no. 6: 113. https://doi.org/10.3390/machines9060113
APA StyleChiriatti, G., Palmieri, G., Scoccia, C., Palpacelli, M. C., & Callegari, M. (2021). Adaptive Obstacle Avoidance for a Class of Collaborative Robots. Machines, 9(6), 113. https://doi.org/10.3390/machines9060113








