Dynamic Modeling of a Front-Loading Type Washing Machine and Model Reliability Investigation
Abstract
:1. Introduction
2. Modeling an FL-Type Washing Machine
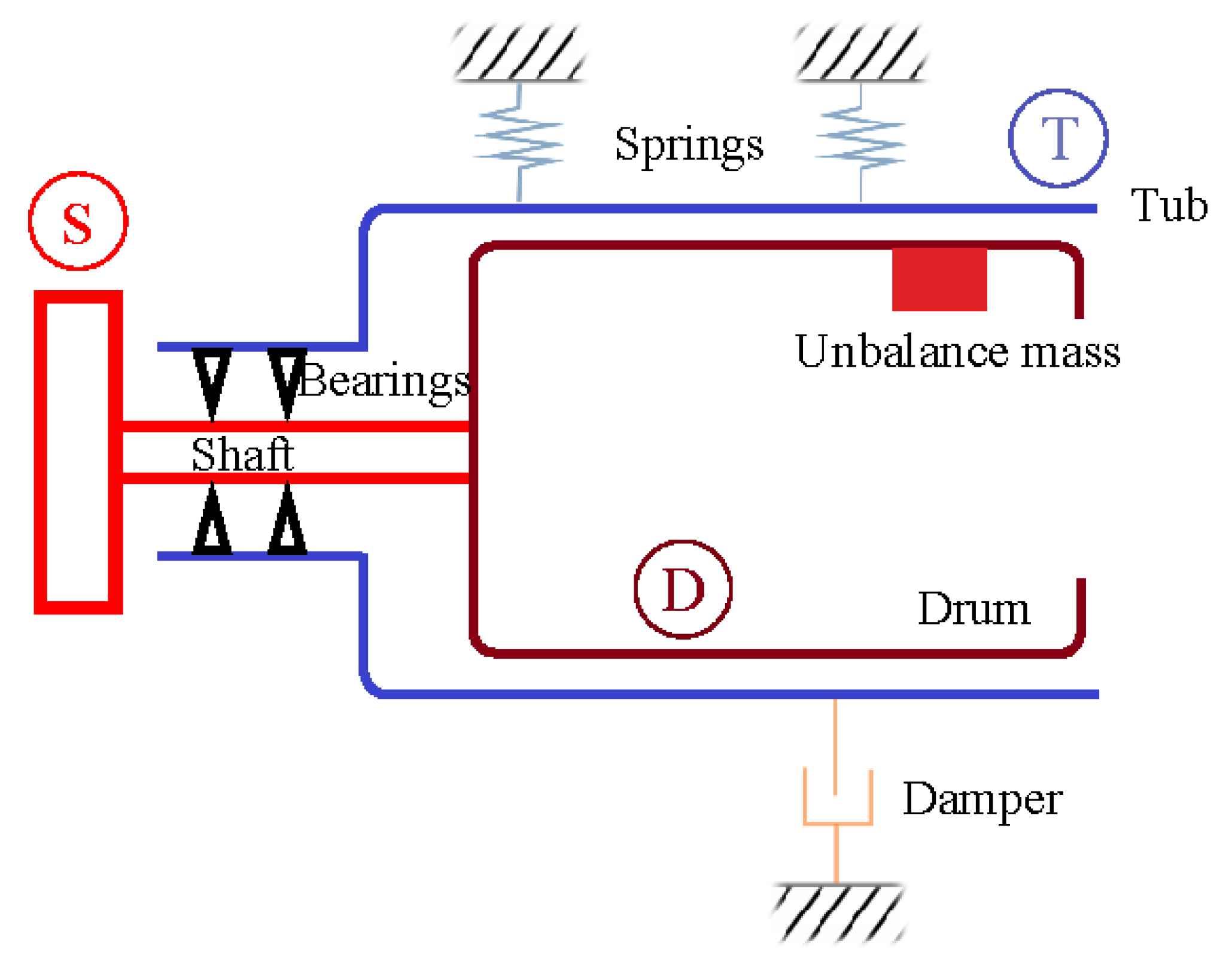
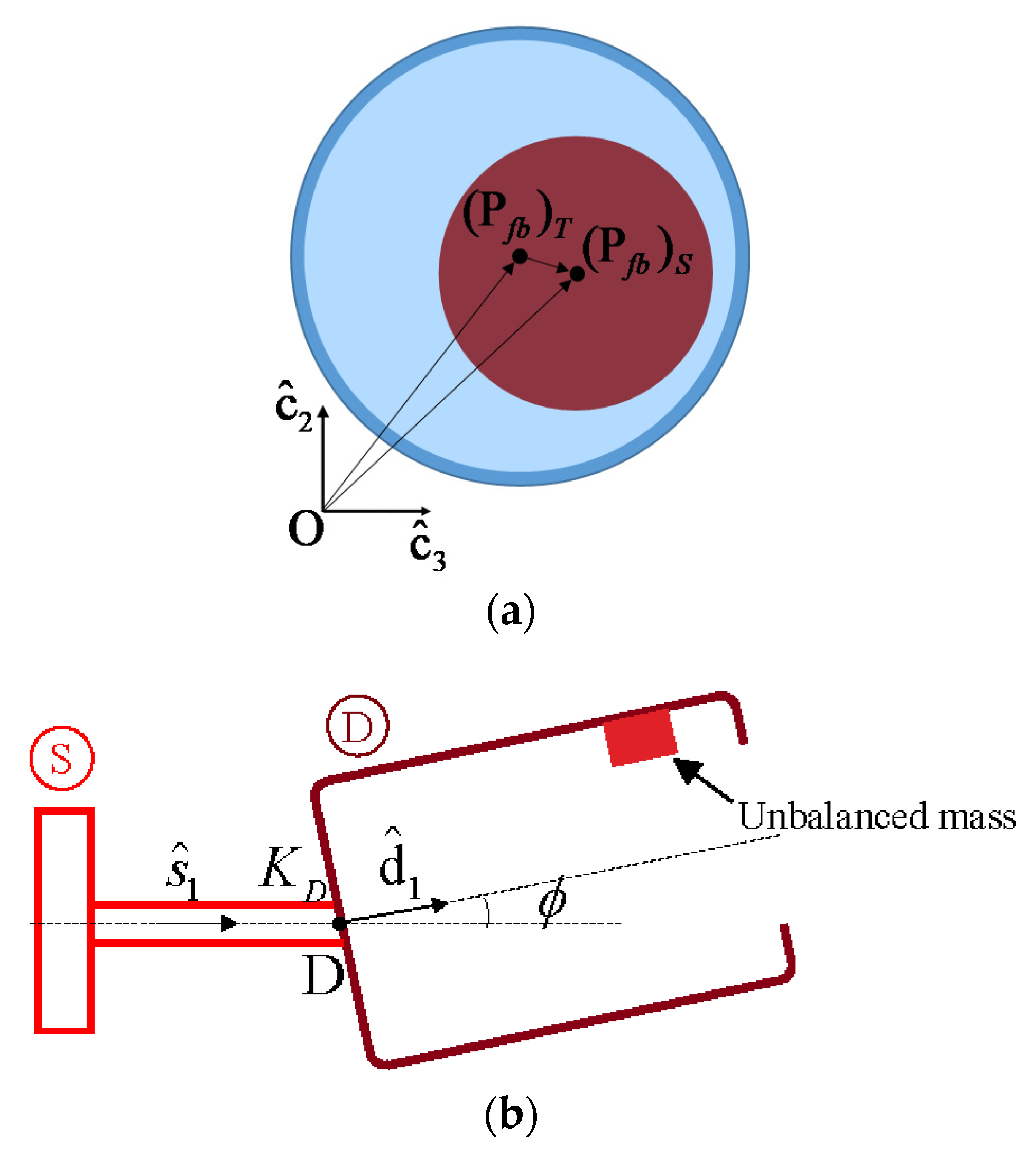
2.1. System Configuration
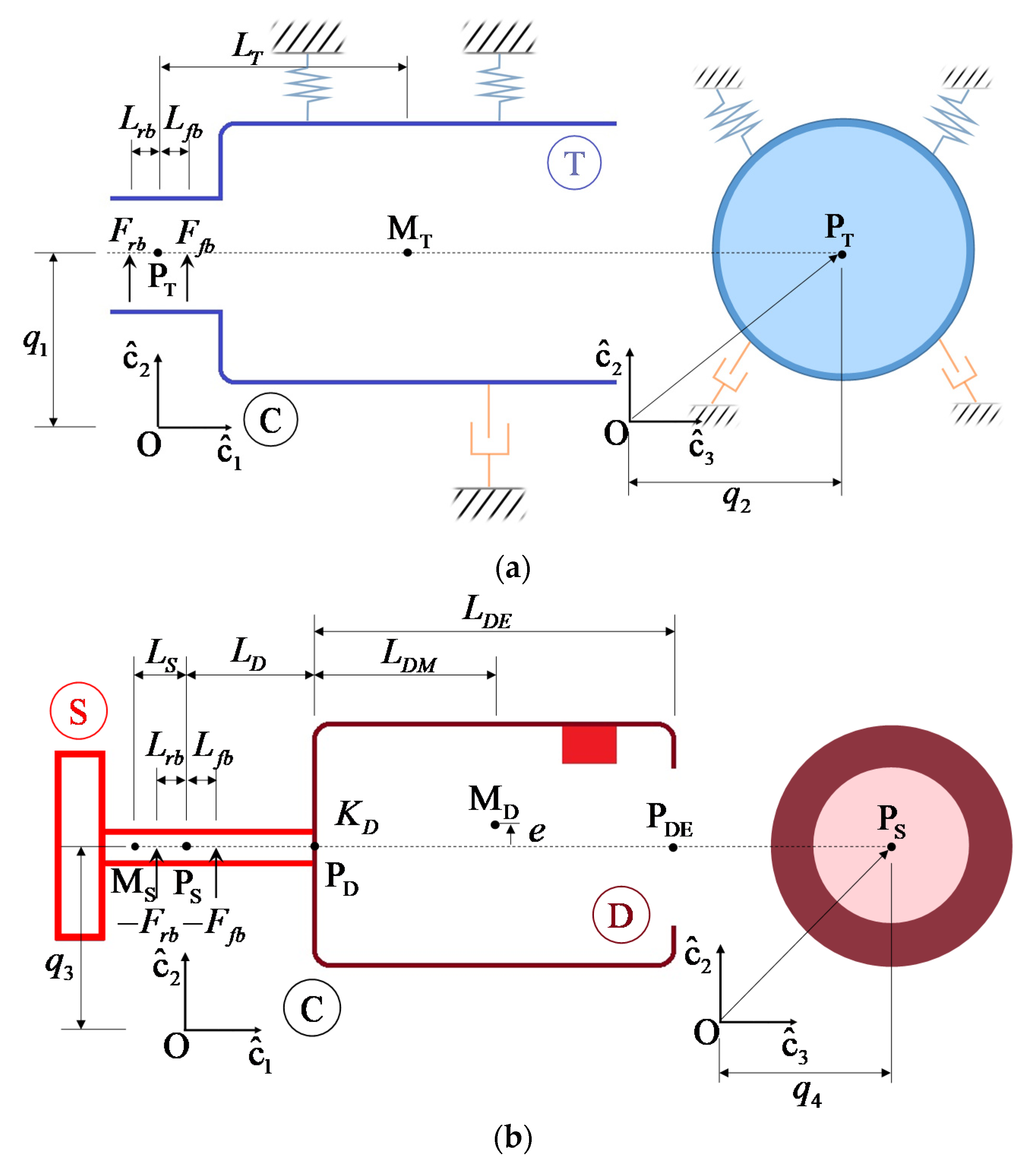
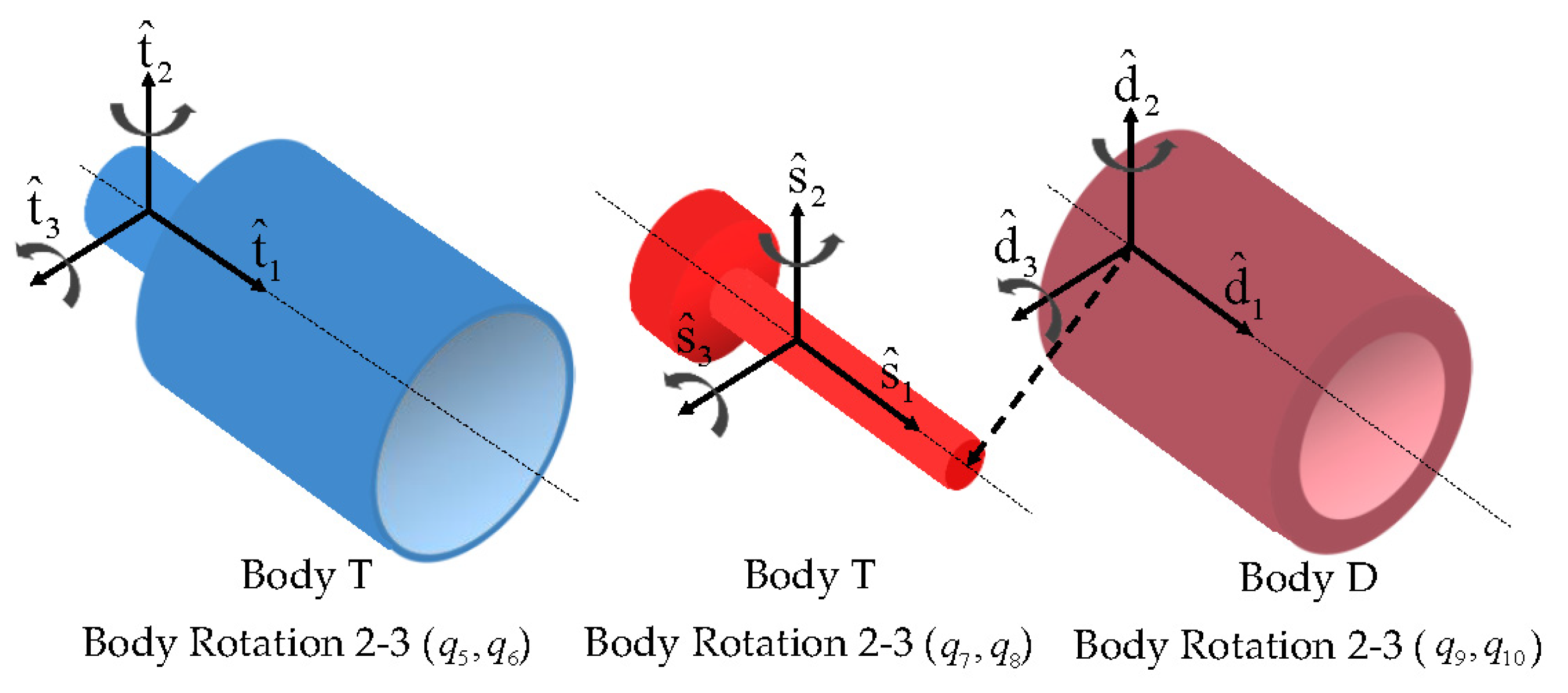
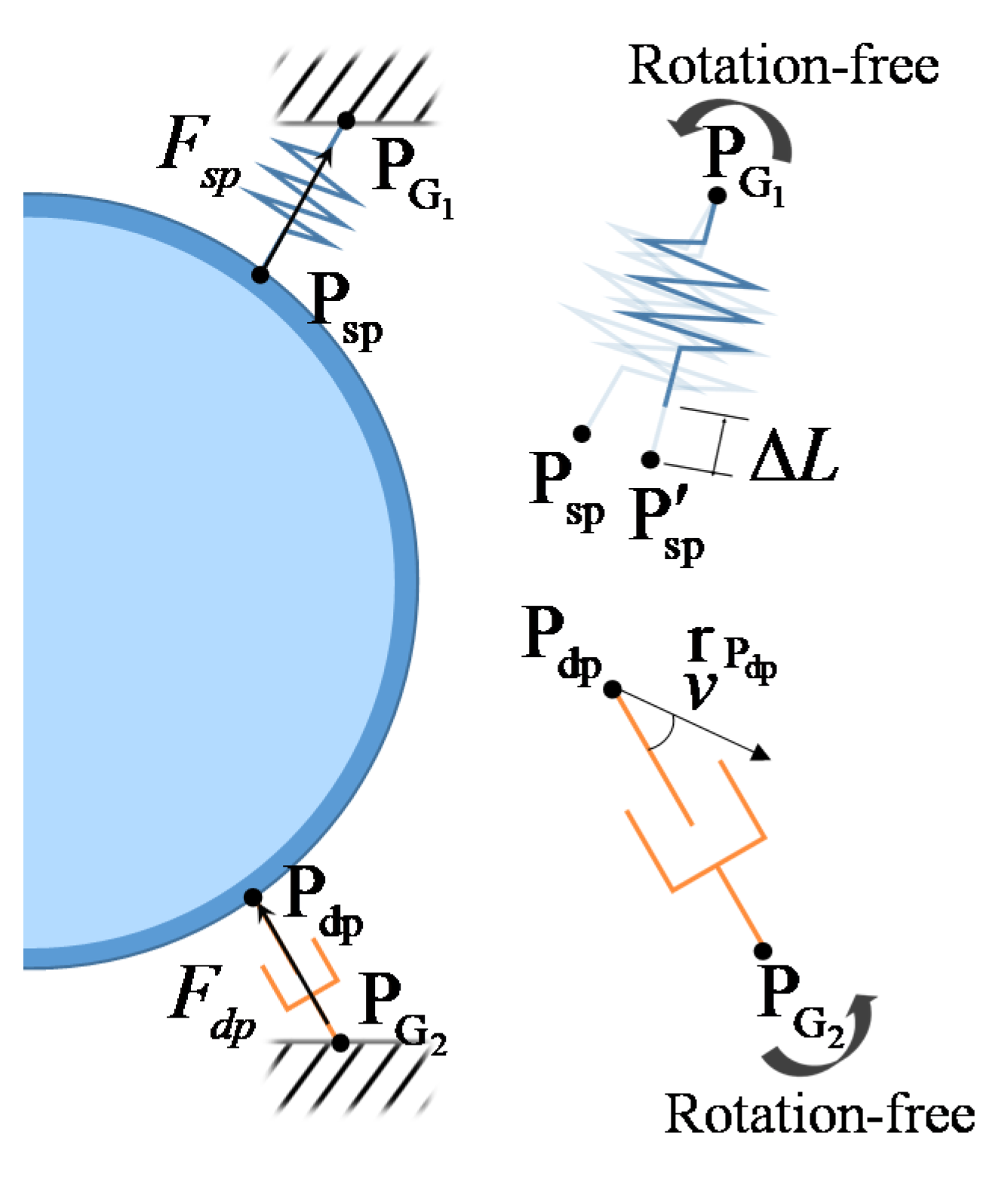
2.2. Derivation of Equations of Motion
- The cabinet is fixed to the ground.
- Axial rotational motion of the tub is ignored.
- Torsional deformation of the shaft relative to the tub is ignored.
- Translational motion of the drum relative to the tub in the axial direction is ignored.
- An unbalance mass is fixed to the drum.
- The rotational motion of the drum is prescribed as a function of time.
2.3. Linearization of the Equations of Motion
3. Numerical Results and Discussion
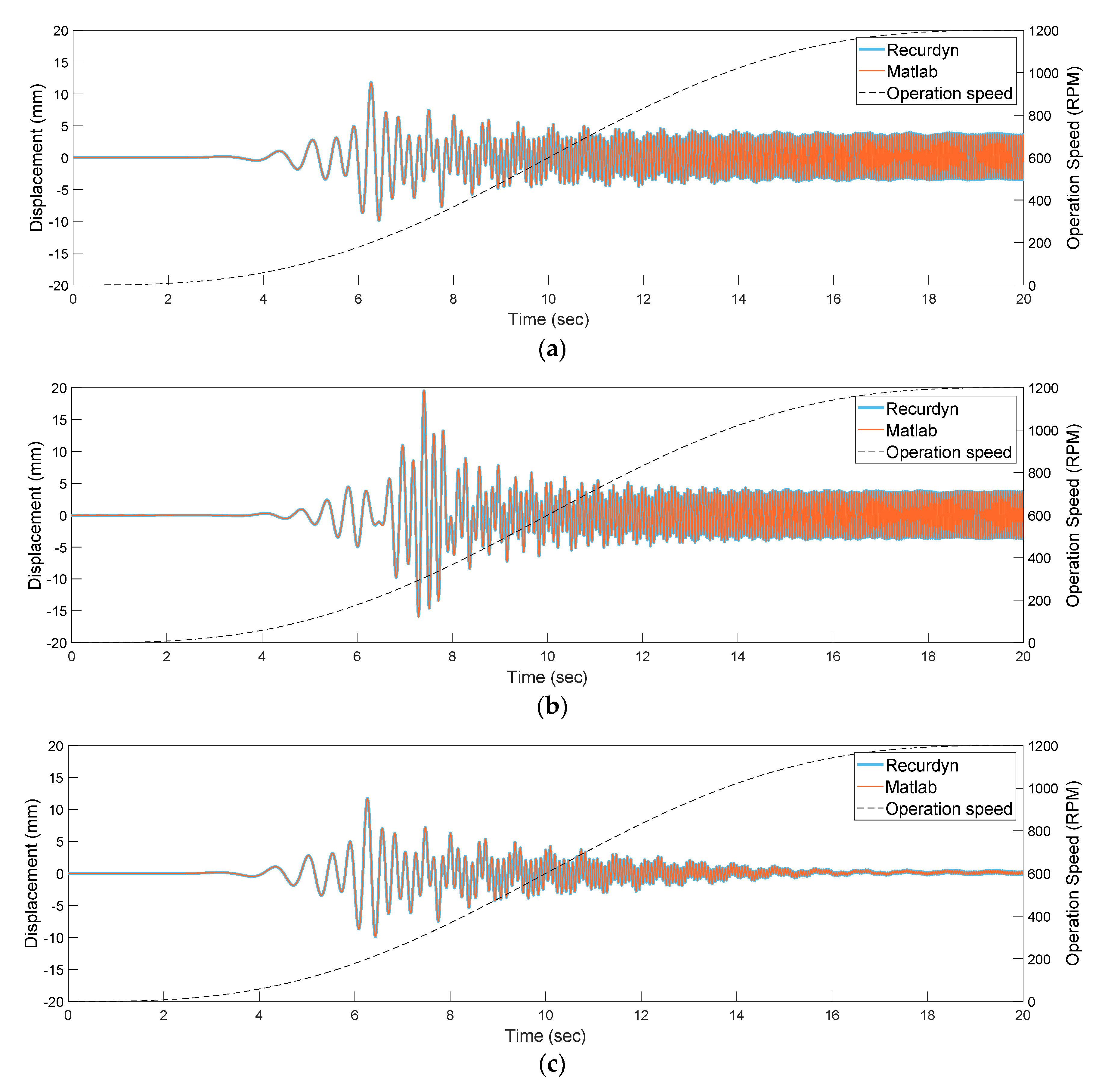
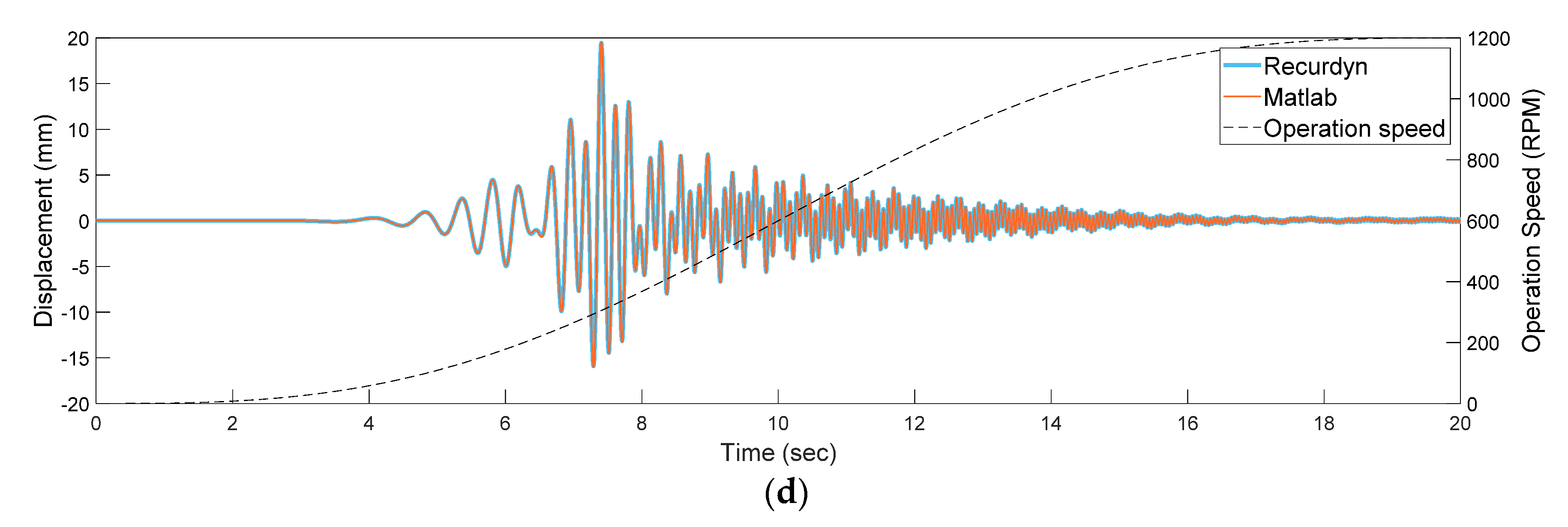
3.1. Validation of the Nonlinear Analytical Model
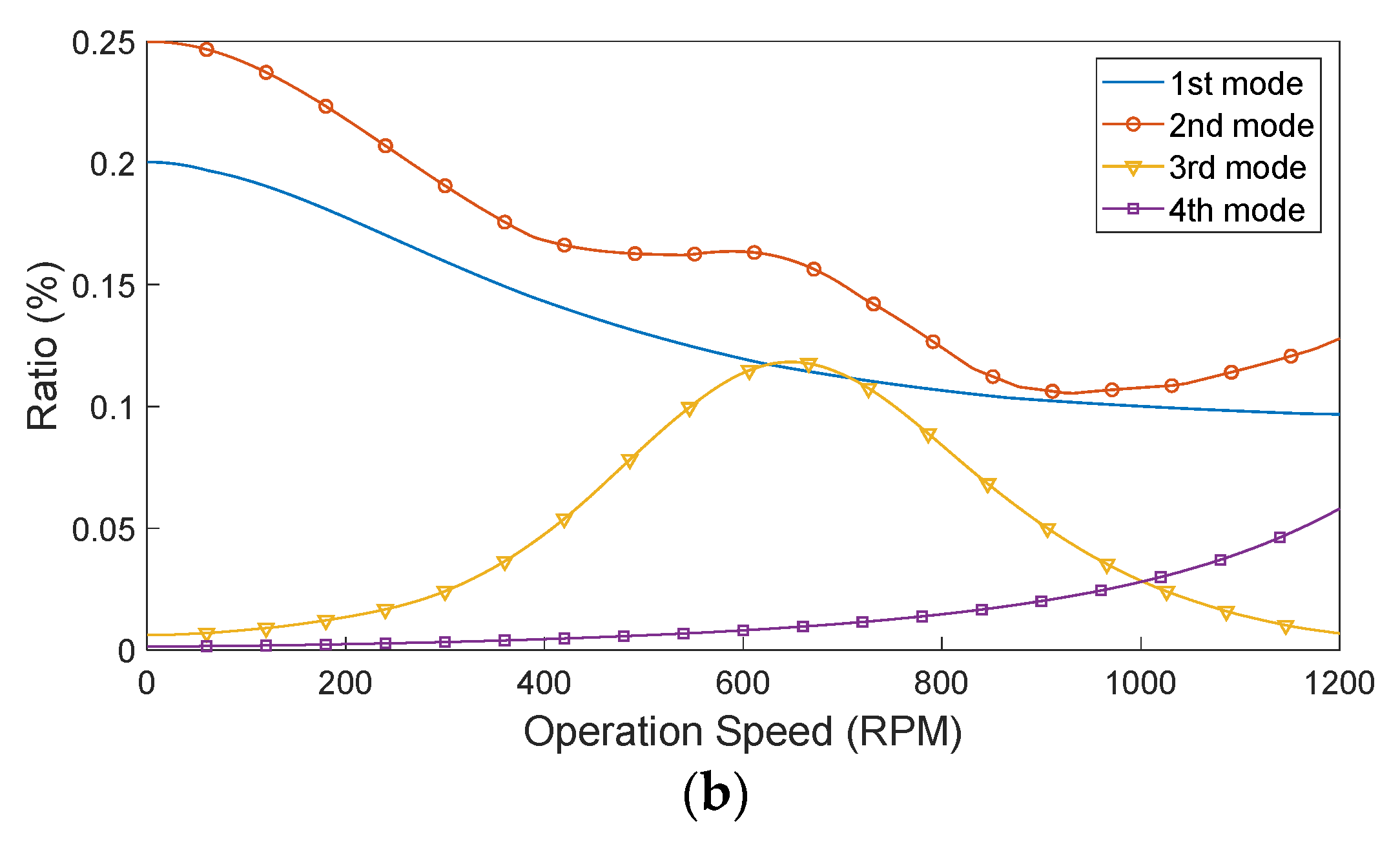
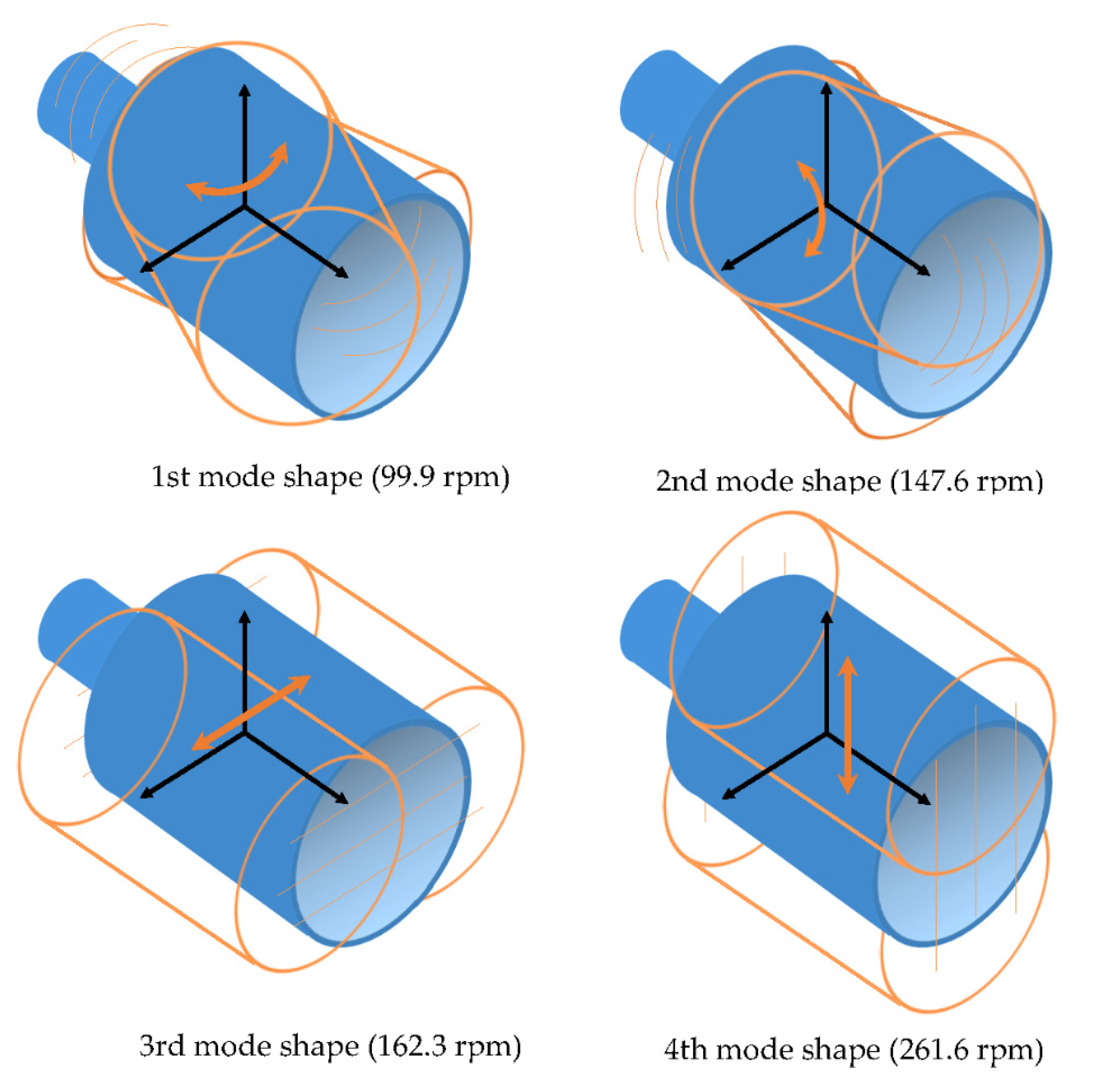
3.2. Modal Analysis with the Linear Model
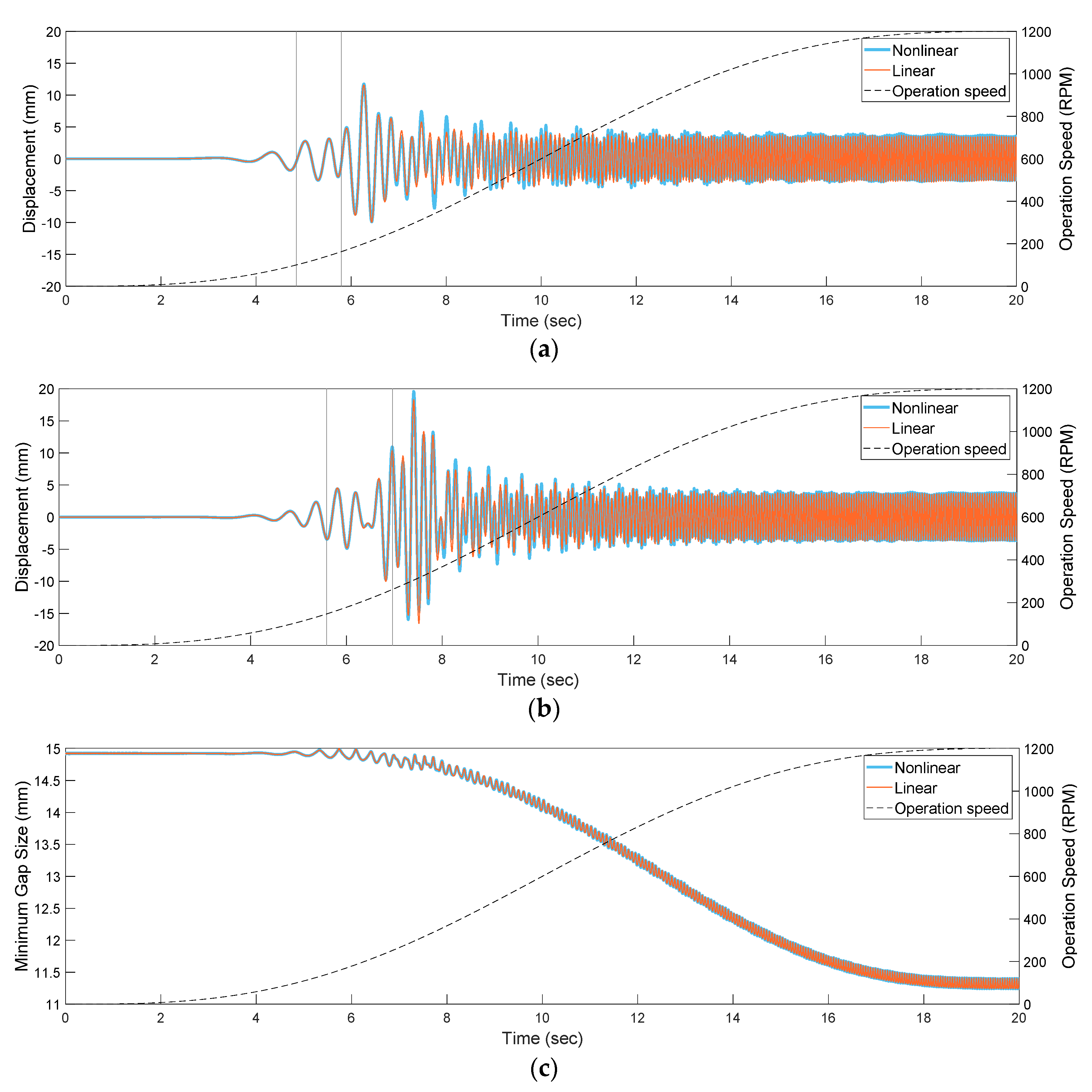
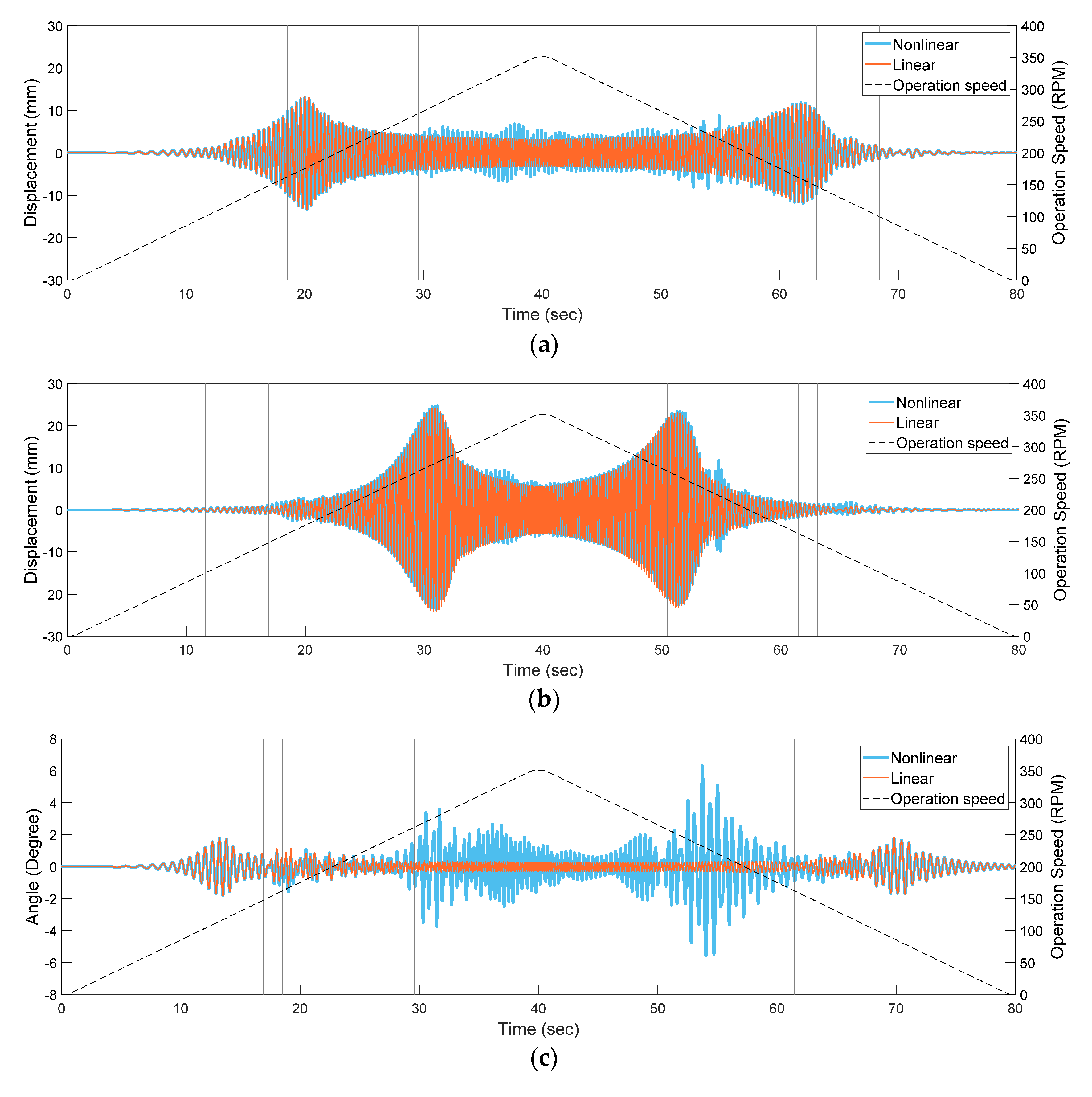
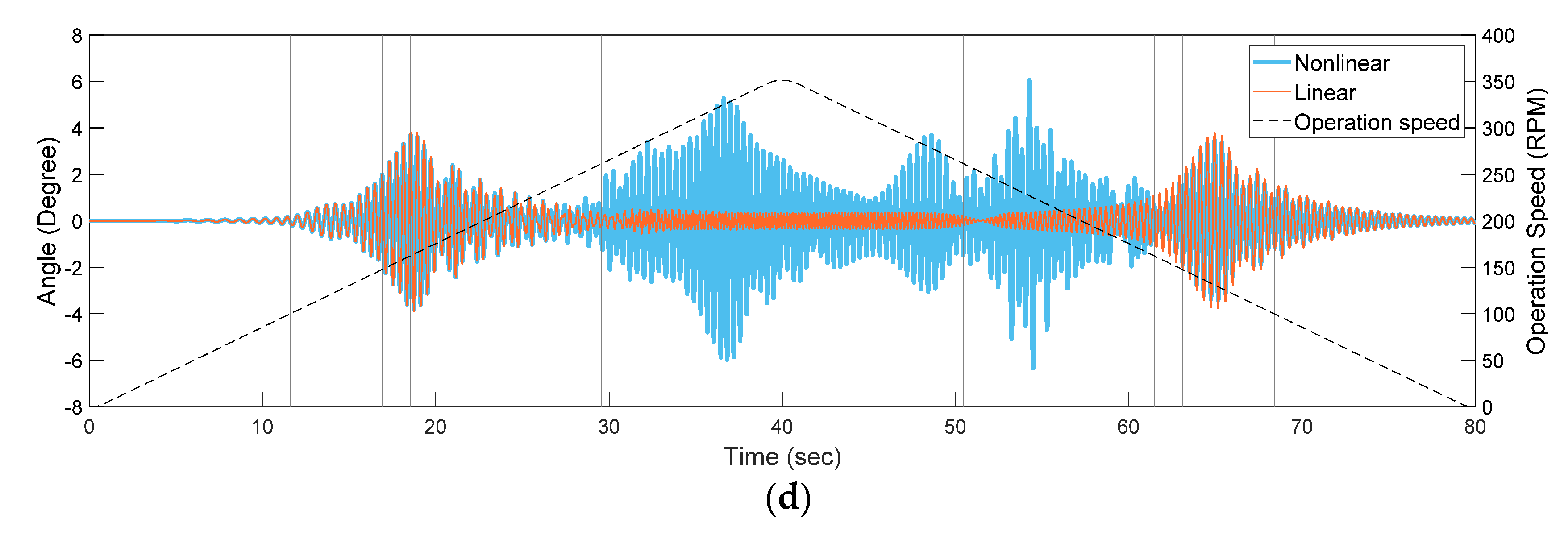
3.3. Comparison of the Nonlinear and Linear Analytical Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Pakula, C.; Stamminger, R. Electricity and water consumption for laundry washing by washing machine worldwide. Energy Effic. 2010, 3, 365–382. [Google Scholar] [CrossRef]
- Ramasubramanian, M.K.; Tiruthani, K. A capacitive displacement sensing technique for early detection of unbalanced loads in a washing machine. Sensors 2009, 9, 9559–9571. [Google Scholar] [CrossRef] [PubMed]
- Conrad, D.; Soedel, W. On the problem of oscillatory walk of automatic washing machines. J. Sound Vib. 1995, 188, 301–314. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Papadimitriou, I. Modeling, design and control of a portable washing machine during the spinning cycle. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Proceedings (Cat. No. 01TH8556), Como, Italy, 8–12 July 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 899–904. [Google Scholar]
- Boyraz, P.; Gündüz, M. Dynamic modeling of a horizontal washing machine and optimization of vibration characteristics using genetic algorithms. Mechatronics 2013, 23, 581–593. [Google Scholar] [CrossRef]
- Buśkiewicz, J.; Pittner, G.; Barczewski, R. Numerical and experimental vibration analysis of domestic washing machine drum. Int. J. Appl. Mech. Eng. 2012, 17, 765–777. [Google Scholar]
- Lim, H.; Jeong, W.; Kim, K. Dynamic modeling and analysis of drum-type washing machine. Int. J. Precis. Eng. Manuf. 2010, 11, 407–417. [Google Scholar] [CrossRef]
- Kamarudin, M.; Rozali, S.; Hairi, M.; Khamis, A.; Husain, A. Linearization-advantages and shortcomings toward control system design. Int. J. Electr. Eng. Appl. Sci. 2019, 2, 17–22. [Google Scholar]
- Kane, T.R.; Levinson, D.A. Dynamics, Theory and Applications; McGraw Hill: New York, NY, USA, 1985. [Google Scholar]
- RecurDyn, V9R1; FunctionBay, Inc.: Seongnam-si, Korea, 2019; Available online: https://getintopc.today/functionbay-recurdyn-v9r1-free-download/ (accessed on 10 November 2021).
- Fearn, R.; Millsaps, K. Constant acceleration of an undamped simple vibrator through resonance. J. R. Aeronaut. Soc. 1967, 71, 567–596. [Google Scholar] [CrossRef]
- Markert, R.; Seidler, M. Analytically based estimation of the maximum amplitude during passage through resonance. Int. J. Solids Struct. 2001, 38, 1975–1992. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations, 1st ed.; Weiley-VCH: Weinheim, Germany, 1979. [Google Scholar]



| 0 | 0 | ||||||||||
| Body | Mass (kg) | |||
| Body T | 23.87 | 240.61 | 0 | 0 |
| Body S | 4.34 | 18.11 | 0 | 0 |
| Body D | 4.04 | 209.9 | 19.8 | 0 |
| Body | ||||
| Body T | 1,030,000 | 1,610,000 | 1,530,000 | 0 |
| Body S | 55300 | 38,400 | 38,400 | 0 |
| Body D | 196,000 | 162,000 | 177,000 | −7207 |
| Point Fixed to Cabinet | Point Fixed to Tub | |
|---|---|---|
| Spring 1 | (326.8, 300.2, 250.6) | (326.8, 162.6, 162.6) |
| Spring 2 | (326.8, 300.2, −250.6) | (326.8, 162.6, −162.6) |
| Spring 3 | (86.8, 300.2, 250.6) | (86.8, 162.6, 162.6) |
| Spring 4 | (86.8, 300.2, −250.6) | (86.8, 162.6, −162.6) |
| Damper 1 | (306.8, −280.0, 280.0) | (306.8, −162.6, 162.6) |
| Damper 2 | (306.8, −280.0, −280.0) | (306.8, −162.6, −162.6) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Jeong, S.; Yoo, H. Dynamic Modeling of a Front-Loading Type Washing Machine and Model Reliability Investigation. Machines 2021, 9, 289. https://doi.org/10.3390/machines9110289
Park J, Jeong S, Yoo H. Dynamic Modeling of a Front-Loading Type Washing Machine and Model Reliability Investigation. Machines. 2021; 9(11):289. https://doi.org/10.3390/machines9110289
Chicago/Turabian StylePark, Jungjoon, Sinwoo Jeong, and Honghee Yoo. 2021. "Dynamic Modeling of a Front-Loading Type Washing Machine and Model Reliability Investigation" Machines 9, no. 11: 289. https://doi.org/10.3390/machines9110289
APA StylePark, J., Jeong, S., & Yoo, H. (2021). Dynamic Modeling of a Front-Loading Type Washing Machine and Model Reliability Investigation. Machines, 9(11), 289. https://doi.org/10.3390/machines9110289






