A Multibody System Approach for the Systematic Development of a Closed-Chain Kinematic Model for Two-Wheeled Vehicles
Abstract
1. Introduction
1.1. Background Information and Research Significance
1.2. Formulation of the Problem of Interest for This Investigation
1.3. Literature Review
1.4. Scope and Contributions of This Study
1.5. Organization of the Manuscript
2. Multibody Approach for the Mechanical Modeling of Two-Wheeled Vehicles as Kinematic Chains
2.1. System Multibody Model
- The rear wheel.
- The rear frame.
- The front fork/handlebars.
- The front wheel.
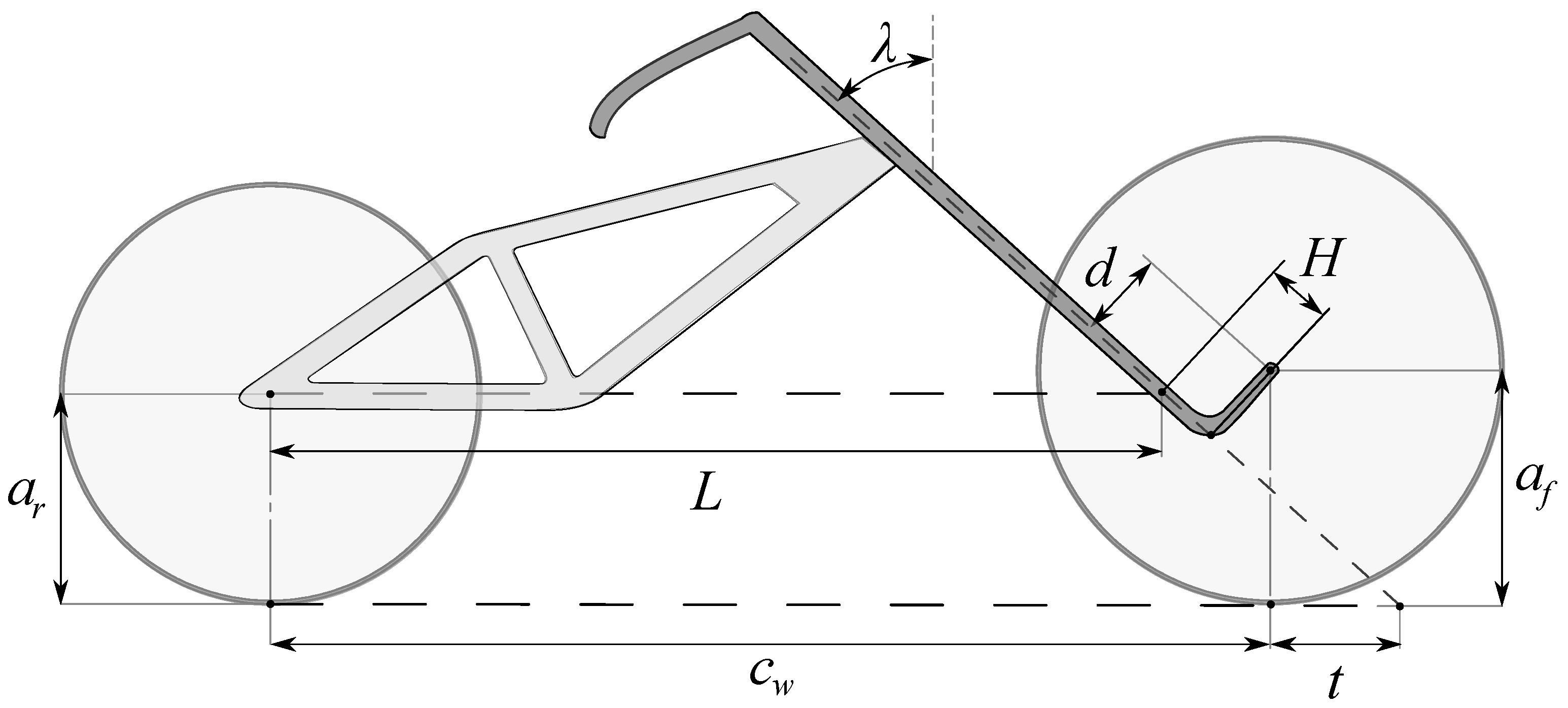
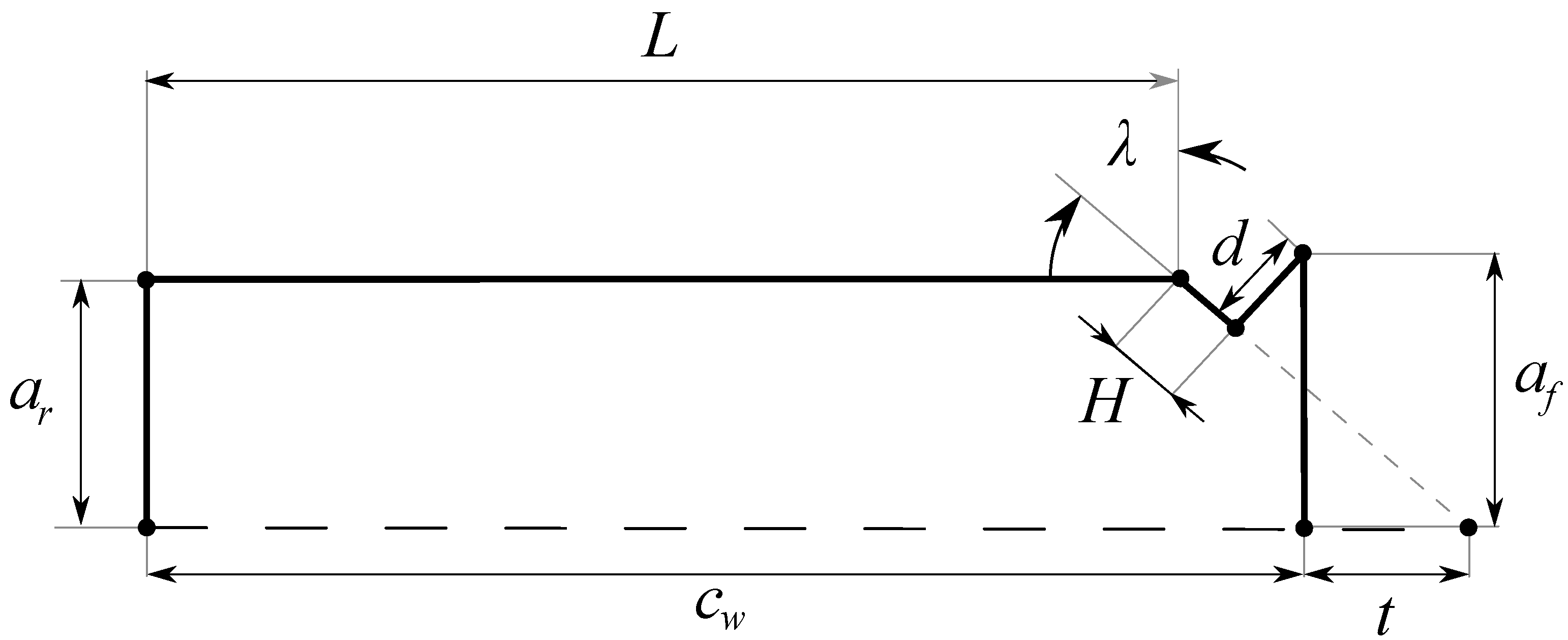
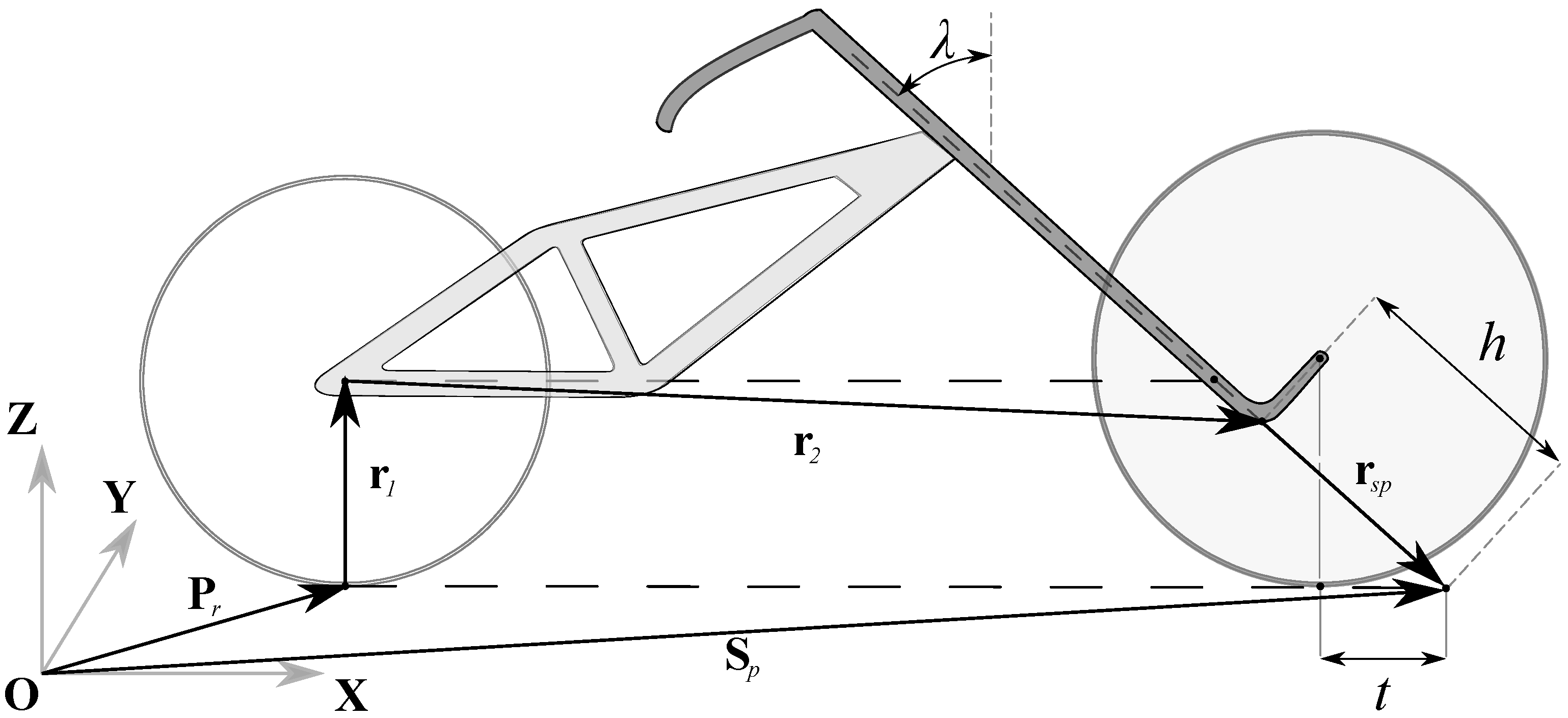
2.2. System Geometry
- The distance between the contact points of the rear and front wheel, known as wheelbase and denoted with .
- The distance between the front contact point and the steering column intersection with the road plane, known as trail and denoted with t.
- The rear and front wheels radii respectively denoted with and .
- The tilt angle of the steering column, known as the caster angle and denoted with .
2.3. Kinematic Analysis
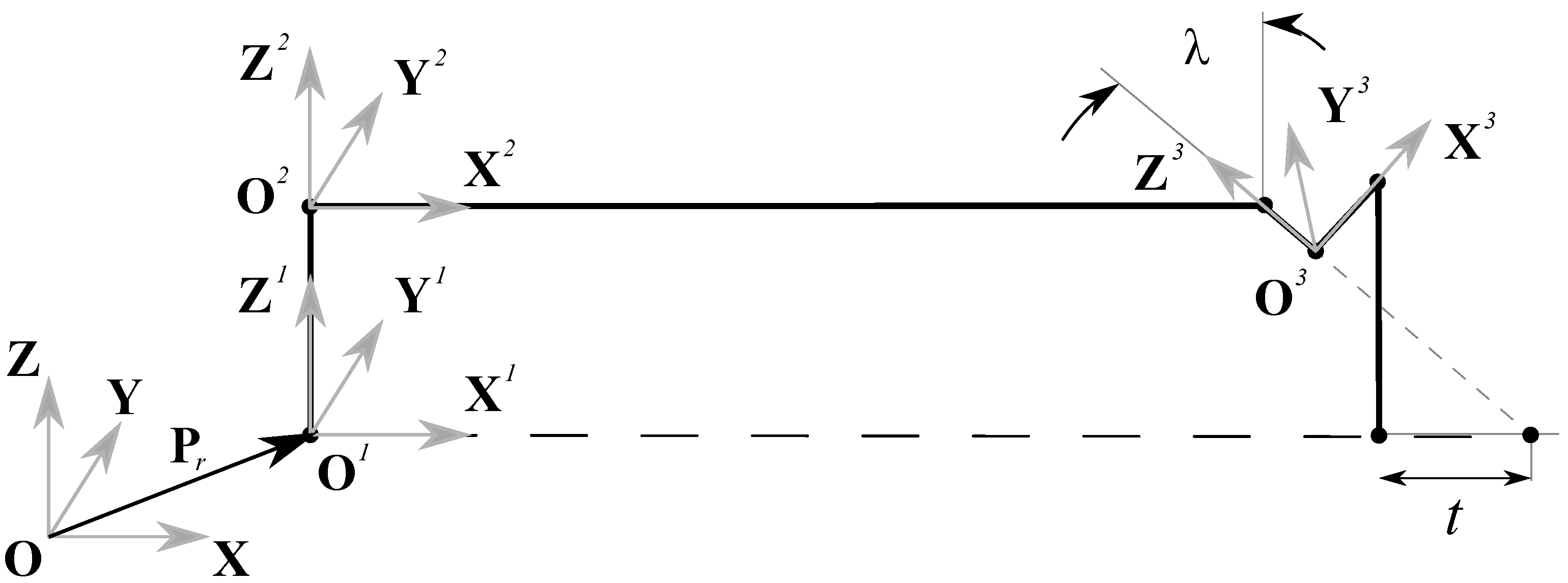
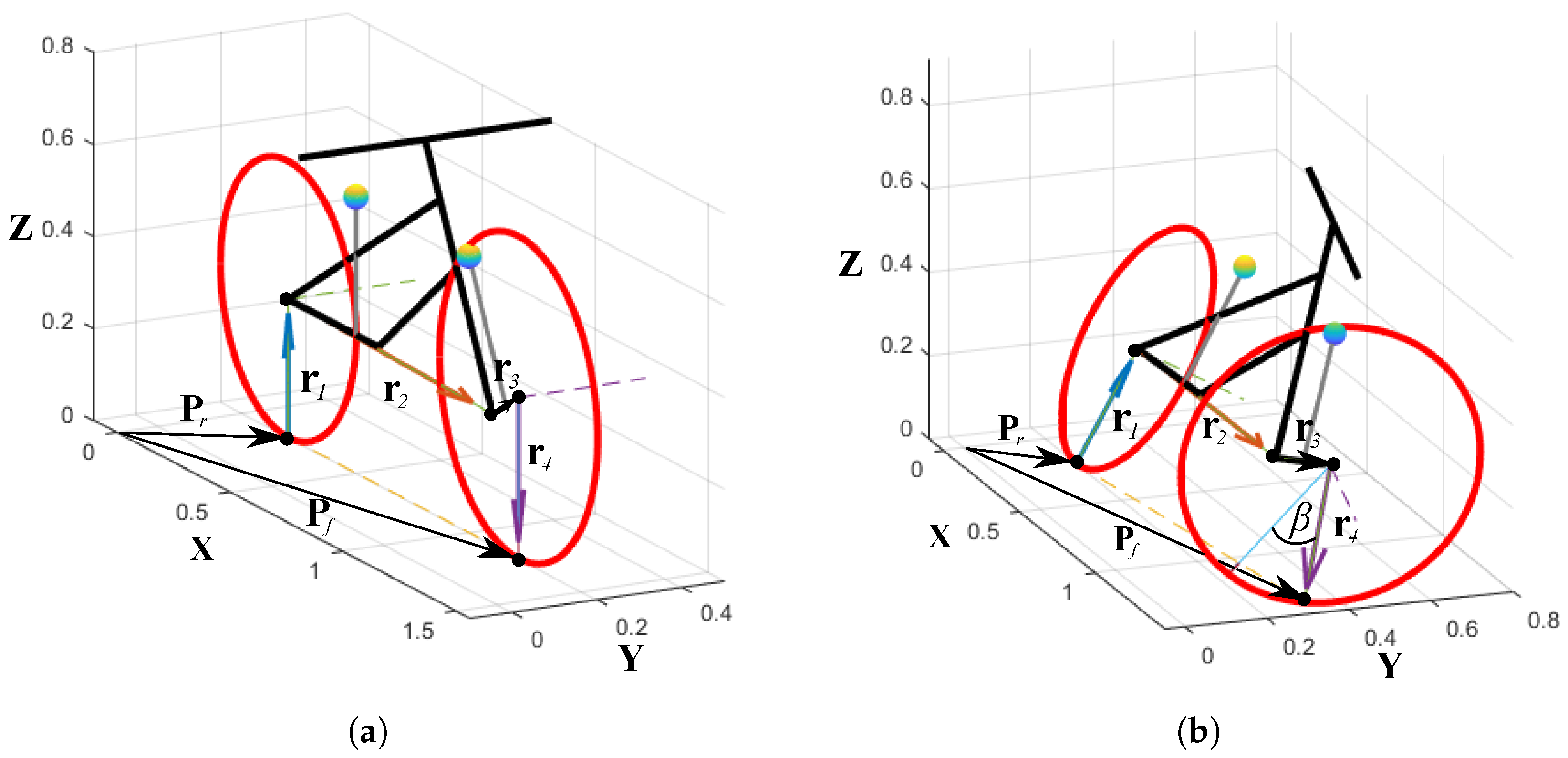
2.4. System Kinematic Chain
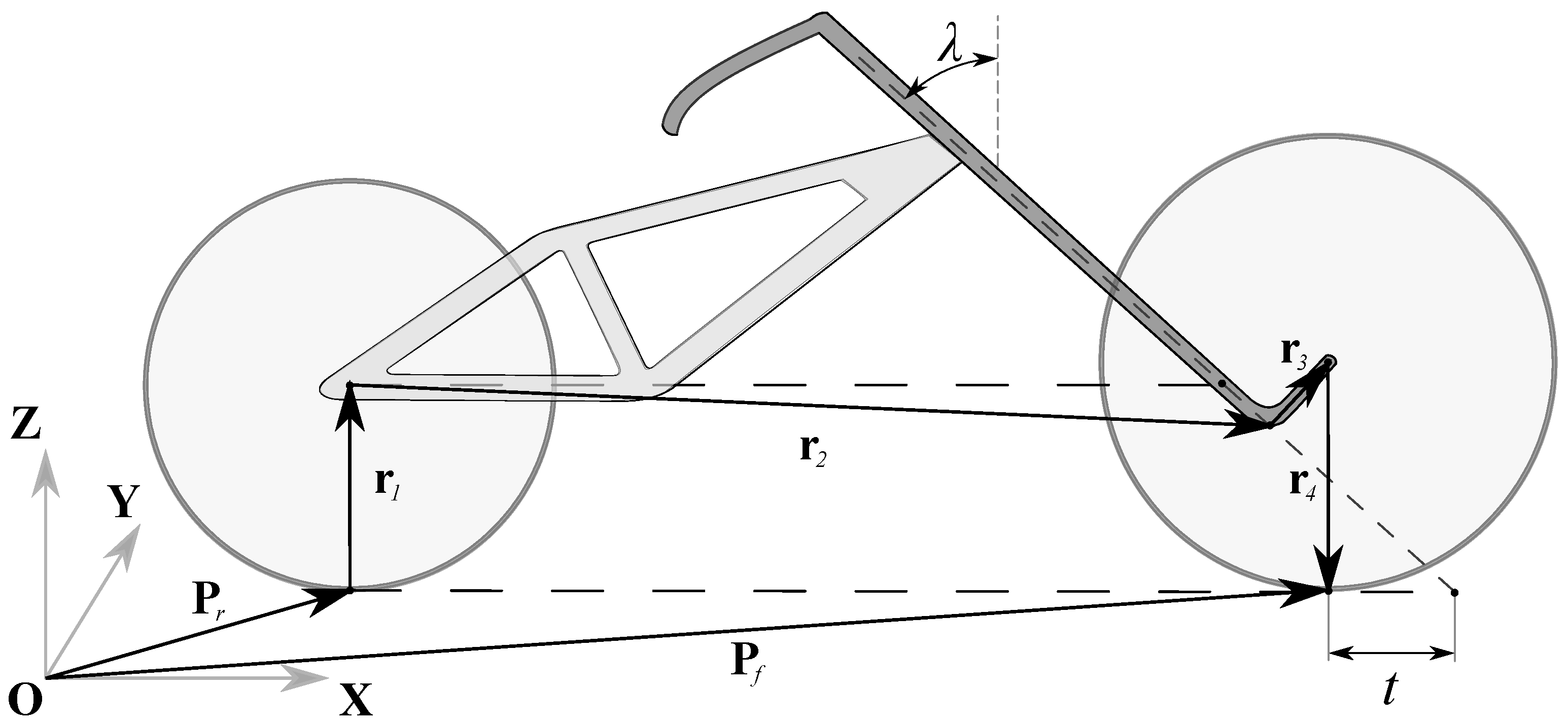
2.5. Cross-Product Model
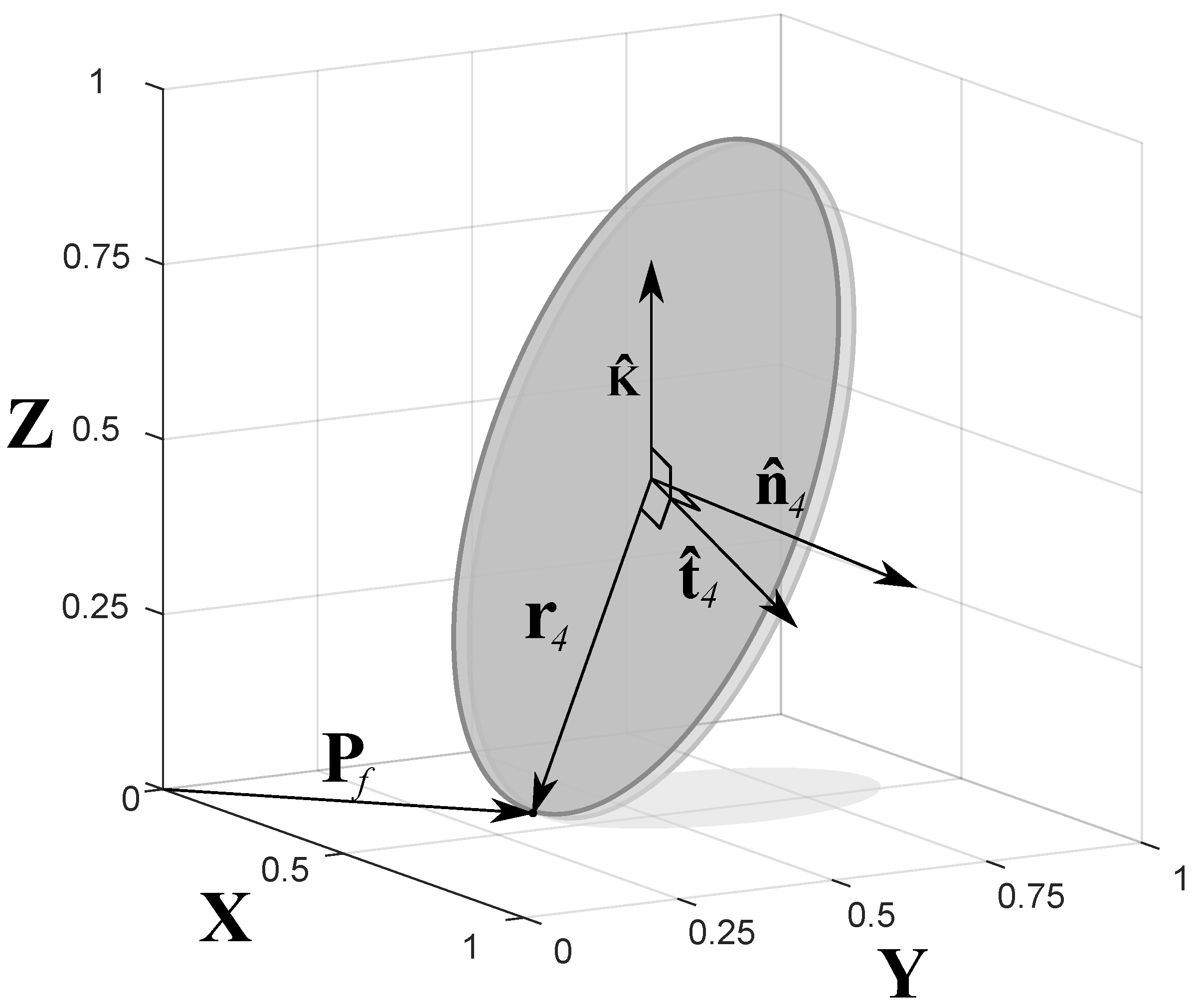
2.6. Surface Parametrization Model
2.7. Steering Point Kinematics
2.8. Front Assembly Orientation
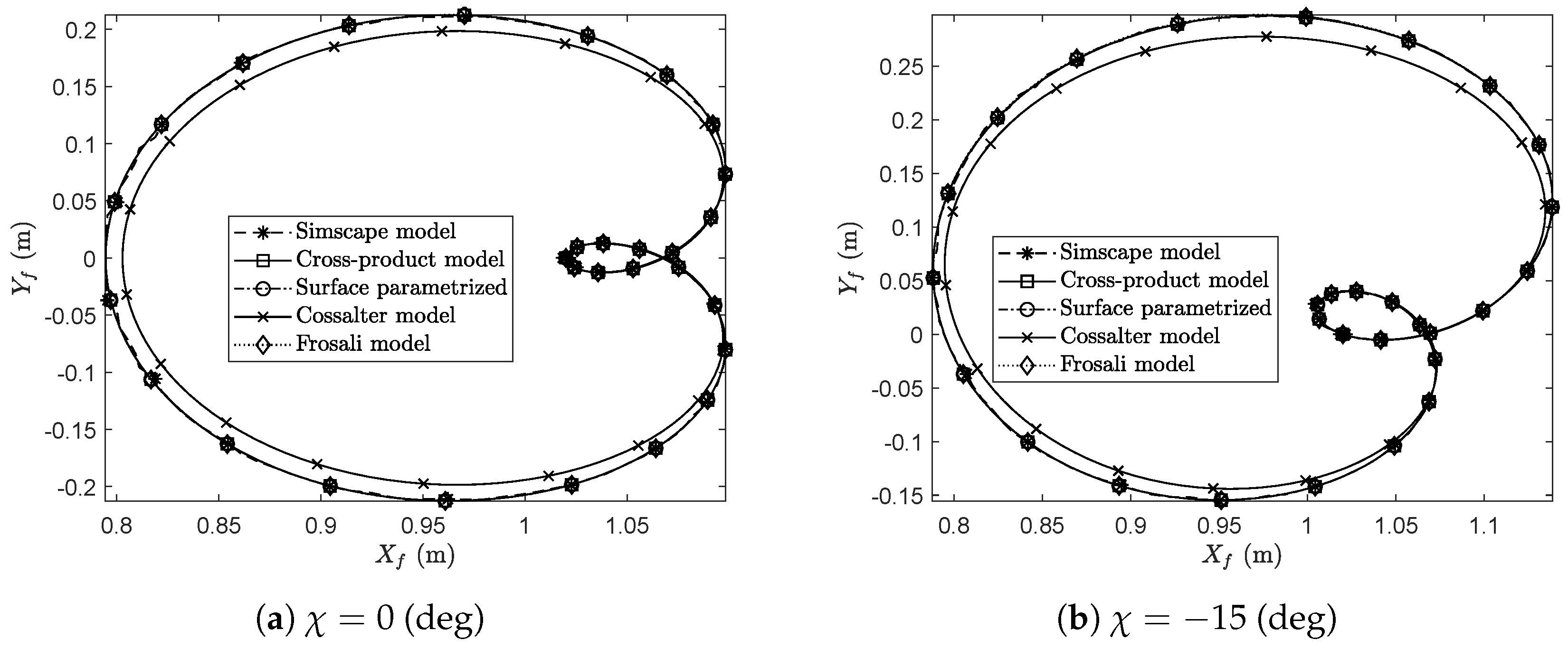
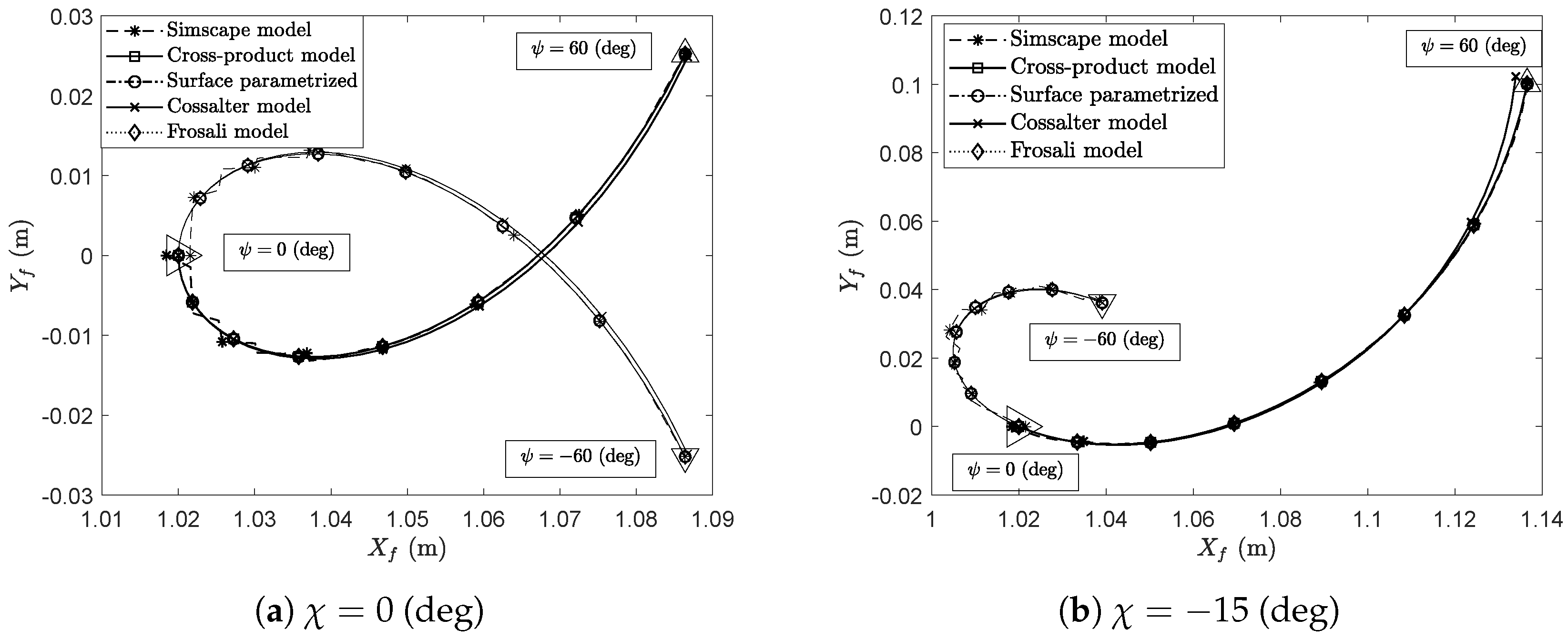
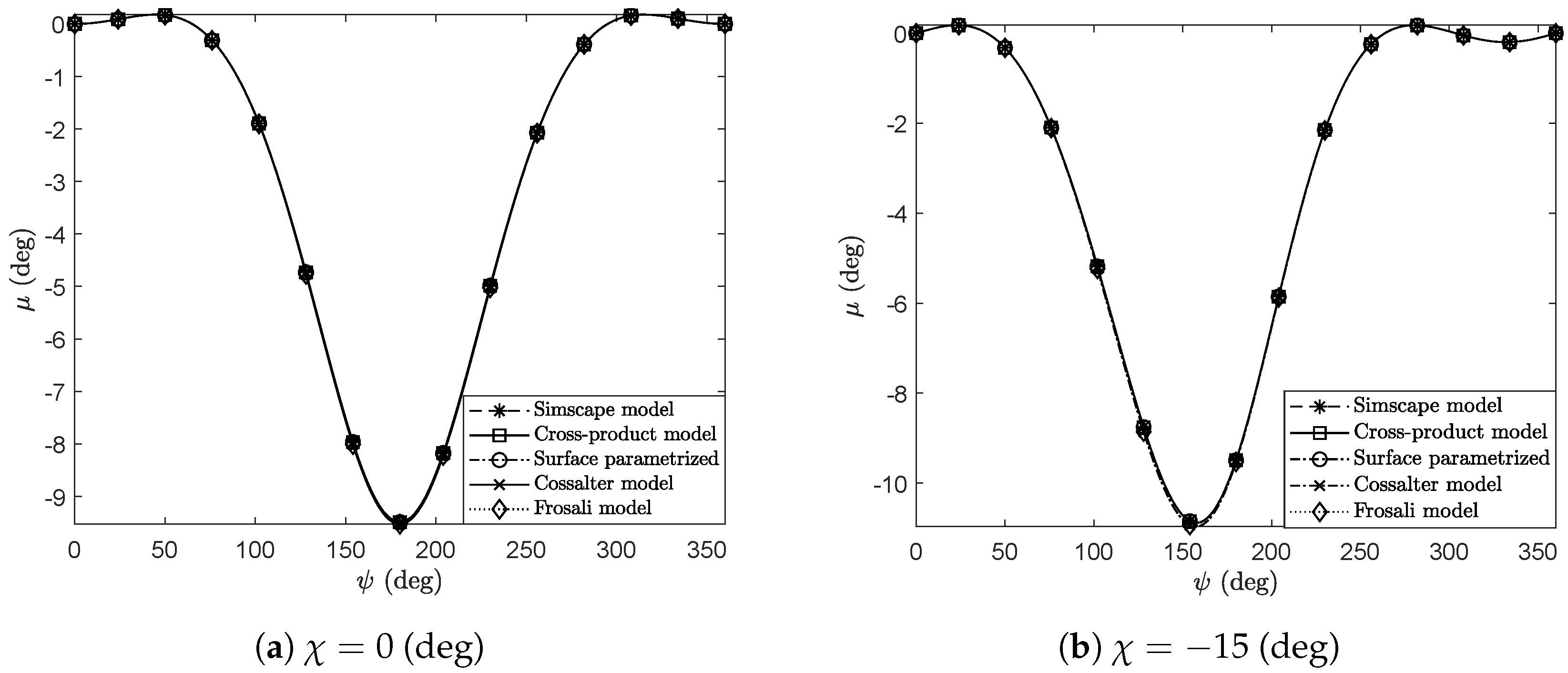
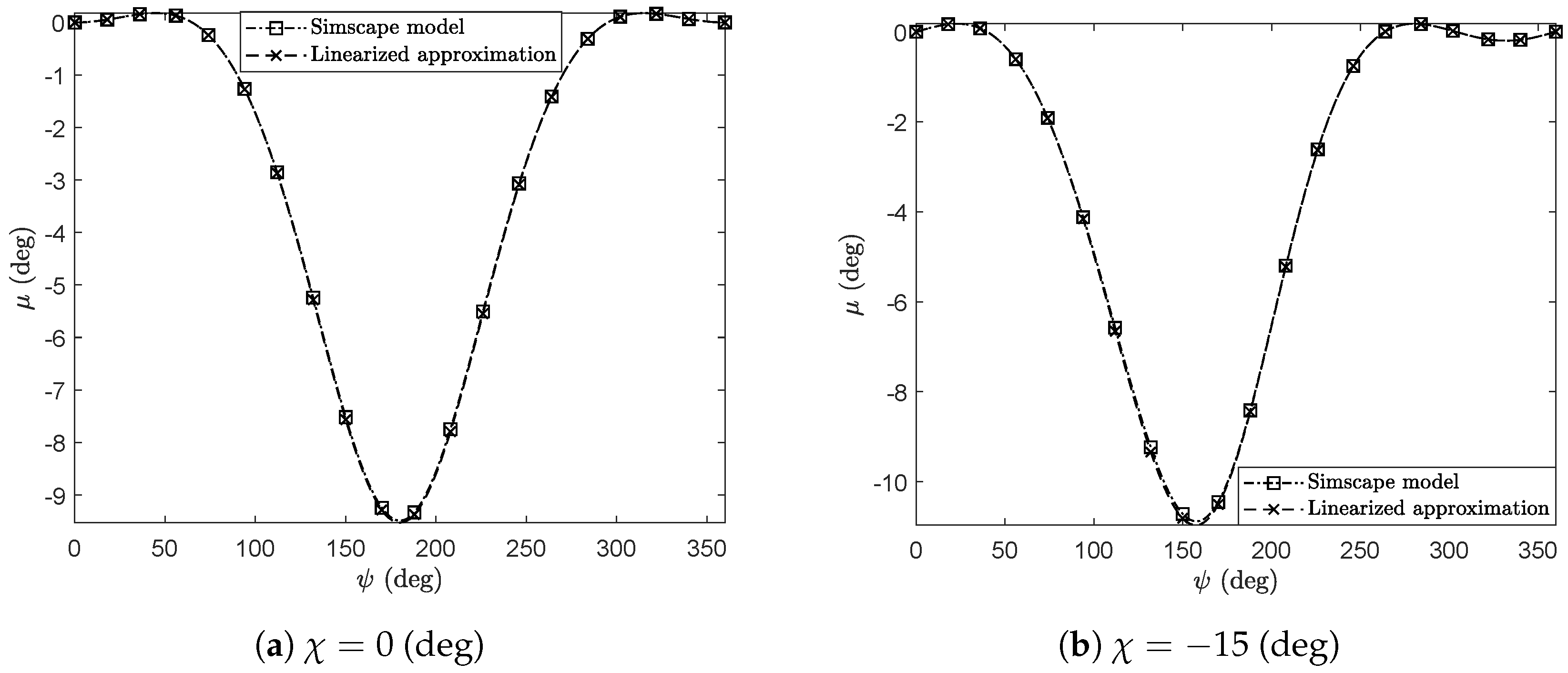
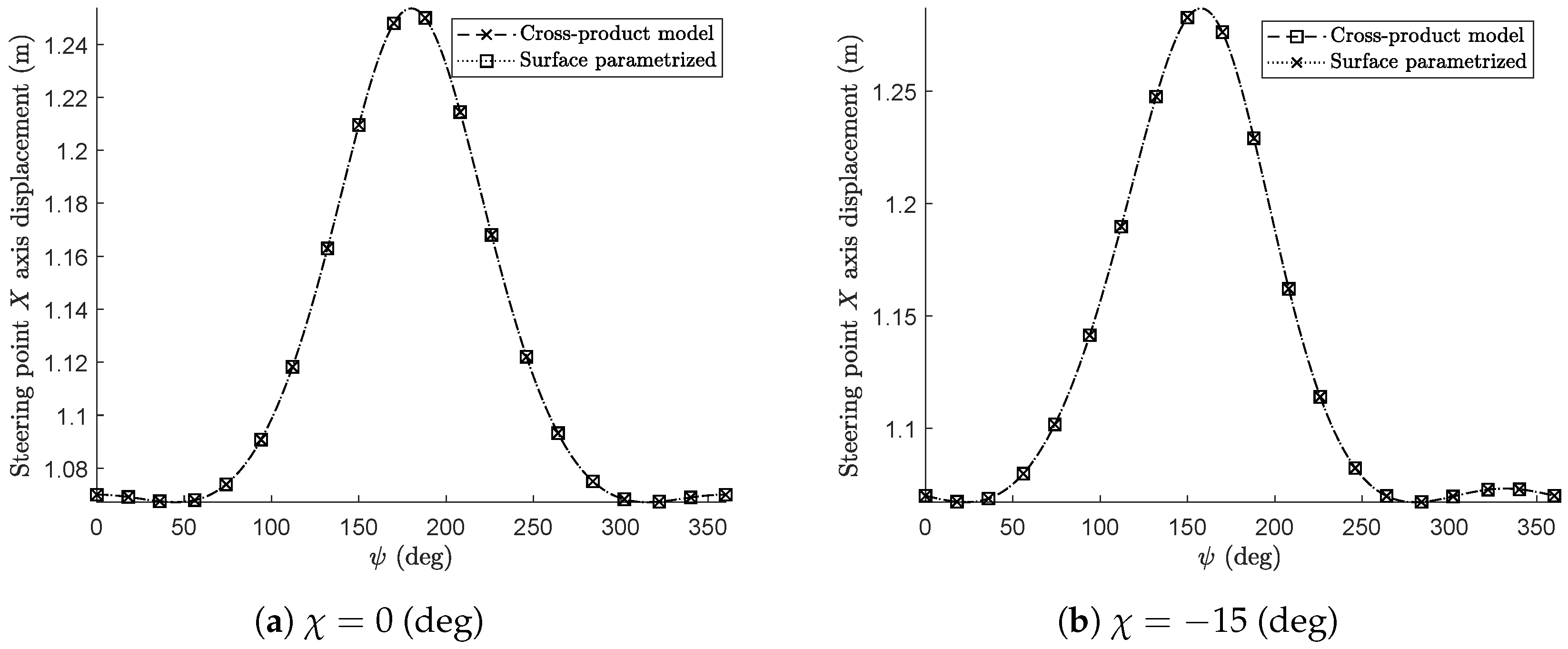
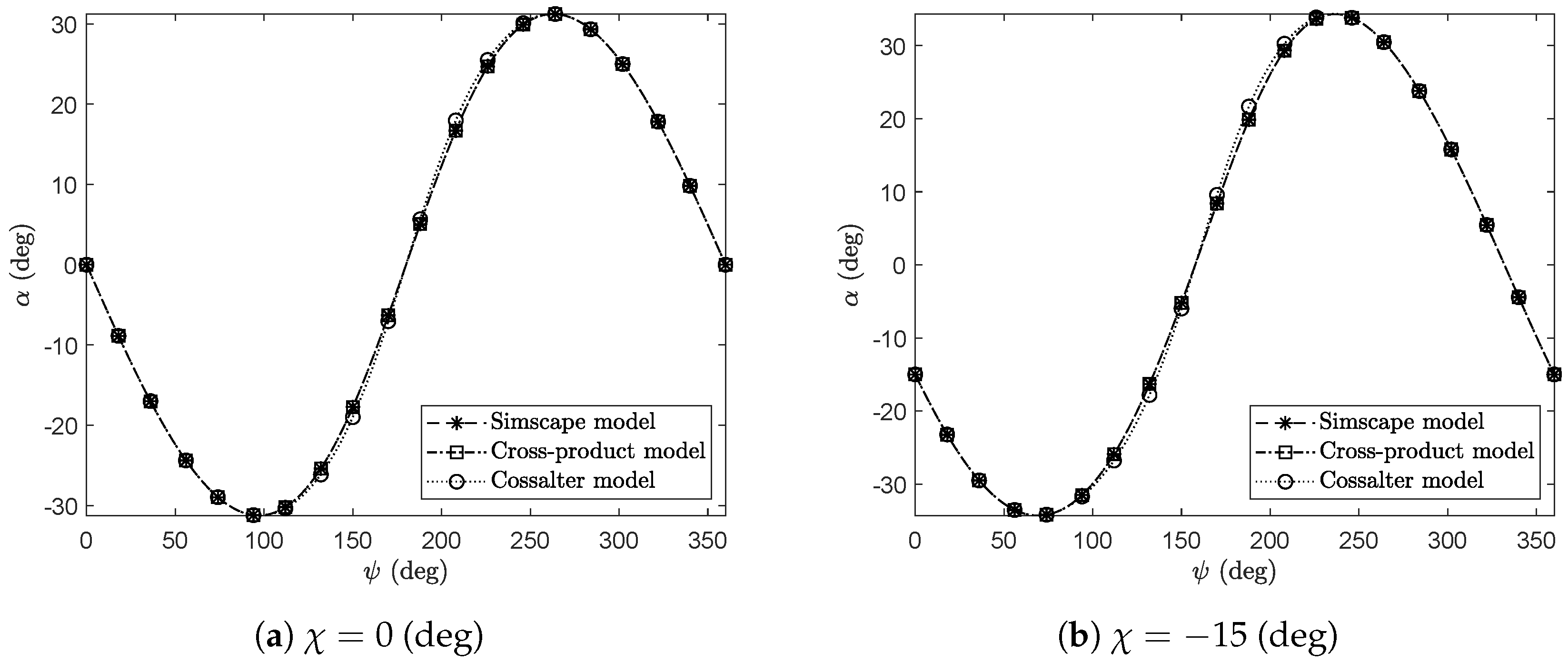
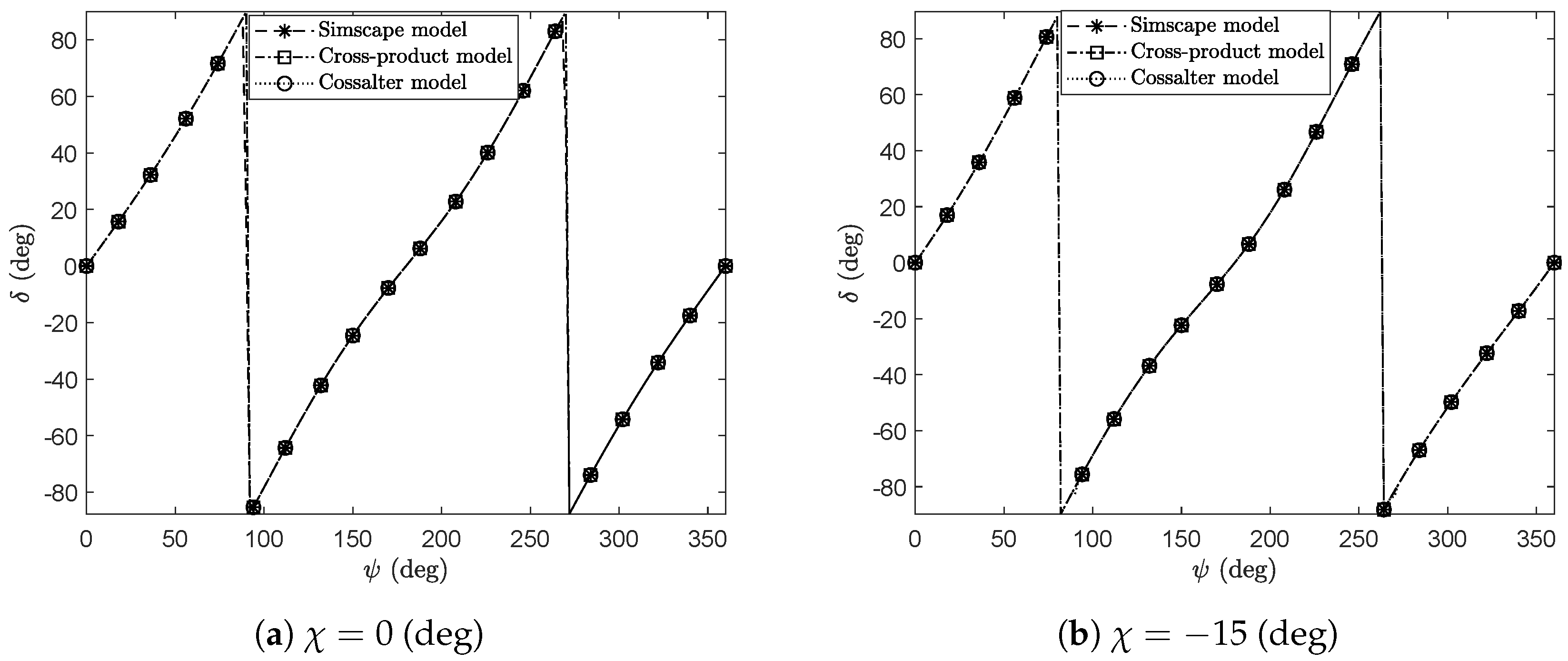
3. Numerical Results and Discussion
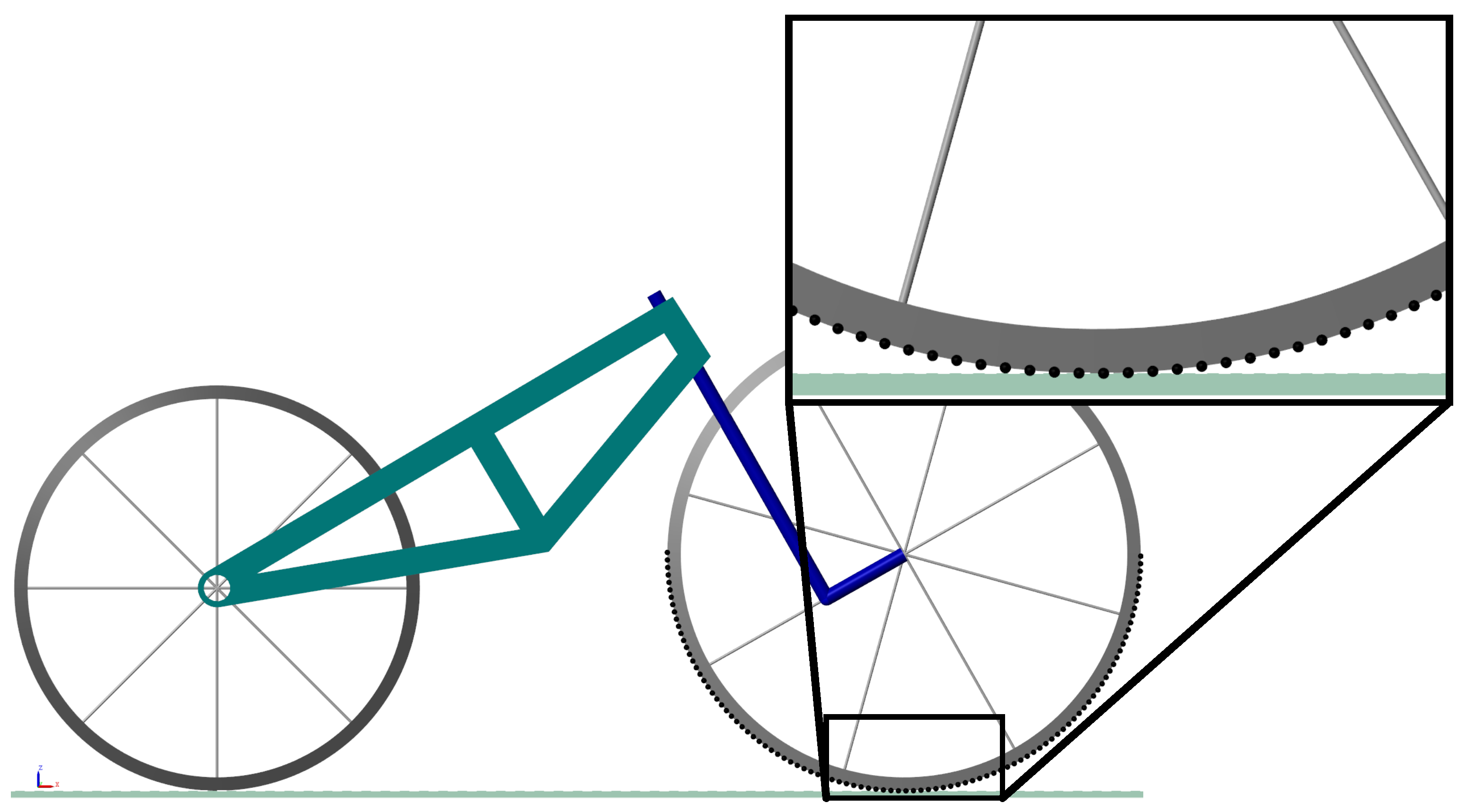
3.1. Description of the Numerical Experiments
- Substitute the components of the given vector into Equation (20).
- Solve numerically this algebraic equation to find the corresponding value of the angle employing the Newton-Raphson method considering an initial estimation (rad) and an appropriate small tolerance denoted with .
- Solve the set of nonlinear equations resulting from the previous step using the Newton-Raphson method considering the initial estimations (rad) and (rad), as well as a sufficiently small tolerance denoted with .
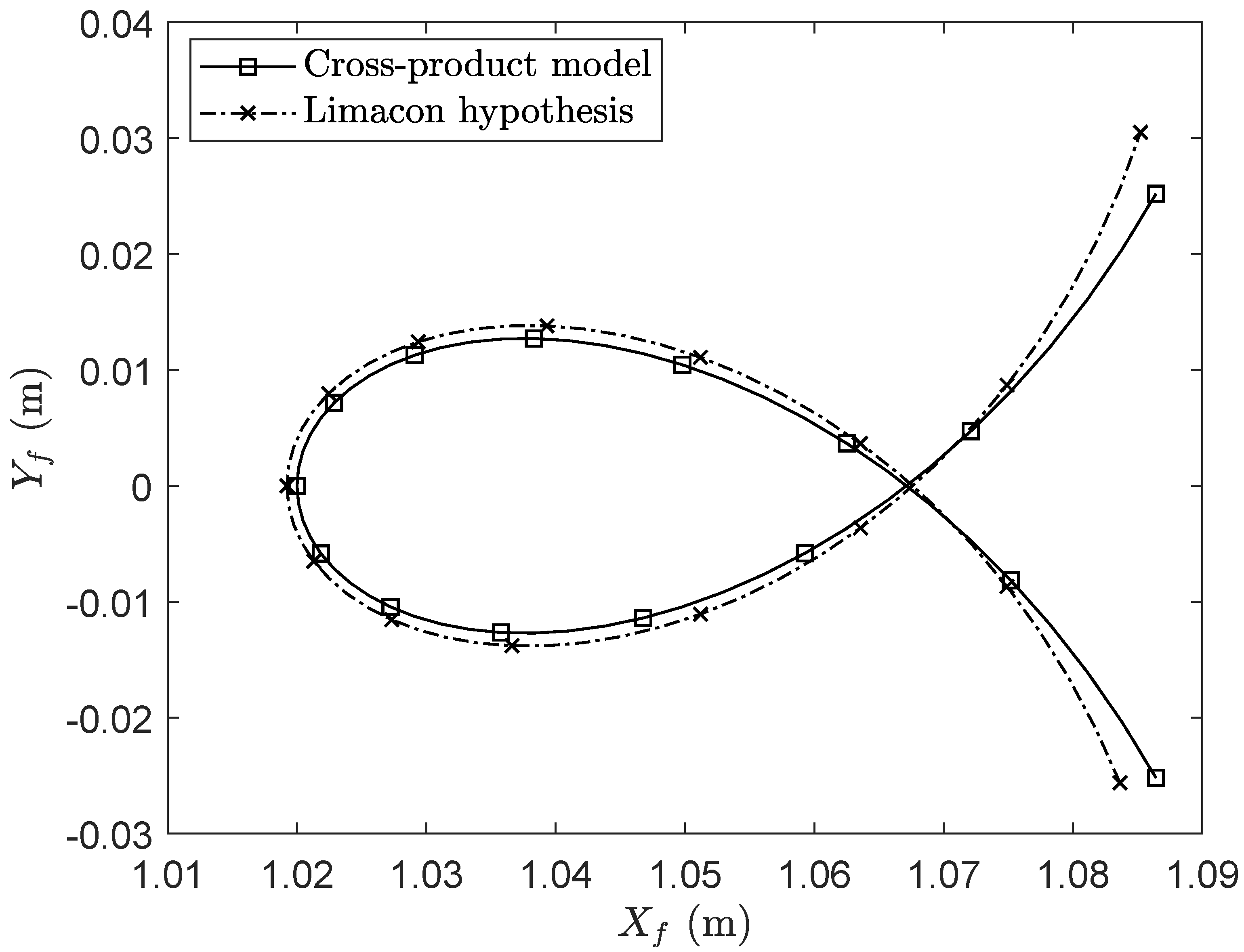
3.2. Kinematically Driven Study and Comparative Analysis
3.3. Discussion and Final Remarks
4. Summary, Conclusions, and Future Directions of Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Kinematic Model Proposed by Cossalter
Appendix A.2. Kinematic Model Proposed by Frosali and Ricci
References
- Whipple, F.J.W. The stability of the motion of a bicycle. Q. J. Pure Appl. Math. 1899, 30, 312–348. [Google Scholar]
- Huang, L. An approach for bicycle’s kinematic analysis. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2017, 231, 278–284. [Google Scholar] [CrossRef]
- Prince, P.; Al-Jumaily, A. Bicycle steering and roll responses. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2012, 226, 95–107. [Google Scholar] [CrossRef]
- Tomiati, N.; Colombo, A.; Magnani, G. A nonlinear model of bicycle shimmy. Veh. Syst. Dyn. 2019, 57, 315–335. [Google Scholar] [CrossRef]
- Baquero-Suárez, M.; Cortés-Romero, J.; Arcos-Legarda, J.; Coral-Enriquez, H. Correction to: A robust two-stage active disturbance rejection control for the stabilization of a riderless bicycle. Multibody Syst. Dyn. 2019, 46, 107. [Google Scholar] [CrossRef]
- Carvallo, E. Théorie du movement du monocycle, part 2: Théorie de la bicyclette. J. Ec. Polytech. Paris 1901, 6, 1–118. [Google Scholar]
- Kooijman, J.D.G.; Meijaard, J.P.; Papadopoulos, J.M.; Ruina, A.; Schwab, A.L. A Bicycle Can Be Self-Stable Without Gyroscopic or Caster Effects. Science 2011, 332, 339–342. [Google Scholar] [CrossRef]
- Sharp, R.S. The Stability and Control of Motorcycles. J. Mech. Eng. Sci. 1971, 13, 316–329. [Google Scholar] [CrossRef]
- Jennings, G. A Study of Motorcycle Suspension Damping Characteristics; National West Coast Meeting; SAE International: Warrendale, PA, USA, 1974. [Google Scholar] [CrossRef]
- Kane, T.R. The Effect of Frame Flexibility on High Speed Weave of Motorcycles; Automotive Engineering Congress and Exposition; SAE International: Warrendale, PA, USA, 1978; pp. 1389–1396. [Google Scholar] [CrossRef]
- Sharp, R.S.; Alstead, C.J. The Influence of Structural Flexibilities on the Straight-running Stability of Motorcycles. Veh. Syst. Dyn. 1980, 9, 327–357. [Google Scholar] [CrossRef]
- Passigato, F.; Eisele, A.; Wisselmann, D.; Gordner, A.; Diermeyer, F. Analysis of the Phenomena Causing Weave and Wobble in Two-Wheelers. Appl. Sci. 2020, 10, 6826. [Google Scholar] [CrossRef]
- Sharp, R.S.; Limebeer, D.J.N. A Motorcycle Model for Stability and Control Analysis. Multibody Syst. Dyn. 2001, 6, 123–142. [Google Scholar] [CrossRef]
- Cossalter, V.; Lot, R. A Motorcycle Multi-Body Model for Real Time Simulations Based on the Natural Coordinates Approach. Veh. Syst. Dyn. 2002, 37, 423–447. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, N.; Liu, C. Stability analysis for the Whipple bicycle dynamics. Multibody Syst. Dyn. 2020, 48, 311–335. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, G.; Li, H. Multibody dynamic modeling and controlling for unmanned bicycle system. ISA Trans. 2021. [Google Scholar] [CrossRef]
- García-Agúndez, A.; García-Vallejo, D.; Freire, E. Linearization approaches for general multibody systems validated through stability analysis of a benchmark bicycle model. Nonlinear Dyn. 2021, 103, 557–580. [Google Scholar]
- Agúndez, A.; García-Vallejo, D.; Freire, E. Linear stability analysis of nonholonomic multibody systems. Int. J. Mech. Sci. 2021, 198, 106392. [Google Scholar]
- Agúndez, A.; García-Vallejo, D.; Freire, E.; Mikkola, A. Stability analysis of a waveboard multibody model with toroidal wheels. Multibody Syst. Dyn. 2021, 53, 173–203. [Google Scholar]
- Pappalardo, C.M.; Lettieri, A.; Guida, D. A General Multibody Approach for the Linear and Nonlinear Stability Analysis of Bicycle Systems. Part I: Methods of Constrained Dynamics. J. Appl. Comput. Mech. 2021, 7, 655–670. [Google Scholar]
- Pappalardo, C.M.; Lettieri, A.; Guida, D. A General Multibody Approach for the Linear and Nonlinear Stability Analysis of Bicycle Systems. Part II: Application to the Whipple–Carvallo Bicycle Model. J. Appl. Comput. Mech. 2021, 7, 671–700. [Google Scholar]
- Cossalter, V.; Lot, R.; Massaro, M. The chatter of racing motorcycles. Veh. Syst. Dyn. 2008, 46, 339–353. [Google Scholar] [CrossRef]
- Sharp, R.S.; Watanabe, Y. Chatter vibrations of high-performance motorcycles. Veh. Syst. Dyn. 2013, 51, 393–404. [Google Scholar] [CrossRef]
- Cattabriga, S.; De Felice, A.; Sorrentino, S. Patter instability of racing motorcycles in straight braking manoeuvre. Veh. Syst. Dyn. 2019, 59, 33–55. [Google Scholar] [CrossRef]
- Klug, S.; Moia, A.; Verhagen, A.; Gorges, D.; Savaresi, S. Modeling of Coupled Vertical and Longitudinal Dynamics of Bicycles for Brake and Suspension Control. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 2018–2024. [Google Scholar] [CrossRef]
- Hung, N.B.; Lim, O. A review of history, development, design and research of electric bicycles. Appl. Energy 2020, 260, 114323. [Google Scholar]
- Slimi, H.; Arioui, H.; Nouveliere, L.; Mammar, S. Motorcycle speed profile in cornering situation. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 1172–1177. [Google Scholar] [CrossRef]
- Kooijman, J.; Schwab, A. A review on bicycle and motorcycle rider control with a perspective on handling qualities. Veh. Syst. Dyn. 2013, 51, 1722–1764. [Google Scholar] [CrossRef]
- Popov, A.; Rowell, S.; Meijaard, J. A review on motorcycle and rider modelling for steering control. Veh. Syst. Dyn. Int. J. Veh. Mech. Mobil. 2010, 48, 775–792. [Google Scholar] [CrossRef]
- Nehaoua, L.; Arioui, H.; Seguy, N.; Mammar, S. Dynamic modelling of a two-wheeled vehicle: Jourdain formalism. Veh. Syst. Dyn. 2013, 51, 648–670. [Google Scholar] [CrossRef]
- Özkan, T.; Lajunen, T.; Doğruyol, B.; Yıldırım, Z.; Çoymak, A. Motorcycle accidents, rider behaviour, and psychological models. Accid. Anal. Prev. 2012, 49, 124–132. [Google Scholar]
- Damon, P.M.; Ichalal, D.; Arioui, H. Steering and Lateral Motorcycle Dynamics Estimation: Validation of Luenberger LPV Observer Approach. IEEE Trans. Intell. Veh. 2019, 4, 277–286. [Google Scholar] [CrossRef]
- Salvati, L.; d’Amore, M.; Fiorentino, A.; Pellegrino, A.; Sena, P.; Villecco, F. Development and Testing of a Methodology for the Assessment of Acceptability of LKA Systems. Machines 2020, 8, 47. [Google Scholar]
- Li, T.; Kou, Z.; Wu, J.; Yahya, W.; Villecco, F. Multipoint Optimal Minimum Entropy Deconvolution Adjusted for Automatic Fault Diagnosis of Hoist Bearing. Shock Vib. 2021, 2021, 6614633. [Google Scholar]
- Villecco, F.; Pellegrino, A. Entropic measure of epistemic uncertainties in multibody system models by axiomatic design. Entropy 2017, 19, 291. [Google Scholar]
- Villecco, F. On the evaluation of errors in the virtual design of mechanical systems. Machines 2018, 6, 36. [Google Scholar]
- Chu, T.D.; Chen, C.K. Modelling and model predictive control for a bicycle-rider system. Veh. Syst. Dyn. 2018, 56, 128–149. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Yi, G. Model analysis of unmanned bicycle and ADRC control. In Proceedings of the 2020 IEEE International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA 2020), Chengdu, China, 28–31 May 2020. [Google Scholar] [CrossRef]
- Sanjurjo, E.; Naya, M.A.; Cuadrado, J.; Schwab, A.L. Roll angle estimator based on angular rate measurements for bicycles. Veh. Syst. Dyn. 2019, 57, 1705–1719. [Google Scholar] [CrossRef]
- Maier, O.; Györfi, B.; Wrede, J.; Kasper, R. Design and validation of a multi-body model of a front suspension bicycle and a passive rider for braking dynamics investigations. Multibody Syst. Dyn. 2018, 42, 19–45. [Google Scholar] [CrossRef]
- Lot, R.; Fleming, J. Gyroscopic stabilisers for powered two-wheeled vehicles. Veh. Syst. Dyn. 2019, 57, 1381–1406. [Google Scholar] [CrossRef]
- Griffin, J.W.; Popov, A.A. Multibody dynamics simulation of an all-wheel-drive motorcycle for handling and energy efficiency investigations. Veh. Syst. Dyn. 2018, 56, 983–1001. [Google Scholar] [CrossRef]
- Slimi, H.; Arioui, H.; Mammar, S. Motorcycle lateral dynamic estimation and lateral tire-road forces reconstruction using sliding mode observer. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 584–589. [Google Scholar] [CrossRef]
- Katagiri, N.; Marumo, Y.; Tsunashima, H. Evaluating Lane-Keeping-Assistance System for Motorcycles by Using Rider-Control Model; SAE International: Warrendale, PA, USA, 2008. [Google Scholar] [CrossRef]
- Meijaard, J.; Papadopoulos, J.M.; Ruina, A.; Schwab, A. Linearized dynamics equations for the balance and steer of a bicycle: A benchmark and review. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 1955–1982. [Google Scholar] [CrossRef]
- Doria, A.; Tognazzo, M.; Cusimano, G.; Bulsink, V.; Cooke, A.; Koopman, B. Identification of the mechanical properties of bicycle tyres for modelling of bicycle dynamics. Veh. Syst. Dyn. 2013, 51, 405–420. [Google Scholar] [CrossRef]
- Turnwald, A.; Liu, S. A Nonlinear Bike Model for Purposes of Controller and Observer Design. IFAC-PapersOnLine 2018, 51, 391–396. [Google Scholar] [CrossRef]
- Ajmi, H.; Aymen, K.; Lotfi, R. Dynamic modeling and handling study of a two-wheeled vehicle on a curved track. Mech. Ind. 2017, 18, 409. [Google Scholar] [CrossRef]
- Teerhuis, A.P.; Jansen, S.T. Motorcycle state estimation for lateral dynamics. Veh. Syst. Dyn. 2012, 50, 1261–1276. [Google Scholar] [CrossRef]
- Wang, E.X.; Zou, J.; Xue, G.; Liu, Y.; Li, Y.; Fan, Q. Development of Efficient Nonlinear Benchmark Bicycle Dynamics for Control Applications. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2236–2246. [Google Scholar] [CrossRef]
- Lake, K.; Thomas, R.; Williams, O. The influence of compliant chassis components on motorcycle dynamics: An historical overview and the potential future impact of carbon fibre. Veh. Syst. Dyn. 2012, 50, 1043–1052. [Google Scholar] [CrossRef]
- Escalona, J.L.; Recuero, A.M. A bicycle model for education in multibody dynamics and real-time interactive simulation. Multibody Syst. Dyn. 2012, 27, 383–402. [Google Scholar] [CrossRef]
- Doria, A.; Favaron, V.; Taraborrelli, L.; Roa, S. Parametric analysis of the stability of a bicycle taking into account geometrical, mass and compliance properties. Int. J. Veh. Des. 2017, 75, 91. [Google Scholar] [CrossRef]
- Astrom, K.; Klein, R.; Lennartsson, A. Bicycle dynamics and control: Adapted bicycles for education and research. IEEE Control Syst. 2005, 25, 26–47. [Google Scholar] [CrossRef]
- Sharp, R.S. On the Stability and Control of the Bicycle. Appl. Mech. Rev. 2008, 61, 060803. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, N.; Liu, C. Bicycle dynamics and its circular solution on a revolution surface. Acta Mech. Sin. 2020, 36, 220–233. [Google Scholar] [CrossRef]
- Saccon, A.; Hauser, J. An efficient Newton method for general motorcycle kinematics. Veh. Syst. Dyn. 2009, 47, 221–241. [Google Scholar] [CrossRef]
- Kane, T.R. Fundamental kinematical relationships for single-track vehicles. Int. J. Mech. Sci. 1975, 17, 499–504. [Google Scholar] [CrossRef]
- Frosali, G.; Ricci, F. Kinematics of a bicycle with toroidal wheels. Commun. Appl. Ind. Math. 2012, 3, 24. [Google Scholar] [CrossRef]
- Cossalter, V. Motorcycle Dynamics; Race Dynamics; Milwaukee: Brookfield, WI, USA, 2002; p. 372. [Google Scholar]
- Manrique, C.; Pappalardo, C.M.; Guida, D. A Model Validating Technique for the Kinematic Study of Two-Wheeled Vehicles. In Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2020; pp. 549–558. [Google Scholar] [CrossRef]
- Boyer, F.; Porez, M.; Mauny, J. Reduced Dynamics of the Non-holonomic Whipple Bicycle. J. Nonlinear Sci. 2018, 28, 943–983. [Google Scholar] [CrossRef]
- Lazarek, M.; Grabski, J.; Perlikowski, P. Derivation of a pitch angle value for the motorcycle. Eur. Phys. J. Spec. Top. 2020, 229, 2225–2238. [Google Scholar] [CrossRef]
- Hess, R.; Moore, J.K.; Hubbard, M. Modeling the manually controlled bicycle. IEEE Trans. Syst. Man Cybern. Syst. 2012, 42, 545–557. [Google Scholar] [CrossRef]
- Genta, G. Motor Vehicle Dynamics: Modeling and Simulation; Series on Advances in Mathematics for Applied Sciences; World Scientific: Singapore, 1997; Volume 43. [Google Scholar] [CrossRef]
- Jones, D.E. The stability of the bicycle. Phys. Today 1970, 23, 34–40. [Google Scholar]
- Doria, A.; Roa Melo, S.D. On the influence of tyre and structural properties on the stability of bicycles. Veh. Syst. Dyn. 2018, 56, 947–966. [Google Scholar] [CrossRef]
- Leonelli, L.; Mancinelli, N. A multibody motorcycle model with rigid-ring tyres: Formulation and validation. Veh. Syst. Dyn. 2015, 53, 775–797. [Google Scholar] [CrossRef]
- Haddout, S. A practical application of the geometrical theory on fibered manifolds to an autonomous bicycle motion in mechanical system with nonholonomic constraints. J. Geom. Phys. 2018, 123, 495–506. [Google Scholar] [CrossRef]
- Manrique Escobar, C.A.; Pappalardo, C.M.; Guida, D. A Parametric Study of a Deep Reinforcement Learning Control System Applied to the Swing-Up Problem of the Cart-Pole. Appl. Sci. 2020, 10, 9013. [Google Scholar]
- Pappalardo, C.M.; Guida, D. Dynamic Analysis and Control Design of Kinematically-Driven Multibody Mechanical Systems. Eng. Lett. 2020, 28, 1125–1144. [Google Scholar]
- Pappalardo, C.M.; De Simone, M.C.; Guida, D. Multibody modeling and nonlinear control of the pantograph/catenary system. Arch. Appl. Mech. 2019, 89, 1589–1626. [Google Scholar]
- Corno, M.; Panzani, G.; Savaresi, S.M. Single-Track Vehicle Dynamics Control: State of the Art and Perspective. IEEE/ASME Trans. Mechatron. 2015, 20, 1521–1532. [Google Scholar] [CrossRef]
- Klug, S.; Moia, A.; Verhagen, A.; Görges, D.; Savaresi, S. The influence of bicycle fork bending on brake control. Veh. Syst. Dyn. 2019, 3114, 1–21. [Google Scholar] [CrossRef]
- Shafiekhani, A.; Mahjoob, M.; Akraminia, M. Design and implementation of an adaptive critic-based neuro-fuzzy controller on an unmanned bicycle. Mechatronics 2015, 28, 115–123. [Google Scholar] [CrossRef][Green Version]

| Symbol | Meaning | Value (Units) |
|---|---|---|
| Wheelbase | (m) | |
| t | Trail | (m) |
| Caster angle | 30 (deg) | |
| Rear wheel radius | (m) | |
| Front wheel radius | (m) | |
| Solver tolerance | (m) or (rad) |
| Model | (m) | (m) | (deg) | (deg) | (deg) | (deg) |
|---|---|---|---|---|---|---|
| Cross-prod. | 7.0868E−4 | E−4 | E−1 | E−3 | E−3 | E−1 |
| Sur. param. | E−4 | E−4 | E−1 | E−3 | - | - |
| Cossalter’s | E−3 | E−3 | E−2 | E−1 | E−3 | |
| Frosali’s | E−4 | E−4 | - | E−2 | - | - |
| Model | (m) | (m) | (deg) | (deg) | (deg) | (deg) |
|---|---|---|---|---|---|---|
| Cross-prod. | E−4 | E−4 | E−1 | E−4 | E−3 | E−4 |
| Sur. param. | E−4 | E−4 | E−1 | E−3 | - | - |
| Cossalter’s | E−3 | E−2 | E−2 | E−1 | E−1 | |
| Frosali’s | E−4 | E−4 | - | E−2 | - | - |
| (deg) | (m) | (m) | (deg) | (deg) |
|---|---|---|---|---|
| 0 | E−17 | E−18 | E−15 | E−17 |
| 15 | E−17 | E−17 | E−15 | E−17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manrique-Escobar, C.A.; Pappalardo, C.M.; Guida, D. A Multibody System Approach for the Systematic Development of a Closed-Chain Kinematic Model for Two-Wheeled Vehicles. Machines 2021, 9, 245. https://doi.org/10.3390/machines9110245
Manrique-Escobar CA, Pappalardo CM, Guida D. A Multibody System Approach for the Systematic Development of a Closed-Chain Kinematic Model for Two-Wheeled Vehicles. Machines. 2021; 9(11):245. https://doi.org/10.3390/machines9110245
Chicago/Turabian StyleManrique-Escobar, Camilo Andres, Carmine Maria Pappalardo, and Domenico Guida. 2021. "A Multibody System Approach for the Systematic Development of a Closed-Chain Kinematic Model for Two-Wheeled Vehicles" Machines 9, no. 11: 245. https://doi.org/10.3390/machines9110245
APA StyleManrique-Escobar, C. A., Pappalardo, C. M., & Guida, D. (2021). A Multibody System Approach for the Systematic Development of a Closed-Chain Kinematic Model for Two-Wheeled Vehicles. Machines, 9(11), 245. https://doi.org/10.3390/machines9110245







