Abstract
Connected and automated vehicles (CAVs) are a very promising alternative for reducing fuel consumption and improving traffic efficiency when vehicles merge at on-ramps. In this study, we propose a graph-based method to coordinate CAVs to merge at the highway ramp. First, the optimized vehicles were divided into groups to pass the merging point. Then we built a directed graph model for each group of vehicles, where each path of the graph corresponds to one of all possible merging sequences. The improved shortest path algorithm is proposed to find the optimal merging sequence for minimizing total fuel consumption. The results of the simulation showed that the proposed graph-based method reduced fuel consumption and ensured high traffic efficiency; moreover, the vehicles can form a platoon after passing the merge point.
1. Introduction
Traffic jams that occur at highway on-ramps are a significant challenge to overcome to improve traffic efficiency [1,2]. Traffic congestion not only adds to travel time and makes drivers anxious but also increases fuel consumption and air pollutants, which violates the concept of green travel. The emergence of cooperative driving technologies provides opportunities to solve the above problems [3,4]. With the help of vehicle to everything technology (V2X) [5,6], including vehicle to vehicle (V2V) and vehicle to infrastructure (V2I), CAVs can shorten the gaps between vehicles, improve response speed and increase traffic efficiency. CAVs can change the modes of future transportation management and organization [7]. Utilizing advanced technology, more intelligent management systems have been developed to coordinate CAVs to merge at freeway on-ramps efficiently [8,9]. These systems roughly contain two main modules: merging sequences optimization and motion planning [10,11]. In this study, we propose a graph-based optimal method to obtain merging sequences and trajectories of CAVs on the highway.
In recent research, the cooperative merging problems were solved sequentially [12]. The merging sequence, namely the passing order of all vehicles, was first determined. Then the trajectory of each vehicle was planned in the motion planning. The methods in the literature rarely consider the impact of merging sequences on the vehicle trajectory while optimizing the merging sequences of the vehicles. Different merging sequences lead to different vehicle trajectories so that the fuel consumption of the vehicles also differs [13]. To the best of our knowledge, there is no study of an optimal model considering merging sequences and vehicle trajectories simultaneously in the literature.
In the study, we propose a graph-based optimal global method for on-ramp merging of CAVs. In this framework, vehicles in the traffic control area send their own information to the central controller through V2I technology. The central controller clusters the vehicles into groups according to the initial state of the vehicles and establishes a graph model that represents all possible merging sequences for each group of vehicles. The weight of the path is calculated by the predicted minimum cost of the vehicle trajectory. The improved shortest path planning algorithm is adopted to find the path representing the optimal merging sequence. For vehicle motion planning, the vehicle trajectories are guaranteed to meet the minimum cost that acts as a weight in the graph model. The central controller finally coordinates vehicles to merge at the highway ramp by sending the optimized control information to vehicles.
The purpose of this study is to improve traffic efficiency and minimize fuel consumption of all CAVs without vehicle collision. Our main contributions in this paper are as follows: (1) to establish a graph-based optimal on-ramp merging sequence model using predicted vehicle fuel consumption as the weight; (2) to solve the problem in real-time and present an improved shortest path algorithm with the quadratic polynomial computational complexity of O(N2) complexity, where N denotes the number of vehicles; (3) to conduct vehicle motion planning so that a group of vehicles passing through the merging point at the highway on-ramp is made to form into a platoon with a constant distance between vehicles.
2. Related Work
Research efforts have focused on optimizing merging sequences and planning vehicle trajectories for coordinating CAVs in merging highways [14]. The approaches of determining the merging sequence can be classified into two categories: optimal and sub-optimal. For vehicle trajectory planning, the methods in recent research mainly include two types: discrete control solution and closed-form analytical solution.
For merging sequence scheduling, several optimization methods are used to solve the merge sequence to maximize traffic efficiency. Pei et al. [15] resolved the problem of on-ramp merging by using a dynamic programming model to get the optimal merging sequence, which reduces the computation complex by defining the state space, state transition and the criterion function. Haigen Min et al. [16] developed a centralized merging control algorithm based on gaming theory aiming to prioritize the merging of cars. The benefit is formulating the priority problem as a double-objective optimization problem to get the best weight of every gaming rule. The proposed method improved fuel economy and saved travel time. Fei Ye et al. [17] proposed a bi-level optimal edge computing model to optimize the merging time and vehicle trajectory for on-merge merging, which aimed to get the minimum vehicle arrival time and energy consumption. The simulation results showed that the proposed model achieves great benefits in vehicle mobility, energy-saving and air pollutant emission reduction. Yuanchang Xie [18] modeled the merging control strategy as a constrained non-linear optimization problem and solved it using the MATLAB optimization toolbox. The study results indicated that the proposed optimal control strategy could effectively improve the average speed and throughput.
Sub-optimization methods are proposed to obtain the merging sequence, which reduces the computational complexity to achieve real-time performance in practical applications. Jackeline Rios-Torres et al. [19] addressed the merging sequence problem by a FIFO-like rule, defining a hierarchical vehicle sequence based on which vehicle is closer to the merging zone. Although this simple method is easy to implement, it sacrifices the optimization of the merge sequence. Jishiyu Ding et al. [20] proposed a rule-based cooperative merging strategy to coordinate vehicles going through the merging zone safely, which tries to allow several vehicles from one direction to pass first if possible and then a group of vehicles from the other direction to pass afterward to avoid the alternating merge. The proposed method struck a good balance between traffic efficiency and computational cost. Wenjing Cao et al. [21] presented a cooperative merging path generation method for vehicles to merge using a Model Predictive Control (MPC) scheme, which controls the slight acceleration or deceleration of vehicles on the main road to let the merging vehicle merge in easily. The results proved that, as long as the initial conditions are reasonable, the proposed method can generate a cooperative merging path. Riccardo Scarinci et al. [22] addressed a novel merging assistant strategy that exploits cooperative systems to reduce congestion at the highway ramp by grouping vehicles together on the main road and adjusting inter-vehicle spaces into gaps that are usable by merging traffic.
For motion planning, in the discrete control solution, Yuanchang Xie et al. [18] proposed a motion planning method that provides individual vehicles with step-by-step control instructions in the ramp merging area. The study results showed that the proposed strategy can effectively coordinate the merging vehicles at freeway on-ramps. In the closed-form analytical solution, Ye et al. [17] obtained the trajectory of each vehicle by selecting the ‘cruise,’ ‘acceleration and cruise’ or ‘deceleration and cruise’ pattern to follow the assigned time to pass the merging zone. The simple method fails to optimize fuel consumption. Rios-Torres and Malikopoulos [23] applied Hamiltonian analysis to derive an analytical closed-form solution that can reduce fuel consumption.
The structure of the paper is as follows. In Section 3, the problem of on-ramp merging for vehicles is formulated; Section 4 proposes a graph-based optimal CAVs merging model and an improved shortest path algorithm to solve it; the simulation results are presented in Section 5; conclusions are outlined in Section 6.
3. Problem Formulation
3.1. General System Description
In a multi-lane scenario, vehicles should not be allowed to change lanes near the ramp for safety. We only focus on the merging of the vehicles on the outermost lane of the road. Therefore, a typical ramp merging scenario includes a single-lane main road and a ramp road, and vehicles on the ramp road merge into the main road after passing the merging point. In the traditional situation without coordination, the vehicles on the ramp and the vehicles on the main road compete to pass through the merging point, leading to traffic jams and even vehicle collisions, which results in low traffic efficiency, high fuel consumption and unsafe conditions [24]. In the scenario we considered, the central controller near the merging point coordinates the CAVs on the main road and ramp road to merge smoothly at the highway ramp. Specifically, within the communication range of V2I, we divided the whole area into two zones: the detecting zone and control zone. The main optimization process occurs in the detecting zone. Obtaining the optimal merging sequence in the detecting zone, the vehicles will follow the trajectory of the lowest fuel consumption until reaching the merging point in the control zone. The architecture of the optimization method proposed in this study is shown in Figure 1, with the following assumptions:
- All vehicles are CAVs that can communicate with the central controller through V2I;
- Overtaking on a single-lane road is not allowed;
- Vehicles on the ramp are forced to merge into the main road at the merging point.
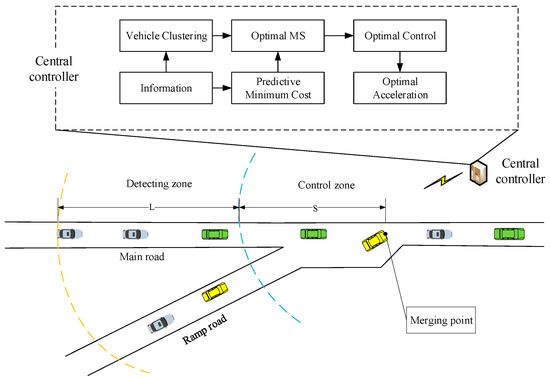
Figure 1.
Framework for merging sequence decisions and control systems.
To simplify the control of the vehicle [25], each vehicle can be modeled as a point mass moving along a specified road with the equation described as:
where , and denote position, speed and acceleration/deceleration of each vehicle, respectively.
3.2. Optimization Problem Formulation
In this section, we formulate a multi-objective cost function that represents travel efficiency and fuel consumption to model the optimal coordination for merging. The multi-objective cost function of vehicle can be expressed as:
where vehicle represents the vehicle passing through the merge point, w1 and w2 are weight coefficients, the time represents the delay of vehicle compared to its minimum time to reach the merge point and and denote the start time at which vehicle is optimized and the optimized time which vehicle arrives at the merging point, respectively.
Considering the acceleration and deceleration capacity of the vehicles and the speed limit of the road, we defined the following constraints as:
where and are the minimum deceleration and maximum acceleration, respectively, and and are the road limit speeds without distinguishing between main road and ramp road.
4. The Graph-Based Optimal Global Method
4.1. Graph-Based Optimal Global Modeling
In actual scenarios, vehicles on the main and ramp road enter continuously and in real-time. The vehicles travel at a constant speed before they are optimized. It is challenging to optimize all the vehicles’ trajectories from the global perspective, so we decided to optimize the entering vehicles round-by-round in the detecting area. In detail, the traffic controller starts to optimize all vehicles in the detecting area when the first entering vehicle (which may be on the main or the ramp road) is about to leave the detecting area. After the optimization, the traffic controller starts to process the next round of incoming vehicles when the first vehicle of the next round of vehicles is about to leave the detecting area.
We divided the vehicles of the detecting zone into several groups before optimizing the merging sequence. A criterion for dividing vehicle groups is proposed to ensure that the leader of each group is not affected by the chaser of the preceding group. Let be the initial state of vehicle , where and are distance to the merge point and speed of vehicle , respectively. The time is the safe gap. The constant is a safety coefficient related to the road. Vehicle acts as the leader of a new vehicle group when its initial state satisfies the equation described as:
Otherwise, vehicle follows vehicle to pass through the merging point. The leader and its followers form a new group. As shown in Figure 2, vehicles 1–9 are divided into two groups, vehicles 1–4 and vehicles 5–9. Vehicle 5 is the leader of the second vehicle group because vehicle 5 fails to follow vehicle 4 with the limitation of vehicle capacity. Each group of vehicles forms a platoon with a constant distance after passing through the merge point. In a group of vehicles, the time where the vehicle arrives at the merging point can be described as:
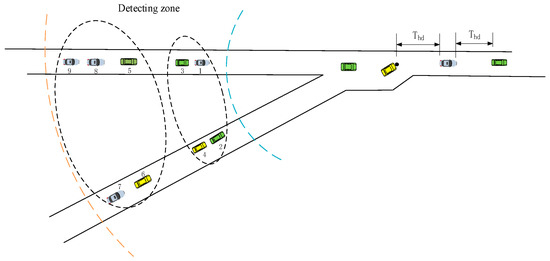
Figure 2.
Vehicles clustered in the detecting zone.
Vehicle , the leader of each vehicle group, is not restricted by the safe gap and can be obtained by optimizing the cost Equation (2). We get the time series of each vehicle arrival to the merging point according to Equation (5) as long as the merging sequence is fixed.
To obtain the optimal merging sequence for one group of clustered vehicles, we modeled the ramp merging as a directed graph shortest path problem to minimize the total fuel consumption while improving traffic efficiency. We construct a directed graph as shown in Figure 3, where and denote vertex and edge set, respectively. As a node of the graph, means that vehicles on the main road and vehicles on the ramp road have the right to go through the merging point. Since overtaking is not allowed on a single-lane road, vehicles on each road obtain the right in an order closer to the merging point.
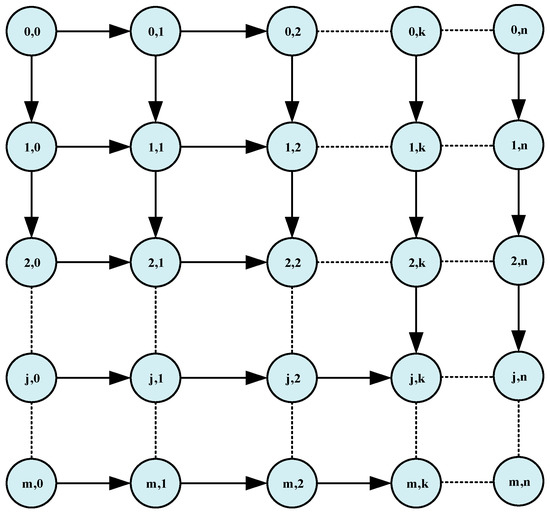
Figure 3.
Graph representing the merging sequences.
The set of directed edge contains two subsets, the set of () and . The directed edge (), from node to node , denotes a vehicle of the main road assigned the right to pass through the merge point at this step. Similarly, () represents that a vehicle of the ramp road obtains the right. We assume that the vehicles of the main road and the vehicles of the ramp road are clustered into the vehicle group. The possible merging sequences of vehicles correspond to the paths from to one-to-one. For example, the path of , and , indicates that the two vehicles of the main road pass the merge point first, and then the two vehicles of the ramp pass. Next, we find the shortest path from to in the graph to solve the optimal merging sequence of vehicles. The weight of the edge represents the predicted fuel consumption of the vehicle. The shortest path from to represents the merging sequence with the smallest total fuel consumption. Therefore, the improved shortest path algorithm ensures that the final merging sequence is optimal.
4.2. The Predicted Fuel Consumption of the Vehicles
In this section, we get an analytical solution for predicting the fuel consumption of the vehicle, reducing computational complexity. For vehicles , the cost function of fuel consumption can be written as:
Following Ding et al.’s solution [9] to the problem, the Pontryagins Maximum Principle is adopted to obtain the analytical solution of each vehicle trajectory. We write the Hamiltonian function for each vehicle as:
where and denotes the co-state variables of vehicle . From Equation (7) and the Pontryagins Maximum Principle, we can get the necessary conditions of optimality as follows:
From (9) and (10) we have:
From (11) and (12) we obtain that:
where are constants. The initial state and final state of vehicle are used as boundary conditions to compute the four constants: , where the velocity represents the speed at which vehicles reach the merge point. The constants and , corresponding to acceleration , are calculated as:
For simplicity, the start time of optimization is set to 0. From (7), (13), (16) and (17), we obtain an analytical solution for predicting the fuel consumption of the vehicle as:
Fuel consumption is infinite when does not meet the limitation of vehicle capacity. In Section 4.1, the weight of the edge represents the predicted fuel consumption of the vehicle. Therefore, the weights of the graph can be obtained from the following equation directly, as:
where and are the minimum and maximum time to reach the merge point within the capacity of vehicle .
4.3. Improved Shortest Path Algorithm to Find Optimal Merging Sequence
In this section, we improve the shortest path algorithm to solve the optimal merging sequence in the characteristic graph constructed by this study. The specific steps of the improved the shortest path algorithm are as follows:
- Determine the time for the first vehicle to pass through the merge point, based on which leading vehicles on the main road and the ramp are closer to the merging point. Then, generate the time series by Equation (5) for the group of vehicles passing the merge point;
- Calculate the weight by Equation (19) to construct the graph. The and store the weights of ) and (), respectively. When or , the weight is infinite;
- Calculate matrix and . The denotes the length of the shortest path from to . Therefore, . The matrix records the shortest path. The is initialized to the zero matrix. When , the is assigned the value 1;
- The optimized merge sequence is obtained from the matrix . Then each vehicle on the main road and the ramp road gets the time to pass the merge point according to the time series in step 1;
- Calculate the trajectory of each vehicle to meet the minimum fuel consumption condition. Therefore, Equation (13) is the analytical solution of the vehicle trajectory.
The graph is two-dimensional in this study. The matrix and are calculated to find the shortest path from to in the graph. The number of each dimension for the matrix is proportional to the number of vehicles on the main and ramp road. Therefore, the improved shortest path algorithm solved the optimal merging sequence with O() computational complexity.
The flow chart of the algorithm is shown in Figure 4.
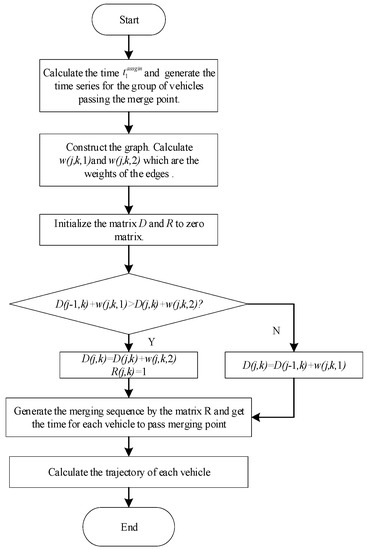
Figure 4.
The flow chart of the improved shortest path algorithm.
5. Simulation Results
All experiments were performed in Matlab 2020a on a computer with Intel i5-9400F CPU with 2.90 GHz and 8 GB RAM. The key simulation parameters are shown in Table 1. The safety coefficient is related to road conditions. We chose a value that performed well in the simulation as in the study. Note that all parameters can be changed according to the actual road conditions.

Table 1.
Simulation parameters.
5.1. Cast Study 1: A Group of Vehicles Passes through the Merging Point
The main purpose of this simulation was to verify the effectiveness of the shortest path planning algorithm for finding the optimal merging sequence. The vehicles are adjusted to the specified speed before entering the detection zone. In the case study, the vehicles on the main road traveled at a speed of 20 m/s, and the vehicles on the ramp traveled at a speed of 15 m/s. Following Poisson distribution, vehicles were randomly generated to enter the detecting area. When the detecting area was full of vehicles, the improved shortest path algorithm was executed to solve the optimal merging sequence for the group of vehicles. The position parameters of the vehicle are shown in Table 2. The position parameter is the opposite of the distance from the vehicle to the merging point when the optimization starts.

Table 2.
The parameters of the vehicles for case study 1.
In case study 1, the vehicles in the detecting area were clustered into a group of vehicles passing through the merging point. The leading vehicle on the ramp was closer to the merging point than the leading vehicle on the main road, so vehicle acted as the first vehicle in the group of vehicles to pass through the merging point. For the other vehicles, including the vehicles and , the possible merging sequences were . The improved shortest path algorithm solved the optimal merging sequence with O() computational complexity, which minimizes the total fuel consumption of the vehicles. In the case study, the final optimal merging sequence was .
The trajectories of the vehicles met the minimum fuel consumption, and the analytical solution was Equation (15). The trajectories of all vehicles are shown in Figure 5. In Figure 5, the red curves are the trajectories of the vehicles on the main road and the blue curves are the trajectories of the vehicles on the ramp. The curves of the same color are not staggered, indicating that the vehicle did not collide. The vehicles formed a vehicle platoon with the constant distance of and the speed of after passing the merging point. The speed and acceleration of the vehicles are shown in Figure 6a,b, respectively.
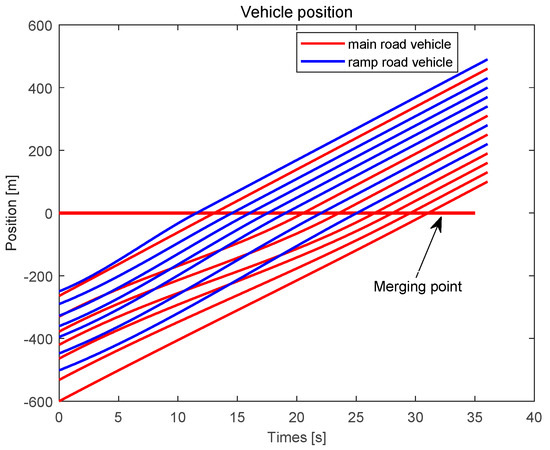
Figure 5.
Position trajectory of vehicles for case study 1.
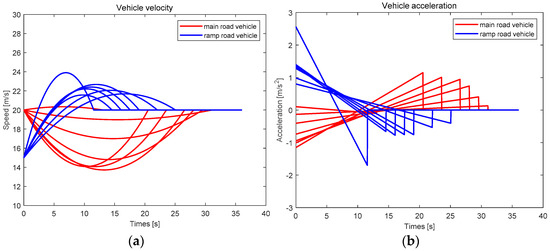
Figure 6.
Speed and acceleration of the vehicles for case study 1: (a) speed of the vehicles and (b) acceleration of the vehicles.
Then, we verified the effect of this method in reducing accumulative fuel consumption. The optimal method was compared with the FIFO-based method. The result is shown in Figure 7. The optimal method decreased accumulative fuel consumption by 45.57% based on the FIFO-based method. It can be seen that the accumulated fuel consumption increases with time quickly at the beginning. The main factor was the large acceleration of the leading vehicle. The leading vehicle in this group of vehicles arrived at the merging point as quickly as possible, which shortened the time for this group of vehicles merging at the highway on-ramp.
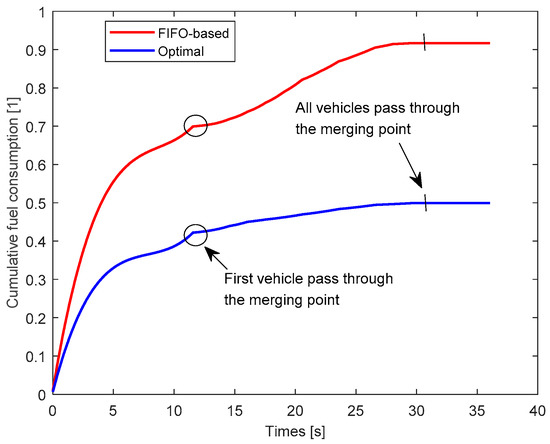
Figure 7.
Cumulative fuel consumption of vehicles for case study 1.
5.2. Case Study 2: Multiple Groups of Vehicles Pass through the Merging Point
When the vehicles in the detecting area were sparse, the vehicles were divided into multiple groups of vehicles to pass through the merging point. To generate discontinuous traffic flow, we randomly generated vehicles entering the detecting area with the random generator pausing for a period of time. When the vehicles filled up the detecting area, the vehicle grouping strategy was carried out, and then the improved shortest path algorithm was performed to solve the optimal merging sequence for each group of vehicles. In case study 2, the position parameters of the vehicles are shown in Table 3.

Table 3.
The parameters of the vehicles for case study 2.
In case study 2, the vehicles in the detecting area were divided into two groups, vehicles and , to pass through the merging point. With the constraints of vehicle capacity, vehicle cannot follow vehicle through the merge point, that is, the speed and position of vehicle and its preceding vehicle satisfied Equation (15). Vehicle acted as the leading vehicle of the next group passing through the merging point. Then, the improved shortest path algorithm solved the optimal merging sequence for each group of vehicles, and the results were and .
The trajectories of the vehicles in two groups are shown in Figure 8. In Figure 8, the vehicles in the detecting area formed two platoons after passing through the merging point. The speed and acceleration of the vehicles were shown in Figure 9a,b, respectively.
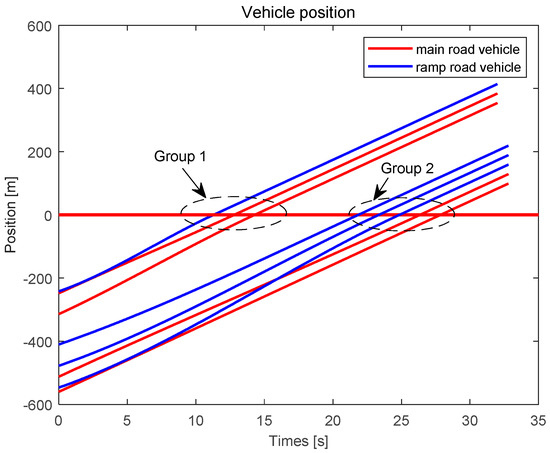
Figure 8.
Position trajectory of vehicles for case study 2.
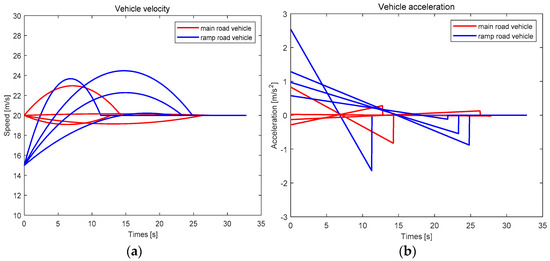
Figure 9.
Speed and acceleration of the vehicles for case study 2: (a) speed of the vehicles and (b) acceleration of the vehicles.
In the case study, eight vehicles in the detecting area were coordinated to merge at the highway. The optimized method reduced cumulative fuel consumption by 20.71% compared to the FIFO-based method, as shown in Figure 10. The effect in reducing fuel consumption of the proposed method improved as the number of coordinated vehicles increased.
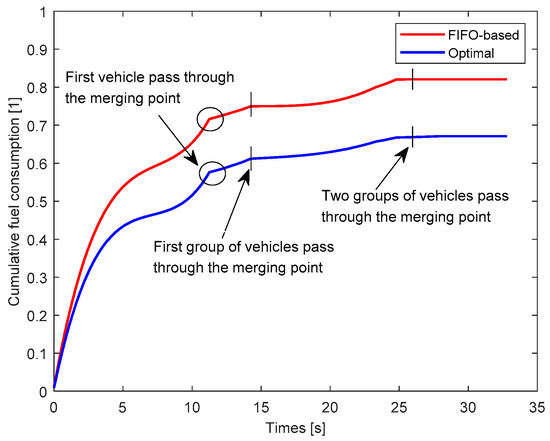
Figure 10.
Cumulative fuel consumption of vehicles for case study 2.
6. Conclusions
The main findings can be summarized as follows. We propose a graph-based method to solve the on-ramp merging for CAVs. First, we clustered the vehicles in the detecting area based on their initial state. Then the graph model was established for each group of vehicles to find the optimal merging sequence. The weights for the graph’s edges were computed by the analytical solution of the predicted fuel consumption. Experiments showed that our method improved fuel consumption by approximately 20% compared to the FIFO-based method while ensuring high traffic efficiency.
Author Contributions
Conceptualization, Y.S. and Z.Y.; methodology, Z.Y.; software, H.Y.; formal analysis, Y.G.; investigation, Y.Q.; resources, Y.S.; data curation, Z.Y.; writing—original draft preparation, Z.Y.; writing—review and editing, H.Y. and Y.G.; visualization, Y.Q.; supervision, Y.S.; project administration, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the China National Key Research and Development Program (NO.2018YFE0197700). This research was derived from the Advanced Driving Use Case in the 5G-MOBIX project. The 5G-MOBIX project received funding from the European Union’s Horizon 2020 program.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bai, Y.; Zhang, Y.; Li, X.; Hu, J. Cooperative weaving for connected and automated vehicles to reduce traffic oscillation. Transp. A Transp. Sci. 2019, 1–19. [Google Scholar] [CrossRef]
- Rios-Torres, J.; Malikopoulos, A.A. A Survey on the Coordination of Connected and Automated Vehicles at Intersections and Merging at Highway On-Ramps. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1066–1077. [Google Scholar] [CrossRef]
- Zou, Y.; Qu, X. On the impact of connected automated vehicles in freeway work zones: A cooperative cellular automata model based approach. J. Intell. Connect. Veh. 2018, 1, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Rios-Torres, J.; Malikopoulos, A.A. Impact of Partial Penetrations of Connected and Automated Vehicles on Fuel Consumption and Traffic Flow. IEEE Trans. Intell. Veh. 2018, 3, 453–462. [Google Scholar] [CrossRef]
- Mahmood, D.A.; Horváth, G. Analysis of the message propagation speed in VANET with disconnected RSUs. Mathematics 2020, 8, 782. [Google Scholar] [CrossRef]
- Shi, Y.; Lv, L.; Yu, H.; Yu, L.; Zhang, Z. A Center-Rule-Based Neighborhood Search Algorithm for Roadside Units Deployment in Emergency Scenarios. Mathematics 2020, 8, 1734. [Google Scholar] [CrossRef]
- Xu, B.; Li, S.E.; Bian, Y.; Li, S.; Ban, X.J.; Wang, J.; Li, K. Distributed conflict-free cooperation for multiple connected vehicles at unsignalized intersections. Transp. Res. Part C Emerg. Technol. 2018, 93, 322–334. [Google Scholar] [CrossRef]
- Ding, J.; Peng, H.; Zhang, Y.; Li, L. Penetration effect of connected and automated vehicles on cooperative on-ramp merging. IET Intell. Transp. Syst. 2020, 14, 56–64. [Google Scholar] [CrossRef]
- Ntousakis, I.A.; Nikolos, I.K.; Papageorgiou, M. Optimal vehicle trajectory planning in the context of cooperative merging on highways. Transp. Res. Part C Emerg. Technol. 2016, 71, 464–488. [Google Scholar] [CrossRef]
- Malikopoulos, A.A.; Hong, S.; Park, B.B.; Lee, J.; Ryu, S. Optimal Control for Speed Harmonization of Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2405–2417. [Google Scholar] [CrossRef] [Green Version]
- Milanes, V.; Godoy, J.; Villagra, J.; Perez, J. Automated on-ramp merging system for congested traffic situations. IEEE Trans. Intell. Transp. Syst. 2011, 12, 500–508. [Google Scholar] [CrossRef] [Green Version]
- Awal, T.; Kulik, L.; Ramamohanrao, K. Optimal traffic merging strategy for communication- and sensor-enabled vehicles. IEEE Conf. Intell. Transp. Syst. Proc. ITSC 2013, 1468–1474. [Google Scholar] [CrossRef]
- Jing, S.; Hui, F.; Zhao, X.; Rios-Torres, J.; Khattak, A.J. Cooperative Game Approach to Optimal Merging Sequence and on-Ramp Merging Control of Connected and Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4234–4244. [Google Scholar] [CrossRef]
- He, Q.; Meng, X.; Qu, R.; Xi, R. Machine learning-based detection for cyber security attacks on connected and autonomous vehicles. Mathematics 2020, 8, 1311. [Google Scholar] [CrossRef]
- Pei, H.; Feng, S.; Zhang, Y.; Yao, D. A Cooperative Driving Strategy for Merging at On-Ramps Based on Dynamic Programming. IEEE Trans. Veh. Technol. 2019, 68, 11646–11656. [Google Scholar] [CrossRef]
- Min, H.; Fang, Y.; Wang, R.; Li, X.; Xu, Z.; Zhao, X. A Novel On-Ramp Merging Strategy for Connected and Automated Vehicles Based on Game Theory. J. Adv. Transp. 2020, 2020, 2529856. [Google Scholar] [CrossRef]
- Ye, F.; Guo, J.; Kim, K.J.; Orlik, P.V.; Ahn, H.; Di Cairano, S.; Barth, M.J. Bi-level optimal edge computing model for on-ramp merging in connected vehicle environment. IEEE Intell. Veh. Symp. Proc. 2019, 2019, 2005–2011. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Zhang, H.; Gartner, N.H.; Arsava, T. Collaborative merging strategy for freeway ramp operations in a connected and autonomous vehicles environment. J. Intell. Transp. Syst. Technol. Plan. Oper. 2017, 21, 136–147. [Google Scholar] [CrossRef]
- Rios-Torres, J.; Malikopoulos, A.; Pisu, P. Online Optimal Control of Connected Vehicles for Efficient Traffic Flow at Merging Roads. IEEE Conf. Intell. Transp. Syst. Proc. ITSC 2015, 2015, 2432–2437. [Google Scholar] [CrossRef]
- Ding, J.; Li, L.; Peng, H.; Zhang, Y. A Rule-Based Cooperative Merging Strategy for Connected and Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3436–3446. [Google Scholar] [CrossRef]
- Cao, W.; Mukai, M.; Kawabe, T.; Nishira, H.; Fujiki, N. Cooperative vehicle path generation during merging using model predictive control with real-time optimization. Control Eng. Pract. 2015, 34, 98–105. [Google Scholar] [CrossRef]
- Scarinci, R.; Heydecker, B.; Hegyi, A. Analysis of traffic performance of a ramp metering strategy using cooperative vehicles. IEEE Conf. Intell. Transp. Syst. Proc. ITSC 2013, 324–329. [Google Scholar] [CrossRef]
- Rios-Torres, J.; Malikopoulos, A.A. Automated and Cooperative Vehicle Merging at Highway On-Ramps. IEEE Trans. Intell. Transp. Syst. 2017, 18, 780–789. [Google Scholar] [CrossRef]
- Meng, T.; Xu, B.; Qin, X.; Huang, J.; Zhong, Z. Cooperative Ramp Merging Control for Connected and Automated Vehicles. SAE Technical Paper; Tsinghua University: Beijing, China, 2020. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, X.; Yin, G. Multi-objective optimal cooperative driving for connected and automated vehicles at non-signalized intersection. IET Intell. Transp. Syst. 2019, 13, 79–89. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).