Research on the Electromagnetic Conversion Method of Stator Current for Local Fault Detection of a Planetary Gearbox
Abstract
:1. Introduction
2. Motor Stator Current Modeling
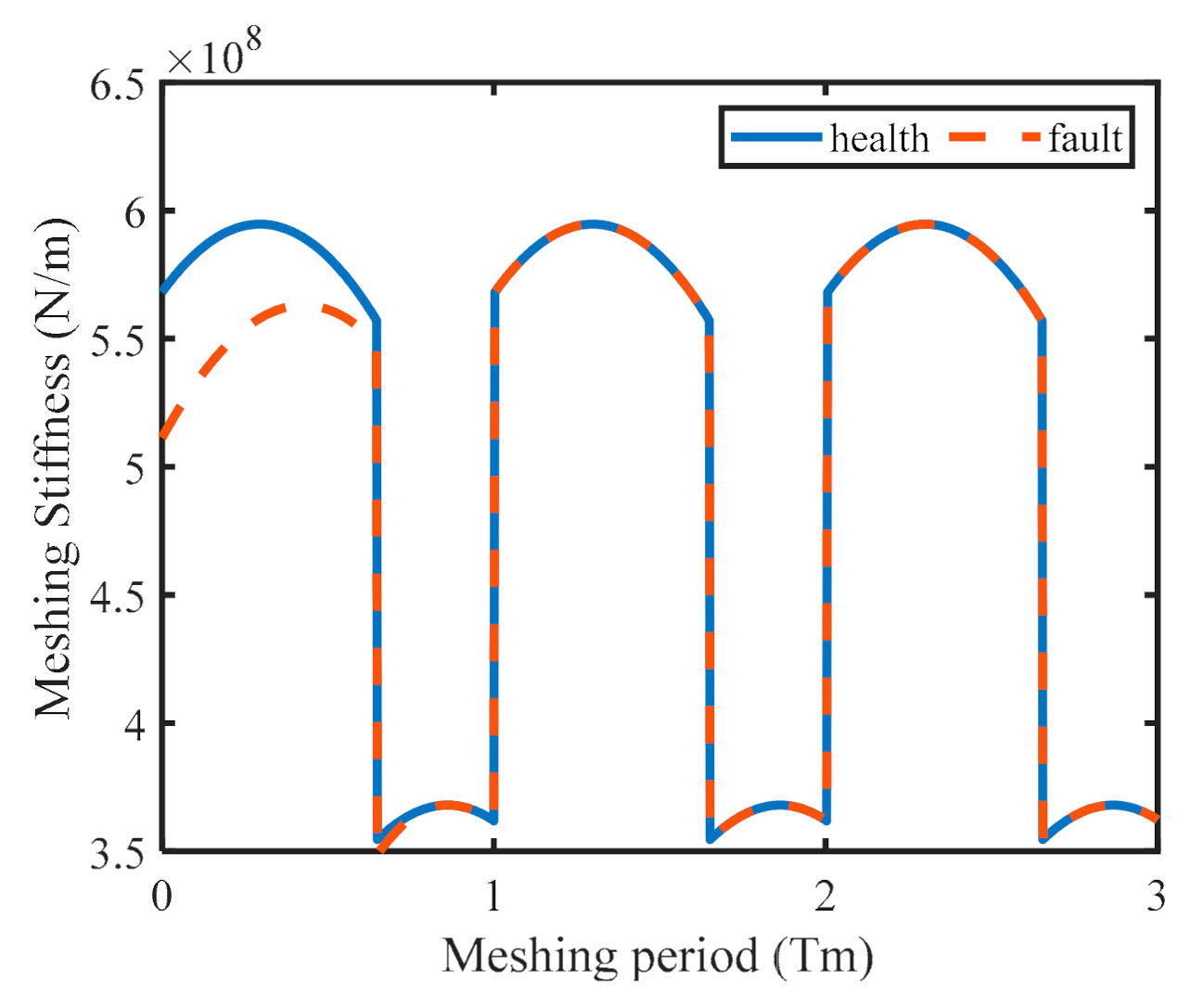
2.1. Planetary Gearbox Dynamic Model
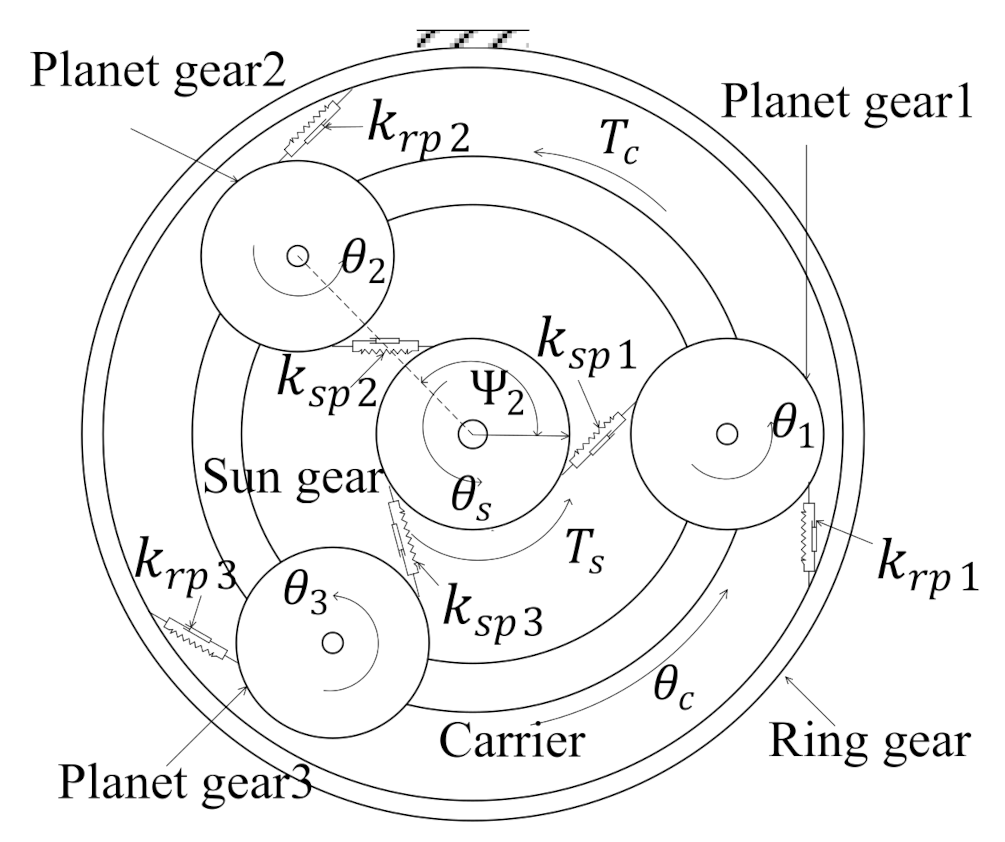
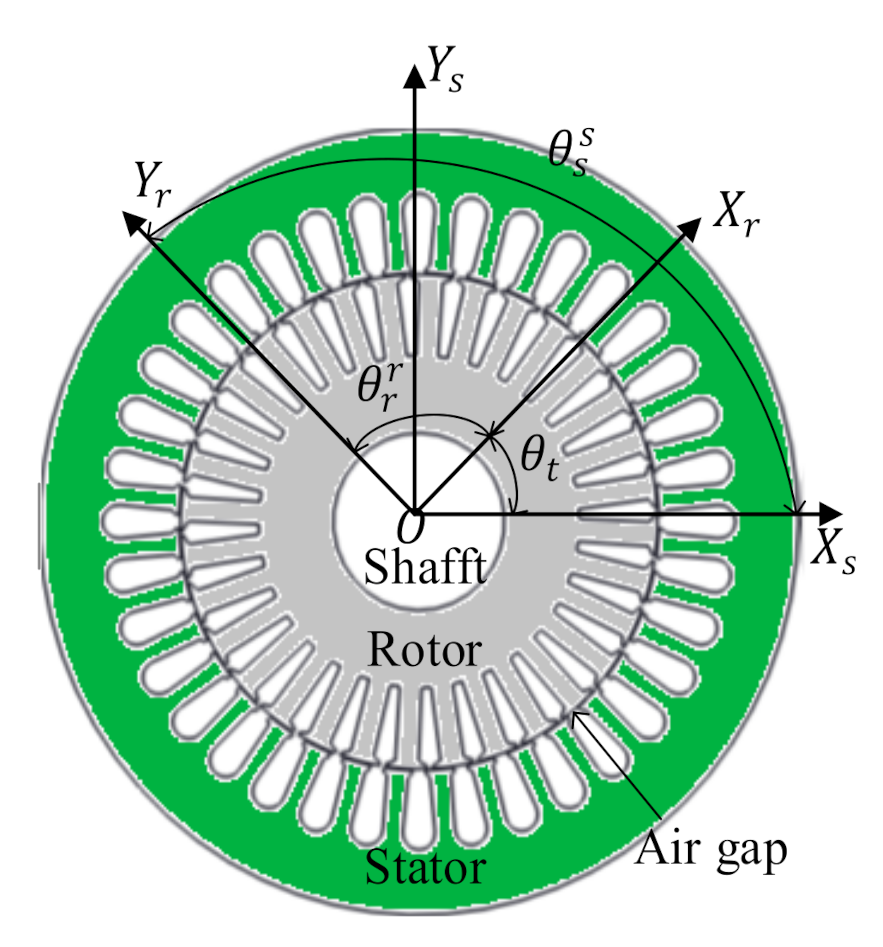
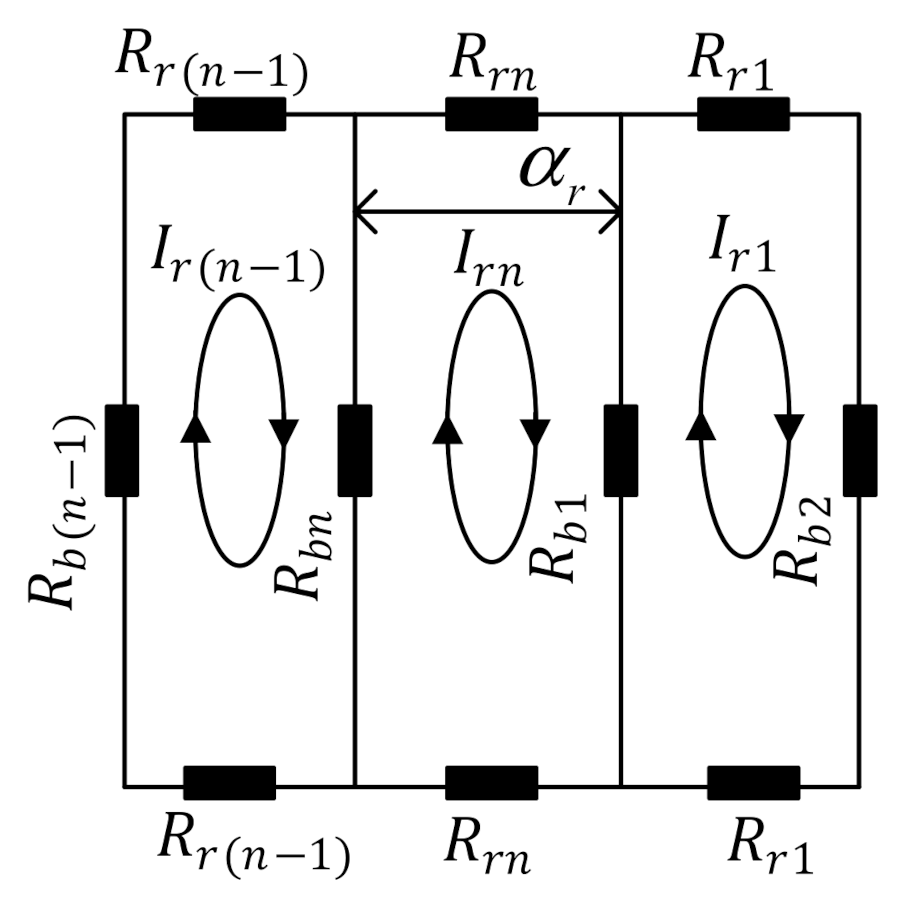
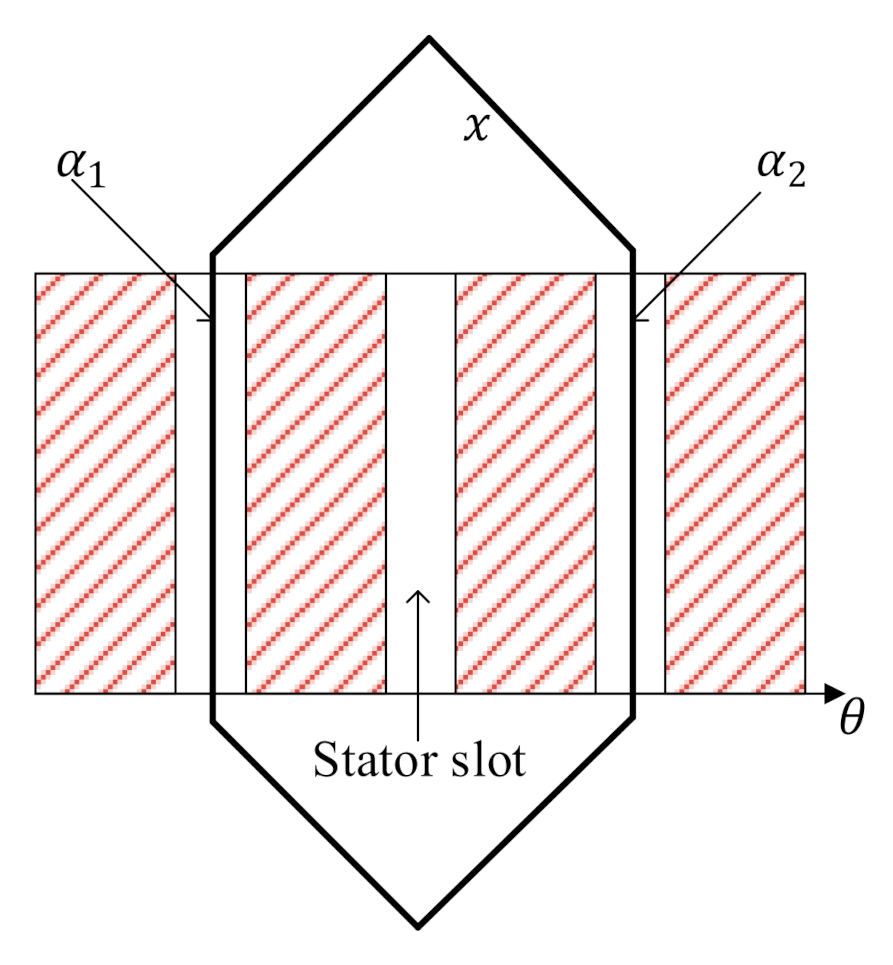
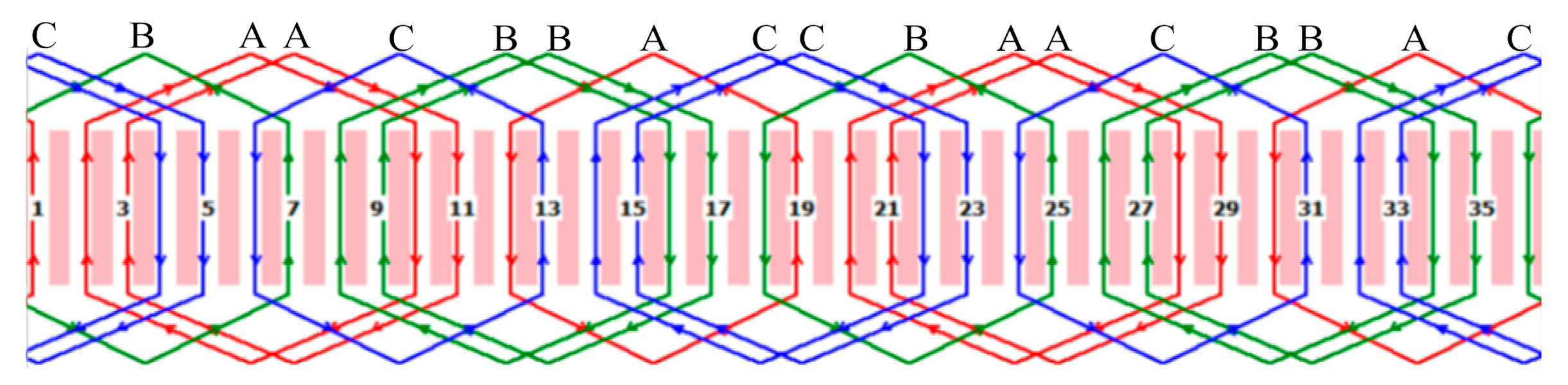
2.2. Stator Current Modeling
3. Stator Current Simulation Analysis
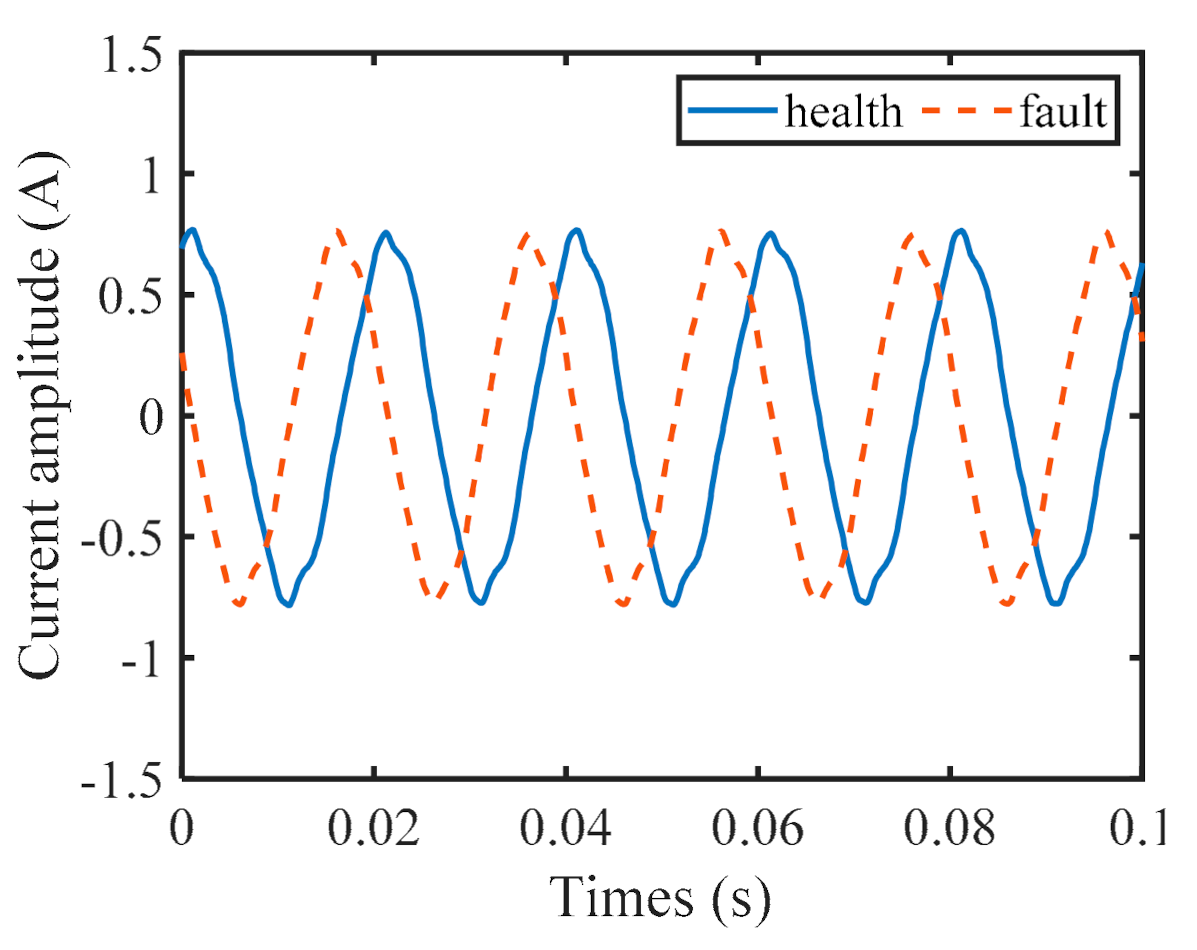
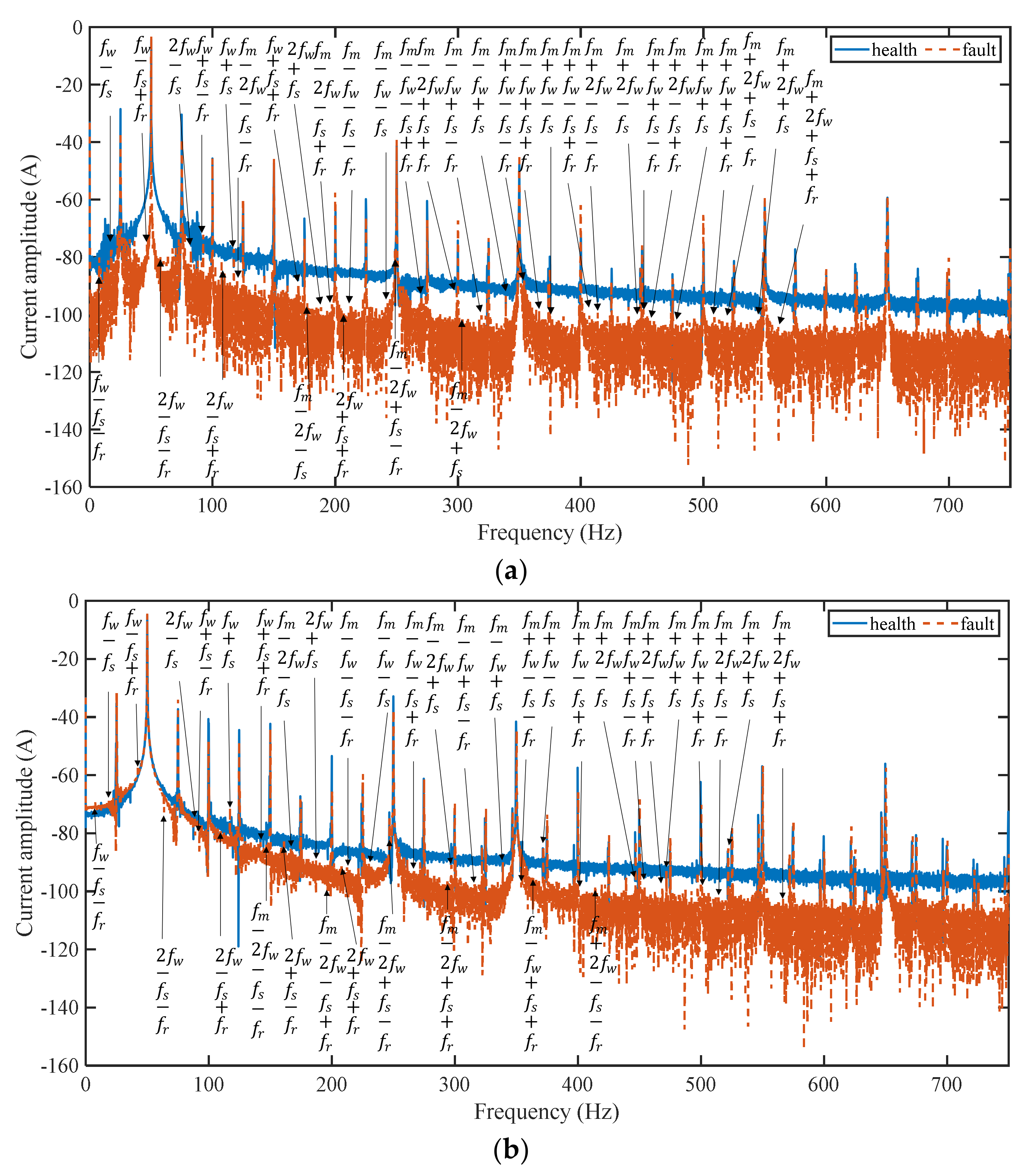
3.1. Stator Three-Phase Current
3.2. Stator Winding Current for Sun Gear Failure
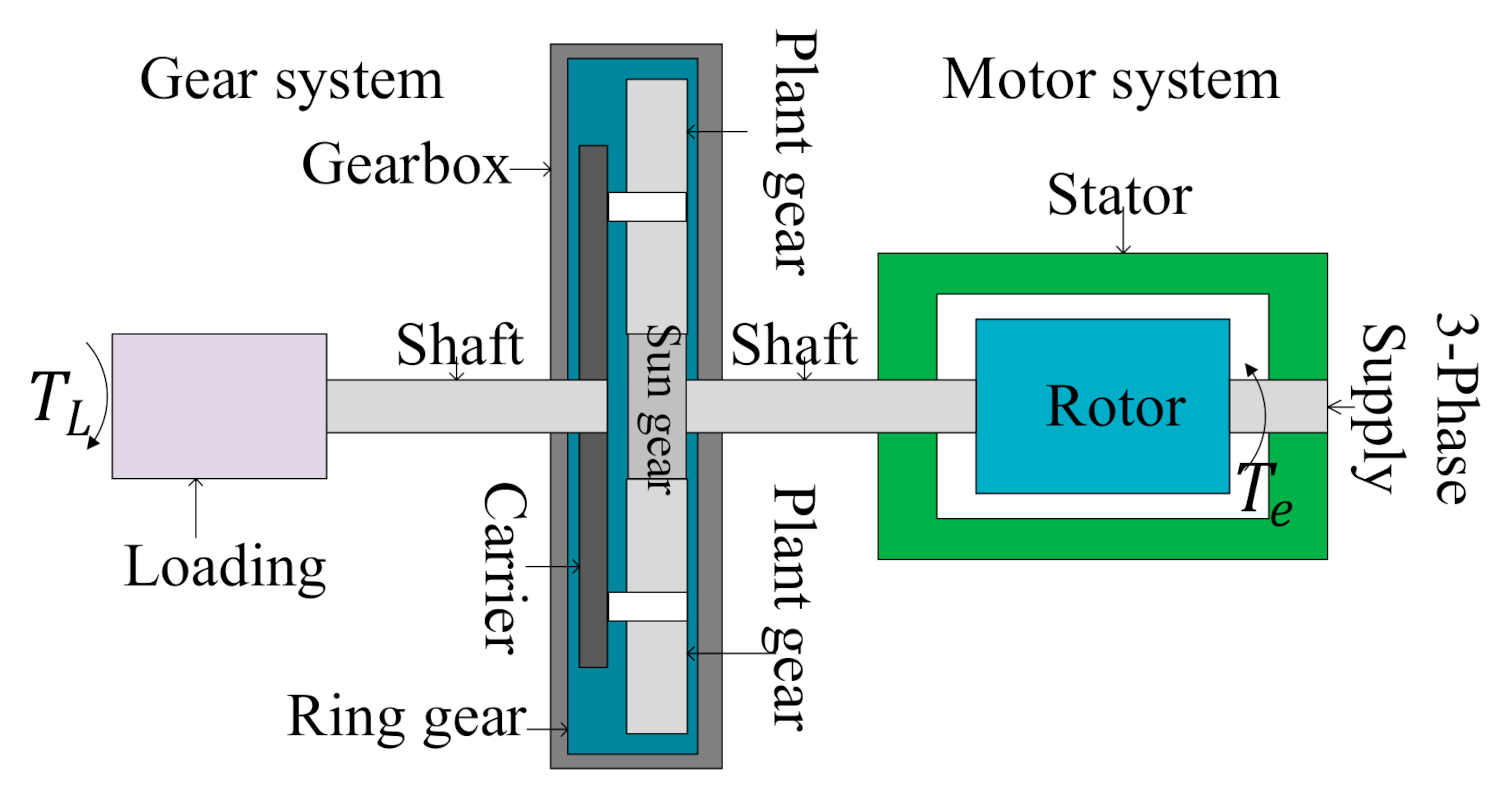
4. Experimental Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, Q.; Wang, T.; Ding, Z.; Xu, X.; Chu, F. Magnetic Equivalent Modeling of Stator Currents for Localized Fault Detection of Planetary Gearboxes Coupled to Electric Motors. IEEE Trans. Ind. Electron. 2020, 68, 2575–2586. [Google Scholar] [CrossRef]
- Toma, S.; Capocchi, L.; Capolino, G.A. Wound-Rotor Induction Generator Inter-Turn Short-Circuits Diagnosis Using a New Digital Neural Network. IEEE Trans. Ind. Electron. 2013, 60, 4043–4052. [Google Scholar] [CrossRef] [Green Version]
- Leite, D.F.; Hell, M.B.; Costa, P.; Gomide, F. Real-Time Fault Diagnosis of Nonlinear Systems. Nonlinear Anal. Theory Methods Appl. 2009, 71, e2665–e2673. [Google Scholar] [CrossRef]
- Touti, W.; Salah, M.; Bacha, K.; Amirat, Y.; Chaari, A.; Benbouzid, M. An Improved Electromechanical Spectral Signature for Monitoring Gear-Based Systems Driven by an Induction Machine. Appl. Acoust. 2018, 141, 198–207. [Google Scholar] [CrossRef]
- Singh, A.; Parey, A. Gearbox Fault Diagnosis under Fluctuating Load Conditions with Independent Angular Re-Sampling Technique, Continuous Wavelet Transform and Multilayer Perceptron Neural Network. IET Sci. Meas. Technol. 2017, 11, 220–225. [Google Scholar] [CrossRef]
- Zhang, R.; Gu, F.; Mansaf, H.; Wang, T.; Ball, A.D. Gear Wear Monitoring by Modulation Signal Bispectrum Based on Motor Current Signal Analysis. Mech. Syst. Signal Process. 2017, 94, 202–213. [Google Scholar] [CrossRef]
- Gligorijevic, J.; Gajic, D.; Brkovic, A.; Savic-Gajic, I.; Gennaro, S.D. Online Condition Monitoring of Bearings to Support Total Productive Maintenance in the Packaging Materials Industry. Sensors 2016, 16, 316. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part II: Fault Diagnosis With Knowledge-Based and Hybrid/Active Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- Ottewill, J.R.; Ruszczyk, A.; Broda, D. Monitoring Tooth Profile Faults in Epicyclic Gearboxes Using Synchronously Averaged Motor Currents: Mathematical Modeling and Experimental Validation. Mech. Syst. Signal Process. 2017, 84, 78–99. [Google Scholar] [CrossRef]
- Capolino, G.A.; Far, Z.D.; Henao, H. Modeling and Simulation of Planetary Gearbox Effects on a Wound Rotor Induction Machine. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Hangzhou, China, 28–31 May 2012. [Google Scholar]
- Feki, N.; Clerc, G.; Velex, P. An Integrated Electro-Mechanical Model of Motor-Gear Units-Applications to Tooth Fault Detection by Electric Measurements. Mech. Syst. Signal Process. 2012, 29, 377–390. [Google Scholar] [CrossRef]
- Kia, S.H.; Henao, H.; Capolino, G.A. A Modeling Approach for Gearbox Monitoring Using Stator Current Signature in Induction Machines. In Proceedings of the Industry Applications Society Annual Meeting, IAS’08, Edmonton, AB, Canada, 5–9 October 2008. [Google Scholar]
- Feki, N.; Clerc, G.; Velex, P. Gear and Motor Fault Modelling and Detection Based on Motor Current Analysis. Electr. Power Syst. Res. 2013, 95, 28–37. [Google Scholar] [CrossRef]
- Cameron, J.R.; Thomson, W.T.; Dow, A.B. Vibration and Current Monitoring for Detecting Airgap Eccentricity in Large Induction Motors. IEE Proc. B Electr. Power Appl. 1986, 133, 155–163. [Google Scholar] [CrossRef]
- Dorrell, D.G.; Thomson, W.T.; Roach, S. Analysis of Airgap Flux, Current, and Vibration Signals as a Function of the Combination of Static and Dynamic Airgap Eccentricity in 3-Phase Induction Motors. IEEE Trans. Ind. Appl. 1995, 1, 24–34. [Google Scholar]
- Schoen, R.R.; Habetler, T.G.; Kamran, F.; Bartfield, R.G. Motor Bearing Damage Detection Using Stator Current Monitoring. IEEE Trans. Ind. Appl. 1995, 31, 1274–1279. [Google Scholar] [CrossRef]
- Nandi, S.; Ilamparithi, T.C.; Lee, S.B.; Hyun, D. Detection of Eccentricity Faults in Induction Machines Based on Nameplate Parameters. IEEE Trans. Ind. Electron. 2011, 58, 1673–1683. [Google Scholar] [CrossRef]
- Chen, X.; Feng, Z. Time-Frequency Space Vector Modulus Analysis of Motor Current for Planetary Gearbox Fault Diagnosis under Variable Speed Conditions. Mech. Syst. Signal Process. 2019, 121, 636–654. [Google Scholar] [CrossRef]
- Blodt, M.; Faucher, J.; Dagues, B.; Chabert, M. Mechanical Load Fault Detection in Induction Motors by Stator Current Time-Frequency Analysis. In Proceedings of the IEEE International Conference on Electric Machines & Drives, San Antonio, TX, USA, 15–18 May 2005. [Google Scholar]
- Kia, S.H.; Henao, H.; Capolino, G.A. Analytical and Experimental Study of Gearbox Mechanical Effect on the Induction Machine Stator Current Signature. IEEE Trans. Ind. Appl. 2009, 45, 1405–1415. [Google Scholar] [CrossRef]
- He, Y.-L.; Deng, W.-Q.; Tang, G.-J.; Sheng, X.-L.; Wan, S.-T. Impact of Different Static Air-Gap Eccentricity Forms on Rotor UMP of Turbogenerator. Math. Probl. Eng. 2016, 2016, 5284815. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef] [Green Version]
- Kahraman, A. Natural Modes of Planetary Gear Trains. J. Sound Vib. 1994, 173, 125–130. [Google Scholar] [CrossRef]
- Balan, A. Theoretical and Experimental Investigations on Radial Electromagnetic Forces in Relation to Vibration Problems of Induction Machines. Ph.D. Thesis, The University of Saskatchewan, Saskatoon, SK, Canada, 1997. [Google Scholar]
- Lipo, T.A. Introduction to AC Machine Design; Wiley-IEEE Press: Hoboken, NJ, USA, 2004. [Google Scholar]
- Bao, X.; Cheng, Z.; Wang, H. Monitoring Magnetic Field of Stator Yoke to Detect Eccentricity Fault in Induction Motor. In Proceedings of the Industrial Electronics & Applications, Kota Kinabalu, Malaysia, 20–22 November 2016. [Google Scholar]
- Joksimovic, G.; Djurovic, M.; Penman, J. Cage Rotor MMF: Winding Function Approach. Power Eng. Rev. IEEE 2001, 21, 64–66. [Google Scholar] [CrossRef]
- IEEE. Electric Machinery; Institute of Electrical and Electronic Engineers: Minneapolis, MN, USA, 1995. [Google Scholar]
- Liang, X.; Zuo, M.J.; Hoseini, M.R. Vibration Signal Modeling of a Planetary Gear Set for Tooth Crack Detection. Eng. Fail. Anal. 2015, 48, 185–200. [Google Scholar] [CrossRef]
- Djeziri, M.A.; Nguyen, L.; Benmoussa, S.; Msirdi, N. Fault Prognosis Based on Physical and Stochastic Models. In Proceedings of the Control Conference, Seattle, WA, USA, 26–28 July 2017. [Google Scholar]







| Parameters | Ring Gear | Sun Gear | Planet Gear |
|---|---|---|---|
| Number of teeth | 143 | 63 | 16 |
| Module (mm) | 2.25 | ||
| Pressure angle | 20 |
| Parameters | Stator | Rotor |
|---|---|---|
| Number of slots | 36 | 32 |
| Number of turns | 31 | 1 |
| Winding type | Single cross | Squirrel cage |
| Rated voltage (U/v) | 220 | |
| Inner diameter () | 98 | |
| Core length (L/mm) | 135 | |
| Number of poles () | 2 | |
| Rated slip () | 0.02 | |
| Air gap length () | 0.3 | |
| PF | 0.83 | |
| Phase Number | Mechanical Angle (Left/Right) | ||
|---|---|---|---|
| A | |||
| B | |||
| C | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Liu, G.; Liang, X. Research on the Electromagnetic Conversion Method of Stator Current for Local Fault Detection of a Planetary Gearbox. Machines 2021, 9, 277. https://doi.org/10.3390/machines9110277
Xu X, Liu G, Liang X. Research on the Electromagnetic Conversion Method of Stator Current for Local Fault Detection of a Planetary Gearbox. Machines. 2021; 9(11):277. https://doi.org/10.3390/machines9110277
Chicago/Turabian StyleXu, Xiangyang, Guanrui Liu, and Xihui Liang. 2021. "Research on the Electromagnetic Conversion Method of Stator Current for Local Fault Detection of a Planetary Gearbox" Machines 9, no. 11: 277. https://doi.org/10.3390/machines9110277
APA StyleXu, X., Liu, G., & Liang, X. (2021). Research on the Electromagnetic Conversion Method of Stator Current for Local Fault Detection of a Planetary Gearbox. Machines, 9(11), 277. https://doi.org/10.3390/machines9110277







