Abstract
Parallel robots with configurable platforms are a class of robots in which the end-effector has an inner mobility, so that its overall shape can be reconfigured: in most cases, the end-effector is thus a closed-loop kinematic chain composed of rigid links. These robots have a greater flexibility in their motion and control with respect to rigid-platform parallel architectures, but their kinematics is more challenging to analyze. In our work, we consider n-RRR planar configurable robots, in which the end-effector is a chain composed of n links and revolute joints, and is controlled by n rotary actuators located on the base of the mechanism. In particular, we study the geometrical design of such robots and their direct and inverse kinematics for , and ; we employ the bilateration method, which can simplify the kinematic analysis and allows us to generalize the approach and the results obtained for the 3-RRR mechanism to n-RRR robots (with ). Then, we study the singularity configurations of these robot architectures. Finally, we present the results from experimental tests that have been performed on a 5–RRR robot prototype.
1. Introduction
A parallel robot with configurable platform (PRCP) is a special parallel mechanism in which the end-effector (EE) has internal Degrees-of-Freedom (DoFs). In most previous works, this is achieved by designing the EE as a closed-loop kinematic chain that can be reconfigured during the motion according to users’ needs. In this work, we will focus on planar PRCPs having only revolute joints (in the rest of this work, R denotes a revolute joint and R an actuated revolute joint; RR...R denotes a chain of revolute joints connected by rigid links, where the number of letters indicates the number of joints).
One of the first examples of PRCPs was in [1], where the authors studied a planar 4-DoF gripper and optimized its design according to suitable kinematic indexes. Later, this concept was extended to 3-DoF spatial mechanisms having translational [2] or spherical [3] motion. In [4], the concept of PRCPs was extended to a larger class of architectures and a general screw-theoretic framework was presented to compute the mobility of these mechanisms. In [5], a 4-DoF PRCP, designed for multi-finger gripping (with two contact points), was studied in terms of its kinematics and singularity analysis. Several robots with a foldable platform were designed by Dahmouche et al., having either 4- [6], 7- [7] or 8-DoFs motion [8]; this way, the EE was provided with cutting [6] or grasping [7,8] functionality. For these robots, screw-theoretical analyses of the wrenches that can be applied to the environment by the EE were presented in [8,9]. In [10], it was shown that a kinematotropic linkage can also be used as the EE of a PRCP. More recently, a systematic design approach was presented in [11] for the development of PRCPs with 4- to 6-DoFs having one internal DoF in the EE; also, a general synthesis method for PRCPs (some of which have closed-loop EEs) was presented in [12].
A number of architectures with an EE having an internal DoF were explored by Pierrot et al., who studied several 4-DoFs spatial PRCPs based on the Delta robot, the first of which was the H4 robot presented in [13]. Later, a control system for the robot was introduced in [14], while in [15], the authors designed a robot prototype; the dynamic model of H4 was presented by Choi et al. in [16]. Other robot architectures derived from the H4, with an articulated EE having internal DoFs, are I4 [17] and Par4 [18,19]; an architecture for a robot conceptually similar to Par4, having 4 DoFs and without parasitic motions, was also presented in [20]. A general approach for the type synthesis of similar mechanisms was later presented in [21]. Another Delta-inspired PRCP was presented in [22]: the robot has a six-bar closed-loop EE and is capable of performing Schönflies motions.
Lambert et al. [23] studied “PentaG”, a 5-DoFs spatial robot with two EEs able to grasp objects and perform Schönflies motion; its architecture was later generalized to a 7-DoFs haptic interface with redundant actuation [24]. Two spatial, 3-DoF PRCPs with a similar concept were presented in [25]. In [26], Lambert and Herder presented a literature review on PRCPs and proposed general results on the singularity and mobility analysis of this class of robots; later, in [27], a general method was presented to derive the complete Jacobians of PRCPs through screw theory. An extension of the configurable-EE concept to cable-driven systems was also presented in [28].
PRCPs’ predicted applications are where extra DoFs beyond those needed to position and orient the EE are required to interact with the environment: for instance, PRCPs can be employed when the robot has to grasp objects [1,2,3,6,7,8]. An alternative solution would be mounting a gripper on the EE of a conventional parallel robot, but the gripper and its motor increase the moving inertia of the EE, which reduces the dynamic performance of the robot. PRCPs, instead, have all the motors located on the robot base and their configurable EE can provide an integrated grasping functionality.
PRCPs were also applied in the design of haptic interfaces where the operator can interact with the robot through several contact points on the EE: this design can lead to a smoother experience of the virtual environment with respect to standard haptic systems [5]. Other proposed applications for PRCPs are for robot surgery such as laparoscopy [6] and for rehabilitation systems [29].
The design and control of parallel robots require solving their Direct and Inverse Kinematic Problem (DKP and IKP, respectively), the former of which can be especially complex, and the more so for robots with many DoFs such as PRCPs [4]. Generally, authors aim at developing analytical approaches: these, albeit slower than numerical methods, provide insight into the number of possible solutions for the DKP and IKP. For planar mechanisms, the usual method is to write loop-closure equations, which can be reduced to a system of polynomial equations (e.g., by using the tangent half-angle substitution). This system of equations can then be reduced to a single characteristic polynomial in one variable, through algebraic manipulation. For example, this method is applied in [30] to a 3-RRR, 3-DoF planar robot; later, these results were extended to 3-DoF planar robots with three general, independent, actuated kinematic chains [31].
An alternative method that is suited to solve the DKP for planar mechanisms is bilateration: here, the goal is to obtain the coordinates of points in the plane from their relative distances (similarly, one speaks of trilateration when considering sets of points in three dimensions). Since this approach is entirely distance-based, it is independent from the choice of the reference frame and does not require variable eliminations nor tangent-half-angle substitutions (unlike conventional analytical methods), which generally lead to numerical instabilities; also, it can be written in a compact form where all quantities have the same unit of length. While the concept of bilateration is old [32,33], its application to robotics is relatively recent. A general review of these methods is in [34,35]. In [36,37], the authors show how to apply bilateration for solving the DKP of planar mechanisms with rigid EE and revolute joints, similar to the ones considered in this work. Bilateration was also applied in several other sectors; we mention the localization of mobile robots [38] and cable-based robot measuring systems [39]. For a review of the state of the art on Euclidean-distance geometry problems and algorithms, we refer the reader to [40].
In the analysis of parallel robots, another necessary step is to identify singular configurations, where the EE has DoFs that cannot be controlled [41]: it is well known that singularities may disrupt the correct operation of robot mechanisms, thus their identification is fundamental for robot control. Early work on the topic is by Gosselin and Angeles [42], who proposed a general classification of the singularities based on the Jacobian matrices of the direct and inverse kinematics. Later, other works on the classification of parallel singularities [43,44] showed the necessity of taking into account also the kinematics of passive joints. In [45], the author proposed an application of Invariant Theory for the purpose of singularity analysis and found conditions for singularity based on Grassmann–Cayley algebra. Regarding the singularities of PRCPs, the first study was in [46] for the H4 and I4 families of architectures; later, in [47] the authors found the full set of singular configurations for the H4 from the Jacobian matrix. An analysis of the singularities for the H4 robot through screw theory was presented in [48].
In this work, we consider planar PRCPs, where the EE is an n-R closed-loop and n RRR chains connect the EE to the base. The paper is organized as follows. We begin with a general introduction to bilateration in Section 2; this method is then applied in Section 3 to the solution of the DKP and the IKP for the PRCPs at hand. Furthermore, we show how to derive the singularity configurations for the inverse and direct kinematics in Section 4. In Section 5, we show the results both from a numerical simulation and a series of experimental tests on a prototype. The tests will also show the behavior of the mechanism close to a singularity configuration. Finally, in Section 6 we discuss our conclusions and suggest possible developments for our work.
The goal of our work is both to apply the bilateration method to the kinematic analysis of a general class of planar manipulators, highlighting its advantages in terms of ease of analysis, and to lay foundational work in the development of a particular 5-DoF PRCP by solving its kinematics and identifying its singular configurations. The PRCP at hand, shown in Section 5, is at present merely a prototype, but it could be usefully developed into a flexible robotic platform capable of grasping, moving and orienting objects in the plane.
This manuscript develops a previous work first presented in [49], by proving several conjectures therein contained (Section 3.2) and by adding the analysis of the singular configurations for the class of the considered PRCPs (Section 4); the behavior of the robot around a singular configuration is also presented in the multimedia attachment (Section 5).
2. Bilateration
Bilateration is a method to find the coordinates of a point , given its distances from two other points and ; the positions , with respect to the fixed coordinate frame are assumed to be known.
For convenience, we define the squared distance between any two points and . The Cayley–Menger bideterminant [34] of two sets of n points and is then defined as the scalar number
For conciseness, we abbreviate the bideterminant of a set with respect to itself as . We can now define the transformation matrix of three points , and as
In Equation (2), is the signed area of triangle , thus
- if points , and are ordered in counterclockwise sense (see Figure 1a), the area is positive;
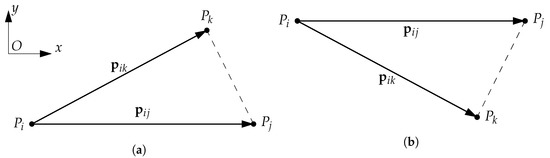 Figure 1. Two possible solutions for bilateration with three points Pi, Pj and Pk on a plane ((a): solution with points in counterclockwise order, (b): solution in clockwise order).
Figure 1. Two possible solutions for bilateration with three points Pi, Pj and Pk on a plane ((a): solution with points in counterclockwise order, (b): solution in clockwise order). - if points , and are ordered in clockwise sense (see Figure 1b), the area is negative.
Defining and , one can prove [32] that
and thus is found from , and the distances between the three points. In the following, we will use the shorthand notation to indicate the procedure of finding point from and , by using the known point distances and Equation (3). Notably, Equations (1)–(3) are independent of the choice of the coordinate frame. Since there are two possible orderings of the points (clockwise or counterclockwise, see Figure 1), bilateration generally provides two possible solutions.
3. Kinematic Analysis
The schematic of a general n-RRR robot is shown in Figure 2a; two example cases are reported for completeness in Appendix A. The centers of the n actuated R joints on the fixed base are denoted as , , and their position vectors are with respect to the base coordinate frame ; the actuated joint variables are angles . The centers of the mobile R joints are denoted as , , and their coordinates are . In the following, all links and all joints are modeled as perfectly rigid; the readers interested in joint-flexibility modeling are referred, for instance, to [50]. The (constant) link lengths are defined as
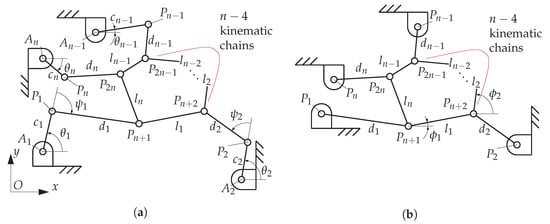
Figure 2.
(a) schematic of the n-RRR robot; (b) the corresponding n-RR structure, obtained by fixing the actuated angles θi. Angles ψi and φi are represented only for the first two RRR chains, for simplicity.
From Grübler’s equation, it can be seen that the PRCP at hand has DoFs; the vector of actuated joint coordinates also has n components, thus the robot is fully actuated. The EE pose can be defined by an n-dimensional vector of independent variables; we choose vector , where angles ’s are those formed by the links of length with the horizontal axis (see Figure 2b). Variables and define the position of (a point of) the EE, whereas variables ’s define the EE shape.
3.1. Inverse Displacement Analysis
For the IKP, one seeks to find the input vector given the desired output pose . Solving the IKP is straightforward, as is usually the case for parallel manipulators. From the coordinates of a point on the EE, one can find the next point on the kinematic chain as
Therefore, since , and are known from , one can find the position of point . Similarly, one can find point from and ; repeatedly applying Equation (5) one finds all points on the kinematic chain up to and including . Finally, we find point from bilateration as (the distances between points , and are all known). Since the actual configuration of the EE is known, we can disregard the spurious solutions out of the two ones for provided by Equations (2) and (3).
At this point, since all ’s are known (for ), the IKP reduces to the well-known problem of the assembly of n RRR dyads, each corresponding to an RRR chain. From the lengths , one finds the coordinates of by using : then, the actuated joint angle of each RRR chain is given by . Applying this equation repeatedly, one may find all the n unknown in vector . Since bilateration provides two positions for , this shows that there are, in the general case, two real and distinct solutions for each RRR chain from the base to the EE. It can be shown that this holds if and only if . Geometrically, this condition defines an annulus comprised between the circles of radii and centered in . If is on the boundary of the annulus, there is one solution for the bilateration between , and ; if is outside the annulus, there are no solutions. In conclusion, the IKP for an n-RRR robot can thus have up to solutions.
3.2. Direct Displacement Analysis
The DKP is more complex than the IKP. In this case, the vector is known, and we seek to derive the EE pose, defined by vector . We will first present a method to analyze a general n–RRR robot (see Figure 2a) by means of bilateration; then, as an example, we will show an application to a 5-RRR robot.
From and the lengths of links , the position of points , is directly found as
We can now simplify the mechanism analysis, by defining an equivalent rigid structure (see Figure 2b) where all links are removed and points are fixed on the ground link: one can see that the structure obtained has indeed DoFs. Solving the DKP is then equivalent to finding points , from the known distances and ; this problem appears suited to be analyzed by means of bilateration.
We start by choosing the unknown variable that we seek to find; at the end of the analysis, we will obtain a single equation in this unknown. Since bilateration is a distance-based method, we could choose the distance between any two points as the unknown, except obviously the fixed distances between points connected by links. Without loss of generality, we choose .
We then choose a bilateration sequence: this is the sequence of n bilateration steps for finding all points on the EE. The simplest choice for this sequence is , namely: from the coordinates of and , we find the coordinates of , then the coordinates of from the points already found, and so on, where all coordinates are written as functions of the unknown . See Figure 3a, where a 5-RR structure is taken as an example. Since each bilateration step provides two solutions, in the DKP we will retain only those which lead to a feasible solution for the complete mechanism.
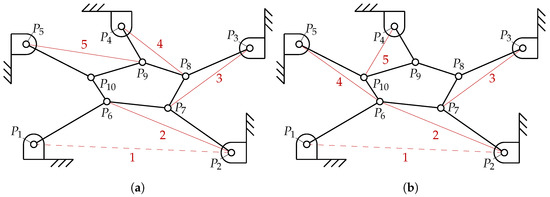
Figure 3.
(a) a bilateration approach for solving the Direct Kinematic Problem (DKP) of a 5-RR structure; (b) a second possible approach. Each bilateration step is denoted in red.
Finally, we write the closure condition, which depends on the remaining link length not used in the bilateration sequence; with the choices we have made so far, this becomes
The final expression for will be an algebraic function in the unknown , containing a number of nested radicals. These can be removed through well-known algebraic techniques, such as those in MATLAB’s Symbolic Math Toolbox; however, the greater the number of RR chains, the more cumbersome the expression for becomes. Notably, as remarked in [36], removing the radicals “is actually the only costly step in the whole process” and can be avoided if a numerical solution is sufficient. Finally, one obtains a univariate polynomial in that can be solved either through algebraic or numerical methods: each real and positive root corresponds to a value of that can be substituted in the expressions for points , to obtain a potential pose for the EE (and thus a solution for the DKP).
As an example, the method seen above will be now applied to a 5–RRR PRCP. We simplify the mechanism, obtaining a 5–RR structure (Figure 3a), by using Equation (6). Then, we define the three parameters for the bilateration:
- (a)
- unknown variable:
- (b)
- bilateration sequence:
- (c)
- closure condition:
The bilateration sequence is shown in Figure 3a.
We have developed a script in MATLAB to solve the DKP for a number of n-RRR robot architectures (with ) by removing all radicals in the equation for the closure condition by an iterative algorithm. In the following, we report our observations.
- The method lends itself easily to generalization for more complex architectures: however, as one may expect, the computational complexity of solving the DKP grows with the number of RRR chains. This is mostly due to the algebraic manipulations required to remove all radicals in the closure equation; these operations are well beyond human feasibility even for and have thus required the use of a symbolic analysis package.
- The time and resources needed to tackle the DKP are dependent on the choice of bilateration sequence and can be greatly reduced through a careful choice. Considering again the example in Figure 3, it was found that using the sequence (see Figure 3b) instead of the one previously indicated in point (b) the time required to obtain a solution is much shorter. The script was run with MATLAB R2019a and an Intel Core processor i7-8700 CPU at 3.20: with this setup, the DKP was solved in two days with the first choice for the bilateration sequence and in ten minutes with the second one. Our empirical observation is that the bilateration sequence is optimized by taking approximately the same number of steps in clockwise sense (such as in the last sequence, see Figure 3b) and in counterclockwise sense (such as ): under this guideline, there are fewer nested radicals in the final closure conditions, which then becomes easier to simplify.
- We conjecture that, for an n-RRR robot, the characteristic univariate polynomial has degree , namely 12, 28, 60 and 124 for, respectively, , 4, 5 and 6.
We verified our conjectures for , by numerically verifying, for a number of generic architectures, that all the (complex) solutions of the final polynomial equation satisfy the closure loop equations of the original mechanism. We also verified that our conjecture is true for . However, in this case, due to the increasing computational cost needed to obtain a univariate polynomial, we preferred to compute all 252 solutions of the problem by a purely numerical approach, such as homotopy continuation, through the software Bertini [51]. Moreover, we found special architectures (in terms of link lengths and positions of the fixed joints) for the 3-, 4- and 5-RR structures such that the DKP has 12, 28 and 60 real and distinct solutions, respectively. Note that the rigid-EE, 3-DoF linkage in [30] can be seen as a special case of the n-RRR architectures considered here for . In [30], it was shown that said linkage can have up to six distinct solutions. In our analysis, for generality, we also include solutions where the EE can “flip” into its symmetric form (which requires the EE to rotate outside the plane of motion): this doubles the number of solutions. It is also possible to analyze the DKP through bilateration without this assumption.
The parameters for the special architectures mentioned above are reported in Table 1, Table 2 and Table 3 and the corresponding solutions are in Table 4, Table 5 and Table 6. These parameters were found by means of a genetic-algorithm search (similarly to the approach used in [52,53] for a spatial robot), using the MATLAB routine ga with a population of 200 individuals and a MATLAB interface to Bertini [54]: for each n, the algorithm iteratively searches for the architecture parameters that lead to the maximum number of real and distinct solutions. For each case, the algorithm converges within 18 generations (or fewer) to an architecture that has as many real and distinct solutions as the characteristic univariate polynomial degree.

Table 1.
Coordinates of fixed points () and link lengths for a 3-RR structure whose DKP has 12 real and distinct solutions. Without loss of generality, points and are taken respectively at the coordinate-system origin and on the x axis; the other values in the table are found by optimization.

Table 2.
Architecture parameters for a 4-RR structure having 28 real and distinct assembly configurations (compare with Table 1).

Table 3.
Architecture parameters for a 5-RR structure having 60 real and distinct assembly configurations (compare with Table 1).

Table 4.
All 12 possible solutions of the DKP for the 3-RR architecture in Table 1. Each solution is defined by the value of the unknown in the characteristic polynomial; from this value, the coordinates of points () are found through bilateration and the pose is derived.

Table 5.
All 28 possible solutions of the DKP for the 4-RR architecture in Table 2.

Table 6.
All 60 possible solutions of the DKP for the 5-RR architecture in Table 3. Notice that some solutions are very close in terms of (and are thus indistinguishable from each other without providing more significant digits that those which can be displayed in the available space), yet lead to clearly different poses.
4. Singularity Analysis
4.1. General Classification
With the definitions of the joint vector and the pose vector given in Section 3, the kinematic constraints of the linkage can be written in the general form:
assuming that all constraints are holonomic, that is, they can be expressed in configuration form.
Differentiating Equation (8) with respect to time, we obtain a relationship between the input joint rates and the EE velocity, as follows:
where and are the Jacobian matrices of the direct and of the inverse kinematics, respectively. Since we only consider fully-actuated robots, where the number of DoFs is equal to the number of actuators, the Jacobians are square matrices and thus they are rank deficient if and only if their determinant is zero, in which case we say that the parallel manipulator is at a singular configuration. Depending on which matrix is rank deficient, there can be different types of singularities. We refer to the standard classification in [42] that distinguishes between three types of singularities. Note also that more refined and complete classifications, which take into account the kinematics of passive joints, can be found in [43,44]. The three types of singularities from [42] are defined in the following.
- (1)
- A type-1 kinematic singularity occurs when . In this case, the null space of is not empty, thus there exists some nonzero that yields in Equation (9). Therefore, infinitesimal motions of the EE along certain directions cannot be accomplished with finite joint rates and the manipulator loses one or more DoFs. Type-1 kinematic singularities usually occur at the workspace boundary or where different branches of the IKP converge [42].
- (2)
- A type-2 kinematic singularity occurs when . In this case, there exist some nonzero that yields . The EE can have infinitesimal motions while all actuators are locked and the EE gains one or more uncontrolled DoFs. Type-2 kinematic singularities usually occur where different branches of the DKP meet.
- (3)
- A type-3 singularity occurs when both and are singular. Generally, this type of singularity can only occur for manipulators with special architectures. At these configurations, Equation (8) degenerates to the identity . The EE can have infinitesimal motions while the actuators are locked and it can also remain stationary while the actuators undergo infinitesimal motions.
4.2. Definition of the Jacobian Matrices
To define the Jacobian matrices and for the PRCPs at hand, we write the loop equation for each RRR chain from the base to the EE:
Differentiating Equation (10) with respect to time (and considering that vectors and have fixed lengths), one has
where is the vector orthogonal to the plane of motion, and we have used , since points are fixed. By dot-multiplying by we obtain an equation without the passive joint angles :
using known properties of the triple vector product.
In a similar fashion, one can also find the velocity of point by writing the closure equation for the first links on the EE kinematic chain (starting from point ) and differentiating with respect to time. One thus obtains from the time derivative of the pose vector as
The term at the left-hand side of Equation (14) depends on , while the terms on the right-hand side only depend on . We thus have linear relationships between the actuated joint velocities and the derivative of the EE pose, from which we can derive the first rows of matrices and . Finally, we use bilateration to find point as and differentiate with respect to time, thus obtaining as a function of ; setting
we find the last row of the Jacobian matrices. By setting the determinants of and and solving the resulting equations for the pose , we can obtain the full set of input-output singularities for the mechanisms at hand.
From Equation (14), it can be seen that the Jacobian of the inverse kinematics is, in general, a diagonal matrix for all PRCPs in the class here considered, having elements on the main diagonal. This matrix is singular if and only if any of these elements is zero; ignoring degenerate cases where one link has zero length, we see that this corresponds to a configuration where two links in a RRR chain from the base to the EE are aligned, either in a stretched-out or folded-back configuration, as shown in Figure 4. These configurations are therefore type-1 kinematic singularities.
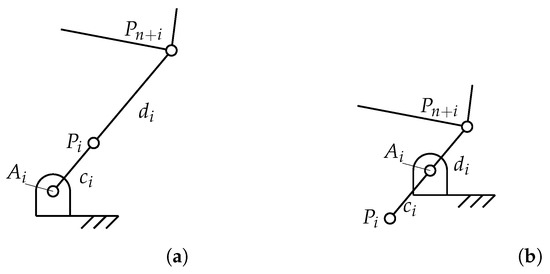
Figure 4.
The two configurations of a type-1 singularity for a generic n-RR structure: (a) stretched-out; (b) folded-back.
Analyzing type-2 kinematic singularities, on the other hand, is more difficult: we will consider the 5–RRR robot as an example.
4.3. Jacobian Matrices of a 5-RRR Pcrp
In this case, we define the joint and pose vectors as and , respectively. By applying the procedure described in Section 4.2, we obtain the matrices
and
where the scalar quantities e, f and g are defined in Appendix B.
Type-1 singularities have already been found, for the most general case, in Section 4.2. Type-2 singularities for this PRCP can be found analyzing matrix . In Figure 5 we present three examples of singular configurations.
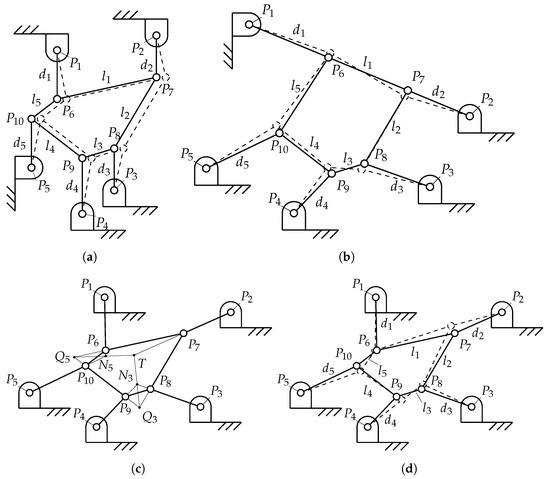
Figure 5.
Some examples of type-2 kinematic singularities of a 5-RR structure (derived from a 5-RRR mechanism): (a) a singularity occurring when all links are parallel; (b) a singularity occurring when three consecutive links are aligned; (c) a singularity configuration derived from [45]; (d) the auxiliary figure of Figure 5c. For each structure, we also show (in dashed lines) a configuration which is close to the singular one; this approximates the infinitesimal motion that the structure can have around its singularity (for Figure 5c, we added the auxiliary Figure 5d)
- (a)
- A type-2 singularity occurs when all links are parallel (Figure 5a). In this case, one can see that the first two columns of from Equation (16) are linearly dependent and thus the matrix is singular. The EE gains a uncontrolled DoF, namely, the rigid translation in the direction orthogonal to the parallel links.
- (b)
- If links , , and are aligned (Figure 5b), then and is a scalar multiple of , so that the first two rows of are linearly dependent. In this configuration, points and move perpendicularly to , while the EE undergoes small deformations. By symmetry, this singular configuration extends to the cases where the links , , or are aligned.
- (c)
- In Figure 5c we show another type of singularity, first noted by Crapo in [45] for a similar type of structure, that can also be applied in our case. For a given link on the EE, we define point , at the intersection of the lines through the links connecting to the base, and point , at the intersection of the lines through the links on the EE connected to ; also, let T be at the intersection of the lines and . If the line (through the distal link on the remaining RR chain connecting the EE to the base) also passes through point T, we have a type-2 singular configuration. Note that this includes the special case where all lines pass through the same point T.
5. Examples
A 5-RRR prototype has been developed at IRI (Institut de Robòtica i Informàtica Industrial, Barcelona, Spain) as shown in Figure 6. Its main parameters are reported in Table 7, together with the input angles for an example configuration for which we solve the DKP using the MATLAB script reported in Section 3.2.
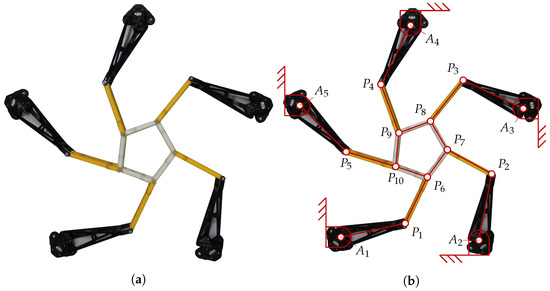
Figure 6.
(a) The 5-RRR prototype developed at IRI; (b) its corresponding schematic.

Table 7.
Coordinates of the ground joints (points ) and the corresponding input angles ; the links’ lengths are , and (for ).
From Section 3.2 we know that the characteristic polynomial can have at most distinct solutions; it is found that, for the geometric parameters in Table 7, the polynomial has six real solutions. Three of them correspond to feasible configurations, which are reported in Table 8; the other solutions are not reachable because of physical constraints, such as interference between the links or because they correspond to unfeasible values of the unknown .

Table 8.
The three real solutions of the DKP for the 5-RR prototype defined in Table 7 and the corresponding poses .
The robot was actuated by five servo units with a DC motor and integrated gear reducer (Robotis Dynamixel AX-12A). The motors have a limited rotation range of 300°, which could limit the reachable workspace; however, this was not found to be an issue for any of the motions considered in our tests. Each motor can be controlled through 1024 discrete steps by a script we developed starting from MATLAB code provided by the manufacturer. At every time-step during the motion, we define the EE pose , which is defined by five variables. Then, using the inverse kinematics formulas from Section 3.1, we calculate the vector of motor angles : these are the angles to be set for the actuators.
The prototype in Figure 6 was studied in terms of position and singularity analysis. Some experimental tests were also performed. In the multimedia attachment for this work (see video abstract) a number of possible motions are presented:
- (i)
- the EE translates and rotates while keeping a fixed configuration, like a conventional (redundantly-actuated) rigid-EE manipulator;
- (ii)
- the robot switches between two different solutions of the IKP for a given EE pose ;
- (iii)
- the robot passes through a type-1 singularity configuration (see Section 4);
- (iv)
- finally, the EE configures itself in order to grip a ball at a first position and moves it to a different position, to present a potential application of having a configurable platform. A schematic of this motion is reported for clarity in Figure 7.
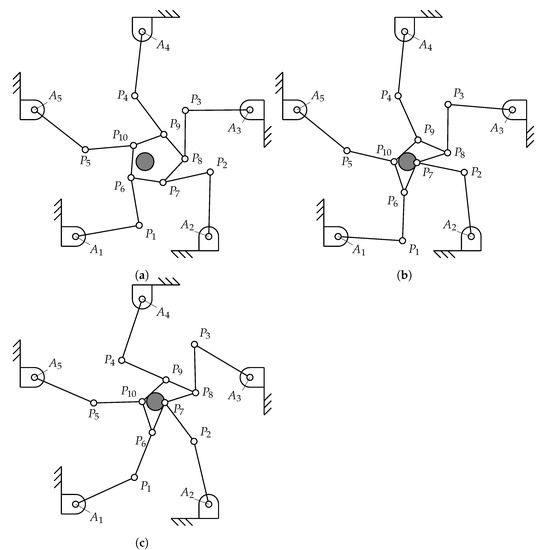 Figure 7. A schematic of a grasping motion with the prototype (see multimedia attachment): an object (in gray) is grasped by reconfiguring the EE and moved to a new pose in the plane, through three successive poses (a–c).
Figure 7. A schematic of a grasping motion with the prototype (see multimedia attachment): an object (in gray) is grasped by reconfiguring the EE and moved to a new pose in the plane, through three successive poses (a–c).
6. Conclusions
In this work, we have considered a general class of planar parallel robots having a configurable platform (PRCPs), for which we performed the position and the singularity analysis. While the inverse kinematics can be readily solved through conventional methods used for planar linkages, the direct kinematics are more challenging; we show that the bilateration method, which has a relatively recent history in robotics research, can be usefully applied to this problem. In particular, we developed a general procedure that can be applied to PRCPs of n-RRR type, having any number n of kinematic chains, and we found heuristics to reduce the solution time. Furthermore, we showed how to derive the Jacobian matrices of these robots, again through bilateration; from the Jacobians, we also showed how to find singular configurations. For an exemplifying PRCP with five kinematic chains, we showed both simulations that illustrate how to solve the direct kinematics and results from experiments performed on a prototype.
Our goals for future work in this field are:
- to prove our conjectures regarding the degree of the characteristic polynomial of the direct kinematics, namely, verifying that it is the polynomial of lowest degree for all n. Furthermore, we aim to find a general example architectures having the maximum possible number of real and distinct solutions (at least for the case );
- to obtain more general results for planar PRCPs with n kinematic chains, for instance including chains that have prismatic joints;
- to perform a statistical analysis of the time required to solve the direct kinematics, both with bilateration and through conventional analytical methods, thus showing the difference in the required computational effort;
- to find the full set of singular configurations for any number of kinematic chains, extending the work in Section 4;
- to further develop the prototype in order to apply it to practical manipulation tasks, for instance by using the flexible EE as a gripper, as shown in Figure 7 and in the multimedia attachment.
Author Contributions
Conceptualization, T.M., J.M.P. and F.T.; methodology, T.M., G.M. and F.T.; software, T.M. and J.M.P.; validation, T.M.; formal analysis, T.M.; investigation, T.M.; resources, J.M.P. and F.T.; writing—original draft preparation, T.M.; writing—review and editing, T.M. and G.M.; visualization, T.M. and G.M.; supervision, G.M., M.C., J.M.P. and F.T.; project administration, M.C., J.M.P. and F.T.; funding acquisition, M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Economy and Competitiveness grants number DPI2017-88282-P and MDM-2016-0656. The APC was funded by Marco Carricato.
Acknowledgments
The support of Patrick Grosch in building the prototype is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| PRCP | Parallel robots with configurable platform |
| EE | End-Effector |
| DoF | Degree of Freedom |
| DKP | Direct Kinematic Problem |
| IKP | Inverse Kinematic Problem |
Appendix A. Example Architectures
For clarity, we report here two selected example architectures: a 3-RRR (Figure A1a) and a 4-RRR (Figure A1b) mechanism. The first one has a rigid platform, while in the second case the platform has an internal DoF for reconfiguring its shape.
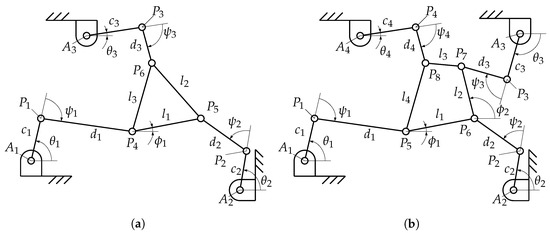
Figure A1.
Schematics of: (a) a general 3-RRR robot; (b) a general 4-RRR robot. They have, respectively, 3 and 4 DoFs.
Appendix B. Singularity Equations
For the sake of completeness, we report here the definitions of quantities e, f, g from Section 4 and their derivations. We find the position of using bilateration; Equations (2) and (3) give
where one obtains (through simplifications)
where the sign of depends on the point ordering as seen for Equation (2) and having defined the auxiliary variable
References
- Yi, B.J.; Na, H.; Lee, J.; Hong, Y.; Oh, S.; Suh, I.H.; Kim, W. Design of a parallel-type gripper mechanism. Int. J. Robot. Res. 2002, 21, 661–678. [Google Scholar] [CrossRef]
- Yi, D.; Yi, B.J.; Kim, W. Design of a new grasper having XYZ translational motions. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 690–695. [Google Scholar] [CrossRef]
- Park, B.J.; Yi, B.J.; Kim, W. Design and analysis of a new parallel grasper having spherical motion. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October 2004; pp. 106–111. [Google Scholar] [CrossRef]
- Mohamed, M.G.; Gosselin, C.M. Design and analysis of kinematically redundant parallel manipulators with configurable platforms. IEEE Trans. Robot. 2005, 21, 277–287. [Google Scholar] [CrossRef]
- Hamaza, S.; Lambert, P.; Carricato, M.; Herder, J.L. The QuadroG robot, a parallel robot with a configurable platform for haptic applications. In Proceedings of the 39th Mechanisms and Robotics Conference, Boston, MA, USA, 2–5 August 2015; p. V05CT08A008. [Google Scholar] [CrossRef]
- Haouas, W.; Dahmouche, R.; Fort-Piat, N.L.; Laurent, G.J. 4-DoF spherical parallel wrist with embedded grasping capability for minimally invasive surgery. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 2363–2368. [Google Scholar] [CrossRef]
- Haouas, W.; Dahmouche, R.; Fort-Piat, N.L.; Laurent, G.J. A new seven degrees-of-freedom parallel robot with a foldable platform. ASME J. Mech. Robot. 2018, 10, 045001. [Google Scholar] [CrossRef]
- Dahmouche, R.; Wen, K.; Gosselin, C.M. Transferability in an 8-DoF parallel robot with a configurable platform. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 6544–6549. [Google Scholar]
- Kang, X.; Dai, J.S. Relevance and transferability for parallel mechanisms with reconfigurable platforms. ASME J. Mech. Robot. 2019, 11, 031012. [Google Scholar] [CrossRef]
- Zeng, Q.; Ehmann, K.F. Design of parallel hybrid-loop manipulators with kinematotropic property and deployability. Mech. Mach. Theory 2014, 71, 1–26. [Google Scholar] [CrossRef]
- Tian, C.; Zhang, D. A new family of generalized parallel manipulators with configurable moving platforms. Mech. Mach. Theory 2020, 153, 103997. [Google Scholar] [CrossRef]
- Jin, X.; Fang, Y.; Zhang, D. Design of a class of generalized parallel mechanisms with large rotational angles and integrated end-effectors. Mech. Mach. Theory 2019, 134, 117–134. [Google Scholar] [CrossRef]
- Pierrot, F.; Company, O. H4: A new family of 4-DOF parallel robots. In Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Atlanta, GA, USA, 19–23 September 1999; pp. 508–513. [Google Scholar] [CrossRef]
- Pierrot, F.; Marquet, F.; Company, O.; Gil, T. H4 parallel robot: modeling, design and preliminary experiments. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; pp. 3256–3261. [Google Scholar] [CrossRef]
- Company, O.; Marquet, F.; Pierrot, F. A new high-speed 4-DOF parallel robot synthesis and modeling issues. IEEE Trans. Robot. 2003, 19, 411–420. [Google Scholar] [CrossRef]
- Choi, H.B.; Konno, A.; Uchiyama, M. Design, implementation, and performance evaluation of a 4-DOF parallel robot. Robotica 2010, 28, 107–118. [Google Scholar] [CrossRef]
- Krut, S.; Company, O.; Benoit, M.; Ota, H.; Pierrot, F. I4: A new parallel mechanism for SCARA motions. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; Volume 2, pp. 1875–1880. [Google Scholar] [CrossRef]
- Nabat, V.; de la O. Rodriguez, M.; Company, O.; Krut, S.; Pierrot, F. Par4: Very high speed parallel robot for pick-and-place. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 553–558. [Google Scholar] [CrossRef]
- Pierrot, F.; Nabat, V.; Company, O.; Krut, S.; Poignet, P. Optimal design of a 4-DOF parallel manipulator: from academia to industry. IEEE Trans. Robot. 2009, 25, 213–224. [Google Scholar] [CrossRef]
- Ye, W.; He, L.; Li, Q. A new family of symmetrical 2T2R parallel mechanisms without parasitic motion. ASME J. Mech. Robot. 2018, 10, 011006. [Google Scholar] [CrossRef]
- Guo, S.; Fang, Y.; Qu, H. Type synthesis of 4-DOF nonoverconstrained parallel mechanisms based on screw theory. Robotica 2012, 30, 31–37. [Google Scholar] [CrossRef]
- Wu, G.; Dong, H. Kinematics of a 6-RUU parallel robots with reconfigurable platforms. In Proceedings of the 7th International Workshop on Computational Kinematics (CK2017); Zeghloul, S., Romdhane, L., Laribi, M.A., Eds.; Springer: Cham, Switzerland, 2018; pp. 331–339. [Google Scholar] [CrossRef]
- Lambert, P.; Langen, H.; Schmidt, R. A novel 5 DOF fully parallel robot combining 3T1R motion and grasping. In Proceedings of the ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 15–18 August 2010; Volume 2, pp. 1123–1130. [Google Scholar] [CrossRef]
- Lambert, P.; Herder, J.L. A 7-DOF redundantly actuated parallel haptic device combining 6-DOF manipulation and 1-DOF grasping. Mech. Mach. Theory 2019, 134, 349–364. [Google Scholar] [CrossRef]
- Hoevenaars, A.; Lambert, P.; Herder, J.L. Kinematic design of two elementary 3DOF parallel manipulators with configurable platforms. In Proceedings of the 6th International Workshop on Computational Kinematics (CK2013); Thomas, F., Gracia, A.P., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 315–322. [Google Scholar] [CrossRef]
- Lambert, P.; Herder, J.L. Parallel robots with configurable platforms: fundamental aspects of a new class of robotic architectures. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2016, 230, 463–472. [Google Scholar] [CrossRef]
- Hoevenaars, A.; Gosselin, C.M.; Lambert, P.; Herder, J.L. A systematic approach for the Jacobian analysis of parallel manipulators with two end-effectors. Mech. Mach. Theory 2017, 109, 171–194. [Google Scholar] [CrossRef]
- Lambert, P.; Cruz, L.D.; Bergeles, C. Design, modelling, and implementation of a 7-DOF cable-driven haptic device with a configurable cable platform. IEEE Robot. Autom. Lett. 2020, 5, 5764–5771. [Google Scholar] [CrossRef]
- Yoon, J.; Ryu, J.; Lim, K.B. Reconfigurable ankle rehabilitation robot for various exercises. J. Robot. Syst. 2006, 22, S15–S33. [Google Scholar] [CrossRef]
- Pennock, G.R.; Kassner, D.J. Kinematic analysis of a planar eight-bar linkage: application to a platform-type robot. ASME J. Mech. Des. 1992, 114, 87–95. [Google Scholar] [CrossRef]
- Merlet, J.P. Direct kinematics of planar parallel manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; pp. 3744–3749. [Google Scholar] [CrossRef]
- Cayley, A. On a theorem in the geometry of position. In The Collected Mathematical Papers; Cambridge Library Collection—Mathematics; Cambridge University Press: Cambridge, UK, 1841; Volume 1. [Google Scholar]
- Menger, K. New foundation of Euclidean geometry. Am. J. Math. 1931, 53, 721–745. [Google Scholar] [CrossRef]
- Thomas, F.; Ros, L. Revisiting trilateration for robot localization. IEEE Trans. Robot. 2005, 21, 93–101. [Google Scholar] [CrossRef]
- Rojas, N.; Thomas, F. The forward kinematics of 3-RPR planar robots: a review and a distance-based formulation. IEEE Trans. Robot. 2011, 27, 143–150. [Google Scholar] [CrossRef]
- Rojas, N.; Thomas, F. Closed-form solution to the position analysis of Watt–Baranov trusses using the bilateration method. ASME J. Mech. Robot. 2011, 3, 031001. [Google Scholar] [CrossRef]
- Rojas, N.; Thomas, F. On closed-form solutions to the position analysis of Baranov trusses. Mech. Mach. Theory 2012, 50, 179–196. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, B.K. Dynamic ultrasonic hybrid localization system for indoor mobile robots. IEEE Trans. Ind. Electron. 2013, 60, 4562–4573. [Google Scholar] [CrossRef]
- Hernandez, E.E.; Valdez, S.I.; Ceccarelli, M.; Hernandez, A.; Botello, S. Design optimization of a cable-based parallel tracking system by using evolutionary algorithms. Robotica 2015, 33, 599–610. [Google Scholar] [CrossRef]
- Liberti, L.; Lavor, C.; Maculan, N.; Mucherino, A. Euclidean distance geometry and applications. SIAM Rev. 2014, 56, 3–69. [Google Scholar] [CrossRef]
- Bohigas, O.; Manubens, M.; Ros, L. Singularities of Robot Mechanisms: Numerical Computation and Avoidance Path Planning; Mechanisms and Machine Science; Springer: Berlin, Germany, 2016; Volume 41. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. Singularity analysis of closed-loop kinematic chains. IEEE Trans. Robot. 1990, 6, 281–290. [Google Scholar] [CrossRef]
- Conconi, M.; Carricato, M. A new assessment of singularities of parallel kinematic chains. IEEE Trans. Robot. 2009, 25, 757–770. [Google Scholar] [CrossRef]
- Zlatanov, D.; Fenton, R.; Benhabib, B. A unifying framework for classification and interpretation of mechanism singularities. ASME J. Mech. Des. 1995, 117, 566–572. [Google Scholar] [CrossRef]
- Crapo, H. Invariant-theoretic methods in scene analysis and structural mechanics. J. Symb. Comput. 1991, 11, 523–548. [Google Scholar] [CrossRef][Green Version]
- Company, O.; Krut, S.; Pierrot, F. Internal singularity analysis of a class of lower mobility parallel manipulators with articulated traveling. IEEE Trans. Robot. 2006, 22, 1–11. [Google Scholar] [CrossRef]
- Choi, H.B.; Ryu, J. Singularity analysis of a four degree-of-freedom parallel manipulator based on an expanded 6 × 6 Jacobian matrix. Mech. Mach. Theory 2012, 57, 51–61. [Google Scholar] [CrossRef]
- Wu, J.; Yin, Z.; Xiong, Y. Singularity analysis of a novel 4-dof parallel manipulator H4. Int. J. Adv. Manuf. Technol. 2006, 29, 794–802. [Google Scholar] [CrossRef]
- Marchi, T.; Mottola, G.; Porta, J.M.; Thomas, F.; Carricato, M. Position analysis of a class of n-RRR planar parallel robots. In Advances in Italian Mechanism Science. The 3rd International Conference of IFToMM Italy (IFIT 2020); Niola, V., Gasparetto, A., Eds.; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2020; Volume 91, pp. 353–361. [Google Scholar] [CrossRef]
- Bottin, M.; Cocuzza, S.; Comand, N.; Doria, A. Modeling and identification of an industrial robot with a selective modal approach. Appl. Sci. 2020, 10, 4619. [Google Scholar] [CrossRef]
- Bates, D.J.; Hauenstein, J.D.; Sommese, A.J.; Wampler, C.W. Bertini: Software for Numerical Algebraic Geometry. Available online: bertini.nd.edu (accessed on 9 January 2021). [CrossRef]
- Abbasnejad, G.; Carricato, M. Real solutions of the direct geometrico-static problem of under-constrained cable-driven parallel robots with 3 cables: A numerical investigation. Meccanica 2012, 47, 1761–1773. [Google Scholar] [CrossRef]
- Dietmaier, P. The Stewart-Gough platform of general geometry can have 40 real postures. In Advances in Robot Kinematics: Analysis and Control; Lenarčič, J., Husty, M.L., Eds.; Springer: Salzburg, Austria, 1998; pp. 7–16. [Google Scholar] [CrossRef]
- Bates, D.J.; Newell, A.J.; Niemerg, M. BertiniLab: A MATLAB interface for solving systems of polynomial equations. Numer. Algorithms 2016, 71, 229–244. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).