End-of-Line Quality Control Based on Mel-Frequency Spectrogram Analysis and Deep Learning

Abstract

This study presents a novel approach to the end-of-line (EoL) quality inspection of brushless DC (BLDC) motors by implementing a deep learning model that combines MEL diagrams, convolutional neural networks (CNNs) and bidirectional gated recurrent units (BiGRUs). The suggested system utilizes raw vibration and sound signals, recorded during the EoL quality inspection process at the end of an industrial manufacturing line. Recorded signals are transformed directly into Mel-frequency spectrograms (MFS) without pre-processing. To remove non-informative frequency bands and increase data relevance, a six-step data reduction procedure was implemented. Furthermore, to improve fault characterization, a reference spectrogram was generated from healthy motors. The neural network was trained on a highly imbalanced dataset, using oversampling and Bayesian hyperparameter optimization. The final classification algorithm achieved classification metrics with high accuracy (99%). Traditional EoL inspection methods often rely on threshold-based criteria and expert analysis, which can be inconsistent, time-consuming, and poorly scalable. These methods struggle to detect complex or subtle patterns associated with early-stage faults. The proposed approach addresses these issues by learning discriminative patterns directly from raw sensor data and automating the classification process. The results confirm that this approach can reduce the need for human expert engagement during commissioning, eliminate redundant inspection steps, and improve fault detection consistency, offering significant production efficiency gains.

1. Introduction

Electric motors are among the most widely produced devices worldwide. To reduce their production costs, they are typically produced on highly automated manufacturing lines. These lines are equipped with 100% end-of-line (EoL) quality inspection systems to check each produced motor for several possible faults and to prevent faulty motors from reaching the market or end-users [1,2].

The presented study is associated with the Slovenian company Domel d.o.o., one of the largest mass-producers of electric motors for vacuum cleaners and other applications [3]. Their motors are integrated into numerous high-end products, thanks to their comprehensive EoL inspection systems. Every manufacturing line at the company has to be equipped with a 100% EoL quality inspection process [1,4,5,6]. Each produced motor undergoes a quality inspection process to verify the quality, absence of faults, and compliance with costumer requirements. The diagnostic process involves a series of tests assessing electrical, vacuum, vibrational, and acoustic characteristics from which a diagnostic report is generated for each motor [2,5].

Motors are becoming more and more complex and they demand specialized diagnosis approaches. Additionally, motor types produced at the same manufacturing line may differ substantially and require unique diagnostic procedures. Therefore, the current solution relies on a variety of sensors and the expertise of skilled experts in order to establish proper diagnosis procedures for each motor type [2,5].

In this study, we propose a diagnostic approach that relies on vibrational and acoustic signals. The selected manufacturing line captures vibration signals (V1, V2, and V3) at three points of the motor (P1, P2, and P3) using a laser vibrometer and acoustic signal (S) using the microphone. Signals are captured during short test runs at nominal (full) rotational speed. This manufacturing line is one of the newest at the company. However, the core principles of the manufacturing processes and diagnostic procedures remain very similar to those in older systems. Notably, when this line was developed, several technical upgrades were implemented to support future improvements, including the integration of machine learning and artificial intelligence in diagnostic workflows.

In the current automatic diagnostic system, these signals undergo traditional signal processing and feature-generating steps. During commissioning, relevant features are selected and their thresholds defined by skilled experts [5]. Despite the robustness of this approach, there are limitations in scalability and adaptability. Feature engineering and threshold setting require domain expertise and are highly specific to motor types and fault conditions. These limitations restrict the ability of traditional systems to generalize across varied conditions or detect emerging failure patterns [4,5,7,8].

This study explores a time–frequency analysis combined with artificial intelligence for fault detection and recognition. Specifically, we propose the use of Mel-frequency spectrograms (MFSs) as input features and neural networks as the classification model, to simplify data processing and improve fault classification performance.

Recently, data-driven methods and machine learning techniques have made progress on industrial quality inspection tasks. Many of the mechanical and assembly-related faults in electric motors can be detected using vibration and acoustic signals. Traditionally, diagnostic systems rely on signal pre-processing steps: filtering, resampling, scaling, Fourier transform, wavelet transforms, etc., followed by classical classification methods using decision trees, support vector machines (SVM), k-nearest neighbours, etc. [4,5,7,8]. These approaches demonstrate solid accuracy and cost-efficiency, but they are typically optimized for specific fault types and depend heavily on specific expertise for feature extraction and threshold settings.

To overcome these limitations, the presented research investigates the use of a combination of convolutional neural networks (CNNs) and bidirectional gated recurrent units (BiGRUs), applied to a time–frequency representation of signals (MFSs). MFSs, originally developed for speech and audio analysis, have become popular in fault detection systems because of their ability to compactly represent relevant frequency content while preserving temporal resolution. CNNs, trained on MFSs, have achieved notable results in fault detection and often outperform classical methods [9,10,11].

However, the integration of such systems in industrial applications also faces several challenges. These include the limited availability of labelled data, interpretability of model decisions, and integration with existing inspection workflows. In recent years, self-supervised and semi-supervised learning methods have emerged as powerful tools to address some of these issues. For example, catenary support rod area masked image modelling (CSRM-MIM) [12] has demonstrated effective self-supervised pretraining for detecting structural faults in railway systems, and multi-modal imitation learning has been successfully applied to arc detection in complex industrial environments [13]. In parallel, focusing enhanced networks (FENets) and physics-informed neural networks (PINNs) are gaining attention for their ability to incorporate domain knowledge, which enhances interpretability and performance in safety-critical monitoring systems [14]. These developments highlight a growing trend toward more adaptable, interpretable, and data-efficient AI models.

The main contributions of this work are summarized as follows:

• A deep learning-based classification model using a CNN–BiGRU architecture trained on MFSs generated from acoustic and vibration signals of BLDC motors.
• An evaluation strategy that includes bootstrap resampling to estimate 95% confidence intervals, providing a more robust estimate of model reliability.
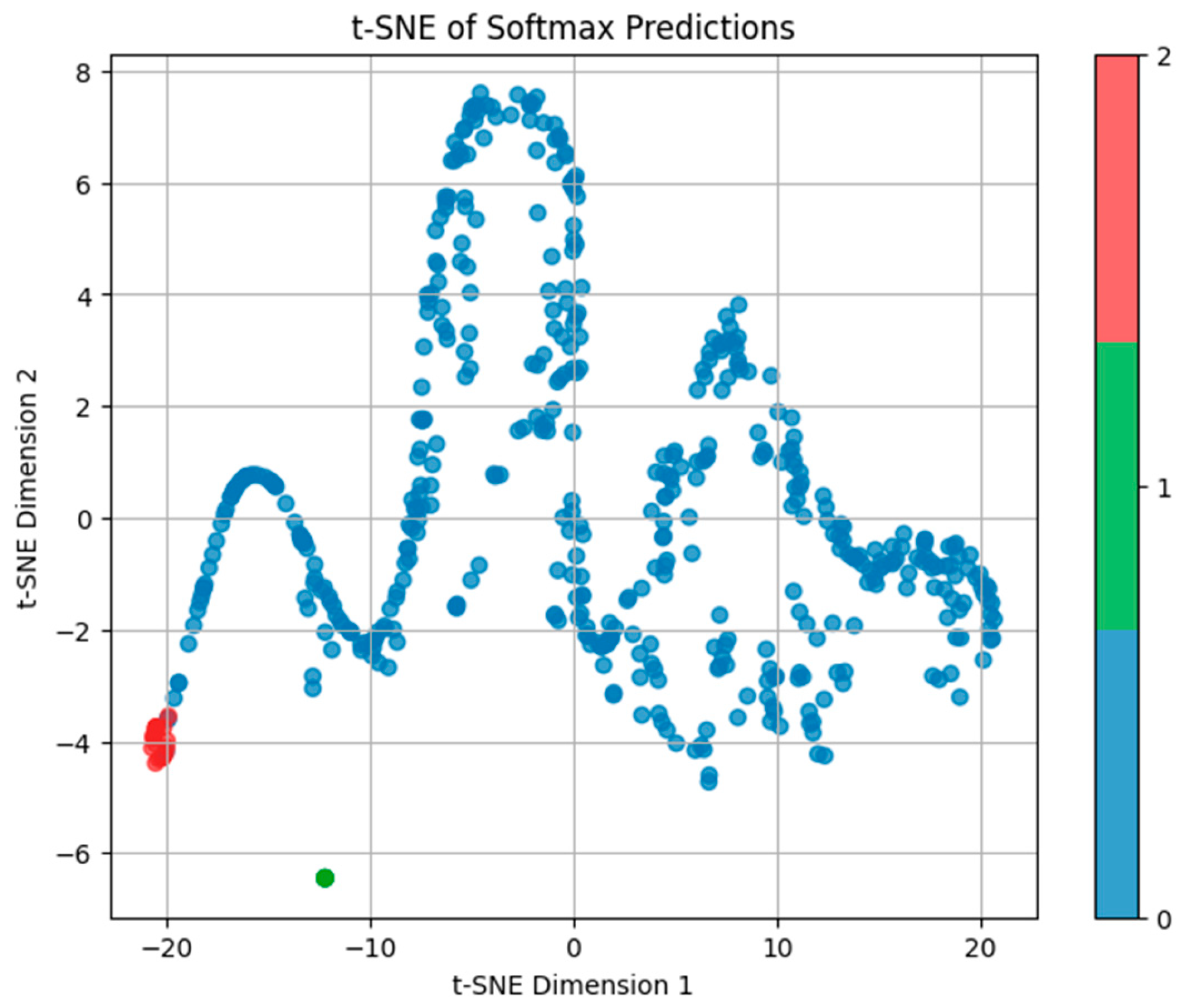
• The use of t-SNE visualization to analyse feature resolution and improve the interpretability of the learned representations in the output space.

The remainder of the paper is organized as follows:

• Section 2 describes the problem and outlines key challenges.
• Section 3 presents the proposed fault detection approach.
• Section 4 explains the data preparation and feature reduction process.
• Section 5 describes the neural network architecture and training procedure.
• Section 6 presents classification results and performance evaluation.
• Section 7 concludes the paper and discusses future directions.

2. Problem Description

2.1. Motor Description

The focus of this study is on brushless DC (BLDC) motors. These motors are produced in many variants. However, we focus on the particular variant with 18 V DC supply voltage, 600 W electric power, and a nominal speed of 38,500 RPM. The motor is shown on the Figure 1. This motor type was selected because the study targets the manufacturing line at its early stage of operation, for which sufficient and relevant data for only this motor type were available. Moreover, this was the first motor type to be mass-produced on the line, making it the most suitable candidate for initial analysis.

2.2. Existing EoL Quality Algorithm and Inspection System

A modular EoL quality inspection system (Figure 2) is installed at the end of the manufacturing line for the inspection of each produced motor. The EoL system consists of three test cells: TC 1, TC 2, and TC 3. Each cell is responsible for evaluating specific aspects of motor performance. During the inspection, each motor undergoes a series of short test runs. In TC 1, electrical characteristics and rotational speed are measured. In TC 2, vibration and acoustic emissions at nominal speed are checked, while TC 3 focuses on detecting bearing and friction faults during a low-speed run. At the time when data for the purposes of this study were collected, only TC 2 had the capability to record and save raw data into files suitable for further analysis. TC 2 was also the most stable and reliable test cell in terms of operation and data handling, which made the recorded data more consistent and trustworthy for subsequent processing.

The measurements result in high-resolution time series data, referred to as raw signals, sampled at rates between 10 and 60 kHz over time spans ranging from 0.1 to 1 s and containing between 1000 and 30,000 samples.

In the current diagnostic procedure, vibration and sound signals undergo a series of signal processing steps (digital filtering, down-sampling, and frequency–domain analysis) to extract meaningful information. As result, a fixed set of features is created, where each feature represents signal (vibration or sound) power at a specific frequency. For the observed motor subtype, a set of 82 features is created. According to the feature values, motors are then classified into one of three quality categories—good, bad, or undefined. In addition to overall classification, the feature values can find the root cause of faults. Details of diagnostic result generation are described in [5] and summarized in

Table 1. Diagnostic result generation [5].

Measurement Status	Features	Diagnostic Result
Completed	All features are within specified ranges.	Good
	One or more features are outside specified range.	Bad
Not completed	Missing features.	Undefined

.

The development of such an inspection system is both complex and resource-intensive. Among other requirements, it requires a specific expertise to select relevant features and determine their acceptable ranges. To reduce this dependency on expert knowledge, our recent work [5] introduced machine learning approaches for automated feature selection and threshold tuning.

Unlike previous approaches, this study considers raw, rather than processed, vibration and acoustic signals that were captured during EoL testing. By using time–frequency representations (MFSs) of raw signals, the proposed method enables a neural network to directly learn discriminative patterns from the data. This approach aims to simplify the development process, reduce expert reliance, and improve adaptability to variations in motor subtypes.

Figure 3 illustrates a comparison between existing and proposed EoL quality inspection systems. Both systems begin with measurement and data acquisition. However, existing system proceeds with manual feature extraction and diagnostic result generation, both of which depend heavily on expert experience and domain knowledge.

In contrast, the proposed system replaces manual feature extraction with automatic MFSs generation, followed by the statistical processing of the MFSs, and ends with diagnostic classification using a CNN-BiGRU neural network. This architecture facilitates a more automated and scalable diagnostic pipeline.

3. Proposed Novel EoL Quality Inspection Algorithm

3.1. Overview

This method is based on raw vibration and acoustic signals, captured at TC 2, and it is composed of two primary parts:

• MFSs are used to transform raw time-series signals into 3D time–frequency representations that can be presented as a colour image;
• A hybrid deep learning architecture that combines a CNN and a BiGRU network.

3.2. MFSs

An MFS is a time-frequency representation of an acoustic or vibrational signal, mapped to the Mel scale. The Mel scale transforms linear frequencies into a scale that approximates the sensitivity of human hearing. MFSs are usually used for purposes of speech recognition and music information retrieval [16,17]. In general, an MFS represents signal power as a function of frequency and time. The diagram shows the power spectrum as a function of time and it is useful for the observation of the dynamic changes within the signal. The x-axis represents the time within the data series and the y-axis represents the frequency. The signal power scalar (the subject of z-axis) is represented by the colour scale (RGB), giving the diagram the appearance of a colour image. An example is shown in Figure 4. Image recognition algorithms can, in principle, be used for the analysis of MFSs [18]. For the analysis, signal power (scalar) can be used, rather than its 3-component RGB representation, which is only used for visual interpretation.

Lately, MFSs were proven to be highly effective in the fault diagnosis of rotating machinery [9,19,20]. In motor diagnostics, MFSs enable the extraction of spectral and temporal features from the raw signal. Compared to traditional feature engineering (which usually relies on the extraction of power bands or harmonics), they provide an information format suitable as input into neural networks.

Compared to linear spectrograms or wavelet transforms, they provide several advantages for fault diagnosis in rotary machines [21]:

• Efficient dimensionality reduction while preserving perceptually and diagnostically relevant features;
• Enhanced sensitivity in the low- and mid-frequency ranges (up to 5 kHz), where mechanical issues such as imbalance, misalignment, and bearing defects usually occur;
• Increased robustness to noise and minor variations in signal phase or speed.

According to recent research, MFSs, combined with CNNs, outperform traditional hand-engineered features in diagnosing faults in electric motors, gearboxes, and rotating machinery [21,22]. Their adaptability for mechanical fault detection tasks is demonstrated by their successful application in vibration and acoustic analysis [23].

3.3. Neural Network Architecture: CNN–BiGRU

In order to classify motor conditions based on MFSs, this study proposes a hybrid neural network architecture, combining CNNs with BiGRUs.

CNNs are typically used to extract hierarchical features and local patterns from image-like inputs such as spectrograms. The convolutional layers use multiple filters that detect frequency components and local spectro-temporal features, such as localized bursts of frequency activity or persistent harmonics, associated with specific fault types. These are critical for identifying motor faults [20,24,25]. CNNs reduce the dimensionality of inputs and preserve crucial spatial structures. That is why they are suitable for analysing the complex patterns in vibration and acoustic data.

However, signals generated by faulty motors often contain evolving patterns over time. To address this issue, a BiGRU layer is proposed. BiGRUs are a type of recurrent neural network, which is capable of learning long-range dependencies in sequential data by bidirectionally processing input sequences [26]. This allows the model to consider both past and future contexts in the time domain, improving sensitivity to dynamic signal changes and the ability to detect fault patterns [23,27]. This eliminates the need for a feature extraction process or manual threshold tuning and allows classification to be established directly from raw signal data.

The combination of CNN-BiGRU allows powerful spatial feature extraction with effective temporal modelling. This enables the learning of discriminative features for fault detection directly from the Mel spectrograms, without relying on extensive pre-processing designed by human experts. Several recent studies have demonstrated that CNN-BiGRU models outperform standalone CNN or recurrent architectures in rotating machinery diagnostics, bearing fault detection, and acoustic signal classification tasks [28,29,30,31]. The effectiveness of this combination has already been demonstrated in various studies that involve audio classification, anomaly detection, and fault diagnosis [32,33].

4. Data Preparation

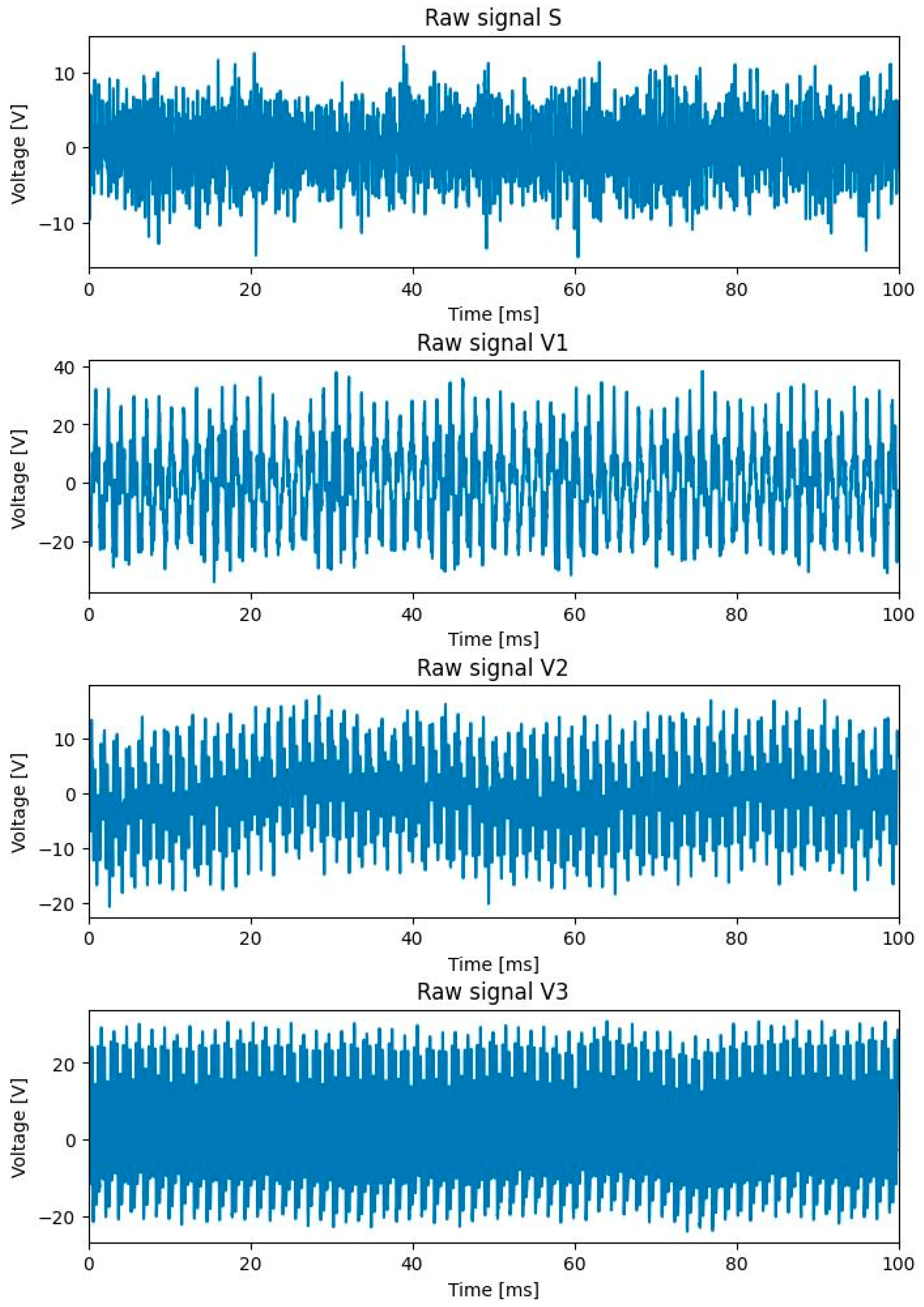
4.1. Data Structure

The dataset used in this study was collected during the production of 1505 pieces of BLDC motors at the manufacturing line. For the purpose of this study, only data acquired at TC 2 was used: vibrations (V1, V2, and V3), and sound (S). Signals were sampled at the nominal motor speed (38,500 RPM) with a sampling frequency of 60 kHz over 100 ms windows, resulting in 6000 samples per signal. No pre-processing (filtering, resampling, scaling, etc.) was used. Figure 5 illustrates examples of raw signals, which served as the direct input to the proposed diagnostic system.

Each motor had already undergone standard diagnostic procedures at the end of the manufacturing line and was classified based on fault detection outcomes. The final classification used in this study is derived from fault localization across the test cells, as follows:

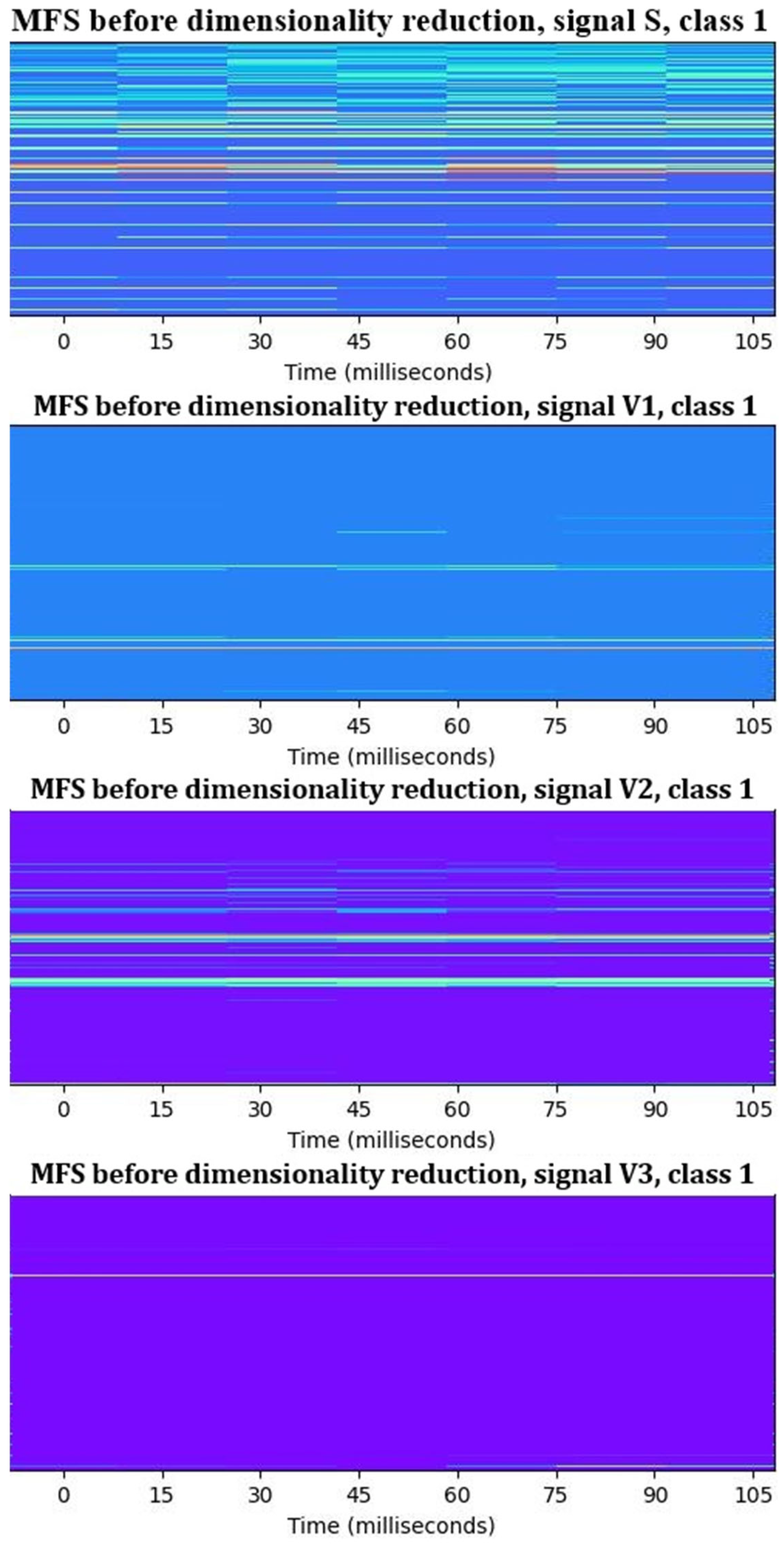
• Class 0: motors with no detected faults (good);
• Class 1: motors with faults detected in TC 2;
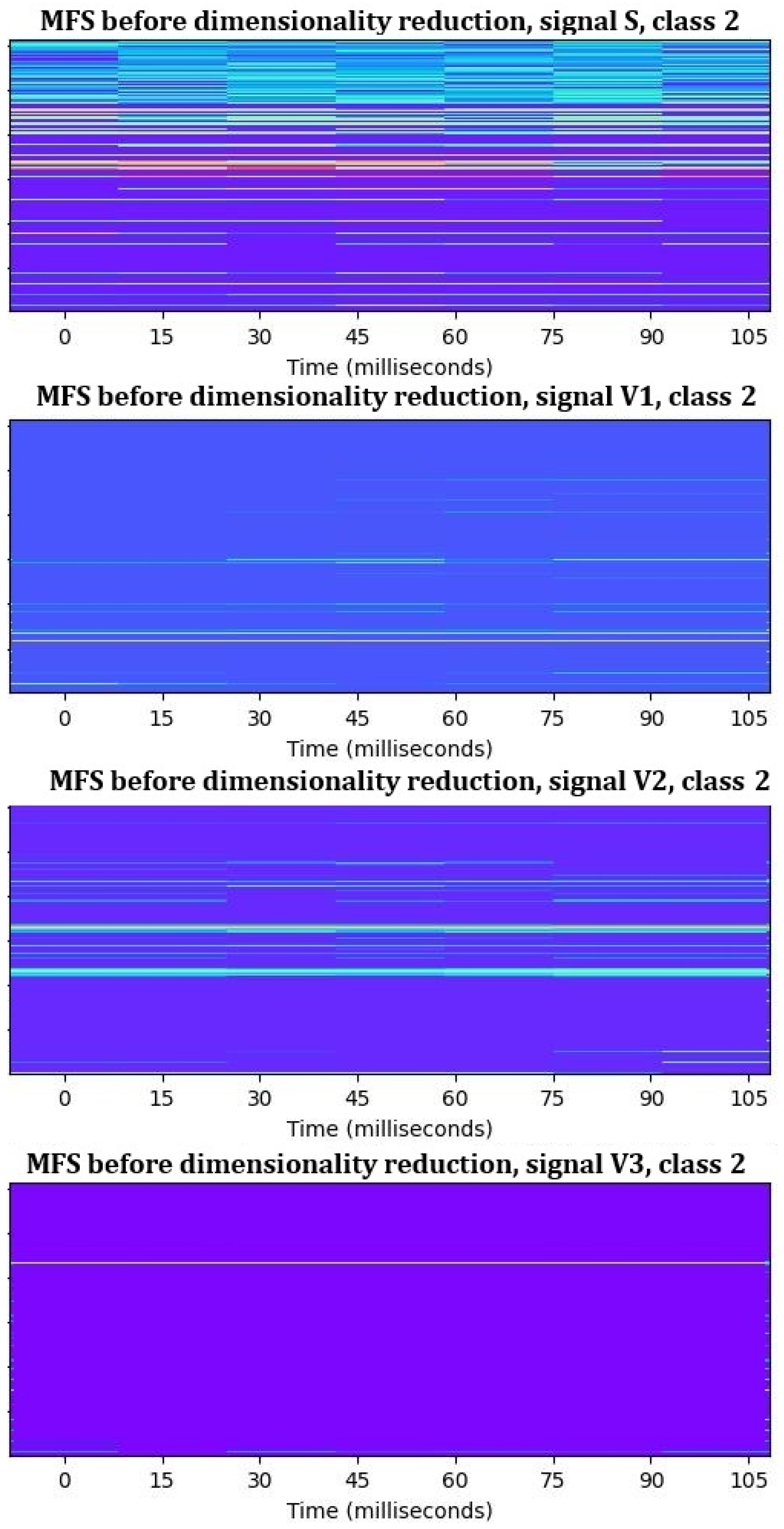
• Class 2: motors with faults detected in TC 3.

It is important to note that no faults were detected in TC 1 for this dataset, therefore it was excluded from class definition. Additionally, an extreme class-imbalance was observed. As expected, the majority of produced motors belonged to class 0 (approximately 95%), while only a few were classified as faulty (around 5%). The class distribution is presented in

Table 2. Class distribution.

Class	Number of Motors	Part [%]
0	1422	94.49
1	16	1.06
2	67	4.45

.

4.2. MFS Generation

In this study, MFSs were generated directly from the raw time–domain signals (Figure 5) without any pre-processing. This approach provides the full frequency content preservation of the signals. For each of the signals (V1, V2, V3, and S), an MFS was created using a standard short-time Fourier transform (STFT)-based method followed by Mel-scale conversion. The spectrogram generation process was configured to retain sufficient resolution for identifying subtle variations in frequency patterns, associated with mechanical faults.

The parameters for MFS computation were chosen carefully to balance time and frequency resolution and to satisfy computational limitations. Those parameters are shown in

Table 3. MFS parameters.

Name of Parameter	Brief Explanation	Value
sampling rate	The sampling frequency of raw input data [Hz], determined by hardware.	60,000
nfft	The length of the FFT window; defines frequency resolution. Set empirically.	2000
win_length	The length of the window for FFT analysis (same or smaller than nfft). Set equal to nfft for maximum frequency detail without truncation.	2000
hop_length	The number of samples between windows (hop); controls the time resolution of the MFS. Tuned empirically to balance the resolution and training stability.	1000
centre	The positioning of the window (symmetric analysis).	True
pad_mode	How the signal at the edge is completed. “Reflect” mirrors the signal at the edges, minimizing boundary artefacts and preserving continuity [34].	Reflect
power	The exponent magnitude of the Mel-frequency spectrogram (1—energy and 2—power).	2
n_mels	The number of Mel-frequency bands. Chosen empirically.	2048
fmin	Low frequency limit; set by experts from the industrial partner.	20
fmax	High frequency limit; set by experts from the industrial partner.	18,000

. MFSs were created in the Python 3.13 programming language, using the librosa library. For improved visualisation and interpretability, the power spectrum magnitude of all MFSs in this study were converted to a logarithmic scale using decibel (dB) scaling. This transformation enhances the contrast of spectral features by compressing the dynamic range of signal power, making low- and high-energy components more visually recognizable.

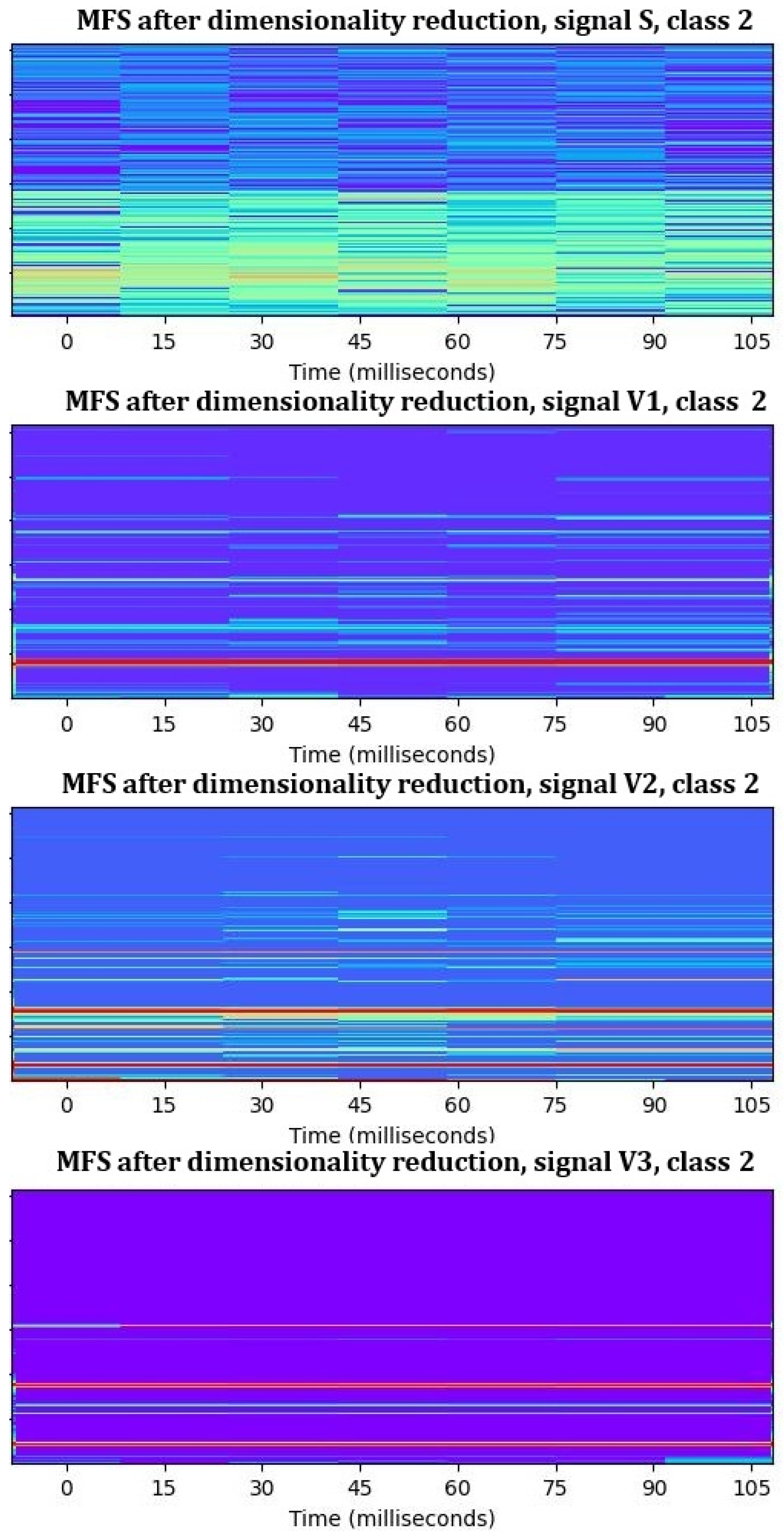
4.3. MFS Processing and Dimensionality Reduction

MFSs preserve the majority of spectral–temporal information. However, not all frequency bands are informative and necessary for classification. Furthermore, their high dimensionality can lead to redundancy, noise, and unnecessary computational complexity and slow down the machine learning process. To address this, a 6-step procedure was created for data reduction where non-informative frequency bands were detected and removed from the dataset:

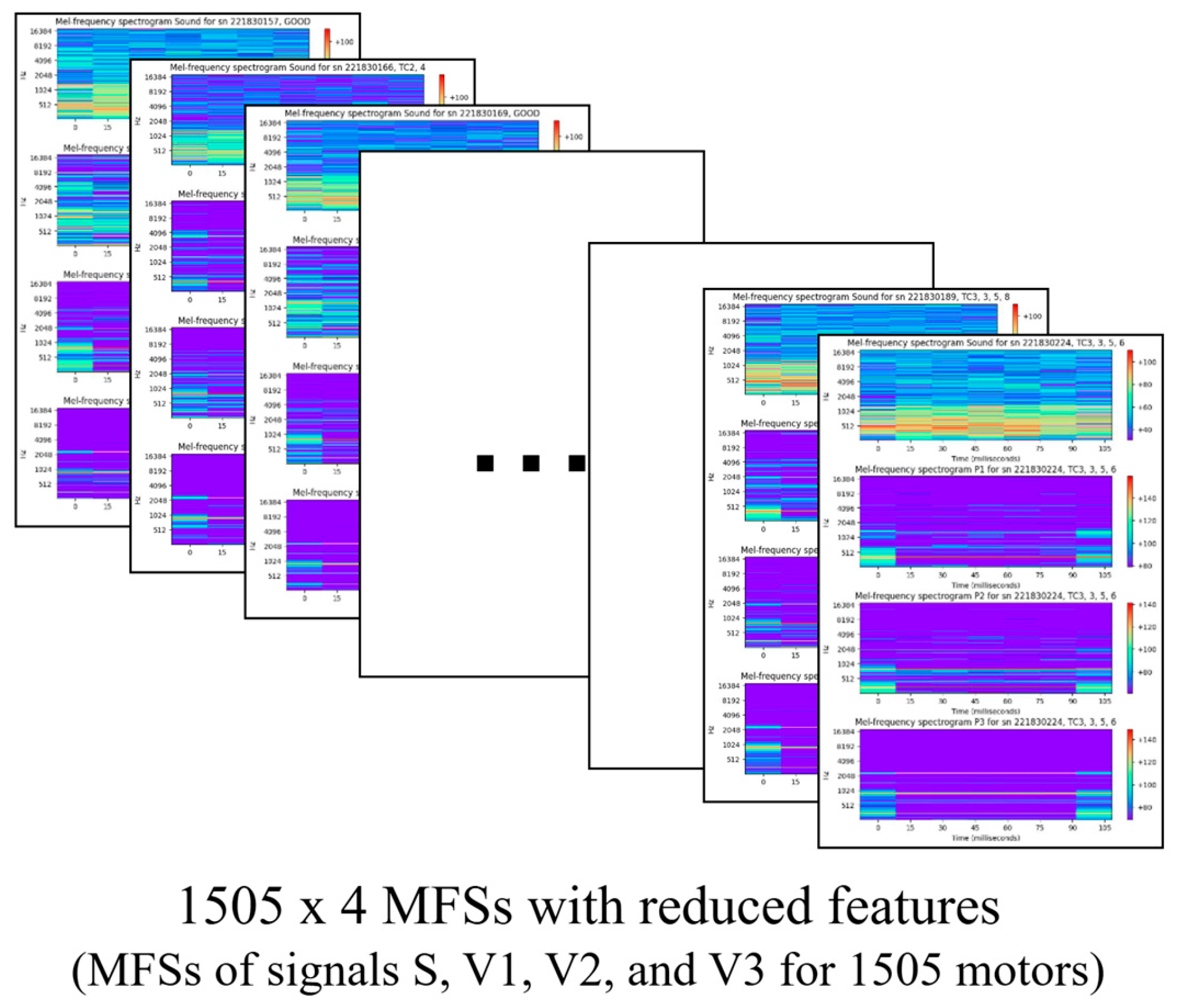
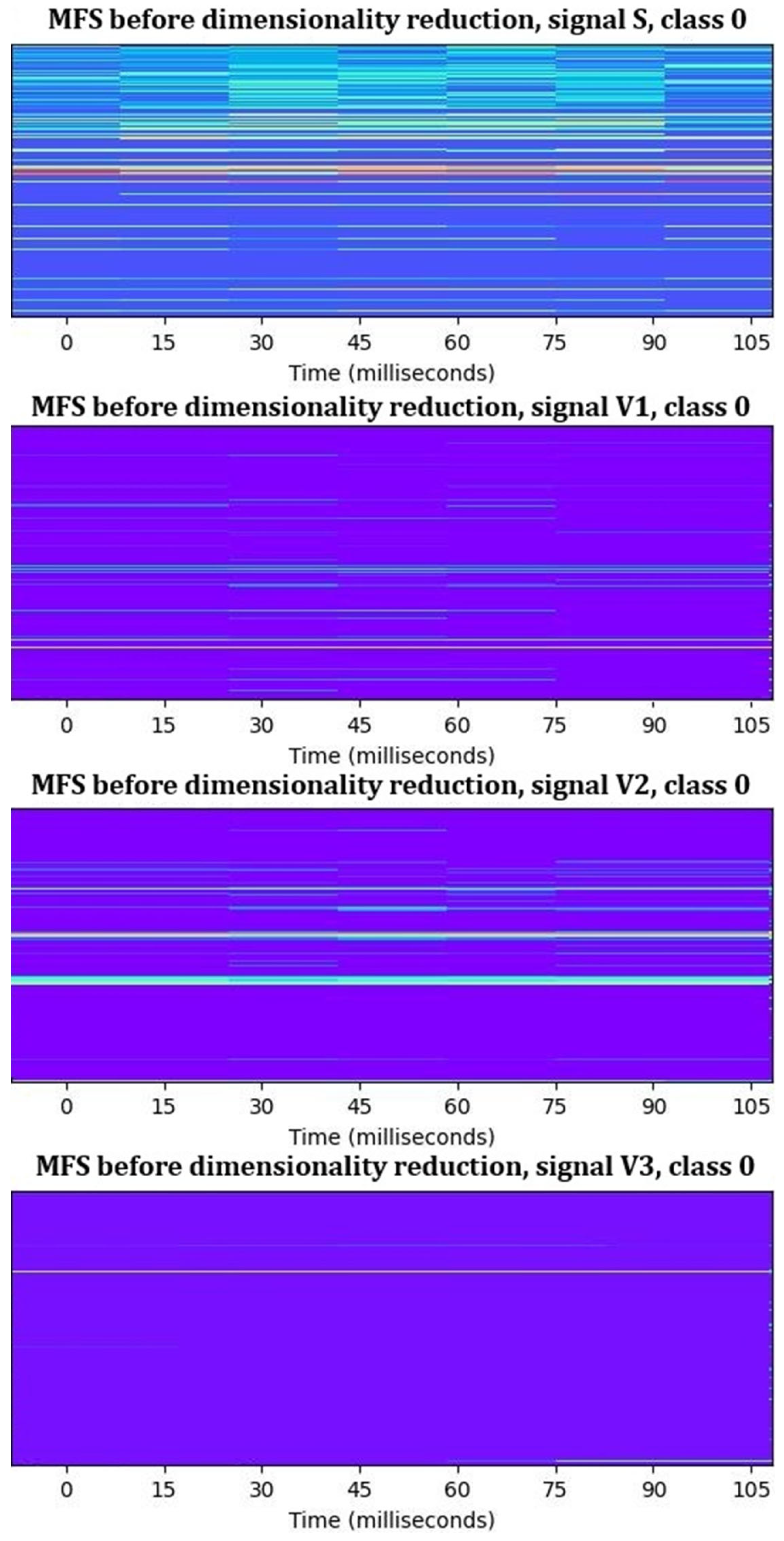
• Step 1: MFS creation. In this step, raw time–domain signals of each motor (V1, V2, V3, and S, explained in Section 4.1) are converted into 4 MFSs, according to parameter settings from 0. The results of this step are 4 MFSs of size 2048 (frequency bands) × 7 (time frames) for each motor. The measured latency for generating all 4 MFSs for one motor is approximately 0.1231 s, which is acceptable and suitable for the requirements of the studied industrial application. Together, 1505 × 4 MFSs were created as shown in Figure 6.

2.

Step 2: Merging MFSs of the same type. In this step, all MFSs of the same type but from all motors (for example, all MFSs of sound) were merged into 4 MFSs. These MFSs were a size of 2048 × 10,535, meaning 2048 frequency bands and 10,535 timeframes, calculated as a sum of all timeframes of all 1505 motors. Figure 7 shows the merged MFSs.

3.

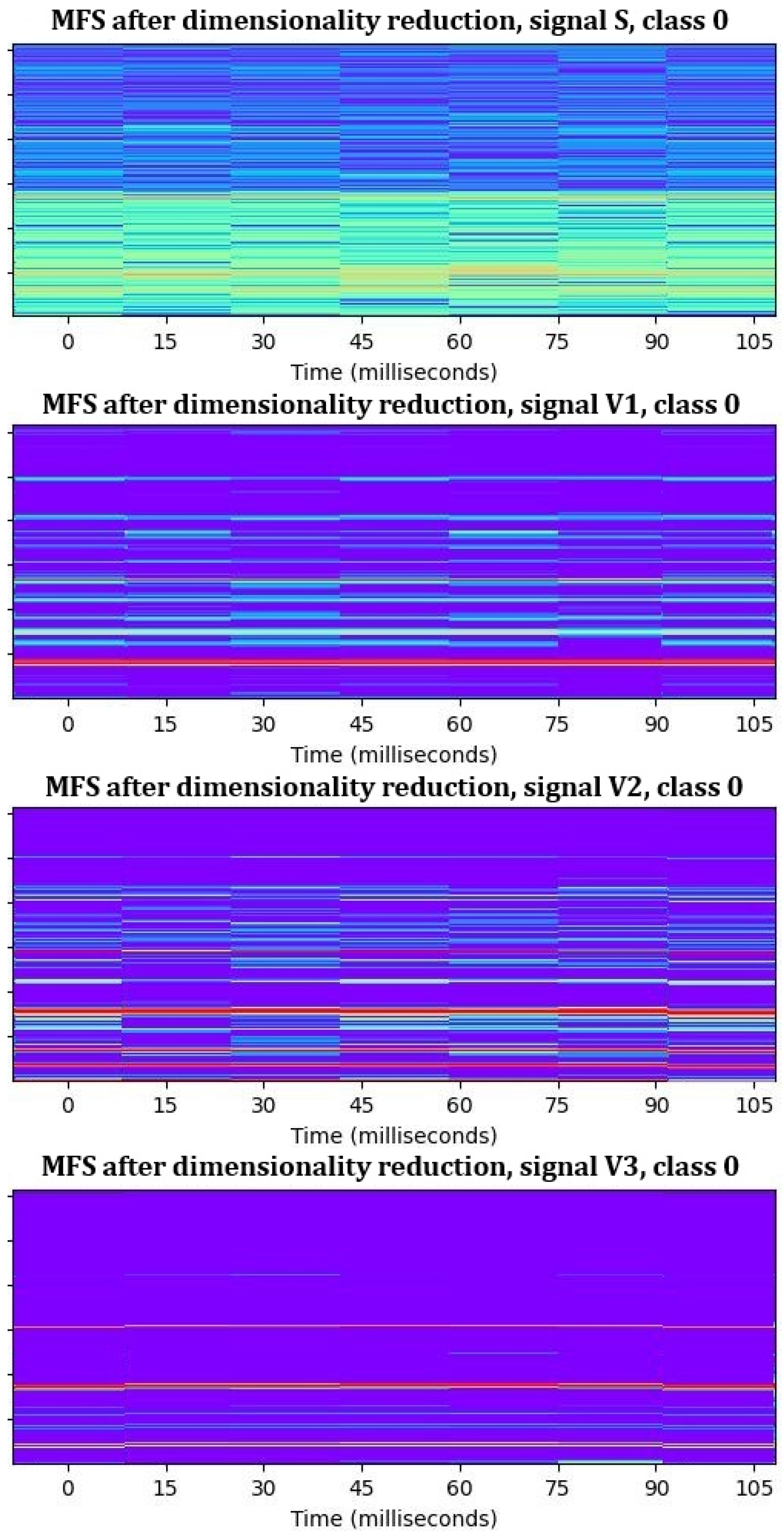
Step 3: Feature reduction. In this step, a feature reduction process was applied to identify and remove non-informative frequency bands from the merged MFSs. Several statistical methods were used to evaluate the distribution and variability of values across each frequency band, including histogram analysis, standard deviation, peak analysis, and kurtosis assessment. Frequency bands were classified as non-informative and excluded from further analysis based on the following criteria:

• Low variance: Bands with values confined to a narrow range (e.g., all values falling within a single histogram bin) and exhibiting very low standard deviation were considered uninformative. Such low variability is typically associated with background noise or redundant data that contribute minimally to classification accuracy. This principle is widely supported in the feature selection literature, where low-variance features are routinely filtered out to improve learning performance and generalization ability [35,36].
• Lack of multimodality: Bands with distributions showing only one prominent peak or no significant peaks were assumed to lack distinctive features. Informative spectral regions, especially in fault diagnosis tasks, often exhibit multimodal behaviour due to the presence of multiple signal patterns or transient components. This behaviour has been observed in fault analysis using wavelet transforms and is emphasized in machine health monitoring literature [37,38].
• Low kurtosis (<3): Bands with a kurtosis value below 3 were identified as statistically flat (platykurtic), indicating the absence of outliers or sharp peaks. Such distributions generally lack impulsive components, which are important indicators of mechanical faults in vibration and acoustic signals. The threshold of kurtosis <3 was chosen based on standard statistical definitions [39,40] and reinforced by prior studies in predictive maintenance and condition monitoring [41,42]. Although not universally prescriptive, this threshold was also verified empirically in our study bands, as kurtosis values above 3 were more frequently observed to contain features contributing to successful fault classification, while those below this threshold consistently lacked discriminative power.

These combined statistical criteria enabled the effective detection of irrelevant or redundant frequency bands. Using this approach, nearly 70% of the total bands were eliminated, significantly reducing input dimensionality while preserving informative content (Figure 8). The results of feature reduction are presented in

Table 4. Number of frequency bands before and after feature reduction.

Signal	Number of Frequency Bands Before Reduction	Number of Frequency Bands After Reduction	Part of Informative Frequency Bands
S	2048	678	0.33
V1	2048	381	0.19
V2	2048	701	0.34
V3	2048	709	0.35
Together	8192	2469	0.30

.

4.

Step 4: Creating new MFSs with only informative frequency bands. From the MFSs from step 1 we eliminated non-informative frequency bands, which were detected as non-informative after step 3. For each signal, we obtained a new dataset of reduced features for each motor, as shown in

Table 5. Size of reduced MFSs for each signal.

Signal	Size of Dataset [Features × Time Frames]
S	678 × 7
V1	381 × 7
V2	701 × 7
V3	709 × 7

. These MFSs with reduced datasets (Figure 9) were used in continuing work.

5.

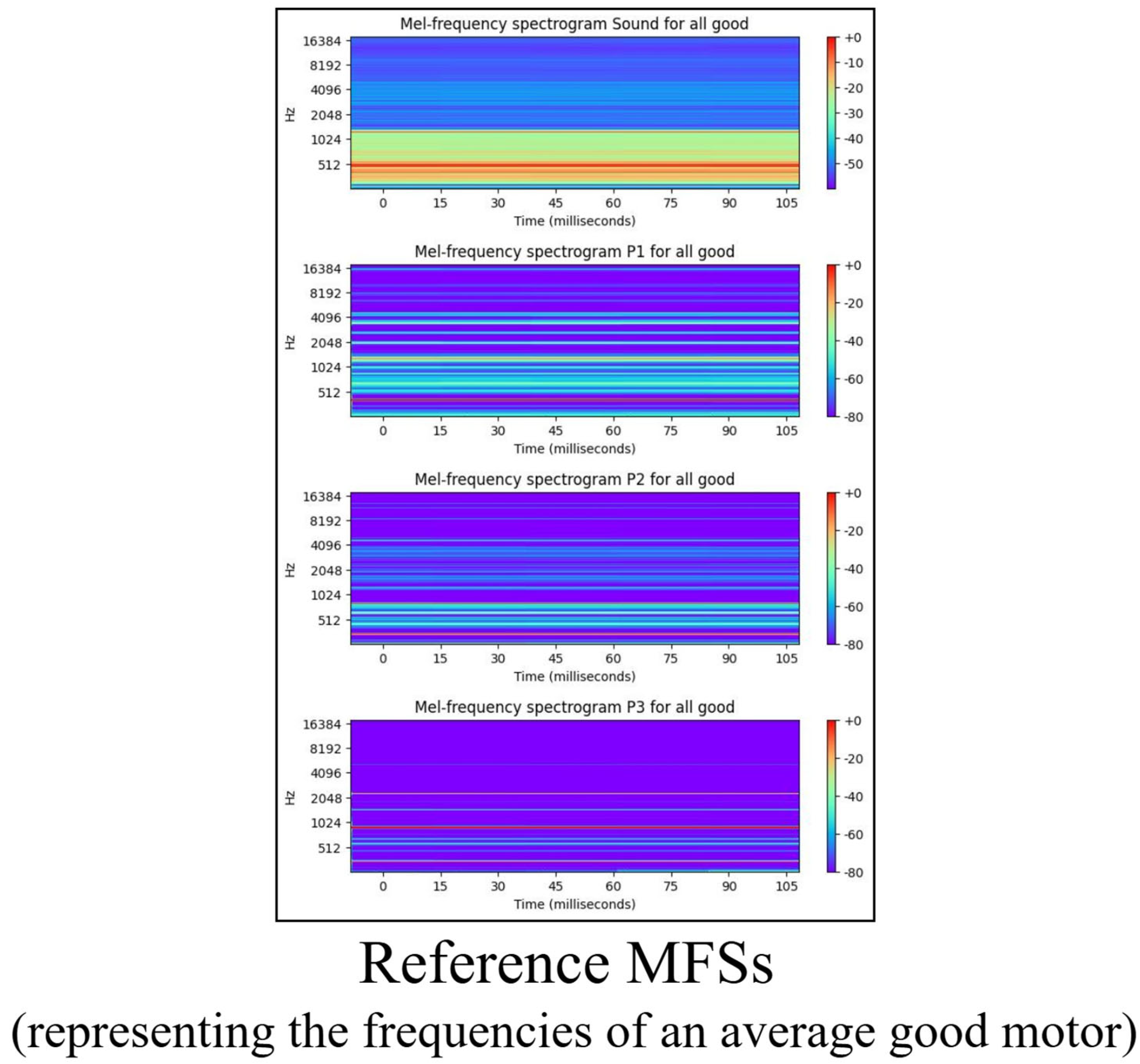
Step 5: Creating the reference MFSs. Next, we selected all MFSs of good motors (class 0). From this group, we calculated an average MFS for each signal. These MFSs represent the typical time–frequency characteristics of non-faulty motors and serve as a baseline profile of a healthy motor. These average MFSs, illustrated in Figure 10, are also referred to as reference MFSs. This step was critical for step 6 where a direct comparison of the MFSs of each individual motor to the reference good motor was performed.

6.

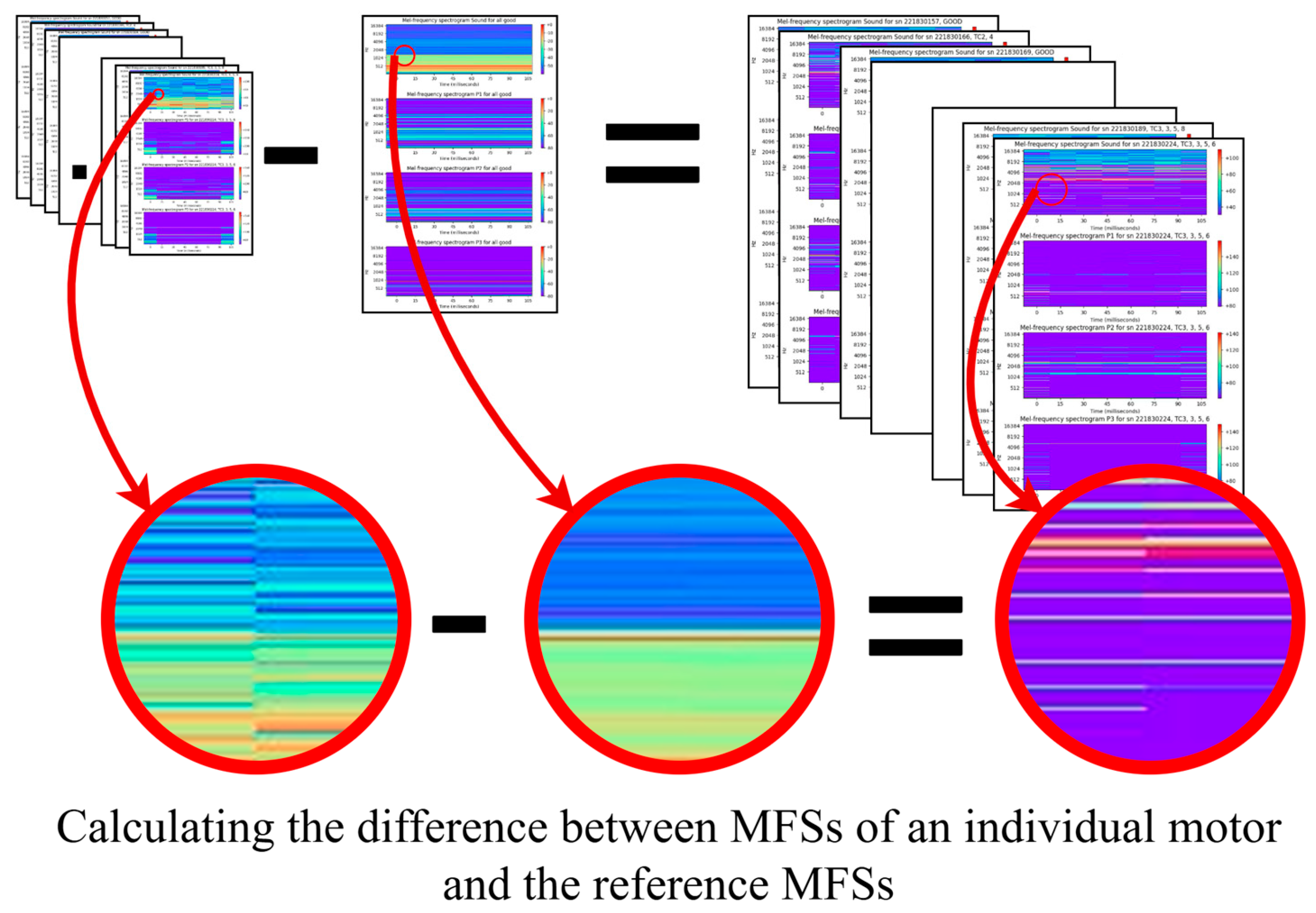
Step 6: Comparing MFSs of an individual motor to reference MFSs. The MFSs of each individual motor from step 4 were compared to the reference MFSs, as shown in Figure 11, and explained with (1). The comparison results reveal the difference between the individual motor and the normal state. This approach allowed for an easy identification of the time–frequency regions that differ from normal behaviour. This difference was used in further machine learning processes. This method is quite common in anomaly detection when fault data are sparse or highly imbalanced. Usually, it simplifies the interpretability of the model and increases the robustness of the classification. This approach also enabled more sensitive and targeted fault detection [43,44].

$${\mathrm{M}\mathrm{E}\mathrm{L}}_{\mathrm{D}}\left(\mathrm{i}\right)=\mathrm{M}\mathrm{E}\mathrm{L}\left(\mathrm{i}\right)-{\mathrm{M}\mathrm{E}\mathrm{L}}_{\mathrm{R}}\hspace{1em}\left(\mathrm{i}=1\dots 1505\right)$$

(1)

At the end of the process, MFSs of the reduced datasets were generated. These MFSs served as inputs for the subsequent machine learning processes. Figure 12 shows the MFSs before dimensionality reduction of motors of class 0. Figure 13 shows its corresponding MFSs after feature reduction. Similar, Figure 14 illustrates the MFSs before dimensionality reduction of class 1 and Figure 15 illustrates its corresponding MFSs after feature reduction. Finally, Figure 16 represents the MFSs before feature reduction of class 2 and Figure 17 its corresponding MFSs after feature reduction.

Importantly, the feature reduction process successfully preserved the essential structure within each class, maintaining critical visual information despite dimensionality simplification. Although non-informative features were eliminated and visual separation between classes was enhanced, the distinction between motor classes based on the visual inspection of MFSs alone remained challenging, even for experienced human experts.

5. Neural Network Architecture and Training

For the purposes of the classification, a hybrid neural network architecture combining CNNs and BiGRUs was employed. The combination of CNNs and BiGRUs has already been explained in Section 3.3 (CNNs are well-suited for extracting local patterns and hierarchical features from image-like inputs, while BiGRUs are suitable for capturing temporal dependencies and sequence dynamics). Based on previous research and empirical testing, the designed architecture includes two CNN and two BiGRU layers.

As explained in Section 4.1, the dataset consisted of 1505 motors, each labelled as one of three classes (class 0—good, class 1—fault in TC2, and class 2—fault in TC3). Figure 18 explains the data manipulation. At the start, the source dataset was split into a test set (ca. 33% of motor instances) and a training set (ca. 67% of motor instances).

The test set remained untouched and was exclusively used for final model evaluation. In the training set, the imbalance was fixed and the set was then used for training the neural network and hyperparameter tuning. Because of the high class imbalance (the low presence of class 1 and 2), we implemented balanced training using the RandomOverSampler method. This oversampling method duplicates minority class samples to balance the class distribution. Among the tested techniques, the RandomOverSampler yielded the most consistent and reliable results for our task. The test set remained imbalanced, presenting real-world distribution.

To optimize the network (the number of neurons in each layer, kernel sizes in CNN, dropout rates, etc.), we employed Bayesian optimization via a Tuner search. This method builds a probabilistic model of the objective function and selects hyperparameters that are most likely to improve model performance based on prior evaluations. Compared to other methods, Bayesian optimization is more efficient and converges faster to optimal parameters [45].

6. Results

A neural network that could successfully classify motors into three classes (0, 1, and 2) was created after the training process was finished. Larger convolutional kernels and layers with relatively few neurons were combined to create the final architecture that performed the best. This suggests that a seemingly simpler network architecture, capable of analysing broader signal patterns, was more effective for this task. Dropout layers were added to prevent overfitting, and batch normalization was used to accelerate and stabilize training. This architecture reflects a well-balanced approach between model complexity and generalization ability. The details of the model are presented in

Table 6. Neural network architecture and hyperparameter configuration used for classification.

Layer (Type)	Output Shape	Details
Input	(None, 7, 2469, 1)	Size of MFS
First Conv2D	(None, 7, 2469, 32)	First 2D convolutional layer with 32 filters, ReLU activation, and kernel size (7 × 7)
First Batch Normalization	(None, 7, 2469, 32)	Normalizes activations, improves training stability
First Max Pooling 2D	(None, 3, 1234, 32)	Down samples feature maps by 2 × 2
First Dropout	(None, 3, 1234, 32)	Prevents overfitting, dropout value 0.5
Second Conv2D	(None, 3, 1234, 64)	Second 2D convolutional layer with 64 filters, ReLU activation, and kernel size (7 × 7)
Second Batch Normalization	(None, 3, 1234, 64)	Further normalization post-convolution
Second Max Pooling 2D	(None, 1, 617, 64)	Further spatial reduction
Second Dropout	(None, 1, 617, 64)	Additional dropout, dropout value 0.5
Reshape	(None, 1, 39,488)	Flattening spatial data into time sequence
First Bidirectional BiGRU	(None, 1, 128)	First BiGRU layer (2 × 64 units) capturing bidirectional context
Second Bidirectional BiGRU	(None, 128)	Second BiGRU layer (2 × 64 units), flattening to vector
First Dense	(None, 64)	Fully connected layer
Third Dropout	(None, 64)	Final dropout before output, dropout value 0.4
Second Dense	(None, 3)	Final layer for 3-class classification (Softmax)

.

To evaluate the accuracy and robustness of the trained neural network, we performed a classification on the test set (explained in 0). The classification performance is shown using a confusion matrix (Figure 19). High values along the diagonal indicate correct classifications and off-diagonal values represent misclassifications. The matrix highlights the model’s strong performance on the majority class (class 0) and its ability to correctly identify minority classes (classes 1 and 2), despite class imbalance. This indicates that the model handles class imbalance effectively, particularly demonstrating a reliable recognition of minority classes (classes 1 and 2), despite their low support.

Detailed evaluation metrics of the classification model’s performance are presented in

Table 7. Classification results on the test set (per class). Values in brackets indicate 95% confidence intervals estimated via bootstrap resampling.

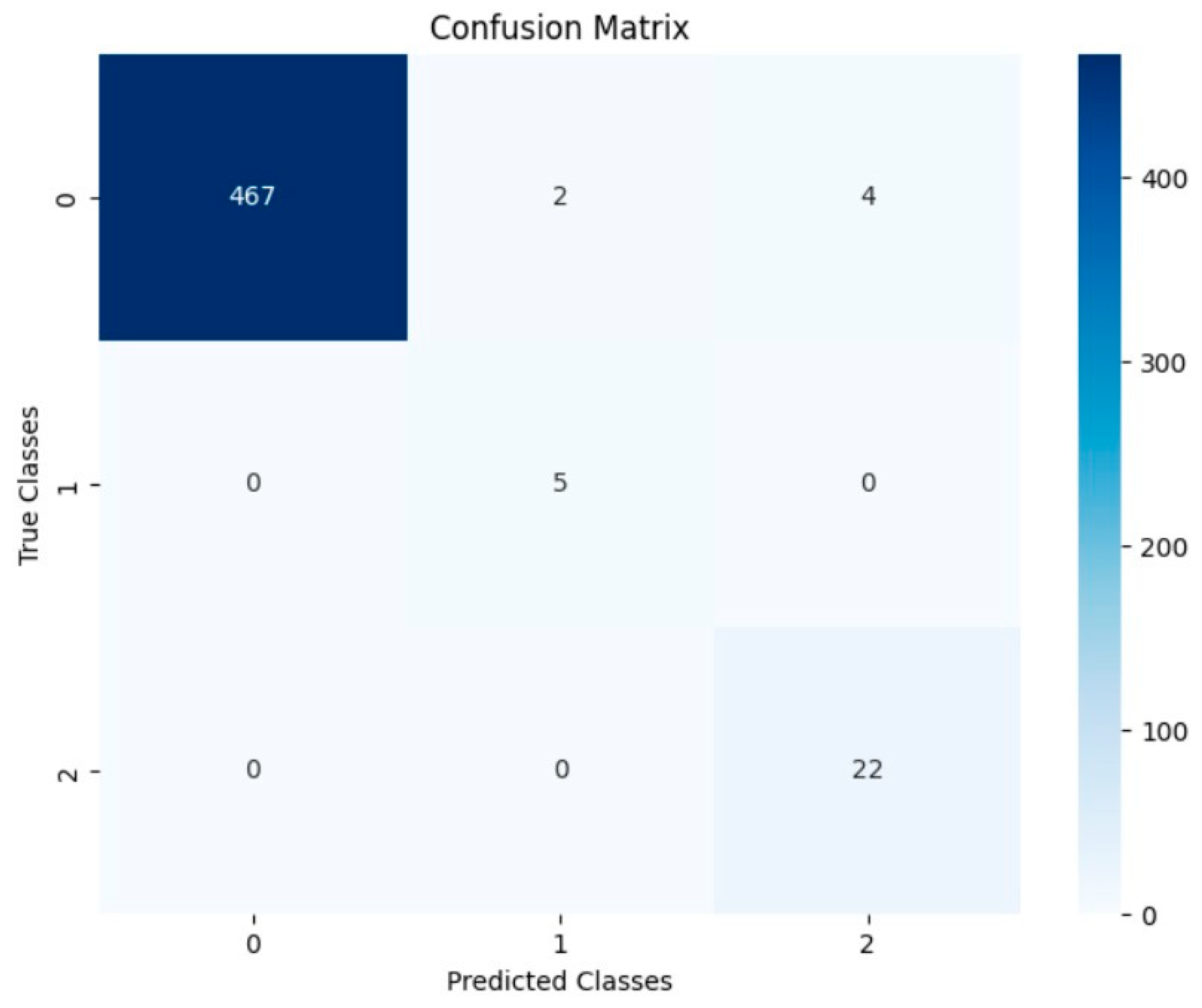
Class	Precision	Recall	F1 Score	Support
0	1 [0.99, 1]	0.99 [0.98, 1]	0.99 [0.98, 1]	473
1	0.71 [0.55, 1]	1 [0.80, 1]	0.83 [0.67, 1]	5
2	0.85 [0.75, 1]	1 [0.92, 1]	0.92 [0.84, 1]	22

and the metrics in

Table 8. Overall evaluation of neural network performance. Values in brackets indicate 95% confidence intervals estimated via bootstrap resampling.

Metrics	Precision	Recall	F1 Score	Support
Accuracy			0.99 [0.98, 1]	500
Macro average	0.85 [0.75, 0.95]	1 [0.99, 1]	0.91 [0.82, 0.98]	500
Weighted average	0.99 [0.98, 1]	0.99 [0.98, 1]	0.99 [0.98, 1]	500

provide more insights into the general effectiveness and class-specific behaviour of the model. The performance was evaluated through following metrics:

• Precision—the proportion of motors classified into a class that truly belong to that class;
• Recall—the proportion of motors of a given class that were correctly identified;
• F1 score—the harmonic mean of precision and recall, offering a balanced view of both metrics;
• Support—the number of motor instances per class;
• Accuracy—the overall percentage of correct predictions across all classes;
• Macro average—the unweighted average of precision, recall, and F1 score across all classes (not accounting for class imbalance);
• Weighted average—The average of precision, recall, and F1 score across all classes (weighted by the number of instances per class, thus incorporating class imbalance).

To provide a more statistically robust evaluation, 95% confidence intervals for each evaluation metric were computed using bootstrap resampling (1000 iterations). This method estimates the variability in model performance by repeatedly sampling the test set and recalculating metrics, offering a clearer picture of metric reliability.

Notably, class 0, which has the highest support (n = 473), achieves near-perfect scores across all metrics—precision, recall, and F1 score—indicating the model’s strong reliability on the majority class. The narrow confidence intervals [0.99, 1.00] suggest that this performance is highly stable and consistent across resampled test sets.

For class 1, despite the perfect recall (1.00), the precision has a much wider confidence interval [0.55, 1.00]. This indicates that while the model consistently identifies all class 1 instances, it sometimes misclassifies samples from other classes as class 1. This variability is primarily due to the very small support size (5), which amplifies statistical uncertainty. The F1 score of 0.83 with an interval of [0.67, 1.00] shows this balance between perfect recall and fluctuating precision.

Class 2, with slightly more support (n = 22), also shows excellent recall (1.00) and strong precision (0.85), with a narrower confidence interval [0.75, 1.00] compared to class 1. This implies more consistent performance, with fewer misclassifications and better stability than class 1.

The model achieves an overall accuracy of 0.99, with a very tight 95% confidence interval [0.98, 1.00], confirming that the performance is statistically robust and generalizes well across the test distribution. The macro average metrics show additional insights: while precision and F1 score show some variability, recall remains consistently high. This suggests that the model rarely misses true instances across any class, even though precision may fluctuate for smaller classes. In contrast, the weighted average shows minimal variability across all metrics. This reflects the model’s overall stability, driven by its strong and consistent performance on the dominant class 0.

Together, these confidence intervals underscore that while the model is highly reliable overall, caution should be exercised when interpreting performance on underrepresented classes, especially class 1, due to inherent statistical uncertainty from the small sample size.

Additionally, a t-distributed stochastic neighbour embedding (t-SNE) projection of the Softmax outputs was generated (Figure 20). t-SNE is a nonlinear dimensionality reduction technique that visualizes high-dimensional data (such as class probabilities) in two dimensions. Each point represents a sample and colours correspond to the predicted class: blue (class 0), green (class 1), and red (class 2.) This plot helps to illustrate how confidently and distinctly the model clusters the classes in its output space. Tight, well-separated clusters generally indicate high confidence and low overlap between class predictions, whereas scattered or overlapping regions may signal confusion between classes. The distinct clustering observed in the t-SNE plot confirms the model’s confidence and clarity in class separation, consistent with the high classification scores reported earlier.

7. Conclusions

The classifier developed in this study has demonstrated excellent efficiency and accuracy in the classification of BLDC motors into three classes (class 0, class 1, and class 2). It performed well, especially in terms of precision and recall. Most importantly, no false negatives were detected (no faulty motors were misclassified as good), which means that no faulty motor is delivered to the market or to the end-users. The rate of false positives (good motors misclassified as faulty) was very low, but not zero, which means a minor operational inconvenience. Beyond high precision and recall, the classifier’s internal feature representation—illustrated through t-SNE—suggests strong class separation and high confidence in its decision boundaries.

Interestingly, the classifier showed the ability to find faults, originally detected in TC3. Using the existing classification algorithm (explained in Section 2.2), it is not possible to detect these faults from the acoustic and vibrational signals of TC2. The confusion matrix confirmed that the algorithm not only detects faults but also localizes them between those originating in TC2 and TC3. This suggests that diagnostic insights traditionally dependent on TC3 can now be inferred from TC2, potentially enabling earlier or more integrated fault detection within the existing TC2 framework. This internal clarity, combined with robust generalization to minority class scenarios, highlights the model’s reliability in diverse and potentially imbalanced real-world conditions.

An important limitation of this study is the absence of motors with faults in TC1, which prevents the trained network’s ability to recognize such faults. Expanding the dataset to include instances with faults at TC1 would be crucial for full coverage of all possible fault classes.

Another limitation is related to model interpretability. While CNN-BiGRU architecture learns discriminative features from raw signals, it functions as a black box. Therefore, it is unclear which specific signal components (frequencies, time intervals, etc.) are most influential in the model’s decision-making. This limits traceability and explainability, which are critical for gaining trust in industrial AI systems.

In future work, it would be valuable to analyse the individual contribution of each input signal (V1, V2, V3, and S) to the overall classification performance. This could lead to further dimensionality reduction by removing redundant or low-impact features, potentially simplifying the hardware configuration for future deployments.

Additionally, the transferability of the trained model to other similar types of motors produced on the manufacturing line should be investigated. Techniques such as domain adaptation or transfer learning [46,47] could enable the model architecture to serve as a foundation for new classifiers, tailored to different motor variants.

Future work should also address model interpretability. Applying explainable AI (XAI) techniques such as Grad-CAM, SHAP, or layer-wise relevance propagation (LRP) can help to identify which features are most influential in the decision-making process. These insights can enhance trust, support model validation, and guide future optimizations.

Moreover, it would be beneficial to compare the performance of the proposed CNN-BiGRU architecture with other deep learning models, such as CNN-LSTM, transformer-based models, or lightweight 1D CNNs [48,49]. These comparisons could identify architectures that offer better accuracy, lower computational cost, or improved generalization to unseen motor types and fault conditions.

This study demonstrates the potential of deep learning models (CNNs combined with BiGRUs) for raw-signal-based industrial fault detection. By eliminating the need for manual feature engineering and expert-driven pre-processing, the proposed system enables faster, more scalable, and more adaptable diagnostics. Moreover, the ability to detect TC3 faults using only TC2 data suggests the potential for reducing system complexity and inspection time in the manufacturing line. Moreover, a combination of broader datasets, interpretability tools, and generalization strategies will be critical for transforming this model into a fully functional, explainable, and adaptable industrial AI solution.