Improved Nonlinear Dynamic Model of Helical Gears Considering Frictional Excitation and Fractal Effects in Backlash
Abstract
1. Introduction
2. Model and Methodology
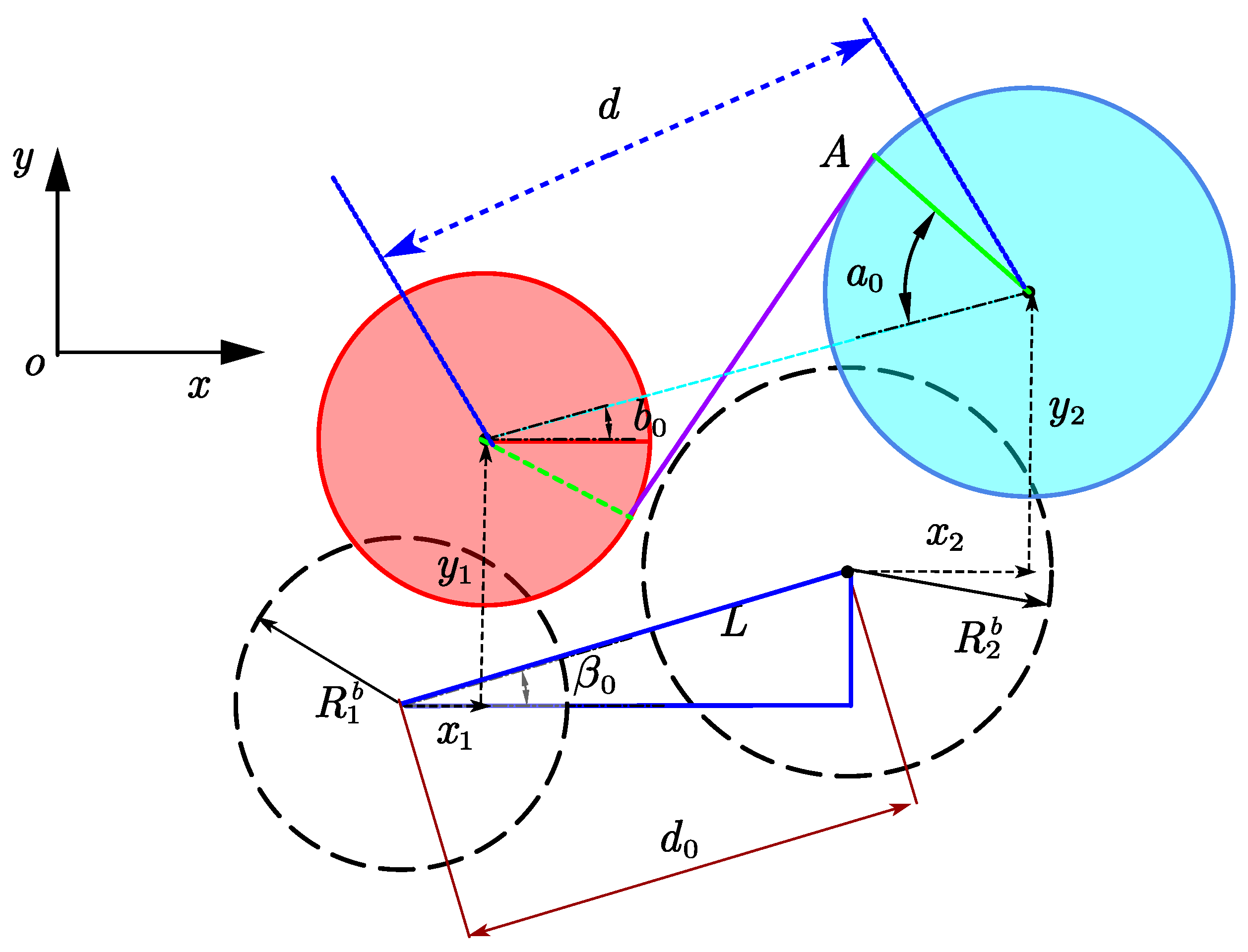
2.1. Time-Varying Gear Backlash Based on Fractal Theory
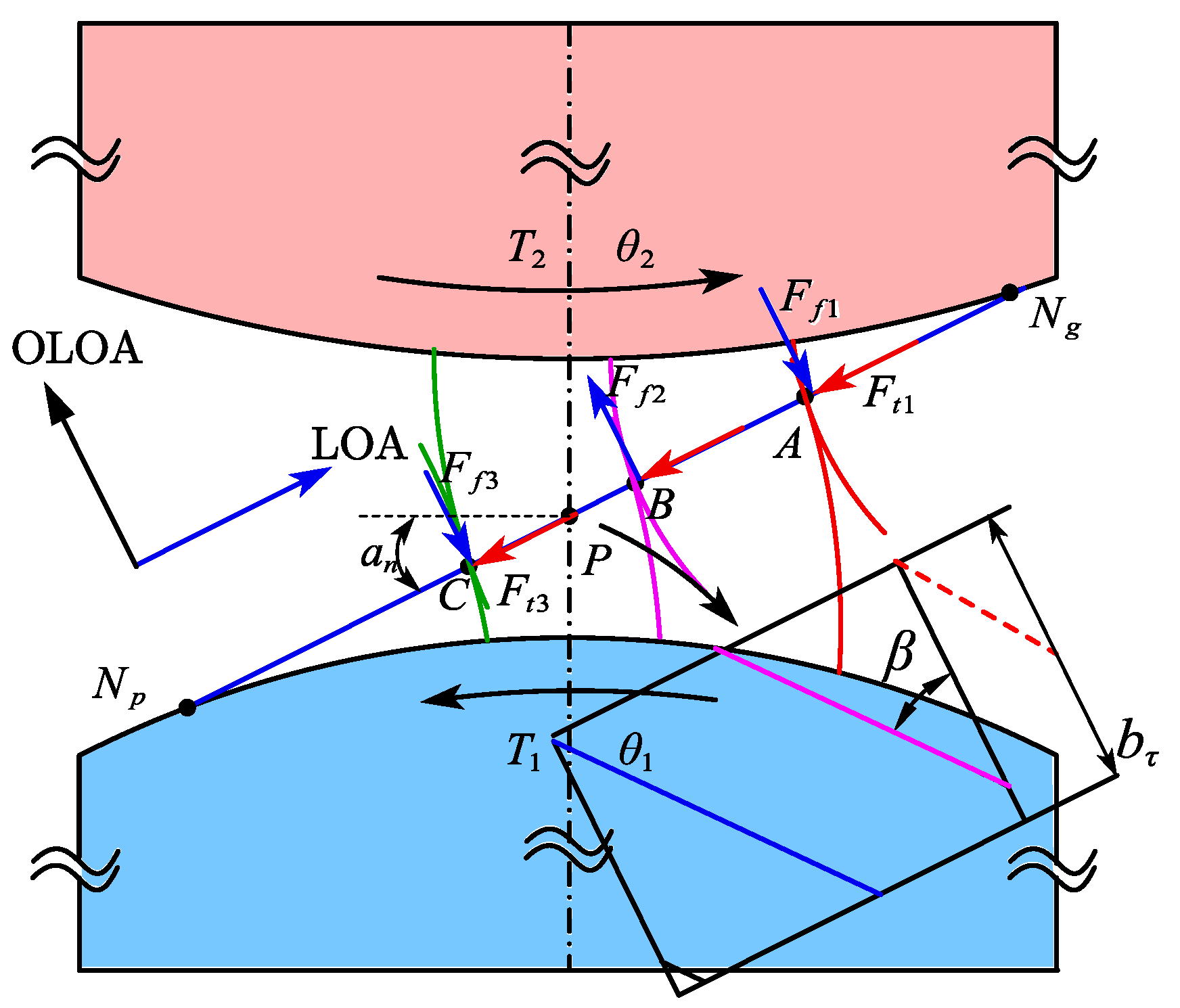
2.2. Dynamic Model of the Gear System
3. Model Validation and Adaptability
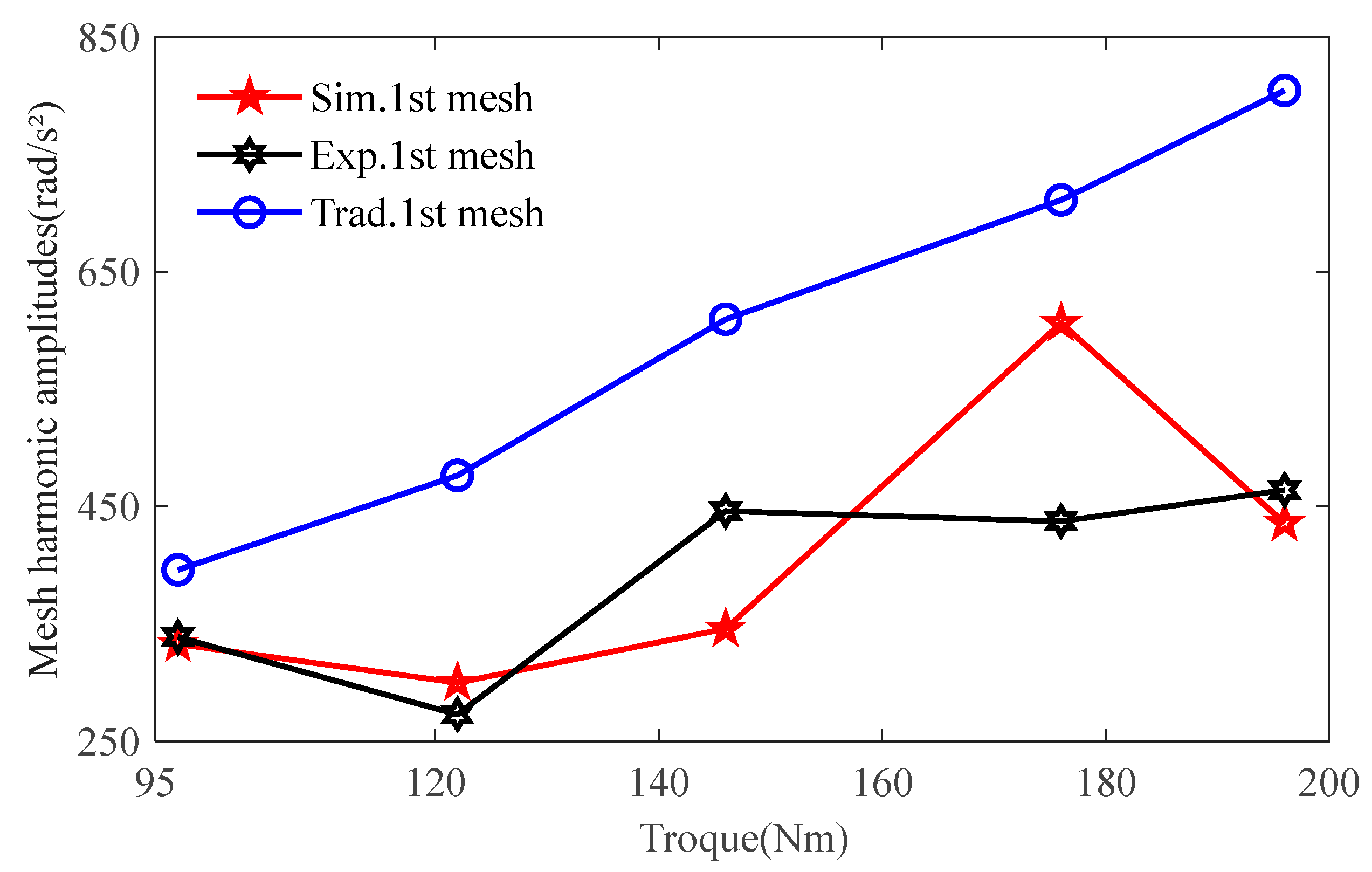
3.1. Model Experimental Verification
3.2. Universal Adaptability of Model
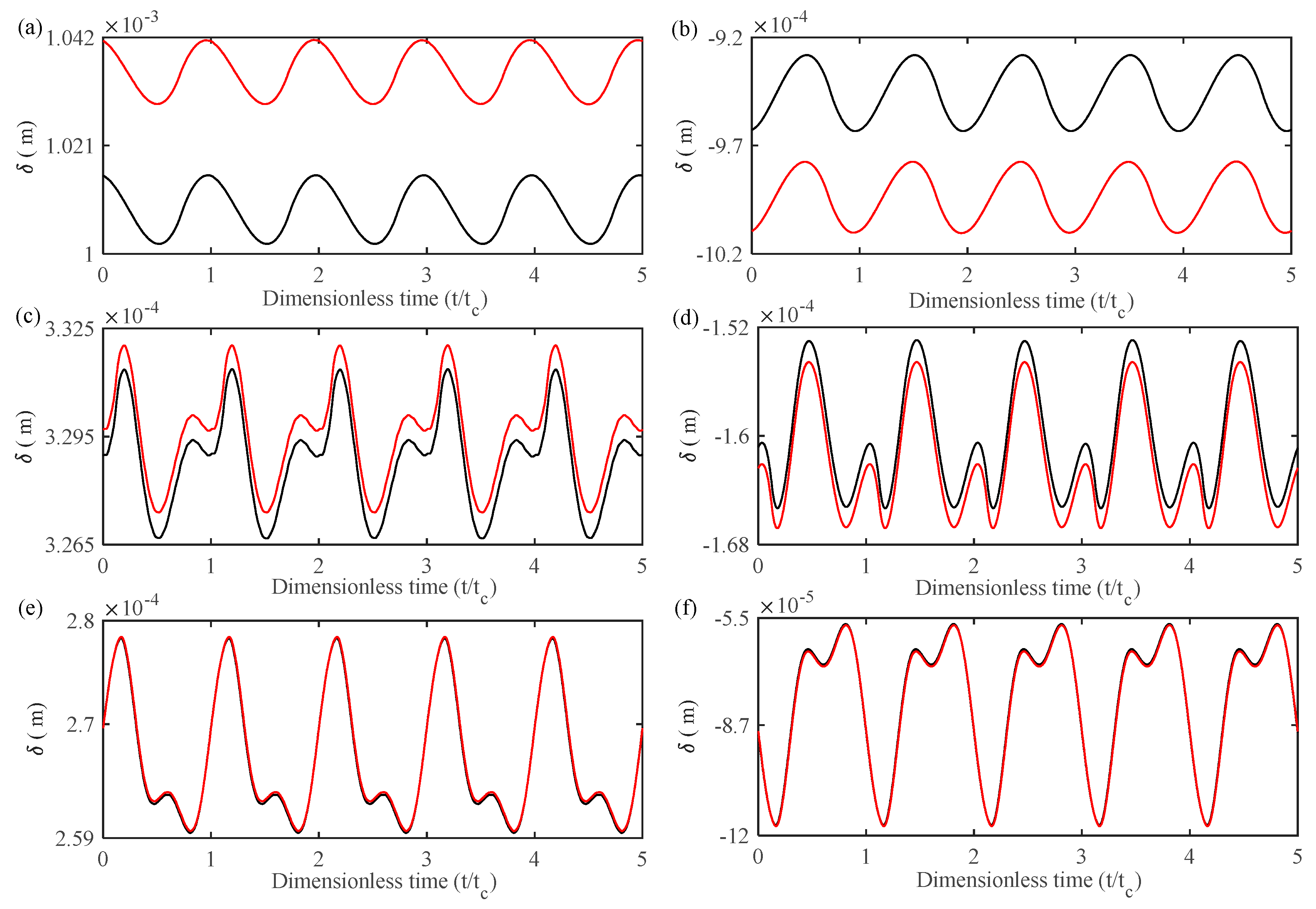
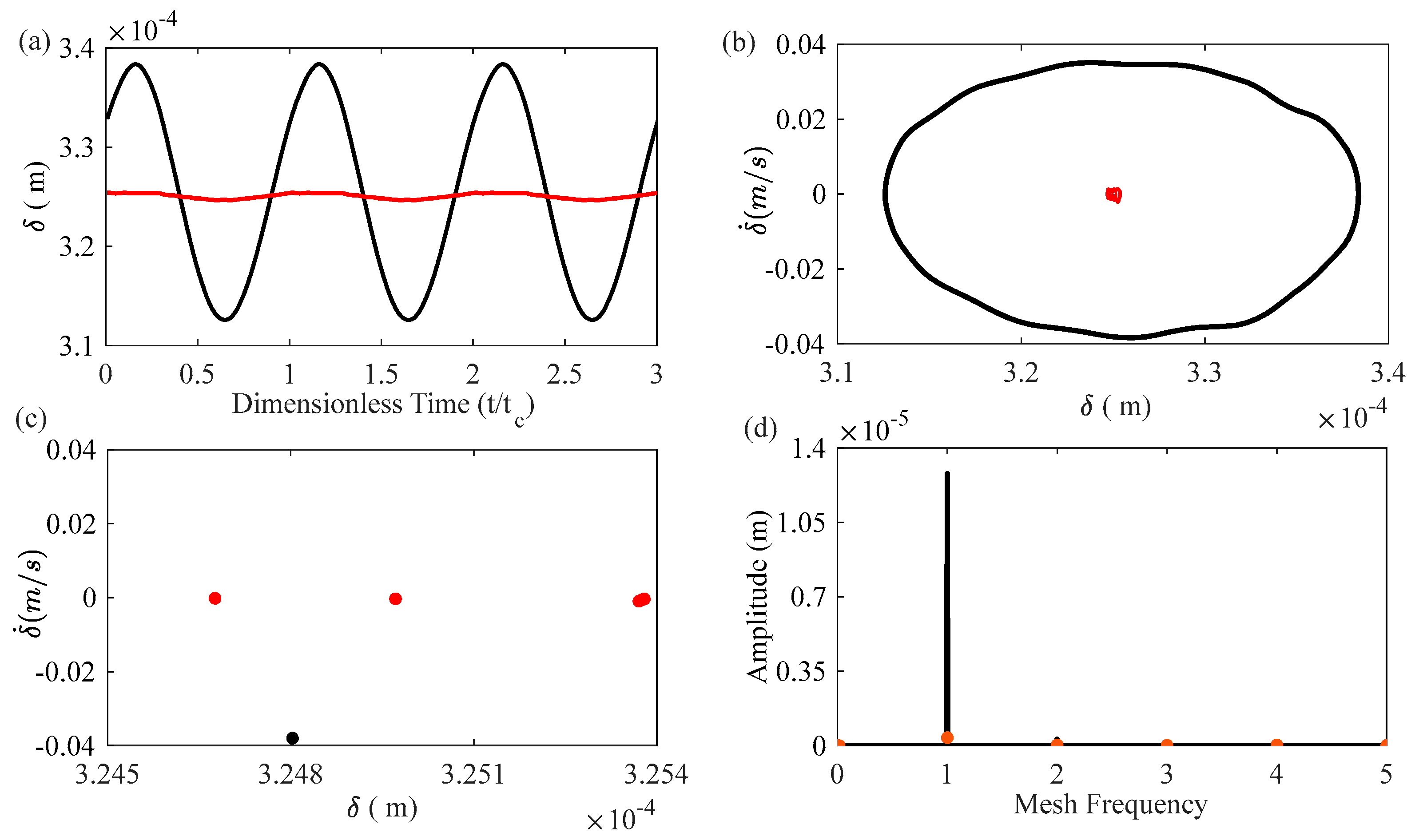
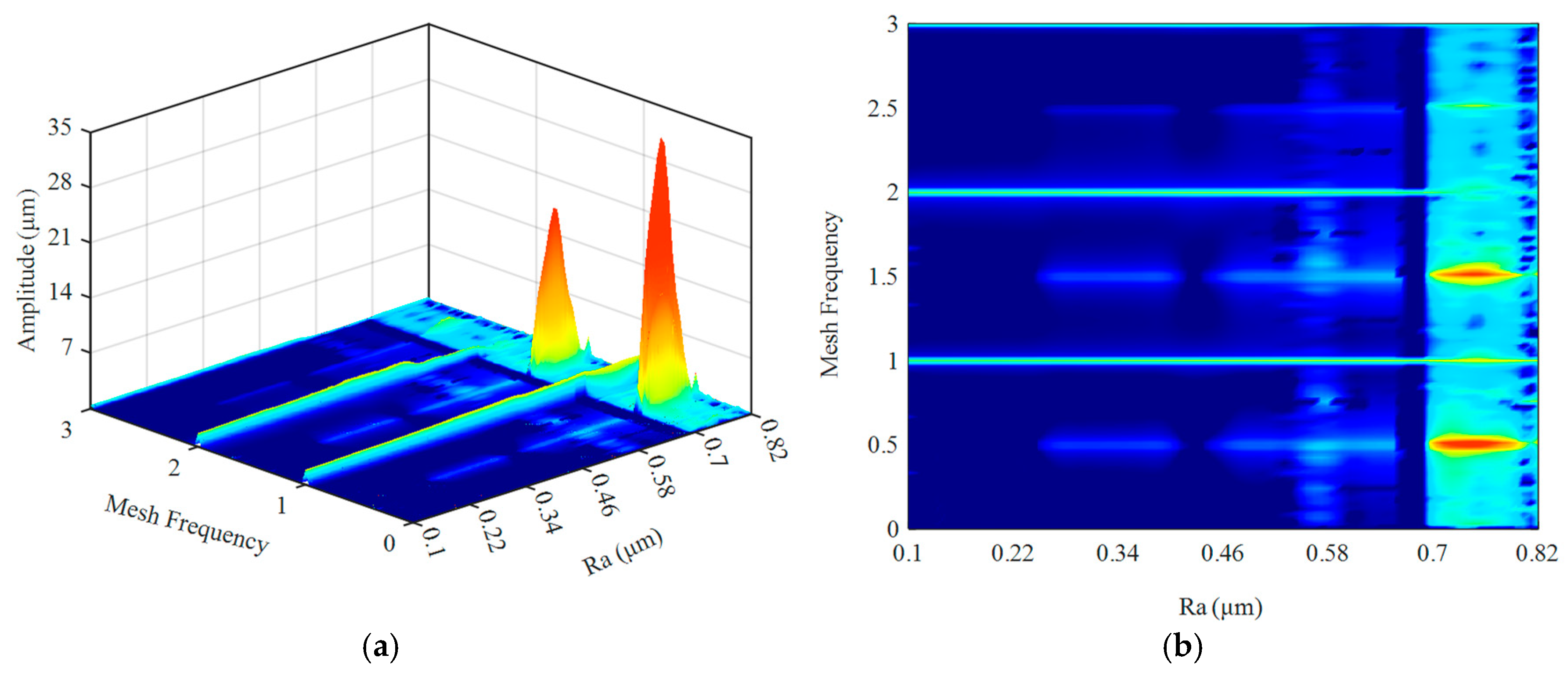
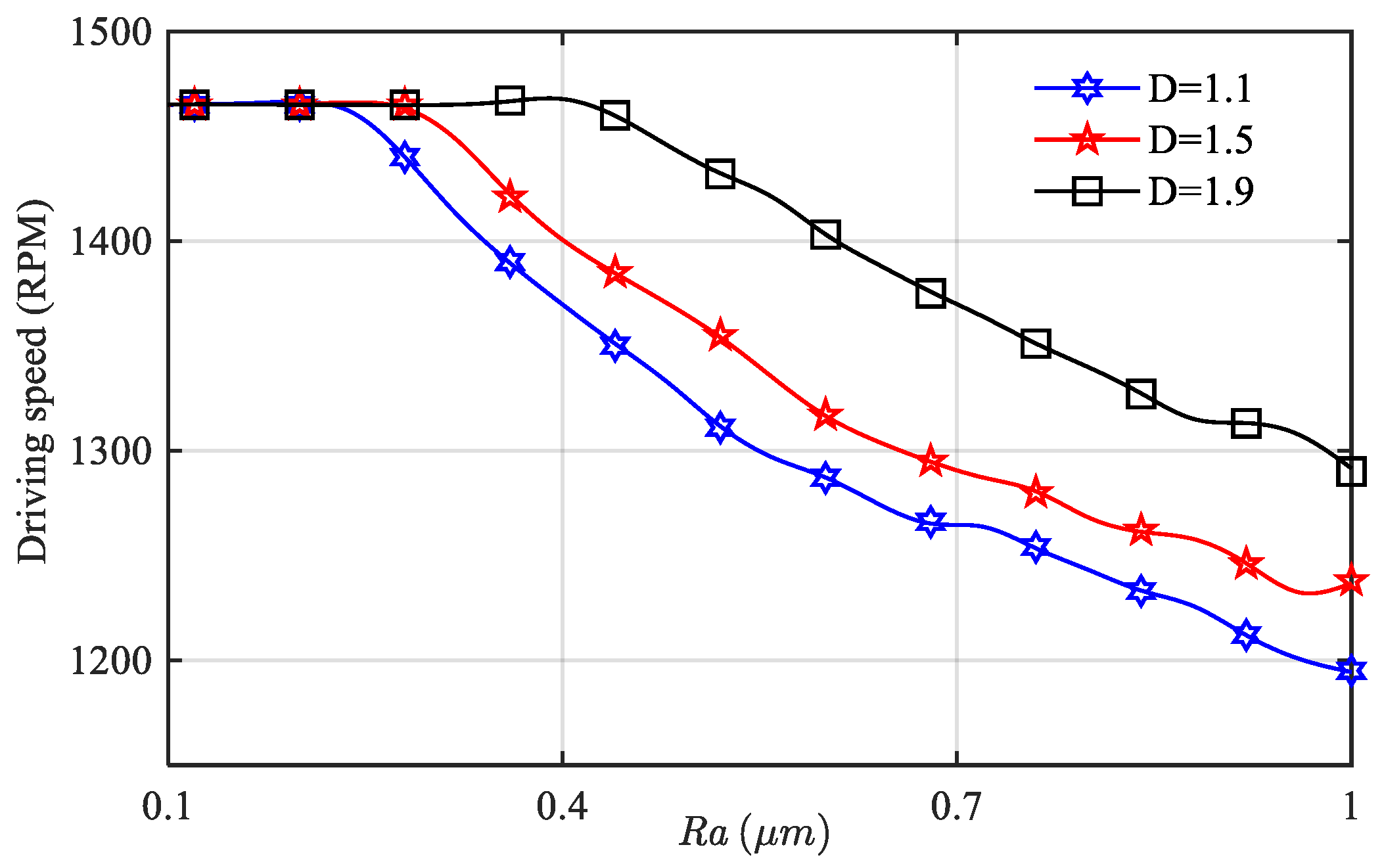
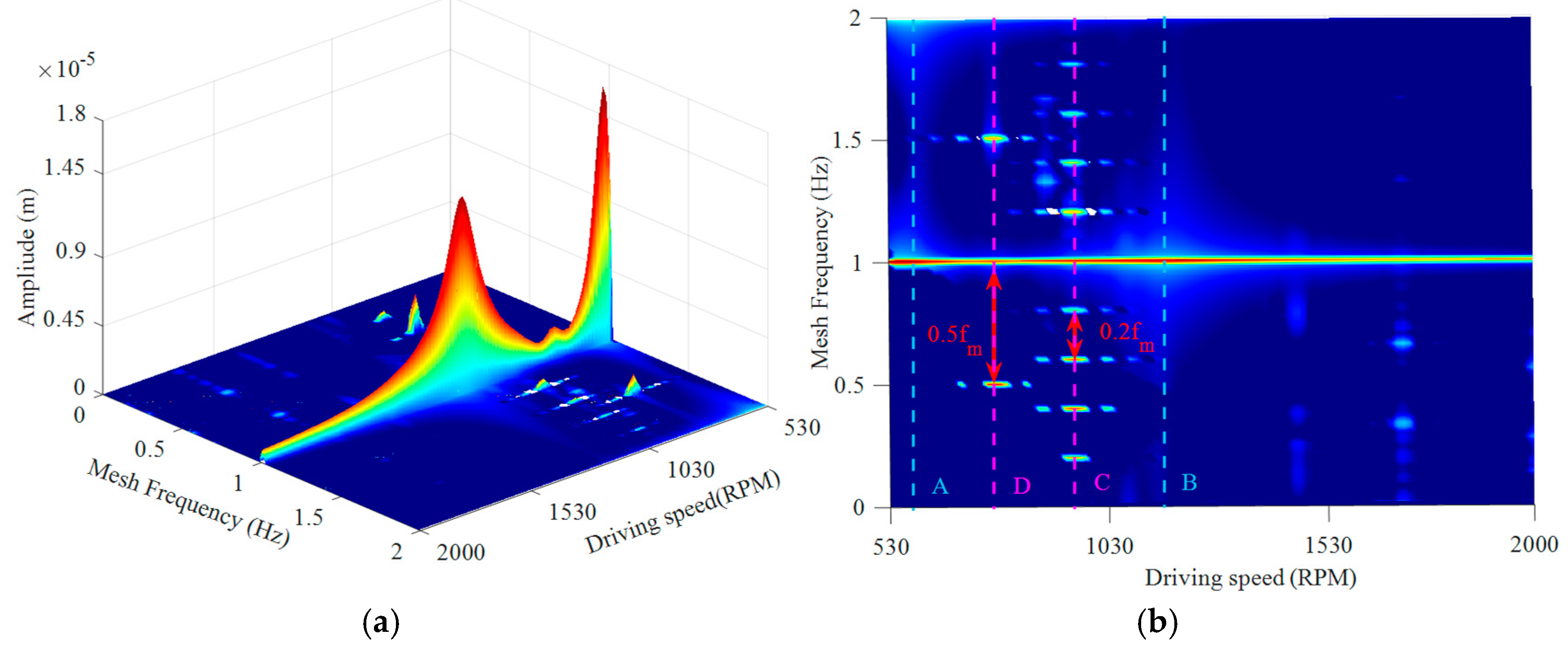
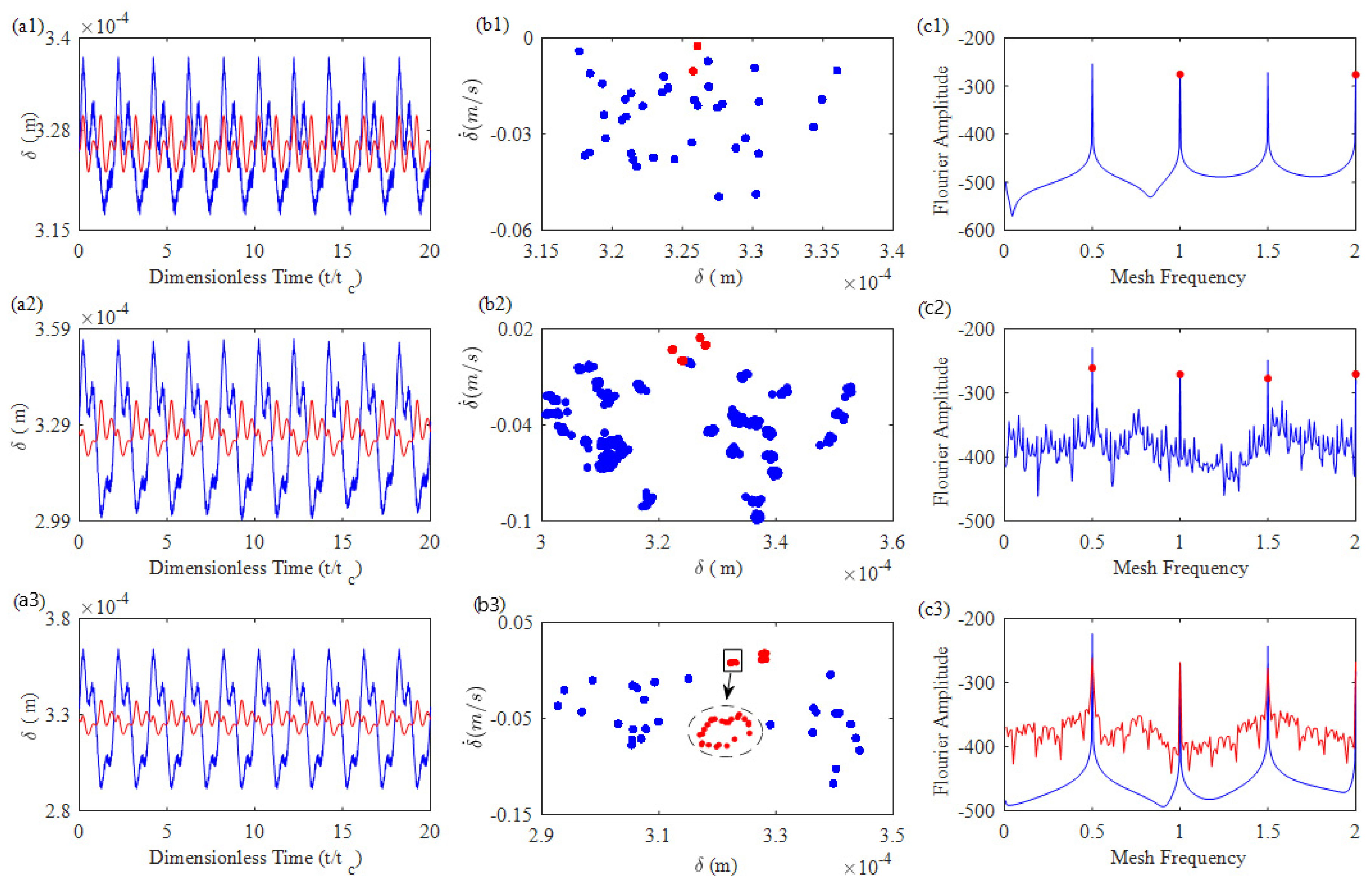
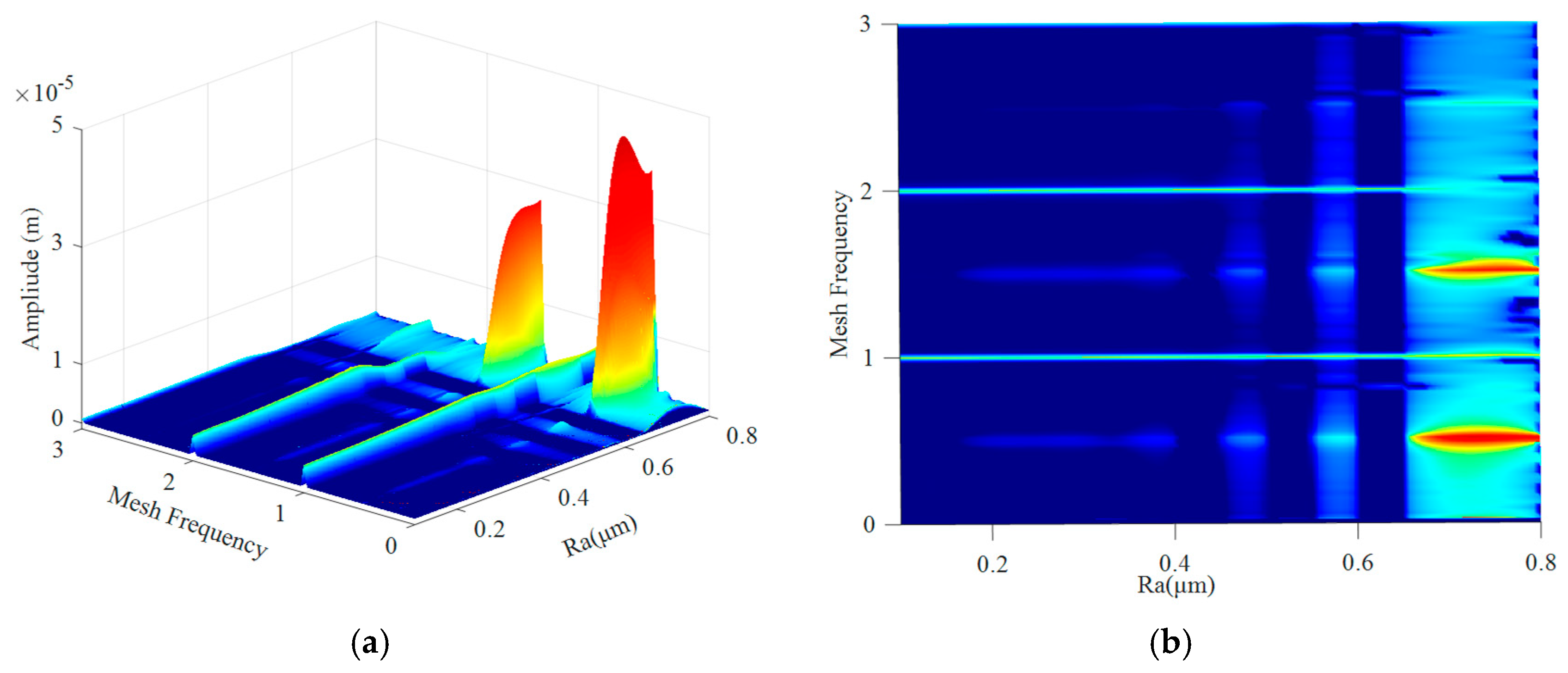
4. Result and Analysis
4.1. Effect of Frictional Excitation on the Gear System
4.2. The Coupling Effect of Frictional Excitation and Fractal Excitation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Alphabets | |
| Initial normal pressure angle | |
| Time-varying normal pressure angle | |
| Initial normal backlash of gears | |
| Time-varying normal position angle | |
| Gear time-varying normal backlash | |
| Time-varying mesh damping | |
| Support damping in the , and directions | |
| The time-varying center distance | |
| Initial Normal center distance of gears | |
| The fractal dimension | |
| Dynamic mesh force of the tooth pair | |
| Dynamic friction force of the tooth pair | |
| The component of meshing force on the , , and axes | |
| The component of fiction force on the , , and axes | |
| The characteristic-scale coefficient | |
| Moment of inertia with respect to the mass center | |
| Time-varying mesh stiffness | |
| Support stiffness in the , and directions | |
| Bearing stiffness in the , and directions | |
| Shaft stiffness in the , and directions | |
| l | Projection distance of theoretical meshing line |
| Initial tooth width | |
| Projection length of base circle tooth pitch | |
| Time-varying contact surface tooth width | |
| Mass of gear | |
| Gear contact ratio | |
| Number of pairs of instantaneously engaged teeth | |
| Base pitch | |
| Generalized force vector | |
| Pitch radius of pinion and gears | |
| Average surface roughness | |
| Radius of the base circle | |
| Total dissipation function | |
| Moment arm of the friction force for the pair | |
| Tooth tip circle radius of gears | |
| Input and output working torque | |
| Kinetic energy of gear system | |
| System engagement cycle | |
| Gear friction torque | |
| Energy generated of gear system | |
| The viscosity coefficient of the gear | |
| The sliding speed | |
| The speed of entraining motion | |
| Normal force of tooth surface contact | |
| Contact wire length | |
| Helical angle of helical gear | |
| Base helix angle | |
| Transmission error along the LOA direction | |
| Translational displacement along the LOA direction | |
| Transmission error along the OLOA direction | |
| Translational displacement along the OLOA direction | |
| Torsional vibration displacement of pinion and gear | |
| Coefficient of friction | |
| Mesh damping ratio | |
| Support damping ratio | |
| Time-varying normal meshing angle | |
| Off-line-of-action | |
| Dynamic transmission error | |
| Line-of-action | |
| Electrohydrodynamic lubrication |
Appendix A
References
- Roda-Casanova, V.; Gonzalez-Perez, I. Investigation of the effect of contact pattern design on the mechanical and thermal behaviors of plastic-steel helical gear drives. Mech. Mach. Theory 2021, 164, 104401. [Google Scholar] [CrossRef]
- Jordan, J.M.; Blockmans, B.; Desmet, W. A linear formulation for misaligned helical gear contact analysis using analytical contact stiffnesses. Mech. Mach. Theory 2023, 187, 105373. [Google Scholar] [CrossRef]
- Guilbert, B.; Velex, P. Investigations on mesh stiffness functions in three-dimensional spur and helical gear models. Definitions and numerical simulations. Mech. Mach. Theory 2024, 203, 105823. [Google Scholar] [CrossRef]
- Bozca, M. Transmission error model-based optimisation of the geometric design parameters of an automotive transmission gearbox to reduce gear-rattle noise. Appl. Acoust. 2018, 130, 247–259. [Google Scholar] [CrossRef]
- He, Z.; Zhang, T.; Lin, T. Novel mathematical modelling method for meshing impact of helical gear. Mech. Mach. Theory 2020, 152, 103949. [Google Scholar] [CrossRef]
- Wang, J.G.; Lv, B.; Sun, R.; Zhao, Y.X. Resonance and stability analysis of a cracked gear system for railway locomotive. Appl. Math. Model. 2020, 77, 253–266. [Google Scholar] [CrossRef]
- Yu, W.; Mechefske, C.K. Analytical modeling of spur gear corner contact effects. Mech. Mach. Theory 2016, 96, 146–164. [Google Scholar] [CrossRef]
- Kim, W.; Yoo, H.H.; Chung, J. Dynamic analysis for a pair of spur gears with translational motion due to bearing deformation. J. Sound Vib. 2010, 329, 4409–4421. [Google Scholar] [CrossRef]
- Kim, W.; Lee, J.Y.; Chung, J. Dynamic analysis for a planetary gear with time-varying pressure angles and contact ratios. J. Sound Vib. 2012, 331, 883–901. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Yao, Z.; Yang, X.; Sun, R.; Zhao, Y. Nonlinear characteristics of a multi-degree-of-freedom spur gear system with bending-torsional coupling vibration. Mech. Syst. Signal Process. 2019, 121, 810–827. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, F. Dynamic features of three-dimensional helical gears under sliding friction with tooth breakage. Eng. Fail. Anal. 2016, 70, 305–322. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, F. Mesh stiffness modelling and dynamic simulation of helical gears with tooth crack propagation. Meccanica 2020, 55, 1215–1236. [Google Scholar] [CrossRef]
- Wan, Z.; Cao, H.; Zi, Y.; He, W.; Chen, Y. Mesh stiffness calculation using an accumulated integral potential energy method and dynamic analysis of helical gears. Mech. Mach. Theory 2015, 92, 447–463. [Google Scholar] [CrossRef]
- Sun, Z.; Chen, S.; Hu, Z.; Lei, D. Vibration response analysis of a gear-rotor-bearing system considering steady-state temperature. Nonlinear Dyn. 2022, 107, 477–493. [Google Scholar] [CrossRef]
- Kong, X.; Hu, Z.; Tang, J.; Chen, S.; Wang, Z. Effects of gear flexibility on the dynamic characteristics of spur and helical gear system. Mech. Syst. Signal Process. 2023, 184, 109691. [Google Scholar] [CrossRef]
- Abdallah, O.; Sassi, S. Contribution of friction-induced vibration to the realistic failure analysis of spur gear cracked teeth. Eng. Fail. Anal. 2024, 158, 107956. [Google Scholar] [CrossRef]
- Vaishya, M.; Singh, R. Analysis of periodically varying gear mesh systems with coulomb friction using floquet theory. J. Sound Vib. 2001, 243, 525–545. [Google Scholar] [CrossRef]
- Vaishya, M.; Singh, R. Sliding friction-induced non-linearity and parametric effects in gear dynamics. J. Sound Vib. 2001, 248, 671–694. [Google Scholar] [CrossRef]
- Gunda, R.; Singh, R. Dynamic Analysis of Sliding Friction in a Gear Pair. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 2–6 September 2003; Volume 2003, pp. 441–448. [Google Scholar]
- He, S.; Gunda, R.; Singh, R. Effect of sliding friction on the dynamics of spur gear pair with realistic time-varying stiffness. J. Sound Vib. 2007, 301, 927–949. [Google Scholar] [CrossRef]
- Kar, C.; Mohanty, A.R. An algorithm for determination of time-varying frictional force and torque in a helical gear system. Mech. Mach. Theory 2007, 42, 482–496. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, R. Nonlinear dynamic analysis of GTF gearbox under friction excitation with vibration characteristics recognition and control in frequency domain. Mech. Syst. Signal Process. 2021, 151, 107373. [Google Scholar] [CrossRef]
- Wang, C.; Shi, Z. A dynamic calculation method of sliding friction losses for a helical gear pair. J. Braz. Soc. Mech. Sci. Eng. 2016, 39, 1521–1528. [Google Scholar] [CrossRef]
- Siyu, C.; Jinyuan, T.; Caiwang, L.; Qibo, W. Nonlinear dynamic characteristics of geared rotor bearing systems with dynamic backlash and friction. Mech. Mach. Theory 2011, 46, 466–478. [Google Scholar] [CrossRef]
- Huang, K.; Xiong, Y.; Wang, T.; Chen, Q. Research on the dynamic response of high-contact-ratio spur gears influenced by surface roughness under EHL condition. Appl. Surf. Sci. 2017, 392, 8–18. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, F.; Zhang, J.; Xiao, Y.; Liu, J.; Xuan, Z.; Li, B.; Yang, X.; Kong, X. Mesh stiffness modeling and dynamic simulation of spur gears with body crack under speed fluctuation condition. Mech. Based Des. Struct. Mach. 2024, 52, 8371–8397. [Google Scholar] [CrossRef]
- Arrospide, E.; Bikandi, I.; García, I.; Durana, G.; Aldabaldetreku, G.; Zubia, J. 7-Mechanical properties of polymer-optical fibres. In Polymer Optical Fibres; Bunge, C.-A., Gries, T., Beckers, M., Eds.; Woodhead Publishing: Cambridge, UK, 2017; pp. 201–216. [Google Scholar] [CrossRef]
- Yilmaz, M.; Kratzer, D.; Lohner, T.; Michaelis, K.; Stahl, K. A study on highly-loaded contacts under dry lubrication for gear applications. Tribol. Int. 2018, 128, 410–420. [Google Scholar] [CrossRef]
- Yan, P.; Liu, H.; Gao, P.; Zhang, X.; Zhan, Z.; Zhang, C. Optimization of distributed axial dynamic modification based on the dynamic characteristics of a helical gear pair and a test verification. Mech. Mach. Theory 2021, 163, 104371. [Google Scholar] [CrossRef]
- Chen, Y.-C. Time-varying dynamic analysis for a helical gear pair system with three-dimensional motion due to bearing deformation. Adv. Mech. Eng. 2020, 12, 1687814020918128. [Google Scholar] [CrossRef]
- Mo, W.; Jiao, Y.; Chen, Z. Dynamic Analysis of Helical Gears With Sliding Friction and Gear Errors. IEEE Access 2018, 6, 60467–60477. [Google Scholar] [CrossRef]
- Yi, Y.; Huang, K.; Xiong, Y.; Sang, M. Nonlinear dynamic modelling and analysis for a spur gear system with time-varying pressure angle and gear backlash. Mech. Syst. Signal Process. 2019, 132, 18–34. [Google Scholar] [CrossRef]
- Chen, Q.; Ma, Y.; Huang, S.; Zhai, H. Research on gears’ dynamic performance influenced by gear backlash based on fractal theory. Appl. Surf. Sci. 2014, 313, 325–332. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Li, H.; Wu, S. Nonlinear characteristics of gear pair considering fractal surface dynamic contact as internal excitation. Int. J. Non-Linear Mech. 2022, 143, 104027. [Google Scholar] [CrossRef]
- Huang, K.; Cheng, Z.; Xiong, Y.; Han, G.; Li, L. Bifurcation and chaos analysis of a spur gear pair system with fractal gear backlash. Chaos Solitons Fractals 2021, 142, 110387. [Google Scholar] [CrossRef]
- Yang, H.; Shi, W.; Chen, Z.; Guo, N. An improved analytical method for mesh stiffness calculation of helical gear pair considering time-varying backlash. Mech. Syst. Signal Process. 2022, 170, 108882. [Google Scholar] [CrossRef]
- Wan, Z.; Cao, H.; Zi, Y.; He, W.; He, Z. An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack. Eng. Fail. Anal. 2014, 42, 157–177. [Google Scholar] [CrossRef]
- He, S.; Cho, S.; Singh, R. Prediction of dynamic friction forces in spur gears using alternate sliding friction formulations. J. Sound Vib. 2008, 309, 843–851. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, F. Dynamic modeling and analysis of spur gears considering friction–vibration interactions. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4911–4920. [Google Scholar] [CrossRef]
- Xie, C.; Yu, W. Gear dynamic modelling based on the concept of dynamic mesh stiffness: Theoretical study and experimental verification. J. Mech. Sci. Technol. 2022, 36, 4953–4965. [Google Scholar] [CrossRef]
- Feng, K. Effect of Shaft and Bearing Flexibility on Dynamic Behavior of Helical Gears: Modeling and Experimental Comparisons. J. Adv. Mech. Des. Syst. Manuf. 2012, 6, 1190–1205. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.; Liu, K.; Wang, J.; Liu, Y.; Long, Y. Nonlinear Dynamic Modeling and Analysis for a Spur Gear System with Dynamic Meshing Parameters and Sliding Friction. Symmetry 2023, 15, 1530. [Google Scholar] [CrossRef]













| Parameters | Pinion/Gear |
|---|---|
| 30/53 | |
| 30 | |
| 20 | |
| 20 | |
| 2.5 | |
| 20 | |
| 2.5 | |
| 79.83/141.04 | |
| 86.60/153.00 | |
| 12.01 | |
| 2.65 | |
| 160 | |
| 50 | |
| 25/30 | |
| Parameters | Pinion/Gear |
|---|---|
| 23/47 | |
| 501.6/8748 | |
| 0.78/3.28 | |
| 2.5 | |
| 8.0 | |
| 20 | |
| 30 | |
| 120 | |
| 0.1 | |
| 1.0 | |
| Damping coefficient of the shaft | 0.05 |
| 0.025 |
| Driving Speed (RPM) | Support Stiffness (Nm) | |||||
|---|---|---|---|---|---|---|
| (1 × 106) | (1 × 106) | (6 × 106) | (6 × 106) | (1.2 × 107) | (1.2 × 107) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, G.; Liu, C.; Liu, G.; Liu, F. Improved Nonlinear Dynamic Model of Helical Gears Considering Frictional Excitation and Fractal Effects in Backlash. Machines 2025, 13, 262. https://doi.org/10.3390/machines13040262
Mo G, Liu C, Liu G, Liu F. Improved Nonlinear Dynamic Model of Helical Gears Considering Frictional Excitation and Fractal Effects in Backlash. Machines. 2025; 13(4):262. https://doi.org/10.3390/machines13040262
Chicago/Turabian StyleMo, Guoyin, Chengyu Liu, Guimian Liu, and Fuhao Liu. 2025. "Improved Nonlinear Dynamic Model of Helical Gears Considering Frictional Excitation and Fractal Effects in Backlash" Machines 13, no. 4: 262. https://doi.org/10.3390/machines13040262
APA StyleMo, G., Liu, C., Liu, G., & Liu, F. (2025). Improved Nonlinear Dynamic Model of Helical Gears Considering Frictional Excitation and Fractal Effects in Backlash. Machines, 13(4), 262. https://doi.org/10.3390/machines13040262








