Road Roughness Recognition: Feature Extraction and Speed-Adaptive Classification Based on Simulation and Real-Vehicle Tests
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation of Vehicle Model
2.2. Simulation of Road Roughness Signal
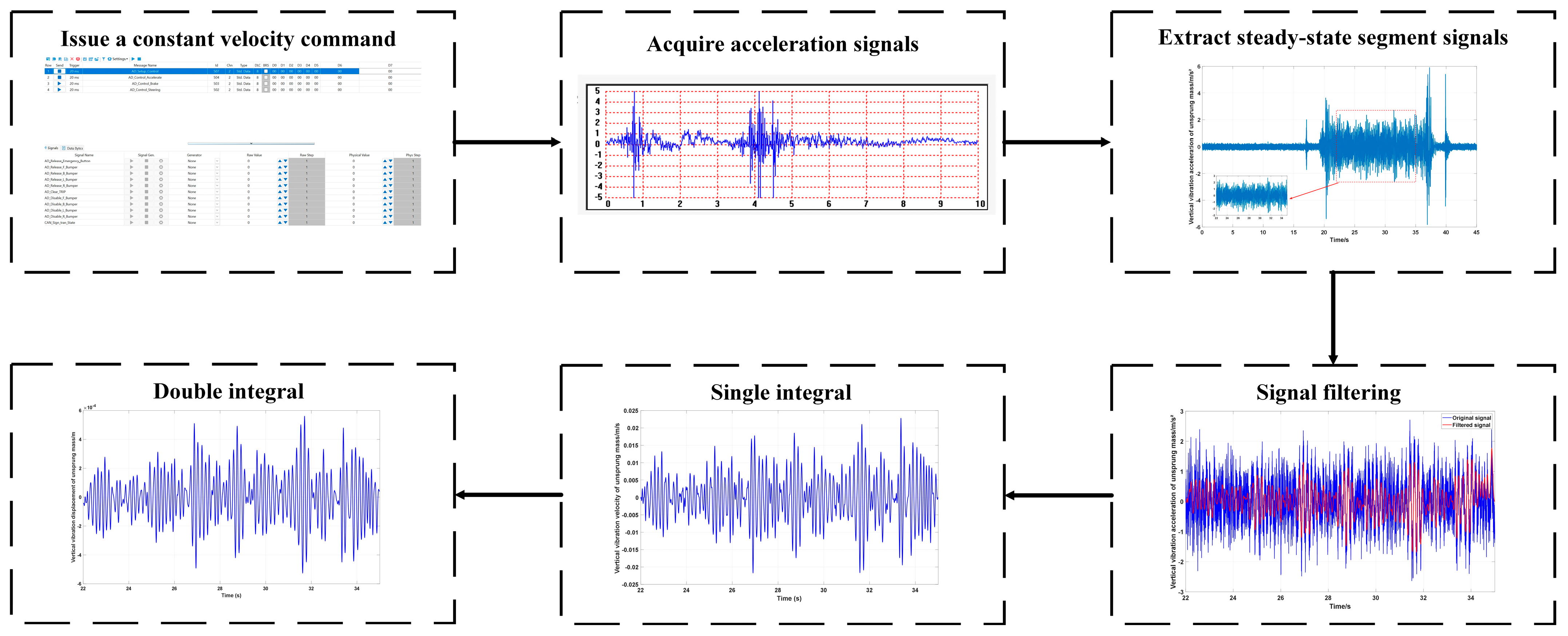
2.3. Construction of Actual Experimental Platform
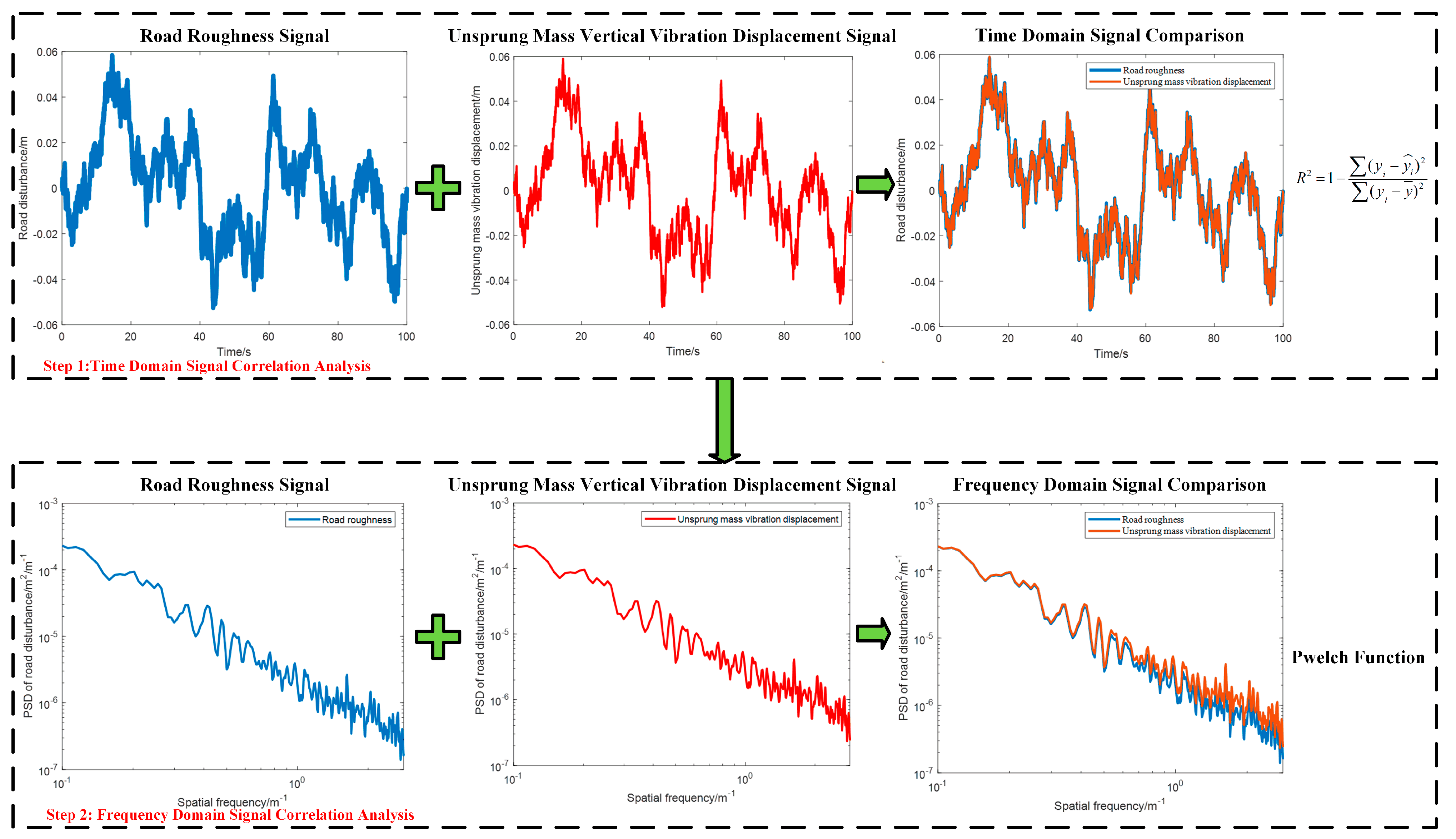
2.4. Signal Consistency Verification Method
2.5. Speed-Adaptive Road Roughness Classifier Design Method
3. Results and Discussion
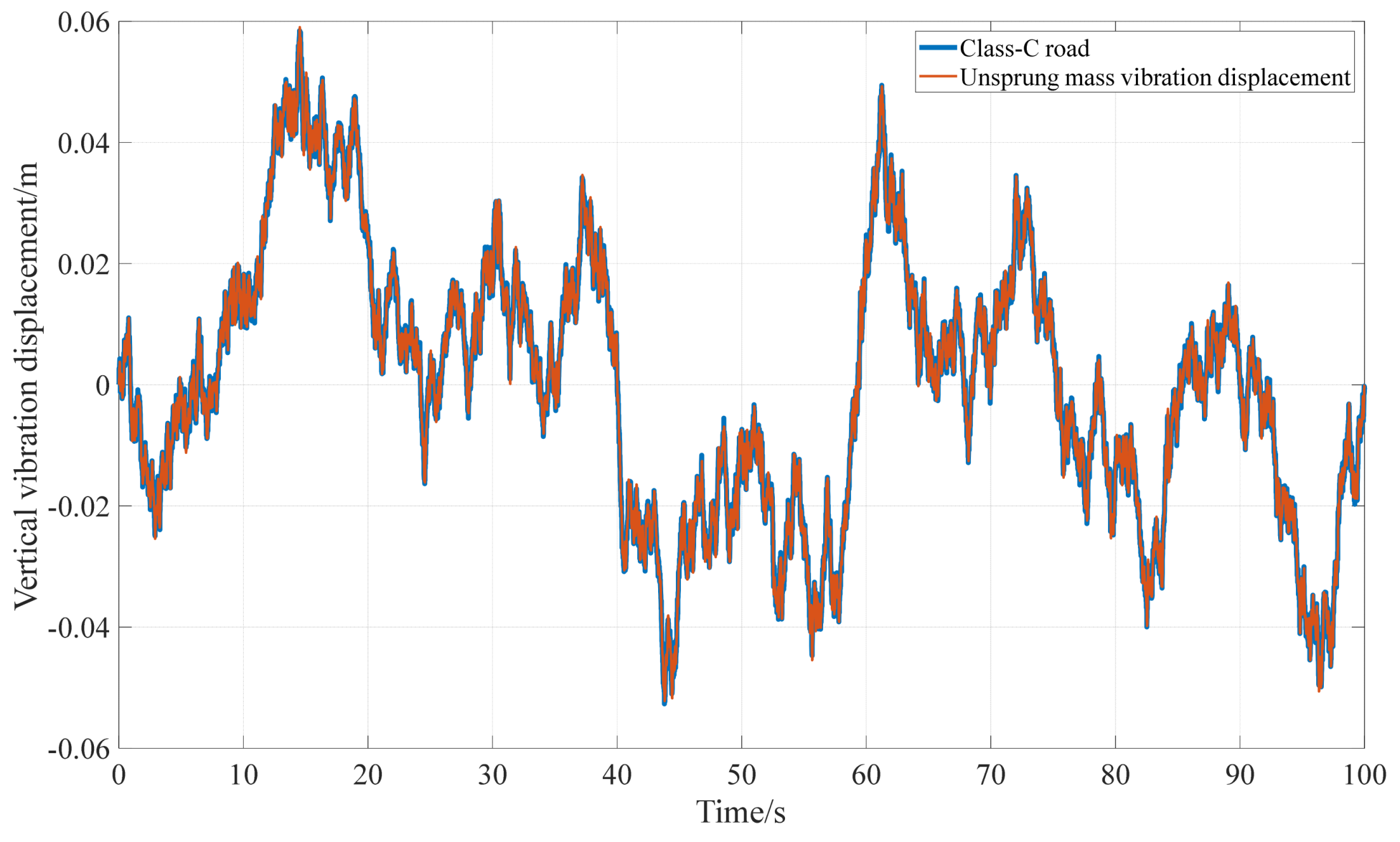
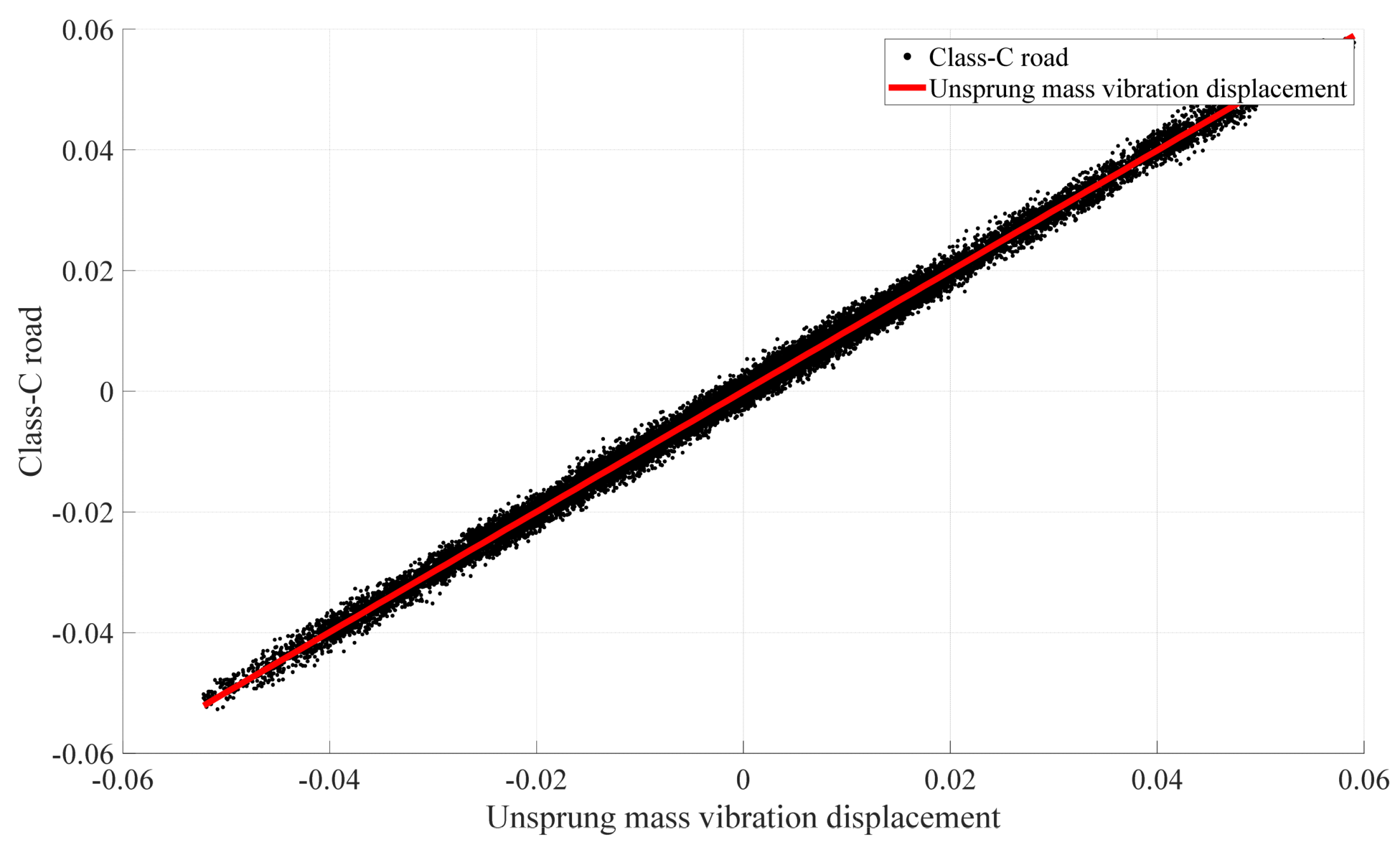
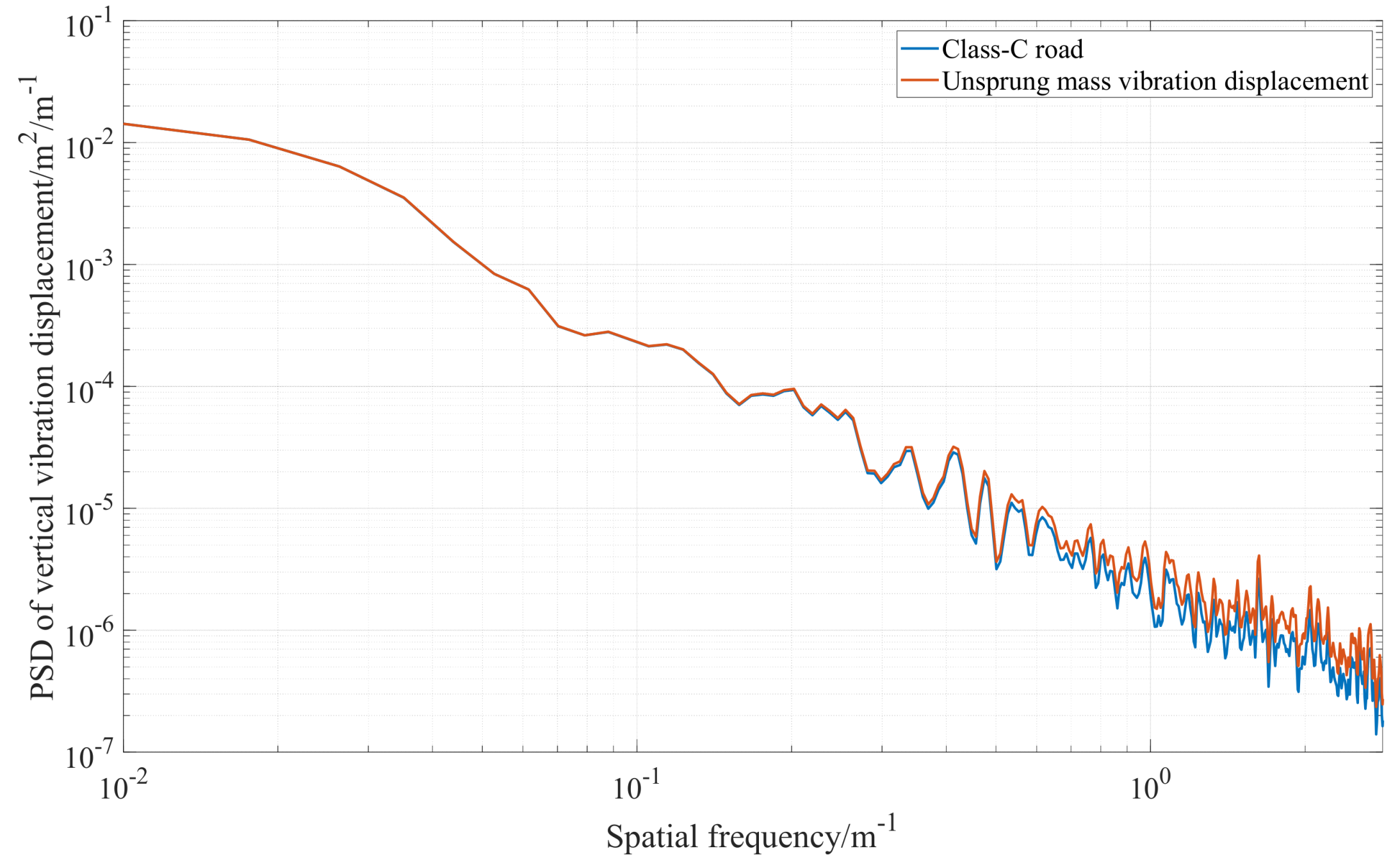
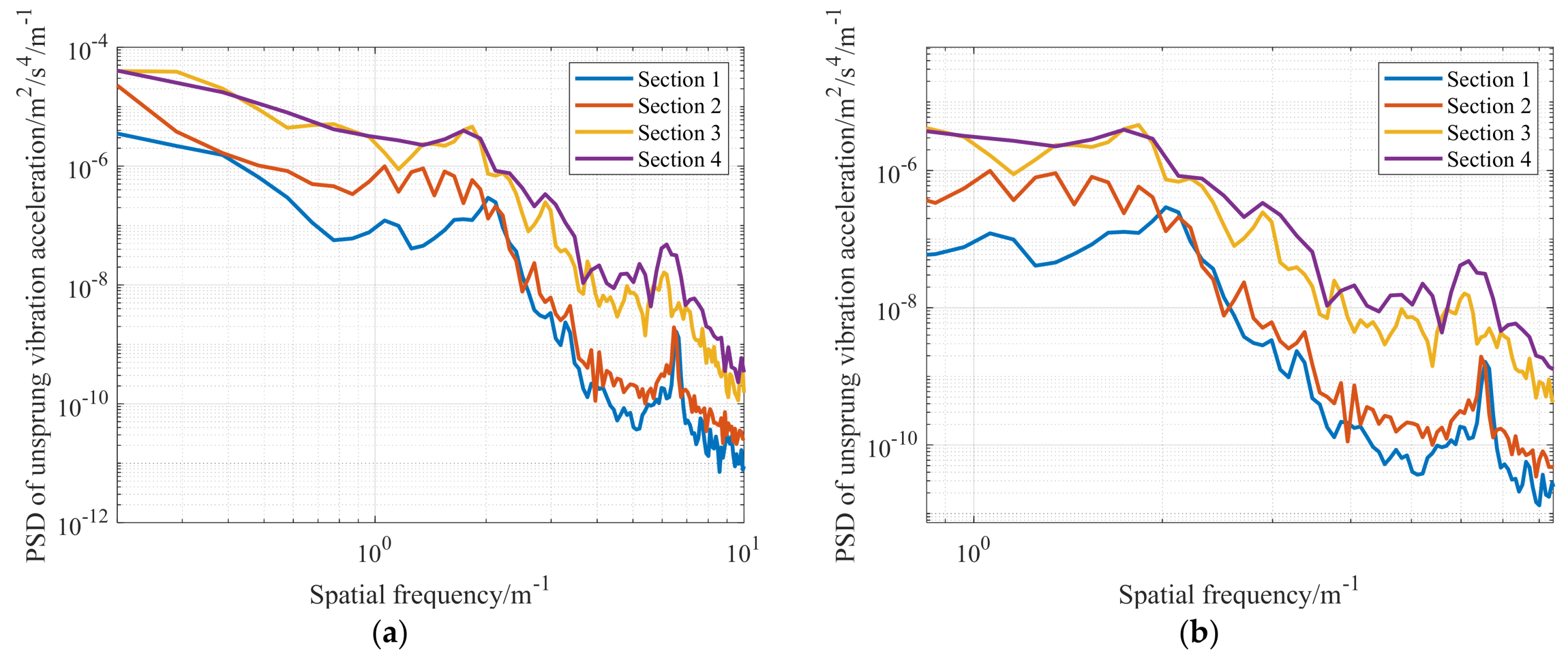
3.1. Time–Frequency Domain Consistency Analysis Based on Theoretical Simulation
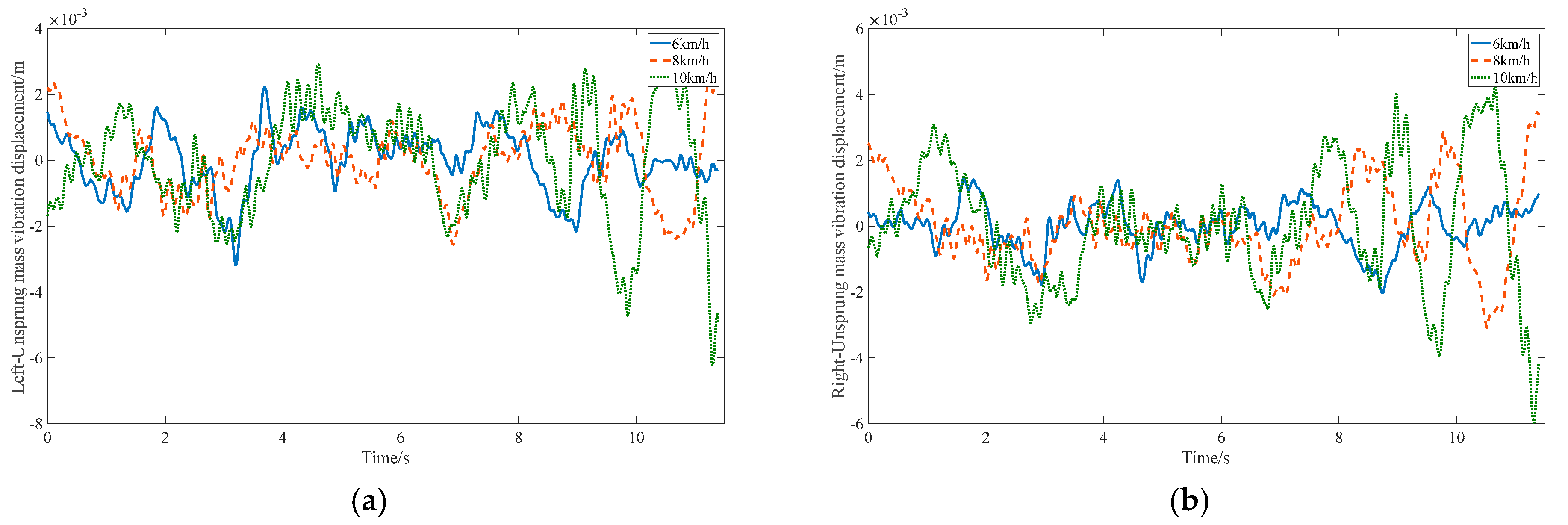
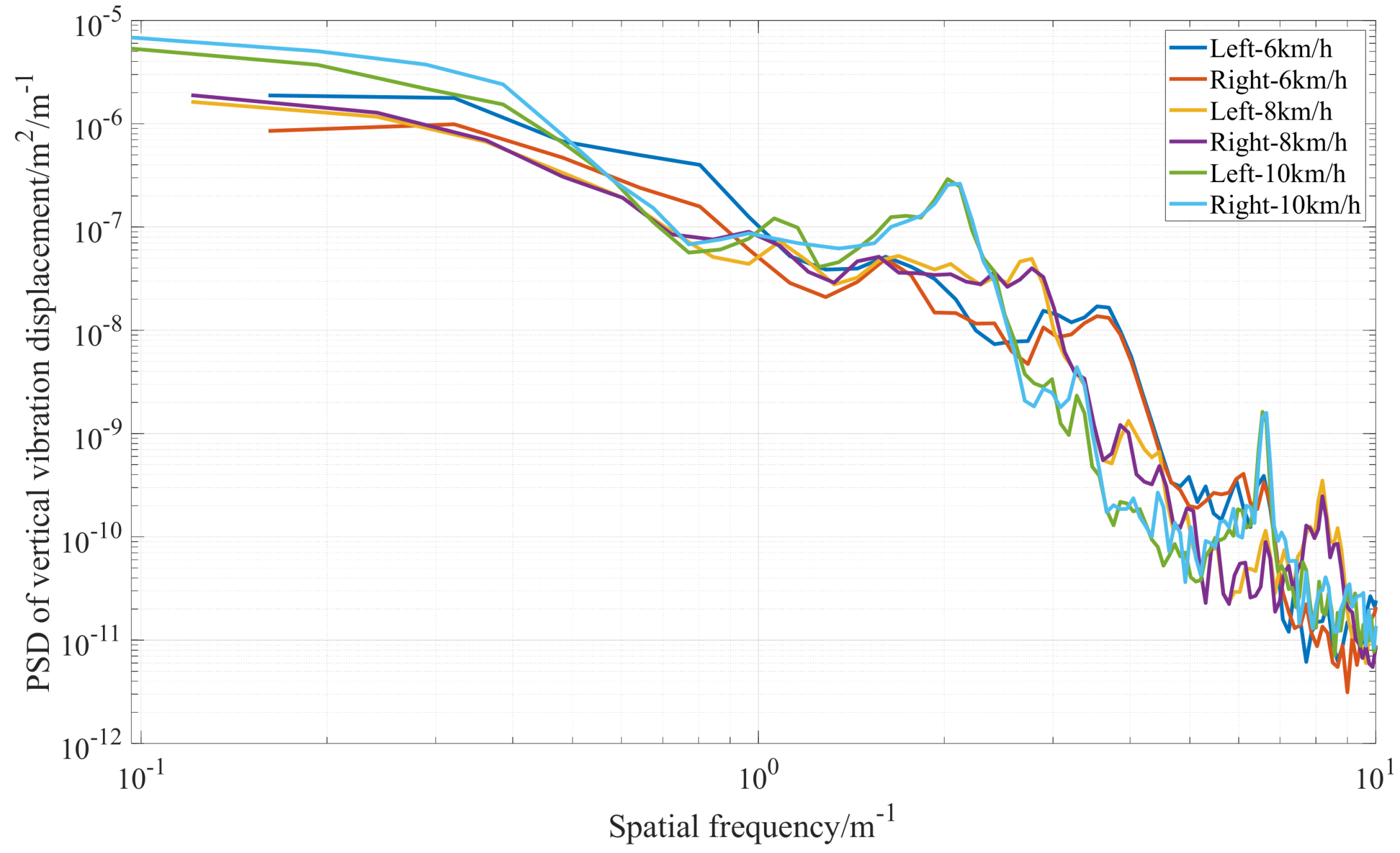
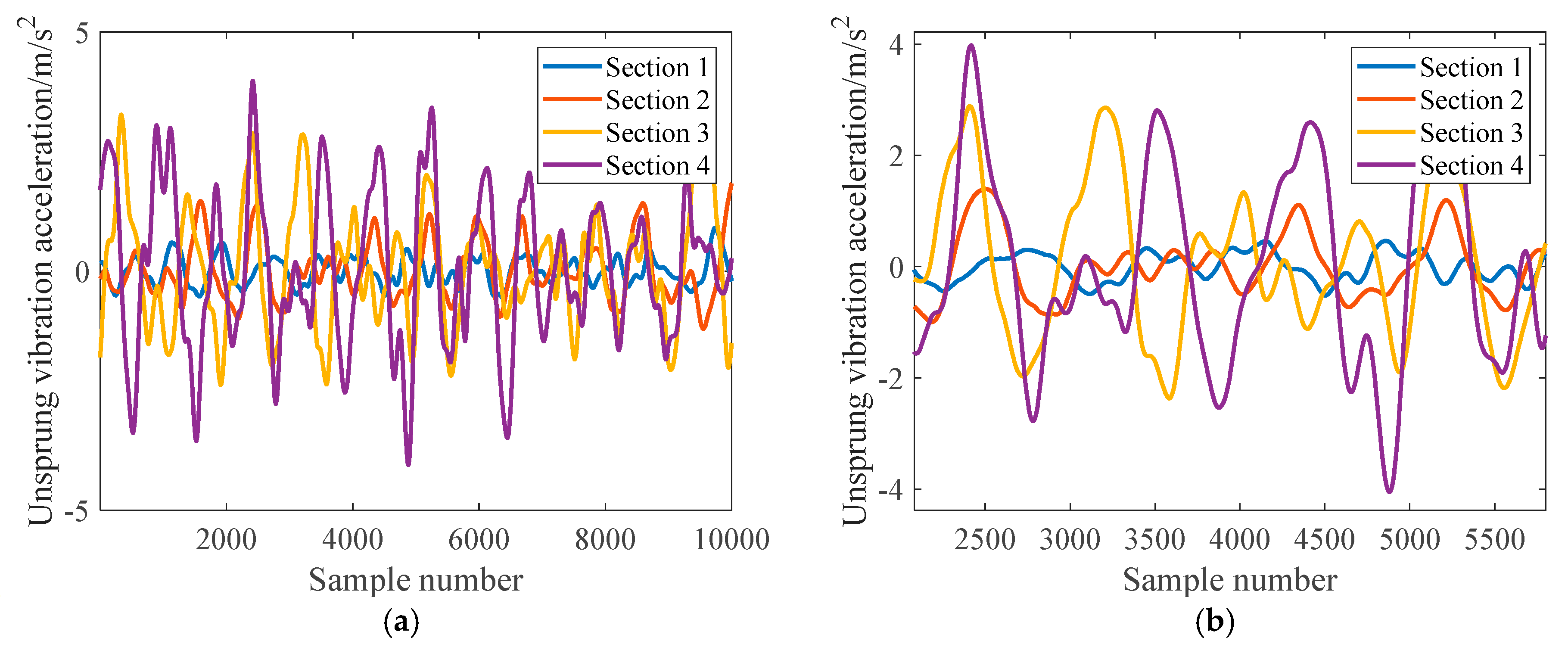
3.2. Consistency Analysis of Left and Right Wheels Based on Real Vehicle Tests
3.3. Construction of Road Roughness Classifier
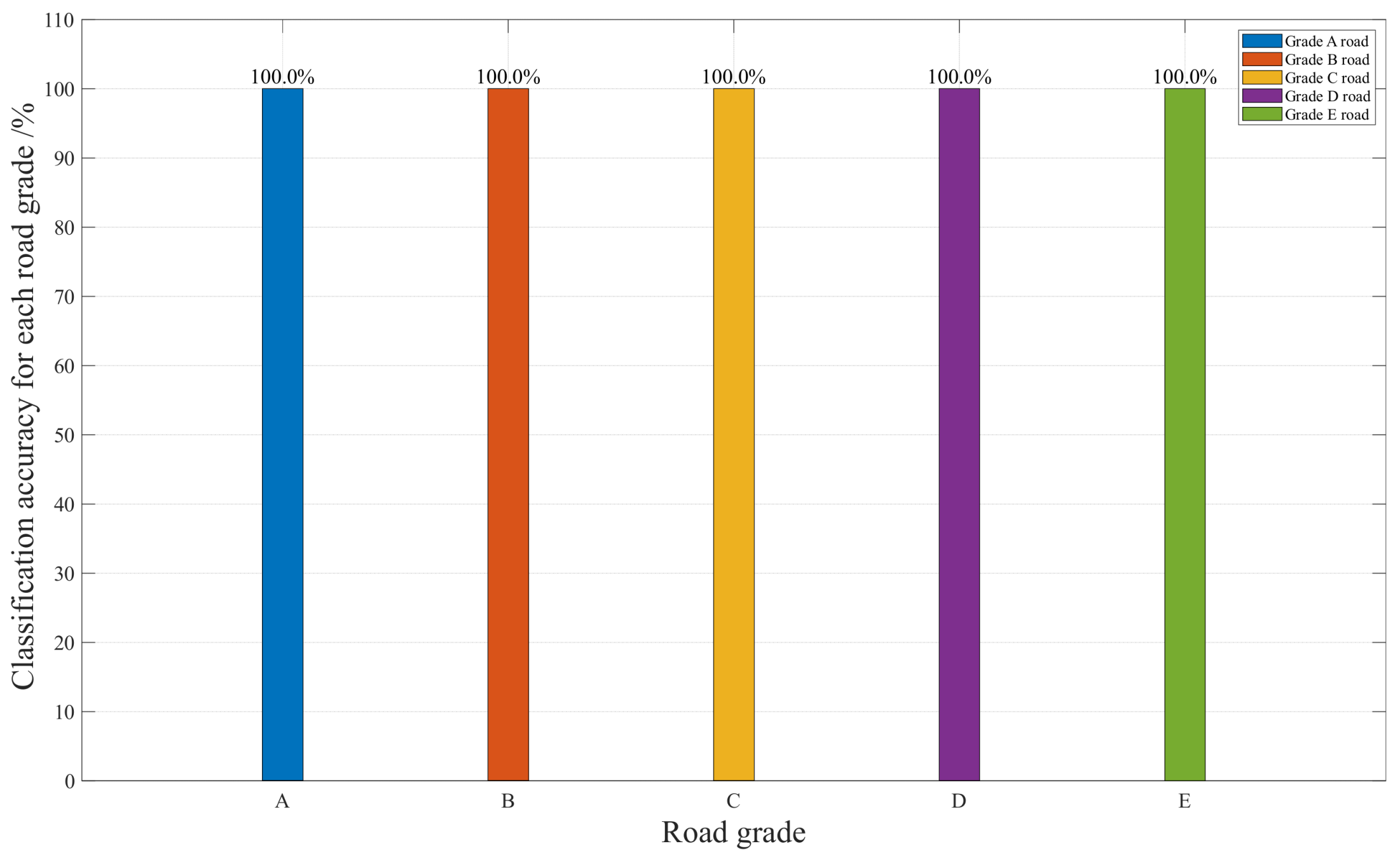
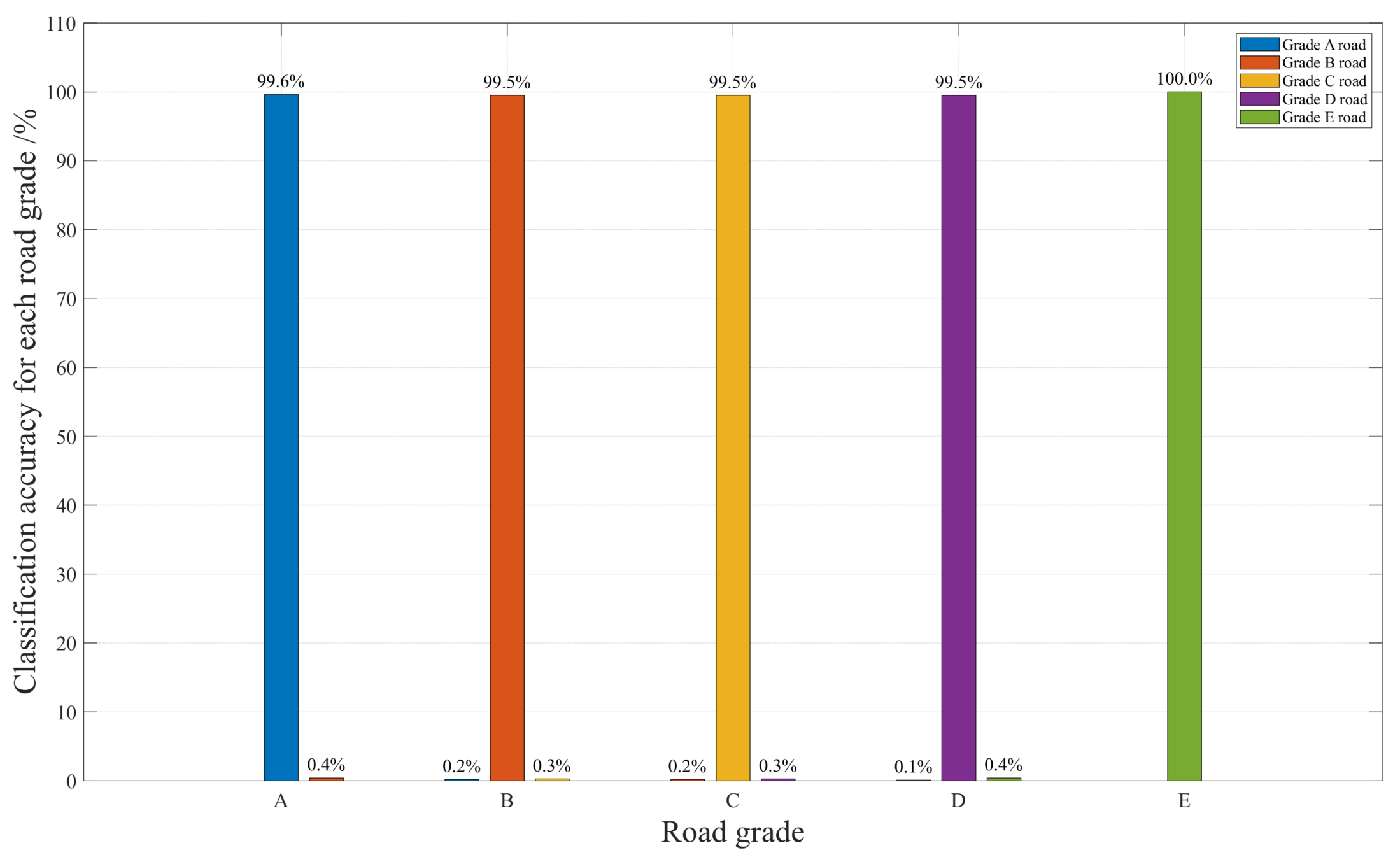
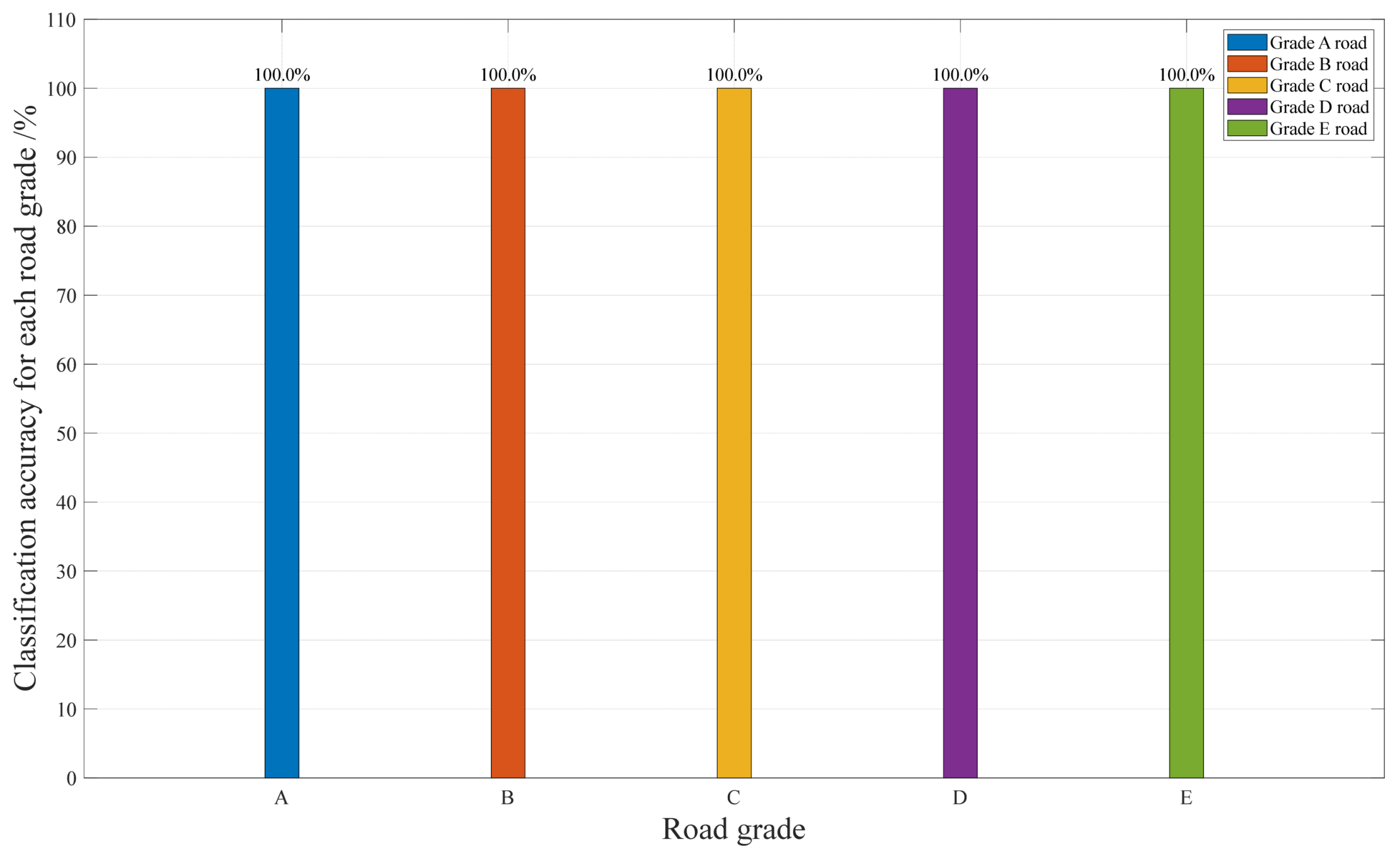
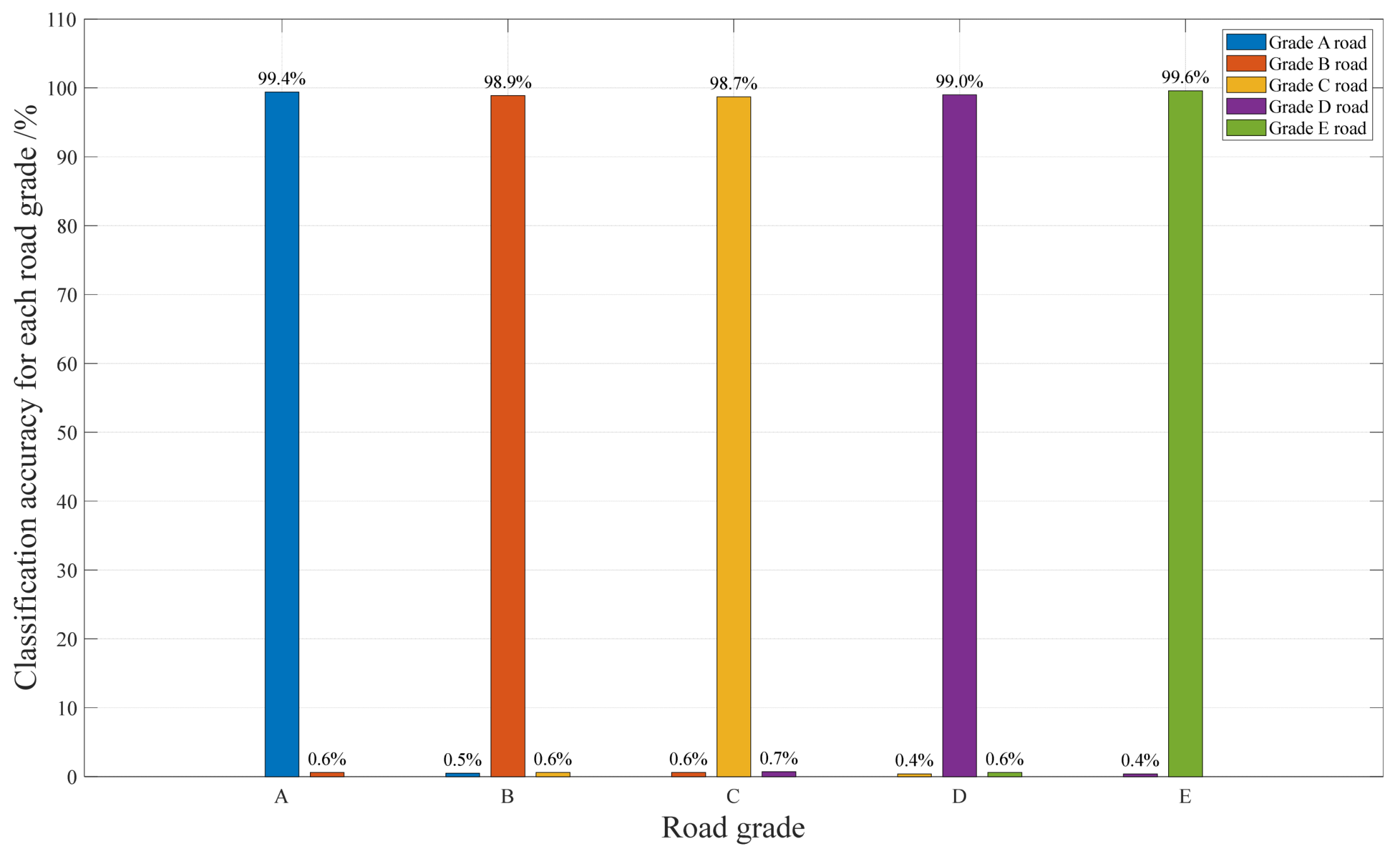
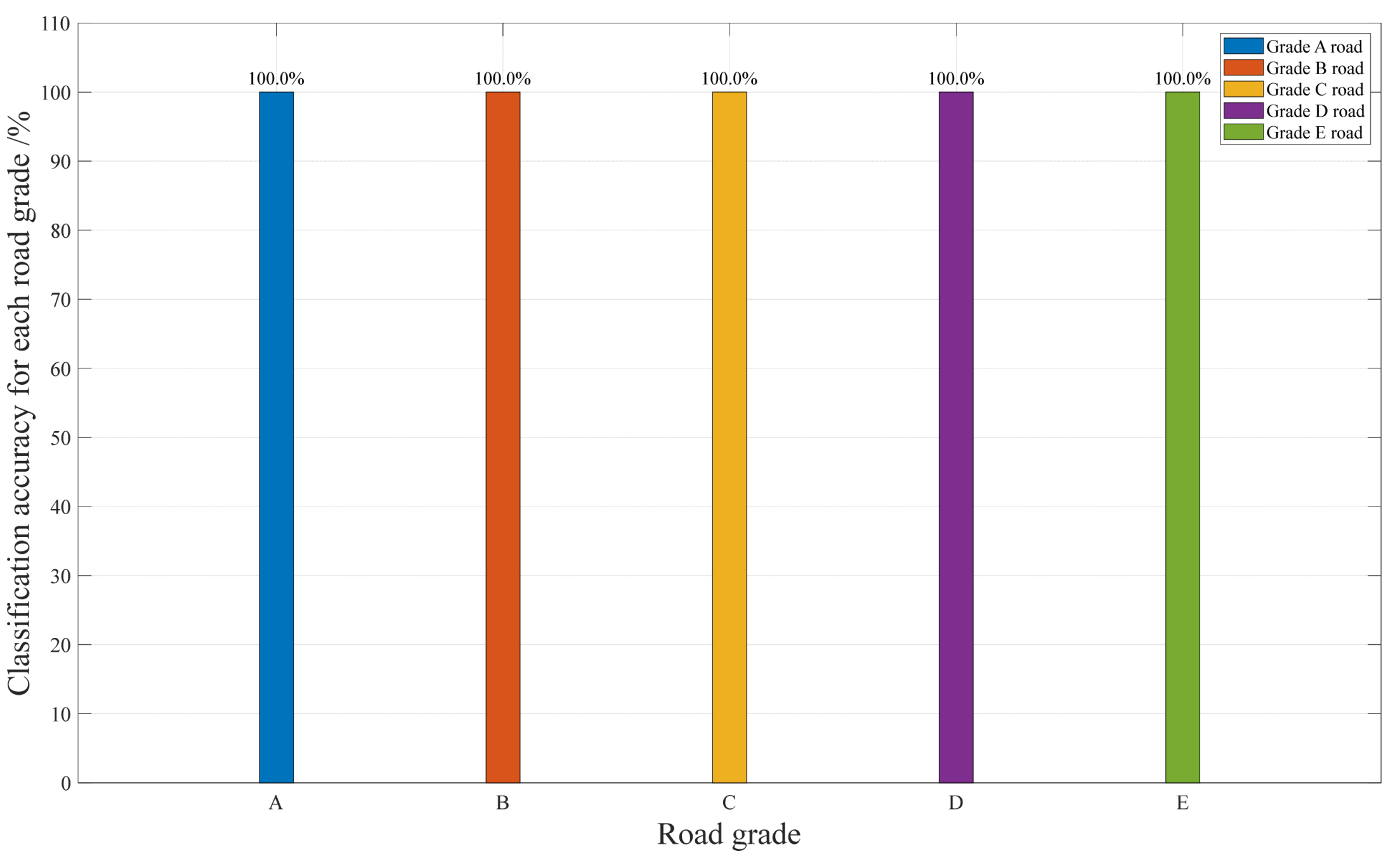
3.4. Construction of Speed-Adaptive Road Roughness Classifier
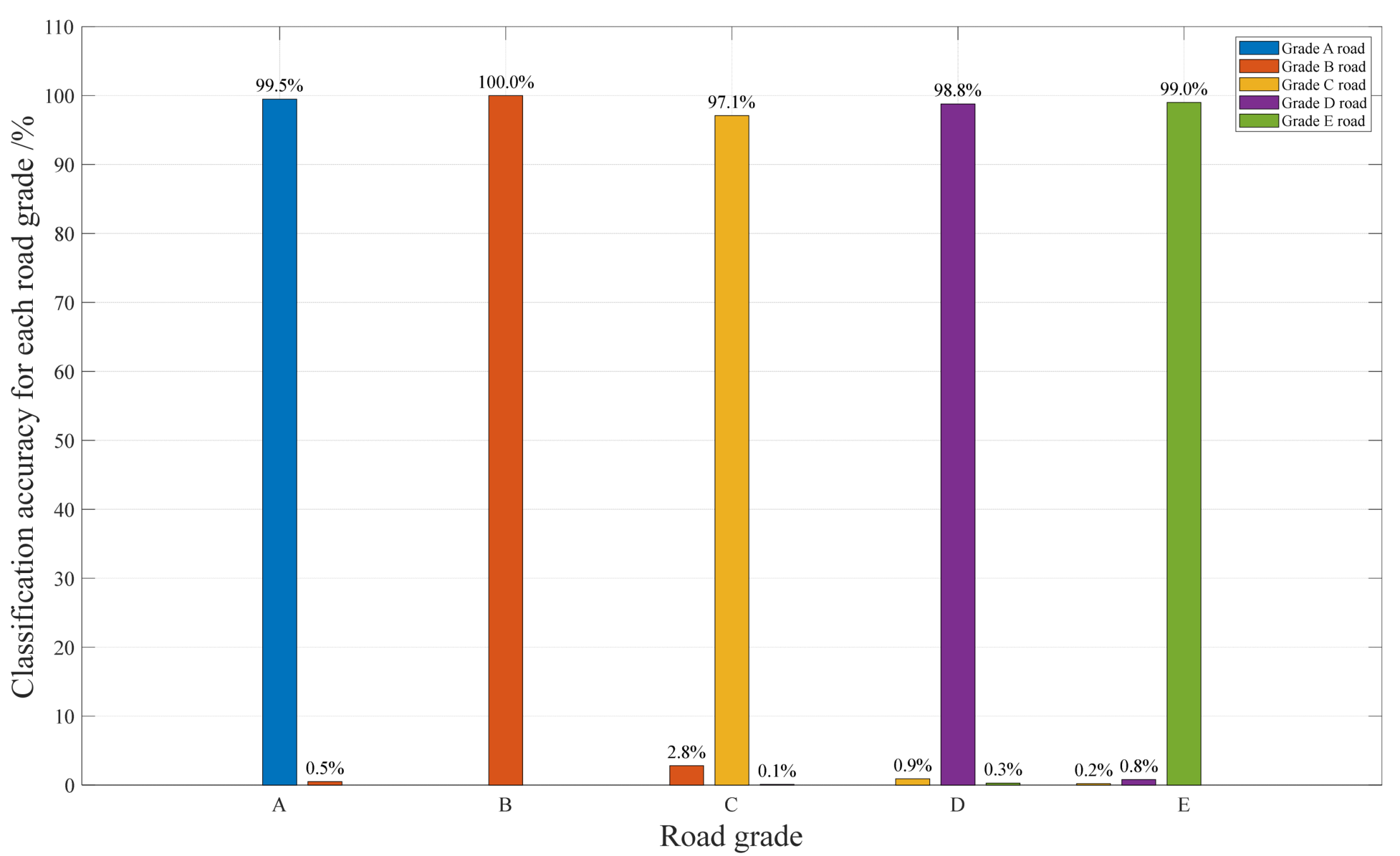
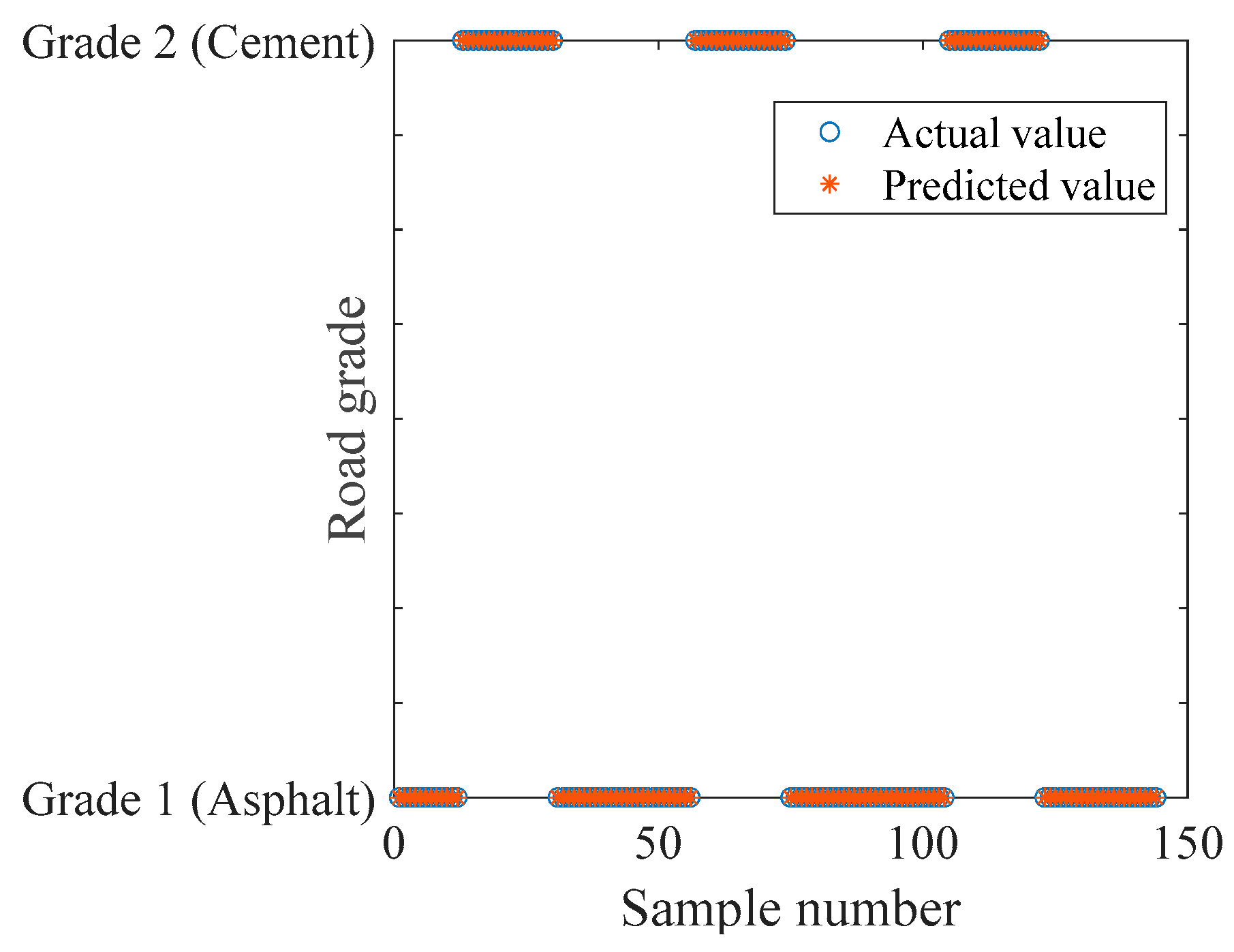
3.5. Real Road Roughness Classification
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, W.; Zhou, Y.; FU, Y.; Zhang, M. Analysis of the Influence of Soil on the Maneuverability of Military Off-road Vehicles. Acta Armamentarii 2024, 45, 288–298. [Google Scholar]
- Franceschetti, B.; Rondelli, V.; Capacci, E. Lateral stability performance of articulated narrow-track tractors. Agronomy 2021, 11, 2512. [Google Scholar] [CrossRef]
- Sun, W.; Li, C.; Wang, J. Research on Ride Comfort of an Off-road Vehicle with Compound Suspension. Automot. Eng. 2022, 44, 105–114+122. [Google Scholar]
- Islam, F.; Nabi, M.; Ball, J. Off-road detection analysis for autonomous ground vehicles: A review. Sensors 2022, 22, 8463. [Google Scholar] [CrossRef]
- Yuan, Y.; Yang, H.; Ding, L. Experimental Study and Modeling Considering the Influence of Wheel Load for Planetary Exploration Rovers. J. Mech. Eng. 2024, 60, 263–271. [Google Scholar]
- Wu, C.; Wen, L.; Chen, Z. Minimum-jerk velocity planning and control for CVT tractor velocity regulation. Trans. Chin. Soc. Agric. Eng. 2023, 39, 28–35. [Google Scholar]
- Chen, Z. Research on System Dynamics Analysis and Continuously Variable Speed of Tractor; Nanjing Agricultural University: Nanjing, China, 2020. [Google Scholar]
- Zheng, E.; Fan, Y.; Zhu, R. Prediction of the vibration characteristics for wheeled tractor with suspended driver seat including air spring and MR damper. J. Mech. Sci. Technol. 2016, 30, 4143–4156. [Google Scholar] [CrossRef]
- Wan, H.; Ou, Y.; Guan, X. Review of the perception technologies for unmanned agricultural machinery operating environment. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2024, 40, 1–18. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Zheng, L. Multi-objective control and optimization of active energy-regenerative suspension based on road recognition. J. Traffic Transp. Eng. 2021, 21, 129–137. [Google Scholar]
- Yang, Z.; Shi, C.; Zheng, Y. A study on a vehicle semi-active suspension control system based on road elevation identification. PLoS ONE 2022, 17, e0269406. [Google Scholar] [CrossRef]
- Zhang, Z. Power Function Model Identification of Road Statistical Characteristics Based on International Roughness Index and Vehicle Vibration Response; Jilin University: Changchun, China, 2019. [Google Scholar]
- Duan, H.; Shi, F.; Zhao, Y. Research and practice of road surface profile measurement. J. Vib. Shock 2011, 30, 155–160. [Google Scholar]
- Zhao, X.; Li, J.; Yue, D. The road roughness acquisition test and analysis of three-dimensional lidar orchard pavement. J. Huazhong Agric. Univ. 2022, 41, 227–236. [Google Scholar]
- Chen, H.; Shao, Y. Measurement method of pavement surface spectrum with multi-sensor coupling based on inertial benchmark. J. Jilin Univ. (Eng. Technol. Ed.) 2023, 53, 2254–2262. [Google Scholar]
- Fares, A.; Zayed, T. Industry-and academic-based trends in pavement roughness inspection technologies over the past five decades: A critical review. Remote Sens. 2023, 15, 2941. [Google Scholar] [CrossRef]
- Berti, M.; Corsini, A.; Daehne, A. Comparative analysis of surface roughness algorithms for the identification of active landslides. Geomorphology 2013, 182, 1–18. [Google Scholar] [CrossRef]
- Gorges, C.; Öztürk, K.; Liebich, R. Impact detection using a machine learning approach and experimental road roughness classification. Mech. Syst. Signal Process. 2019, 117, 738–756. [Google Scholar] [CrossRef]
- Zhang, Q.; Hou, J.; Hu, X. Vehicle parameter identification and road roughness estimation using vehicle responses measured in field tests. Measurement 2022, 199, 111348. [Google Scholar] [CrossRef]
- Ngwangwa, H.; Heyns, P.; Labuschagne, F. Reconstruction of road defects and road roughness classification using vehicle responses with artificial neural networks simulation. J. Terramech. 2010, 47, 97–111. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, W.; Liu, Q. Study on road roughness recognition based on analysis of wheel vertical dynamic load. Chin. J. Sci. Instrum. 2006, 2132–2133. [Google Scholar] [CrossRef]
- Li, J.; Guo, W.; Gu, S. Road Roughness Identification Based on NARX Neural Network. Automot. Eng. 2019, 41, 807–814. [Google Scholar]
- Liu, L.; Zhang, Z.; Lu, H. Road Roughness Identification Based on Augmented Kalman Filtering with Consideration of Vehicle Acceleration. Automot. Eng. 2022, 44, 247–255+297. [Google Scholar]
- Li, S.; Li, J.; Feng, G. Road roughness recognition based on GA-LSTM adaptive Kalman filtering. J. Vib. Shock 2024, 43, 121–130. [Google Scholar]
- Chen, K.; Shi, S.; Cheng, S. Research on Road Roughness Recognition Algorithm Based on ReliefF-RBF. Chin. J. Automot. Eng. 2024, 14, 49–59. [Google Scholar]
- Rahman, M.; Rideout, G. Using the lead vehicle as preview sensor in convoy vehicle active suspension control. Veh. Syst. Dyn. 2012, 50, 1923–1948. [Google Scholar] [CrossRef]
- Fergani, S.; Menhour, L.; Sename, O. A new LPV/H∞ semi-active suspension control strategy with performance adaptation to roll behavior based on non linear algebraic road profile estimation. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10 December 2013. [Google Scholar]
- Imine, H.; Delanne, Y.; M’sirdi, N. Road profile input estimation in vehicle dynamics simulation. Veh. Syst. Dyn. 2006, 44, 285–303. [Google Scholar] [CrossRef]
- Doumiati, M.; Martinez, J.; Sename, O. Road profile estimation using an adaptive Youla–Kučera parametric observer: Comparison to real profilers. Control Eng. Pract. 2017, 61, 270–278. [Google Scholar] [CrossRef]
- Alatoom, Y.; Al-Suleiman, T. Development of pavement roughness models using Artificial Neural Network (ANN). Int. J. Pavement Eng. 2022, 23, 4622–4637. [Google Scholar] [CrossRef]
- Lugner, P.; Ploechl, M.; Imine, H. Road Profile Inputs for Evaluation of The Loads on The Wheels. Tyre Models for Vehicle Dynamics Analysis. In Proceedings of the 3rd International Colloquium on Tyre Models for Vehicle Dynamics Analysis (Tmvda), Vienna, Austria, 29–31 August 2004; Volume 2005, p. 43. [Google Scholar]
- Qin, Y. Study on Load Control System of Combined Harvester; Jiangsu University: Zhenjiang, China, 2012. [Google Scholar]
- Yin, J.; Chen, X.; Wu, L. Simulation Method of Road Excitation in Time Domain Using Filtered White Noise and Dynamic Analysis of Suspension. J. Tongji Univ. (Nat. Sci.) 2017, 45, 398–407. [Google Scholar]
- Shi, X.; Jiang, X.; Zhao, J.; Zhao, P.; Zeng, J. Seven Degrees of Freedom Vehicle Response Characteristic under Four Wheel Random Pavement Excitation. Sci. Technol. Eng. 2018, 18, 71–78. [Google Scholar]
- Chen, M.; Long, H.Y.; Ju, L.Y.; Li, Y.G. Stochastic road roughness modeling and simulation in time domain. Mech. Eng. Autom. 2017, 2, 40–41. [Google Scholar]
- ISO 8608:2016; Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data. International Organization for Standardization: Geneva, Switzerland, 2016.
- Wang, J.; Li, P.; Han, Y. Road roughness measurement based on multi—Sensor data comprehension. Eng. J. Wuhan Univ. 2012, 45, 361–365. [Google Scholar]
- Wang, X.; Cheng, Z.; Ma, L. Road Recognition Based on Vehicle Vibration Signal and Comfortable Speed Strategy Formulation Using ISA Algorithm. Sensors 2022, 22, 6682. [Google Scholar] [CrossRef]
- Shen, Z.; Peng, Y.; Shu, N. A Road Damage Identification Method Based on Scale-span Image and SVM. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 993–997. [Google Scholar]
- Zhen, J.; Zhang, J.; Cao, D.; Wu, Y. Intelligent Roughness Detection of Asphalt Pavements by the kNN Method. J. South China Univ. Technol. (Nat. Sci. Ed.) 2022, 50, 50–56. [Google Scholar]
- Yu, T.; Pei, L.; Li, W.; Hu, Y. Pavement condition index prediction based on random forest algorithm. J. Road Transp. Res. Development. 2021, 38, 16–23. [Google Scholar] [CrossRef]
- Gu, S. Research on Neural Network Method for Pavement Roughness Recognition Based on Vehicle Response Neural Network Approach for Pavement Roughness Recognition Based on Vehicle Response; Jilin University: Changchun, China, 2018. [Google Scholar]
- Qin, Y.; Dong, M.; Zhao, F. Road Profile Classification for Vehicle Semi-Active Suspension System Based on Adaptive Neuro-Fuzzy Inference System. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; IEEE: Piscataway NJ, USA, 2015; pp. 1533–1538. [Google Scholar]
- Liang, G.; Zhao, T.; Wang, Y.; Wei, Y. Road Unevenness Identification Based on LSTM Network. Automot. Eng. 2021, 43, 509–517+628. [Google Scholar]
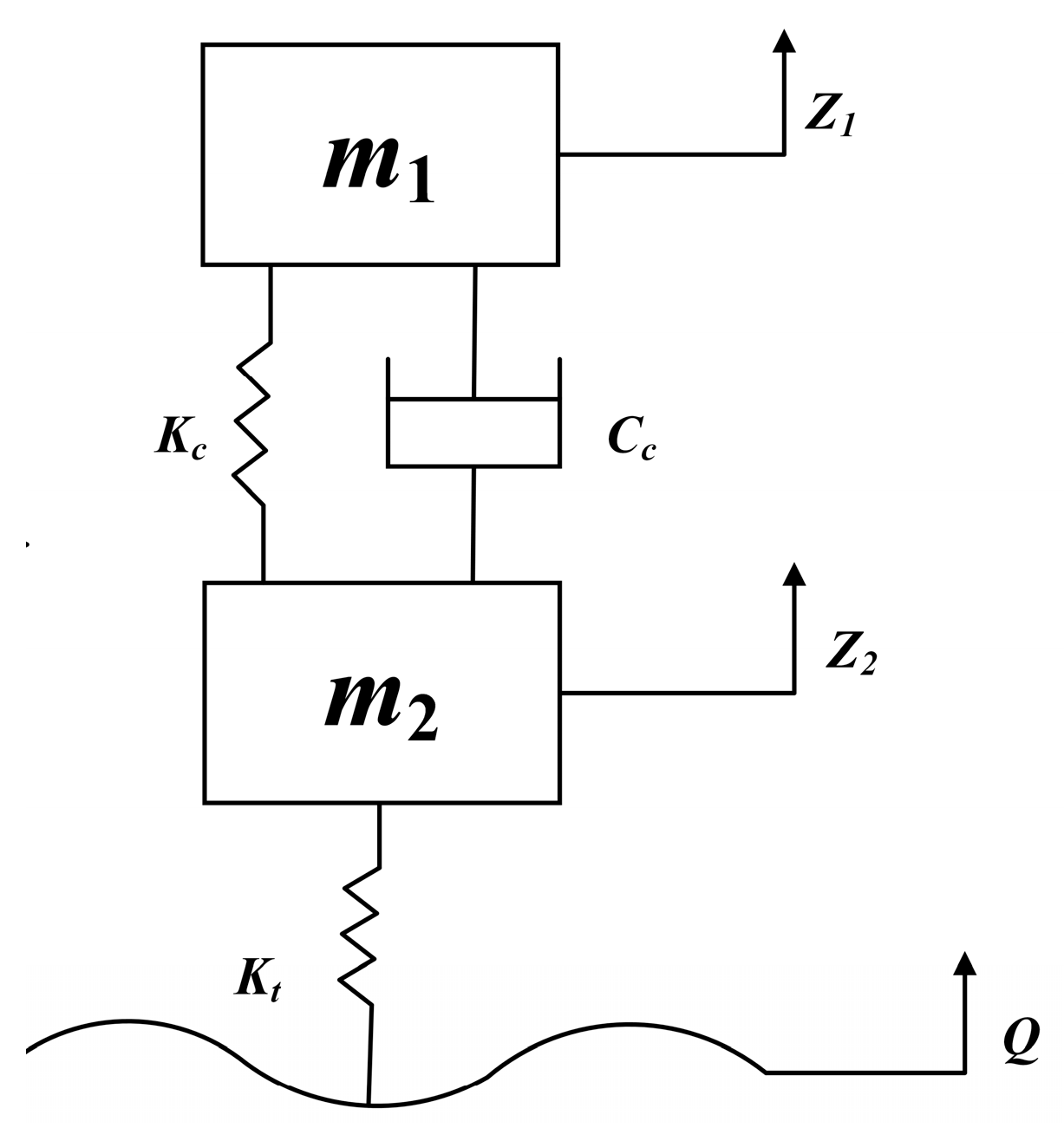




| Parameter | Value |
|---|---|
| Sprung mass m1 | 133 kg |
| Unsprung mass m2 | 25 kg |
| Suspension stiffness Kc | 13,000 N/m |
| Suspension damping coefficient Cc | 2403.8 N·s/m |
| Tire stiffness Kt | 178,950 N/m |
| Road Grade | ·10−6 (m3) | ||
|---|---|---|---|
| Lower Limit | Geometric Mean | Upper Limit | |
| A | 8 | 16 | 32 |
| B | 32 | 64 | 128 |
| C | 128 | 256 | 512 |
| D | 512 | 1024 | 2048 |
| E | 2048 | 4096 | 8192 |
| F | 8192 | 16,384 | 32,768 |
| G | 32,768 | 65,536 | 131,072 |
| H | 131,072 | 262,144 | 524,288 |
| Parameter | Value |
|---|---|
| Operating Voltage Measurement Range | 9–57 V ±16 g |
| Measurement Frequency | 266,667 Hz |
| Operating Temperature | −40–85 °C |
| Communication Interface | Ethernet |
| Road Grades | Vehicle Speed (km/h) | Simulation Duration |
|---|---|---|
| A | 5,10,15,20,25,30,35,40,45,50,55,60 | 1000 s for each speed |
| B | 5,10,15,20,25,30,35,40,45,50,55,60 | 1000 s for each speed |
| C | 5,10,15,20,25,30,35,40,45,50,55,60 | 1000 s for each speed |
| D | 5,10,15,20,25,30,35,40,45,50,55,60 | 1000 s for each speed |
| E | 5,10,15,20,25,30,35,40,45,50,55,60 | 1000 s for each speed |
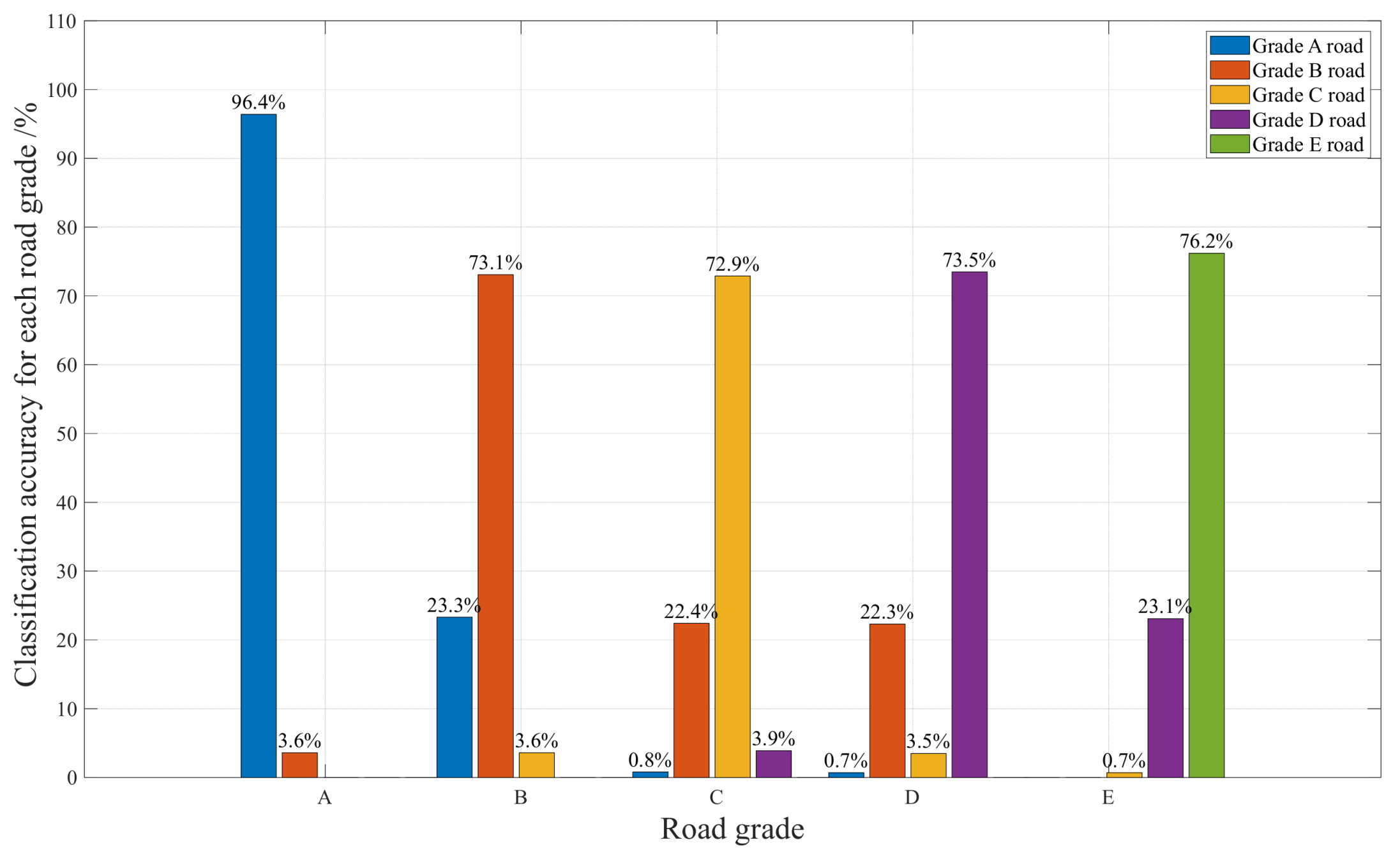
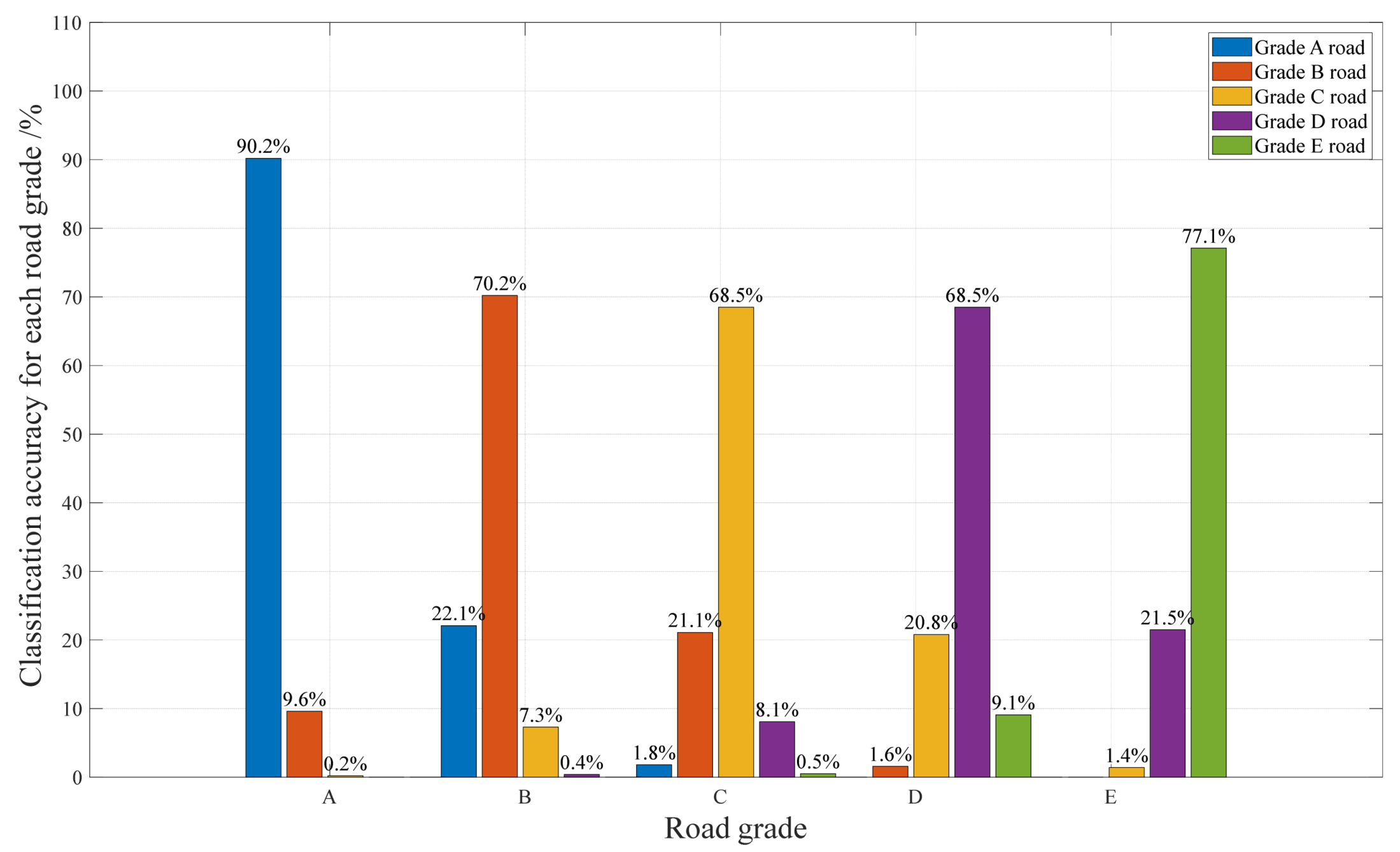
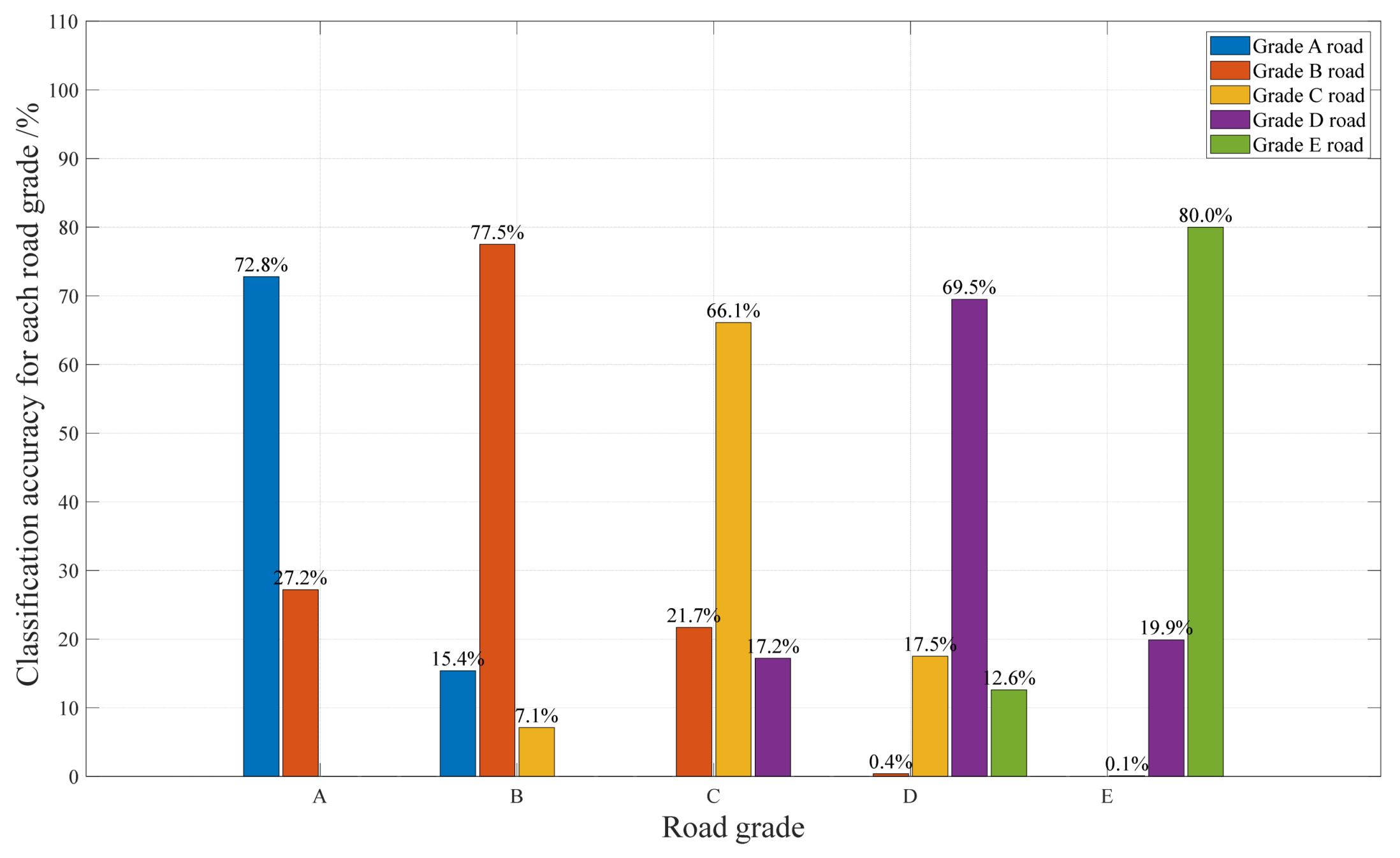
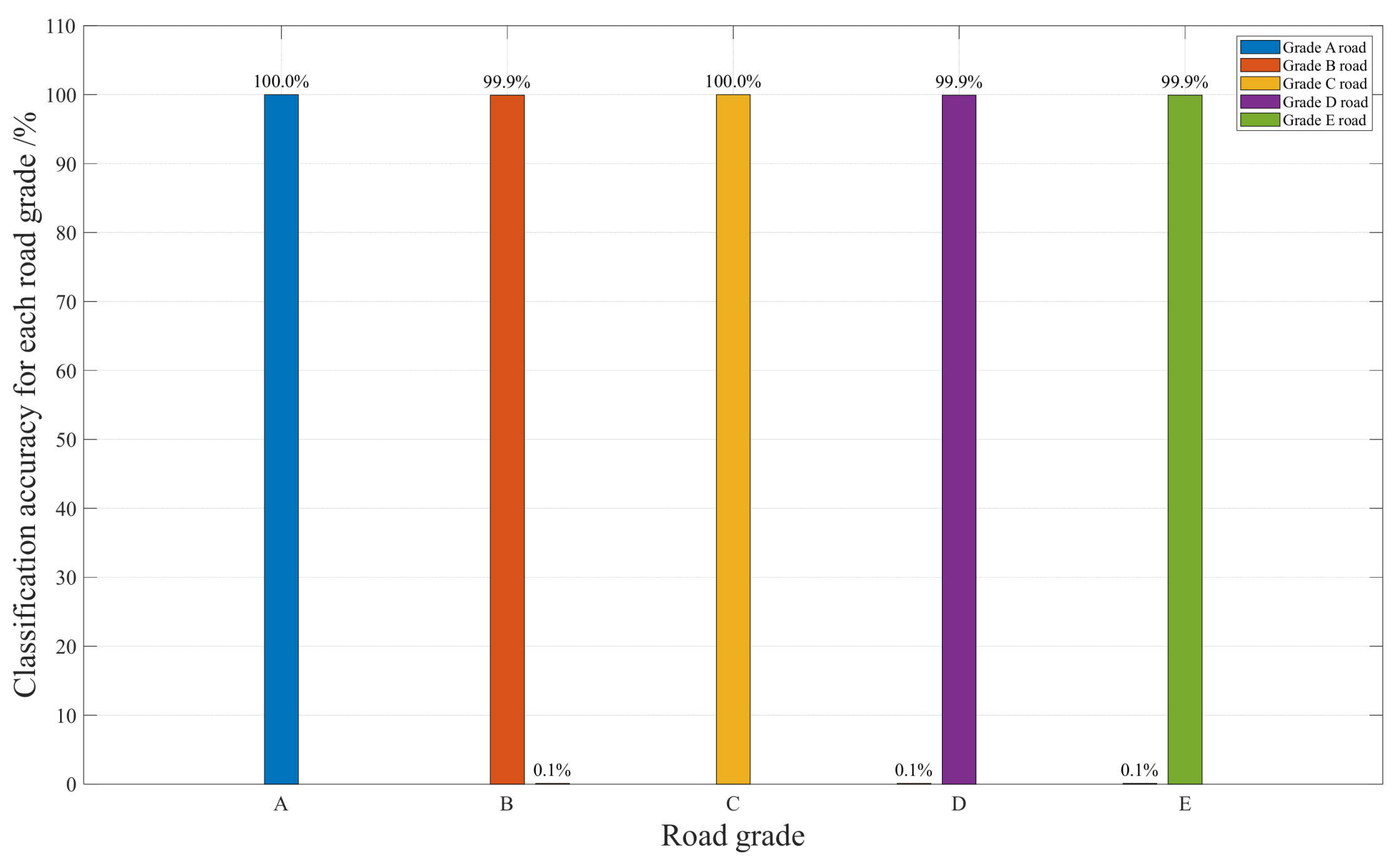
| Classifier | Classification Accuracy |
|---|---|
| SVM KNN | 78.41% 74.92% |
| RF | 74.32% |
| RBF | 73.18% |
| Classifier | Classification Accuracy |
|---|---|
| SVM KNN | 99.94% 100% |
| RF | 99.62% |
| RBF | 98.88% |
| Feature Selection | Classification Accuracy |
|---|---|
| Vehicle Speed, Mean Absolute Value Vehicle Speed, Absolute Standard Deviation | 100% 100% |
| Vehicle Speed, Peak Absolute Value | 99.12% |
| Vehicle Speed, Root Mean Square Value | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, J.; Cheng, Z.; Ye, S.; Liu, S.; Lin, J. Road Roughness Recognition: Feature Extraction and Speed-Adaptive Classification Based on Simulation and Real-Vehicle Tests. Machines 2025, 13, 391. https://doi.org/10.3390/machines13050391
Xing J, Cheng Z, Ye S, Liu S, Lin J. Road Roughness Recognition: Feature Extraction and Speed-Adaptive Classification Based on Simulation and Real-Vehicle Tests. Machines. 2025; 13(5):391. https://doi.org/10.3390/machines13050391
Chicago/Turabian StyleXing, Jie, Zhun Cheng, Shuai Ye, Songwei Liu, and Jiawei Lin. 2025. "Road Roughness Recognition: Feature Extraction and Speed-Adaptive Classification Based on Simulation and Real-Vehicle Tests" Machines 13, no. 5: 391. https://doi.org/10.3390/machines13050391
APA StyleXing, J., Cheng, Z., Ye, S., Liu, S., & Lin, J. (2025). Road Roughness Recognition: Feature Extraction and Speed-Adaptive Classification Based on Simulation and Real-Vehicle Tests. Machines, 13(5), 391. https://doi.org/10.3390/machines13050391






