Abstract
Nowadays, motor type plays a significant role in the vehicle performances. This article compares various types of permanent magnet vernier motors (PMVMs) with different shapes of field modulation teeth and different numbers of field modulation poles (FMPs). Based on this, the electromagnetic performance of permanent magnet synchronous motors (PMSMs) and PMVMs is compared. First, the back EMF, air gap flux density, flux density distribution, and torque of PMVMs with different shapes of FMPs are compared. Based on the selected PMVMs, the rated torque and overload capacity of PMVMs with different slot–pole combinations are compared. Subsequently, the comprehensive electromagnetic performance of PMVMs and PMSMs is compared, where the strength and weakness of PMSMs and PMVMs are concluded. Finally, a prototype is manufactured and tested, verifying the correctness and accuracy of the simulation model.
1. Introduction
In recent years, a new type of permanent magnet vernier motor (PMVM) based on the magnetic field modulation principle has received widespread attention. This type of motor achieves rotor speed reduction and torque enhancement through magnetic field energy conversion and has excellent application prospects in low-speed and high-torque situations [1,2]. Therefore, PMVMs that use magnetic field modulation have become a research hotspot in the field of motors in the past decade. Additionally, PMVMs are being extensively explored in theoretical analysis, structural innovation, design optimization, and multi-physics field research [3,4]. It is shown that PMVMs have multiple advantages such as low speed and high torque and are one of the important development trends for motors in the future.
The principle of magnetic field modulation, also known as the magnetic gear effect, is commonly used in magnetic field modulation motors to generate higher amplitude or higher-order magnetic field modulation harmonics [5,6]. PMVMs are considered a type of magnetic field modulation motor. Therefore, understanding the distribution of air gap magnetic fields is crucial for the design and optimization of PMVMs. As shown in [7], in recent years, analytical methods and the FEM have been commonly used to analyze the air gap magnetic field of motors. As shown in [8], the FEM can usually provide the most intuitive waveform. In [9], the working principle and design process of traditional PMVMs are introduced, and it is confirmed that this analytical method can usually provide accurate mathematical prediction models. The simultaneous use of both methods further improves the accuracy of the model, as shown in [10].
Based on the gradual improvement in various magnetic field analysis methods, various new structures of PMVMs have also emerged. In [11], a novel modular stator fractional pole-pair PMVM is proposed. The torque fluctuation and cogging torque are significantly reduced, but the torque does not increase significantly. In [12], an unequal stator modulated teeth structure is proposed to reduce the electromagnetic vibration. At the same time, the torque of PMVMs can be increased by an uneven distribution of the number of modulation teeth, as seen in [13]. Additionally, reference [14] optimized electromagnetic performance by using coding-shaped tooth. What is more, the loss performance and torque performance of spoke-type PMVMs with different stator topologies are studied in [15,16]. What is more, reference [17] compared and studied the loss distribution characteristics of single-tooth PMVMs and PMSMs and pointed out that eddy current losses of permanent magnets for a relatively high proportion of the total losses of PMVMs. Reference [18] compared and studied the electromagnetic performance characteristics such as torque, efficiency, and power factor between single-tooth PMVMs and PMSMs. Reference [3] compared the performance advantages and disadvantages of permanent magnet vernier wind turbines and permanent magnet synchronous wind turbines. In summary, there have been many studies on new types of PMVMs, but most of the literature focus on traditional single-tooth PMVMs, split-tooth PMVMs with auxiliary slot structures, and analytical modeling methods for PMVMs. Although split-tooth PMVMs have been proposed, there are basically no papers that study in detail the relationship between the number of FMPs and the number of permanent magnet poles of split-tooth PMVMs and their magnetic field modulation ability.
In this paper, PMVMs with different shapes of FMPs are proposed; at the same time, the performance differences in PMVMs with various slot numbers/FMP numbers/pole numbers are analyzed in this paper in detail. In addition, this paper aims to provide a comparison between PMSMs and PMVMs, and discussions on the comparison results between PMSMs and PMVMs are carried out; all performances, e.g., the back EMF characteristics, cogging torque, output torque, power factor and efficiency, are schematically shown and compared, which provide a reference for the selection of the two-type high-performance motors. Finally, a prototype is manufactured for a type of motor, and its electromagnetic performance is tested.
2. Comparison Between Different Types of PMVMs
In order to explore the influence of various structural parameters on the electromagnetic performance of PMVMs, PMVMs with different shapes of FMPs, different numbers of FMPs, and different slot–pole combinations are compared in this section, and changing laws of the performance of PMVMs with different topologies and structural parameters are obtained. All models in this article are built by using ANSYS Maxwell 2022R2 software, and the finite element analysis method (FEM) is used to compare the electromagnetic performance of all PMVMs and PMSMs.
2.1. Comparison of Different Shapes of FMPs
When exploring the effects of the pole slot combination, number of permanent magnet poles, and electromagnetic reduction ratio on the electromagnetic performance of a PMVM, it is first necessary to select a suitable shape for the modulation teeth (FMPs) of the PMVMs to avoid the disadvantage of slot type of FMPs on performance analysis.
Therefore, this section takes 12-slot/18-FMP/13-pole-pair PMVMs as the research object to study the influence of different shapes of FMPs on the comprehensive performance of the motor.
Different shapes of FMPs are shown in Figure 1. In order to accurately evaluate the differences in the magnetic field modulation ability of different topologies, different stator topologies of PMVMs are kept with the same cross-sectional area of the stator core to explore the performance differences in PMVMs with different FMP shapes while ensuring consistent structural parameters and the same amount of silicon steel material. The common structural parameters of PMVMs are shown in Table 1.
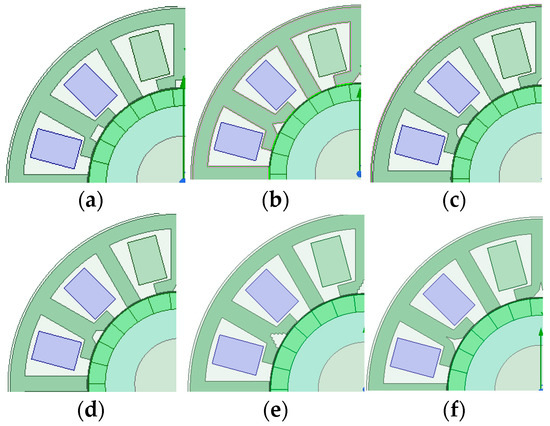
Figure 1.
Different kinds of stator topologies: (a) conventional teeth; (b) triangular teeth; (c) circular teeth; (d) trapezoidal teeth; (e) staircase teeth; (f) tower-shaped teeth.

Table 1.
Common structural parameter of 12-slot/18-FMP/13-pole-pair PMVMs.
The no-load characteristics of PMVMs with six different FMP structures are studied separately, as shown in Figure 2 and Figure 3. Keeping the motor speed at 500 rpm, it is found that the no-load back EMF amplitude of PMVMs with five special tooth structures is greater than that of PMVMs with conventional tooth structures. The no-load back EMF amplitude of PMVMs with triangular teeth is the largest. At the same time, from the Fourier decomposition results of the no-load air gap magnetic density, the main harmonic orders contained in the six different PMVMs remain the same, but the amplitudes of the main harmonics are different. After conducting a comparison, it is found that the 5th harmonic, 13th harmonic, 23rd harmonic, 31st harmonic, and 39th harmonic of PMVMs with triangular teeth have significant advantages over conventional PMVMs. As shown in Figure 3, although the fundamental harmonic amplitude of PMVMs with tower-shaped teeth and PMVMs with trapezoidal teeth is higher than that of conventional PMVMs, their other low-order modulation harmonics do not have advantages. Therefore, the triangular tooth-shaped PMVM has best magnetic field modulation ability.
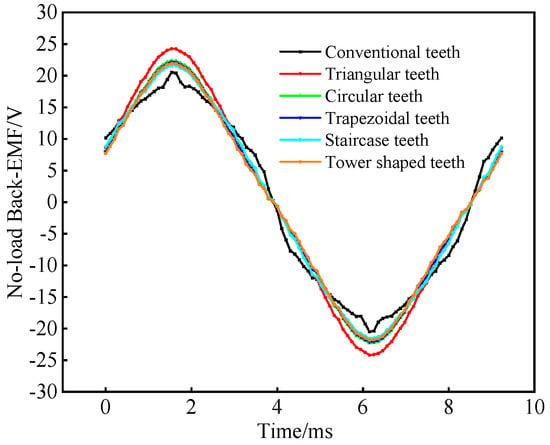
Figure 2.
No-load phase back EMF of PMVMs.
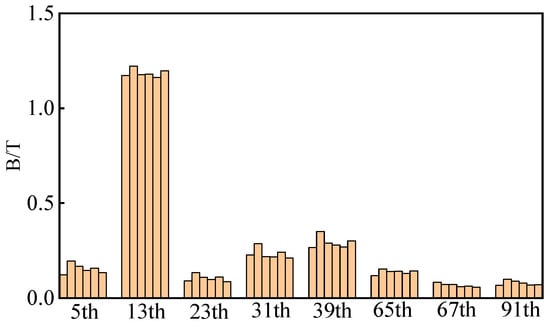
Figure 3.
Fourier decomposition of no-load air gap magnetic density of different PMVMs (corresponding to Figure 1. (a)–(f) from left to right in sequence).
The magnetic flux density distribution of different kinds of FMPs of the PMVMs is analyzed under rated conditions, as shown in Figure 4, it can be found that PMVMs with conventional tooth structures are very prone to the saturation of the yoke of modulation teeth, which causes a large amount of magnetic leakage in the stator teeth and greatly limits the improvement in and optimization of torque density. Under the same conditions, the saturation degree of the triangular tooth structure and the tower-shaped structure is smaller, and the magnetic density distribution is more uniform compared to the PMVMs with conventional tooth structures, which is conducive to an improvement in torque density.
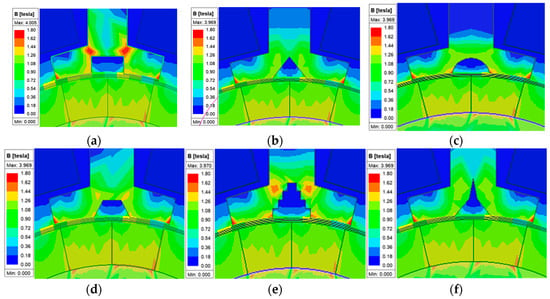
Figure 4.
No-load magnetic flux density distribution of different PMVMs: (a) conventional teeth; (b) triangular teeth; (c) circular teeth; (d) trapezoidal teeth; (e) staircase teeth; (f) tower-shaped teeth.
In addition, based on the previous research results, it can be concluded that the order and quantity of modulation harmonics are determined by the number of FMPs of PMVMs, the number of permanent magnet poles, and the electromagnetic reduction ratio. Different shapes of FMPs can change the amplitude of each order harmonic, which is of great help in improving the torque capability of PMVMs.
In order to verify the correctness of the air gap magnetic density Fourier decomposition and magnetic flux density distribution results and more accurately evaluate the electromagnetic performance of PMVMs with different types of FMPs, parameterized modeling is carried out on the stator teeth of these six PMVMs. The parameterized variables of PMVMs with different shapes of FMPs are shown in Figure 5, and the value ranges of different variables are shown in Table 2. While all other structural parameters maintain their original proportions or remain unchanged, 50 parameter combinations are selected by using the symmetric reverse equidistant parameter scanning method within the range of Table 2 values, and their torque and torque fluctuations are analyzed separately. The results are shown in Figure 6. It can be found that the torque ranges of PMVMs with triangular teeth, PMVMs with circular teeth and PMVMs with trapezoidal teeth have certain advantages compared to traditional PMVMs, and the advantage of PMVMs with triangular teeth is the most obvious, which verifies the correctness of the previous analysis.
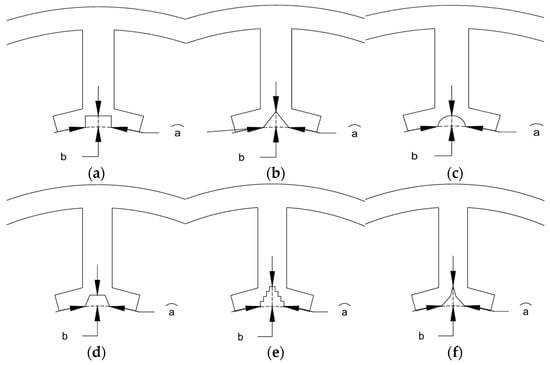
Figure 5.
Different combinations of FMP shape parameters: (a) conventional teeth; (b) triangular teeth; (c) circular teeth; (d) trapezoidal teeth; (e) staircase teeth; (f) tower-shaped teeth.

Table 2.
Common structural parameter.
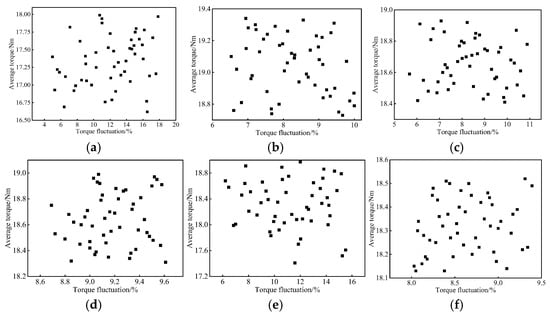
Figure 6.
Distribution of torque performance of PMVMs under different parameter combinations: (a) conventional teeth; (b) triangular teeth; (c) circular teeth; (d) trapezoidal teeth; (e) staircase teeth; (f) tower-shaped teeth.
2.2. Comparison of Different Slot–Pole Combinations of PMVMs
In this section, the number of slots for the motors are set to 6 or 12, respectively, which is used to explore the electromagnetic performance of the PMVMs under different combinations of slot numbers and permanent magnet pole numbers. All FMP shapes of motors are set to triangles. By comparing the no-load back EMF, torque, and overload capacity of different PMVM topologies, the changing law of motor performance with the number of FMPs under different slot numbers is obtained.
For six-slot motors, all motor topologies are shown in Figure 7 below. is defined as the electromagnetic reduction ratio of a motor, which is equal to the ratio of the number of permanent magnet poles to the number of stator winding poles. When the number of slots in the motor is six, the number of FMPs on each tooth gradually increases, resulting in multiple slot–pole combinations, as seen in Table 3. A1 in Table 3 corresponds to Figure 6a, A2 in Table 3 corresponds to Figure 6b, A3 in Table 3 corresponds to Figure 6c, A4 in Table 3 corresponds to Figure 6d, and A1–A4 corresponds to four six-slot PMVM topologies in Figure 7. While keeping the number of armature winding pole-pairs constant, the total number of FMPs gradually increases. At this time, the number of permanent magnet pole pairs and electromagnetic deceleration ratio of the PMVM also gradually increase.
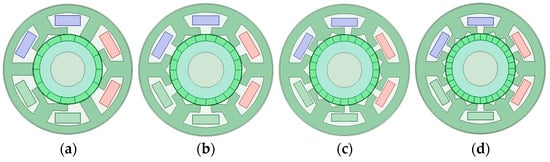
Figure 7.
Stator topologies of 6-slot PMVMs: (a) A1; (b) A2; (c) A3; (d) A4.

Table 3.
Matching parameters of 6-slot PMVMs.
These six-slot PMVMs have the same structural parameters except for the number of FMPs on the stator and the number of permanent magnets on the rotor. The outer diameter of the stator for all topologies remains 82 mm, and they are all in the form of a single-layer concentrated winding structure. In order to explore the changes in the electromagnetic properties of the motors under different slot–pole combinations, the back EMF, air gap flux density, and torque of different kinds of PMVMs are analyzed under the no-load condition and load current amplitudes of 50 A. The variation in torque with current is also analyzed. To verify the fault tolerance of the single-layer concentrated winding structure, self-inductance and mutual inductance are analyzed, too.
When the motor speed is 500 rpm, the no-load back EMF and cogging torque of different types of PMVMs are analyzed, as shown in Figure 8 and Figure 9 below. It can be found that the amplitude of the no-load back EMF of the 6-slot/15-FMP/13-pole-pair PMVM corresponding to A3 is the largest. As the number of FMPs increases and the number of permanent magnet poles increases, the amplitude of the no-load back EMF of six-slot PMVMs first increases and then gradually decreases. At the same time, the peak-to-peak value of cogging torque also gradually decreases. It can be inferred that when the number of FMPs is small, the width of the slot opening is large. As the number of FMPs increases, the slot opening also gradually decreases. Therefore, the number of cogging torque cycles increases and the amplitude decreases.
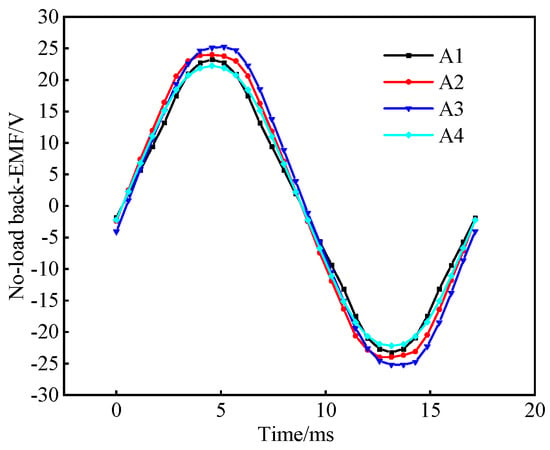
Figure 8.
No-load phase back EMF of 6-slot PMVMs.
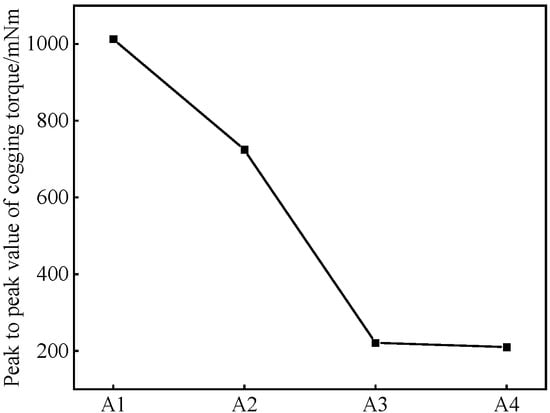
Figure 9.
Cogging torque of 6-slot PMVMs.
The Fourier decomposition results of the air gap flux density of different six-slot PMVMs under no-load conditions are shown in Figure 10, Figure 11, Figure 12 and Figure 13. The main harmonics of the six-slot PMVMs are listed in Table 4. In this table, is the number of pole pairs for different PMVMs, and corresponds to the number of FMPs for different PMVMs. The table displays the main harmonic orders of various PMVMs. It can be observed that the 6-slot/9-FMP/7-pole-pair PMVM has the highest number of air gap flux density harmonics, as shown in Figure 10.
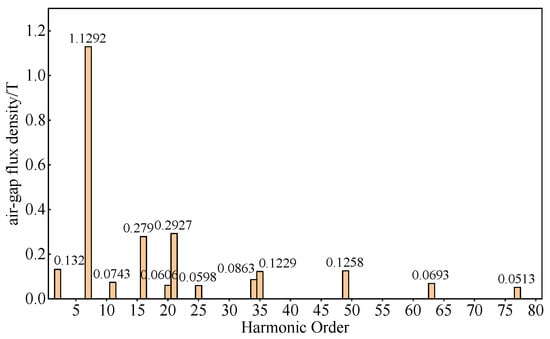
Figure 10.
Fourier decomposition of no-load air gap magnetic density of A1.
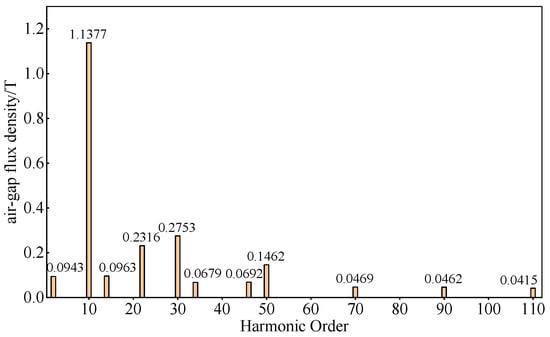
Figure 11.
Fourier decomposition of no-load air gap magnetic density of A2.
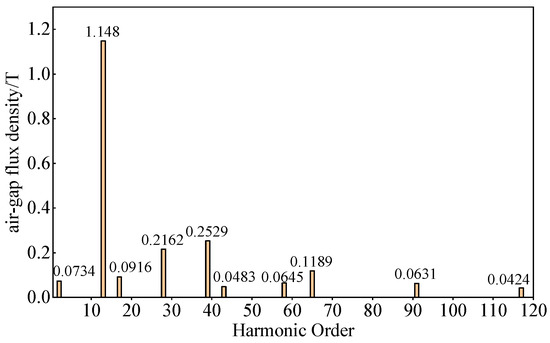
Figure 12.
Fourier decomposition of no-load air gap magnetic density of A3.
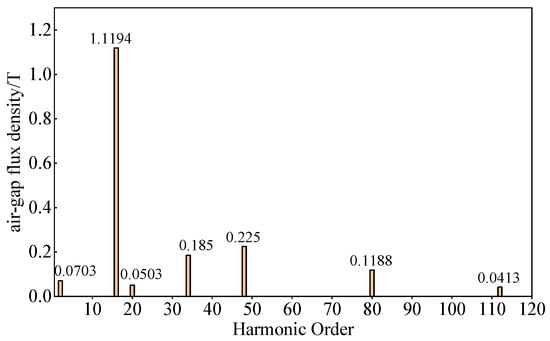
Figure 13.
Fourier decomposition of no-load air gap magnetic density of A4.

Table 4.
Matching methods of 6-slot PMVMs.
As for Table 4, it can be observed that with the increase in FMPs and the number of permanent magnet pole pairs, the highest harmonic order of the air gap flux density gradually increases, the fundamental order of the rotor gradually increases, and the amplitude of -order harmonics gradually decrease, especially in Figure 11, which is particularly evident.
As the electromagnetic reduction ratio of the PMVMs increases, the amplitude of the -order fundamental wave of the air gap magnetic density gradually increases, and the amplitude of the -order magnetic field modulation harmonic gradually decreases. For the -order magnetic field modulation harmonic, since the number of permanent magnet pole pairs and winding pole pairs of the stator of the PMVMs satisfies the relationship in Equation (1), it can be concluded that for the above four PMVMs, their -order harmonics are all 2. Therefore, when the amplitude of the -order magnetic field modulation harmonic gradually decreases, the number of permanent magnet pole pairs also gradually increases, which can offset the effect of the decrease in the amplitude of the -order harmonic. As can be seen from the torque equation derived from the previous section, the fundamental wave and harmonic have the greatest impact on torque among all harmonic orders. Therefore, as the number of permanent magnet poles increases, the back EMF of PMVMs first increases. However, when the number of permanent magnet poles is too large, the distance between adjacent magnetic poles becomes very small, causing serious problems such as increased magnetic resistance, local saturation, and large leakage flux. Therefore, the back EMF of A4 decreases. In summary, as the number of permanent magnet poles increases, the magnetic field modulation capability of the PMVMs first increases and then decreases.
In addition, the rated torque values of different motors are analyzed under a rated condition with a load current amplitude of 50 A, as shown in Figure 14. It can be found that as the number of FMPs and the number of permanent magnet poles increase, the average torque of the motor basically first increases and then decreases. At the same time, the torque fluctuation of all motors is greater than 6%, which is speculated to be due to the small number of slots limiting the minimum size of the width of slot openings. As shown in Figure 15, it can be observed that as the number of FMPs increases, the overload torque coefficient (100 A) first increases and then decreases. This is because increasing the number of permanent magnet pole pairs will increase the electrical frequency of the motor. As the current gradually increases to the overload state, the armature reaction of the motor will be stronger, resulting in a decrease in the power factor and an increase in core loss. Therefore, the overload torque of PMVMs with large numbers of pole pairs is relatively reduced.
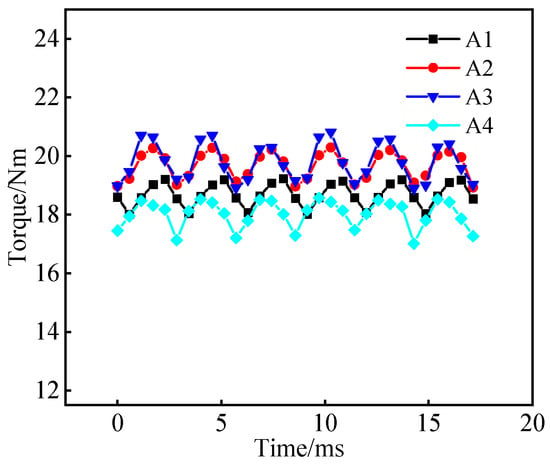
Figure 14.
Rated torque of 6-slot PMVMs.
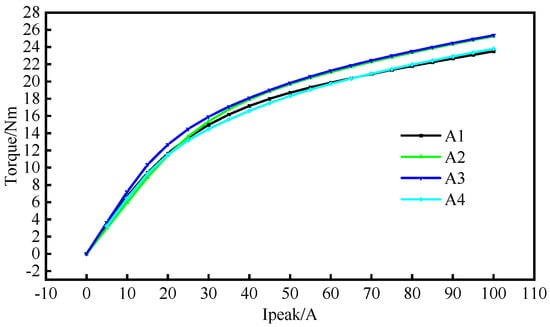
Figure 15.
Relationship of torque and current of 6-slot PMVMs.
Based on the changing law of number of FMPs and permanent magnet pole pairs of a 6-slot PMVMs, different topological structures of 12-slot PMVMs are determined, as shown in Figure 16 and Table 5. Their specific parameters are shown in Table 4. B1 in Table 4 corresponds to Figure 16a, B2 in Table 4 corresponds to Figure 16b, B3 in Table 4 corresponds to Figure 16c, and B4 in Table 4 corresponds to Figure 16d, and B1–B4 corresponds to four 12-slot PMVM topologies in Figure 16. It should be noted that the outer diameter of the stator and rotor and axial length of the stator and rotor of the 12-slot PMVMs are the same as those of the 6-slot PMVMs.
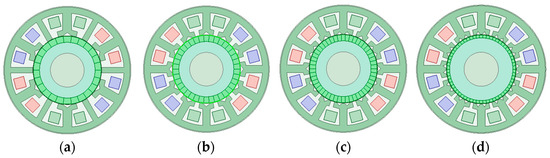
Figure 16.
Stator topologies of 12-slot PMVMs: (a) B1; (b) B2; (c) B3; (d) B4.

Table 5.
Matching parameters of 12-slot PMVMs.
From Table 6, it can be concluded that as the number of FMPs and the number of permanent magnet pole pairs increase, the amplitude of the no-load phase back EMF of 12-slot PMVMs first increases and then decreases. The cogging torque of B1 corresponding to 12-slot/18-FMP/13-pole-pair PMVMs is the largest, and the cogging torque of B2 corresponding to 12-slot/24-FMP/19-pole-pair PMVMs is the second largest. After analysis, it can be concluded that this is because the minimum common multiple of their FMP number and the number of permanent magnet pole pairs are relatively small.

Table 6.
Comparison of no-load performances.
In order to conduct a detailed comparative study on the differences in the magnetic field modulation ability of different types of 12-slot PMVMs, Fourier analysis is performed on the no-load air gap magnetic density of different types of 12-slot PMVMs. The results are shown in Figure 17, Figure 18, Figure 19 and Figure 20 and Table 7.
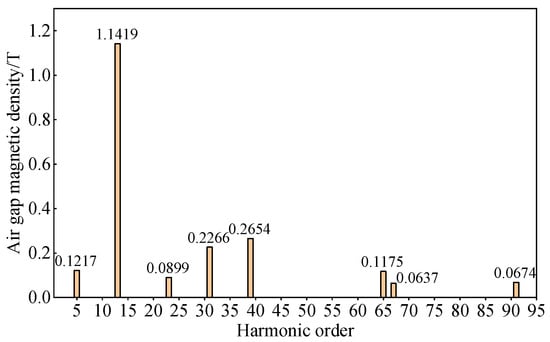
Figure 17.
Fourier decomposition of no-load air gap magnetic density of B1.
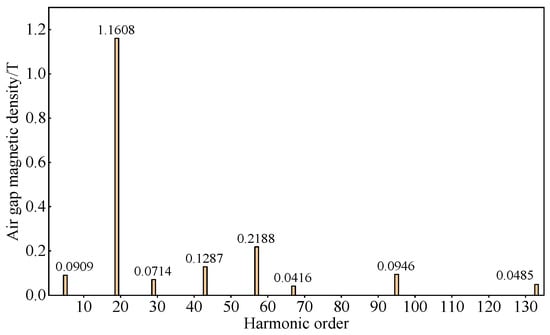
Figure 18.
Fourier decomposition of no-load air gap magnetic density of B2.
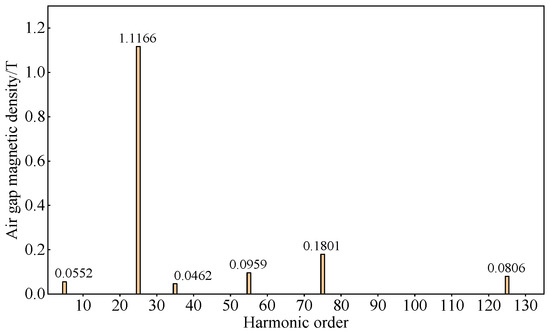
Figure 19.
Fourier decomposition of no-load air gap magnetic density of B3.
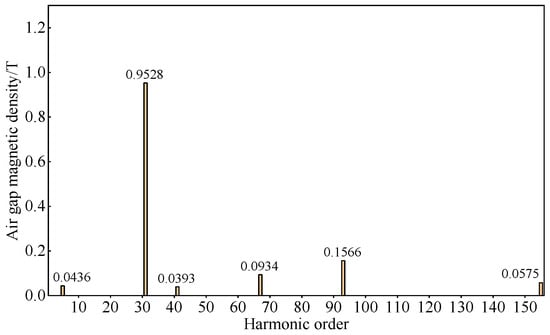
Figure 20.
Fourier decomposition of no-load air gap magnetic density of B4.

Table 7.
Matching methods of 12-slot PMVMs.
Based on the above results, it can be seen that for 12-slot PMVMs, as the number of FMPs increases, the amplitude of the fundamental order of the rotor first increases and then decreases, and other low-order harmonics gradually decrease, and the magnitude of reduction is greater than that of 6-slot PMVMs. It can be found that this corresponds to the results of six-slot PMVMs.
As the number of FMPs increases, the amplitude of the fundamental magnetic field gradually increases, while the amplitude of the modulation harmonic gradually decreases. However, at this time, the number of permanent magnets also gradually increases, thus offsetting the negative effect of the decrease in the amplitude of the harmonic on the amplitude of the no-load back EMF. Therefore, as the electromagnetic reduction ratio increases, the no-load back EMF first increases. When the number of permanent magnet poles is too large, it causes problems such as local saturation and increased leakage flux, so the no-load back EMF decreases again at this time.
In order to better evaluate the magnetic field modulation capability of different types of 12-slot PMVMs, the torque characteristics of 12-slot PMVMs are analyzed at a rated load current amplitude of 50 A, as shown in Figure 21. It can be found that as the number of FMPs and permanent magnet poles increases, the average torque of 12-slot PMVMs gradually first increases and then decreases. At the same time, the torque fluctuation values of 12-slot PMVMs are all less than 7%. Compared to the results of six-slot PMVMs, it can be concluded that increasing the number of slots and poles can effectively reduce the motor torque fluctuation.
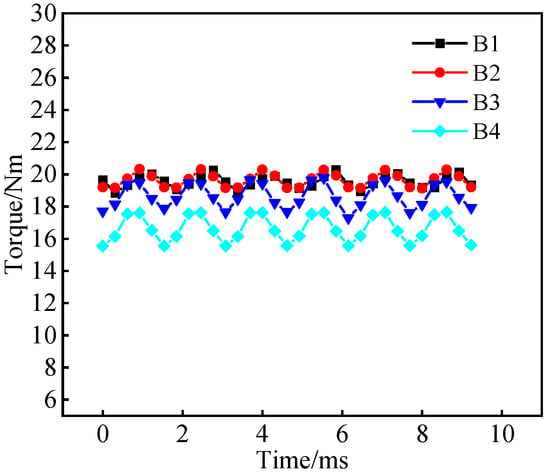
Figure 21.
Rated torque of 12-slot PMVMs.
The torque of 12-slot PMVMs under different load conditions is analyzed, as shown in Figure 22. It can be seen that as the number of FMPs and the number of permanent magnet poles increase, the overload torque coefficient of the motor gradually decreases when the load current amplitude is 100 A.
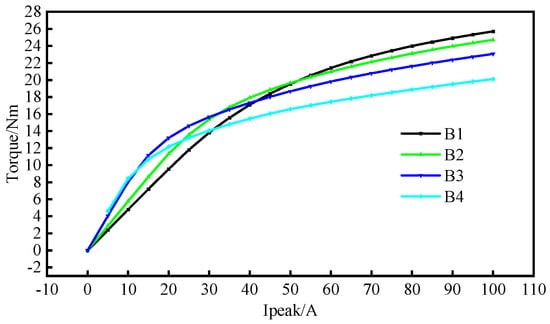
Figure 22.
Relationship of torque and current of 12-slot PMVMs.
Based on the results of 6-slot PMVMs and 12-slot PMVMs, it can be concluded that when the basic structural parameters of the motor remain unchanged, the electromagnetic reduction ratio of PMVMs increases with the increase in the number of FMPs and number of permanent magnet poles. This will lead to an increase in the amplitude of the fundamental modulation order of the magnetic field but a decrease in the number and amplitude of low-order magnetic field modulation harmonics. However, the increase in the number of permanent magnet pole pairs will compensate for the side effect of the decrease in the amplitude of the harmonic.
At the same time, increasing the number of pole pairs of PMVMs within a certain range can enhance the torque performance of the motor. Therefore, in order to ensure that the torque of the motor meets the requirements, for 6-slot PMVMs with an inner diameter less than 82 mm, the number of FMPs on each tooth of the stator should be not over three; for 12-slot PMVMs, the number of FMPs on each tooth of the stator should not exceed two as much as possible.
In order to verify the good fault tolerance of 12-slot PMVMs, self-inductance and mutual inductance are analyzed. As shown in Table 8, the ratio of mutual inductance to self-inductance is all not greater than 2%. Combined with the results of six-slot PMVMs, it can be concluded that single-layer concentrated windings have high fault tolerance and excellent phase-to-phase isolation capability.

Table 8.
Matching methods of 12-slot PMVMs.
Based on the above research results, in order to accurately evaluate the torque density and torque density coefficient of PMVMs under different slot–pole combinations, the increase in axial length of PMVMs caused by end winding is considered in detail. When the axial lengths of the stator core of 6-slot PMVMs and 12-slot PMVMs are basically the same, 6-slot PMVMs have longer winding ends than 12-slot PMVMs, which causes the axial length of 6-slot PMVMs to be greater than that of 12-slot PMVMs. Based on the above analysis, a modified variation relationship of torque density and current is given, as shown in Figure 23.

Figure 23.
Relationship of torque density and current of 6-slot PMVMs and 12-slot PMVMs.
As shown in Figure 23, as the load current gradually increases, B1 corresponding to 12-slot/18-FMP/13-pole-pair PMVMs has the highest torque density and torque density coefficient, while B2 corresponding to 12-slot/24-FMP/19-pole-pair PMVMs has the second highest torque density and torque density coefficient. It can be seen that 12-slot PMVMs have certain advantages in electromagnetic performance compared to 6-slot PMVMs.
2.3. Comparison of Different Flatness Ratio of PMVMs
In order to investigate the influence of structural parameters on the electromagnetic performance changes in PMVMs with different numbers of FMPs, a variable named the flatness ratio is defined in this section, which is equal to the ratio of the outer diameter of the stator to the axial length of the stator core , as shown in Equation (1). The variation in the electromagnetic performance of six-slot PMVMs with the number of FMPs under different flatness ratios is studied.
The motor parameters for each flatness ratio are shown in Table 9. The simulation results of each flatness ratio are shown in Figure 24. When the flatness ratio of the motor does not exceed 1.82, the outer diameter of the motor stator does not exceed 164 mm. At this time, as the number of FMPs increases, and the average torque of PMVMs under rated load gradually increases and then gradually decreases. Among the four 6 slot-PMVMs, the 6-slot/15-FMP/13-pole-pair PMVM has the highest average rated torque. When the flatness ratio of the motor exceeds 2.73, the outer diameter of the motor stator is greater than 246 mm. As the number of motor FMPs increases, the average rated torque of PMVMs gradually increases, and the average rated torque of 6-slot/18-FMP/16-pole-pair PMVMs is the highest.

Table 9.
Matching methods of 12-slot PMVMs.
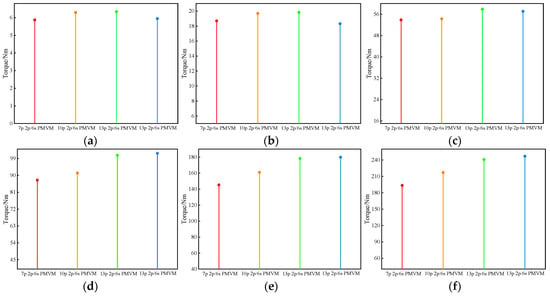
Figure 24.
The torque variation law of PMVMs with different flatness ratios. (a) ; (b) ; (c) ; (d) ; (e) ; (f) .
In summary, for six-slot split-tooth PMVMs, when the motor flatness ratio is small, an excessive number of permanent magnet poles will reduce the utilization rate of permanent magnets of motors, thereby deteriorating the motor’s magnetic field modulation ability and load torque performance. When the flatness ratio of the motor is very large, the outer diameter of the rotor increases, and the distance between adjacent permanent magnet poles relatively increases, which will make the motor less prone to the problem of increased leakage magnetic flux. Therefore, when the flatness ratio of the PMVMs increases, appropriately increasing the number of FMPs will improve the electromagnetic reduction ratio of the motor and enhance its load torque capacity.
3. Comparison Between PMVM and PMSM
In the previous section, a detailed study was conducted on various PMVMs with different structures, and their differences in magnetic field modulation ability were compared in detail. Different kinds of PMVMs with new stator tooth structures were proposed, and their performance advantages compared to traditional PMVM were demonstrated. In order to compare PMVMs with PMSMs in different load conditions, this section selects the 12-slot/18-FMP/13-pole-pair PMVM with triangular teeth, which has excellent electromagnetic performance, and compares it to the traditional 24-slot/13-pole-pair PMSM and 12-slot/5-pole-pairs PMSM; the number of permanent magnet poles for the 12-slot/18 FMP/13 pole-pair PMVM and 24 slot/13-pole-pair PMSM is the same, and the number of slots for the 12-slot/18-FMP/13-pole-pair PMVM and 12-slot/5-pole-pair PMSM is the same. All PMVMs and PMSMs in this article are at the 1.0~1.5 kW power level. Within this power level range, the electromagnetic performance of the 12-slot/5-pole-pair PMSM, 12-slot/18-FMP/13-pole-pair PMVM, and 24-slot/13-pole-pair PMSM is relatively good. Therefore, the 12-slot/5-pole-pair PMSM and 24-slot/13-pole-pair PMSM are taken as typical representative structures of PMSMs at this power level, and the 12-slot/18-FMP/13-pole-pair PMVM is taken as a typical representative structure of PMVMs at this power level.
The selected PMVMs and PMSMs are shown in Figure 25. The outer diameter of the stator and core axial length of the three motors are exactly the same, with a speed of 500 rpm and a load current of 50 A. All three motors are in a rated operating condition.
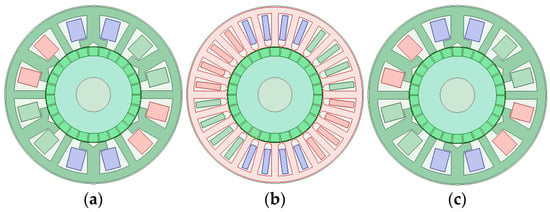
Figure 25.
Flux density under no-load condition: (a) 12-slot/18-FMP/13-pole-pair PMVM; (b) 24-slot/13-pole-pair PMSM; (c) 12-slot/5-pole-pair PMSM.
In order to ensure fairness in the comparison of electromagnetic performance, it is necessary to ensure that the some parameters of PMSMs and PMVM are consistent, as shown in Table 10.

Table 10.
Common parameters of PMSMs and PMVMs.
The no-load back EMF amplitude of PMVMs and PMSMs by the FEA method under different speeds is shown in Figure 26. It can be seen that the no-load back EMF amplitudes of PMSMs are larger than those of PMVMs under the same rotating speed, and the peak-to-peak value of the cogging torque of PMVMs is significantly higher than that of PMSMs, as shown in Figure 27. This is because the PMVM contains rich magnetic field modulation harmonics. Therefore, reducing the cogging torque of PMVMs is also one of the main directions to optimize the electromagnetic performance of PMVMs.
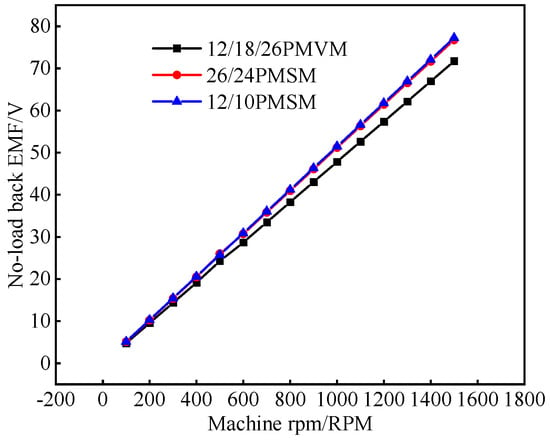
Figure 26.
No-load back EMF amplitude under different speeds.
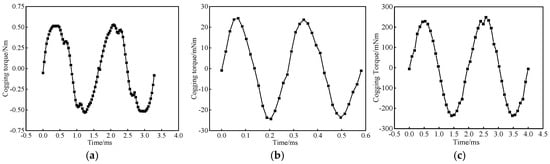
Figure 27.
Cogging torque of PMVM and PMSM: (a) 12-slot/18-FMP/13-pole-pair PMVM; (b) 24-slot/13-pole-pair PMSM; (c) 12-slot/5-pole-pair PMSM.
In order to evaluate the load torque characteristics of the motors in detail, the load current amplitude is set from 5 A to 100 A with a step size of 5 A. The average torque variation in PMVMs and PMSMs is studied as the load current increased. It is found that the load torque of PMVMs is always lower than that of different kinds of PMSMs, as shown in Figure 28. As is seen from Figure 28, when the amplitude of the load current is greater than 20 A, the load torque of the PMSM has a significant advantage. When the load current is 50 A, the average rated torque of the 24-slot/13-pole-pair PMSM is 22.53 Nm, the average rated torque of the 12-slot/5-pole-pair PMSM is 23.15 Nm, and the average rated torque of the 12-slot/18-FMP/13-pole-pair PMVM is 18.94 Nm, which is significantly lower than the two types of PMSMs. When the load current amplitude is 70 A, the overload torque of the 24-slot/13-pole-pair PMSM is 4.64 Nm higher than that of the PMVM, and the overload torque of the 12-slot/5-pole-pair PMSM is 8.82 Nm higher than that of the PMVM, indicating that the steady-state and overload performances of PMSMs are significantly better than those of PMVMs.
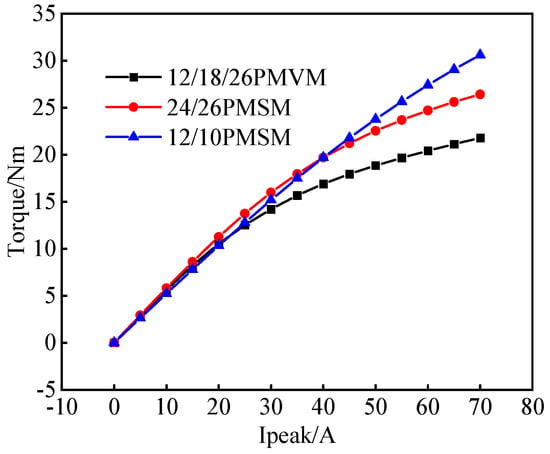
Figure 28.
Torque versus phase current of PMVM and PMSM.
A power factor analysis of PMVMs and PMSMs is shown in Figure 29. It can be seen that the power factor of PMVMs is always lower than that of PMSMs, which explains why the overload performance of PMVMs is a lot more inferior to PMSMs.
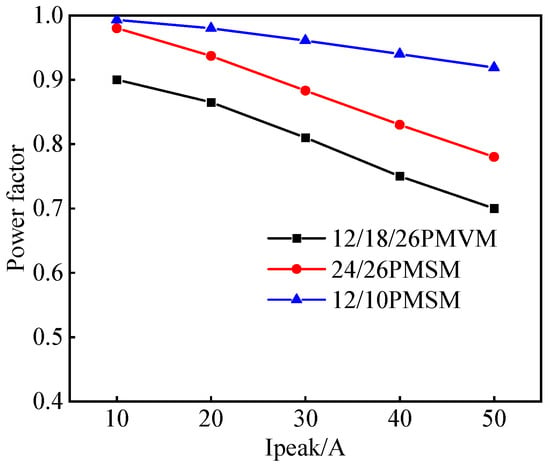
Figure 29.
Power factor versus phase current of PMVM and PMSM.
As shown in Figure 30 and Table 11, the constant speed range of PMVMs is smaller than that of PMSMs, but PMVMs can still maintain high torque at low speeds. Therefore, it can be concluded that the PMVM is suitable for some low-speed and high-torque applications. In addition, the highest efficiency of the 12-slot/18-FMP/13-pole-pair PMVM is 94.5%, the highest efficiency of the 24-slot/13-pole-pair PMSM reaches 94.7%, and the highest efficiency of the 12-slot/5-pole-pair PMSM is 96.3%, indicating that the 12-slot/5-pole-pair PMSM and 24-slot/13-pole-pair PMSM have a higher efficiency than the 12-slot/18-FMP/13-pole-pair PMVM. At the same time, compared to the PMVM, the 12-slot/5-pole-pair PMSM has a larger efficient area (efficiency > 92%), which is due to the abundant air gap magnetic density modulation harmonics in the PMVM, resulting in significant losses. However, the efficiency of the PMVM is relatively high in high-speed light-load areas; therefore, PMVMs have certain applicability in high-speed light-load applications.
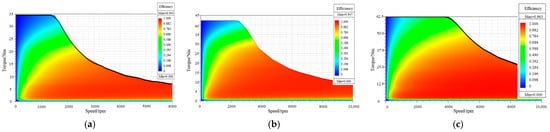
Figure 30.
Measured efficient map: (a) 12-slot/18-FMP/13-pole-pair PMVM; (b) 24-slot/13-pole-pair PMSM; (c) 12-slot/5-pole-pair PMSM.

Table 11.
Efficiency comparison between PMSMs and PMVM.
As shown in Table 12, for all motors, copper loss accounts for a relatively large proportion. The copper losses of the 12-slot/5-pole-pair PMSM and 12-slot/18-FMP/13-pole-pair PMVM are similar, but the copper loss of the 24-slot/13-pole-pair PMSM is smaller than that of the first two motors because the length of the winding end of the 24-slot/13-pole-pair PMSM is shorter and the phase resistance of the 24-slot/13-pole-pair PMSM is smaller. The core losses of the 12-slot/18-FMP/13-pole-pair PMVM and 24-slot/13-pole-pair PMSM are both relatively large because the electrical frequencies of the 12-slot/18-FMP/13-pole-pair PMVM and 24-slot/13-pole-pair PMSM are relatively high, and at the same time, 12-slot/18-FMP/13-pole-pair PMVM’s air gap magnetic field contains rich harmonics, so the core loss of the 12-slot/18-FMP/13-pole-pair PMVM is relatively large.

Table 12.
Losses of PMSMs and PMVM.
4. Experimental Verification
In order to verify the accuracy and correctness of the simulation models of the PMSMs and PMVM, a prototype is manufactured for the 12-slot/5-pole-pair PMSM, as shown in Figure 31, and the no-load back EMF and load torque of the motor are tested in Figure 32 and Figure 33.

Figure 31.
Prototype of 12-slot/5-pole-pair PMSM.
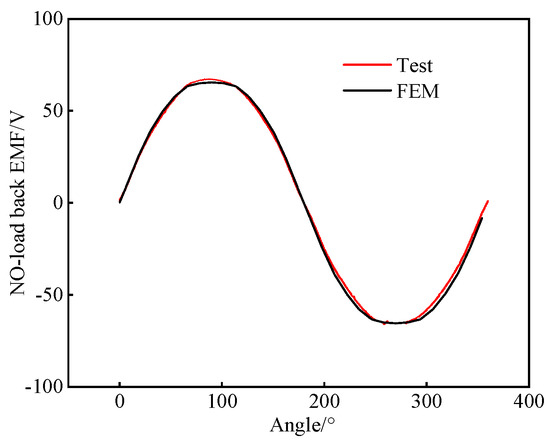
Figure 32.
Comparison of no-load back EMF between prototype and simulation.
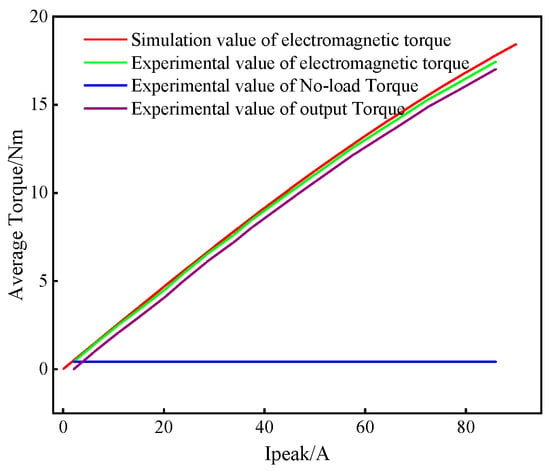
Figure 33.
Comparison of torque between prototype and simulation.
In the no-load back EMF test, the prototype is driven by a motor at a speed of 4272 rpm, and the no-load back EMF force is tested by an oscilloscope. When measuring the electromagnetic torque of a motor, the output torque of the motor under a specific load current and the no-load torque of the motor are measured separately and added to obtain the motor electromagnetic torque. Firstly, the output torque under a specific load current is measured. The motor driver drives the prototype to a specific speed, the clamp ammeter measures the effective value of the input current, and the output torque data are collected by using the upper computer. At the same speed, the prototype is driven and the no-load torque is measured. The average electromagnetic torque of the motor under this operating condition can be obtained by adding the average torque obtained from the two experiments.
The no-load back EMF of the 12-slot/5-pole-pair PMSM at 4272 rpm is measured, and the shape of the measured waveform is almost the same as that obtained from the simulation. The maximum error between the amplitude of the simulation and the measured value is within 2.6%, which is in a small range. This verifies that the constructed simulation model of motors has high accuracy.
The torque of the 12-slot/5-pole-pair PMSM is measured. It can be found that the measured electromagnetic torque is relatively small, and the maximum error between the prototype value of the electromagnetic torque and simulation value of the electromagnetic torque is within 2%, which verifies that the constructed torque simulation model has high accuracy. The possible reasons for errors mainly include the following: the prototype is powered on for a long time, resulting in significant heating and a certain decrease in electromagnetic performance, and during the measurement of output torque, frictional resistance causes the test results to decrease.
The consistency between the prototype and the simulation calculation results is good, so there is no problem with the simulation modeling calculation method. The same calculation method and software are used to calculate the electromagnetic performance of the 12-slot/18-FMP/13-pole-pair PMVM and 24-slot/13-pole-pair PMSM, so the calculation results are reliable.
5. Conclusions
In this paper, firstly, the electromagnetic performance differences in 12-slot PMVMs with different shapes of FMPs are studied, and multiple new shapes of FMPs are proposed. It is concluded that the PMVM with triangular teeth has stronger magnetic field modulation ability and higher torque density. Additionally, the PMVM with different types of slot–pole combinations and PMVMs with different numbers of FPMs and permanent magnet pole pairs are studied, revealing the mapping relationship between the number of FMPs/number of permanent magnet pole pairs/electromagnetic reduction ratio and torque characteristics under different slot–pole combinations. Then, the comprehensive performances of typical PMVMs and PMSMs are compared, and their performance in terms of the back EMF coefficient, torque coefficient, power factor, efficiency, etc., under various operating conditions is compared. It is proved that the PMSM indeed has better performance. If other effective measures are taken to reduce losses and improve the power factor, the advantage of PMVMs can be greatly expanded. Finally, a prototype of the 12-slot/5-pole pair PMSM is manufactured, and the no-load back EMF and torque under different currents are tested.
Author Contributions
Conceptualization, Y.L. and J.Z.; methodology, Y.L.; software, Y.L.; validation, Y.L., J.Z. and W.W.; formal analysis, J.F.; investigation, Y.L.; resources, Y.X.; data curation, X.L.; writing—original draft preparation, Y.L.; writing—review and editing, J.Z.; visualization, J.F.; supervision, Y.X.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets presented in this article are not readily available due to technical and time limitations. Requests to access the datasets should be directed to 3120220849@bit.edu.cn.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, Y.; Li, D.; Ren, X.; Qu, R. Investigation of Permanent Magnet Vernier Machines from Armature Field Perspective. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2934–2945. [Google Scholar] [CrossRef]
- Ma, Y.; Xiao, Y.; Wang, J.; Zhou, L. Multicriteria Optimal Latin Hypercube Design-Based Surrogate-Assisted Design Optimization for a Permanent-Magnet Vernier Machine. IEEE Trans. Magn. 2022, 58, 1–5. [Google Scholar] [CrossRef]
- Tlali, P.M.; Wang, R.-J.; Gerber, S.; Botha, C.D.; Kamper, M.J. Design and Performance Comparison of Vernier and Conventional PM Synchronous Wind Generators. IEEE Trans. Ind. Appl. 2020, 56, 2570–2579. [Google Scholar] [CrossRef]
- Xie, S.; Cai, S.; Zuo, Y.; Cao, L.; Zhu, J.; Li, A.; Yan, Y.; Lee, C.H.T. A New Hybrid Concentrated-Winding Concept With Improved Power Factor for Permanent Magnet Vernier Machine. IEEE Trans. Ind. Electron. 2023, 70, 11109–11120. [Google Scholar] [CrossRef]
- Ishizaki, A.; Tanaka, T.; Takasaki, K.; Nishikata, S. Theory and optimum design of PM vernier motor. In Proceedings of the 1995 Seventh International Conference on Electrical Machines and Drives (Conf. Publ. No. 412), Durham, UK, 11–13 September 1995; pp. 208–212. [Google Scholar]
- Kim, B.; Lipo, T.A. Operation and Design Principles of a PM Vernier Motor. IEEE Trans. Ind. Appl. 2014, 50, 3656–3663. [Google Scholar] [CrossRef]
- Kim, H.-W.; Kang, D.H.; Jun, S.-B.; Jung, S.-W.; Jung, S.-Y. Comparative Study of PMVM According to Gear Ratio With Power Factor Improvement. In Proceedings of the 2022 IEEE 20th Biennial Conference on Electromagnetic Field Computation (CEFC), Denver, CO, USA, 24–26 October 2022. [Google Scholar]
- Wang, T.; Zhu, X.; Xiang, Z.; Fan, D.; Quan, L. Torque Ripple Suppression of a Permanent Magnet Vernier Motor From Perspective of Shifted Air-Gap Permeance Distribution. IEEE Trans. Magn. 2022, 58, 1–6. [Google Scholar] [CrossRef]
- Jian, L.; Xu, G.; Mi, C.C.; Chau, K.T.; Chan, C.C. Analytical Method for Magnetic Field Calculation in a Low-Speed Permanent-Magnet Harmonic Machine. IEEE Trans. Energy Convers. 2011, 26, 862–870. [Google Scholar] [CrossRef]
- Du, Y.; He, Z.; Zhu, X.; Xiao, F.; Zhang, C.; Xu, L.; Zuo, Y.; Quan, L. A Novel Pole-Changing Permanent Magnet Vernier Motor. IEEE Trans. Ind. Electron. 2023, 70, 6110–6120. [Google Scholar] [CrossRef]
- Li, R.; Shi, C.; Qu, R.; Li, D.; Ren, X.; Fedida, V.; Zhou, Y. A Novel Modular Stator Fractional Pole-Pair Permanent-Magnet Vernier Machine With Low Torque Ripple for Servo Applications. IEEE Trans. Magn. 2021, 57, 1–6. [Google Scholar] [CrossRef]
- Liu, G.; Guan, R.; Xu, L. Unequal Stator Modulated Teeth Structure to Reduce Electromagnetic Vibration in Permanent Magnet Vernier Machine. IEEE Trans. Ind. Electron. 2023, 70, 12036–12047. [Google Scholar] [CrossRef]
- He, Z.; Xiao, F.; Du, Y.; Zhu, X. Comparison of Permanent Magnet Vernier Motors with Evenly and Unevenly Distributed Modulation Teeth. IEEE Trans. Magn. 2023, 59, 1–5. [Google Scholar] [CrossRef]
- Fang, L.; Li, D.; Ren, X.; Qu, R. A Novel Permanent Magnet Vernier Machine with Coding-Shaped Tooth. IEEE Trans. Ind. Electron. 2022, 69, 6058–6068. [Google Scholar] [CrossRef]
- Yu, Y.; Chai, F.; Pei, Y.; Doppelbauer, M. Investigation of PM Loss in Spoke-Type Permanent Magnet Vernier Motors With Different Stator Topologies for In-Wheel Direct Drive. IEEE Trans. Ind. Appl. 2022, 58, 4562–4574. [Google Scholar] [CrossRef]
- Raza, M.; Zhao, W.; Lipo, T.A.; Kwon, B.-I. Performance Comparison of Dual Airgap and Single Airgap Spoke-Type Permanent-Magnet Vernier Machines. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Yu, Y.; Chai, F.; Pei, Y.; Doppelbauer, M.; Lee, C.H.T. Comparative Study of Loss Characteristic Between Permanent Magnet Synchronous Machine and Vernier Machine for In-Wheel Direct Drive. IEEE Trans. Transp. Electrif. 2025, 11, 2035–2048. [Google Scholar] [CrossRef]
- Yu, Y.; Pei, Y.; Chai, F.; Doppelbauer, M. Performance Comparison Between Permanent Magnet Synchronous Motor and Vernier Motor for In-Wheel Direct Drive. IEEE Trans. Ind. Electron. 2023, 70, 7761–7772. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).