Nonlinear Vibration Analysis of Turbocharger Rotor Supported on Rolling Bearing by Modified Incremental Harmonic Balance Method
Abstract
1. Introduction
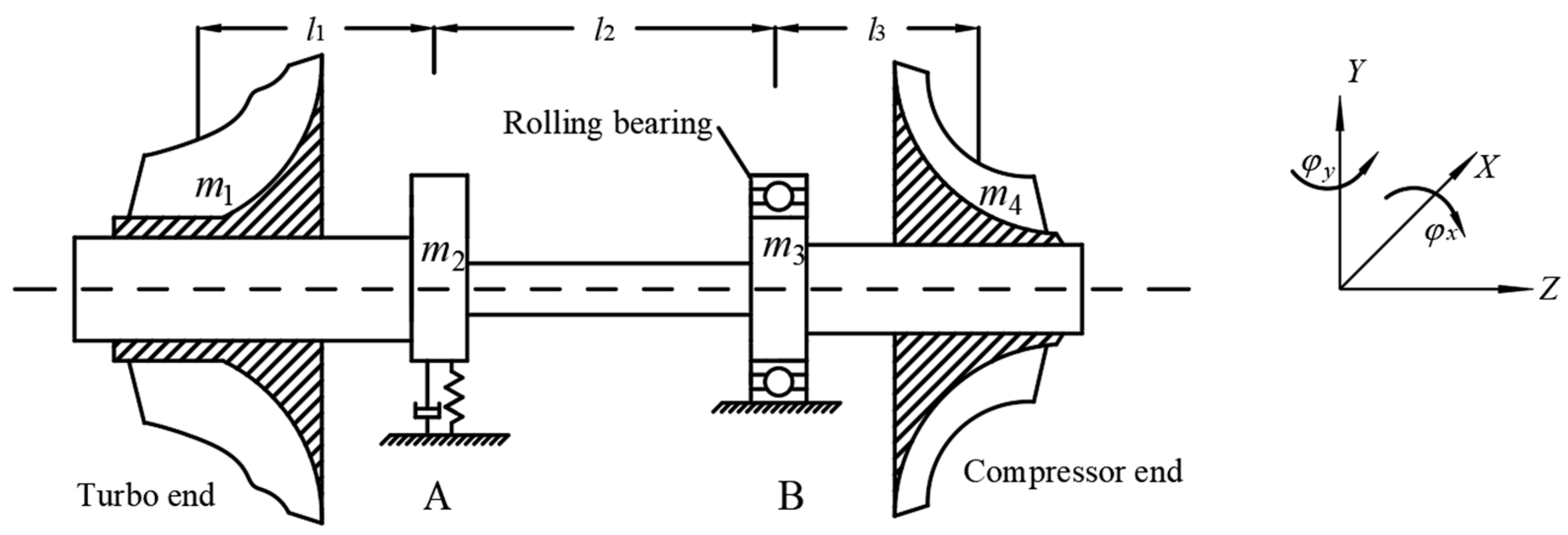
2. Rolling Bearing-Supported Turbocharger Rotor Model
2.1. Dynamic Model of Rotor System
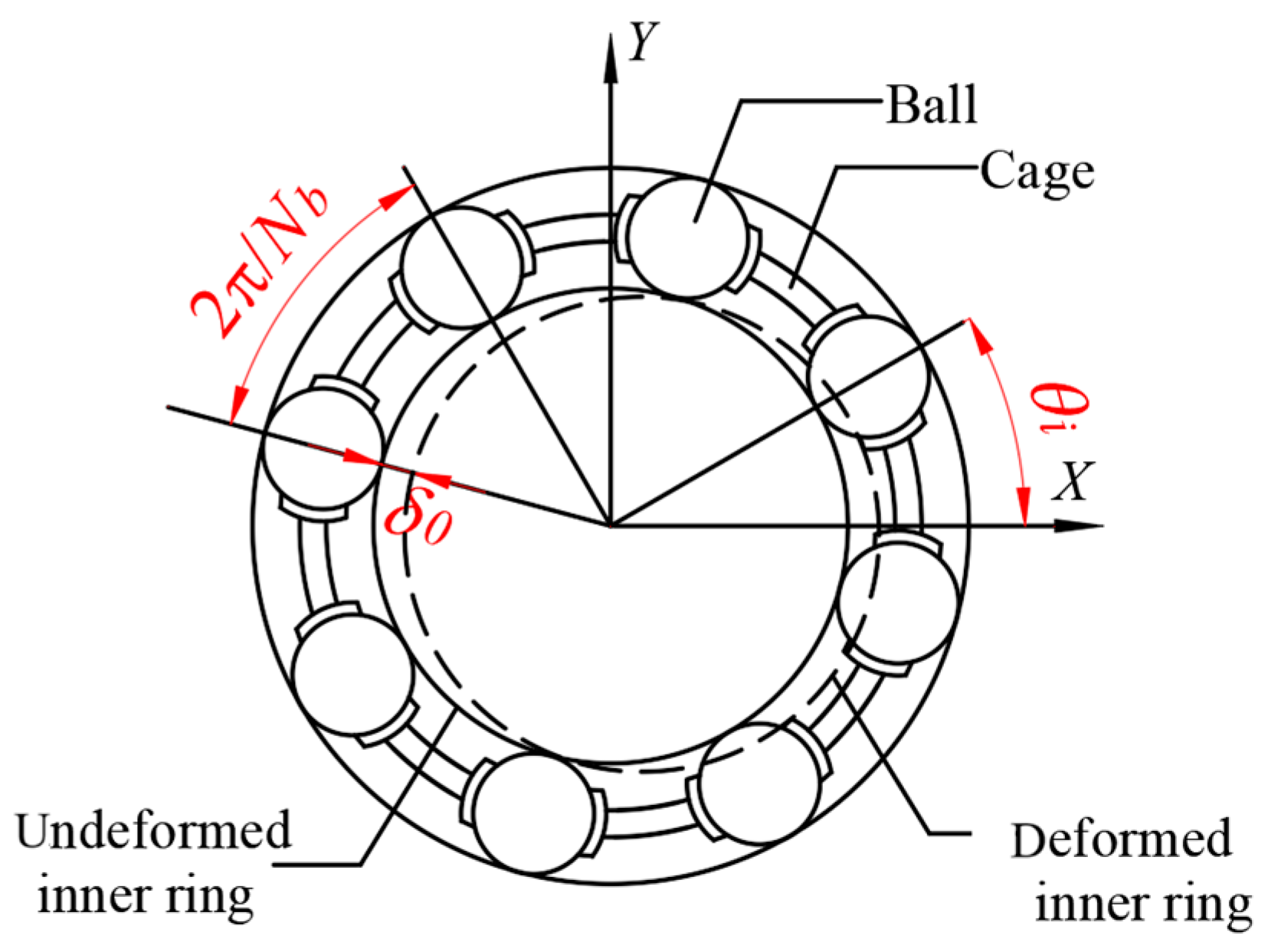
2.2. Dynamic Model of Rolling Bearings
2.3. Dynamic Model of the Rotor-Rolling Bearing System
3. The MIHB Method for Nonlinear Dynamic Analysis
3.1. IHB Method Based on Tensor Contraction and FFT
3.2. MIHB Method for Embedding Arc-Length Continuation
3.3. Stability Analysis of Periodic Solution
4. Verification
4.1. Model Validation
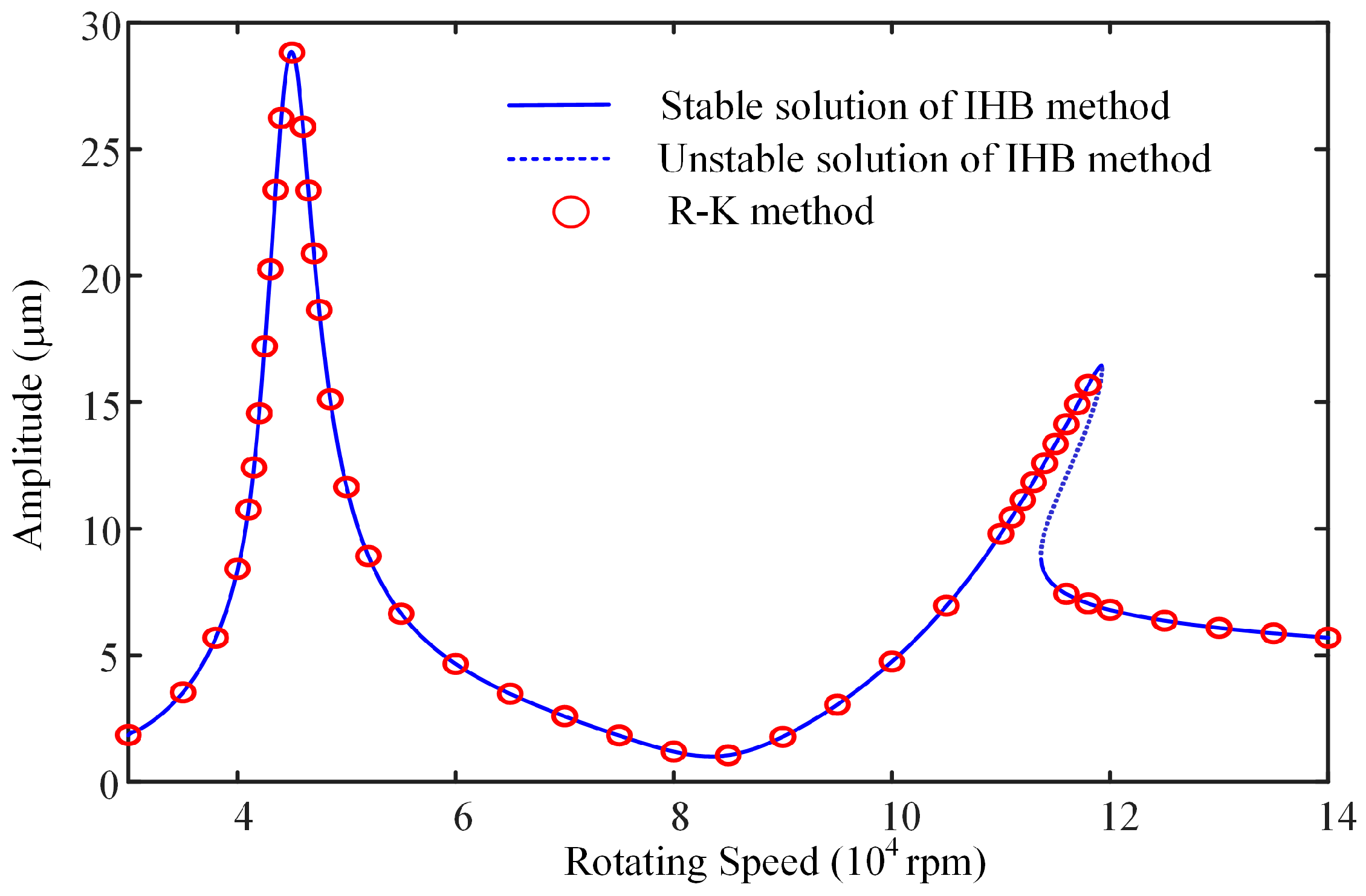
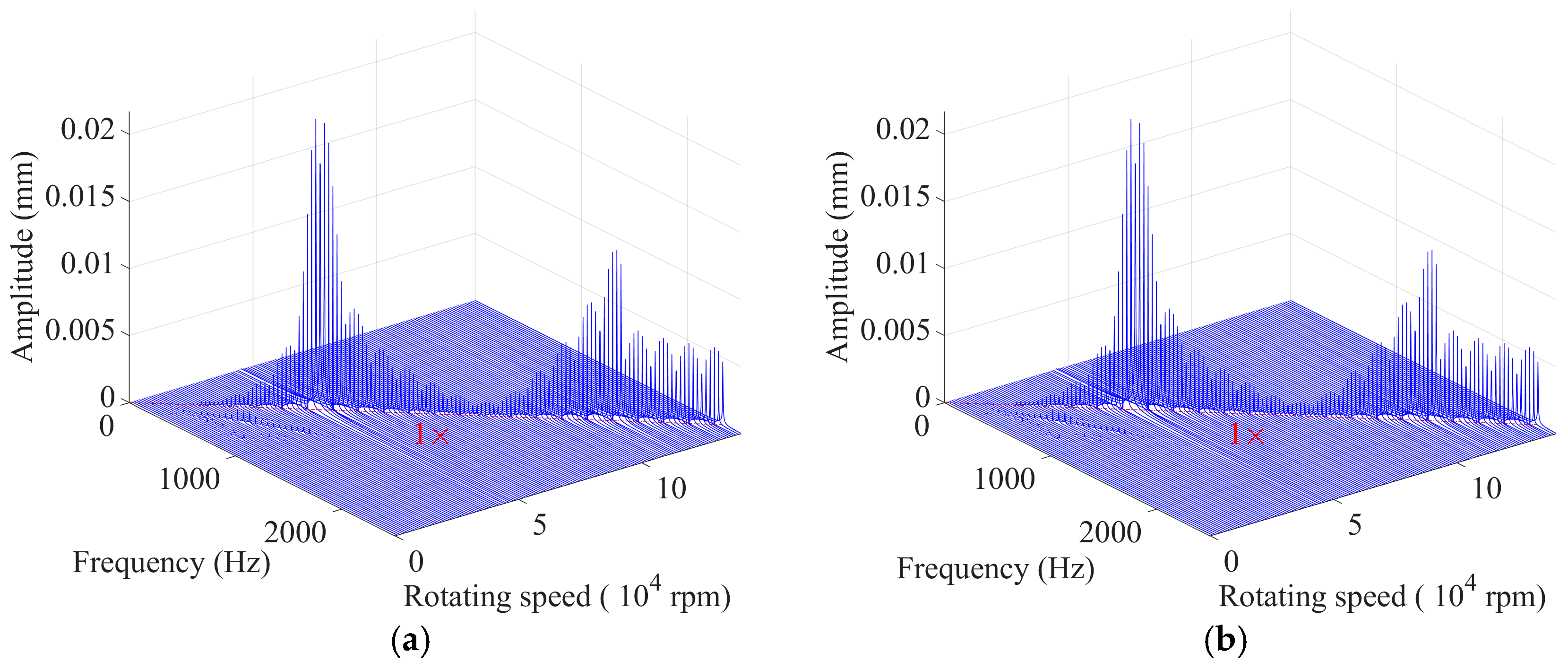
4.2. The Validation for the MIHB Method
5. Discussion
6. Conclusions
- (1)
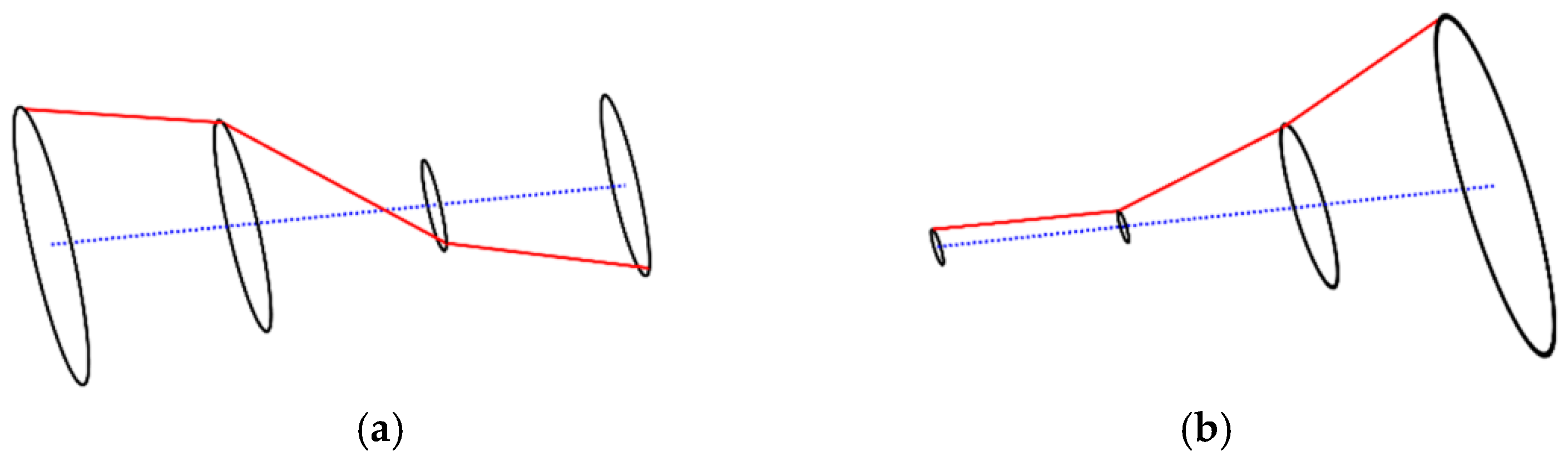
- The resonance modes of the system at low speed (around 4.5 × 104 rpm) and high speed (around 11 × 104 rpm) are conical mode and bending mode, respectively, with a bistable phenomenon appearing at the resonance peak of the bending mode.
- (2)
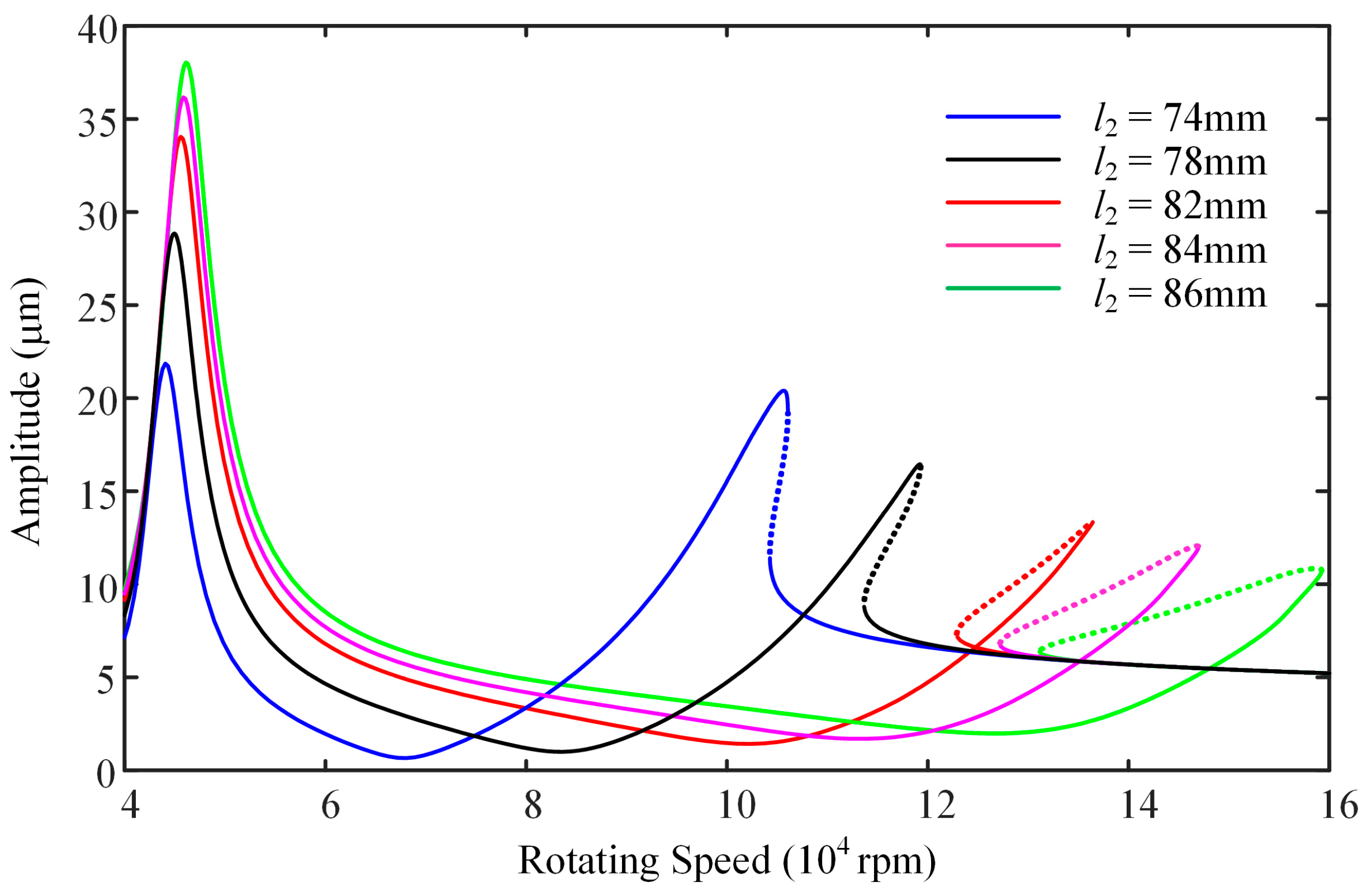
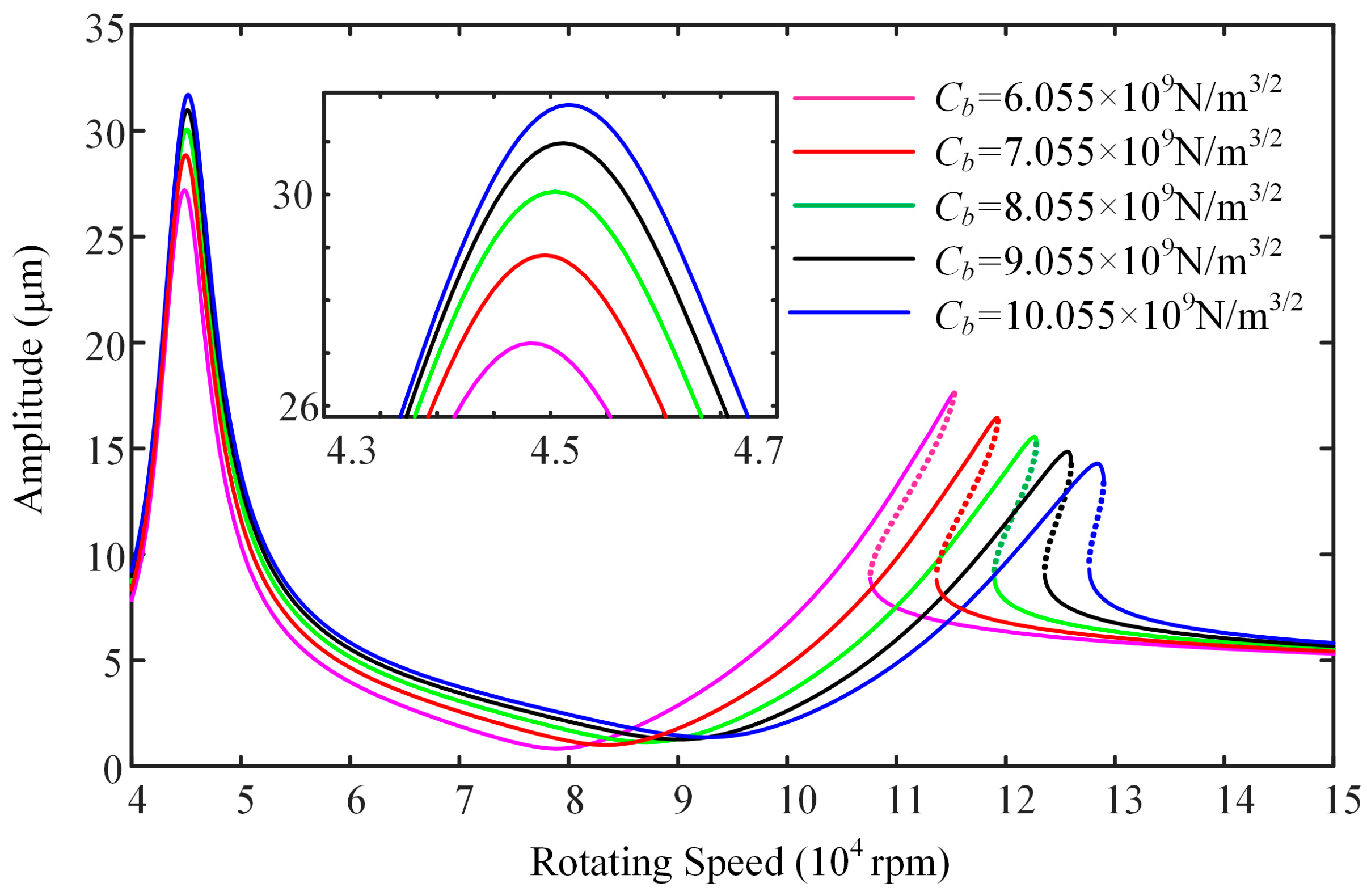
- The conical mode resonance peak demonstrates notable sensitivity to both bearing clearance and the spacing between the two bearings. The amplitude of the system in the non-resonant speed range is positively correlated with the resonance peak of the conical mode. Therefore, when designing a turbocharger, the resonance peak of the conical mode should be suppressed. To achieve this, it is necessary to increase the equivalent stiffness of another bearing and reduce the distance between the two bearings.
- (3)
- The bending mode’s resonance frequency and amplitude are highly sensitive to the spacing between the two bearings. Due to the fact that the resonance peak value of the bending mode is smaller than that of the conical mode, it is more important to reduce its bistable range compared to suppressing amplitude.
- (4)
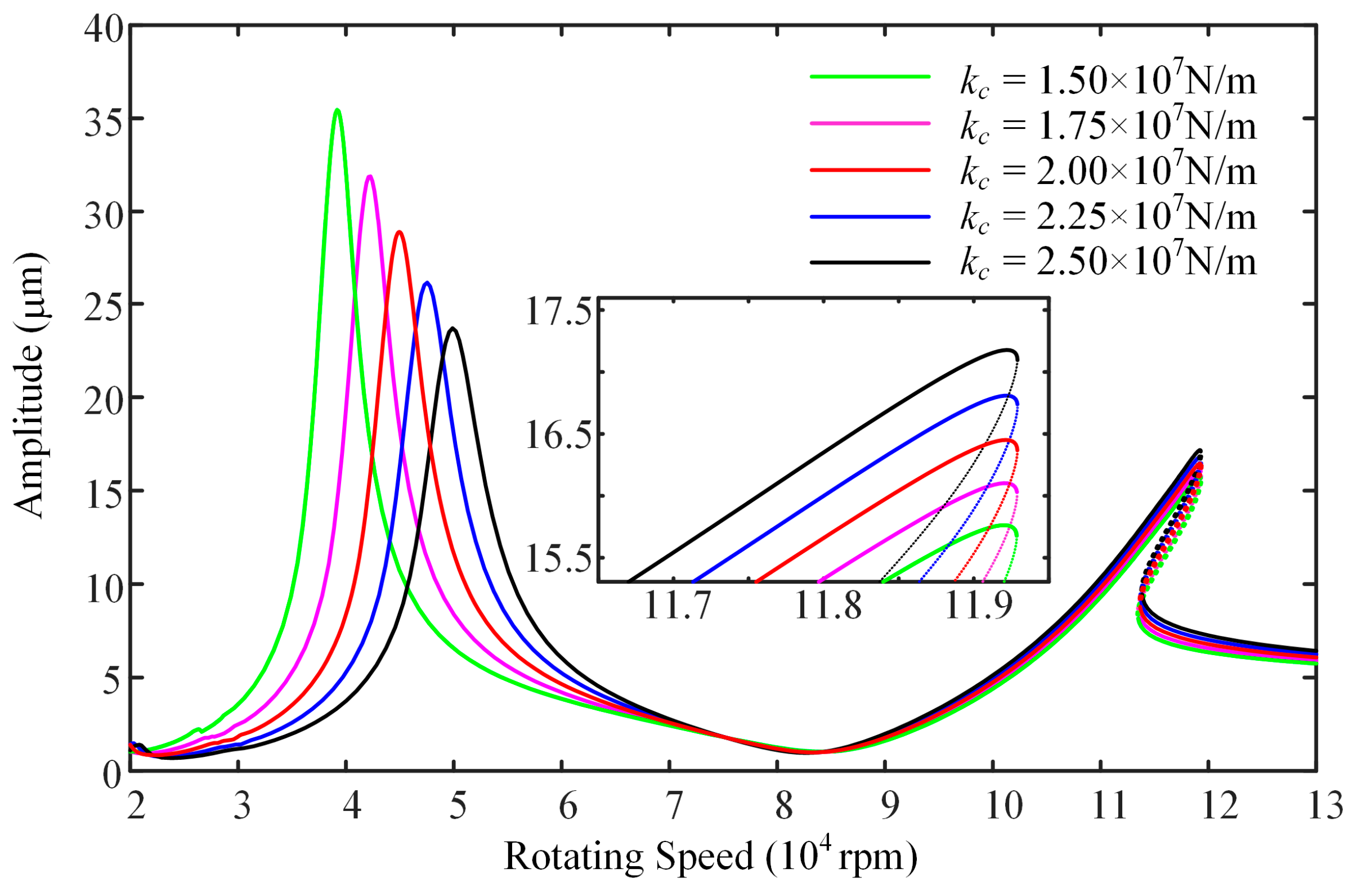
- In general, the decrease of one vibration peak is often in the wake of the increase of another one unless increasing the modal damping ratio. Choosing bearings with a large number of ball bearings, high Hertz contact stiffness, and small bearing clearance can effectively prevent amplitude jumps and enhance the system’s impact resistance at high speeds. However, under non-resonant rotating speed, the amplitude will increase. Therefore, the equivalent stiffness of another bearing needs to be adjusted simultaneously. The distance between two bearings should be as small as possible while meeting other parameter requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nyongesa, A.; Park, M.; Lee, C.; Choi, J.H.; Hur, J.J.; Lee, W.J. Experimental evaluation of the significance of scheduled turbocharger reconditioning on marine diesel engine efficiency and exhaust gas emissions. Ain Shams Eng. J. 2024, 15, 102845. [Google Scholar] [CrossRef]
- Wang, L.; Wang, A.; Yin, Y.; Heng, X.; Jin, M. Effects of unbalance orientation on the dynamic characteristics of a double overhung rotor system for high-speed turbochargers. Nonlinear Dyn. 2022, 107, 665–681. [Google Scholar] [CrossRef]
- Cao, H.; Niu, L.; Xi, S.; Chen, X. Mechanical model development of rolling bearing-rotor systems: A review. Mech. Syst. Signal Proc. 2018, 102, 37–58. [Google Scholar] [CrossRef]
- Singh, A.; Gupta, T.C. Effect of rotating unbalance and engine excitations on the nonlinear dynamic response of turbocharger flexible rotor system supported on floating ring bearings. Arch. Appl. Mech. 2020, 90, 1117–1134. [Google Scholar] [CrossRef]
- Smolík, L.; Dyk, S. Towards efficient and vibration-reducing full-floating ring bearings in turbochargers. Int. J. Mech. Sci. 2020, 175, 105516. [Google Scholar] [CrossRef]
- Peixoto, T.F.; Nordmann, R.; Cavalca, K.L. Dynamic analysis of turbochargers with thermo-hydrodynamic lubrication bearings. J. Sound Vib. 2021, 505, 116140. [Google Scholar] [CrossRef]
- Ishida, Y.; Yamamoto, T. Linear and Nonlinear Rotordynamics: A Modern Treatment with Applications; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Sawalhi, N.; Randall, R.B.; Endo, H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis. Mech. Syst. Signal Proc. 2007, 21, 2616–2633. [Google Scholar] [CrossRef]
- Tian, J.; Wang, P.; Xu, H.; Ma, H.; Zhao, X. Nonlinear vibration characteristics of rolling bearing considering flexible cage fracture. Int. J. Non-Linear Mech. 2023, 156, 104478. [Google Scholar] [CrossRef]
- Sunnersjö, C. Varying compliance vibrations of rolling bearings. J. Sound Vib. 1978, 58, 363–373. [Google Scholar] [CrossRef]
- Fukata, S.; Gad, E.; Kondou, T.; Ayabe, T.; Tamura, H. On the radial vibration of ball bearings: Computer simulation. Bull. JSME 1985, 28, 899–904. [Google Scholar] [CrossRef]
- Mevel, B.; Guyader, J. Routes to chaos in ball bearings. J. Sound Vib. 1993, 162, 471–487. [Google Scholar] [CrossRef]
- Mevel, B.; Guyader, J. Experiments on routes to chaos in ball bearings. J. Sound Vib. 2008, 318, 549–564. [Google Scholar] [CrossRef]
- Zhao, Y.; Hou, Y.; Wang, X.; Wei, J.; Shi, H.; Sha, C. A multiaxial fatigue method for rolling contact fatigue life prediction of axle box bearing under wheel-rail excitation conditions. Eng. Fail. Anal. 2024, 159, 108086. [Google Scholar] [CrossRef]
- Andres, L.; Rivadeneria, J.; Chinta, M.; Gjika, K.; LaRue, G. Nonlinear rotordynamics of automotive turbochargers: Predictions and comparisons to test data. J. Eng. Gas Turbines Power 2007, 129, 488–493. [Google Scholar] [CrossRef]
- Andres, L.; Rivadeneria, J.; Gjika, K.; Groves, C.; LaRue, G. A virtual tool for prediction of turbocharger nonlinear dynamic response: Validation against test data. J. Eng. Gas Turbines Power 2007, 129, 1035–1046. [Google Scholar] [CrossRef]
- Andres, L.; Rivadeneria, J.; Gjika, K.; Groves, C.; LaRue, G. Rotordynamics of small turbochargers supported on floating ring bearings—Highlights in bearing analysis and experimental validation. J. Tribol. 2007, 129, 391–397. [Google Scholar] [CrossRef]
- Bonello, P. Transient modal analysis of the non-linear dynamics of a turbocharger on floating ring bearings. J. Tribol. 2009, 223, 79–93. [Google Scholar] [CrossRef]
- Tian, L.; Wang, W.J.; Peng, Z.J. Dynamic behaviours of a full floating ring bearing supported turbocharger rotor with engine excitation. J. Sound Vib. 2011, 330, 4851–4874. [Google Scholar] [CrossRef]
- Tian, L.; Wang, W.J.; Peng, Z.J. Nonlinear effects of unbalance in the rotor-floating ring bearing system of turbochargers. Mech. Syst. Signal Process. 2013, 34, 298–320. [Google Scholar] [CrossRef]
- Tian, L.; Wang, W.; Peng, Z. Effects of bearing outer clearance on the dynamic behaviours of the full floating ring bearing supported turbocharger rotor. Mech. Syst. Signal Process. 2012, 31, 155–175. [Google Scholar] [CrossRef]
- Ouyang, X.; Guo, H.; Wu, X.; Men, R.; Li, M.; Cao, S. Investigation of weight effects on the critical speed of inclined turbocharger rotor system. J. Nonlinear Math. Phys. 2022, 29, 403–422. [Google Scholar] [CrossRef]
- Kong, X.; Guo, H.; Cheng, Z.; Men, R. Dynamic characteristics of electrically assisted turbocharger rotor system under strong impacts. J. Vib. Eng. Technol. 2024, 12, 7955–7967. [Google Scholar] [CrossRef]
- Mutra, R.R.; Srinivas, J.; Shaik, J.H.; Obaiah, M.C.; Balamurali, G.; Kumar, P. Turbocharger rotor vibration reduction methodology with an active control scheme. Noise Vib. Worldw. 2021, 52, 347–355. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H. A coupled model of angular-contact ball bearing-elastic rotor system and its dynamic characteristics under asymmetric support. J. Vib. Eng. Technol. 2021, 9, 1175–1192. [Google Scholar] [CrossRef]
- Ghaisas, N.; Wassgren, C.; Sadeghi, F. Cage instabilities in cylindrical roller bearings. J. Tribol. 2004, 126, 681–689. [Google Scholar] [CrossRef]
- Zhao, H.; Fu, C.; Zhang, Y.Q.; Zhu, W.D.; Lu, K.; Francis, E.M. Dimensional decomposition-aided metamodels for uncertainty quantification and optimization in engineering: A review. Comput. Methods Appl. Mech. Eng. 2024, 428, 117098. [Google Scholar] [CrossRef]
- Omid, M.; Saleh, M. Adaptive sliding mode control for finite-time stability of quad-rotor UAVs with parametric uncertainties. ISA Trans. 2018, 72, 1–14. [Google Scholar]
- Fu, C.; Zhang, K.F.; Cheng, H.; Zhu, W.D.; Zheng, Z.L.; Lu, K.; Yang, Y.F. A comprehensive study on natural characteristics and dynamic responses of a dual-rotor system with inter-shaft bearing under non-random uncertainty. J. Sound Vib. 2024, 570, 118091. [Google Scholar] [CrossRef]
- Ashtekar, A.; Tian, L.; Lancaster, C. An analytical investigation of turbocharger rotor-bearing dynamics with rolling element bearings and squeeze film dampers. In Proceedings of the 11th International Conference on Turbochargers and Turbocharging, London, UK, 13–14 May 2014; pp. 361–373. [Google Scholar]
- Chang, Z.; Hou, L.; Chen, Y. Nonlinear dynamics and thermal bidirectional coupling characteristics of a rotor-ball bearing system. Appl. Math. Model. 2023, 119, 513–533. [Google Scholar] [CrossRef]
- Kim, K.; Ri, K.; Yun, C.; Jong, Y.; Han, P. Nonlinear forced vibration and stability analysis of nonlinear systems combining the IHB method and the AFT method. Comput. Struct. 2022, 264, 106771. [Google Scholar] [CrossRef]
- Lu, W.; Ge, F.; Wu, X.; Hong, Y. Nonlinear dynamics of a submerged floating moored structure by incremental harmonic balance method with FFT. Mar. Struct. 2013, 31, 63–81. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, W. A modified incremental harmonic balance method based on the fast Fourier transform and Broyden’s method. Nonlinear Dyn. 2015, 81, 981–989. [Google Scholar] [CrossRef]
- Zhang, W.; Huseyin, K. Complex formulation of the IHB technique and its comparison with other methods. Appl. Math. Model. 2002, 26, 53–75. [Google Scholar] [CrossRef]
- Ri, K.; Ri, Y.; Yun, C.; Kim, K.; Han, P. Analysis of nonlinear vibration and stability of Jeffcott rotor supported on squeeze-film damper by IHB method. AIP Adv. 2022, 12, 025127. [Google Scholar] [CrossRef]
- Ri, K.; Jang, J.; Yun, C.; Pak, C.; Kim, K. Analysis of subharmonic and quasi-periodic vibrations of a Jeffcott rotor supported on a squeeze-film damper by the IHB method. AIP Adv. 2022, 12, 055328. [Google Scholar] [CrossRef]
- Ju, R.; Fan, W.; Zhu, W. An efficient Galerkin averaging-incremental harmonic balance method based on the fast Fourier transform and tensor contraction. J. Vib. Acoust. 2020, 142, 1–38. [Google Scholar] [CrossRef]
- Chang, Z.; Hou, L.; Lin, R.; Jin, Y.; Chen, Y. A modified IHB method for nonlinear dynamic and thermal coupling analysis of rotor-bearing systems. Mech. Syst. Signal Proccess. 2023, 200, 110586. [Google Scholar] [CrossRef]
- Chang, Z.Y.; Hou, L.; Masarati, P.; Lin, R.Z.; Li, Z.G.; Chen, Y.S. Modeling and nonlinear analysis of a coupled thermo-mechanical dual-rotor system. Nonlinear Dyn. 2024, 112, 17811–17842. [Google Scholar] [CrossRef]
- Chen, Y.; Hou, L.; Lin, R.Z.; Song, J.Z.; Ng, T.Y.; Chen, Y.S. A harmonic balance method combined with dimension reduction and FFT for nonlinear dynamic simulation. Mech. Syst. Signal Proccess. 2024, 221, 111758. [Google Scholar] [CrossRef]
- Chen, Y.; Hou, L.; Lin, R.Z.; Toh, W.; Ng, T.Y.; Chen, Y.S. A general and efficient harmonic balance method for nonlinear dynamic simulation. Int. J. Mech. Sci. 2024, 276, 109388. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.; Lai, S.K.; Chen, Z.; Chen, L. Frequency-dependent equivalent impedance analysis for optimizing vehicle inertial suspensions. Nonlinear Dyn. 2025, 113, 9373–9398. [Google Scholar] [CrossRef]
- Zhou, Y.; Luo, Z.; Bian, Z.; Wang, F. Nonlinear vibration characteristics of the rotor bearing system with bolted flange joints. Proc. Inst. Mech. Eng. Part K 2019, 233, 910–930. [Google Scholar] [CrossRef]
- Roy, H.; Chandraker, S.; Dutt, J.K.; Roy, T. Dynamics of multilayer, multidisc viscoelastic rotor-An operator based higher order classical model. J. Sound Vib. 2016, 369, 87–108. [Google Scholar] [CrossRef]
- Kluger, J.; Crevier, L.; Udengaard, M. Speed-dependent eigenmodes for efficient simulation of transverse rotor vibration. Vibration 2022, 5, 732–754. [Google Scholar] [CrossRef]
- Harris, T.; Kotzalas, M. Rolling Bearing Analysis: Essential Concepts of Bearing Technology; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Zhang, H.; Zhai, J.; Han, Q.; Sun, W. Dynamics of a geared parallel-rotor system subjected to changing oil-bearing stiffness due to external loads. Finite Elem. Anal. Des. 2015, 106, 32–40. [Google Scholar] [CrossRef]
- Chen, Y.; Hou, L.; Lin, R.; Wang, Y.; Saeed, N.A.; Chen, Y. Combination resonances of a dual-rotor-bearing-casing system. Nonlinear Dyn. 2024, 112, 4063–4083. [Google Scholar] [CrossRef]
- Han, Y.; Ri, K.; Yun, C.; Kim, K.; Kim, K. Nonlinear vibration analysis and stability analysis of rotor systems supported on SFD by combining DQFEM, CMS and IHB methods. Appl. Math. Model. 2023, 121, 828–842. [Google Scholar] [CrossRef]
- Zhu, G.; Lu, K.; Cao, Q.; Huang, P.; Zhang, K. Dynamic behavior analysis of tethered satellite system based on Floquet theory. Nonlinear Dyn. 2022, 109, 1379–1396. [Google Scholar] [CrossRef]
- Berenguer, M.; Garbayo, A.; Mas, J.; Ramallo, A.V. Holographic Floquet states in low dimensions (II). J. High Energy Phys. 2022, 2022, 20. [Google Scholar] [CrossRef]

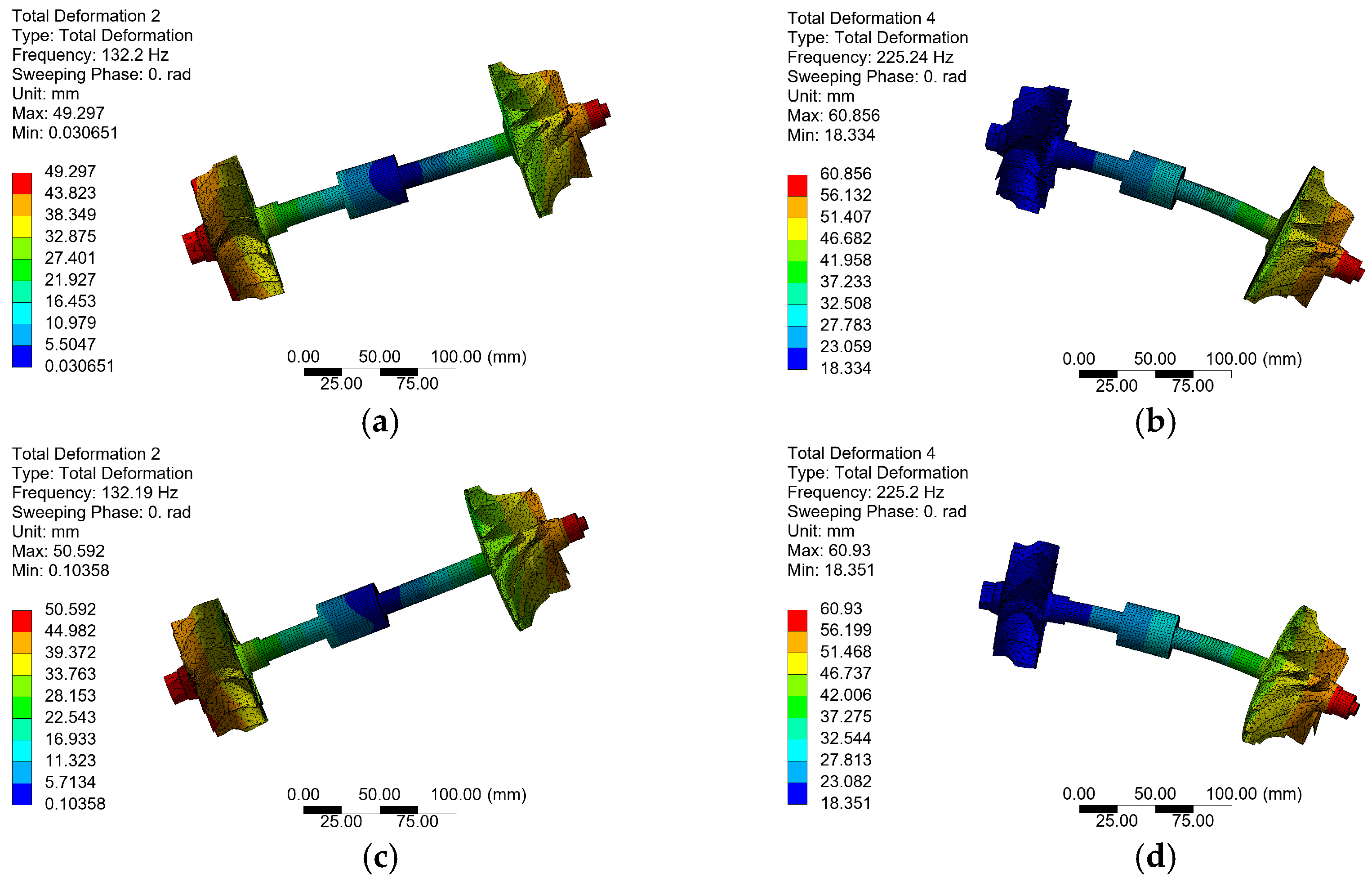



| First Resonance Mode | Second Resonance Mode | |
|---|---|---|
| Mesh Type 1 (rpm) | 9146 | 15,204 |
| Mesh Type 2 (rpm) | 9146 | 15,203 |
| Mesh Type 3 (rpm) | 9147 | 15,205 |
| Lumped Mass Model | Finite Element Model (Mesh Type 1) | Relative Error | |
|---|---|---|---|
| First mode (rpm) | 9956 | 9146 | 8.8% |
| Second mode (rpm) | 14,020 | 15,204 | 7.8% |
| Variable | Value | Variable | Value |
|---|---|---|---|
| m1 (kg) | 0.46 | Ja1 (kg·m2) | 1.35 × 10−4 |
| m2 (kg) | 0.16 | Ja2 (kg·m2) | 5.83 × 10−6 |
| m3 (kg) | 0.17 | Ja3 (kg·m2) | 5.75 × 10−6 |
| m4 (kg) | 0.23 | Ja4 (kg·m2) | 6.71 × 10−5 |
| l1 (mm) | 16.0 | Jp1 (kg·m2) | 1.73 × 10−4 |
| l2 (mm) | 78.1 | Jp2 (kg·m2) | 1.17 × 10−5 |
| l3 (mm) | 22.6 | Jp3 (kg·m2) | 1.15 × 10−5 |
| E1 (Pa) | 2.1 × 1011 | Jp4 (kg·m2) | 9.35 × 10−5 |
| E2 (Pa) | 1.78 × 1011 | e1 (m) | 6.43 × 10−6 |
| E3 (Pa) | 2.08 × 1011 | e4 (m) | 1.28 × 10−6 |
| I1 (m4) | 3.87 × 10−9 | I2 (m4) | 1.29 × 10−8 |
| I3 (m4) | 1.99 × 10−9 |
| Physical Parameter | Variable | Value |
|---|---|---|
| Hertz contact stiffness (N/m1.5) | Cb | 7.055 × 109 |
| Number of rolling bearings | Nb | 9 |
| Initial radial clearances of rolling bearing (μm) | δ0 | 1.5 |
| Equivalent linear stiffness (N/m) Equivalent linear damping coefficient (N·s/m) | kc cn | 2.2 × 107 87 |
| Diameter of inner ring (mm) | di | 20.4 |
| Diameter of outer ring (mm) | do | 30.1 |
| The first-order modal damping ratios | ξ1 | 0.021 |
| The second-order modal damping ratios | ξ1 | 0.034 |
| Preset Parameter | Variable | Value |
|---|---|---|
| Number of truncated harmonic terms | h | 4 |
| Error tolerance | Rt | 1 × 10−9 |
| Stepsize of iteration | z | 10 |
| Number of sampling points Maximum speed (rpm) | N ωmax | 215 14 × 104 |
| Parameter | The Variation of the Parameter | The Variation Rate of the First-Order Resonant Frequency | The Variation Rate of the Second-Order Resonant Frequency | The Variation Rate of the First-Order Resonance Peak | The Variation Rate of the Second-Order Resonance Peak |
|---|---|---|---|---|---|
| l2 (mm) | 74~86 | −1.9~2.2% | −11.6~34.6% | −24.4~33.6% | 27.1~−36.9% |
| Nb | 8~12 | −0.3~0.1% | −2.6~6.0% | −4.2~8.5% | 2.8~−12.0% |
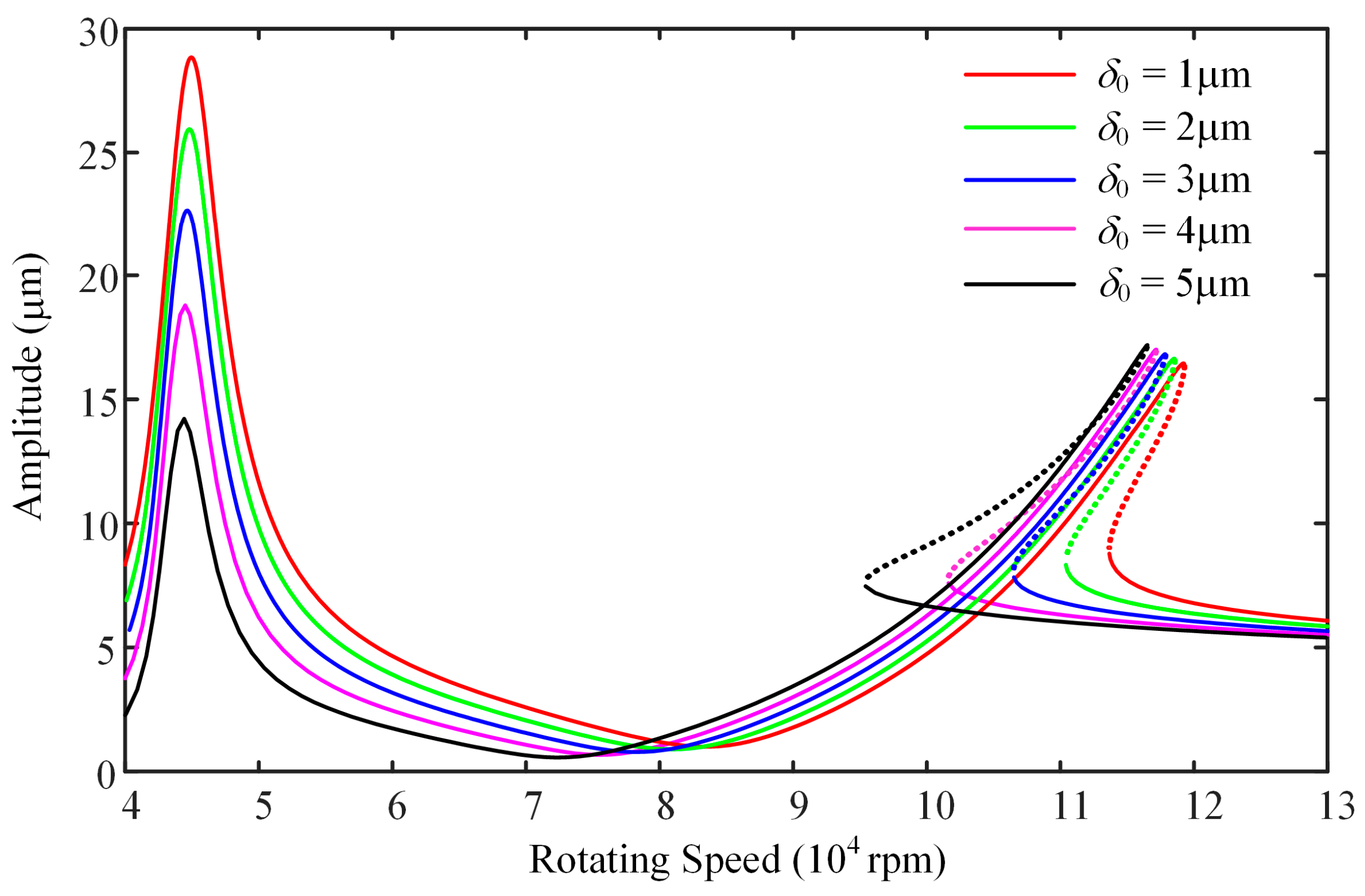
| δ0 (μm) | 1~5 | 0.0~−1.3% | 0.0~−1.8% | 0.0~−50.87% | 0.0~3.4% |
| Cb (N/m1.5) | 6.055~10.055 | −0.4~0.2% | −3.1~7.5% | −5.7~10.0% | 6.5~−12.2% |
| kc (N/m) | 1.5 × 107~2.5 × 107 | −12.6~10.9% | −0.1~0.0% | 15.9~−14.5% | −3.9~4.3% |
| ξ2 | 0.030~0.038 | 0.0~−0.1% | 1.8~−1.2% | 23.0~−16.0% | 13.9~−9.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Guo, H.; Cheng, Z.; Men, R.; Li, J.; Chen, Y. Nonlinear Vibration Analysis of Turbocharger Rotor Supported on Rolling Bearing by Modified Incremental Harmonic Balance Method. Machines 2025, 13, 360. https://doi.org/10.3390/machines13050360
Li T, Guo H, Cheng Z, Men R, Li J, Chen Y. Nonlinear Vibration Analysis of Turbocharger Rotor Supported on Rolling Bearing by Modified Incremental Harmonic Balance Method. Machines. 2025; 13(5):360. https://doi.org/10.3390/machines13050360
Chicago/Turabian StyleLi, Tangwei, Hulun Guo, Zhenyu Cheng, Rixiu Men, Jun Li, and Yushu Chen. 2025. "Nonlinear Vibration Analysis of Turbocharger Rotor Supported on Rolling Bearing by Modified Incremental Harmonic Balance Method" Machines 13, no. 5: 360. https://doi.org/10.3390/machines13050360
APA StyleLi, T., Guo, H., Cheng, Z., Men, R., Li, J., & Chen, Y. (2025). Nonlinear Vibration Analysis of Turbocharger Rotor Supported on Rolling Bearing by Modified Incremental Harmonic Balance Method. Machines, 13(5), 360. https://doi.org/10.3390/machines13050360






