Abstract
The job shop scheduling problem (JSSP) is a classical NP-hard combinatorial optimization challenge that plays a crucial role in manufacturing systems. Deep reinforcement learning has shown great potential in solving this problem. However, it still has challenges in reward function design and state feature representation, which makes it suffer from slow policy convergence and low learning efficiency in complex production environments. Therefore, a human feedback-based large language model-assisted deep reinforcement learning (HFLLMDRL) framework is proposed to solve this problem, in which few-shot prompt engineering by human feedback is utilized to assist in designing instructive reward functions and guiding policy convergence. Additionally, a self-adaptation symbolic visualization Kolmogorov–Arnold Network (KAN) is integrated as the policy network in DRL to enhance state feature representation, thereby improving learning efficiency. Experimental results demonstrate that the proposed framework significantly boosts both learning performance and policy convergence, presenting a novel approach to the JSSP.
1. Introduction
Efficient production scheduling is a critical factor in optimizing the cost-effectiveness and productivity of manufacturing systems. Job shop environments, known for their flexibility in handling a wide range of tasks, are widely employed in industries such as the aerospace, automotive, and semiconductor industries. The job shop scheduling problem (JSSP) is a classical combinatorial optimization challenge that arises in these settings and has been extensively studied. The JSSP is classified as an NP-hard problem, which makes finding optimal solutions computationally intractable for large-scale instances [1]. Current approaches to solving the JSSP are generally categorized into exact methods and approximate methods. Exact methods [2], such as branch-and-bound and integer programming, offer high optimization accuracy but are computationally expensive, making them suitable only for small-scale problems. As manufacturing environments become more dynamic and complex, especially with the growing competition in global markets and increasingly diversified customer demands, the need for fast and efficient solutions has become more pressing. Consequently, approximate methods, which are more scalable and capable of handling larger, more complex problem instances, have become more prevalent in practice.
Recent advancements in deep reinforcement learning (DRL) offer transformative potential by enabling autonomous decision-making in dynamic production scenarios [3]. However, deploying DRL in the JSSP remains hindered by two critical bottlenecks: the labor-intensive design of reward functions [4,5] and the inadequate representation of high-dimensional, time-varying state features [6]. Conventional reward mechanisms rely heavily on domain expertise, while static state representations fail to encapsulate the dynamic interplay of machine availability, job sequences, and processing constraints. These limitations impede learning efficiency and policy convergence, particularly in large-scale, real-world scheduling tasks.
Recent advancements in automated reinforcement learning (AutoRL) partially address these issues by adjusting hyperparameters and reward functions via predefined templates [7]. However, these methods still require the manual initialization of reward parameters, limiting their scalability in complex scenarios [8]. Concurrently, large language models (LLMs), a cornerstone of generative AI [9], demonstrate unique capabilities in contextual reasoning, knowledge integration [10], and task automation. Their application spans natural language processing [11], combinatorial optimization [12], and even reward function design through few-shot prompting [13]. However, LLMs’ reliance on natural language generation introduces uncertainty in structured industrial tasks such as the JSSP, where precision and domain-specific constraints are paramount.
Equally critical is the challenge of state representation in dynamic scheduling environments. Traditional methods struggle to encode high-dimensional features—such as machine availability and job sequences—into actionable inputs for DRL agents [14]. This gap underscores the need for adaptive neural architectures that capture evolving system states while maintaining interpretability, a prerequisite for trust in industrial applications.
To bridge these gaps, this study proposes a human feedback-based LLM-assisted deep reinforcement learning framework that synergizes LLM-driven semantic understanding with adaptive neural architectures. Innovatively, the framework leverages LLMs’ contextual reasoning through human-guided few-shot prompting to automate reward function design, aligning policies with operational objectives while reducing dependency on specialized expertise. Simultaneously, a self-adaptive symbolic visualization network is integrated to dynamically encode complex state features, addressing the limitations of traditional representation methods. By harmonizing generative AI’s contextual intelligence with DRL’s adaptive learning, the framework advances key intelligent manufacturing objectives: autonomous decision-making in complex scheduling, reduced reliance on manual programming, and enhanced convergence in dynamic production ecosystems.
2. Literature Review
2.1. Job Shop Scheduling Problem
A standard JSSP instance contains a job set and a machine set . Each job . consists of process operations, which must be performed in a specific sequence. represents the -th process of the -th job. This process can only be processed on one machine, and each machine can only process one job at a time, with no pre-emption allowed. The objective of the JSSP is typically to minimize the makespan. This involves finding an optimal schedule where the start time and the end time for each operation are determined, ensuring that all constraints are satisfied. The size of a JSSP instance is denoted as . The JSSP is one of the NP-hard combinatorial optimization problems and it is a thriving area of scheduling research that has been concentrated on and studied widely by scholars in engineering and academic fields. Current methods for solving the JSSP are mainly divided into two types: exact methods and approximate methods. Exact algorithms (e.g., mathematical programming methods [15] and bounded dynamic programming methods [16]) are classical methods for solving the JSSP. However, the actual manufacturing processes are more complex and dynamic, and a fast response time and effective optimization method for solving this problem are strictly required. On the other hand, with the problem scale expanding, the exact algorithms often need to consume a lot of computing time to find high-quality solutions. Therefore, there are many approximate algorithms (e.g., meta-heuristic [17], heuristic [18], and artificial intelligence (AI) algorithms [19]). They can yield appropriate solutions after a period of running.
2.2. Deep Reinforcement Learning
As one of the most active areas in AI research, deep reinforcement learning (DRL) combines the perceptual abilities of deep learning with the decision-making abilities of reinforcement learning. In Atari games and the game of Go, DRL has shown intelligence beyond that of the leading human experts. DRL has also been successfully applied to solve combinatorial optimization problems. Mazyavkina et al. [20] present a DRL framework to tackle combinatorial optimization problems. Kallestad et al. [21] proposed a heuristic framework that utilizes deep reinforcement learning to replace adaptive layers in order to more effectively select lower-level heuristic operators, thereby improving the performance of solving combinatorial optimization problems. The effectiveness of the framework was validated on various problems, including the capacitated vehicle routing problem, the parallel job scheduling problem, the pickup and delivery problem, and the pickup and delivery problem with a time window. Yuan et al. [22] modeled the job shop scheduling problem as a Markov decision process and proposed a new state representation method. They introduced an effective deep reinforcement learning approach to address this issue. Serrano-Ruiz et al. [23] developed a smart manufacturing scheduling approach using deep reinforcement learning in a job shop environment, achieving high flexibility levels and outperforming traditional heuristic rules from a multi-objective perspective. However, production-scheduling methods based on DRL require a considerable length of time to be trained, but after training, they respond quickly and can be applied to daily rolling scheduling or even real-time scheduling in the factory [2]. The reward function is the key factor for the performance of policy learning and training time in DRL. To further reduce the training time, some researchers used a reward-shaping method to design the reward function [24]. Due to the excellent generative ability of LLMs, some scholars have also employed them as reward function designers [25]. Because of the cost-effectiveness of using LLMs, it is advantageous for enhancing the application capability of DRL in the JSSP. Inspired by this, the present study also utilizes LLMs for reward function design.
2.3. Reward Function Design
The concept of a reward design problem (RDP) was introduced by Singh et al. [26]. An RDP is defined as a tuple , where represents the world model with state space , action space , and transition function . is the space of reward functions. is a learning algorithm that outputs a policy optimizing the reward in the . is a fitness function used to evaluate the effectiveness of any policy . The goal in an RDP is to find out a reward function , where the policy generates the optimized and obtains the highest fitness score. The primary methodologies for designing reward functions encompass preference-based reward design [27] and inverse reinforcement learning [28]. Preference-based reward design involves the adaptation of the reward function based on feedback from users or experts to more accurately correspond with real requirements. On the other hand, inverse reinforcement learning deduces the concealed reward function by analyzing the behavior of experts. Both of these methodologies heavily rely on human expertise, consequently increasing the costs linked to the design phase. LLMs [29], through their enormous reservoirs of existing common sense knowledge, are poised to be of enormous help in developing reward functions. Recent research has already demonstrated that LLMs can be used to guide how rewards should be shaped in reinforcement learning, for example, by Carta et al. [30]. It is through the analysis of natural language instructions that LLMs adeptly merge task specifications with user preferences into reward functions [31]. It is satisfactory in terms of both cost and reward functions designed for LLMs. Therefore, this paper also adopts LLMs to design the reward functions for the JSSP.
2.4. Kolmogorov–Arnold Network
To enhance the performance of deep reinforcement learning (DRL) in complex environments, it is crucial to improve the representation of state features [32]. The ability to accurately capture and represent the dynamic state space directly affects the learning efficiency and optimization results. In the early stages, traditional neural networks [33], such as backpropagation (BP) networks, are used to model the relationship between inputs and outputs. These shallow networks typically consist of one or two hidden layers and are suitable for relatively simple problems with low-dimensional state spaces. However, when facing a complex environment with a high-dimensional state space, shallow networks often struggle to capture complex patterns and dependencies.
As the complexity of DRL tasks increases, architectures such as deep neural networks (DNNs), especially multilayer perceptrons (MLPS), are used to improve the representation of state features. By stacking multiple layers [34], DNNs can learn a hierarchical representation and model nonlinear relationships more effectively. While DNNs have shown great potential in representing high-dimensional state spaces, they still face challenges in capturing highly complex, multidimensional dependencies that are common in dynamic environments, such as job shop scheduling.
To address these limitations, the KAN [35] has emerged as an alternative approach. The KAN was introduced by Liu Ziming et al. in May 2024 and provides a more efficient way to represent multivariate continuous functions. By decomposing these functions into compositions of univariate functions, the KAN provides a more flexible and expressive way to model complex relationships in the state space. This ability to better capture complex patterns in the data makes the KAN ideal for deep reinforcement learning tasks, especially in job shop environments with high dimensionality and dynamic state spaces.
The KAN relies on the Kolmogorov–Arnold representation theorem [36], also known as the Kolmogorov–Arnold superposition theorem. The Kolmogorov–Arnold representation theorem states that any multivariate continuous function can be represented as a composition of univariate functions and the addition operation:
where represents univariate functions that map each input variable such that and . The KAN layer is:
where is the parametrized function of learnable parameters. The KAN layer with and , and the outer functions form a KAN layer with and . A generic deeper KAN can be expressed by the composition L layers:
Notice that all the operations are differentiable. The KAN differentiates itself from traditional MLPs by using learnable activation functions on the edges and parametrized activation functions as weights, eliminating the need for linear weight matrices. This design allows KANs to achieve comparable or superior performance with smaller model sizes [37]. Moreover, their structure enhances model interpretability without compromising performance, making them suitable for applications such as scientific discovery. In cognitive diagnostic tasks, KANs may offer a precise diagnosis and analysis of learners’ knowledge structures, aiding personalized teaching and precision education with intuitive data interpretation.
3. The HFLLMDRL Framework for the JSSP Based on Disjunctive Graphs
3.1. Constructing the Framework for HFLLMDRL
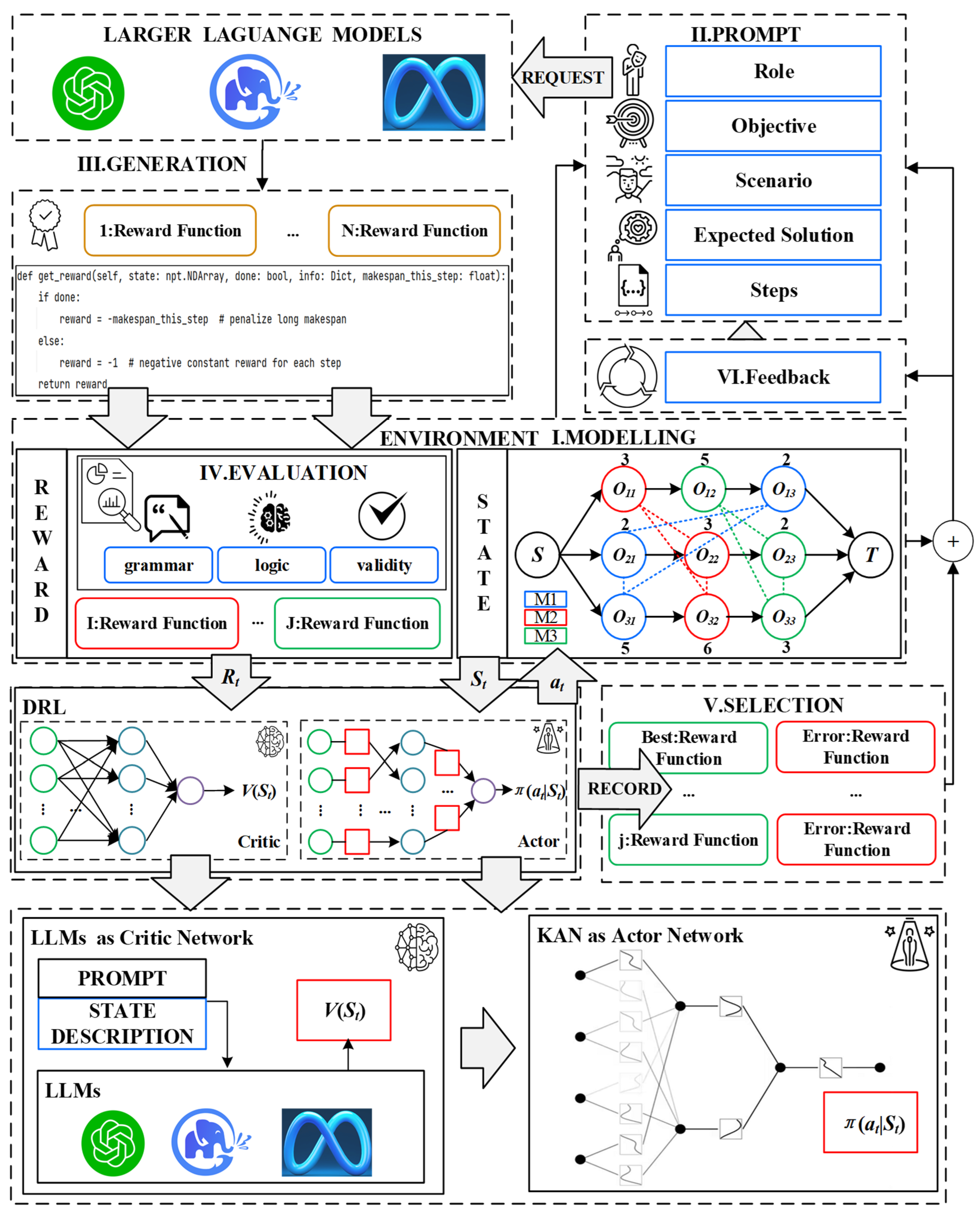
A novel large language model (LLM)-assisted deep reinforcement learning (HFLLMDRL) framework was constructed to solve the job shop scheduling problem (JSSP). The framework focuses on automating the design of reward functions and improving the efficiency of policy convergence. The framework consists of five key stages: problem modeling, reward generation, evaluation and selection, self-improvement iteration, and DRL model design. Figure 1 gives an overview of the framework.
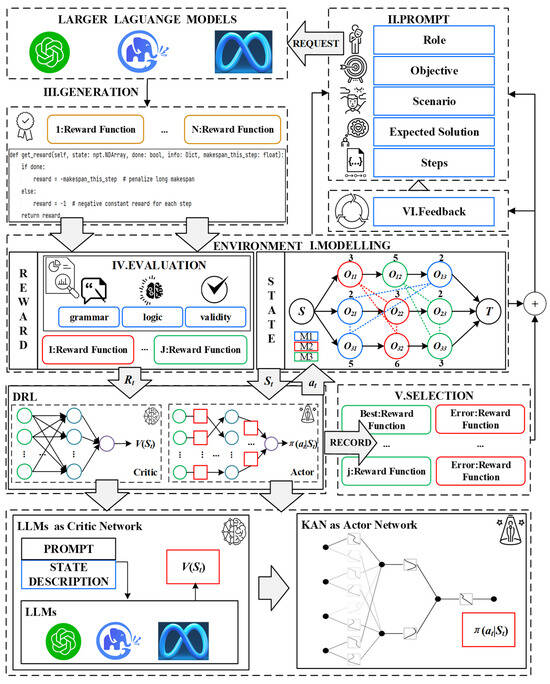
Figure 1.
The overall framework.
The preparation phase, shown in the middle part of Figure 1, involves modeling the JSSP in a discrete graph environment. This environment is used to establish the state representation as a base reference for hints. It is important to note that the problem is modeled only once, providing the basis for subsequent phases.
In the reward generation phase, the LLM is provided with the environment specification, which includes the problem context of the JSSP. To guide the LLM to generate an effective reward function, context-specific prompts based on the ROSES (role/goal/scenario/expected solution/step) framework are fed into the model. The prompts outline the semantic context of the environment and highlight the key variables used to formulate the reward function. The cue is located in the upper right corner of Figure 1.
Since the LLM generates output in string format, the resulting reward function cannot be executed directly. Therefore, a conversion process is required. Although rose-based hints can effectively guide the LLM to generate appropriate rewards, further evaluation is needed to ensure the effectiveness of the reward function. We designed an evaluation process based on human experience at this stage. This evaluation process includes syntax checking, logical consistency verification, and correctness evaluation, as shown on the left side of Figure 1.
To enhance the generation ability of the LLM, an elite feedback mechanism inspired by the idea of swarm intelligence optimization is used. This mechanism provides the LLM with feedback on the performance of the generated reward function, encouraging the model to generate improved reward functions over time. In addition, human feedback prompts based on the ROSES framework are incorporated to further optimize the reward generation process.
In order to further improve the efficiency and stability of reinforcement learning for solving the JSSP, a deep reinforcement learning method based on the actor-critic (AC) framework was used. In this framework, the KAN was used as the decision network to enhance the state feature representation. The KAN is based on representation theory, and an ensemble is used to capture complex state information more effectively, thus improving learning efficiency. Given the strong general knowledge capabilities of the LLM, it is used as an evaluation network. LLMs act as expert guides, generating action candidates (high-level task plans) to narrow down the action selection space or provide reference strategies. This feedback mechanism guides the policy update process in the reinforcement learning model and promotes faster policy convergence.
3.2. Modeling the Disjunctive Graphs for the JSSP
Solving a JSSP instance can be viewed as a task of determining the direction of each disjunction. Therefore, we consider the dispatching decisions as actions of changing the disjunctive graph and formulate the model as .
State: At decision step t, the states is represented by a disjunctive graph ) that reflects the current status of the solution, where encompasses all the directed disjunctive arcs that have been assigned a direction up to step t, and includes the remaining ones. The initial state is the disjunctive graph representing the original JSSP instance, and the terminal state is a complete solution where , indicating that all disjunctive arcs have been assigned a direction. Each operation that is represented by a node has four features: start time, end time, processing time, and scheduling status. The start time represents the start time of the operation o. The end time represents the end time of the operation. The processing time represents the processing time of the operation, and the scheduling status indicates whether the operation has been processed. For each edge D, there are four features: start node, end node, weight, and arc type. The start node represents the starting node number of the edge, the end node represents the ending node number of the edge, and the weight represents the difference between the start time of the head node and the start time of the tail node. A positive value indicates that the head node starts later than the tail node, and the arc type presents the type of edge, with a value of 1 representing a conjunctive arc and 0 representing a disjunctive arc. For the graph G, there are two features: critical path and distance. The critical path represents the set of all points on the longest path required for the graph from start to finish. The distance represents the length of the critical path. This measure provides an estimate of the total time required to complete all operations.
Action: An action is a valid operation at decision step t. Each job can only have one maximum operation ready at t, and the maximum size of the action space is , which depends on the instance being solved. During solving, becomes smaller as more jobs are completed.
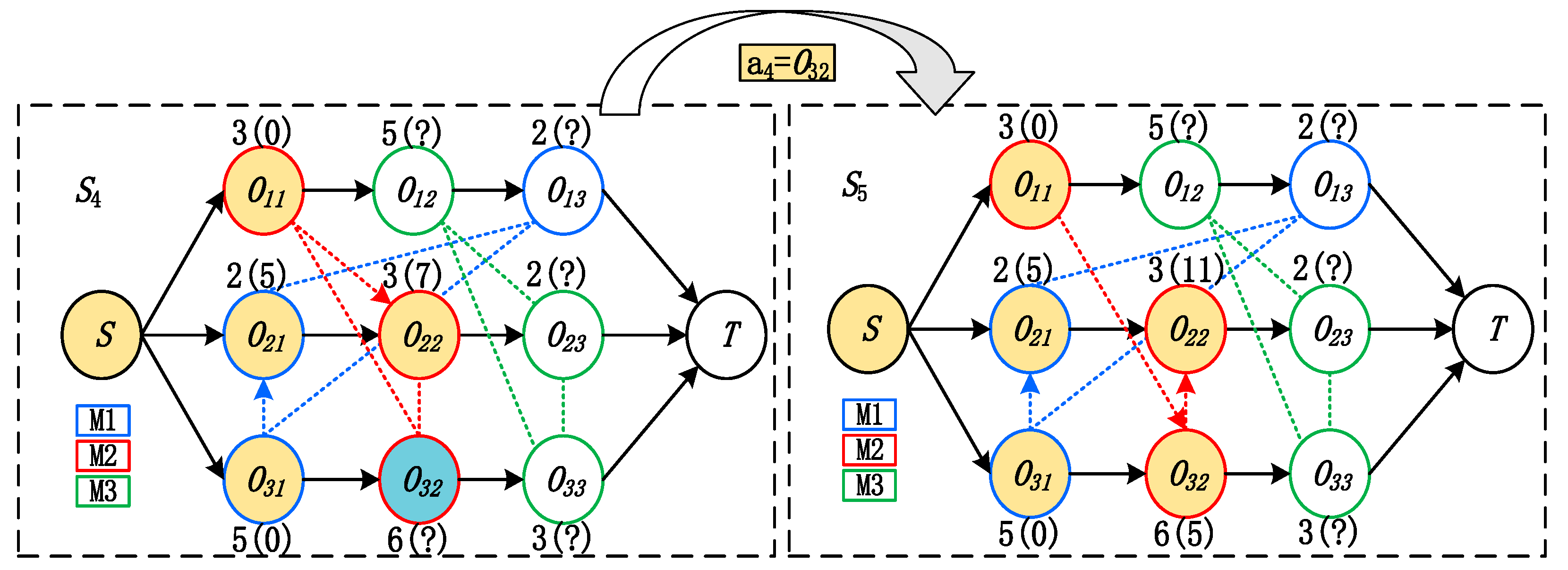
State transition: Once an operation has been determined to dispatch next, the directions of the disjunctive arcs of that machine will be updated by the earliest feasible time period to allocate at on the required machine. A new disjunctive graph is engendered as the new state . An example is given in Figure 2, where action is chosen at state from action space . On the required machine M2, we find that can be allocated in the time period before the already scheduled ; therefore, the direction of the disjunctive arc between and is determined as , as shown in the new state . Note that the starting time of is changed from 7 to 11 since is scheduled before .
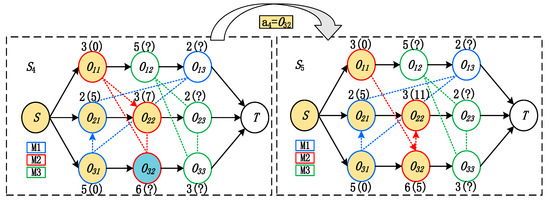
Figure 2.
Example of state transition.
Objective: The objective of the JSSP is makespan, which is equal the distance of the critical path in the disjunctive graph, such that the value of S4 is 14 and the value of S5 is 16.
3.3. Generating a Reward Function Based on ROSES
The ROSES framework is used to guide reward function design in the JSSP, providing a structured approach that ensures compatibility with the environment and consistency with the problem context. The framework is tailored to automate the generation of efficient reward functions using LLMs. It consists of five core components: role, objective, scenario, expected solution, and steps, each tailored specifically to the requirements of the JSSP.
Role: The LLM is designated as a reward engineer and is responsible for developing reward functions for reinforcement learning agents running in a JSSP environment. By defining this role, the generation focus of the LLM is directed towards optimizing scheduling goals, ensuring relevance to the problem domain. In this context, the LLM’s role is to create mathematically sound and task-specific reward functions to improve agent performance in dynamic and complex job shop environments.
Goal: The main goal of the reward function is to guide the reinforcement learning agent to optimize scheduling metrics specific to the job shop production system. These metrics include minimizing total completion time, balancing machine workloads, avoiding task delays, and improving resource utilization. The reward function must promote policy convergence by converting these scheduling objectives into signals that the agent can act on. In addition, the reward function should also improve learning efficiency by providing clear and interpretable guidance to the agent during training.
Scenario: The JSSP environment is modeled as a disjointed graph, where nodes represent tasks and weighted edges represent task priority relationships and processing times. The status representation of the agent contains key characteristics:
- Captures the adjacency matrix of priority constraints between tasks;
- Indicates the task-to-machine mapping assigned to the machine for each task;
- The task duration is normalized by the maximum processing time;
- The reward function must take these state characteristics into account and align with the specific characteristics of job shop scheduling, such as the need to manage task priorities and minimize delays throughout the production process. This culture ensures that the generated reward functions are specific to the scheduling domain.
Expected solution: This describes the ideal outcome or type of solution that the LLM should aim to produce, guiding its response towards fulfilling user needs. The expected solution specifies that the reward function must fulfill the following:
- Use only the environment variables explicitly defined in the JSSP environment class;
- Be compatible with TorchScript, requiring the use of torch. It should use a tensor for all variables and ensure device consistency between tensors;
- Returns a single output, the total reward, formatted as a string of Python code. Rewards may include penalties for task delay, incentives for the early completion of tasks, and components of balancing machine workloads. For example, transformations such as torch.exp can be applied to normalize rewards or emphasize specific scheduling priorities.
Steps: This step outlines a sequence of actions or considerations that the LLM should follow in formulating its response, ensuring a structured approach to problem-solving:
- Identify key variables from the environment, such as task dependencies, processing time, and machine allocation;
- Define mathematical expressions for the reward components, ensuring that they capture trade-offs inherent in job shop scheduling (for example, penalizing idle machine time or task completion delays);
- Normalized and scaled rewards where necessary, introducing temperature parameters to control the sensitivity of the converted reward components;
- Format the final reward function as a TorchScript-compatible string of Python code and ensure that all implementation constraints are met.
By applying the ROSES framework, the LLM-generated reward function is optimized for the JSSP environment. This structured approach ensures that functions reflect the complexities of job shop scheduling, such as managing task dependencies, machine constraints, and processing time, while also improving policy convergence and learning efficiency. The framework enables the automated design of high-quality reward functions, reduces reliance on manual engineering, and facilitates scalable deployment in real-world production systems. The details of examples are provided in Box A1, Box A2, Box A2, Box A4 and Box A5.
3.4. Evaluating and Selecting for Reward Functions
To improve the generation and selection of reward functions, a feedback-driven evaluation process is established. We incorporate human feedback into our workflow to refine reward functions generated by LLMs, ensuring their correctness, feasibility, and performance. By incorporating human expertise as a guiding factor, the process is better aligned with the task requirements while minimizing automated manual intervention.
The evaluation and selection process first starts with the automated validation of the reward function generated by the LLM. Since the initial outputs are string-based and non-executable, a series of filtering steps are required to transform these outputs into a reliable and efficient reward function:
- Correctness verification via human-guided rules: Human feedback was initially used to establish rules for checking the correctness of the reward function. This includes defining acceptable syntax, logical structure, and environment-specific constraints. Automated tools, such as Python’s ast library, are then used to verify that the generated code obeyed these rules. Any reward function that fails syntactic or logical validation is excluded from further evaluation.
- Operational testing based on human-defined criteria: Reward functions that pass syntactic and logical checks are executed in the environment. We use human feedback to define correctness evaluation criteria, such as whether a reward function meets the intended goal or produces a meaningful output. At this stage, functions that cause runtime exceptions or deviations from human-defined correctness criteria are discarded.
Once the reward functions have been verified for correctness, their performance was evaluated using human-centric metrics:
- Objective metrics defined by human goals: In the job shop scheduling problem (JSSP), minimizing the total completion time (makespan) is the main objective. During reinforcement learning, human feedback informs the selection of key metrics, such as maximum, minimum, and average completion times, to evaluate the effectiveness of the reward function in achieving this goal.
- Reward quality: While reward metrics (such as maximum, minimum, and average rewards) are recorded, they are not directly used for ranking as they are themselves influenced by the reward function. Human feedback helps to identify this limitation and prioritize objective metrics.
To refine the selection process and incorporate high-quality reward functions into the framework, an elitist selection strategy is applied. This approach uses automated evaluation results and human feedback to identify and retain superior reward functions:
- Correctness filtering: Human feedback is embedded in the correctness verification process to ensure that only valid and executable reward functions, with correctness = 0, are considered for further evaluation.
- Ranking based on human-defined goals: The reward functions are ranked according to the goal metrics defined by the human goals. Functions that achieve smaller makespan values are preferred.
- Elite feedback mechanism: The top N selected elite reward functions are fed back into the LLM framework to guide subsequent iterations. This iterative refinement ensures that the new reward function is consistent with the human-defined goals and builds on previous successful designs.
By incorporating human feedback into the evaluation and refinement process, the framework achieves a balance between automation efficiency and human supervision. Human insights are used to establish rules, define goals, and guide iterations, while automated tools perform validation and ranking steps. This synergy ensures that the generated reward function satisfies the correctness and feasibility criteria.
3.5. Establishing the Human Feedback Iteration Mechanism
To improve the quality of the reward function design, a self-improvement mechanism based on human feedback is embedded in the framework. This mechanism operates as a closed-loop process, using feedback on the generated reward functions to iteratively improve their design. By combining LLMs and human-provided evaluation guidance, this approach ensures that the reward function can better synchronize with the objective of the job shop scheduling problem (JSSP).
The feedback starts with an evaluation of the generated reward function. Key performance metrics are computed, such as the average, maximum, and minimum rewards achieved during reinforcement learning. At the same time, the corresponding metrics related to the specific objectives of the JSSP, such as average, maximum, and minimum span values, are evaluated. If the reward function fails, the evaluation statement explicitly highlights these reasons. Reasons for failure include invalid calculations, improper use of variables, or other problems. This ensures that the feedback provided to the LLM is comprehensive and actionable, as shown in Box A6 and Box A7.
The feedback also provides specific suggestions for improving the reward function based on the observed problems in the policy performance:
- If the span values consistently lead to “NaN” (not a number—an undefined or unrepresentable value), the feedback suggests rewriting the entire reward function;
- If the value of a reward component changes very little, the LLM is guided to perform the following steps:
- Adjust the scale or temperature parameters of the components;
- Overwrite or replace invalid components;
- A component is discarded if it contributes little to the optimization.
- For reward components with significantly larger magnitudes compared to the other components, the LLM is instructed to rescale it to the appropriate range. These actionable insights guide the LLM to refine its reward function design approach.
To ensure a structured refinement process, the feedback included step-by-step instructions for analyzing and improving each component of an existing reward function. This step-by-step guidance helps the LLM maintain consistency and coherence in the revised reward function, as shown in Box A8 and Box A9.
The iterative mechanism continuously improves the reward function based on the provided feedback. At each iteration, the LLM analyzes the performance of the current reward function using the evaluation and expected solution components. It then follows the prescribed production steps to generate a refined reward function. This process is repeated until the reward function reaches a predefined performance criterion or a maximum number of iterations is reached. By incorporating human knowledge and task-specific insights into the LLM-guided refinement loop, this mechanism ensures that the reward function evolves to match the unique requirements of the JSSP. It facilitates the identification and resolution of problems in reward design, such as improper scaling or invalid components, ultimately leading to a high-quality reward function that drives faster policy convergence and improves learning efficiency. This closed-loop system not only automates the reward refinement process but also minimizes the need for direct human intervention while retaining the benefits of human expertise.
3.6. Designing DRL Based on KANs and LLMs
The action network of deep reinforcement learning (DRL) serves as the action decision-maker, observing the current JSSP state and selecting appropriate job operations. Given that the state of a JSSP possesses a graph structure, directly employing it as an input to a multilayer perceptron (MLP) could lead to the loss of spatial structure information and computational inefficiency. Consequently, it is prevalent to utilize a combination of convolutional neural networks (CNNs) and MLPs within a DRL actor network. In this architecture, a CNN is deployed for feature extraction, and the resultant feature vectors are used as inputs to the MLP. Subsequently, the MLP makes action decisions based on these extracted features. However, the weak interpretability of an MLP reduces the reliability of these decisions, making trained DRL less applicable to practical job shop scheduling.
To further enhance the reliability of DRL, we use a KAN based on representation theory, which offers stronger interpretability and has been proven to be a viable alternative to an MLP. Therefore, the MLP has been replaced with a two-layer (two-depth) KAN network as the action network. The KAN can be expressed by the composition of these two layers:
where the output function generates the by doing the transformation from the previous layers. An example of a KAN architecture is shown in the bottom-right part of Figure 1.
Due to the comprehensive understanding and evaluation capabilities of LLMs, the critic network of DRL in this study is composed of LLMs, as depicted in the bottom-left section of Figure 1. The prompts are constructed to inform the LLM of the current state and the action generated by the KAN. The LLM is then tasked with scoring for the task. These scores are subsequently used to update the loss of the action network, thereby enhancing the overall performance and reliability of the decision-making process. The loss function of the action network is as follows:
To clearly show the synergy of the LLM-driven reward generation mechanism, elite selection strategy, and DRL training in the HFLLMDRL framework, Algorithm 1 shows the complete algorithm flow. The algorithm integrates the three core modules described above: (1) an LLM reward function generation based on the ROSES framework (Section 3.3); (2) an elite reward evaluation mechanism for human–machine collaboration (Section 3.4 and Section 3.5); and (3) DRL training with a KAN network and LLM evaluation.
Through the formulation of the algorithm steps, the data flow and control logic between each module can be systematically presented. The following pseudocode translates the theoretical framework into a programmable implementation:
| Algorithm 1. HFLLMDRL Framework | |
| Input: | |
| Output: | |
| 1. | Initialize,Task context TC, human-defined criteria HC and human goals HG. |
| 2. | while do: |
| 3. | Reward Generation Phase (Section 3.3) Prompt engineering: Candidate generation: Validation: |
| 4. | Elite Selection Phase (Section 3.4) with HG |
| 5. | |
| 6. | DRL Training Phase (Section 3.6) for do: State representation Action selection Environment transition Experience storage Value estimation Parameter update |
| 7. | Human Feedback Loop (Section 3.5) Equations (6) and (7) |
| 8. | return Computational Complexity |
The algorithm’s time and space complexity are mainly affected by three key parameters: M—the maximum number of reinforcement learning iterations; N—the number of reward candidates generated by the LLM in each round; and E—the number of empirical replay buffer samples.
4. Case Study
Four experiments were carried out to assess the performance of the HFLLMDRL model. The primary objective of the first experiment was to confirm the convergence of HFLLMDRL. The second experiment was designed to contrast the performance disparities between the reward function formulated by HFLLMDRL and that crafted by human designers. The third experiment, aimed at evaluating the efficacy of the elite strategy, involved a comparison of various reward retention strategies. The final experiment was conducted to authenticate the interpretability of the HFLLMDRL model.
All tests were run on a 3.1 GHz E5-2603V4 processor and a 64 GB server using the python3.10 programming language.
4.1. Experimental Setup
This section provides a description of the experimental setup, including examples, artificial design reward functions for comparison, performance evaluation metrics, iteration strategies for comparison, and DRL algorithm parameters.
In order to validate the stability and efficiency of the HFLLMDRL model, we employed three moderately sized job shop scheduling instances, namely ft06, ft10, and ft20, as proposed by Thompson in 1963. To evaluate the scalability of HFLLMDRL, we utilized large-scale instances, specifically swv19 and swv20, and well-known large-scale benchmark instances from the Taillard (ta) dataset, specifically ta51 (50 × 15) and ta71 (100 × 20) [38]. As shown in Table 1, n denotes the number of jobs, m denotes the number of machines, and optimal solution denotes the optimal makespan.

Table 1.
The basic information of the instances.
The four reward functions are zhang [38], nasuta [39], samsonov [40], and tassel [41], which have been manually designed and sourced from the existing literature or benchmarks (Table 2).

Table 2.
The details of the crafted reward functions.
The metric below is used to evaluate the performance of HFLLMDRL and other manually designed reward functions, where a smaller value reflects a better reward function.
where
Two reward function selection strategies were employed as control groups, specifically the greedy strategy [42] and the roulette wheel selection strategy [43]. The greedy strategy preserves the optimal (i.e., smallest ) reward function from each set of reward functions generated by the LLM. The roulette wheel selection strategy computes the probability of each reward function in the set based on the corresponding , retaining the generated reward functions according to these probabilities.
The experiment settings consist of various parameters. The number of samples generated by the LLM, denoted as N, is set to 20. The number of loop iterations, denoted as M, is 100. Additionally, the number of elite individuals, denoted as BN, is three, the number of reward function evaluations, denoted as ET, is 50, and the total number of steps for each reinforcement learning algorithm learning is 10,000. The learning rate is set to 0.0003, the buffer size is 100,000, gamma is 0.99, and the optimizer used is Adam.
4.2. The Convergence of HFLLMDRL with Different Instances
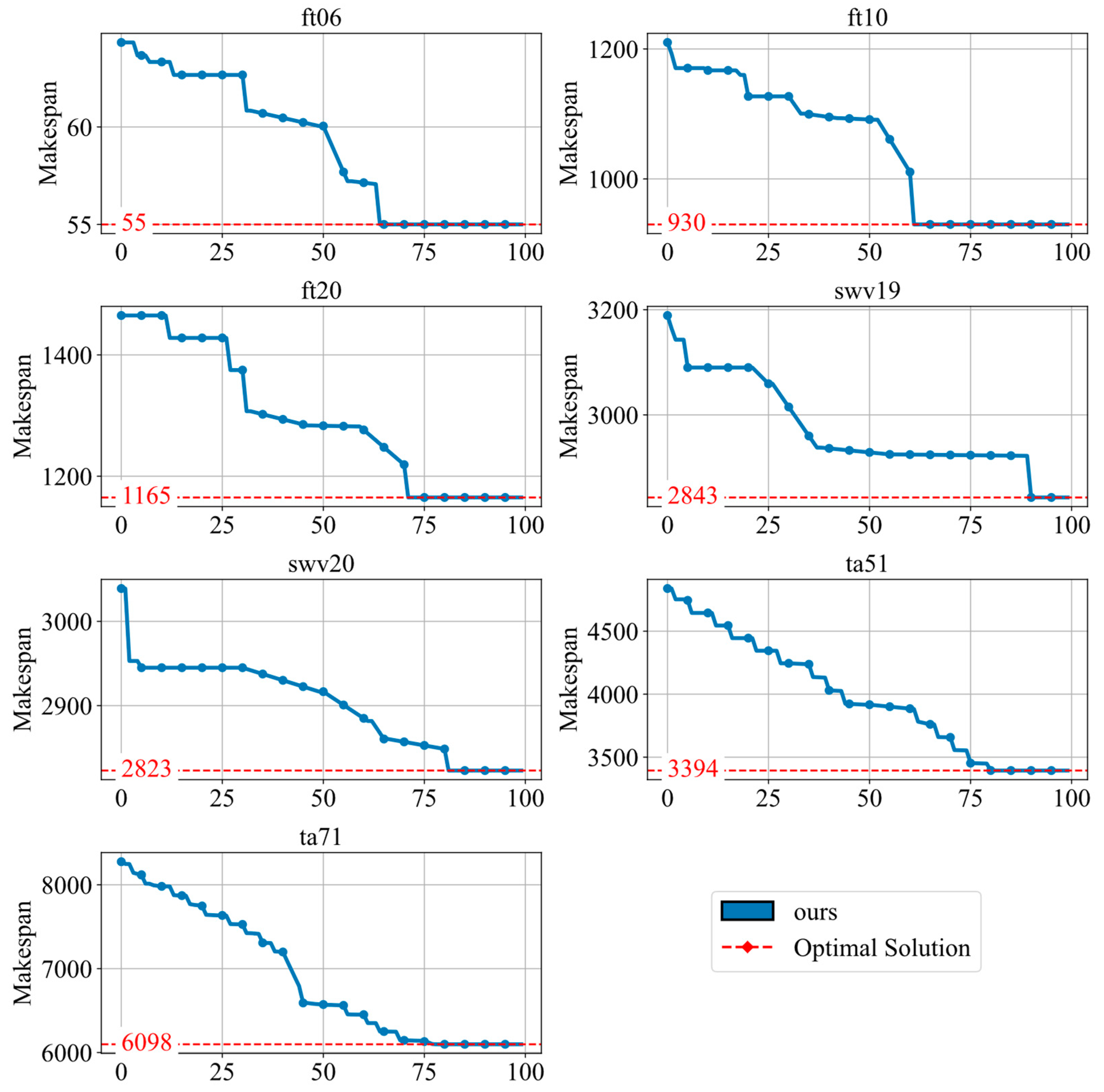
To evaluate the convergence behavior of the HFLLMDRL framework, we conducted experiments on instances of different sizes, including small-, medium-, and large-scale problems. As shown in Figure 3, the results demonstrate a clear trend: as the number of iterations increases, the performance curve steadily approaches the optimal value.
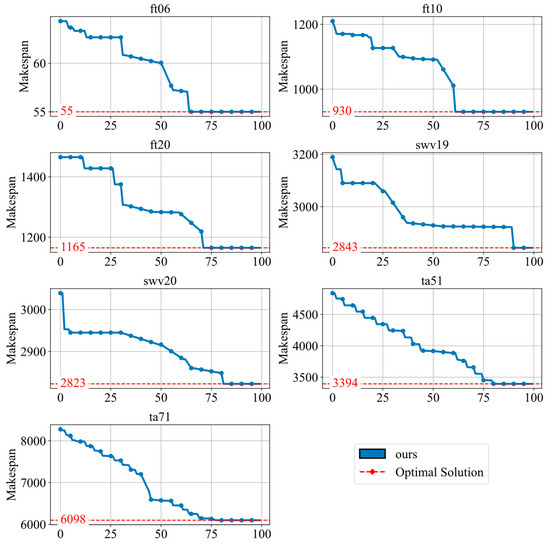
Figure 3.
The result of convergence of the HFLLMDRL framework.
Although the convergence rate decreases as the instance size grows, the framework is always able to achieve convergence to the optimal solution. This shows that HFLLMDRL maintains robust convergence performance across different problem sizes, demonstrating its adaptability and effectiveness in dealing with various instances of the JSSP.
The convergence performance was further tested on large-scale Taillard instances, namely ta51 (50 × 20) and ta71 (100 × 20). As shown in the updated Figure 3, HFLLMDRL continues to demonstrate convergence capabilities even on these significantly larger problems, although it requires more iterations compared to for smaller instances. This highlights the framework’s robustness and scalability.
4.3. The Convergence of HFLLMDRL with Different Reward Functions
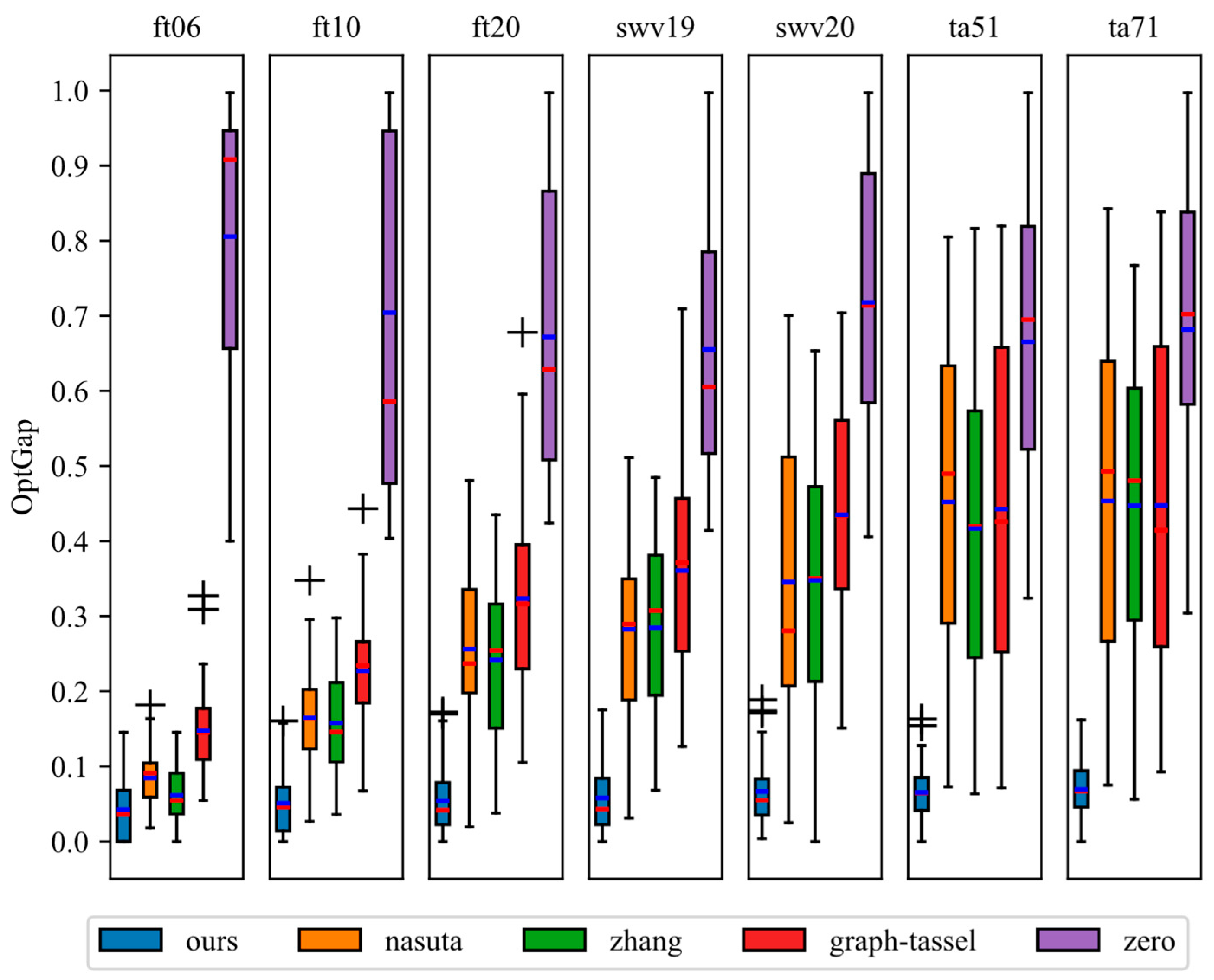
To test the effectiveness of the reward function designed by the framework, comparative experiments were carried out with four manually designed reward functions. The results are shown in Figure 4. In the experiments, the DRL algorithm learns from the job shop scheduling environment using different reward functions, calculates the completion time, and evaluates the performance gap using Equation (6).
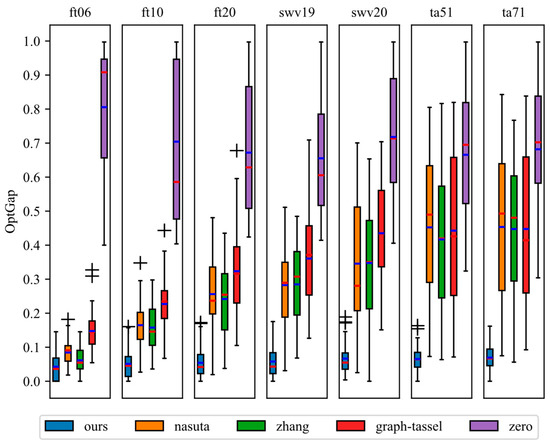
Figure 4.
The boxplot of the comparison with various reward functions.
As shown in Figure 4, the red line represents the median and the blue line represents the mean. The reward function generated by the framework consistently outperforms the human-designed reward function. Moreover, as the dataset size increases, the differences in under various reward functions become more pronounced. The reward function designed by the proposed framework achieves a smaller , indicating that it has a stronger guiding effect on the deep reinforcement learning process and can effectively improve the scheduling performance.
The performance gap analysis, which was extended to include ta51 and ta71 (Figure 4), reveals that the reward function generated by HFLLMDRL consistently yields lower OptGap values. This advantage is particularly pronounced on the 100 × 20 instance (ta71), suggesting that the LLM-guided reward design is highly effective for navigating the extremely large state action spaces of a large-scale JSSP.
4.4. Comparison with Different Selection Policies
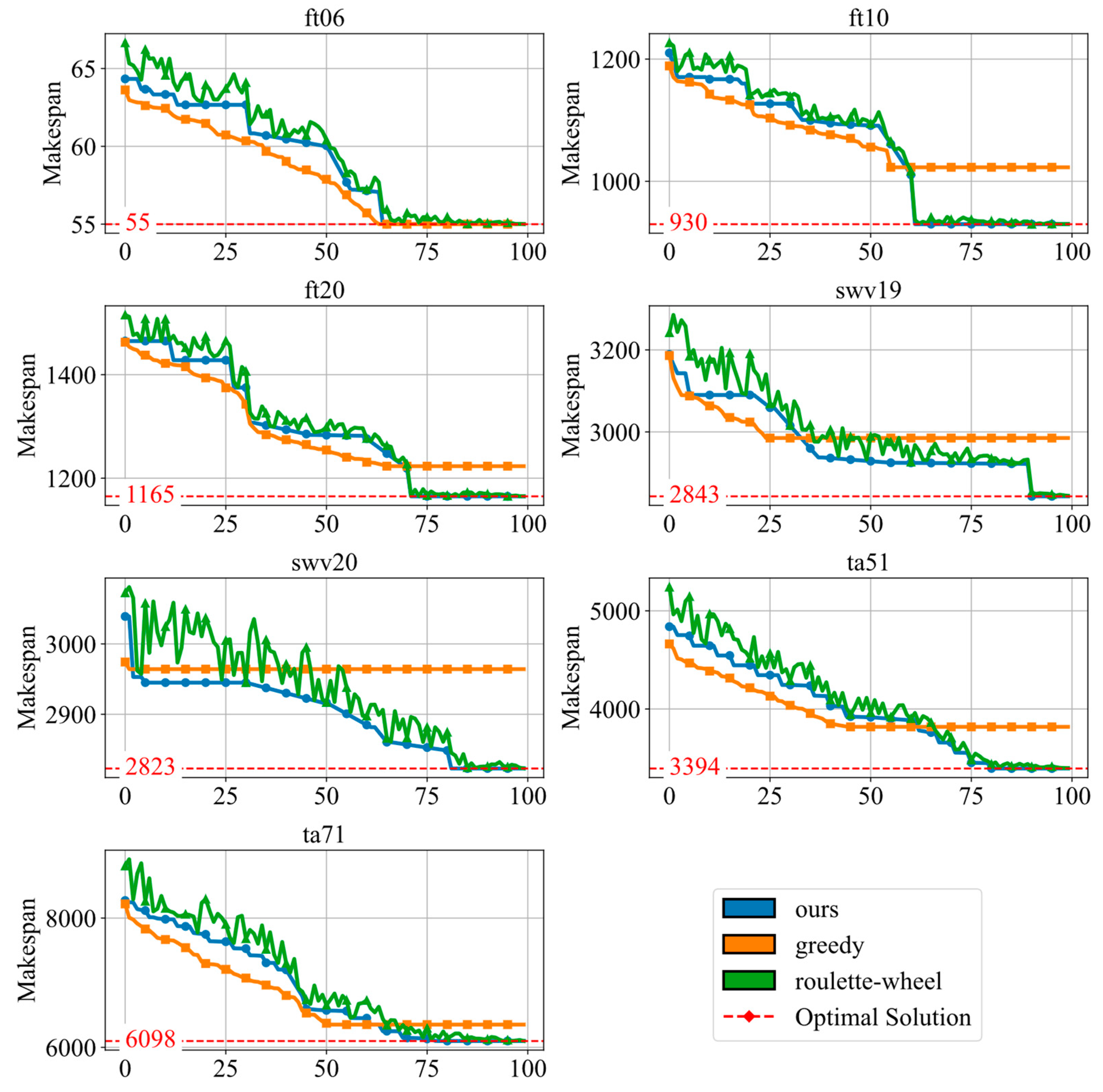
To investigate the effectiveness of the proposed elitist selection strategy on the reward function generated by the LLM, we compared it with two alternative strategies: greedy and roulette. As shown in Figure 5, the results show that the elite strategy consistently outperforms the other strategies as the problem instance size increases.
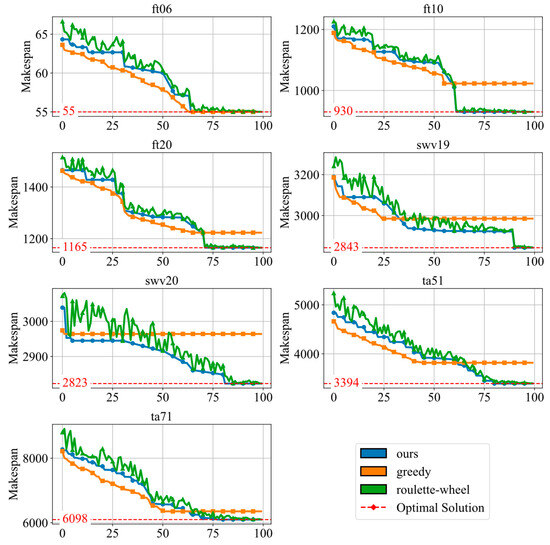
Figure 5.
The convergence of the comparison with various policies.
In the small-scale instance ft06, the greedy strategy has the best performance, followed by the elite strategy and the roulette wheel strategy. This advantage arises because the greedy strategy focuses on exploiting high-performance solutions, which reduces the diversity of solutions and speeds up convergence. However, this lack of diversity can become a limitation as the problem instance size grows.
For larger instances, the greedy strategy gets into trouble due to its tendency to converge prematurely to a local optimum. In contrast, the elite and roulette strategies maintain greater solution diversity, allowing them to avoid local optima and achieve better overall performance. Among them, the elitist strategy shows more stable convergence because it effectively balances exploration and exploitation.
4.5. Visualization and Performance of the Actor Network
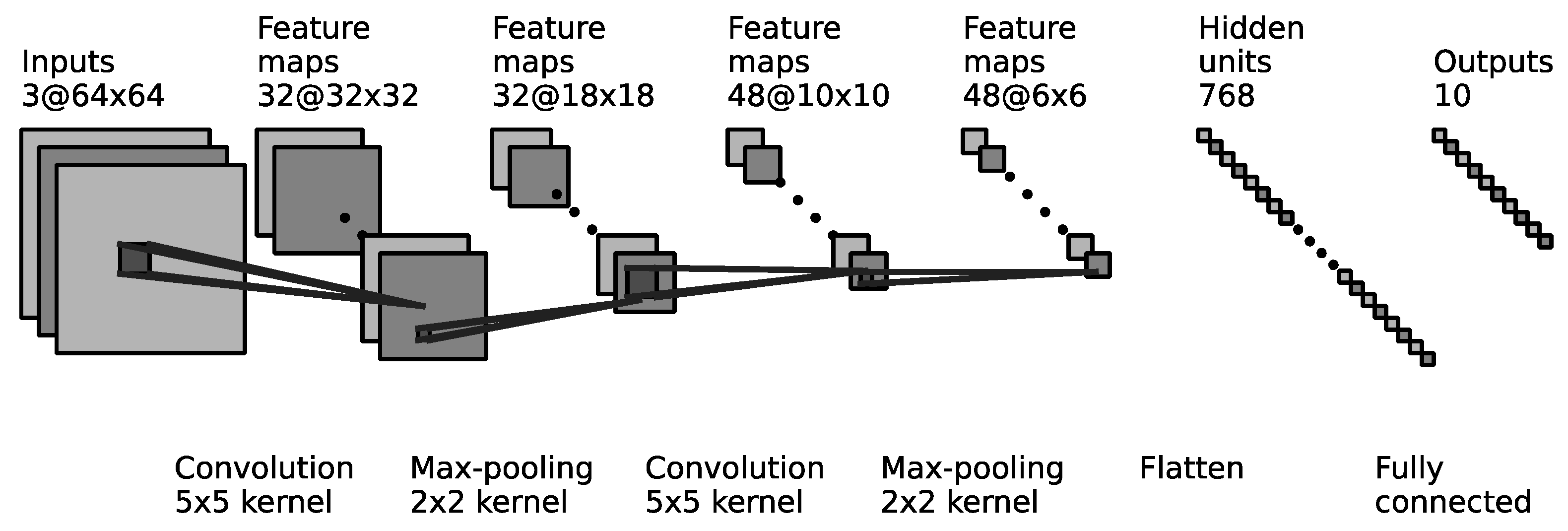
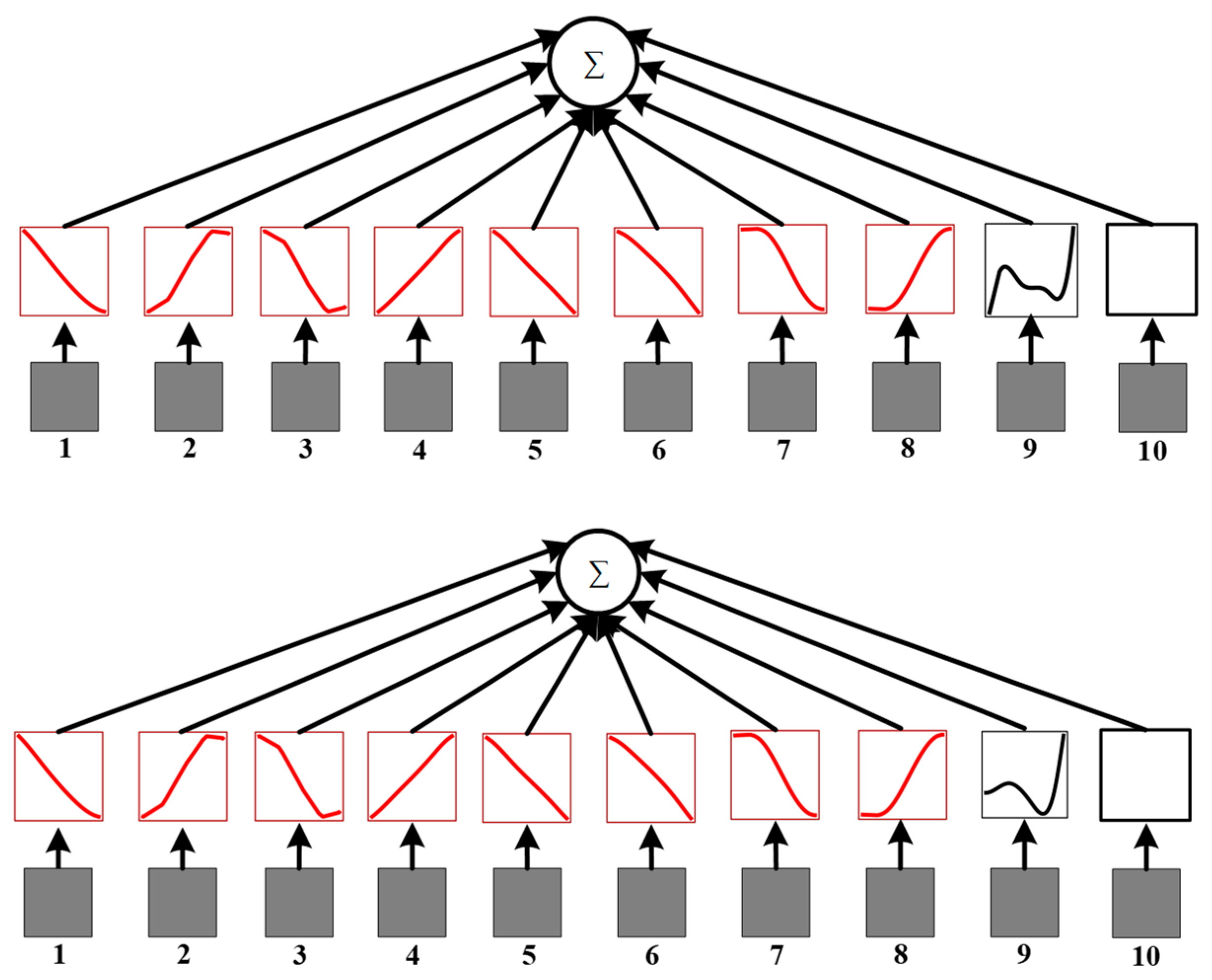
Visualization is a powerful tool used to address the complexity of machine learning models, improving their interpretability. In this study, we performed multiple visualizations of the actor network using the ft06 instance, focusing on its internal structures: the convolutional neural network (CNN) and the KAN. These visualizations are presented in Figure 6 and Figure 7.
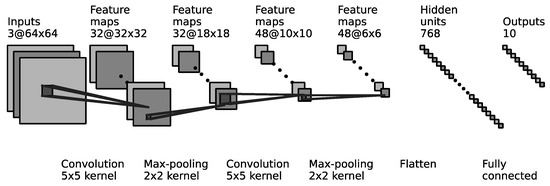
Figure 6.
The visualization of the CNN in the actor network.
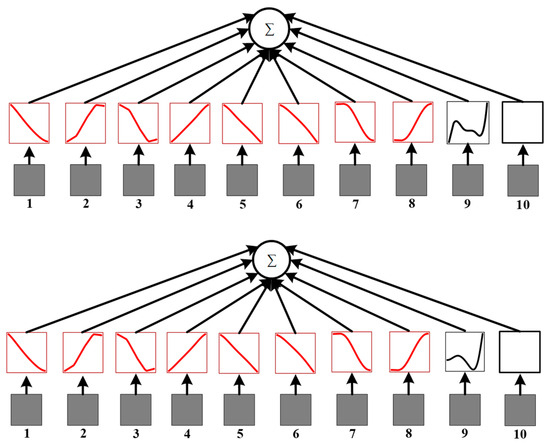
Figure 7.
The visualization of the KAN in the actor network.
As shown in Figure 6, the CNN in the actor network initially extracts ten distinct features, including the following:
- Node features: start time, end time, process time, and scheduling status.
- Edge features: start node, end node, weight, and arc type.
- Graph features: the critical path and the distance of the critical path.
These features serve as the foundation for decision-making and are passed to the KAN for further symbolic representation.
Figure 7 highlights the KAN’s role in transforming the CNN-extracted features into combinatorial symbols that represent decision-making actions. The red line represents features without obvious changes, while the black line represents features with prominent changes. Observations from the visualization reveal:
- The ninth feature (critical path of the disjunctive graph) is represented by differing symbols in the top and bottom subgraphs. This inconsistency arises because a disjunctive graph can contain multiple critical paths, resulting in varied symbolic representations for this feature;
- The tenth feature (distance of the critical path) does not generate a symbol. This is because once the critical path is identified, the distance becomes a fixed value, leaving no variability to be symbolically represented.
These results demonstrate that the KAN significantly enhances the interpretability of the actor network by providing a clear, symbolic mapping of features, offering insights into the decision-making process.
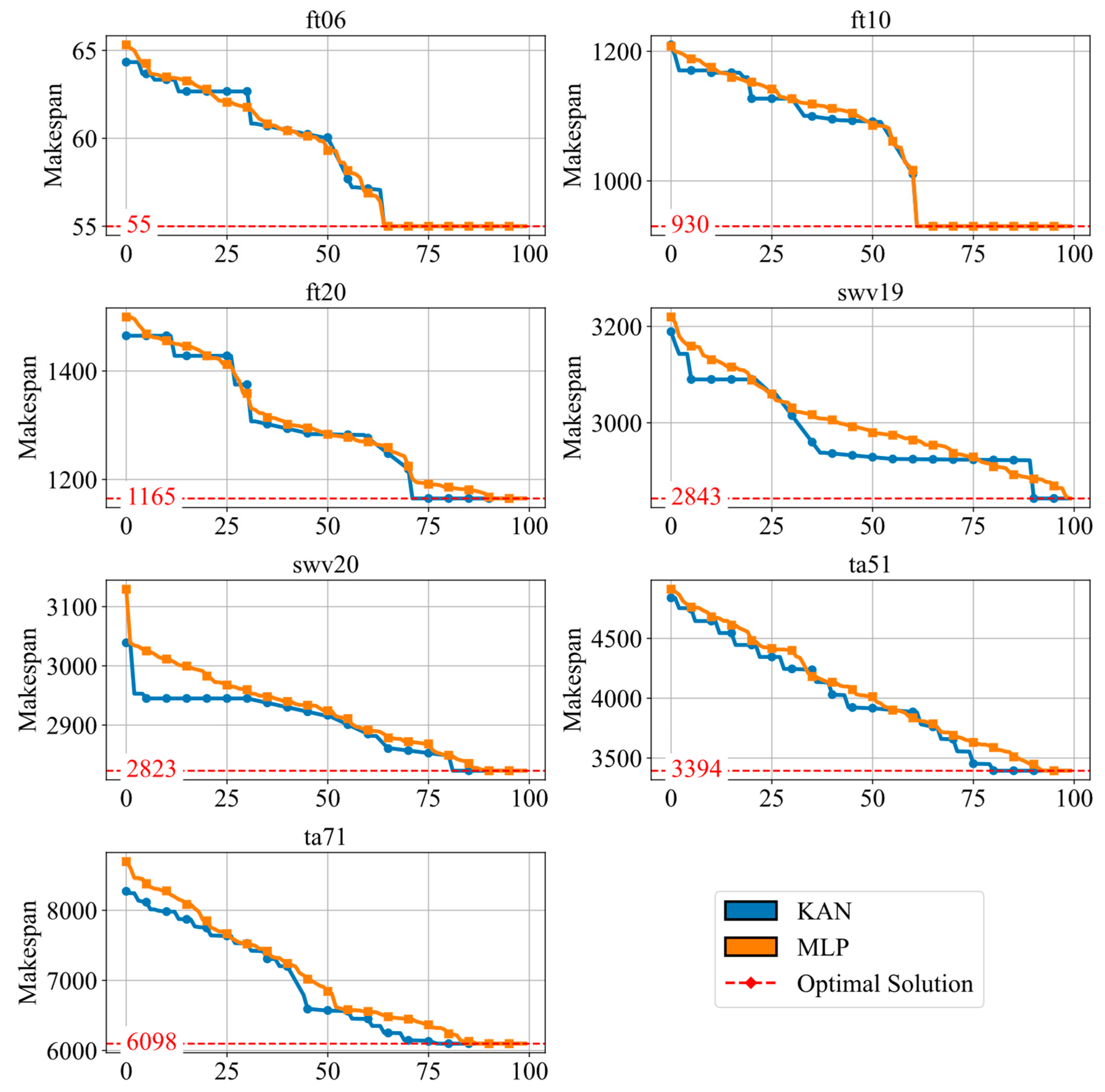
To assess the impact of the KAN compared to a traditional multilayer perceptron (MLP) on algorithm performance, we conducted a comparison using convergence curves across ten instances, as shown in Figure 8. The analysis reveals the following:
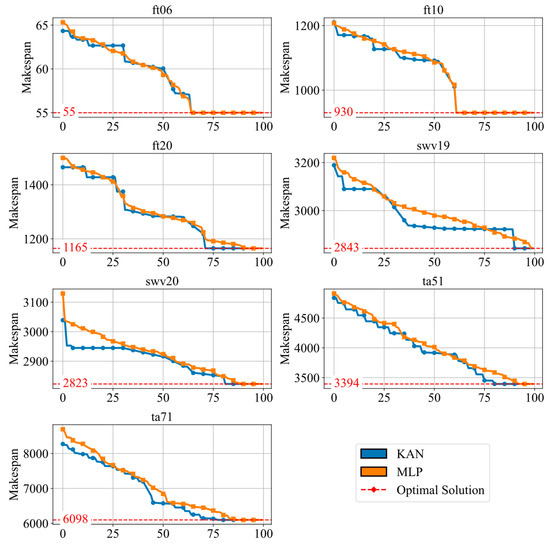
Figure 8.
The convergence of the comparison with various networks.
- For small-scale problems, the performance differences between the KAN and the MLP are negligible;
- For large-scale problems, the KAN exhibits a clear advantage, achieving optimal solutions with fewer iterations. This efficiency in complex scheduling problems highlights the robustness of the KAN in handling higher-dimensional feature spaces.
4.6. Computational Performance Analysis
The computational complexity of the HFLLMDRL framework, outlined as O(M·(E|| + N||)), is primarily influenced by the number of iterations (M), LLM generations per iteration (N), DRL training episodes (E), and the experience buffer size (||). While the core JSSP remains NP-hard, the complexity mainly lies in the training phase. The integration of the KAN, while offering better interpretability and performance on larger scales, maintains a comparable computational footprint to MLPs during inference. The LLM-based critic introduces computational overhead during training compared to simpler value networks, dependent on the chosen LLM’s size and API call latency. However, a significant advantage of DRL approaches, including HFLLMDRL, is the fast inference time after training, allowing for the rapid generation of schedules in dynamic environments.
As demonstrated in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, HFLLMDRL exhibits robust convergence across various instance sizes. Compared to standard DRL approaches for the JSSP referenced in the literature, the integration of LLM-designed rewards and the KAN architecture contributes to faster convergence towards high-quality solutions, which is particularly evident in larger instances where the KAN outperforms the MLP. The elite selection strategy further stabilizes and potentially accelerates convergence compared to greedy or roulette methods, especially for complex problems (Figure 5). While training time remains a consideration for DRL methods, the framework shows competitive or improved convergence speeds relative to other advanced DRL techniques by effectively guiding the policy search through better reward shaping and state representation.
In our experimental setup (3.1 GHz E5-2603V4 CPU, 64 GB RAM), the training phase for larger instances (e.g., swv20 and ta71) required several hours, influenced by the number of iterations (M = 100) and DRL steps per evaluation (10,000). Factors impacting computational time include the complexity of the KAN architecture, the number of reward candidates generated by the LLM (N = 20), and potentially the latency if interacting with external LLM APIs. However, once trained, the policy network (KAN) can generate scheduling decisions in milliseconds or seconds, making HFLLMDRL suitable for practical applications such as daily rescheduling or even near-real-time adjustments in dynamic manufacturing environments, where rapid responses are crucial.
5. Conclusions
In this paper, a human feedback-based large language model-assisted deep reinforcement learning framework is proposed (HFLLMDRL) to solve the job shop scheduling problem (JSSP), a classical NP-hard combinatorial optimization challenge in manufacturing systems. The proposed framework addresses two key challenges in JSSP reinforcement learning: the design of effective reward functions and the representation of state features. By incorporating human feedback into prompting engineering, our framework leverages the generative power of LLMs to design instructive reward functions that accelerate policy convergence. At the same time, a KAN was integrated as a policy network to enhance the representation of state features so as to improve learning efficiency in a complex production environment.
The job shop scheduling environment is modeled by a disjunctive graph, which simplifies the representation of the problem and effectively applies reinforcement learning techniques. The ROSES framework proposes an engineering framework built around roles, goals, scenarios, intended solutions, and steps to ensure that the reward functions generated by LLMs are aligned with human-defined goals, improving their quality and relevance. In addition, guided by human feedback, an automatic evaluation and selection mechanism is implemented to validate, rank, and retain elite reward functions. This process minimizes human intervention while maintaining high-quality outputs and enables the iterative optimization of reward design. The experimental results verify the effectiveness of the proposed framework. Compared with traditional methods, the proposed framework has significant improvements in policy convergence and learning performance. The framework achieves a reward function that is competitive with or superior to human-designed reward functions, highlighting the potential of combining human feedback with LLM functions. In addition, by incorporating the KAN architecture, the proposed framework enhances the feature representation and further improves its robust performance in task scheduling. This study provides a new method for the application of deep reinforcement learning in manufacturing systems, which reduces the dependence on manual reward function design and improves optimization efficiency. By demonstrating the utility of human feedback and LLMs in reinforcement learning, our framework contributes to the wider adoption of automated approaches in scheduling problems. Furthermore, the effectiveness and scalability of HFLLMDRL were rigorously validated on a wide range of instances, including challenging large-scale benchmarks such as Taillard instances of up to 100 jobs and 20 machines, demonstrating its potential for tackling complex real-world scheduling problems.
In future research, the framework can be extended by fine-tuning LLMs for JSSP-specific tasks. Although the proposed method includes a feedback mechanism, the experimental results show that LLMs occasionally produce an invalid reward function due to the illusion effect. Fine-tuning LLMs with domain-specific data has the potential to alleviate these issues, reduce the generation of invalid reward functions, and further improve the performance of the framework. Furthermore, leveraging open-source LLMs can protect tacit knowledge and lower barriers to industrial adoption, paving the way for wider applications of reinforcement learning in areas such as scheduling.
Author Contributions
All authors contributed to this study’s conception and design. Conceptualization, Y.Z.; Data curation, Y.Z., P.L., J.H. (Jianmin Hu) and C.F.; Funding acquisition, P.L. and J.H. (Jianmin Hu); Investigation, P.L. and J.H. (Jiwei Hu); Methodology, Y.Z. and P.L.; Project administration, Q.L.; Supervision, J.H. (Jianmin Hu) and Q.L.; Validation, C.F.; Writing—original draft, Y.Z.; Writing—review and editing, Y.Z., P.L., C.F. and J.H. (Jiwei Hu). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Hubei Province of China under Grant 2025AFA055 and the National Key Research and Development Program of China under Grant 2020YFB1710804.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors have no relevant financial or non-financial interests to disclose.
Abbreviations
The following abbreviations are used in this manuscript:
| LLMs | Large language models |
| JSSP | Job Shop Scheduling Problem |
| KAN | Kolmogorov–Arnold Network |
| DRL | Deep Reinforcement Learning |
| HFLLMDRL | Human feedback-based Large Language Model-assisted deep reinforcement learning framework |
Appendix A
This section mainly shows the prompt design descriptions of some implementation examples. Box A1, Box A2, Box A3, Box A4 and Box A5 are the prompt templates of the role, objective, scenario, expected solution, and steps, respectively.
Box A1. The role of generating a reward function.
You are a reward engineer trying to write reward functions to solve reinforcement learning tasks as effective as possible.
Box A2. The objective for the reward prompt.
Your goal is to write a reward function for the environment that will help the agent learn the task described in text.
Box A3. The state of the problem.
The Python environment is
class DisjunctiveGraphJspEnv(gym.Env):
def get_state(self) -> npt.NDArray:
"""
returns the state of the environment as numpy array.
"""
adj = nx.to_numpy_array(self.G)[1:−1, 1:−1].astype(dtype = int) # remove dummy tasks
task_to_machine_mapping = np.zeros(shape = (self.total_tasks_without_dummies, 1),
dtype = int)
task_to_duration_mapping = np.zeros(shape = (self.total_tasks_without_dummies, 1),
dtype = self.dtype)
for task_id, data in self.G.nodes(data=True):
if task_id == self.src_task or task_id == self.sink_task:
continue
else:
# index shift because of the removed dummy tasks
task_to_machine_mapping[task_id − 1] = data[“machine”]
task_to_duration_mapping[task_id − 1] = data[“duration”]
if self.normalize_observation_space:
# one hot encoding for task to machine mapping
task_to_machine_mapping = task_to_machine_mapping.astype(int).ravel()
n_values = np.max(task_to_machine_mapping) + 1
task_to_machine_mapping = np.eye(n_values)[task_to_machine_mapping]
# normalize
adj = adj/self.longest_processing_time # note: adj matrix contains weights
task_to_duration_mapping = task_to_duration_mapping
/self.longest_processing_time
# merge arrays
res = np.concatenate((adj, task_to_machine_mapping, task_to_duration_mapping),
axis = 1, dtype = self.dtype)
if self.env_transform == ‘mask’:
res = OrderedDict({“action_mask”:
np.array(self.valid_action_mask()).astype(np.int32),
“observations”:res})
return res
Box A4. The expected solution for the reward prompt.
Your reward function should use useful variables from the environment as inputs. As an example, the reward function signature can be: @torch.jit.script
def get_reward(self, state: npt.NDArray, done: bool, info: Dict, makespan_this_step: float):
…
return reward
Since the reward function will be decorated with @torch.jit.script,
please make sure that the code is compatible with TorchScript (e.g., use torch tensor instead of numpy array).
Make sure any new tensor or variable you introduce is on the same device as the input tensors.
Box A5. The steps for the reward prompt.
The output of the reward function should consist of one item:
(1) the total reward,
The code output should be formatted as a python code string: “```python … ```”.
Some helpful tips for writing the reward function code:
(1) You may find it helpful to normalize the reward to a fixed range by applying transformations like torch.exp to the overall reward or its components
(2) If you choose to transform a reward component, then you must also introduce a temperature parameter inside the transformation function; this parameter must be a named variable in the reward function and it must not be an input variable. Each transformed reward component should have its own temperature variable
(3) Make sure the type of each input variable is correctly specified; a float input variable should not be specified as torch.Tensor
(4) Most importantly, the reward code’s input variables must contain only attributes of the provided environment class definition (namely, variables that have prefix self.). Under no circumstance can you introduce new input variables.
Box A6, Box A7, Box A8 and Box A9 present a template for human feedback, including an error statement, a successful statement, and expected solutions and steps.
Box A6. The error statement of the feedback prompt.
The generated reward function is invalid, primarily due to incorrect syntax formatting.
There are the errors code:
(1)#@torch.jit.script
def get_reward(self, state: npt.NDArray, done: bool, info: Dict, makespan_this_step: float):
reward = -makespan_this_step # penalize long makespan
return reward
reward = get_reward(state, done, info, makespan_this_step)
reward_normalized = torch.exp(reward) # normalize the reward using torch.exp
reward_normalized.
Box A7. The best statement of the feedback prompt.
These are relatively superior reward function codes:
(1)@torch.jit.script
def get_reward(self, state: npt.NDArray, done: bool, info: Dict, makespan_this_step: float):
if done:
reward = -makespan_this_step # penalize long makespan
else:
reward = −1 # negative constant reward for each step
return reward
(2)@torch.jit.script
def get_reward(self, makespan_this_step: float) -> float:
reward = -makespan_this_step
return reward
(3)def get_reward(self, state: torch.Tensor, done: bool, info: Dict, makespan_this_step: float):
if done:
# Penalize for not completing the task
reward = −100.0
else:
# Calculate makespan reward: make it negative to minimize
makespan_reward = -makespan_this_step
# Additional rewards based on the information provided in the state
# Add more components based on the state if needed
reward = makespan_reward
return reward
and their evaluation rewards and completion time statistics are as follows:
(1) rewards: [−103.66, −102.85, −106.40, −106.92, …], Max: −102.86, Mean: −108.21, Min: −110.98
makespan: [68.66, 67.85, 71.40, 71.92,…], Max: 75.98, Mean: 73.21, Min: 67.86
(2) rewards: [−2096.00, −2148.00, −2141.19, −2108.85, …], Max: −2096.00, Mean: −2114.38, Min: −2148.00
makespan: [66.00, 73.28, 76.50, 75.42, …], Max: 76.50, Mean: 73.91, Min: 66.00
(3) rewards: [−1988.33, −2067.14, −2093.30, −2124.92,…], Max: −1988.33, Mean: −2126.47, Min: −2145.38
makespan: [64.33, 67.57, 69.40, 71.07, 72.00,…], Max: 73.10, Mean: 72.30, Min: 64.33
Box A8. The expected solution of the feedback prompt.
Please carefully analyze the policy feedback and provide a new, improved reward function that can better solve the task.
Box A9. The steps of the feedback prompt.
Some helpful tips for analyzing the policy feedback:
- (1)
- If the makespen are always near nan, then you must rewrite the entire reward function
- (2)
- If the values for a certain reward component are near identical throughout, then this means RL is not able to optimize this component as it is written. You may consider
- (a)
- Changing its scale or the value of its temperature parameter
- (b)
- Re-writing the reward component
- (c)
- Discarding the reward component
- (3)
- If some reward components’ magnitude is significantly larger, then you must re-scale its value to a proper range
Please analyze each existing reward component in the suggested manner above first, and then write the reward function code.
References
- Xiong, H.; Shi, S.; Ren, D.; Hu, J. A Survey of Job Shop Scheduling Problem: The Types and Models. Comput. Oper. Res. 2022, 142, 105731. [Google Scholar] [CrossRef]
- Chen, R.; Li, W.; Yang, H. A Deep Reinforcement Learning Framework Based on an Attention Mechanism and Disjunctive Graph Embedding for the Job-Shop Scheduling Problem. IEEE Trans. Ind. Inf. 2023, 19, 1322–1331. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Liang, X.; Zhao, D.; Huang, J.; Xu, X.; Dai, B.; Miao, Q. Deep Reinforcement Learning: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5064–5078. [Google Scholar] [CrossRef] [PubMed]
- Eschmann, J. Reward Function Design in Reinforcement Learning. In Reinforcement Learning Algorithms: Analysis and Applications; Belousov, B., Abdulsamad, H., Klink, P., Parisi, S., Peters, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 25–33. ISBN 978-3-030-41188-6. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning, Second Edition: An Introduction; MIT Press: Cambridge, MA, USA, 2018; ISBN 978-0-262-35270-3. [Google Scholar]
- Yuan, E.; Wang, L.; Cheng, S.; Song, S.; Fan, W.; Li, Y. Solving Flexible Job Shop Scheduling Problems via Deep Reinforcement Learning. Expert Syst. Appl. 2024, 245, 123019. [Google Scholar] [CrossRef]
- Parker-Holder, J.; Rajan, R.; Song, X.; Biedenkapp, A.; Miao, Y.; Eimer, T.; Zhang, B.; Nguyen, V.; Calandra, R.; Faust, A.; et al. Automated Reinforcement Learning (AutoRL): A Survey and Open Problems. J. Artif. Int. Res. 2022, 74, 517–568. [Google Scholar] [CrossRef]
- Chiang, H.-T.L.; Faust, A.; Fiser, M.; Francis, A. Learning Navigation Behaviors End-to-End with AutoRL. IEEE Rob. Autom. Lett. 2019, 4, 2007–2014. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Y.; Yan, M.; Su, Z.; Luan, T.H. A Survey on ChatGPT: AI–Generated Contents, Challenges, and Solutions. IEEE Open J. Comput. Soc. 2023, 4, 280–302. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, W.S.; Hsu, D. Large Language Models as Commonsense Knowledge for Large-Scale Task Planning. Adv. Neur. In. 2023, 36, 31967–31987. [Google Scholar]
- Otter, D.W.; Medina, J.R.; Kalita, J.K. A Survey of the Usages of Deep Learning for Natural Language Processing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 604–624. [Google Scholar] [CrossRef]
- Romera-Paredes, B.; Barekatain, M.; Novikov, A.; Balog, M.; Kumar, M.P.; Dupont, E.; Ruiz, F.J.R.; Ellenberg, J.S.; Wang, P.; Fawzi, O.; et al. Mathematical Discoveries from Program Search with Large Language Models. Nature 2024, 625, 468–475. [Google Scholar] [CrossRef]
- Kwon, M.; Xie, S.M.; Bullard, K.; Sadigh, D. Reward Design with Language Models. arXiv 2023, arXiv:2303.00001. [Google Scholar]
- Song, W.; Chen, X.; Li, Q.; Cao, Z. Flexible Job-Shop Scheduling via Graph Neural Network and Deep Reinforcement Learning. IEEE Trans. Ind. Inf. 2023, 19, 1600–1610. [Google Scholar] [CrossRef]
- Seifi, C.; Schulze, M.; Zimmermann, J. A New Mathematical Formulation for a Potash-Mine Shift Scheduling Problem with a Simultaneous Assignment of Machines and Workers. Eur. J. Oper. Res. 2021, 292, 27–42. [Google Scholar] [CrossRef]
- Ozolins, A. Bounded Dynamic Programming Algorithm for the Job Shop Problem with Sequence Dependent Setup Times. Oper. Res. 2020, 20, 1701–1728. [Google Scholar] [CrossRef]
- Gui, L.; Li, X.; Zhang, Q.; Gao, L. Domain Knowledge Used in Meta-Heuristic Algorithms for the Job-Shop Scheduling Problem: Review and Analysis. Tsinghua Sci. Technol. 2024, 29, 1368–1389. [Google Scholar] [CrossRef]
- Syarif, A.; Pamungkas, A.; Kumar, R.; Gen, M. Performance Evaluation of Various Heuristic Algorithms to Solve Job Shop Scheduling Problem (JSSP). Int. J. Intell. Eng. Syst. 2021, 14, 334–343. [Google Scholar] [CrossRef]
- Kotary, J.; Fioretto, F.; Hentenryck, P.V. Fast Approximations for Job Shop Scheduling: A Lagrangian Dual Deep Learning Method. Proc. AAAI Conf. Artif. Intell. 2022, 36, 7239–7246. [Google Scholar] [CrossRef]
- Mazyavkina, N.; Sviridov, S.; Ivanov, S.; Burnaev, E. Reinforcement Learning for Combinatorial Optimization: A Survey. Comput. Oper. Res. 2021, 134, 105400. [Google Scholar] [CrossRef]
- Kallestad, J.; Hasibi, R.; Hemmati, A.; Sörensen, K. A General Deep Reinforcement Learning Hyperheuristic Framework for Solving Combinatorial Optimization Problems. Eur. J. Oper. Res. 2023, 309, 446–468. [Google Scholar] [CrossRef]
- Yuan, E.; Cheng, S.; Wang, L.; Song, S.; Wu, F. Solving Job Shop Scheduling Problems via Deep Reinforcement Learning. Appl. Soft Comput. 2023, 143, 110436. [Google Scholar] [CrossRef]
- Serrano-Ruiz, J.C.; Mula, J.; Poler, R. Job Shop Smart Manufacturing Scheduling by Deep Reinforcement Learning. J. Ind. Inf. Integr. 2024, 38, 100582. [Google Scholar] [CrossRef]
- Liu, R.; Piplani, R.; Toro, C. A Deep Multi-Agent Reinforcement Learning Approach to Solve Dynamic Job Shop Scheduling Problem. Comput. Oper. Res. 2023, 159, 106294. [Google Scholar] [CrossRef]
- Ma, Y.J.; Liang, W.; Wang, G.; Huang, D.-A.; Bastani, O.; Jayaraman, D.; Zhu, Y.; Fan, L.; Anandkumar, A. Eureka: Human-Level Reward Design via Coding Large Language Models. arXiv 2023, arXiv:2310.12931. [Google Scholar]
- Singh, S.; Lewis, R.L.; Barto, A.G. Where Do Rewards Come From? In Proceedings of the International Symposium on AI-Inspired Biology, Leicester, UK, 29 March–1 April 2010; pp. 111–116. [Google Scholar]
- Wirth, C.; Akrour, R.; Neumann, G.; Fürnkranz, J. A Survey of Preference-Based Reinforcement Learning Methods. J. Mach. Learn. Res. 2017, 18, 4945–4990. [Google Scholar]
- Arora, S.; Doshi, P. A Survey of Inverse Reinforcement Learning: Challenges, Methods and Progress. Artif. Intell. 2021, 297, 103500. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, H.; Cheng, Y.; Shu, T.; Liu, G.; Liang, G.; Zhao, J.; Li, Y. Survey on Large Language Model-Enhanced Reinforcement Learning: Concept, Taxonomy, and Methods. IEEE Trans. Neural Netw. Learn. Syst. 2024. [Google Scholar] [CrossRef]
- Carta, T.; Oudeyer, P.-Y.; Sigaud, O.; Lamprier, S. EAGER: Asking and Answering Questions for Automatic Reward Shaping in Language-Guided RL. Adv. Neural Inf. Process. Syst. 2022, 35, 12478–12490. [Google Scholar]
- Hu, H.; Sadigh, D. Language Instructed Reinforcement Learning for Human-AI Coordination. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; Volume 202, pp. 13584–13598. [Google Scholar]
- Yan, Z.; Ge, J.; Wu, Y.; Li, L.; Li, T. Automatic Virtual Network Embedding: A Deep Reinforcement Learning Approach with Graph Convolutional Networks. IEEE J. Sel. Areas Commun. 2020, 38, 1040–1057. [Google Scholar] [CrossRef]
- Li, S.E. Deep Reinforcement Learning. In Reinforcement Learning for Sequential Decision and Optimal Control; Li, S.E., Ed.; Springer Nature: Singapore, 2023; pp. 365–402. ISBN 978-981-19-7784-8. [Google Scholar]
- Li, K.; Chen, J.; Yu, D.; Dajun, T.; Qiu, X.; Lian, J.; Ji, R.; Zhang, S.; Wan, Z.; Sun, B.; et al. Deep Reinforcement Learning-Based Obstacle Avoidance for Robot Movement in Warehouse Environments. In Proceedings of the 2024 IEEE 6th International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Hangzhou, China, 23–25 October 2024. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Schmidt-Hieber, J. The Kolmogorov–Arnold Representation Theorem Revisited. Neural Netw. 2021, 137, 119–126. [Google Scholar] [CrossRef]
- Vaca-Rubio, C.J.; Blanco, L.; Pereira, R.; Caus, M. Kolmogorov-Arnold Networks (KANs) for Time Series Analysis. arXiv 2024, arXiv:2405.08790. [Google Scholar]
- Zhang, C.; Song, W.; Cao, Z.; Zhang, J.; Tan, P.S.; Chi, X. Learning to Dispatch for Job Shop Scheduling via Deep Reinforcement Learning. Adv. Neural Inf. Process. Syst. 2020, 33, 1621–1632. [Google Scholar]
- Nasuta, A.; Kemmerling, M.; Lütticke, D.; Schmitt, R.H. Reward Shaping for Job Shop Scheduling. In Proceedings of the Machine Learning, Optimization, and Data Science, Grasmere, UK, 22–26 September 2023; Nicosia, G., Ojha, V., La Malfa, E., La Malfa, G., Pardalos, P.M., Umeton, R., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 197–211. [Google Scholar]
- Samsonov, V.; Kemmerling, M.; Paegert, M.; Lütticke, D.; Sauermann, F.; Gützlaff, A.; Schuh, G.; Meisen, T. Manufacturing Control in Job Shop Environments with Reinforcement Learning. In Proceedings of the 13th International Conference on Agents and Artificial Intelligence, Online, 4–6 February 2021; pp. 589–597. [Google Scholar]
- Tassel, P.; Kovács, B.; Gebser, M.; Schekotihin, K.; Stöckermann, P.; Seidel, G. Semiconductor Fab Scheduling with Self-Supervised and Reinforcement Learning. In Proceedings of the 2023 Winter Simulation Conference (WSC), San Antonio, TX, USA, 10–13 December 2023. [Google Scholar]
- Zhu, Y.; Zhao, D. Online Minimax Q Network Learning for Two-Player Zero-Sum Markov Games. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1228–1241. [Google Scholar] [CrossRef]
- Zhou, K.; Oh, S.-K.; Qiu, J.; Pedrycz, W.; Seo, K.; Yoon, J.H. Design of Hierarchical Neural Networks Using Deep LSTM and Self-Organizing Dynamical Fuzzy-Neural Network Architecture. IEEE Trans. Fuzzy Syst. 2024, 32, 2915–2929. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).