Abstract
Accurate fault diagnosis remains a critical but unresolved issue in predictive maintenance, as industrial environments typically involve large amounts of electromagnetic interference and mechanical noise that can severely degrade the signal quality. In this study, we propose an innovative diagnostic framework to address the challenging problem of bearing fault diagnosis in vibration signals under complex noise conditions. We develop the VMD-CNN-BiLSTM-CBAM model by systematically integrating the variational mode decomposition (VMD), convolutional neural network (CNN), bi-directional long and short-term memory network (BiLSTM), and convolutional block attention module (CBAM). The framework starts with VMD-based signal decomposition, which effectively separates the noise component from the bearing vibration features. Based on this denoising, a CNN architecture is employed to extract multi-scale spatio-temporal features through its hierarchical learning mechanism. The subsequent BiLSTM layer captures bidirectional temporal dependencies to model fault-evolution patterns, while the CBAM module strategically highlights key diagnostic features through adaptive channel spatial attention. Experimental validation using the Case Western Reserve University and Jiangnan University bearing datasets demonstrates the excellent performance of the model, with average accuracies of 99.76% and 99.40%, respectively. Finally, additional validation through our customized testbed confirms the usefulness of the model with an average accuracy of 99.70%. These results demonstrate that the proposed approach greatly improves fault diagnosis in noisy industrial environments through its synergistic architectural design and enhanced noise immunity.
1. Introduction
The ongoing advancement in industrial automation and innovative manufacturing technologies has led to increasingly sophisticated equipment with enhanced automation capabilities. In this context, bearing systems play a pivotal role in maintaining optimal production efficiency and ensuring consistent product quality standards [1]. However, in practice, environmental noise and the variety of fault types and causes in complex systems make the early detection and diagnosis of bearing faults particularly challenging [2]. Traditional fault-diagnosis methods rely on simple signal processing and thresholding, which are less effective in the face of highly noisy or nonlinear systems and difficult to cope with rapidly changing industrial requirements [3].
Aiming at the shortcomings of traditional CNN models that make it challenging to capture global statistical features, Yannis L. Karnavas [4] proposed a dual-stream attention model architecture. By learning the global statistical features and local spatial correlations of the input vectors, respectively, through parallel neural streams, high-precision fault identification is achieved based on the CWRU and Paderborn bearing datasets, which verifies the advantages of the global–local feature fusion mechanism in cross-dataset generalization. Andressa Borré [5] constructed a hybrid CNN-LSTM model based on quantile regression, which effectively solves the false alarm problem of traditional models under data noise and working condition fluctuations. Y Keshun [6] addresses the dual challenges of a large number of model parameters and poor interpretability and innovatively fuses a quadratic neural network (QNN) and bidirectional LSTM to achieve high classification accuracy in the CWRU dataset and effectively reduces the number of model parameters. Ting Huang [7] proposed a research method combining a convolutional neural network (CNN) and long and short-term memory network (LSTM), which effectively improves the fault-diagnosis performance of complex systems by comprehensively considering the feature extraction and the time delay of fault occurrence. FangDao [8] came up with a model based on Bayesian optimization, combining a convolutional neural network and long and short-term memory network (BO-CNN-LSTM) that improves the accuracy and stability of rotating machine fault diagnosis and solves the shortcomings of the traditional model in fault feature extraction and time series analysis by optimizing the hyperparameters. Baoye Song [9] proposed an optimized CNN-BiLSTM network method to solve the problem of limited training samples in bearing fault diagnosis under multiple operating conditions. Aiming at the issue of the insufficient extrapolation of fault-diagnosis models for wind turbine bearings in complex environments, Zifei Xu [10] proposed an MSCNN-BiLSTM model with multi-sensor information fusion combined with a weighted majority voting rule to improve the diagnostic accuracy. Dong Z [11] proposed a one-dimensional-ISACNN combined with Empirical Wavelet Transform (EWT) and an improved attention mechanism model, which achieves better classification performance through multi-frequency feature extraction and an optimized loss function. Aiming at the complexity of multi-fault vibration signals, Xue Y [12] proposed a fault-diagnosis method combining a deep convolutional neural network (DCNN) and support vector machine (SVM), which utilizes DCNN to extract fault features automatically and combines them with manually designed time-domain features, which significantly improves the accuracy of the composite fault diagnosis.
While current deep learning methodologies have achieved notable advancements in enhancing fault diagnostic accuracy and system reliability, critical gaps persist in addressing nonlinear signal characteristics and multi-scale data relationships. Particularly under noise-intensive operational conditions, these approaches continue to demonstrate limitations in diagnostic precision and model adaptability across variable industrial scenarios.
This research introduces an innovative diagnostic framework that synergistically integrates Variational Mode Decomposition (VMD) with a multi-component deep learning architecture comprising Convolutional Neural Networks (CNNs), Bidirectional Long Short-Term Memory networks (BiLSTMs), and Convolutional Block Attention Mechanisms (CBAMs). The developed VMD-CNN-BiLSTM-CBAM methodology aims to significantly enhance the effectiveness of bearing-fault-identification systems. The algorithm effectively improves the bearing-fault-diagnosis capability in complex environments through multiple levels of feature extraction and processing. Experimental results show that the algorithm has significant advantages in improving the diagnostic accuracy generalization ability and exhibits good adaptability and robustness. However, there exists the disadvantage of a long computation time, which is a part that needs to be improved in the future.
2. Theoretical Foundation
2.1. Optimizing the VMD Algorithm
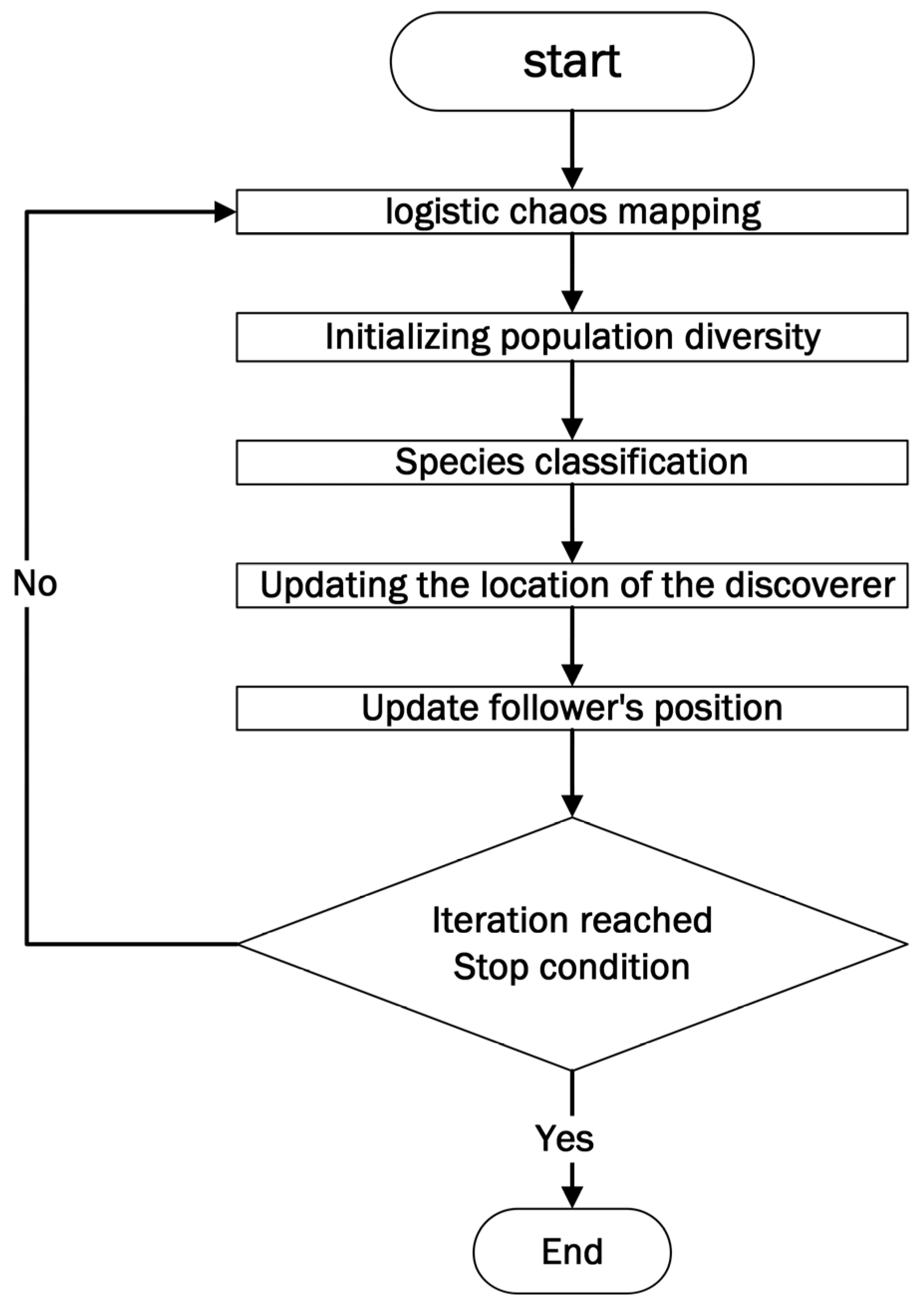
The VMD Algorithm-Fishhawk-Corsi Sparrow Search Algorithm (FCSSA-VMD) was optimized. By combining the Fishhawk optimization algorithm with the Cauchy variation strategy, it aims to improve the original sparrow optimization algorithm [13]. The optimization algorithm flow is shown in Figure 1.
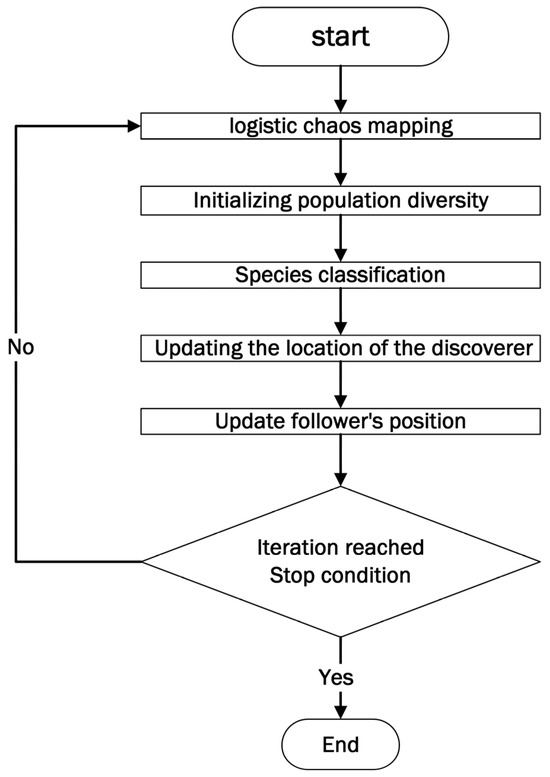
Figure 1.
Overall flow chart of FCSSA-VMD.
Logistic chaotic mapping [14] was first used to initialize the diversity of the population; the mathematical expression for the logistic mapping was defined as follows:
where ∈ [3.57, 4] controls the chaotic behavior (set to 4 in this study) and ∈ (0, 1). With this deterministic but non-repetitive sequence-generation mechanism, we obtain initial sparrow locations that cover the entire search space while avoiding clustering in suboptimal regions. Compared to traditional random initialization, chaotic mapping significantly improves the probability of discovering potentially dominant regions in early iterations. Then, in dividing the population into discoverers and followers, the discoverer positions updated by using the Fishhawk optimization algorithm [15] and the follower positions updated by using the Cauchy variation strategy [16] are designed to extend the search range of the sparrow algorithm, thus enhancing the ability of the algorithm to jump out of the local optimal solution. At the same time, it can correct the limitation of the original sparrow algorithm that overly relies on the previous generation of sparrow position updates.
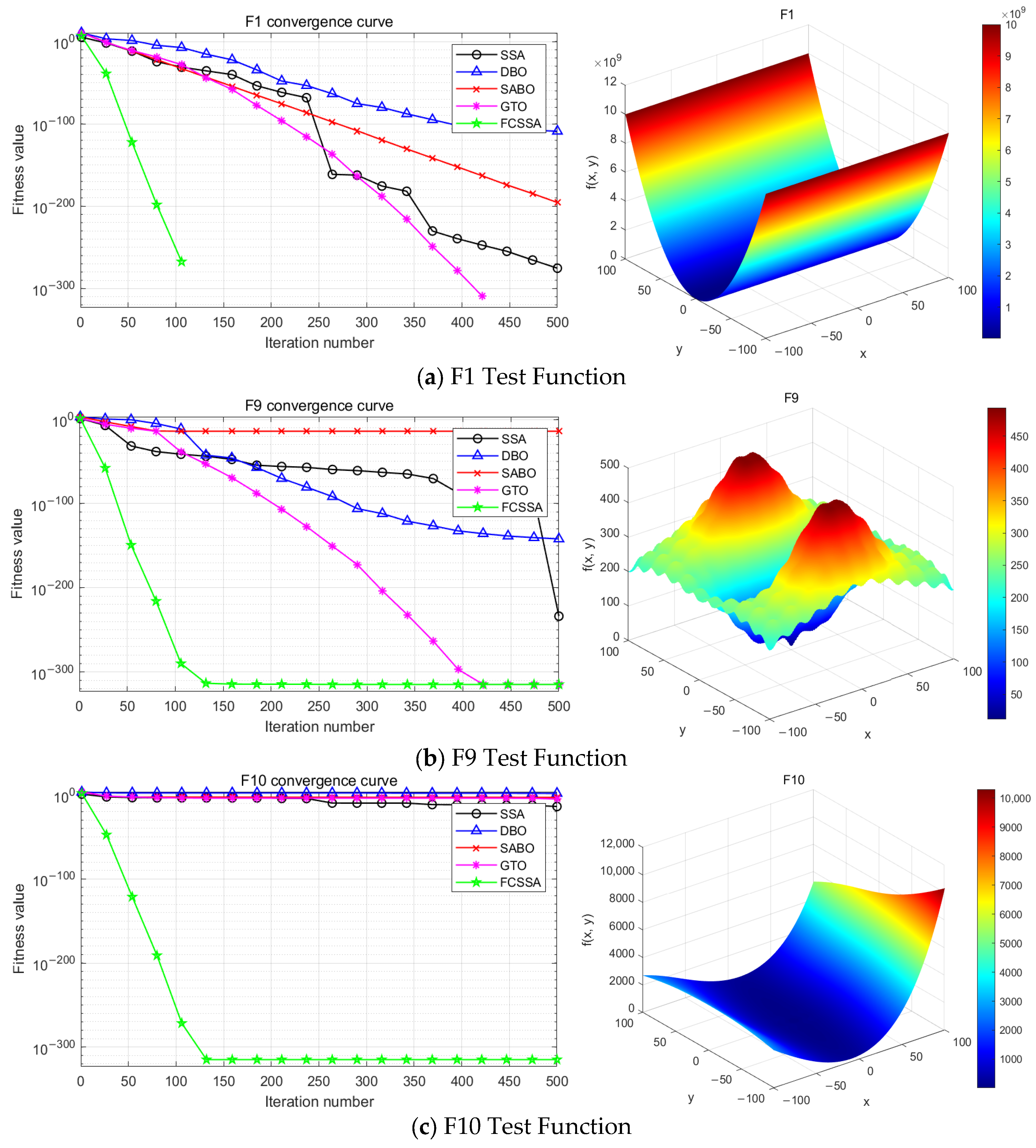
In order to verify the effectiveness of the optimisation algorithm proposed in this paper, matlab 2021a was chosen as the experimental tool and the CEC2021 function set [17] was used as the test object, and three functions, namely, single-peak function F1 and multi-peak functions F9 and F10, were used for testing. And compared with other four original algorithms which are Dung Beetle Optimisation Algorithm (DBO), Primitive Sparrow Algorithm (SSA), Artificial Gorilla Troop Optimisation Algorithm (GTO) and Subtractive Averaging Optimisation Algorithm (SABO).
Figure 2 shows the experimental comparison results. The five algorithms’ convergence curves are shown on the left, and the test function’s 3D modeling diagram is on the right.
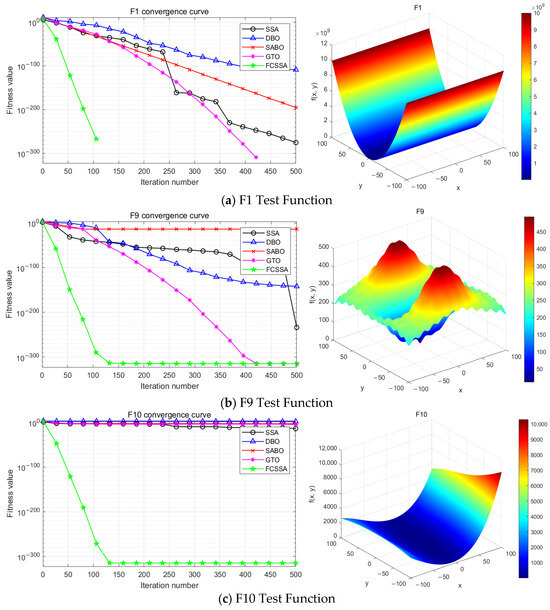
Figure 2.
Comparison of optimization algorithms.
The comparative analysis in Figure 2 reveals that the FCSSA-VMD approach demonstrates superior convergence characteristics, achieving optimal solutions with reduced iteration counts relative to alternative algorithmic implementations.
2.2. Convolutional Neural Network (CNN)
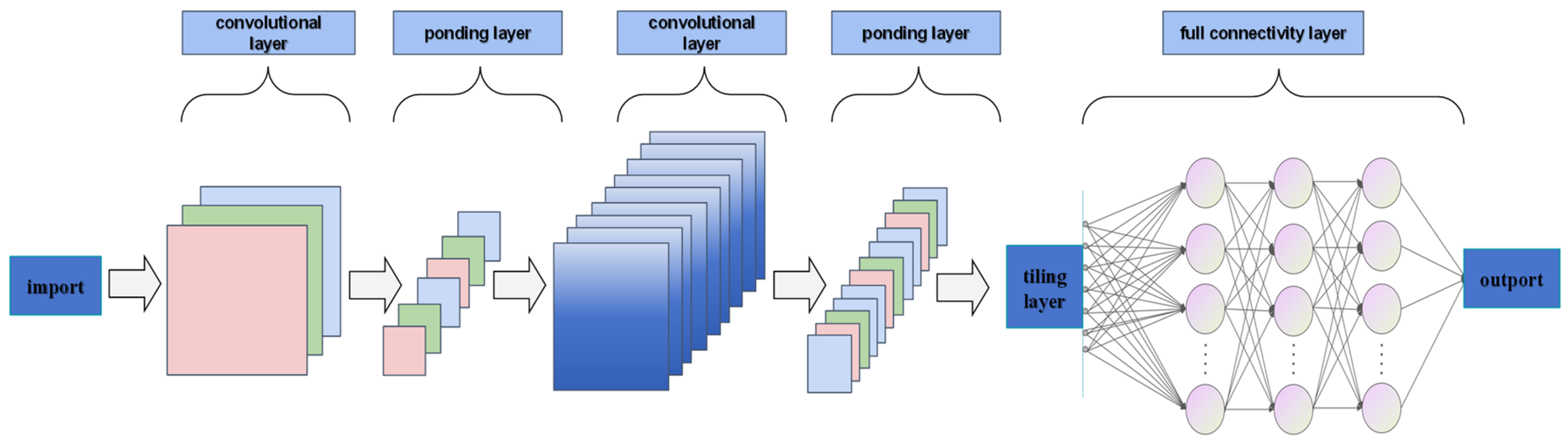
CNN is a feed-forward neural network in deep learning, which is mainly used to process data with a grid structure, such as image or sequence data [18]. The architecture’s fundamental characteristic lies in its employment of convolutional filters for feature extraction, where these filters systematically traverse input matrices, executing localized weighted computations that enhance both processing efficiency and model adaptability. The system demonstrates its computational framework, typically structured with five principal components—including data input, feature convolution, dimensionality reduction pooling, comprehensive connection, and result output layers. Illustrated in Figure 3, the implemented neural network configuration incorporates dual convolutional processing stages integrated with a feature abstraction layer. The convolution operation is calculated as follows [19]:
where: denotes the features of the ()-th layer following the convolution operation; represents the size of the convolution kernel; denotes the number of convolution channels; is the jth eigenvalue of the ith eigenmap of layer l; is the convolution kernel; is the bias term.
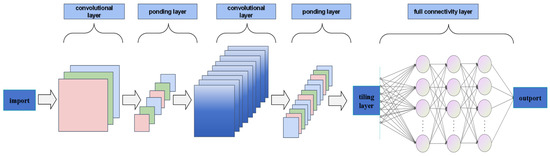
Figure 3.
CNN structure diagram.
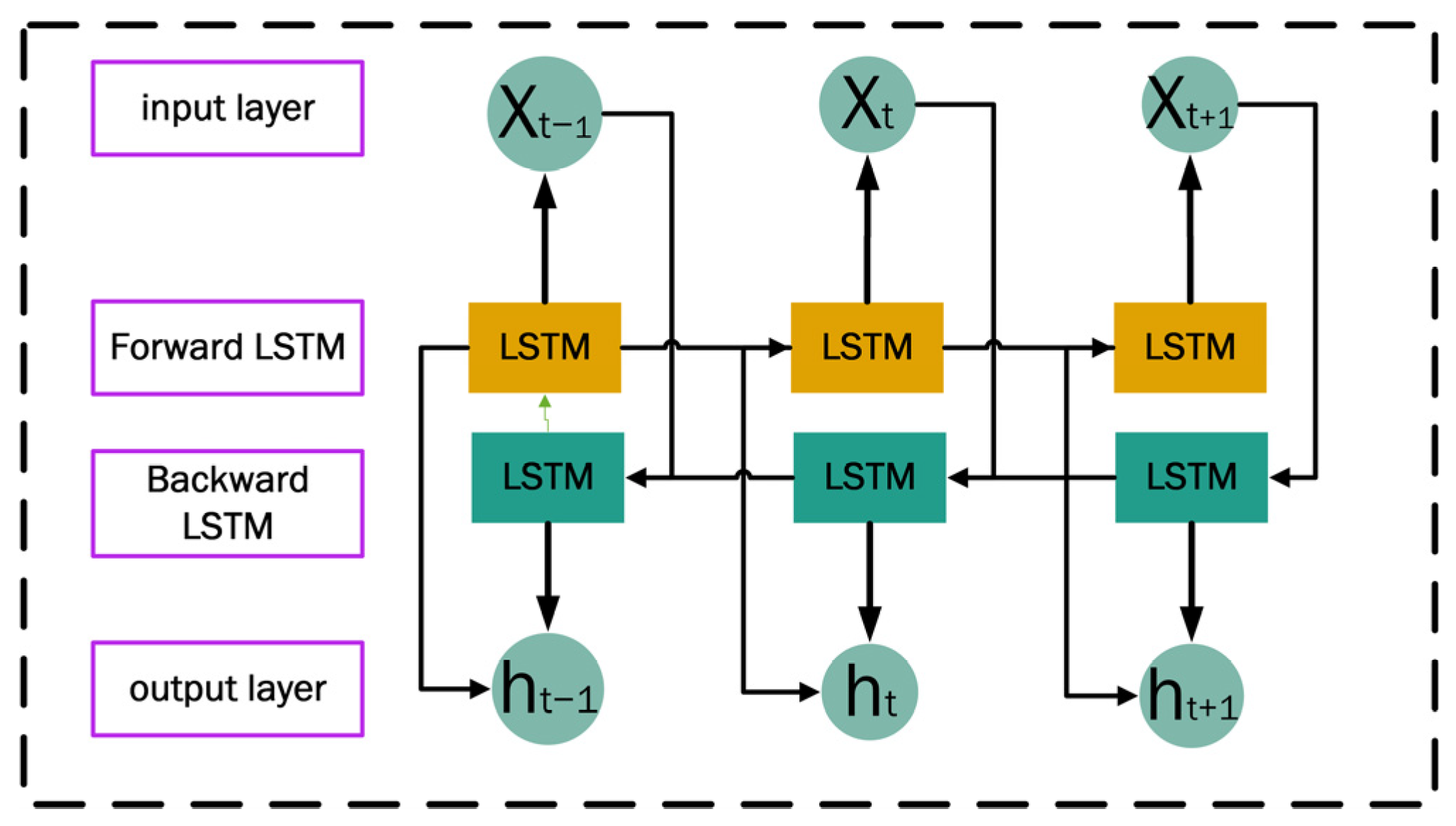
2.3. Bidirectional Long Short-Term Memory Network (BiLSTM)
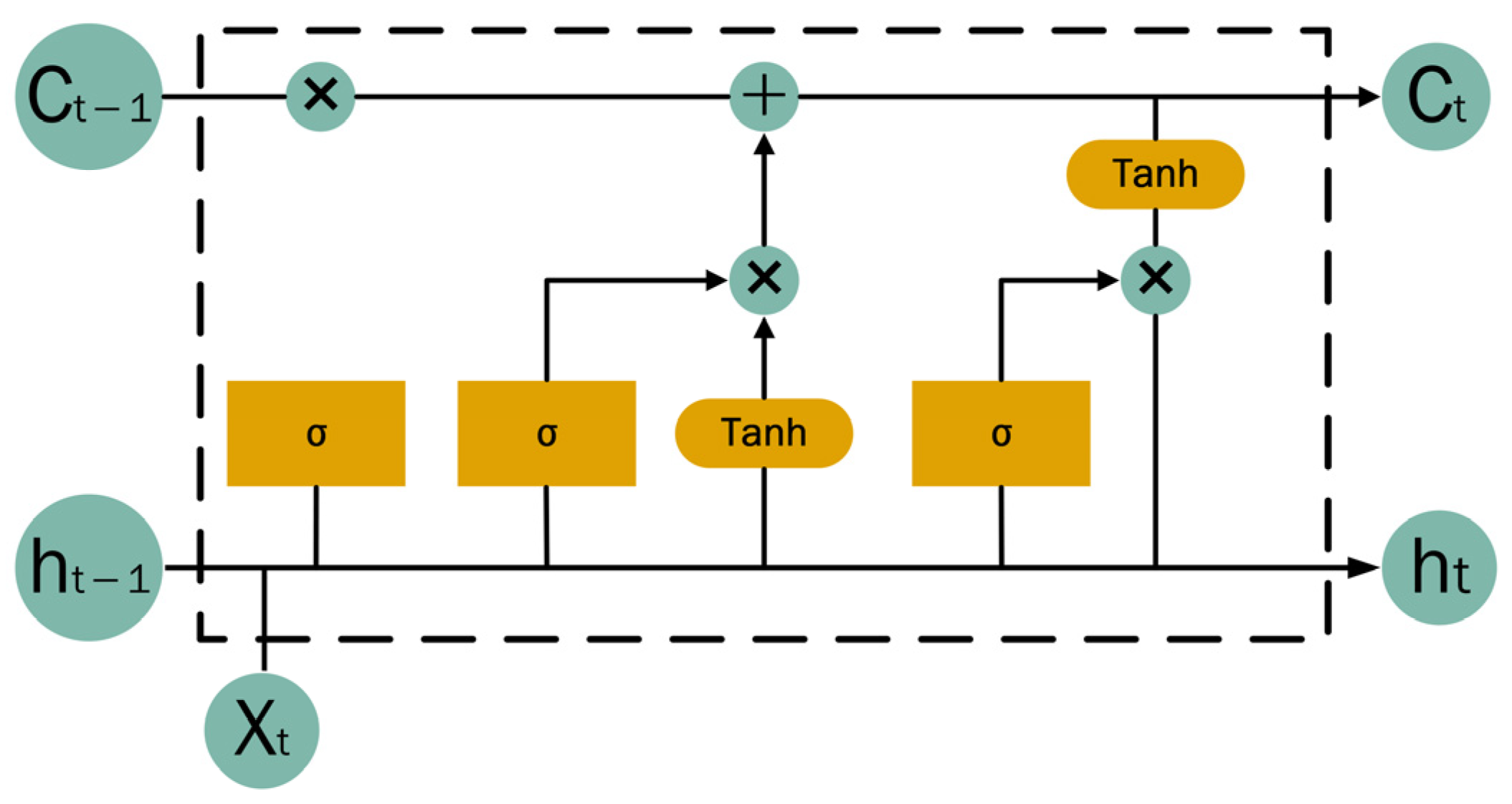
The Long Short-Term Memory (LSTM) architecture represents a refined variant of Recurrent Neural Networks (RNNs) designed to mitigate issues, such as gradient vanishing and explosion that often arise in standard RNNs when handling long sequential data [20]. The architecture of the LSTM unit incorporates three distinct gates: the input gate, the forget gate, and the output gate. The LSTM cell information transfer process at the moment is shown in Figure 4, where is the input of the t moment, is the output of the cell at the moment, ⊕ is the addition operation, and ⊗ is the multiplication operation.
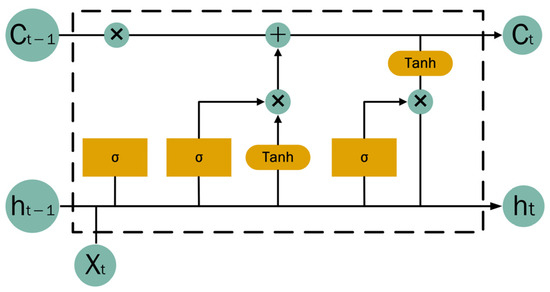
Figure 4.
LSTM structure diagram.
The formulas for input gates, oblivion gates, and output gates in the LSTM cell are as follows [21]:
where the variable corresponds to the sigmoid activation function; and are the output vectors of the moment forgetting gate and the input gate, the forget gate is defined by weight matrix and bias vector , which regulate the retention or discarding of historical information; the input gate, parameterized by weight matrix and bias vector , controls the integration of new input data into the current state; temporal continuity is maintained through state units and , representing stored information at the preceding and current time steps, respectively; is the output value of the output gate; is the output value of the state unit of the moment; and and are the weight matrix and the bias vector of the output gate, respectively.
The conventional Long Short-Term Memory (LSTM) architecture primarily processes temporal sequences in a unidirectional manner, leveraging historical data to predict subsequent states. However, real-world temporal sequences often exhibit bidirectional dependencies, where current observations are interconnected not only with preceding events but also with future contextual patterns. To address this limitation, we developed the Bidirectional Long Short-Term Memory (BiLSTM) framework. This enhanced architecture concurrently analyzes input sequences through both forward (past-to-future) and reverse (future-to-past) temporal pathways, thereby capturing comprehensive bidirectional contextual relationships and improving the model’s capacity to interpret complex temporal interdependencies within sequential data.
The structure of the Bidirectional Long Short-Term Memory Network (BiLSTM) [22] consists of two independent LSTMs corresponding to the forward LSTM layer and the backward LSTM layer, as shown in Figure 5. BiLSTM performs feature extraction by feeding inputs into two independent LSTM networks in a forward and backward manner, respectively, and then splicing the two sets of output vectors together to generate new vectors as the final feature representation. This is why BiLSTM can utilize the information before and after the current moment to obtain more comprehensive contextual information and improve the model’s understanding and modeling ability of sequence data. Especially when dealing with long sequence data, BiLSTM not only effectively mitigates the gradient vanishing problem through the forward and backward information flow but also enhances the training throughput and the convergence dynamics of the model, making it easier to train and optimize the model [23]. Its calculation formula is as follows:
where variables and , respectively, denote the hidden state outputs of the forward and backward LSTM layers at time step , while and represent the distinct LSTM cell units dedicated to processing sequential data in their respective temporal directions (forward: past-to-future; backward: future-to-past). This dual-path architecture enables the integration of contextual dependencies from both temporal orientations, enhancing the model’s ability to synthesize bidirectional sequential patterns; variable denotes the input feature vector at time step , whereas encapsulates the hidden state inherited from the forward LSTM layer at the prior time step , thereby preserving sequential dependencies for contextual feature propagation; variable encapsulates the hidden state propagated by the reverse temporal processing (backward LSTM) at the prior time step , while represents the concatenated composite of the forward and backward hidden states at the current time step .
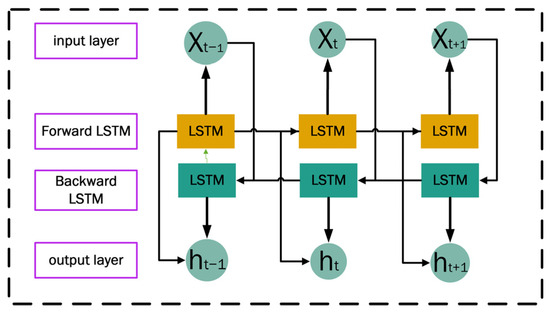
Figure 5.
BiLSTM structure diagram.
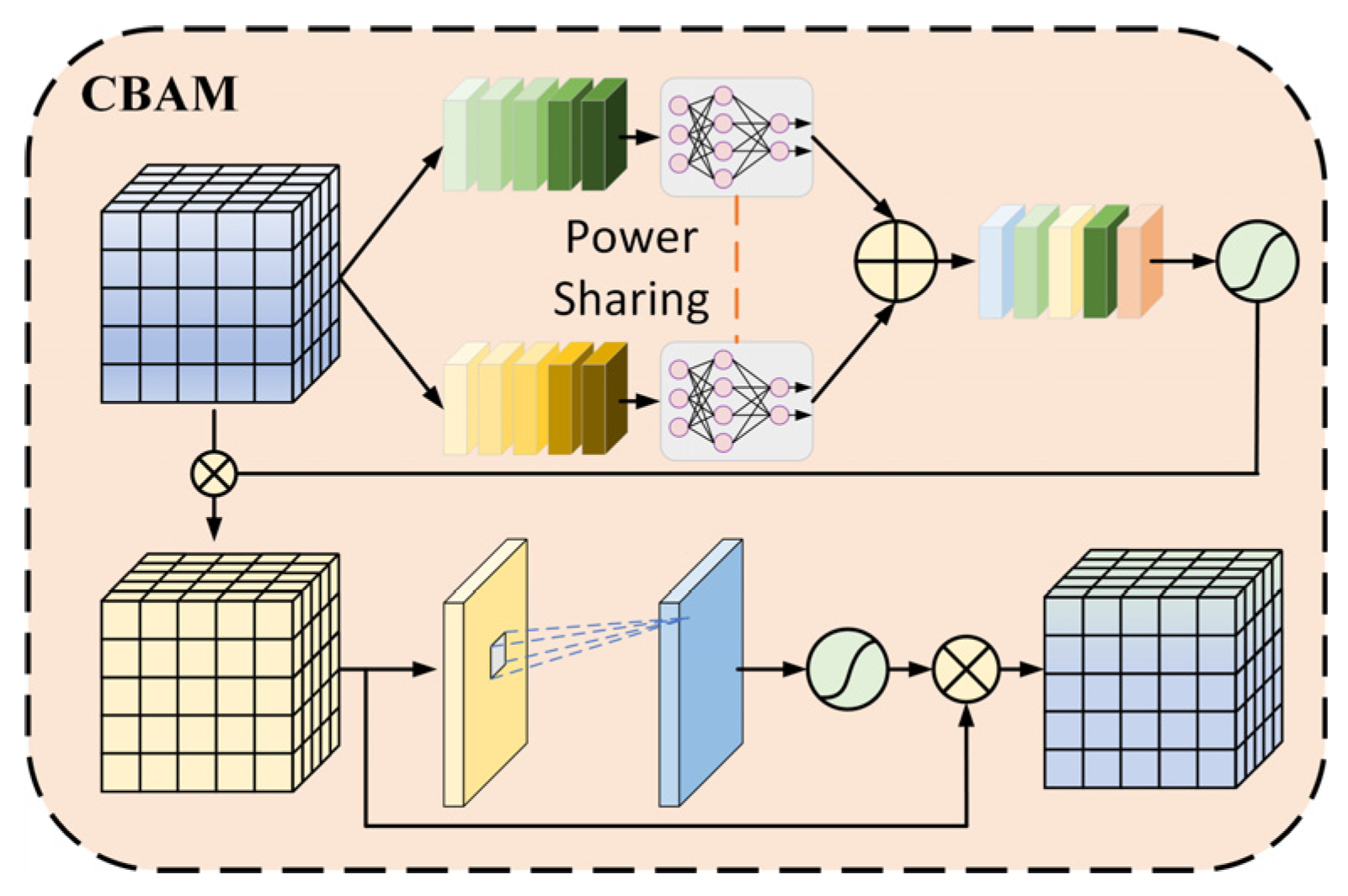
2.4. CBAM Convolutional Block Attention Module
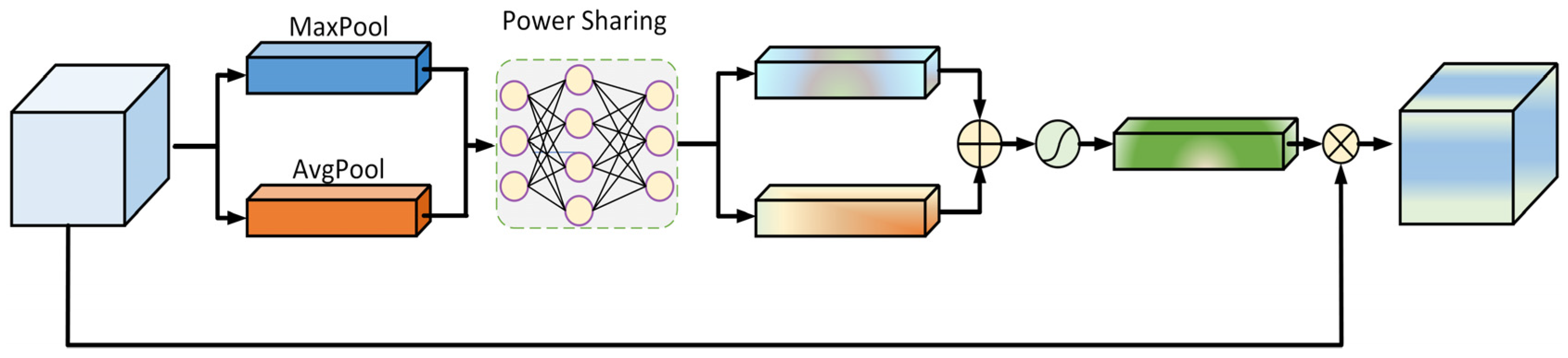
The Convolutional Block Attention Module (CBAM), introduced by Woo [24], is a dual-attention framework that synergistically integrates channel-wise feature weighting and spatial feature prioritization to refine convolutional feature representations adaptively.
The channel attention mechanism [25] operates through an adaptive feature recalibration workflow. Initially, dual parallel pooling operations (global max-pooling and average-pooling) are applied to the input feature maps to extract complementary spatial statistics. These pooled features are then processed through a shared multilayer perceptron (MLP) to generate independent channel-wise descriptors. The MLP outputs undergo element-wise summation followed by Sigmoid activation, producing normalized attention weights (0–1 range) that prioritize salient channels. These weights are subsequently applied via channel-wise scaling to the original input features, enhancing discriminative feature representation while suppressing irrelevant channels. This architecture enables the dynamic refinement of channel-wise feature importance, as illustrated in Figure 6.
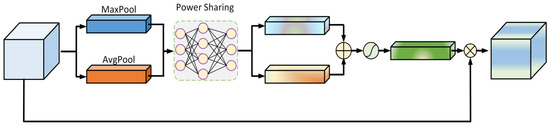
Figure 6.
Channel attention structure.
The calculation formula is as follows:
where denotes the feature multiplication operation; + denotes the feature stacking operation; the activation function is Sigmoid; variables and represent the input features obtained through global average pooling and max pooling operations, respectively, while corresponds to the shared weight mechanism in the joint feature mapping layer; and is the feature that contains the feature weights.
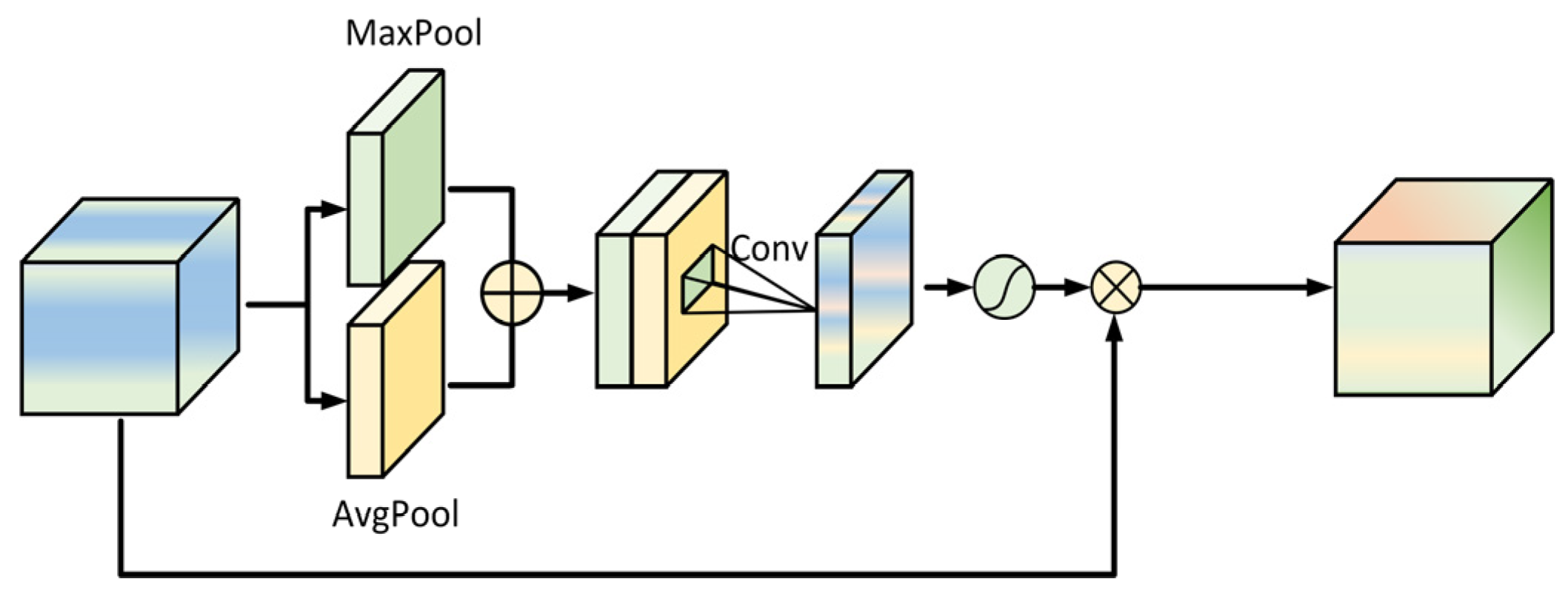
The Spatial Attention Mechanism [26] utilizes the output from the channel attention mechanism as its input. It applies both average and max pooling operations to combine weighted feature information, subsequently processes the data through a convolutional layer and Sigmoid activation, and ultimately generates enhanced features through dual-module refinement. The detailed structure is illustrated in Figure 7.
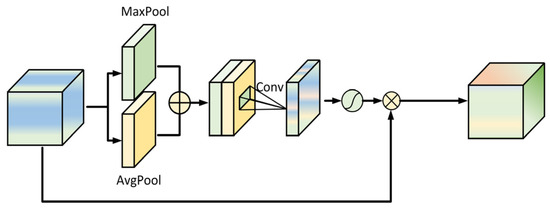
Figure 7.
Spatial attention structure.
The calculation formula is as follows:
where sigmoid is the activation function, denotes a 7 × 7 convolution kernel, denotes the convolution operation, denotes the features after global average pooling and maximum pooling, is the final feature information obtained after bimodule enhancement.
The convolutional attention module is integrated to prioritize features critical for diagnostic identification, thereby enhancing the fault classification accuracy and model adaptability. The system’s architecture is detailed in Figure 8. The method focuses on the key features and ignores the secondary information by adjusting the weight values according to the importance of the feature information. Features with elevated weight values receive a greater computational emphasis, enabling the model to prioritize essential characteristics while de-emphasizing less significant data elements, thus focusing on the key features and ignoring the secondary information.
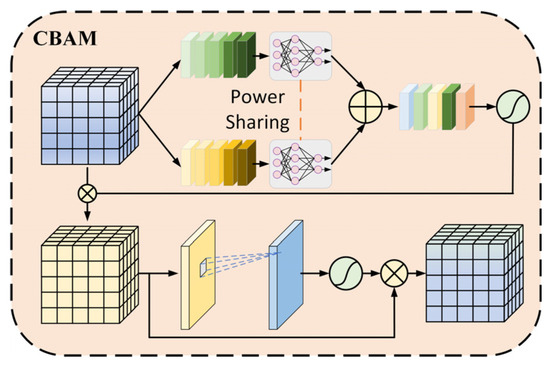
Figure 8.
Schematic diagram of CBAM structure.
3. Diagnostic Models
Figure 9 illustrates the structural framework of the developed diagnostic system, which integrates Variational Mode Decomposition with a hybrid deep learning architecture combining CNN, BiLSTM, and CBAM components. The operational workflow of this model can be described through the following sequential stages:
- (1)
- Acquisition of vibration signals from bearings under varying operational conditions;
- (2)
- Feature extraction through Variational Mode Decomposition (VMD) applied to raw signals to mitigate noise interference;
- (3)
- Division of processed data into training and testing subsets with a 70–30% allocation ratio;
- (4)
- Development of the trained model using the CNN-BiLSTM-CBAM architecture on the training dataset;
- (5)
- Implementation of diagnostic evaluation by introducing the test set into the trained model to generate final classification outcomes.
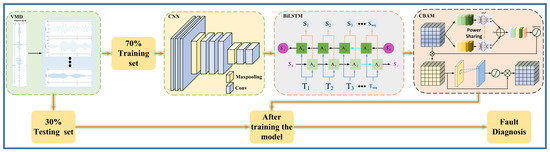
Figure 9.
Overall model architecture.
Figure 9.
Overall model architecture.
4. Experimental Case Analysis
4.1. Experimental Data
This study employs two open-access bearing fault datasets for methodology validation: the Case Western Reserve University (CWRU, Cleveland, OH, USA) Bearing Data Center repository [27] and Jiangnan University (JNU, Wuxi, China) experimental database [28]. The corresponding test configurations are illustrated in Figure 10, where the a and b panels, respectively, display the CWRU and JNU experimental setups. These benchmark datasets were selected to evaluate diagnostic performance under different operational conditions.

Figure 10.
CWRU and JiangNan University Bearing Data Collection Platforms.
4.1.1. Introduction to CWRU Experimental Datasets
The experimental analysis utilized SKF-6205 (Svenska Kullager-Fabriken, headquartered in Gothenburg, Sweden) deep groove ball bearings with three geometrically defined defect types: inner raceway (IR), outer raceway (OR), and rolling element (RE) faults. The CWRU dataset was acquired under controlled conditions (1750 RPM rotational speed, no-load operation) with a 12 kHz sampling frequency. Artificially induced defects through electrical discharge machining spanned three severity levels: 0.18, 0.36, and 0.53 mm (equivalent to 0.007, 0.014, and 0.021 inches), establishing ten operational states (9 fault conditions + normal condition). To construct the training samples, 2048-point vibration signatures were extracted using a sliding window technique with a 50% overlap ratio—a strategic approach to enhance model generalization while preventing overlearning. The mathematical implementation of this segmentation process is formalized in Equation (7). Since the faulty bearings used in the CWRU experiments had three fault sizes for each fault condition and three labels for each faulty bearing, the three faulty bearings had a total of nine labels, plus the label for one normal bearing for a total of ten labels. Please see Table 1 for details.
where is the total length of data, is the length of individual sample data, is the number of samples obtained, and is the step size to obtain 500 samples for each fault type.

Table 1.
Experimental data of CWRU bearing.
4.1.2. Introduction to the Experimental Dataset of JNU
The experimental investigation utilized the bearing dataset from Jiangnan University, comprising N205 cylindrical roller bearings under four distinct operational states: normal operation, inner race defects, outer race defects, and rolling element faults. Each data sample consists of 1024 discrete points, with 500 samples collected per condition. The testing parameters included a rotational velocity of 1000 rpm and a sampling rate of 50 kHz. In contrast to the CWRU dataset, there are only four labels in total, due to the fact that there is only one fault size for each of the three fault types for each faulty bearing in the JNU, plus one label for the normal bearing. Detailed specifications are shown in Table 2.

Table 2.
Bearing experimental data of JNU.
4.2. Analysis of Ablation Experiment Results
4.2.1. CWRU Dataset Ablation Experiments
In order to verify the effectiveness of the method in this paper, we conducted comparison experiments with commonly used diagnostic models, including CNN-LSTM, CNN-BiLSTM, VMD-CNN-LSTM, VMD-CNN-BiLSTM, VMD-CNN-LSTM-CBAM, and VMD-CNN-BiLSTM-CBAM, with a total of six models.
The initial dataset employed was the experimental dataset from Case Western Reserve University. The training process incorporated a stepped learning rate strategy, starting with an initial rate of 0.005. L2 regularization was used to reduce overfitting. In addition, the learning rate was reduced by 0.001 per 200 iterations and 500 iterations per model category.
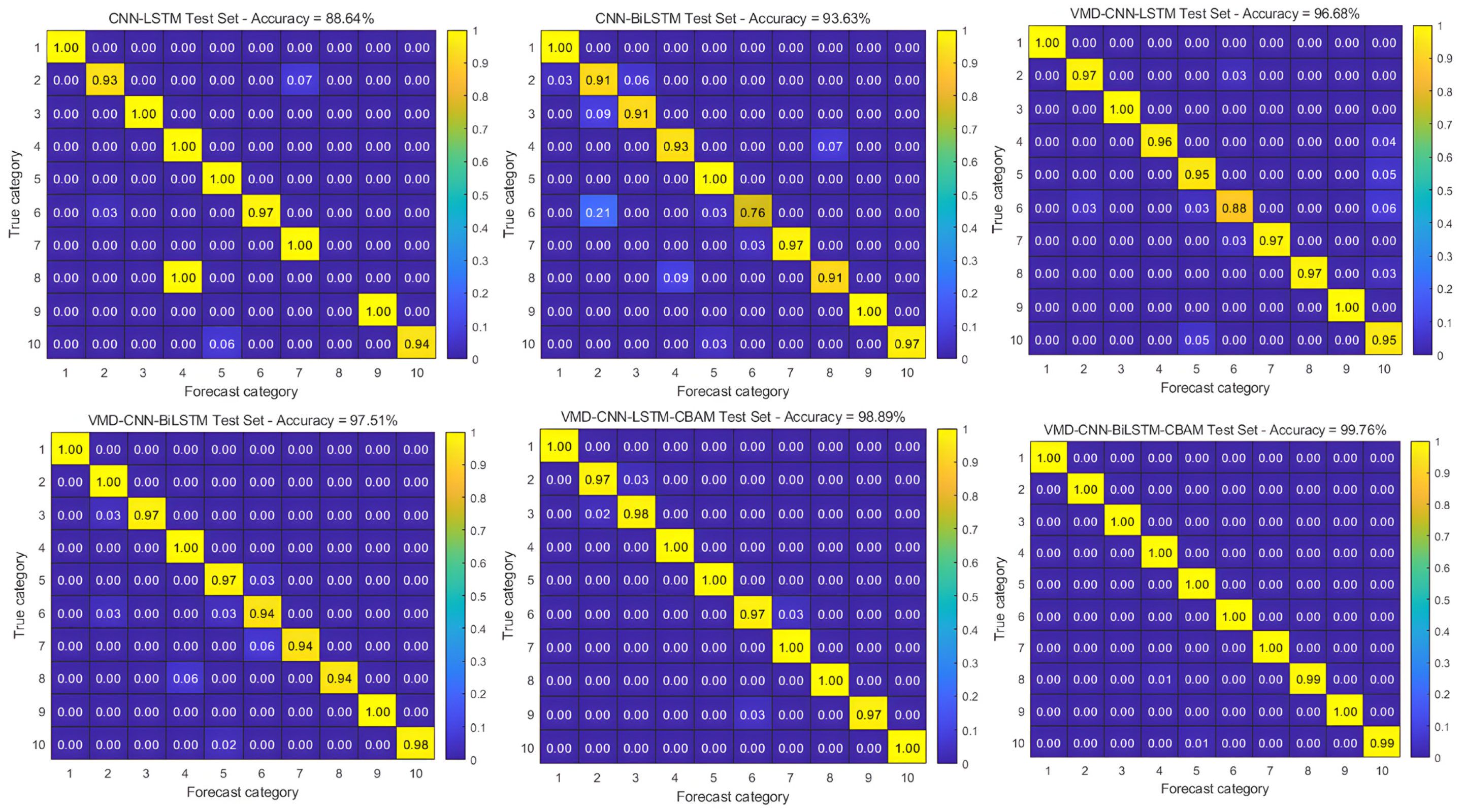
The diagnostic accuracy results are shown in Table 3, and the training confusion matrix is shown in Figure 11. When evaluating the six models, the VMD-CNN-BILSTM-CBAM model performs excellently, with the highest classification accuracy and F1 score of 99.76% and 0.996, respectively. This result highlights the model’s strong classification ability and good generalization capability. However, the drawback is that the computational time is long due to the complexity of the computational timing problem caused by the bidirectional long and short-term memory network (BILSTM) used in the model.

Table 3.
Analysis of ablation experiment results.
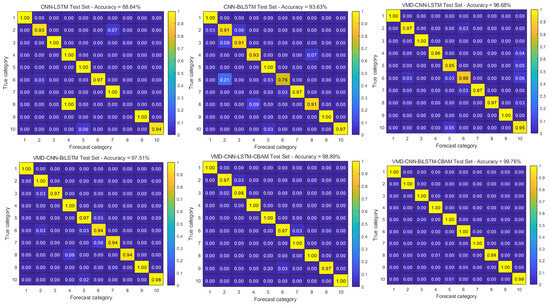
Figure 11.
Confusion matrix for Case Western Reserve University dataset.
4.2.2. JNU Dataset Ablation Experiment
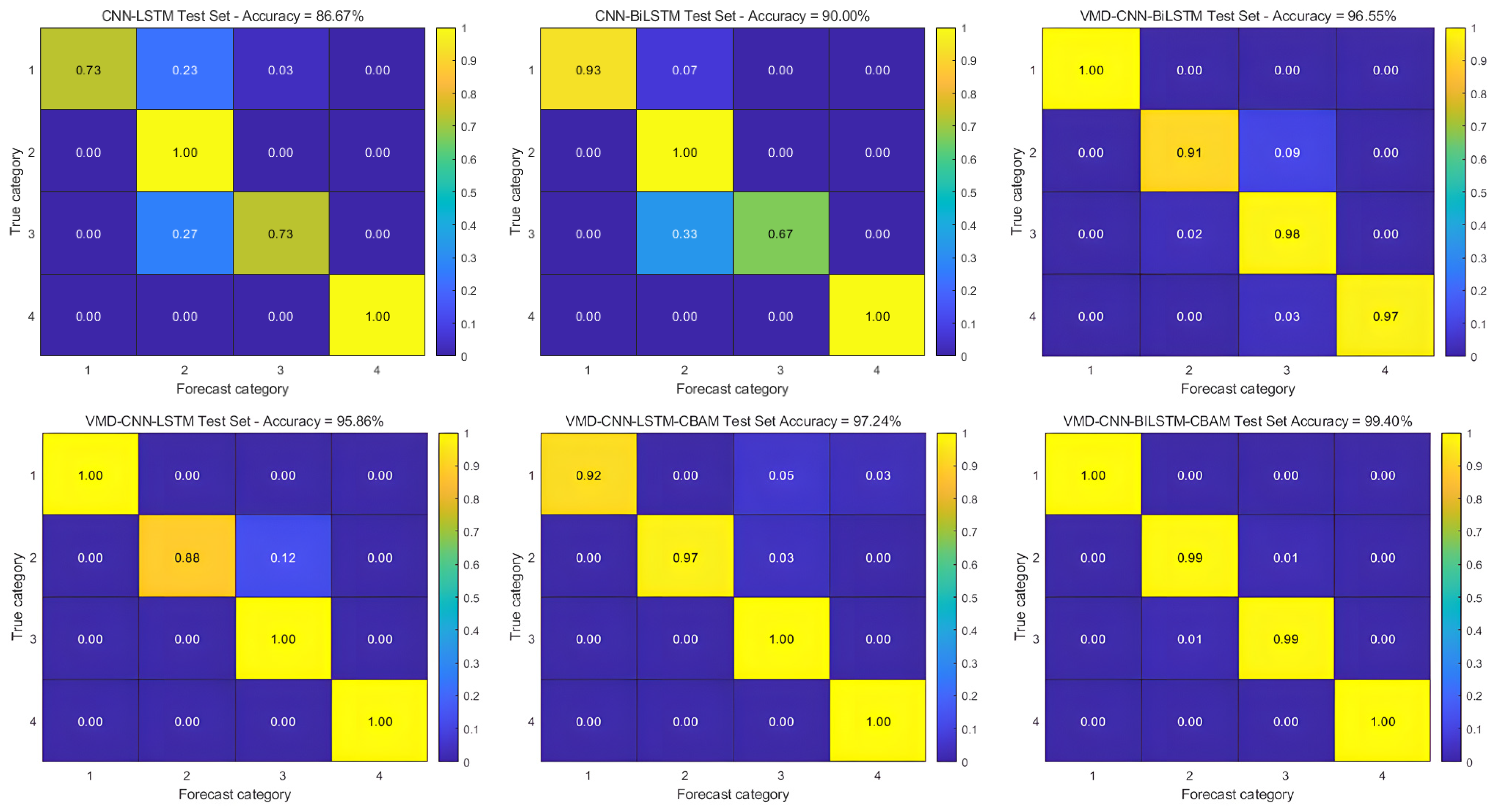
To verify the generalization ability of the models, we also conducted additional experiments using the JNU dataset under a consistent training protocol. The experimental setup maintained uniform parameters across all models, including a stepwise learning rate scheduler with an initial learning rate of 0.005, L2 regularization to prevent overfitting, and a learning rate that decreased by 0.001 every 200 times throughout the 500 iterations of training. The results of the quantitative analysis of the classification performance metrics are presented in Table 4, and the corresponding training confusion matrix is shown in Figure 12 to visualize the results.

Table 4.
Analysis of ablation experiment results.
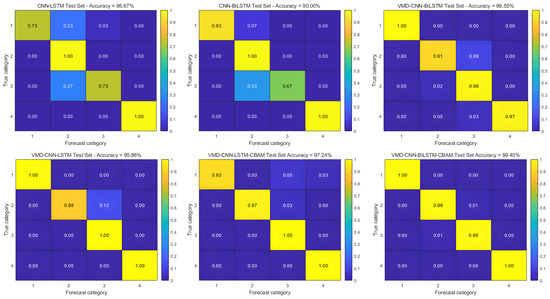
Figure 12.
Confusion matrix for JNU dataset.
It can be concluded that in the dataset of Jiangnan University, the classification result of the VMD-CNN-BILSTM-CBAM model has an accuracy of 99.40% and an F1 score of 0.995, which indicates that the diagnostic accuracy of this model for different datasets is relatively high, and at the same time, it better reflects the model’s ability of recognizing a few classes, and its generalization ability is relatively good.
4.3. Self-Constructed Data Validation
In order to further test the effectiveness of the VMD-CNN-BILSTM-CBAM model on the bearing fault diagnosis and its other generalization ability, the author independently designed a bearing data-acquisition experimental platform, as shown in Figure 13, which consists of a motor controller, a motor, a coupling, a shaft support, a bearing, a vibration sensor, and a vibration signal acquisition card. The bearing model is a 6001-SKF deep groove ball bearing, with an empty load, the acquisition frequency is 10,240 Hz, the acquisition time is 10 s, and the bearing rotational speed is 1200 r/min. The same data overlap segmentation method is used, and the acquired bearing fault data are divided into the training set and the test set according to the ratio of 70% and 30%. Since there is also one fault size for each fault type, there are also a total of four labels. The specific data are shown in Table 5.

Figure 13.
Bearing data acquisition platform.

Table 5.
Bearing experimental data.
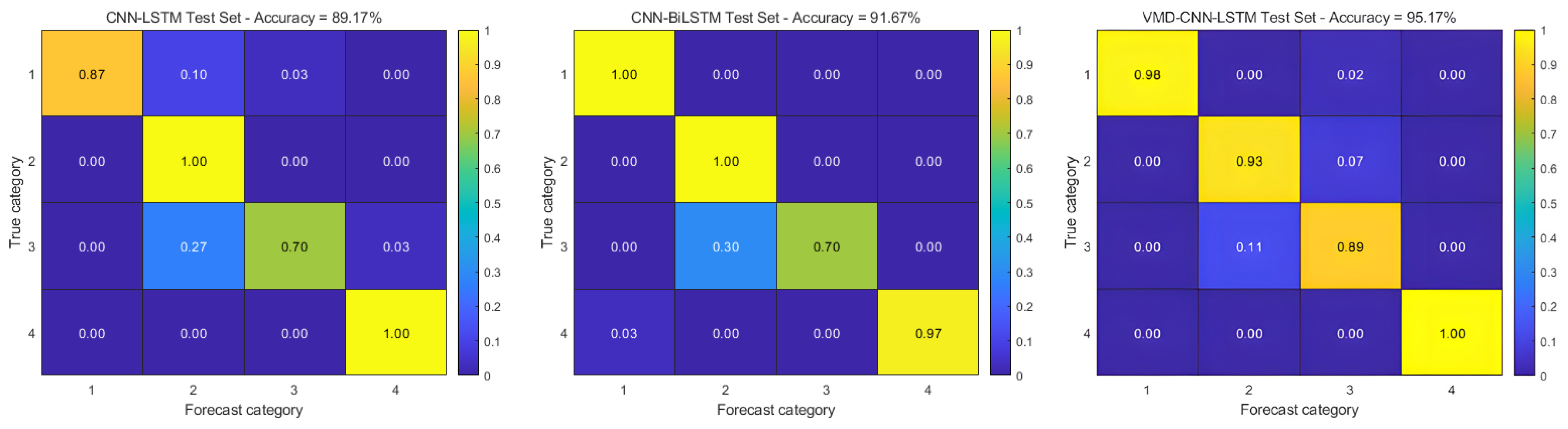
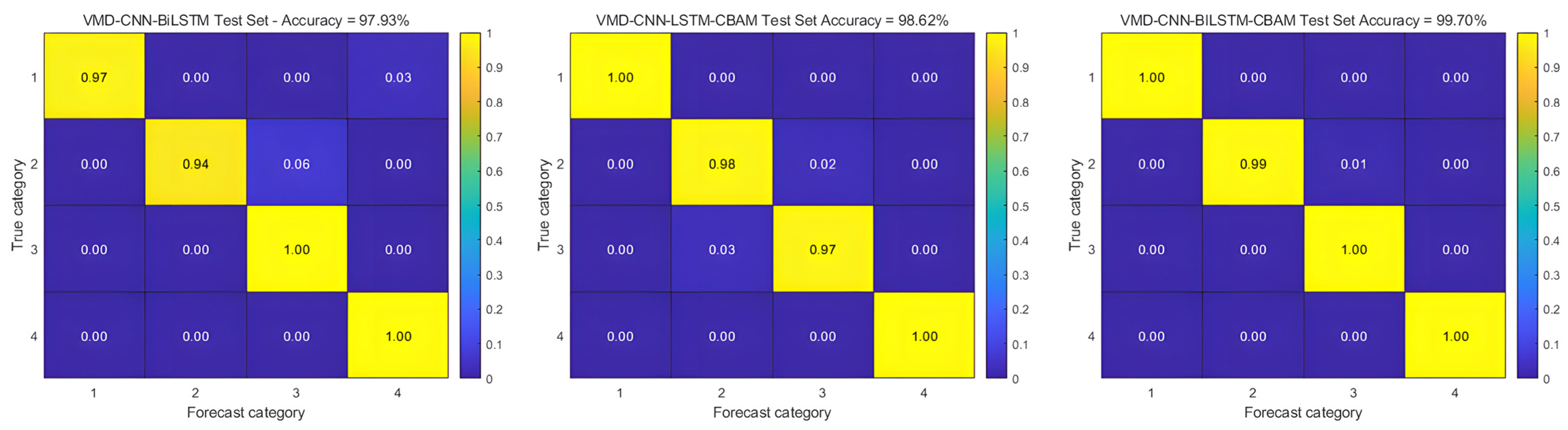
Figure 14 demonstrates the classification performance through confusion matrix visualization, while Table 6 provides a detailed quantitative analysis of the prediction results. The experimental results show that the integrated VMD-CNN-BiLSTM-CBAM framework achieves a remarkable diagnostic accuracy of 99.70% and an F1 score of 0.998, confirming its excellent fault-identification capability and strong generalization performance across a wide range of operating conditions; however, because of the increased computational complexity of the model with respect to the temporal sequences due to the bi-directional long and short-term memory network, the computational time of the model is increased, and this is an area for future improvement.
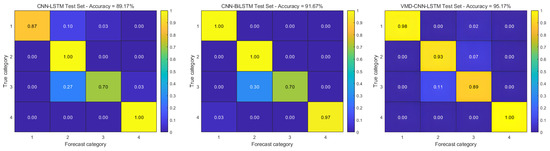

Figure 14.
Confusion matrix for the measured dataset.

Table 6.
Analysis of ablation experiment results.
5. Conclusions
This study addresses the challenge of bearing fault diagnosis and classification by proposing a novel integrated deep learning approach (VMD-CNN-BILSTM-CBAM). A comparative analysis reveals its enhanced diagnostic precision, achieving accuracies of 99.76%, 99.40%, and 99.70% across distinct experimental datasets, thereby outperforming conventional methodologies.
The signal processing begins with optimized FCSSA-VMD decomposition, enhancing the model’s noise resistance through refined feature extraction. A bidirectional LSTM (BILSTM) architecture is implemented to analyze sequential data in both temporal directions, effectively capturing complex temporal dependencies. Further, the framework integrates dual attention mechanisms (CBAM), merging channel-wise feature weighting with spatial feature prioritization to optimize information utilization. Experimental validation across multiple datasets confirms the model’s superior generalization performance, while its structural innovations establish a valuable reference framework for advancing bearing fault diagnostic methodologies. However, the model also has some limitations. For example, the calculation time will be longer, which is also part of the future improvement.
Subsequent studies may extend this framework by incorporating non-bearing operational datasets and evaluating its generalization capacity and noise robustness across diverse operational environments, thereby enhancing its adaptability for broader industrial applications.
Author Contributions
Conceptualization, L.L.; Methodology, L.L.; Software, L.L.; Validation, L.L.; Formal Analysis, L.L.; Investigation, L.L.; Resources, L.L.; Data Curation, L.L.; Writing—Original Draft, L.L.; Writing—Review and Editing, L.L.; Visualization, L.L.; Supervision, B.Y.; Project Administration, B.Y. and S.C.; Funding Acquisition, B.Y. and S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Zhejiang Provincial ‘Pioneer’ and ‘Leading Wild Goose’ Research and Development Project, grant number 2023C02008, and the Zhejiang Provincial ‘Pioneer & Leading Wild Goose + X’ Research and Development Project, grant number 2024C04037.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hoang, D.T.; Kang, H.J. A Survey on Deep Learning Based Bearing Fault Diagnosis. Neurocomputing 2019, 335, 327–335. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. A Review on Signal Processing Techniques Utilized in the Fault Diagnosis of Rolling Element Bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Abid, A.; Khan, M.T.; Iqbal, J. A Review on Fault Detection and Diagnosis Techniques: Basics and Beyond. Artif. Intell. Rev. 2021, 54, 3639–3664. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Plakias, S.; Chasiotis, I.D. Extracting Spatially Global and Local Attentive Features for Rolling Bearing Fault Diagnosis in Electrical Machines Using Attention Stream Networks. IET Electr. Power Appl. 2021, 15, 903–915. [Google Scholar] [CrossRef]
- Borré, A.; Seman, L.O.; Camponogara, E.; Stefenon, S.F.; Mariani, V.C.; Coelho, L.D.S. Machine Fault Detection Using a Hybrid CNN-LSTM Attention-Based Model. Sensors 2023, 23, 4512. [Google Scholar] [CrossRef]
- Keshun, Y.; Puzhou, W.; Yingkui, G. Towards Efficient and Interpretative Rolling Bearing Fault Diagnosis via Quadratic Neural Network with Bi-LSTM. IEEE Internet Things J. 2024, 11, 23002–23019. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, Q.; Tang, X.; Zhao, S.; Lu, X. A Novel Fault Diagnosis Method Based on CNN and LSTM and Its Application in Fault Diagnosis for Complex Systems. Artif. Intell. Rev. 2022, 55, 1289–1315. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Qian, J. Fault Diagnosis of Hydro-Turbine via the Incorporation of Bayesian Algorithm Optimized CNN-LSTM Neural Network. Energy 2024, 290, 130326. [Google Scholar] [CrossRef]
- Song, B.; Liu, Y.; Fang, J.; Liu, W.; Zhong, M.; Liu, X. An Optimized CNN-BiLSTM Network for Bearing Fault Diagnosis Under Multiple Working Conditions with Limited Training Samples. Neurocomputing 2024, 574, 127284. [Google Scholar] [CrossRef]
- Xu, Z.; Mei, X.; Wang, X.; Yue, M.; Jin, J.; Yang, Y.; Li, C. Fault Diagnosis of Wind Turbine Bearing Using a Multi-Scale Convolutional Neural Network with Bidirectional Long Short Term Memory and Weighted Majority Voting for Multi-Sensors. Renew. Energy 2022, 182, 615–626. [Google Scholar] [CrossRef]
- Dong, Z.; Zhao, D.; Cui, L. An Intelligent Bearing Fault Diagnosis Framework: One-Dimensional Improved Self-Attention-Enhanced CNN and Empirical Wavelet Transform. Nonlinear Dyn. 2024, 112, 6439–6459. [Google Scholar] [CrossRef]
- Xue, Y.; Dou, D.; Yang, J. Multi-Fault Diagnosis of Rotating Machinery Based on Deep Convolution Neural Network and Support Vector Machine. Measurement 2020, 156, 107571. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Li, B.; Ding, H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Optimization Algorithms; Academic Press: London, UK, 2020; pp. 45–80. [Google Scholar]
- Dehghani, M.; Trojovský, P. Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front. Mech. Eng. 2023, 8, 1126450. [Google Scholar] [CrossRef]
- Chang, Y.; Bao, G. Enhancing rolling bearing fault diagnosis in motors using the OCSSA-VMD-CNN-BiLSTM model: A novel approach for fast and accurate identification. IEEE Access 2024, 12, 78463–78479. [Google Scholar] [CrossRef]
- Zhu, R.; Li, T.; Tang, B. Research on short-term photovoltaic power generation forecasting model based on multi-strategy improved squirrel search algorithm and support vector machine. Sci. Rep. 2024, 14, 14348. [Google Scholar] [CrossRef]
- Ruan, D.; Wang, J.; Yan, J.; Gühmann, C. CNN parameter design based on fault signal analysis and its application in bearing fault diagnosis. Adv. Eng. Inform. 2023, 55, 101877. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A Deep Convolutional Neural Network with New Training Methods for Bearing Fault Diagnosis under Noisy Environment and Different Working Load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Qin, C.; Chen, L.; Cai, Z.; Liu, M.; Jin, L. Long short-term memory with activation on gradient. Neural Netw. 2023, 164, 135–145. [Google Scholar] [CrossRef]
- Zeng, J.; Qiao, W. Support vector machine-based short-term wind power forecasting. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–8. [Google Scholar]
- Nacer, S.M.; Nadia, B.; Abdelghani, R.; Mohamed, B. A novel method for bearing fault diagnosis based on BiLSTM neural networks. Int. J. Adv. Manuf. Technol. 2023, 125, 1477–1492. [Google Scholar] [CrossRef]
- Rathore, M.S.; Harsha, S.P. An attention-based stacked BiLSTM framework for predicting remaining useful life of rolling bearings. Appl. Soft Comput. 2022, 131, 109765. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Qin, Y.; Chen, D.; Xiang, S.; Zhu, C. Gated dual attention unit neural networks for remaining useful life prediction of rolling bearings. IEEE Trans. Ind. Inform. 2020, 17, 6438–6447. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Z.; Chen, Y.; Jin, Y.; Bai, G. Selective kernel convolution deep residual network based on channel-spatial attention mechanism and feature fusion for mechanical fault diagnosis. ISA Trans. 2023, 133, 369–383. [Google Scholar] [CrossRef] [PubMed]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64, 100–131. [Google Scholar] [CrossRef]
- Li, K.; Ping, X.; Wang, H.; Chen, P.; Cao, Y. Sequential fuzzy diagnosis method for motor roller bearing in variable operating conditions based on vibration analysis. Sensors 2013, 13, 8013–8804. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).