Simulation Analysis of an Electric Locomotive with a Hydraulic Wheelset Guidance System for Improved Performance in Curved Tracks
Abstract
1. Introduction
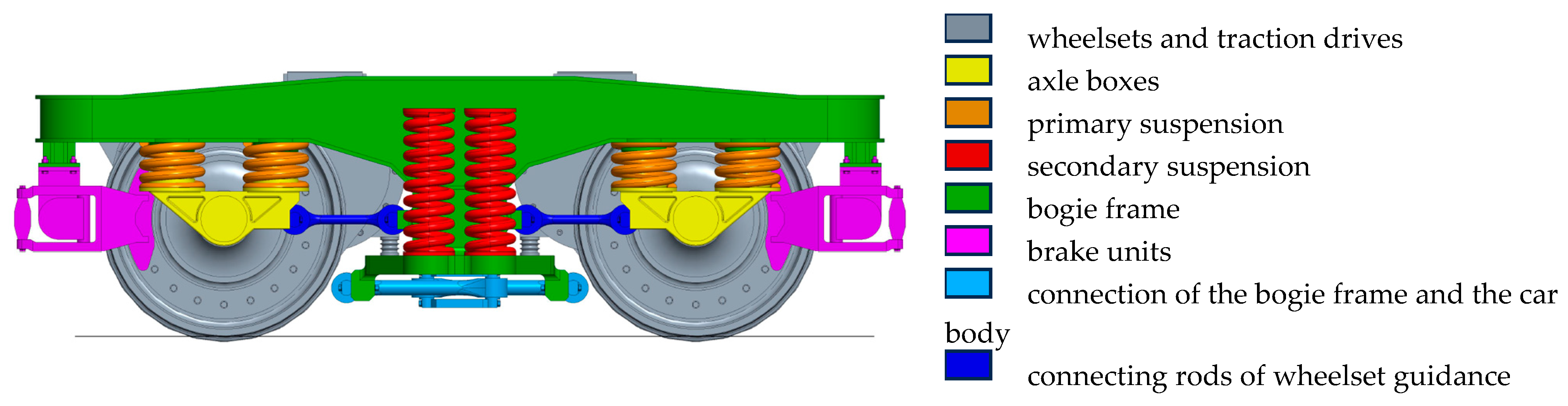
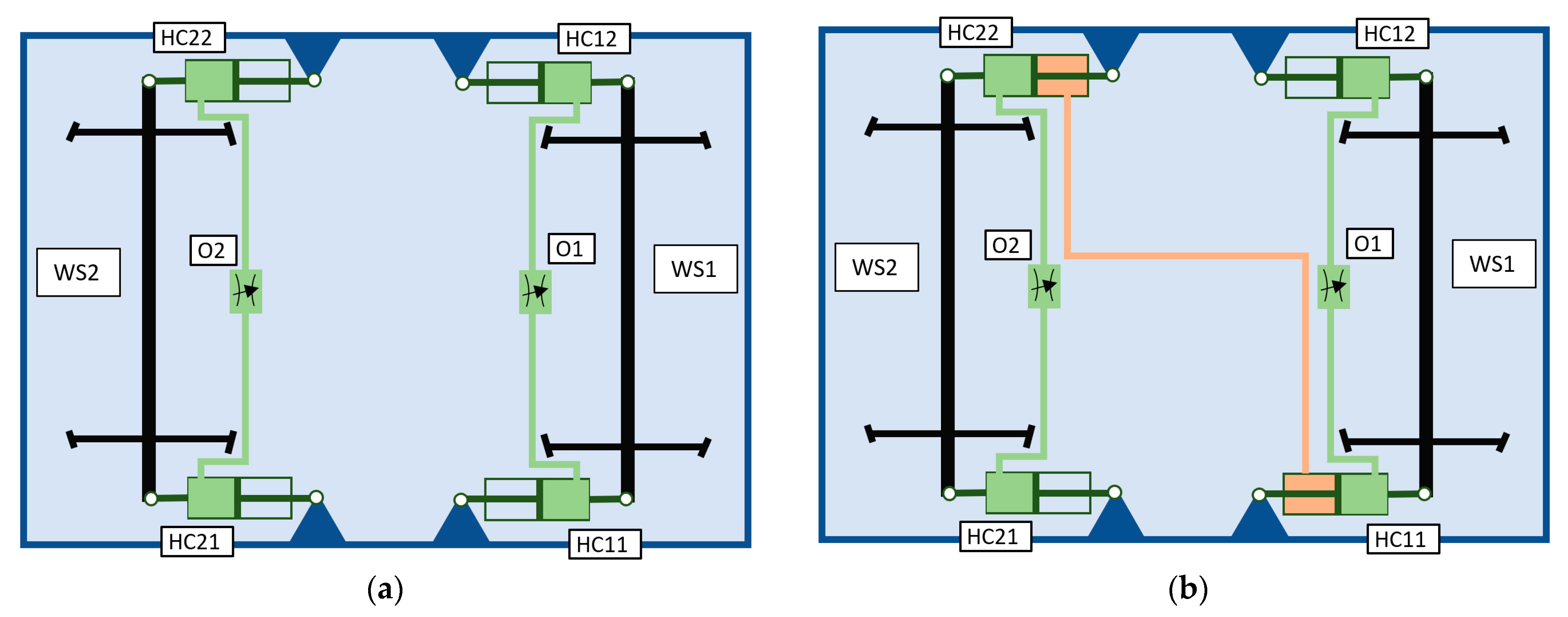
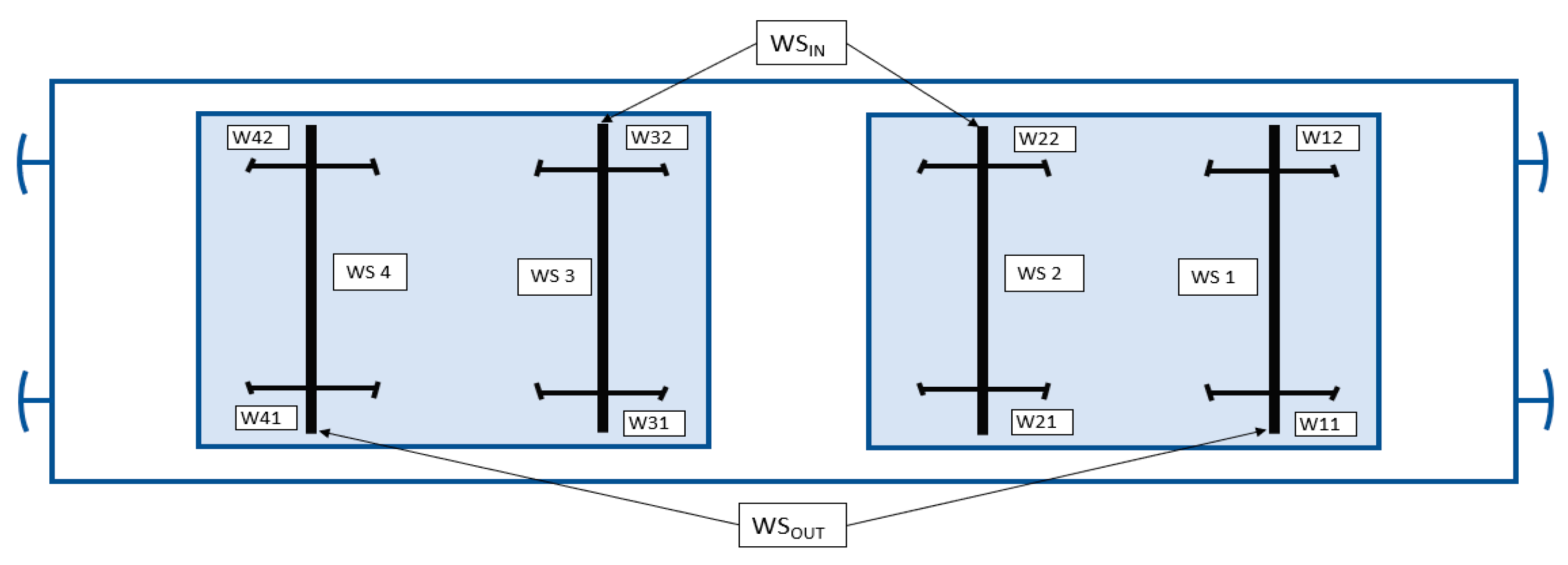
2. Description of the Analysed Vehicle and Its Simulation Model
3. Simulation Results
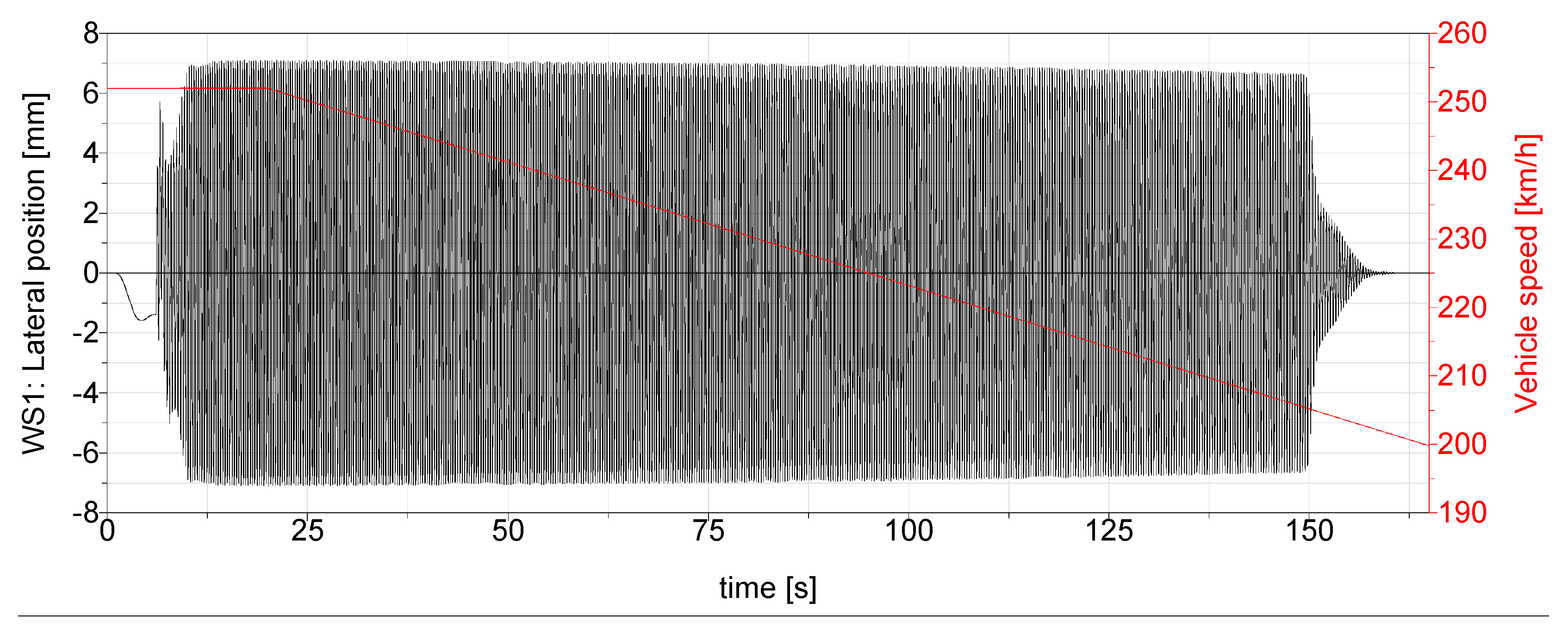
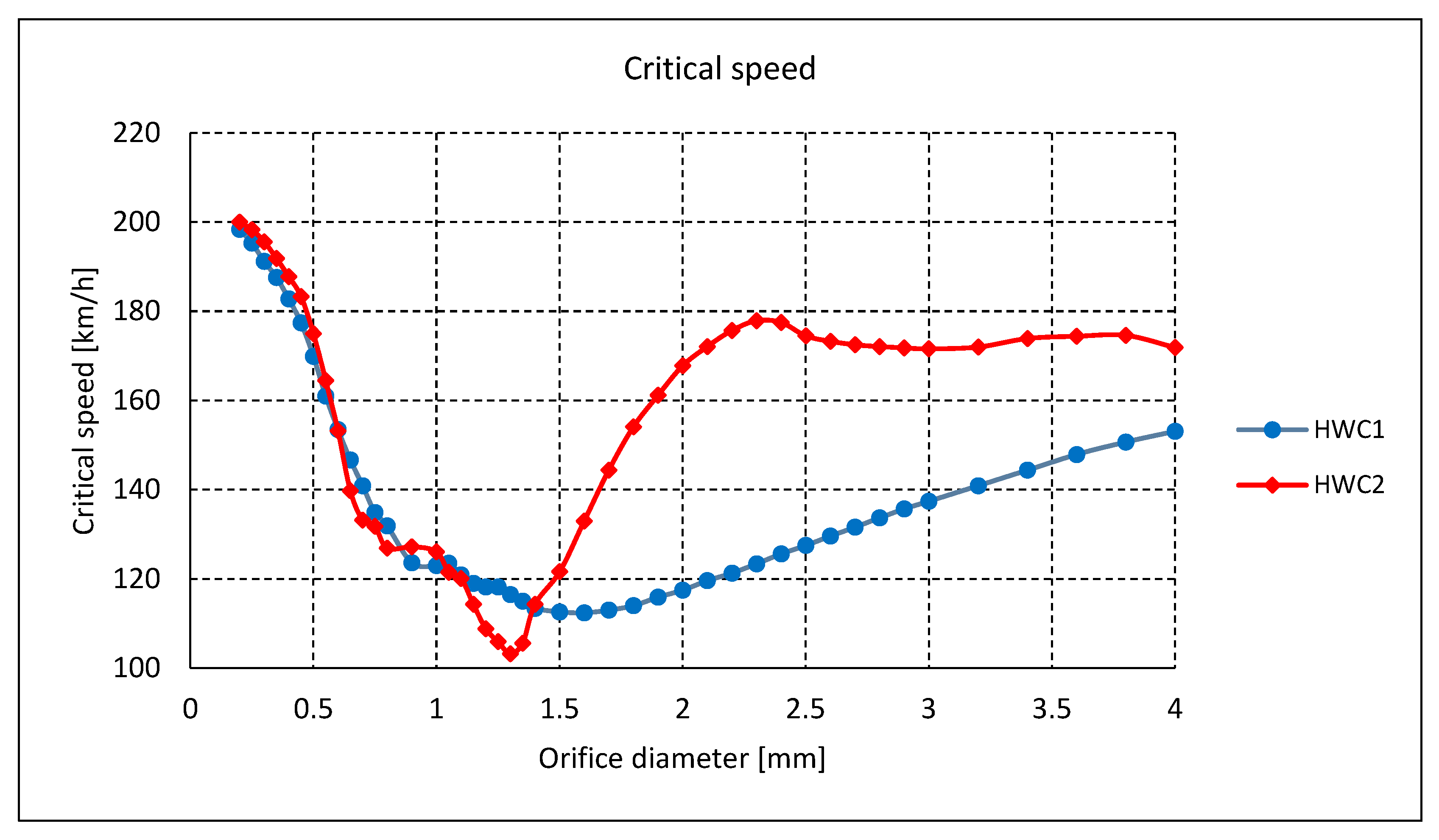
3.1. High-Speed Stability
3.2. Curving Behavior
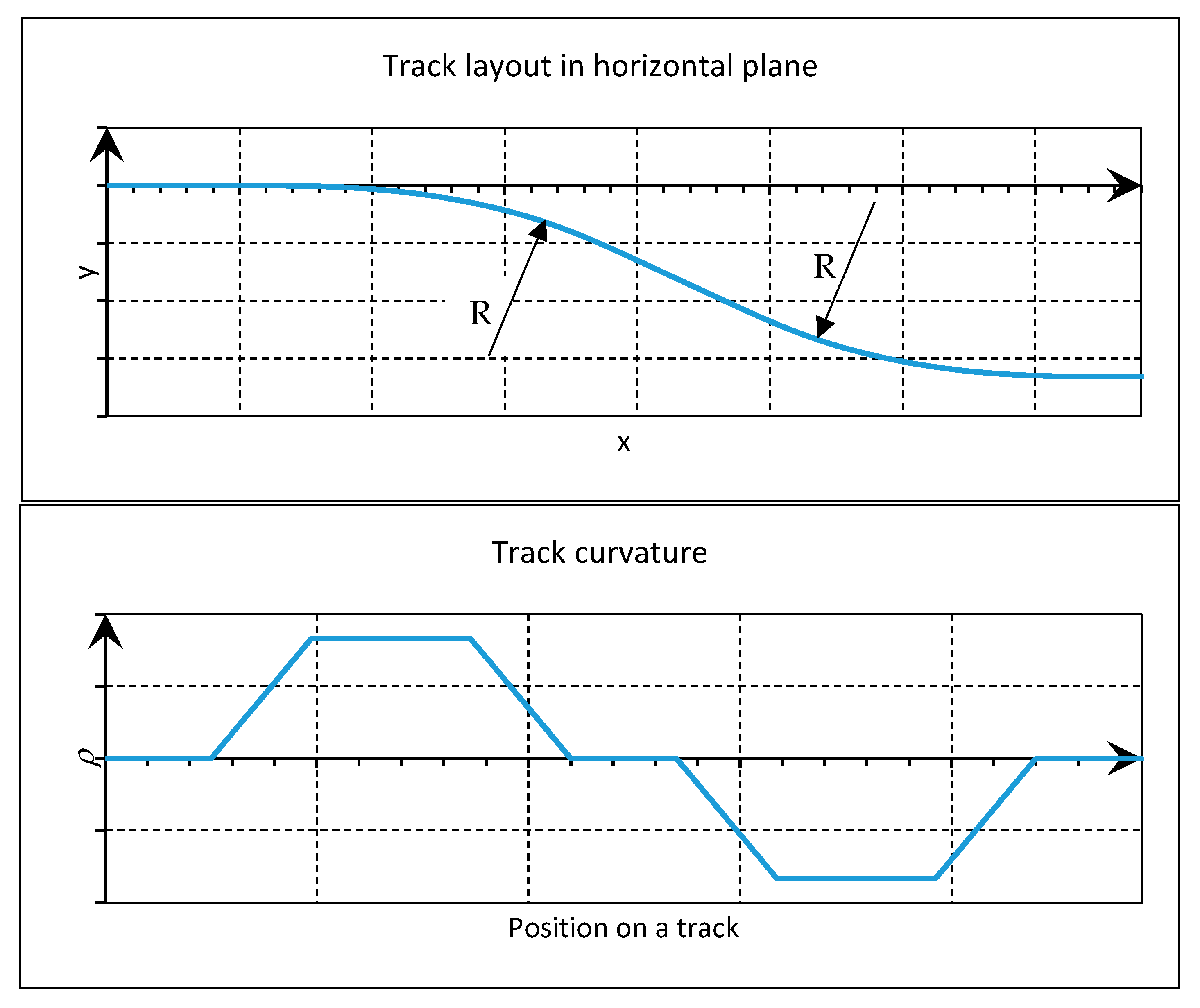
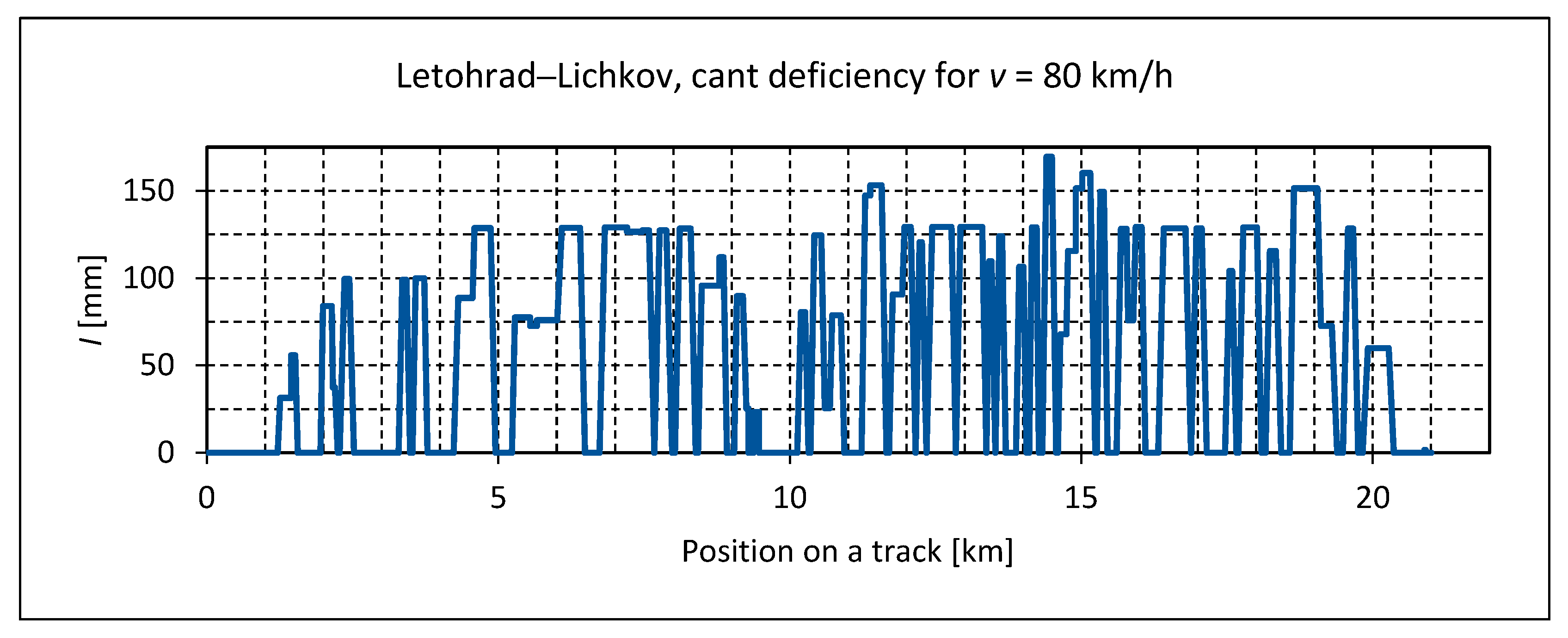
3.3. Running in a Real Track
4. Conclusions
- The critical speed of a vehicle equipped with the proposed hydraulic system is lower compared to a standard vehicle with otherwise identical parameters;
- The diameter of the orifice significantly influences the flow rate of the hydraulic fluid, affecting vehicle stability and critical speed;
- The expected advantage of the HWC2 arrangement in achieving a higher critical speed compared to the HWC1 arrangement was confirmed, particularly for larger orifice diameters (od > 2 mm). In the range of small orifice diameters (od = 0.2 to 1 mm), the critical speed of both arrangements is very similar;
- With an orifice diameter of od = 0.35 mm, the critical speed of the vehicle was 187.6 km/h for HWC1 and 191.9 km/h for HWC2. The critical speed of a standard vehicle with the same parameters was 202.4 km/h. Thus, the reduction in critical speed is 7.3% for HWC1 and 5.2% for HWC2;
- Simulations of passing through curves of different radii with minimal length of the transition sections showed that, for the applied hydraulic fluid and hydraulic cylinder sizes, an orifice diameter of od = 0.35 mm is sufficient for the timely adaptation of the wheelset position in the transition track sections;
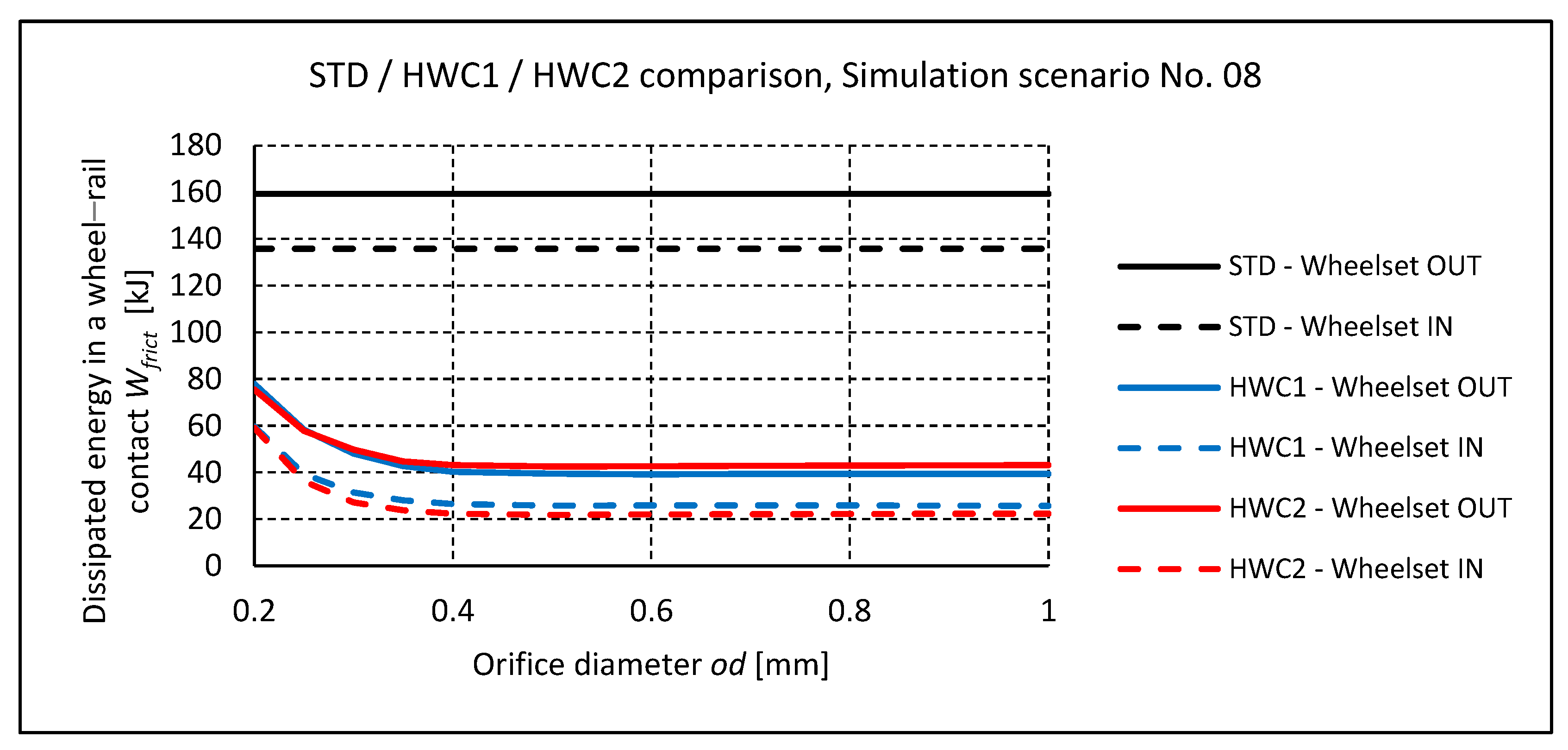
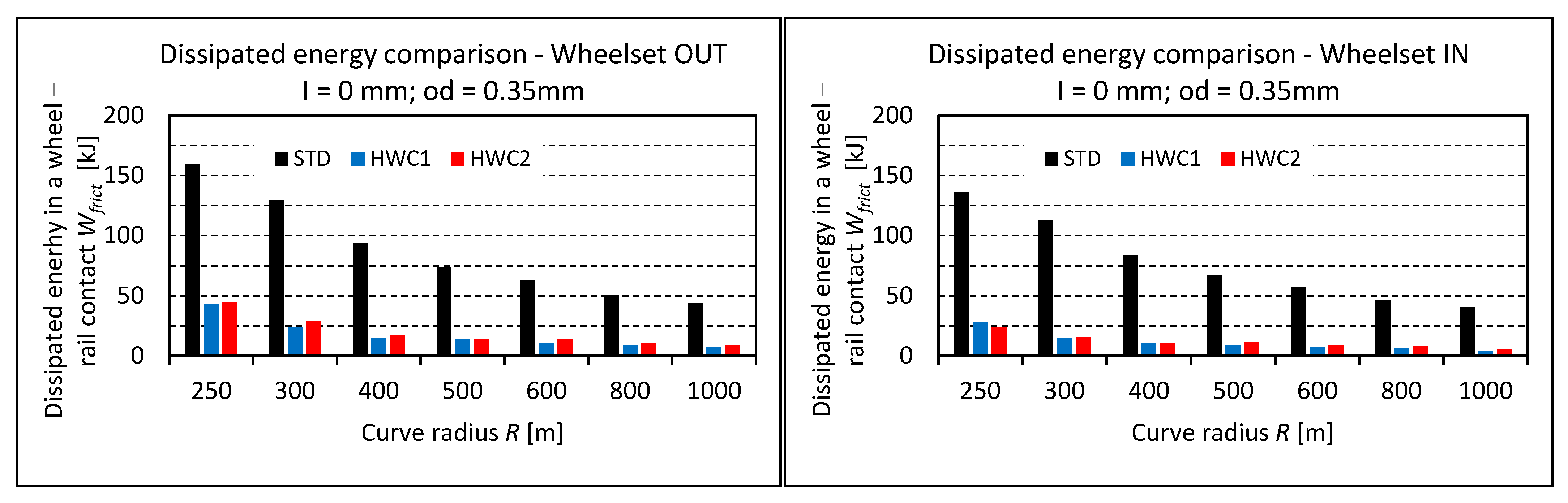
- Simulations of running on a 20 km section of a real track with a number of curved sections demonstrated a significant benefit of both hydraulic systems in reducing frictional work in wheel–rail contacts, thereby decreasing wheel and rail wear. This reduction reaches 75–82% on the outer wheelsets and 79–87% on the inner wheelsets for HWC1 and 72–79% on the outer wheelsets and 79–87% on the inner wheelsets for HWC2. As the track irregularities increase, the benefit of the hydraulic system decreases, but even for a high level of irregularities, it does not drop below 70%;
- The benefit of the hydraulic wheelset guidance systems in reducing the frictional work at the wheel–rail contacts is relatively lower under deteriorated adhesion conditions compared to a dry rail. Nevertheless, there is still a significant improvement. The reduction in frictional work ranges from 41 to 48% for both arrangements of the hydraulic system.
Funding
Data Availability Statement
Conflicts of Interest
References
- Andersson, E.; Stichel, S.; Orvnäs, A.; Persson, R. How to Find a Compromise between Track Friendliness and the Ability to Run at High Speed. In Proceedings of the First International Conference on Railway Technology: Research, Development and Maintenance; Civil-Comp Press: Stirlingshire, Scotland, 2012; p. 68. [Google Scholar]
- Ye, Y.; Sun, Y.; Dongfang, S.; Shi, D.; Hecht, M. Optimizing wheel profiles and suspensions for railway vehicles operating on specific lines to reduce wheel wear: A case study. Multibody Syst. Dyn. 2021, 51, 91–122. [Google Scholar] [CrossRef]
- Polach, O. Curving and Stability Optimisation of Locomotive Bogies using Interconnected wheelsets. Veh. Syst. Dyn. 2004, 41, 53–62. [Google Scholar]
- Zhang, Z.; Zhou, J.; Sun, W.; Thompson, D.; Shen, G.; Gong, D.; Wang, Z.; Wang, T.; Li, X. Analytical study and evaluation of self-steering ability of elastically constrained wheelsets under traction/braking conditions. Veh. Syst. Dyn. 2024, 63, 333–350. [Google Scholar] [CrossRef]
- Carballeira, J.; Baeza, L.; Rovira, A.; García, E. Technical characteristics and dynamic modelling of Talgo trains. Veh. Syst. Dyn. 2008, 46, 301–316. [Google Scholar] [CrossRef]
- Shimokawa, Y.; Mizuno, M. Development of the New Concept Steering Bogie. Nippon. Steel Sumitomo Met. Tech. Rep. 2013, 41–47. [Google Scholar]
- Hecht, M. Wear and energy-saving freight bogie designs with rubber primary springs: Principles and experiences. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 105–110. [Google Scholar] [CrossRef]
- Megna, G.; Bracciali, A. Gearless Track-Friendly Metro with Guided Independently Rotating Wheels. Urban Rail Transit 2021, 7, 285–300. [Google Scholar] [CrossRef]
- Fu, B.; Giossi, R.; Persson, R.; Stichel, S.; Bruni, S.; Goodall, R. Active suspension in railway vehicles: A literature survey. Railw. Eng. Sci. 2020, 28, 3–35. [Google Scholar] [CrossRef]
- Farhat, N.; Ward, C.; Goodall, R.; Dixon, R. The benefits of mechatronically-guided railway vehicles: A multi-body physics simulation study. Mechatronics 2018, 51, 115–126. [Google Scholar] [CrossRef]
- Persson, R.; Goodall, R.; Sasaki, K. Carbody tilting—Technologies and benefits. Veh. Syst. Dyn. 2009, 47, 949–981. [Google Scholar] [CrossRef]
- Persson, R. Tilting Trains: Benefits and Motion Sickness. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2010, 224, 513–522. [Google Scholar] [CrossRef]
- Park, J.; Yang, H. Design of a lateral active suspension controller for railway vehicles: A focus on ride comfort and perturbations. J. Mech. Sci. Technol. 2023, 37, 5781–5788. [Google Scholar] [CrossRef]
- Park, J.; Shin, Y.; Hur, H.; You, W. A practical approach to active lateral suspension for railway vehicles. Meas. Control 2019, 52, 1195–1209. [Google Scholar] [CrossRef]
- Mei, T.; Goodall, R. Recent Development in Active Steering of Railway Vehicles. Veh. Syst. Dyn. 2003, 39, 415–436. [Google Scholar] [CrossRef]
- Perez, J.; Goodall, R. Control strategies for active steering of bogie-based railway vehicles. Control Eng. Pract. 2002, 10, 1005–1012. [Google Scholar] [CrossRef]
- Hur, H.; Shin, Y.; Ahn, D. Analysis on Steering Performance of Active Steering Bogie According to Steering Angle Control on Curved Section. Appl. Sci. 2020, 10, 4407. [Google Scholar] [CrossRef]
- Giossi, R.; Persson, R.; Stichel, S. Improved curving performance of an innovative two-axle vehicle: A reasonable feedforward active steering approach. Veh. Syst. Dyn. 2022, 60, 516–539. [Google Scholar] [CrossRef]
- Wei, J.; Lu, Z.; Yin, Z.; Jing, Z. Multiagent Reinforcement Learning for Active Guidance Control of Railway Vehicles with Independently Rotating Wheels. Appl. Sci. 2024, 14, 1677. [Google Scholar] [CrossRef]
- Fu, B.; Bruni, S. Fault-tolerant design and evaluation for a railway bogie active steering system. Veh. Syst. Dyn. 2022, 60, 810–834. [Google Scholar] [CrossRef]
- Podolski, M.; Słabuszewski, M.; Firlik, B.; Staśkiewicz, T. Bogie Steering System Improving Alignment of the Urban Railway Vehicle in a Track. Eng. Trans. 2018, 66, 375–390. [Google Scholar] [CrossRef]
- Zhou, Y.; Tian, Q.; Hecht, M. Application of Hydraulic Arm Bushings with Frequency-Dependent Stiffness to Compromise Hunting Stability and Curve Negotiation Performance for a Passenger Coach. J. Vib. Eng. Technol. 2024, 12, 8839–8849. [Google Scholar] [CrossRef]
- Qu, C.; Li, Y.; Jiang, J.; Tucker, G.; Neild, S.; Smith, M.; Gleeson, A.; Odetunde, S.; Muhamedsalih, Y. Reducing wheel–rail surface damage by incorporating hydraulic damping in the Bogie primary suspension. Veh. Syst. Dyn. 2023, 61, 1916–1936. [Google Scholar] [CrossRef]
- Evans, J. Application of the hall hydraulic radial arm bush to a 200 km/h inter-city coach. In Proceedings of the International Symposium on Dynamics of Vehicle on Road and Tracks, IAVSD, Manchester, UK, 14–19 August 2011; p. 6. [Google Scholar]
- Kumar, P.; Park, S.; Zhang, Y.; Jo, S.; Kim, H.; Kim, T. A Review of Hydraulic Cylinder Faults, Diagnostics, and Prognostics. Int. J. Precis. Eng. Manuf.-Green Technol. 2024, 11, 1637–1661. [Google Scholar] [CrossRef]
- True, H. Multiple attractors and critical parameters and how to find them numerically: The right, the wrong and the gambling way. Veh. Syst. Dyn. 2013, 51, 443–459. [Google Scholar] [CrossRef]
- Polach, O. On non-linear methods of bogie stability assessment using computer simulations. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2006, 220, 13–27. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, W.; Lewis, R.; Yan, W.; Lewis, S.; Ding, H. A Review on Wear Between Railway Wheels and Rails Under Environmental Conditions. J. Tribol. 2019, 141, 120801. [Google Scholar] [CrossRef]
- Smith, A.; Iwnicki, S.; Kaushal, A.; Odolinski, K.; Wheat, P. Estimating the relative cost of track damage mechanisms: Combining economic and engineering approaches. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 620–636. [Google Scholar] [CrossRef]
- Magelli, M.; Zampieri, N. Calculation of Wear of Railway Wheels with Multibody Codes: Benchmarking of the Modelling Choices. Machines 2024, 12, 644. [Google Scholar] [CrossRef]
- Lewisa, R.; Dwyer-Joyce, R. Wear mechanisms and transitions in railway wheel steels. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2004, 218, 467–478. [Google Scholar] [CrossRef]
- de Paula Pacheco, P.; Magelli, M.; Lopes, M.; Correa, P.; Zampieri, N.; Bosso, N.; dos Santos, A. The effectiveness of different wear indicators in quantifying wear on railway wheels of freight wagons. Railw. Eng. Sci. 2024, 32, 307–323. [Google Scholar] [CrossRef]
- Krause, H.; Poll, G. Wear of wheel-rail surfaces. Wear 1986, 113, 103–122. [Google Scholar] [CrossRef]
- N.N.: Benchmark Problem Results and Assessment. In Bogies with Steered or Steering Wheelsets; ORE (ERRI) B 176/3, DT290; ORE (ERRI): Utrecht, The Netherlands, 1993.
- White, B.; Lewis, R.; Fletcher, D.; Harrison, T.; Hubbard, P.; Ward, C. Rail-wheel friction quantification and its variability under lab and field trial conditions. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2024, 238, 569–579. [Google Scholar] [CrossRef]
- Alonso, A.; Giménez, J.; Gomez, E. Yaw damper modelling and its influence on railway dynamic stability. Veh. Syst. Dyn. 2011, 49, 1367–1387. [Google Scholar] [CrossRef]
- Isacchi, G.; Ripamonti, F.; Corsi, M.; Dongen, T. Modelling of Innovative Yaw Dampers for Railway Vehicles. In Proceedings of the 15th World Congress on Computational Mechanics (WCCM-XV) and 8th Asian Pacific Congress on Computational Mechanics (APCOM-VIII), Yokohama, Japan, 31 July–5 August 2022. [Google Scholar]
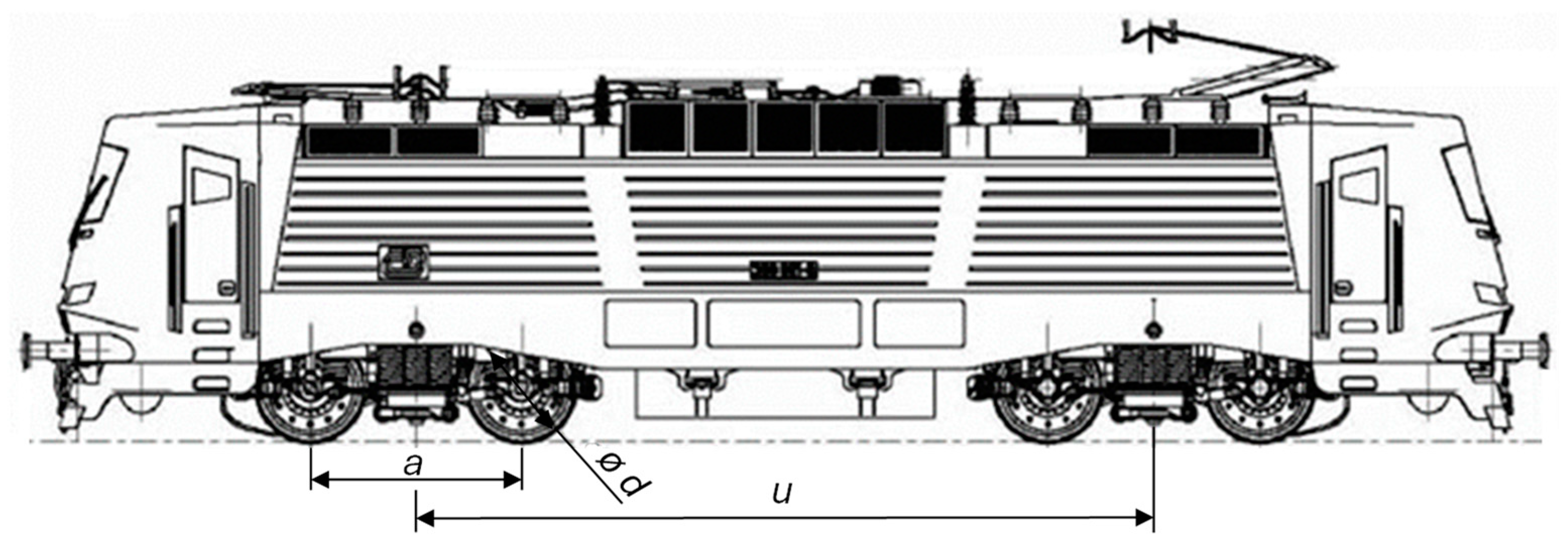





| Parameter | Unit | Value | |
|---|---|---|---|
| Overall weight | mv | [kg] | 90,200 |
| Maximal speed | vmax | [km/h] | 200 |
| Track gauge | G | [mm] | 1,435 |
| Bogie wheelbase | a | [mm] | 2,500 |
| Bogie to bogie distance | u | [mm] | 8,700 |
| Wheel diameter | dk | [mm] | 1,250 |
| Connecting rod stiffness | kvd | [N/mm] | 85,000 |
| Primary suspension stiffness transverse | k1x, k1y | [N/mm] | 3,800 |
| Primary suspension stiffness vertical | k1z | [N/mm] | 2,200 |
| Secondary suspension stiffness longitudinal | k2x | [N/mm] | 300 |
| Secondary suspension stiffness lateral | k2y | [N/mm] | 300 |
| Secondary suspension stiffness vertical | k2z | [N/mm] | 1,000 |
| Simulation Scenario No | R | I | v | Lt |
|---|---|---|---|---|
| [-] | [m] | [mm] | [kmh−1] | [m] |
| 01 | 250 | 0 | 56.5 | 85.0 |
| 02 | 300 | 0 | 61.9 | 95.0 |
| 03 | 400 | 0 | 71.5 | 110.0 |
| 04 | 500 | 0 | 79.9 | 120.0 |
| 05 | 600 | 0 | 87.6 | 130.0 |
| 06 | 800 | 0 | 101.1 | 150.0 |
| 07 | 1000 | 0 | 113.0 | 170.0 |
| 08 | 250 | 150 | 80.2 | 85.0 |
| 09 | 300 | 150 | 87.9 | 95.0 |
| 10 | 400 | 150 | 101.5 | 110.0 |
| 11 | 500 | 150 | 113.4 | 120.0 |
| 12 | 600 | 150 | 124.3 | 130.0 |
| 13 | 800 | 150 | 143.5 | 150.0 |
| 14 | 1000 | 150 | 160.4 | 170.0 |
| 15 | 250 | −100 | 33.0 | 85.0 |
| 16 | 300 | −100 | 36.1 | 95.0 |
| 17 | 400 | −100 | 41.7 | 110.0 |
| 18 | 500 | −100 | 46.7 | 120.0 |
| 19 | 600 | −100 | 51.1 | 130.0 |
| 20 | 800 | −100 | 59.0 | 150.0 |
| 21 | 1000 | −100 | 66.0 | 170.0 |
| Arrangement | Orifice Diameter od [mm] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | ||
| HWC1 | WSOUT | 74.7% | 81.9% | 84.5% | 85.6% | 85.7% | 85.7% | 85.7% | 85.6% | 85.3% | 84.0% | 83.9% |
| WSIN | 78.6% | 85.1% | 87.2% | 87.9% | 88.0% | 87.9% | 87.7% | 87.5% | 87.3% | 85.9% | 85.6% | |
| HWC2 | WSOUT | 76.0% | 80.9% | 82.4% | 83.1% | 83.2% | 83.2% | 83.0% | 83.0% | 82.9% | 81.9% | 81.4% |
| WSIN | 79.8% | 85.3% | 87.0% | 87.6% | 87.6% | 87.5% | 87.3% | 87.2% | 87.1% | 86.0% | 85.4% | |
| Scenario No | Dissipated Energy [kJ] | Improvement Over STD [%] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| STD | HWC1 | HWC2 | HWC1 | HWC2 | ||||||
| Wfrict,OUT | Wfrict,IN | Wfrict,OUT | Wfrict,IN | Wfrict,OUT | Wfrict,IN | ΔWfrict,OUT | ΔWfrict,IN | ΔWfrict,OUT | ΔWfrict,IN | |
| 01 | 173.3 | 152.3 | 42.1 | 30.2 | 42.5 | 25.0 | 75.7 | 82.6 | 75.5 | 85.5 |
| 02 | 142.7 | 127.4 | 23.8 | 16.3 | 27.2 | 14.1 | 83.3 | 88.5 | 80.9 | 90.1 |
| 03 | 103.7 | 93.6 | 10.5 | 7.1 | 13.5 | 6.5 | 89.9 | 93.1 | 86.9 | 93.7 |
| 04 | 80.5 | 73.6 | 7.2 | 4.7 | 8.2 | 4.6 | 91.0 | 94.2 | 89.8 | 94.2 |
| 05 | 66.9 | 61.6 | 5.2 | 3.7 | 6.4 | 4.1 | 92.3 | 94.4 | 90.4 | 93.9 |
| 06 | 51.3 | 47.7 | 3.5 | 2.3 | 4.6 | 3.3 | 93.1 | 95.4 | 91.0 | 93.5 |
| 07 | 42.6 | 39.7 | 2.0 | 1.8 | 3.8 | 3.3 | 95.3 | 95.7 | 91.2 | 92.2 |
| 08 | 159.3 | 135.8 | 42.7 | 28.0 | 44.7 | 23.7 | 73.2 | 82.4 | 71.9 | 85.1 |
| 09 | 129.2 | 112.6 | 23.9 | 14.7 | 29.1 | 15.4 | 81.5 | 88.6 | 77.5 | 88.1 |
| 10 | 93.6 | 83.4 | 14.8 | 10.4 | 17.4 | 10.6 | 84.2 | 88.9 | 81.4 | 88.6 |
| 11 | 73.7 | 66.6 | 14.2 | 9.0 | 14.0 | 11.2 | 80.8 | 87.8 | 81.0 | 84.9 |
| 12 | 62.5 | 57.0 | 10.6 | 7.5 | 14.1 | 9.0 | 83.0 | 87.9 | 77.5 | 85.6 |
| 13 | 50.2 | 46.4 | 8.4 | 6.2 | 10.3 | 7.8 | 83.4 | 87.6 | 79.5 | 84.6 |
| 14 | 43.7 | 40.7 | 6.8 | 4.3 | 9.1 | 5.7 | 84.4 | 90.1 | 79.2 | 86.8 |
| 15 | 189.2 | 163.1 | 49.1 | 40.5 | 48.6 | 35.1 | 74.0 | 78.6 | 74.3 | 81.5 |
| 16 | 149.3 | 134.5 | 29.3 | 24.7 | 31.0 | 21.8 | 80.4 | 83.4 | 79.2 | 85.4 |
| 17 | 111.4 | 102.2 | 13.8 | 11.9 | 16.2 | 11.0 | 87.6 | 89.3 | 85.5 | 90.1 |
| 18 | 87.0 | 80.3 | 8.5 | 8.3 | 10.3 | 8.1 | 90.2 | 90.5 | 88.2 | 90.7 |
| 19 | 71.4 | 66.3 | 6.4 | 6.5 | 8.1 | 6.6 | 91.0 | 90.9 | 88.6 | 90.8 |
| 20 | 53.6 | 50.2 | 4.9 | 4.9 | 6.3 | 5.4 | 90.9 | 90.8 | 88.2 | 90.0 |
| 21 | 43.6 | 40.9 | 4.3 | 4.1 | 6.3 | 4.9 | 90.1 | 90.6 | 85.5 | 88.9 |
| Scenario | Dissipated Energy [kJ] | Improvement Over STD [%] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| STD | HWC1 | HWC2 | HWC1 | HWC2 | ||||||
| Wfrict,OUT | Wfrict,IN | Wfrict,OUT | Wfrict,IN | Wfrict,OUT | Wfrict,IN | ΔWfrict,OUT | ΔWfrict,IN | ΔWfrict,OUT | ΔWfrict,IN | |
| Irr no | 2505 | 2202 | 437.9 | 277.2 | 522.4 | 272.2 | 82.5 | 87.4 | 79.2 | 87.6 |
| Irr low | 2527 | 2216 | 505.2 | 351.9 | 593.3 | 347.6 | 80.0 | 84.1 | 76.5 | 84.3 |
| Irr high | 2564 | 2242 | 618.6 | 464.1 | 698.3 | 454.8 | 75.9 | 79.3 | 72.8 | 79.7 |
| Irr meas | 2554 | 2238 | 579.1 | 429.9 | 658.8 | 420.9 | 77.3 | 80.8 | 74.2 | 81.2 |
| Scenario | Dissipated energy [kJ] | Improvement over STD [%] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| STD | HWC1 | HWC2 | HWC1 | HWC2 | ||||||
| Wfrict,OUT | Wfrict,IN | Wfrict,OUT | Wfrict,IN | Wfrict,OUT | Wfrict,IN | ΔWfrict,OUT | ΔWfrict,IN | ΔWfrict,OUT | ΔWfrict,IN | |
| Irr no | 887.7 | 716.1 | 491.3 | 372.6 | 490.4 | 370.6 | 44.7 | 48.0 | 44.8 | 48.3 |
| Irr low | 900.1 | 726.5 | 511.9 | 390.8 | 511.0 | 388.6 | 43.1 | 46.2 | 43.2 | 46.5 |
| Irr high | 917.4 | 740.9 | 542.2 | 422.5 | 540.5 | 414.8 | 40.9 | 43.0 | 41.1 | 44.0 |
| Irr meas | 908.1 | 733.8 | 524.1 | 406.7 | 523.3 | 401.3 | 42.3 | 44.6 | 42.4 | 45.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalivoda, J. Simulation Analysis of an Electric Locomotive with a Hydraulic Wheelset Guidance System for Improved Performance in Curved Tracks. Machines 2025, 13, 321. https://doi.org/10.3390/machines13040321
Kalivoda J. Simulation Analysis of an Electric Locomotive with a Hydraulic Wheelset Guidance System for Improved Performance in Curved Tracks. Machines. 2025; 13(4):321. https://doi.org/10.3390/machines13040321
Chicago/Turabian StyleKalivoda, Jan. 2025. "Simulation Analysis of an Electric Locomotive with a Hydraulic Wheelset Guidance System for Improved Performance in Curved Tracks" Machines 13, no. 4: 321. https://doi.org/10.3390/machines13040321
APA StyleKalivoda, J. (2025). Simulation Analysis of an Electric Locomotive with a Hydraulic Wheelset Guidance System for Improved Performance in Curved Tracks. Machines, 13(4), 321. https://doi.org/10.3390/machines13040321





