Resonant Fatigue Tests on Polished Drill Pipe Specimens
Abstract
1. Introduction
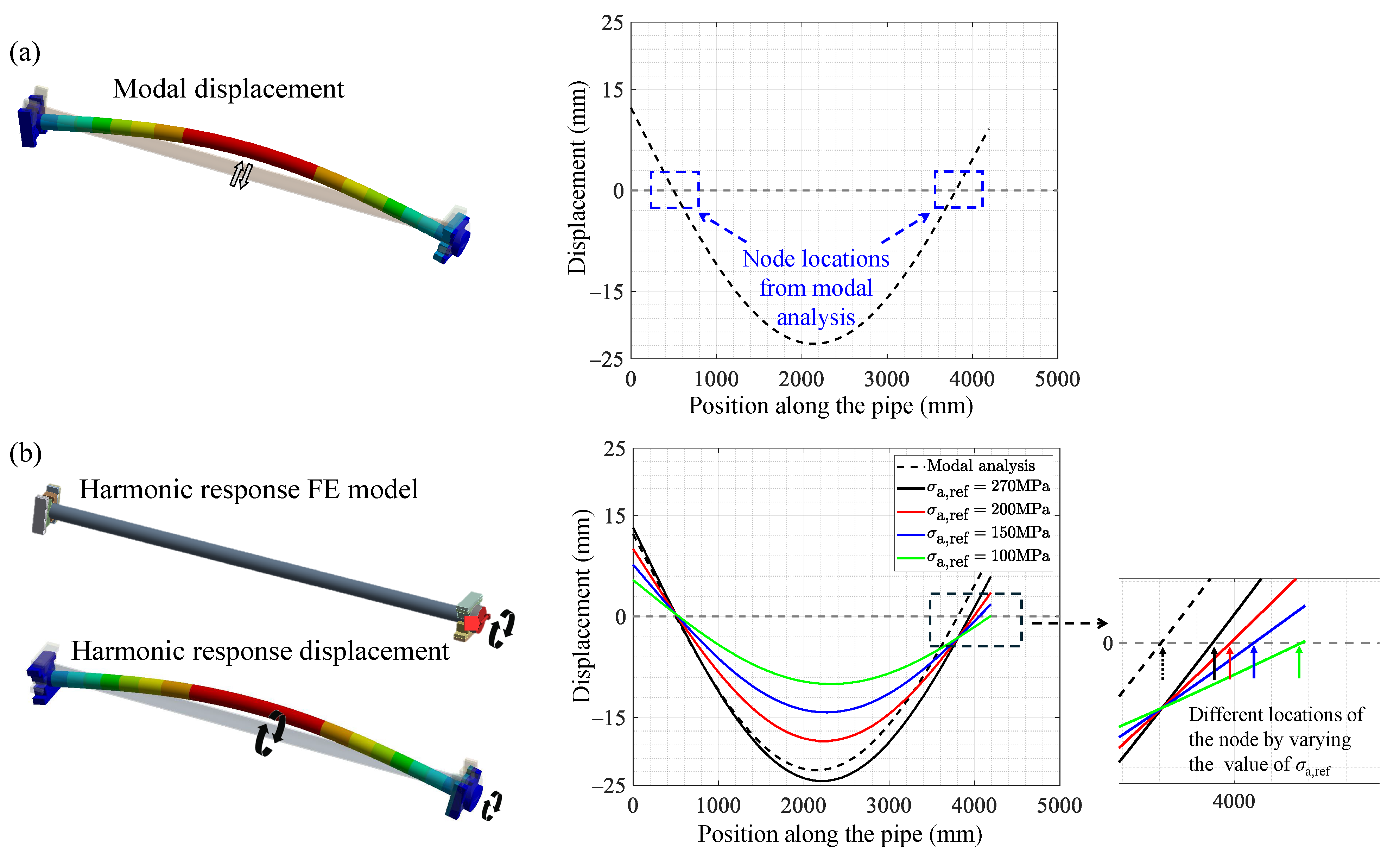
2. Theoretical Background
3. Materials and Methods
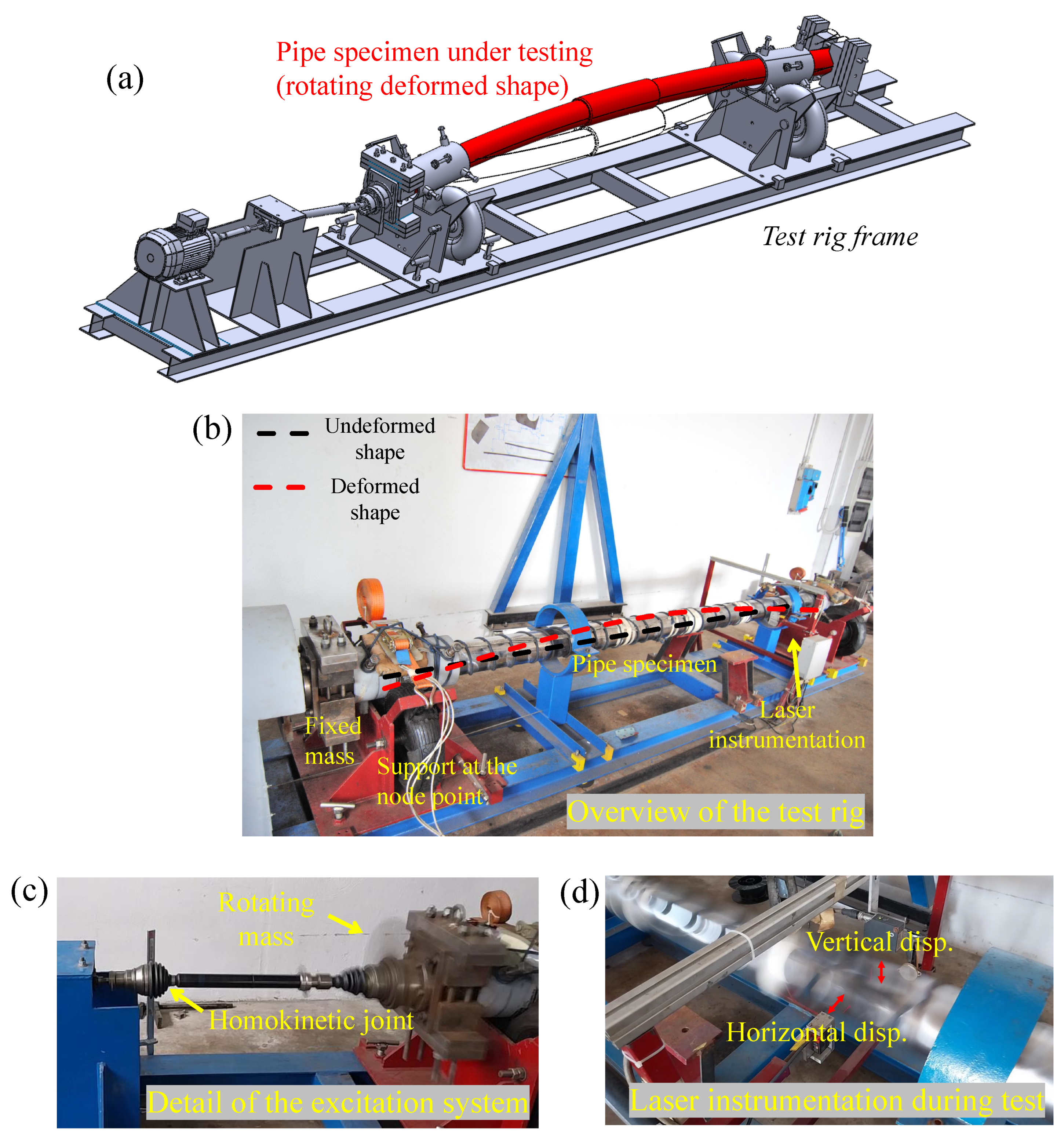
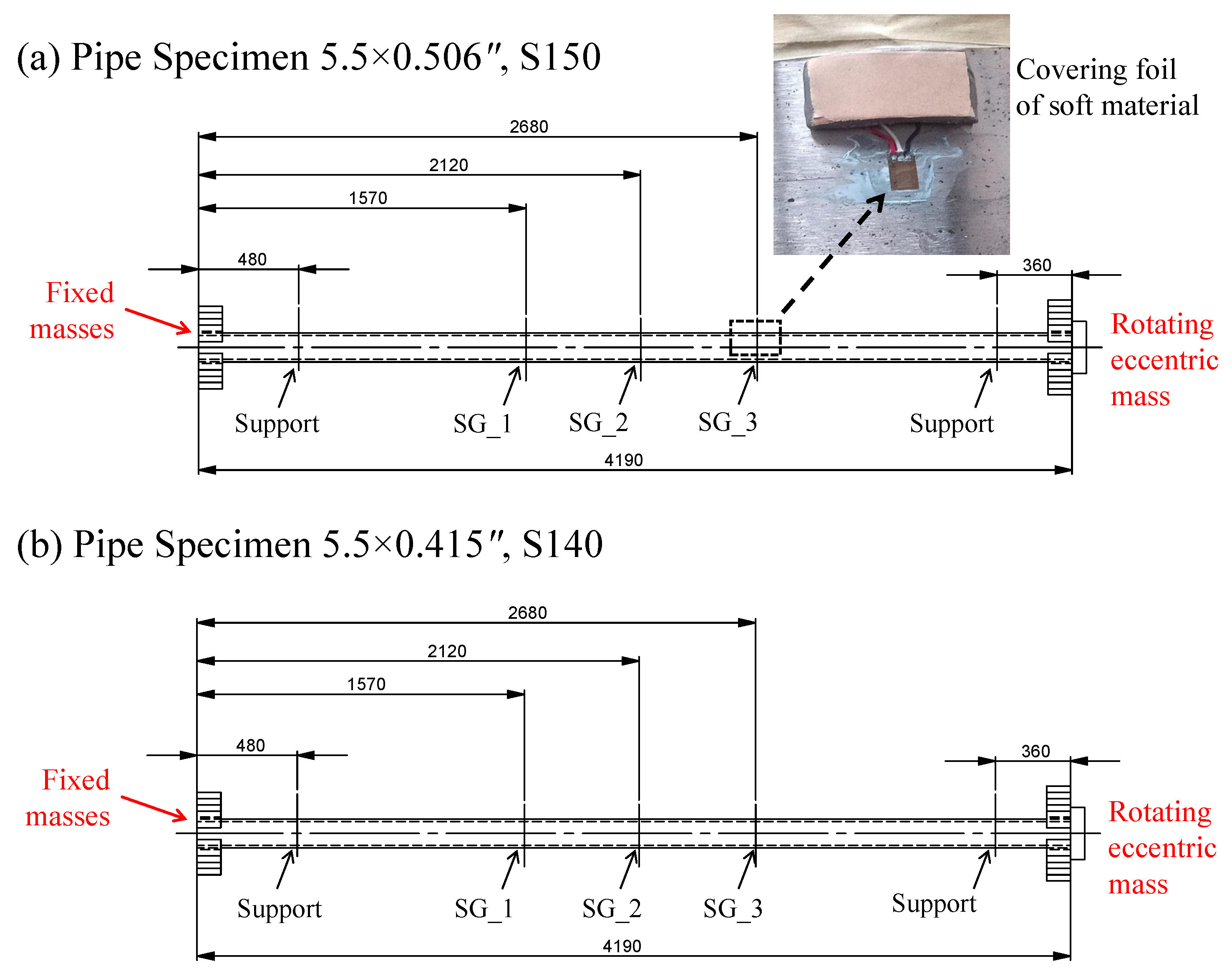
3.1. Description of the Resonant Test Rig and the Tested Specimens
3.2. Strain Gauges and Lasers Calibrations
3.3. Test Rig for the Polishing Operations
4. Results
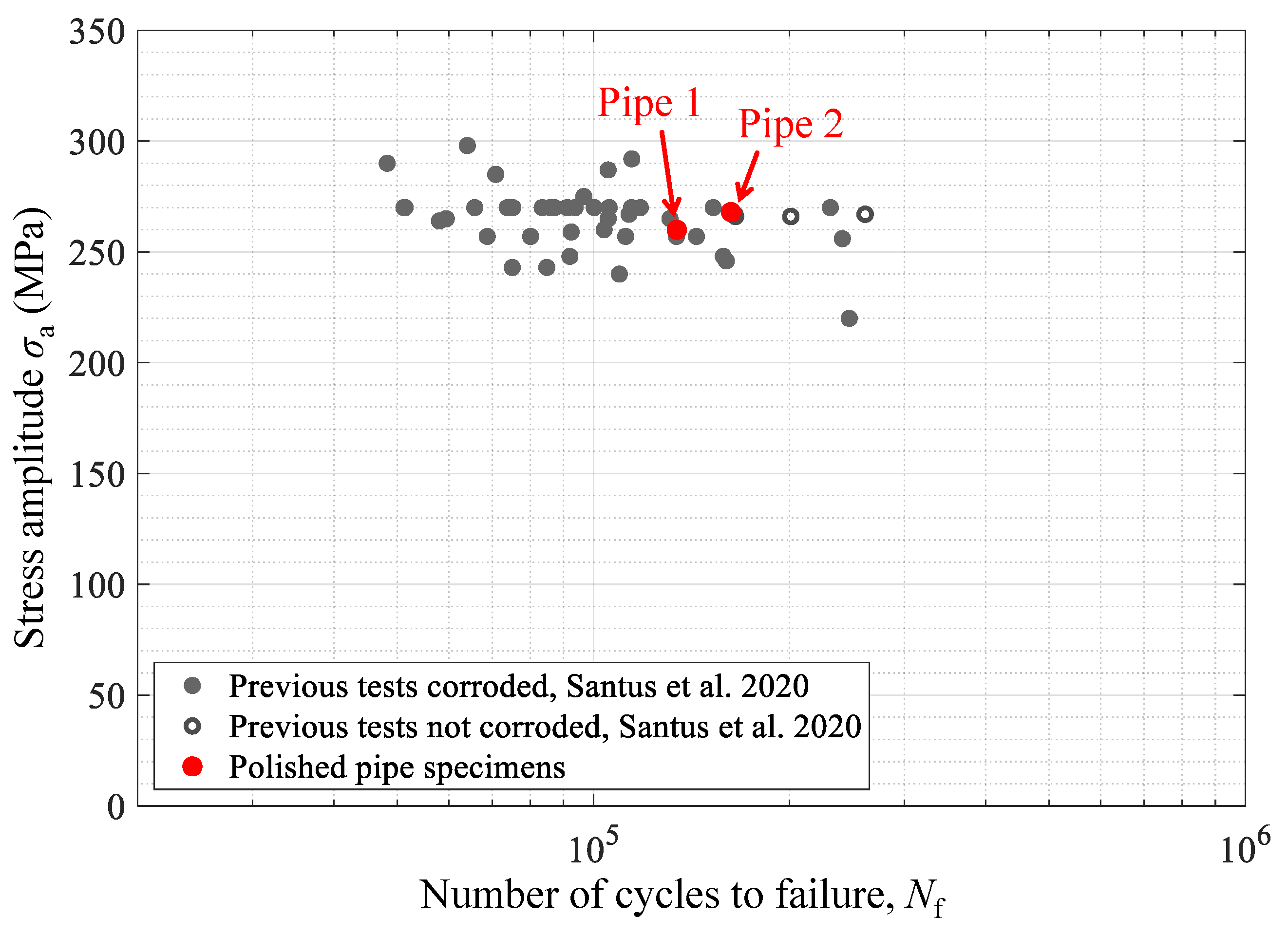
4.1. Fatigue Strength Results and Crack Location Analyses
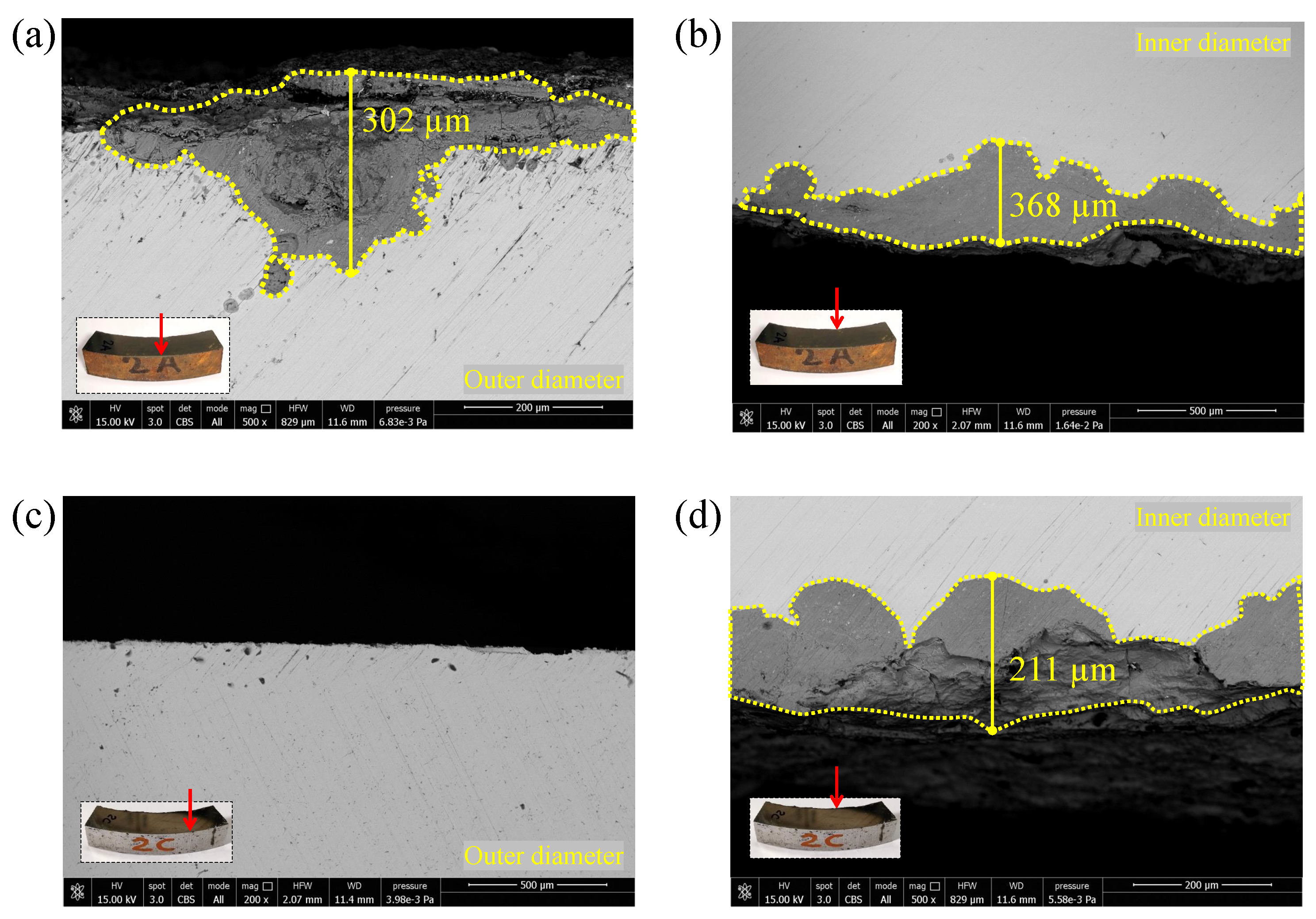
4.2. Performed Investigations with the SEM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| API | American petroleum institute |
| FE | Finite element |
| LET | Last engaged thread |
| FET | First engaged thread |
| SG_1 | Strain gauge 1 |
| SG_2 | Strain gauge 2 |
| SG_3 | Strain gauge 3 |
| SEM | Scanning electronic mycroscope |
References
- Dong, G.; Chen, P. A Review of the Evaluation, Control, and Application Technologies for Drill String Vibrations and Shocks in Oil and Gas Well. Shock Vib. 2016, 2016, 7418635. [Google Scholar] [CrossRef]
- Ma, T.; Chen, P.; Zhao, J. Overview on vertical and directional drilling technologies for the exploration and exploitation of deep petroleum resources. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 365–395. [Google Scholar] [CrossRef]
- Inoue, T.; Wada, K.; Miyazaki, E.; Miyazaki, T. Scientific Drilling Program of Drilling Vessel Chikyu and Drilling Data Acquisition for Future Technical Development. In Proceedings of the Volume 5: Ocean Space Utilization; Ocean Renewable Energy. ASMEDC, Rotterdam, The Netherlands, 19–24 June 2011. OMAE2011. [Google Scholar] [CrossRef]
- Inoue, T.; Kyo, M.; Sakura, K. Fatigue Strength Evaluation of Drill Pipe for Challenging Deep Drilling Project-Japan Trench Fast Drilling (JFAST). In Proceedings of the Twenty-Third International Offshore and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
- Inoue, T.; Kyo, M.; Sakura, K.; Fukui, T. Fatigue Strength Investigation of Drill Pipe for Challenging Scientific Deep Drilling and Utilization of Drilling Data to Estimate Cumulative Fatigue. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014. 14OTC. [Google Scholar] [CrossRef]
- American Petroleum Institute. Specification for Rotary Drill Stem Elements; American Petroleum Institute: Washington, DC, USA, 2006. [Google Scholar]
- Santus, C. Fretting fatigue of aluminum alloy in contact with steel in oil drill pipe connections, modeling to interpret test results. Int. J. Fatigue 2008, 30, 677–688. [Google Scholar] [CrossRef]
- Fangpo, L.; Yonggang, L.; Xinhu, W.; Caihong, L. Failure analysis of ⌀ 127mm IEU G105 drill pipe wash out. Eng. Fail. Anal. 2011, 18, 1867–1872. [Google Scholar] [CrossRef]
- Haagensen, P.J.; Grøttum, T.I. Fatigue Assessment of Drill Pipes. In Proceedings of the Volume 4: Materials Technology. American Society of Mechanical Engineers, Trondheim, Norway, 25–30 June 2017. OMAE2017. [Google Scholar] [CrossRef]
- Luo, S.; Liu, M.; Zheng, X. Characteristics and life expression of fatigue fracture of G105 and S135 drill pipe steels for API grade. Eng. Fail. Anal. 2020, 116, 104705. [Google Scholar] [CrossRef]
- Inoue, T.; Fujikubo, M. Fatigue evaluation of drill pipe by considering ship motions and its application in scientific drilling. J. Mar. Sci. Technol. 2020, 26, 525–540. [Google Scholar] [CrossRef]
- Zamani, S.M.; Hassanzadeh-Tabrizi, S.A.; Sharifi, H. Failure analysis of drill pipe: A review. Eng. Fail. Anal. 2016, 59, 605–623. [Google Scholar] [CrossRef]
- Ferjani, M.; Averbuch, D.; Constantinescu, A. A computational approach for the fatigue design of threaded connections. Int. J. Fatigue 2011, 33, 610–623. [Google Scholar] [CrossRef]
- Tafreshi, A.; Dover, W. Stress analysis of drillstring threaded connections using the finite element method. Int. J. Fatigue 1993, 15, 429–438. [Google Scholar] [CrossRef]
- Macdonald, K.; Deans, W. Stress analysis of drillstring threaded connections using the finite element method. Eng. Fail. Anal. 1995, 2, 1–30. [Google Scholar] [CrossRef]
- Macdonald, K.A. The effectiveness of stress relief features in austenitic drillcollar connections. Eng. Fail. Anal. 1996, 3, 267–279. [Google Scholar] [CrossRef]
- Van Wittenberghe, J.; De Pauw, J.; De Baets, P.; De Waele, W.; Ost, W.; De Roeck, G.; Bui, T.T. Fatigue investigation of threaded pipe connections. Int. J. Sustain. Constr. Des. 2010, 1, 182–189. [Google Scholar] [CrossRef]
- Van Wittenberghe, J.; De Baets, P.; De Waele, W.; Galle, T.; Bui, T.T.; De Roeck, G. Design characteristics that improve the fatigue life of threaded pipe connections. Int. J. Sustain. Constr. Des. 2011, 2, 334–341. [Google Scholar] [CrossRef]
- Luo, S.; Wu, S. Effect of stress distribution on the tool joint failure of internal and external upset drill pipes. Mater. Des. (1980–2015) 2013, 52, 308–314. [Google Scholar] [CrossRef]
- Ozguc, O. Analysis of fatigue behaviour of drill pipe on pin-box connection. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2020, 235, 68–80. [Google Scholar] [CrossRef]
- Liu, H.; He, Y.; Wan, J.; Chen, L.; Yi, X.; Hou, S.; Wang, Y.; He, D.; Li, G. New design method of unequal taper thread (UTT) pairs and its application in API NC38 thread improvement. Petroleum 2023, 9, 439–453. [Google Scholar] [CrossRef]
- Lin, Y.; Qi, X.; Zhu, D.; Zeng, D.; Zhu, H.; Deng, K.; Shi, T. Failure analysis and appropriate design of drill pipe upset transition area. Eng. Fail. Anal. 2013, 31, 255–267. [Google Scholar] [CrossRef]
- Yonggang, L.; Fangpo, L.; Xin, X.; biyu, Y.; caihong, L. Simulation Technology in Failure Analysis of Drill Pipe. Procedia Eng. 2011, 12, 236–241. [Google Scholar] [CrossRef]
- Zhu, H.; Lin, Y.; Zeng, D.; Zhou, Y.; Xie, J. Simulation analysis of flow field and shear stress distribution in internal upset transition zone of drill pipe. Eng. Fail. Anal. 2012, 21, 67–77. [Google Scholar] [CrossRef]
- Spasova, D.; Argirov, Y.; Atanasov, N.; Yankova, R. Analysis of failure causes of S135 drill pipe. Mater. Today Proc. 2022, 59, 1719–1725. [Google Scholar] [CrossRef]
- Yu, Z.; Zeng, D.; Hu, S.; Zhou, X.; Lu, W.; Luo, J.; Fan, Y.; Meng, K. The failure patterns and analysis process of drill pipes in oil and gas well: A case study of fracture S135 drill pipe. Eng. Fail. Anal. 2022, 138, 106171. [Google Scholar] [CrossRef]
- Luo, S.; Liu, M.; Shen, Y.; Lin, X. Sulfide Stress Corrosion Cracking Behavior of G105 and S135 High-Strength Drill Pipe Steels in H2S Environment. J. Mater. Eng. Perform. 2019, 28, 1707–1718. [Google Scholar] [CrossRef]
- Yu, H.; Peng, X.; Lian, Z.; zhang, Q.; Shi, T.; Wang, J.; Zhao, Z. Experimental and numerical simulation of fatigue corrosion behavior of V150 high-strength drill pipe in air and H2S-dilling mud environment. J. Nat. Gas Sci. Eng. 2022, 98, 104392. [Google Scholar] [CrossRef]
- Lu, S.; Feng, Y.; Luo, F.; Qin, C.; Wang, X. Failure analysis of IEU drill pipe wash out. Int. J. Fatigue 2005, 27, 1360–1365. [Google Scholar] [CrossRef]
- Han, Y.; Zhao, X.; Bai, Z.; Yin, C. Failure Analysis on Fracture of a S135 Drill Pipe. Procedia Mater. Sci. 2014, 3, 447–453. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y.; Chen, W.; Shi, T.; Singh, A.; Lu, Q. Longitudinal crack failure analysis of box of S135 tool joint in ultra-deep well. Eng. Fail. Anal. 2015, 48, 283–296. [Google Scholar] [CrossRef]
- Liu, Y.; Lian, Z.; Lin, T.; Shen, Y.; Zhang, Q. A study on axial cracking failure of drill pipe body. Eng. Fail. Anal. 2016, 59, 434–443. [Google Scholar] [CrossRef]
- Liu, M.; Luo, S.; Shen, Y.; lin, X. Corrosion fatigue crack propagation behavior of S135 high–strength drill pipe steel in H2S environment. Eng. Fail. Anal. 2019, 97, 493–505. [Google Scholar] [CrossRef]
- Zeng, D.; Li, H.; Tian, G.; Liu, F.; Li, B.; Yu, S.; Ouyang, Z.; Shi, T. Fatigue behavior of high-strength steel S135 under coupling multi-factor in complex environments. Mater. Sci. Eng. A 2018, 724, 385–402. [Google Scholar] [CrossRef]
- Han, L.; Liu, M.; Luo, S.; Lu, T.J. Fatigue and corrosion fatigue behaviors of G105 and S135 high–strength drill pipe steels in air and H2S environment. Process Saf. Environ. Prot. 2019, 124, 63–74. [Google Scholar] [CrossRef]
- Peng, X.; Yu, H.; Lian, Z.; Dong, B.; Zhong, W.; Zhang, Y.; Hu, Z. Material optimization of drill pipe in complex wellbore environments by comparing fatigue life and cost. Energy Rep. 2021, 7, 5420–5430. [Google Scholar] [CrossRef]
- Ziomek-Moroz, M. Environmentally Assisted Cracking of Drill Pipes in Deep Drilling Oil and Natural Gas Wells. J. Mater. Eng. Perform. 2011, 21, 1061–1069. [Google Scholar] [CrossRef]
- Kryzhanivskyi, E.I.; Nykyforchyn, H.M.; Student, O.Z.; Krechkovska, H.V.; Chudyk, I.I. Role of Nonmetallic Inclusions in Premature Stress-Corrosion Fractures of Drill Pipes. Mater. Sci. 2020, 55, 822–830. [Google Scholar] [CrossRef]
- Zhao, J.; Bai, X.; Qu, T.; Li, D.; Liu, W.; Wei, Z.; Xiaolong, L. Corrosion Failure Analysis of a S135 Drill Pipe. J. Fail. Anal. Prev. 2024, 24, 368–379. [Google Scholar] [CrossRef]
- Santus, C.; Bertini, L.; Beghini, M.; Merlo, A.; Baryshnikov, A. Torsional strength comparison between two assembling techniques for aluminium drill pipe to steel tool joint connection. Int. J. Press. Vessel. Pip. 2009, 86, 177–186. [Google Scholar] [CrossRef]
- Belkacem, L.; Abdelbaki, N.; Otegui, J.L.; Gaceb, M.; Bettayeb, M. Using a supperficially treated 2024 aluminum alloy drill pipe to delay failure during dynamic loading. Eng. Fail. Anal. 2019, 104, 261–273. [Google Scholar] [CrossRef]
- Liu, W.; Li, J.; Zhong, Y.; Shi, T.; Zhang, J.; Li, S. Failure analysis on aluminum alloy drill pipe with pits and parallel transverse cracks. Eng. Fail. Anal. 2022, 131, 105809. [Google Scholar] [CrossRef]
- Mou, Y.; Lian, Z.; Li, W.; Zhong, X.; Li, J.; He, Y.; Cao, J.; Eliaz, N. The effect of friction welding on the mechanical properties and corrosion fatigue resistance of titanium alloy drill pipe. Fatigue Fract. Eng. Mater. Struct. 2021, 45, 466–481. [Google Scholar] [CrossRef]
- Miscow, G. Techniques to characterize fatigue behaviour of full size drill pipes and small scale samples. Int. J. Fatigue 2004, 26, 575–584. [Google Scholar] [CrossRef]
- Teodoriu, C. Oil Country Tubular Goods Fatigue Testing: Do We Test Them Enough? In Proceedings of the Volume 4: Materials Technology, American Society of Mechanical Engineers, Trondheim, Norway, 25–30 June 2017. OMAE2017. [Google Scholar] [CrossRef]
- Zou, H.; Tan, Z. Fatigue life analysis of rotary drill pipe. Int. J. Press. Vessel. Pip. 2023, 201, 104874. [Google Scholar] [CrossRef]
- Huertas, J.I.; Navarrete, N.; Giraldo, M.; Uribe, J.D.; Gasca, J.J. Resonant fatigue test bench for shaft testing. Fatigue Fract. Eng. Mater. Struct. 2016, 40, 364–374. [Google Scholar] [CrossRef]
- Bertini, L.; Beghini, M.; Santus, C.; Baryshnikov, A. Resonant test rigs for fatigue full scale testing of oil drill string connections. Int. J. Fatigue 2008, 30, 978–988. [Google Scholar] [CrossRef]
- Santus, C.; Bertini, L.; Burchianti, A.; Inoue, T.; Sakurai, N. Fatigue resonant tests on drill collar rotary shouldered connections and critical thread root identification. Eng. Fail. Anal. 2018, 89, 138–149. [Google Scholar] [CrossRef]
- Santus, C.; Burchianti, A.; Inoue, T.; Ishiguro, H. Fatigue resonant tests on S140 and S150 grade corroded drill pipe connections and pipe bodies. Int. J. Press. Vessel. Pip. 2020, 184, 104107. [Google Scholar] [CrossRef]
- Santus, C.; Romanelli, L.; Burchianti, A.; Inoue, T. Resonant Fatigue Tests on Drill Pipe Connections with Different Geometries and Sizes. Appl. Sci. 2023, 13, 8006. [Google Scholar] [CrossRef]
- Van Wittenberghe, J.; De Baets, P.; De Waele, W.; Ost, W.; Verstraete, M.; Hertelé, S. Resonant Bending Fatigue Test Setup for Pipes With Optical Displacement Measuring System. J. Offshore Mech. Arct. Eng. 2012, 134. [Google Scholar] [CrossRef]
- Oku, Y.; Sugino, M.; Ando, Y.; Makino, T.; Komoda, R.; Takazaki, D.; Kubota, M. Fretting fatigue on thread root of premium threaded connections. Tribol. Int. 2017, 108, 111–120. [Google Scholar] [CrossRef]
- Schneider, S.; Herrmann, R.; Marx, S. Development of a resonant fatigue testing facility for large-scale beams in bending. Int. J. Fatigue 2018, 113, 171–183. [Google Scholar] [CrossRef]
- Schramm, C.; Birkner, D.; Marx, S. Resonance-based testing facility for fatigue tests of different axially loaded structural elements. Eng. Struct. 2024, 298, 117045. [Google Scholar] [CrossRef]
- Thomas, C.; Sainz-Aja, J.; Setien, J.; Cimentada, A.; Polanco, J.A. Resonance fatigue testing on high-strength self-compacting concrete. J. Build. Eng. 2021, 35, 102057. [Google Scholar] [CrossRef]
- Chuan, W.; Zhu, H.; Wang, D. Test System and Model for Fatigue Performance Evaluation of Marine Riser. J. Appl. Sci. 2013, 13, 854–861. [Google Scholar] [CrossRef][Green Version]
- Xu, Z.; An, C.; Xie, Z.; Zhang, J.; Lim, F.; Zhang, Y. Full-scale resonant bending fatigue testing of casing joints under bending moment load. Int. J. Press. Vessel. Pip. 2024, 207, 105105. [Google Scholar] [CrossRef]
- Snowberg, D.; Dana, S.; Hughes, S.; Berling, P. Implementation of a Biaxial Resonant Fatigue Test Method on a Large Wind Turbine Blade; National Renewable Energy Lab.: Golden, CO, USA, 2014. [Google Scholar] [CrossRef]
- Melcher, D.; Bätge, M.; Neßlinger, S. A novel rotor blade fatigue test setup with elliptical biaxial resonant excitation. Wind Energy Sci. 2020, 5, 675–684. [Google Scholar] [CrossRef]
- Van Wittenberghe, J.; Vanden Haute, C.; Shirzadeh, R.; Thibaux, P. On the Feasibility of Large-Scale Resonant Fatigue Testing to Study Bolt Force Relaxation. In Proceedings of the Volume 3: Materials Technology; Pipelines, Risers, and Subsea Systems, Hamburg, Germany, 5–10 June 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022. OMAE2022. [Google Scholar] [CrossRef]
- Luo, S.; Liu, M.; Lin, X. Corrosion fatigue behavior of S135 high-strength drill pipe steel in a simulated marine environment. Mater. Corros. 2018, 70, 688–697. [Google Scholar] [CrossRef]
- Murakami, Y. Metal Fatigue; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Macoretta, G.; Romanelli, L.; Santus, C.; Romoli, L.; Lutey, A.H.A.; Uriati, F.; Nicoletto, G.; Raghavendra, S.; Benedetti, M.; Monelli, B.D. Modelling of the surface morphology and size effects on fatigue strength of L-PBF Inconel 718 by comparing different testing specimens. Int. J. Fatigue 2024, 181, 108120. [Google Scholar] [CrossRef]
- Łagoda, T.; Vantadori, S.; Głowacka, K.; Kurek, M.; Kluger, K. Using the Smith-Watson-Topper Parameter and Its Modifications to Calculate the Fatigue Life of Metals: The State-of-the-Art. Materials 2022, 15, 3481. [Google Scholar] [CrossRef] [PubMed]
- Santus, C.; Romanelli, L.; Grossi, T.; Neri, P.; Romoli, L.; Lutey, A.H.A.; Pedranz, M.; Benedetti, M. Torsional-loaded notched specimen fatigue strength prediction based on mode I and mode III critical distances and fracture surface investigations with a 3D optical profilometer. Int. J. Fatigue 2022, 161, 106913. [Google Scholar] [CrossRef]
- Santus, C.; Romanelli, L.; Grossi, T.; Bertini, L.; Le Bone, L.; Chiesi, F.; Tognarelli, L. Elastic–plastic analysis of high load ratio fatigue tests on a shot-peened quenched and tempered steel, combining the Chaboche model and the Theory of Critical Distances. Int. J. Fatigue 2023, 174, 107713. [Google Scholar] [CrossRef]






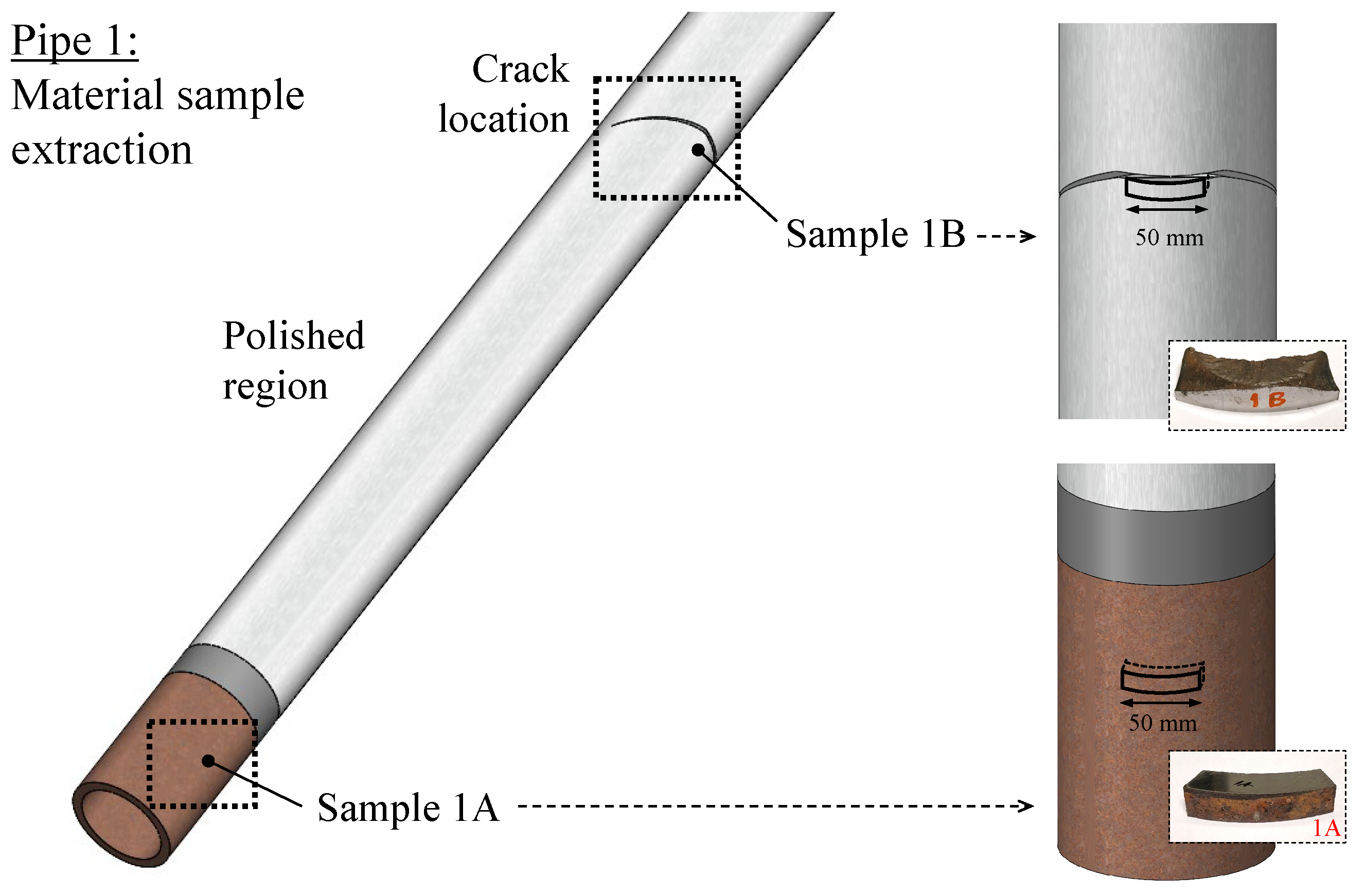
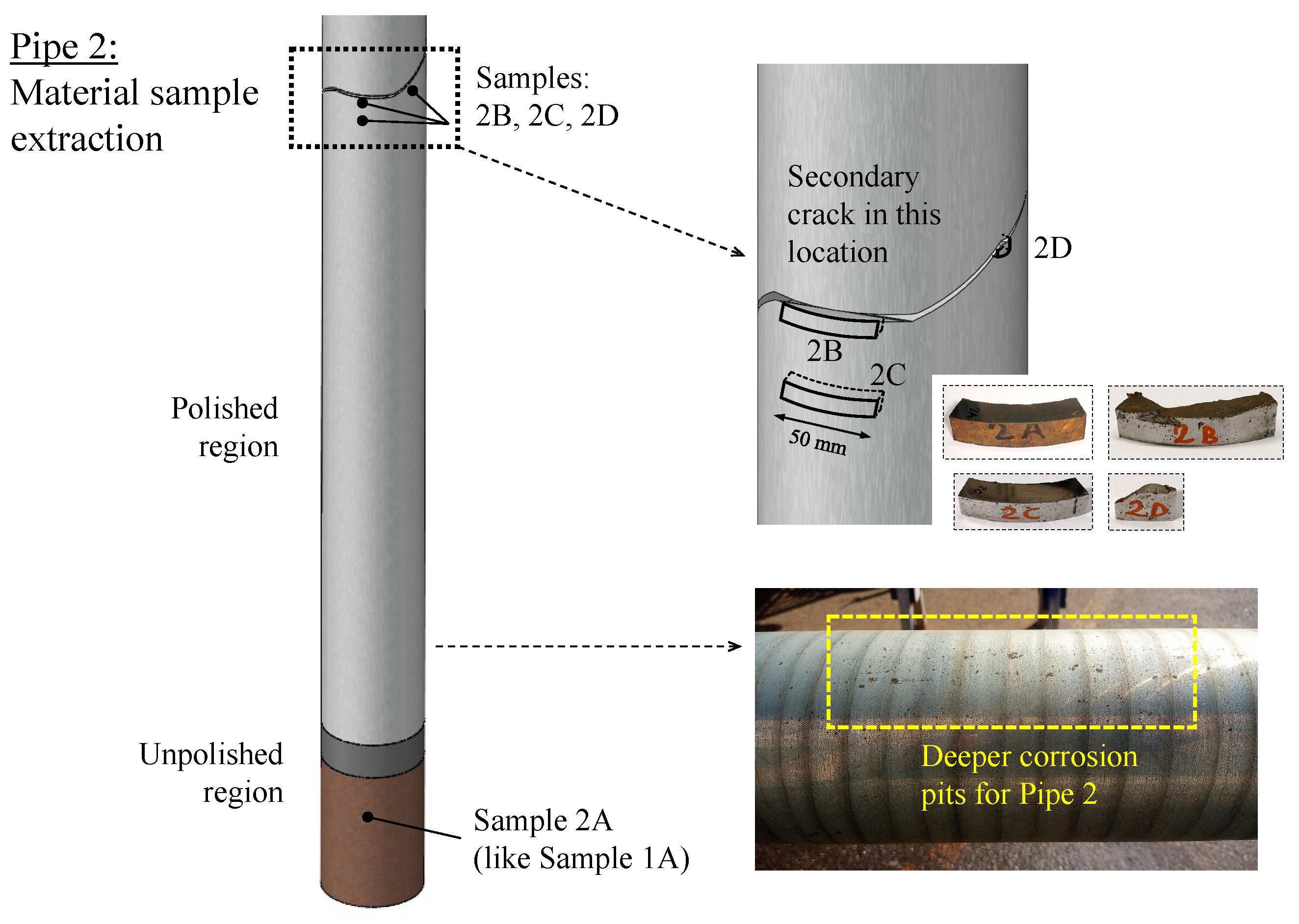



| Step of the Polishing Operation | Grinding Wheel Rotational Speed (rpm) | Pipe Specimen’s Rotational Speed (rpm) | Grinding Wheel Diameter (mm) |
|---|---|---|---|
| First step (coarse grinding | 5000 | 60 | 150 |
| Second step (coarse polishing) | 8000–10,000 | 60 | 100 |
| Third step (fine polishing) | 5000 | 60 | 125 |
| Sample Number | Location | (mm) | (MPa) |
|---|---|---|---|
| Sample 1A | outer diameter | 0.263 | 281 |
| Sample 1A | inner diameter | 1.28 | 216 |
| Sample 1B | outer diameter | — | — |
| Sample 1B | inner diameter | 0.463 | 256 |
| Sample 2A | outer diameter | 0.333 | 256 |
| Sample 2A | inner diameter | 0.632 | 230 |
| Sample 2B | outer diameter | 0.327 | 257 |
| Sample 2C | outer diameter | — | — |
| Sample 2C | inner diameter | 0.349 | 254 |
| Sample 2D | outer diameter | 0.361 | 252 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santus, C.; Romanelli, L.; Bertini, L.; Burchianti, A.; Inoue, T. Resonant Fatigue Tests on Polished Drill Pipe Specimens. Machines 2024, 12, 314. https://doi.org/10.3390/machines12050314
Santus C, Romanelli L, Bertini L, Burchianti A, Inoue T. Resonant Fatigue Tests on Polished Drill Pipe Specimens. Machines. 2024; 12(5):314. https://doi.org/10.3390/machines12050314
Chicago/Turabian StyleSantus, Ciro, Lorenzo Romanelli, Leonardo Bertini, Alessandro Burchianti, and Tomoya Inoue. 2024. "Resonant Fatigue Tests on Polished Drill Pipe Specimens" Machines 12, no. 5: 314. https://doi.org/10.3390/machines12050314
APA StyleSantus, C., Romanelli, L., Bertini, L., Burchianti, A., & Inoue, T. (2024). Resonant Fatigue Tests on Polished Drill Pipe Specimens. Machines, 12(5), 314. https://doi.org/10.3390/machines12050314







