Analytical Model of Tapered Thread Made by Turning from Different Machinability Workpieces
Abstract
1. Introduction
2. Materials and Methods
2.1. Modern Approaches for Choosing Materials for Hard-Loaded Screw Threads
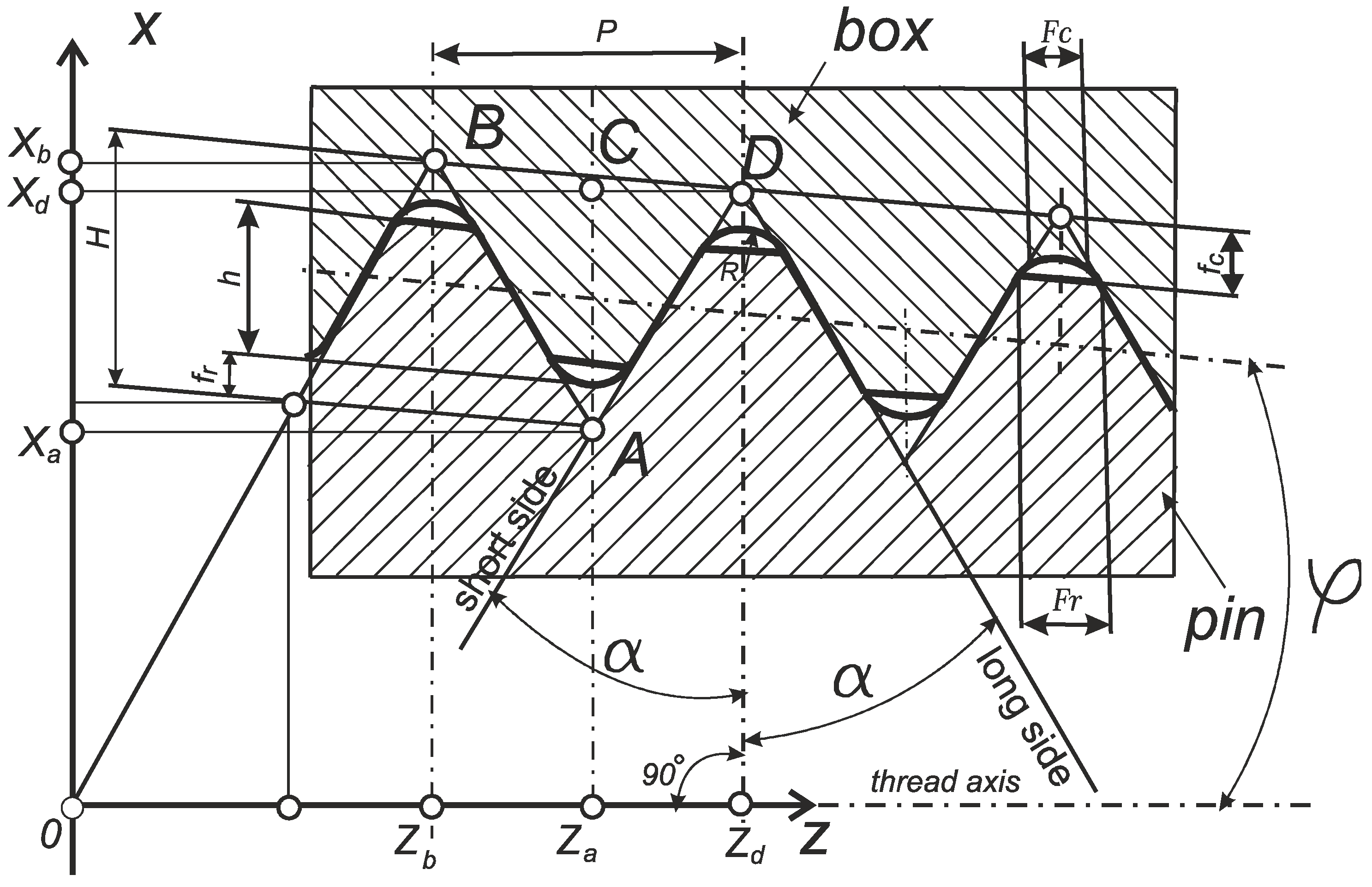
2.2. Geometrical Explanation of Manufactured Screw Thread as Convolute Helicoid Surface
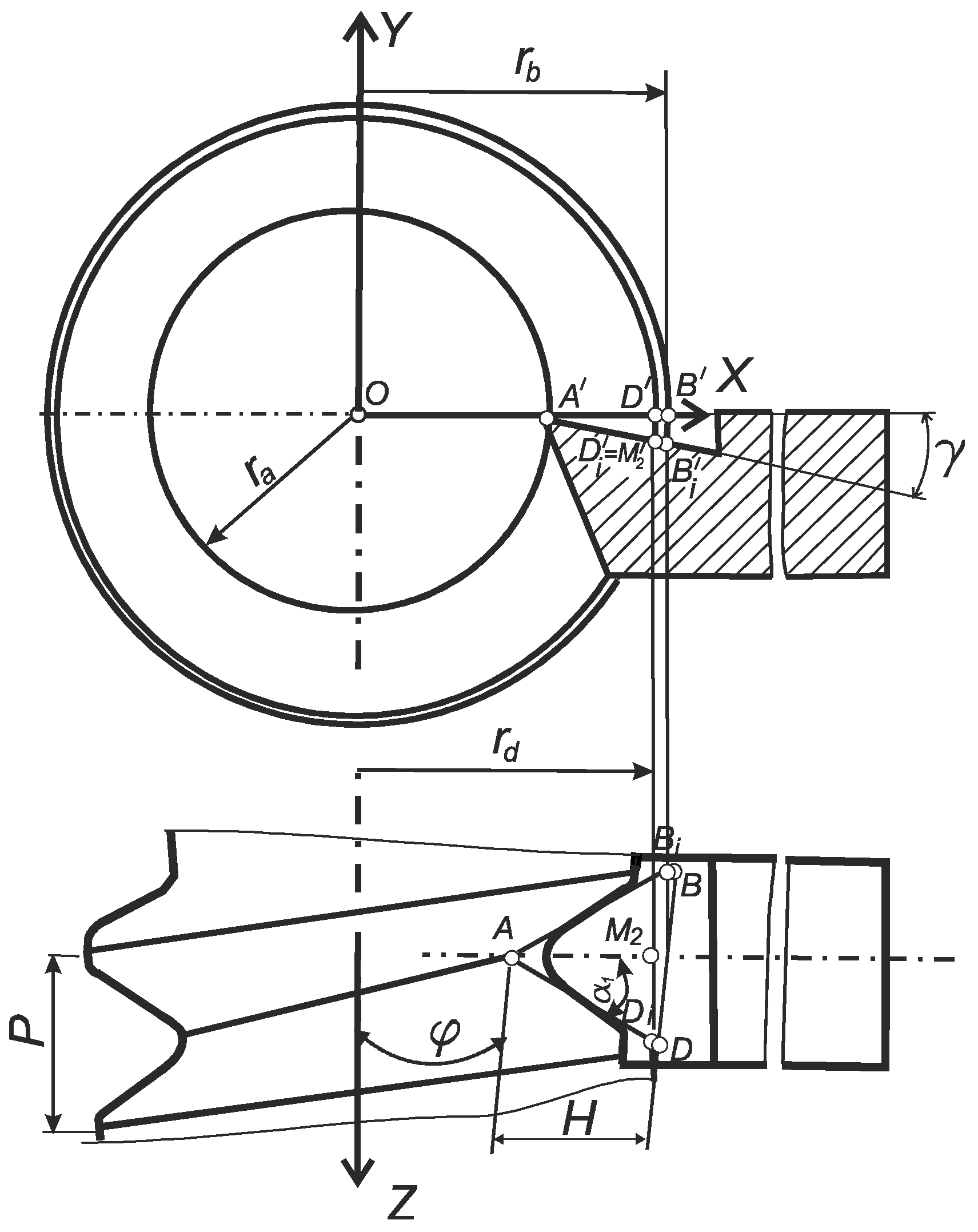
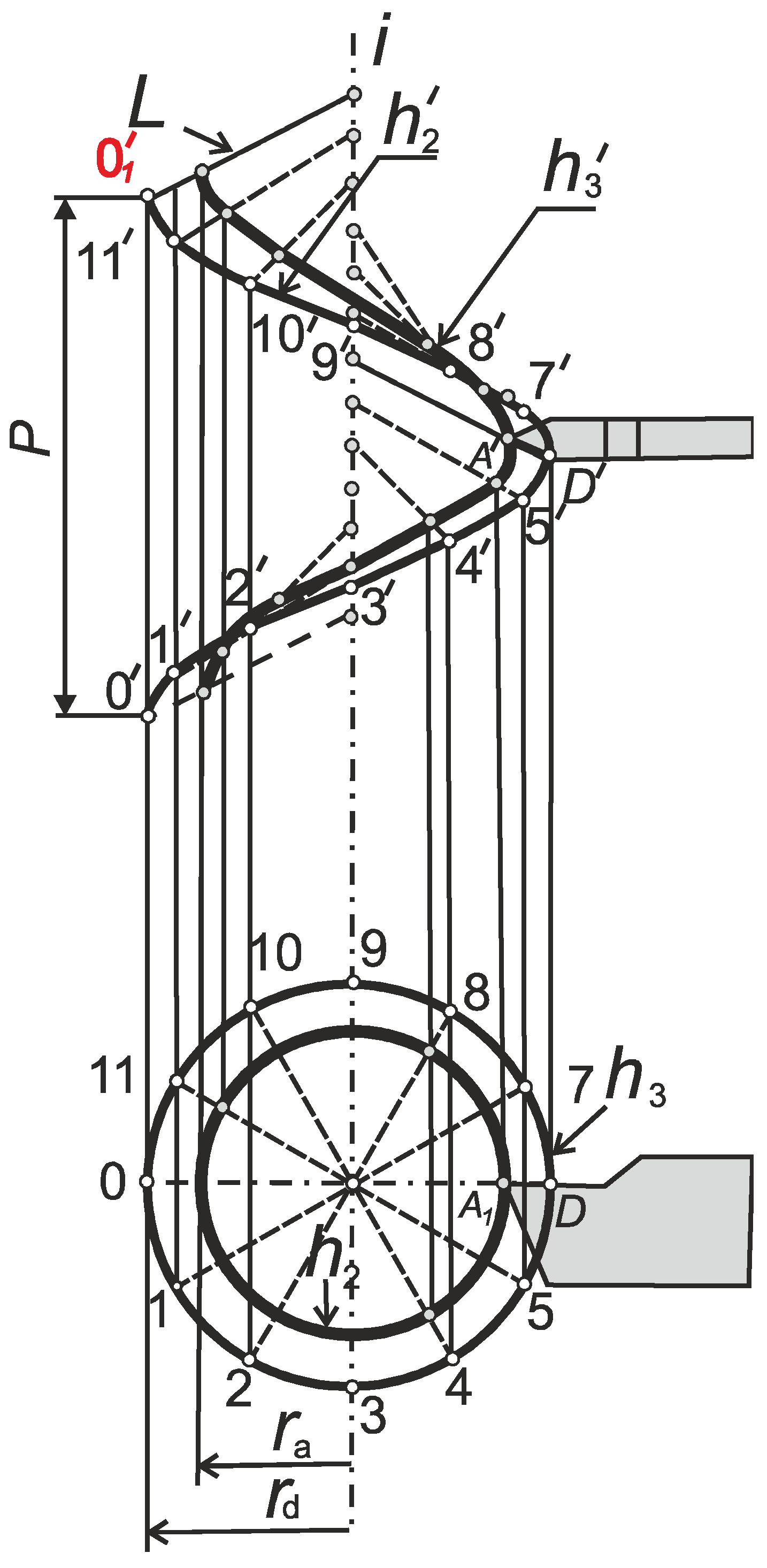
2.3. Analytical Method of Screw Thread Model Using Tool Back-Rake Parameter
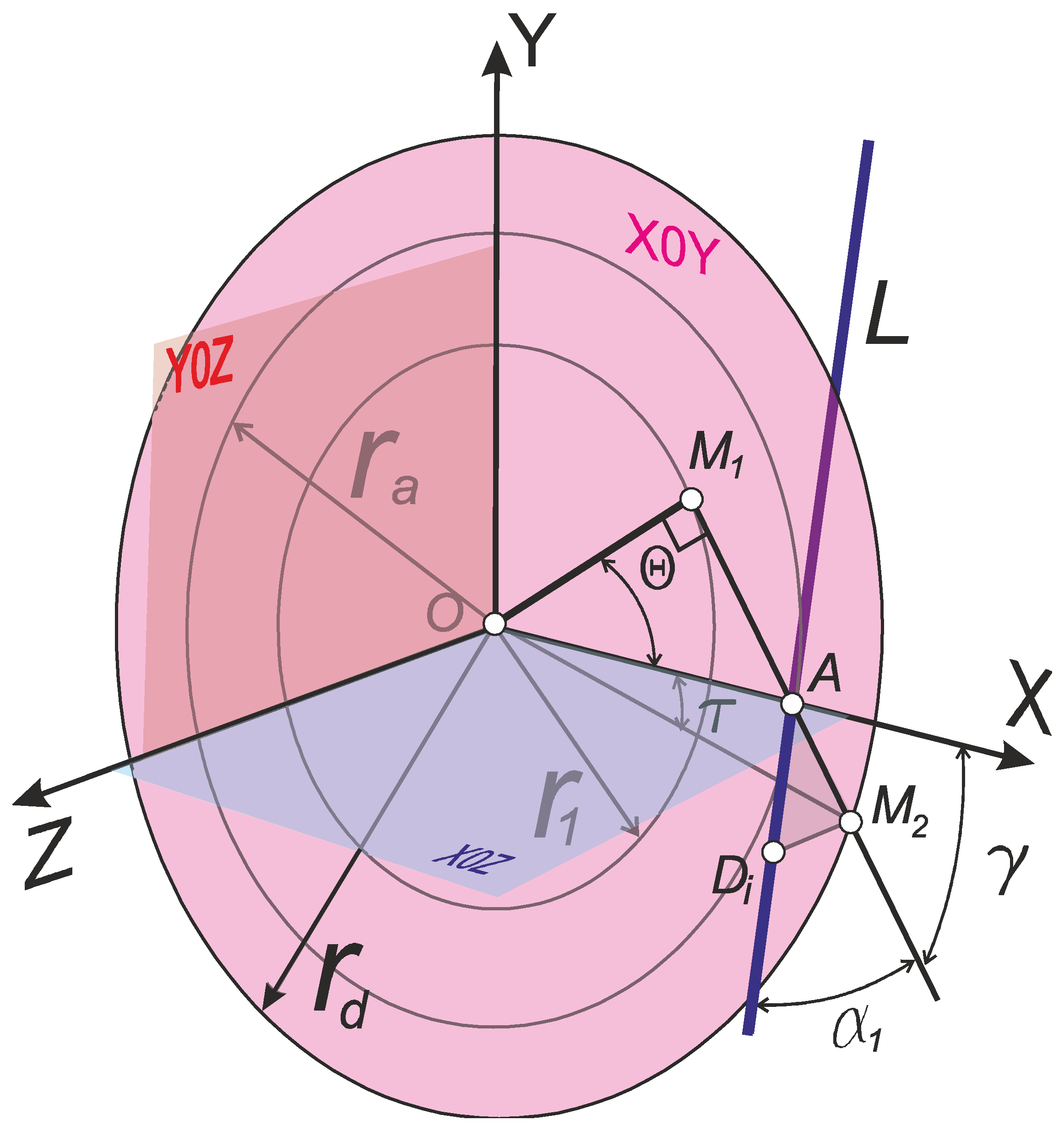
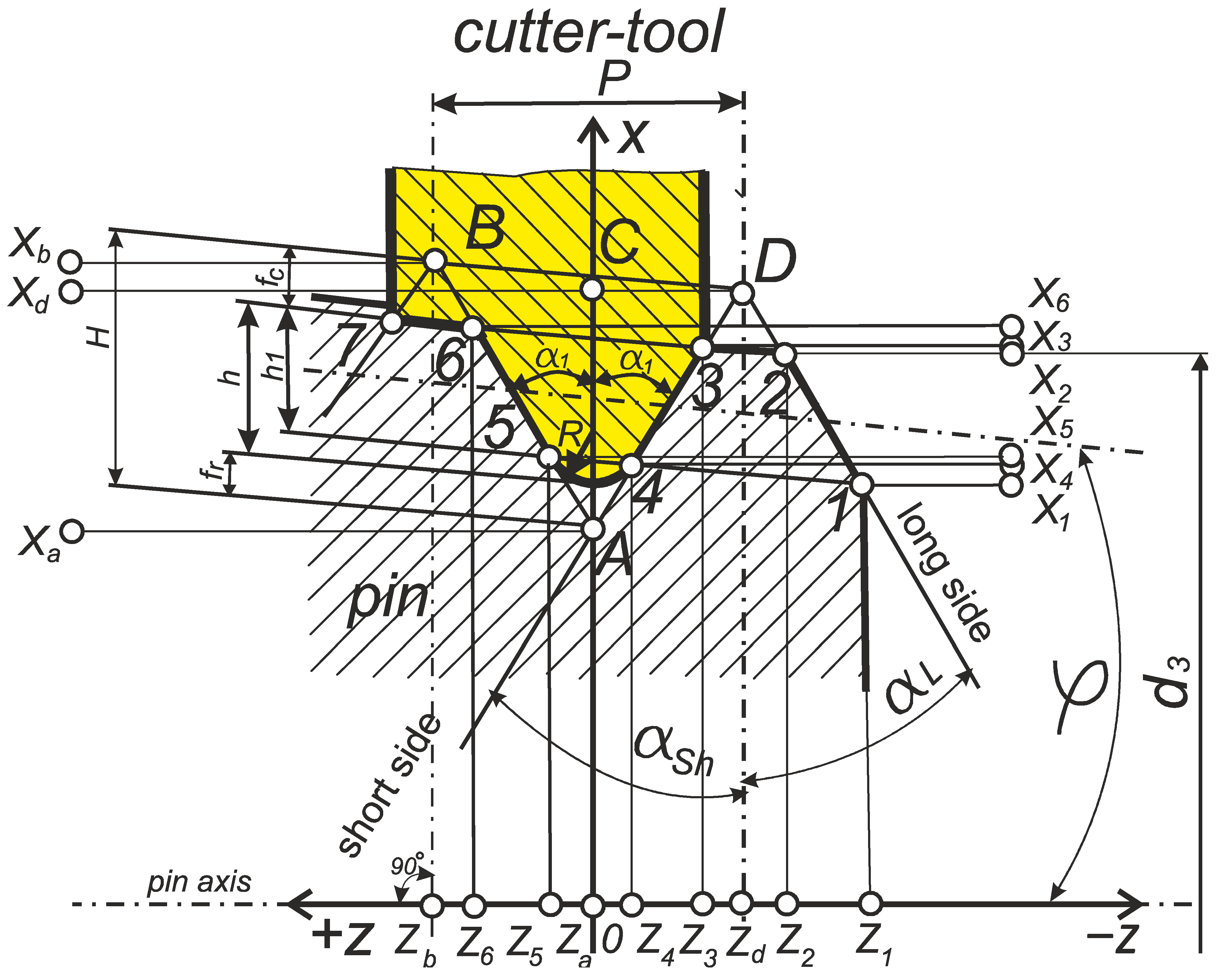
2.3.1. Parametric Equations of the Helical Surface and Equations of Its Axial Section in General Form
- —
- Parameters τ and Ɵ determine the position of a point on the surface and are its curvilinear coordinates. At the same time, the parameter τ determines the position of an arbitrary point of the line M1M2 on the projection of the generating line L on the X0Y plane. The parameter Ɵ determines the amount of rotation of the generator L around the Z-axis.
- —
- The value p is a parameter of the screw and is determined by the formulawhere P is the pitch of the helicoid.
2.3.2. The Influence of the Back-Rake Angle at the Nose of the Lathe Tool on the Profile of the Helical Convoluted Surface
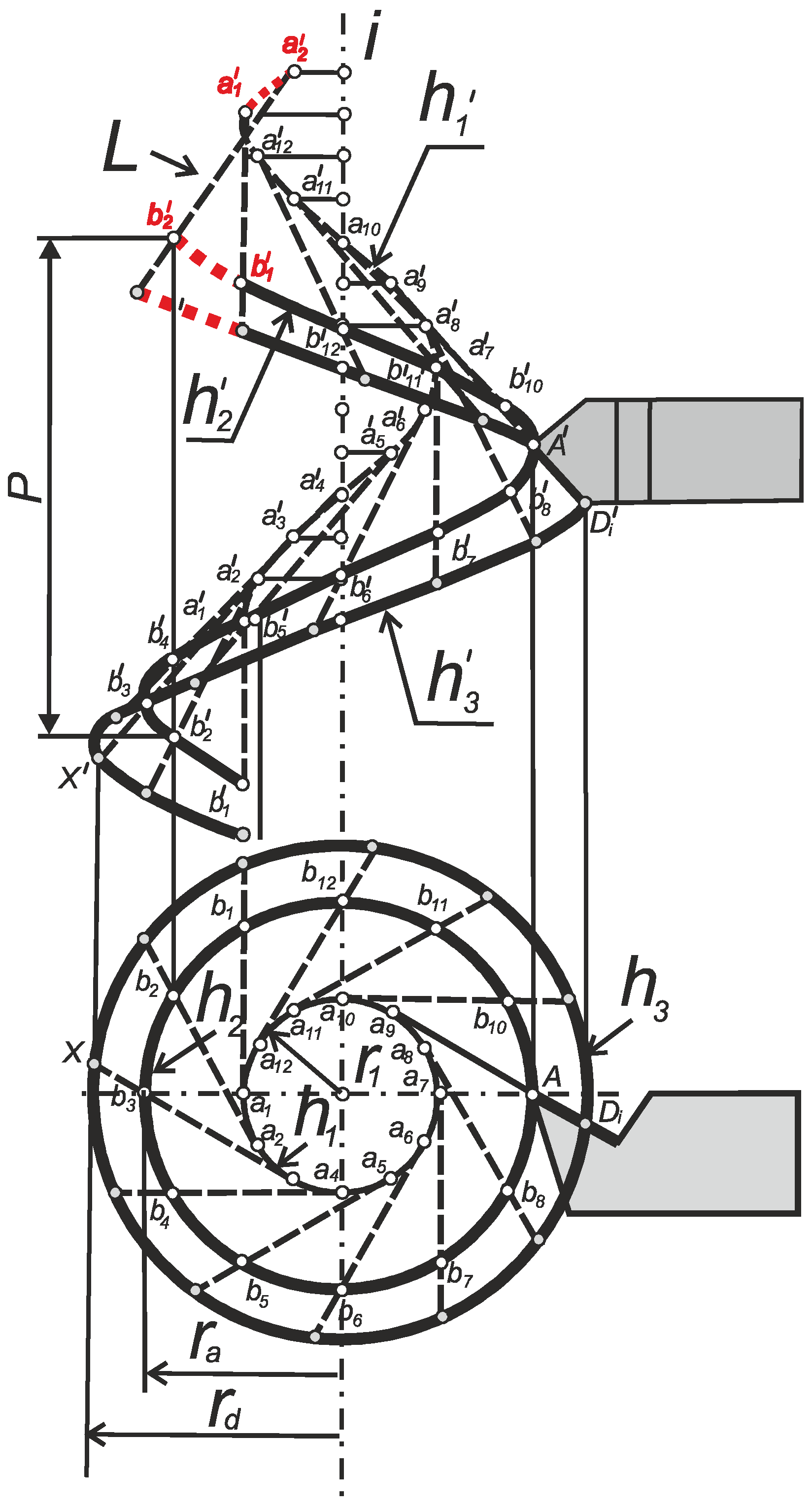
2.4. Analytical Method of Screw Thread Model Using Tool Cutting-Edge Inclination Angle Parameter
3. Theoretical Results
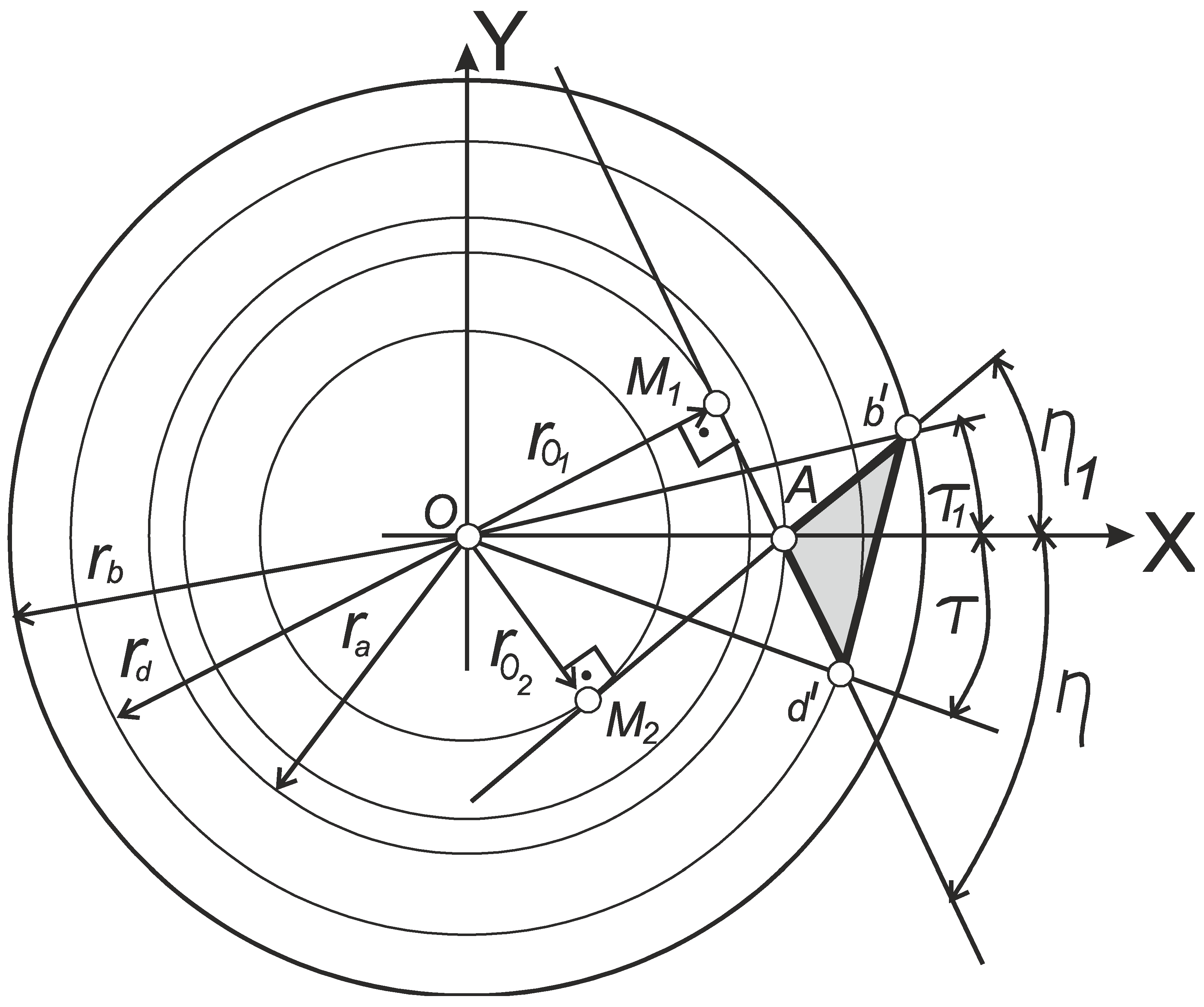
3.1. Function Dependence of Thread Profile on Double Parameter: Rake and Cutting-Edge Inclination Angle
3.2. Definition of Angles η and η1
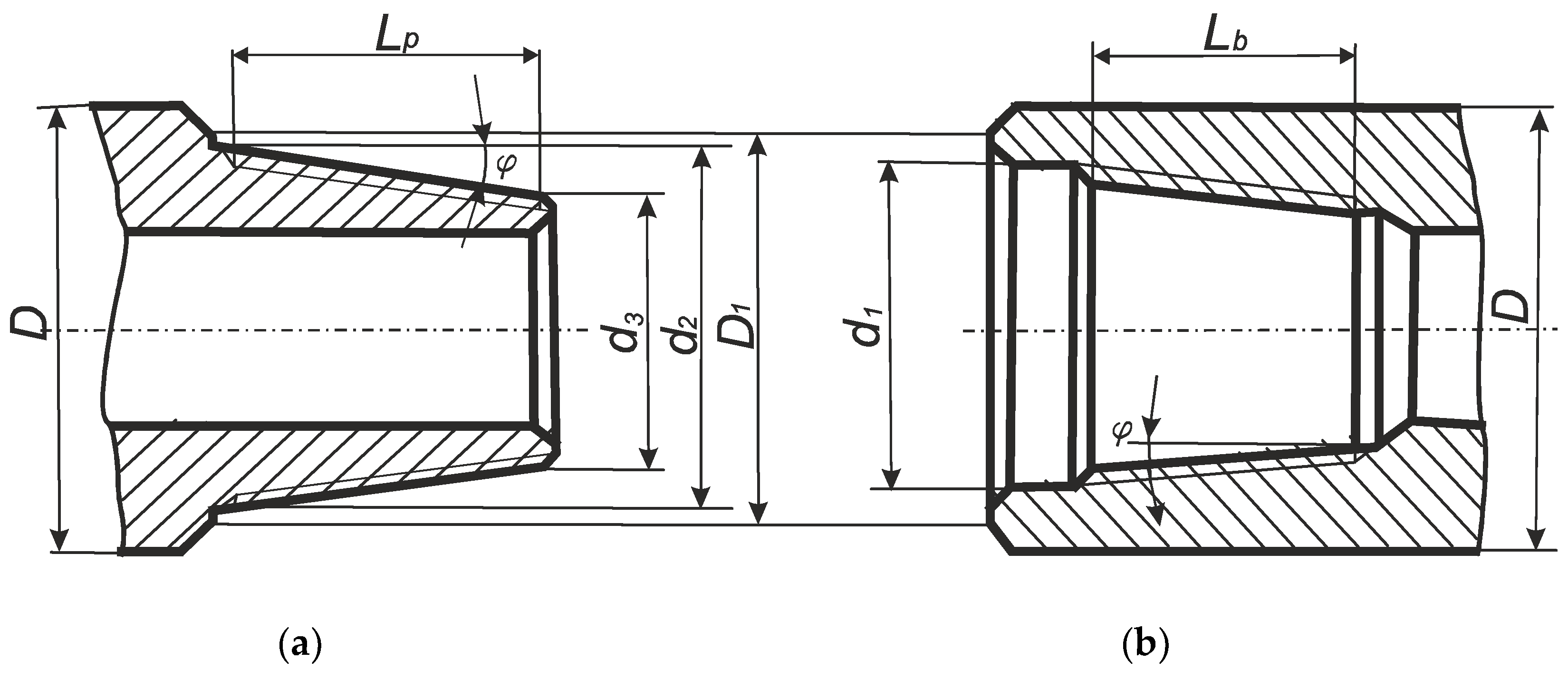
4. Modeling a Tapered Thread Profile for Drill Strings
4.1. Investigation of NC23 Drill-String Tool-Joint Thread Profile Accuracy
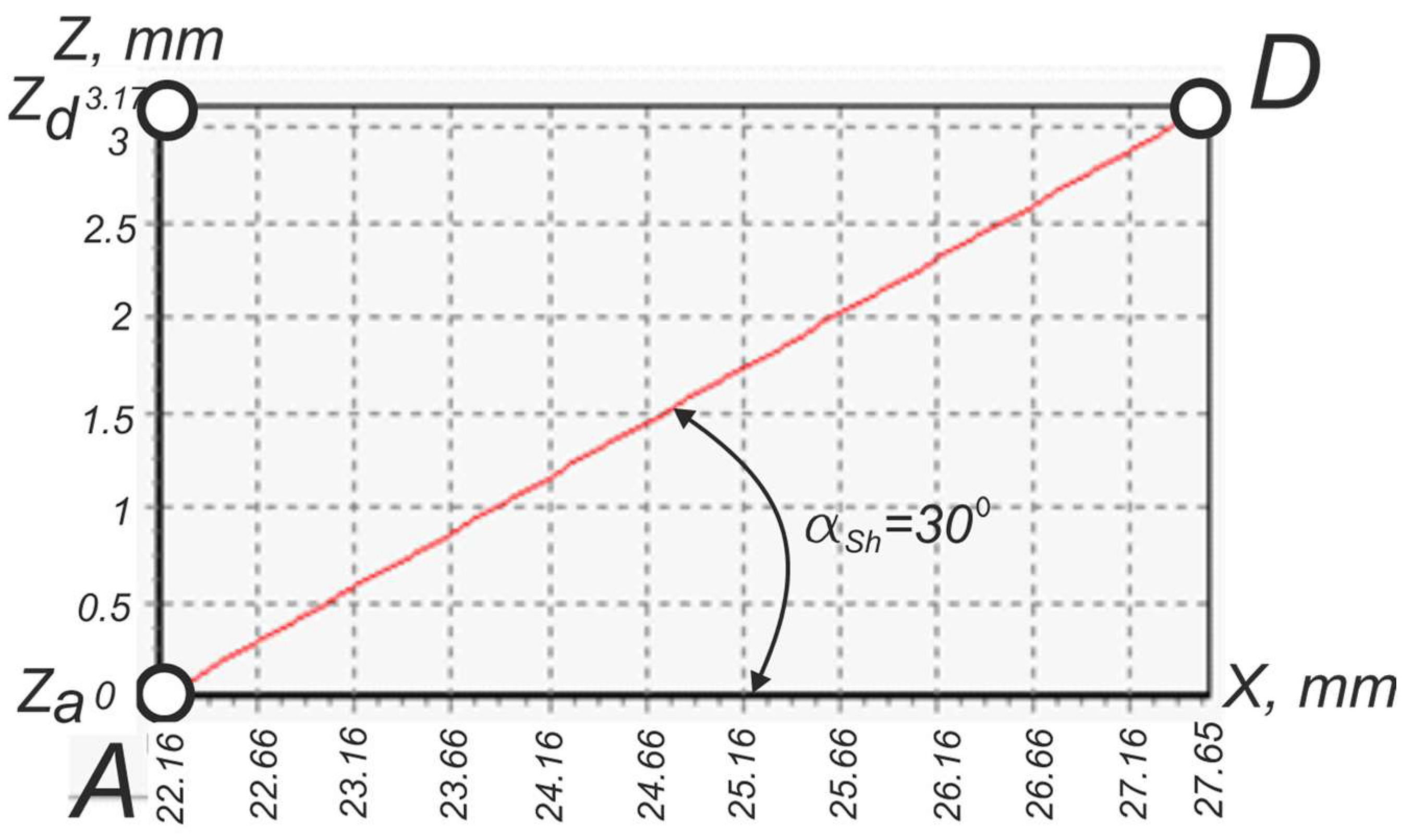
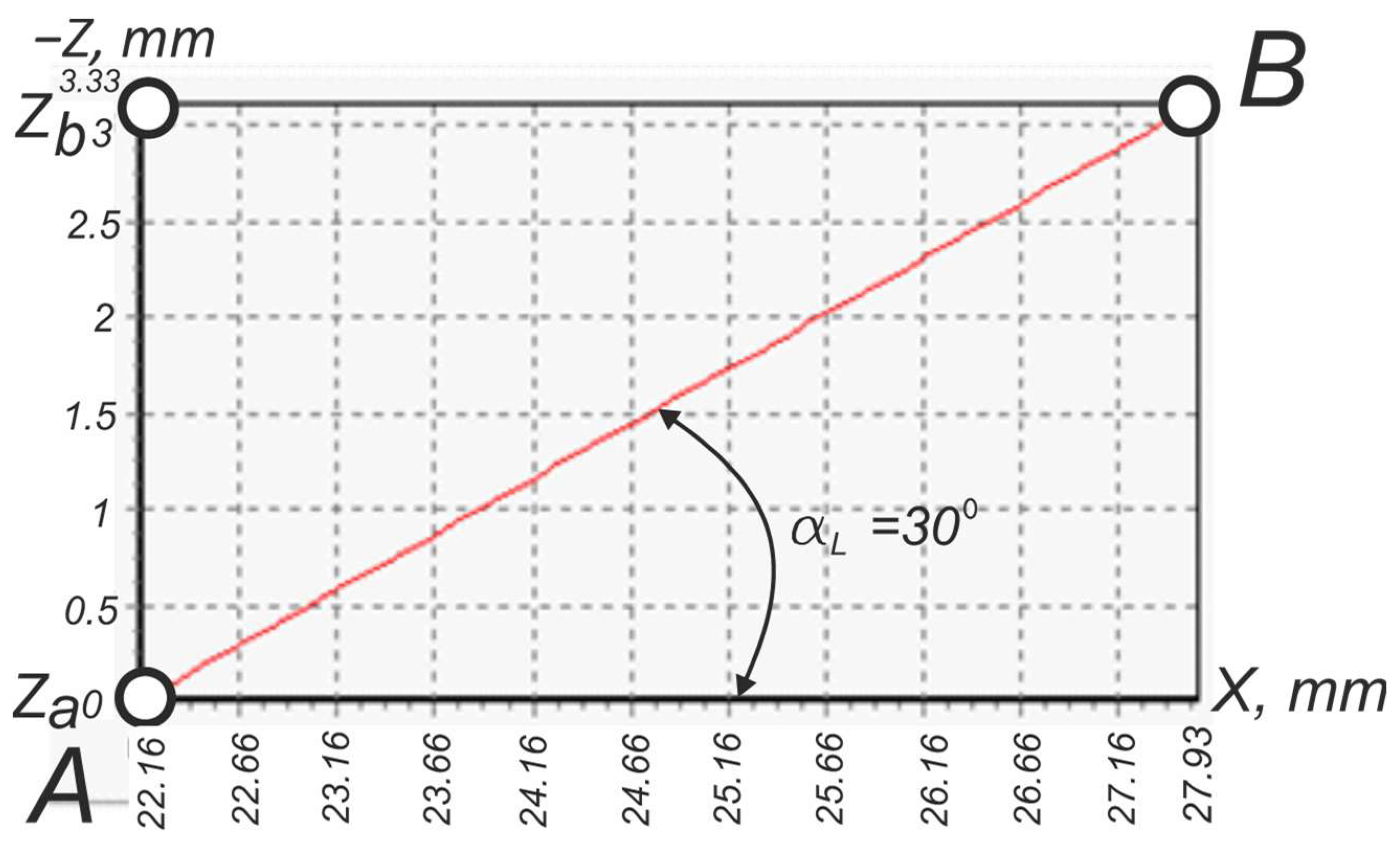
4.2. Visual Analytical Research of NC23 Made by Lathe Cutter with Zero-Angle Parameters
4.3. Visual Analytical Research of NC23 Made by Lathe Cutter with Non-Zero-Angle Parameters
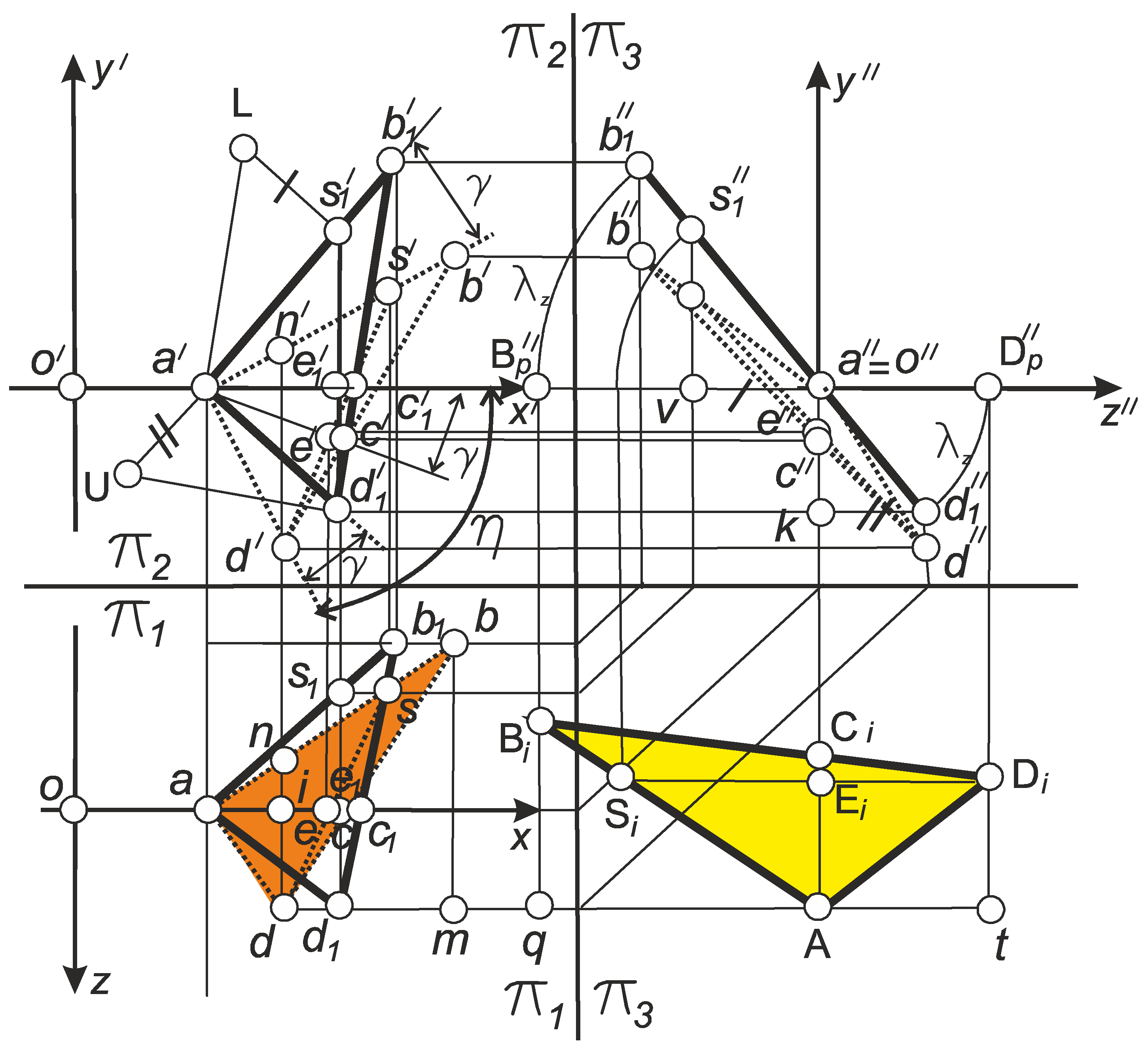
4.3.1. Analysis of the Flank Profile Models of Thread
4.3.2. Modeling of the Side Profile of the NC23 Drill-String Thread Made by Turning Tool with Rake Angle γ = 12°
4.4. The Results of Side Profile Modeling of the NC56 Drill-String Thread Made by Turning Tool with Non-Zero Rake Angle
5. Conclusions
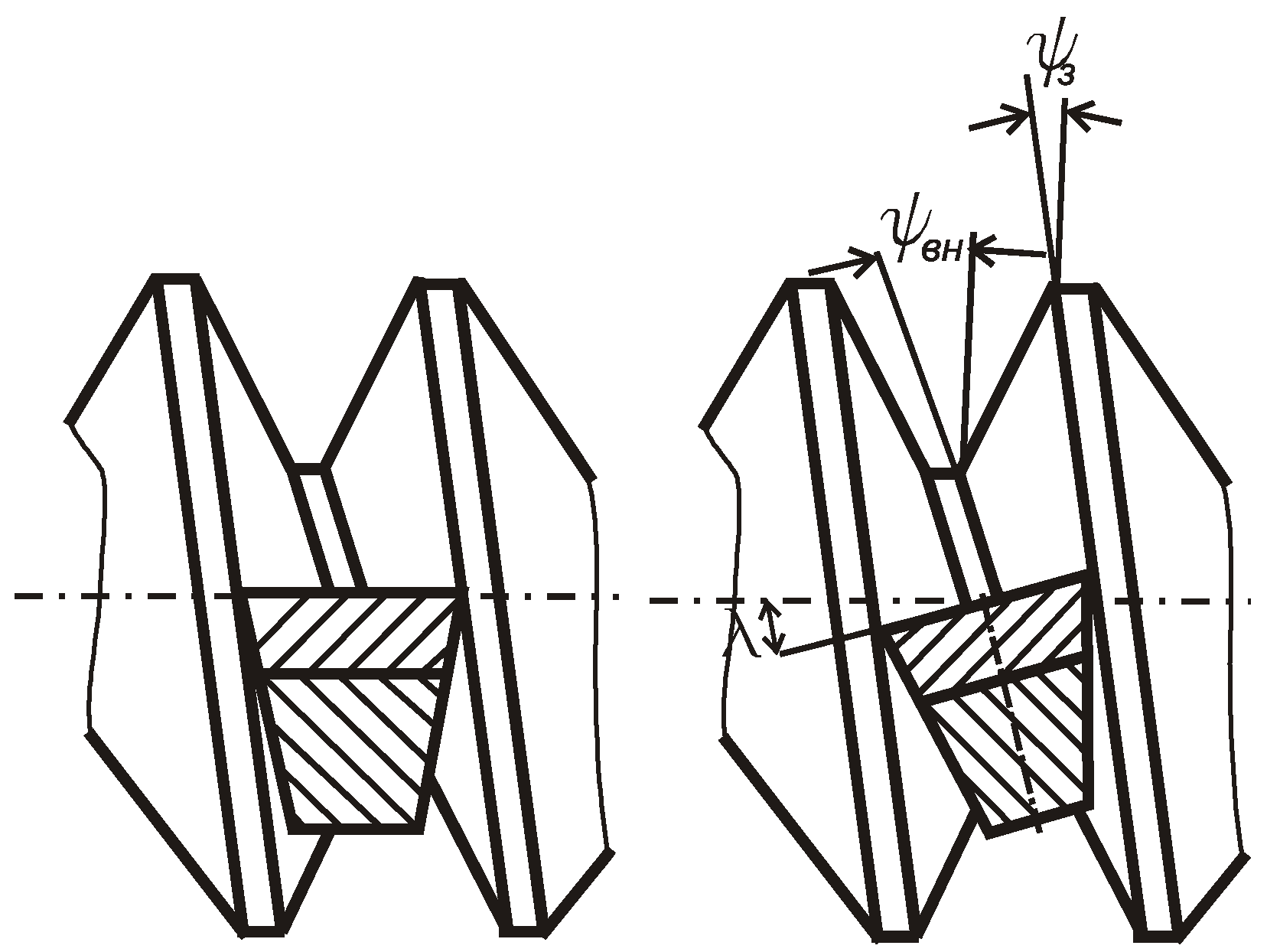
- For an effective threading process on workpieces made of different machinability materials, cutters should be used with selected non-zero geometric parameters, namely the rake angle and the inclination angle of the cutting edge. This causes the surfaces of the conical or cylindrical threads to be obtained with the help of the specified cutters which consist of two convolute helicoids.
- The axial profile of a thread formed in this way does not contain rectilinear lateral flanks, but only curved ones.
- The curvilinear profile of the lateral flanks is mathematically represented as a transcendental function, in which the parameters are the actual parameters of the thread: the diameter, pitch, and geometric parameters of the thread cutter: rake angle, half-profile angle, and inclination angle of its cutting edge.
- In case of using the known or scientifically justified values of the rake angles of thread-turning cutters up to 8–12°, the obtained flank profile of the thread becomes close to rectilinear, and the value of the thread half-profile angles can be within the tolerance field for angular deviation.
- As the value of the tool rake angle decreases to 4° and the threaded part diameter increases from 65 up to 117 (mm), the value of the predicted thread half-profile angle approaches the nominal value.
- In the case of using zero values of the geometric parameters of the thread-turning cutter, the convolute helicoid as part of the thread surface changes to an oblique closed helicoid (Archimedes’ screw), and its profile contains a straight flank line.
- In the case of exactly zero values of the geometric parameters of the thread-turning cutter, namely the inclination angle of the edge and the rake angle, the transcendental expression describing the lateral thread profiles turns into a linear algebraic equation describing the profile of standard threads.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Huang, H.; Bi, W.; Ji, G.; Zhou, B.; Zhuo, L. Deep and ultra-deep oil and gas well drilling technologies: Progress and prospect. Nat. Gas Ind. B 2022, 9, 141–157. [Google Scholar] [CrossRef]
- Sharmin, T.; Rodoshi Khan, N.; Md Saleh Akram; Ehsan, M.A. State-of-the-Art Review on Geothermal Energy Extraction, Utilization, and Improvement Strategies: Conventional, Hybridized, and Enhanced Geothermal Systems. Int. J. Thermofluids 2023, 18, 100323. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, K.; Meng, G.; Suo, X. Optimization of Recharge Schemes for Deep Excavation in the Confined Water-Rich Stratum. Sustainability 2023, 15, 5432. [Google Scholar] [CrossRef]
- Chen, F.; Huo, Y.; Zhao, H.; Di, Q.; Wang, W.; Zhou, X.; Zhang, Y. The effect of axial tension and borehole curvature on torsion limit of drill string threaded connections. Eng. Fail. Anal. 2021, 127, 105555. [Google Scholar] [CrossRef]
- ISO 11961:2018; International Standard. Petroleum and Natural Gas Industries—Steel Drill Pipe (MOD), 2nd ed. 1 November 2008. ISO: Geneva, Switzerland, 2008.
- GOST R 50278-92; Drill Pipes with Weld-On Tool Joints. Specifications IS: Moscow, Russia, 1992. (In Russian)
- Vlasiy, O.; Mazurenko, V.; Ropyak, L.; Rogal, O. Improving the aluminum drill pipes stability by optimizing the shape of protector thickening. East. Eur. J. Enterp. Technol. 2017, 1, 25–31. [Google Scholar] [CrossRef]
- Bazaluk, O.; Slabyi, O.; Vekeryk, V.; Velychkovych, A.; Ropyak, L.; Lozynskyi, V. A technology of hydrocarbon fluid production intensification by productive stratum drainage zone reaming. Energies 2021, 14, 3514. [Google Scholar] [CrossRef]
- Chudyk, I.; Velychkovych, A.; Grydzhuk, J. A Modeling of the Inertia Properties of a Drill String Section as a Continual Bent Rotating Rod. SOCAR Proc. 2021, 2021, 24–32. [Google Scholar] [CrossRef]
- Prysyazhnyuk, P.; Molenda, M.; Romanyshyn, T.; Ropyak, L.; Romanyshyn, L.; Vytvytskyi, V. Development of a hardbanding material for drill pipes based on high-manganese steel reinforced with complex carbides. Acta Montan. Slovaca 2022, 27, 685–696. [Google Scholar]
- Bembenek, M.; Prysyazhnyuk, P.; Shihab, T.; Machnik, R.; Ivanov, O.; Ropyak, L. Microstructure and Wear Characterization of the Fe-Mo-B-C—Based Hardfacing Alloys Deposited by Flux-Cored Arc Welding. Materials 2022, 15, 5074. [Google Scholar] [CrossRef]
- Grydzhuk, J.S.; Dzhus, A.P.; Grydzhuk, J.S.; Dzhus, A.P.; Yurych, A.R.; Yurych, L.R.; Riznychuk, A.I.; Pylypaka, O.P. Approbation of the method for ensuring operational reliability and evaluating the residual life of drill string elements. In Proceedings of the 16th International Conference Monitoring of Geological Processes and Ecological Condition of the Environment, Monitoring 2022, Kyiv, Ukraine, 15–18 November 2022; EAGE: Amsterdam, The Netherlands, 2022; pp. 1–5. [Google Scholar]
- Kopei, V.; Onysko, O.; Kusyi, Y.; Vriukalo, V.; Lukan, T. Investigation of the Influence of tapered Thread Pitch Deviation on the Drill-String Tool-Joint Fatigue Life. In Lecture Notes in Networks and Systems, New Technologies, Development and Application V. NT 2022; Karabegović, I., Kovačević, A., Mandžuka, S., Eds.; Springer: Cham, Switzerland, 2023; Volume 472, pp. 144–154. [Google Scholar]
- Shatskyi, I.; Ropyak, L.; Velychkovych, A. Model of contact interaction in threaded joint equipped with spring-loaded collet. Eng. Solid Mech. 2020, 8, 301–312. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Fini, S.; Mele, M.; Olmi, G.; Scapecchi, C.; Tariq, M.H.B. Failure of Threaded Connections: A Literature Review. Machines 2023, 11, 212. [Google Scholar] [CrossRef]
- Ropyak, L.Y.; Vytvytskyi, V.S.; Velychkovych, A.S.; Pryhorovska, T.O.; Shovkoplias, M.V. Study on grinding mode effect on external conical thread quality. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1018, 012014. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, C.; Kong, L.; Zhou, Q.; Gong, J. Design Optimization for the Thin-Walled Joint Thread of a Coring Tool Used for Deep Boreholes. Appl. Sci. 2020, 10, 2669. [Google Scholar] [CrossRef]
- Grydzhuk, J.; Chudyk, I.; Velychkovych, A.; Andrusyak, A. Analytical estimation of inertial properties of the curved rotating section in a drill string. East. Eur. J. Enterp. Technol. 2019, 1, 6–14. [Google Scholar] [CrossRef]
- Pryhorovska, T.O.; Ropyak, L. Machining Error Influnce on Stress State of Conical Thread Joint Details. In Proceedings of the 8th International Conference on Advanced Optoelectronics and Lasers (CAOL 2019), Sozopol, Bulgaria, 6–8 September 2019; pp. 493–497. [Google Scholar]
- Tutko, T.; Dubei, O.; Ropyak, L.; Vytvytskyi, V. Determination of Radial Displacement Coefficient for Designing of Thread Joint of Thin-Walled Shells. In Lecture Notes in Mechanical Engineering, Advances in Design, Simulation and Manufacturing IV. DSMIE 2021; Ivanov, V., Trojanowska, J., Pavlenko, I., Zajac, J., Peraković, D., Eds.; Springer: Cham, Switzerland, 2021; pp. 153–162. [Google Scholar]
- Onysko, O.; Panchuk, V.; Kusyi, Y.; Odosii, Z.; Lukan, T. Impact of the Tool’s Flank Clearance Angle on the Pitch Diameter Accuracy of the Tool-Joint Tapered Thread. In Lecture Notes in Mechanical Engineering, Advances in Design, Simulation and Manufacturing V. DSMIE 2022; Ivanov, V., Trojanowska, J., Pavlenko, I., Rauch, E., Peraković, D., Eds.; Springer: Cham, Switzerland, 2022; pp. 312–321. [Google Scholar]
- Kopei, V.; Onysko, O.; Odosii, Z.; Pituley, L.; Goroshko, A. Investigation of the influence of tapered thread profile accuracy on the mechanical stress, fatigue safety factor and contact pressure. In Lecture Notes in Networks and Systems, New Technologies, Development and Application IV. NT 2021; Karabegović, I., Ed.; Springer: Cham, Switzerland, 2021; Volume 233, pp. 177–185. [Google Scholar]
- Dubei, O.Y.; Tutko, T.F.; Ropyak, L.Y.; Shovkoplias, M.V. Development of Analytical Model of Threaded Connection of Tubular Parts of Chrome-Plated Metal Structures. Metallofiz. Noveishie Tekhnol. 2022, 44, 251–272. [Google Scholar] [CrossRef]
- Rong, L.; Tie, Z.; Wu, X.J.; Wang, C.H. Crack closure effect on stress intensity factors of an axially and a circumferentially cracked cylindrical shell. Int. J. Fract. 2004, 125, 227–248. [Google Scholar]
- Shats’kyi, I.P. Closure of a longitudinal crack in a shallow cylindrical shell in bending. Mater. Sci. 2005, 41, 186–191. [Google Scholar] [CrossRef]
- Shatskii, I.P.; Makoviichuk, N.V. Effect of closure of collinear cracks on the stress-strain state and the limiting equilibrium of bent shallow shells. J. Appl. Mech. Tech. Phys. 2011, 52, 464–470. [Google Scholar] [CrossRef]
- Adizova, A.; Abdieva, G.; Mavlanov, T. Computer modelling of dynamics of the thread in technological process. J. Phys. Conf. Ser. 2022, 2373, 022060. [Google Scholar] [CrossRef]
- Saber, M.; Chouikhi, H. Finite Element Analyses of Bolted Joints Using Different Thread Modelling Techniques. Teh. Vjesn. 2022, 30, 178–184. [Google Scholar] [CrossRef]
- Merticaru, V.; Nagît, G.; Dodun, O.; Merticaru, E.; Ripanu, M.I.; Mihalache, A.M.; Slatineanu, L. Influence of Machining Conditions on Micro-Geometric Accuracy Elements of Complex Helical Surfaces Generated by Thread Whirling. Micromachines 2022, 13, 1520. [Google Scholar] [CrossRef] [PubMed]
- Bracken, P. Helicoidal Surfaces and Their Relationship to Bonnet Surfaces. Adv. Pure Math. 2017, 7, 31–40. [Google Scholar] [CrossRef][Green Version]
- Bazaluk, O.; Velychkovych, A.; Ropyak, L.; Pashechko, M.; Pryhorovska, T.; Lozynskyi, V. Influence of heavy weight drill pipe material and drill bit manufacturing errors on stress state of steel blades. Energies 2021, 14, 4198. [Google Scholar] [CrossRef]
- Demirpolat, H.; Binali, R.; Patange, A.D.; Pardeshi, S.S.; Gnanasekaran, S. Comparison of Tool Wear, Surface Roughness, Cutting Forces, Tool Tip Temperature, and Chip Shape during Sustainable Turning of Bearing Steel. Materials 2023, 16, 4408. [Google Scholar] [CrossRef] [PubMed]
- Sitarz, P.; Powałka, B. A new approach to improve noncircular turning process. Int. J. Adv. Manuf. Technol. 2019, 104, 3343–3360. [Google Scholar] [CrossRef]
- Zhao, G.; Zhao, B.; Ding, W.; Xin, L.; Nian, Z.; Peng, J.; He, N.; Xu, J. Nontraditional energy-assisted mechanical machining of difficult-to-cut materials and components in aerospace community: A comparative analysis. Int. J. Extrem. Manuf. 2024, 6, 022007. [Google Scholar] [CrossRef]
- Baizeaua, T.; Campocasso, S.; Fromentin, G.; Rossi, F.; Poulachon, G. Effect of rake angle on strain field during orthogonal cutting of hardened steel with c-BN tools. Procedia CIPR 2015, 31, 166–171. [Google Scholar] [CrossRef]
- Litvin, F.; Gonzalez-Perez, I.; Yukishima, K.; Fuentes, A.; Hayasaka, K. Design, simulation of meshing, and contact stresses for an improved worm gear drive. Mech. Mach. Theory 2007, 42, 940–959. [Google Scholar] [CrossRef]
- Kusyi, Y.; Stupnytskyy, V.; Onysko, O.; Dragašius, E. Optimization synthesis of technological parameters during manufacturing of the parts. Eksploat. I Niezawodn. 2022, 24, 655–667. [Google Scholar] [CrossRef]
- Ivchenko, O.; Ivanov, V.; Trojanowska, J.; Zhyhylii, D.; Ciszak, O.; Zaloha, O.; Pavlenko, I.; Hladyshev, D. Method for an Effective Selection of Tools and Cutting Conditions during Precise Turning of Non-Alloy Quality Steel C45. Materials 2022, 15, 505. [Google Scholar] [CrossRef]
- Petrakov, Y.; Danylchenko, M. A Time-Frequency Approach to Ensuring Stability of Machining by Turning. East. Eur. J. Enterp. Technol. 2022, 6, 85. [Google Scholar]
- Pasternak, S.; Danylchenko, Y.M.; Storchak, M.; Okhrimenko, O.A. Gear Cutting with Disk-Shaped Milling Cutters. In Advances in Gear Theory and Gear Cutting Tool Design; Radzevich, S.P., Storchak, M., Eds.; Springer: Cham, Switzerland, 2022; pp. 151–179. [Google Scholar]
- Danylchenko, Y.M.; Kryvosheia, A.V.; Melnyk, V.Y.; Tkach, P.M. Generalizing Structural Unified Model of the Synthesis of Links of Flat-Toothed Gearing Systems. In Advances in Gear Theory and Gear Cutting Tool Design; Radzevich, S.P., Storchak, M., Eds.; Springer: Cham, Switzerland, 2022; pp. 445–483. [Google Scholar]
- Gu, W.; Li, C.; Miao, J.; Wang, P.; Chen, B. Wear Prediction Method of Differential Planetary Roller Screws Considering the Ambient Temperature Variations. Appl. Sci. 2023, 13, 10609. [Google Scholar] [CrossRef]
- Yeh, S.-S.; Jiang, W.-J. Development of Pitch Cycle-Based Iterative Learning Contour Control for Thread Milling Operations in CNC Machine Tools. Appl. Sci. 2023, 13, 6447. [Google Scholar] [CrossRef]
- Del Val, A.G.; Veiga, F.; Pereira, O.; De Lacalle, L.N.L. Threading Performance of Different Coatings for High Speed Steel Tapping. Coatings 2020, 10, 464. [Google Scholar] [CrossRef]
- Del Val, A.G.; Veiga, F.; Suárez, A.; Arizmendi, M. Thread Quality Control in High-Speed Tapping Cycles. J. Manuf. Mater. Process. 2020, 4, 9. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Xu, K. Automatic Measurement of External Thread at the End of Sucker Rod Based on Machine Vision. Sensors 2022, 22, 8276. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Jiang, L.; Chen, M. Experimental Study on the Influence of Cutting Parameters on Thread Precision of External Thread Turning. MSF 2013, 770, 7–12. [Google Scholar] [CrossRef]
- Araujo, A.C.; Mello, G.M.; Cardoso, F.G. Thread milling as a manufacturing process for API threaded connection: Geometrical and cutting force analysis. J. Manuf. Process. 2015, 18, 75–83. [Google Scholar] [CrossRef]
- Lin, E.-Y.; Chen, J.-C.; Lien, J.-J.J. Intelligent Tapping Machine: Tap Geometry Inspection. Sensors 2023, 23, 8005. [Google Scholar] [CrossRef]
- Li, Z.; Fu, X.; Li, J.; Jiang, B.; Wang, F. Establishment of vibration wear model for turning large-pitch thread tools and its wear suppression method. Int. J. Adv. Manuf. Technol. 2020, 109, 857–876. [Google Scholar] [CrossRef]
- Khoshdarregi, M.R.; Altintas, Y. Dynamics of Multipoint Thread Turning—Part I: General Formulation. J. Manuf. Sci. Eng. 2018, 140, 061003. [Google Scholar] [CrossRef]
- Koleva, S.; Enchev, M.; Szecsi, T. Compensation of the deviations caused by mechanical deformations during machining of threads. Procedia Manuf. 2017, 13, 480–486. [Google Scholar] [CrossRef]
- Khoshdarregi, M.R.; Altintas, Y. Generalized modeling of chip geometry and cutting forces in multi-point thread turning. Int. J. Mach. Tools Manuf. 2015, 98, 21–32. [Google Scholar] [CrossRef]
- Khani, S.; Shahabi, H.S.; Razfar, M.R.; Farahnakian, M. Improvement of thread turning process using micro-hole textured solid-lubricant embedded tools. Proc. Inst. Mech. Eng. Part. B J. Eng. Manuf. 2021, 235, 1727–1738. [Google Scholar] [CrossRef]
- Khoshdarregi, M.R.; Altintas, Y. Dynamics of Multipoint Thread Turning—Part II: Application to Thin-Walled Oil Pipes. J. Manuf. Sci. Eng. 2018, 140, 041016. [Google Scholar] [CrossRef]
- Krawczyk, B.; Szablewski, P.; Mendak, M.; Gapiński, B.; Smak, K.; Legutko, S.; Wieczorowski, M.; Miko, E. Surface Topography Description of Threads Made with Turning on Inconel 718 Shafts. Materials 2022, 16, 80. [Google Scholar] [CrossRef] [PubMed]
- Neshta, A.; Kryvoruchko, D.; Hatala, M.; Ivanov, V.; Botko, F.; Radchenko, S.; Mital, D. Technological Assurance of High-Efficiency Machining of Internal Rope Threads on Computer Numerical Control Milling Machines. J. Manuf. Sci. Eng. 2018, 140, 071012. [Google Scholar] [CrossRef]
- He, Q.; Jiang, Y.; Jing, X.; Jiang, Y.; Zhou, H.; Fu, B. Research and Optimization of Process Parameters for Internal Thread Forming Based on Numerical Simulation and Experimental Analysis. Materials 2022, 15, 3160. [Google Scholar] [CrossRef]
- Chen, T.-C.; Lian, J.-J.; Wang, C.-C. Analysis of Micro-Machining Process for External Thread of Micro Round Tube. Materials 2021, 14, 4327. [Google Scholar] [CrossRef]
- Zanger, F.; Sellmeier, V.; Klose, J.; Bartkowiak, M.; Schulze, V. Comparison of modeling methods to determine cutting tool profile for conventional and synchronized whirling. Procedia CIPR 2017, 58, 222–227. [Google Scholar] [CrossRef]
- Onysko, O.; Panchuk, V.; Kopei, V.; Pituley, L.; Lukan, T. Influence of Back Rake Angle of a Threading Cutter on the Drill-String Tool-Joint Pitch Diameter. In Lecture Notes in Mechanical Engineering, Grabchenko’s International Conference on Advanced Manufacturing Processes (InterPartner 2022); Tonkonogyi, V., Ivanov, V., Eds.; Springer: Cham, Switzerland, 2023; pp. 200–210. [Google Scholar]
- Kacalak, W.; Majewski, M.; Budniak, Z.; Ponomarenkow, J. Worm Gear Drives with Improved Kinematic Accuracy. Materials 2021, 14, 7825. [Google Scholar] [CrossRef]
- API SREC 7-2; Specification for Threading and Gauging of Rotary Shouldered Thread Connection, Second Edition. API: Washington, DC, USA, 2020.
- Sandvik Coromant. Tread Turning Tools. Available online: https://www.sandvik.coromant.com/en-us/tools/threading-tools/thread-turning-tools (accessed on 11 March 2024).
- Costa, C.E.; Polli, M.L. Effects of the infeed method on thread turning of AISI 304L stainless steel. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 253. [Google Scholar] [CrossRef]
- Günay, M. Investigation of the Effects on Screw Thread of Infeed Angle during External Threading. Gazi Univ. J. Sci. 2011, 24, 153–160. [Google Scholar]
- An, Q.L.; Guo, G.G.; Zheng, X.H.; Chen, M.; Liu, G.; Zhang, Y.S. Experimental Study on Cutting Characteristics for Buttress Thread Turning of 13%Cr Stainless Steel. Key Eng. Mater. 2010, 443, 262–267. [Google Scholar] [CrossRef]
- Onysko, O.; Kopei, V.; Vytvytskyi, V.; Vriukalo, V.; Lukan, T. Calculation of the Accuracy of the Drill-String NC13 Thread Profile Turned from Difficult-to-Machine Steel. In Lecture Notes in Mechanical Engineering; Advanced Manufacturing Processes V. InterPartner 2023; Tonkonogyi, V., Ivanov, V., Eds.; Springer: Cham, Switzerland, 2024; pp. 182–192. [Google Scholar] [CrossRef]
- Workpiece Material Group. Available online: https://5wyuco84ao39w9tsgkkmnmx.blob.core.windows.net/cms/WMG_summary.pdf (accessed on 19 April 2024).
- 630 (1.4542) Stainless Steel. Available online: https://bircelik.com/en/category/630-1-4542 (accessed on 19 April 2024).
- Onysko, O.; Medvid, I.; Panchuk, V.; Rodic, V.; Barz, C. Geometric Modeling of Lathe Cutters for Turning High-Precision Stainless Steel Tapered Threads. In Lecture Notes in Mechanical Engineering, Advances in Design, Simulation and Manufacturing IV. DSMIE 2021; Ivanov, V., Trojanowska, J., Pavlenko, I., Zajac, J., Peraković, D., Eds.; Springer: Cham, Switzerland, 2021; pp. 472–480. [Google Scholar]
- Caltaru, M.; Ripeanu, R.; Badicioiu, R.; Zisopol, D.R. Experimental Researches to Establish the Optimum Hardbanding Technology and Materials of the Heavy Weight Drill Pipe. MATEC Web Conf. 2020, 318, 01017. [Google Scholar] [CrossRef]
- JFE-TC. UHPTM-15CR-125. Available online: https://jfetc.com/product/uhp-15cr/ (accessed on 19 April 2024).
- Medvid, I.; Onysko, O.; Panchuk, V.; Pituley, L.; Schuliar, I. Kinematics of the Tapered Thread Machining by Lathe: Analytical Study. In Lecture Notes in Mechanical Engineering, Advanced Manufacturing Processes II (InterPartner 2020); Tonkonogyi, V., Ivanov, V., Trojanowska, J., Oborskyi, G., Grabchenko, A., Pavlenko, I., Edl, M., Kuric, I., Dasic, P., Eds.; Springer: Cham, Switzerland, 2021; pp. 555–565. [Google Scholar]
- Slătineanu, L.; Radovanovic, M.; Coteață, M.; Beșliu, I.; Dodun, O.; Coman, I.; Olaru, S.-C. Requirements in designing a device for experimental investigation of threading accuracy. MATEC Web Conf. 2017, 112, 01005. [Google Scholar] [CrossRef]
- Boral, P.; Gołębski, R. Technology of Manufacturing of ZC Cylindrical Worm. Materials 2022, 15, 6412. [Google Scholar] [CrossRef]
- Andrianto, M.; Wu, Y.R.; Arifin, A. Mathematical modeling on a novel manufacturing method for roller-gear cams using a whirl-machining process. Int. J. Adv. Manuf. Technol. 2023, 125, 5015–5029. [Google Scholar] [CrossRef]
- Kacalak, W.; Szafraniec, F. Analiza kształtu i położenia strefy obróbki w procesie szlifowania powierzchni śrubowych ślimaków stożkowych. Mechanik 2015, 8–9, 159–163. [Google Scholar]
- Onysko, O.; Kopei, V.; Kusyj, Y.; Kornuta, O.; Schuliar, I. Turning of NC10 Threads for Drill Pipes: Theoretical Study of the Designed Profile. In Lecture Notes in Mechanical Engineering, Advances in Design, Simulation and Manufacturing VI. DSMIE 2023; Ivanov, V., Trojanowska, J., Pavlenko, I., Rauch, E., Piteľ, J., Eds.; Springer: Cham, Switzerland, 2023; pp. 356–366. [Google Scholar]
- Onysko, O.R. The Theoretical Foundations of the Threading Tool Bits Designing for Lathe Machining of the Drill String Tool-Joint Connectors with the Increased Operating Characteristics. Ph.D. Thesis, Odessa National Polytechnic University, Odessa, Ukraine, 2020. (In Ukrainian). [Google Scholar]
- Fromentin, G.; Poulachon, G. Geometrical analysis of thread milling—Part 1: Evaluation of tool angles. Int. J. Adv. Manuf. Technol. 2010, 49, 73–80. [Google Scholar] [CrossRef]
- Fu, X.; Li, K.; Li, Z.; Wang, X. A SVM-based design method for cutting edge profile stability of large-pitch thread turning tool considering vibration. Int. J. Adv. Manuf. Technol. 2023, 125, 4529–4547. [Google Scholar] [CrossRef]




| Name of Property, Unit | Values of Mechanical Properties due to Strength Groups of Steel | |||||
|---|---|---|---|---|---|---|
| D | E | X | G | S | Y (GOST Only) | |
| Tensile strength σ, MPa | 655 | 689 | 724 | 793 | 1000 | 1241 |
| Flow stress σf, MPa (min) | 379 | 517 | 655 | 724 | 931 | 1170 |
| Flow stress σf, MPa (max) | - | 724 | 862 | 931 | 1138 | - |
| Group of Machine Parts | Grade of Steel | Machinability Range MC Code/WMG | Rake Angle | Reference |
|---|---|---|---|---|
| Pump shafts, marine applications, petrochemical industries | AISI 630 stainless steel DIN X5CrNiCuNb16-4 EN 1.4542 | P5.0.Z.PH M3.3 2800 N/mm2 | - | [70] |
| Automotive part production, machine industry | AISI 416 stainless steel DIN X12CrS13 | P5.0.Z.PH 2800 N/mm2 | +12° | [67,71] |
| Machine parts in corrosion environment | AISI 304L stainless steel DIN X5CrNi18-10 | M3.1 M1.1.Z.AQ 2000 N/mm2 | - | [66] |
| Heavy-weight drill pipes, bolts, gears | AISI 4145 H 46MoMnCr01 low-alloy steel | P3.3 | - | [72] |
| Drill pipes provide superior corrosion resistance at high temperatures | JFE-UHPTM –15CR-125 (Japan) 0.03C-15Cr-6Ni-2Mo-1Cu stainless steel | M2.3 | - | [73] |
| Heavy-weight drill pipes | GOST 35X3HMA high-alloy steel | P3.3 | −7° | [68] |
| Drill-string pipes and tool joints | high-strength low-alloy steels | −5° | [61] |
| No. | Parameter Name, Dimension | Marking | Value |
|---|---|---|---|
| 1 | Pitch, mm | P | 6.35 |
| 2 | Tapered angle, ° | φ | 4.763 |
| 3 | Thread height (not truncated), mm | H | 5.487 |
| 4 | Thread height (truncated), mm | h | 3.095 |
| 5 | Root truncation, mm | fc | 1.427 |
| 6 | Crest truncation, mm | fr | 0.965 |
| 7 | Angular depth, mm | h1 | 2.633 |
| 8 | The outer thread diameter of the small base of the cone of pin, mm | d3 | 52.433 |
| 9 | Half-profile angle, ° | α | 30 |
| Long Side | Root | Short Side | Short Side Truncated | Long Side Truncated | ||
|---|---|---|---|---|---|---|
| mm | ||||||
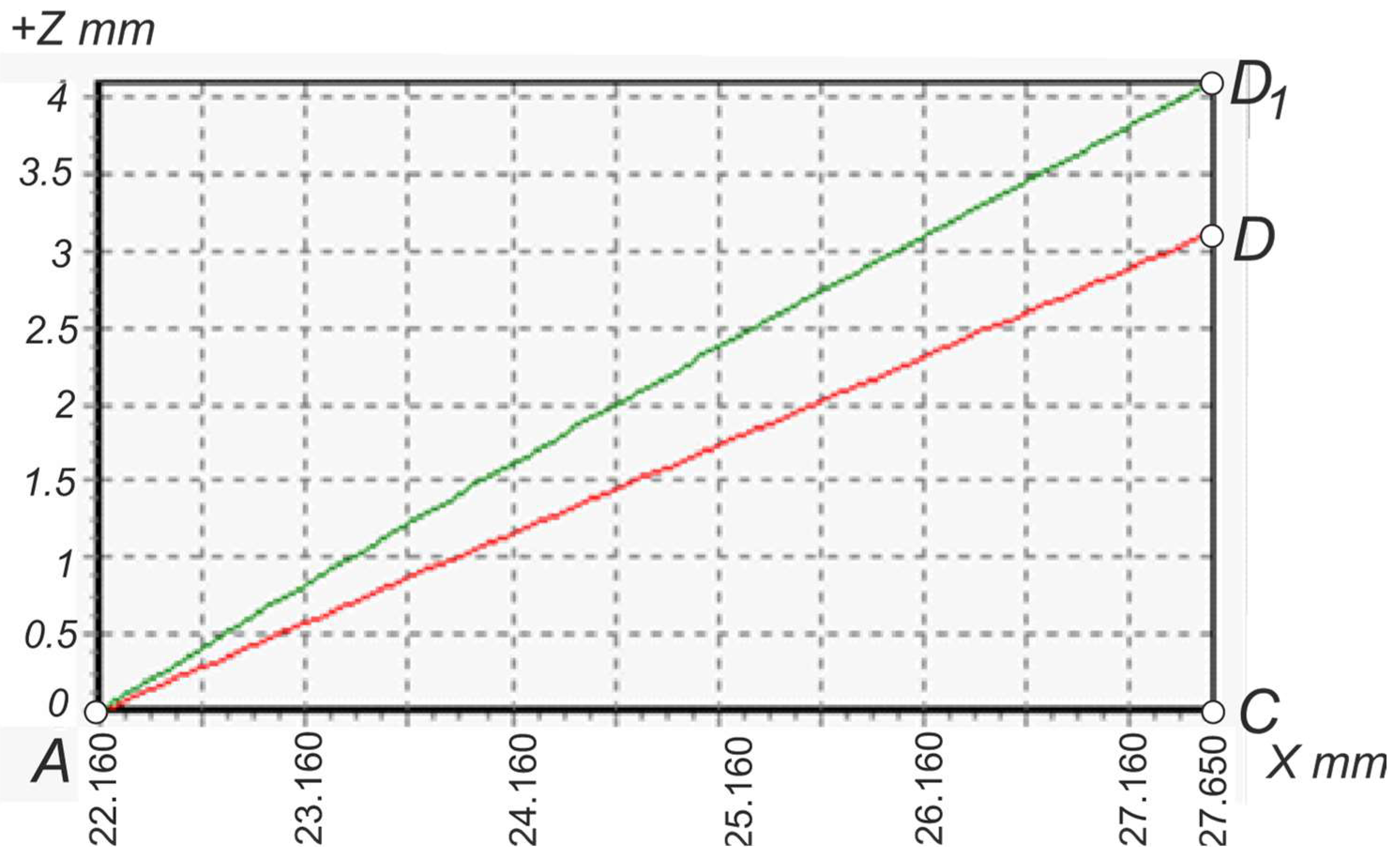
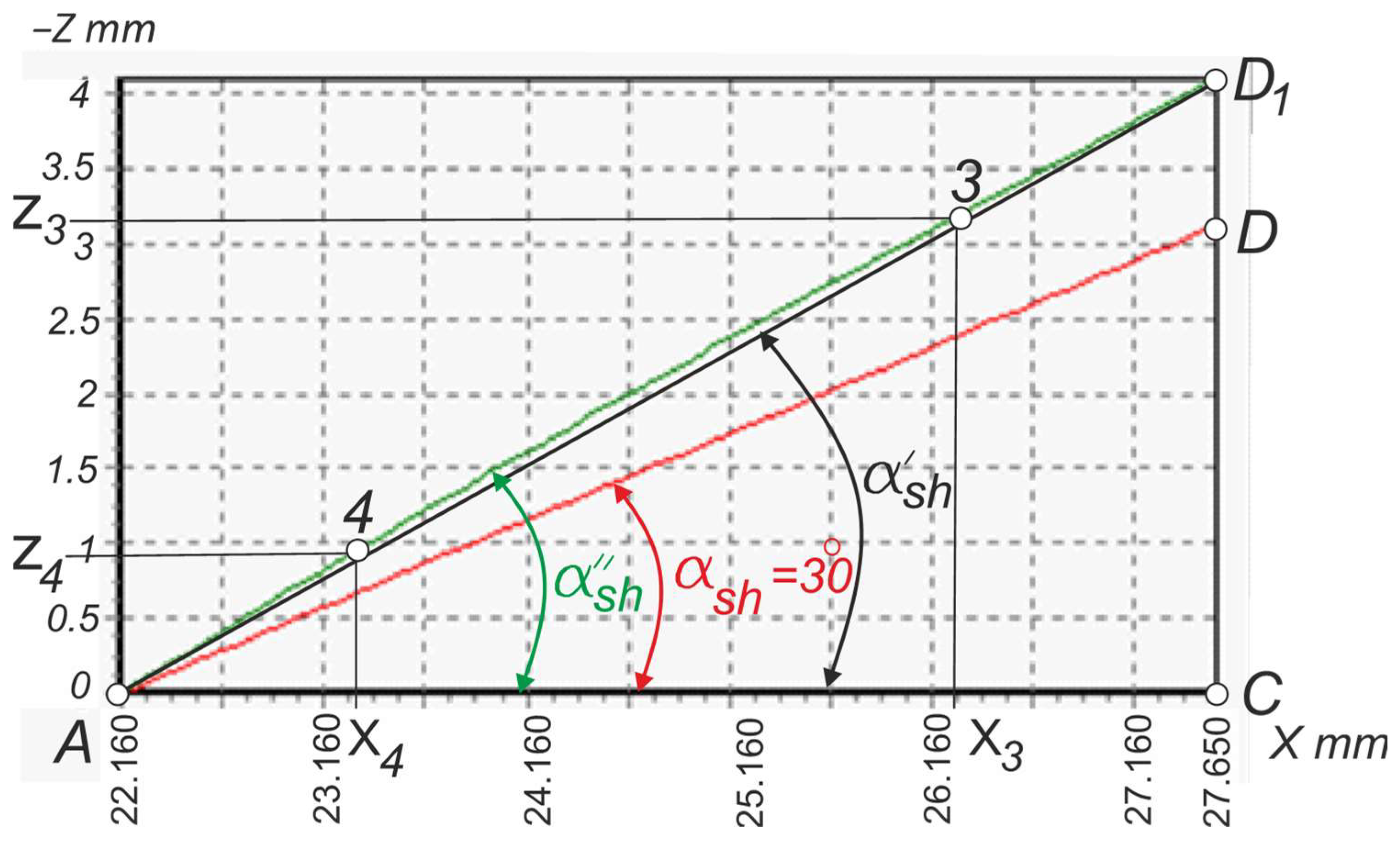
| Xb1 | Xa | Xd1 | X3 | X4 | X5 | X6 |
| 27.93 | 22.16 | 27.65 | 26.22 | 23.59 | 23.87 | 26.50 |
| Zb1 | Za = Zc | Zd1 | Z3 | Z4 | Z5 | Z6 |
| 4.73 | 0 | 4.17 | 3.42 | 1.28 | 1.52 | 3.64 |
| Half-profile angles, ° | ||||||
| αl′ | αsh′ | αsh″ | αl″ | |||
| 39.34 | 37.22 | 39.14 | 38.87 | |||
| Half-Profile Angles, ° | |||
|---|---|---|---|
| Side AB | Side AD | Flank 34 | Flank 56 |
| αl′ | αsh′ | αsh″ | αl″ |
| 30.58 | 30.08 | 30.04 | 30.15 |
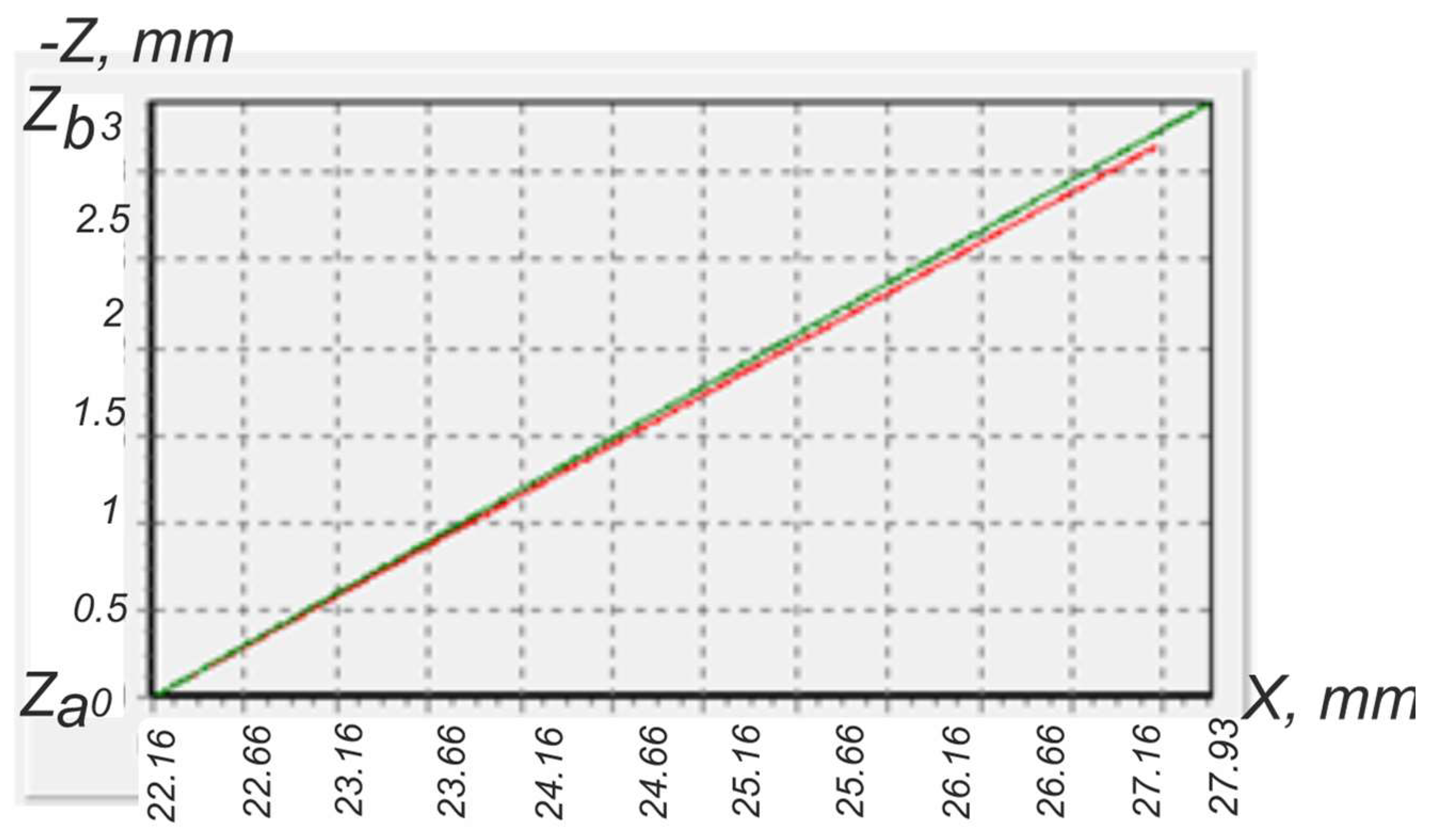
| No. | Parameter Name, Dimension | Marking | Value |
|---|---|---|---|
| 1 | Pitch, mm | P | 5.471 |
| 2 | Tapered angle, ° | φ | 7°7′30″ |
| 3 | Thread height (not truncated), mm | H | 5.471 |
| 4 | Thread height (truncated), mm | h | 3.083 |
| 5 | Root truncation, mm | fc | 1.423 |
| 6 | Crest truncation, mm | fr | 0.965 |
| 7 | Angular depth, mm | h1 | 2.625 |
| 8 | The outer thread diameter of the small base of the cone of pin, mm | d3 | 117.5 |
| 9 | Half-profile angle, ° | α | 30 |
| Parameters | Half-Profile Angles, ° | ||||
|---|---|---|---|---|---|
| Side AB | Side AD | Flank 34 | Flank 56 | ||
| λ, ° | γ, ° | αl′ | αsh′ | αsh″ | αl″ |
| 1.060 | −8 | 29.99 | 30.39 | 30.35 | 29.91 |
| 1.060 | 8 | 30.17 | 30.28 | 30.35 | 30.11 |
| 1.060 | 4 | 30.10 | 29.97 | 29.95 | 30.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onysko, O.; Kopei, V.; Barz, C.; Kusyi, Y.; Baskutis, S.; Bembenek, M.; Dašić, P.; Panchuk, V. Analytical Model of Tapered Thread Made by Turning from Different Machinability Workpieces. Machines 2024, 12, 313. https://doi.org/10.3390/machines12050313
Onysko O, Kopei V, Barz C, Kusyi Y, Baskutis S, Bembenek M, Dašić P, Panchuk V. Analytical Model of Tapered Thread Made by Turning from Different Machinability Workpieces. Machines. 2024; 12(5):313. https://doi.org/10.3390/machines12050313
Chicago/Turabian StyleOnysko, Oleh, Volodymyr Kopei, Cristian Barz, Yaroslav Kusyi, Saulius Baskutis, Michal Bembenek, Predrag Dašić, and Vitalii Panchuk. 2024. "Analytical Model of Tapered Thread Made by Turning from Different Machinability Workpieces" Machines 12, no. 5: 313. https://doi.org/10.3390/machines12050313
APA StyleOnysko, O., Kopei, V., Barz, C., Kusyi, Y., Baskutis, S., Bembenek, M., Dašić, P., & Panchuk, V. (2024). Analytical Model of Tapered Thread Made by Turning from Different Machinability Workpieces. Machines, 12(5), 313. https://doi.org/10.3390/machines12050313











