Study on the Potential of New Load-Carrying Capacity Descriptions for the Service Life Calculations of Gears
Abstract
1. Introduction
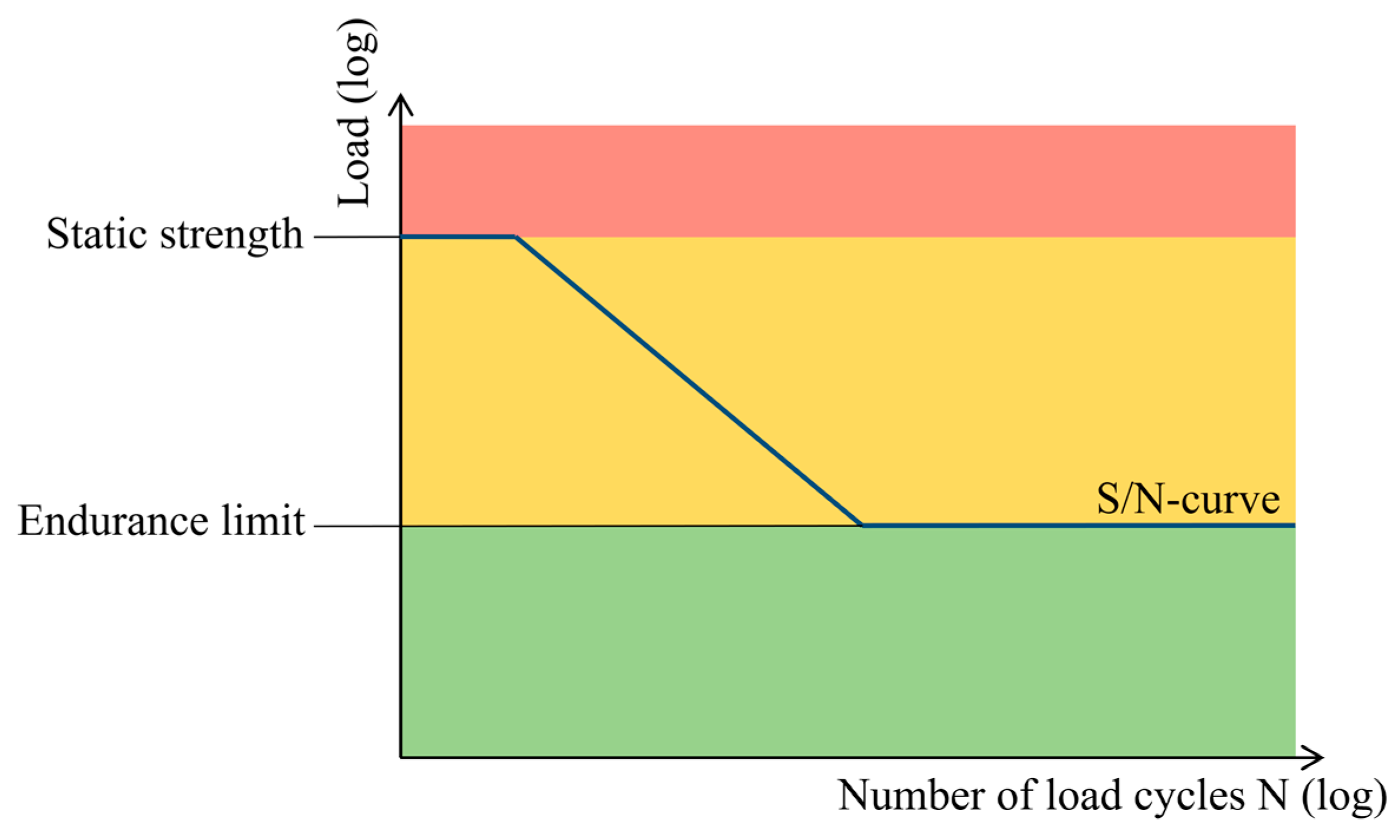
2. Load-Carrying Capacity of Gears
- Loads greater than the static strength cannot be tolerated for a relevant number of load cycles (red area in Figure 1).
- Loads less than the endurance limit can be tolerated for an infinite number of load cycles (green area in Figure 1).
- Loads between these two characteristic values can be tolerated for a limited number of load cycles (yellow area in Figure 1).
- The determination of the endurance limit of the gear;
- The specification of the S/N curve in the load range of limited service life.
- The horizon method uses a certain number of stress levels, which must be determined by the user. At every load level, a certain number of test points are conducted. This basis is used to calculate the endurance limit.
- The staircase procedure includes a certain number of test runs. The load level of each test run is determined by the result of the previous test run. If a failure occurs, the next test will be performed at a lower load level. On the other hand, if a runout is observed, the next test run applies a higher load. The endurance limit is usually calculated using the method according to Hück [12]. Additional information about this method and its accuracy can be found in [13].
3. Basics of Machine Learning and Application in the Field of Fatigue Life Analysis
- Neural network (NN);
- Support vector machine/support vector regression (SVR);
- Random forest (RF);
- Gaussian process regression (GPR).
3.1. Support Vector Machine
3.2. Random Forest
3.3. Neural Network
3.4. Gaussian Process Regression
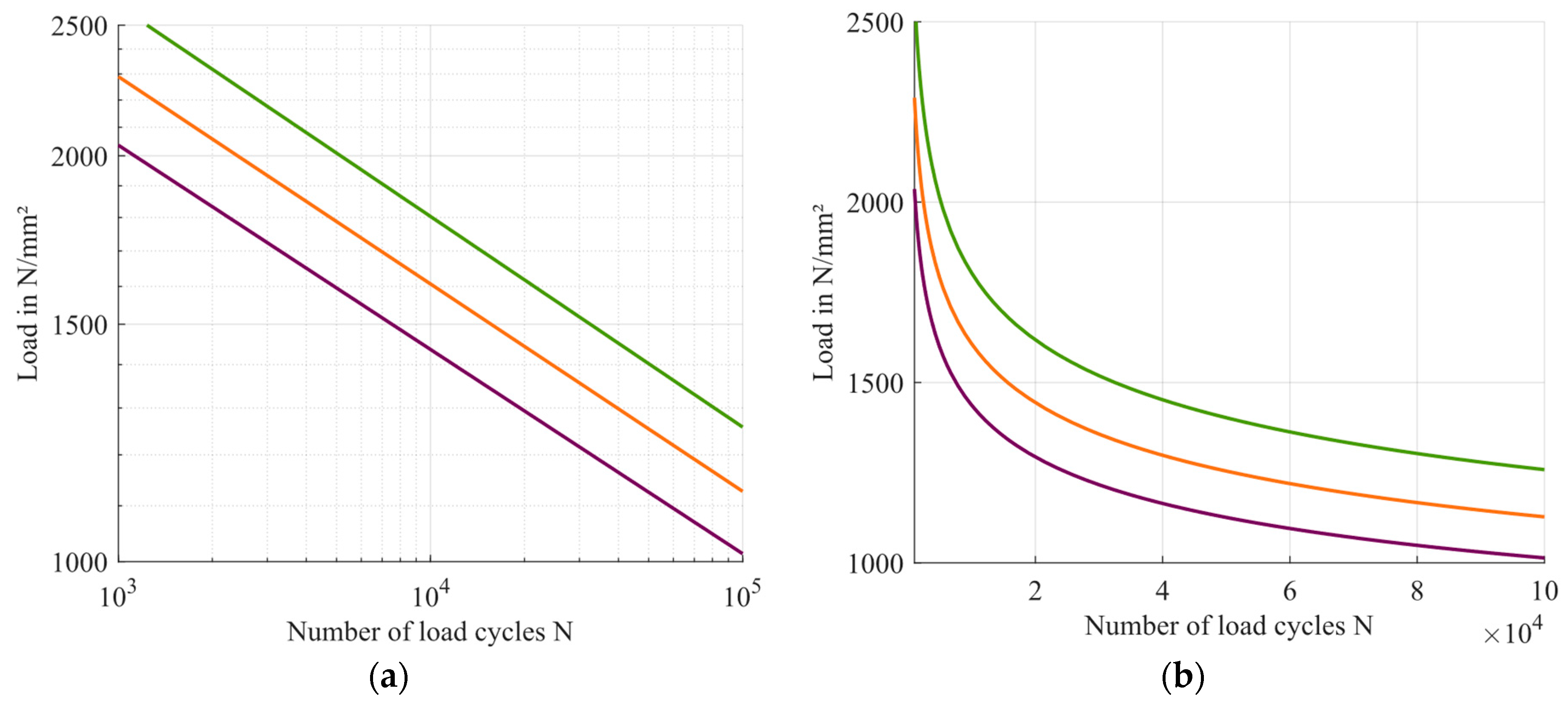
4. Experimental Data for the Determination of the S/N Curve
5. Methods for the Advanced Description of the Load-Carrying Capacity of Gears
5.1. Polynomial Regression
5.2. Approaches Based on Machine Learning
5.3. Overview
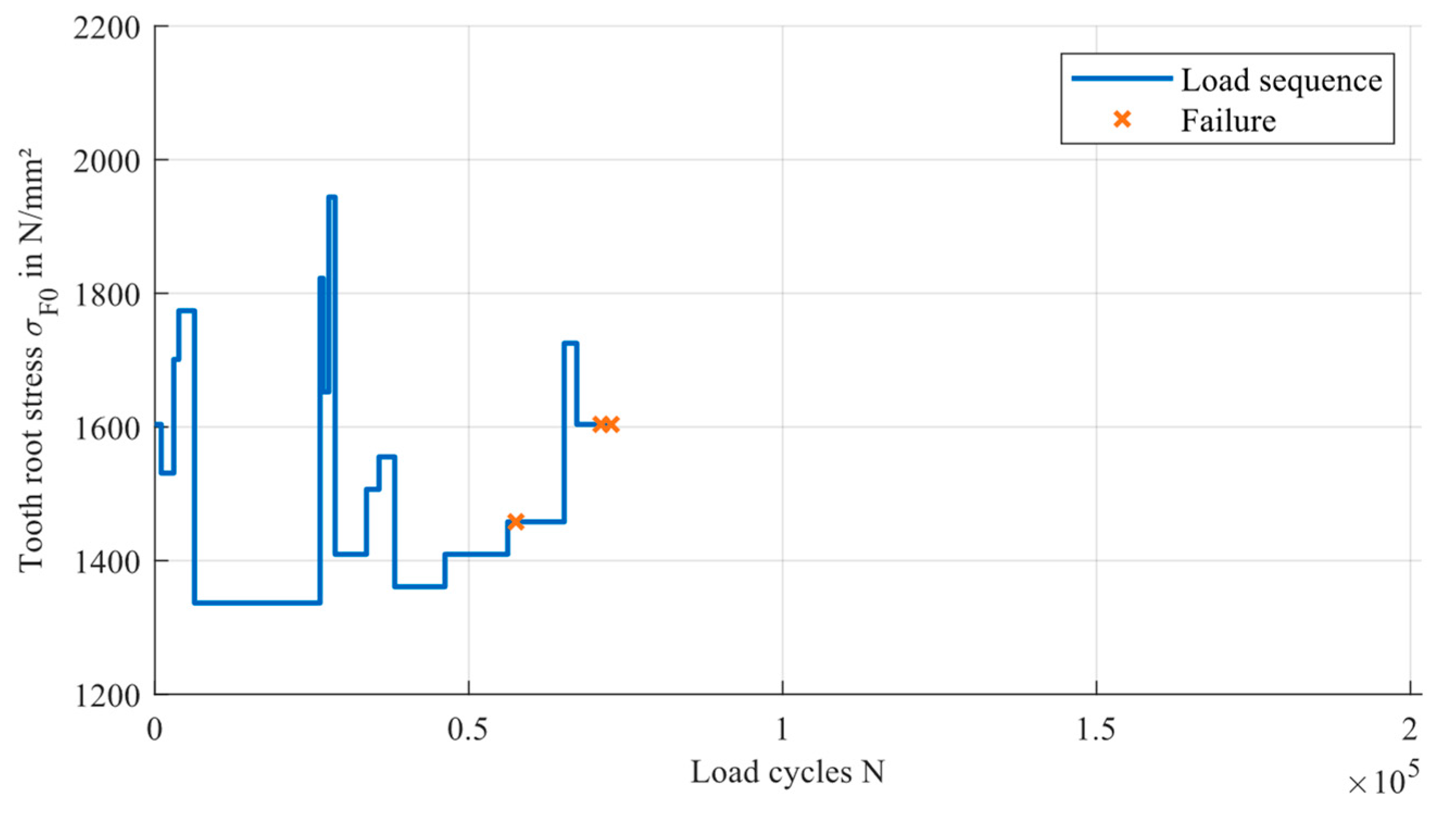
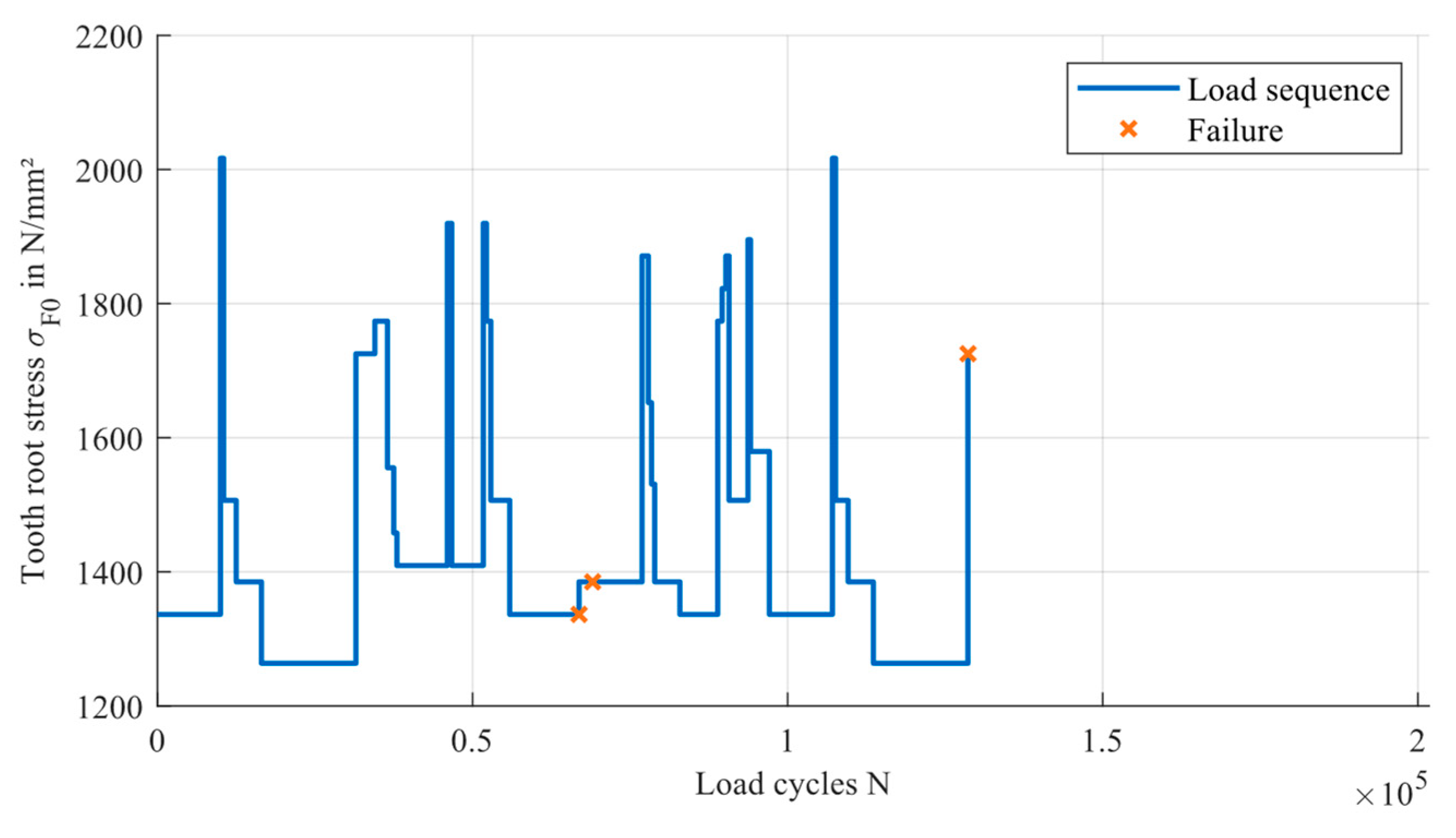
6. Experimental Data for Validation
7. Results of the Validation
- The range of the damage sum at failure of all data points (total scattering);
- The range of the damage sum at failure of the inner 50% of the data points.
8. Conclusion and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Unit | ||
| Face width | mm | |
| Constant of the S/N curve | - | |
| Coefficients of the polynomial | - | |
| Damage sum | - | |
| Pulsator force | N | |
| Slope of the S/N curve | - | |
| Load | N/mm2 or N | |
| Normal module | mm | |
| Number of endurable load cycles | - | |
| Number of load cycles at the knee point of the S/N curve | - | |
| Form factor | - | |
| Stress correction factor | - | |
| Tooth root stress | N/mm2 |
References
- Niemann, G.; Winter, H. Machine Elements—Part 2 (In German: Maschinenelemente—Band 2: Getriebe Allgemein, Zahnradgetriebe—Grundlagen, Stirnradgetriebe), 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Basquin, O. The exponential law of endurance tests. In Proceedings of the Thirteenth Annual Meeting, Trenton, NJ, USA, 8 November 1910; pp. 625–630. [Google Scholar]
- ISO 6336-1:2019-11; Calculation of Load Capacity of Spur and Helical Gears—Part 1: Basic Principles, Introduction and General Influence Factors. ISO: Geneva, Switzerland, 2019.
- ISO 6336-6:2019-11; Calculation of Load Capacity of Spur and Helical Gears—Part 6: Calculation of Service Life under Variable Load. ISO: Geneva, Switzerland, 2019.
- Dong, Z.; Zhao, D.; Cui, L. An intelligent bearing fault diagnosis framework: One-dimensional improved self-attention-enhanced CNN and empirical wavelet transform. Nonlinear Dyn. 2024, 112, 6439–6459. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, T.; Chu, F. Deep convolutional neural network based planet bearing fault classification. Comput. Ind. 2019, 107, 59–66. [Google Scholar] [CrossRef]
- Dong, Z.; Zhao, D.; Cui, L. Non-negative wavelet matrix factorization-based bearing fault intelligent classification method. Meas. Sci. Technol. 2023, 34, 115013. [Google Scholar] [CrossRef]
- Hein, M. Holistic Approach for Fatigue Life Design and Testing of Gearwheels (In German: Zur Ganzheitlichen Betriebsfesten Auslegung und Prüfung von Getriebezahnrädern). Ph.D. Thesis, Technical University of Munich, München, Germany, 2018. [Google Scholar]
- Tobie, T.; Matt, P. FVA 563 I—FVA Guideline: Recommendations for the Standardisation of Load Capacity Tests on Hardened and Tempered Cylindrical Gears; Research Association for Drive Technology (FVA): Frankfurt am Main, Germany, 2012. [Google Scholar]
- Wöhler, A. Report on the experiments carried out on the Royal Lower Silesian-Mark Railway with devices for measuring the bending and twisting of railroad car axles during travel. (In German: Bericht über die Versuche, welche auf der Königl. Niederschlesisch-Märkischen Eisenbahn mit Apparaten zum Messen der Biegung und Verdrehung von Eisenbahnwagen-Achsen während der Fahrt angestellt wurden). Z. Bauwes. 1858, 8, 641–678. [Google Scholar]
- DIN 50100:2022-12; Load Controlled Fatigue Testing—Execution and Evaluation of Cyclic Tests at Constant Load Amplitudes on Metallic Specimens and Components. DIN: Berlin, Germany, 2022.
- Hück, M. An improved procedure for the evaluation of staircase procedure tests (In German: Ein verbessertes Verfahren zur Auswertung von Treppenstufenversuchen). Z. Werkst. 1982, 14, 147–176. [Google Scholar]
- Müller, C.; Wächter, M.; Masendorf, R.; Esderts, A. Accuracy of fatigue limits estimated by the staircase method using different evaluation techniques. Int. J. Fatigue 2017, 100, 296–307. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach, 4th ed.; Pearson: Hoboken, NJ, USA, 2021. [Google Scholar]
- He, L.; Wang, Z.; Akebono, H.; Sugeta, A. Machine learning-based predictions of fatigue life and fatigue limit for steels. J. Mater. Sci. Technol. 2021, 90, 9–19. [Google Scholar] [CrossRef]
- Zhan, Z.; Li, H. A novel approach based on the elastoplastic fatigue damage and machine learning models for life prediction of aerospace alloy parts fabricated by additive manufacturing. Int. J. Fatigue 2021, 145, 106089. [Google Scholar] [CrossRef]
- Mudabbir, M.; Mosavi, A. Machine Learning for Modeling Service Life: Comprehensive Review, Bibliometrics Analysis and Taxonomy. In Proceedings of the 2023 IEEE 27th International Conference on Intelligent Engineering Systems (INES), Nairobi, Kenya, 26–28 July 2023; pp. 235–244. [Google Scholar] [CrossRef]
- Liu, D.P.; Ferri, G.; Heo, T.; Marino, E.; Manuel, L. On long-term fatigue damage estimation for a floating offshore wind turbine using a surrogate model. Renew. Energy 2024, 225, 120238. [Google Scholar] [CrossRef]
- Wilkie, D.; Galasso, C. Gaussian process regression for fatigue reliability analysis of offshore wind turbines. Struct. Saf. 2021, 88, 102020. [Google Scholar] [CrossRef]
- Karolczuk, A.; Słoński, M. Application of the Gaussian process for fatigue life prediction under multiaxial loading. Mech. Syst. Signal Process. 2022, 167, 108599. [Google Scholar] [CrossRef]
- Döbel, I.; Leis, M.; Vogelsang, M.; Neustroev, D.; Patzka, H.; Rüping, S.; Voss, A.; Wegele, M.; Welz, J. BMBF Nr. 01IS17019—Machine Learning—Competence, Applications and Research Deamnd (In German: Maschinelles Lernen—Kompetenzen, Anwendungen und Forschungsbedarf—Ergebnisbericht); Fraunhofer Society: Munich, Germany, 2018. [Google Scholar]
- The MathWorks, Inc. MATLAB Version 2023b. Available online: https://de.mathworks.com/products/matlab.html (accessed on 19 April 2024).
- The MathWorks, Inc. MATLAB Documentation—Fitrensemble. Available online: https://de.mathworks.com/help/stats/fitrensemble.html (accessed on 22 April 2024).
- The MathWorks, Inc. MATLAB Help Center—Fitrnet. Available online: https://de.mathworks.com/help/stats/fitrnet.html#mw_f074fe92-8d2f-48a0-b8f9-8c7d7a6ddf54 (accessed on 19 April 2024).
- Wang, J. An Intuitive Tutorial to Gaussian Process Regression. Comput. Sci. Eng. 2023, 25, 4–11. [Google Scholar] [CrossRef]
- Vietze, D.; Pellkofer, J.; Stahl, K. Non-Linear Analysis of Gear-Fatigue-Damage under Variable Load: 23FTM08. In Proceedings of the AGMA Fall Technical Meeting, FTM 2023, Detroit, MI, USA, 16–18 October 2023. [Google Scholar]
- Illenberger, C.; Tobie, T.; Stahl, K. FVA-Nr. 610/III—Booklet 1328—Gearing steel worldwide Part III (fina report) (In German: Zahnradstähle weltweit III—Abschlussbericht—Referenzwerte zur Zahnradtragfähgikeit moderner Zahnradstähle im Weltmarkt—Teil III); Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2019. [Google Scholar]
- Saddei, P.; Schurer, S.; Güntner, C.; Steinbacher, M.; Tobie, T.; Zoch, H.-W.; Stahl, K. IGF-Nr. 17903 N/2—FVA-Nr. 513/III—Heft 1248—Randschichtgefüge—Abschlussbericht—Alternative mehrphasige Randschichtgefüge beim Einsatzhärten zur Steigerung der Festigkeitseigenschaften von verzahnten Getriebebauteilen; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2017. [Google Scholar]
- Weber, C.; Tobie, T.; Stahl, K. Rapid and Precise Manufacturing of Special Involute Gears for Prototype Testing: 19FTM20. In Proceedings of the AGMA Fall Technical Meeting, FTM 2019, Detroit, MI, USA, 14–16 October 2019. [Google Scholar]
- Bonaiti, L.; Rosa, F.; Rao, P.M.; Concli, F.; Gorla, C. Gear root bending strength: Statistical treatment of Single Tooth Bending Fatigue tests results. Eng. Res. 2022, 86, 251–258. [Google Scholar] [CrossRef]
- ISO 6336-3:2019-11; Calculation of Load Capacity of Spur and Helical Gears—Part 3: Calculation of Tooth Bending Strength: Corrected Version 2020-11. ISO: Geneva, Switzerland, 2019.
- The MathWorks, Inc. Machine Learning with MATLAB. 2022. Available online: https://de.mathworks.com/content/dam/mathworks/ebook/gated/machine-learning-ebook-all-chapters.pdf (accessed on 19 April 2024).
- The MathWorks, Inc. MATLAB Documentation—Fitrgp. Available online: https://de.mathworks.com/help/stats/fitrgp.html (accessed on 22 April 2024).
- The MathWorks, Inc. MATLAB Documentation—Fitrsvm. Available online: https://de.mathworks.com/help/stats/fitrsvm.html#buxgtub (accessed on 22 April 2024).
- Pålmgren, A. Service Life of Ball Gearings (In German: Die Lebensdauer von Kugellager). Z. Vereines Dtsch. Ingenieure 1924, 58, 339–341. [Google Scholar]
- Miner, M.A. Cumulative Damage in Fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar] [CrossRef]
- Haibach, E. Operational Strength—Methods and Data for Calculation (In German: Betriebsfestigkeit—Verfahren und Daten zur Bauteilberechnung), 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- DIN 3990-6:1994-12; Calculation of Load Capcity of Cylindrical Gears—Part 6: Calculation of Service Strength. DIN: Berlin, Germany, 1994.
- DNVGL-CG-0036:2015-12; Calculation of Gear Rating for Marine Transmissions. DNVGL: Bærum, Norway, 2015.
- ANSI/AGMA 2101-D04; Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth. AGMA: Alexandria, VA, USA, 2004.
- Stahl, K.; Michaelis, K.; Höhn, B.-R.; Winter, H. IGF-Nr. 11154, FVA-Nr. 304—Booklet 580—Service Life Statistics (Final Report) (In German: Lebensdauerstatistik—Statistische Methoden zur Beurteilung von Bauteillebensdauer und Zuverlässigkeit und ihre Beispielhafte Anwendung auf Zahnräder); Research Association for Drive Technology (FVA): Frankfurt, Germany, 1999. [Google Scholar]
- Geitner, M.; Tobie, T.; Stahl, K. FVA-Nr. 610 IV—Booklet 1432—Materials 4.0 (Final Report) (In German: Werkstoffe 4.0—Erweiterte Datenanalyse zur Bewertung des Einflusses von Werkstoff und Wärmebehandlungseigenschaften auf die Zahnradtragfähigkeit); Research Association for Drive Technology (FVA): Frankfurt, Germany, 2021. [Google Scholar]
- Götz, S.; Eulitz, K.-G. Fatgiue Life Analysis (In German: Betriebsfestigkeit), 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Gudehus, H.; Zenner, H. Guideline for Fatigue Life Analysis (In German: Leitfaden für eine Betriebsfestigkeitsrechnung), 4th ed.; Verlag Stahleisen: Düsseldorf, Germany, 1999. [Google Scholar]
- Foulard, S.; Rinderknecht, S.; Ichchou, M.; Perret-Liaudet, J. Real-time and online lifetime monitoring of automotive transmissions: Determining of the remaining lifetime of transmission components with the aid of torque measure. In Proceedings of the International Conference on Gears: VDI-Berichte 2199, München, Germany, 7–9 October 2013. [Google Scholar]
- Foulard, S.; Rinderknecht, S.; Perret-Liaudet, J.; Ichchou, M. Online and real-time damage calculation in automotive transmissions Application to remaining service life estimation. In Proceedings of the International Gear Conference 2014: Conference Proceedings Volume II, Lyon Villeurbanne, France, 26–28 August 2014; pp. 933–949. [Google Scholar]



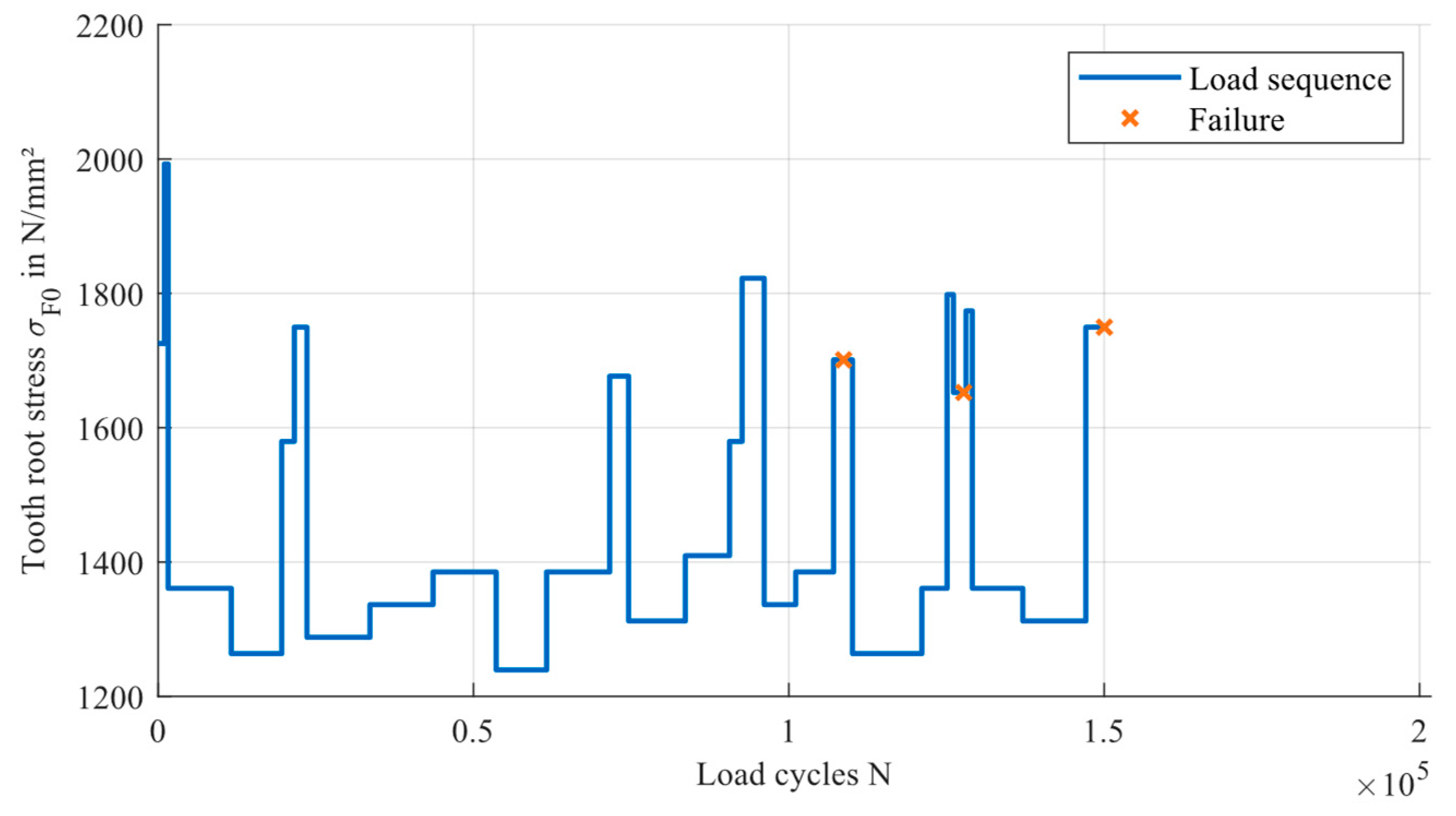
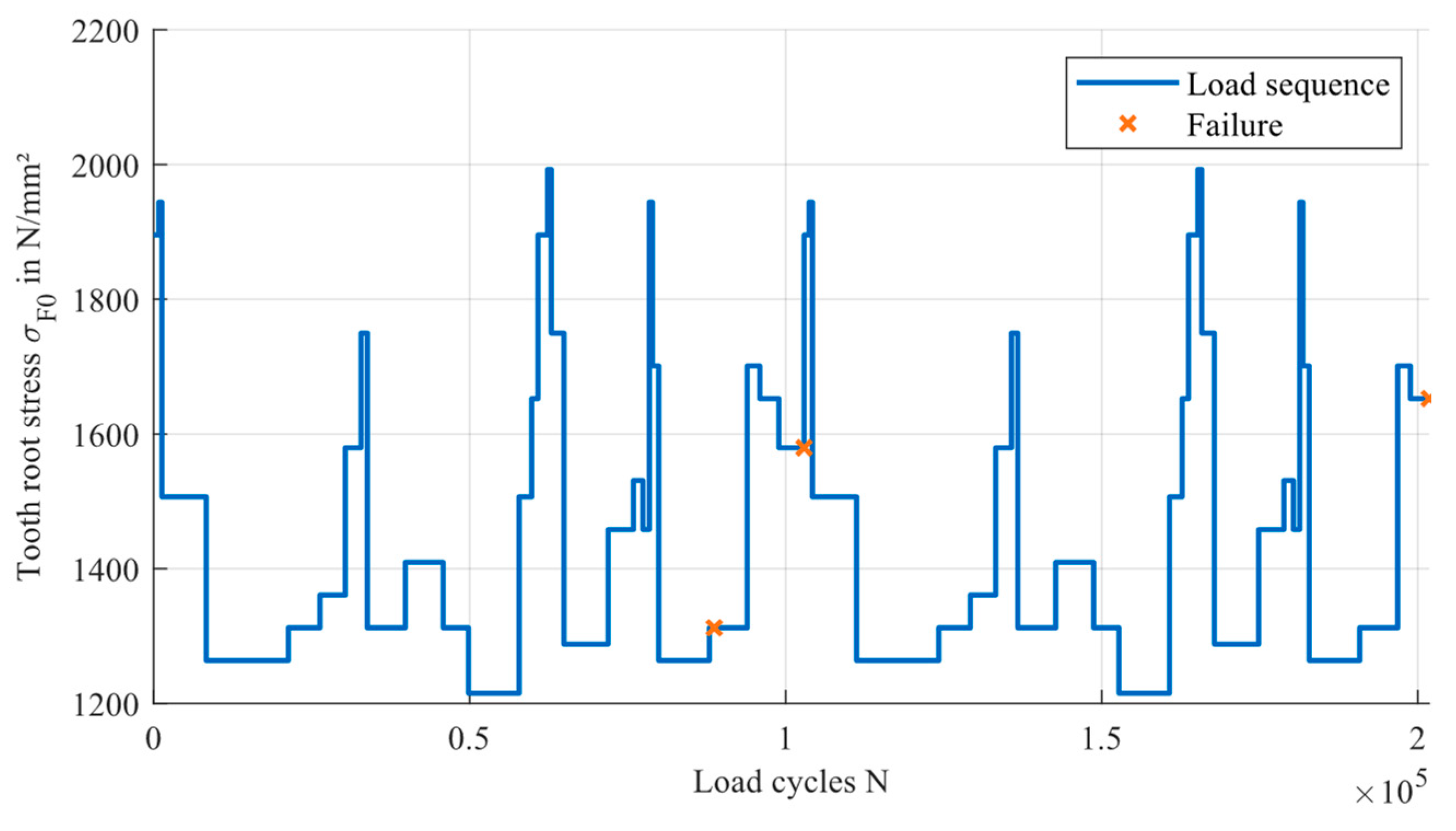
| Gear | Spur Gear |
|---|---|
| 5 mm | |
| Number of teeth | 24 |
| 20 mm | |
| Machining | Milling and grinding |
| Material | Steel 18CrNiMo7-6 |
| Heat treatment | Case-hardened |
| Endurance limit | 1375.81 N/mm2 |
| Slope k | 6.33 |
| Constant C | 6.90 × 1024 |
| 2274.519 | |
| −0.033 | |
| 4.067 × 10−7 | |
| −1.697 × 10−12 |
| Data Point | Damage Sum According to DAH Miner Original Calculated with the Load-Carrying Description Based On | |||||
|---|---|---|---|---|---|---|
| Basquin | Polynomial | SVR | RF | NN | GPR | |
| 1 | 0.699 | 0.806 | 0.786 | 0.771 | 0.789 | 0.779 |
| 2 | 1.017 | 1.187 | 1.173 | 1.156 | 1.179 | 1.161 |
| 3 | 1.063 | 1.241 | 1.232 | 1.216 | 1.241 | 1.226 |
| 4 | 0.803 | 0.893 | 0.876 | 0.827 | 0.847 | 0.849 |
| 5 | 0.779 | 0.865 | 0.847 | 0.802 | 0.824 | 0.821 |
| 6 | 1.462 | 1.607 | 1.593 | 1.513 | 1.512 | 1.583 |
| 7 | 1.091 | 1.172 | 1.218 | 1.119 | 1.111 | 1.152 |
| 8 | 1.263 | 1.347 | 1.412 | 1.309 | 1.295 | 1.325 |
| 9 | 1.473 | 1.551 | 1.639 | 1.510 | 1.505 | 1.511 |
| 10 | 0.992 | 1.092 | 1.064 | 1.090 | 1.062 | 1.096 |
| 11 | 2.455 | 2.696 | 2.702 | 2.778 | 2.698 | 2.751 |
| 12 | 1.279 | 1.410 | 1.417 | 1.462 | 1.421 | 1.450 |
| Arithmetic Mean | Median | Scattering (Inner 50%) | Total Scattering | |||
|---|---|---|---|---|---|---|
| Basquin | 1.20 | 1.08 | 0.47 | Reference | 0.77 | Reference |
| Polynomial | 1.32 | 1.21 | 0.49 | +4.26% | 0.80 | +3.90% |
| SVR | 1.33 | 1.23 | 0.54 | +14.89% | 0.85 | +10.39% |
| RF | 1.30 | 1.20 | 0.53 | +12.77% | 0.74 | −3.90% |
| NN | 1.29 | 1.21 | 0.51 | +8.51% | 0.72 | −6.49% |
| GPR | 1.31 | 1.19 | 0.51 | +8.51% | 0.80 | +3.90% |
| Arithmetic Mean | Median | Scattering (Inner 50%) | Total Scattering | |||
|---|---|---|---|---|---|---|
| Basquin | 1.00 | 0.90 | 0.40 | Reference | 0.65 | Reference |
| Polynomial | 1.00 | 0.92 | 0.37 | −7.50% | 0.61 | −6.15% |
| SVR | 1.00 | 0.92 | 0.40 | ±0% | 0.64 | −1.54% |
| RF | 1.00 | 0.92 | 0.41 | +2.50% | 0.57 | −12.31% |
| NN | 1.00 | 0.94 | 0.39 | −2.50% | 0.56 | −13.85% |
| GPR | 1.00 | 0.91 | 0.39 | −2.50% | 0.61 | −6.15% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vietze, D.; Pellkofer, J.; Stahl, K. Study on the Potential of New Load-Carrying Capacity Descriptions for the Service Life Calculations of Gears. Machines 2024, 12, 304. https://doi.org/10.3390/machines12050304
Vietze D, Pellkofer J, Stahl K. Study on the Potential of New Load-Carrying Capacity Descriptions for the Service Life Calculations of Gears. Machines. 2024; 12(5):304. https://doi.org/10.3390/machines12050304
Chicago/Turabian StyleVietze, Daniel, Josef Pellkofer, and Karsten Stahl. 2024. "Study on the Potential of New Load-Carrying Capacity Descriptions for the Service Life Calculations of Gears" Machines 12, no. 5: 304. https://doi.org/10.3390/machines12050304
APA StyleVietze, D., Pellkofer, J., & Stahl, K. (2024). Study on the Potential of New Load-Carrying Capacity Descriptions for the Service Life Calculations of Gears. Machines, 12(5), 304. https://doi.org/10.3390/machines12050304









