Abstract
With the progressive development of new energy technologies, high-power lithium batteries have been widely used in ship power systems due to their high-power density and low environmental pollution, and they have gradually become one of their main propulsion energy sources. However, the large-scale deployment of lithium batteries has also brought a series of safety problems to ship operations, especially the battery internal short circuit (ISC). Battery ISC faults are very hidden and unpredictable at the initial stage and often fail to be detected in time, ultimately leading to overheating, fire or even an explosion of the ship’s power system. Based on this, this paper proposes a fast and accurate method for early-stage ISC fault location and detection of lithium batteries. Initially, voltage variations across the lithium battery packs are quantified using curvilinear Manhattan distances to pinpoint faulty battery units. Subsequently, the localized characteristics of voltage variance among adjacent batteries are leveraged to detect an early-stage ISC fault. Simulation results indicate that the proposed method can quickly and accurately locate the position of 5 Ω, 10 Ω and 15 Ω ISC faulty batteries within the battery pack, as well as detect the abnormal batteries in a timely manner with considerable sensitivity and reliability.
1. Introduction
With increased environmental awareness and tightened international emission standards in recent years, the shipping industry has placed increasing emphasis on energy efficiency and carbon emission control. According to Marpol Annex VI, the standards for emissions of exhaust gases such as sulfur oxides (SOX) and nitrogen oxides (NOX) from ships during navigation have become more rigorous [1]. In response to this imperative, electric ship power propulsion systems have emerged as a compelling solution for the maritime sector, fostering intelligence and environmental responsibility. With electric ship systems, batteries and other electric components assume direct control over energy transmission and power propulsion operations [2,3]. This transformative approach yields substantial reductions in both fossil fuel consumption and carbon emissions, thereby offering vital support for the sustainable evolution of ship transportation in the years ahead.
As a pivotal constituent of electric ship propulsion systems, lithium batteries are esteemed for their high energy density, prolonged cycle life, and minimal self-discharge rates [4,5]. In practical engineering, lithium batteries are often combined in series or parallel to provide power requirements for the propulsion system of ships. However, the harsh and complex operating environment at the ocean makes these battery components susceptible to mechanical, electrical, and thermal stresses, which can lead to battery degradation, failure, and faults [6]. Thus, the precise and effective detection of incipient faults within ship lithium battery packs, and the mitigation of potential power failures and safety incidents, have emerged as paramount concerns for optimizing and enhancing the reliability of ship electric propulsion systems.
A lithium battery failure or fault is usually triggered by changes in its internal structure or materials, and it can be broadly categorized into a progressive or sudden type [7]. Firstly, the progressive failure or fault of lithium batteries is manifested by the gradual decrease in battery capacity and power over time, which is characterized by battery aging, charge/discharge cycling, loss of active material, and increase in internal resistance. The sudden failure or fault of lithium batteries, on the other hand, is triggered by events such as its internal short circuit (ISC), thermal runaway, and capacity drop and can lead to a significant degradation of the battery performance in a short period of time [8,9]. At the same time, the occurrence of an ISC in lithium batteries generates ultra-high currents, leading to a rapid increase in the battery temperature, as well as fire and explosions [10].
To ensure the safety and reliability of ships during navigation, experts and scholars have conducted extensive research on fault detection and diagnosis (FDD) methods for lithium battery ISCs. Presently, FDD methods for lithium battery ISC faults can be broadly classified into three categories: threshold-based methods [11], model-based methods [12], and data-driven methods [13]. Threshold-based methods diagnose battery ISC faults by establishing a voltage threshold. This approach is characterized by its simplicity, ease of implementation, and computational efficiency, rendering it widely employed in battery management systems (BMS). However, the effectiveness of threshold-based diagnosis is heavily reliant on the precise setting of the threshold [14,15,16]. If the threshold is set too low, there is an increased risk of normal voltage triggering false alarms, thereby elevating the false alarm rate for system faults [17]. Conversely, if the threshold is set too high, abnormal voltages may fail to surpass the threshold, resulting in reduced detection sensitivity for the diagnostic method.
The model-based approach for diagnosing ISC faults in Li-ion batteries entails achieving FDD through the establishment of an accurate mathematical model of the battery [18], followed by a comparison of actual measured battery state parameters with those predicted by the model. Various mathematical models have been employed for this purpose, including electrochemical models [19], equivalent circuit models [20], thermal models [21], and multiphysics-field coupling models [22]. Dey et al. [23] developed a one-dimensional thermal model to describe the dynamic changes in surface and core temperatures of lithium batteries, enabling a detailed examination of temperature distribution in the radial direction of column batteries. Feng et al. [24] established an electrochemical–thermal coupled model of batteries by analyzing the evolutionary characteristics of battery ISC faults, effectively bridging the gap between ISC fault detection and their evolutionary characteristics. Additionally, Gao et al. [25] aiming to quantitatively analyze initial ISC, utilized a battery difference model to estimate the difference of state of charge (SOC) within the battery pack through extended Kalman filtering (KF). Subsequently, recursive least squares (RLS) were employed to derive the short circuit resistance value, and while the model-based ISC fault diagnosis method yields commendable diagnostic outcomes, it is susceptible to parameter uncertainty and battery cell inconsistencies during the diagnostic process [26,27]. Maintaining robustness to perturbations and sensitivity to faults concurrently presents a challenge.
With the continuous development of mobile internet and smart sensor technology, data-driven FDD methods for lithium batteries have gained wide attention. Unlike model-based methods, data-driven battery FDD methods do not rely on an accurate battery model, while FDD is performed by real-time data such as voltage, current, and temperature generated during battery operation. Commonly employed data-driven diagnostic techniques encompass entropy analysis (EA) [28], statistical analysis (SA) [29], and machine learning (ML) [30]. Xia et al. [31] introduced a fault detection method for lithium batteries based on the voltage profile correlation coefficient. This method utilizes a recursive moving window to compute the voltage correlation coefficient, thereby enhancing fault detection sensitivity. Wang et al. [32] proposed an ICA-PCA diagnostic model for the rapid and accurate diagnosis of ISC and sensor faults in Li-ion battery systems. This model, based on independent component analysis (ICA) and principal component analysis (PCA), enables efficient fault diagnosis. Furthermore, Xie et al. [33] investigated the thermal effects of battery ISC and established a pseudo-distributed model structure based on a limit learning machine. They employed a multi-class correlation vector machine to detect the intensity of the ISC fault. Experimental results conducted on 18650 Li-ion batteries demonstrate the efficacy of this FDD method, achieving an ISC fault recognition rate with a state misclassification rate as low as 3.13%.
Motivated by the literature [31,32,34], this paper proposes a method for ISC fault localization and detection of lithium batteries based on curvilinear Manhattan distance and voltage variance analysis. Different from the FDD methods proposed in the studies [25,30], the proposed method in this paper is accurate and efficient, which can realize the online monitoring and localization of lithium battery ISC faults, and thus, it is more in line with practical industrial application scenarios. Specifically, the curvilinear Manhattan distance between the cell voltages of a lithium battery pack is calculated to rapidly and accurately locate the position of the faulty cell. Meanwhile, the exact location and occurrence time of the fault are detected in a timely manner by the localized voltage variance difference in the battery with a sliding window, which in turn feeds back the detection results to the ship operators and guides the repairers to make repairs. Finally, the efficacy and applicability of the proposed method are validated on an established experimental platform.
The structure of the paper proceeds as follows. In Section 2, a thorough elucidation is provided regarding the evolutionary mechanisms of ISC faults, along with detailed insights into the experimental platforms utilized and the modes of fault injection. Section 3 delineates the proposed ISC detection method, outlining its specific diagnostic steps and operational procedures. Subsequently, Section 4 undertakes simulation verification utilizing the constructed experimental platform, followed by a meticulous analysis and discussion of the experimental findings. Section 5 summarizes the conclusions and suggests the next steps in the research.
2. ISC Fault Experimental Platform and Injection Method
2.1. ISC Fault Triggering Mechanism
The ISC faults of lithium battery packs include safety risks such as battery internal circuit anomalies, elevated temperatures, and potential thermal runaway (TR) incidents, which occur during the complex charging and discharging operations of lithium batteries. Figure 1 illustrates the triggering modes of lithium battery ISC failure. Based on the diaphragm failure mechanism and various abuse conditions, ISC faults in lithium battery packs can be classified into three primary types: (1) mechanical abuse-induced ISC; (2) electrical abuse-induced ISC; and (3) thermal abuse-induced ISC. ISC resulting from mechanical or thermal abuse tends to rapidly generate significant heat, often leading directly to thermal runaway [35]. Conversely, ISC triggered by electrical abuse typically generates less heat that is insufficient to provoke thermal runaway. This discrepancy arises from the propensity of mechanical and thermal abuse-induced ISC to generate substantial heat, thus precipitating the onset of thermal runaway, whereas electrical abuse-induced ISC generally lacks the magnitude of heat required to trigger TR.
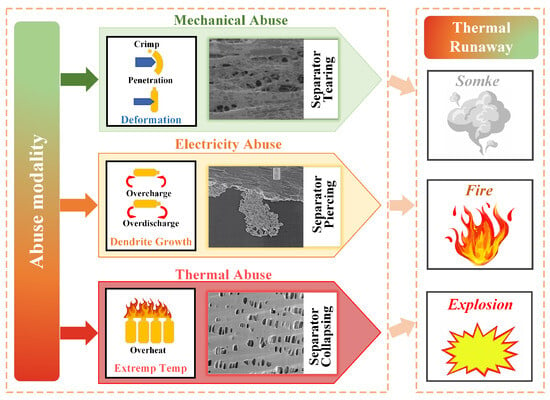
Figure 1.
Lithium battery ISC fault trigger mode.
Furthermore, the evolution of lithium battery ISC failure can be delineated into three distinct stages. In the initial stage, the single cell experiencing ISC failure exhibits self-extinguishing characteristics, characterized by slow self-discharge and minimal heat generation. Subsequently, in the second stage, the ISC characteristics become more pronounced, with a rapid drop in battery voltage and a significant rise in temperature. Finally, in the third stage, the battery pack experiences a widespread short circuit, resulting in instantaneous generation of substantial heat, ultimately culminating in battery thermal runaway. This phase is of exceedingly brief duration and cannot be halted. Given the potential for significant damage to the system of ships, timely and effective detection and isolation of ISC failures in lithium-powered vessels are imperative to avert adverse.
2.2. ISC Fault Experiment Platform
The acquisition of reliable and realistic experimental data stands as paramount for the accurate detection of faults by data-driven methods. For this reason, we have built an experimental platform to simulate ISC faults in battery packs. Figure 2 shows the built experimental platform for lithium battery ISC faults. The platform includes a voltage collection unit (VCU) based on the special chip LTC6811, a field control unit (FCU) based on a relay and a main control board, a central control program (CCP) based on LabView, a battery charging and discharging device, and six single lithium batteries.
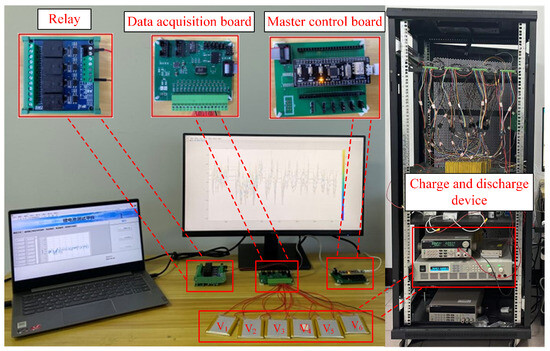
Figure 2.
ISC fault experiment platform.
The functions of the various parts for the platform illustrated in Figure 2 are as follows: the VCU is responsible for synchronizing the voltage measurement of each battery; the FCU manages the charging and discharging states of the batteries by controlling the sequential switching of the controllable DC power supply; the CCP is responsible for the global coordinated control, and the charging and discharging devices carry out the charging and discharging operations of the battery packs according to the given profiles. In addition, the serial peripheral interface (SPI) protocol and RS-232 bus are used for data acquisition and command communication among devices, respectively. In the experiment, a series-connected battery pack consisting of six Li-ion ternary batteries was inserted into the experimental platform, and the profile of the charging and discharging device was set to Federal Urban Driving Schedule (FUDS). The sampling frequency of the data acquisition board was set to 100 Hz. The specifications of the experimental lithium batteries are detailed in Table 1.

Table 1.
Experimental battery specifications.
2.3. ISC Fault Injection Method
Unlike external short circuit (ESC) faults, which are obviously characterized by faults, battery ISC faults are initially very hidden and often difficult to detect. Moreover, battery ISC can quickly cause a large amount of heat to be generated inside the battery, which can lead to a fire or explosion, while ESC is less harmful because it occurs outside the battery and does not directly affect the battery interior. Therefore, industry and academia have paid more attention to the ISC fault diagnosis of batteries.
Currently, researchers have designed a variety of ISC fault triggering mechanisms under laboratory conditions. For example, the study [36] induces ISC faults by overcharging and overdischarging the battery cells to cause damage. This approach is feasible but less controllable. The study [37] triggers ISC with different failure strengths by connecting resistors with different resistance values in parallel at both ends of the battery cell, which is considered that the ISC failure of the battery is manifested as the change in equivalent internal resistance in the electrical behavior, and therefore, the ISC with different failure levels can be simulated by changing the magnitude of the equivalent resistance through the external parallel resistance. This method is simple to trigger, and it has very good controllability. This method is simple and very controllable.
In this paper, different intensities of ISC faults are triggered by connecting resistors in parallel at both ends of the battery. Assuming the original equivalent internal resistance (EIR) of the cell is , and the value of the external parallel resistance is , then the EIR of the battery after the parallel resistance changes as follows [37]:
where is the EIR of the battery during normal operation; and is the value of the battery parallel resistance. The larger the value of the parallel resistance, the smaller the ISC fault triggered, and vice versa.
Figure 3 depicts the first-order equivalent circuit model of the battery under both normal operating conditions and ISC faults. Figure 4 illustrates the ISC fault injection method. To facilitate the control of ISC fault injection and removal, relay contacts (, , ) are utilized to control the access or disconnection of the external parallel resistor. Building upon these ISC fault injection methods, three distinct ISC fault scenarios have been designed for testing purposes [38].
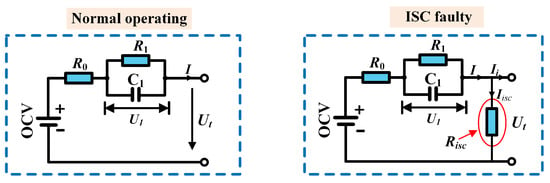
Figure 3.
Lithium battery first-order equivalent circuit model.
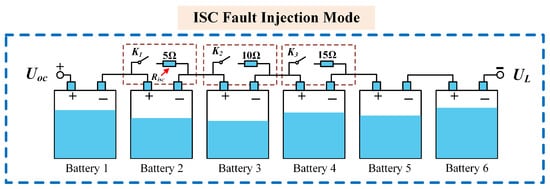
Figure 4.
ISC fault injection method.
- Case 1: At the 1816-th sampling moment, close contact and insert a 5 Ω resistances in parallel across battery 2 to induce a high-intensity ISC fault;
- Case 2: At the 3285-th sampling moment, close contact and insert a 10 Ω resistances in parallel across battery 3 to induce a medium-intensity ISC fault;
- Case 3: At the 3706-th sampling moment, close contact and connect a 15 Ω resistances in parallel with both ends of battery 4 to induce a weak-intensity ISC fault.
3. ISC Fault Detection and Diagnosis Process
3.1. ISC Fault Location Based on Curvilinear Manhattan Distance
The curvilinear Manhattan distance is a metric that measures the differences between two series. Similar to the traditional Manhattan distance, the curvilinear Manhattan distance is defined as the shortest curvilinear path on the grid structure that moves horizontally and vertically. The larger the curved path, the greater the difference between the sample data and the lower the similarity, i.e., there may be outliers. Conversely, the smaller the curved path, the higher the similarity between the sample data points. The Manhattan distance between two locations in two-dimensional space can be expressed by the following mathematical formula:
where denotes the Manhattan distance between the , and the .
The Euclidean distance is another commonly used metric for measuring differences between series, which evaluates differences between data samples by calculating the straight-line distance between two positions. This method is known for its simplicity in calculation, ease of comprehension, and resilience to noise. However, it is more susceptible to the influence of outliers and less robust in nature. In contrast, the Manhattan distance primarily focuses on the disparity between two positions relative to the coordinate axes, rather than considering the absolute distance between them [34]. This approach prevents compression and distortion of the original distance, thereby offering a better reflection of the true disparity between the positions. Figure 5 illustrates schematic diagrams of the Manhattan distance and Euclidean distance. The blue line A and orange line C depict equivalent Manhattan distances, while the pink line B represents the Euclidean distance.
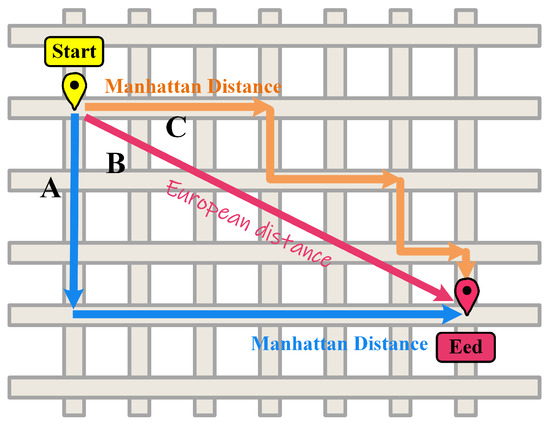
Figure 5.
The schematic diagrams of the Manhattan distance and Euclidean distance. The blue line A and orange line C depict equivalent Manhattan distances, while the pink line B represents the Euclidean distance.
To quantify the distance between multiple locations in a two-dimensional space, this paper introduces an modified method to the Manhattan distance termed the curvilinear Manhattan distance. This improvement involves calculating the sum of the relative offsets between two curves of the same length to quantify the Manhattan distance between them. For two curves, and , each of length n, their curvilinear Manhattan distance can be computed using the following equation.
where and denote the nth sample point of curve and curve , respectively; denotes the curvilinear Manhattan distance between curve and curve .
For a lithium battery pack system, the voltage matrix is as follows.
where denotes the voltage profile of the mth lithium battery; denotes the nth sampling voltage of the mth lithium battery; n denotes the number of samples; and m denotes the number of single cells in the lithium battery pack.
Based on the voltage profile data of each cell, the curvilinear Manhattan distance between each cell in the lithium battery pack is computed. Specifically, the Manhattan distance between cell i and cell j can be calculated using the following formula:
Building the curvilinear Manhattan matrix of the lithium battery pack based on the Manhattan distances between all cells, [34] is shown below:
To mitigate inconsistencies in the voltage amplitudes of different cells, the curvilinear Manhattan distance matrix is normalized:
where ; ; and denotes the normalized curvilinear Manhattan distance between cell i and cell j.
In a normally operating lithium battery pack system, the voltage curves of each cell exhibit a similar trend, as depicted in Figure 6a. However, due to various factors such as production processes, external environmental conditions, and usage patterns, ISC faults may arise during the operation of lithium-powered ships. Figure 6b illustrates the voltage curve of each battery under 5 Ω ISC fault. It is evident that the battery with an ISC fault experiences a sudden voltage drop, leading to desynchronization among the battery pack voltages. Furthermore, upon calculating the curvilinear Manhattan distance of the battery pack under normal operation and ISC fault conditions, we observe that the values of each lithium battery fall within a smaller range under normal operation, while they fall within a larger range under ISC fault conditions. Hence, in this paper, we quantify the Manhattan distance of the curves between the voltages of each cell in the lithium battery pack to accurately and sensitively detect and locate the ISC cell position.
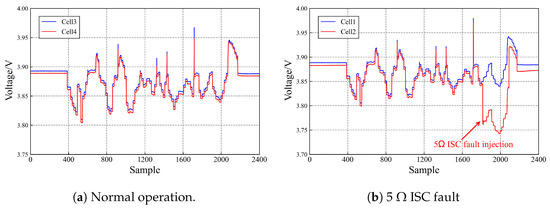
Figure 6.
Battery pack voltage curve.
3.2. ISC Fault Detection Based on Voltage Variance Analysis
Variance serves as a pivotal statistical metric employed to quantify the extent of dispersion within a dataset or random variable. Within the realm of probability theory, variance elucidates the degree of deviation between a random variable and its anticipated value. In statistical parlance, variance is delineated as the mean of the squared deviations between individual sample values and their respective mean. The formula for the variance of the ith battery voltage series as follows:
where denotes the voltage of the ith battery at moment t; is the mean of ; and is the ith battery variance.
According to Equation (8), the voltage amplitude change exhibited by each battery within the battery pack ought to remain within a narrow range under standard operating conditions. During such periods, the majority of voltage series values closely approximate the mean, resulting in minimal variance within the series. However, if the battery pack suffers an ISC, the voltage of the affected cells will drop suddenly, which will change the distribution of the voltage series and lead to an increase in the variance. Based on this, the current proposal is to diagnose the battery ISC fault by analyzing the variance variation between cells. Figure 7 demonstrates the variance variation in the voltage of the battery in the normal operation state and in the ISC operation state.
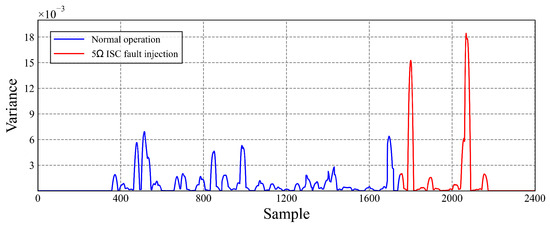
Figure 7.
Variation of cell voltage variance.
Detecting battery ISC faults solely through the computational outcomes of Equation (8) presents certain inherent challenges. Primarily, the initial synchronization of voltage data collected with the VCU tends to mask variance fluctuations caused by ISC faults. In addition, prolonged data sampling may overload the on-board microcontroller unit (MCU) storage, resulting in the increased computation of the Vari, thereby enabling us to monitor the lithium battery status in real time. Addressing these issues, Qin et al. [39] introduced a novel approach rooted in sliding window-based variance calculation methodology. This innovative technique circumvents the aforementioned limitations by segmenting variance alterations attributed to faults from the overarching variance through the implementation of a fixed-length sliding window w. This method ensures precise and expeditious diagnosis of battery ISC faults, facilitating prompt alert notifications to operators. The formula governing the sliding window-based localized variance calculation is as follows [39]:
where w denotes the sliding window width; denotes the mean value of cell i in the pth sliding window; and denotes the local variance in the pth sliding window. Note that the sampling time is .
During battery voltage measurements, the voltage amplitude is particularly susceptible to external noise and disturbance. Detecting faults within environments characterized by elevated noise levels poses a significant challenge, as methodologies reliant on local variance differences in battery voltage may erroneously interpret such noise as indicative of faults, consequently triggering false alarms within the system. In response to this inherent challenge, this paper proposes an ISC fault detection method based on the local variance difference of battery voltage. Drawing from the preceding variance analysis, it is observed that during the ISC event within a battery, the voltage of the affected battery experiences a precipitous decline, thereby yielding an increase in variance. Conversely, the variance in unaffected battery voltages remains relatively stable within a defined range. Figure 8 illustrates the variance difference values between battery 3 and its adjacent batteries. Leveraging this observation, ISC fault detection accuracy is proposed to be improved by calculating the local variance difference value between neighboring cell voltages. The mathematical formulation encapsulating the variance difference between neighboring battery voltages is articulated as follows.
where denotes the variance difference between the ith cell and the jth cell in the pth sliding window; denotes the series consisting of the variance difference between cell i and cell j, and k denotes the length of the current difference series.
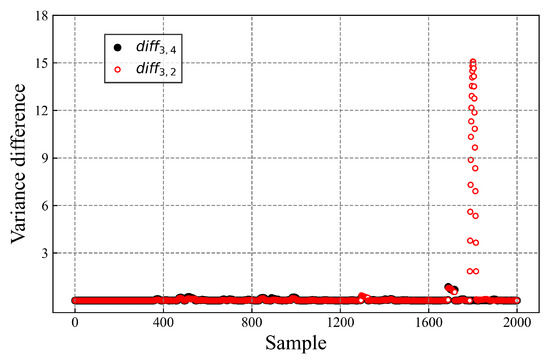
Figure 8.
Variance difference values between cell 3 and its neighboring cells.
3.3. ISC Fault Localization and Diagnosis Framework
The ISC fault location and detection process delineated in this paper is elucidated in Figure 9. The precise steps comprising the proposed ISC fault location and detection method are expounded below:
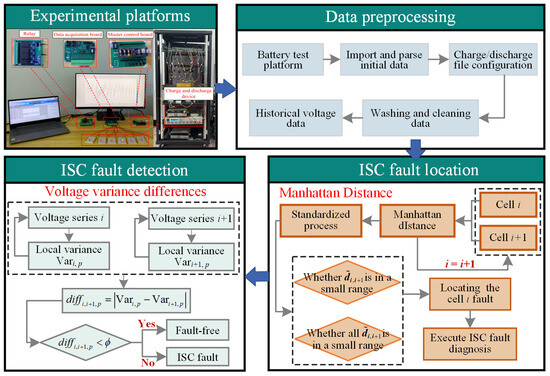
Figure 9.
ISC fault location and detection process.
Step 1: Voltage data for each cell in a lithium battery pack are collected via the established battery experimental platform, and data cleaning is performed.
Step 2: Computation of the curvilinear Manhattan distance between each cell, subsequently subjecting the calculated distances to normalization.
Step 3: Construction and comprehensive analysis of the Manhattan matrix pertaining to the Li-ion battery pack, aimed at identifying potential ISC-faulty cell locations.
Step 4: Calculation of the local variance pertaining to the voltages of the potential ISC-faulty battery and its neighboring batteries, based on the localization outcomes derived from Step 3. Subsequent analysis involves evaluating the variance disparity between the two batteries utilizing Equation (9).
Step 5: Evaluation of whether the calculated variance difference exceeds the predetermined threshold . If , then battery i is considered to have an ISC failure at time period p. If , then battery i is considered not to have an ISC failure at time period p.
4. Experimental Results and Analysis
To realistically replicate the manifestation of ISC faults in lithium battery-powered ship battery packs, we meticulously simulate three distinct intensities of ISC faults, as delineated in the experimental configuration expounded upon in Section 2. The voltage exhibited by each battery amidst the three ISC faults is graphically illustrated in Figure 10. Evidently depicted in Figure 10, the battery pack demonstrates robust uniformity, manifesting analogous real-time voltage amplitudes across each cell during normal operation. However, upon introduction of an ISC fault into the battery pack, a discernible plummet in voltage is observed in the affected cell, disrupting the harmonious synchronization among the cells. Following the introduction of varying levels of ISC faults, the voltage of short-circuited cells experiences an abrupt decline. Therefore, the methods of curvilinear Manhattan distance analysis and voltage variance analysis is introduced to accurately locate and identify the battery ISC faults.
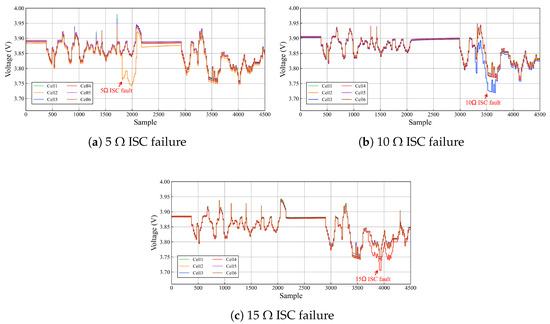
Figure 10.
Battery pack voltage curves under different intensities of ISC faults.
4.1. ISC Fault Detection Based on Manhattan Distance
Taking into account the voltage fluctuations across diverse ISC fault scenarios, the computed outcomes of the Manhattan distance were standardized to uniformly assess battery malfunction across varying degrees of ISC faults. The inter-cell Manhattan distances across distinct ISC fault injection instances are delineated in Figure 11. It is pertinent to highlight that the shading of cell colors corresponds to the magnitude of the Manhattan distance between them: cells exhibiting a greater Manhattan distance are depicted with darker hues, while those with lesser distances are depicted with lighter shades. Furthermore, as the Manhattan distance between a cell and itself inherently equals 0, the cell is rendered in white.
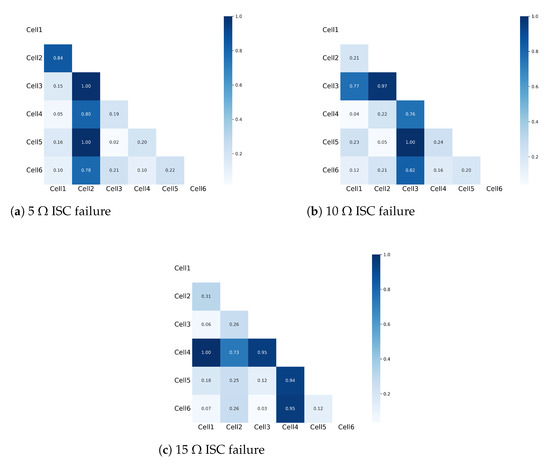
Figure 11.
Curvilinear Manhattan distances between cells for different intensities of ISC failures.
It is widely recognized that during the initial phases of operation in lithium battery-powered vessels, the cells within the battery pack exhibit optimal health. Nevertheless, as the service lifespan of lithium batteries progresses, individual cells may encounter varying degrees of ISC failures. Consequently, during the nascent stages of ISC failure, the vast majority of cells within the battery pack remain unaffected. This discernible phenomenon is elucidated in Figure 11a, where cell 2 distinctly exhibits a substantial Manhattan distance from the other batteries, while the remaining batteries maintain a close proximity to each other, with Manhattan distances ranging between [0, 0.25]. This observation facilitates the localization of the ISC failure within cell 2, thereby affirming the normalcy of the other batteries. Similarly, in Figure 11b,c, despite the attenuation in the severity of injected ISC faults, conspicuous deviations in Manhattan distances are still discernible for cell 3 and cell 4, markedly exceeding the Manhattan distances observed between the remaining batteries. Consequently, this enables the unequivocal identification of cell 3 and cell 4 as the defective cells. Hence, through the meticulous quantification of Manhattan distances between batteries, this paper engenders an accurate and dependable method for promptly discerning the occurrence of early ISC failures within battery packs.
4.2. ISC Fault Detection Based on Voltage Variance Analysis
To reduce the risk of false alarms and to improve the accuracy of ISC fault detection, voltage variance analysis is performed on the collected voltage data to determine when an ISC fault occurs. In this context, a moving window w of local variance is set to 30, alongside the threshold , derived from multiple experimental trials. Figure 12a illustrates the temporal evolution of the local variance disparity between cell 2 and cell 3 for the 5 Ω ISC fault scenario. From the depicted graph, it is discernible that at the 1816-th sampling instance, the differential value experiences a dramatic surge, surpassing the predefined threshold abruptly. This notable deviation signifies that, at this juncture, the introduction of the ISC fault disrupts the coherence between the batteries, resulting in an alteration in the variance distribution between battery 2 and battery 3, thereby culminating in a sudden escalation of the differential value. Consequently, predicated upon the aforementioned analysis, the occurrence of ISC in either battery 2 or battery 3 can be reliably detected. Furthermore, in conjunction with the localization findings from the Manhattan curve, it is conclusively determined that battery 2 malfunctions around the 1816th sampling moment.
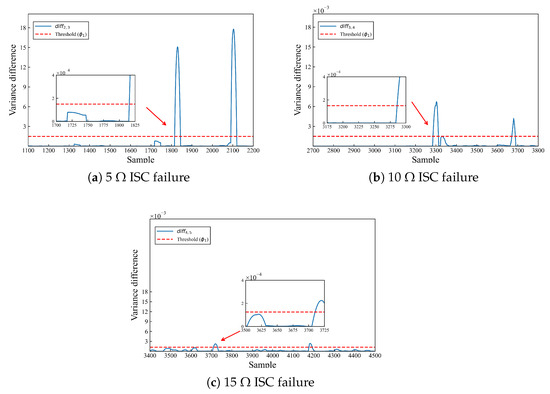
Figure 12.
Detection results of localized variance difference methods under different intensities of ISC faults.
The second instance where the threshold is surpassed in Figure 12a can be attributed to the cessation of the 5 Ω ISC fault injection during the experiment. During the 5 Ω ISC fault experiments, the disconnection of the relay stops the fault injection, prompting the battery voltage to return to normal. As a result, the distribution of the voltage data changes accordingly. In addition, the detection results shown in Figure 12b,c indicate that the proposed method is able to accurately identify the early-stage ISC faults in lithium battery packs.
In the context of ISC fault detection relying on local variance difference analysis, the selection of the moving window poses a pertinent issue warranting investigation. Hence, this paper explores the impact of values within the range of [0, 50] at intervals of 10 on the detection outcomes. Figure 13 presents the detection results of 5 Ω ISC faults under varying moving windows. It is evident from Figure 13a that false alarms manifest around the 1720th sampling instances. This occurrence can be attributed to the excessively small w value, which permits variance changes induced by external noise to be erroneously recognized as ISC faults, thereby compromising the sensitivity of the detection algorithm. Furthermore, Figure 13b–d illustrate that as the value escalates, the impact of noise-induced variance changes gradually diminishes, thereby mitigating false alarms. However, the incremental augmentation of the w value also engenders an increase in computational complexity. Consequently, the detection process necessitates the judicious selection of a suitable sliding window to balance detection sensitivity and computational complexity effectively.
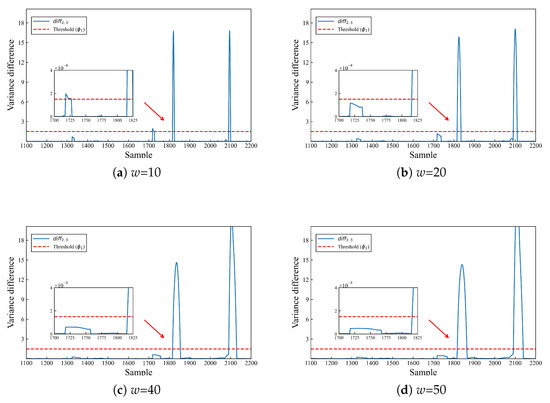
Figure 13.
The 5 Ω ISC fault detection results under different sliding windows w.
4.3. Compared to Other Detection Methods
To delve deeper into the efficacy of the proposed method, the comparative analysis is conducted against established methodologies, namely the correlation coefficient (CC), relative entropy (RE), and principal component analysis (PCA). The detection results obtained from the CC method are depicted in Figure 14, while those from the RE method are illustrated in Figure 15. Additionally, the detection results derived from the PCA method are showcased in Figure 16. Subsequently, the results of the proposed method and the detection with CC, RE and PCA methods are discussed and analyzed.
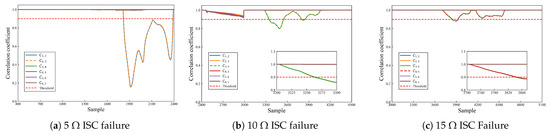
Figure 14.
Experimental results of the CC method under different intensities of ISC faults.

Figure 15.
Experimental results of the RE method under different intensities of ISC faults.
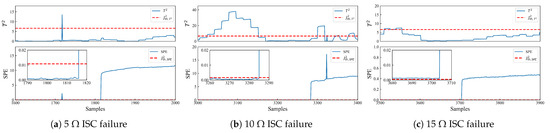
Figure 16.
Experimental results of the PCA method under different intensities of ISC faults.
As depicted in Figure 14, the CC method demonstrates effectiveness in detecting high-intensity ISC faults, yet it exhibits delays and failures in identifying minor ISC faults. This limitation is due to the fact that the voltage changes that occur with minor ISC are extremely small and there is still a robust correlation between the faulty and normal cell voltages, which ultimately hinders the effectiveness of the CC-based detection method.
On the other hand, the relative entropy (RE) method, as inferred from its calculation results, proves adept at detecting ISC faults of varying intensities. However, unlike the approach outlined in this paper, the RE method solely determines the location of the faulty battery based on the relative entropy between different batteries, without discerning the time of fault occurrence. Examining the results derived from the and squared prediction error (SPE) statistics in Figure 16, it is apparent that the principal component analysis (PCA) method effectively detects ISC faults by monitoring and SPE statistics. Nevertheless, the PCA method is susceptible to false alarms, particularly when detecting high-intensity ISC faults, where its statistics exhibit deficiencies. In summary, the methodology expounded in this paper proves accurate and efficient in early ISC fault localization and detection. Moreover, it surpasses the CC, RE, and PCA methods in terms of sensitivity and accuracy, thereby establishing its superiority in ISC fault detection.
4.4. Discussion of Different Detection Methods
To further demonstrate the advantages of the proposed method, we discuss and analyze its detection results with those of classical methods such as CC, RE, and PCA. Compared with the classical methods, the proposed method of battery ISC fault diagnosis based on the variance difference in battery voltage has the following advantages: (1) it fully takes into account the internal physical properties and dynamic changes of the battery and can provide more intuitive and interpretable results; (2) it works flexibly for batteries with different specifications and working conditions and has wider applicability and robustness; and (3) it has a low computational complexity, which improves the detection efficiency and practicability. In summary, the proposed method exhibits obvious advantages in applicability and computational efficiency and provides a more reliable and practical solution for battery ISC fault diagnosis.
5. Conclusions
This paper presents a data-driven method for the early-stage ISC fault location and detection of shipping lithium batteries. At first, based on the synchronization of voltages during normal operation of lithium battery packs, the curvilinear Manhattan distance between batteries is proposed to locate the faulty batteries. Afterwards, the local voltage variance difference values between neighboring batteries are analyzed to further detect ISC faults. The simulation results obtained on the devised battery test platform affirm that, for ISC faults of 5 Ω, 10 Ω, and 15 Ω, the curvilinear Manhattan distance and cell variance analysis methods exhibit notable efficacy in accurately localizing and detecting early-stage ISC faults in batteries, boasting high sensitivity and reliable monitoring performance.
Presently, although the proposed method can effectively and accurately detect early-stage ISC faults in batteries, it has some potential limitations. On the one hand, our study mainly focuses on FDD for early-stage ISC faults of batteries and fails to explore more kinds of battery faults, such as external short-circuit faults, sensor faults, connection anomalies, and other battery-related anomalies. On the other hand, for the collected battery data, we currently only focus on the voltage data information, without exploiting the effect of temperature, capacity, and internal resistance on the battery behavior. Therefore, we will cover more types of battery failures in our future research while enriching the scope of battery data collection.
Author Contributions
Investigation, Y.G. and H.N.; writing—original draft preparation, Y.G.; writing—review and editing, Y.G., H.N. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, H.; Oterkus, E.; Oterkus, S. Peridynamic modelling of fracture in marine lithium-ion batteries. Ocean Eng. 2018, 151, 257–267. [Google Scholar] [CrossRef]
- Peralta, P.C.O.; Vieira, G.T.T.; Meunier, S.; Vale, R.J.; Salles, M.B.C.; Carmo, B.S. Evaluation of the CO2 Emissions Reduction Potential of Li-ion Batteries in Ship Power Systems. Energies 2019, 12, 375. [Google Scholar] [CrossRef]
- Williard, N.; Hendricks, C.; Sood, B.; Chung, J.S.; Pecht, M. Evaluation of Batteries for Safe Air Transport. Energies 2016, 9, 340. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Luo, L.; Fan, Y.; Du, Z. A review on thermal management of lithium-ion batteries for electric vehicles. Energy 2022, 238, 121652. [Google Scholar] [CrossRef]
- Chen, S.; Dai, F.; Cai, M. Opportunities and Challenges of High-Energy Lithium Metal Batteries for Electric Vehicle Applications. ACS Energy Lett. 2020, 5, 3140–3151. [Google Scholar] [CrossRef]
- Zhang, F.; Feng, X.; Xu, C.; Jiang, F.; Ouyang, M. Thermal runaway front in failure propagation of long-shape lithium-ion battery. Int. J. Heat Mass Transfer 2022, 182, 121928. [Google Scholar] [CrossRef]
- Ren, D.; Feng, X.; Lu, L.; He, X.; Ouyang, M. Overcharge behaviors and failure mechanism of lithium-ion batteries under different test conditions. Appl. Energy 2019, 250, 323–332. [Google Scholar] [CrossRef]
- Hu, J.; He, H.; Wei, Z.; Li, Y. Disturbance-Immune and Aging-Robust Internal Short Circuit Diagnostic for Lithium-Ion Battery. IEEE Trans. Ind. Electron. 2022, 69, 1988–1999. [Google Scholar] [CrossRef]
- Lai, X.; Jin, C.; Yi, W.; Han, X.; Feng, X.; Zheng, Y.; Ouyang, M. Mechanism, modeling, detection, and prevention of the internal short circuit in lithium-ion batteries: Recent advances and perspectives. Energ. Storage Mater. 2021, 35, 470–499. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, X.; Tang, X.; Zhu, J.; Chen, S.; Dai, H. Internal short circuit mechanisms, experimental approaches and detection methods of lithium-ion batteries for electric vehicles: A review. Renew. Sustain. Energ. Rev. 2021, 141, 110790. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, D.; Lai, X.; Zheng, Y.; Wei, X.; Dai, H. A novel method of quantitative internal short circuit diagnosis based on charging electric quantity in fixed voltage window. J. Energy Storage 2023, 70, 108096. [Google Scholar] [CrossRef]
- Feng, X.; He, X.; Lu, L.; Ouyang, M. Analysis on the Fault Features for Internal Short Circuit Detection Using an Electrochemical-Thermal Coupled Model. J. Electrochem. Soc. 2018, 165, A155. [Google Scholar] [CrossRef]
- Schmid, M.; Kleiner, J.; Endisch, C. Early detection of Internal Short Circuits in series-connected battery packs based on nonlinear process monitoring. J. Energy Storage 2022, 48, 103732. [Google Scholar] [CrossRef]
- Gao, H.; Li, Z.; Yu, X.; Qiu, J. Hierarchical Multiobjective Heuristic for PCB Assembly Optimization in a Beam-Head Surface Mounter. IEEE Trans. Cybern. 2022, 52, 6911–6924. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Huang, W.; Huang, D.; Chen, H.; Chai, Y.; Ma, M.; Zheng, W.X. A Reduced-Order Observer-Based Method for Simultaneous Diagnosis of Open-Switch and Current Sensor Faults of a Grid-Tied NPC Inverter. IEEE Trans. Power Electron. 2023, 38, 9019–9032. [Google Scholar] [CrossRef]
- Zheng, Y.; Luo, Q.; Cui, Y.; Dai, H.; Han, X.; Feng, X. Fault Identification and Quantitative Diagnosis Method for Series-Connected Lithium-Ion Battery Packs Based on Capacity Estimation. IEEE Trans. Ind. Electron. 2022, 69, 3059–3067. [Google Scholar] [CrossRef]
- Amirkhani, S.; Chaibakhsh, A.; Ghaffari, A. Nonlinear robust fault diagnosis of power plant gas turbine using Monte Carlo-based adaptive threshold approach. ISA Trans. 2020, 100, 171–184. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Jin, S. Investigating the Distribution of Flatness Measurements in Battery Manufacturing through Empirical Investigation and Statistical Theory. Machines 2023, 11, 723. [Google Scholar] [CrossRef]
- Rahman, M.A.; Anwar, S.; Izadian, A. Electrochemical Model-Based Condition Monitoring via Experimentally Identified Li-Ion Battery Model and HPPC. Energies 2017, 10, 1266. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Liu, P.; Wang, Z.; Zhang, L. Battery Fault Diagnosis for Electric Vehicles Based on Voltage Abnormality by Combining the Long Short-Term Memory Neural Network and the Equivalent Circuit Model. IEEE Trans. Power Electron. 2021, 36, 1303–1315. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Lyapunov-Based Thermal Fault Diagnosis of Cylindrical Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2020, 67, 4670–4679. [Google Scholar] [CrossRef]
- Zhang, H.; Dai, K.; Yin, Q. Ammunition Reliability Against the Harsh Environments During the Launch of an Electromagnetic Gun: A Review. IEEE Access 2019, 7, 45322–45339. [Google Scholar] [CrossRef]
- Dey, S.; Perez, H.E.; Moura, S.J. Model-Based Battery Thermal Fault Diagnostics: Algorithms, Analysis, and Experiments. IEEE Trans. Control Syst. Technol. 2019, 27, 576–587. [Google Scholar] [CrossRef]
- Feng, X.; Pan, Y.; He, X.; Wang, L.; Ouyang, M. Detecting the internal short circuit in large-format lithium-ion battery using model-based fault-diagnosis algorithm. J. Energy Storage 2018, 18, 26–39. [Google Scholar] [CrossRef]
- Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Lai, X.; Hu, X. Micro-Short-Circuit Diagnosis for Series-Connected Lithium-Ion Battery Packs Using Mean-Difference Model. IEEE Trans. Ind. Electron. 2019, 66, 2132–2142. [Google Scholar] [CrossRef]
- Wang, G.; Jin, S.; Jiao, J.; Xie, J. Voltage measurement-based recursive adaptive method for internal short circuit fault diagnosis in lithium-ion battery packs. Contr. Eng. Pract. 2024, 145, 105857. [Google Scholar] [CrossRef]
- Park, S.; Song, Y.; Kim, S.W. Simultaneous diagnosis of cell aging and internal short circuit faults in lithium-ion batteries using average leakage interval. Energy 2024, 290, 130220. [Google Scholar] [CrossRef]
- Qiu, Y.; Cao, W.; Peng, P.; Jiang, F. A novel entropy-based fault diagnosis and inconsistency evaluation approach for lithium-ion battery energy storage systems. J. Energy Storage 2021, 41, 102852. [Google Scholar] [CrossRef]
- Sun, R.B.; Du, F.P.; Yang, Z.B.; Chen, X.F.; Gryllias, K. Cyclostationary Analysis of Irregular Statistical Cyclicity and Extraction of Rotating Speed for Bearing Diagnostics with Speed Fluctuations. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Zhu, G.; Sun, T.; Xu, Y.; Zheng, Y.; Zhou, L. Identification of Internal Short-Circuit Faults in Lithium-Ion Batteries Based on a Multi–Machine Learning Fusion. Batteries 2023, 9, 154. [Google Scholar] [CrossRef]
- Xia, B.; Shang, Y.; Nguyen, T.; Mi, C. A correlation based fault detection method for short circuits in battery packs. J. Power Sources 2017, 337, 1–10. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, J.; Yang, J.; Jiao, J.; Xie, J.; Feng, F. Multivariate statistical analysis based cross voltage correlation method for internal short-circuit and sensor faults diagnosis of lithium-ion battery system. J. Energy Storage 2023, 62, 106978. [Google Scholar] [CrossRef]
- Xie, J.; Yao, T. Quantified Assessment of Internal Short-Circuit State for 18 650 Batteries Using an Extreme Learning Machine-Based Pseudo-Distributed Model. IEEE Trans. Transp. Electrificat. 2021, 7, 1303–1313. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, S.; Yang, Z.; He, Y. A multi-fault diagnosis method for lithium-ion battery pack using curvilinear Manhattan distance evaluation and voltage difference analysis. J. Energy Storage 2023, 67, 107575. [Google Scholar] [CrossRef]
- Grabow, J.; Klink, J.; Benger, R.; Hauer, I.; Beck, H.P. Particle Contamination in Commercial Lithium-Ion Cells—Risk Assessment with Focus on Internal Short Circuits and Replication by Currently Discussed Trigger Methods. Batteries 2023, 9, 9. [Google Scholar] [CrossRef]
- Xie, J.; Peng, H.; Li, Z.; Wang, G.; Li, X. Data-Driven Diagnosis of Multiple Faults in Series Battery Packs Based on Cross-Cell Voltage Correlation and Feature Principal Components. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 109–119. [Google Scholar] [CrossRef]
- Kang, Y.; Duan, B.; Zhou, Z.; Shang, Y.; Zhang, C. Online multi-fault detection and diagnosis for battery packs in electric vehicles. Appl. Energy 2020, 259, 114170. [Google Scholar] [CrossRef]
- Wang, G.; Yang, J.; Jiao, J. Voltage Correlation-Based Principal Component Analysis Method for Short Circuit Fault Diagnosis of Series Battery Pack. IEEE Trans. Ind. Electron. 2023, 70, 9025–9034. [Google Scholar] [CrossRef]
- Qin, Y.; Yan, Y.; Ji, H.; Wang, Y. Recursive Correlative Statistical Analysis Method With Sliding Windows for Incipient Fault Detection. IEEE Trans. Ind. Electron. 2022, 69, 4185–4194. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).