A Fault Diagnosis Method for Key Components of the CNC Machine Feed System Based on the DoubleEnsemble–LightGBM Model

Abstract

To solve the problem of fault diagnosis for the key components of the CNC machine feed system under the condition of variable speed conditions, an intelligent fault diagnosis method based on multi-domain feature extraction and an ensemble learning model is proposed in this study. First, various monitoring signals including vibration signals, noise signals, and current signals are collected. Then, the monitoring signals are preprocessed and the time domain, frequency domain, and time–frequency domain feature indices are extracted to construct a multi-dimensional mixed-domain feature set. Finally, the feature set is entered into the constructed DoubleEnsemble–LightGBM model to realize the fault diagnosis of the key components of the feed system. The experimental results show that the model can achieve good diagnosis results under different working conditions for both the widely used dataset and the feed system test bench dataset, and the average overall accuracy is 91.07% and 98.06%, respectively. Compared with XGBoost and other advanced ensemble learning models, this method demonstrates better accuracy. Therefore, the proposed method provides technical support for the stable operation and intelligence of CNC machines.

1. Introduction

Among the failures in CNC machines, mechanical body failure accounts for about 57% and electrical system failure accounts for about 37.5%, according to statistics. CNC system failure accounts for only 5.5%, and most of the current CNC machines have the self-diagnosis function of electrical and CNC systems [1]. The failure of the mechanical body is the key and most challenging point of the current research. With the continuous development of data acquisition technology, information technology, and artificial intelligence technology, fault diagnosis methods have also experienced the development process from artificial experience diagnosis to intelligent diagnosis, and from single-sensor diagnosis to multi-sensor fusion diagnosis. A CNC machine is a kind of efficient processing equipment. The working stability and positioning accuracy of the feed system are very important components of CNC machines that ensure processing quality and efficiency. The mechanical transmission structure of the CNC machine feed system is mainly composed of a servo motor, coupling, ball screw pair, rolling bearing, and guide rail pair.

Grether et al. [2] conducted a study on Siemens CNC machines. According to expert knowledge in the field of fault diagnosis, an ontology-based knowledge representation structure was proposed, and then the SimRank algorithm was used to calculate the similarity between the fault phenomenon and the fault caused in the case base to realize the fault diagnosis of the CNC machine. However, the relationship between mechanical ontology failures and critical components was not further analyzed.

Wang et al. [3] established the fault tree model of CNC machines and, on this basis, a deep neural network model was constructed to classify and identify the features. The average recognition rate of the back-propagation (BP) network after feature reduction was found to be 86%. Kemal et al. [4] used Morlet wavelet analysis to extract the features of vibration signals of CNC machines and then proposed a deep long short-term memory (LSTM) model for fault classification, which effectively improves the classification accuracy. However, the influence of the vibration signal fault diagnosis accuracy under the variable speed working condition of CNC machines was not considered.

In recent years, many scholars have studied the fault diagnosis of key components of the CNC machine feed system, such as roller bearings, ball screws, and so on.

Shan et al. [5] proposed to arrange multiple sensors at different positions of the ball screw. The fault location of the ball screw was realized by carrying out weight distribution on the fault sensitivity indices of different sensors and combining it with a convolutional neural network (CNN). The effectiveness of the method was verified by testing it on the ball screw bench; however, the model requires a larger sample dataset for training.

Zhang et al. [6] applied a new unsupervised learning method, generalized normalized sparse filtering, to rolling bearing intelligence under complex working conditions. The experiment proves that the method can obtain higher diagnosis accuracy with fewer training samples. However, the validity of the algorithm was verified with the Western Reserve University roller bearing dataset as well as the planetary gearbox test bed dataset, and the accuracy of fault diagnosis under variable speed conditions was not analyzed.

Chen et al. [7] proposed a multi-scale feature alignment CNN for bearing fault diagnosis under different working conditions, which improves the displacement invariance of the CNN. The effectiveness and advancement of the method were verified by using the Nippon Seiko Kabushiki-gaisha (NSK) 40BR10 rolling bearing dataset and the rolling bearing data set of CNC machines under three load conditions and four speed operating conditions in experiments. Moslem et al. [8] proposed a domain adaptive method based on deep learning for cross-domain ball screw fault diagnosis. A deep convolutional neural network was used for feature extraction, and the maximum average difference metric was proposed to measure and optimize the data distribution under different working conditions. The effectiveness of the proposed method was proved by the experiment with the monitoring data of the ball screw under real working conditions. Pandhare et al. [9] collected the vibration acceleration signals at five different positions on the ball screw test bench and proposed a data domain-adaptive fault diagnosis method based on the CNN, which minimizes the maximum average difference of high-level representations between the source domain data and the target domain data, and the average diagnostic accuracy of the model reached 98.25%, which provides a kind of diagnostic method for diagnosing the faults of the key components of the feed system. However, the methods proposed in the literature [7,8,9] require larger sample datasets.

Jin et al. [10] proposed an end-to-end adaptive anti-noise neural network framework (AAnNet) without manual feature selection and denoising processing. The convolutional feature extraction part of the network takes the exponential linear unit as the activation function, and the extracted features are learned and classified by a gated recurrent neural network improved by an attention mechanism. The accuracy of bearing fault diagnosis under the conditions of noise and variable load was effectively improved. However, the validity of the algorithm was verified with the Western Reserve University roller bearing dataset as well as the bearing failure test bed bench dataset, and the accuracy of fault diagnosis under variable speed conditions was not analyzed.

Patel et al. [11] modeled the mixed fault, analyzed its vibration signal, and then recognized the mixed fault pattern. Abbasion et al. [12] applied the combination of wavelet packet decomposition and support vector machine to the mixed fault diagnosis of bearings. Lei et al. [13] proposed a classification method based on adaptive fuzzy neural inference to diagnose the composite faults of electric locomotives. Delgado et al. [14] extracted fault features from the motor current signal and vibration signal and used partial least squares to reduce the dimensionality of the extracted features and construct feature vectors. Finally, they used a support vector machine (SVM) model to achieve the diagnosis of motor inter-turn short-circuit fault. The authors of [11,12,13,14] provided effective methods and ideas for nonlinear feature extraction and fault diagnosis of rolling bearings.

Wang et al. [15] used a multi-task shared classifier based on incremental learning to achieve better fault diagnosis of support bearings under various working conditions. Li et al. [16] proposed a method based on an attention mechanism to solve the problem of low accuracy and poor stability of the model caused by unbalanced datasets. The experimental results of their study show that the method has a good diagnosis effect under unbalanced data conditions. Xu et al. [17] used an improved method of combining a multi-scale convolutional neural network with a feature attention mechanism to improve the generalization ability of the model. Wu et al. [18] adopted a fault diagnosis method combining domain antagonistic neural networks and attention mechanisms. The experimental results of their study show that this method has great potential in the cross-domain diagnosis of rolling bearings. Huang et al. [19] proposed a method to solve the problem of data distribution deviation in the fault diagnosis of support-bearing migration. The experimental results of their study show that the method can support bearing migration fault diagnosis suitable for different working conditions. The authors of [15,16,17,18,19] provided effective methods and models for bearing fault diagnosis under different operating conditions.

Zhang et al. [20] proposed an instance-based transfer learning method to solve the problem of insufficient labeled samples in the application of ball screw fault diagnosis. The authors of [20] provided effective methods and models for ball screw fault diagnosis under complex operating conditions.

Based on a comprehensive analysis of the research status of fault diagnosis of key components of the CNC machine feed system, this study’s primary contributions can be summarized as follows:

• To solve the problem of the fault diagnosis of key components of the CNC machine feed system under variable speed conditions and the issue of too few fault samples being available in practical work, a fault diagnosis method based on multi-monitoring signals, multi-domain feature extraction, and the DoubleEnsemble–LightGBM integrated learning model is proposed in this study. The experimental results show that this method can realize the fault diagnosis of key components of the feed system with fewer data samples, and the method achieves a better diagnosis effect than Xgboost and other advanced integrated learning models.
• Various monitoring signals including vibration signals, noise signals, and current signals are collected. The monitoring signals are preprocessed by using singularity elimination, trend item elimination, and wavelet threshold denoising. Next, the time domain, frequency–domain feature indices, and IMF information entropy of the monitoring signals are extracted. Finally, the multi-dimensional mixed-domain feature set is constructed.
• Based on the LightGBM model, the DoubleEnsemble–LightGBM fault diagnosis model is constructed by introducing the sample re-weighting mechanism based on learning trajectory and the feature selection mechanism based on shuffling technology, which realizes the intelligent fault diagnosis of the CNC machine feed system.

The remainder of this article is structured as follows: The main theories and approaches behind the proposed model are introduced in Section 2. The proposed method is explained in Section 3. The experimental findings are summarized in Section 4. The pertinent conclusions are summarized in Section 5.

2. Relevant Theories

2.1. CEEMDAN Decomposition and IMF Information Entropy

2.1.1. CEEMDAN Decomposition

The CEEMDAN (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise) algorithm overcomes the mode mixing problem of EMD by adding adaptive white noise. This model can effectively reduce the residual white noise in the IMF components obtained after decomposition [21].

The specific process of CEEMDAN decomposition is as follows:

1. Add k times of random Gaussian white noise with a mean value of 0 into the signal $x(t)$ to be decomposed; next, construct the sequence $x_i(t)$ of the k times experiment according to Formula (1): $i=1,2,\cdot \cdot \cdot ,K$

$$x_i(t)=x(t)+{\epsilon }_0{\delta }_i(t)$$

(1)

where ${\delta }_i(t)$ is the random Gaussian white noise added in the ith experiment; ${\epsilon }_0$ is the weight coefficient of the Gaussian white noise.

2. Carry out EMD decomposition on the sequence, $x_i(t)$, by taking the average value of the first IMF component obtained from the k times the experiment as the first IMF component obtained from the CEEMDAN decomposition, and refer to Formula (2) for calculation. Refer to Formula (3) for the calculation of the residual signal after the first decomposition.

$${\overline{IMF}}_1(t)=\frac{1}{K}{\displaystyle \sum _{i=1}^{K}IM{F_1}^i(t)}$$

(2)

$$r_1(t)=x(t)-{\overline{IMF}}_1(t)$$

(3)

3. A new sequence $r_1(t)+{\epsilon }_1{E}_1\left({\delta }_i(t)\right)$ is obtained by adding k times specific noise $r_1(t)$. Next, the EMD decomposition is carried out by calculating the second IMF component obtained by using the CEEMDAN decomposition according to Formula (4),

$${\overline{IMF}}_2(t)=\frac{1}{K}{\displaystyle \sum _{i=1}^K{E}_1\left(r_1(t)+{\epsilon }_1{E}_1\left({\delta }_i(t)\right)\right)}$$

(4)

where $E_1\left(\cdot \right)$ is the first IMF component obtained after EMD decomposition; ${\epsilon }_1$ is the weight coefficient for adding noise to $r_1(t)$.

4. Calculate a margin signal $r_m(t)$$m=2,\cdot \cdot \cdot ,M$ according to Formula (5), and obtain the m+1th IMF component of the CEEMDAN in the same way as step 3. Refer to Formula (6) for calculation.

$$r_m(t)=r_{m-1}(t)-{\overline{IMF}}_m(t)$$

(5)

$${\overline{IMF}}_{m+1}(t)=\frac{1}{K}{\displaystyle \sum _{i=1}^K{E}_1\left(r_m(t)+{\epsilon }_m{E}_m\left({\delta }_i(t)\right)\right)}$$

(6)

The formula $E_m\left(\cdot \right)$ represents the mth IMF component obtained after the EMD decomposition of a certain sequence; ${\epsilon }_m$ is the weight coefficient for adding noise $r_m(t)$.

5. Repeat step 4 to calculate other IMF components of the CEEMDAN decomposition until the number of extreme points $r_m(t)$ is less than two. Eventually, the signal $x(t)$ is decomposed into m IMF components and a residual component $R(t)$ is obtained.

$$R(t)=x(t)-{\displaystyle \sum _{m=1}^M{\overline{IMF}}_m(t)}$$

(7)

2.1.2. False Modal Component Rejection

The IMF components obtained by using the CEEMDAN decomposition may contain false modal components, and the spurious modal components need to be rejected. The correlation coefficient can describe the degree of correlation between the IMF component and the original signal. The closer the correlation coefficient is to 1, the more useful the information contained by the component, and, thus, the stronger the correlation with the original signal. Therefore, the false modal components obtained after the CEEMDAN decomposition can be adaptively eliminated through the correlation coefficient.

The correlation coefficient $C_m$ between the mth IMF component and the original signal is calculated as follows:

$$C_m=\frac{{\displaystyle \sum _{i=1}^N(x_i-\overline{x})(y_i-\overline{y})}}{\sqrt{{\displaystyle \sum _{i=1}^N{(x_i-\overline{x})}^2}}\sqrt{{\displaystyle \sum _{i=1}^N{(y_i-\overline{y})}^2}}}$$

(8)

where $x_i$ is the ith element value in the original signal sequence; $\overline{x}$ is the average value of the original signal sequence; $y_i$ is the value of the ith element in the mth IMF component; $\overline{y}$ is the average value of the mth IMF component; and $N$ is the signal sequence length.

Albert et al. [22] developed a formula for calculating the adaptive threshold of the correlation coefficient, as shown in Equation (9). If $C_m<\mu$, then the mth IMF component will be rejected.

$$\mu =\frac{\max (C_m)}{10\times \max (C_m)-3},m=1,2,\cdot \cdot \cdot ,M$$

(9)

In the formula, M is the number of IMF components decomposed from the original signal and $\max (C_m)$ is the maximum correlation coefficient value.

2.1.3. Calculation of IMF Information Entropy

In the field of fault diagnosis, entropy can effectively reflect the complexity of the signal and describe its nonlinear characteristics. It is often difficult to describe the signal characteristics of a single entropy value; therefore, multiple information entropy eigenvalues are extracted simultaneously. It is assumed that K effective IMF components are obtained after the signal $x(t)$ is decomposed by using CEEMDAN, denoted as $u_i(t),i=1,2,\cdot \cdot \cdot ,k$.

1. Energy entropy of IMF

Energy entropy is an index that can characterize the energy complexity of a signal. The IMF energy entropy is calculated as follows:

First, the energy value of each effective IMF component is calculated by Equation (10):

$$E_i={\displaystyle {\int }_{-\infty }^{+\infty }{\left|u_i(t)\right|}^2}dt,i=1,2,\cdot \cdot \cdot ,k$$

(10)

Then, the total energy value is calculated by Equation (11):

$$E={\displaystyle \sum _{i=1}^k{E}_i}$$

(11)

Finally, the IMF energy entropy is calculated by Equation (12):

$$H_{\mathrm{E}}=-{\displaystyle \sum _{i=1}^k{h}_i\lg h_i}$$

(12)

where $h_i=E_i/E$ represents the proportion of the energy value of the ith IMF component to the total energy value.

2. Power spectrum entropy of IMF

Power spectrum entropy can reflect the change in signal energy in the frequency domain. The IMF power spectrum entropy is calculated as follows: First, each effective IMF component $u_i(t)$ is Fourier-transformed to obtain $u_i(\omega ),i=1,2,\cdot \cdot \cdot ,k$. Then, the power spectrum of each effective IMF component is calculated by Equation (13):

$$S_i=\frac{1}{2\pi N}{\left|u_i(\omega )\right|}^2$$

(13)

Finally, the IMF power spectrum entropy is calculated by Equation (14):

$$H_{\mathrm{F}}=-{\displaystyle \sum _{i=1}^k{p}_i\lg p_i}$$

(14)

where $p_i=S_i/{\displaystyle \sum _{i=1}^k{S}_i}$ represents the proportion of the power spectrum of the ith IMF component to the total power spectrum.

3. The singular spectral entropy of IMF

Singular spectral entropy can quantitatively describe the complex state characteristics of time series. The calculation of the IMF singular spectral entropy is as follows:

First, each IMF component is formed into a characteristic matrix A:

$$\mathit{A}={\left[u_1(t),\cdot \cdot \cdot ,u_k(t)\right]}^{\mathrm{T}}$$

(15)

Then, the singular values ${\lambda }_i,i=1,2,\cdot \cdot \cdot ,k$ of the characteristic matrix A are computed.

Finally, the IMF singular spectral entropy is calculated by Equation (16):

$$H_{\mathrm{S}}=-{\displaystyle \sum _{i=1}^k{q}_i\lg q_i}$$

(16)

where $q_i={\lambda }_i/{\displaystyle \sum _{i=1}^k{\lambda }_i}$ represents the proportion of the ith singular value to the sum of all singular values.

2.2. LightGBM Algorithm

LightGBM [23] (Light Gradient Boosting Machine) is a lightweight gradient lifting model. It is an optimized framework based on the classical ensemble learning model GBDT [24]. The principle of GBDT is shown in Figure 1.

The basic idea is to use the decision tree as a weak classifier. A plurality of weak classifiers are iteratively trained through a gradient lifting strategy, and all the weak classifiers are combined in a linear addition mode to form a strong classifier with a better classification effect.

Based on the GBDT model, LightGBM is optimized as follows:

(1) The gradient-based one-sided sampling (GOSS) algorithm is used to compress the training data samples without loss of accuracy, and its basic idea is to discard some samples that are not helpful to the calculation of information gain. Then, the data calculation amount can be reduced, and the operation cost is greatly reduced.

(2) The Exclusive Feature Bundling (EFB) algorithm is used to merge the mutually exclusive features in high-dimensional data into one feature, which can effectively reduce the feature dimension and reduce the computational load.

(3) The histogram algorithm is used to improve the node segmentation strategy of the decision tree. The basic idea is to discretize the continuous floating-point eigenvalues into K integers and construct a histogram with width K. This can greatly reduce the computational time and memory consumption, and it has little impact on the overall classification accuracy of the model under the framework of gradient boosting. At the same time, it has the effect of regularization, which can prevent the model from overfitting and enhance the stability and robustness of the model.

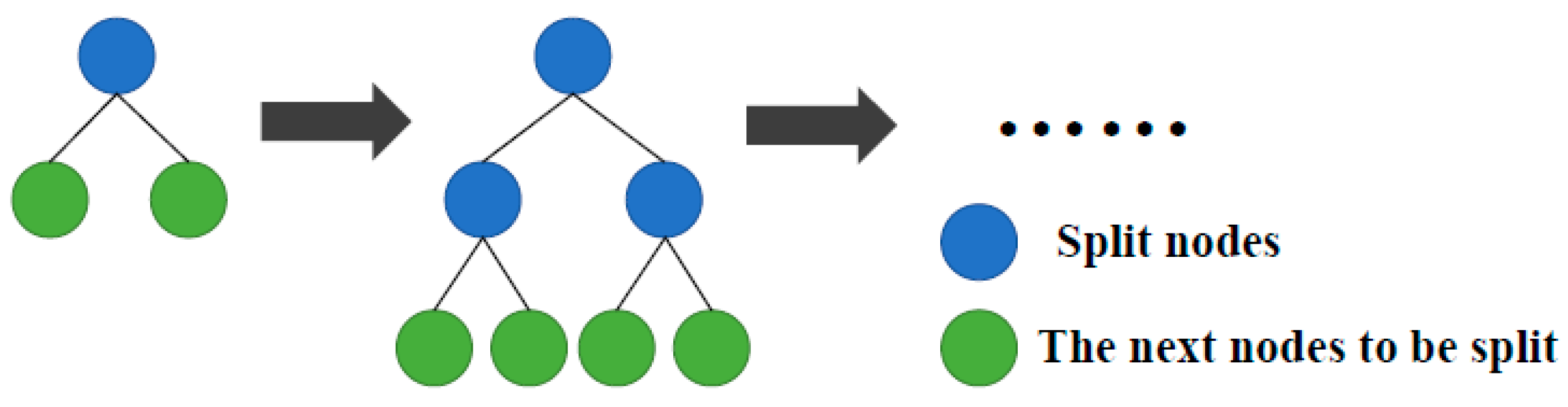
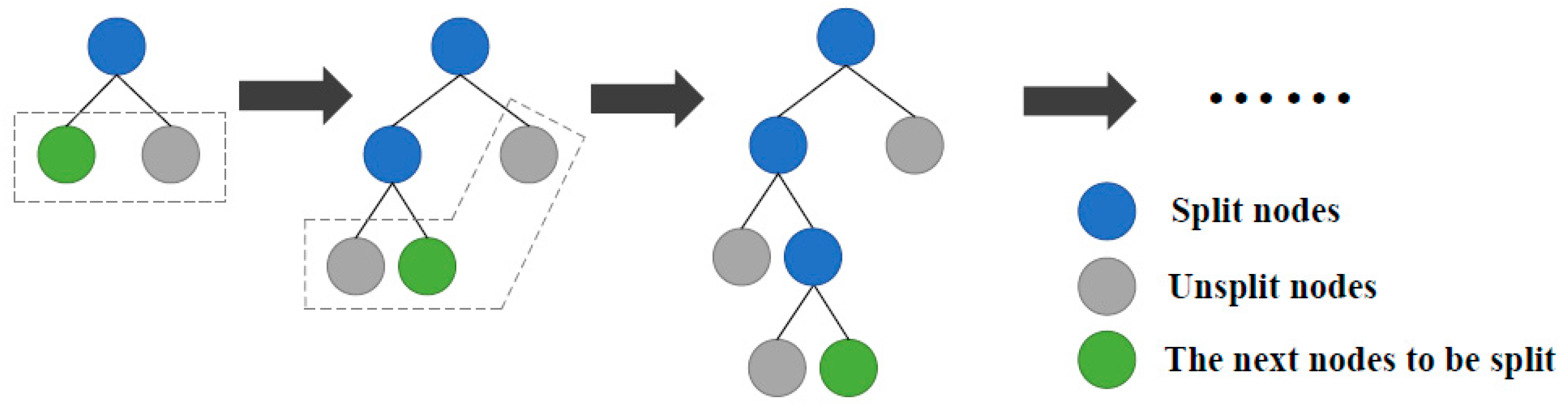
(4) The decision tree growth strategy used by GBDT is grow-by-layer, as shown in Figure 2, which treats all leaf nodes in the same layer indiscriminately and is computationally very inefficient. LightGBM instead uses a grow-by-leaf strategy, the principle of which is shown in Figure 3. This strategy identifies the leaf node with the largest splitting gain from all current leaf nodes to split each time, and so on. With the same number of splits, the grow-by-leaf strategy can reduce errors and achieve better accuracy. However, this approach may result in deeper decision trees, leading to model overfitting; therefore, LightGBM adds another maximum depth limit to the grow-by-leaf strategy.

In summary, LightGBM not only inherits the advantages of GBDT but also greatly improves the training efficiency and memory consumption. Compared with other integrated learning models, this model more easily addresses large-scale data and requires low computing power. Therefore, LightGBM is the basic model for mechanical fault diagnosis of CNC machine feed systems.

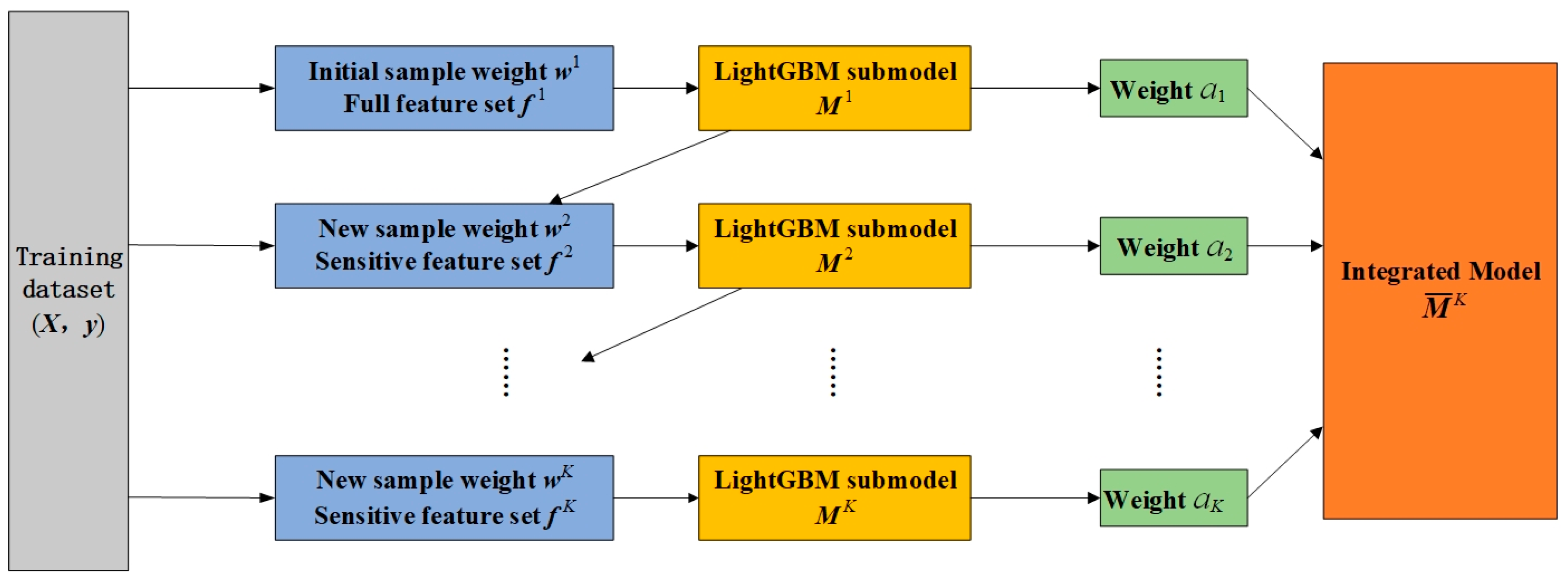
2.3. DoubleEnsemble Algorithm

DoubleEnsemble is a new ensemble algorithm framework that can be used with various machine learning models. It includes two key technologies, one of which is the sample re-weighting technology based on learning trajectory, which can give different weights to different samples in the model training process, thus reducing the interference of simple samples and noise samples and enhancing the training of key samples. The feature selection technology based on the shuffling mechanism can help the model automatically screen sensitive features in the training process, thus effectively improving the model’s accuracy and reducing the risk of overfitting.

The algorithm flow (pseudocode) of DoubleEnsemble is shown in Algorithm 1.

Algorithm 1: DoubleEnsemble

1: Input: Training data (X, y), number of sub-models K, and sub-model weights $\mathit{a}=(a_1,\cdots ,a_K)$

2: Set the initial sample weights ${\mathit{w}}^1$ = (1, ⋯⋯, 1)

3: Select initial feature set ${\mathit{f}}^1$ = [F]

4: for k = 1 to K:

5: ${\mathit{M}}^k$←Train sub-model (X, y, ${\mathit{w}}^k$, ${\mathit{f}}^k$)

6: Retrieve the loss curve ${\mathit{C}}^k$ of the sub-model ${\mathit{M}}^k$ and the loss ${\mathit{L}}^k$ of the current integrated model ${\overline{\mathit{M}}}^k$

7: Update sample weights based on the sample re-weighting technique ${\mathit{w}}^{k+1}$←SR (${\mathit{C}}^k$, ${\mathit{L}}^k$, K)

8: Update the feature set based on the feature selection technique ${\mathit{f}}^{k+1}$←FS (${\overline{\mathit{M}}}^k$, X, y)

9: Return: Integrated model ${\overline{\mathit{M}}}^K(\cdot )$

The algorithm sequentially trains K machine learning sub-models, denoted as ${\mathit{M}}^1$,⋯,${\mathit{M}}^K$; all sub-models are weighted and integrated according to Formula (17), and the integrated model ${\overline{\mathit{M}}}^K(\cdot )$ is taken as the final output of the algorithm,

$${\overline{\mathit{M}}}^K(\cdot )=\frac{1}{K}{\displaystyle \sum _{i=1}^K{a}_i{\mathit{M}}^i(\cdot )}$$

(17)

where $a_i$ is the weight coefficient of the ith sub-model ${\mathit{M}}^i$.

The training data comprise a feature matrix X and a label vector y. $\mathit{X}={[{\mathit{x}}_1,\cdot \cdot \cdot ,{\mathit{x}}_N]}^{\mathrm{T}}\in {\mathrm{R}}^{N\times F}$, where ${\mathit{x}}_i$ represents the feature set of the ith sample, N is the total number of training samples, and F is the dimension of the feature set. $\mathit{y}=(y_1,\cdot \cdot \cdot ,y_N)$, $y_i$ represents the fault label of the ith sample. For the first sub-model ${\mathit{M}}^1$, the algorithm will use all the feature indices in the feature set of the training data for training, i.e., ${\mathit{f}}^1$ = [F]; the initial sample weights are set to ${\mathit{w}}^1$ = (1,⋯,1). The subsequent sub-models are trained based on the newly selected feature set ${\mathit{f}}^k\subseteq [F]$ and the updated sample weights ${\mathit{w}}^k=(w_1^k,\cdot \cdot \cdot ,w_N^k)$, where ${\mathit{w}}^k$ and ${\mathit{f}}^k$ are obtained through sample re-weighting based on learning trajectory and feature selection based on the shuffling mechanism algorithm, respectively.

3. Model: Multi-Domain Feature and DoubleEnsemble–LightGBM

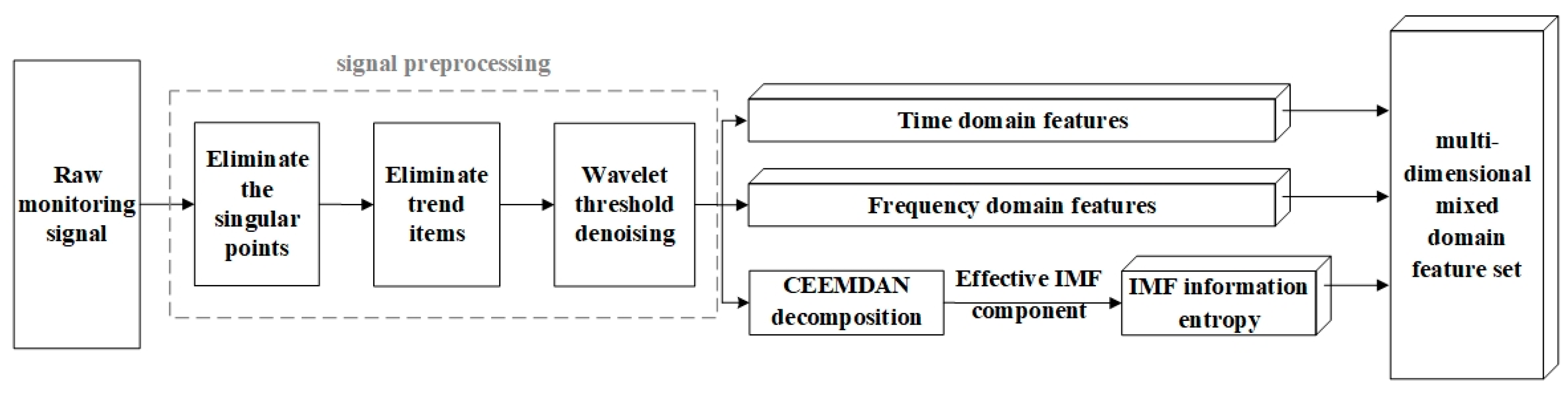
The CNC machine feed system is a complex system with multi-mechanical components, and it is difficult to describe its fault state by the characteristics in a single domain. To reflect the operational status of the feed system more comprehensively, the time domain characteristic indices, the frequency domain characteristic indices, and the time–frequency domain characteristic indices of various monitoring signals including vibration signals, noise signals, and current signals are first extracted, and a multi-dimensional mixed domain feature set, as shown in Figure 4, is constructed.

In addition, considering that the total dimension of the multi-dimensional mixed domain feature set reaches hundreds of dimensions, it may contain invalid features, which will impair the model training process. In addition, there may be simple samples and useless high-noise samples in the collected training samples, which leads to poor training performance of the model and overfitting. Therefore, the fault diagnosis model is further optimized and multiple LightGBM classification sub-models are trained and integrated through the DoubleEnsemble algorithm. Finally, the DoubleEnsemble–LightGBM model is constructed, as shown in Figure 5, for intelligent identification of the fault mode of the CNC machine feed system.

The ${\mathit{w}}^k$ and ${\mathit{f}}^k$ parameters in the model are obtained through sample re-weighting using learning trajectory and feature selection based on the shuffling mechanism algorithm, respectively.

(1) Sample re-weighting based on the learning trajectory algorithm

The algorithm flow (pseudocode) of sample re-weighting based on the learning trajectory is shown in Algorithm 2. The algorithm aims to reduce the training weight of simple samples (samples that are easy to be correctly classified by the model) and noisy samples (samples that are easy to be overwhelmed with information) so that the model can focus on learning difficult samples (samples that are challenging for the model to correctly classify) during training, and thus improve the classification performance of the model.

Algorithm 2: Sample re-weighting based on learning trajectory

1: Input: the loss curve ${\mathit{C}}^k$ of the sub-model ${\mathit{M}}^k$, the index value K of the loss ${\mathit{L}}^k$ and ${\mathit{M}}^k$ of the current integrated model ${\overline{\mathit{M}}}^k$

2: Parameters: coefficient ${\alpha }_1$ and ${\alpha }_2$, number of sample subsets $B$, attenuation factor $\gamma$

3: Calculate the value $h$ of each sample according to Formula (18)

4: Divide the sample into $B$ sample subsets based on the values $h$

5: Calculate the sample weights ${\mathit{w}}^{k+1}=(w_1^{k+1},\cdot \cdot \cdot ,w_N^{k+1})$ according to Formula (19)

6: Return: Sample weight ${\mathit{w}}^{k+1}$

The algorithm uses the loss curve ${\mathit{C}}^k$ of the current sub-model ${\mathit{M}}^k(k=1,\cdot \cdot \cdot ,K-1)$ during training and the loss ${\mathit{L}}^k$ of the current ensemble model ${\overline{\mathit{M}}}^k$ to update the sample weights ${\mathit{w}}^{k+1}$ to be used in the next sub-model ${\mathit{M}}^{k+1}$ training. It is assumed that the sub-model ${\mathit{M}}^k$ has been trained for T iterations (for the LightGBM sub-model, each iteration will build a new decision tree); then, ${\mathit{C}}^k\in R^{N\times T}$ is a matrix composed of elements $c_{i,t}$, which are the errors of the ith sample after the tth iteration of the sub-model ${\mathit{M}}^k$. ${\mathit{L}}^k\in R^{N\times 1}$ is the vector of elements $l_i$, which is the error of the current ensemble model ${\overline{\mathit{M}}}^k$ on the ith sample (i.e., the difference between ${\overline{\mathit{M}}}^k({\mathit{x}}_i)$ and $y_i$). The specific measures are as follows:

First, the value of h for each sample is calculated based on ${\mathit{C}}^k$ and ${\mathit{L}}^k$, as shown in Equation (18), and the calculation is performed element by element. For robustness considerations, ${\mathit{C}}^k$ and ${\mathit{L}}^k$ are normalized in order, respectively, $\widetilde{{\mathit{C}}^k}=\mathrm{norm}({\mathit{C}}^k)$, $\widetilde{-{\mathit{L}}^k}=\mathrm{norm}(-{\mathit{L}}^k)$ (inverse normalization), $\mathrm{norm}(\cdot )$ is the rank normalization function,

$$\mathit{h}={\alpha }_1{\mathit{h}}_1+{\alpha }_2{\mathit{h}}_2={\alpha }_1(\widetilde{-{\mathit{L}}^k})+{\alpha }_2\mathrm{norm}(\frac{{\mathit{C}}_{\mathrm{end}}^k}{{\mathit{C}}_{\mathrm{start}}^k})$$

(18)

where $\mathit{h}\in R^{N\times 1}$ is the vector consisting of the values h of all samples. ${\mathit{C}}_{\mathrm{start}}^k,{\mathit{C}}_{\mathrm{end}}^k\in R^{N\times 1}$ is the average loss of the first 10% of T iterations and the last 10% of T iterations of $\widetilde{{\mathit{C}}^k}$, respectively, representing the loss of the sub-model ${\mathit{M}}^k$ at the beginning and end of training. ${\alpha }_1$ and ${\alpha }_2$ are constant coefficients, and their function is to adjust the calculated proportion of ${\mathit{h}}_1$ and ${\mathit{h}}_2$, which is generally taken as ${\alpha }_1={\alpha }_2=1$.

Then, the algorithm divides all the samples into B subsets by sorting the h values of the samples; the samples in the same subset are assigned the same weight, and the samples in different subsets are assigned different weights. Assuming that the ith sample is divided into the bth subset, its weight $w_i$ is calculated as shown in Equation (19):

$$w_i=\frac{1}{\gamma h_b+0.1}$$

(19)

where $h_b$ is the average value of h values of all samples in the bth subset. $\gamma$ is the attenuation factor, whose function is to make the distribution of sample weights more uniform, and $\gamma$ is generally taken at 0.5.

In general, the value $h_1$ of simple samples is large and the value $h_2$ is moderate; moreover, the value $h_1$ of noise samples is large and the value $h_2$ is small. However, the $h_1$ and $h_2$ values of difficult samples are small. Therefore, through the calculation of Equations (18) and (19), the difficult sample will obtain a larger training weight. The training weights of simple samples and noise samples are relatively small.

(2) Feature selection based on the shuffling mechanism algorithm

The algorithm flow (pseudocode) of feature selection based on the shuffling mechanism is shown in Algorithm 3. The algorithm calculates a value of g for each feature index in the current feature set ${\mathit{f}}^k$. The value is used to measure the contribution of the feature to the current integration model ${\overline{\mathit{M}}}^k$ (it also represents the importance of the feature; a larger value of g indicates that the feature is more important to the training of the model).

Algorithm 3: Feature selection based on the shuffling mechanism

1: Input: Current integrated model ${\overline{\mathit{M}}}^k$ and training data (X, y)

2: Parameter: feature sampling ratio r%

3: ${\mathit{L}}^k=\mathrm{loss}({\overline{\mathit{M}}}^k(\mathit{X}),\mathit{y})$

4: For the index value f of each feature in ${\mathit{f}}^k$

5: The fth column feature of ${\mathit{X}}_f$←X is disrupted

6: ${\mathit{L}}_f^k=\mathrm{loss}({\overline{\mathit{M}}}^k({\mathit{X}}_f),\mathit{y})$

7: $g_f=\mathrm{mean}({\mathit{L}}_f^k-{\mathit{L}}^k)/\mathrm{std}({\mathit{L}}_f^k-{\mathit{L}}^k)$

8: Sort all feature indicators in the feature set ${\mathit{f}}^k$ in the descending order of their values $g$

9: Select the top r% of ranked features as sensitive features to obtain the sensitive feature set ${\mathit{f}}^{k+1}=r\%{\mathit{f}}^k$

10: Return: ${\mathit{f}}^{k+1}$

The value g is obtained by the feature shuffling mechanism as follows:

For feature f, its arrangement in the training dataset X is disrupted to obtain a new dataset ${\mathit{X}}_f$ (in which the role of feature f has been invalidated), and the integrated model loss ${\mathit{L}}_f^k$ when feature f is invalidated is computed by Equation (20):

$${\mathit{L}}_f^k=\mathrm{loss}({\overline{\mathit{M}}}^k({\mathit{X}}_f),\mathit{y})$$

(20)

Then, the value g of feature f is calculated by Equation (21):

$$g_f=\mathrm{mean}({\mathit{L}}_f^k-{\mathit{L}}^k)/\mathrm{std}({\mathit{L}}_f^k-{\mathit{L}}^k)$$

(21)

where ${\mathit{L}}^k$ is the normal integrated model loss, $\mathrm{mean}(\cdot )$ is the mean function, and $\mathrm{std}(\cdot )$ is the standard deviation function.

After calculating the value g of each feature by using the above method, all the features can be sorted according to the size of the value g from high to low importance. Finally, according to the preset feature sampling ratio, the top r% of features are retained to form the filtered sensitive feature set ${\mathit{f}}^{k+1}$, which is used for the training of the next sub-model ${\mathit{M}}^{k+1}$.

Compared with other feature selection methods, feature selection based on the shuffling mechanism has the following advantages: firstly, this method takes into account the contribution of the feature to the model as a whole when filtering the features, instead of only considering the nature of the feature itself, such as the feature data relevance. Secondly, compared with the direct removal of a feature, this approach eliminates the contribution of a feature by perturbing the arrangement of a column of features in the dataset, and its contribution can be evaluated without re-training the model, which is more efficient in terms of computational efficiency. Moreover, this approach does not change the overall distribution of the model training data, which is more reasonable than the direct zeroing of features.

Li et al. [25] proposed a multi-scale weighted ensemble model based on LightGBM for fault diagnosis without requiring cross-domain data. In the MWE–LightGBM model, multiple LightGBMs were considered as multiple weak learners and integrated as strong learners for classification. Moreover, the MWE–LightGBM model adopted multi-scale sliding windows to achieve data augmentation. Specifically, sliding windows with different scales are employed to subsample the raw samples and construct multiple subsample datasets. The focus of the model is on fault diagnosis with few samples, which can reduce the number of required feature signals and multi-domain features; moreover, it can also provide another method of conducting the fault diagnosis of key components of the CMC machine feed system.

4. Experimental Results

4.1. Data Set Description

4.1.1. University of Ottawa Variable Speed Bearing Failure Widely Used Dataset

The vibration data of ER16K deep groove ball bearings under different speed conditions were collected from the variable speed bearing fault dataset of the University of Ottawa in Canada, and the sampling frequency was 200 kHz. The fault types of bearings include normal, inner ring fault, outer ring fault, rolling element fault, and compound fault of inner and outer rings and rolling elements. Speed changes include speed up (from 846 r/min to 1428 r/min), speed down (from 1734 r/min to 822 r/min), speed up first and then speed down (from 882 r/minute to 1518 r/minute and then to 1260 r/minute), and first decrease and then increase (from 1452 r/min to 888 r/min and then to 1236 r/min).

Firstly, five kinds of original data collected from the dataset under four speed conditions (speed up, speed down, speed up and then speed down, and speed down and then speed up) were divided into samples, and each sample contained 2000 data points. Since the key components of the CNC machine feed system do not have a large number of fault samples in actual operation, we used a smaller number of samples to simulate the reality. Initially, the number of training samples was set at 480 and the number of test samples was set at 120. Then, the obtained samples were divided into the training set and the test set in a ratio of 8:2. The sample distribution of the dataset and the corresponding relationship of the fault labels are shown in

Table 1. Sample distribution of the widely used dataset and corresponding relationship of fault labels.

Label	Category	Number of Training Set Samples	Number of Test Set Samples
1	Normal	480	120
2	Bearing inner ring fault	480	120
3	Bearing ball fault	480	120
4	Bearing outer ring fault	480	120
5	Bearing compound fault	480	120

.

4.1.2. Dataset of Feed System Test Bench

Based on the transmission principle and mechanical structure of the X-direction feed system of the vertical machining center, a feed system test bench made of heavy steel, as shown in Figure 6, was built. The model and specification of the key parts used in the test are the same as those of the vertical machining center. The model of the ball screw pair is Taiwan Shangyin R4010FSI, the model of the rolling bearing is Japan NSK angular contact ball bearing 30TAC62B, the guide rail pair is a roller-type rail with good rigidity, and the driving motor is a three-phase AC servo motor.

The model and parameters of the data acquisition equipment used in the experiment are shown in

Table 2. Model and parameters of data acquisition instrument and sensor.

Device Name	Equipment Model	Device Parameters
Data acquisition instrument	INV3062C	Sampling frequency range: 0.4~216 kHz; resolution: 24 bits; number of channels: 8
Three-direction vibration sensor	INV9832	Frequency range: 1–10 kHz; sensitivity: 100 mV/G
Noise sensor	INV9206	Frequency range: 20 Hz~20 kHz; sensitivity: 50 mV/Pa
Hall current sensor	CHK-100R1	Frequency range: from 0 to 20 kHz

. Among them, the data acquisition instrument uses a high-precision distributed acquisition instrument developed by the Beijing Dongfang Vibration Research Institute. The device has Ethernet and WiFi interfaces, supports multiple synchronous cascades, and can perform data acquisition using DASP software. The used sensors are three-directional vibration acceleration sensors, noise sensors produced by the Beijing Dongfang Vibration Research Institute (Beijing, China), and open-loop Hall current sensors produced by the Beijing Senshe Electronics Co., Ltd (Beijing, China).

According to the historical fault statistics of the CNC machine feed system, the fault frequency of the rolling bearing is the highest, accounting for 42% of all faults, and the fault frequency of the ball screw pair is the second highest, accounting for 26% [26]. Therefore, to collect data on common fault types of rolling bearings and ball screw pairs, tools such as files and electric grinding needles were used to produce different degrees of wear or damage scars on the inner and outer rings of bearings and the raceways of screws, and the bearing balls were polished with sandpaper to produce wear faults. Figure 7 shows the tools used and some of the manufactured fault parts.

In this experiment, the normal data and fault data of three common feeding conditions were collected, respectively. The feed rates of cases 1 to 3 were set as 1000 mm/min, 2000 mm/min, and 3000 mm/min, respectively. Fault types included bearing inner ring fault, bearing outer ring fault, bearing ball fault, screw wear, screw bending, screw wear and bearing inner ring composite fault, screw wear and bearing outer ring composite fault, and screw wear and bearing ball composite fault. The collected signals included vibration signals, noise signals, and current signals. The sampling frequency was 10 kHz, and the sampling time for each fault was 120 s. The fault dataset divided by 2000 data points per sample is shown in

Table 3. Self-built fault dataset of feed system test bench.

Type of Fault	Number of Samples
	Condition 1	Condition 2	Condition 3
Normal	600	600	600
Bearing inner ring fault	600	600	600
Bearing outer ring fault	600	600	600
Bearing ball fault	600	600	600
Worn lead screw	600	600	600
Screw bending	600	600	600
Screw wear and bearing inner ring composite fault	600	600	600
Screw wear and bearing outer ring composite fault	600	600	600
Screw wear and bearing ball composite fault	600	600	600

.

4.2. Signal Preprocessing

(1) Elimination of singular point

By setting the upper and lower threshold limits for the signal, the abnormal values outside the threshold range are eliminated. The empirical formula for the upper and lower limits of the threshold is the signal mean ± 4 signal standard deviations. Taking the noise sensor signal shown in Figure 8a as an example, the calculated upper and lower threshold values are 5 and −5, respectively. The signal after removing the singular points is shown in Figure 8b.

(2) Elimination of trend term

To ensure the accuracy of the original data as much as possible, the signal trend line was fitted by using the least squares method and subtracted. Figure 9a,b show the comparison of the X-direction vibration signals before and after the removal of the trend item.

(3) Wavelet threshold denoising

Wavelet threshold denoising is a nonlinear denoising method based on wavelet transform. This method is very suitable for processing non-stationary fault signals of CNC machines. In industrial signals, the fault signal mostly exists in the low-frequency component of the signal, while the noise is usually a high-frequency signal with a small amplitude [27]. The process of wavelet threshold denoising is shown in Figure 10.

Sym5 is selected as the wavelet base for signal denoising, and the original signal is decomposed by using a three-layer wavelet. Then, the soft and hard threshold compromise method is used for noise reduction, and the expression of the threshold function is shown as Formula (22):

$${\sigma }_{\lambda }(\omega )=\left\{\begin{array}{c}\mathrm{sgn}(\omega )·(\left|\omega \right|-\alpha \lambda ),\left|\omega \right|\ge \lambda \\ 0,\left|\omega \right|<\lambda \end{array}\right.$$

(22)

where $\omega$ is the wavelet coefficient; $\lambda$ is the threshold; and $\alpha$ is the scaling factor. The value of $\alpha$ in this study is 0.5.

Figure 11 shows the comparison between the original vibration signal and the signal after the application of the above-mentioned wavelet threshold denoising method. It can be observed that this method effectively eliminates the high-frequency noise while retaining the main characteristic information of the original signal, and the denoising effect is good.

4.3. Signal Feature Extraction

(1) Time domain feature extraction

To reflect the overall situation of the signal and reflect the sudden change in the signal, 13 time domain characteristic indices with dimension and non-dimension were extracted, as shown in

Table 4. Time domain characteristic indices and their calculation formula.

Dimensional Characteristic Index	Calculation Formula	Dimensionless Characteristic Index	Calculation Formula
Maximum value	$X_{\max }=\max \left\{x_i\right\}$	Peak factor	$C_{\mathrm{f}}=\frac{X_{\mathrm{pk}}}{X_{\mathrm{rms}}}$
Peak value	$X_{\mathrm{pk}}=\max \left\{x_i\right\}-\min \left\{x_i\right\}$	Pulse factor	$I=\frac{X_{\mathrm{pk}}}{X^{\prime }}$
Average amplitude	$\overline{X}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{x}_i}$	Waveform factor	$C_{\mathrm{s}}=\frac{X_{\mathrm{rms}}}{X^{\prime }}$
Absolute mean	$X^{\prime }=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|x_i\right|}$	Margin factor	$C_{\mathrm{e}}=\frac{X_{\mathrm{pk}}}{X_{\mathrm{r}}}$
Square root magnitude	$X_{\mathrm{r}}={(\frac{1}{N}{\displaystyle \sum _{i=1}^N\sqrt{\left|x_i\right|}})}^2$	Kurtosis	$K=\frac{\frac{1}{N}{\displaystyle \sum _{i=1}^N{(x_i-\overline{X})}^4}}{{(\frac{1}{N}{\displaystyle \sum _{i=1}^N{(x_i-\overline{X})}^2})}^2}-3$
Variance	${\sigma }^2=\frac{1}{N-1}{\displaystyle \sum _{i=1}^N{(x_i-\overline{X})}^2}$
Root mean square value	$X_{\mathrm{rms}}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{x_i}^2}}$	Skewness	$S=\frac{\frac{1}{N}{\displaystyle \sum _{i=1}^N{(x_i-\overline{X})}^3}}{{(\frac{1}{N}{\displaystyle \sum _{i=1}^N{(x_i-\overline{X})}^2})}^{3/2}}$

. In the table, $\left\{x_i\right\}$ is the discrete signal and $i=1,2,\cdot \cdot \cdot ,N$, N is the number of sampling points.

(2) Feature extraction in the frequency domain

Spectrum analysis can reflect the distribution and change in frequency components in the signal and provide effective fault information in the signal. The three extracted frequency domain characteristic indices and their calculations are shown in

Table 5. Frequency domain characteristic indices and their calculation formula.

Frequency Domain Characteristic Index	Calculation Formula
Center of gravity frequency	$X_{\mathrm{fc}}=\frac{{\displaystyle \sum _{i=1}^N{f}_{i}F(f_i)}}{{\displaystyle \sum _{i=1}^{N}F(f_i)}}$
Mean square frequency	$X_{\mathrm{msf}}=\frac{{\displaystyle \sum _{i=1}^N{f_i}^{2}F(f_i)}}{{\displaystyle \sum _{i=1}^{N}F(f_i)}}$
Frequency variance	$X_{\mathrm{vf}}=\frac{{\displaystyle \sum _{i=1}^N{(f_i-X_{\mathrm{fc}})}^{2}F(f_i)}}{{\displaystyle \sum _{i=1}^{N}F(f_i)}}$

.

(3) Feature extraction in the time-frequency domain

The CEEMDAN algorithm was used to decompose the preprocessed signal to extract and select the effective IMF components, and then the information entropy values of IMF components, such as energy, power spectrum, and singular spectrum, were calculated. Taking the X-direction vibration signal of the bearing ball wear fault as an example, the result of CEEMDAN decomposition is shown in Figure 12. The correlation coefficient between each IMF component and the original signal is shown in

Table 6. The correlation coefficient between the IMF component and the original signal.

IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7	IMF8	IMF9	IMF10
0.150	0.239	0.200	0.286	0.185	0.220	0.611	0.684	0.132	0.009

, and the correlation coefficient threshold can be calculated as 0.178 according to Formula (9). Therefore, IMF 1, IMF 9, and IMF 10 were removed, and then the seven effective IMF components, IMF 2~IMF8, were used to compute three information entropies containing energy entropy, power spectrum entropy, and singularity spectrum entropy.

Finally, the multi-dimensional mixed domain feature set was constructed by stitching the above 13 time domain characteristic indices, three frequency domain characteristic indices, and three IMF information entropies, totaling 19 features, into feature vectors.

4.4. Experimental Environment, Hyper-Parameter Setting, and Model Evaluation Index

(1) Experimental environment configuration

The experiment uses a self-configured server with an Intel core i9 11900k CPU, 128 GB running memory, and a 64-bit Windows 10 operating system. The development environment is LightGBM 3.2.1.99, Python 3.8.

(2) Hyperparameter setting

The training hyperparameters of the DoubleEnsemble–LightGBM fault diagnosis model are set as follows:

LightGBM key hyperparameters: the number of iterations (num_iterations) is 100, the learning_rate is 0.14, the maximum depth of the decision tree (Max_depth) is 7, the number of leaf nodes (num_leaves) is 21, and the minimum sample number of leaf nodes (min_data _in_leaf) is 30.

DoubleEnsemble key hyperparameters: the number of sub-models is five, and the weight of the sub-models is (1,1,1,1,1). The number of sample subsets is four, the feature sampling ratio is 80%, and the loss function is the classification cross-entropy loss.

(3) Model evaluation index

A confusion matrix [28] is often used to judge the performance of multi-classification models.

Table 7. Confusion matrix of fault category prediction results.

Predictive Failure Category (Label)	Actual Fault Category (Label)
	1	2	3	$\begin{array}{cc}\cdots & \cdots \end{array}$	N
1	$a_{11}$	$a_{12}$	$a_{13}$	$\begin{array}{cc}\cdots & \cdots \end{array}$	$a_{1N}$
2	$a_{21}$	$a_{22}$	$a_{23}$	$\begin{array}{cc}\cdots & \cdots \end{array}$	$a_{2N}$
3	$a_{31}$	$a_{32}$	$a_{33}$	$\begin{array}{cc}\cdots & \cdots \end{array}$	$a_{3N}$
$\begin{array}{l}⋮\\ ⋮\end{array}$	$\begin{array}{l}⋮\\ ⋮\end{array}$	$\begin{array}{l}⋮\\ ⋮\end{array}$	$\begin{array}{l}⋮\\ ⋮\end{array}$	$\begin{array}{cc}\ddots & \\ & \ddots \end{array}$	$\begin{array}{l}⋮\\ ⋮\end{array}$
N	$a_{N1}$	$a_{N2}$	$a_{N3}$	$\begin{array}{cc}\cdots & \cdots \end{array}$	$a_{NN}$

shows the confusion matrix of the fault category prediction results, where the number in the main diagonal position indicates the number of samples that the model correctly classifies for each fault; a larger number indicates better model diagnostic performance. The numbers in the remaining positions represent the number of misclassified samples, and the smaller the number, the better the diagnostic performance of the model. Which kinds of faults are easily confused by the model can be clearly distinguished through the confusion matrix.

The overall diagnosis accuracy and individual diagnosis accuracy are used as the evaluation indices of the fault diagnosis model. The overall diagnostic accuracy can reflect the overall diagnostic performance of the model, as calculated in Equation (23). The individual diagnostic accuracy can reflect the diagnostic performance of the model for a specific type of fault, as calculated in Equation (24):

$$T=\frac{{\displaystyle \sum _{i=1}^N{a}_{ii}}}{{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^N{a}_{ji}}}}$$

(23)

$$I_i=\frac{a_{ii}}{{\displaystyle \sum _{j=1}^N{a}_{ji}}},i=1,2,3,\cdot \cdot \cdot N$$

(24)

where $T$ is the overall diagnostic accuracy rate; $I_i$ is the individual diagnostic accuracy rate; and $a_{ji}$ is the element value of the ith column of the jth row in the confusion matrix.

4.5. Analysis of Experimental Results

4.5.1. Analysis of Experimental Results of a Widely Used Dataset

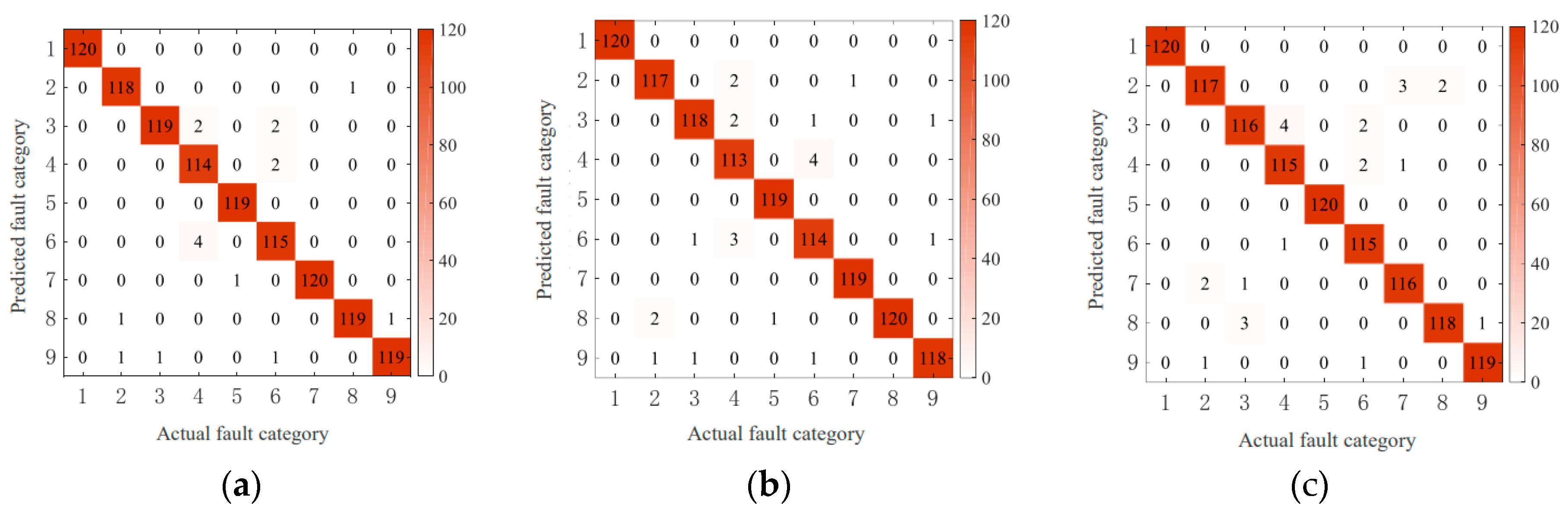
Considering the influence of random factors on model training and testing, 10 repeated experiments were carried out. Figure 13 shows the confusion matrix of the last experimental test result.

The overall diagnostic accuracy and individual diagnostic accuracy of the DoubleEnsemble–LightGBM model under each speed condition were calculated by analyzing the confusion matrix, and the calculation results are shown in

Table 8. Calculation of model evaluation indices of experimental test results.

Speed Change	Individual Accuracy Ii/%					Overall Accuracy T/%
	I1	I2	I3	I4	I5
Speed up	99.17	93.33	88.33	86.67	92.50	92.00
Slow down	95.00	90.83	86.67	93.33	87.50	90.67
First up, then down	96.67	91.67	93.33	85.83	89.17	91.33
First down, then up	95.00	91.67	85.83	85.83	90.83	89.83
Average value	96.46	91.88	88.54	87.92	90.00	90.96

. It can be observed from the table that the overall diagnostic accuracy of the model is 90.96% after averaging the calculation results under four speed conditions, which can achieve better overall diagnostic performance. The individual diagnostic accuracies from Category 1 to Category 5 are 96.46%, 91.88%, 88.54%, 87.92%, and 90%, respectively. It can be observed that the diagnostic accuracy of the model for Category 1 (normal) is the highest, and the diagnostic accuracy for Category 3 (bearing ball failure) and Category 4 (bearing outer ring failure) is lower.

In addition, the diagnosis performance of the constructed DoubleEnsemble–LightGBM model was compared with that of the original LightGBM model and three other ensemble learning models with excellent performance in the field of fault diagnosis: the RF model used in [29], the AdaBoost model used in [30], and the XGBoost model used in [31]. The average value of the overall fault diagnosis accuracy of 10 experiments was taken as the evaluation index, and the experimental comparison results are shown in

Table 9. Comparison of diagnostic performance of different models on the widely used dataset.

Comparison Model	Overall Accuracy T/%				$\mathbf{Average} \mathbf{Overall} \mathbf{Accuracy} \overline{\mathit{T}}$/%
	Speed Up	Slow Down	First Up, Then Down	First Down, Then Up
RF	85.02	84.36	85.14	83.46	84.50
AdaBoost	85.23	84.15	84.92	83.54	84.46
XGBoost	88.54	87.23	87.96	86.87	87.65
LightGBM	87.83	86.92	87.25	86.05	87.01
DoubleEnsemble–LightGBM	91.96	90.83	91.33	90.17	91.07

. It can be observed from the table that the average overall diagnostic accuracy of the DoubleEnsemble–LightGBM model is the highest, which increased by 6.57%, 6.61%, 3.42%, and 4.06%, respectively, compared with the RF model, AdaBoost model, XGBoost model, and LightGBM original model. Figure 14 shows the comparison of the overall diagnostic accuracy of the five models under different speed conditions. The diagnostic performance of the DoubleEnsemble–LightGBM model is significantly better than that of other models.

4.5.2. Analysis of Experimental Results of Feed System Test Bench Dataset

The feed system fault dataset established by the feed system test bench in Section 4.1.2 was divided into the training set and the test set at a ratio of 8:2. The distribution of the divided samples and the corresponding relationship of the fault labels are shown in

Table 10. Sample distribution of the test bench dataset and corresponding relationship of fault labels.

Label	Category	Number of Training Set Samples	Number of Test Set Samples
1	Normal	480	120
2	Bearing inner ring fault	480	120
3	Bearing ball fault	480	120
4	Bearing outer ring fault	480	120
5	Worn lead screw	480	120
6	screw bending	480	120
7	Worn lead screw and bearing inner ring complex fault	480	120
8	Worn lead screw and bearing ball complex fault	480	120
9	Worn lead screw and bearing outer ring complex fault	480	120

.

To ensure the reliability of the model, 10 repeated experiments were also carried out. Figure 15 shows the confusion matrix for the last experimental test result.

The overall diagnostic accuracy and individual diagnostic accuracy of the DoubleEnsemble–LightGBM model under each feed condition were calculated by analyzing the confusion matrix, and the calculation results are shown in

Table 11. Calculation of model evaluation index of the last experimental test result.

Working Condition	Individual Accuracy Ii/%									Overall Accuracy T/%
	I1	I2	I3	I4	I5	I6	I7	I8	I9
1	100	98.33	99.17	95.00	99.17	95.83	100	99.17	99.17	98.43
2	100	97.50	98.33	94.17	99.17	95.00	99.17	100	98.33	97.96
3	100	97.50	96.67	95.83	100	95.83	96.67	98.33	99.17	97.78
Average value	100	97.78	98.06	95.00	99.45	95.55	98.61	99.17	98.89	98.06

. In the table, the feed speeds corresponding to working condition 1, working condition 2, and working condition 3 are 1000 mm/min, 2000 mm/min, and 3000 mm/min, respectively. It can be observed from the table that, after averaging the calculation results under the three feeding conditions, the overall diagnostic accuracy of the model is 98.06%, and the individual diagnostic accuracy of categories 1 to 9 is 100%, 97.78%, 98.06%, 95%, 99.45%, 95.55%, 98.61%, 99.17%, and 98.89%, respectively. The results show that the DoubleEnsemble–LightGBM model can achieve high-precision fault diagnosis, and the classification accuracy of normal data (class 1) reaches 100%.

In addition, the RF model, AdaBoost model, XGBoost model, and LightGBM original model were also selected to compare the diagnostic performance with the DoubleEnsemble–LightGBM model. The average value of the overall fault diagnosis accuracy of 10 experiments was taken as the evaluation index, and the experimental comparison results are shown in

Table 12. Comparison of diagnostic performance of different models on the test bench dataset.

Comparison Model	Overall Accuracy T/%			$\mathbf{Average} \mathbf{Overall} \mathbf{Accuracy} \overline{\mathit{T}}$/%
	Condition 1	Condition 2	Condition 3
RF	93.99	93.75	92.99	93.58
AdaBoost	94.56	94.18	93.83	94.19
XGBoost	95.73	95.32	95.15	95.4
LightGBM	95.42	95.05	94.98	95.15
DoubleEnsemble–LightGBM	98.46	97.98	97.75	98.06

. It can be observed from the table that, compared with the original LightGBM model, the average overall diagnostic accuracy of the constructed DoubleEnsemble–LightGBM model is improved by 2.91% under three feeding conditions, indicating that the introduction of sample re-weighting and the feature selection mechanism can effectively improve the overall diagnostic performance of the model. Compared with the RF model, AdaBoost model, and XGBoost model, the average overall diagnostic accuracy of the DoubleEnsemble–LightGBM model is still the highest, which is improved by 4.48%, 3.87%, and 2.66%, respectively. Figure 16 shows more intuitively the comparison of the overall diagnostic accuracy of the five models at different feed rates. The diagnostic performance of the DoubleEnsemble–LightGBM model is significantly better than that of the other models.

5. Conclusions and Future Work

To solve the problem of intelligent fault diagnosis of the CNC machine feed system under variable speed conditions, a variety of signals such as current signal, vibration signal, and noise signal were used as monitoring data. Firstly, the above signals were preprocessed by using singularity elimination, trend item elimination, and wavelet threshold denoising. Then, time domain analysis and frequency domain analysis were carried out for each signal, and 13 time domain characteristic indices and three frequency domain characteristic indices were extracted. The time–frequency domain analysis of the signal was carried out using the CEEMDAN algorithm, and three IMF information entropies were calculated. The multi-dimensional mixed domain feature set was constructed by stitching the above multiple feature indices into feature vectors. Finally, LightGBM was selected as the basic fault diagnosis model. In addition, to further improve the training performance of the model and improve the diagnosis accuracy, the sample re-weighting mechanism based on learning trajectory and the feature selection mechanism based on shuffling technology were introduced to build a DoubleEnsemble–LightGBM fault diagnosis model. The experimental results show that the average diagnostic accuracy of the DoubleEnsemble–LightGBM model is 91.07% on the public variable speed bearing fault dataset, and 98.06% on the self-built fault dataset of the feed test bench. Compared with the RF, AdaBoost, Xgboost, and other advanced ensemble learning models and the original LightGBM model, the proposed DoubleEnsemble–LightGBM model effectively improves the diagnostic accuracy of both datasets.

The experimental results show that the proposed model effectively solves the fault diagnosis of the key components of the CNC machine feed system in the case of fewer samples as well as under variable speed and noise conditions.

Based on the above conclusions, the author believes that the model can be applied to the fault diagnosis of key rotating parts of large equipment such as high-speed railways and wind turbines under complex working conditions. Due to the limitation of the experimental conditions, the fault data of the key mechanical components of the feed system were mainly collected by building a feed test bench and artificially producing simulated faults. Our follow-up research will aim to accumulate real fault data from actual working conditions and production of the CNC machine feed system. Moreover, the values of rotation speed, different accelerations, and decelerations could be increased in order to further expand the types of faults tested.