Feature Extraction of a Planetary Gearbox Based on the KPCA Dual-Kernel Function Optimized by the Swarm Intelligent Fusion Algorithm
Abstract
1. Introduction
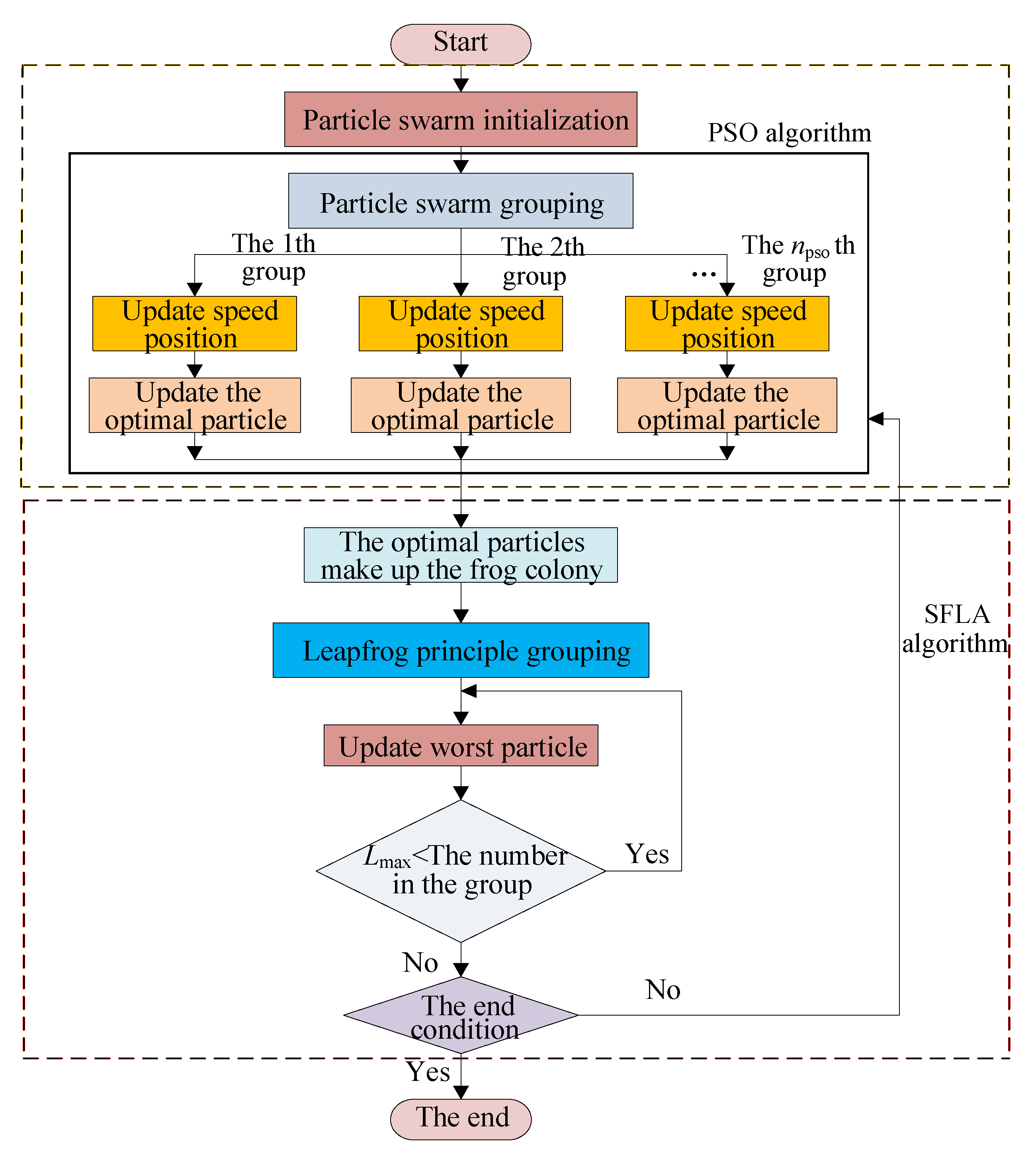
2. Swarm Intelligence Fusion Algorithm
2.1. The SFLA and PSO Fusion Mechanism
2.2. Fusion Algorithm Flow
- (1)
- Relevant parameters of the SFLA-PSO fusion algorithm are set.
- (2)
- The particle swarm is initialized, and each particle is initialized. After the fitness is sorted, each particle is divided into npso groups with np particles in each group.
- (3)
- The PSO mode iterative optimization is carried out for each group, the fitness of each particle is evaluated, and the optimal particle Pjid of each group is recorded.
- (4)
- According to Formulas (1) and (2) for PSO, the velocity and position of each group particle are updated to complete the optimization of the first level.
- (5)
- Each group of optimal particles (called elites) optimized by PSO are regarded as all the frogs of the SFLA, and their fitness is evaluated and ranked.
- (6)
- According to the SFLA grouping mechanism, the elite particles are divided into m groups with n particles in each group.
- (7)
- According to the updating Formulas (3)–(5) of the SFLA, the local optimal value and the local worst value for the population are recorded. After all the groups are updated, the global optimal value is updated to find the best Xgd, and the second-level optimization is completed.
- (8)
- If the end condition is satisfied, that is, the predetermined accuracy requirement is met or the set maximum iteration number is reached, Xgd is the output, and the algorithm is stopped; otherwise, the procedure returns to (4).
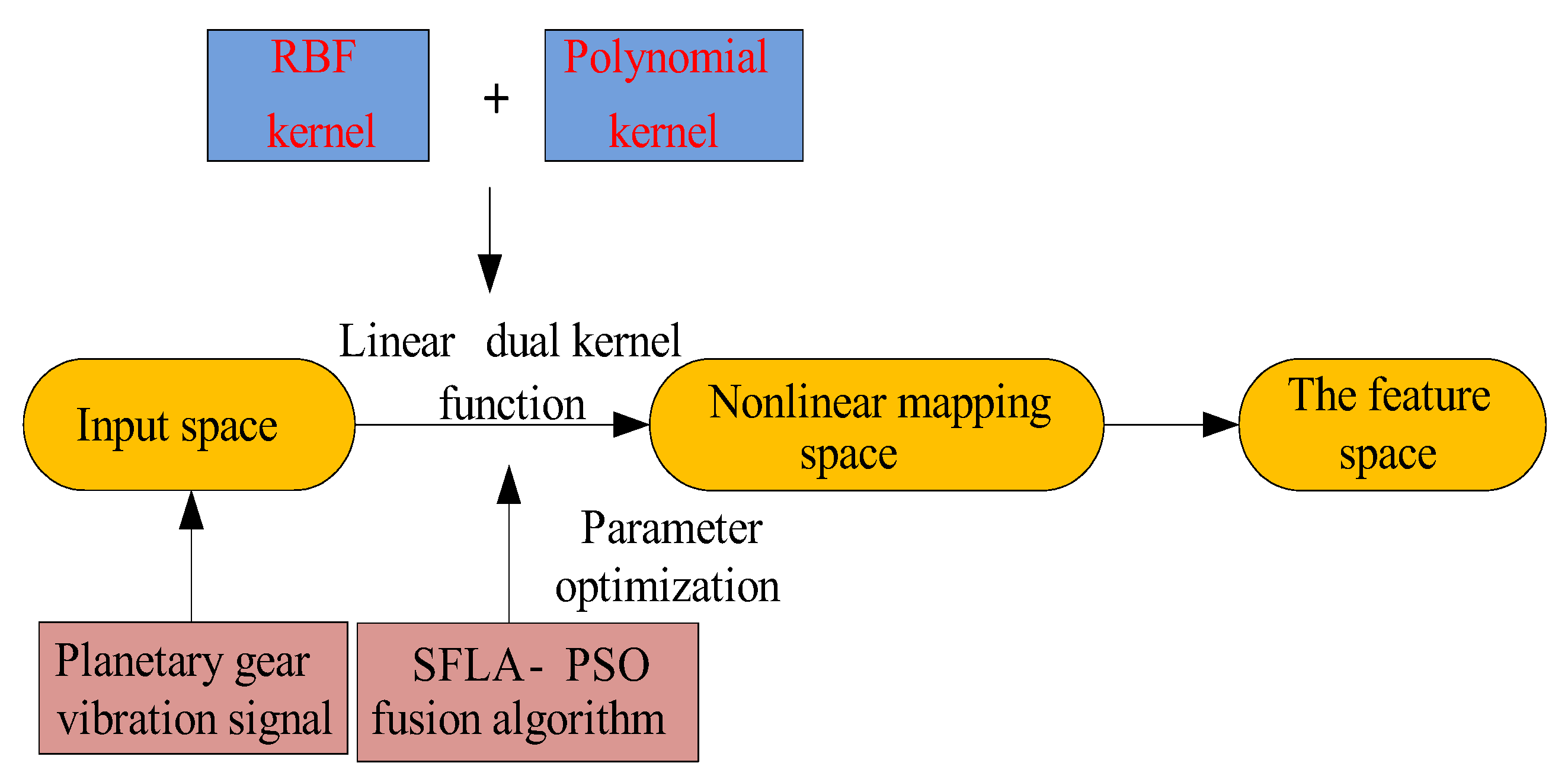
3. The Composition and Optimization of the Dual-Kernel Function of KPCA
3.1. The Principle of KPCA Algorithm Feature Extraction
- (1)
- The data are mapped to the high-dimensional feature space via the nonlinear transformation Φ(yi), and the kernel matrix can be calculated. The covariance matrix CF in the feature space of the training sample after mapping iswhere M is the number of training samples. The kernel matrix K is defined aswhere K is the kernel function, which is defined as a function that represents the inner product of vector yi and yj through nonlinear mapping to a feature space, using two vectors in the original space as a function in order to achieve nonlinear mapping.
- (2)
- Data centralization: Ifthen the centralized processing is carried out. K is replaced by K* = K – AK – KA + AKA. In the formula, .
- (3)
- The eigenvalues and eigenvectors v of the covariance matrix C F are calculated, satisfying the following conditions:
- (4)
- Extraction of the principal component: the projection on the feature vector space is calculated:where Φ(yi)·Φ(y) can be calculated using the kernel technique, which is a type of function that makes Kij = Φ(yi)·Φ(yj) hold. Letwhere K is the kernel function and becomes the kth nonlinear kernel principal component corresponding to Φ(y), and all projected values are used as the feature vectors of the samples.
3.2. The Composition of the Dual-Kernel Function of Flexible Weight Linear Combination
3.3. The Specific Steps of Dual-Kernel Parameter Optimization
- (1)
- According to Fisher’s criterion, the samples are input, and the sum of the square of the distance between class Db and within class Dw1 and Dw2 are calculated using Formulas (20)–(22).
- (2)
- The optimized objective function JFisher is constructed using Equation (23) and is used as the fitness of the swarm intelligence optimization.
- (3)
- The parameters of the SFLA-PSO swarm intelligent fusion algorithm are set, and the particle swarm optimization is initialized.
- (4)
- The initial population is generated randomly, the fitness of the individuals are calculated, and the velocity and position are updated according to Formulas (1) and (2) of the PSO strategy.
- (5)
- The optimal particles optimized in the first layer of PSO are taken as all the initial frogs of the SFLA and are grouped once more.
- (6)
- According to the fitness size, the frog’s velocity and position are updated based on the frog leaping update Formulas (3)–(5) to determine the best advantage.
- (7)
- If the objective function JFisher satisfies the termination condition, the optimal value JFisher (γ*, d1*, σ*) is output, and the algorithm is stopped. Otherwise, it returns to (4).
3.4. Simulation and Comparative Analysis
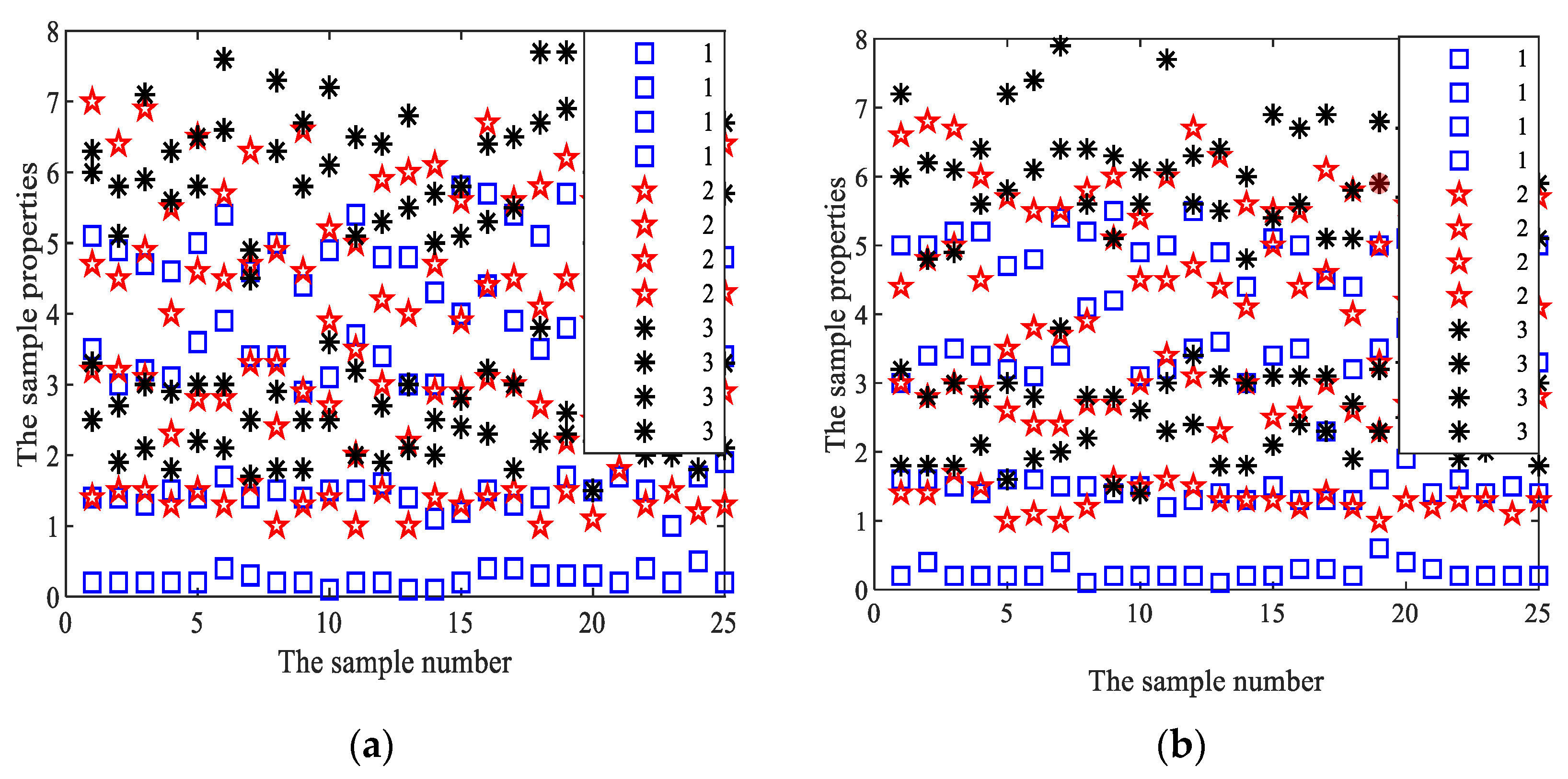
3.4.1. Iris Plant Database
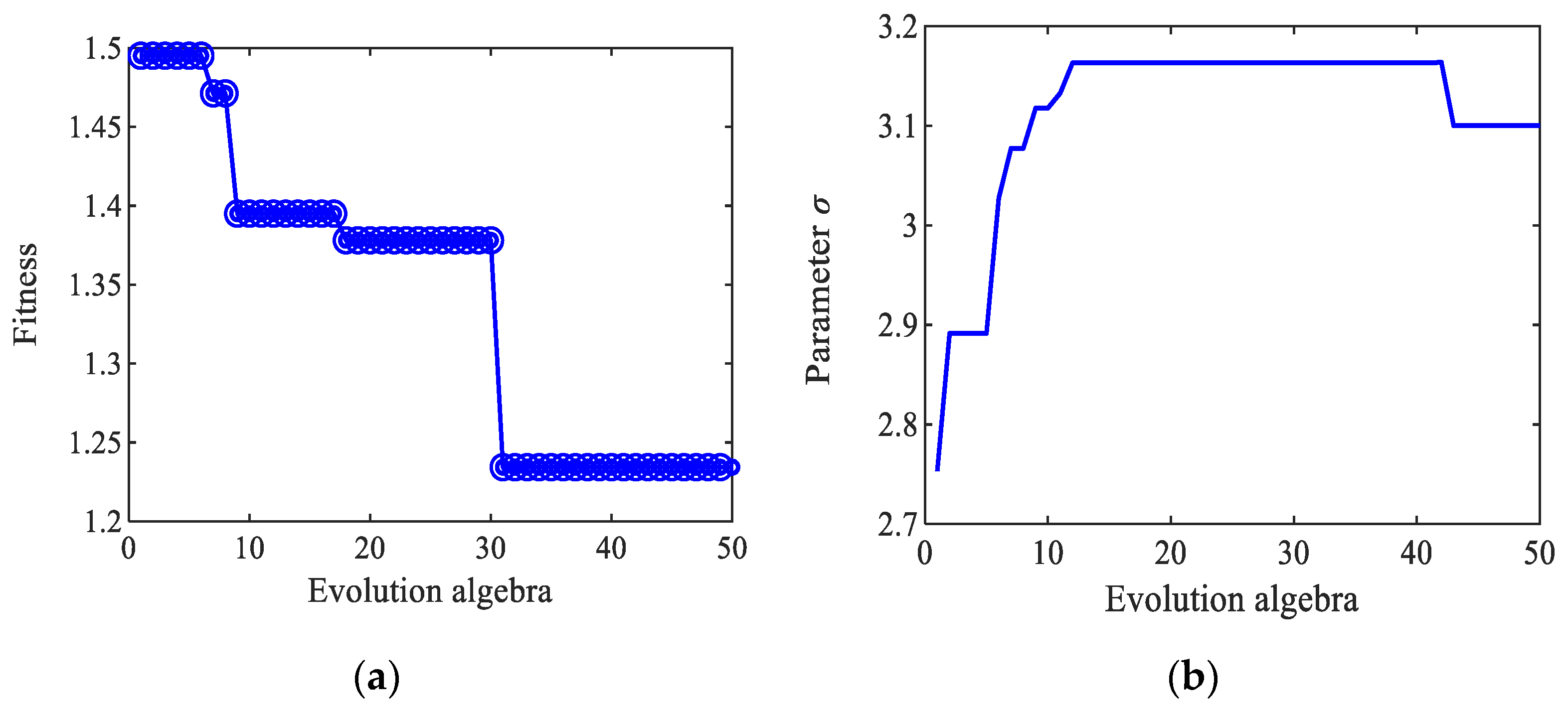
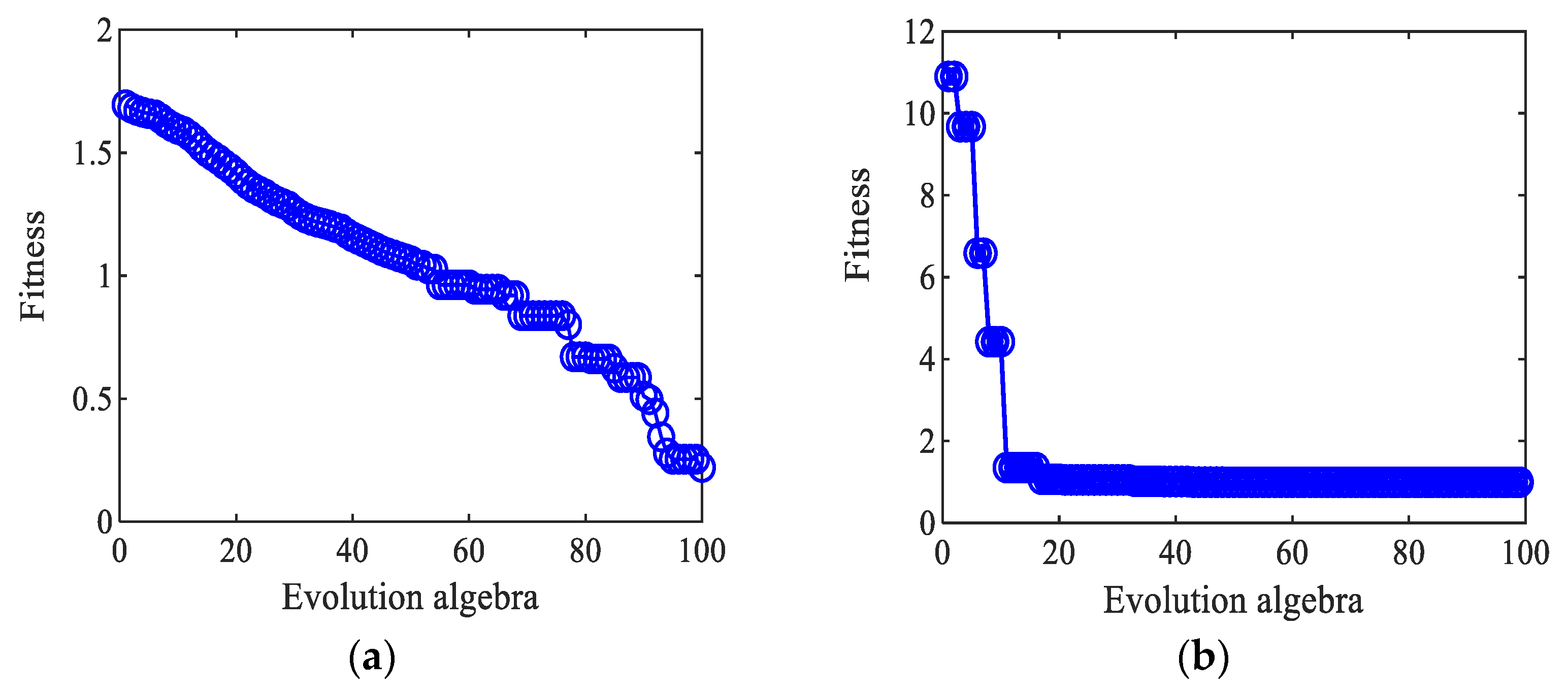
3.4.2. Parameter Optimization of the Iris Data Set with the Dual-Kernel Function Based on the SFLA-PSO
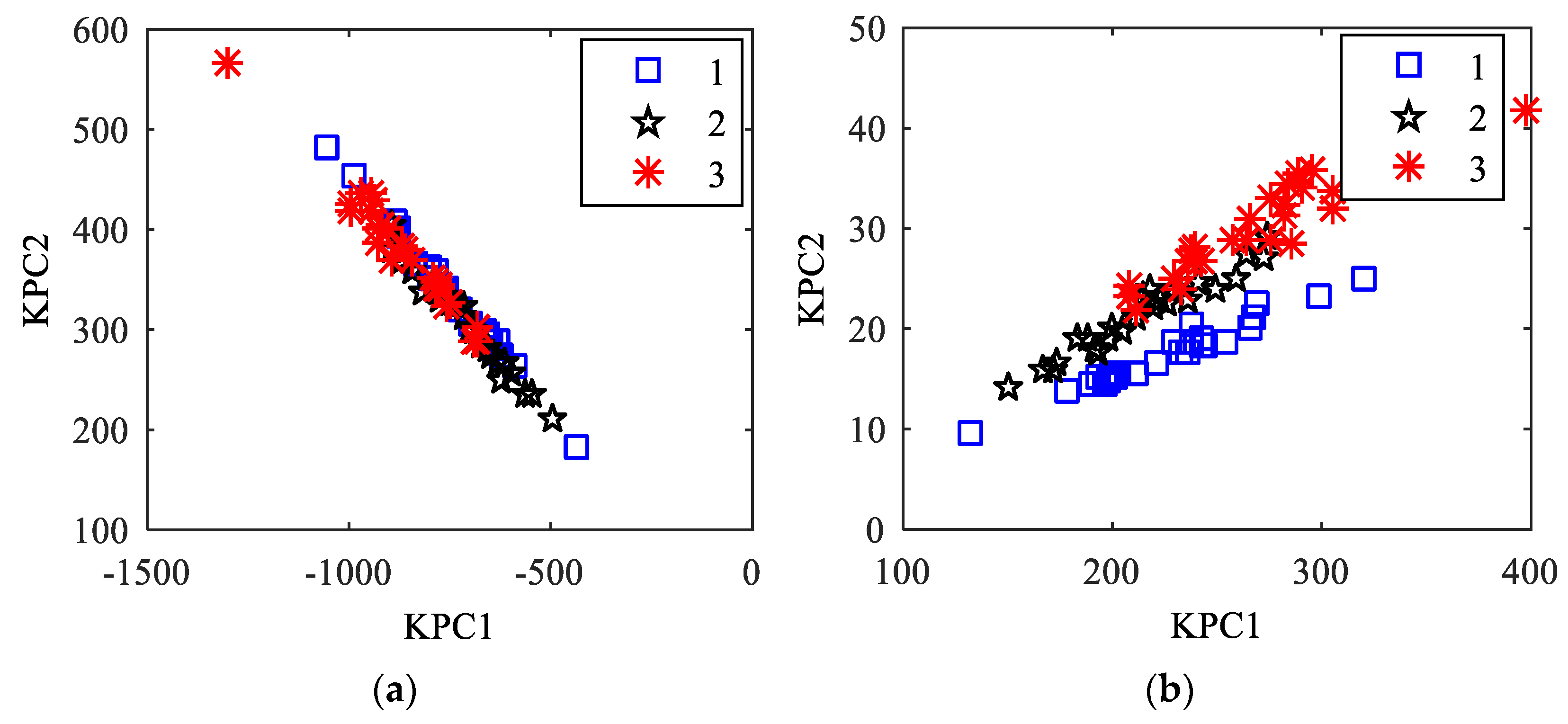
3.4.3. DKKPCA Feature Extraction of the Iris Data
4. The Simulation Failure Experiment for the Planetary Gearbox
4.1. Experimental Scheme of the Planetary Gearbox
4.2. Analysis of Vibration Signal
5. Feature Extraction of the Planetary Gearbox Based on the KPCA Dual-Kernel Parameter Optimized by the SFLA-PSO
5.1. Optimization of the Dual-Kernel Parameters of KPCA Based on the SFLA-PSO
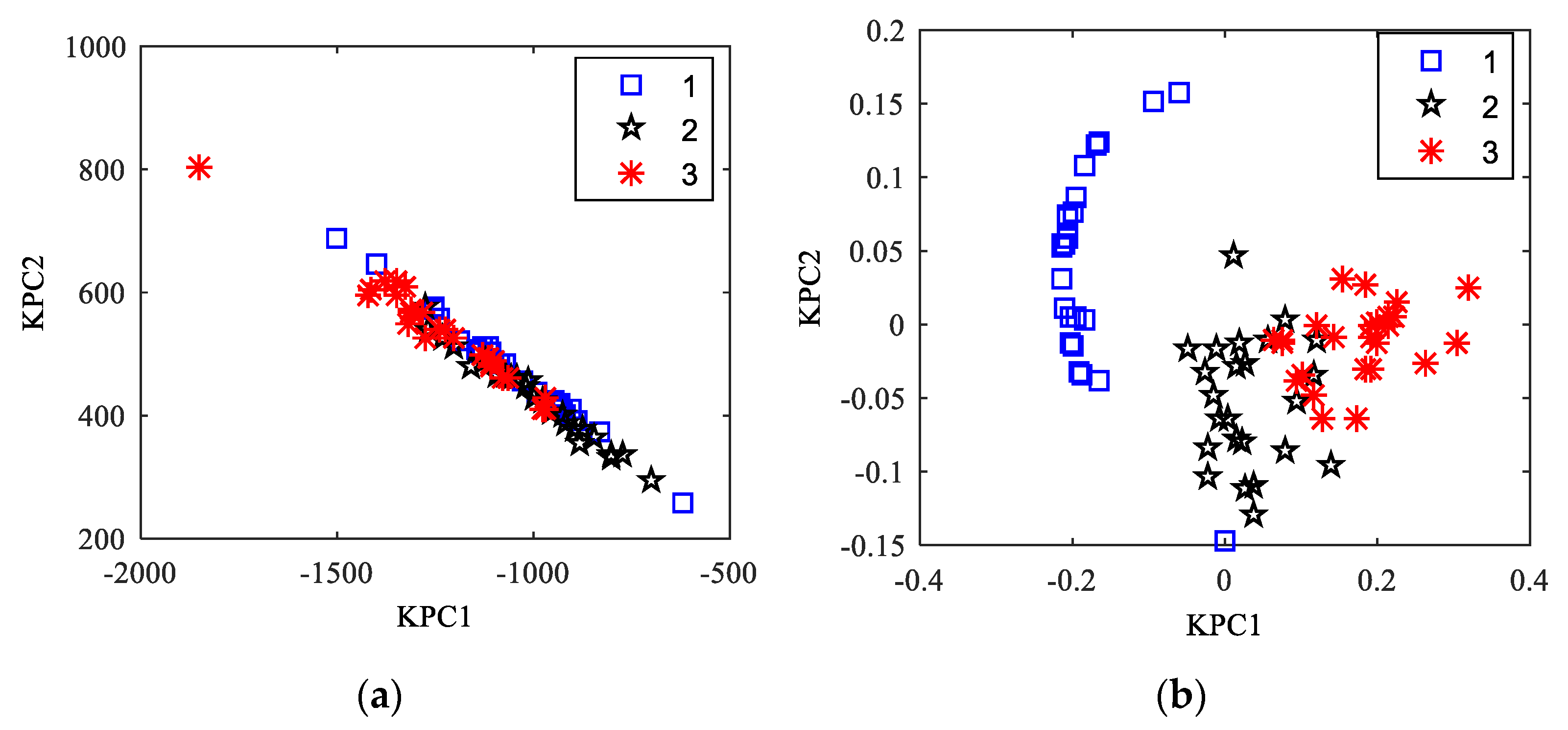
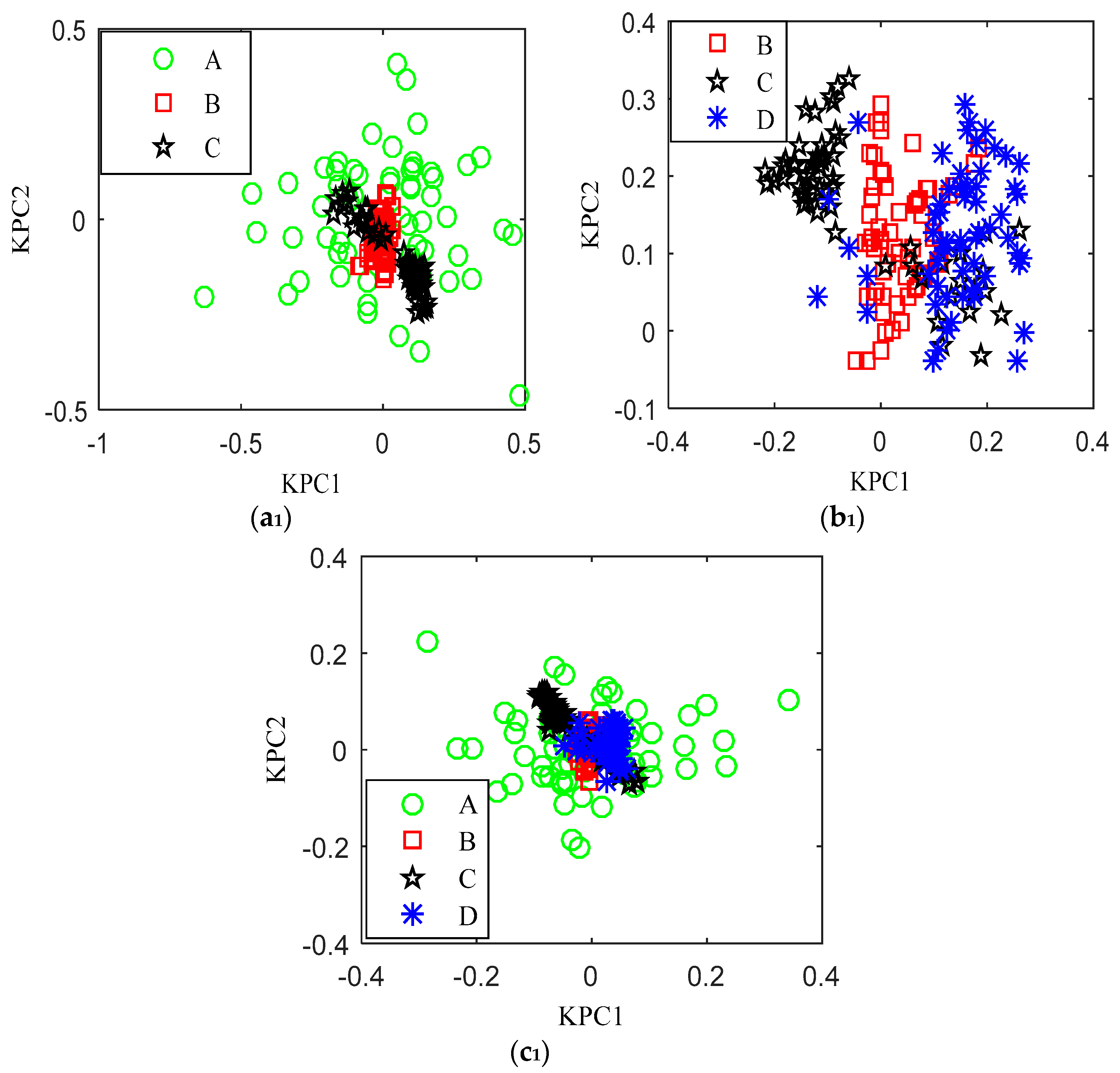
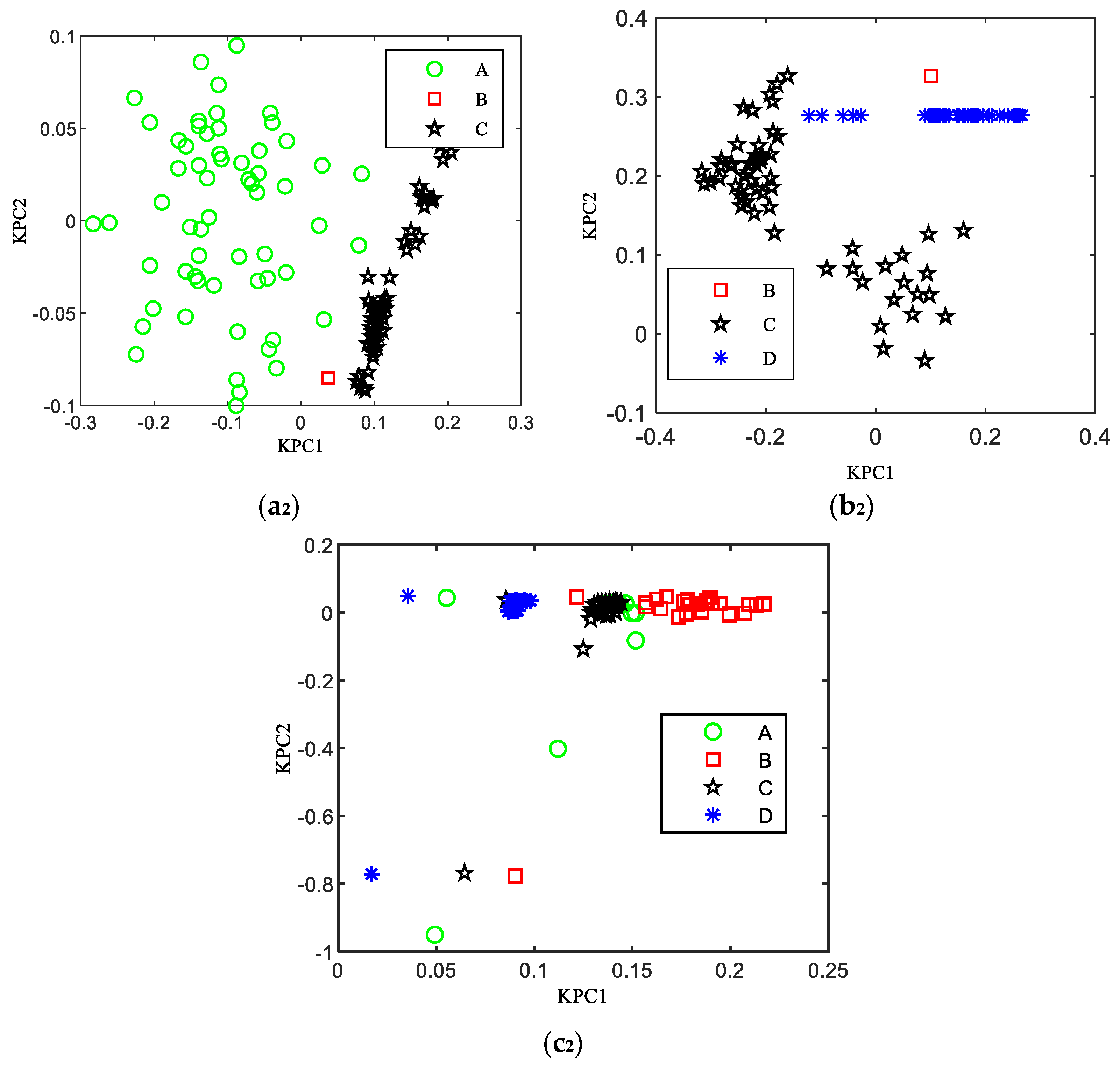
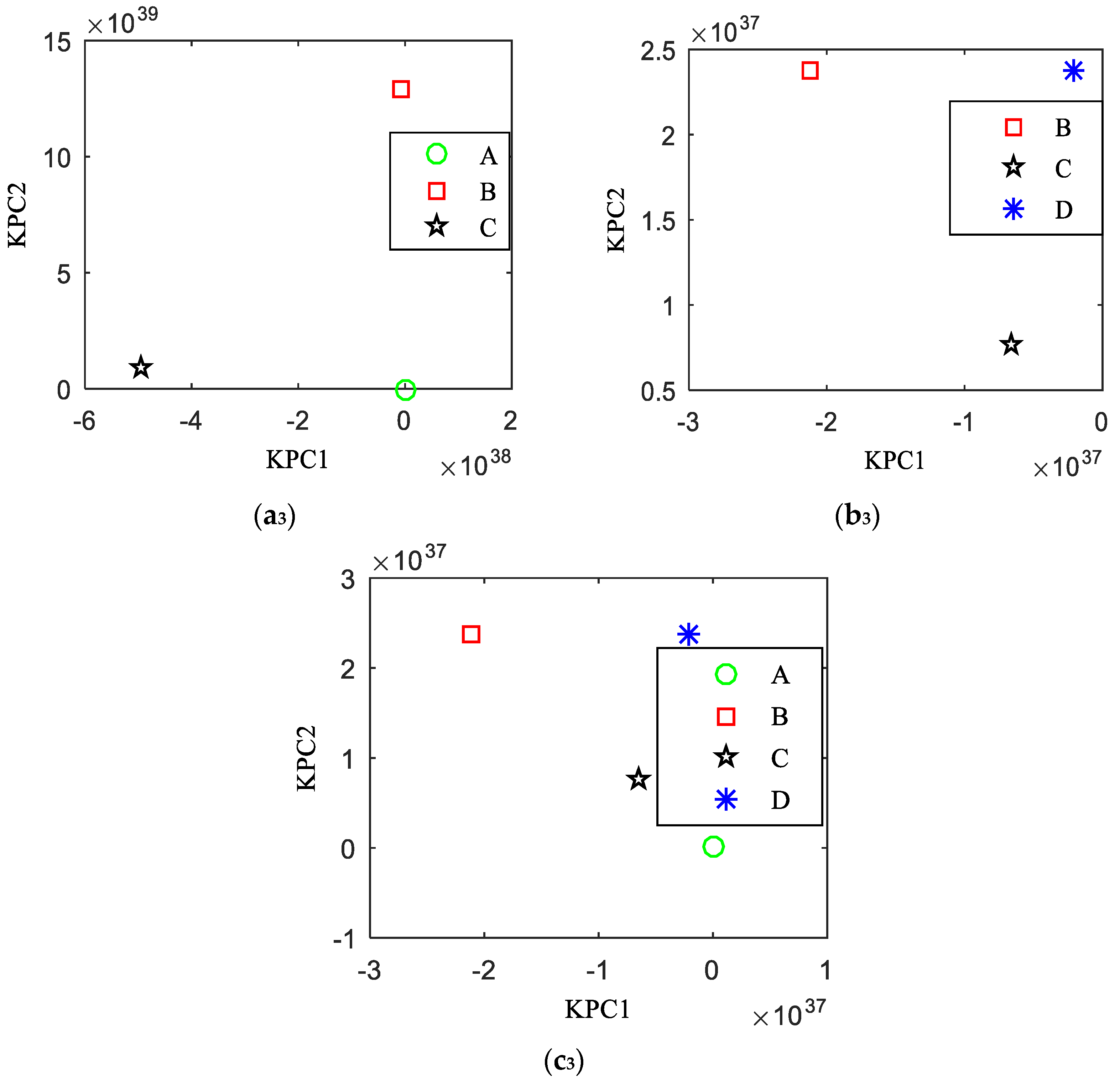
5.2. KPCA Feature Extraction of the Planetary Gear Wear Based on the Dual-Kernel Optimization
5.3. The Analysis of the Obtained Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, H.; Zheng, J.; Yang, Y.; Cheng, J. Nonlinear sparse mode decomposition and its application in planetary gearbox fault diagnosis. Mech. Mach. Theory 2021, 155, 104082. [Google Scholar] [CrossRef]
- Wang, C.; Li, H.; Ou, J.; Hu, R.; Hu, S.; Liu, A. Identification of planetary gearbox weak compound fault based on parallel dual-parameter optimized resonance sparse decomposition and improved momeda. Measurement 2020, 165, 108079. [Google Scholar] [CrossRef]
- Schölkof, B.S.; Muller, K.R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Xiao, Y.; Feng, L. A novel neural-network approach of analog fault diagnosis based on kernel discriminant analysis and particle swarm optimization. Appl. Soft Comput. 2012, 12, 904–920. [Google Scholar] [CrossRef]
- Fatma, L.; Lotfi, M.; Wiem, A.; Hedi, D.; Khaled, Y. Investigating Machine Learning and Control Theory Approaches for Process Fault Detection: A Comparative Study of KPCA and the Observer-Based Method. Sensors 2023, 23, 6899. [Google Scholar]
- Wang, Y.; Dong, R.; Wang, X.; Zhang, X. Research on Rolling Bearing Fault Diagnosis Based on Volterra Kernel Identification and KPCA. Shock. Vib. 2023, 2023, 1–9. [Google Scholar] [CrossRef]
- Shao, R.; Hu, W.; Wang, Y.; Qi, X. The fault feature extraction and classification of gear using principal component analysis and kernel principal component analysis based on the wavelet packet transform. Measurement 2014, 54, 118–132. [Google Scholar] [CrossRef]
- Lei, Y.; Chen, W.; Li, N.; Lin, J. A relevance vector machine prediction method based on adaptive multi-kernel dual and its application to remaining useful life prediction of machinery. J. Mech. Eng. 2016, 52, 87–93. [Google Scholar] [CrossRef]
- Fu, H.; Ren, R.; Yan, Z.; Ma, Y. Fault diagnosis method of power transformers using multi-kernel RVM and QPSO. High Volt. Appar. 2017, 53, 131–135. [Google Scholar]
- Deng, X.; Lei, W. Modified kernel principal component analysis using dual-weighted local outlier factor and its application ton on linear process monitoring. ISA Trans. 2018, 72, 218–228. [Google Scholar] [CrossRef]
- Pan, C.; Li, H.; Chen, B.; Zhou, M. Fault Diagnosis method with class mean kernel principal component analysis based on combined kernel function. Comput. Simul. 2019, 36, 414–419. [Google Scholar]
- Wang, H.; Cai, Y.; Sun, F.; Zhao, Z. Adaptive sequence learning and application of multi-scale kernel method. Pattern Recognit. Artif. Intell. 2011, 24, 72–81. [Google Scholar]
- Lv, L.; Wang, W.; Zhang, Z.; Liu, X. A novel intrusion detection system based on an optimal hybrid kernel extreme learning machine. Knowl.-Based Syst. 2020, 195, 105648. [Google Scholar] [CrossRef]
- Nithya, A.; Appathurai, A.; Venkatadri, N.; Ramji, D.R.; Anna, P.C. Kidney disease detection and segmentation using artificial neural network and multi-kernel k-means clustering for ultrasound images. Measurement 2020, 149, 106952. [Google Scholar] [CrossRef]
- Ouyang, A.; Liu, Y.; Pei, S.; Peng, X.; He, M.; Wang, Q. A hybrid improved kernel LDA and PNN algorithm for efficient face recognition. Neurocomputing 2020, 393, 214–222. [Google Scholar] [CrossRef]
- Afzal, A.L.; Asharaf, S. Deep multiple multilayer kernel learning in core vector machines. Expert Syst. Appl. 2018, 96, 149–156. [Google Scholar]
- Li, X.; Gao, X.; Li, K.; Hou, Y. Prediction for dynamic fluid Level of oil well based on GPR with AFSA optimized combined kernel function. J. Northeast. Univ. (Nat. Sci.) 2017, 38, 11–15. [Google Scholar]
- Xie, F.; Chen, H.; Xie, S.; Jiang, W.; Liu, B.; Li, X. Bearing state recognition based on kernel principal component analysis of particle swarm optimization. Meas. Control Technol. 2018, 37, 28–35. [Google Scholar]
- Bernal, D.; Lázaro, J.M.; Prieto, M.A.; Llanes, S.O.; da Silva, N.A.J. Optimizing kernel methods to reduce dimensionality in fault diagnosis of industrial systems. Comput. Ind. Eng. 2015, 87, 140–149. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks; IEEE Computer Society: Washington, DC, USA, 1995; pp. 1942–1948. [Google Scholar]
- Eusuff, M.M.; Lansey, K.E. Optimization of water distribution network design using shuffled frog leaping algorithm. J. Water Resour. Plan. Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wild fire probability. Agric. For. Meteorol. 2019, 266–267, 198–207. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, L.; Wang, B.; Bao, S.; Jiang, R. Fault Diagnosis of Wind Turbine Planetary Gear Based on a Digital Twin. Appl. Sci. 2023, 13, 4776. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Swarm Intelligence; Morgan Kaufmann Division of Academic Press: San Francisco, CA, USA, 2001; pp. 11–15. [Google Scholar]
- Rajamohana, S.P.; Umamaheswari, K. Hybrid approach of improved binary particle swarm optimization and shuffled frog leaping for feature selection. Comput. Electr. Eng. 2018, 67, 497–508. [Google Scholar] [CrossRef]
- Wang, H.; Sun, F.; Cai, Y.; Chen, N.; Ding, L. Multi-kernel learning method. Acta Autom. Sin. 2010, 36, 1037–1050. [Google Scholar] [CrossRef]
- Li, J.; Qiao, J.; Yin, H.; Liu, D. Kernel Adaptive Learning and Application in Pattern Recognition; Publishing House of Electronics Industry: Beijing, China, 2013; pp. 23–25. [Google Scholar]
- Chen, W.; Panahi, M.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Panahi, S.; Li, S.; Jaafari, A.; Bin Ahmad, B. Applying population-based evolutionary algorithms and a neuro-fuzzy system for modeling landslide susceptibility. Catena 2019, 172, 212–231. [Google Scholar] [CrossRef]
- Zhao, Y. Pattern Recognition; Shanghai Jiao Tong University: Shanghai, China, 2013; pp. 12–16. [Google Scholar]
- He, Y.; Wang, Z. Regularized kernel function parameter of kpca using WPSO-FDA for feature extraction and fault recognition of gearbox. J. Vibroengineering 2018, 20, 225–239. [Google Scholar] [CrossRef]




| Serial Number | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Algorithm | |||||
| DKKPCA | Kernel principal component eigenvalue | 2.518 | 0.2996 | 0.1014 | 0.0284 |
| Contribution % | 85.431 | 10.165 | 3.441 | 0.963 | |
| Cumulative contribution rate % | 85.431 | 95.595 | 99.036 | 100.000 | |
| KPCA_Poly | Kernel principal component eigenvalue | 49.566 | 4.0559 | 0.3441 | 0.0217 |
| Contribution % | 91.8099 | 7.5126 | 0.6373 | 0.0402 | |
| Cumulative contribution rate % | 91.8099 | 99.3225 | 99.9558 | 100.00 | |
| KPCA_RBF | Kernel principal component eigenvalue | 3.0601 | 0.5177 | 0.0946 | 0.0127 |
| Contribution % | 83.0404 | 14.0486 | 2.5666 | 0.3444 | |
| Cumulative contribution rate % | 83.0404 | 97.089 | 99.6556 | 100.000 | |
| Component | Name | Parameter |
|---|---|---|
| Helical gear box | Gear | Large gear: modules = 2, number of teeth = 77 Pinion: modules = 2, number of teeth = 55 |
| Bear | Deep groove ball rolling bearing 6206 | |
| Planetary gearbox | Gear | Inner gear ring: modules = 2, number of teeth = 72 |
| Planetary gear: modules = 2, number of teeth = 27, quantity = 3 | ||
| Sun gear: modules = 2, number of teeth = 18 | ||
| Bear | Deep groove ball rolling bearing: for the planet wheel 6202, for the planet shelf = 6206, for the sun wheel 6205 | |
| Brake | The loading form is magnetic, and the loading torque is 0–100 N·m | |
| Motor | Converter motor | 2.2 kW, the rotational speed is 1500 RPM, and the rated speed is 1410 RPM |
| Algorithm | Parameters |
|---|---|
| SFLA-PSO | N = 200, nPSO = 20, nP = 10, c1 = c2 = 2, F = 20, m = 5, n = 4, Lmax = 10, Tmax = 100, d = 20, Smax = 20 |
| Type | Model | KPCA Kernel Parameter | JFnsher | ||
|---|---|---|---|---|---|
| γ* | d1* | σ* | |||
| 3-type | ABC | 0.005 | 0.8 | 23.37 | 0.3497 |
| BCD | 0.038 | 0.896 | 5.4438 | 0.8970 | |
| 4-type | ABCD | 0.055 | 1.03 | 13.1 | 0.9949 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Ye, L.; Liu, Y. Feature Extraction of a Planetary Gearbox Based on the KPCA Dual-Kernel Function Optimized by the Swarm Intelligent Fusion Algorithm. Machines 2024, 12, 82. https://doi.org/10.3390/machines12010082
He Y, Ye L, Liu Y. Feature Extraction of a Planetary Gearbox Based on the KPCA Dual-Kernel Function Optimized by the Swarm Intelligent Fusion Algorithm. Machines. 2024; 12(1):82. https://doi.org/10.3390/machines12010082
Chicago/Turabian StyleHe, Yan, Linzheng Ye, and Yao Liu. 2024. "Feature Extraction of a Planetary Gearbox Based on the KPCA Dual-Kernel Function Optimized by the Swarm Intelligent Fusion Algorithm" Machines 12, no. 1: 82. https://doi.org/10.3390/machines12010082
APA StyleHe, Y., Ye, L., & Liu, Y. (2024). Feature Extraction of a Planetary Gearbox Based on the KPCA Dual-Kernel Function Optimized by the Swarm Intelligent Fusion Algorithm. Machines, 12(1), 82. https://doi.org/10.3390/machines12010082










