A New Cable-Driven Model for Under-Actuated Force–Torque Sensitive Mechanisms

Abstract

Force–torque sensors are used in many and different domains (i.e., space, medicine, biology, etc.). Design solutions of force–torque sensors can be conceived by using many types of connections or components; however, there are only a few sensors designed using cable-driven systems. This could be related to many reasons, one of which being that cables are able only to pull and not push. In this paper, a new cable-driven model for under-actuated force–torque sensing mechanisms is proposed, simulated, and tested, underlining the novelty of using cables for force–torque sensing. Analytical formulations, simulations, and physical implementations are presented in this paper. Results confirm that the new proposed model can be used for force–torque sensing mechanisms in micro- and macro- applications where under-actuation is a fundamental requirement, as in robotic surgery. The proposed model and mechanism can be used in the design of sensors and actuators. The innovative model is validated with two different test benches, opening new challenges in the design and development of under-actuated force–torque transducers.

1. Introduction

Nowadays, sensors are used in many different contexts and domains (i.e., space, medicine, engineering, biology, etc.), allowing users to analyse the behaviour of the systems.

Force–torque sensors are used to measure the forces and torques exchanged between two or more systems in order to define their physical interaction.

Among the possible sensor configurations, the conceptual architecture of parallel mechanisms is very useful for the design of force–torque sensors. The motion of a mobile part, connected with joints and links to a fixed part, is the core of a force–torque sensor’s design. The local reference system (on the mobile part) can be moved with respect to the absolute reference system (on the fixed part). The displacement between the two reference systems is one aspect which permits the exchanged forces and torques between the two parts and their physical connections to be reconstructed to find the applied forces/torques. The types of physical connection between the two parts (mobile and fixed) have been explored by many researchers. An overview on force–torque sensors for microscopic and macroscopic applications, including the surgical robotic field, can be found in Muscolo and Fiorini [1]. One output of the review is that the force–torque sensors developed in the literature can be divided on the basis of three types of physical connections between mobile and fixed parts: rigid connections (e.g., using beams), soft connections (e.g., using cables or membranes), or no connections (e.g., using magnets). Nowadays, the most used sensors are those with rigid connections.

The Stewart platform is an example of a parallel mechanism used for its design architecture in the design and development of force–torque sensors [2]. In [3], the authors present a review of Stewart platform manipulators, in which a mobile part is connected to a fixed part using links, spherical joints, and prismatic actuators. Sorli and Pastorelli defined the general design of a force–torque sensor, conceived with the Stewart platform architecture [4]. Many research papers have been published in which an architecture with a Stewart platform is used for force–torque sensor design. In [5], the authors use a near-singular configuration to define a force–torque sensor based on a Stewart platform. Rotary joints are replaced with flexible hinges, and strain-gauges are used as sensing elements in the developed prototype. In [6], applications in minimally invasive robotic surgery are proposed. The realized system is conceived with the Stewart platform architecture and with reduced dimensions because the mobile and fixed parts must be included in the surgical instrument with a diameter of around 10 mm. Flexural hinges are used instead of joints; six strain gauges are used as sensing elements and mounted on each of the six links of the Stewart platform. In [7], a six-component contact force measurement device is presented with a Stewart platform structure. Each of the six physical connections between mobile and fixed parts is composed of a wire connected to a strain-gauged cantilever.

Force–torque sensors can be designed using many other physical architectures, such as the one based on a Maltese Cross shape [8,9], but also in this case, the sensor can be designed with fixed and mobile parts connected by links. In the Maltese Cross shape case, the motion of the mobile part, generated by an external load, can be evaluated via the analysis of the deformation of the links positioned in the cruciform shape.

Other architectures for force–torque sensor design can be defined by using different structures (e.g.: a combination between the Stewart platform and the Maltese Cross shape). Some examples of mixed architectures can be found in [1,10,11,12].

Cable-driven systems [13,14] or membranes [15,16,17] are examples of soft physical connections which can be used as sensitive elements. Cable-driven mechanisms are used in different contexts, such as rehabilitation [18], the design of exoskeletons [19], industry [20], or in mechanical designs for general applications [21,22,23].

Some researchers used the pretension of fibre Bragg gratings to wrap the fibre around the mechanical transducer [24]. In [25], the authors presented a minimally invasive robotic surgery instrument in which the sensor is included in the rear part of the surgical instrument, analysing the tension of cables. Recently, researchers studied a cable-driven robotic system for aeronautical applications [26]. The differences in the cable tension are amplified to read the force sensitivity of the cables. The paper [26] underlines the advantages of using cable-driven parallel robots (CDPR) instead of rigid links parallel robots, as follows:

• Their convenient disassembly/reassembly;
• Their light-weight structures;
• Their high payload-to-weight ratios.

These three advantages are very useful in the robotic surgery research field.

In this paper, we propose a new model of a cable-driven force–torque sensing mechanism that can be used as an under-actuated force–torque sensor or actuator. The mechanism consists of one mobile part and one fixed part connected to each other by soft physical connections (e.g., using cables). The mechanism has been conceived to solve problems in the robotic surgery research field. For example, robotic tools must be sterilized for use in minimally invasive robotic surgery, and the process of sterilization is dangerous for the electronic components and sensing elements of the instrument [1]. The invention shown in this paper is a sensorized mechanism consisting of an under-actuated platform connected with cables. If this mechanism is included in a minimally invasive robotic surgery tool, the part of the robotic tool that can be sterilized is composed of cables and a rigid structure, and the electronic part remains outside the human body and does not need sterilization. The cable-driven model and mechanism presented in this paper can be used in many different domains, as well as outside the robotic surgery field. The proposed architecture can be used as a sensor or an actuator and for micro- and macro- applications.

The paper is organized as follows: Section 2 shows the problem statement of the force feedback during robotic surgery and the proposed innovation in comparison to cable-driven parallel manipulators; Section 3 presents the kinematic model of the proposed solution and some configurations; Section 4 shows the simulation of and comparison between two configurations; Section 5 presents the analytical formulation of the sensing mechanism; Section 6 shows the developed test bench prototypes for the experiments; Section 7 includes results and discussion. The paper ends with the conclusions and future research directions.

2. Problem Statement and Proposed Solution

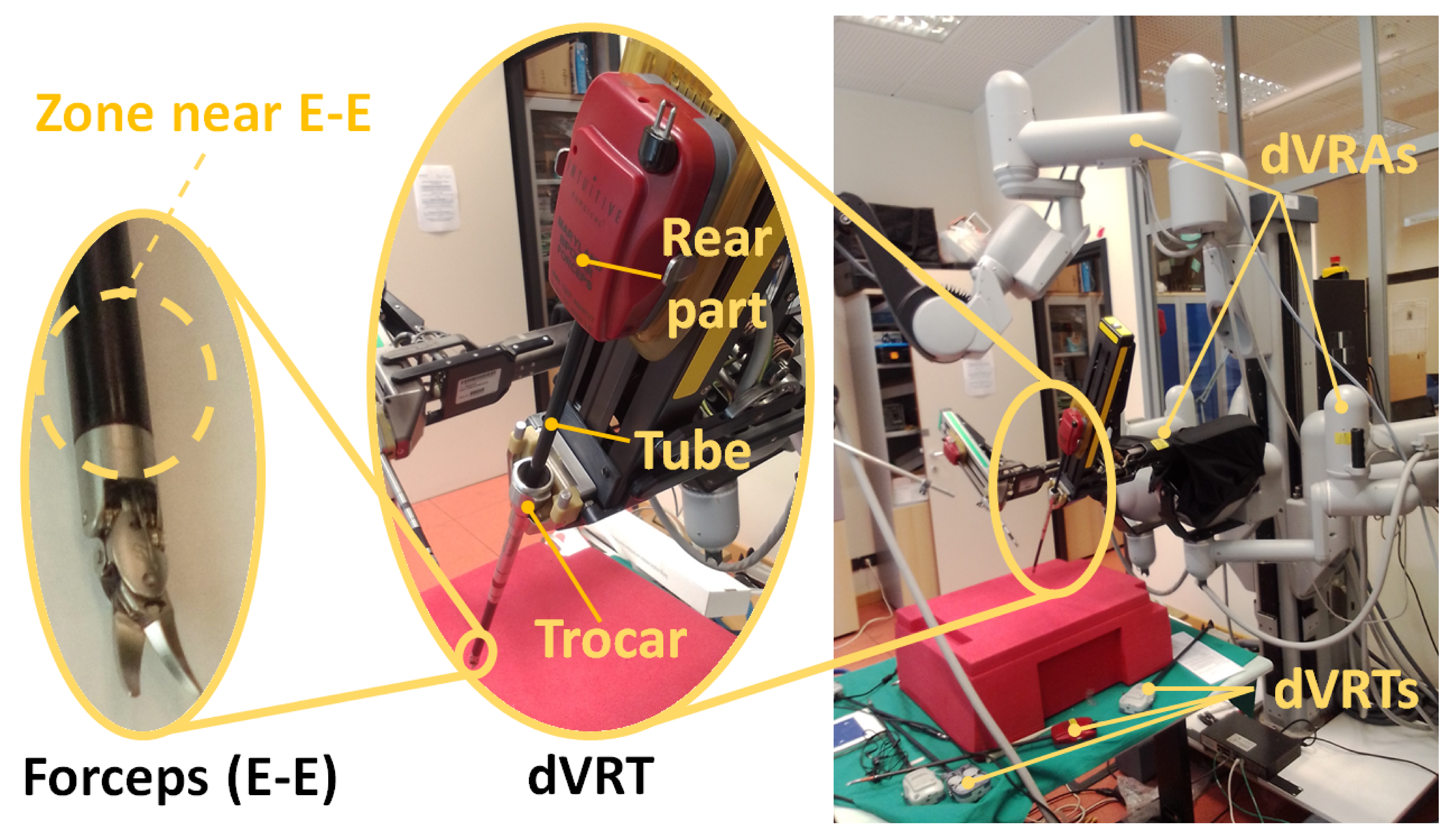
2.1. Da Vinci Robotic Tools (dVRTs)

The da Vinci Robot is a Minimally Invasive Robotic Surgery (MIRS) system, developed by Intuitive Surgical, Sunnyvale, CA, USA [1]. It is composed of two parts, located in two different places and connected by tele-operation:

• Local part: located near the surgeon and controlled directly by the hands of the surgeon;
• Remote part: located near the patient and tele-operated by the local part.

The local part does not give force feedback to the surgeon but permits them to control the remote part (in open-loop) using only a vision system. The remote part consists of the da Vinci Robotic Arms (dVRAs) and da Vinci Robotic Tools (dVRTs) or Minimally Invasive Robotic Tools (MIRTs), as shown in Figure 1 [1].

The dVRT is composed of a rear part (assembled on the robotic arm), a tube, and an End-Effector (E-E), constituted by forceps, or other systems used for MIRS. The dVRT uses cable-driven mechanisms to move the forceps [1]. Cables passing inside the tube connect the E-E to the pulleys in the rear part.

During MIRS operations, the dVRT is forced to pass through a trocar (see Figure 1), i.e., a connection and separation system between the external environment and the interior of the human body. All tools in contact with the human body must be sterilized.

2.2. Problem Statement: Force Feedback in Robotic Surgery

In order to give force feedback to the surgeon (via the local part of the robot), many solutions were proposed [1]. One of the desirable solutions is the inclusion of sensitive elements in the surgical instrument (on the remote part). This solution is not simple to implement because many constraints should be considered. One of these constraints is to develop a sensor able to resist the routine sterilization process at high temperature.

Many research solutions proposed the implementation of sensitive elements in the rear part of the surgical instrument [25,27,28,29], or on the robotic arm [30]. This approach is good because it allows the sterilization of the sensor to be avoided (because it is not near the E-E). However, the signals of the sensor are corrupted by many disturbances, amplified by the connections between the E-E (of the surgical instrument) and the robotic arm.

Other solutions include an added sensitive element near the E-E of the tool (see zone near E-E, Figure 1) [6,31,32]. In this case, the errors in the signal data of the sensor are reduced, but problems emerge during the sterilization process of the electronic components.

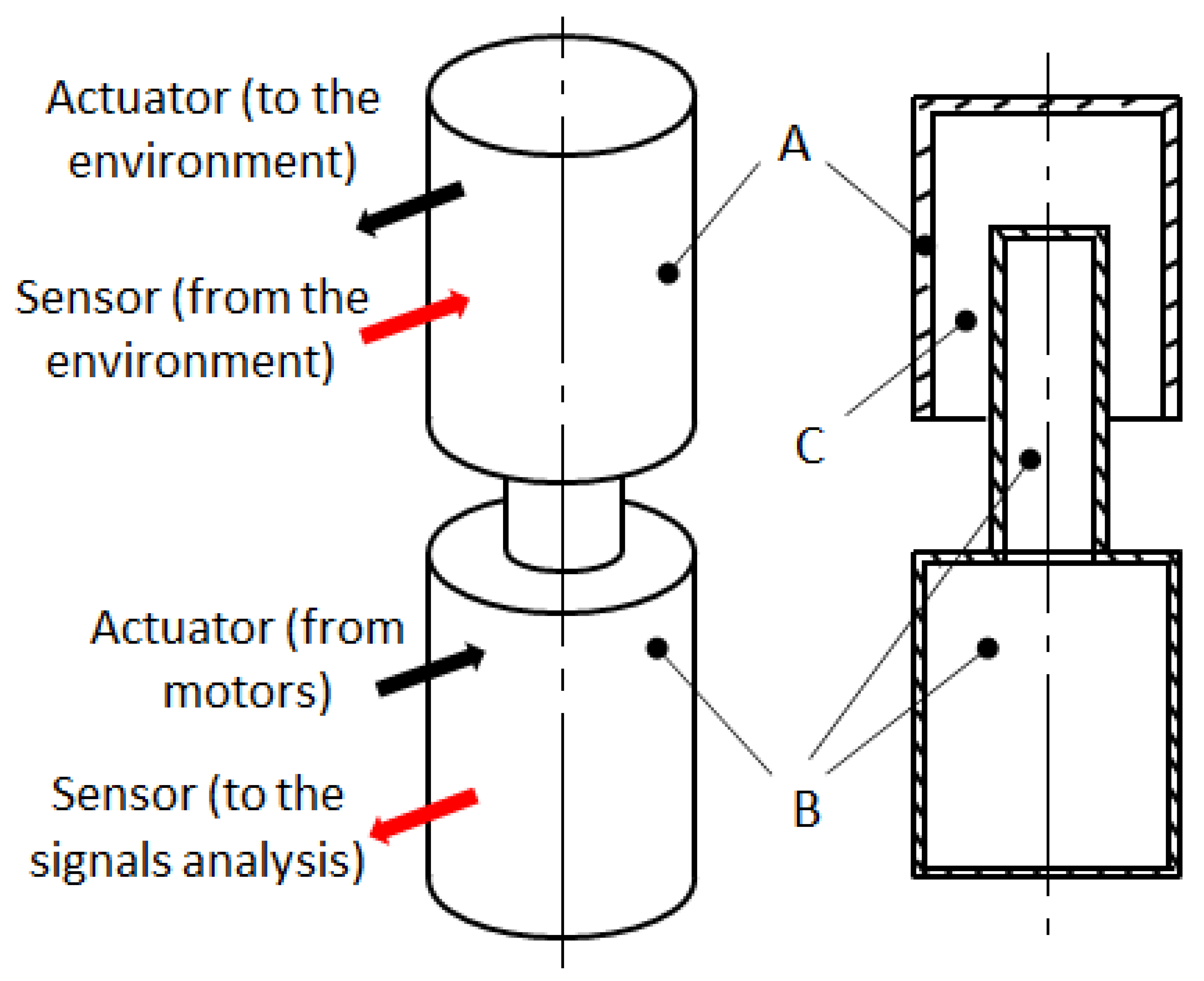
2.3. Proposed Solution: Cable-Driven Force–Torque Sensing Mechanism

We thought to use cable-driven systems, also used in the dVRT for the actuation of the E-E, to design our force–torque sensitive mechanism. The under-actuation of cables is convenient in robotic surgery, since it allows direct contact between the electronic part and the sterilized zone of the surgical instrument to be avoided. In the proposed solution in this paper, we tried to merge the advantages of the two approaches presented above: we include the sensitive mechanism near the E-E of the tool (reducing gap errors in the signal data) and the electronic components of the mechanism outside of the sterilizing zone (thanks to the cable connections and avoiding the sterilization of the electronic part).

Some innovations of the cable-driven sensitive mechanism proposed in this paper are given below:

• Hybrid System: the mechanism can be used as a sensor and/or actuator;
• Modelling: the model of the mechanism is constituted by an external mobile part connected with cables to an internal fixed structure;
• Application: micro- and macro- applications can be performed with the proposed mechanism;
• Under-actuation: the mechanism is composed of a cable-driven, under-actuated system.

2.3.1. Hybrid System: Sensor and/or Actuator

The proposed solution in this paper allows devices to be created which can be used as sensors or actuators, respectively measuring forces from the environment or implementing forces on the environment.

In its general form, our solution is composed of two elements, A and B, as shown in Figure 2, divided by a C zone. Element A can interact with the external environment as a sensor (measuring force resultants) or as an actuator (acting force resultants). Element A can be stationary or in motion with respect to the fixed element B. The C zone can be constituted by different types of elements or connections between A and B: membranes, cables, tendons, magnets, etc. Based on the deformation or displacement of the elements in C, the forces on A (when used as a sensor) or from A (when used as an actuator) can be determined.

In this paper, the mechanism is used as a sensor, using cables in the C zone.

2.3.2. Modelling: An Internal Cable-Driven Fixed Structure

The classical model used to describe CDPR is composed of an external parallelepiped connected to an internal parallelepiped using cables (pulleys are approximated to points) [21,22,23,26]. The fixed and mobile parts are the external and the internal parallelepipeds, respectively. The motion of the internal parallelepiped is calculated with respect to the external one by using screw theory [7], or other analytical methods, and computing the tension of the cables.

In order to integrate our solution in the cylindrical tube of the surgical instrument (with a tube diameter of around 10 mm, see Figure 1), it is convenient to conceive different models, in which the mobile part (A) is external and the fixed part (B) is internal. Cables can pass inside the fixed part to connect B to A. We simplified the classical model with parallelepipeds using the cylindrical symmetry of the system.

Figure 3 shows two cylindrical configurations of our cable-driven mechanism. The two presented configurations will be analysed in detail in the following sections and represent the two extreme conditions in which the length of part B ($b_i$) is shorter or longer than the length of part A ($a_i$):

$$b_{min}<b_{iI}<a_{max}$$

(1)

$$a_{min}<b_{iII}<b_{max}$$

(2)

where $b_{iI}$ and $b_{iII}$ are the lengths of the internal cylinder (part B) in the two configurations I and II; $a_i$ is the length of the external cylinder (part A); $a_{max}$, $b_{max}$, $a_{min}$, and $b_{min}$ are the maximum and minimum values of the height of the two cylinders; and $D_A$ and $D_B$ are the diameters of the mobile (A) and fixed (B) cylinders, respectively.

Another condition to be respected is the following one:

$$D_A>D_B$$

(3)

2.3.3. Application: Micro/Macro Cable-Driven Applications

From the application point of view, the model has been conceived for micro- applications (e.g., containing the system in a minimum cylinder of 10 mm diameter). However, macro-applications can be found in different contexts and domains. This point can be considered as an open challenge.

Figure 4 shows an example of the implemented configurations on the tube of the surgical instrument. The analysis of the tension of eight cables allows the external resultant forces on the mobile part A to be defined.

2.3.4. Under-Actuation: Cable-Driven System

The under-actuation allows the use of a light system and separates the zone of motion of the mobile part from the zone of the electronics part and the sensor’s implementation. This is very convenient in robotic surgery, bypassing the sterilization problem related to the use of electronic components. The under-actuation also allows more accurate sensors to be used because in the rear part of the instrument, minor constraints on dimensions, permeability, and other features are required.

3. Analysis of the Mechanism’s Configurations

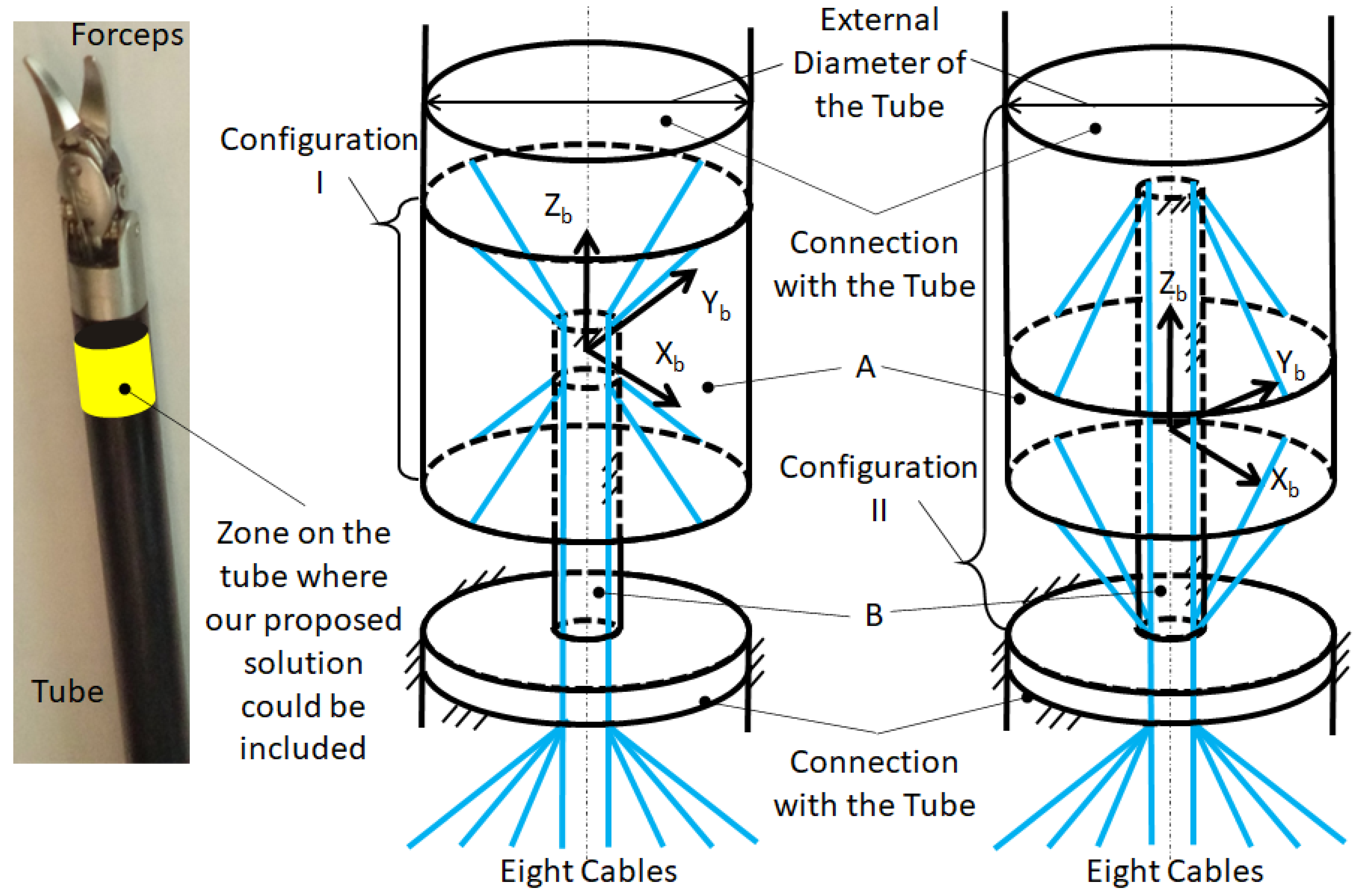
3.1. Details of the Kinematic Model

Figure 5 shows the two reference systems on the fixed B ($O_B-X_B{Y}_B{Z}_B$) and mobile A platforms ($O_A-X_A{Y}_A{Z}_A$), where i is the cable number from 1 to k and j is the equilibrium positions, initial $j=0$ and final $j=1$. The reference system of the mobile platform A ($O_A-X_A{Y}_A{Z}_A$) is applied to its centre of mass G ($O_A=G$), and in the position $j=0$, it is coincident with $O_B$. $N_{Bij}$, $N_{Aij}$, ${\mathbf{p}}_{Bi}$, and ${\mathbf{p}}_{Ai}$ are the two anchor points of the cables ($N_{Bij}$, $N_{Aij}$) and their two position vectors (${\mathbf{p}}_{Bi}$, ${\mathbf{p}}_{Ai}$), respectively; ${\mathbf{C}}_{ij}$ is the vector of the cables, and ${\mathbf{r}}_{ij}$ the unit vector of the cables. The position of the mobile platform A with respect to the fixed one B is shown by the vector ${\mathbf{p}}_G$. P is a general point on A, and ${\mathbf{p}}_P$ and ${\mathbf{p}}_z$ are the position vectors of the point P with respect to the reference systems in B (${\mathbf{p}}_P$) and A (${\mathbf{p}}_z$). It is possible to write the kinematic equation of the k cables in a general form, using the rotational matrix Q to transform the vectors calculated in the mobile platform A with respect to the fixed platform B:

$${\mathbf{C}}_{ij}=-{\mathbf{p}}_{Bi}+{\mathbf{p}}_G+\mathbf{Q}{\mathbf{p}}_{Ai};i=1,\dots ,k;j=0,1.$$

(4)

If part A is in equilibrium, the resultants of forces ($\mathbf{F}$) and torques ($\mathbf{M}$) are zero:

$$\sum \mathbf{F}=0=\sum _{i=1}^k{\mathbf{T}}_{ij}+m{\mathbf{g}}_G+{\mathbf{F}}_P$$

(5)

$$\sum \mathbf{M}=0=\sum _{i=1}^k(\mathbf{Q}{\mathbf{p}}_{Ai}\wedge {\mathbf{T}}_{ij})+({\mathbf{p}}_G\wedge m{\mathbf{g}}_G)+({\mathbf{p}}_P\wedge {\mathbf{F}}_P)+{\mathbf{M}}_P$$

(6)

where ${\sum }_{i=1}^k{\mathbf{T}}_{ij}={\sum }_{i=1}^k{T}_{ij}{\mathbf{r}}_{ij}$ is the tension of cables applied to the mobile platform A in $N_{Aij}$; ${\sum }_{i=1}^k(\mathbf{Q}{\mathbf{p}}_{Ai}\wedge {\mathbf{T}}_{ij})={\sum }_{i=1}^k(\mathbf{Q}{\mathbf{p}}_{Ai}\wedge T_{ij}{\mathbf{r}}_{ij})$ is the torque produced by the cables; $m{\mathbf{g}}_G$ is the gravity; and ${\mathbf{F}}_P$ and ${\mathbf{M}}_P$ are the external forces and torques applied to the point P, respectively. In a more compact form:

$$\left[\begin{array}{ccc}{\mathbf{r}}_{1j}& \cdots & {\mathbf{r}}_{kj}\\ \mathbf{Q}{\mathbf{p}}_{A1}\wedge {\mathbf{r}}_{1j}& \cdots & \mathbf{Q}{\mathbf{p}}_{Ak}\wedge {\mathbf{r}}_{kj}\end{array}\right]\left[\begin{array}{c}{T}_{1j}\\ ⋮\\ T_{kj}\end{array}\right]=-\left[\begin{array}{c}m{\mathbf{g}}_G\\ ({\mathbf{p}}_G\wedge m{\mathbf{g}}_G)\end{array}\right]-\left[\begin{array}{c}{\mathbf{F}}_P\\ ({\mathbf{p}}_P\wedge {\mathbf{F}}_P)+{\mathbf{M}}_P\end{array}\right]$$

(7)

$$\mathbf{S}{\mathbf{T}}_j=-{\mathbf{W}}_G-{\mathbf{W}}_{Pj}$$

(8)

where $\mathbf{S}$ is the force transformation matrix [5]; ${\mathbf{T}}_j$ is the vector of the cables’ tension; and ${\mathbf{W}}_G$ is the gravity vector [26]. The vector of the external forces and torques, applied in the point P (${\mathbf{W}}_{Pj}$), is calculated by analysing the variation in the tension of the cables $\Delta \mathbf{T}={\mathbf{T}}_1-{\mathbf{T}}_0$, in which ${\mathbf{T}}_0$ is the vector of the tension of the cables, used as an offset and calculated at the equilibrium condition $j=0$:

$$\mathbf{S}{\mathbf{T}}_0=\mathbf{S}\left[\begin{array}{c}{T}_{10}\\ ⋮\\ T_{k0}\end{array}\right]=-{\mathbf{W}}_G-{\mathbf{W}}_{P0}$$

(9)

By the analysis of Equation (8) and using the difference between the condition $j=1$ and $j=0$, ${\mathbf{W}}_{Pj}$ is obtained:

$${\mathbf{W}}_{Pj}={\left[\begin{array}{c}{F}_{PX},F_{PY},F_{PZ},M_{PX},M_{PY},M_{PZ}\end{array}\right]}^T={\mathbf{W}}_{P0}-\mathbf{S}\Delta \mathbf{T}$$

(10)

If the proposed cable-driven mechanism is used as a force–torque sensor, in order to increase the sensitivity of the entire system, the geometry of the mechanism must be optimised to obtain low variations in cable tension for small displacements of the mobile part A.

In line with [26], we optimise the geometrical dimensions of the two configurations of the mechanism (shown in Figure 3) to find the best solution providing more sensitivity; however, we use a different method than the one proposed in [26].

Figure 3 shows the two studied configurations. The difference between the two configurations is underlined by the different positions of cables with respect to the two parts, A and B. In configuration I, the height of cylinder B ($b_{iI}$) is less than the height of cylinder A, as shown in Equation (1). The opposite is shown in configuration II, Equation (2), in which the height of cylinder B ($b_{iII}$) is larger than the height of cylinder A. Part A is in equilibrium: the resultant of forces and torques are zero ($\sum \mathbf{F}=0$ and $\sum \mathbf{M}=0$).

Our final objective is to find the most optimised geometry for the two presented configurations in order to measure the tension of the cables. If the external forces/torques are applied to the system, the variation in the tension of the cables gives us information on the entity of the external forces/torques.

3.2. Configuration I

Figure 6 (on the left) shows a general representation of the configuration I. Thanks to the cylindrical symmetry of the entire system, the calculations can be simplified and the mechanism can be studied in the planar case. Part B is partially fixed, only allowing the rotation around the axial cylindrical axis, and part A is in equilibrium. The forces acting on part A are:

• External forces and torques in condition $j=1$: ${\mathbf{W}}_{P1}={[F_{PX},F_{PY},F_{PZ},M_{PX},M_{PY},M_{PZ}]}^T$;
• Gravity: ${\mathbf{W}}_G={[0,0,-m{g}_G,0,0,0]}^T$;
• Tension of cables in condition $j=1$: ${\mathbf{T}}_1={[T_{11},T_{21},T_{31},T_{41},T_{51},T_{61},T_{71},T_{81}]}^T$;
• Offset in condition $j=0$: ${\mathbf{T}}_0={[T_{10},T_{20},T_{30},T_{40},T_{50},T_{60},T_{70},T_{80}]}^T$.

Using the equilibrium conditions ($\sum \mathbf{F}=0$, $\sum \mathbf{M}=0$), the vector ${\mathbf{W}}_{P1}$ can be determined by finding the $S_I$ matrix for configuration I with $c{\theta }_I=cos\left({\theta }_I\right)$ and $s{\theta }_I=sin\left({\theta }_I\right)$:

$$\begin{array}{c}\hfill {\mathbf{S}}_{I0}=\left[\begin{array}{cccccccc}-s\theta & -s{\theta }_I& +s{\theta }_I& +s{\theta }_I& 0& 0& 0& 0\\ 0& 0& 0& 0& -s{\theta }_I& -s{\theta }_I& +s{\theta }_I& +s{\theta }_I\\ +c{\theta }_I& -c{\theta }_I& +c{\theta }_I& -c{\theta }_I& +c{\theta }_I& -c{\theta }_I& +c{\theta }_I& -c{\theta }_I\\ 0& 0& 0& 0& -h_{I0}& -h_{I1}& +h_{I0}& +h_{I1}\\ +h_{I0}& -h_{I1}& -h_{I0}& +h_{I1}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\end{array}$$

(11)

where

$$h_{I0}=((L_2-a_{max}/2)sin\left({\theta }_I\right)+(D_A/2)cos\left({\theta }_I\right))$$

(12)

$$h_{I1}=((L_2+a_{max}/2)sin\left({\theta }_I\right)-(D_A/2)cos\left({\theta }_I\right))$$

(13)

The geometrical dimensions $a_{max}$, $b_i$, $D_A$, and $D_B$ can be optimised and can be included in the angle ${\theta }_I$ and in the length of the cable $C_I$:

$$C_I=\sqrt{{((a_{max}-b_i)/2)}^2+{((D_A-D_B)/2)}^2}$$

(14)

$${\theta }_I=arctan((D_A-D_B)/(a_{max}-b_i))$$

(15)

3.3. Configuration II

Figure 6 (on the right) shows configuration II, following the relative equations with $S_{II}$ matrix for configuration II and with $c{\theta }_{II}=cos\left({\theta }_{II}\right)$ and $s{\theta }_{II}=sin\left({\theta }_{II}\right)$:

$$\begin{array}{c}\hfill {\mathbf{S}}_{II0}=\left[\begin{array}{cccccccc}-s{\theta }_{II}& -s{\theta }_{II}& +s{\theta }_{II}& +s{\theta }_{II}& 0& 0& 0& 0\\ 0& 0& 0& 0& -s{\theta }_{II}& -s{\theta }_{II}& +s{\theta }_{II}& +s{\theta }_{II}\\ -c{\theta }_{II}& +c{\theta }_{II}a& -c{\theta }_{II}& +c{\theta }_{II}& -c{\theta }_{II}& +c{\theta }_{II}& -c{\theta }_{II}& +c{\theta }_{II}\\ 0& 0& 0& 0& -h_{II0}& -h_{II1}& +h_{II0}& +h_{II1}\\ +h_{II0}& +h_{II1}& -h_{II0}& -h_{II1}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\end{array}$$

(16)

where

$$h_{II0}=(L_2-a_i/2)sin\left({\theta }_{II}\right)-(D_A/2)cos\left({\theta }_{II}\right)$$

(17)

$$h_{II1}=(L_2+a_i/2)sin\left({\theta }_{II}\right)+(D_A/2)cos\left({\theta }_{II}\right)$$

(18)

The geometrical dimensions $b_{max}$, $a_i$, $D_A$, and $D_B$, can be optimised and can be included in the angle ${\theta }_{II}$ and in the length of the cable $C_{II}$:

$$C_{II}=\sqrt{{((b_{max}-a_i)/2)}^2+{((D_A-D_B)/2)}^2}$$

(19)

$${\theta }_{II}=arctan((D_A-D_B)/(b_{max}-a_i))$$

(20)

4. Configurations I and II: Comparison and Simulation

The elements of the two matrices (${\mathbf{S}}_{I0}$ and ${\mathbf{S}}_{II0}$) have their first three rows function according to the two angles (${\theta }_I$ and ${\theta }_{II}$).

Equation (10) shows that the first three rows of the matrix $\mathbf{S}$ allow one to find the three force components ($F_{PX}$, $F_{PY}$, $F_{PZ}$) of the applied vector in P (${\mathbf{W}}_{P1}$). The advantage of using one configuration over another one is not underlined by the values of ${\theta }_I$ and ${\theta }_{II}$. If ${\theta }_I\to \pi /2^{-}$ and ${\theta }_{II}\to \pi /2^{-}$, or ${\theta }_I\to 0^{+}$ and ${\theta }_{II}\to 0^{+}$, it is possible to note that the first three rows of the matrices have the same values with the opposite signs. This means that the geometry of the configuration cannot give any other contribution to optimise the entire system.

The advantage of using one configuration instead of the other is identified by analysing the last three rows of the matrices, which allows one to find the three torque components ($M_{PX}$, $M_{PY}$, $M_{PZ}$) applied in P, as shown in Equation (10). The last three rows of the two matrices ${\mathbf{S}}_{I0}$ and ${\mathbf{S}}_{II0}$ (shown in Equations (11) and (16)) have the same forms, and the differences between the two configurations are represented by the four elements $h_{I0}$, $h_{I1}$, $h_{II0}$, and $h_{II1}$, as shown in Equations (12), (13), (17) and (18) and by their signs. A detailed comparison is shown in Figure 7 between the four elements, modifying the two angles ${\theta }_I$ and ${\theta }_{II}$ and using the dimensions shown in Figure 6: $L_2$ = 50 mm, $a_{max}=b_{max}$ = 40 mm, $D_A$ = 10 mm, $D_B$ = 4 mm, $a_i=b_i={[10,...,40]}^T$ mm.

In order to find the best configuration between the two mentioned above, the two force transformation matrices ${\mathbf{S}}_{I0}$ and ${\mathbf{S}}_{II0}$ (shown in Equations (11) and (16)) and their elements should be analysed. Using Equation (10), it is possible to write:

$$\Delta \mathbf{W}={\mathbf{W}}_{P0}-{\mathbf{W}}_{P1}=\mathbf{S}\Delta \mathbf{T}$$

(21)

and then

$${\parallel S\Delta T-\Delta W\parallel }_2=0$$

(22)

In order to obtain the minimum in the Equation (22), based on the properties of the norms and modifying only the matrix $\mathbf{S}$, we should have a minimum value of ${\parallel S\parallel }_2$.

Unfortunately, ${\mathbf{S}}_{I0}$ and ${\mathbf{S}}_{II0}$ are rectangular matrices, and this aspect does not permit us to use simplifications for the square matrices. However, we used the singular value decomposition method [33] in order to find the singular values of the two matrices and to have an index on their characteristics. The singular values of $\mathbf{S}$ are correlated to the eigenvalues of the matrix ${\mathbf{S}}^T\mathbf{S}$ and with the Euclidean norm of $\mathbf{S}$ (${\parallel S\parallel }_2$). The following formulation is true:

$${\sigma }_s\left(S\right)=\sqrt{{\lambda }_s\left(S^{T}S\right)}$$

(23)

$${\parallel S\parallel }_2={\sigma }_1\left(S\right)$$

(24)

where ${\sigma }_s$ and ${\lambda }_s$ are the s singular values of $\mathbf{S}$ and s eigenvalues of the matrix ${\mathbf{S}}^T\mathbf{S}$ ($s=1,...,p$ and ${\sigma }_1>{\sigma }_2>...>{\sigma }_p\ne 0$); ${\parallel S\parallel }_2$ is the Euclidean norm of $\mathbf{S}$; and ${\sigma }_1$ the largest singular value of $\mathbf{S}$.

The following results have been found:

• The two matrices ${\mathbf{S}}_{I0}$ and ${\mathbf{S}}_{II0}$ have the same rank, equal to 5;
• $\parallel S_{I0}{\parallel }_2<{\parallel S_{II0}\parallel }_2$.

To simplify the Equation (22), it is convenient to use configuration I with a smaller value of its Euclidean norm. However, configuration I has geometrical limitations with respect to configuration II. All cables in configuration I converge to the point $O_B$, and this limits the capacity of the structure to be fixed. Furthermore, the difference between two elements of the same configuration ($h_{I0}$, $h_{I1}$, or $h_{II0}$, $h_{II1}$) is smaller in configuration I compared to configuration II; this is shown in Figure 7. For these reasons, configuration II is selected as the best for our scope.

5. Analytical Formulation of Configuration II

5.1. Force Transformation Matrix

The matrices ${\mathbf{S}}_{I0}$ and ${\mathbf{S}}_{II0}$ (found in Equations (11) and (16), respectively) are the simplified matrices for the two configurations in starting position (condition $j=0$). Based on the analysis performed in previous sections, configuration II is the one recommended for our scope.

In order to use Equation (21) and to find the vector of the external forces and torques (${\mathbf{W}}_{Pj}$), the force transformation matrix (${\mathbf{S}}_{IIj}$) and the vector of the variation in the tension of cables between the two conditions $j=0$ and $j=1$ ($\Delta \mathbf{T}$) must be calculated. In order to simplify the calculation, we used the model of configuration II shown in Figure 8, obtained with $a_i=0$. In our case, ${\mathbf{W}}_{P0}=0$, and we can re-write Equation (10) it as:

$${\mathbf{W}}_{Pj}={\left[\begin{array}{c}{F}_{PX},F_{PY},F_{PZ},M_{PX},M_{PY},M_{PZ}\end{array}\right]}^T=-{\mathbf{S}}_{IIj}\Delta \mathbf{T}$$

(25)

The new force transformation matrix ${\mathbf{S}}_{IIj}$ is:

$$\begin{array}{c}\hfill {\mathbf{S}}_{IIj}=\left[\begin{array}{cccccccc}{S}_{11j}& S_{12j}& S_{13j}& S_{14j}& S_{15j}& S_{16j}& S_{17j}& S_{18j}\\ S_{21j}& S_{22j}& S_{23j}& S_{24j}& S_{25j}& S_{26j}& S_{27j}& S_{28j}\\ S_{31j}& S_{32j}& S_{33j}& S_{34j}& S_{35j}& S_{36j}& S_{37j}& S_{38j}\\ S_{41j}& S_{42j}& S_{43j}& S_{44j}& S_{45j}& S_{46j}& S_{47j}& S_{48j}\\ S_{51j}& S_{52j}& S_{53j}& S_{54j}& S_{55j}& S_{56j}& S_{57j}& S_{58j}\\ S_{61j}& S_{62j}& S_{63j}& S_{64j}& S_{65j}& S_{66j}& S_{67j}& S_{68j}\end{array}\right]\end{array}$$

(26)

where the elements of the ${\mathbf{S}}_{IIj}$ matrix are shown in the following:

$$\begin{array}{c}\hfill S_{11j}=-sin\left({\alpha }_{11}\right)cos({\gamma }_b+\psi );S_{12j}=-sin\left({\alpha }_{21}\right)cos({\gamma }_b+\psi );S_{13j}=sin\left({\alpha }_{31}\right)cos\left({\gamma }_a\right);\end{array}$$

(27)

$$\begin{array}{c}\hfill S_{14j}=sin\left({\alpha }_{41}\right)cos\left({\gamma }_a\right);S_{15j}=sin\left({\alpha }_{51}\right)sin\left({\gamma }_c\right);S_{16j}=sin\left({\alpha }_{61}\right)sin\left({\gamma }_c\right);\end{array}$$

(28)

$$\begin{array}{c}\hfill S_{17j}=sin\left({\alpha }_{71}\right)sin({\gamma }_d+\psi );S_{18j}=sin\left({\alpha }_{81}\right)sin({\gamma }_d+\psi );\end{array}$$

(29)

$$\begin{array}{c}\hfill S_{21j}=sin\left({\alpha }_{11}\right)sin({\gamma }_b+\psi );S_{22j}=sin\left({\alpha }_{21}\right)sin({\gamma }_b+\psi );S_{23j}=sin\left({\alpha }_{31}\right)sin\left({\gamma }_a\right);\end{array}$$

(30)

$$\begin{array}{c}\hfill S_{24j}=sin\left({\alpha }_{41}\right)sin\left({\gamma }_a\right);S_{25j}=sin\left({\alpha }_{51}\right)cos\left({\gamma }_c\right);S_{26j}=sin\left({\alpha }_{61}\right)cos\left({\gamma }_c\right);\end{array}$$

(31)

$$\begin{array}{c}\hfill S_{27j}=sin\left({\alpha }_{71}\right)cos({\gamma }_d+\psi );S_{28j}=sin\left({\alpha }_{81}\right)cos({\gamma }_d+\psi );\end{array}$$

(32)

$$\begin{array}{c}\hfill S_{31j}=-cos\left({\alpha }_{11}\right);S_{32j}=cos\left({\alpha }_{21}\right);S_{33j}=-cos\left({\alpha }_{31}\right);S_{34j}=cos\left({\alpha }_{41}\right);\end{array}$$

(33)

$$\begin{array}{c}\hfill S_{35j}=-cos\left({\alpha }_{51}\right);S_{36j}=cos\left({\alpha }_{61}\right);S_{37j}=-cos\left({\alpha }_{71}\right);S_{38j}=cos\left({\alpha }_{81}\right);\end{array}$$

(34)

$$\begin{array}{c}\hfill S_{41j}=C_{11}sin\left({\alpha }_{11}\right)sin({\gamma }_b+\psi )cos\left({\alpha }_{11}\right);S_{42j}=-C_{21}sin\left({\alpha }_{21}\right)sin({\gamma }_b+\psi )cos\left({\alpha }_{21}\right);\end{array}$$

(35)

$$\begin{array}{c}\hfill S_{43j}=C_{31}sin\left({\alpha }_{31}\right)sin\left({\gamma }_a\right)cos\left({\alpha }_{31}\right);S_{44j}=-C_{41}sin\left({\alpha }_{41}\right)sin\left({\gamma }_a\right)cos\left({\alpha }_{41}\right);\end{array}$$

(36)

$$\begin{array}{c}\hfill S_{45j}=C_{51}sin\left({\alpha }_{51}\right)cos\left({\gamma }_c\right)cos\left({\alpha }_{51}\right);S_{46j}=-C_{61}sin\left({\alpha }_{61}\right)cos\left({\gamma }_c\right)cos\left({\alpha }_{61}\right);\end{array}$$

(37)

$$\begin{array}{c}\hfill S_{47j}=C_{71}sin\left({\alpha }_{71}\right)cos({\gamma }_d+\psi )cos\left({\alpha }_{71}\right);S_{48j}=-C_{81}sin\left({\alpha }_{81}\right)cos({\gamma }_d+\psi )cos\left({\alpha }_{81}\right);\end{array}$$

(38)

$$\begin{array}{c}\hfill S_{51j}=-C_{11}sin\left({\alpha }_{11}\right)cos({\gamma }_b+\psi )cos\left({\alpha }_{11}\right);S_{52j}=C_{21}sin\left({\alpha }_{21}\right)cos({\gamma }_b+\psi )cos\left({\alpha }_{21}\right);\end{array}$$

(39)

$$\begin{array}{c}\hfill S_{53j}=C_{31}sin\left({\alpha }_{31}\right)cos\left({\gamma }_a\right)cos\left({\alpha }_{31}\right);S_{54j}=-C_{41}sin\left({\alpha }_{41}\right)cos\left({\gamma }_a\right)cos\left({\alpha }_{41}\right);\end{array}$$

(40)

$$\begin{array}{c}\hfill S_{55j}=C_{51}sin\left({\alpha }_{51}\right)sin\left({\gamma }_c\right)cos\left({\alpha }_{51}\right);S_{56j}=-C_{61}sin\left({\alpha }_{61}\right)sin\left({\gamma }_c\right)cos\left({\alpha }_{61}\right);\end{array}$$

(41)

$$\begin{array}{c}\hfill S_{57j}=C_{71}sin\left({\alpha }_{71}\right)sin({\gamma }_d+\psi )cos\left({\alpha }_{71}\right);S_{58j}=-C_{81}sin\left({\alpha }_{81}\right)sin({\gamma }_d+\psi )cos\left({\alpha }_{81}\right);\end{array}$$

(42)

$$\begin{array}{c}\hfill S_{61j}=S_{62j}=S_{63j}=S_{64j}=S_{65j}=S_{66j}=S_{67j}=S_{68j}=0.\end{array}$$

(43)

The terms of the elements of the ${\mathbf{S}}_{IIj}$ matrix are described below, with the help of Figure 8, Figure 9 and Figure 10. Angle ${\alpha }_{ij}$ is the angle between the cable i (in the condition j) and the fixed central cylinder; $C_{ij}$ is the length of the part of the cable i (in the condition j) between the two points $N_{Aij}$ and $N_{Bij}$; $\psi$ is the angle that the component of the applied force in the XY plane has with respect to the $Y_B$ axis; and ${\gamma }_a$, ${\gamma }_b$, ${\gamma }_c$, and ${\gamma }_d$ are the angles in the XY plane, formed by the cables as shown in the sketch of Figure 10, after displacement and rotation of the mobile reference system (centred in $O_A$), with respect to the absolute reference system (centred in $O_B$).

Using Carnot’s theorem, the angle between two cables and the angle ${\alpha }_{ij}$ can be calculated as a function of the lengths $p_3$ and $C_{ij}$, shown in Figure 8, for the condition $j=0$. In the following, this formulation is used to obtain ${\alpha }_{ij}$:

$$\begin{array}{c}\hfill {\alpha }_{121}=arccos((C_{11}^2+C_{21}^2-p_3^2)/\left(2C_{11}{C}_{21}\right));\end{array}$$

(44)

$$\begin{array}{c}\hfill {\alpha }_{341}=arccos((C_{31}^2+C_{41}^2-p_3^2)/\left(2C_{31}{C}_{41}\right));\end{array}$$

(45)

$$\begin{array}{c}\hfill {\alpha }_{561}=arccos((C_{51}^2+C_{61}^2-p_3^2)/\left(2C_{51}{C}_{61}\right));\end{array}$$

(46)

$$\begin{array}{c}\hfill {\alpha }_{781}=arccos((C_{71}^2+C_{81}^2-p_3^2)/\left(2C_{71}{C}_{81}\right));\end{array}$$

(47)

$$\begin{array}{c}\hfill {\alpha }_{11}=arccos((p_3^2+C_{11}^2-C_{21}^2)/\left(2C_{11}{p}_3\right));\end{array}$$

(48)

$$\begin{array}{c}\hfill {\alpha }_{21}=arccos((p_3^2+C_{21}^2-C_{11}^2)/\left(2C_{21}{p}_3\right));\end{array}$$

(49)

$$\begin{array}{c}\hfill {\alpha }_{31}=arccos((p_3^2+C_{31}^2-C_{41}^2)/\left(2C_{31}{p}_3\right));\end{array}$$

(50)

$$\begin{array}{c}\hfill {\alpha }_{41}=arccos((p_3^2+C_{41}^2-C_{31}^2)/\left(2C_{41}{p}_3\right));\end{array}$$

(51)

$$\begin{array}{c}\hfill {\alpha }_{51}=arccos((p_3^2+C_{51}^2-C_{61}^2)/\left(2C_{51}{p}_3\right));\end{array}$$

(52)

$$\begin{array}{c}\hfill {\alpha }_{61}=arccos((p_3^2+C_{61}^2-C_{51}^2)/\left(2C_{61}{p}_3\right));\end{array}$$

(53)

$$\begin{array}{c}\hfill {\alpha }_{71}=arccos((p_3^2+C_{71}^2-C_{81}^2)/\left(2C_{71}{p}_3\right));\end{array}$$

(54)

$$\begin{array}{c}\hfill {\alpha }_{81}=arccos((p_3^2+C_{81}^2-C_{71}^2)/\left(2C_{81}{p}_3\right)).\end{array}$$

(55)

With the obtained ${\alpha }_{ij}$, the Z components of the length $C_{ij}$ can be computed as a function of $C_{ij}$:

$$\begin{array}{c}\hfill C_{11z}=-C_{11}cos\left({\alpha }_{11}\right);C_{21z}=C_{21}cos\left({\alpha }_{21}\right);C_{31z}=-C_{31}cos\left({\alpha }_{31}\right);C_{41z}=C_{41}cos\left({\alpha }_{41}\right);\end{array}$$

(56)

$$\begin{array}{c}\hfill C_{51z}=-C_{51}cos\left({\alpha }_{51}\right);C_{61z}=C_{61}cos\left({\alpha }_{61}\right);C_{71z}=-C_{71}cos\left({\alpha }_{71}\right);C_{81z}=C_{81}cos\left({\alpha }_{81}\right).\end{array}$$

(57)

Then, the angles that $O_A-X_A{Y}_A{Z}_A$ forms with respect to $O_B-X_B{Y}_B{Z}_B$ in X (${\alpha }_X$) and Y (${\alpha }_Y$) are obtained, and $\psi$ and ${\alpha }_A$ (shown in Figure 10) can be calculated.

$$\begin{array}{c}\hfill {\alpha }_X=arctan\left(\right(|C_{5z}-C_{7z}\left|\right)/p_1);{\alpha }_Y=arctan\left(\right(|C_{3z}-C_{1z}\left|\right)/p_1);\end{array}$$

(58)

$$\begin{array}{c}\hfill \psi =arctan(\left(tan\left({\alpha }_Y\right)\right)/\left(tan\left({\alpha }_X\right)\right);\end{array}$$

(59)

$$\begin{array}{c}\hfill {\alpha }_A=arctan(tan\left({\alpha }_X\right)/cos\left(\psi \right))=arctan(tan\left({\alpha }_Y\right)/sin\left(\psi \right)).\end{array}$$

(60)

In conclusion, the four angles ${\gamma }_a$, ${\gamma }_b$, ${\gamma }_c$, and ${\gamma }_d$ (shown in Figure 10) can be obtained as follows:

$$\begin{array}{c}\hfill {\gamma }_a=arccos(\left(p_{2}cos\left(\psi \right)\right)/\left(C_{31}sin\left({\alpha }_{31}\right)\right))-\psi ;\end{array}$$

(61)

$$\begin{array}{c}\hfill {\gamma }_b=arccos(\left(p_{2}cos\left(\psi \right)\right)/\left(C_{11}sin\left({\alpha }_{11}\right)\right));\end{array}$$

(62)

$$\begin{array}{c}\hfill {\gamma }_c=arccos(\left(p2cos(\pi /2-\psi )\right)/\left(C_{51}sin\left({\alpha }_{51}\right)\right))-\pi /2+\psi ;\end{array}$$

(63)

$$\begin{array}{c}\hfill {\gamma }_d=\pi /2-{\gamma }_c-arccos(\left(p2sin\left(\psi \right)\right)/\left(C_{71}sin\left({\alpha }_{71}\right)\right)).\end{array}$$

(64)

Using the formulations in the previous equations, the X and Y components of the $C_{ij}$ are obtained:

$$\begin{array}{c}\hfill C_{11x}=-C_{11}sin\left({\alpha }_{11}\right)cos({\gamma }_b+\psi );C_{11y}=-C_{11}sin\left({\alpha }_{11}\right)sin({\gamma }_b+\psi );\end{array}$$

(65)

$$\begin{array}{c}\hfill C_{21x}=C_{11x};C_{21y}=C_{11y};C_{31x}=C_{31}sin\left({\alpha }_{31}\right)cos\left({\gamma }_a\right);\end{array}$$

(66)

$$\begin{array}{c}\hfill C_{31y}=-C_{31}sin\left({\alpha }_{31}\right)sin\left({\gamma }_a\right);C_{41x}=C_{31x};C_{41y}=C_{31y};\end{array}$$

(67)

$$\begin{array}{c}\hfill C_{51x}=C_{51}sin\left({\alpha }_{51}\right)sin\left({\gamma }_c\right);C_{51y}=-C_{51}sin\left({\alpha }_{51}\right)cos\left({\gamma }_c\right);\end{array}$$

(68)

$$\begin{array}{c}\hfill C_{61x}=C_{51x};C_{61y}=C_{51y};C_{71x}=C_{71}sin\left({\alpha }_{71}\right)sin({\gamma }_d+{\gamma }_c);\end{array}$$

(69)

$$\begin{array}{c}\hfill C_{71y}=-C_{71}sin\left({\alpha }_{71}\right)cos({\gamma }_d+{\gamma }_c);C_{81x}=C_{71x};C_{81y}=C_{71y}.\end{array}$$

(70)

Now, it is possible to compute the displacement of the centre of the mobile system $O_A$ ($x_1$, $y_1$, $z_1$) and of the point P ($x_P$, $y_P$, $z_P$) of the applied external forces:

$$\begin{array}{c}\hfill x_1=|C_{31x}|-|C_{11x}|;y_1=|C_{71y}|-|C_{51y}|;\end{array}$$

(71)

$$\begin{array}{c}\hfill z_1=p_3/2-\left(\right|C_{51z}|+|C_{71z}|+|C_{31z}|+|C_{11z}\left|\right)/4.\end{array}$$

(72)

$$\begin{array}{c}\hfill x_P=x_1+J_{1}sin\left({\alpha }_Y\right);y_P=y_1+J_{1}sin\left({\alpha }_X\right);z_P=z_1-J_1(1-cos\left({\alpha }_A\right))+J_3.\end{array}$$

(73)

5.2. Vector of the Cable’s Tension

All formulations shown in the last sub-section are functions of the cable’s length $C_{ij}$, computed with the following equations.

In our proposed idea, the cables are supposed to be non-extensible. Figure 11 (left) shows a planar sketch of the behaviour of the entire sensor in the two conditions (e.g., $j=0$ and $j=1$). Each cable is connected with a spring with a stiffness coefficient $k_i$. The variation in the length $C_{ij}$ is a function of the displacement in each spring of the sensor:

$$\begin{array}{c}\hfill \Delta C_{i10}=\Delta L_{mi10};\Delta C_{i10}=C_{i1}-C_{i0};\Delta L_{mi10}=L_{mi1}-L_{mi0};\end{array}$$

(74)

$$\begin{array}{c}\hfill C_{i1}=C_{i0}+L_{mi1}-L_{mi0}.\end{array}$$

(75)

In Equation (75), the cable’s length in the condition j = 1 is obtained. $L_{mij}$ is the difference between the length of the spring i (in the condition j) and its initial length. The values of $C_{ij}$ in the initial conditions ($j=0$) are obtained as follows:

$$\begin{array}{c}\hfill C_{10}=C_{20}=C_{30}=C_{40}=C_{50}=C_{60}=C_{70}=C_{80}=\sqrt{{(p_3/2)}^2+{\left(p_2\right)}^2};\end{array}$$

(76)

$$\begin{array}{c}\hfill {\alpha }_{10}={\alpha }_{20}={\alpha }_{30}={\alpha }_{40}={\alpha }_{50}={\alpha }_{60}={\alpha }_{70}={\alpha }_{80}=arctan(p_3/2p_2).\end{array}$$

(77)

Using the same approach, it is possible to calculate the ideal cable tension near the spring in the two conditions $T_{i1m}$ and $T_{i0m}$:

$$\begin{array}{c}\hfill T_{i1m}=k_i{L}_{mi1};T_{i0m}=k_i{L}_{mi0};\Delta T_{i10m}=T_{i1m}-T_{i0m}.\end{array}$$

(78)

Figure 11 (right) shows the tensions of cables 1 and 2. Based on the forces shown in the picture, the cable’s tension near the mobile part ($T_{11p}$ or $T_{21p}$) is function of the force of the spring ($T_{11m}$ or $T_{21m}$).

In order to calculate the cables’ tension on the mobile part, the following formulations can be obtained for cables 1 and 2. $\mu$ is the friction coefficient between the cable and the pulley. If the pulley is fixed, the cable crawls on the cylindrical surface of the pulley. This is the case analysed in this paper.

$$\begin{array}{c}\hfill (T+dT)cos(d\sigma /2)-Tcos(d\sigma /2)-d{F}_T=0;\end{array}$$

(79)

$$\begin{array}{c}\hfill d{F}_N-(T+dT)sin(d\sigma /2)-Tsin(d\sigma /2)=0.\end{array}$$

(80)

$$\begin{array}{c}\hfill cos(d\sigma /2)\approx 1;sin(d\sigma /2)\approx d\sigma /2;\end{array}$$

(81)

$$\begin{array}{c}\hfill dT=d{F}_T;d{F}_N-Td\sigma =0;d{F}_T=\mu d{F}_N;\mu Td\sigma =dT;\end{array}$$

(82)

$$\begin{array}{c}\hfill T_2=T_1{e}^{\mu \lambda }.\end{array}$$

(83)

$$\begin{array}{c}\hfill T_{11p}=T_{11m}{e}^{\mu (3\pi /2-{\alpha }_{11})};T_{21p}=T_{21m}{e}^{\mu (pi/2+{\alpha }_{21})};T_{31p}=T_{31m}{e}^{\mu (3\pi /2-{\alpha }_{31})};\end{array}$$

(84)

$$\begin{array}{c}\hfill T_{41p}=T_{41m}{e}^{\mu (pi/2+{\alpha }_{41})};T_{51p}=T_{51m}{e}^{\mu (3\pi /2-{\alpha }_{51})};T_{61p}=T_{61m}{e}^{\mu (pi/2+{\alpha }_{61})};\end{array}$$

(85)

$$\begin{array}{c}\hfill T_{71p}=T_{71m}{e}^{\mu (3\pi /2-{\alpha }_{71})};T_{81p}=T_{81m}{e}^{\mu (pi/2+{\alpha }_{81})};\end{array}$$

(86)

$$\begin{array}{c}\hfill T_{10p}=T_{10m}{e}^{\mu (3\pi /2-{\alpha }_{10})};T_{20p}=T_{20m}{e}^{\mu (pi/2+{\alpha }_{20})};T_{30p}=T_{30m}{e}^{\mu (3\pi /2-{\alpha }_{30})};\end{array}$$

(87)

$$\begin{array}{c}\hfill T_{40p}=T_{40m}{e}^{\mu (pi/2+{\alpha }_{40})};T_{50p}=T_{50m}{e}^{\mu (3\pi /2-{\alpha }_{50})};T_{60p}=T_{60m}{e}^{\mu (pi/2+{\alpha }_{60})};\end{array}$$

(88)

$$\begin{array}{c}\hfill T_{70p}=T_{70m}{e}^{\mu (3\pi /2-{\alpha }_{70})};T_{80p}=T_{80m}{e}^{\mu (pi/2+{\alpha }_{80})};\end{array}$$

(89)

The general equation can be obtained as follows:

If $i=1,3,5,7$:

$$\begin{array}{c}\hfill T_{ijp}=T_{ijm}{e}^{\mu (3\pi /2-{\alpha }_{ij})};\end{array}$$

(90)

If $i=2,4,6,8$:

$$\begin{array}{c}\hfill T_{ijp}=T_{ijm}{e}^{\mu (pi/2+{\alpha }_{ij})}.\end{array}$$

(91)

The vector of the cable tension can be obtained using the following equation:

$$\begin{array}{c}\hfill \Delta T_{1p}=T_{11p}-T_{10p};\Delta T_{2p}=T_{21p}-T_{20p};\Delta T_{3p}=T_{31p}-T_{30p};\Delta T_{4p}=T_{41p}-T_{40p};\end{array}$$

(92)

$$\begin{array}{c}\hfill \Delta T_{5p}=T_{51p}-T_{50p};\Delta T_{6p}=T_{61p}-T_{60p};\Delta T_{7p}=T_{71p}-T_{70p};\Delta T_{8p}=T_{81p}-T_{80p}.\end{array}$$

(93)

$$\begin{array}{c}\hfill \Delta {\mathbf{T}}_p={[\Delta T_{1p}\Delta T_{2p}\Delta T_{3p}\Delta T_{4p}\Delta T_{5p}\Delta T_{6p}\Delta T_{7p}\Delta T_{8p}]}^T.\end{array}$$

(94)

The final equation to consider in order to find the external forces and torques is:

$$\begin{array}{c}\hfill {\mathbf{W}}_p=-{\mathbf{S}}_{IIj}\Delta {\mathbf{T}}_p.\end{array}$$

(95)

6. Model Validation and Physical Implementation with Two Test Bench Prototypes

6.1. Model Validation

In order to test how much the physical dimensions of the mechanism and the friction on the cables influence the proposed model, we decided to test our model in two test benches of different dimensions of the mechanism and with different levels of cable friction. Our basic idea is that if our model gives good answers in different dimensions of the mechanism, this would confirm the feasibility of recreating our system in reduced dimensions and its ability to be used (in the near future) inside a surgical instrument of a maximum diameter of 10 mm. Test bench I (TBI) is the bigger and planar mechanism. Test bench II (TBII) is the smaller spatial mechanism. The dimensions of the two test benches used are shown in

Table 1. Dimensions of the test bench prototypes. Measures ($p_1$, $p_2$, $p_3$, $p_4$, $p_6$, $p_{10}$) are shown in Figure 8.

	${\mathit{p}}_1$ (mm)	${\mathit{p}}_2$ (mm)	${\mathit{p}}_3$ (mm)	${\mathit{p}}_4$ (mm)	${\mathit{p}}_6$ (mm)	${\mathit{p}}_{10}$ (mm)	$\mathit{\mu }$
TBI	23	85	100	43	7	82	0
TBII	16	8.75	13.5	11.8	12	2.5	0.3; 0.25 [34]

.

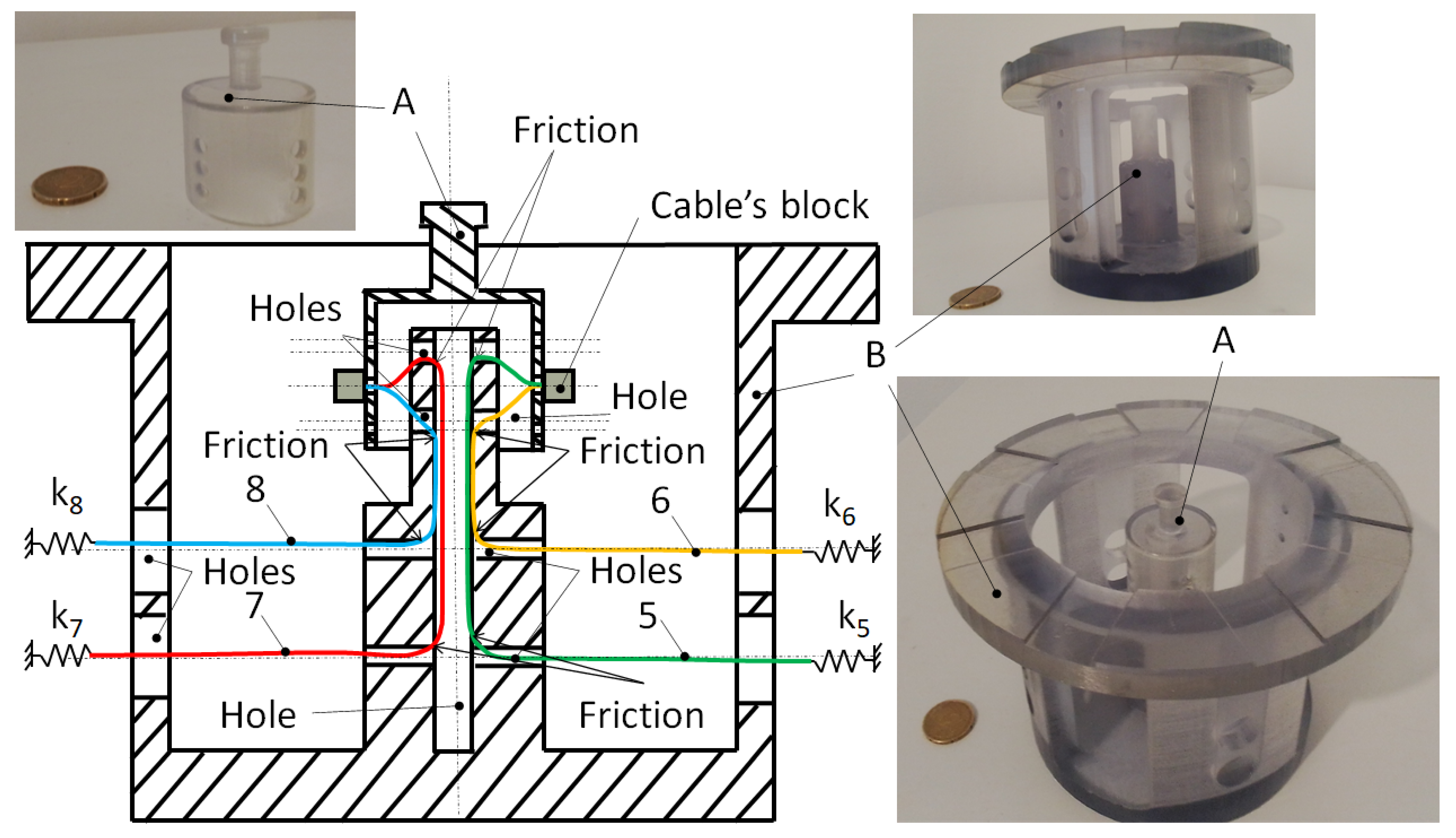
6.2. Planar Test Bench Prototype: TBI

Figure 12 shows the scheme of TBI, and Figure 13 shows the prototype developed to validate and implement the proposed cable-driven mechanism. In TBI, we analysed the planar application using four cables. Part B is fixed and part A is the mobile part. Pulleys are attached to part B, and four cables connect part A with part B. Four springs are connected to the four cables, and thanks to their movements, the motion of point P is found. Another cable connects the applied load to point P. The spherical joints are attached between the mobile part A and the planar base (fixed plane) in order to enable the motion of part A in the plane, reducing friction. The pulleys in the Figure 13 are used to validate the behaviour of the mechanism without friction acting on the cables.

6.3. Spatial Test Bench Prototype: TBII

Figure 14 shows the TBII prototype realized with a 3D printer and used to study the sensing mechanism. Part A is the mobile part consisting of a hollow cylinder with radial holes for the cable connections and a central shaft for the application of the external forces. Part B consists of a central shaft and an external hollow cylinder fixed on a plane. Part B includes holes that facilitate the connection with the cables. Part A is assembled on the central shaft of part B, in its zone with a minimum diameter. A planar section is shown in Figure 14 with cables $5,6,7,8$ and stiffness coefficients $k5,k6,k7,k8$. Two cable blocks are used to fix cables 6 and 5 and cables 8 and 7 to part A. The motion of part A can be evaluated using the displacement of the springs.

Figure 15 shows the TBII used for the experiments. An external force F is applied in the YZ plane, modifying the cables’ tension. Measuring the displacement of the springs allows us to find the displacement of the point of the applied force F, and thanks to Equation (94), the vector of the cables’ tension ($\Delta {\mathbf{T}}_p$) is computed. Using Equation (95), the external forces and torques are measured.

6.4. Springs and Cables

In order to test the sensitive mechanism, we tried many types of cables and springs, and in the following, we will show only the selection used in the experiments. The material of the cable is nylon, with a diameter of 0.6 mm. The dimensions of the spring used in the experiments are shown in

Table 2. Dimensions of the type of spring used in the experiment: $D_e$ is the external diameter; d is the diameter of the wire; $L_m$ is the initial length of the spring; n is the number of wraps; k is the stiffness coefficient.

	${\mathit{D}}_{\mathit{e}}$ (mm)	d (mm)	${\mathit{L}}_{\mathit{m}}$ (mm)	$\mathit{n}$	k (N/mm)
Spring	9.4	1	24.8	25	0.6786

. The stiffness coefficient of the spring is calculated by applying a load (after a preload condition) and measuring the displacement of the spring obtained with the applied load.

The springs are connected between the cable and external fixed connections. Manual calibration of the cable tension is performed on the external connections using screws.

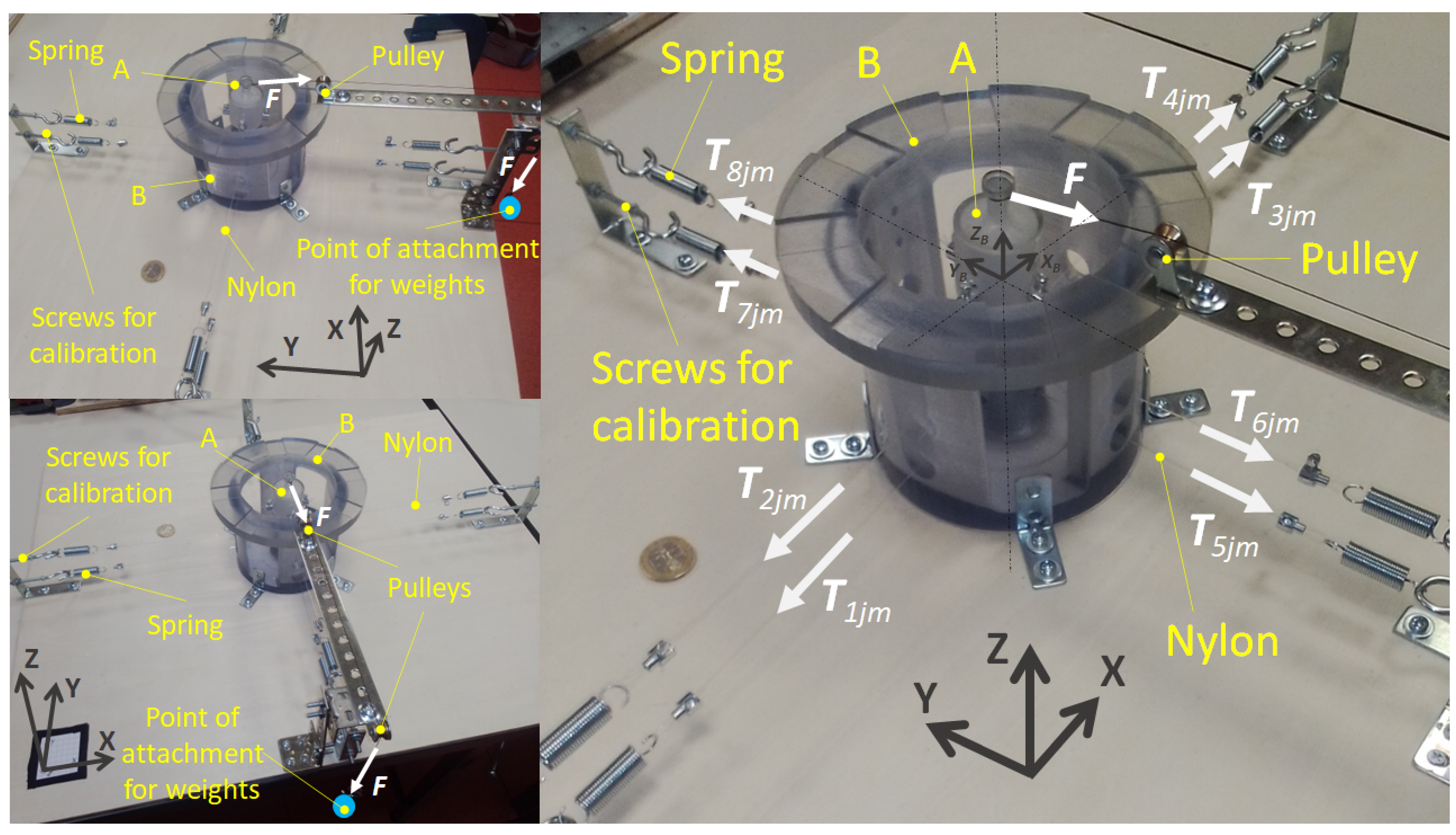
6.5. Implementation

Part B of the test bench prototype is fixed on a plane using screws. Part A is connected to part B, as described in the previous sections. In the first step, we attached the nylon cable to part A, after passing the cables through part B (in the pulleys of TBI or in the holes of TBII). An external force F is applied on part A, as shown in Figure 13 and Figure 15. Force is created by adding different weights to the point of attachment for the weights, shown in Figure 13 and Figure 15. In each experiment using TBI or TBII, we performed the same process, described as follows:

1

Attachment of the spring to the cable;

2

Attachment of the spring to the fixed part;

3

Centring of part A and calibration using screws in the fixed part;

4

Measuring the spring’s length in the condition $j=0$;

5

Applying weights to the point of attachment for the weights;

6

Measuring the spring’s length in the condition $j=1$.

In each test (TBI and TBII), we applied loads in the sequence shown in

Table 3. Sequence of the Applied Loads.

	1 (N)	2 (N)	3 (N)	4 (N)	5 (N)	6 (N)	7 (N)
TBI	6.46	7.48	8.49	9.85	10.94
TBII	3.25	4.26	5.27	6.46	7.48	8.49	9.57

.

Using the formulations shown in the previous sections, we considered only the positive cable tension values in order to transfer the information to the software that the cable is only able to pull and not to push.

7. Comparison between Measured and Calculated Forces: Results and Discussion

7.1. Results

In following, the results of the comparison between measured and calculated forces on the point P are shown. By using formulations shown in the last sections, the values shown in Table 1, Table 2 and Table 3 and Figure 16 and Figure 17 are obtained. The black points represent the measured applied loads on point P; the blue points represent the points computed using the following formulation (96) to calculate the applied resultant forces:

$$\begin{array}{c}\hfill F_{calculated}=\sqrt{F_X^2+F_Y^2+F_Z^2}.\end{array}$$

(96)

where $F_X$, $F_Y$, and $F_Z$ are the first three elements of the vector ${\mathbf{W}}_{Pj}$.

7.2. Discussion

Figure 16 shows the comparison between measured and computed external forces on the point P if the planar TBI is used. Figure 17 shows the same situation in which TBII is used. In TBI, it seems that if the sequence of load increases, the error is reduced. A different behaviour is noted in TBII, in which the error seems to have a more constant behaviour, maybe influenced by the friction.

In TBII, it is possible to note a maximum absolute error of around 0.64 N and a minimum error of around of 0.03 N if the friction coefficient $\mu =0.25$ is used. The mean of all errors obtained for the seven loads are around 0.33 N. In case of using $\mu =0.3$, the maximum absolute error is around 2 N, and a minimum error is around 0.13 N. The mean of all errors noted in each applied load is around 1.13 N. In conclusion, in TBII, the maximum percentage of relative error to calculate the external force is around $28\%$ if $\mu =0.3$ is used, and $9\%$ if $\mu =0.25$ is used. The absolute error is calculated as the difference between the measured and calculated value of the force (or displacement). The percentage of the relative error is calculated as the ratio between the absolute error and the measured value multiplied by 100.

Based on the obtained results, it is important to underline that this is a first test of these prototypes, and two points of contact between each cable and the part B are present in TBI and TBII. This generates many errors, because no pulley is used in TBII. However, the model presented in this paper gives the same behaviour of the forces in the two different test bench prototypes. This is a very good initial result and opens new possibilities for future developments of the mechanism.

8. Conclusions

In this paper, we present a new cable-driven model of an under-actuated sensing mechanism for robotic surgery and micro/macro applications, where the under-actuation is a fundamental aspect of the design. The proposed mechanism is conceived with an under-actuated system with cables and could solve the big problem of sterilization in robotic surgery, permitting the use of electronic parts in surgical instruments while avoiding their sterilization. This paper presents the first results of the implementation of the proposed model in two test bench prototypes of different dimensions. Future works are oriented toward realizing another spatial test bench with reduced dimensions and to perform other tests with digital sensors for comparison. We would like to reduce the dimensions of the test bench of the mechanism in order to implement the model in a prototype of a 10 mm diameter, which will be directly mounted on the robotic surgery tool. Furthermore, we will try to reduce friction, including pulleys, in the spatial test bench.