Shock Absorption for Legged Locomotion through Magnetorheological Leg-Stiffness Control
Abstract
1. Introduction
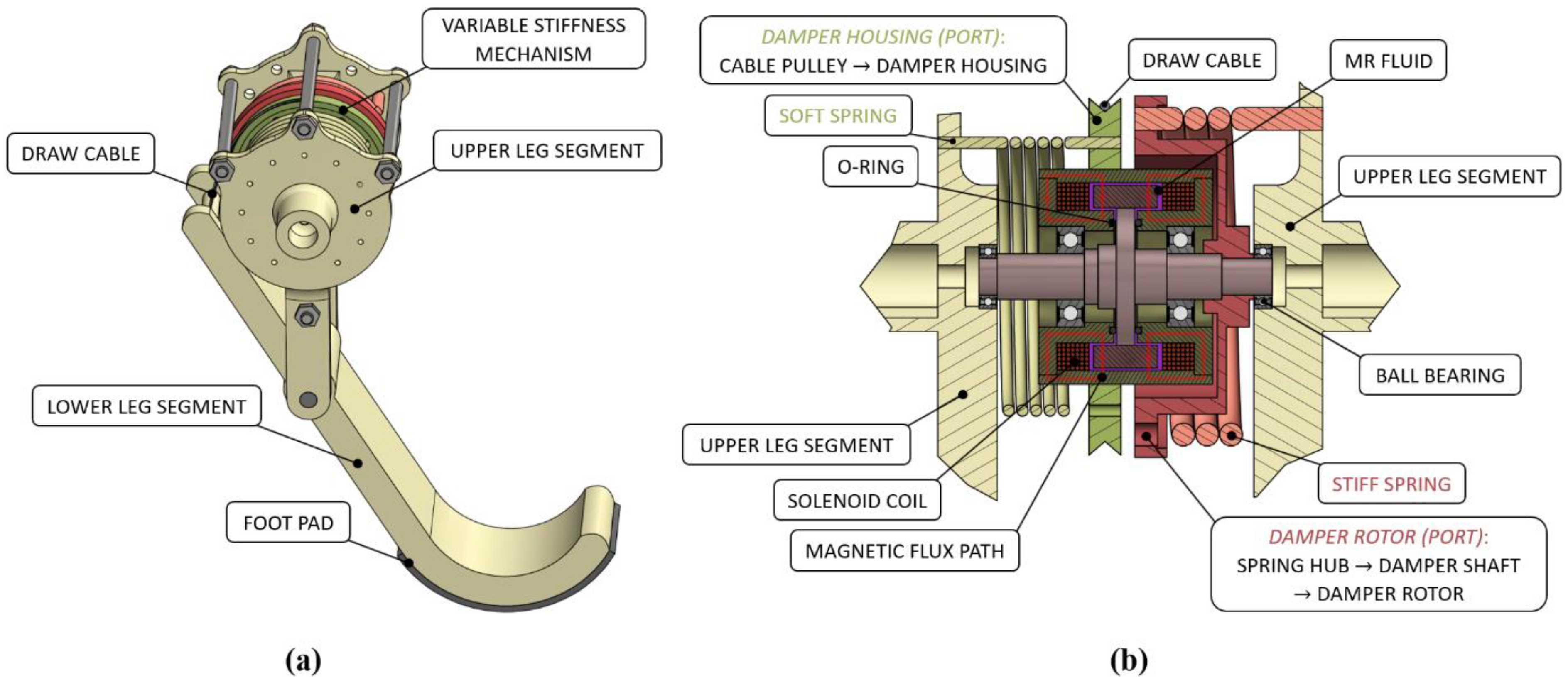
2. MRVSAL-II Mechanism
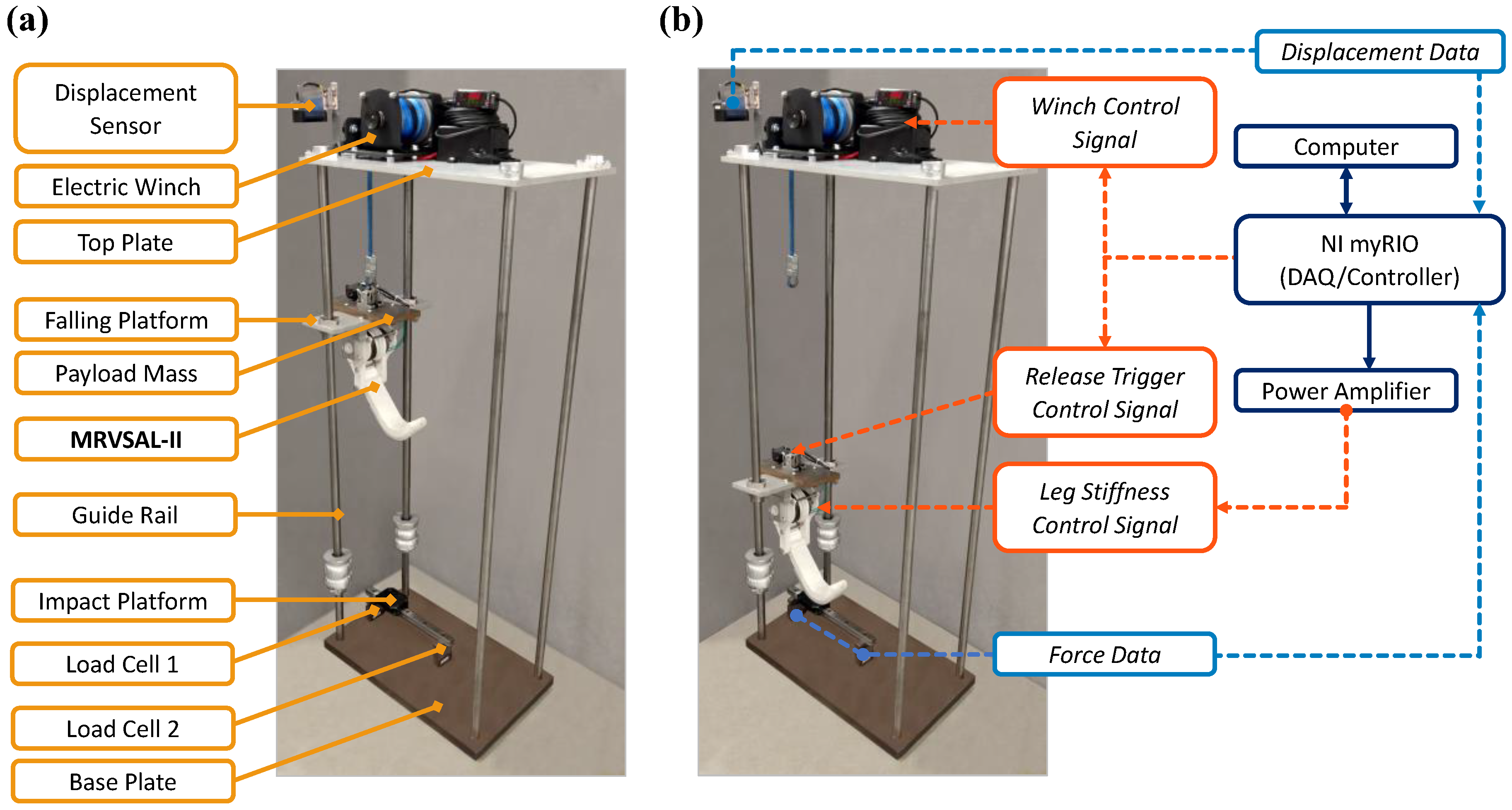
3. Experimental Setup
4. Experimental Procedure
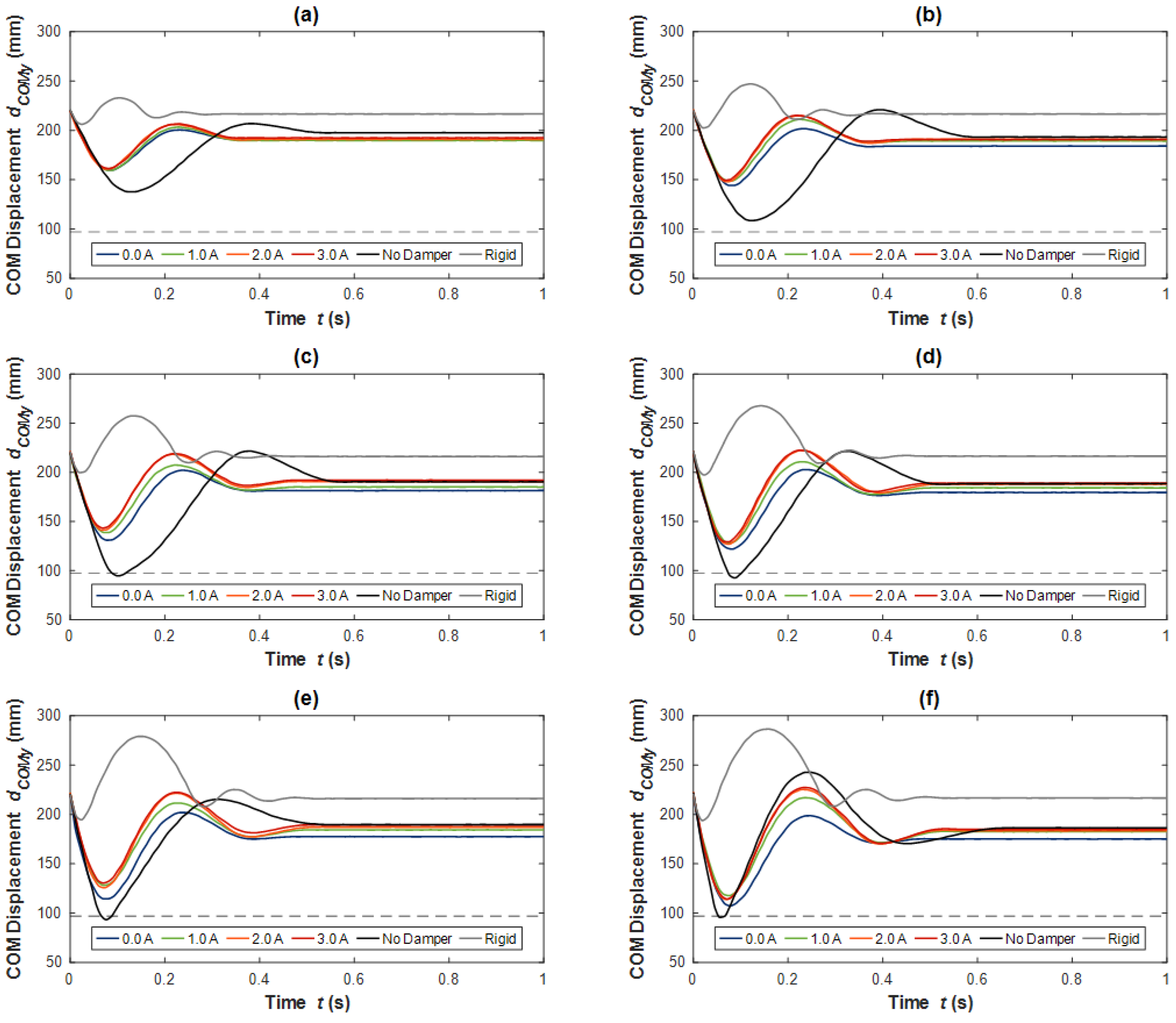
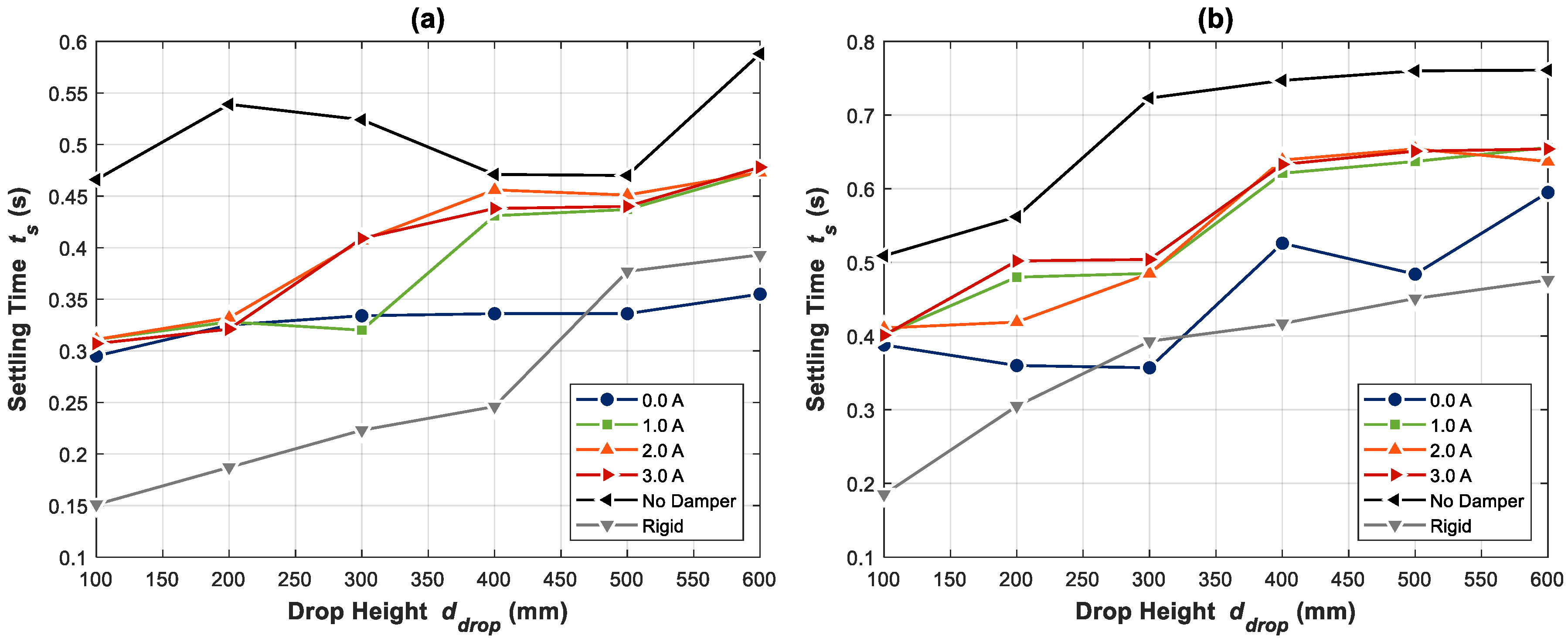
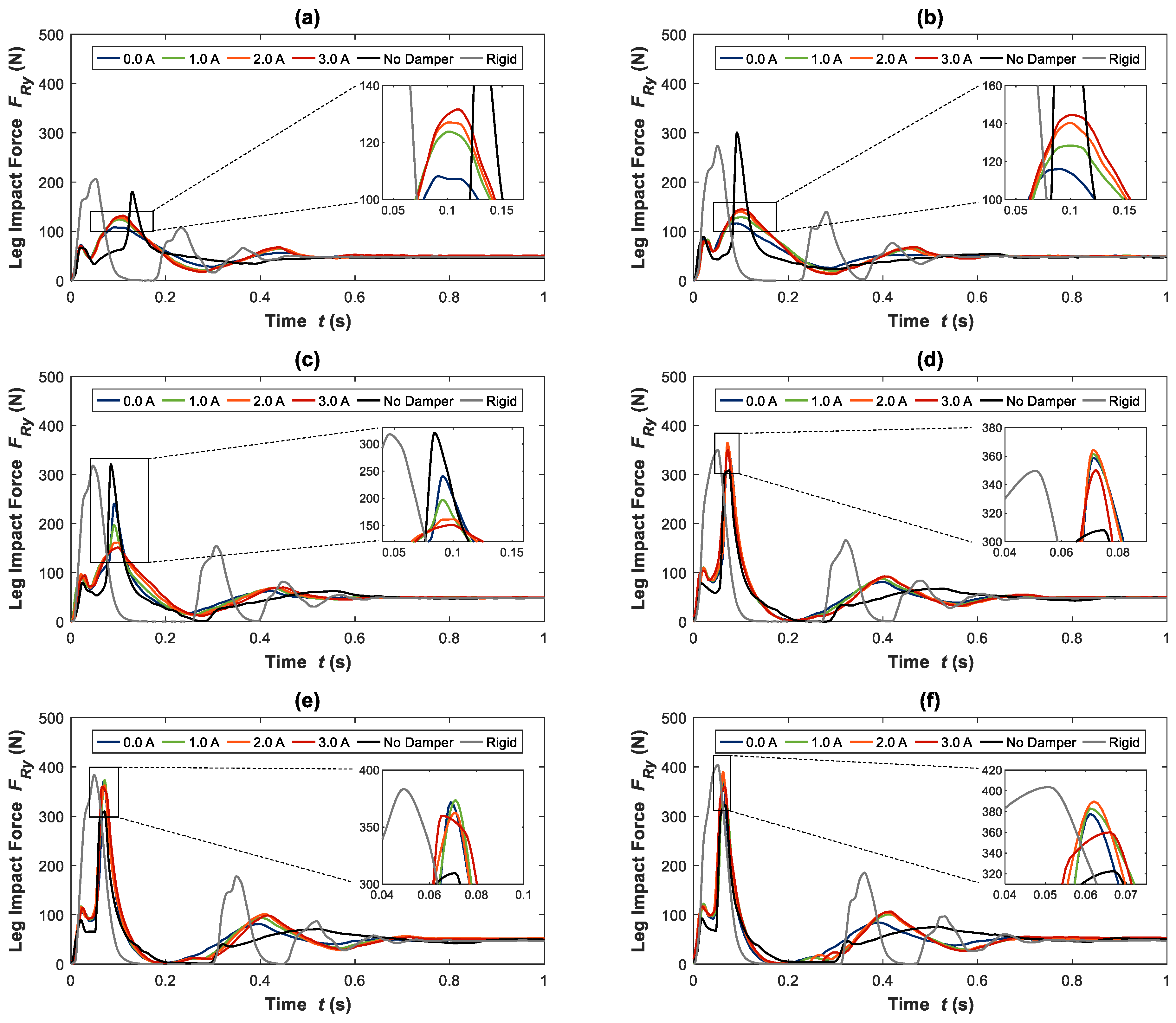
5. Passive Control
6. Impact Force Control
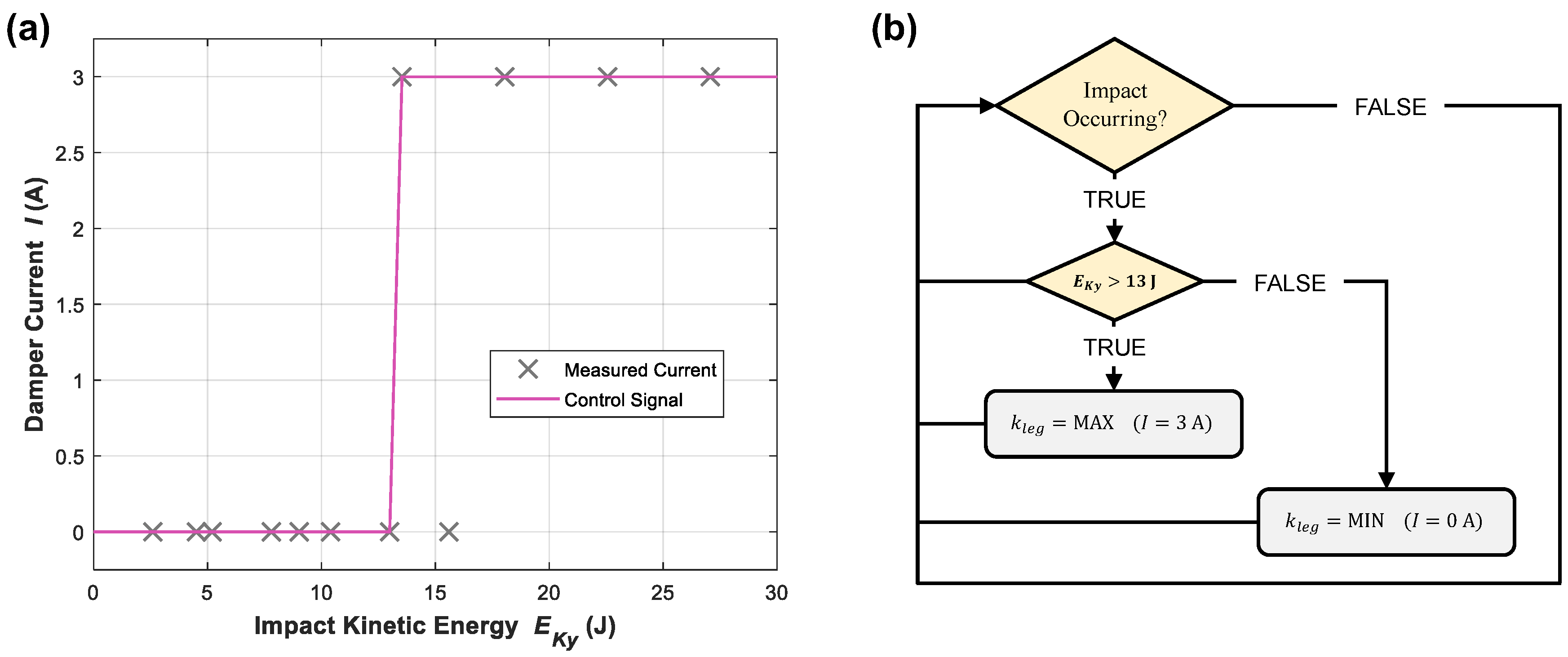
6.1. Controller Development
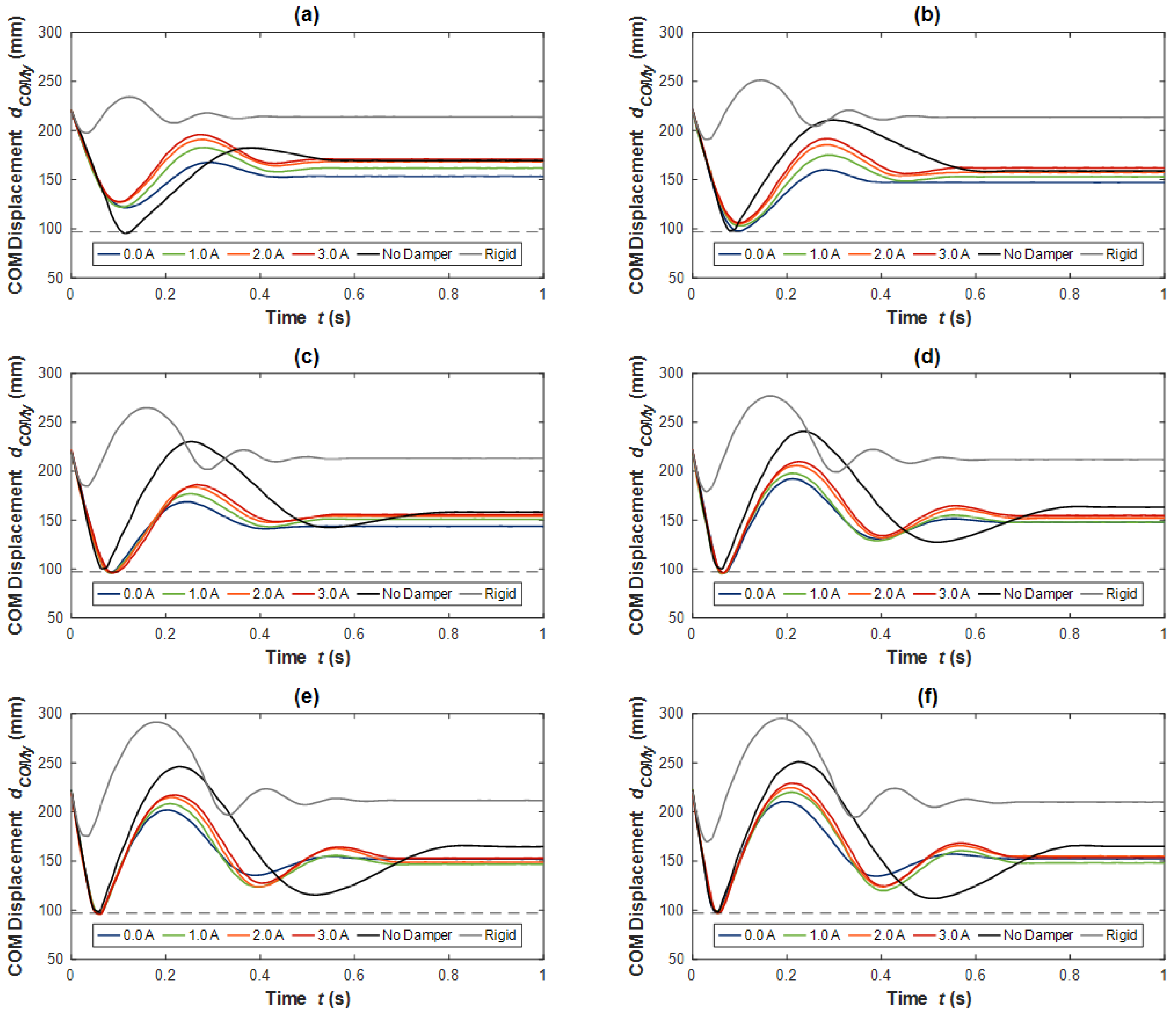
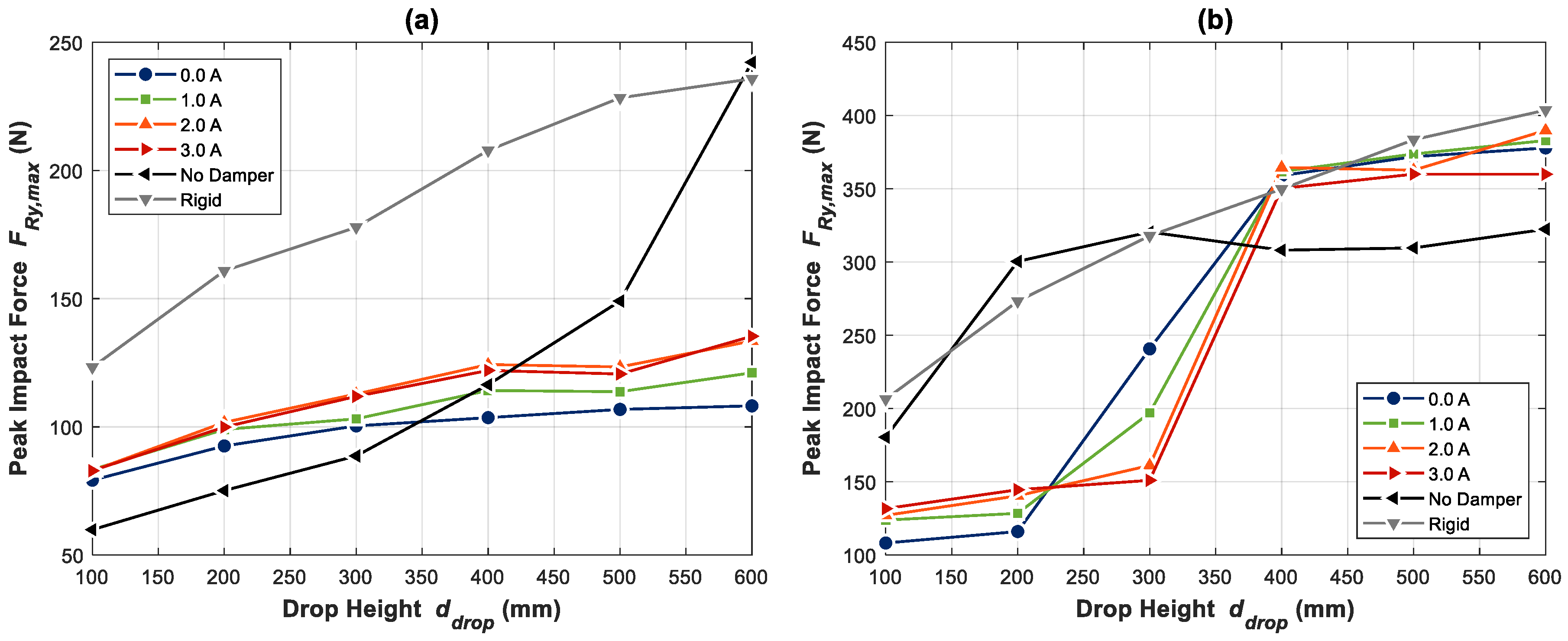
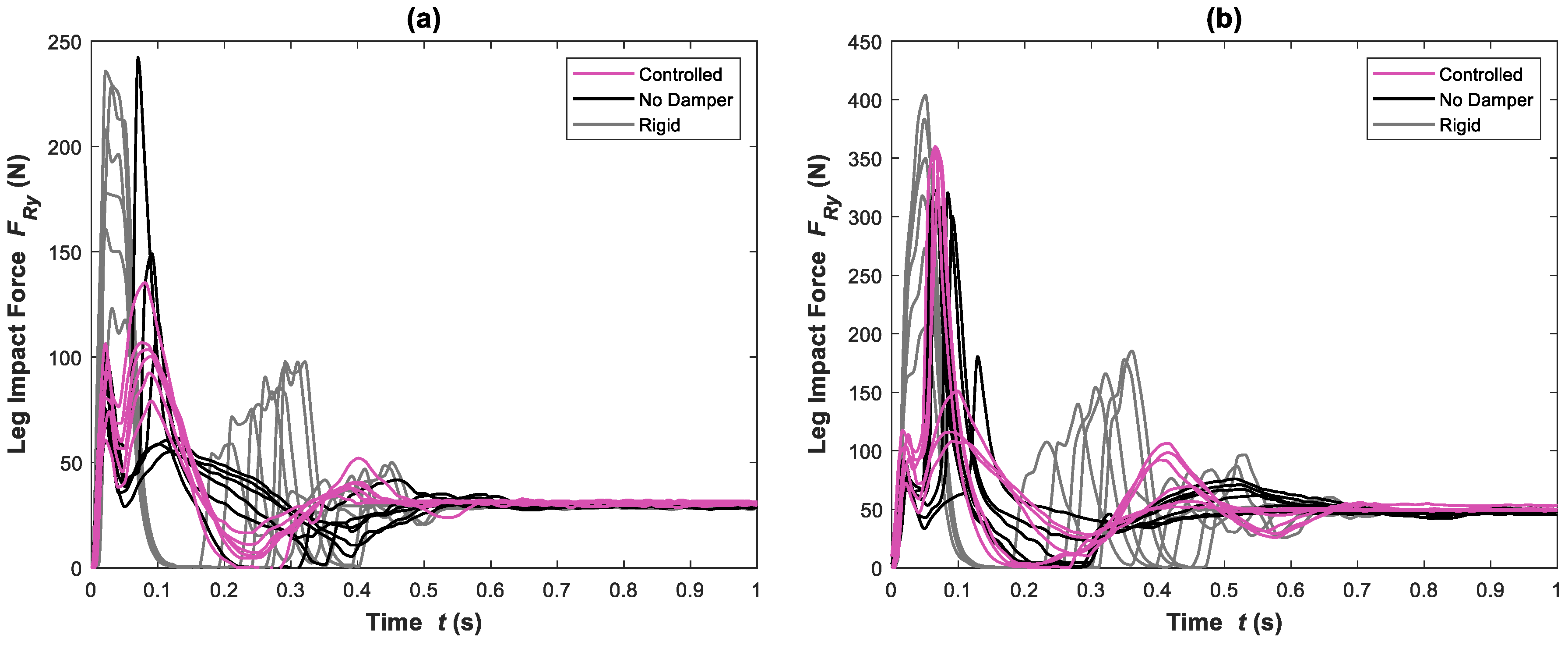
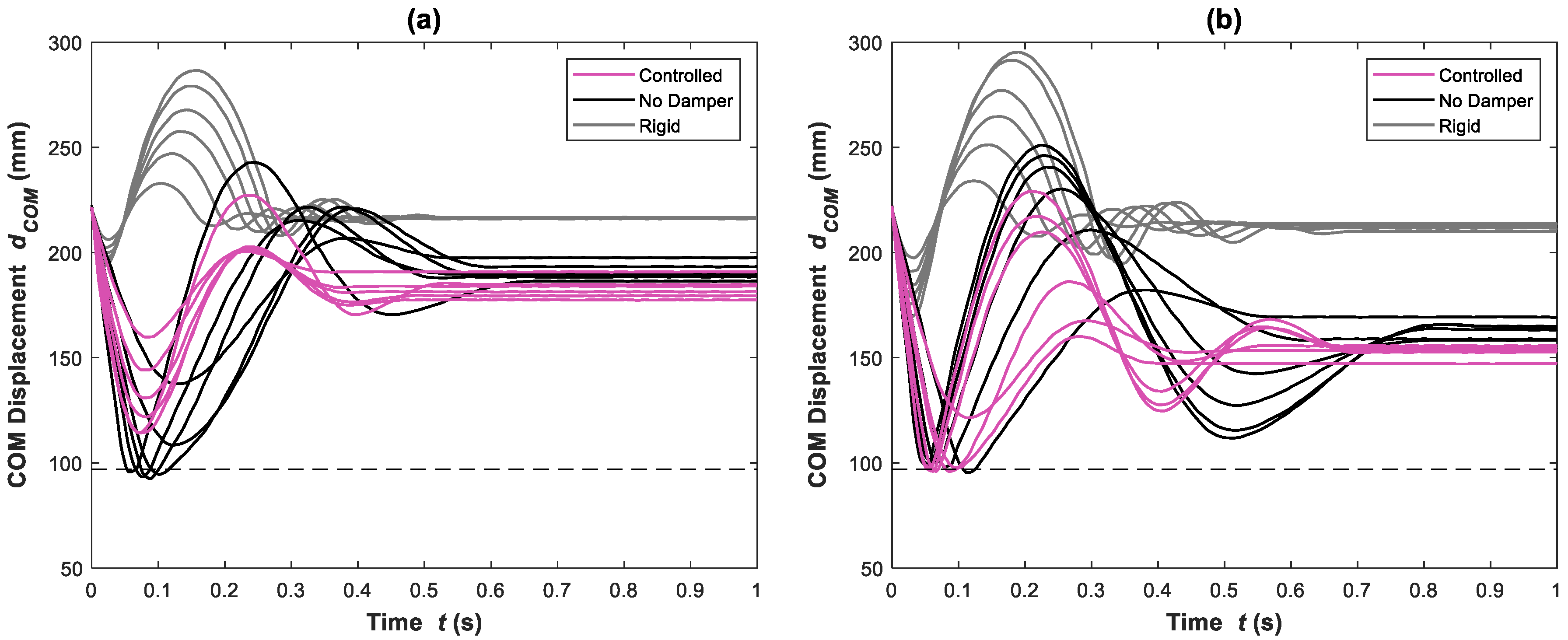
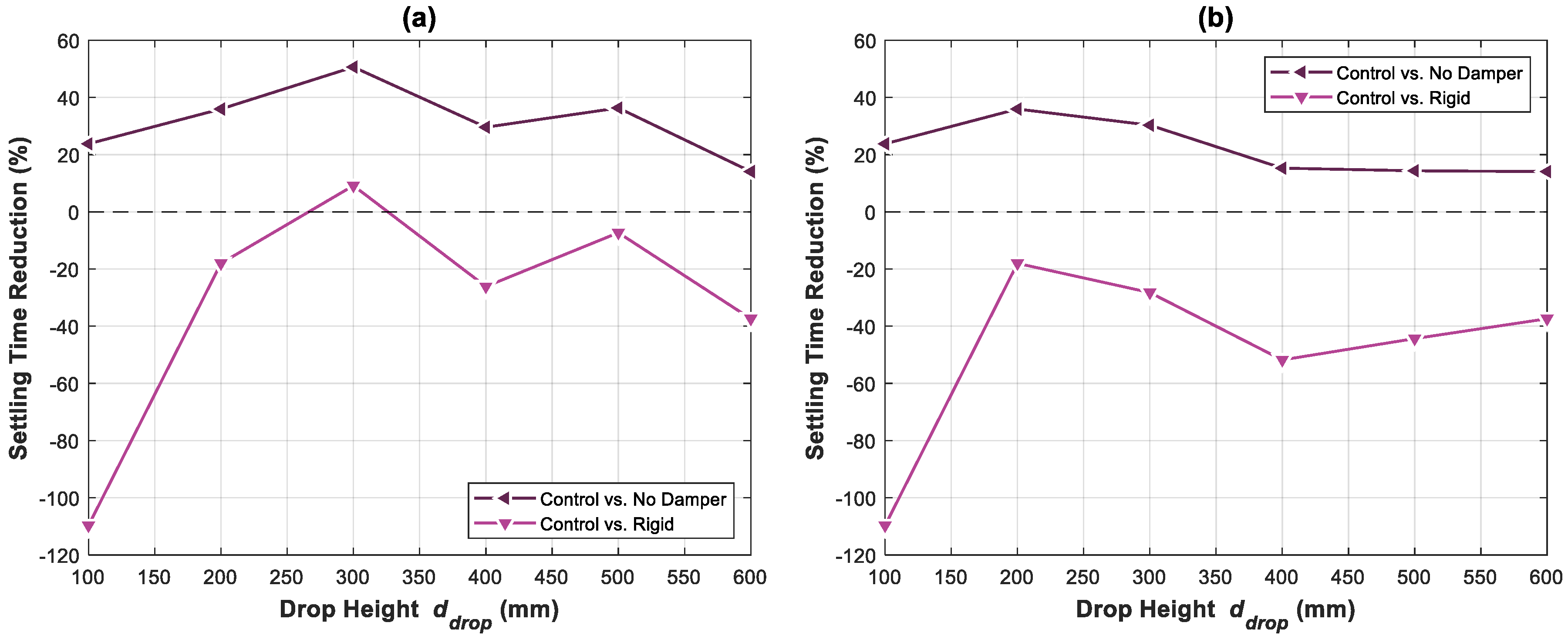
6.2. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dickinson, M.H.; Farley, C.T.; Full, R.J.; Koehl, M.A.R.; Kram, R.; Lehman, S. How animals move: An integrative view. Science 2000, 288, 100–106. [Google Scholar] [CrossRef]
- Farley, C.T.; Houdijk, H.H.P.; Van Strien, C.; Louie, M. Mechanism of leg stiffness adjustment for hopping on surfaces of different stiffnesses. J. Appl. Physiol. 1998, 85, 1044–1055. [Google Scholar] [CrossRef]
- Devita, P.; Skelly, W.A. Effect of landing stiffness on joint kinetics and energetics in the lower extremity. Med. Sci. Sport. Exerc. 1992, 24, 108–115. [Google Scholar] [CrossRef]
- Roy, M.; Tobias, S.; Reinhard, B. Muscle Preactivation Control: Simulation of Ankle Joint Adjustments at Touchdown During Running on Uneven Ground. J. Appl. Biomech. 2012, 28, 718–725. [Google Scholar] [CrossRef]
- Dyhre-Poulsen, P.; Simonsen, E.B.; Voigt, M. Dynamic control of muscle stiffness and H reflex modulation during hopping and jumping in man. J. Physiol. 1991, 437, 287–304. [Google Scholar] [CrossRef]
- Müller, R.; Ernst, M.; Blickhan, R. Leg adjustments during running across visible and camouflaged incidental changes in ground level. J. Exp. Biol. 2012, 215, 3072. [Google Scholar] [CrossRef]
- Grimmer, S.; Ernst, M.; Günther, M.; Blickhan, R. Running on uneven ground: Leg adjustment to vertical steps and self-stability. J. Exp. Biol. 2008, 211, 2989. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.; Birn-Jeffery, A.V.; Blum, Y. Human and avian running on uneven ground: A model-based comparison. J. R. Soc. Interface 2016, 13, 20160529. [Google Scholar] [CrossRef]
- Müller, R.; Blickhan, R. Running on uneven ground: Leg adjustments to altered ground level. Hum. Mov. Sci. 2010, 29, 578–589. [Google Scholar] [CrossRef] [PubMed]
- Clites, T.R.; Arnold, A.S.; Singh, N.M.; Kline, E.; Chen, H.; Tugman, C.; Billadeau, B.; Biewener, A.A.; Herr, H.M. Goats decrease hindlimb stiffness when walking over compliant surfaces. J. Exp. Biol. 2019, 222, jeb198325. [Google Scholar] [CrossRef]
- Moritz, C.T.; Farley, C.T. Passive dynamics change leg mechanics for an unexpected surface during human hopping. J. Appl. Physiol. 2004, 97, 1313–1322. [Google Scholar] [CrossRef]
- Moritz, C.T.; Greene, S.M.; Farley, C.T. Neuromuscular changes for hopping on a range of damped surfaces. J. Appl. Physiol. 2004, 96, 1996–2004. [Google Scholar] [CrossRef] [PubMed]
- Jill, L.M.-G. Kinematics and Impulse Characteristics of Drop Landings from Three Heights. Int. J. Sport Biomech. 1991, 7, 201–224. [Google Scholar] [CrossRef]
- Ozgüven, H.N.; Berme, N. An experimental and analytical study of impact forces during human jumping. J. Biomech. 1988, 21, 1061–1066. [Google Scholar] [CrossRef]
- Mizrahi, J.; Susak, Z. Analysis of parameters affecting impact force attenuation during landing in human vertical free fall. Eng. Med. 1982, 11, 141–147. [Google Scholar] [CrossRef]
- Hackney, J.M.; Clay, R.L.; James, M. Force-displacement differences in the lower extremities of young healthy adults between drop jumps and drop landings. Hum. Mov. Sci. 2016, 49, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Decker, M.J.; Torry, M.R.; Wyland, D.J.; Sterett, W.I.; Richard Steadman, J. Gender differences in lower extremity kinematics, kinetics and energy absorption during landing. Clin. Biomech. 2003, 18, 662–669. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.N.; Bates, B.T.; Dufek, J.S. Contributions of lower extremity joints to energy dissipation during landings. Med. Sci. Sport. Exerc. 2000, 32, 812–819. [Google Scholar] [CrossRef]
- Podraza, J.T.; White, S.C. Effect of knee flexion angle on ground reaction forces, knee moments and muscle co-contraction during an impact-like deceleration landing: Implications for the non-contact mechanism of ACL injury. Knee 2010, 17, 291–295. [Google Scholar] [CrossRef]
- Whitting, J.W.; Steele, J.R.; McGhee, D.E.; Munro, B.J. Effects of passive ankle dorsiflexion stiffness on ankle mechanics during drop landings. J. Sci. Med. Sport 2012, 15, 468–473. [Google Scholar] [CrossRef]
- Batterbee, D.C.; Sims, N.D.; Stanway, R.; Wolejsza, Z. Magnetorheological landing gear: 1. A design methodology. Smart Mater. Struct. 2007, 16, 2429–2440. [Google Scholar] [CrossRef]
- Choi, Y.-T.; Wereley, N.M. Shock Isolation Systems Using Magnetorheological Dampers. J. Vib. Acoust. 2008, 130, 024503. [Google Scholar] [CrossRef]
- Choi, Y.-T.; Wereley, N.M. Biodynamic Response Mitigation to Shock Loads Using Magnetorheological Helicopter Crew Seat Suspensions. J. Aircr. 2005, 42, 1288–1295. [Google Scholar] [CrossRef]
- Choi, Y.-T.; Wereley, N.M. Vibration Control of a Landing Gear System Featuring Electrorheological/Magnetorheological Fluids. J. Aircr. 2003, 40, 432–439. [Google Scholar] [CrossRef]
- Robinson, D.W.; Pratt, J.E.; Paluska, D.J.; Pratt, G.A. Series elastic actuator development for a biomimetic walking robot. In Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (Cat. No.99TH8399), Atlanta, GA, USA, 19–23 September 1999; pp. 561–568. [Google Scholar]
- Hutter, M.; Remy, C.D.; Hoepflinger, M.A.; Siegwart, R. Efficient and Versatile Locomotion With Highly Compliant Legs. IEEE/ASME Trans. Mechatron. 2013, 18, 449–458. [Google Scholar] [CrossRef]
- Vanderborght, B.; Albu-Schaeffer, A.; Bicchi, A.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.; Eiberger, O.; Friedl, W.; Ganesh, G.; et al. Variable impedance actuators: A review. Robot. Auton. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Wolf, S.; Grioli, G.; Eiberger, O.; Friedl, W.; Grebenstein, M.; Hoppner, H.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.G.; et al. Variable Stiffness Actuators: Review on Design and Components. IEEE/ASME Trans. Mechatron. 2016, 21, 2418–2430. [Google Scholar] [CrossRef]
- Christie, M.D.; Sun, S.; Deng, L.; Du, H.; Zhang, S.W.; Li, W.H. Real-time adaptive leg-stiffness for roll compensation via magnetorheological control in a legged robot. Smart Mater. Struct. 2022, 31, 045003. [Google Scholar] [CrossRef]
- Christie, M.D.; Sun, S.; Ning, D.H.; Du, H.; Zhang, S.W.; Li, W.H. A highly stiffness-adjustable robot leg for enhancing locomotive performance. Mech. Syst. Signal Process. 2019, 126, 458–468. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christie, M.D.; Sun, S.; Deng, L.; Du, H.; Zhang, S.; Li, W. Shock Absorption for Legged Locomotion through Magnetorheological Leg-Stiffness Control. Machines 2023, 11, 236. https://doi.org/10.3390/machines11020236
Christie MD, Sun S, Deng L, Du H, Zhang S, Li W. Shock Absorption for Legged Locomotion through Magnetorheological Leg-Stiffness Control. Machines. 2023; 11(2):236. https://doi.org/10.3390/machines11020236
Chicago/Turabian StyleChristie, Matthew Daniel, Shuaishuai Sun, Lei Deng, Haiping Du, Shiwu Zhang, and Weihua Li. 2023. "Shock Absorption for Legged Locomotion through Magnetorheological Leg-Stiffness Control" Machines 11, no. 2: 236. https://doi.org/10.3390/machines11020236
APA StyleChristie, M. D., Sun, S., Deng, L., Du, H., Zhang, S., & Li, W. (2023). Shock Absorption for Legged Locomotion through Magnetorheological Leg-Stiffness Control. Machines, 11(2), 236. https://doi.org/10.3390/machines11020236








