Semi-Active Vibration Control of Seat Suspension Equipped with a Variable Equivalent Inertance-Variable Damping Device
Abstract
1. Introduction
- A novel concept of the VEI–VD device is proposed and tested experimentally to verify its controllability.
- A novel semi-active force tracking controller is designed to achieve better seat vibration control.
2. VEI–VD Seat Suspension System
2.1. Motivation
2.2. System Analysis
3. VEI and VD Device Test
3.1. Prototype of VEI and VD Device
3.2. Test Design
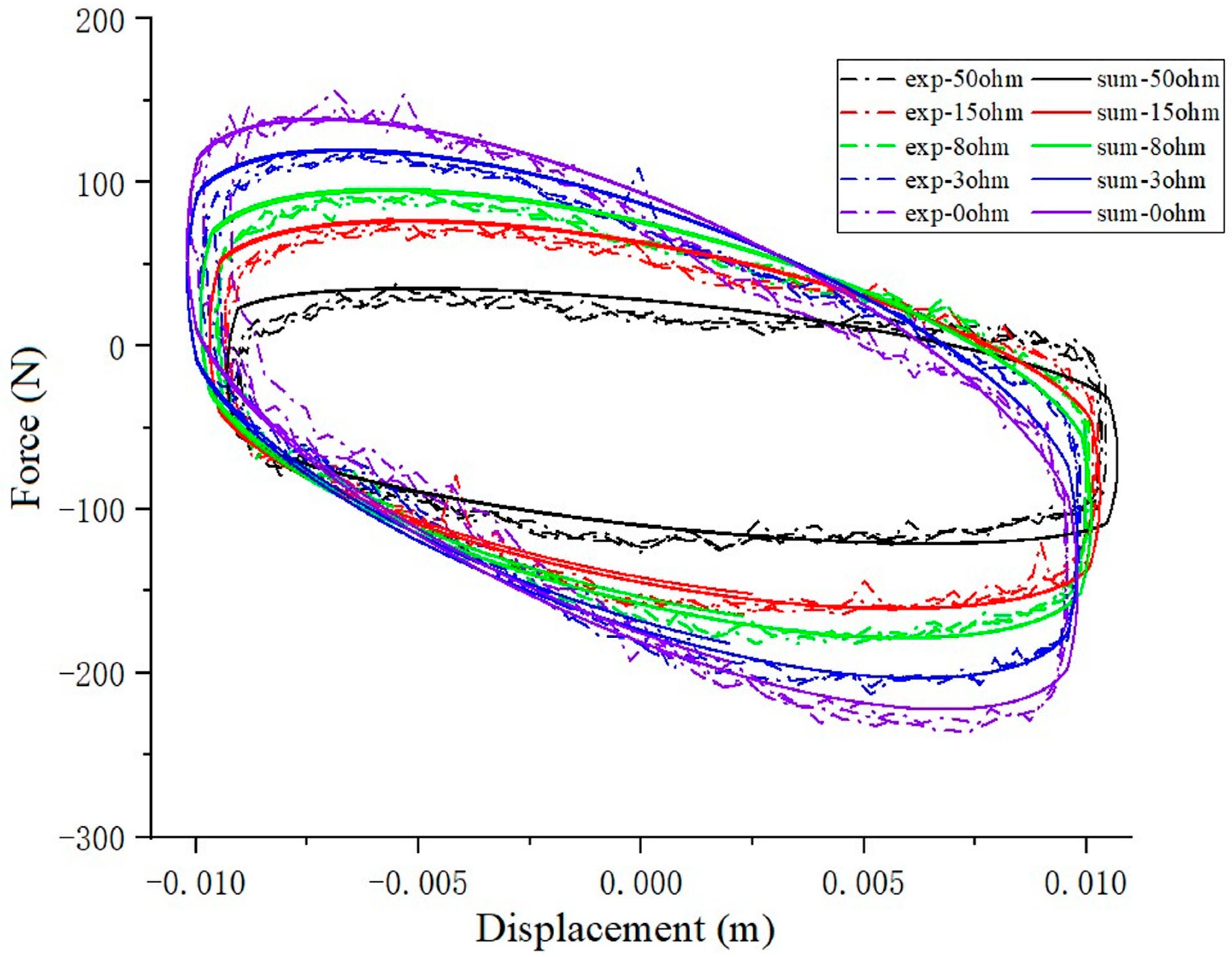
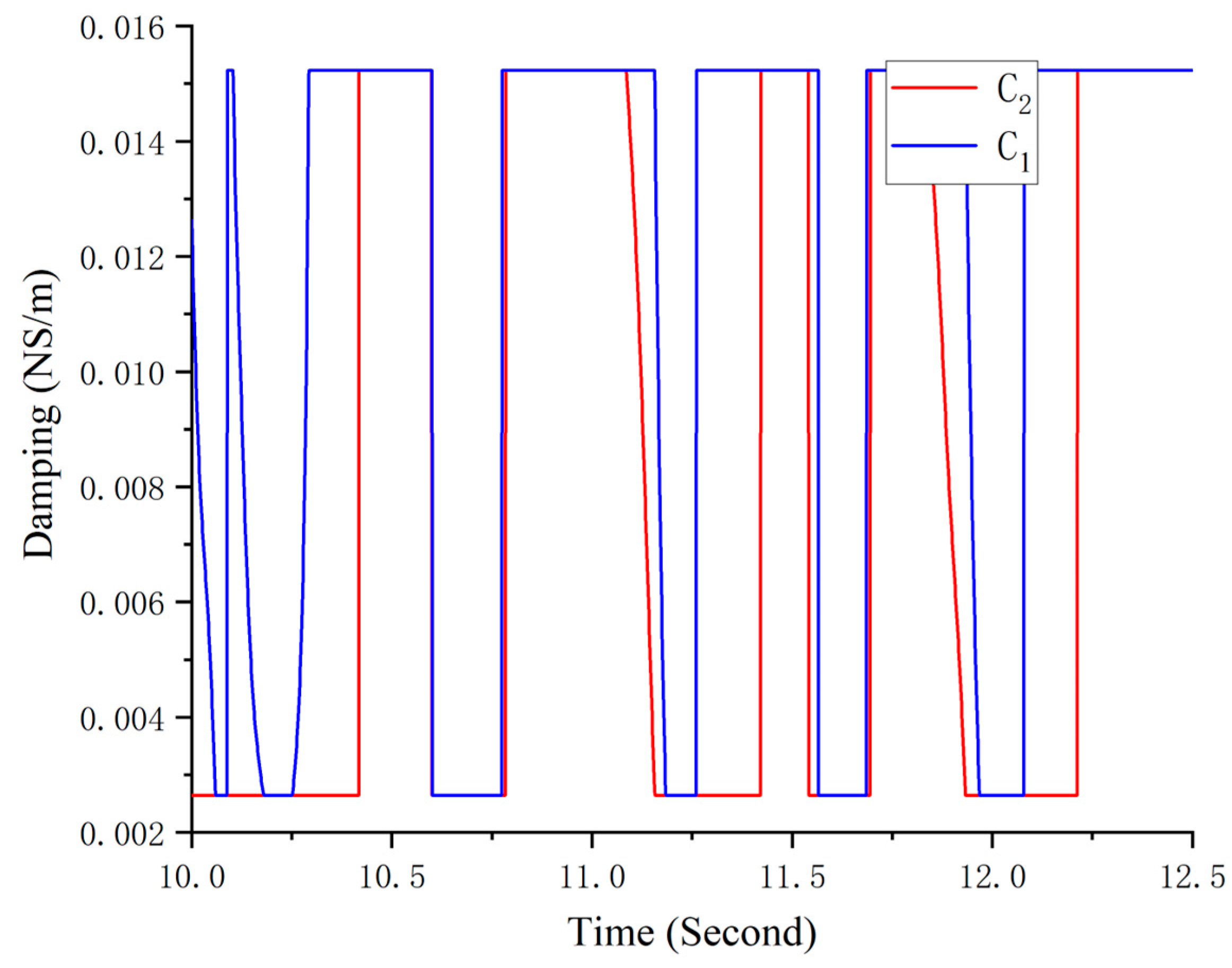
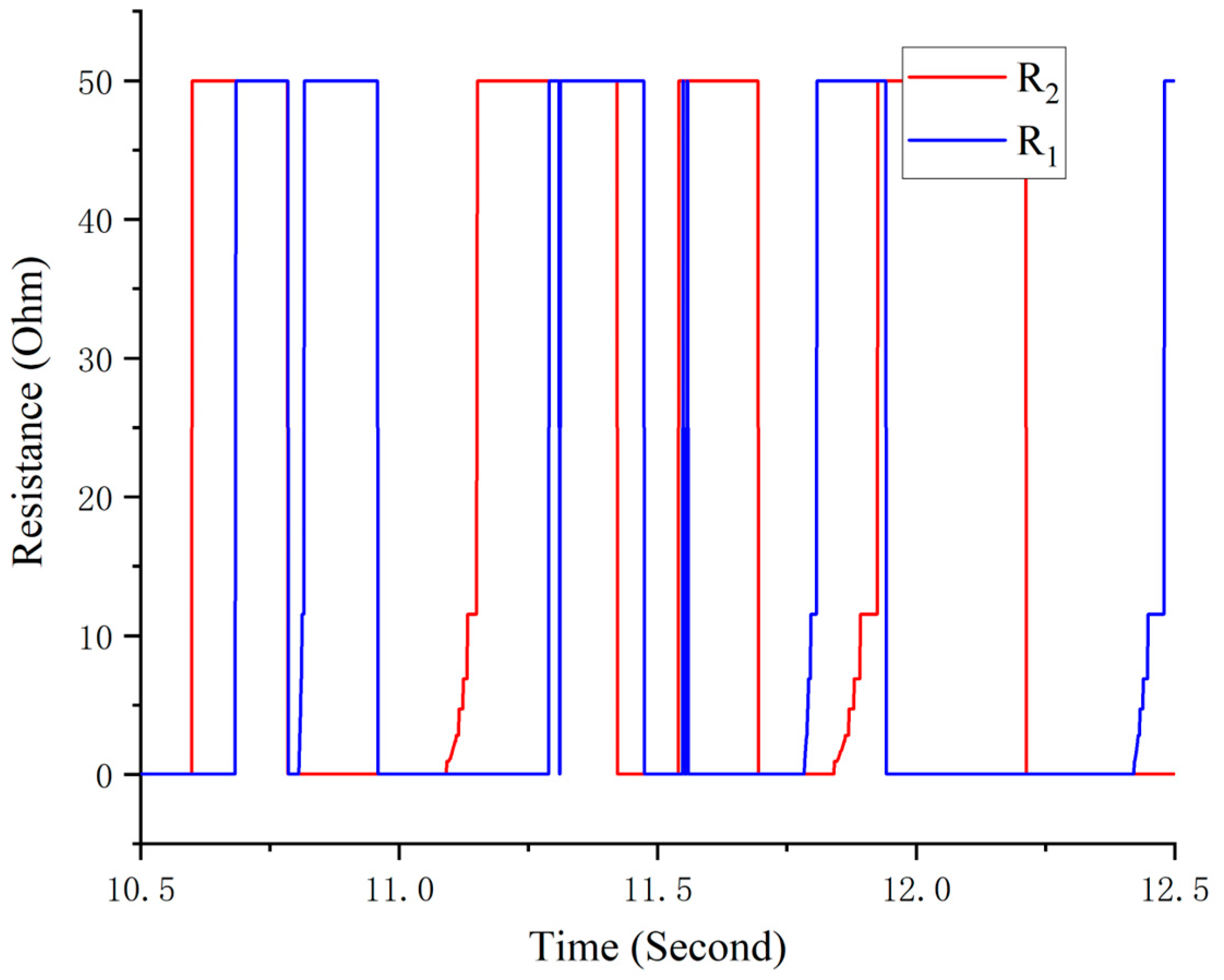
3.3. Time-Domain Characteristic
4. Controller Design
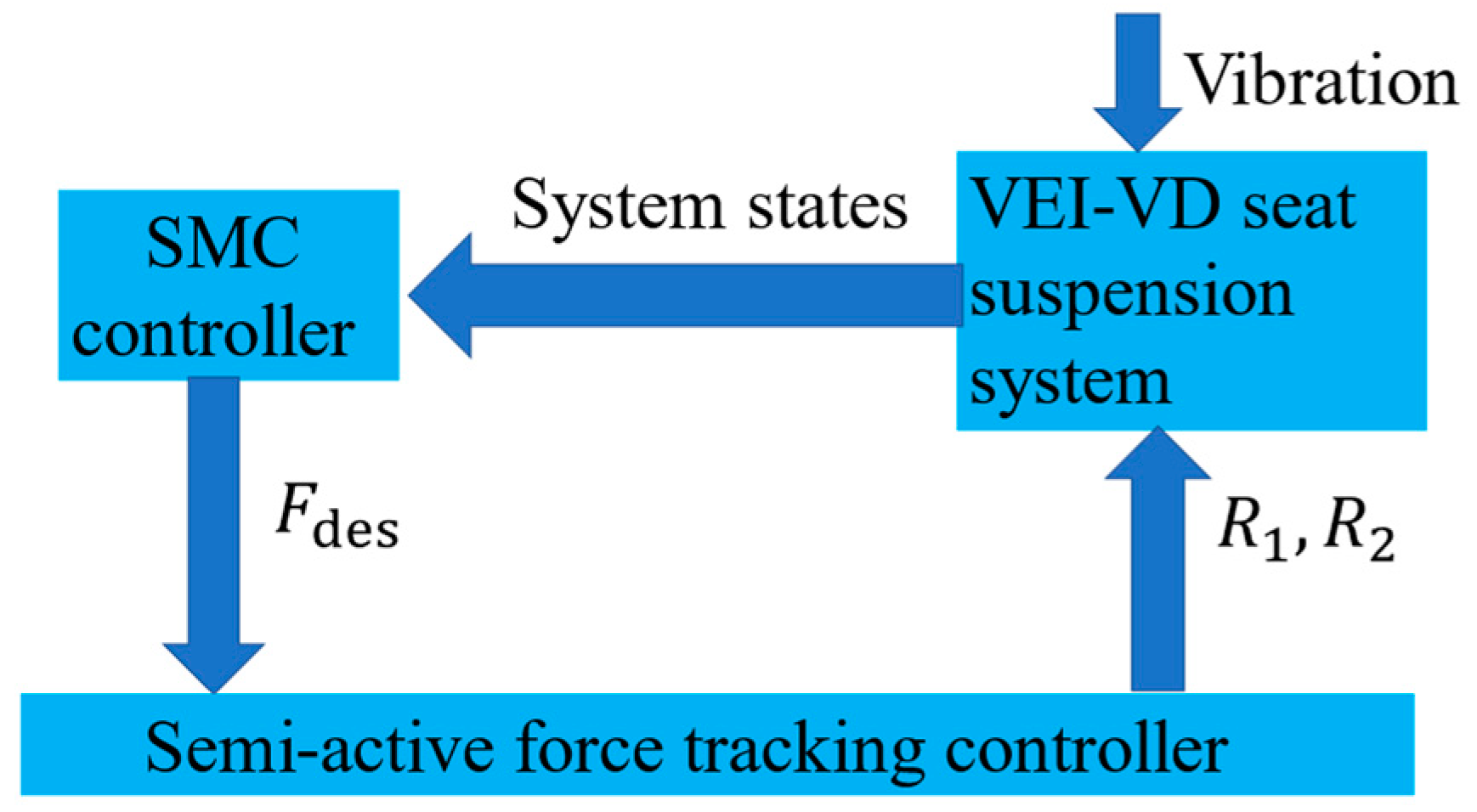
4.1. Control Scheme
4.2. Sliding Mode Control
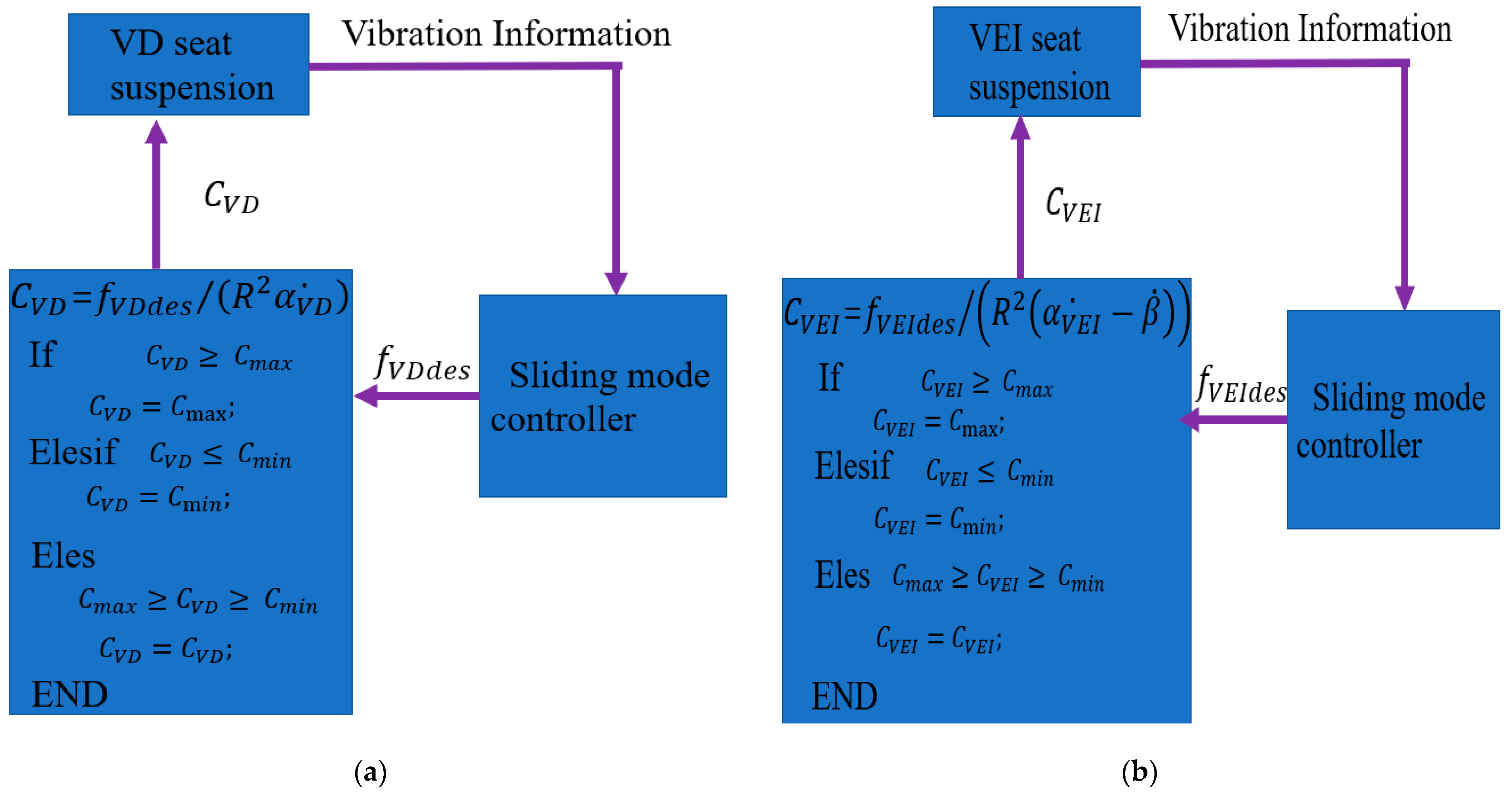
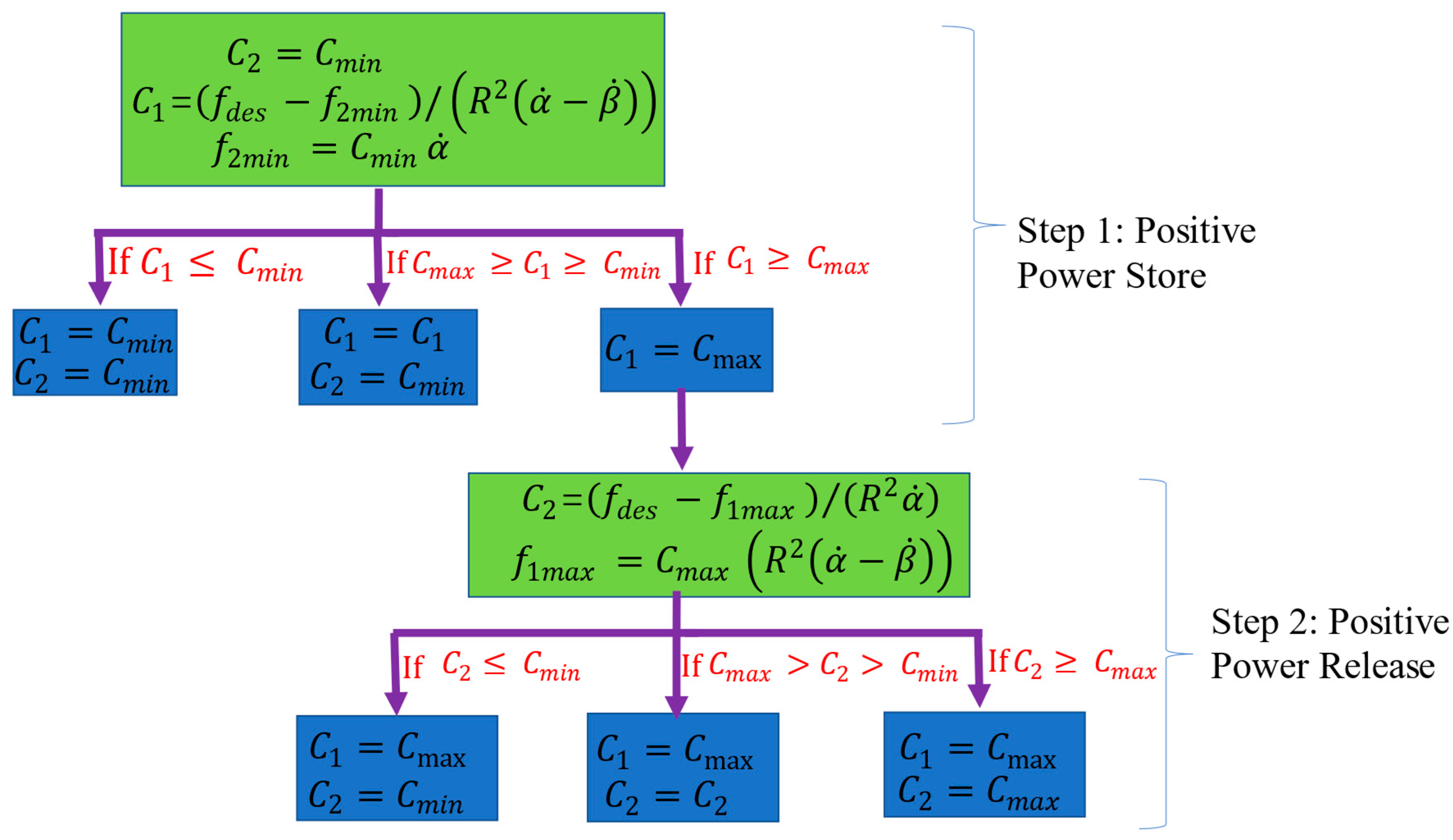
4.3. Force Track Control Strategy
5. Numerical Validation
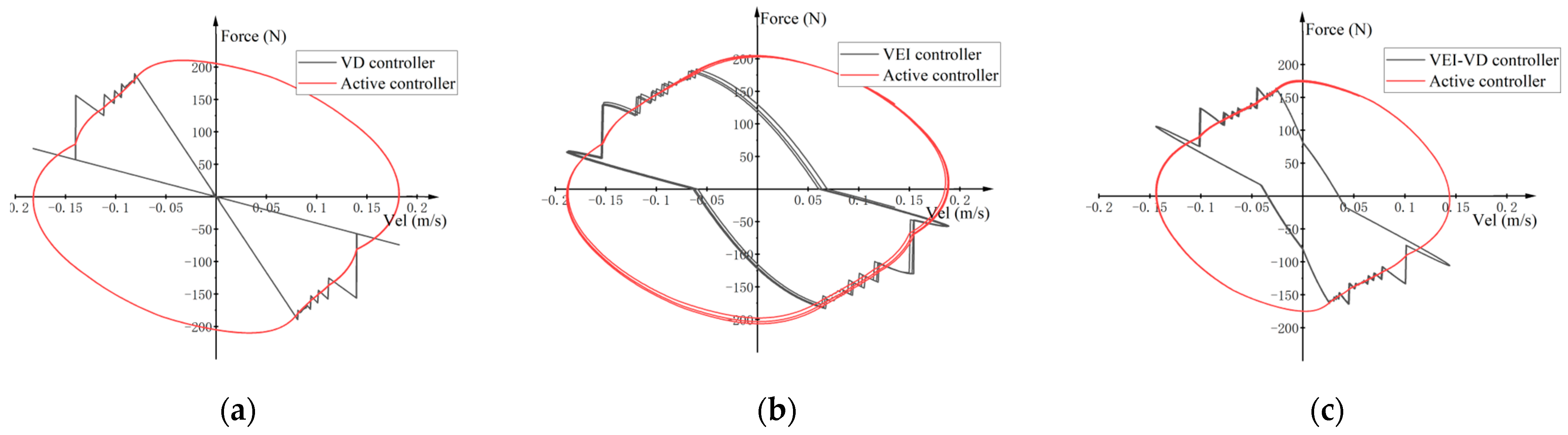
5.1. Feasibility Test
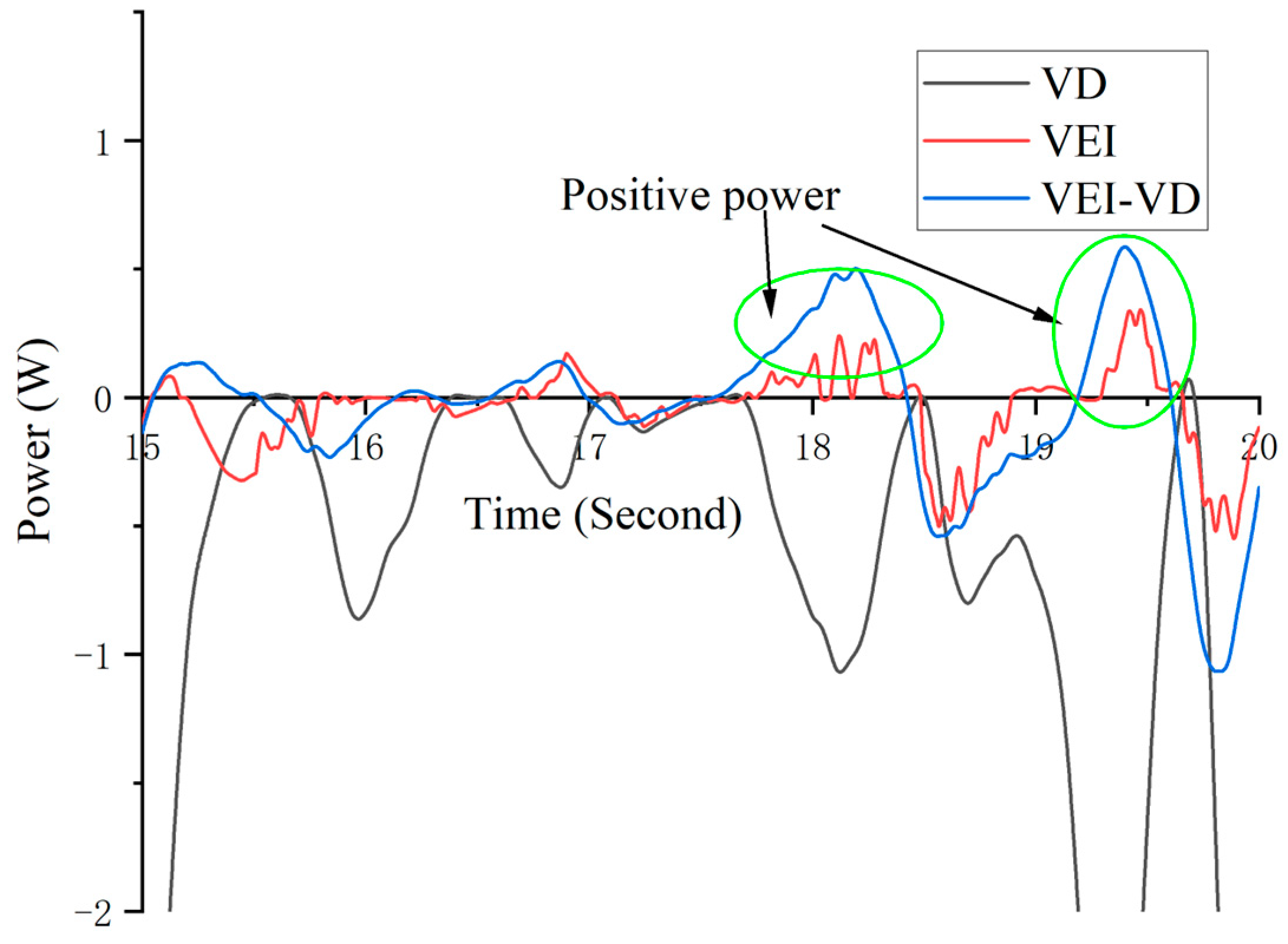
5.2. Sinusoidal Excitation Test
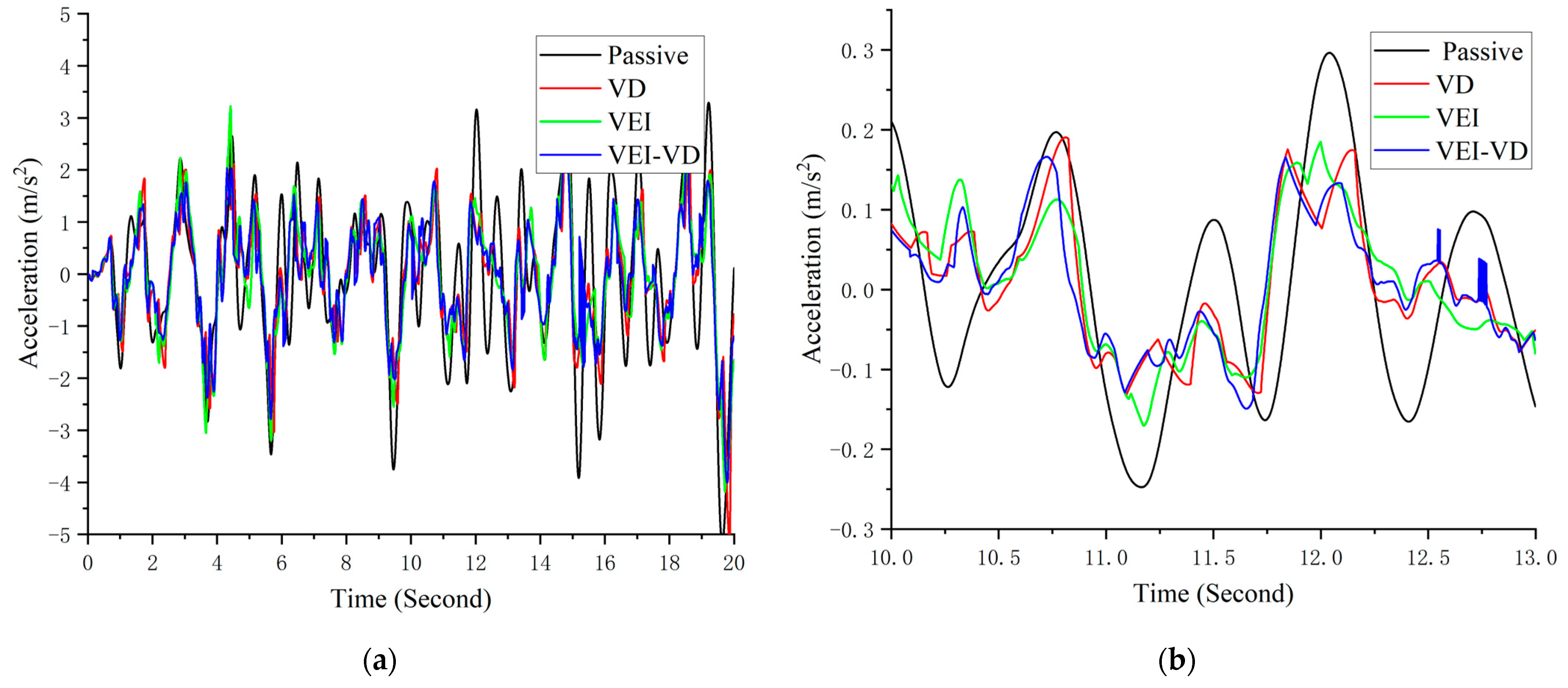
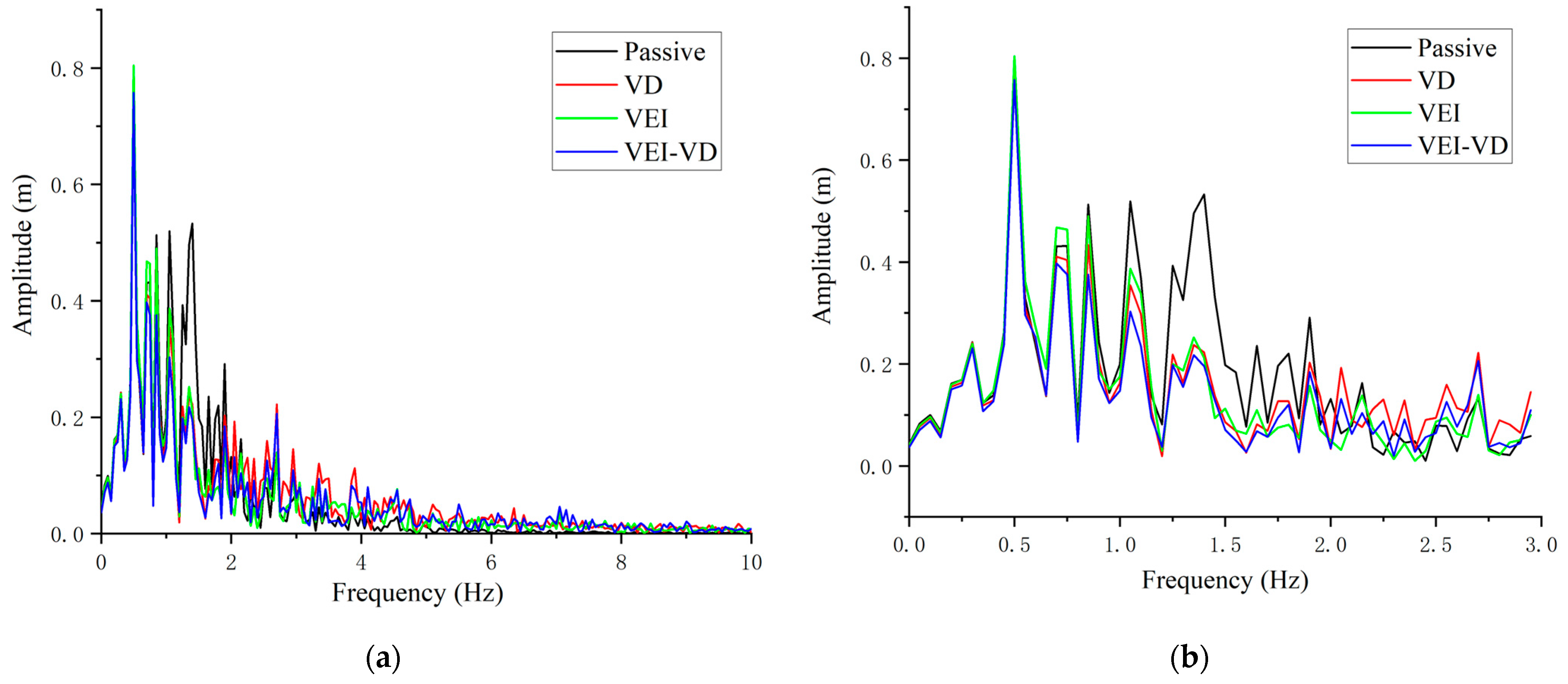
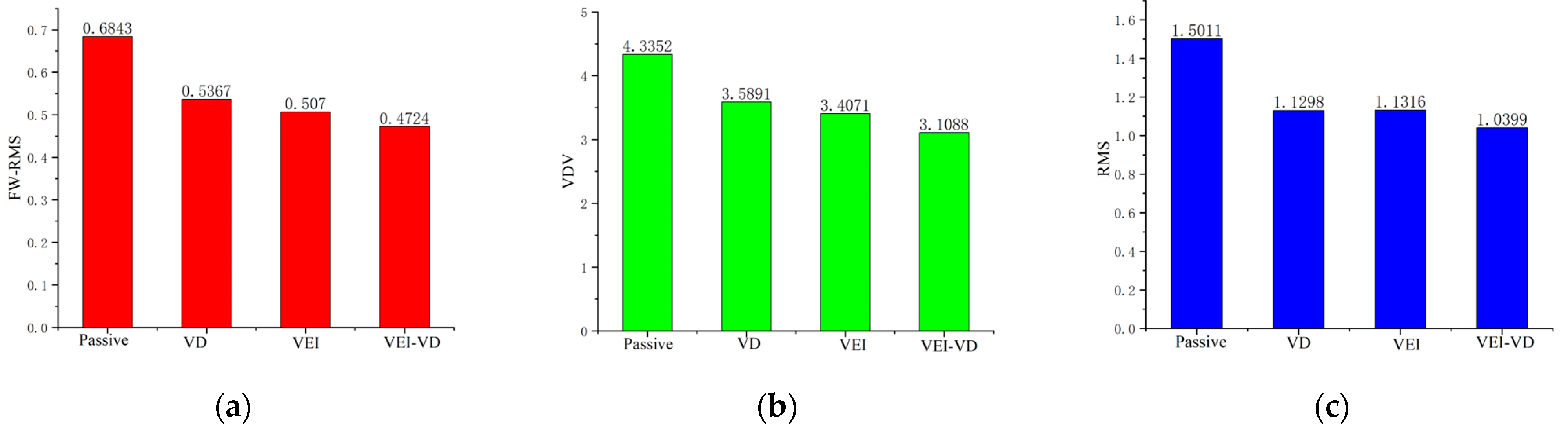
5.3. Radom Vibration Test
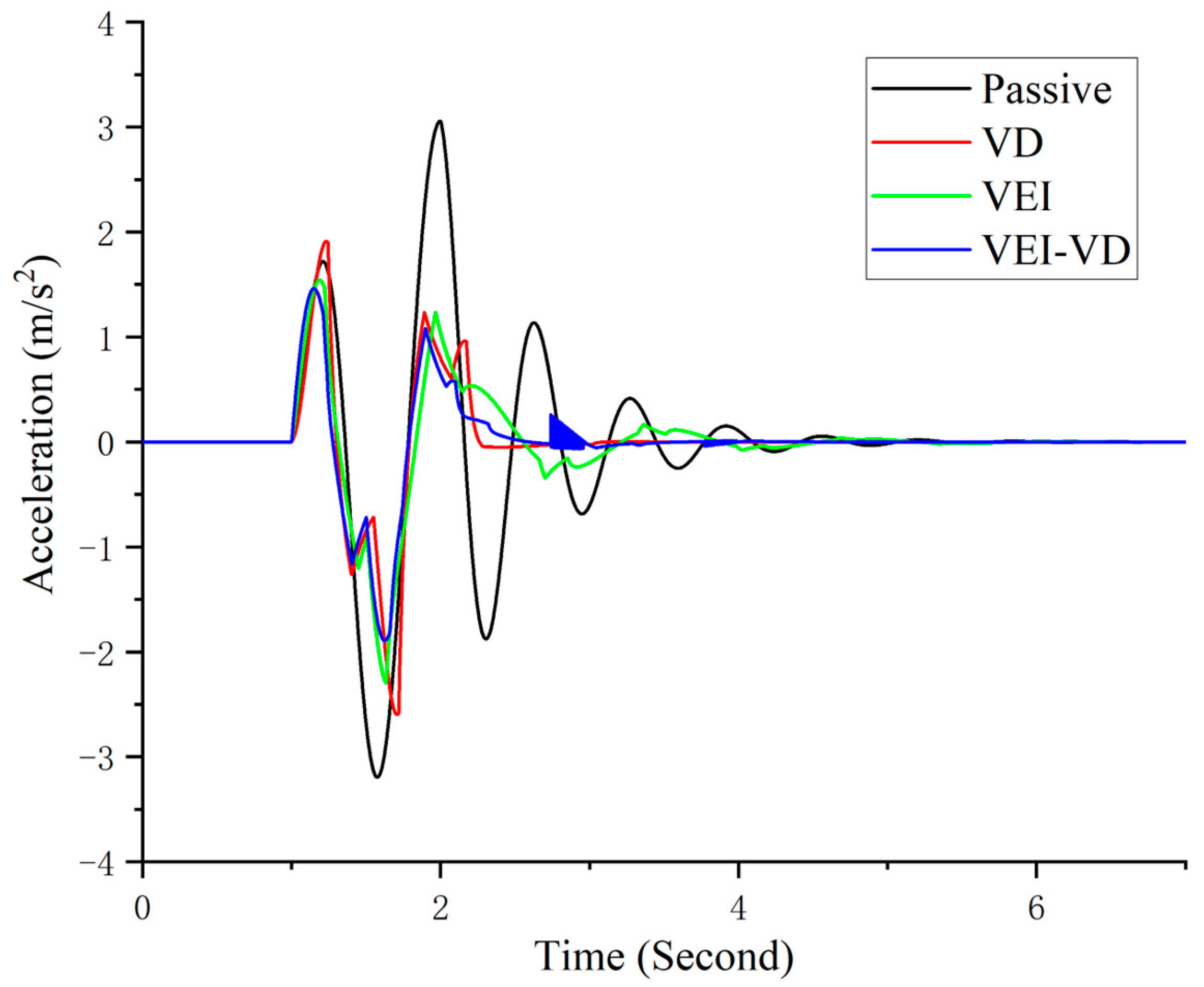
5.4. Bump Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krajnak, K. Health effects associated with occupational exposure to hand-arm or whole body vibration. J. Toxicol. Environ. Health B Crit. Rev. 2018, 21, 320–334. [Google Scholar] [CrossRef]
- Lee, C.M.; Goverdovskiy, V.N.; Temnikov, A.I. Design of springs with “negative” stiffness to improve vehicle driver vibration isolation. J. Sound Vib. 2007, 302, 865–874. [Google Scholar] [CrossRef]
- Maciejewski, I.; Meyer, L.; Krzyzynski, T. Modelling and multi-criteria optimisation of passive seat suspension vibro-isolating properties. J. Sound Vib. 2009, 324, 520–538. [Google Scholar] [CrossRef]
- Nguyen, V.; Jiao, R.; Zhang, J. Control Performance of Damping and Air Spring of Heavy Truck Air Suspension System with Optimal Fuzzy Control. SAE Int. J. Veh. Dyn. Stab. NVH 2020, 4, 179–194. [Google Scholar] [CrossRef]
- Tseng, H.E.; Hrovat, D. State of the art survey: Active and semi-active suspension control. Veh. Syst. Dyn. 2015, 53, 1034–1062. [Google Scholar] [CrossRef]
- Chen, M.Z.Q.; Yinlong, H.; Chanying, L.; Guanrong, C. Performance Benefits of Using Inerter in Semiactive Suspensions. IEEE Trans. Control. Syst. Technol. 2015, 23, 1571–1577. [Google Scholar] [CrossRef]
- Du, H.; Li, W.; Zhang, N. Semi-active variable stiffness vibration control of vehicle seat suspension using an MR elastomer isolator. Smart Mater. Struct. 2011, 20. [Google Scholar] [CrossRef]
- Du, X.-M.; Yu, M.; Fu, J.; Peng, Y.-X.; Shi, H.-F.; Zhang, H. H∞ control for a semi-active scissors linkage seat suspension with magnetorheological damper. J. Intell. Mater. Syst. Struct. 2018, 30, 708–721. [Google Scholar] [CrossRef]
- Choi, S.-B.; Han, Y.-M. Vibration control of electrorheological seat suspension with human-body model using sliding mode control. J. Sound Vib. 2007, 303, 391–404. [Google Scholar] [CrossRef]
- Gohari, H.D.; Zarastvand, M.R.; Talebitooti, R.; Loghmani, A.; Omidpanah, M. Radiated sound control from a smart cylinder subjected to piezoelectric uncertainties based on sliding mode technique using self-adjusting boundary layer. Aerosp. Sci. Technol. 2020, 106, 106141. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, L.; Yang, X.; Shi, D.; Yang, J. Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension. J. Sound Vib. 2016, 361, 148–158. [Google Scholar] [CrossRef]
- Liu, Y.; Matsuhisa, H.; Utsuno, H. Semi-active vibration isolation system with variable stiffness and damping control. J. Sound Vib. 2008, 313, 16–28. [Google Scholar] [CrossRef]
- Choi, S.-B.; Nam, M.-H.; Lee, B.-K. Vibration Control of a MR Seat Damper for Commercial Vehicles. J. Intell. Mater. Syst. Struct. 2000, 11, 936–944. [Google Scholar] [CrossRef]
- Ning, D.; Du, H.; Sun, S.; Zheng, M.; Li, W.; Zhang, N.; Jia, Z. An Electromagnetic Variable Stiffness Device for Semiactive Seat Suspension Vibration Control. IEEE Trans. Ind. Electron. 2020, 67, 6773–6784. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Du, H.; Li, W.; Zhang, N.; Zheng, M.; Luo, L. An electromagnetic variable inertance device for seat suspension vibration control. Mech. Syst. Signal Process. 2019, 133. [Google Scholar] [CrossRef]
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Autom. Control. 2002, 47, 1648–1662. [Google Scholar] [CrossRef]
- Bailey, T.; Hubbard, J., Jr. Distributed Piezoelectric-Polymer Active Vibration Control of a Cantilever Beam. J. Guid. Control. Dyn. 1984, 8, 23. [Google Scholar] [CrossRef]
- Choi, H.D.; Lee, C.J.; Lim, M.T. Fuzzy Preview Control for Half-vehicle Electro-hydraulic Suspension System. Int. J. Control. Autom. Syst. 2018, 16, 2489–2500. [Google Scholar] [CrossRef]
- Bai, X.-X.; He, G. Pseudo-active actuators: A concept analysis. Int. J. Mech. Syst. Dyn. 2021, 1, 230–247. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Yu, J.; Zheng, M.; Du, H.; Zhang, N.; Li, W. A rotary variable admittance device and its application in vehicle seat suspension vibration control. J. Frankl. Inst. 2019. [Google Scholar] [CrossRef]
- Smith, M.; Wang, F.-C. Performance Benefits in Passive Vehicle Suspensions Employing Inerters. Veh. Syst. Dyn. 2004, 42, 235–257. [Google Scholar] [CrossRef]
- Chen, L. Performance Analysis of Two-stage Series-connected Inerter-spring-damper Suspension Based on Half-car Model. J. Mech. Eng. 2012, 48, 102. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, M.; Shu, Z. Passive vehicle suspensions employing inerters with multiple performance requirements. J. Sound Vib. 2014, 333, 2212–2225. [Google Scholar] [CrossRef]
- Zhu, A.-D.; Zhong, W.; Bai, X. Design and analysis of a shock absorber with both tunable inertance and 522 damping. In Proceedings of the Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Denver, Colorado, 3–7 March 2019. [Google Scholar]
- Chen, M.Z.Q.; Hu, Y.; Li, C.; Chen, G. Semi-active suspension with semi-active inerter and semi-active damper. IFAC Proc. Vol. 2014, 47, 11225–11230. [Google Scholar] [CrossRef]
- Firestone, F.A. A New Analogy Between Mechanical and Electrical Systems. J. Acoust. Soc. Am. 1933, 4, 249–267. [Google Scholar] [CrossRef]
- Li, J.-Y.; Zhu, S. Versatile Behaviors of Electromagnetic Shunt Damper With a Negative Impedance Converter. IEEE/ASME Trans. Mechatron. 2018, 23, 1415–1424. [Google Scholar] [CrossRef]
- Liu, P.; Ning, D.; Luo, L.; Zhang, N.; Du, H. An Electromagnetic Variable Inertance and Damping Seat Suspension With Controllable Circuits. IEEE Trans. Ind. Electron. 2021, 69, 2811–2821. [Google Scholar] [CrossRef]
- Ning, D.; Du, H.; Zhang, N.; Jia, Z.; Li, W.; Wang, Y. A semi-active variable equivalent stiffness and inertance device implemented by an electrical network. Mech. Syst. Signal Process. 2021, 156, 107676. [Google Scholar] [CrossRef]
- Ning, D.; Du, H.; Sun, S.; Li, W.; Li, W. An energy saving variable damping seat suspension system with regeneration capability. IEEE Trans. Ind. Electron. 2018, 65, 8080–8091. [Google Scholar] [CrossRef]


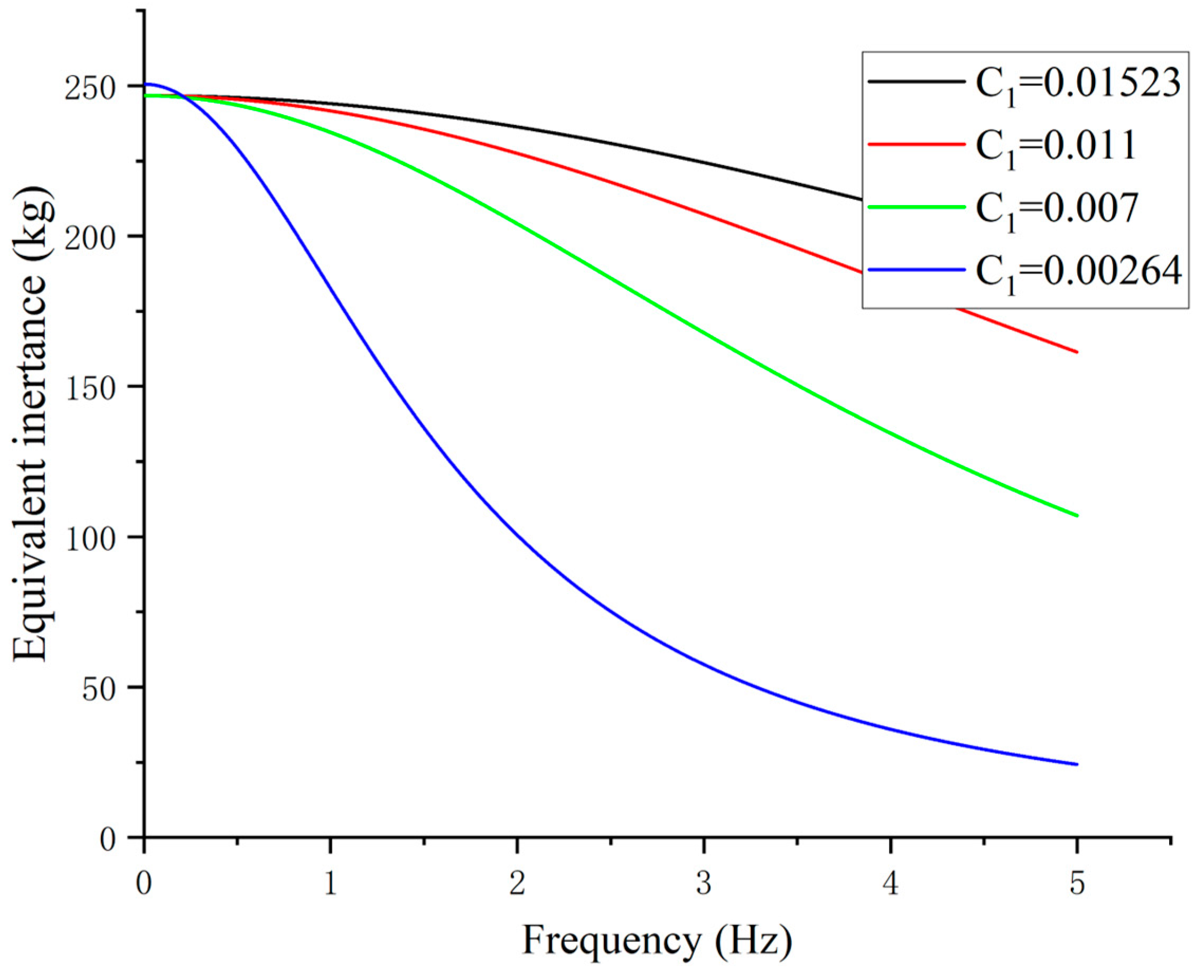
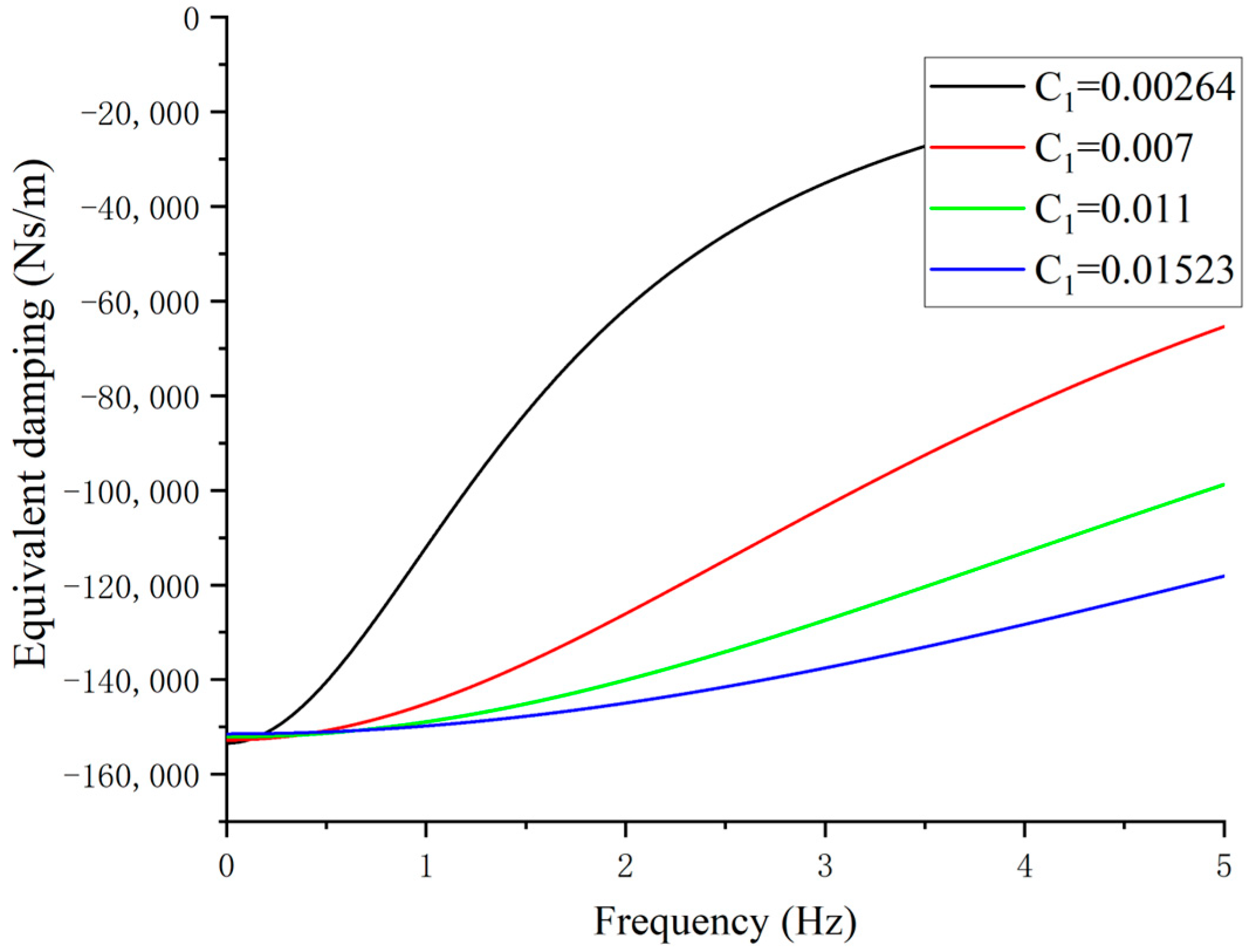
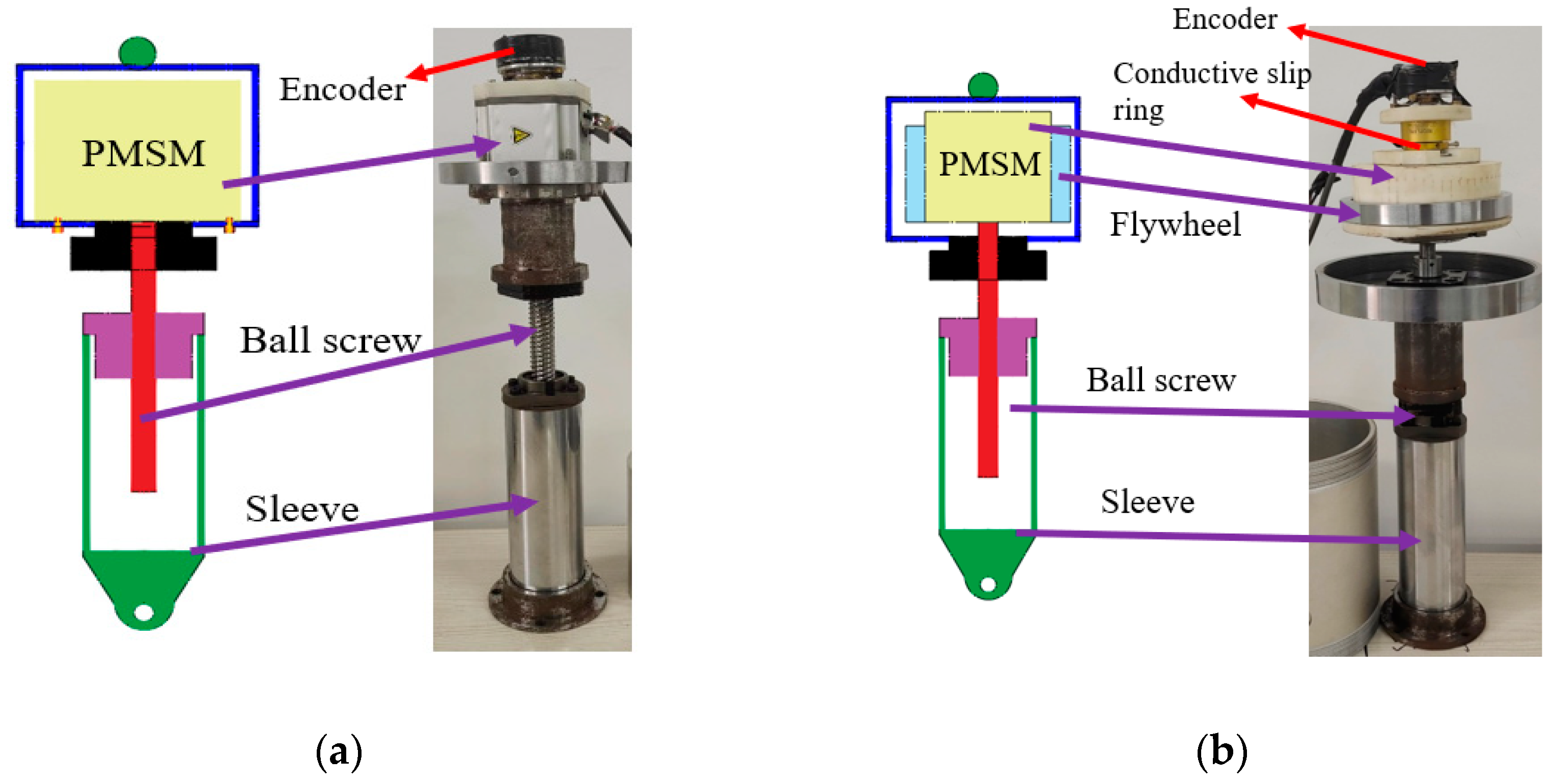
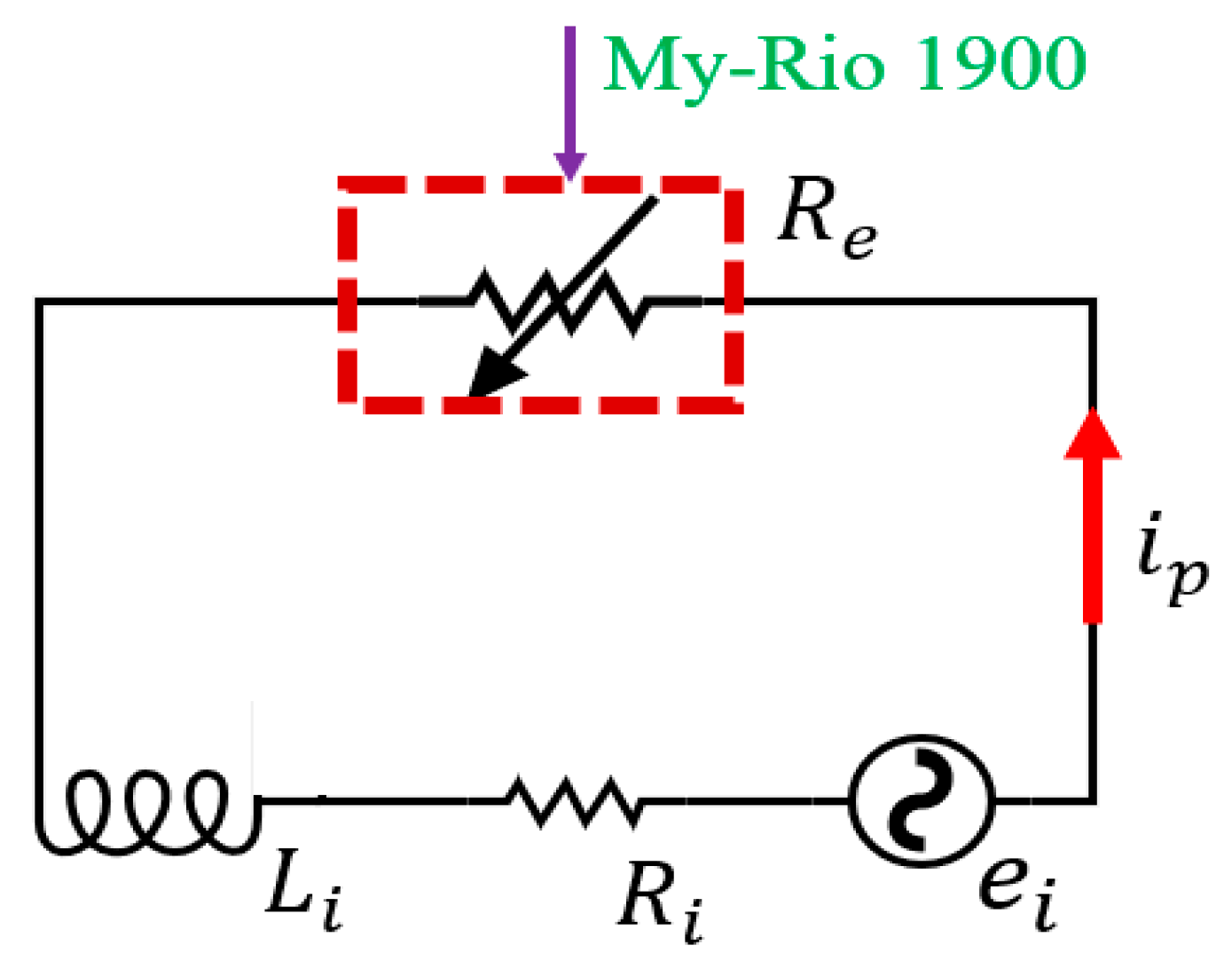





| Semiactive Device | Parameter | Symbol | Value |
|---|---|---|---|
| VEI device | Friction coefficient | 35 N | |
| Inherent moment of inertia | |||
| Moment of inertia of flywheel | |||
| Friction coefficient | 30 N | ||
| Inherent moment of inertia | |||
| VD device | Constant of PMSM | ||
| Internal resistance of PMSM |
| Device | 1.0 Hz | 1.5 Hz | 2.0 Hz | 2.5 Hz |
|---|---|---|---|---|
| Passive | --- | --- | --- | --- |
| VD | 10.72% | 50.67% | 51.69% | 49.37% |
| VEI | 27.64% | 60.13% | 48.89% | 40.97% |
| VEI–VD | 33.07% | 59.13% | 35.87% | 22.56% |
| Device | FW-RMS | VDV | RMS |
|---|---|---|---|
| Passive | --- | --- | -- |
| VD | 21.57% | 17.21% | 23.28% |
| VEI | 25.91% | 21.41% | 24.62% |
| VEI–VD | 30.97% | 28.29% | 30.72% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, G.; Liu, P.; Ning, D.; Liu, G.; Du, H. Semi-Active Vibration Control of Seat Suspension Equipped with a Variable Equivalent Inertance-Variable Damping Device. Machines 2023, 11, 284. https://doi.org/10.3390/machines11020284
Luan G, Liu P, Ning D, Liu G, Du H. Semi-Active Vibration Control of Seat Suspension Equipped with a Variable Equivalent Inertance-Variable Damping Device. Machines. 2023; 11(2):284. https://doi.org/10.3390/machines11020284
Chicago/Turabian StyleLuan, Guangrui, Pengfei Liu, Donghong Ning, Guijie Liu, and Haiping Du. 2023. "Semi-Active Vibration Control of Seat Suspension Equipped with a Variable Equivalent Inertance-Variable Damping Device" Machines 11, no. 2: 284. https://doi.org/10.3390/machines11020284
APA StyleLuan, G., Liu, P., Ning, D., Liu, G., & Du, H. (2023). Semi-Active Vibration Control of Seat Suspension Equipped with a Variable Equivalent Inertance-Variable Damping Device. Machines, 11(2), 284. https://doi.org/10.3390/machines11020284








