A Refined Dynamic Model for the Planetary Gear Set Considering the Time-Varying Nonlinear Support Stiffness of Ball Bearing
Abstract
:1. Introduction
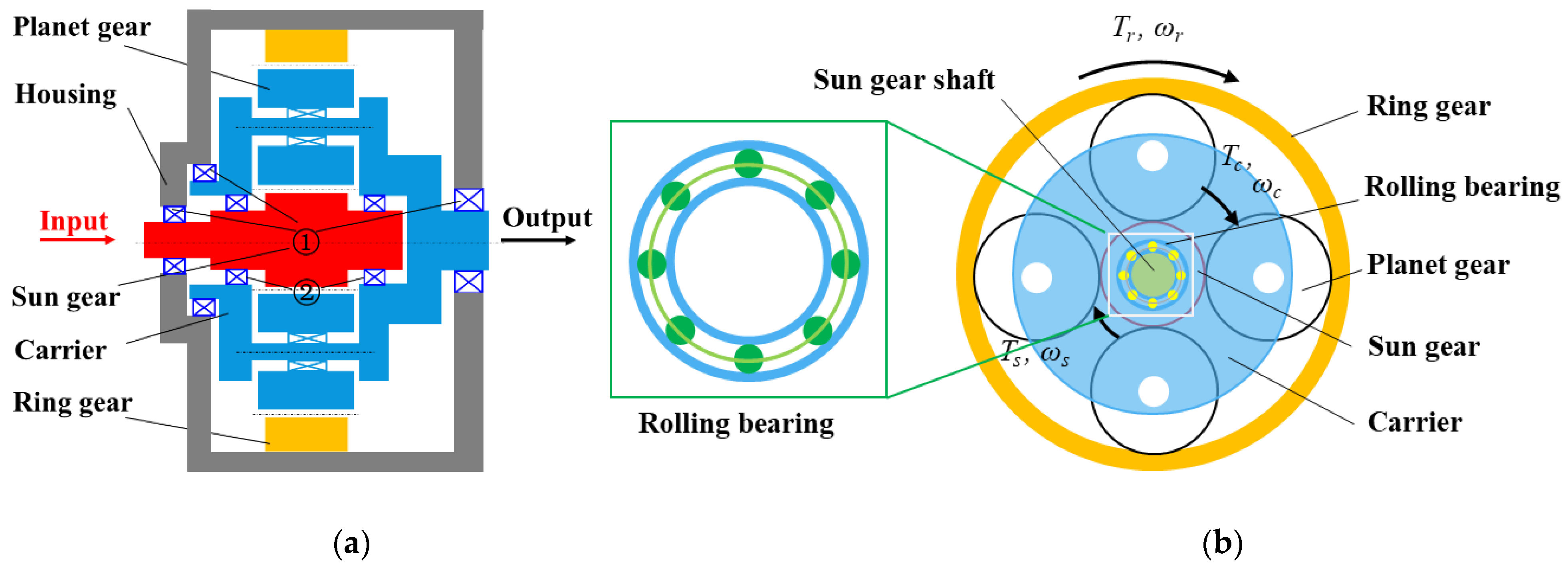
2. Dynamics Model of a Planetary Gear Set with Time-Varying Nonlinear Support Stiffness
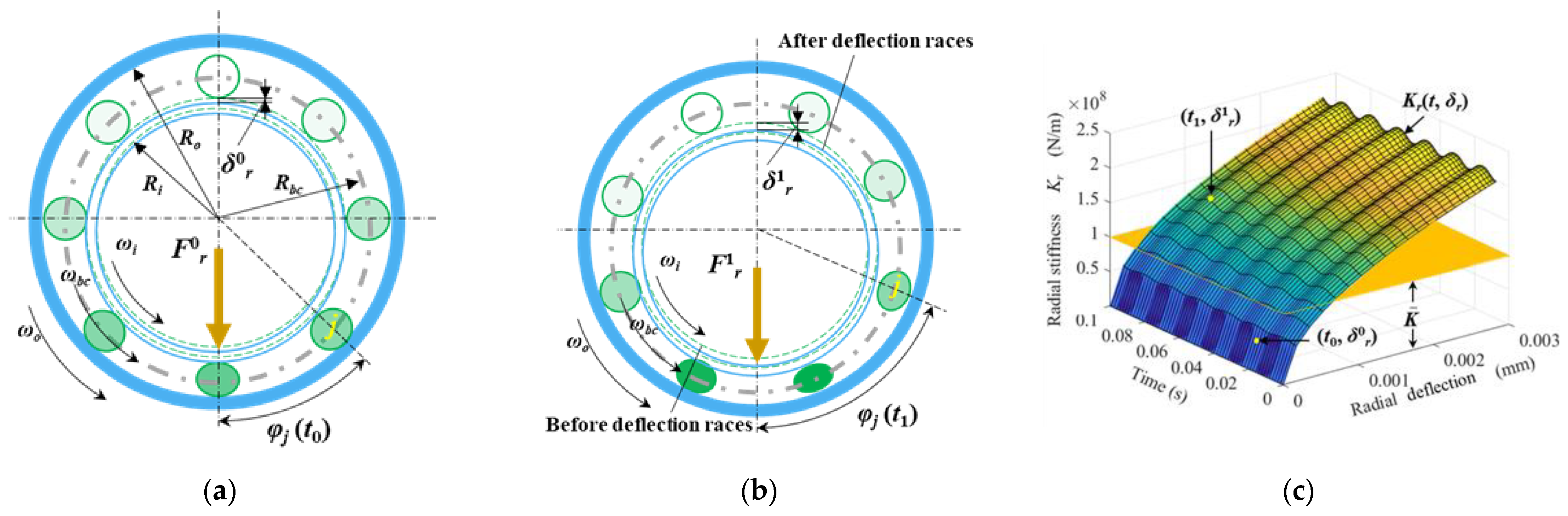
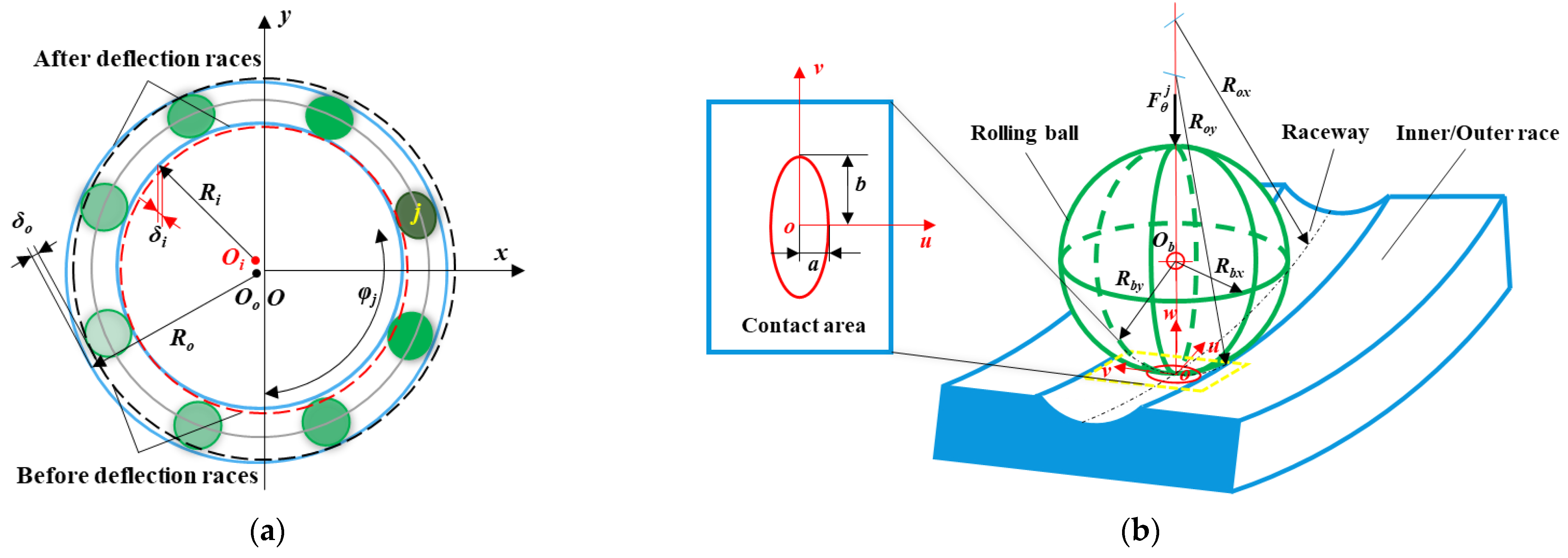
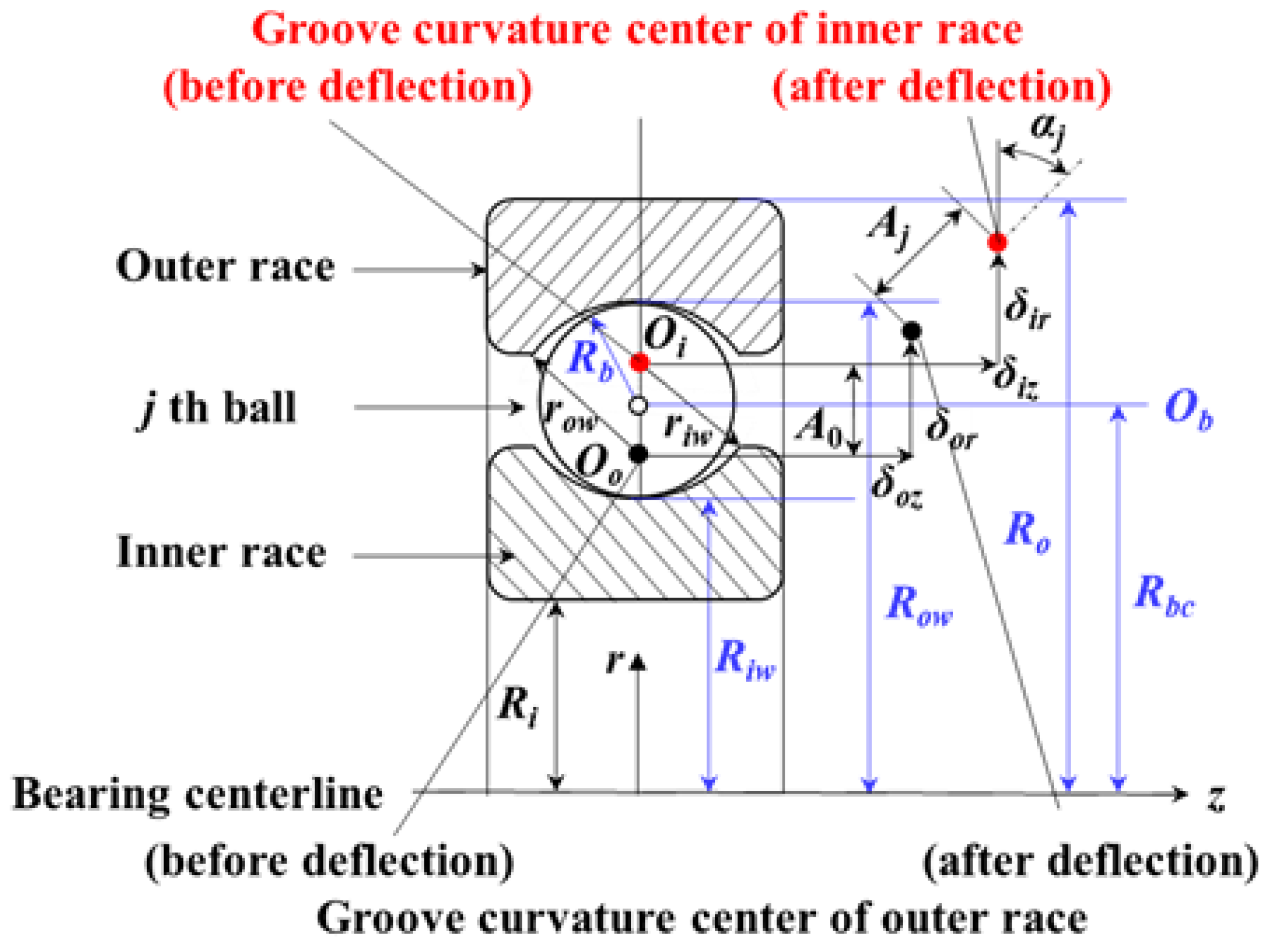
2.1. Actual Support Stiffness and Translation of the Ball Bearing
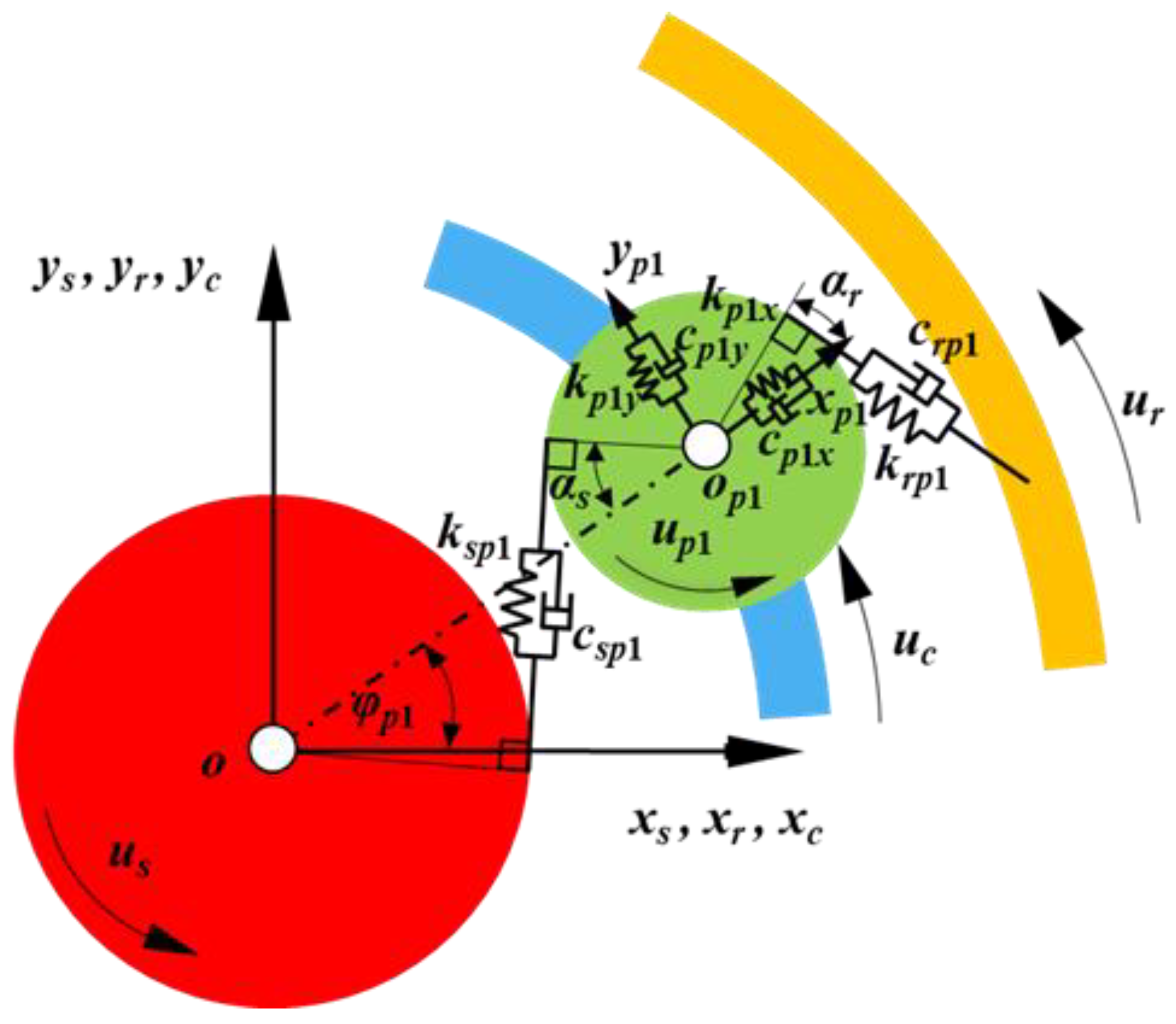
2.2. Lumped Parameter Model of a PGS Coupled with the Time-Varying Nonlinear Support Stiffness
2.3. The Solving Algorithm of the Refined Dynamics Model
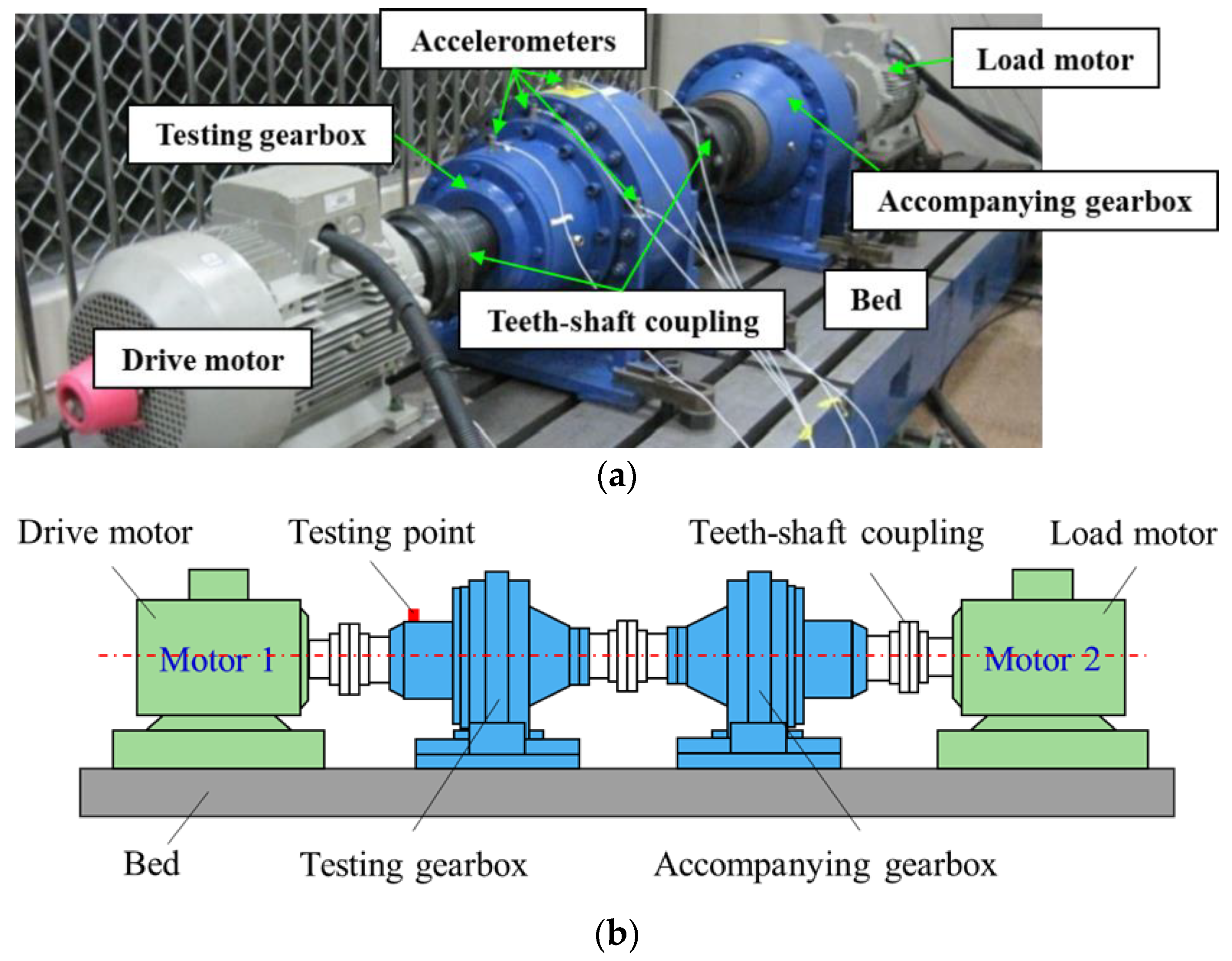
3. Experiment and Comparisons
4. Dynamic Simulation and Discussion
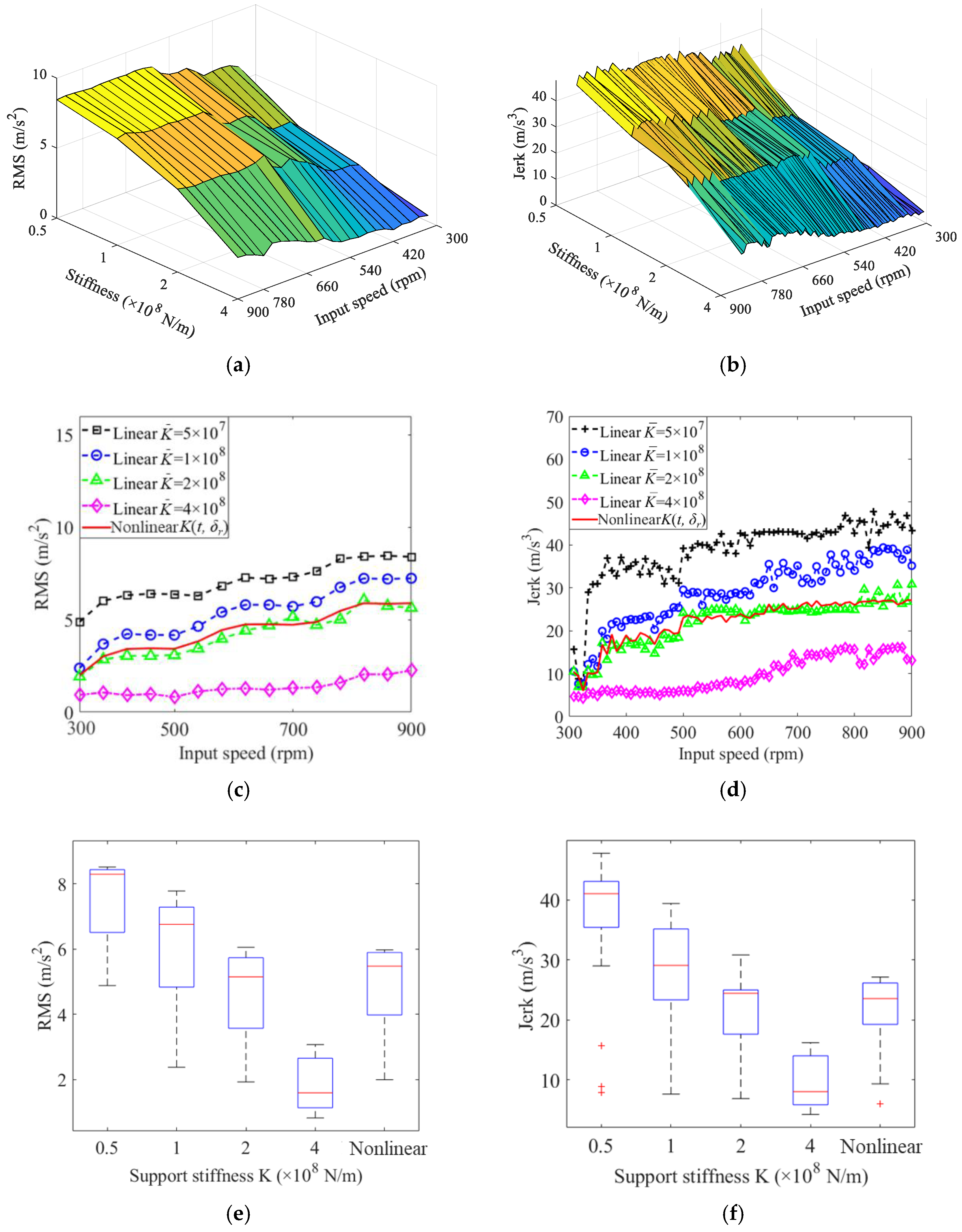
4.1. Influence of Support Stiffness and Input Speed on the Vibrations
4.2. Influence of Support Stiffness and Input Speed on the Load-Sharing Factor
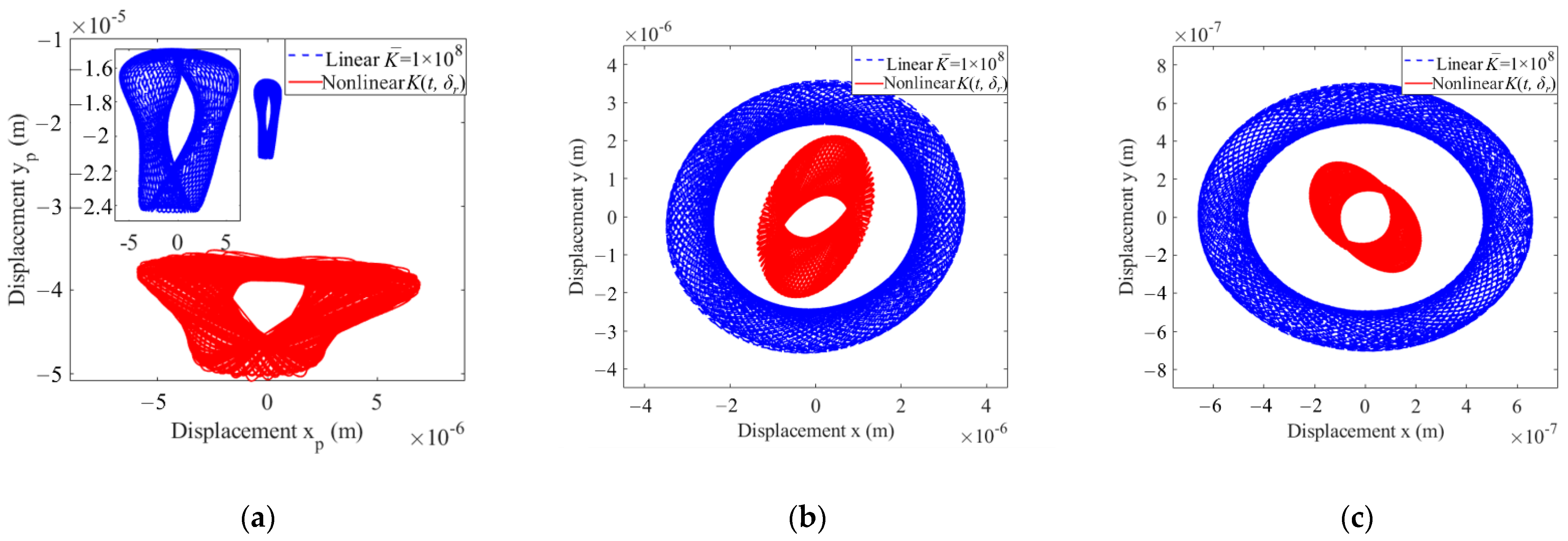
4.3. Influence of Support Stiffness and Input Speed on the Center Trajectories
5. Conclusions
- Compared to the static linear bearing support stiffness conditions, the sidebands of the time-varying nonlinear support stiffness condition in the logarithm frequency spectrum possess additional ball passing frequencies (fbc, fp, fbpfi, and fbpfo), which are much closer to the real scenario.
- The conventional static linear bearing support stiffness models, which usually assume an empirical constant value, cannot faithfully reflect the dynamic scenario of the system. The proposed refined support stiffness model is close to the actual situation, which may provide theoretical guidance for the condition monitoring and fault diagnosis of PGSs’ bearings.
- The vibration amplitudes of the sun gear and the center trajectories of the sun gear, carrier, and planet gear are greatly affected by the time-varying nonlinear support stiffness of bearings.
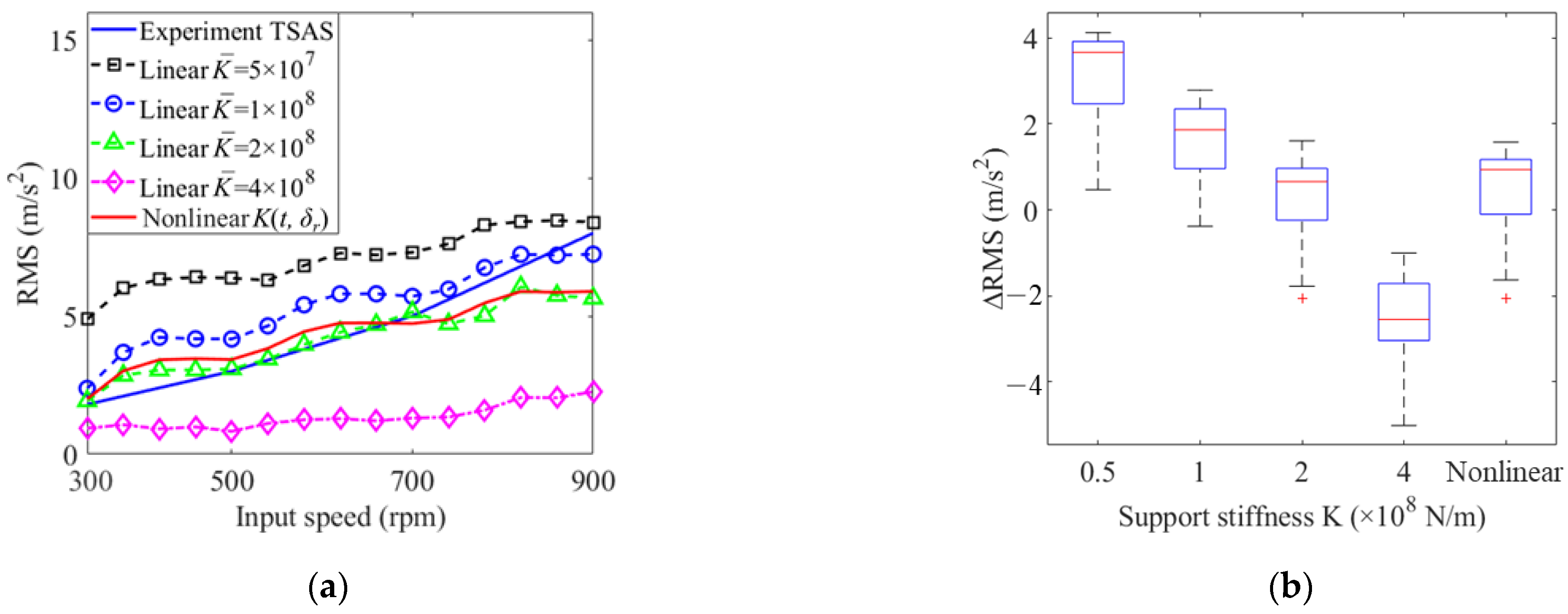
- The vibration responses of the time-varying nonlinear case and the static linear case with = 2 × 108 N/m are very close to that of the experiment. However, the dynamic responses of the time-varying nonlinear case are stabler.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moshrefzadeh, A.; Fasana, A. Planetary gearbox with localised bearings and gears faults: Simulation and time/frequency analysis. Meccanica 2017, 52, 3759–3779. [Google Scholar] [CrossRef]
- Yang, X.; Shao, Y.; Wang, L.; Yu, W.; Yue, N.; Du, W. Configuration design of dual-input compound power-split mechanism for in-wheel motor-driven electrical vehicles based on an improved lever analogy method. J. Mech. Des. 2021, 143, 104501. [Google Scholar] [CrossRef]
- Wang, L.; Shao, Y. Crack fault classification for planetary gearbox based on feature selection technique and K-means clustering method. Chin. J. Mech. Eng. 2018, 31, 242–252. [Google Scholar] [CrossRef]
- Carrella, A.; Friswell, M.I.; Zotov, A.; Ewins, D.J.; Tichonov, A. Using nonlinear springs to reduce the whirling of a rotating shaft. Mech. Syst. Signal Process. 2009, 23, 2228–2235. [Google Scholar] [CrossRef]
- Lim, T.C.; Singh, R. Vibration transmission through rolling element bearings, part I: Bearing stiffness formulation. J. Sound Vib. 1990, 139, 179–199. [Google Scholar] [CrossRef]
- Kahraman, A.; Singh, R. Nonlinear dynamics of a geared rotor-bearing system with multiple clearances. J. Sound Vib. 1991, 144, 469–506. [Google Scholar] [CrossRef]
- Atanasovska, I. The mathematical phenomenological mapping in non-linear dynamics of spur gear pair and radial ball bearing due to the variable stiffness. Int. J. Nonlinear Mech. 2015, 73, 114–120. [Google Scholar] [CrossRef]
- Kahraman, A. Effect of axial vibrations on the dynamics of a helical gear pair. J. Vib. Acoust. 1993, 115, 33–39. [Google Scholar] [CrossRef]
- Kim, W.; Hong, H.Y.; Chung, J. Dynamic analysis for a pair of spur gears with translational motion due to bearing deformation. J. Sound Vib. 2010, 329, 4409–4421. [Google Scholar] [CrossRef]
- Shi, Z.; Li, S. Nonlinear dynamics of hypoid gear with coupled dynamic mesh stiffness. Mech. Mach. Theory 2022, 168, 104589. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, L.; Gou, X.; Shi, J.; Jin, G. Dynamics modeling and analyzing of spur gear pair with pitch deviation considering time-varying contact ratio under multi-state meshing. J. Sound Vib. 2021, 513, 116411. [Google Scholar] [CrossRef]
- Cirelli, M.; Valentini, P.; Pennestrì, E. A study of the non-linear dynamic response of spur gear using a multibody contact based model with flexible teeth. J. Sound Vib. 2019, 445, 148–167. [Google Scholar] [CrossRef]
- Cirelli, M.; Giannini, O.; Valentini, P.; Pennestrì, E. Influence of tip relief in spur gears dynamic using multibody models with movable teeth. Mech. Mach. Theory 2020, 152, 103948. [Google Scholar] [CrossRef]
- Zheng, X.; Luo, W.; Hu, Y.; He, Z.; Wang, S. Study on the mesh stiffness and nonlinear dynamics accounting for centrifugal effect of high-speed spur gears. Mech. Mach. Theory 2022, 170, 104686. [Google Scholar] [CrossRef]
- Zhu, L.; Shi, J.; Gou, X. Modeling and dynamics analyzing of a torsional-bending-pendular face-gear drive system considering multi-state engagements. Mech. Mach. Theory 2020, 149, 103790. [Google Scholar] [CrossRef]
- Fei, Z.; Tong, S.; Wei, C. Investigation of the dynamic characteristics of a dual rotor system and its start-up simulation based on finite element method. J. Zhejiang Univ. Sci. A 2013, 14, 268–280. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D. Vibration response characteristics of a dual-rotor with unbalance-misalignment coupling faults: Theoretical analysis and experimental study. Mech. Mach. Theory 2018, 125, 207–219. [Google Scholar] [CrossRef]
- Hu, Q.; Deng, S.; Teng, H. A 5-DOF model for aeroengine spindle dual-rotor system analysis. Chin. J. Aeronaut. 2011, 24, 224–234. [Google Scholar] [CrossRef]
- Deng, S.; Fu, J.; Wang, Y.; Yang, H. Analysis on dynamic characteristics of aero-engine rolling bearing/dual-rotor system. J. Aerosp. Power 2013, 28, 195–204. [Google Scholar]
- Gupta, K.; Gupta, K.D.; Athre, K. Unbalance response of a dual rotor system: Theory and experiment. J. Vib. Acoust. 1993, 115, 427–435. [Google Scholar] [CrossRef]
- Chiang, H.; Hsu, C.N.; Tu, S.H. Rotor-bearing analysis for turbomachinery single- and dual-rotor systems. J. Propul. Power 2012, 20, 1096–1104. [Google Scholar] [CrossRef]
- Luo, G.; Zhou, H.; Wang, F.; Yang, X. Dynamic response of co-rotating and counter-rotating dual-rotor system supported on ball bearing. J. Aerosp. Power 2012, 27, 1887–1894. [Google Scholar]
- Gao, P.; Chen, Y.; Hou, L. Nonlinear thermal behaviors of the inter-shaft bearing in a dual-rotor system subjected to the dynamic load. Nonlinear Dyn. 2020, 101, 191–209. [Google Scholar] [CrossRef]
- Fukata, S.; Gad, E.H.; Kondou, T.; Ayabe, T.; Tamura, H. On the radial vibration of ball bearings: Computer simulation. Bull. JSME 1985, 28, 899–904. [Google Scholar] [CrossRef]
- Tiwari, M.; Gupta, K.; Prakash, O. Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor. J. Sound Vib. 2000, 238, 723–756. [Google Scholar] [CrossRef]
- Tiwari, M.; Gupta, K.; Prakash, O. Dynamic response of an unbalanced rotor supported on ball bearings. J. Sound Vib. 2000, 238, 757–779. [Google Scholar] [CrossRef]
- Ghafari, S.H.; Abdel-Rahman, E.M.; Golnaraghi, F.; Ismail, F. Vibrations of balanced fault-free ball bearings. J. Sound Vib. 2010, 329, 1332–1347. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Cao, Q. Bifurcations and hysteresis of varying compliance vibrations in the primary parametric resonance for a ball bearing. J. Sound Vib. 2015, 350, 171–184. [Google Scholar] [CrossRef]
- Gao, P.; Chen, Y.; Hou, L. Bifurcation analysis for a simple dual-rotor system with nonlinear intershaft bearing based on the singularity method. Shock Vib. 2020, 2020, 7820635. [Google Scholar] [CrossRef]
- Yi, G.; Parker, R.G. Dynamic analysis of planetary gears with bearing clearance. J. Comput. Nonlinear Dyn. 2012, 7, 041002. [Google Scholar]
- Yi, G.; Parker, R.G. Dynamic modeling and analysis of a spur planetary gear involving tooth wedging and bearing clearance nonlinearity. Eur. J. Mech. A-Solids 2010, 29, 1022–1033. [Google Scholar]
- Kim, W.; Ji, Y.L.; Chung, J. Dynamic analysis for a planetary gear with time-varying pressure angles and contact ratios. J. Sound Vib. 2012, 331, 883–901. [Google Scholar] [CrossRef]
- Wu, X.; Parker, R.G. Vibration of rings on a general elastic foundation. J. Sound Vib. 2006, 295, 194–213. [Google Scholar] [CrossRef]
- Liu, C.; Cooley, C.G.; Parker, R.G. Parametric instability of spinning elastic rings excited by fluctuating space-fixed stiffnesses. J. Sound Vib. 2017, 400, 533–549. [Google Scholar] [CrossRef]
- Bahgat, B.M.; Osman, M.O.M.; Dukkipati, R.V. On the dynamic gear tooth loading of planetary gearing as affected by bearing clearances in high-speed machinery. J. Mech. Des. 1985, 107, 430–436. [Google Scholar] [CrossRef]
- Guo, Y.; Parker, R.G. Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters. J. Vib. Acoust. 2010, 132, 655–672. [Google Scholar] [CrossRef]
- Tatar, A.; Schwingshackl, C.W.; Friswell, M.I. Dynamic behaviour of three-dimensional planetary geared rotor systems. Mech. Mach. Theory 2019, 134, 39–56. [Google Scholar] [CrossRef]
- Qiu, X.; Han, Q.; Chu, F. Load-sharing characteristics of planetary gear transmission in horizontal axis wind turbines. Mech. Mach. Theory 2015, 92, 391–406. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Ma, J.; Shao, Y. Effect of the radial support stiffness of the ring gear on the vibrations for a planetary gear system. J. Low Freq. Noise 2020, 39, 1024–1038. [Google Scholar] [CrossRef]
- Liu, W.; Shuai, Z.; Guo, Y.; Wang, D. Modal properties of a two-stage planetary gear system with sliding friction and elastic continuum ring gear. Mech. Mach. Theory 2019, 135, 251–270. [Google Scholar] [CrossRef]
- Chen, H.; Hu, N.; Cheng, Z.; Zhang, L.; Zhang, Y. A deep convolutional neural network based fusion method of two-direction vibration signal data for health state identification of planetary gearboxes. Measurement 2019, 146, 268–278. [Google Scholar] [CrossRef]
- Li, F.; Chen, Y.; Wang, J.; Zhou, X.; Tang, B. A reinforcement learning unit matching recurrent neural network for the state trend prediction of rolling bearings. Measurement 2019, 145, 191–203. [Google Scholar] [CrossRef]
- Rajab, M. Modeling of the Transmissibility through Rolling-Element Bearings under Radial and Moment Loads. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 1982. [Google Scholar]
- Harris, T.A.; Kotzalas, M.N. Advanced Concepts of Bearing Technology: Rolling Bearing Analysis; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Chen, Z. Study on Gear Mesh Nonlinear Excitation Modelling and Vibration Features of Planetary Gear System. Ph.D. Thesis, Chongqing University, Chongqing, China, November 2013. [Google Scholar]








| Parameters | Sun Gear | Ring Gear | Planet Gear | Carrier |
|---|---|---|---|---|
| Tooth number | 16 | 84 | 33 | -- |
| Module (mm) | 4 | 4 | 4 | -- |
| Face width (mm) | 25 | 25 | 25 | -- |
| Mass (kg) | 0.5075 | 1.646 | 0.6762 | 5.2 |
| Moment of inertia I/r2 (kg) | 0.304 | 1.352 | 0.371 | 2.08 |
| Base circle radius (m) | 0.03 | 0.1579 | 0.062 | -- |
| Pressure angle (°) | 20 | |||
| Number of planet gear | 4 | |||
| Young’s modulus (MPa) | 2.05 × 105 | |||
| Poisson’s ratio | 0.3 | |||
| Translational support stiffness (N/m) | kpx,y = krx,y = 108 | |||
| Torsional support stiffness (N/m) | krt = 109; kst = kct = 0 | |||
| Cases | Parameters | Value |
|---|---|---|
| Static linear | Ksx,y, Kcx,y (N/m) | sx,y = cx,y = [0.5, 1, 2, 4] × 108 |
| Time-varying nonlinear | Ksx,y, Kcx,y (N/m) | Kx,y (t, δr) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, C.; Yu, W.; Huang, W.; Xu, Z.; Nie, C. A Refined Dynamic Model for the Planetary Gear Set Considering the Time-Varying Nonlinear Support Stiffness of Ball Bearing. Machines 2023, 11, 206. https://doi.org/10.3390/machines11020206
Yang X, Zhang C, Yu W, Huang W, Xu Z, Nie C. A Refined Dynamic Model for the Planetary Gear Set Considering the Time-Varying Nonlinear Support Stiffness of Ball Bearing. Machines. 2023; 11(2):206. https://doi.org/10.3390/machines11020206
Chicago/Turabian StyleYang, Xiaodong, Chaodong Zhang, Wennian Yu, Wenbin Huang, Zhiliang Xu, and Chunhui Nie. 2023. "A Refined Dynamic Model for the Planetary Gear Set Considering the Time-Varying Nonlinear Support Stiffness of Ball Bearing" Machines 11, no. 2: 206. https://doi.org/10.3390/machines11020206
APA StyleYang, X., Zhang, C., Yu, W., Huang, W., Xu, Z., & Nie, C. (2023). A Refined Dynamic Model for the Planetary Gear Set Considering the Time-Varying Nonlinear Support Stiffness of Ball Bearing. Machines, 11(2), 206. https://doi.org/10.3390/machines11020206






