Active Disturbance Rejection Control for Piezoelectric Smart Structures: A Review
Abstract
1. Introduction
- Small size and light weight;
- Wide applicable frequency band;
- High electromechanical conversion efficiency;
- …
2. Disturbance Sources of Piezoelectric Smart Structures
2.1. System Modeling
2.1.1. Constitutive Equations
2.1.2. Electromechanical Coupling Model
2.2. Disturbances/Uncertainties in Smart Structures
2.2.1. Unmodeled Dynamics
2.2.2. Parametric Uncertainties
2.2.3. Control–Structure Interaction
2.2.4. Measurement Error Effects and Measurement Noise
2.2.5. Time Delay
2.2.6. External Disturbances
2.3. Piezoelectric Modal Sensors
3. Formulation and Applications of ADRC
3.1. System Re-Modeling with Total Disturbances
3.1.1. Single Modal
3.1.2. Multi-Modal
3.2. Design Principles of Convention Linear ADRC for Smart Structure
4. Theoretical Analysis and Modifications of ADRC
4.1. Theoretical Analysis and Parameter Selection
4.2. Modified ADRC for Smart Structure
4.2.1. Modified ADRC for Specific Problems
4.2.2. Modified ADRC by Nonlinear Function
4.2.3. Composite Control Based on ADRC
4.2.4. ADRC Based on Other Models
5. Overview of Other Anti-Disturbance-Based Vibration Control Methods of Piezoelectric Smart Structures
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anumodh, R.; Singh, B.; Zuber, M. Morphing applications in automobiles: A review. Int. J. Veh. Des. 2021, 85, 1–31. [Google Scholar] [CrossRef]
- Crawley, E.F. Intelligent structures for aerospace: A technology overview and assessment. AIAA J. 1994, 32, 1689–1699. [Google Scholar] [CrossRef]
- Ghorbani, H.; Vatankhah, R.; Farid, M. Adaptive nonsingular fast terminal sliding mode controller design for a smart flexible satellite in general planar motion. Aerosp. Sci. Technol. 2021, 119, 107100. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, L.; Luo, Y.; Ding, R.; Jiang, F. A piezoelectric sensor network with shared signal transmission wires for structural health monitoring of aircraft smart skin. Mech. Syst. Signal Process. 2020, 141, 106730. [Google Scholar] [CrossRef]
- Chen, Y.; Xue, X. Advances in the structural health monitoring of bridges using piezoelectric transducers. Sensors 2018, 18, 4312. [Google Scholar] [CrossRef] [PubMed]
- Sobczyk, M.; Wiesenhutter, S.; Noennig, J.R.; Wallmersperger, T. Smart materials in architecture for actuator and sensor applications: A review. J. Intell. Mater. Syst. Struct. 2022, 33, 379–399. [Google Scholar] [CrossRef]
- Mohith, S.; Karanth, N.; Kulkarni, S.M.; Desai, V.; Patil, S.S. Performance comparison of piezo actuated valveless micropump with central excitation and annular excitation for biomedical applications. Smart Mater. Struct. 2021, 30, 105019. [Google Scholar] [CrossRef]
- Ambrokiewicz, B.; Grabowski, L.; Czy, Z.; Karpiski, P.; Staczek, P.; Litak, G. Ceramic-based piezoelectric material for energy harvesting using hybrid excitation. Materials 2021, 14, 5816. [Google Scholar] [CrossRef]
- Wang, J.; Geng, L.; Ding, L.; Zhu, H.; Yurchenko, D. The state-of-the-art review on energy harvesting from flow-induced vibrations. Appl. Energy 2020, 267, 114902. [Google Scholar] [CrossRef]
- Zhang, S.; Schmidt, R.; Qin, X. Active vibration control of piezoelectric bonded smart structures using PID algorithm. Chin. J. Aeronaut. 2015, 28, 305–313. [Google Scholar] [CrossRef]
- Shahraeeni, M. Assessment of shunted piezoelectric devices for simultaneous noise and vibration reduction: Comparison of passive, active and hybrid networks. Meccanica 2018, 53, 3209–3231. [Google Scholar] [CrossRef]
- Tian, J.; Guo, Q.; Shi, G. Laminated piezoelectric beam element for dynamic analysis of piezolaminated smart beams and GA-based LQR active vibration control. Compos. Struct. 2020, 252, 112480. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Y. High precision tracking of a piezoelectric nano-manipulator with parameterized hysteresis compensation. Smart Mater. Struct. 2018, 27, 065018. [Google Scholar] [CrossRef]
- Bai, L.; Feng, Y.W.; Li, N.; Xue, X.F. Robust model-free adaptive iterative learning control for vibration suppression based on evidential reasoning. Micromachines 2019, 10, 196. [Google Scholar] [CrossRef]
- Yousefpour, A.; Haji Hosseinloo, A.; Reza Hairi Yazdi, M.; Bahrami, A. Disturbance observerbased terminal sliding mode control for effective performance of a nonlinear vibration energy harvester. J. Intell. Mater. Syst. Struct. 2020, 31, 1495–1510. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Zhang, X.Y.; Ji, H.L.; Ying, S.-S.; Schmidt, R. A refined disturbance rejection control for vibration suppression of smart structures under unknown disturbances. J. Low Freq. Noise Vib. Act. Control 2021, 40, 427–441. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, S.Q.; Wang, Z.-X.; Qin, X.S.; Wang, R.-X.; Schmidt, R. Disturbance rejection control with H∞; Optimized observer for vibration suppression of piezoelectric smart structures. Mech. Ind. 2019, 20, 202. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Wang, R.X.; Zhang, S.Q.; Wang, Z.X.; Qin, X.S.; Schmidt, R. Generalized-Disturbance Rejection Control for Vibration Suppression of Piezoelectric Laminated Flexible Structures. Shock Vib. 2018, 2018, 1538936. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Guo, B.; Bacha, S.; Alamir, M.; Hably, A.; Boudinet, C. Generalized Integrator-Extended State Observer with Applications to Grid-Connected Converters in the Presence of Disturbances. IEEE Trans. Control Syst. Technol. 2021, 29, 744–755. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, Z.; Zhu, X.; Wang, Z. Responses and suppression of Joined-Wing UAV in wind field based on distributed model and active disturbance rejection control. Aerosp. Sci. Technol. 2021, 115, 106803. [Google Scholar] [CrossRef]
- Madonski, R.; Ramirez-Neria, M.; Stankovi, M.; Shao, S.; Gao, Z.; Yang, J.; Li, S. On vibration suppression and trajectory tracking in largely uncertain torsional system: An error-based ADRC approach. Mech. Syst. Signal Process. 2019, 134, 106300. [Google Scholar] [CrossRef]
- Fareh, R.; Khadraoui, S.; Abdallah, M.Y.; Baziyad, M.; Bettayeb, M. Active disturbance rejection control for robotic systems: A review. Mechatronics 2021, 80, 102671. [Google Scholar] [CrossRef]
- Chen, S.; Xue, W.; Zhong, S.; Huang, Y. On comparison of modified ADRCs for nonlinear uncertain systems with time delay. Sci. China Inf. Sci. 2018, 61, 70223. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, A. Active disturbance rejection control of DCDC boost converter: A review with modifications for improved performance. IET Power Electron. 2019, 12, 2095–2107. [Google Scholar] [CrossRef]
- Wu, Z.H.; Zhou, H.-C.; Guo, B.Z.; Deng, F. Review and new theoretical perspectives on active disturbance rejection control for uncertain finite-dimensional and infinite-dimensional systems. Nonlinear Dyn. 2020, 101, 935–959. [Google Scholar] [CrossRef]
- Preumont, A. Vibration Control of Active Structures; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zhang, S.Q.; Schmidt, R. Large rotation FE transient analysis of piezolaminated thin-walled smart structures. Smart Mater. Struct. 2013, 22, 105025. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Hosseini, S.H.S.; Singhal, A. A comprehensive review on the modeling of smart piezoelectric nanostructures. Struct. Eng. Mech. 2020, 74, 611–633. [Google Scholar] [CrossRef]
- Shivashankar, P.; Gopalakrishnan, S. Review on the use of piezoelectric materials for active vibration, noise, and flow control. Smart Mater. Struct. 2020, 29, 053001. [Google Scholar] [CrossRef]
- Mustapha, K.B.; Metwalli, K.M. A review of fused deposition modelling for 3D printing of smart polymeric materials and composites. Eur. Polym. J. 2021, 156, 110591. [Google Scholar] [CrossRef]
- Mallek, H.; Jrad, H.; Wali, M.; Dammak, F. Nonlinear dynamic analysis of piezoelectric-bonded FG-CNTR composite structures using an improved FSDT theory. Eng. Comput. 2021, 37, 1389–1407. [Google Scholar] [CrossRef]
- Li, L.L.; Xue, C.X. Chaotic motion of piezoelectric material hyperbolic shell under thermoelastic coupling. Wuli Xuebao/Acta Phys. Sin. 2019, 68, 010501. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, Z.; Zuo, M. Phase leading active disturbance rejection control for a nanopositioning stage. ISA Trans. 2021, 116, 218–231. [Google Scholar] [CrossRef] [PubMed]
- Pu, Y.; Yao, C.; Li, X.; Liu, Z. Adaptive active vibration control for piezoelectric smart structure with online hysteresis identification and compensation. J. Vib. Control 2022, 28, 626–636. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Rakotondrabe, M.; Al-Darabsah, I.; Aljanaideh, O. Internal model-based feedback control design for inversion-free feedforward rate-dependent hysteresis compensation of piezoelectric cantilever actuator. Control Eng. Pract. 2018, 72, 29–41. [Google Scholar] [CrossRef]
- Shao, S.; Xu, M.; Zhang, S.; Xie, S. Stroke maximizing and high efficient hysteresis hybrid modeling for a rhombic piezoelectric actuator. Mech. Syst. Signal Process. 2016, 75, 631–647. [Google Scholar] [CrossRef]
- Zhang, X.; Su, C.Y.; Lin, Y.; Ma, L.; Wang, J. Adaptive Neural Network Dynamic Surface Control for a Class of Time-Delay Nonlinear Systems with Hysteresis Inputs and Dynamic Uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2844–2860. [Google Scholar] [CrossRef]
- Wang, G.; Wang, S.; Bai, F. Modeling and identification of piezoelectric hysteresis by an asymmetric Bouc-Wen model. In Proceedings of the 36th Chinese Control Conference, CCC 2017, Dalian, China, 26–28 July 2017; pp. 2000–2005. [Google Scholar]
- Mao, X.; Du, H.; Sun, S.; Liu, X.; Shan, J.; Feng, Y. A fast sparse least squares support vector machine hysteresis model for piezoelectric actuator. Smart Mater. Struct. 2022, 31, 117001. [Google Scholar] [CrossRef]
- Huang, D.; Min, D.; Jian, Y.; Li, Y. Current-Cycle Iterative Learning Control for High-Precision Position Tracking of Piezoelectric Actuator System via Active Disturbance Rejection Control for Hysteresis Compensation. IEEE Trans. Ind. Electron. 2020, 67, 8680–8690. [Google Scholar] [CrossRef]
- Dal Borgo, M.; Tehrani, M.G.; Elliott, S.J. Active nonlinear control of a stroke limited inertial actuator: Theory and experiment. J. Sound Vib. 2020, 465, 115009. [Google Scholar] [CrossRef]
- Peng, H.; Li, F.; Kan, Z. A novel distributed model predictive control method based on a substructuring technique for smart tensegrity structure vibrations. J. Sound Vib. 2020, 471, 115171. [Google Scholar] [CrossRef]
- Peng, H.; Li, F.; Zhang, S.; Chen, B. A novel fast model predictive control with actuator saturation for large-scale structures. Comput. Struct. 2017, 187, 35–49. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J.; Gabbert, U. Compensation for hysteresis with input saturation: An anti-saturation block approach. Smart Mater. Struct. 2018, 27, 117001. [Google Scholar] [CrossRef]
- Mevada, J.R.; Prajapati, J.M. Active vibration control of smart beam under parametric variations. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 394. [Google Scholar] [CrossRef]
- Deng, F.; Remond, D.; Gaudiller, L. Self-adaptive modal control for time-varying structures. J. Sound Vib. 2011, 330, 3301–3315. [Google Scholar] [CrossRef]
- Bendine, K.; Satla, Z.; Boukhoulda, F.B.; Nouari, M. Active Vibration damping of Smart composite beams based on system identification technique. Curved Layer. Struct. 2018, 5, 43–48. [Google Scholar] [CrossRef]
- Rodriguez, J.; Collet, M.; Chesne, S. Experimental modal identification of smart composite structure applied to active vibration control. Smart Mater. Struct. 2021, 30, 115008. [Google Scholar] [CrossRef]
- Alkhatib, R.; Golnaraghi, M.F. Active structural vibration control: A review. Shock Vib. Dig. 2003, 35, 367–383. [Google Scholar] [CrossRef]
- Dong, X.; Ye, L.; Peng, Z.; Hua, H.; Meng, G. A study on controller structure interaction of piezoelectric smart structures based on finite element method. J. Intell. Mater. Syst. Struct. 2014, 25, 1401–1413. [Google Scholar] [CrossRef]
- Yan, X.; Xu, Z.D.; Shi, Q.X.; Dai, J. Effect of Control-Structure Interaction Using Torsional Servomotor for Active Tuned Mass Damper Control System. Int. J. Struct. Stab. Dyn. 2022, 22, 2250142. [Google Scholar] [CrossRef]
- Yao, H.; Tan, P.; Zhou, H.; Zhou, F. Real-time hybrid testing for active mass driver system based on an improved control strategy against control-structure-interaction effects. J. Build. Eng. 2023, 63, 105477. [Google Scholar] [CrossRef]
- Jiao, P.; Egbe, K.-J.I.; Xie, Y.; Nazar, A.M.; Alavi, A.H. Piezoelectric sensing techniques in structural health monitoring: A state-of-the-art review. Sensors 2020, 20, 3730. [Google Scholar] [CrossRef] [PubMed]
- Hoshyarmanesh, H.; Maddahi, Y. Poling Process of Composite Piezoelectric Sensors for Structural Health Monitoring: A Pilot Comparative Study. IEEE Sens. Lett. 2018, 2, 6000304. [Google Scholar] [CrossRef]
- He, Y.; Chen, X.; Liu, Z.; Qin, Y. Piezoelectric self-sensing actuator for active vibration control of motorized spindle based on adaptive signal separation. Smart Mater. Struct. 2018, 27, 065011. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, A. On Active Disturbance Rejection Control in Presence of Measurement Noise. IEEE Trans. Ind. Electron. 2022, 69, 11600–11610. [Google Scholar] [CrossRef]
- Lakomy, K.; Madonski, R. Cascade extended state observer for active disturbance rejection control applications under measurement noise. ISA Trans. 2021, 109, 1–10. [Google Scholar] [CrossRef]
- Du, Y.; Cao, W.; She, J. Analysis and Design of Active Disturbance Rejection Control With an Improved Extended State Observer for Systems With Measurement Noise. IEEE Trans. Ind. Electron. 2023, 70, 855–865. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Zhu, C.; Su, J.; Li, J. Nonlinear ESO-based vibration control for an all-clamped piezoelectric plate with disturbances and time delay: Design and hardware implementation. J. Intell. Mater. Syst. Struct. 2022, 33, 2321–2335. [Google Scholar] [CrossRef]
- Li, S.; Zhu, C.; Mao, Q.; Su, J.; Li, J. Active disturbance rejection vibration control for an all-clamped piezoelectric plate with delay. Control Eng. Pract. 2021, 108, 104719. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, G.; Xiang, M.; Sun, H.; Wang, X.; Xie, X. Vibration control for the nonlinear resonant response of a piezoelectric elastic beam via time-delayed feedback. Smart Mater. Struct. 2019, 28, 095010. [Google Scholar] [CrossRef]
- Feng, B.; Özer, A.Ö. Exponential stability results for the boundary-controlled fully-dynamic piezoelectric beams with various distributed and boundary delays. J. Math. Anal. Appl. 2022, 508, 125845. [Google Scholar] [CrossRef]
- Peng, J.; Xiang, M.; Wang, L.; Xie, X.; Sun, H.; Yu, J. Nonlinear primary resonance in vibration control of cable-stayed beam with time delay feedback. Mech. Syst. Signal Process. 2020, 137, 106488. [Google Scholar] [CrossRef]
- Warminski, J.; Kloda, L.; Latalski, J.; Mitura, A.; Kowalczuk, M. Nonlinear vibrations and time delay control of an extensible slowly rotating beam. Nonlinear Dyn. 2021, 103, 3255–3281. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H.G.; Cai, G.P. Time delay stability analysis for vibration suppression of a smart cantilever beam with hysteresis property. J. Low Freq. Noise Vib. Act. Control 2021, 40, 898–915. [Google Scholar] [CrossRef]
- Li, D.; Jiang, J.; Liu, W.; Fan, C. A New Mechanism for the Vibration Control of Large Flexible Space Structures with Embedded Smart Devices. IEEE/ASME Trans. Mechatron. 2015, 20, 1653–1659. [Google Scholar] [CrossRef]
- Callipari, F.; Sabatini, M.; Angeletti, F.; Iannelli, P.; Gasbarri, P. Active vibration control of large space structures: Modelling and experimental testing of offset piezoelectric stack actuators. Acta Astronaut. 2022, 198, 733–745. [Google Scholar] [CrossRef]
- Azimi, M.; Joubaneh, E.F. Dynamic modeling and vibration control of a coupled rigid-flexible high-order structural system: A comparative study. Aerosp. Sci. Technol. 2020, 102, 105875. [Google Scholar] [CrossRef]
- Varelis, D.; Saravanos, D.A. Coupled nonlinear mechanics for the electromechanical response of multi-stable piezoelectric shallow shells with piezoelectric films. Aerosp. Sci. Technol. 2021, 109, 106444. [Google Scholar] [CrossRef]
- Andreades, C.; Fierro, G.P.M.; Meo, M.; Ciampa, F. Nonlinear ultrasonic inspection of smart carbon fibre reinforced plastic composites with embedded piezoelectric lead zirconate titanate transducers for space applications. J. Intell. Mater. Syst. Struct. 2019, 30, 2995–3007. [Google Scholar] [CrossRef]
- Preumont, A.; Voltan, M.; Sangiovanni, A.; Mokrani, B.; Alaluf, D. Active tendon control of suspension bridges. Smart Struct. Syst. 2016, 18, 31–52. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, C.; Golub, M.V. Physics-informed neural networks for analysis of 2D thin-walled structures. Eng. Anal. Bound. Elem. 2022, 145, 161–172. [Google Scholar] [CrossRef]
- Zeng, Y.; Pan, P.; Cao, Y.; He, Z. Shear deformation detection in smart rubber bearing (SRB) using active sensing method. Eng. Struct. 2021, 242, 112573. [Google Scholar] [CrossRef]
- Wang, X.; Xia, P.; Masarati, P. Active aeroelastic control of aircraft wings with piezo-composite. J. Sound Vib. 2019, 455, 1–19. [Google Scholar] [CrossRef]
- Librescu, L.; Na, S.; Marzocca, P.; Chung, C.; Kwak, M.K. Active aeroelastic control of 2-D wing-flap systems operating in an incompressible flowfield and impacted by a blast pulse. J. Sound Vib. 2005, 283, 685–706. [Google Scholar] [CrossRef]
- Morgan, D.R. An adaptive modal based active control systems. J. Acoust. Soc. Am. 1991, 89, 248–256. [Google Scholar] [CrossRef]
- Lee, C.K.; Moon, F.C. Modal sensors/actuator. J. Appl. Mech. 1990, 57, 434–441. [Google Scholar] [CrossRef]
- Lee, C.K.; Chiang, W.W.; O’Sullivan, T.C. Piezoelectric modal sensor/actuator pairs for critical active damping vibration control. J. Acoust. Soc. Am. 1991, 90, 374–384. [Google Scholar] [CrossRef]
- Mao, Q.; Pietrzko, S. Design of shaped piezoelectric modal sensor for beam with arbitrary boundary conditions by using Adomian decomposition method. J. Sound Vib. 2010, 329, 2068–2082. [Google Scholar] [CrossRef]
- Mao, Q.; Pietrzko, S. Design of shaped piezoelectric modal sensor for a type of non-uniform beams using adomian-modified decomposition method. J. Intell. Mater. Syst. Struct. 2011, 22, 149–159. [Google Scholar] [CrossRef]
- Friswell, M.I. Partial and segmented modal sensors for beam structures. J. Vib. Control 1999, 5, 619–637. [Google Scholar] [CrossRef]
- Adhikari, S.; Friswell, M.I. Shaped modal sensors for linear stochastic beams. J. Intell. Mater. Syst. Struct. 2009, 20, 2269–2284. [Google Scholar] [CrossRef]
- Sullivan, J.M.; Hubbard, J.E.; Burke, S.E. Distributed transducer design for plates: Spatial shape and shading as design parameters. In Proceedings of the Smart Structures and Materials 1994: Mathematics and Control in Smart Structures, Orlando, FL, USA, 13–18 February 1994; pp. 132–144. [Google Scholar]
- Donoso, A.; Bellido, J.C.; Chacon, J.M. Numerical and analytical method for the design of piezoelectric modal sensors/actuators for shell-type structures. Int. J. Numer. Methods Eng. 2010, 81, 1700–1712. [Google Scholar] [CrossRef]
- Donoso, A.; Guest, J.K. Topology optimization of piezo modal transducers considering electrode connectivity constraints. Comput. Methods Appl. Mech. Eng. 2019, 356, 101–115. [Google Scholar] [CrossRef]
- Porn, S.; Nasser, H.; Coelho, R.F.; Belouettar, S.; Deraemaeker, A. Level set based structural optimization of distributed piezoelectric modal sensors for plate structures. Int. J. Solids Struct. 2016, 80, 348–358. [Google Scholar] [CrossRef]
- Sanada, A.; Higashiyama, K.; Tanaka, N. Active control of sound transmission through a rectangular panel using point-force actuators and piezoelectric film sensors. J. Acoust. Soc. Am. 2015, 137, 458–469. [Google Scholar] [CrossRef]
- Zahui, M.B.; Naghshineh, K.; Kamman, J.W. Narrow band active control of sound radiated from a baffled beam using local volume displacement minimization. Appl. Acoust. 2001, 62, 47–64. [Google Scholar] [CrossRef]
- Rozema, R.; Zellers, B.; Naghshineh, K.; Zahui, M. Development of a PVDF sensor for the measurement of the acoustic local volume displacement of vibrating beams. J. Vib. Acoust. Trans. ASME 2004, 126, 352–358. [Google Scholar] [CrossRef]
- Zhong, H.; Wu, J.; Bao, B.; Mao, Q. A composite beam integrating an in-situ FPCB sensor membrane with PVDF arrays for modal curvature measurement. Measurement 2020, 166, 108241. [Google Scholar] [CrossRef]
- Mao, Q.; Zhong, H. Sound power estimation for beam and plate structures using polyvinylidene fluoride films as sensors. Sensors 2017, 17, 1111. [Google Scholar] [CrossRef]
- Trindade, M.A.; Pagani, C.C.; Oliveira, L.P.R. Semi-modal active vibration control of plates using discrete piezoelectric modal filters. J. Sound Vib. 2015, 351, 17–28. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z.L. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Yang, X.; Huang, Y. Capabilities of extended state observer for estimating uncertainties. In Proceedings of the 2009 American Control Conference, ACC 2009, St. Louis, MO, USA, 10–12 June 2009; pp. 3700–3705. [Google Scholar]
- Qi, X.; Li, J.; Xia, Y.; Gao, Z. On the Robust Stability of Active Disturbance Rejection Control for SISO Systems. Circuits Syst. Signal Process. 2017, 36, 65–81. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Xiong, S.; Du, L.; Li, Y. An extended state observer for a class of nonlinear systems with a new frequency-domain analysis on convergence. ISA Trans. 2020, 107, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Li, D.; Gao, Z.; Yang, Z.; Zhao, S. Combined feedforward and model-assisted active disturbance rejection control for non-minimum phase system. ISA Trans. 2016, 64, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.L.; Guo, B.Z. A novel extended state observer for output tracking of MIMO systems with mismatched uncertainty. IEEE Trans. Autom. Control 2018, 63, 211–218. [Google Scholar] [CrossRef]
- Skupin, P.; Nowak, P.; Czeczot, J. On the stability of active disturbance rejection control for first-order plus delay time processes. ISA Trans. 2022, 125, 179–188. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Xue, W.; Huang, Y. Analytical design of active disturbance rejection control for nonlinear uncertain systems with delay. Control Eng. Pract. 2019, 84, 323–336. [Google Scholar] [CrossRef]
- Patelski, R.; Dutkiewicz, P. On the stability of ADRC for manipulators with modelling uncertainties. ISA Trans. 2020, 102, 295–303. [Google Scholar] [CrossRef]
- Gao, Z. Active disturbance rejection control for nonlinear fractional-order systems. Int. J. Robust Nonlinear Control 2016, 26, 876–892. [Google Scholar] [CrossRef]
- Wei, W.; Xia, P.; Chen, N.; Zuo, M. Frequency characteristics of a phase optimised active disturbance rejection control. Int. J. Model. Identif. Control 2020, 36, 222–232. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and Bandwidth-Parameterization based Controller Tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Teppa-Garran, P.; Garcia, G. Optimal Tuning of PI/PID/PID(n-1) Controllers in Active Disturbance Rejection Control. Control Eng. Appl. Inform. 2013, 15, 26–36. [Google Scholar]
- Zhou, R.; Tan, W. Analysis and tuning of general linear active disturbance rejection controllers. IEEE Trans. Ind. Electron. 2019, 66, 5497–5507. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, H.; Zhao, B.; Zhao, L. A GA-based parameters tuning method for an ADRC controller of ISP for aerial remote sensing applications. ISA Trans. 2018, 81, 318–328. [Google Scholar] [CrossRef]
- Benrabah, A.; Xu, D.; Gao, Z. Active Disturbance Rejection Control of LCL-Filtered Grid-Connected Inverter Using Pade Approximation. IEEE Trans. Ind. Appl. 2018, 54, 6179–6189. [Google Scholar] [CrossRef]
- Zheng, Q.; Gao, Z. Predictive active disturbance rejection control for processes with time delay. ISA Trans. 2014, 53, 873–881. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Gao, Z. Modified active disturbance rejection control for time-delay systems. ISA Trans. 2014, 53, 882–888. [Google Scholar] [CrossRef]
- Sun, L.; Xue, W.; Li, D.; Zhu, H.; Su, Z.-G. Quantitative Tuning of Active Disturbance Rejection Controller for FOPTD Model with Application to Power Plant Control. IEEE Trans. Ind. Electron. 2022, 69, 805–815. [Google Scholar] [CrossRef]
- Wei, W.; Duan, B.; Zhang, W.; Zuo, M. Active disturbance rejection control for nanopositioning: A robust U-model approach. ISA Trans. 2022, 128, 599–610. [Google Scholar] [CrossRef]
- Wei, W.; Xia, P.; Xue, W.; Zuo, M. On the Disturbance Rejection of a Piezoelectric Driven Nanopositioning System. IEEE Access 2020, 8, 74771–74781. [Google Scholar] [CrossRef]
- Yang, C.; Wang, Y.; Youcef-Toumi, K. Hierarchical Antidisturbance Control of a Piezoelectric Stage via Combined Disturbance Observer and Error-Based ADRC. IEEE Trans. Ind. Electron. 2022, 69, 5060–5070. [Google Scholar] [CrossRef]
- Zhao, Z.L.; Guo, B.Z. A nonlinear extended state observer based on fractional power functions. Automatica 2017, 81, 286–296. [Google Scholar] [CrossRef]
- Li, S.; Zhu, C.; Li, J.; Mao, Q. A nonlinear disturbance rejection vibration control for an all-clamped piezoelectric panel. Int. J. Appl. Electromagn. Mech. 2020, 64, 403–411. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Li, Z.; Zhao, C.; Gao, F.; Xu, F.; Wang, P. Extended-State-Observer Based Model Predictive Control of a Hybrid Modular DC Transformer. IEEE Trans. Ind. Electron. 2021, 69, 1561–1572. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, T.; Sun, X.; Dong, J.; Wang, Z.; Yang, C. Sliding mode control combined with extended state observer for an ankle exoskeleton driven by electrical motor. Mechatronics 2021, 76, 102554. [Google Scholar] [CrossRef]
- Nie, Z.Y.; Zhang, B.; Wang, Q.-G.; Liu, R.-J.; Luo, J.-L. Adaptive active disturbance rejection control guaranteeing uniformly ultimate boundedness and simplicity. Int. J. Robust Nonlinear Control 2020, 30, 7278–7294. [Google Scholar] [CrossRef]
- Wang, S.; Li, S.; Su, J.; Li, J.; Zhang, L. Extended state observer-based nonsingular terminal sliding mode controller for a DC-DC buck converter with disturbances: Theoretical analysis and experimental verification. Int. J. Control. 2022. [Google Scholar] [CrossRef]
- Li, S.; Li, J.; Mo, Y. Piezoelectric multimode vibration control for stiffened plate using ADRC-based acceleration compensation. IEEE Trans. Ind. Electron. 2014, 61, 6892–6902. [Google Scholar] [CrossRef]
- Xu, Z.; Li, S.; Li, J.; Zhang, L.; Wang, S. Nonsingular Terminal Sliding-Mode Controller Based on Extended State Observer for Two-Mode Vibration of a Piezoelectric Plate: Design, Analysis and Experiments. Int. J. Struct. Stab. Dyn. 2022. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Y.; Huang, J. Application of fractional-order active disturbance rejection controller on linear motion system. Control Eng. Pract. 2018, 81, 207–214. [Google Scholar] [CrossRef]
- Zheng, Y.; Huang, Z.; Tao, J.; Sun, H.; Sun, Q.; Sun, M.; Dehmer, M.; Chen, Z. A Novel Chaotic Fractional-Order Beetle Swarm Optimization Algorithm and Its Application for Load-Frequency Active Disturbance Rejection Control. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1267–1271. [Google Scholar] [CrossRef]
- Al-Saggaf, U.M.; Mansouri, R.; Bettayeb, M.; Mehedi, I.M.; Munawar, K. Robustness Improvement of the Fractional-Order LADRC Scheme for Integer High-Order System. IEEE Trans. Ind. Electron. 2021, 68, 8572–8581. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y. A Two-Degree-of-Freedom Controller Design Satisfying Separation Principle with Fractional-Order PD and Generalized ESO. IEEE/ASME Trans. Mechatron. 2022, 27, 137–148. [Google Scholar] [CrossRef]
- Abdallah, M.; Fareh, R. Fractional order active disturbance rejection control for trajectory tracking for 4-DOF serial link manipulator. Int. J. Model. Identif. Control 2020, 36, 57–65. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y.; Zheng, W.; Gao, Z.; Chen, Y. Fractional order active disturbance rejection control with the idea of cascaded fractional order integrator equivalence. ISA Trans. 2021, 114, 359–369. [Google Scholar] [CrossRef]
- Muresan, C.I.; Folea, S.; Birs, I.R.; Ionescu, C. A novel fractional-order model and controller for vibration suppression in flexible smart beam. Nonlinear Dyn. 2018, 93, 525–541. [Google Scholar] [CrossRef]
- Wang, J.; Tang, S.X.; Pi, Y.; Krstic, M. Exponential regulation of the anti-collocatedly disturbed cage in a wave PDE-modeled ascending cable elevator. Automatica 2018, 95, 122–136. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, J.; Zong, X. Leader-follower synchronization controller design for a network of boundary-controlled wave PDEs with structured time-varying perturbations and general disturbances. J. Frankl. Inst. 2021, 358, 834–855. [Google Scholar] [CrossRef]
- Jin, H.; Song, J.; Lan, W.; Gao, Z. On the characteristics of ADRC: A PID interpretation. Sci. China Inf. Sci. 2020, 63, 209201. [Google Scholar] [CrossRef]
- Rojas, H.D.; Cortes-Romero, J. On the equivalence between Generalized Proportional Integral Observer and Disturbance Observer. ISA Trans. 2022, in press. [CrossRef]
- Sira-Ramirez, H.; Zurita-Bustamante, E.W. On the equivalence between ADRC and Flat Filter based controllers: A frequency domain approach. Control Eng. Pract. 2021, 107, 104656. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Zurita-Bustamante, E.W.; Huang, C. Equivalence among flat filters, dirty derivative-based PID controllers, ADRC, and integral reconstructor-based sliding mode control. IEEE Trans. Control Syst. Technol. 2020, 28, 1696–1710. [Google Scholar] [CrossRef]
- Cai, Z.; Wang, Z.; Zhao, J.; Wang, Y. Equivalence of LADRC and INDI controllers for improvement of LADRC in practical applications. ISA Trans. 2022, 126, 562–573. [Google Scholar] [CrossRef]
- Li, S.; Qiu, J.; Li, J.; Ji, H.; Zhu, K. Multi-modal vibration control using amended disturbance observer compensation. IET Control Theory Appl. 2012, 6, 72–83. [Google Scholar] [CrossRef]
- Li, S.; Zhao, R.; Li, J.; Mo, Y.; Sun, Z. DOB-based piezoelectric vibration control for stiffened plate considering accelerometer measurement noise. Smart Struct. Syst. 2014, 14, 327–345. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Li, H.N.; Schmidt, R.; Muller, P.C. Disturbance rejection control for vibration suppression of piezoelectric laminated thin-walled structures. J. Sound Vib. 2014, 333, 1209–1223. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Schmidt, R.; Muller, P.C.; Qin, X.S. Disturbance rejection control for vibration suppression of smart beams and plates under a high frequency excitation. J. Sound Vib. 2015, 353, 19–37. [Google Scholar] [CrossRef]
- Miyamoto, K.; She, J.; Imani, J.; Xin, X.; Sato, D. Equivalent-input-disturbance approach to active structural control for seismically excited buildings. Eng. Struct. 2016, 125, 392–399. [Google Scholar] [CrossRef]
- Zhu, Q.; Yue, J.Z.; Liu, W.Q.; Wang, X.D.; Chen, J.; Hu, G.D. Active vibration control for piezoelectricity cantilever beam: An adaptive feedforward control method. Smart Mater. Struct. 2017, 26, 047003. [Google Scholar] [CrossRef]
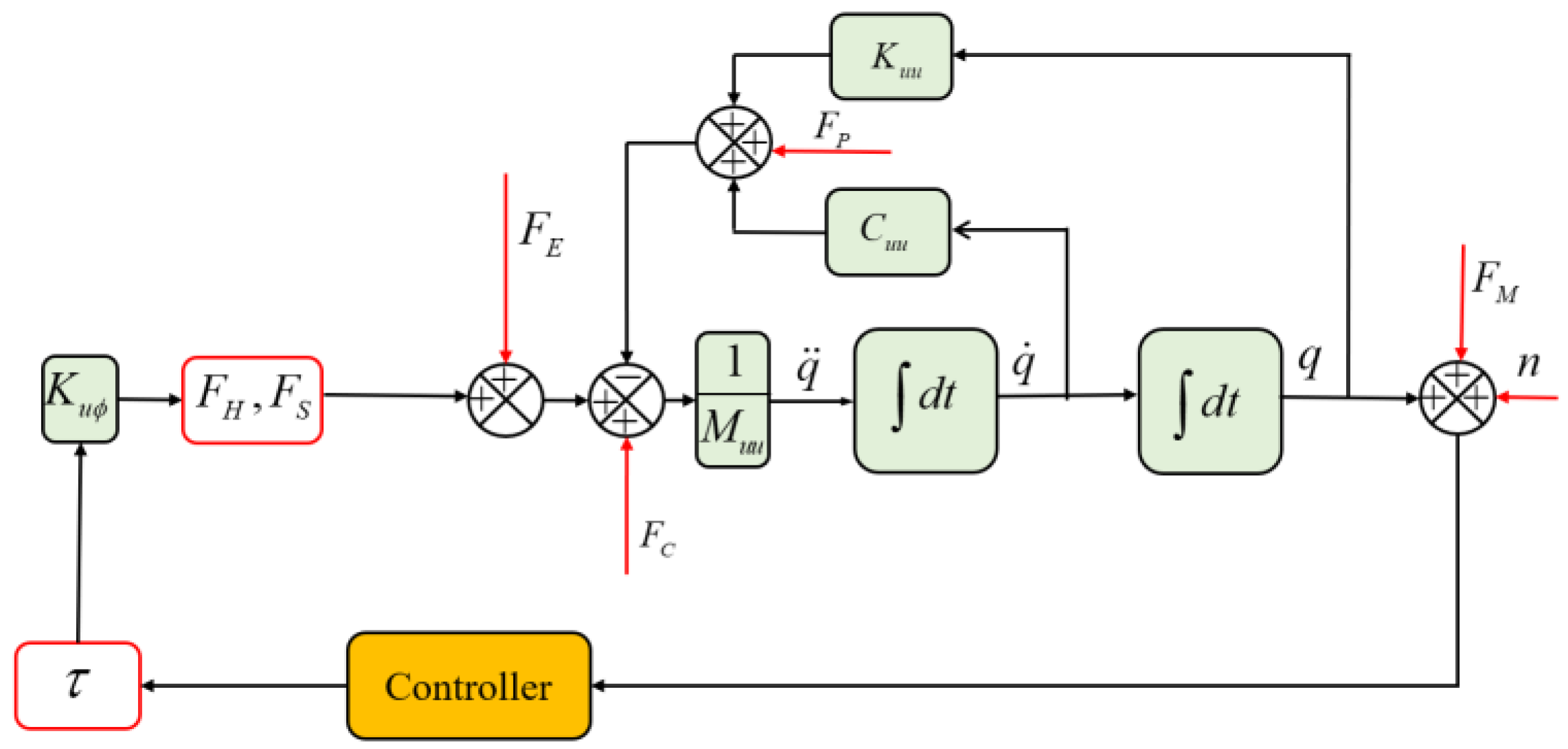
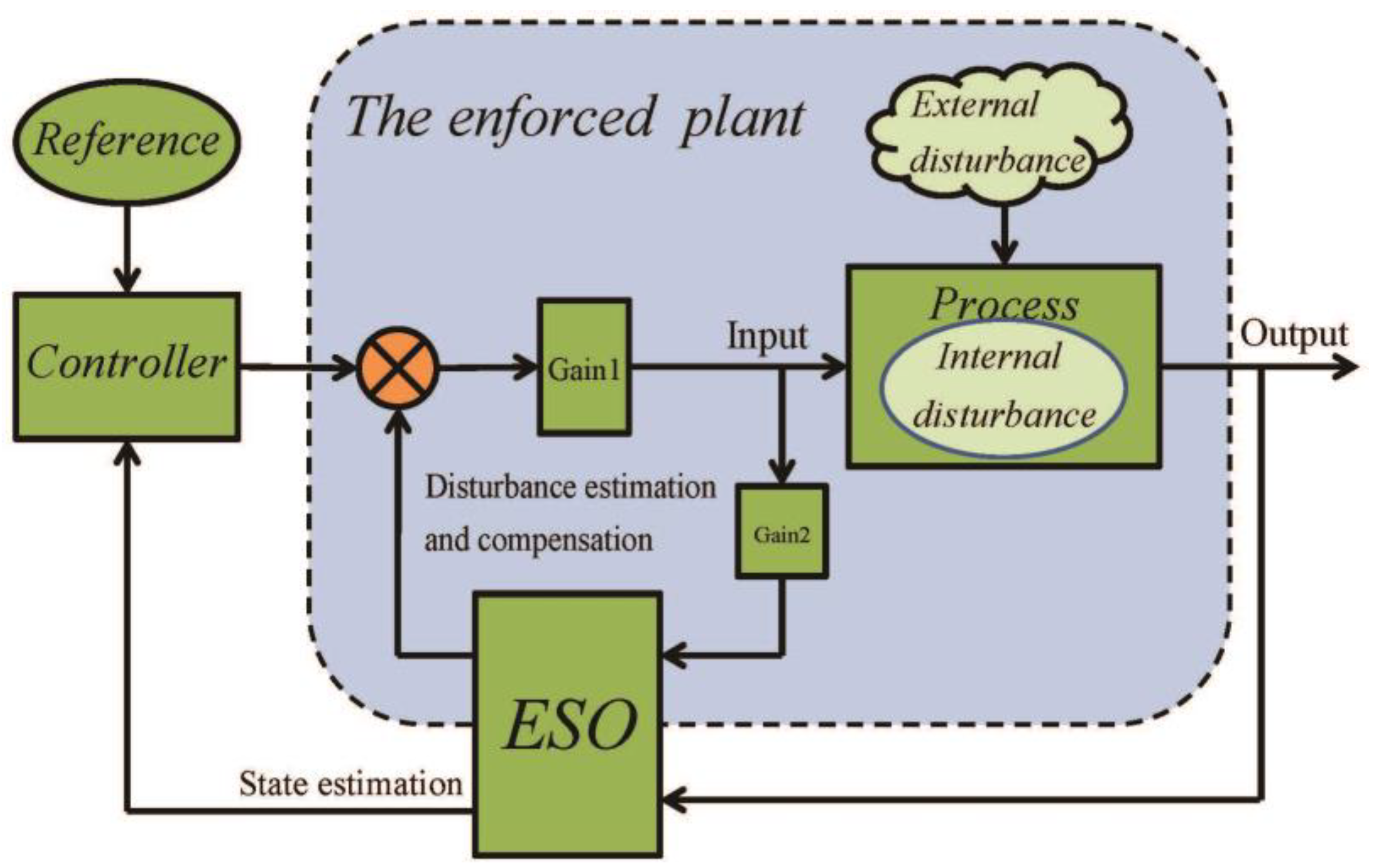

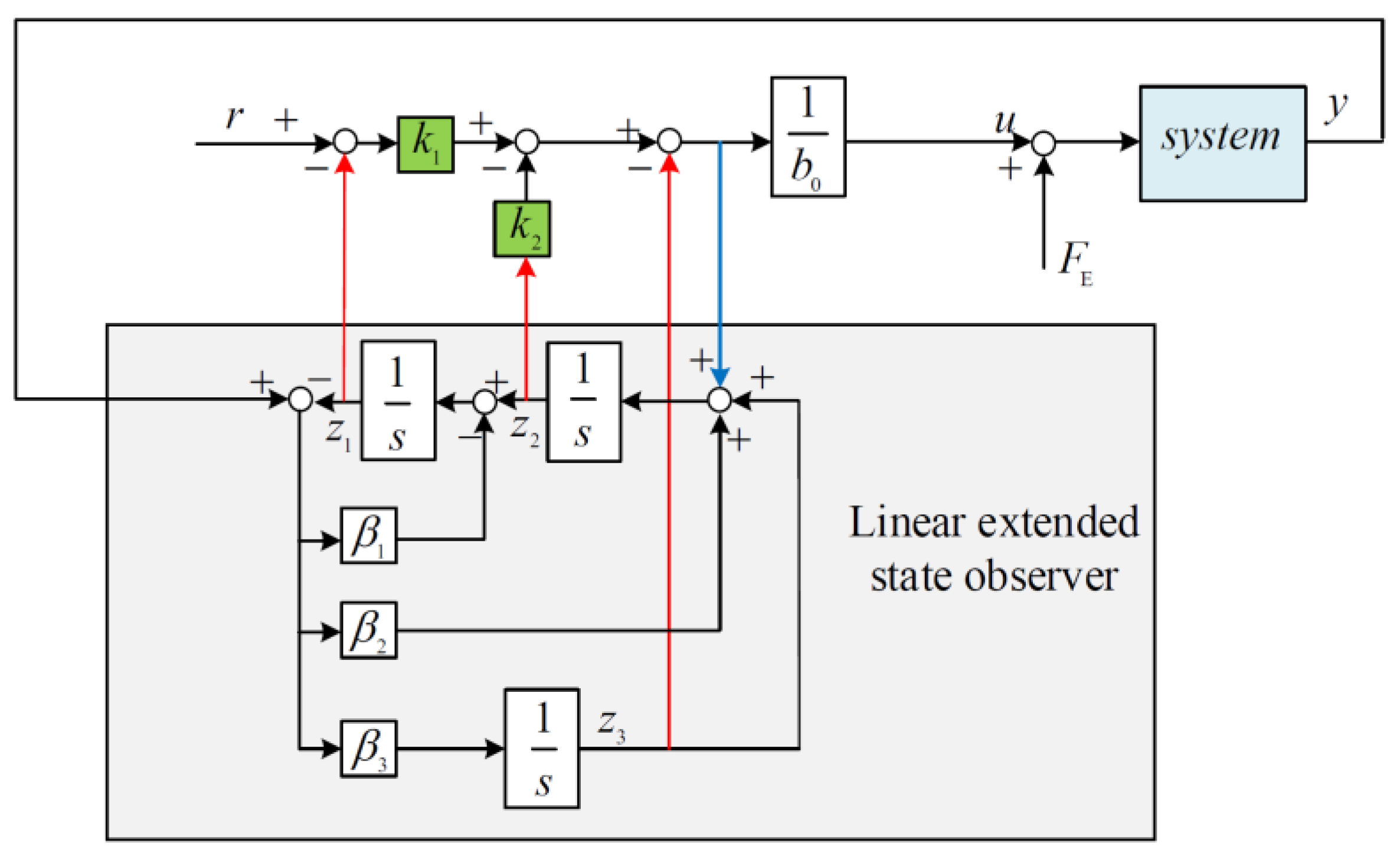
| Symbol | Meaning |
|---|---|
| Δ | Nonlinear dynamics of structures |
| FH | Hysteresis property of piezoelectric actuator |
| FS | Saturation nonlinearity |
| FP | Parametric uncertainties |
| FC | Control–structure interaction |
| FM | Measurement error effects |
| n | Measurement noise |
| τ | Time delay |
| FE | External disturbances |
| Typical Structures | Common External Disturbances | References |
|---|---|---|
| Large space structures |
| [3,30,67,68,69,70,71] |
| Civil structures |
| [72,73,74] |
| Rotor system of the helicopters |
| [75,76] |
| Methods | References | Characteristics |
|---|---|---|
| Combined ADRC and Smith predictor | [60,61] |
|
| Phase-leading extended state observer | [34] |
|
| Combined ADRC and current-cycle iterative learning control | [41] |
|
| Combined disturbance observer and error-based ADRC | [115] |
|
| Nonlinear ADRC based on “fa” function | [117] |
|
| Combined ADRC and nonsingular terminal sliding mode control | [123] |
|
| ADRC based on fractional order controller | [127] |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhang, L.; Li, S.; Mao, Q.; Mao, Y. Active Disturbance Rejection Control for Piezoelectric Smart Structures: A Review. Machines 2023, 11, 174. https://doi.org/10.3390/machines11020174
Li J, Zhang L, Li S, Mao Q, Mao Y. Active Disturbance Rejection Control for Piezoelectric Smart Structures: A Review. Machines. 2023; 11(2):174. https://doi.org/10.3390/machines11020174
Chicago/Turabian StyleLi, Juan, Luyao Zhang, Shengquan Li, Qibo Mao, and Yao Mao. 2023. "Active Disturbance Rejection Control for Piezoelectric Smart Structures: A Review" Machines 11, no. 2: 174. https://doi.org/10.3390/machines11020174
APA StyleLi, J., Zhang, L., Li, S., Mao, Q., & Mao, Y. (2023). Active Disturbance Rejection Control for Piezoelectric Smart Structures: A Review. Machines, 11(2), 174. https://doi.org/10.3390/machines11020174







