Window Shape Estimation for Glass Façade-Cleaning Robot
Abstract
1. Introduction
- A glass façade-cleaning robot moves on a window surface with a rectangular frame.
- The robot needs to estimate the window shape it is on with its own external sensor.
2. Related Work
- (1)
- A testbed for observing a window frame, called a window scanning robot, is presented: The window scanning robot having a 2D laser range scanner installed perpendicularly to a window surface is developed on the basis of a concept of nested reconfigurable robots for façade cleaning, detailed in the next section. This allows robots to observe window frames with little or no rising on the window surface they work on and to independently perform cleaning and exploration tasks. The window scanning robot offers an idea to acquire environmental data on a glass façade of a building for façade cleaning.
- (2)
- A method for façade-cleaning robots to estimate a window shape is proposed: The window shape estimation is achieved by arranging points obtained by an external sensor and performing the loop closure based on the robot’s pose estimated by the EKF. This is due to the environment on a window that has fewer features required for incorporating feature matching in a pose estimation, such as SLAM [38,39]. The method to obtain window shapes on the window surface a robot is on has not been presented to the knowledge of the authors.
- (3)
- The validities of the window scanning robot and the window shape estimation method are demonstrated: Focusing on demonstrating the effectiveness of the ideas of window scanning and window shape estimation, we experiment with the window scanning robot developed on a window placed on the ground. The experimental results show that the robot can acquire the window shape by scanning the window frame, and the proposed method is effective for estimating the shape of the window the robot works on.
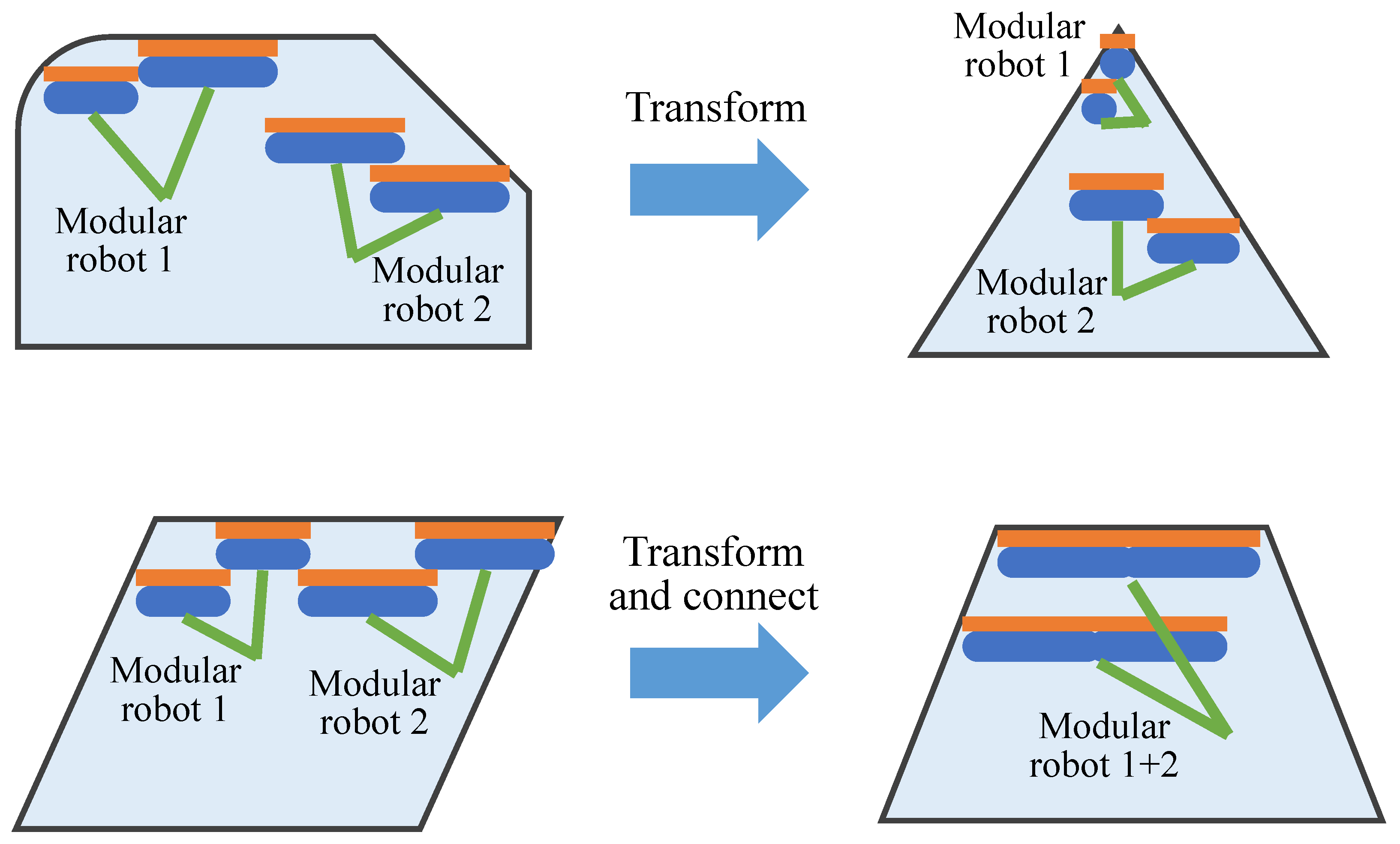
3. Concept of Nested Reconfigurable Robots for Façade Cleaning
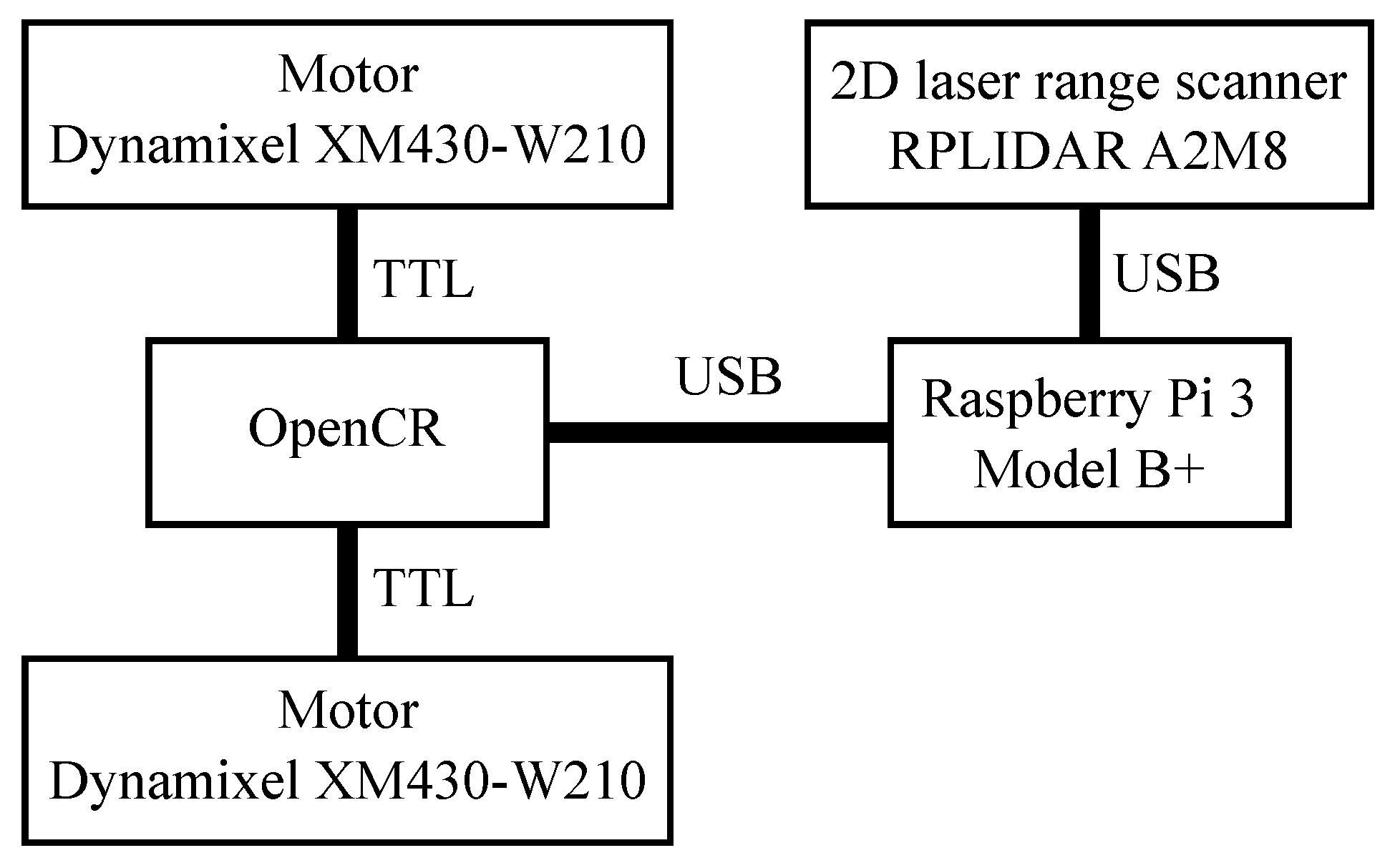
4. Window Scanning Robot
5. Window Shape Estimation
5.1. Pose Estimation
5.1.1. Model of the Window Scanning Robot
5.1.2. Extended Kalman Filter
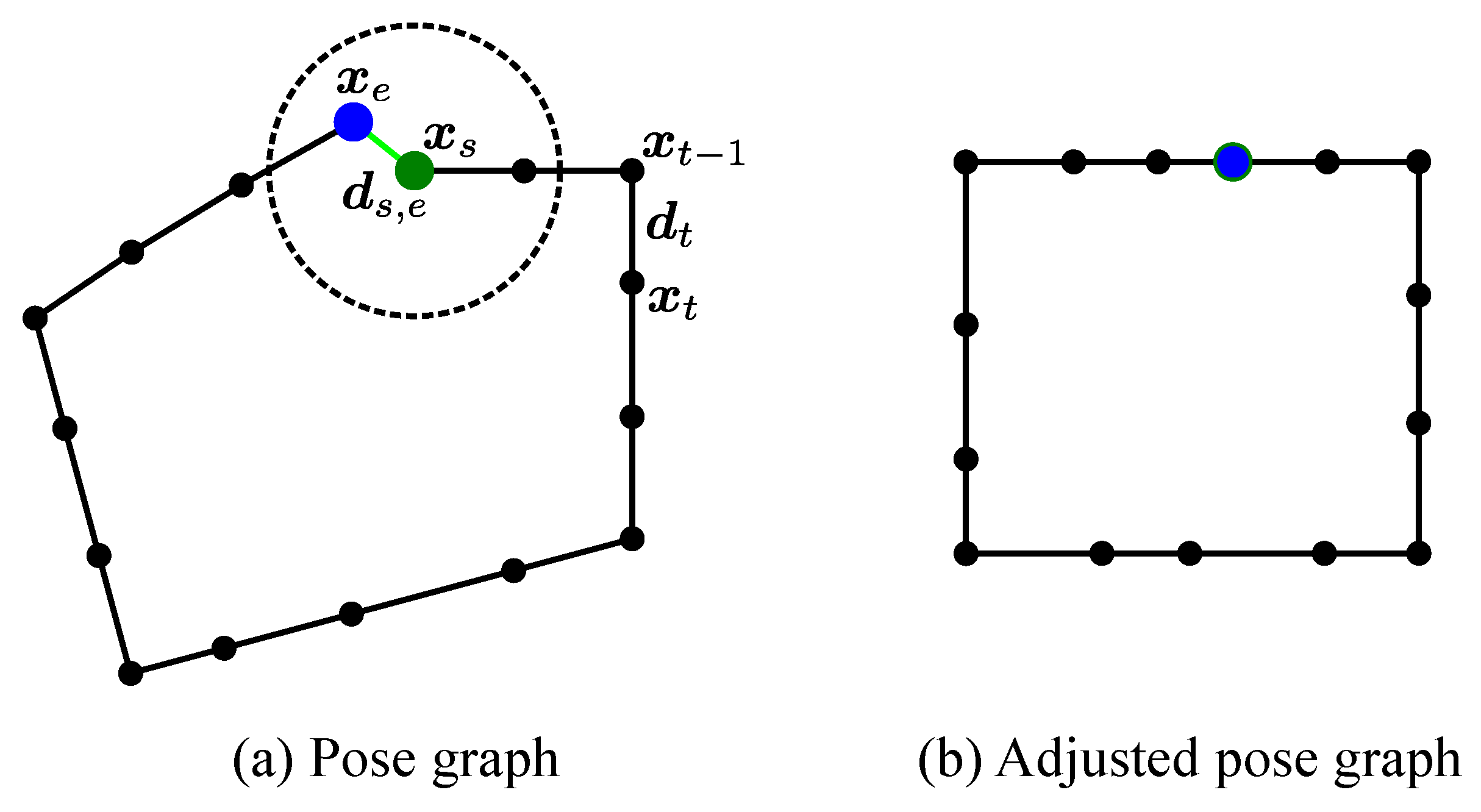
5.2. Loop Closure
5.2.1. Loop Detection
5.2.2. Pose Adjustment
| Algorithm 1 Loop detection. |
|
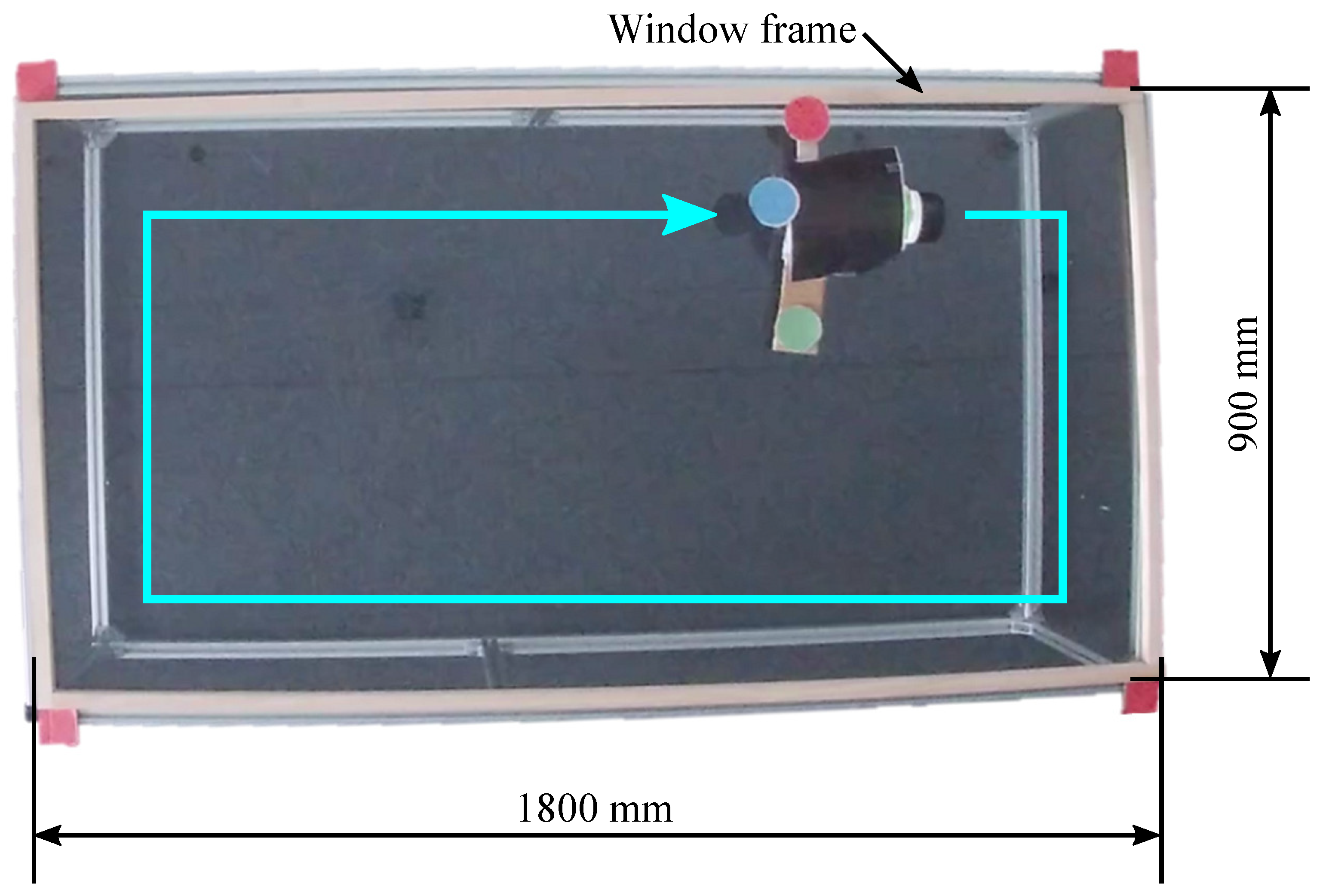
6. Experiment
6.1. ROS-Based Experimental System
6.2. Variable and Parameter Settings
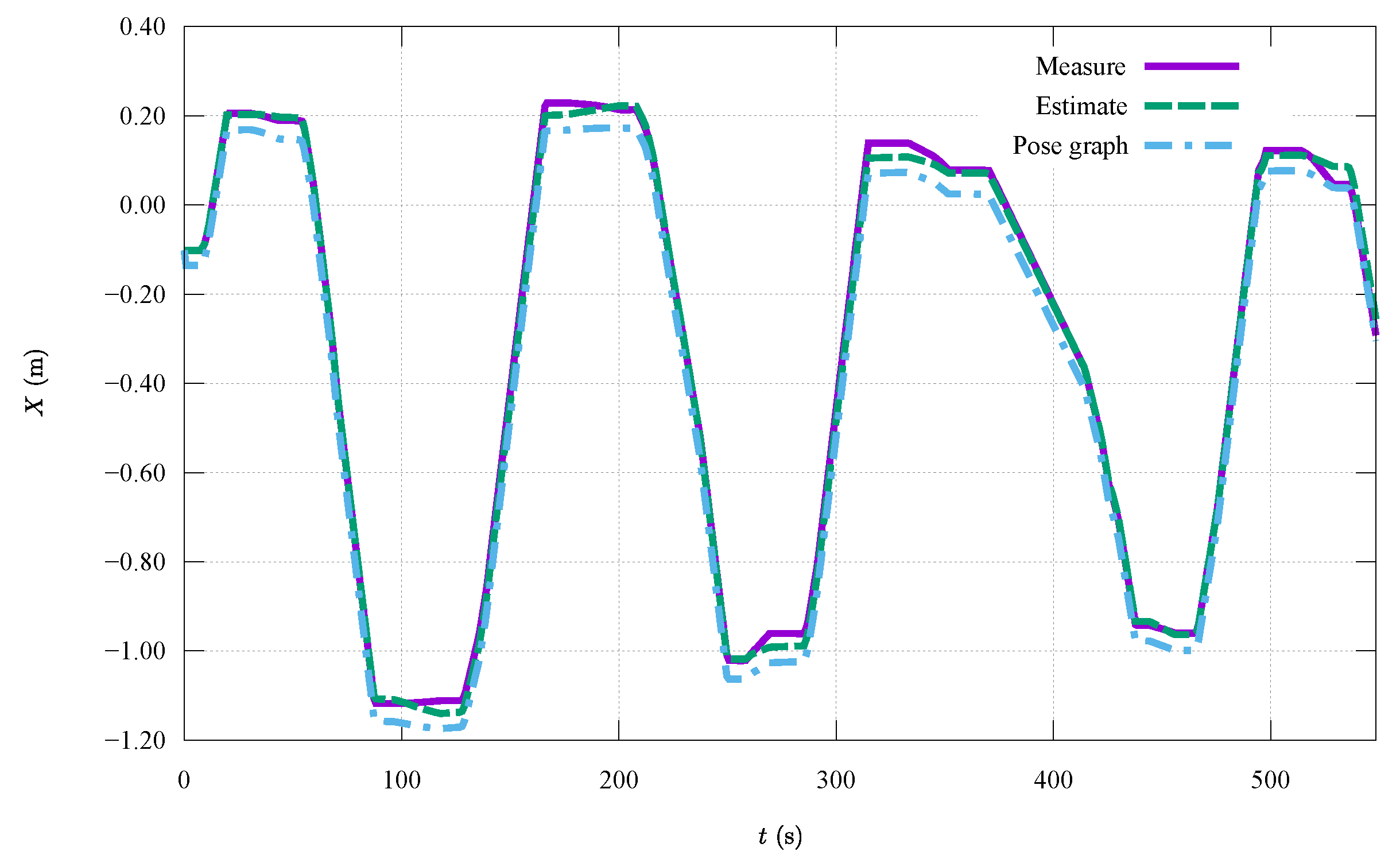
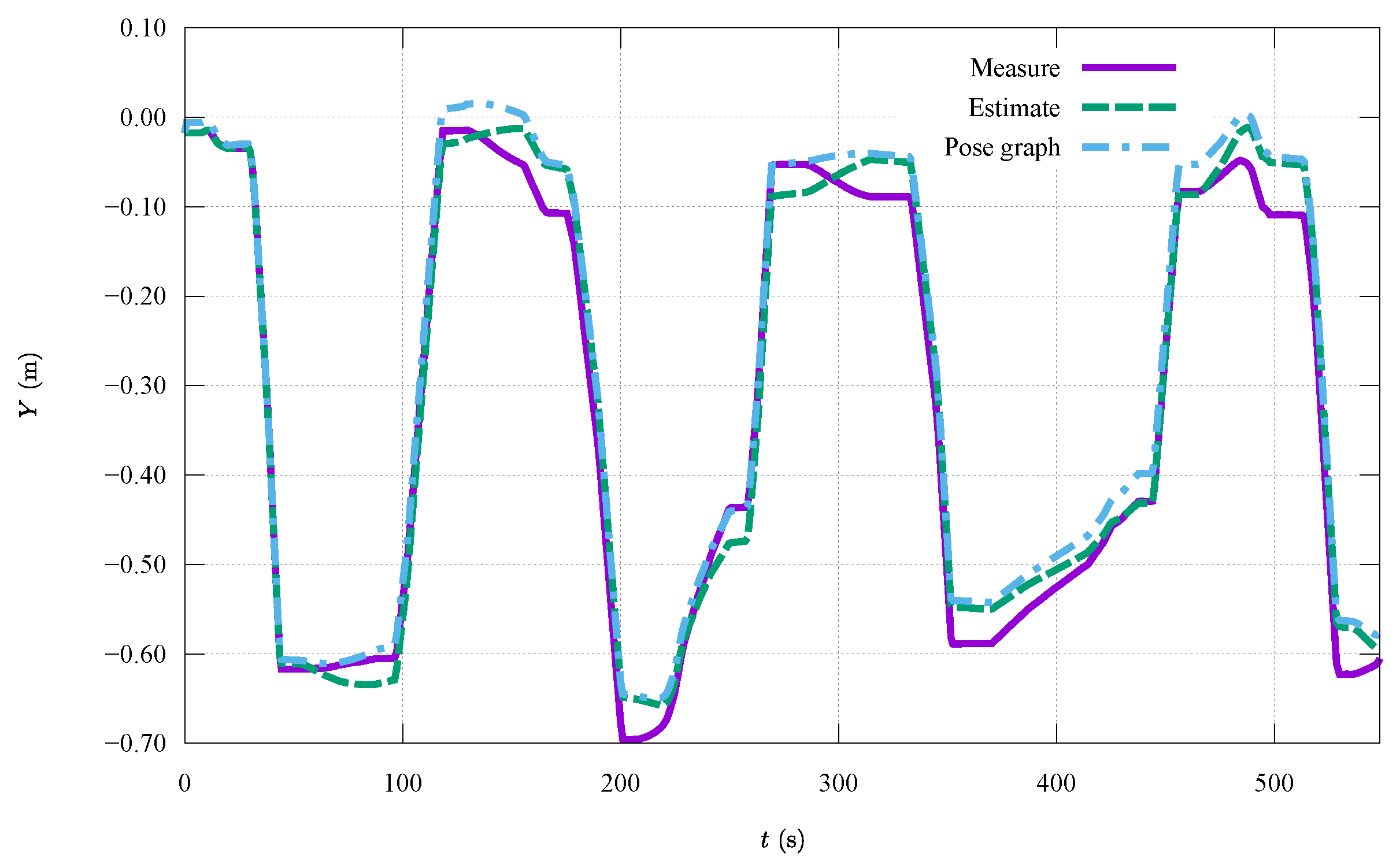
6.3. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EKF | Extended Kalman filter |
| ROS | Robot operating system |
| IMU | Inertial measurement unit |
References
- BBC. Shanghai window cleaning cradle swings out of control. BBC News, 3 April 2015.
- BBC. Window washers rescued from high up world trade center. BBC News, 12 November 2014.
- Elkmann, N.; Hortig, J.; Fritzsche, M. Cleaning automation. In Springer Handbook of Automation; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1253–1264. [Google Scholar] [CrossRef]
- Seo, T.; Jeon, Y.; Park, C.; Kim, J. Survey on glass and façade-cleaning robots: Climbing mechanisms, cleaning methods, and applications. Int. J. Precis. Eng.-Manuf.-Green Technol. 2019, 6, 367–376. [Google Scholar] [CrossRef]
- Elkmann, N.; Felsch, T.; Sack, M.; Saenz, J.; Hortig, J. Innovative service robot systems for facade cleaning of difficult-to-access areas. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; Volume 1, pp. 756–762. [Google Scholar] [CrossRef]
- Elkmann, N.; Kunst, D.; Krueger, T.; Lucke, M.; Böhme, T.; Felsch, T.; Stürze, T. SIRIUSc—Façade cleaning robot for a high-rise building in Munich, Germany. In Climbing and Walking Robots; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1033–1040. [Google Scholar] [CrossRef]
- Elkmann, N.; Lucke, M.; Krüger, T.; Kunst, D.; Stürze, T.; Hortig, J. Kinematics, sensors and control of the fully automated façade-cleaning robot SIRIUSc for the Fraunhofer headquarters building, Munich. Ind. Robot Int. J. 2008. [Google Scholar] [CrossRef]
- Lee, S.; Kang, M.S.; Han, C.S. Sensor based motion planning and estimation of highrise building façade maintenance robot. Int. J. Precis. Eng. Manuf. 2012, 13, 2127–2134. [Google Scholar] [CrossRef]
- Moon, S.M.; Hong, D.; Kim, S.W.; Park, S. Building wall maintenance robot based on built-in guide rail. In Proceedings of the 2012 IEEE International Conference on Industrial Technology, Athens, Greece, 19–21 March 2012; pp. 498–503. [Google Scholar] [CrossRef]
- Shin, C.; Moon, S.; Kwon, J.; Huh, J.; Hong, D. Force control of cleaning tool system for building wall maintenance robot on built-in guide rail. In Proceedings of the International Symposium on Automation and Robotics in Construction, Sydney, Australia, 9–11 July 2014; Volume 31, p. 1. [Google Scholar] [CrossRef]
- Moon, S.M.; Shin, C.Y.; Huh, J.; Oh, K.W.; Hong, D. Window cleaning system with water circulation for building façade maintenance robot and its efficiency analysis. Int. J. Precis. Eng.-Manuf.-Green Technol. 2015, 2, 65–72. [Google Scholar] [CrossRef]
- Lee, Y.S.; Kim, S.H.; Gil, M.S.; Lee, S.H.; Kang, M.S.; Jang, S.H.; Yu, B.H.; Ryu, B.G.; Hong, D.; Han, C.S. The study on the integrated control system for curtain wall building façade cleaning robot. Autom. Constr. 2018, 94, 39–46. [Google Scholar] [CrossRef]
- Lee, C.; Chu, B. Three-modular obstacle-climbing robot for cleaning windows on building exterior walls. Int. J. Precis. Eng. Manuf. 2019, 20, 1371–1380. [Google Scholar] [CrossRef]
- Yoo, S.; Joo, I.; Hong, J.; Park, C.; Kim, J.; Kim, H.S.; Seo, T. Unmanned high-rise façade cleaning robot implemented on a gondola: Field test on 000-building in Korea. IEEE Access 2019, 7, 30174–30184. [Google Scholar] [CrossRef]
- Hong, J.; Park, G.; Lee, J.; Kim, J.; Kim, H.S.; Seo, T. Performance comparison of adaptive mechanisms of cleaning module to overcome step-shaped obstacles on façades. IEEE Access 2019, 7, 159879–159887. [Google Scholar] [CrossRef]
- Park, G.; Hong, J.; Yoo, S.; Kim, H.S.; Seo, T. Design of a 3-DOF parallel manipulator to compensate for disturbances in facade cleaning. IEEE Access 2020, 8, 9015–9022. [Google Scholar] [CrossRef]
- Chae, H.; Park, G.; Lee, J.; Kim, K.; Kim, T.; Kim, H.S.; Seo, T. Façade cleaning robot with manipulating and sensing devices equipped on a gondola. IEEE/ASME Trans. Mechatron. 2021, 26, 1719–1727. [Google Scholar] [CrossRef]
- Zhu, J.; Sun, D.; Tso, S.K. Application of a service climbing robot with motion planning and visual sensing. J. Robot. Syst. 2003, 20, 189–199. [Google Scholar] [CrossRef]
- Sun, D.; Zhu, J.; Lai, C.; Tso, S. A visual sensing application to a climbing cleaning robot on the glass surface. Mechatronics 2004, 14, 1089–1104. [Google Scholar] [CrossRef]
- Sun, D.; Zhu, J.; Tso, S.K. A Climbing Robot for Cleaning Glass Surface with Motion Planning and Visual Sensing. In Climbing and Walking Robots: Towards New Applications; IntechOpen: London, UK, 2007. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Zong, G. Requirements of glass cleaning and development of climbing robot systems. In Proceedings of the 2004 International Conference on Intelligent Mechatronics and Automation, Chengdu, China, 26–31 August 2004; pp. 101–106. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Zong, G. Realization of a service climbing robot for glass-wall cleaning. In Proceedings of the 2004 IEEE International Conference on Robotics and Biomimetics, Shenyang, China, 22–26 August 2004; pp. 395–400. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Liu, R.; Zong, G. A novel approach to pneumatic position servo control of a glass wall cleaning robot. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)(IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 1, pp. 467–472. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Zong, G. Effective pneumatic scheme and control strategy of a climbing robot for class wall cleaning on high-rise buildings. Int. J. Adv. Robot. Syst. 2006, 3, 28. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Zong, G.; Wang, W.; Liu, R. Sky cleaner 3: A real pneumatic climbing robot for glass-wall cleaning. IEEE Robot. Autom. Mag. 2006, 13, 32–41. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Zong, G. Effective nonlinear control algorithms for a series of pneumatic climbing robots. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 994–999. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Liu, R.; Zong, G. Realization of a service robot for cleaning spherical surfaces. Int. J. Adv. Robot. Syst. 2005, 2, 7. [Google Scholar] [CrossRef]
- Seo, K.; Cho, S.; Kim, T.; Kim, H.S.; Kim, J. Design and stability analysis of a novel wall-climbing robotic platform (ROPE RIDE). Mech. Mach. Theory 2013, 70, 189–208. [Google Scholar] [CrossRef]
- Kim, T.Y.; Kim, J.H.; Seo, K.C.; Kim, H.M.; Lee, G.U.; Kim, J.W.; Kim, H.S. Design and control of a cleaning unit for a novel wall-climbing robot. Appl. Mech. Mater. 2014, 541, 1092–1096. [Google Scholar] [CrossRef]
- Kim, T.; Seo, K.; Kim, J.; Kim, H.S. Adaptive impedance control of a cleaning unit for a novel wall-climbing mobile robotic platform (ROPE RIDE). In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besacon, France, 8–11 July 2014; pp. 994–999. [Google Scholar] [CrossRef]
- Tun, T.T.; Elara, M.R.; Kalimuthu, M.; Vengadesh, A. Glass facade cleaning robot with passive suction cups and self-locking trapezoidal lead screw drive. Autom. Constr. 2018, 96, 180–188. [Google Scholar] [CrossRef]
- Vega-Heredia, M.; Mohan, R.E.; Wen, T.Y.; Siti’Aisyah, J.; Vengadesh, A.; Ghanta, S.; Vinu, S. Design and modelling of a modular window cleaning robot. Autom. Constr. 2019, 103, 268–278. [Google Scholar] [CrossRef]
- Vega-Heredia, M.; Muhammad, I.; Ghanta, S.; Ayyalusami, V.; Aisyah, S.; Elara, M.R. Multi-sensor orientation tracking for a façade-cleaning robot. Sensors 2020, 20, 1483. [Google Scholar] [CrossRef]
- Chae, H.; Moon, Y.; Lee, K.; Park, S.; Kim, H.S.; Seo, T. A Tethered Façade Cleaning Robot Based on a Dual Rope Windlass Climbing Mechanism: Design and Experiments. IEEE/ASME Trans. Mechatron. 2022. [Google Scholar] [CrossRef]
- Nansai, S.; Elara, M.R.; Tun, T.T.; Veerajagadheswar, P.; Pathmakumar, T. A novel nested reconfigurable approach for a glass façade cleaning robot. Inventions 2017, 2, 18. [Google Scholar] [CrossRef]
- Nansai, S.; Onodera, K.; Veerajagadheswar, P.; Rajesh Elara, M.; Iwase, M. Design and experiment of a novel façade cleaning robot with a biped mechanism. Appl. Sci. 2018, 8, 2398. [Google Scholar] [CrossRef]
- Nansai, S.; Itoh, H. Foot location algorithm considering geometric constraints of façade cleaning. J. Adv. Simul. Sci. Eng. 2019, 6, 177–188. [Google Scholar] [CrossRef]
- Singandhupe, A.; La, H.M. A review of slam techniques and security in autonomous driving. In Proceedings of the 2019 third IEEE international conference on robotic computing (IRC), Naples, Italy, 25–27 February 2019; pp. 602–607. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, L.; Chen, Q.; Hu, X.; Cai, J. A review of visual SLAM methods for autonomous driving vehicles. Eng. Appl. Artif. Intell. 2022, 114, 104992. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; MIT Press: Cambridge, MA, USA, 2005; ISBN 0-262-20162-3. [Google Scholar]
- Adachi, S.; Maruta, I. Fundamentals of Kalman Filter; Tokyo Denki University Press: Tokyo, Japan, 2012. (In Japanese) [Google Scholar]
- Tomono, M. Simultaneous Localization and Mapping; Ohmsha: Tokyo, Japan, 2018. (In Japanese) [Google Scholar]
- Kim, D.Y.; Yoon, J.; Sun, H.; Park, C.W. Window detection for gondola robot using a visual camera. In Proceedings of the 2012 IEEE International Conference on Automation Science and Engineering (CASE), Seoul, Republic of Korea, 20–24 August 2012; pp. 998–1003. [Google Scholar] [CrossRef]
- Kim, D.Y.; Yoon, J.; Cha, D.H.; Park, C.W. Tilted Window Detection for Gondolatyped Facade Robot. Int. J. Control Theory Comput. Model. (IJCTCM) 2013, 3, 1–10. [Google Scholar] [CrossRef]
- Pu, S.; Vosselman, G. Extracting windows from terrestrial laser scanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 36, 12–14. [Google Scholar]
- Pu, S.; Vosselman, G. Knowledge based reconstruction of building models from terrestrial laser scanning data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 575–584. [Google Scholar] [CrossRef]
- Wang, R.; Bach, J.; Ferrie, F.P. Window detection from mobile LiDAR data. In Proceedings of the 2011 IEEE Workshop on Applications of Computer Vision (WACV), Kona, HI, USA, 5–7 January 2011; pp. 58–65. [Google Scholar] [CrossRef]
- Zolanvari, S.I.; Laefer, D.F. Slicing Method for curved façade and window extraction from point clouds. ISPRS J. Photogramm. Remote Sens. 2016, 119, 334–346. [Google Scholar] [CrossRef]
- Qasem, S.N.; Ahmadian, A.; Mohammadzadeh, A.; Rathinasamy, S.; Pahlevanzadeh, B. A type-3 logic fuzzy system: Optimized by a correntropy based Kalman filter with adaptive fuzzy kernel size. Inf. Sci. 2021, 572, 424–443. [Google Scholar] [CrossRef]




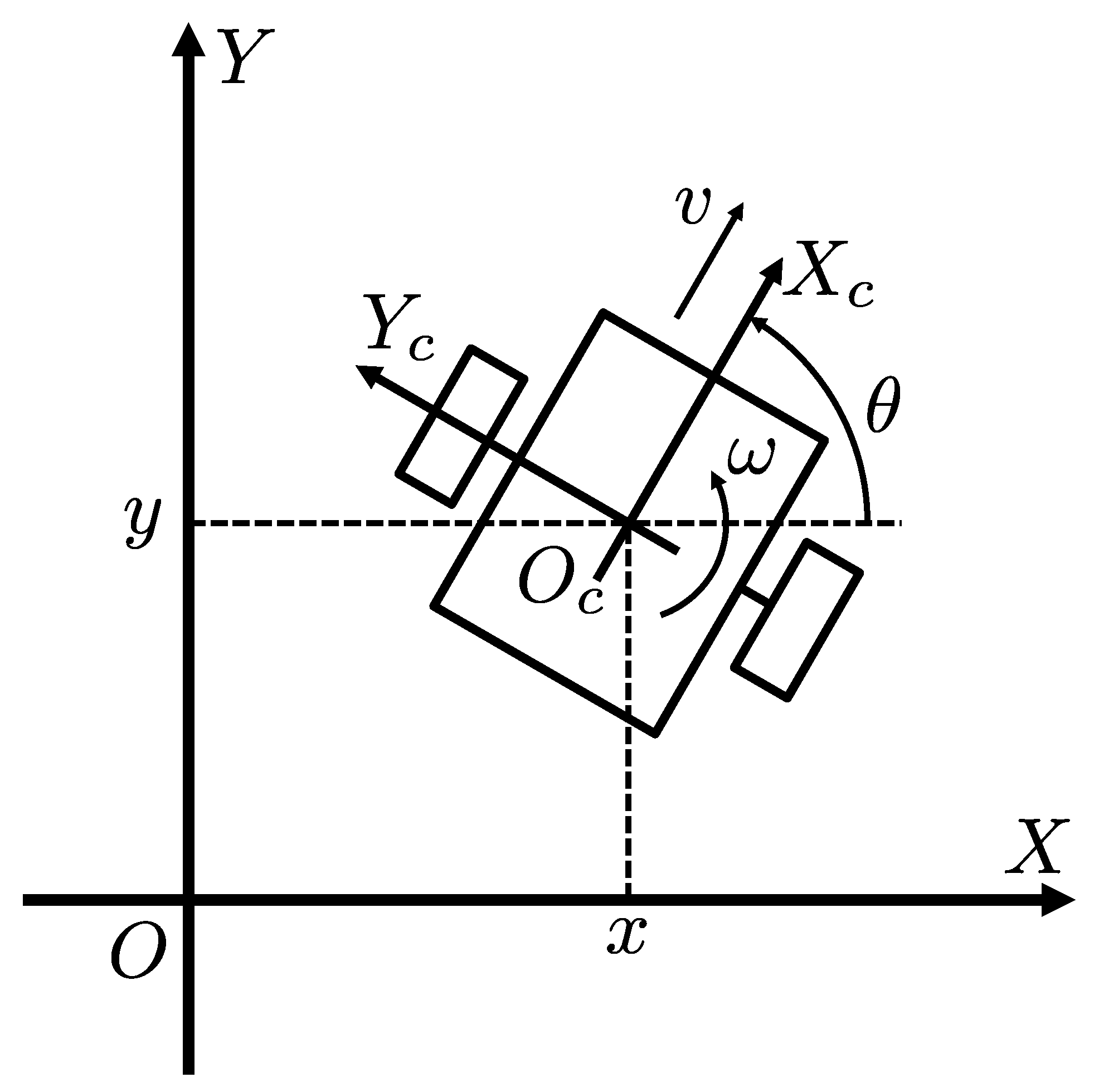



| Symbol | Description |
|---|---|
| x | Robot position in X direction |
| y | Robot position in Y direction |
| Robot heading angle | |
| v | Translational velocity input |
| Rotational velocity input | |
| t | Timestep |
| Robot’s pose: | |
| Robot’s observation: | |
| Robot’s input: | |
| Relative robot’s pose: | |
| Input noise: | |
| Observation noise: | |
| Covariance of input noise: | |
| Covariance of observation noise: | |
| Covariance of robot’s pose: | |
| Covariance of relative robot’s pose: | |
| Set of robot’s poses: | |
| Set of relative robot’s poses: | |
| Set representing pose graph: |
| Symbol | Description |
|---|---|
| Travel time | |
| T | Time of the end of robot movement |
| s | Time stamp at the start point of a loop |
| e | Time stamp at the end point of a loop |
| Traveling distance threshold | |
| Evaluation value threshold | |
| Relative pose between start and end points: | |
| Covariance of relative pose between start and end points: | |
| Covariance for the initial pose settlement: | |
| Weight matrix: | |
| Set of pairs of the time stamps s and e: |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nemoto, T.; Nansai, S.; Iizuka, S.; Iwase, M.; Itoh, H. Window Shape Estimation for Glass Façade-Cleaning Robot. Machines 2023, 11, 175. https://doi.org/10.3390/machines11020175
Nemoto T, Nansai S, Iizuka S, Iwase M, Itoh H. Window Shape Estimation for Glass Façade-Cleaning Robot. Machines. 2023; 11(2):175. https://doi.org/10.3390/machines11020175
Chicago/Turabian StyleNemoto, Takuma, Shunsuke Nansai, Shohei Iizuka, Masami Iwase, and Hiroshi Itoh. 2023. "Window Shape Estimation for Glass Façade-Cleaning Robot" Machines 11, no. 2: 175. https://doi.org/10.3390/machines11020175
APA StyleNemoto, T., Nansai, S., Iizuka, S., Iwase, M., & Itoh, H. (2023). Window Shape Estimation for Glass Façade-Cleaning Robot. Machines, 11(2), 175. https://doi.org/10.3390/machines11020175








