Abstract
Autonomous robots are designed to discover and interpret their surroundings and orient themselves around obstacles to reach the destination point from an initial point. Robot autonomous navigation is a requirement for maze-solving systems, where the solver robot is required to navigate the maze area to get its desire destination location using the fastest route possible. In this paper, a new, modified wall-follower system for a maze-solving robot was proposed that overcame the infinite loop-back issue in the traditional wall-follower approaches. We also investigated and analyzed the performance of three different maze-solving algorithms and compared them with the proposed, modified wall-follower robotic system by conducting several real experiments to validate the efficiency of the developed wall-follower robotic system.
1. Introduction
Dense city streets, disaster regions, and war environments have common navigational difficulties. These difficulties range from navigation through obstructions on a possible route to navigation through dead-ends. Autonomous robot navigation involves the robot’s ability to navigate its environment independently and its ability to determine its location and direction and then plan a path towards the goal location. The robot must avoid dangerous areas, including collisions and unsafe places [1,2].
The maze-solving robot is one of the most popular intelligent robots; it is an independent robot that can solve the maze area from a known initial point to a destination point. The maze-solving robot generally requires navigating the maze area to explore the existing paths to the destination point. The maze-solving robot can process multiple runs in the maze area, navigate the maze area to construct a map, and then store the obtained map in the robot’s memory [3,4].
Usually, the navigation process consists of three main fundamental functions: self-localization, path-planning, and map building. Self-localization is the robot’s ability to explore its current position using one of the available localization techniques (RFID, GPS, inertial navigation, etc.). Path-planning includes exploring the possible paths for traveling from one point to the other. Lastly, map building includes constructing a map of the paths for the navigation area [5,6].
Maze-solver robots may be applied in various applications, ranging from accomplishing simple tasks, such as transferring goods through factories, office buildings, classrooms, and other workspaces, to dangerous tasks, such as reaching areas to evacuate people from buildings, bomb-sniffing, etc. [7,8,9].
Several maze-solving robotic systems have been developed recently, with various capabilities surveyed in [10,11,12]. However, in this paper, we focus on the wall-follower maze solving robotic systems for three main reasons: First, wall-follower systems can be implemented with any robotic system (no need for complicated hardware architecture); second, wall-follower systems are easy to deploy and are based on simple sensing technology; and third, wall-follower systems need low-memory requirements and low-processing overhead. However, most wall-follower systems fail in the maze areas that consist of more than one path to the destination point, as the loop-back issue arises, and the solver robot fails to reach the destination point. Therefore, this paper discusses the design and development of an efficient maze-solving robotic system based on a modified wall-follower method. The main contributions of this paper lie in the following aspects:
- Reviewing the recently developed wall-follower maze-solving robotic systems.
- Designing and implementing a maze-solving robotic system by employing a modified wall-follower method.
- Validating the implemented wall follower system through different maze environments by conducting real experiments using different maze structures.
- Comparing the obtained results from the modified wall-follower method with three different maze-solving algorithms.
The subsequent sections are organized as follows: Section 2 discusses the recent development of wall-follower-based, maze-solving robotic systems. In Section 3, the proposed, modified wall-follower system is introduced. Section 4 presents the experimental results obtained from several real experiments conducted in maze environments. In Section 5, we discuss and compare the obtained results and the recently developed maze-solving systems. Finally, Section 6 concludes the work presented in this paper and proposes suggestions for future research.
2. Related Works
Various maze-solving robotic systems have been developed recently, driven by the requirement to build an efficient solver robot that can reach the target destination with the minimum time and the shortest path possible. Authors of [11] discussed and analyzed the existing maze-solving algorithms employed in the maze-solving robotic systems and categorized them into two main categories, based on the deployment area: known and unknown environment-based systems. In addition, authors investigated the recent development of autonomous maze-solving robotic systems. They categorized them into two main categories: camera-based and sensor-based solutions, where the latter was further categorized into two subcategories: line-follower and wall-follower systems. Both systems employ the same navigation strategy. However, they differ in the employed navigation technology, where the first one follows the lines placed on the ground, and the second one follows the heading walls.
The wall-follower is the most common maze-solving approach that has been employed in robotics, where the robot solver follows walls in the maze area and observes the right wall or the left wall throughout the maze area until it finds its way out. The wall-follower system works according to one of two rules: the right-hand rule or the left-hand rule. According to the rule decision, the turning priority is either right or left.
Several wall-follower robotic systems have been designed and implemented recently. For instance, the authors of [9] developed an autonomous maze-solving robot with independent mapping and localization functions. The developed robot consisted of three infrared sensors, where two of them were used for sidewall detection, and the third one was employed to detect the obstacles ahead of the robot. The developed robot system was tested and offered efficient accuracy to solve the maze area successfully without interruption.
Authors [13] presented a hybrid maze-solving robot system based on a wall-follower method combined with left-hand and right-hand rules and implemented it in several configurations. The authors revealed that the hybrid algorithm had improved the maze-solving capabilities using robot systems. On the other hand, a wall-follower robot system was proposed in [14], which employed the left-hand rule using three infrared sensors to read the environmental patterns. An artificial neural network method was adopted to process the data received from onboard sensors and make suitable decisions accordingly. The obtained results showed that the solver robot was able to complete the labyrinth path, consisting of eight intersection points and a dead-end point with a distance of 595 cm, and complete another maze pattern containing four intersection points with a distance of 360 cm.
The work presented in [15] included a maze-solving robot that could solve the labyrinth by adopting the wall-follower algorithm. The developed robot consisted of an array of proximity sensors to navigate the robot safely by avoiding obstacles in the maze area.
As discussed above, the developed wall-follower, maze-solving robotic systems assumed the existence of a single path to the destination point, with no other assumptions to deal with multiple paths to reach the destination point. In addition, wall-follower systems failed in the maze area with more than one path to the destination point. Therefore, developing an efficient maze-solving robotic system is important to work with multiple paths and overcome the infinite loop issue.
3. Modified Wall-Follower Solver Robot System
The existing wall-follower systems [9,13,14] suffer from the loop-back issue, where the solver robot might go in an infinite loop and hence never finds the destination point. In addition, the existing wall-follower-, Pledge-, random mouse-, and Tremaux-based maze solving systems cannot explore all possible routes between the source and the destination points. Hence, these methods cannot find the shortest possible path(s).
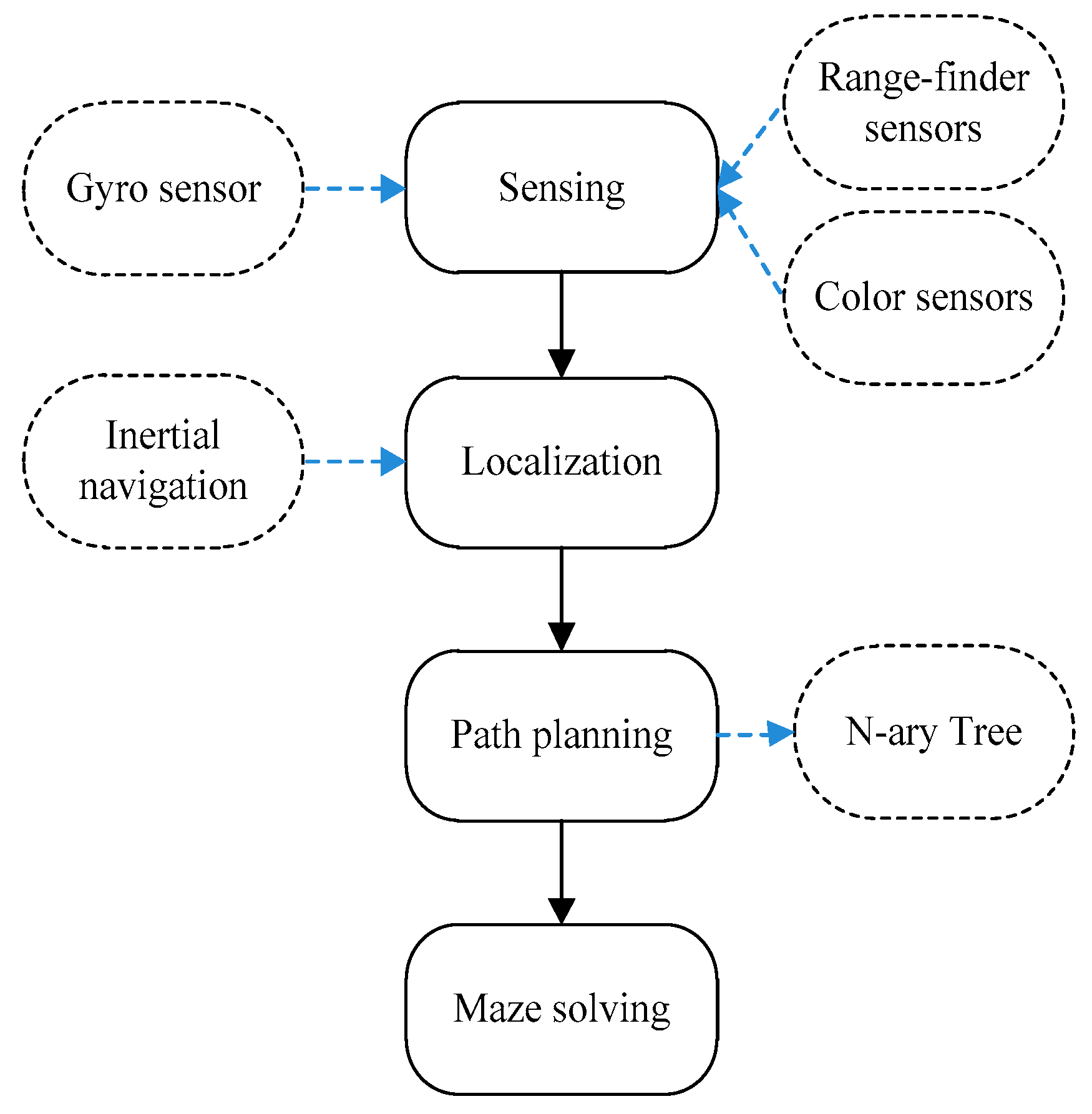
This section discusses an efficient, modified, wall-follower system (MWFS) to solve the above issue. Through the proposed approach, the solver robot never goes in an infinite loop, hence finding the location of the destination point. In addition, MWFS can find all the possible paths between any two points in the maze area, and hence, the shortest paths can be easily computed. Algorithm 1 presents the pseudo-code for the MWFS concept, whereas Figure 1 presents the general stages for the MWFS, including sensing, localization, path planning, and maze solving, which are discussed below.
| Algorithm 1: The modified wall-follower method |
| 1: let be the solver mobile 2: let be the default direction value at the source point 3: let ( be the 2D coordinates for a point 4: let ( be the 2D coordinates for the destination point 5: let be the node in the maze area 5: let be the list of nodes in the maze area 5: let be the list of coordinates that traveled through 6: let ( be the 2D coordinates for the solver robot 7: while ( ( != ( 8: { moves in the maze area until it finds an intersection point ( 9: if ( then 10: rotate_180() 11: else add ( to } 12: end |
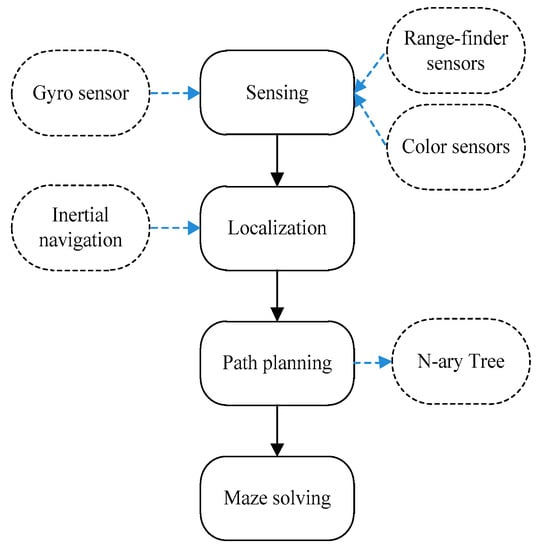
Figure 1.
General stages of the modified wall-follower maze-solving system.
3.1. Sensing
This involves collecting several data from onboard sensors, including the data from the gyro, range-finder, and color, to allow the solver robot to obtain information about the surrounding environment, hence performing the navigation task. For instance, the gyro sensor offers two functions to the solver robot: identify the robot direction and balance the solver robot to travel in straight lines. Equation (1) calculates the variance in direction for the solver robot.
where is the variance (degree) in direction between the obtained rotation value from sensor at time , and is the default rotation value at the time . The auto-balance algorithm is presented in Algorithm 2.
| Algorithm 2: Auto Balance Function |
| 1: let be the rotation value obtained from the rotation sensor, where (180 > Sd > −180)
2: let SR be the solver robot 3: let be the default rotation value at the start point 4: while ( != 0) 5: { if ( < 0) then 6: else } 7: end |
The auto-balance algorithm (Algorithm 2) was adopted to balance the robot when traveling between two points. On the other hand, the range-finder sensor could measure the distance between the solver robot and the heading walls to discover obstacle-free paths. The color sensor was employed to recognize the labels’ color placed in the maze area (for instance, the green label was an intersection point, whereas the black label was a destination point) and then perform a suitable action.
3.2. Localization
In robot navigation, robot localization is an important task for two reasons: exploring the shortest possible paths between any two nodes and calculating the solver robot’s location. The solver robot must localize itself to navigate the terrain efficiently, estimate the traveled distance between nodes in the maze area, and then obtain the shortest path between the source and destination points. Several localization methods [16,17,18,19,20] may be employed to calculate the distance traveled by the solver robot and to estimate the robot’s new position with various localization accuracies. However, these approaches offer high localization errors, which drastically affect the navigation process. Therefore, in this project, we employed an inertial navigation function, where the robot obtained its current location based on an inertial sensor that counted the number of the wheels’ rotations and then employed a method to estimate the traveled distance by the solver robot.
3.3. Path Planning
Path planning is the computation of a path through a map area that represents the map area. The robot’s path is selected based on the problem objectives, where the expected destination can be obtained. According to the sensed data obtained from the gyro, inertial, color, and range-finder sensors, the 2D map for the maze area is constructed and planned, where the map contains all the possible routes that may exist between any two points.
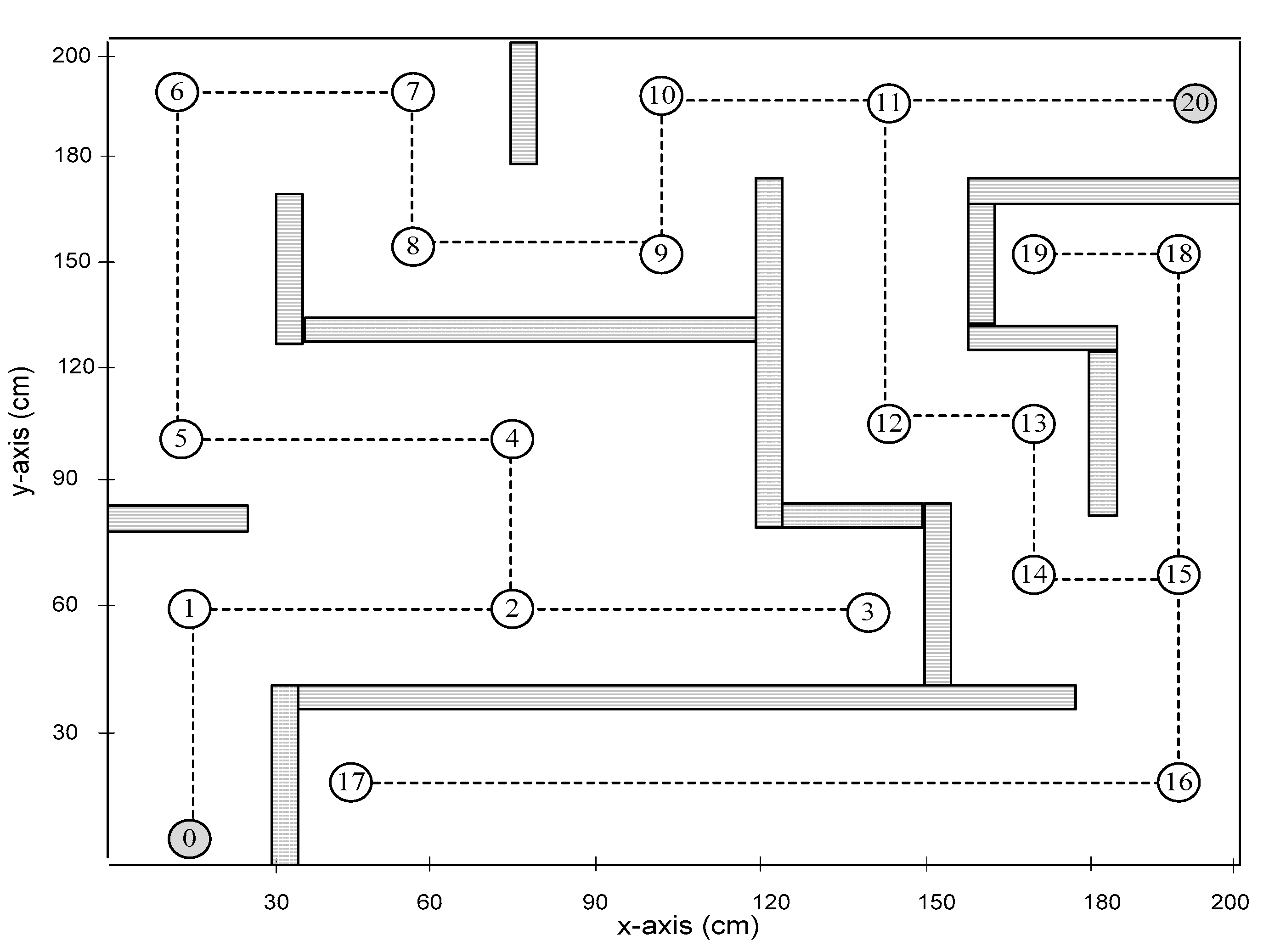
The intersection points are presented in the map area using nodes, where the map area is represented as an N-ary tree. N-ary is a tree that allows owning n number of children for a particular node (n ≥ 0). We implemented a node class in C# code to represent the maze area, as depicted in Figure 2, and obtained the directions and distances in the maze area. Figure 3 presents an example of the tree nodes established for the maze area. As soon as the solver robot starts navigation, the destination and intersection points are represented as nodes, where each visited node is assigned a unique identifier (ID) number.

Figure 2.
Class node attributes.
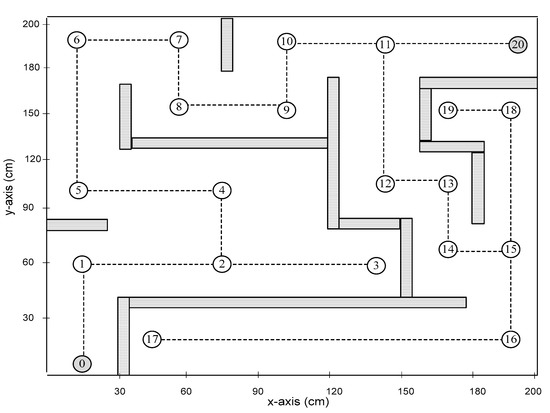
Figure 3.
The constructed N-ary tree after performing the navigation task.
As soon as the map area is constructed using the N-ary tree, the Dijkstra’s algorithm is employed to find out the shortest path between the source and destination points. Then, the solver robot follows the obtained path from the Dijkstra algorithm.
3.4. Maze Solving
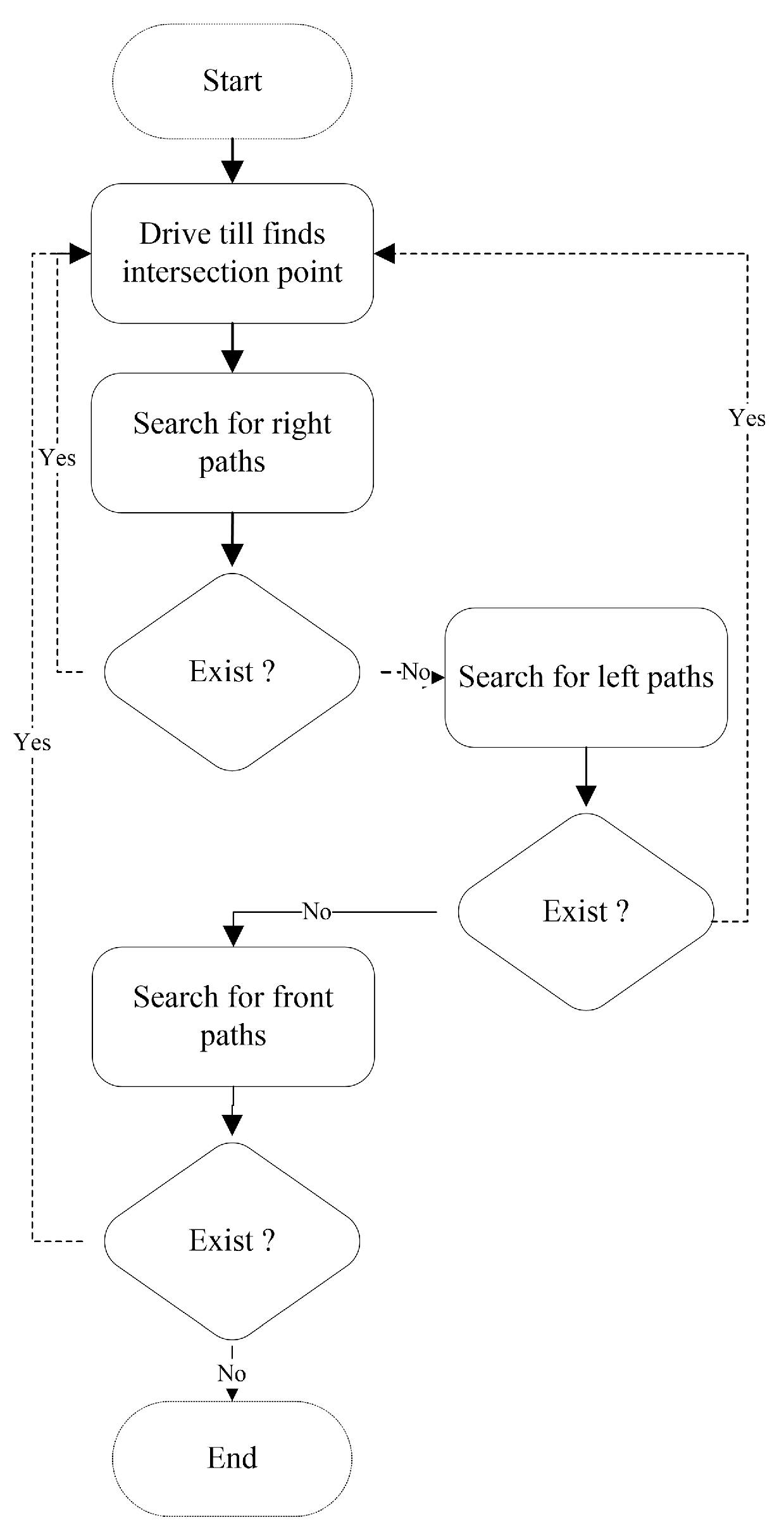
The modified wall-follower algorithm was based on the following searching priority (Right–Left–Front hand rule). Figure 4 presents the flowchart for the implemented Right–Left–Front hand rule, where the right paths are searched first, then the left paths are searched next, and finally, the solver robot searches the front paths. This algorithm is beneficial when the whole maze area is required to be searched, and all possible paths can be explored, where the possible shortest paths can be estimated.
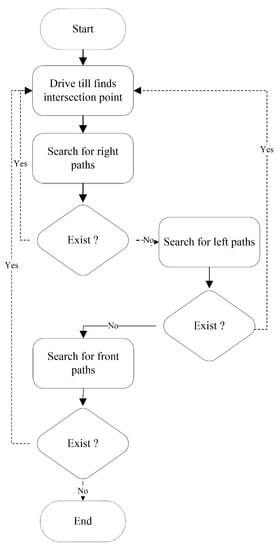
Figure 4.
The flowchart for the MWFS approach.
4. Experimental Results
This section discusses the experimental testbed in terms of the solver-robot platform and the experiment testbed area. In addition, this section discusses the results obtained from several real experiments conducted in three different maze areas.
4.1. Expeirment Testbed
The experiment testbed consisted of two main components: the solver robot and the testbed area. First, the Lego EV3 robot depicted in Figure 5 was employed in the validation process. Lego EV3 was used as a development kit to test the efficiency of the proposed, modified wall-follower system. The Lego EV3 development kit was employed in various research works [21,22,23,24] and proved its capabilities in proof-of-concept tasks.

Figure 5.
The customized Lego EV3 robot platform.
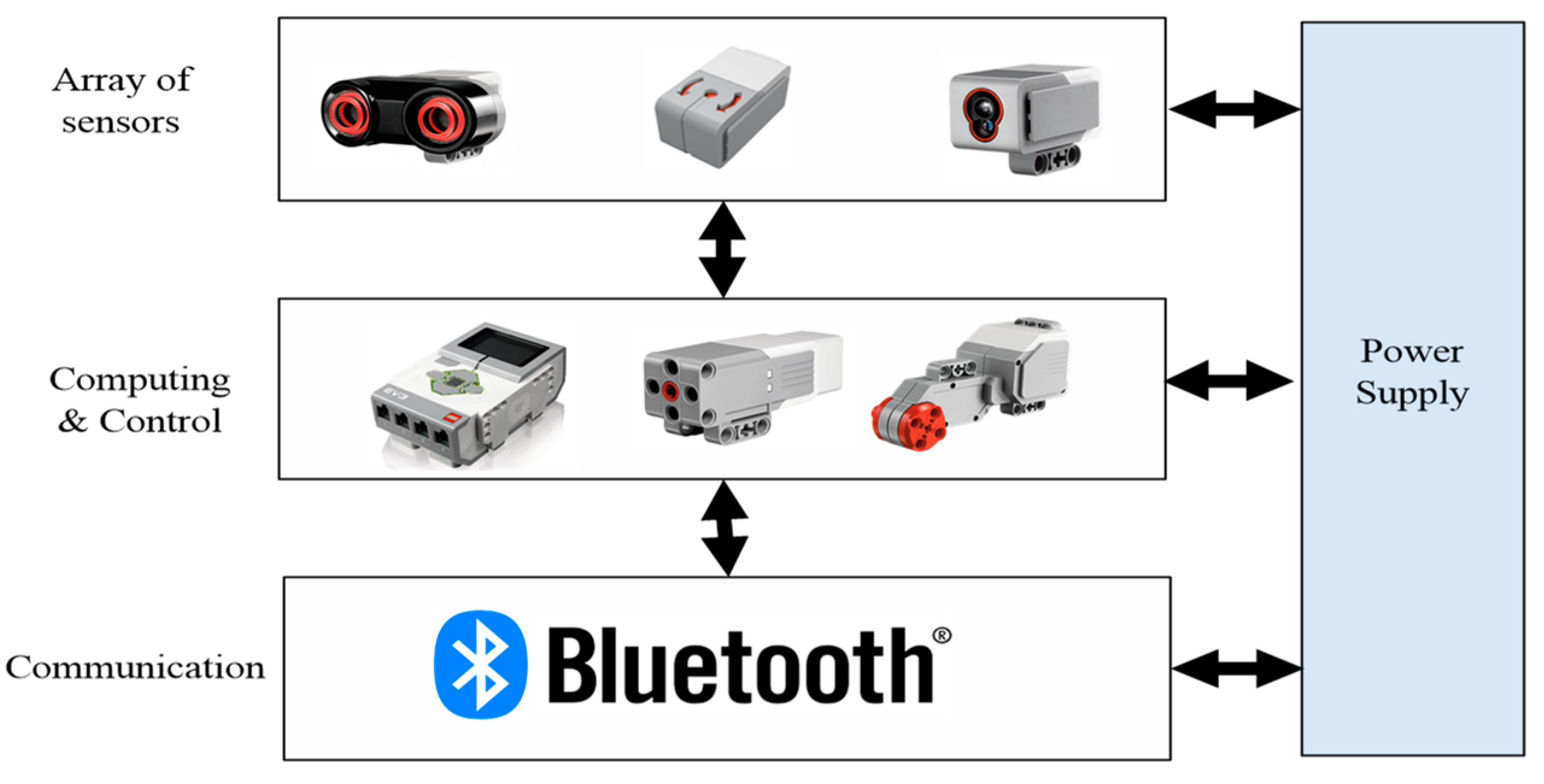
The robot architecture is presented in Figure 6, and the robot architecture consists of four main units.
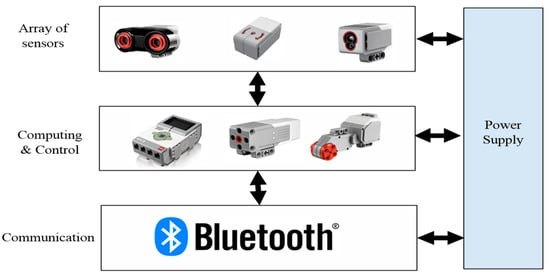
Figure 6.
Lego EV3 robot architecture.
- Sensing unit: includes four different sensors that are required to sense the solver robot’s surrounding environment, including: ultrasonic, gyro, color, and inertial navigation sensors. Table 1 presents the general specifications for the ultrasonic sensor. The specifications for the gyro sensor are shown in Table 2, whereas Table 3 presents the specifications for the color sensor, and finally, the specifications for the inertial sensor are presented in Table 4.
- Computing and control unit: this collects sensed data from onboard sensors, processes the data, and makes suitable decisions accordingly.
- Communication unit: this includes exchanging the processed data between the solver robot and the GUI located in the computer unit.
- Power supply unit: this involves feeding the units mentioned above with the required energy.
Second, the testbed area was considered. For a proof-of-concept purpose, we conducted several real experiments using the maze area depicted in Figure 7 with the dimension of 200 × 200 cm. Through this experiment testbed, we set different initial and destination points to assess the efficiency of four different maze-solving algorithms. Therefore, three different testbeds were available for evaluation purposes. The green labels are the intersection points in the maze area, whereas the black label is the destination point. The testbed’s initial (source) location might be at any point. Table 5 presents several parameters for the experimental testbed.

Figure 7.
Experiment testbed area.

Table 1.
General specification parameters for the ultrasonic sensor.
Table 1.
General specification parameters for the ultrasonic sensor.
| Parameter | Value |
|---|---|
| Distance measurement | 0–255 cm |
| Accuracy | +/−1 cm |
| Frequency | 40 KHz |
| Beam angle | 90 degree |

Table 2.
General specification parameters for the gyro sensor.
Table 2.
General specification parameters for the gyro sensor.
| Parameter | Value |
|---|---|
| Maximum rotation speed | 440 degree/second |
| Accuracy | +/−3 degrees |
| Control unit | 8-bit microcontroller |
| Frequency | 1 KHz |

Table 3.
General specification parameters for the color sensor.
Table 3.
General specification parameters for the color sensor.
| Parameter | Value |
|---|---|
| Sensitivity | 900 nm |
| Frequency | 1 KHz |
| Reading distance | 0.5–1.5 cm |
| Sensor output | 0–100 |

Table 4.
General specification parameters for the inertial sensor.
Table 4.
General specification parameters for the inertial sensor.
| Parameter | Value |
|---|---|
| Resolution | 1 count/degree |
| Rotation speed | 175 RPM |
| Power consumption | 60 mA |

Table 5.
Several parameters for the experiment.
Table 5.
Several parameters for the experiment.
| Parameter | Value |
|---|---|
| Maze area | 2D (200 × 200) cm |
| Robot platform | Lego EV3 |
| Robot speed | 0.05 m/s |
| # of intersections | 3 |
| # of maze layouts | 3 |
| Ultrasonic range | 100 cm |
| Green label | An intersection point |
| Black label | Destination point |
4.2. Results
As mentioned earlier, we implemented four different maze-solving systems (wall-follower (right-hand and left-hand), Pledge, and modified wall-follower) through three different maze areas and compared the results obtained with the proposed modified wall-follower system. All the experiments were carried out in the same maze area and under the same circumstances to validate the efficiency of each maze-solving system. The maze solving systems’ efficiency was validated through assessing the following parameters:
- Average time to solve the maze: this refers to the total time (in minutes) required to solve the maze, i.e., the time required for the solver robot to travel from the start point to the destination point. Average time depended on the maze solving algorithm and the taken path to reach the destination point.
- Distance to target point: this refers to the total distance (in centimeters) traveled by the solver robot from the start point to the destination point.
- Total distance traveled in the maze: this indicates the total distance (in centimeters) traveled by the solver robot through the maze area.
- Number of visited paths: this refers to the total number of paths that the solver robot visited during the navigation process, i.e., the path from the source (initial) point to the destination point.
- Robot deviation: this estimates the deviation angle for the maze-solver robot while traveling between any two points in the maze area.
- Robot positioning accuracy: this refers to the measurement of the difference between the estimated location of the solver robot and the real robot’s location.
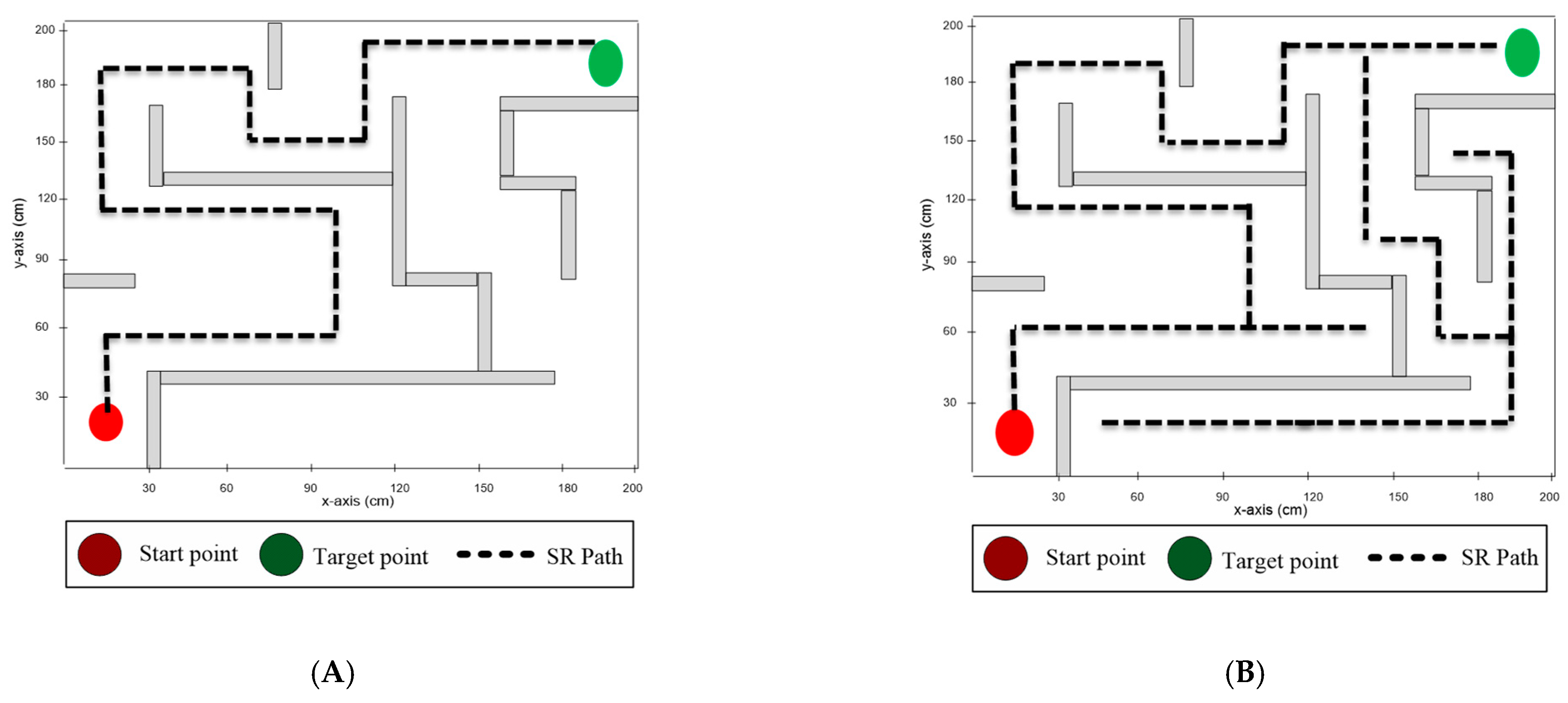
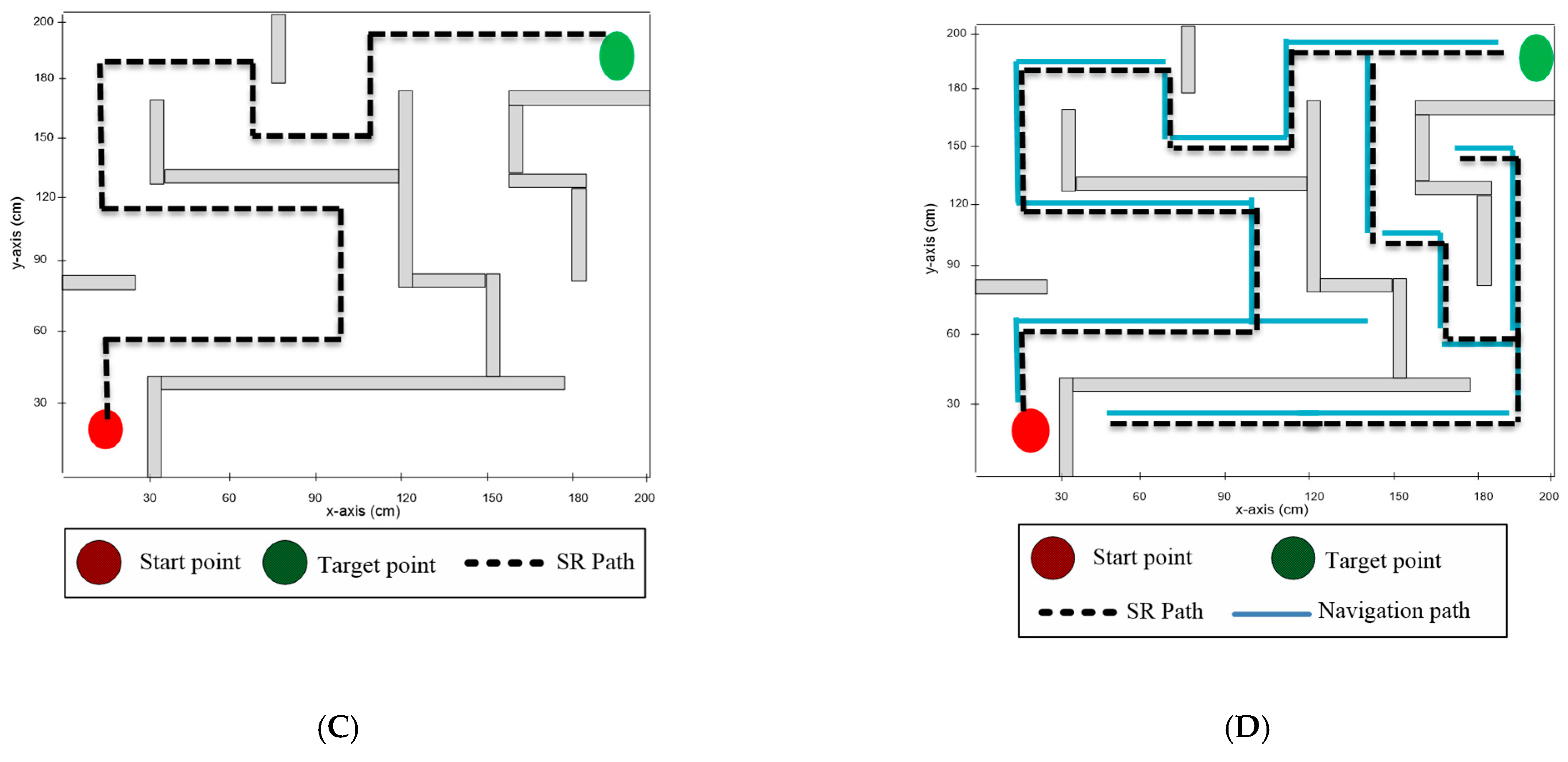
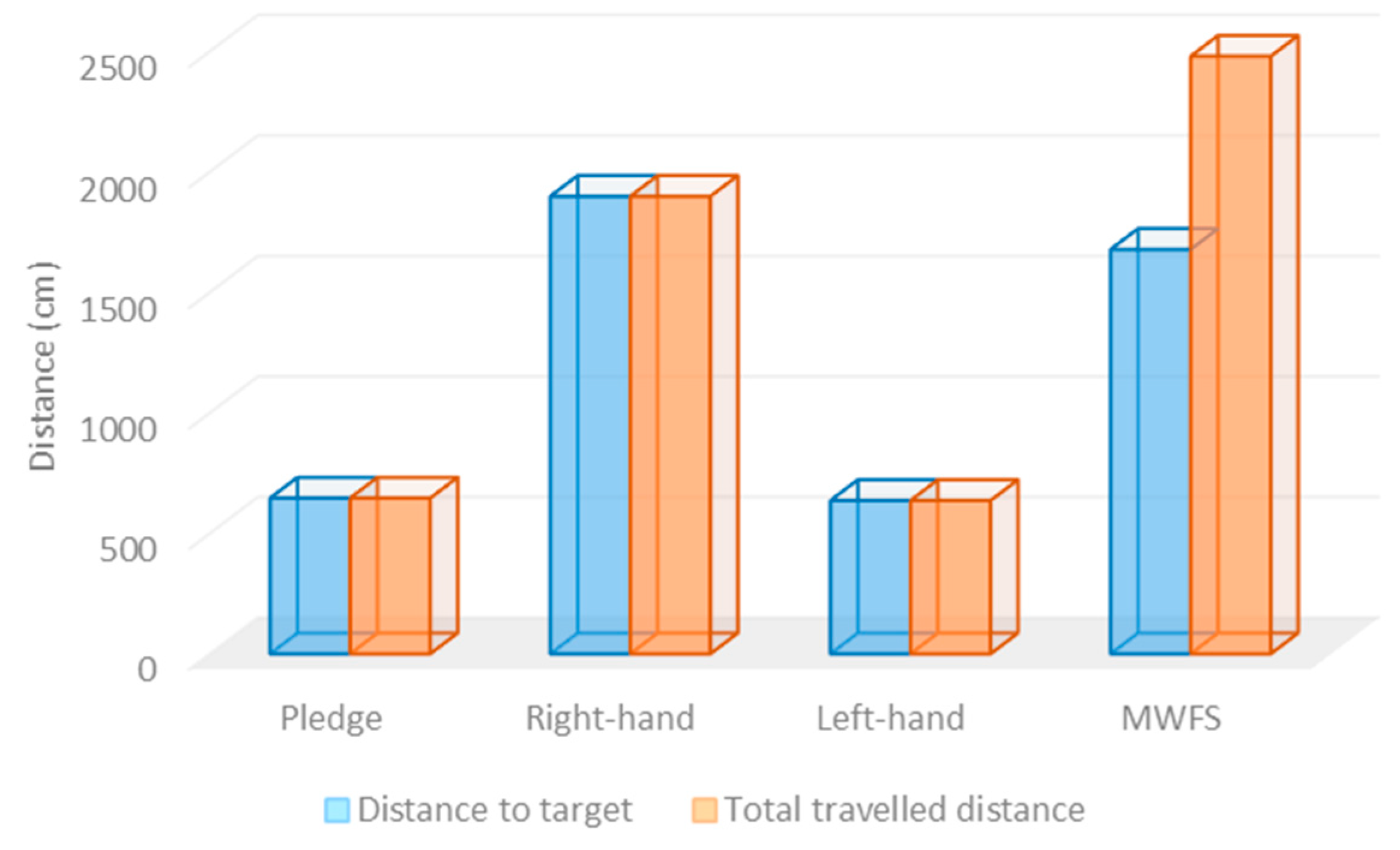
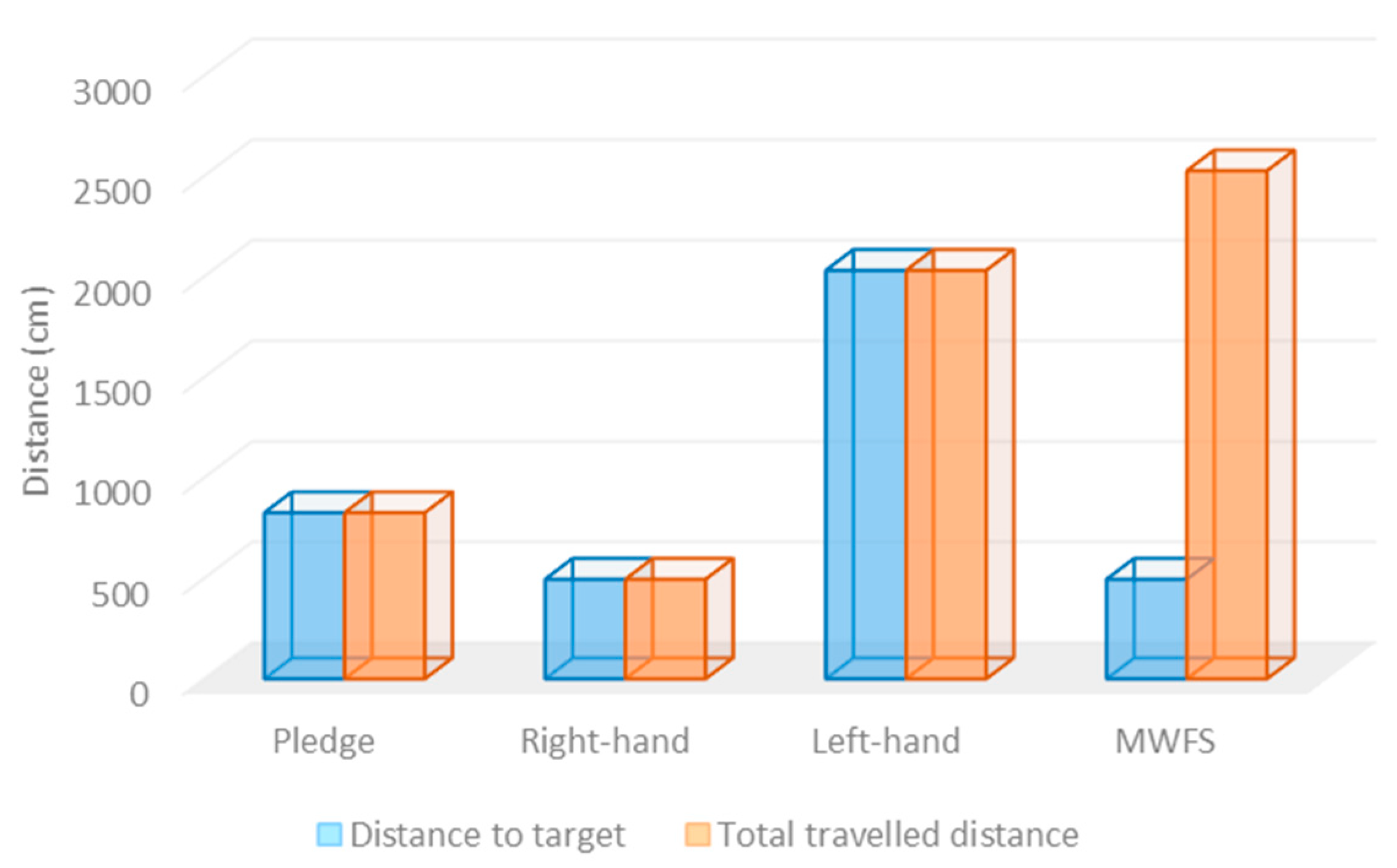
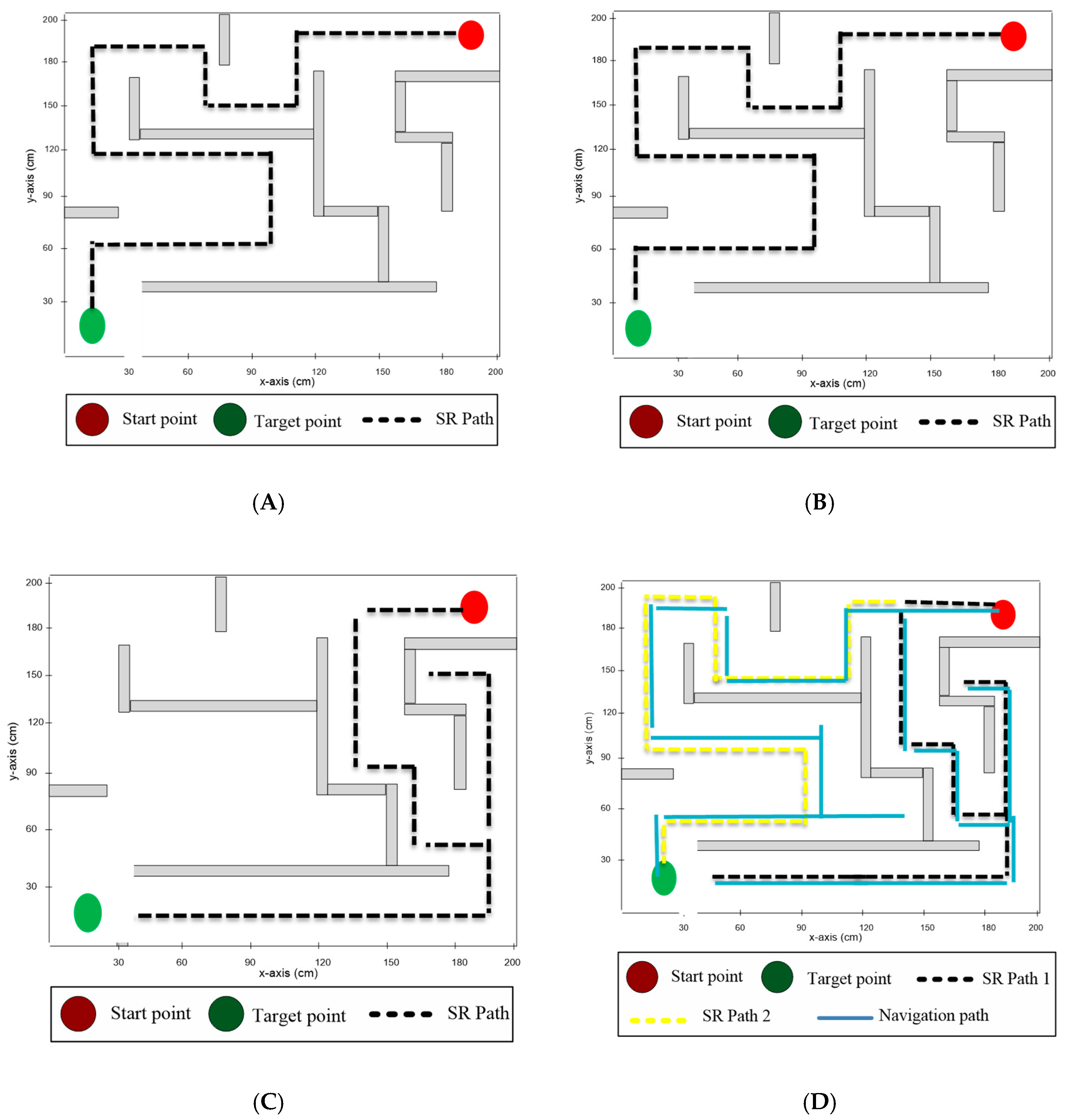
In the first experiment testbed, both the start and the destination points were located at the corners, as shown in Figure 8. The solver robot traveled autonomously in the maze area and navigated the paths according to the employed maze-solving system. As presented in Table 6, the left-hand rule required the minimum time to solve the maze and arrive at the destination point (4 min and 18 s), with a total traveled distance of 636 cm. However, the right-hand rule required the longest time (13 min and 40 s), with a total traveled distance equal to 1898 cm. All the algorithms explored a single path to the destination point, since no other paths existed. The modified wall-follower algorithm navigated the whole maze area to discover all paths between the start and destination points, with the total distance traveled being 2479 cm.
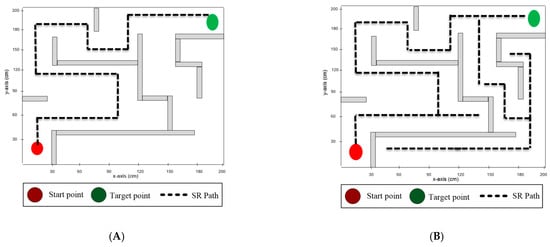
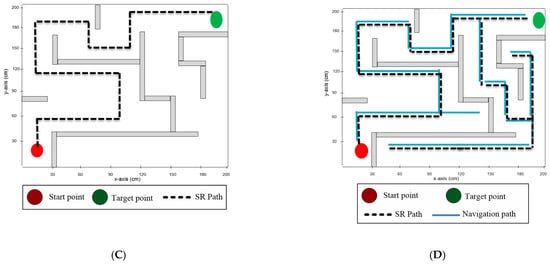
Figure 8.
The route of the solver robot using 4 algorithms in testbed # 1. (A) Pledge algorithm; (B) right-hand algorithm; (C) left-hand algorithm; (D) MWFS.

Table 6.
Experimental results obtained from the first experiment testbed.
Figure 8 presents the routes of the solver robot in maze area 1 through deploying different maze-solving algorithms. Figure 8A shows the route of the solver robot in maze area 1 using the Pledge maze-solving algorithm. In Figure 8B, the route of the solver robot is presented when employing the right-hand algorithm. Figure 8C depicts the solver-robot route for the left-hand algorithm. finally, Figure 8D presents the solver-robot route for the modified wall-follower algorithm.
As presented in Table 2, the right-hand algorithm required the maximum time to reach the destination point. In addition, all algorithms found a single path. In contrast, the modified wall-follower algorithm kept looking for new paths, even if a single path had been found, as presented in Figure 8D, where the navigation path is presented with a blue color. Figure 9 shows the total distance traveled to the destination point and the total distance traveled in the maze area in the four solving-robot systems.
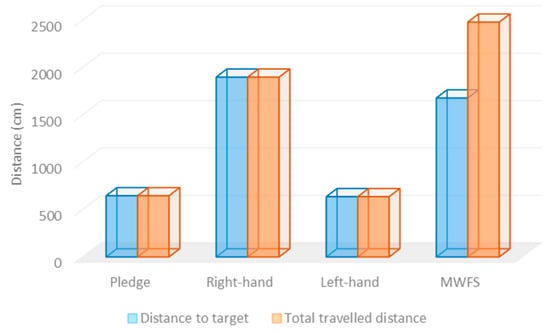
Figure 9.
The total traveled distance of the solver robot for 4 algorithms in testbed # 1.
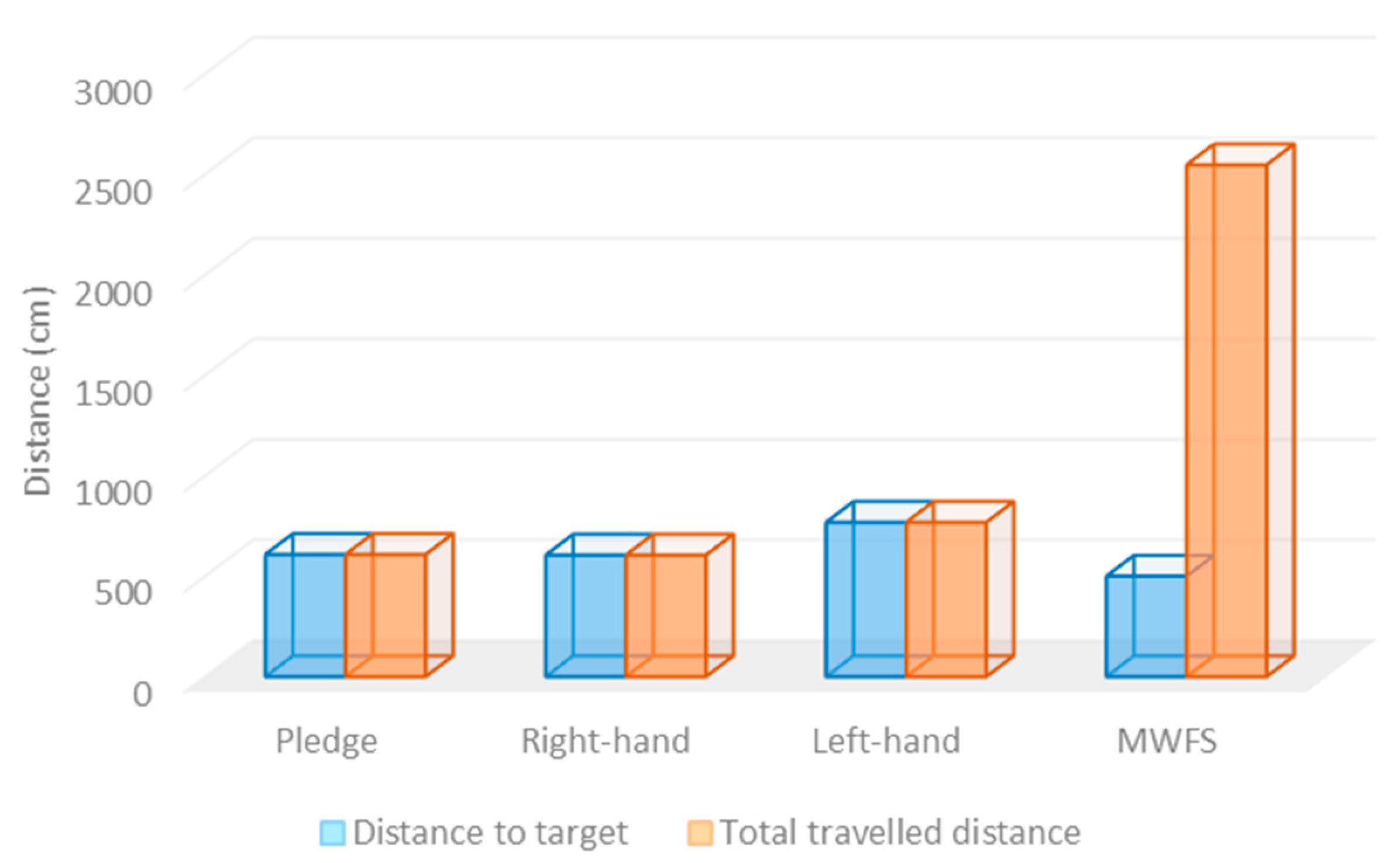
In the second experiment testbed, the initial and the destination points were located in different positions, as presented in Figure 10. Table 7 shows the experimental results obtained from deploying four different maze-solving algorithms in maze area 2. As presented, the modified wall-follower algorithm and the right-hand algorithm required the minimum time and distance to reach the target location, with a total traveled distance of 495 cm. On the other hand, the left-hand rule needed the maximum time and distance, with a total traveled distance of 2031 cm. However, the total distance traveled was around 2526 cm for the modified wall-follower algorithm. This was because the modified wall-follower algorithm needed to navigate the whole maze area to explore all the available routes to the destination location.
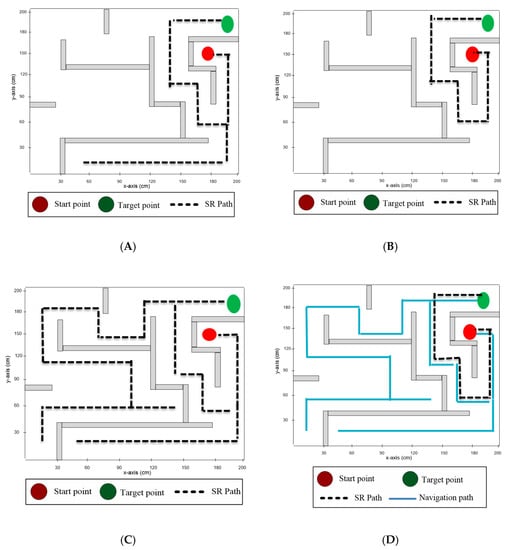
Figure 10.
The route of the solver robot using 4 algorithms in testbed # 2. (A) Pledge algorithm; (B) right-hand algorithm; (C) left-hand algorithm; (D) MWFS.

Table 7.
Experimental results obtained from the second experiment testbed.
Figure 10 shows the routes of the solver robot in the experiment testbed 2 through deploying four different maze-solving algorithms. Figure 10A shows the route traveled by the solver robot when deploying the Pledge algorithm. Figure 10B presents the route when adopting the right-hand algorithm. In Figure 10C, the solver-robot route when employing the left-hand rule is depicted, and finally, Figure 10D shows the route when adopting the modified wall-follower algorithm. The modified wall-follower algorithm navigated the whole maze area to search for other paths from the initial point to the target point. Figure 11 shows the total distance traveled to the destination point and the total distance traveled in the maze area for the four maze-solving robot systems.
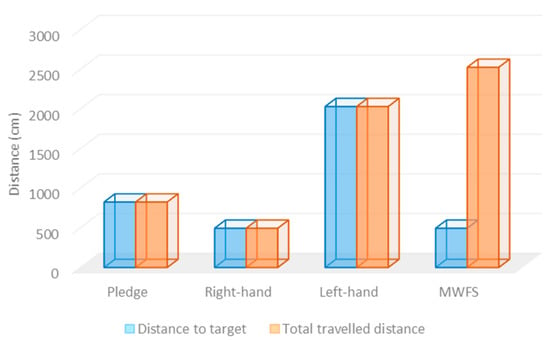
Figure 11.
The total traveled distance of the solver robot for 4 algorithms in testbed # 2.
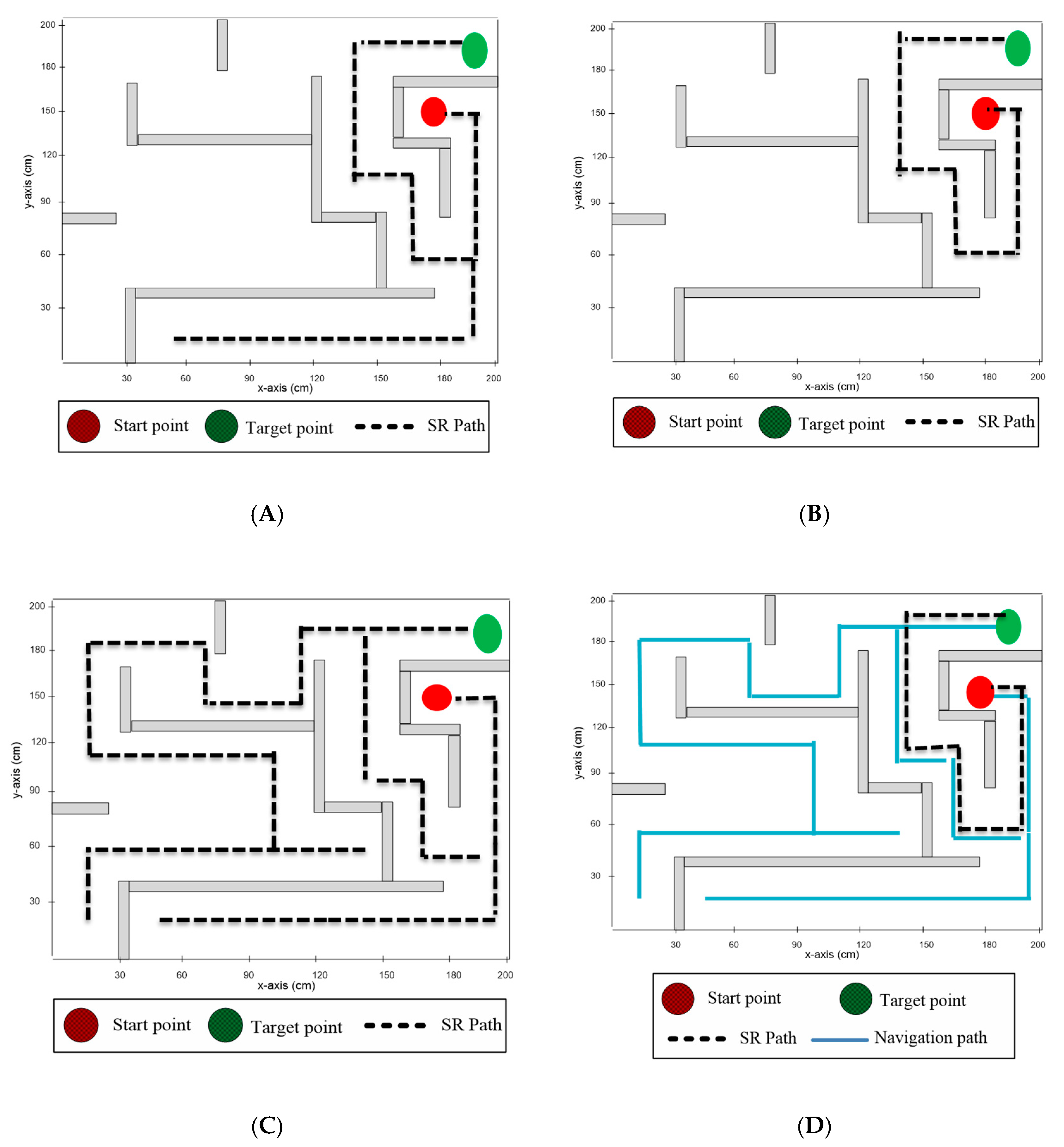
The initial and destination points were placed at the corners in the third experiment testbed, and more than one path existed between them. Table 8 shows the results obtained from deploying four different maze-solving algorithms in experiment testbed 3. The modified wall-follower algorithm required the minimum time to travel between the initial location and the target location, with a total traveled distance of 500 cm. On the other hand, the left-hand algorithm required the maximum time to reach the target location, with a total traveled distance of 768 cm.

Table 8.
Experimental results obtained from the third experiment testbed.
As presented in Table 4, the modified wall-follower algorithm required the minimum time to reach the target point, with a total traveled distance of 500 cm. In contrast, the left-hand algorithm required the maximum time to reach the target point, with a total traveled distance of 768 cm. However, in the modified wall-follower algorithm, the robot needed to navigate the whole maze area to look for another route, and the robot found two routes in this maze area. All other maze-solving algorithms found a single path to the target point.
Figure 12 presents the routes of the solver robot in experiment testbed 3 when employing the four maze-solving algorithms. Figure 12A shows the solver-robot route when using the Pledge algorithm, whereas in Figure 12B, the route of the solver robot is presented using the right-hand algorithm. Figure 12C presents the solver-robot route using the left-hand algorithm, and finally, Figure 12D shows the solver-robot route when the modified wall-follower algorithm was employed. Figure 13 presents the total distance traveled to the destination point and the total distance traveled in the maze area for each maze-solving robot system.
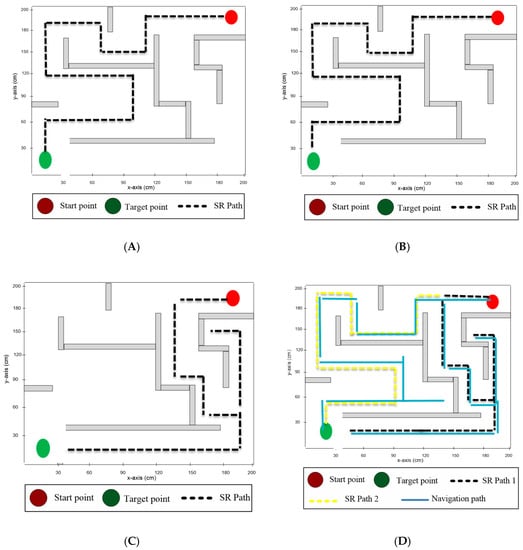
Figure 12.
The route of the solver robot using 4 algorithms in testbed # 3. (A) Pledge algorithm; (B) right-hand algorithm; (C) left-hand algorithm; (D) MWFS.
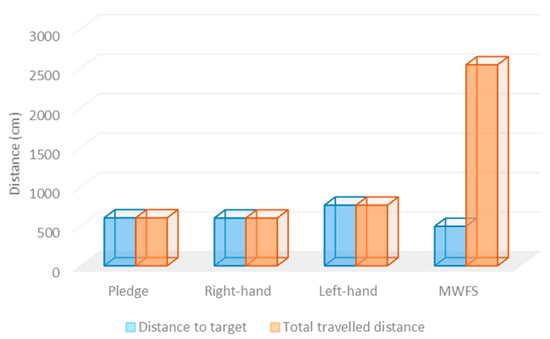
Figure 13.
The total traveled distance of the solver robot for 4 algorithms in testbed # 3.
As presented in Figure 12D, the robot found two possible routes between the initial and destination points (black and yellow routes), since the solver robot navigated the maze area even after finding out the first route.
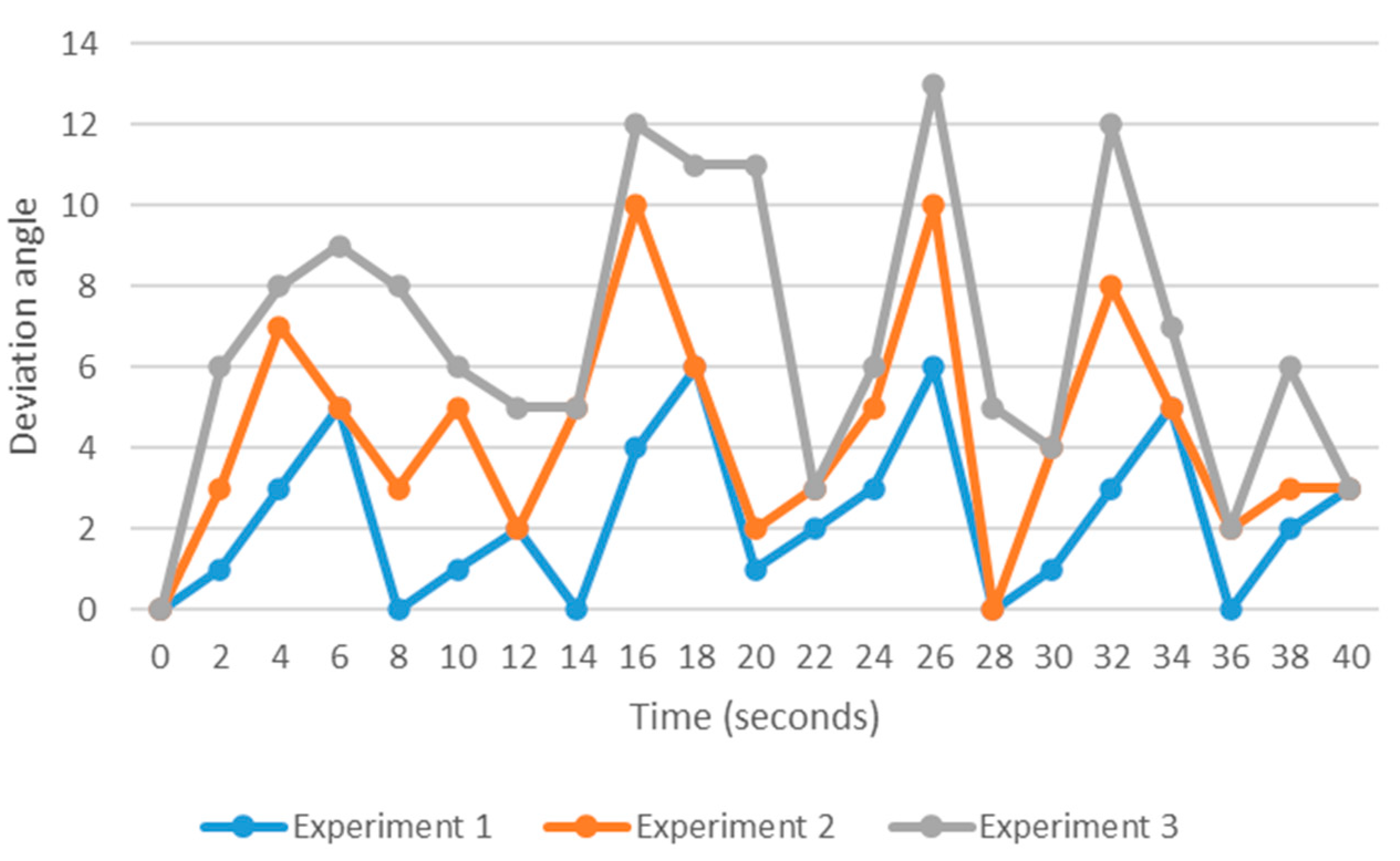
The robot deviation was evaluated by assessing the deviation angle in three different experiments using the MWFS approach. As depicted in Figure 14, the average deviation angle was almost 3 degrees; however, in all experiments, the solver robot balanced (rotate to 0 degrees, which is the straight mode) itself as soon as it deviated. For all experiments, the robot deviation angle was almost the same, with no noticeable variance.
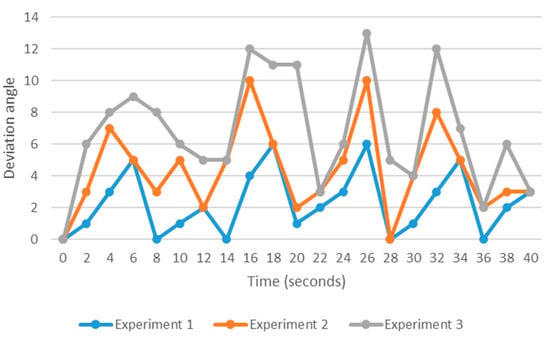
Figure 14.
Estimating the deviation angle using the MWFS approach for 3 different experiments.
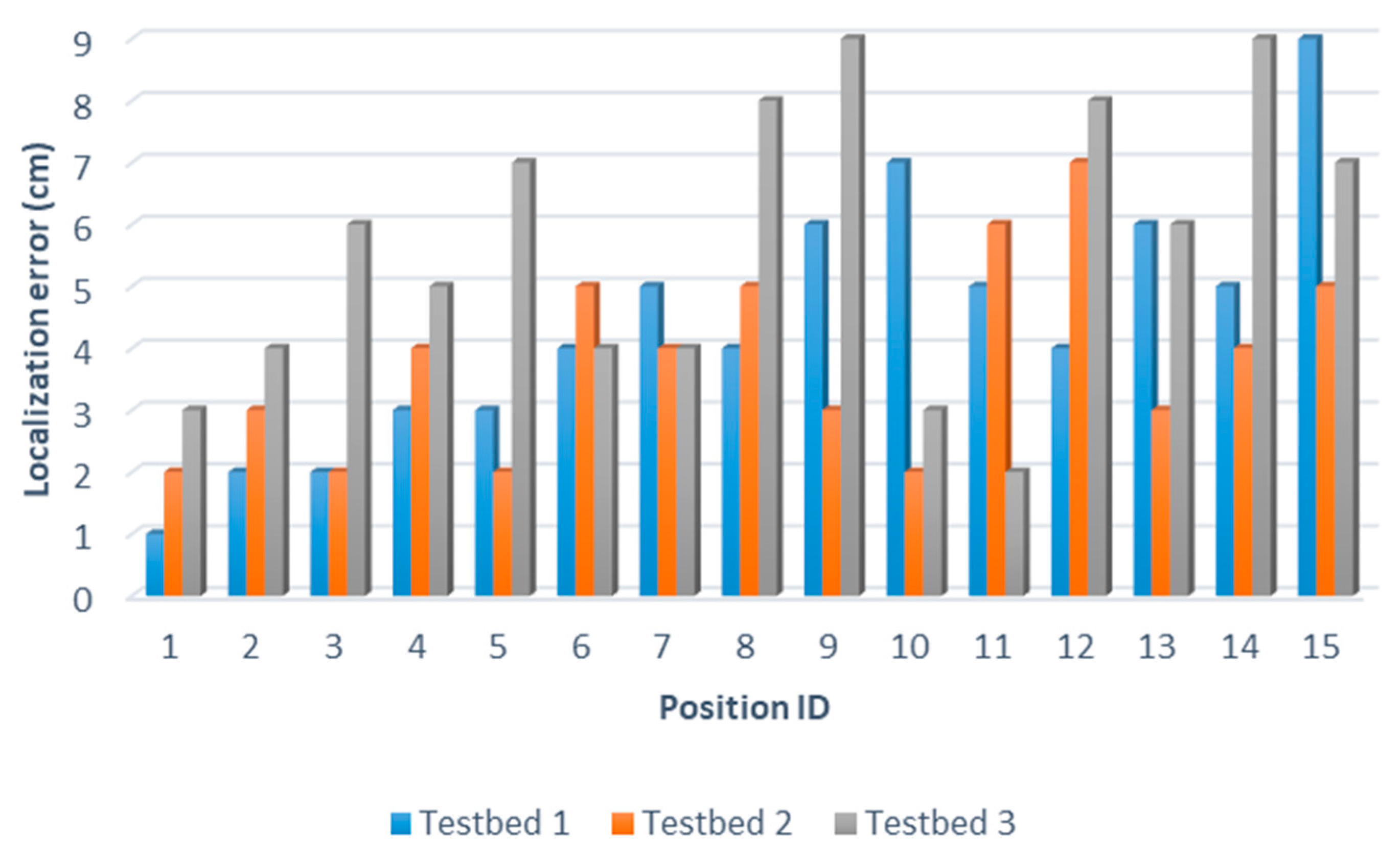
In addition, robot localization is a significant task in the navigation process. Therefore, it is important to study and analyze the performance of the employed positioning system. The localization accuracy was estimated by measuring the difference between the estimated position by the localization system and the robot’s actual position. The localization accuracy of the solver-robot system was evaluated in three different scenarios by estimating the solver robot’s location in twelve different reference locations. Figure 15 presents the localization accuracy for three different experiment testbeds through twelve locations using the MWFS approach. As noticed, the average localization error for the solver robot was around 9 cm in three different experiments.
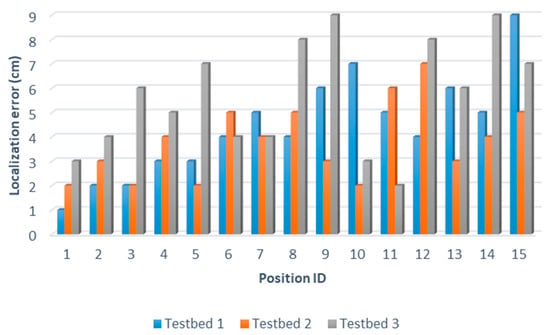
Figure 15.
The localization error using the MWFS approach for 3 different testbeds.
5. Discussion
In general, autonomous robots are expected to work independently in the area of interest, where the solver robot needs to move from one point to another in an autonomous way [25]. Wall-follower maze-solving systems have been deployed in several robotic applications. In this section, we discuss the key differences between the proposed wall-follower robotic system and the recently developed wall-follower robotic systems. The recently developed systems were evaluated according to the following metrics:
- Maze solving algorithm: this refers to the algorithm that was employed to solve the maze area.
- Sensors: this refers to the arrays of sensors that were employed to achieve the navigation task.
- Experiment testbed: this refers to the type of validation testbed that was used to validate the maze-solving robotic system.
- Ability to find out the shortest path: this refers to the robot’s ability to explore all the existing paths between the start and the destination points and hence determine the robot’s ability to find out the shortest path possible.
The work presented in [8,9] was based on simulation experiments, where several real metrics were not considered. On the other hand, the developed systems in [7,9,10] did not have the ability to navigate in the whole maze area and hence did not have the ability to retrieve the possible paths. Moreover, most of the existing wall-follower systems [7,8,9,10] do not take into consideration the localization and self-balancing issues, while in this paper, we presented an efficient maze-solving solution to deal with such issues. Table 9 presents a comparison among the recently developed wall-follower maze-solving systems.

Table 9.
A comparison between the recently developed wall-follower systems.
In addition, the average time required to solve the maze area was also considered in this study. Time is an important factor in robot maze-solving applications, where the maze-solver robot needs to navigate the unknown environment and reach the destination point with the minimum possible time. As noticed in the obtained results, no algorithm guarantees the shortest time, and the average time mainly depends on the environment structure.
To conclude the results obtained from the conducted real experiments, no single maze-solving algorithm is guaranteed to solve the maze in the shortest time possible. In general, solving the maze area depends on the maze structure and the location of the initial and the destination points. However, the proposed modified wall-follower robotic system usually guarantees finding a single path (at least) if it exists in the maze area. In addition, the proposed system never enters into an infinite loop-back, since it records the coordinates for every possible node in the tree and compares the coordinates of a new node with the coordinates of the tree’s nodes. As a result, the developed modified wall-follower system overcomes two main limitations in the existing wall-follower solving systems:
- The developed maze-solver robot system solves the infinite loop issues that exist in the recently developed wall-follower systems.
- The developed MWFS can explore all possible paths in the maze area, and hence, MWFS is able to find out all the possible paths between the initial and the destination points.
6. Conclusions
In this paper, we designed and implemented a modified wall-follower system (MWFS) based on the wall-follower algorithm, with tiny changes on the searching priority and with an off-loopback. Three different maze solving systems were experimentally tested, and the results were compared to the proposed MWFS’ results. The developed MWFS could solve the loop-back issue that existed in the existing wall-follower systems. In addition, the proposed maze solving robotic system efficiently navigated the maze area, found out all the possible paths, and then estimated the shortest path possible. For future research, we aim to develop various maze-solving algorithms and assess the speed and efficiency for each one. Finally, we aim to conduct our experiments in large maze areas to verify the effectiveness of the maze-solving algorithm and conduct some real experiments using different robot platforms.
Author Contributions
S.A. (Shatha Alamri), H.A. and S.A. (Shuruq Alshehri) completed the experimental study including the experiment setup and the achieved results. W.A. and A.A. surveyed the recent developed maze solving robotic systems. T.A. developed the enhanced maze solving robotic system, discussed the obtained results and finalized the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gul, F.; Rahiman, W.; Nazli Alhady, S.S. A comprehensive study for robot navigation techniques. Cogent Eng. 2019, 6, 1632046. [Google Scholar] [CrossRef]
- Pandey, A.; Pandey, S.; Parhi, D.R. Mobile robot navigation and obstacle avoidance techniques: A review. Int. Rob. Auto. J. 2017, 2, 00022. [Google Scholar] [CrossRef]
- Wyard-Scott, L.; Meng, Q.H. A potential maze solving algorithm for a micro mouse robot. In Proceedings of the IEEE Pacific Rim Conference on Communications, Computers, and Signal Processing, Victoria, BC, Canada, 17–19 May 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 614–618. [Google Scholar]
- Coufal, P.; Hubálovský, Š.; Hubálovská, M. Application of Basic Graph Theory in Autonomous Motion of Robots. Mathematics 2021, 9, 919. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path planning for the mobile robot: A review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Tullu, A.; Endale, B.; Wondosen, A.; Hwang, H.Y. Machine learning approach to real-time 3D path planning for autonomous navigation of unmanned aerial vehicle. Appl. Sci. 2021, 11, 4706. [Google Scholar] [CrossRef]
- Tirian, G.O. Maze-solving mobile robot. Ann. Fac. Eng. Hunedoara 2015, 13, 199. [Google Scholar]
- Husain, Z.; Al Zaabi, A.; Hildmann, H.; Saffre, F.; Ruta, D.; Isakovic, A.F. Search and rescue in a maze-like environment with ant and dijkstra algorithms. Drones 2022, 6, 273. [Google Scholar] [CrossRef]
- Kumar, R.; Jitoko, P.; Kumar, S.; Pillay, K.; Prakash, P.; Sagar, A.; Singh, R.; Mehta, U. Maze solving robot with automated obstacle avoidance. Procedia Comput. Sci. 2017, 105, 57–61. [Google Scholar] [CrossRef]
- Kaur, N.K.S. A review of various maze-solving algorithms based on graph theory. IJSRD 2019, 6, 431–434. [Google Scholar]
- Alamri, S.; Alshehri, S.; Alshehri, W.; Alamri, H.; Alaklabi, A.; Alhmiedat, T. Autonomous Maze Solving Robotics: Algorithms and Systems. Int. J. Mech. Eng. Robot. Res. 2021, 10, 668–675. [Google Scholar] [CrossRef]
- Niemczyk, R.; Zawiślak, S. Review of Maze Solving Algorithms for 2D Maze and Their Visualisation. In Engineer of the XXI Century; Springer: Cham, Switzerland, 2020; pp. 239–252. [Google Scholar]
- Saman, A.B.S.; Abdramane, I. Solving a reconfigurable maze using a hybrid wall follower algorithm. Int. J. Comput. Appl. 2013, 82, 0975–8887. [Google Scholar]
- Zarkasi, A.; Ubaya, H.; Amanda, C.D.; Firsandaya, R. Implementation of RAM Based Neural Networks on Maze Mapping Algorithms for Wall Follower Robot. J. Phys. Conf. Ser. 2019, 1196, 012043. [Google Scholar] [CrossRef]
- Del Rosario, J.R.B.; Sanidad, J.G.; Lim, A.M.; Uy, P.S.L.; Bacar, A.J.C.; Cai, M.A.D.; Dubouzet, A.Z.A. Modeling and characterization of a maze-solving mobile robot using wall follower algorithm. Appl. Mech. Mater. 2014, 446, 1245–1249. [Google Scholar]
- Pire, T.; Fischer, T.; Civera, J.; De Cristóforis, P.; Berlles, J.J. Stereo parallel tracking and mapping for robot localization. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1373–1378. [Google Scholar]
- Alhmiedat, T.; Salem, A.A. A Hybrid Range-free Localization Algorithm for ZigBee Wireless Sensor Networks. Int. Arab. J. Inf. Technol. (IAJIT) 2017, 14, 647–653. [Google Scholar]
- Junior, C.M.D.; da Silva, S.P.; da Nobrega, R.V.; Barros, A.C.; Sangaiah, A.K.; Reboucas Filho, P.P.; de Albuquerque, V.H.C. A new approach for mobile robot localization based on an online IoT system. Future Gener. Comput. Syst. 2019, 100, 859–881. [Google Scholar]
- Alhmiedat, T. An adaptive indoor positioning algorithm for ZigBee WSN. In Proceedings of the Fifth International Conference on the Innovative Computing Technology (INTECH 2015), Galicia, Spain, 20–22 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 51–55. [Google Scholar]
- Alhmiedat, T.; Aborokbah, M. Social distance monitoring approach using wearable smart tags. Electronics 2021, 10, 2435. [Google Scholar] [CrossRef]
- Alhmiedat, T.A.; Abutaleb, A.; Samara, G. A prototype navigation system for guiding blind people indoors using NXT Mindstorms. Int. J. Online Biomed. Eng. (IJOE) 2013, 9, 52–58. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, Y.N.; Tang, P.; Chen, R.; Jiang, Z.N.; Deng, A.B. Indoor Simultaneous Localization and Mapping for Lego Ev3. DEStech Trans. Comput. Sci. Eng. (CCNT) 2018, 500–504. [Google Scholar] [CrossRef]
- Alhawas, S.; Sabha, M.; Alhmiedat, T.A. The design and development of a smart fire-fighter robotic system. Int. Rob. Auto. J. 2017, 3, 00073. [Google Scholar]
- Bienias, Ł.; Szczepański, K.; Duch, P. Maze Exploration Algorithm for Small Mobile Platforms. Image Process. Commun. 2016, 21, 15–26. [Google Scholar] [CrossRef]
- Alenzi, Z.; Alenzi, E.; Alqasir, M.; Alruwaili, M.; Alhmiedat, T.; Alia, O.M.D. A Semantic Classification Approach for Indoor Robot Navigation. Electronics 2022, 11, 2063. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).