Abstract
In the case of simultaneous localization and mapping, route planning and navigation are based on data captured by multiple sensors, including built-in cameras. Nowadays, mobile devices frequently have more than one camera with overlapping fields of view, leading to solutions where depth information can also be gathered along with ordinary RGB color data. Using these RGB-D sensors, two- and three-dimensional point clouds can be recorded from the mobile devices, which provide additional information for localization and mapping. The method of matching point clouds during the movement of the device is essential: reducing noise while having an acceptable processing time is crucial for a real-life application. In this paper, we present a novel ISVD-based method for displacement estimation, using key points detected by SURF and ORB feature detectors. The ISVD algorithm is a fitting procedure based on SVD resolution, which removes outliers from the point clouds to be fitted in several steps. The developed method removes these outlying points in several steps, in each iteration examining the relative error of the point pairs and then progressively reducing the maximum error for the next matching step. An advantage over relevant methods is that this method always gives the same result, as no random steps are included.
1. Introduction
Controlling autonomous mobile robots is based on various sensors and the fusion of sensors [1]. Different types of cameras and computer vision are widely applied for recognition of the environment. The choice of sensors depends on the use case; however, it is generally useful for the robot to understand the environment to perform the specified task. For navigational tasks, knowledge of the position of the robot is essential, and additionally, information of obstacles and the desired target is crucial.
During navigation to the destined location, previously unknown, pop-up obstacles have to be detected by sensors, and avoidance is performed by the robot. In case a map is not available before operation, it has to be created by the vehicle during movement. These navigation methods are referred to as simultaneous localization and mapping, or SLAM, systems [2].
Movement of the vehicle can happen indoors or outdoors. In the case of outdoor navigation, we can rely on the global positioning system (GPS), which can give the absolute position of the vehicle relatively precisely [3,4]. Unfortunately, the application of GPS for indoor navigation is not recommended, due to lack of precision. For indoor localization, computer vision based solutions are applied: the detection of object feature points can help. Feature points [5] are detected by the camera and based on distances and other objects, the position of the vehicle can be determined. A possible solution is to put QR codes to predetermined places [6].
In some cases, it is not necessary to know the exact map of the environment, for example, in the case of warehousing cargo-bots [7,8,9]. For the warehouse automation, the line follower machines can detect and follow a line drawn on the floor. One significant disadvantage of this solution is that a pre-established infrastructure is necessary.
Movement estimation can happen using an accelerometer and a gyroscope. An autonomous system is able to estimate its own displacement based on these sensors; however, the estimation accuracy is imperfect. By using more sensors, localization can be further improved. In the paper by Csaba et al. [10], a localization and map building method was described based only on displacement sensory data from the wheels. As faults were accumulated continuously, self-positioning became more and more inaccurate as the robot moved.
In this paper, we present a solution for displacement estimation: a three-dimensional point cloud matching method referred to as ISVD. Displacement estimation is based on reduced point sets obtained from feature detectors with low computational power needs, using the proposed ISVD algorithm. The ISVD algorithm is a point cloud matching method based on singular value decomposition that gradually eliminates false pairs from point clouds. Outliers are deleted successively such that point pairs with a Euclidean distance greater than a threshold value are omitted in a certain step. This way, the error diminishes constantly, thus ensuring improving fitting accuracy. The advantage of this method is determinism, i.e., always providing the same output, in contrast to the RANSAC method, for instance, which gives different results for different executions due to its intrinsic randomness. The resulting visual odometry (VO) can be further refined by sensor fusion.
The structure of the paper is the following: in Section 2, a literature overview is given, concentrating on related work; in Section 3, the device used during the experiments is introduced; Section 4 contains the detailed description of the methods used for localization and mapping; in Section 5, the results are presented and evaluated; and finally, Section 6 summarizes the findings.
2. Related Work
In recent years, a number of small-sized relatively cheap sensors became available in computer vision applications, such as the Xtion [11], PrimeSense and Kinect sensors [12,13,14]. These devices are mostly used in prototyping; however, their implementation in production is also possible, as the depth sensing accuracy is feasible for small-sized mobile robots.
By using RGB-D cameras or stereo cameras, a detailed three-dimensional map can be created from the environment [13]. There are multiple works describing stereo-camera-based SLAM methods [15,16]. Similar results can be achieved using the LIDAR sensor, or even single cameras [17,18,19]. There are applications of LIDAR sensors in multi-robot environments [20], and recently a learning-based method was applied using a loop-closing algorithm to further improve the covered trajectory [21].
The method of position estimation using the RGB-D sensor starts with selecting feature points using the cameras [22]. This is followed by estimating the relative displacement between them, based on the knowledge of the spatial position of feature points [23,24]. Recent papers recommended using feature-based three-dimensional alignment [25,26,27,28].
For any method, the main difference is in the selected feature detector: robust feature detectors are computationally complex and, therefore, slow; simpler detectors may run in real-time, but the selected feature points might not be as reliable and stable as in the case of more sophisticated methods.
The SIFT feature detector [29] was applied in a paper describing 3D mapping of indoor environment [30]. The presented system used the PrimeSense sensor. A transformation between the resulting point clouds can be defined; the authors defined an RGBD-ICP algorithm to solve this. A loop closure detection [31] specifies the position of the vehicle on map building, continuously.
Images taken by unmanned aerial vehicles (UAVs) are often used in precision agriculture [32]. A solution to control a UAV based on an RGB-D camera was presented in [33]. FAST feature point detector [34] was applied, which is known for being less computationally expensive compared to the SIFT method. On the other hand, while the processing time is shorter, it is more sensitive for transformations.
An improved solution was presented in [35], similarly using FAST feature points. The performance can be further increased by using robust feature detectors [36].
3. Experimental Setup
A mobile robot was made for testing the algorithm and collecting measurement data (Figure 1). The robot includes drive electronics, onboard computer, and sensors.

Figure 1.
The mobile robot built and used for experiments. The experimental setup contains ultrasonic sensors and a commercially available Kinect sensor.
Main features of the robot:
- Two layer architecture leaves enough space for the electronics and controlling laptop;
- Driving wheels with 2 DC motor encoder;
- 4 inflated tire with air;
- Two 12V accumulator;
- 5 distance sensor;
- Integrated control electronics;
Custom motor controller electronics was developed, which is connected to the control computer. Ultrasonic sensors and a Kinect sensor are placed on the robot. Originally, the robot was built for data collection, which was processed offline on a PC, along other sources to comparatively evaluate different methods. Finally, the navigational algorithm of the robot is capable of running on the built-in computer in real time.
The system only uses colorful and pixel-level depth picture of a camera for movement following. Estimation of displacement is based on joined point clouds. To simplify navigation and route planning, the three-dimensional point cloud was reduced to a two-dimensional binary map. On the 2D map, obstacles with the minimum height similar as the robots were taken into account [10].
The robot is capable of navigating without storing 3D point clouds, and navigates simply based on calculated displacement. The elemental displacement is estimated during movement, and spatial place of the vehicle is therefore given from the starting position. This type of usage results in an RGBD sensor based IMU (RGBD-IMU) [37,38].
The Kinect sensor is a popular, low-budget RGB-D camera, with accuracy enough for controlling a vehicle indoors, and outdoor use is limited. Originally, it was developed for game control: the camera gives a colorful camera picture and pixel-level depth information from the area in front of it. Regarding accuracy, in the case of objects of at least 1 m distance, the standard deviation of sensors accuracy is maximum 5 mm. In case of further measurements, it is maximum 20 mm. A modified average filter can reduce this fault to 3 mm [39]. The few meters’ detection proximity of the sensor makes it able to be used on smaller sized robots indoors.
4. Methodology
During the movement of the robot, colorful and depth pictures are made continuously with the help of the Kinect sensor. Every colorful camera picture and pixel level depth information of the actual environment of the robot can be transformed into a three-dimensional point cloud (). Three dimensional piles (, ...) can be attached to each other. New point clouds can be attached to earlier sets if the sensor was displaced a little bit. Displacement is defined between earlier point cloud and the newest measurement. The latest measurement is given to the global map in every case, and this is the base of displacement estimation from an earlier place. If the latest sensor data are not able to attach to an earlier point cloud reliably, the data are trashed. During the movement, the measurement faults are accumulated to each other; in this way, the location of the vehicle will be more and more inaccurate. Knowing an earlier place from the traveled area, we have the chance to specify the position and reduction of faults accumulated earlier (loop-closure algorithm). The processing system is shown on Figure 2.
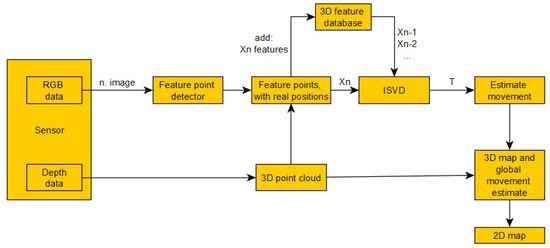
Figure 2.
Processing pipeline of the movement estimation and map building system.
The algorithm uses three-dimensional feature points to define displacement between point clouds made at different times. The searching of feature points happens on the colorful camera picture. These have determinative spatial location using depth data of the RGB-D camera. Using feature points, a displacement can be defined between measurements made at different places. The estimation of displacement between point clouds is based on SVD resolution.
Most research works deal with the feature-based 3D join topic. One significant difference is the feature detector used because these react for picture transformations in different ways. The running time of easier feature detectors (FAST) is much smaller than more complicated ones (SIFT, PCA-SIFT and SURF), but it reacts worse to each picture transformation. The best performance is achieved when applying the SIFT detector [40], as it gives the best results in the case of transformations or blurring. The main disadvantage of SIFT is the high processing time [30]. The most important conditions for real-time map building is choosing the fast feature point searching algorithm.
The FAST algorithm is a less robust detector with better runtime; however, it is less invariant for transformations [33]. For these experiments, we chose the SURF detector because of its robust work and speed. We recently presented a comparative analysis of available detectors, including ORB [41], SIFT [29], SURF [42] and FAST [34].
For the fast definition of the feature points spatial position, each depth point is indexed by its pixel pair on a colorful camera picture. In this way, if we search the depth information to a feature point on the colorful camera picture, it can be found in a short time due to indexing. Feature points are in the set. In this set, the position on a colorful camera picture and spatial position in the depth camera coordinate system are stored.
As the RGB-D sensor produces more noisy measurements for larger distances, feature points more than 5.5 meters away were discarded during the matching procedure based on our previous results [39]. Therefore, set only contains these pre-filtered feature points.
The system calculates displacement based on the newest feature points of point cloud and earlier (1, 4, 8, ...pieces feature points made in earlier points). Feature points of the latest measurement are paired to earlier measurements, then transformation between the point clouds is calculated based on feature point pairs which know their spatial location. In this way, we obtain the relative displacement compared to the earlier known point.
The transformation between them is defined by a multi-level join method based on feature point pairs (Algorithm 1). During the processing of the algorithm, the goal is to find the minimal join fault between the two sets of Equation (1).
| Algorithm 1 The proposed multistage three dimensional point cloud matcher (ISVD) |
procedure ISVD(D, S, , , ) for do for do if then end if end for if then Return else = end if end for end procedure |
In the two feature point sets, where the spatial location of points are known and all points have a pair, the algorithm gives transformation between them (Algorithm 1). It starts from initial transformation, which is an estimated value. During each iteration, the wrong point pairs are examined by the join method. It deletes those point pairs whose Euclidean distance is more than . The is the biggest allowed difference between the join points. The initial value is , and gives the value of the join fault.
First, the algorithm removes those feature pairs that have high error values. The value of decreases successively in every step, as better quality feature pairs become available for SVD-based joining. This way, transformation T become more and more accurate between the two sets. Successively discarding outlier points step by step makes the procedure more and more accurate, as the matching has to consider fewer and fewer misleading points. The SVD-based matching [43] finds the transformation with minimal error during the iteration. The optimal transformation between two point sets is defined by the algorithm using the aforementioned singular value decomposition. Then, the translation vector is created using the center of gravity of the sets. This process is repeated multiple times until termination, i.e., when it reaches the maximum number of steps , or the fitting has the desired accuracy .
The pairs of points that are associated incorrectly by feature detector are removed from the system. Figure 3 shows an example of points associated correctly, also considering their spatial information on top of the feature vector. This procedure is also appropriate to filter feature points of homogeneous surfaces or those with recurring patterns.

Figure 3.
Visualized results for the 3D feature matching, and the reconstructed environment.
Figure 4 shows the reduction in coherent point pairs during the joining of two point sets, and it gives the quality of joining as well (). An estimated displacement is defined by the joining of feature point from actual measurement and its earlier () and previous () feature points. Almost 200 feature pairs were reduced to less than 50 by the algorithm during four iterations. There is enough overlap on some picture made before the actual measurement to run the algorithm.
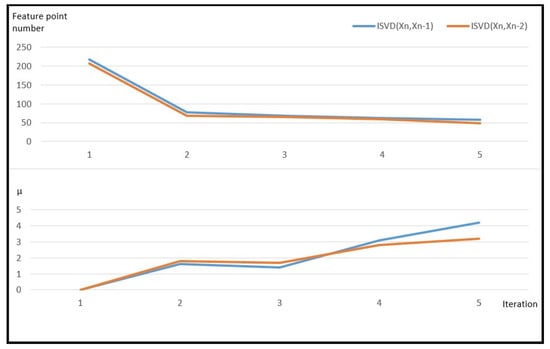
Figure 4.
Processing time for the ISVD algorithm. The upper diagram shows the feature point pair number in each iteration. Below, the diagram shows quality of the transformation first and last iteration.
Quality of two point sets is shown by the . The overlap of the two point sets is given in Equation (2) for an estimated T transformation. The join is unsuccessful if its value is zero. The quality of the join is much better if its value is much bigger.
where .
In the case of final the measurement, the estimation of the position is given by the algorithm for previously known estimation and some earlier (4 or 8) cases. Each estimation contains the accuracy of the join to earlier cases. The new estimation of the position is given by the earlier measurements quality.
5. Evaluation and Results
The advantage of the algorithm is that the transformation between the point pairs is defined defined; in this way, the running time of the algorithm is reduced significantly.The system calculates with just a few predetermined points. The ISVD algorithm takes into consideration that every point pair in the point sets has its own pairs. Accumulated fault after sixty 3D joins in the case of the ICP is 2.86 and 343 mm and in case of the ISVD is 1.48 and 248 mm. During measurement, the sensor is rotated 360 degrees around. In the case of the same feature detectors and parameters, the rotational and translational faults at ISVD algorithm are smaller than in the case of using an ICP algorithm [30,44].
Algorithm testing happened on some sets from two different sources. Data sets were made with our own robot system in university buildings, laboratories and corridors. As a second source, data sets made at Poznan University were used. They were made for mobile robot developments [45].
In case of our own measurements, the real spatial position of the robot is unknown. The starting and target positions are always the same. The robot takes a whole circle in every case, so its first and last positions are the same. In this way, the absolute translation and rotation fault accumulated can be examined. The sensor goes back to the starting point in every case. Its accurate route is unknown. The reconstruction is made by our own application and then shown in the application (Figure 5). The vehicle completes a whole circle in the laboratory in this measurement. All of the accumulated absolute translation faults on each axis are x = −250 mm, y = 2.5 mm, z = 15 mm. The absolute rotational fault is , , .
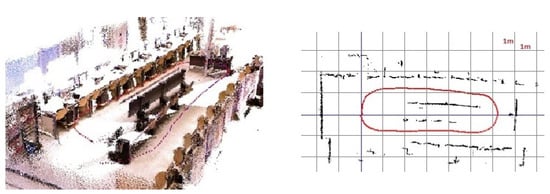
Figure 5.
The 2D and 3D visualizations of the results on custom, self-collected data. The data set contains 300 images.
In the case of data sets [45] made at Poznan University, the actual spatial position of the robot is also available in addition to the regular and depth-image pairs produced by the Kinect sensor. Four such image sequences were recorded by the sensor applied to a WifiBot. The location of the vehicle was registered by five cameras from the ceiling. The produced data set contains all color and depth images as well as camera parameters and information about vehicle movement. Images were captured every 100 ms.
In most similar research, there are two measurement numbers for displacement estimation on data series containing real spatial position [46]. The absolute trajectory error (ATE) shows how far the robot is from the real position in a given position. The relative pose error (RPE) examines only the relative displacement between two pictures made one after another. In the case of displacement estimation, small faults generated at each join are added up; in this way, if there is a fault in one join, they exist at the other ones as well. RPE based in an actual join fault can be calculated from the difference between the actual and previous real and estimated displacement. There is an average fault in the case of ATE and RPE, which is the average of faults made at every measurement. It is called the RMSE. On Figure 6, the left image showing the result of the three-dimensional reconstruction generated by joins run on data series can be seen. Figure 6, the right image, shows the two-dimensional version.

Figure 6.
The 3D reconstruction of the Poznan University data set [45]. The blue line represents the ground truth movement, the red line shown the estimated movement. For these results 700 images were used from the data set; SURF was applied for feature detection.
We made comparison measurements from 300 pictures joining on trajectory1 [45] data set. During testing, there were parameters next to SURF and ORB feature detectors to show how many earlier pictures the actual measurement is joined to. The average result of the joins is shown in Figure 7. Figure 8 and Figure 9 show the relative displacement faults detailed in the point pairs.

Figure 7.
RMSE value on trajectory1 [45] data sets. The blue bar shows the translation error in millimeters, and the orange chart shows the rotation error in degrees.

Figure 8.
Relative pose error (RPE) on a trajectory1 [45] datasets. The blue line shows the error when ORB feature detector is used and the red line shows the error when SURF detector is used. Used orb2 and surf2 joining (trajectory error in and rotation error in degree).

Figure 9.
Relative pose error (RPE) on a trajectory1 [45] datasets. The blue line shows the error when ORB feature detector is used, and the red line shows the error when SURF detector is used. Used orb4 and surf4 joining (trajectory error in mm and rotation error in degree).
In the case of the orb2 data set, two previous measurements were used with the ORB feature detection. For surf1, surf2, surf4 and surf8, one, two, four and eight measurements were taken into account, respectively, using the SURF feature detector. When multiple measurements were evaluated, custom weights for the transformations were calculated by Equation (2). For surf4-avg and surf8-avg data sets, the SURF feature detector was applied with four and eight measurements, respectively, but the transformation was determined based on the average values. It can be seen that SURF provides better results compared to the ORB feature detection. Additionally, taking more previous measurements into account, the accuracy can be further improved. Using the SURF feature detection with 4 and 8 measurements at least, the best results were obtained when their weighted averages were taken.
On a mid-level computer, the average run time of the algorithm was 180 ms (Intel Core 2 Quad Q9400 @2.66 GHz). The process consists of three major parts: finding feature points on new images (which is more time consuming in the case of SURF); constructing a three-dimensional point cloud (which consumes negligible time and is independent of the feature detector used); and determining the transformation between the two sets of points (which is also time consuming). The run time of the latter part is mainly governed by the number of previous measurements, which is considered during the alignment.
The matching procedure is extended with a loop-closure (LC) algorithm, which continuously monitors the matches between the current image and the keyframes. It determines the match by comparing the feature descriptors of the current image with the feature descriptors of the previous keyframes. The feature vectors of the key images are stored continuously, the keyframes are selected linearly, and every 20th frame is selected for this purpose. If a match is found with a previous image, the ISVD algorithm attempts to provide a relative displacement estimate between the frame and the current image, then the resulting offset is used to refine the odometry. The execution time of the algorithm increases significantly for larger data sets.
The performance of the proposed system is compared with four similar solutions. The comparison was made using the fr1/desk [46] dataset. The ATE (RMSE [m]) values of the results are shown in Table 1. In our previous work, where the LC procedure was not applied (surf8 pre. work) [47], we managed to slightly improve the results using the SURF detector for the surf4 parameter. By extending the system with the LC procedure, we achieved a further increase in accuracy (surf4+LC). The table also shows that we were able to match the results of the four similar systems and achieve higher accuracy for one of them.

Table 1.
The achieved results in comparison with other relevant techniques using the fr1/desk [46] dataset. In the table, ATE values are expressed in RMSE [m]. Columns 2 to 4 show the results of our own methods, while the remaining columns show the values of relevant geometric approximations.
6. Conclusions
Two- and the three-dimensional maps are made by our own join algorithm introduced in the article from the data of a RGB-D camera put on a mobile robot. The information needed for the navigation of the robot is provided by these maps. The method gives a spatial displacement of the sensor and robot in an unknown area, and global maps made from the traveled area. A robust feature detector and point cloud join method based in SVD resolution are used for displacement estimation.
During tests, mainly the SURF and ORB detectors are chosen. The selected feature detectors are well known, and many implementations exist; an important argument for our system is the relatively low computational cost. Further investigation with additional feature detectors can be done in the future, which should lead to further improvements. The proposed algorithm searches feature points on every measurement point in real time. In the next step, the three-dimensional point cloud is made, and feature points found earlier are indicated in this point cloud. Tests are run on their own and on other data sets which were made for mobile robots.This developed algorithm () gives the estimated displacement compared to the final measurement during more steps. During this time, not related points, which are detected as wrong by the feature detector, are deleted by the method. During measurements, using the SURF detector, a 9.9 mm average displacement and 0.38 rotational fault are generated by examination of the trajectory1 data set.
Future plans include the application of deep learning for data-driven feature detection [52]: for indoor environments, a wide dataset can be prepared and used to find general features of objects, which could optimize feature selection and, therefore, reduce the computational costs.
Author Contributions
Conceptualization, L.S. and Z.V.; methodology, L.S. and Z.V.; software, L.S.; validation, Z.V.; formal analysis, Z.V.; investigation, L.S.; resources, Z.V.; data curation, L.S.; writing—original draft preparation, L.S.; writing—review and editing, Z.V.; visualization, L.S.; supervision, Z.V.; project administration, Z.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the colleagues at the John von Neumann Faculty of Informatics for their comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ATE | Absolute Trajectory Error |
| FAST | FAST Feature Detector |
| GPS | Ground Positioning System |
| ICP | Iterative Closest Point |
| IMU | Inertial Movement Unit |
| ISVD | Iterative SVD |
| LC | Loop Closure |
| LIDAR | Light Detection and Ranging |
| ORB | Oriented FAST and Rotated BRIEF |
| PC | Personal Computer |
| PCA | Principal Component Analysis |
| QR | Quick Response Code |
| RGB | Red Green Blue Color Representation |
| RGBD | RGB+Depth Sensor |
| RMSE | Root Mean Square Error |
| RPE | Relative Pose Error |
| SIFT | Scale-Invariant Feature Transform |
| SLAM | Simultaneous Localization and Mapping |
| SURF | Sped-Up Robust Features |
| SVD | Singular Value Decomposition |
| UAV | Unmanned Aerial Vehicle |
| VO | Visual Odometry |
References
- Filipenko, M.; Afanasyev, I. Comparison of various slam systems for mobile robot in an indoor environment. In Proceedings of the 2018 International Conference on Intelligent Systems (IS), Funchal, Portugal, 25–27 September 2018; pp. 400–407. [Google Scholar]
- Scaramuzza, D.; Fraundorfer, F. Visual odometry [tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Ross, R.; Hoque, R. Augmenting GPS with geolocated fiducials to improve accuracy for mobile robot applications. Appl. Sci. 2019, 10, 146. [Google Scholar] [CrossRef] [Green Version]
- Szénási, S.; Kertész, G.; Felde, I.; Nádai, L. Statistical accident analysis supporting the control of autonomous vehicles. J. Comput. Methods Sci. Eng. 2021, 21, 85–97. [Google Scholar] [CrossRef]
- Cristinacce, D.; Cootes, T.F. Feature Detection and Tracking with Constrained Local Models. In Proceedings of the British Machine Vision Conference, Edinburgh, UK, 4–7 September 2006; BMVA Press: Swansea, UK, 2006; pp. 95.1–95.10. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, H. A new proposal for self-localization of mobile robot by self-contained 2d barcode landmark. In Proceedings of the 2012 of SICE Annual Conference (SICE), Akita, Japan, 20–23 August 2012; pp. 2080–2083. [Google Scholar]
- Elayaraja, D.; Ramabalan, S. Investigation in autonomous line follower robot. J. Sci. Ind. Res. 2017, 76, 212–216. [Google Scholar]
- Yildiz, H.; Korkmaz Can, N.; Ozguney, O.C.; Yagiz, N. Sliding mode control of a line following robot. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–13. [Google Scholar] [CrossRef]
- Goyal, N.; Aryan, R.; Sharma, N.; Chhabra, V. Line Follower Cargo-Bot For Warehouse Automation. Int. Res. J. Eng. Technol. 2021, 8, 1–8. [Google Scholar]
- Csaba, G.; Somlyai, L.; Vámossy, Z. Differences between Kinect and structured lighting sensor in robot navigation. In Proceedings of the 2012 IEEE 10th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 26–28 January 2012; pp. 85–90. [Google Scholar]
- Wasenmüller, O.; Meyer, M.; Stricker, D. CoRBS: Comprehensive RGB-D benchmark for SLAM using Kinect v2. In Proceedings of the 2016 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Placid, NY, USA, 7–10 March 2016; pp. 1–7. [Google Scholar]
- Kuan, Y.W.; Ee, N.O.; Wei, L.S. Comparative study of intel R200, Kinect v2, and primesense RGB-D sensors performance outdoors. IEEE Sens. J. 2019, 19, 8741–8750. [Google Scholar] [CrossRef]
- Zhou, T.; Fan, D.P.; Cheng, M.M.; Shen, J.; Shao, L. RGB-D salient object detection: A survey. Comput. Vis. Media 2021, 7, 37–69. [Google Scholar] [CrossRef]
- Tadic, V.; Toth, A.; Vizvari, Z.; Klincsik, M.; Sari, Z.; Sarcevic, P.; Sarosi, J.; Biro, I. Perspectives of RealSense and ZED Depth Sensors for Robotic Vision Applications. Machines 2022, 10, 183. [Google Scholar] [CrossRef]
- Zhou, Y.; Gallego, G.; Shen, S. Event-based stereo visual odometry. IEEE Trans. Robot. 2021, 37, 1433–1450. [Google Scholar] [CrossRef]
- Kostavelis, I.; Boukas, E.; Nalpantidis, L.; Gasteratos, A. Stereo-based visual odometry for autonomous robot navigation. Int. J. Adv. Robot. Syst. 2016, 13, 21. [Google Scholar] [CrossRef] [Green Version]
- Dieterle, T.; Particke, F.; Patino-Studencki, L.; Thielecke, J. Sensor data fusion of LIDAR with stereo RGB-D camera for object tracking. In Proceedings of the 2017 IEEE Sensors, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Qi, X.; Wang, W.; Liao, Z.; Zhang, X.; Yang, D.; Wei, R. Object semantic grid mapping with 2D LiDAR and RGB-D camera for domestic robot navigation. Appl. Sci. 2020, 10, 5782. [Google Scholar] [CrossRef]
- Vokhmintcev, A.; Timchenko, M. The new combined method of the generation of a 3d dense map of evironment based on history of camera positions and the robot’s movements. Acta Polytech. Hung. 2020, 17, 95–108. [Google Scholar] [CrossRef]
- Amanatiadis, A.; Henschel, C.; Birkicht, B.; Andel, B.; Charalampous, K.; Kostavelis, I.; May, R.; Gasteratos, A. Avert: An autonomous multi-robot system for vehicle extraction and transportation. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1662–1669. [Google Scholar]
- Chen, X.; Läbe, T.; Milioto, A.; Röhling, T.; Vysotska, O.; Haag, A.; Behley, J.; Stachniss, C. OverlapNet: Loop closing for LiDAR-based SLAM. arXiv 2021, arXiv:2105.11344. [Google Scholar]
- Kostavelis, I.; Gasteratos, A. Learning spatially semantic representations for cognitive robot navigation. Robot. Auton. Syst. 2013, 61, 1460–1475. [Google Scholar] [CrossRef]
- Fuentes-Pacheco, J.; Ruiz-Ascencio, J.; Rendón-Mancha, J.M. Visual simultaneous localization and mapping: A survey. Artif. Intell. Rev. 2015, 43, 55–81. [Google Scholar] [CrossRef]
- Mac, T.T.; Lin, C.Y.; Huan, N.G.; Duc, L.; Nhat, P.C.H.; Hai, H.H. Hybrid SLAM-based exploration of a mobile robot for 3D scenario reconstruction and autonomous navigation. Acta Polytech. Hung 2021, 18, 197–212. [Google Scholar]
- Hana, X.F.; Jin, J.S.; Xie, J.; Wang, M.J.; Jiang, W. A comprehensive review of 3D point cloud descriptors. arXiv 2018, arXiv:1802.02297. [Google Scholar]
- Renò, V.; Nitti, M.; di Summa, M.; Maglietta, R.; Stella, E. Comparative analysis of multimodal feature-based 3D point cloud stitching techniques for aeronautic applications. In Proceedings of the 2020 IEEE 7th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Pisa, Italy, 22–24 June 2020; pp. 398–402. [Google Scholar]
- Xu, T.; An, D.; Jia, Y.; Yue, Y. A review: Point cloud-based 3d human joints estimation. Sensors 2021, 21, 1684. [Google Scholar] [CrossRef]
- Fernandes, D.; Silva, A.; Névoa, R.; Simoes, C.; Gonzalez, D.; Guevara, M.; Novais, P.; Monteiro, J.; Melo-Pinto, P. Point-cloud based 3D object detection and classification methods for self-driving applications: A survey and taxonomy. Inf. Fusion 2021, 68, 161–191. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Henry, P.; Krainin, M.; Herbst, E.; Ren, X.; Fox, D. RGB-D mapping: Using depth cameras for dense 3D modeling of indoor environments. In Experimental Robotics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 477–491. [Google Scholar]
- Ho, K.L.; Newman, P. Loop closure detection in SLAM by combining visual and spatial appearance. Robot. Auton. Syst. 2006, 54, 740–749. [Google Scholar] [CrossRef]
- Kiss, D.; Stojcsics, D. Eigenvector based segmentation methods of high resolution aerial images for precision agriculture. In Proceedings of the 5th ICEEE-2014 International Conference: Global Environmental Change and Population Health: Progress and Challenges, Budapest, Hungary, 19–21 November 2014; pp. 155–162. [Google Scholar]
- Huang, A.S.; Bachrach, A.; Henry, P.; Krainin, M.; Maturana, D.; Fox, D.; Roy, N. Visual odometry and mapping for autonomous flight using an RGB-D camera. In Robotics Research; Springer: Berlin/Heidelberg, Germany, 2017; pp. 235–252. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 430–443. [Google Scholar]
- Nowicki, M.; Skrzypezyński, P. Combining photometric and depth data for lightweight and robust visual odometry. In Proceedings of the 2013 European Conference on Mobile Robots, Barcelona, Spain, 25–27 September 2013; pp. 125–130. [Google Scholar]
- Endres, F.; Hess, J.; Engelhard, N.; Sturm, J.; Cremers, D.; Burgard, W. An evaluation of the RGB-D SLAM system. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1691–1696. [Google Scholar]
- Laidlow, T.; Bloesch, M.; Li, W.; Leutenegger, S. Dense RGB-D-inertial SLAM with map deformations. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6741–6748. [Google Scholar]
- Deng, X.; Jin, G.; Wang, M.; Li, J. Robust 3D-SLAM with tight RGB-D-inertial fusion. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 4389–4396. [Google Scholar]
- Somlyai, L.; Vámossy, Z. Map building with rgb-d camera for mobil robot. In Proceedings of the 2012 IEEE 16th International Conference on Intelligent Engineering Systems (INES), Lisbon, Portugal, 13–15 June 2012; pp. 489–493. [Google Scholar]
- Juan, L.; Gwun, O. A comparison of sift, pca-sift and surf. Int. J. Image Process. (IJIP) 2009, 3, 143–152. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-squares fitting of two 3-D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar] [CrossRef] [Green Version]
- Seeger, S.; Laboureux, X.; Häusler, G. An accelerated ICP-algorithm. In Lehrstuhl für Optik; Annual Report; Springer: Berlin/Heidelberg, Germany, 2001; p. 32. [Google Scholar]
- Schmidt, A.; Fularz, M.; Kraft, M.; Kasiński, A.; Nowicki, M. An indoor RGB-D dataset for the evaluation of robot navigation algorithms. In Proceedings of the International Conference on Advanced Concepts for Intelligent Vision Systems, Poznań, Poland, 28–31 October 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 321–329. [Google Scholar]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Somlyai, L.; Csaba, G.; Vámossy, Z. Benchmark system for novel 3D SLAM algorithms. In Proceedings of the 2018 IEEE 16th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Kosice and Herlany, Slovakia, 7–10 February 2018; pp. 000131–000136. [Google Scholar]
- Whelan, T.; Kaess, M.; Johannsson, H.; Fallon, M.; Leonard, J.J.; McDonald, J. Real-time large-scale dense RGB-D SLAM with volumetric fusion. Int. J. Robot. Res. 2015, 34, 598–626. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Li, R.; Hu, H.; Gu, D. Building semantic maps for blind people to navigate at home. In Proceedings of the 2016 8th Computer Science and Electronic Engineering (CEEC), Colchester, UK, 28–30 September 2016; pp. 12–17. [Google Scholar]
- Endres, F.; Hess, J.; Sturm, J.; Cremers, D.; Burgard, W. 3-D mapping with an RGB-D camera. IEEE Trans. Robot. 2013, 30, 177–187. [Google Scholar] [CrossRef]
- Stückler, J.; Behnke, S. Multi-resolution surfel maps for efficient dense 3D modeling and tracking. J. Vis. Commun. Image Represent. 2014, 25, 137–147. [Google Scholar] [CrossRef]
- Arshad, S.; Kim, G.W. Role of deep learning in loop closure detection for visual and lidar SLAM: A survey. Sensors 2021, 21, 1243. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).