Mechanical Design and a Novel Structural Optimization Approach for Hexapod Walking Robots
Abstract
:1. Introduction
1.1. Related Work
1.2. Contribution of the Paper
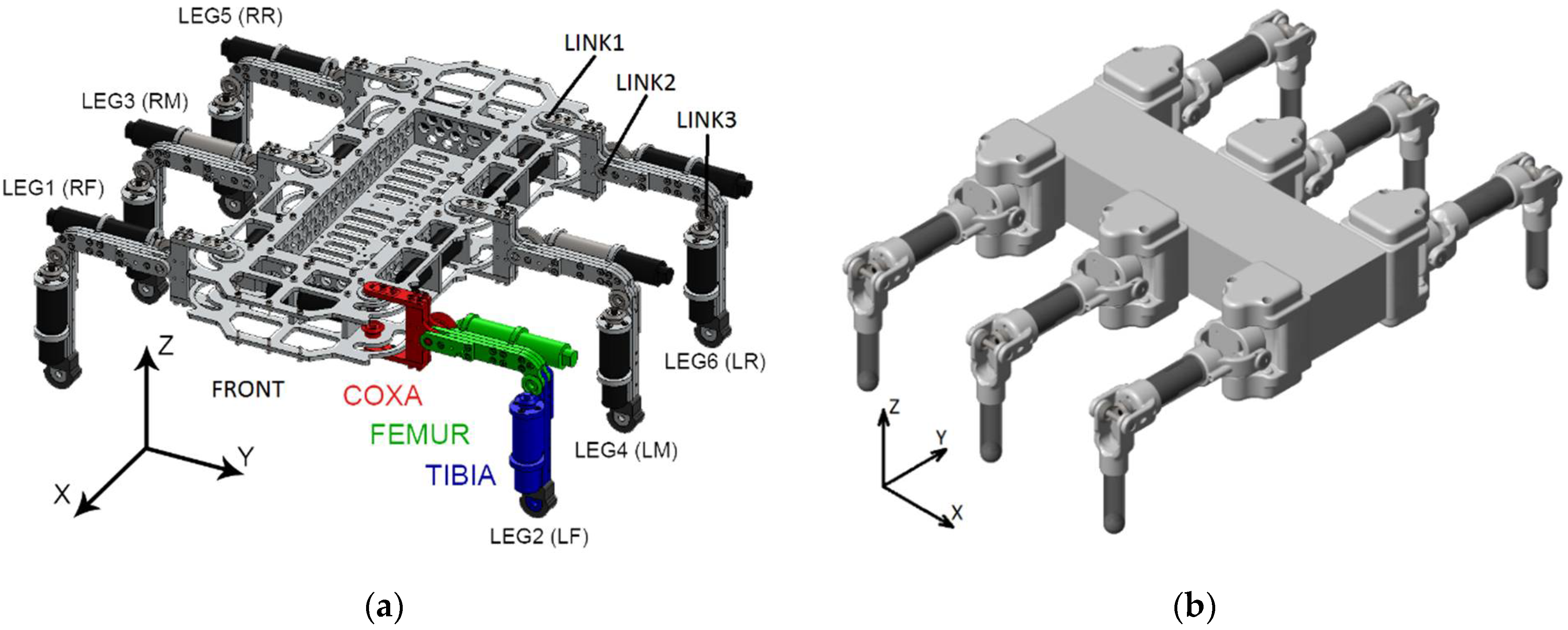
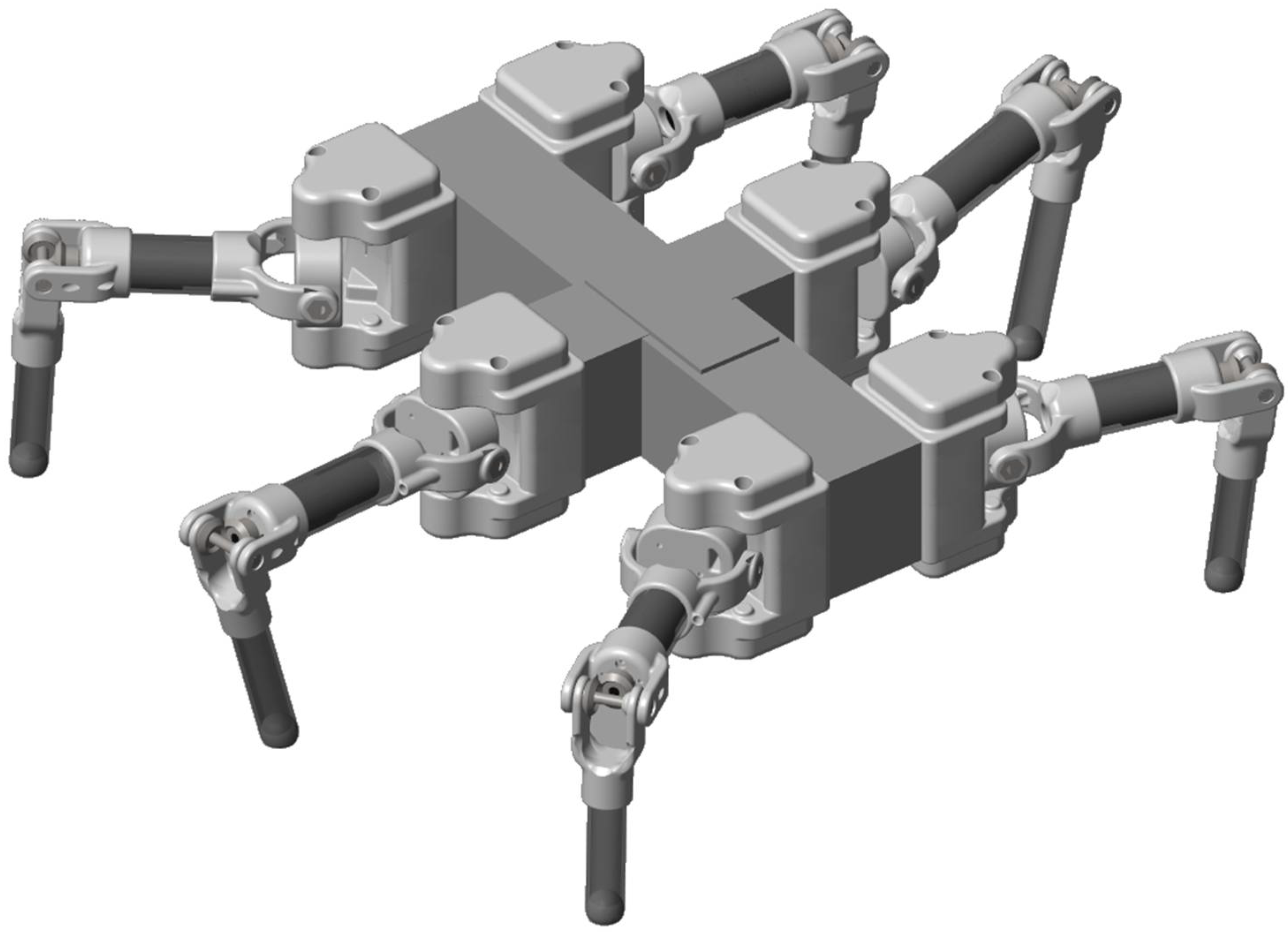
2. The Mechanical System of the Szabad(ka)-III Robot
3. Szabad(ka)-III Robot Model
- -
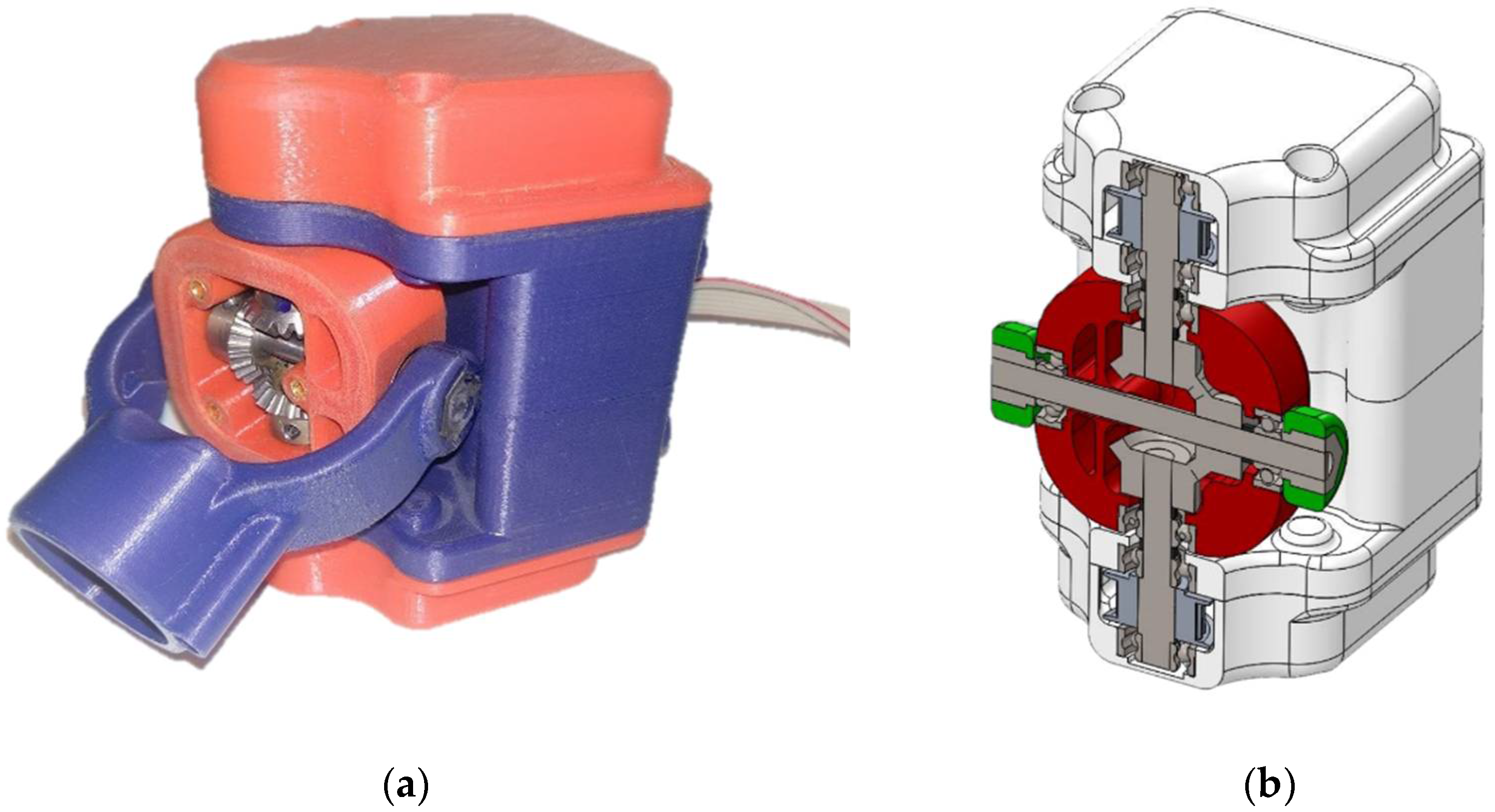
- The pre-designed elements (the differential joint connecting the body and femur, and the joint between the femur and tibia);
- -
- Variable-parameter elements (the tibia and femur segments and the body itself).
4. Formulating the Optimization Problem
4.1. Optimization Objectives (Fitness Function)
- -
- Minimizing energy consumption,
- -
- Minimizing mass,
- -
- Maximizing speed and dexterity,
- -
- Minimizing unwanted body motion,
- -
- Minimizing adverse effects on the structure, and
- -
- Minimizing differences between joint torques.
4.2. Optimization Parameters
- -
- Axisymmetric;
- -
- Symmetrical only along the longitudinal axis;
- -
- Symmetrical along the longitudinal and lateral axes.
- -
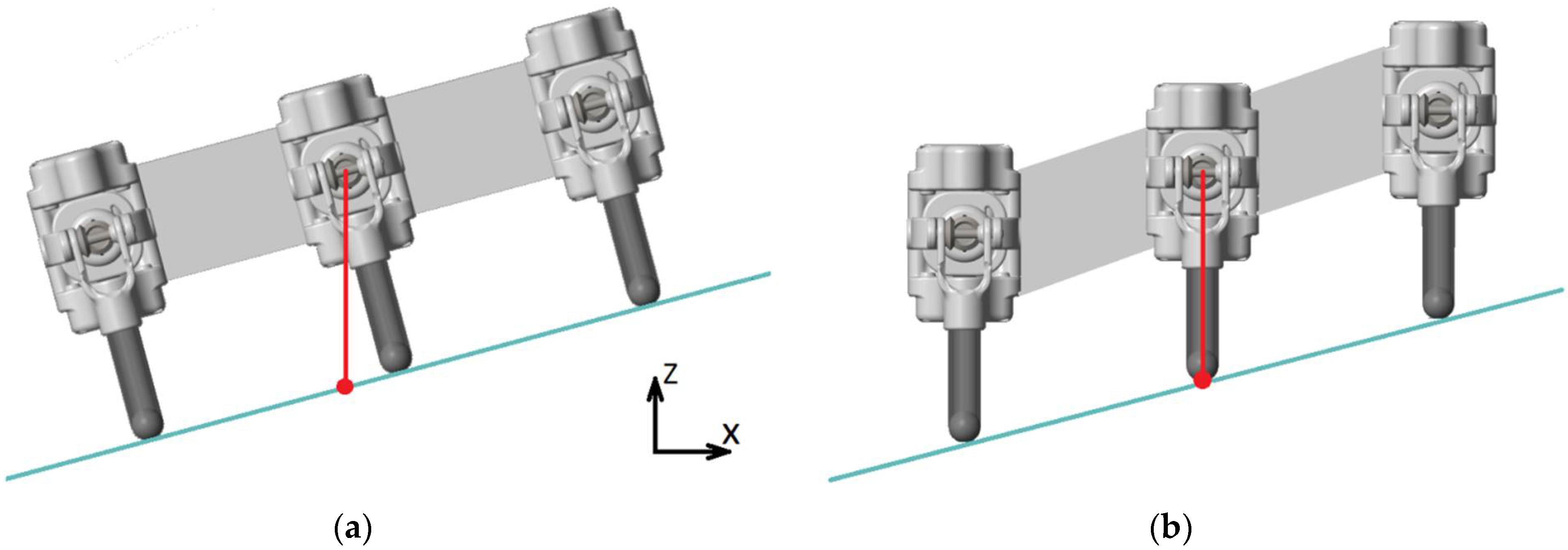
- Leg segment length: This includes the length of the tibia and femur. For Szabad(ka)-III, the coxa has zero length due to the differential joint, and a separate tarsus segment is not present due to the design of the foot. The tibia and femur (whose lengths are interpreted between the rotational axes of the joints) are shown in Figure 5b.
- -
- -
- Positioning of the center of gravity in the body: The center of gravity of the electronics and the battery can be moved inside the body along the x- and z-axis relative to the center of the robot (Figure 5d).
- -
- Choice of motors and reductors: Unlike before, these two parameters are not continuous but can take discrete values, i.e., it is possible to choose which of a given manufacturer’s products can deliver the appropriate torques.
- -
- Spring constant and damping coefficient of the feet: The main function of the triple spring-damper system in the tibia segment is to absorb vibrations during walking. The triple spring-damper system is described in detail in [28]. Therefore, the optimization involves the determination of three spring constants and three damping coefficient parameters.
- -
- Posture: This includes the height of the body above the ground (other posture parameters should be taken into account when optimizing the walking algorithm).
- -
- Foot trajectory: This includes the height and the length of the trajectory (same for all feet), its offset in the direction of travel and its distance from the body (per pair of feet).
4.3. Reducing the Number of Parameters
- -
- If the goal is to achieve a given speed (step length), the same result can be achieved by changing the position of the legs, the length of the segments, or the length of the trajectory.
- -
- If the goal is to achieve sufficiently low joint torques for a given mass, this will be influenced by the torque of the motors, the positioning of the legs, the length of the segments, and the posture.
- -
- The number of parameters can be reduced if it is likely to be unnecessary to optimize all of them.
- -
- If the same result can be achieved by modifying several different parameters, than the parameters that are more expedient to determine based on the production conditions can be taken out of the optimization.
- -
- The optimization can be broken down into a number of sub-optimizations if the appropriate objectives and the associated parameters that influence them the most can be categorized.
4.3.1. Investigating the Reduction in the Number of Structural Parameters
4.3.2. Investigating the Reduction in the Number of Spring-Damper Parameters
4.3.3. Investigating the Reduction in the Number of Walking Algorithm Parameters
4.4. Optimization Scenarios
- -
- The robot’s walking velocity;
- -
- The terrain characteristics;
- -
- The selected walking algorithm.
- -
- Ground slip (friction between the ground and the foot);
- -
- Ground slope (the angle between the horizontal and the ground plane);
- -
- The nature and size of obstacles on the ground.
- -
- Wave gait is the slowest gait, with five feet on the ground and one foot in the air at a time.
- -
- The ripple gait is a medium-speed gait with four feet on the ground and two feet in the air at a time.
- -
- The tripod gait is the fastest gait, with three feet on the ground and three feet in the air [36].
5. Optimization
5.1. Search Method
5.2. Fitness Function
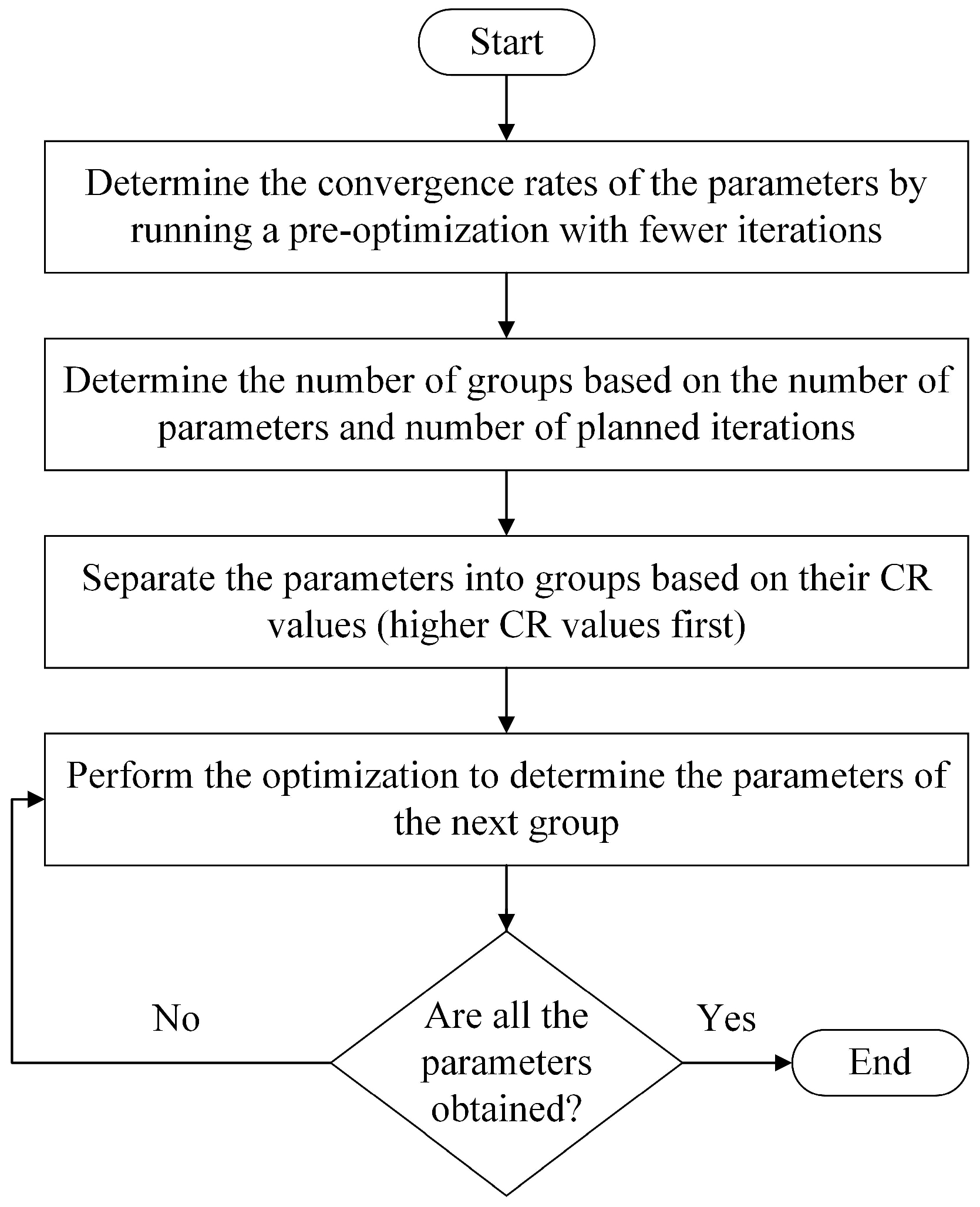
5.3. Multi-Step Optimization
5.4. Optimization Results
- -
- The connection points of the inner legs along the y-axis are further away from the body, and those of the outer legs are closer. This more uniform distribution around the robot’s center of gravity increases its stability.
- -
- The trajectories of the outer feet have moved away from the center of the body along the direction of travel (x-axis), while the trajectories of the inner feet have changed minimally. This allows for the robot to take longer steps, and the feet in contact with the ground can cover more surface area, which also improves stability.
- -
- The length of the trajectory is close to the maximum allowed, which determines the size of the step. Larger steps reduce energy consumption.
- -
- The spring constant of the foot is also close to the maximum value. This may result in high-frequency vibrations; however, it may significantly reduce the low-frequency and high-amplitude wobbling of the body.
- -
- The center of gravity of the electronics has not changed much from its original central position. This helps to achieve a uniform distribution of mass around the geometric center of the body (this is the point at which the rotational movement of the body is measured).
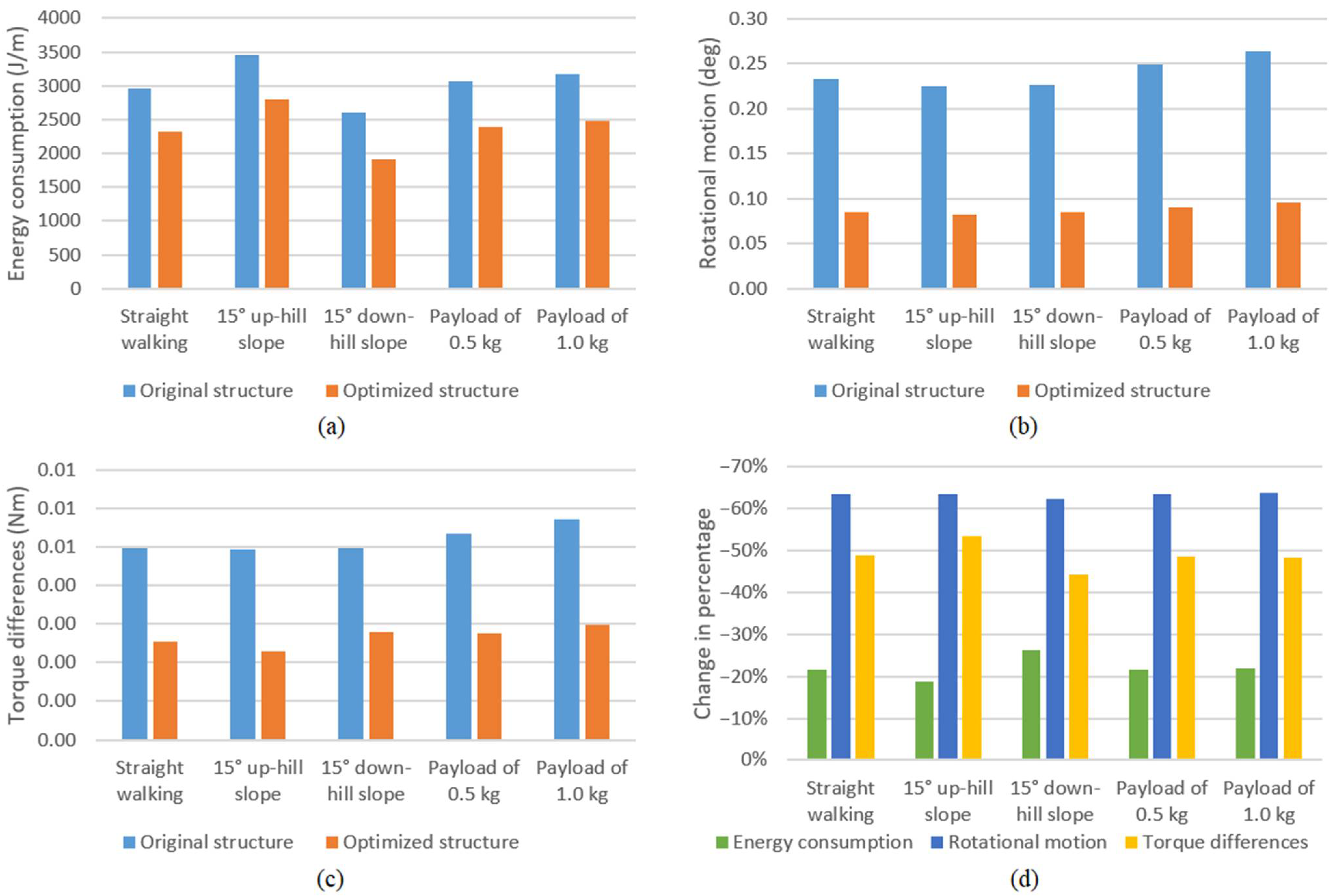
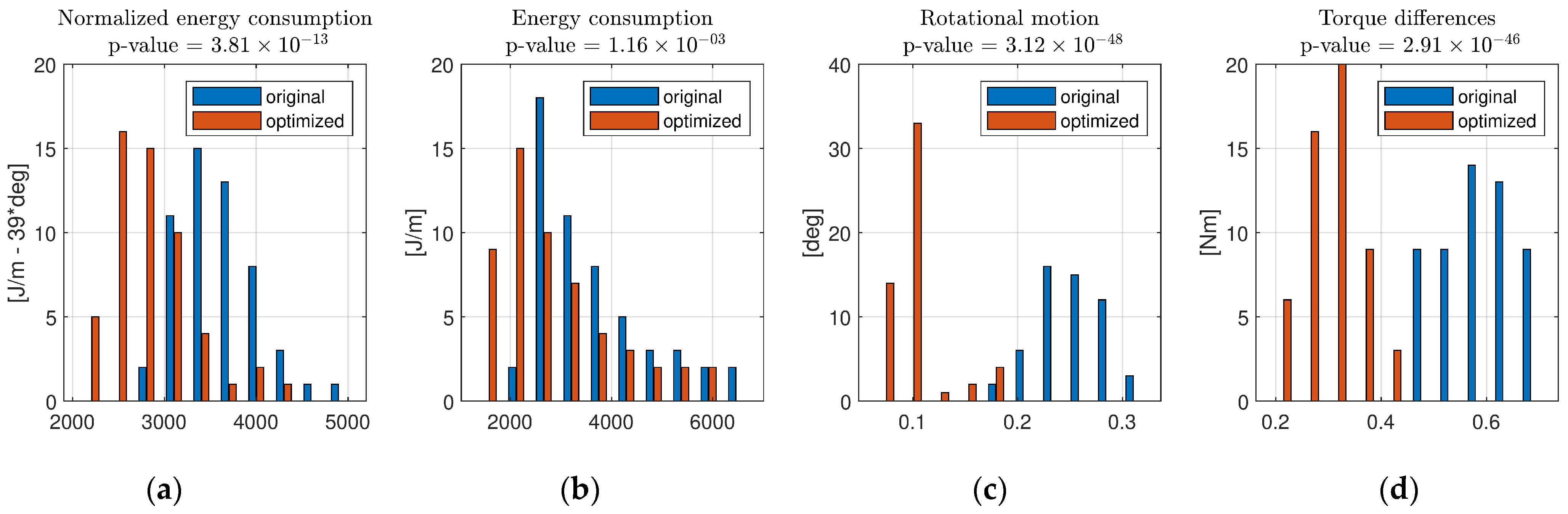
5.5. Verification of the Optimization on Independent Scenarios
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kecskés, I.; Burkus, E.; Bazsó, F.; Odry, P. Model validation of a hexapod walker robot. Robotica 2015, 35, 419–462. [Google Scholar] [CrossRef]
- Silva, M.F.; Machado, J.A.T. A literature review on the optimization of legged robots. J. Vib. Control 2011, 18, 1753–1767. [Google Scholar] [CrossRef]
- Ding, X.; Yang, F. Study on hexapod robot manipulation using legs. Robotica 2016, 34, 468–481. [Google Scholar] [CrossRef]
- Grzelczyk, D.; Stańczy, B.; Awrejcewicz, J. Power consumption analysis of different hexapod robot gaits. In Proceedings of the 13th International Conference on Dynamical Systems: Theory and Applications, Lodz, Poland, 7–10 December 2015. [Google Scholar]
- Grzelczyk, D.; Stanczyk, B.; Awrejcewicz, J. Kinematics, Dynamics and Power Consumption Analysis of the Hexapod Robot During Walking with Tripod Gait. Int. J. Struct. Stab. Dyn. 2016, 17, 1740010. [Google Scholar] [CrossRef]
- Mahapatra, A.; Roy, S.S.; Pratihar, D.K. Study on feet forces’ distributions, energy consumption and dynamic stability measure of hexapod robot during crab walking. Appl. Math. Model. 2019, 65, 717–744. [Google Scholar] [CrossRef]
- Wang, G.; Ding, L.; Gao, H.; Deng, Z.; Liu, Z.; Yu, H. Minimizing the Energy Consumption for a Hexapod Robot Based on Optimal Force Distribution. IEEE Access 2019, 8, 5393–5406. [Google Scholar] [CrossRef]
- Rastgar, H.; Naeimi, H.; Agheli, M. Characterization, validation, and stability analysis of maximized reachable workspace of radially symmetric hexapod machines. Mech. Mach. Theory 2019, 137, 315–335. [Google Scholar] [CrossRef]
- Komatsu, H.; Endo, G.; Hodoshima, R.; Hirose, S.; Fukushima, E.F. How to optimize the slope walking motion by the quadruped walking robot. Adv. Robot. 2015, 29, 1497–1509. [Google Scholar] [CrossRef]
- Gülhan, M.M.; Erbatur, K. Kinematic arrangement optimization of a quadruped robot with genetic algorithms. Meas. Control 2018, 51, 406–416. [Google Scholar] [CrossRef]
- Bartsch, S.; Birnschein, T.; Römmermann, M.; Hilljegerdes, J.; Kühn, D.; Kirchner, F. Development of the six-legged walking and climbing robot SpaceClimber. J. Field Robot. 2012, 29, 506–532. [Google Scholar] [CrossRef]
- Rommerman, M.; Kuhn, D.; Kirchner, F. Robot design for space missions using evolutionary computation. In Proceedings of the IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009. [Google Scholar]
- Roennau, A.; Heppner, G.; Pfotzer, L.; Dillmann, R. LAURON V: Optimized Leg Configuration for the Design of a Bio-Inspired Walking Robot. In Proceedings of the 16th International Conference on Climbing and Walking Robots, Sydney, Australia, 14–17 July 2013. [Google Scholar]
- Roennau, A.; Heppner, G.; Nowicki, M.; Dillmann, R. LAURON V: A versatile six-legged walking robot with advanced maneuverability. In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besançon, France, 8–11 July 2014; pp. 82–87. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Zhao, J.; Chen, J.; Yan, J. Development of a Bionic Hexapod Robot for Walking on Unstructured Terrain. J. Bionic Eng. 2014, 11, 176–187. [Google Scholar] [CrossRef]
- Ma, R.R.; Dollar, A.M. On Dexterity and Dexterous Manipulation. In Proceedings of the 15th International Conference on Advanced Robotics, Tallinn, Estonia, 20–23 June 2011. [Google Scholar]
- Liu, Y.; Wang, C.; Zhang, H.; Zhao, J. Research on the Posture Control Method of Hexapod Robot for Rugged Terrain. Appl. Sci. 2020, 10, 6725. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, H.; Liu, Y.; Yan, J.; Zang, X.; Zhou, Z. Development of the Hexapod Robot HITCR-II for Walking on Unstructured Terrain. In Proceedings of the International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012. [Google Scholar]
- Burkus, E.; Awrejcewicz, J.; Odry, P. A validation procedure to identify joint friction, reductor self-locking and gear backlash parameters. Arch. Appl. Mech. 2020, 90, 1625–1641. [Google Scholar] [CrossRef]
- Kecskés, I.; Odry, P. Full kinematic and dynamic modeling of Szabad(ka)-Duna Hexapod. In Proceedings of the IEEE 7th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 25–26 September 2009. [Google Scholar]
- Kecskés, I.; Odry, P. Multi-Scenario Multi-Objective Optimization of a Fuzzy Motor Controller for the Szabad(ka)-II Hexapod Robot. Acta Polytech. Hung. 2018, 15, 157–178. [Google Scholar]
- Kecskés, I.; Székács, L.; Fodor, J.C.; Odry, P. PSO and GA optimization methods comparison on simulation model of a real hexapod robot. In Proceedings of the 2013 IEEE 9th International Conference on Computational Cybernetics (ICCC), Tihany, Hungary, 8–10 July 2013; pp. 125–130. [Google Scholar] [CrossRef]
- Kecskés, I.; Odry, Á.; Burkus, E.; Odry, P. Embedding optimized trajectory and motor controller into the Szabad(ka)-II hexapod robot. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics, Budapest, Hungary, 9–12 October 2016. [Google Scholar] [CrossRef]
- Kecskés, I.; Odry, P. Optimization of PI and Fuzzy-PI Controllers on Simulation Model of Szabad(ka)-II Walking Robot. Int. J. Adv. Robot. Syst. 2014, 11, 186. [Google Scholar] [CrossRef]
- Kecskés, I.; Burkus, E.; Odry, P. Gear efficiency modeling in a simulation model of a DC gearmotor. In Proceedings of the IEEE 18th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 21–22 November 2018. [Google Scholar]
- Kecskés, I.; Odry, Á.; Tadić, V.; Odry, P. Simultaneous Calibration of a Hexapod Robot and an IMU Sensor Model Based on Raw Measurements. IEEE Sens. J. 2021, 21, 14887–14898. [Google Scholar] [CrossRef]
- Kecskés, I.; Odry, P. Robust optimization of multi-scenario many-objective problems with auto-tuned utility function. Eng. Optim. 2021, 53, 1135–1155. [Google Scholar] [CrossRef]
- Burkus, E.; Odry, Á.; Kecskés, I.; Tadić, V.; Odry, P. A Novel Leg Design for the Szabad(ka) III Robot. In Proceedings of the IEEE 18th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 17–19 September 2020. [Google Scholar]
- Bjelonic, M.; Kottege, N.; Homberger, T.; Borges, P.; Beckerle, P.; Chli, M. Weaver: Hexapod robot for autonomous navigation on unstructured terrain. J. Field Robot. 2018, 35, 1063–1079. [Google Scholar] [CrossRef]
- Seok, S.; Wang, A.; Chuah, M.Y.; Otten, D.; Lang, J.; Kim, S. Design principles for highly efficient quadrupeds and implementation on the MIT Cheetah robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Karlsson, M.; Hörnqvist, F. Robot Condition Monitoring and Production Simulation. Master’s Thesis, Luleå Tekniska Universitet, Luleå, Sweden, 2018. [Google Scholar]
- Gierlak, P.; Kurc, K.; Szybicki, D. Mobile crawler robot vibration analysis in the contexts of motion speed selection. J. Vibroeng. 2017, 19, 2403–2412. [Google Scholar] [CrossRef]
- Odry, Á.; Fullér, R.; Rudas, I.J.; Odry, P. Kalman filter for mobile-robot attitude estimation: Novel optimized and adaptive solutions. Mech. Syst. Signal Process. 2018, 110, 569–589. [Google Scholar] [CrossRef]
- Yang, J.-M.; Kim, J.-H. Fault-tolerant locomotion of the hexapod robot. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1998, 28, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.-M. Fault-Tolerant Gait Planning for a Hexapod Robot Walking Over Rough Terrain. J. Intell. Robot. Syst. 2008, 54, 613–627. [Google Scholar] [CrossRef]
- Campos, R.; Matos, V.; Santos, C. Hexapod Locomotion: A Nonlinear Dynamical Systems Approach. In Proceedings of the 36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010. [Google Scholar]
- Burkus, E.; Fodor, J.C.; Odry, P. Structural and gait optimization of a hexapod robot with Particle Swarm Optimization. In Proceedings of the IEEE 11th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 26–28 September 2013. [Google Scholar]

| Feature | Szabad(ka)-II | Szabad(ka)-III |
|---|---|---|
| Robot length | 440 mm | 400 mm |
| Distance between front and rear pairs of legs | 320 mm | 320 mm |
| Joints | Traditional joints | Differential gear drive system |
| Motor-reductor position | On the side of the segments | In the segment, closer to the body |
| Foot design | Rubber-like coating | Triple spring-damper system |
| Tibia segment length | 120 mm | Adjustable |
| Femur segment length | 80 mm | Adjustable |
| Coxa segment length | 60 mm | 0 mm |
| Motor-reductor combinations | 4 combinations | 1 combination |
| Manufacturing technology | Aluminum sheets | 3D printed PLA, Aluminum tubes |
| Bearings | Plain bearing with offset | Ball bearing, aligned |
| Motor | Several types | Faulhaber 2232U 012SR, 10 mNm |
| Reductor | Several types | Faulhaber 26 A, 1–1.5 Nm |
| Joint 1, 2 continuous and intermittent torque | Several types | 1.5 Nm, 2.25 Nm |
| Joint 3 continuous and intermittent torque | Several types | 1.0 Nm, 1.5 Nm |
| Structural Parameters | Initial Values | Limits Set during Optimization |
|---|---|---|
| Body length (X distance between outer pairs of legs) | 320 mm | fixed |
| Y distance between legs within the outer pairs | 100 mm | +/−40 mm |
| Y distance between legs within the inner pair | 100 mm | +/−40 mm |
| Inner coxa X position (offset) | 0 mm (middle) | +/−40 mm |
| Inner coxa Z position (offset) | 0 mm (middle) | +/−5 mm |
| Outer femur length | 160 mm | 140–180 mm |
| Inner femur length | 160 mm | 160–180 mm |
| Outer tibia length | 120 mm | 120–160 mm |
| Inner tibia length | 120 mm | 120–160 mm |
| Body mass parameters | ||
| Body electronics mass | 2 kg | fixed |
| Body electronics dimensions | 100 × 50 × 50 mm | fixed |
| Electronics center of gravity X position (offset) | 0 mm (middle) | +/−50 mm |
| Electronics center of gravity Z position (offset) | 0 mm (middle) | +/−50 mm |
| Spring-damper parameters | ||
| Feet spring constant | 10000 N/m | 15,000–20,000 |
| Feet damping coefficient | 100 Ns/m | 50–500 |
| Walking algorithm parameters | ||
| Walking algorithm | Ripple Gait | fixed |
| Body height (Z) | 120 mm | 70–120 mm |
| Trajectory height (Z) | 50 mm | 10–100 |
| Trajectory length (X) | 40 mm | 45–50 mm |
| Outer leg trajectory offset in X direction | 0 mm | +/−40 mm |
| Inner leg trajectory offset in X direction | 0 mm | +/−40 mm |
| Outer leg trajectory offset in Y direction | 160 mm | 120–140 mm |
| Inner leg trajectory offset in Y direction | 160 mm | 120–200 mm |
| Friction parameters | ||
| Feet friction in X and Y directions | 1 | fixed |
| Stribeck friction | 0.0 Nm | fixed |
| Coulomb friction | 0.5 Nm | fixed |
| Viscous friction | 0.25 Nm/(rad/s) | fixed |
| Battery parameters | ||
| Battery voltage | 12 V | fixed |
| Internal battery resistance | 0.2 Ohm | fixed |
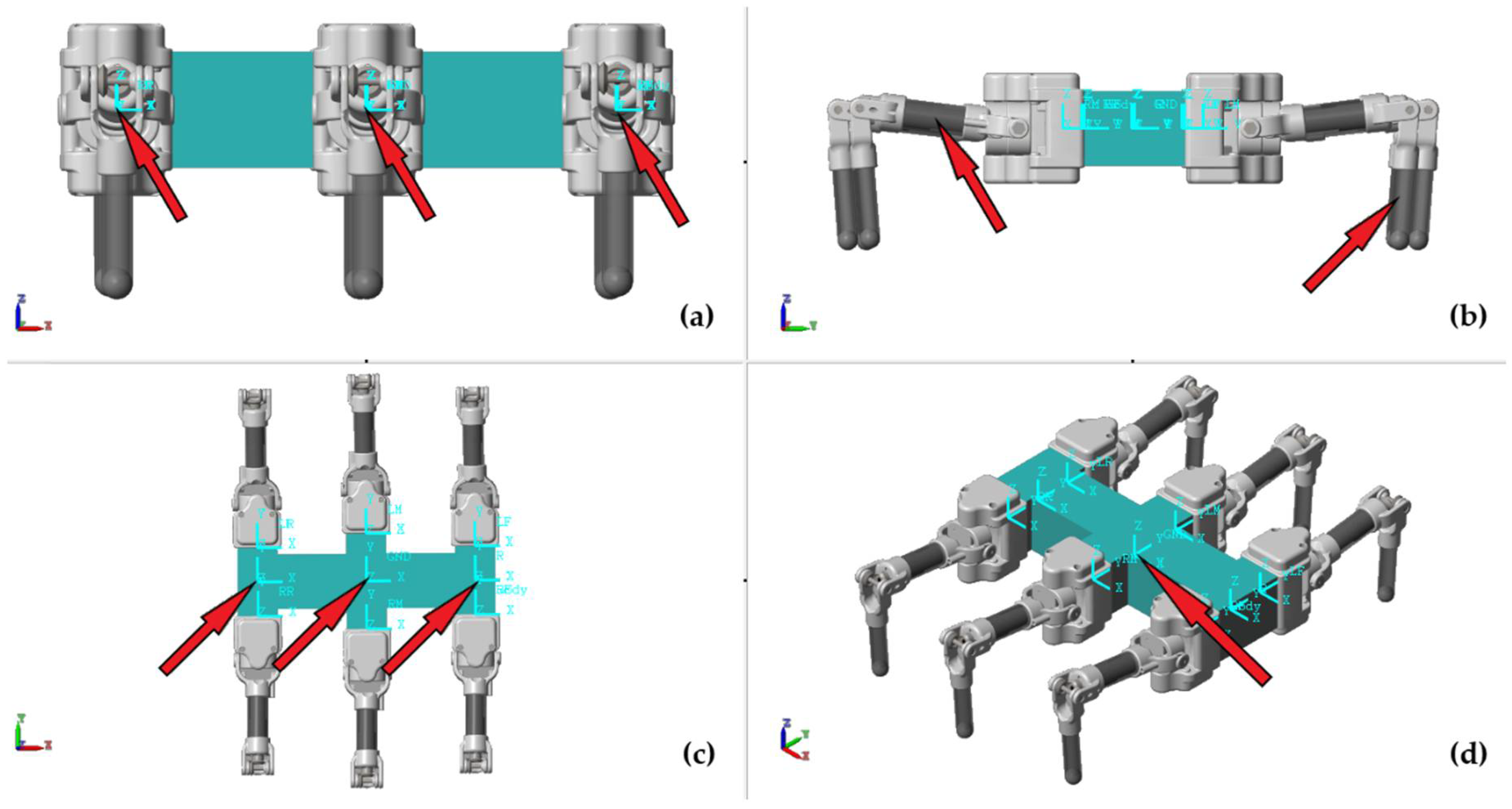
| Output Variable: | Related Objective Function: | Multibody Naming: (See Figure 4) |
|---|---|---|
| Energy consumption (see Equation (2)) | simout_Ubat, simout_Isum, simout_p | |
| Dexterity (see Equation (5)) | simout_IK | |
| Translational motion (see Equation (6)) | simout_p | |
| Rotational motion (see Equation (7)) | simout_Q | |
| Torque differences (see Equation (10)) | simout_M | |
| Desired angles | - | simout_a |
| Actual angles | - | simout_q |
| Motor currents | - | simout_I |
| Foot forces | - | simout_F |
| Optimization Objectives: | Characteristics | Identification | Formula |
|---|---|---|---|
| Minimizing energy consumption | Important | Simple | |
| Minimizing mass | Minimally influenceable | Simple | |
| Maximizing dexterity | Predetermined | Simple | |
| Minimizing unwanted body motion (trans. + rot.) | Important | Medium | |
| Minimizing adverse effects on the structure | Relatively important | Complex (FFT) | |
| Minimizing differences between joint torques | Important | Simple |
| Structural Parameters | No. of Parameters | Walking Algorithm Parameters | No. of Parameters |
|---|---|---|---|
| Length of tibia | 3 | Height of body in Z | 1 |
| Length of femur | 3 | Height of trajectory in Z | 1 |
| Position of coxa in X | 3 | Length of trajectory in X | 1 |
| Position of coxa in Z | 3 | Trajectory offset in X-direction | 3 |
| Distance between legs in Y | 3 | Trajectory offset in Y-direction | 3 |
| Position of CoG in X and Z | 2 | ||
| Spring-Damper Parameters | |||
| Spring constant | 3 | ||
| Damping coefficient | 3 |
| Structural Parameters | No. of Parameters | Walking Algorithm Parameters | No. of Parameters |
|---|---|---|---|
| Length of tibia | 2 | Height of body in Z | 1 |
| Length of femur | 2 | Height of trajectory in Z | 1 |
| Position of coxa in X | 1 | Length of trajectory in X | 1 |
| Position of coxa in Z | 1 | Trajectory offset in X-direction | 2 |
| Distance between legs in Y | 2 | Trajectory offset in Y-direction | 2 |
| Position of CoG in X and Z | 2 | ||
| Spring-Damper Parameters | |||
| Spring constant | 1 | ||
| Damping coefficient | 1 |
| Optimization | All Parameters | Two-Step First Step | Two-Step Second Step | |||
|---|---|---|---|---|---|---|
| Population and generation no. | 80 × 30 | 120 × 40 | 80 × 30 | 120 × 40 | 80 × 30 | 120 × 40 |
| Performed iterations | 202 | 475 | 481 | 695 | 445 | 757 |
| Y distance between legs within the outer pairs | 93.68 | 82.18 | - | - | 60.14 | 64.41 |
| Y distance between legs within the inner pair | 112.73 | 101.34 | - | - | 135.10 | 139.37 |
| Inner coxa X position (offset) | −38.98 | 2.78 | 1.97 | 0.56 | - | - |
| Inner coxa Z position (offset) | 0.17 | 0.48 | 0.48 | 0.67 | - | - |
| Outer femur length | 140.28 | 143.24 | 141.84 | 141.55 | - | - |
| Inner femur length | 168.38 | 173.78 | 160.64 | 166.79 | - | - |
| Outer tibia length | 124.37 | 121.00 | - | - | 126.02 | 139.55 |
| Inner tibia length | 149.51 | 139.45 | - | - | 144.43 | 142.41 |
| Electronics center of gravity X position (offset) | −25.10 | 33.61 | - | - | 23.69 | 19.52 |
| Electronics center of gravity Z position (offset) | −44.81 | 11.41 | - | - | 14.98 | 0.32 |
| Feet spring constant | 19,191 | 19,516 | 19,589 | 19,592 | - | - |
| Feet damping coefficient | 302.94 | 294.08 | - | - | 419.05 | 319.16 |
| Body height (Z) | 109.72 | 108.10 | 100.30 | 86.72 | 118.90 | 119.51 |
| Trajectory height (Z) | 49.44 | 13.30 | - | - | 11.98 | 11.37 |
| Trajectory length (X) | 48.98 | 49.37 | 48.97 | 47.97 | - | - |
| Outer leg trajectory offset in X-direction | 36.46 | 36.40 | 37.41 | 39.24 | - | - |
| Inner leg trajectory offset in X-direction | −4.41 | 22.08 | - | - | 21.29 | 17.94 |
| Outer leg trajectory offset in Y-direction | 122.50 | 128.36 | 122.82 | 120.23 | - | - |
| Inner leg trajectory offset in Y-direction | 126.42 | 122.83 | 120.87 | 120.33 | 123.16 | 124.59 |
| Fitness result: | 7.34 | 7.04 | 7.18 | 7.23 | 6.65 | 6.68 |
| Objective Function (3 Scenario Average) | Original Structure (Normalized) | Optimized Structure (Normalized) | Change in Percentage |
|---|---|---|---|
| Energy consumption | 1.0000 | 0.7785 | −22.16% |
| Rotational motion | 1.0000 | 0.3817 | −61.83% |
| Torque differences | 1.0000 | 0.5087 | −49.13% |
| Dexterity | 0.0000 | 0.0000 | 0.00% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burkus, E.; Odry, Á.; Awrejcewicz, J.; Kecskés, I.; Odry, P. Mechanical Design and a Novel Structural Optimization Approach for Hexapod Walking Robots. Machines 2022, 10, 466. https://doi.org/10.3390/machines10060466
Burkus E, Odry Á, Awrejcewicz J, Kecskés I, Odry P. Mechanical Design and a Novel Structural Optimization Approach for Hexapod Walking Robots. Machines. 2022; 10(6):466. https://doi.org/10.3390/machines10060466
Chicago/Turabian StyleBurkus, Ervin, Ákos Odry, Jan Awrejcewicz, István Kecskés, and Péter Odry. 2022. "Mechanical Design and a Novel Structural Optimization Approach for Hexapod Walking Robots" Machines 10, no. 6: 466. https://doi.org/10.3390/machines10060466
APA StyleBurkus, E., Odry, Á., Awrejcewicz, J., Kecskés, I., & Odry, P. (2022). Mechanical Design and a Novel Structural Optimization Approach for Hexapod Walking Robots. Machines, 10(6), 466. https://doi.org/10.3390/machines10060466









