Velocity and Singularity Analysis of a 5-DOF (3T2R) Parallel-Serial (Hybrid) Manipulator
Abstract
:1. Introduction
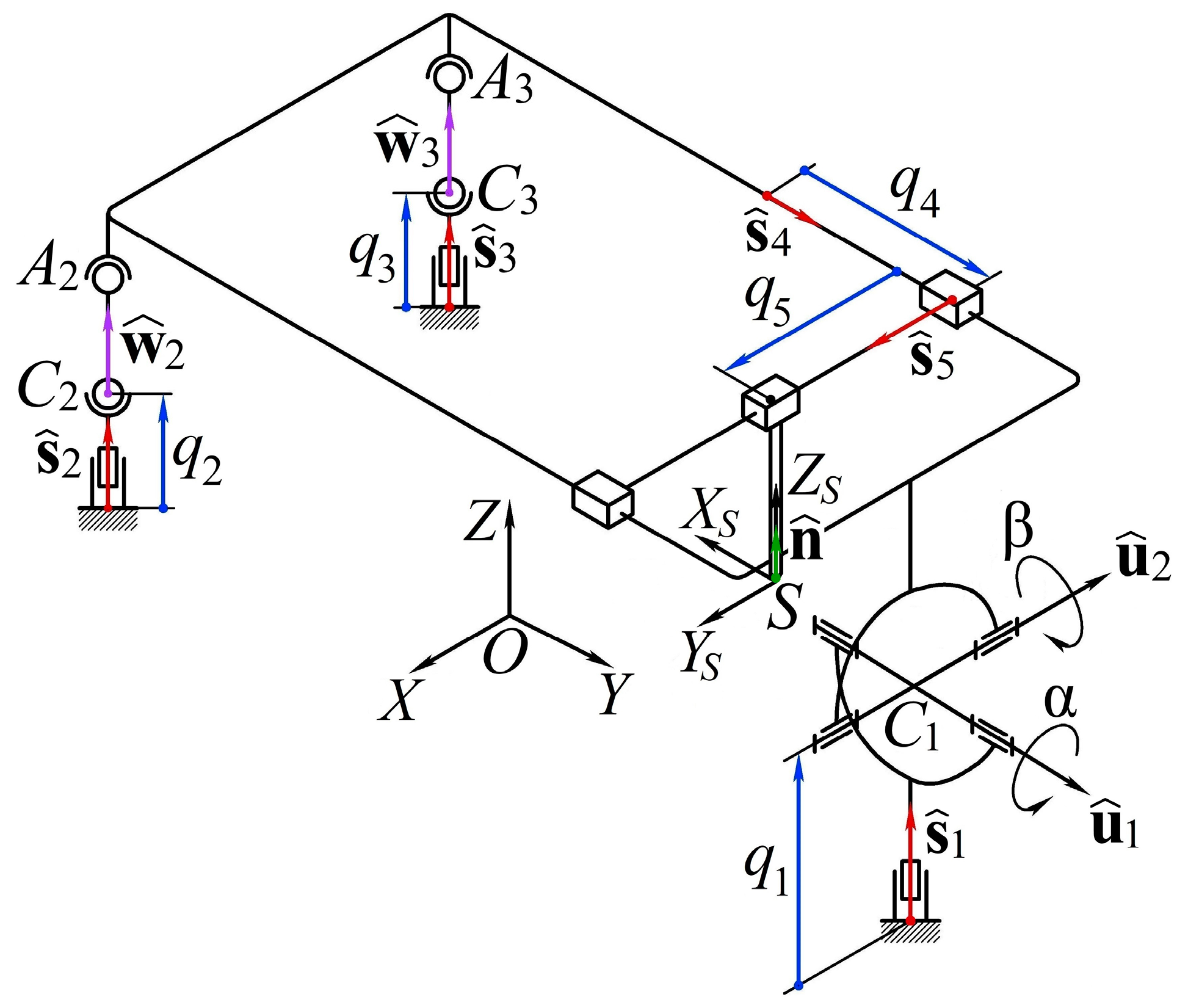
2. Manipulator Design
3. Position Analysis
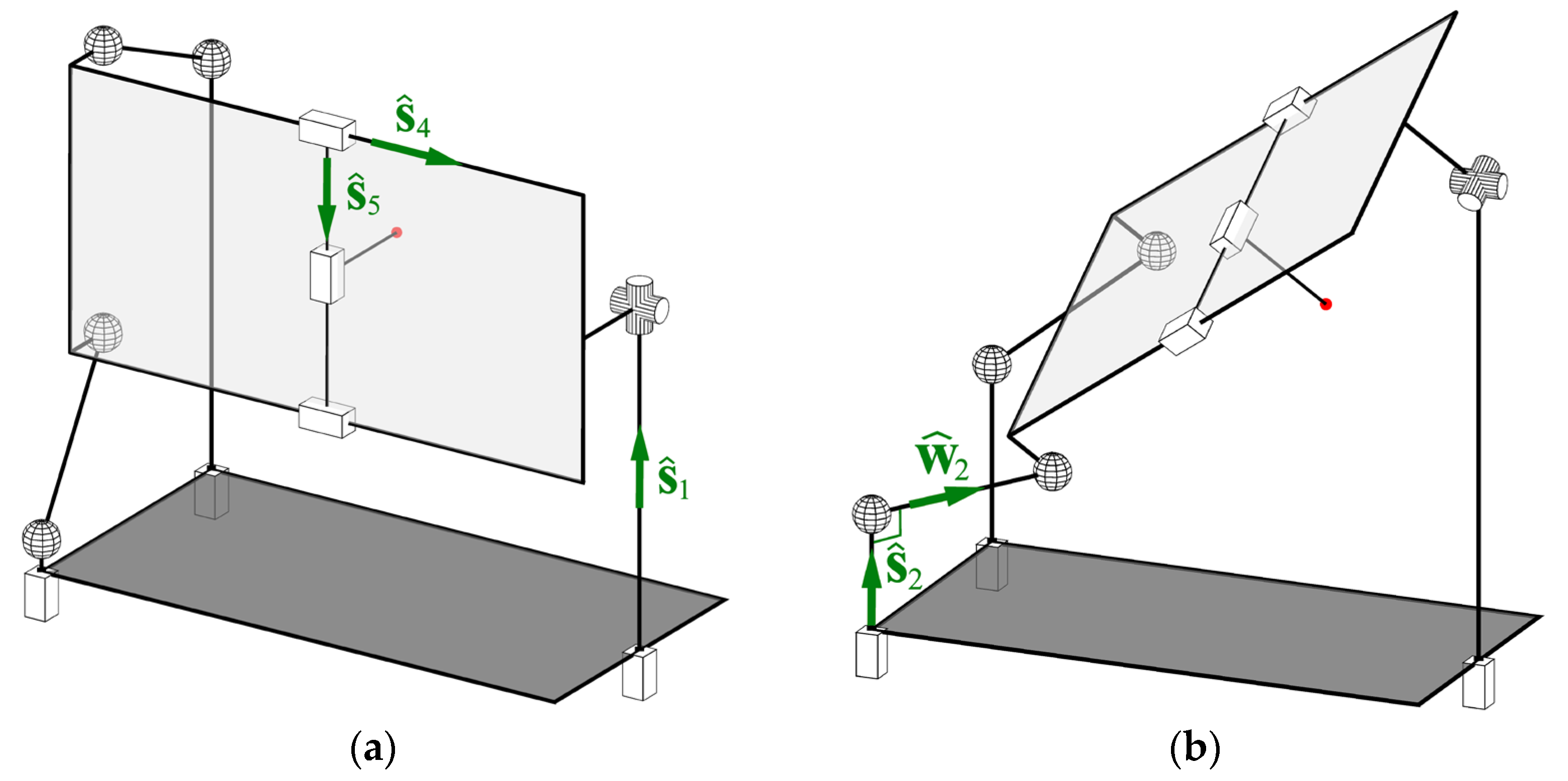
- is a stationary reference frame attached to the base arbitrarily.
- is a reference frame attached to the end-effector such that axis is directed along the tool (unit vector ) and the remaining axes ( and ) have an arbitrary direction; vector and rotation matrix define the position and orientation of relative to .
- are the actuated coordinates according to the previous section; all these coordinates are measured about the axes defined by unit vectors (in ).
- and are the angles in the universal joint measured about its axes defined by unit vectors and (in ).
- As the end-effector connects with the platform by two prismatic joints, vector uniquely defines the orientation of the latter. The platform orientation, on the other hand, depends only on two angles and in the universal joint. This condition allows us to express as a function of and and find these angles from the corresponding equations.
- Having found and , we can write a vector loop equation for . This vector depends only on parameters , , and , which we find from the obtained equation.
- Having found , we know the platform configuration relative to . Hence, we know the coordinates of platform spherical joints and relative to the same frame. We can also write coordinates of spherical joints and as functions of and . Coordinates of the spherical joints in each kinematic chain are connected by a known and constant distance between the joints. This allows us to form corresponding equations and find parameters and .
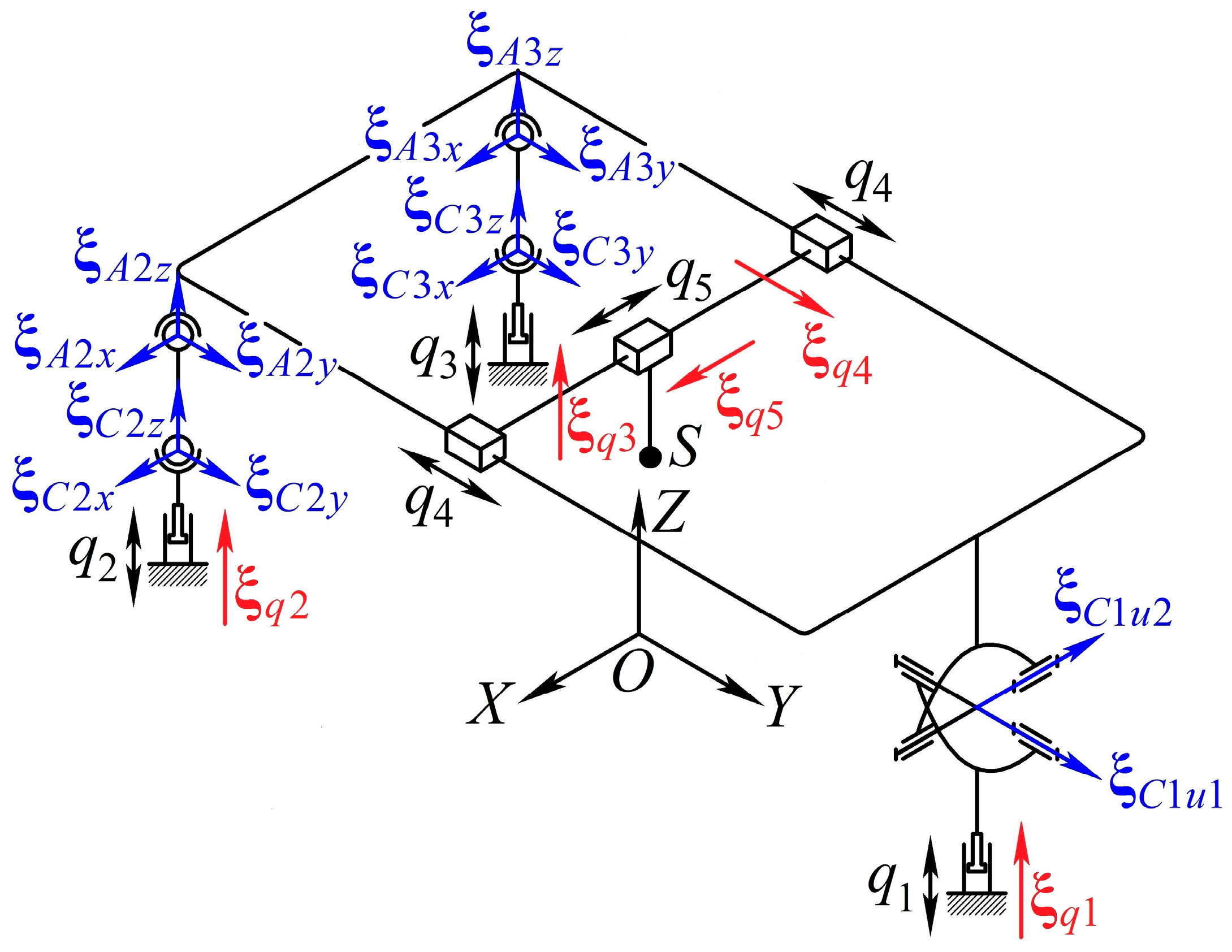
4. Velocity Analysis
4.1. Theory
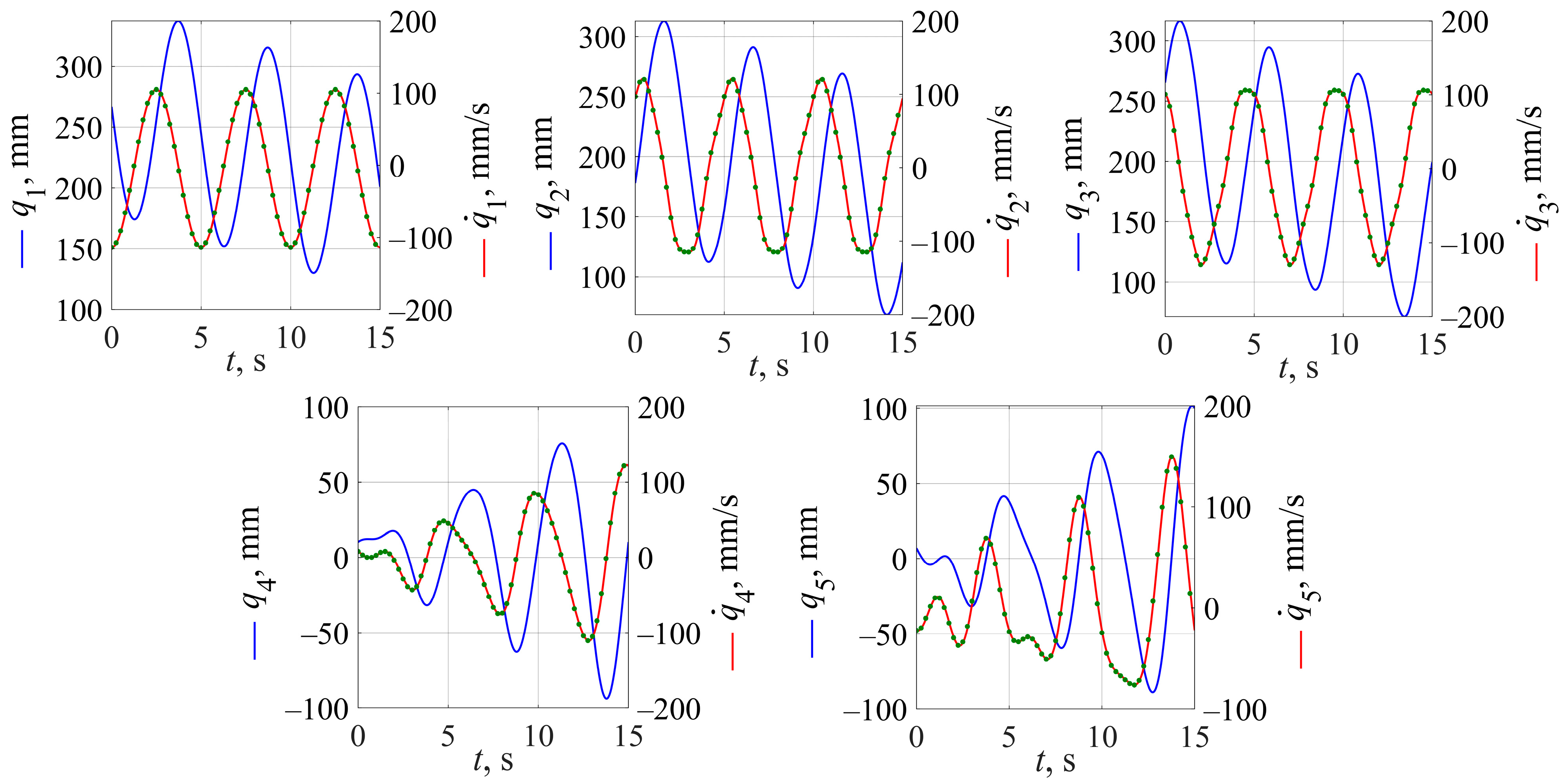
4.2. Numerical Example
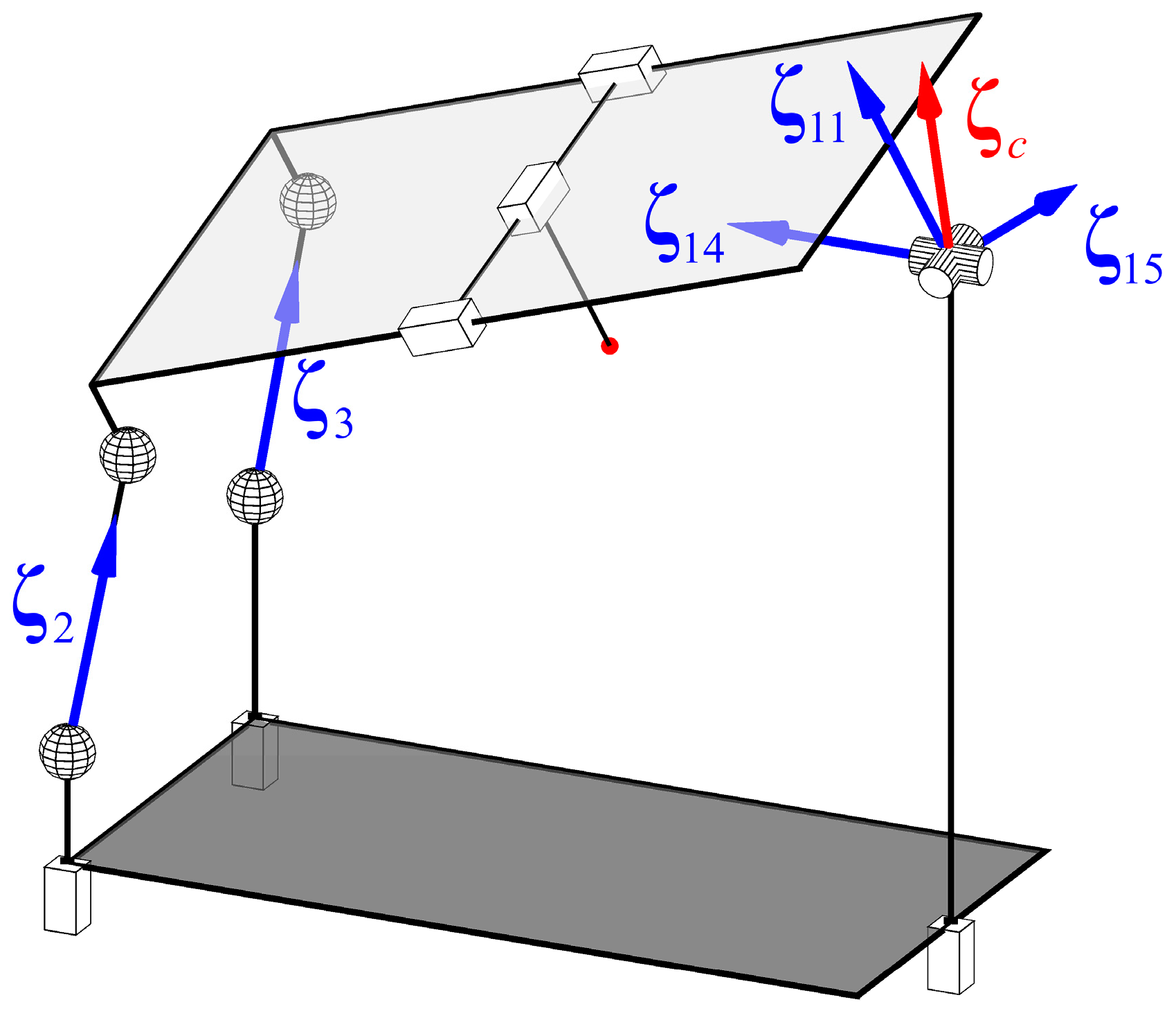
5. Singularity Analysis
5.1. Serial Singularities
5.2. Parallel Singularities
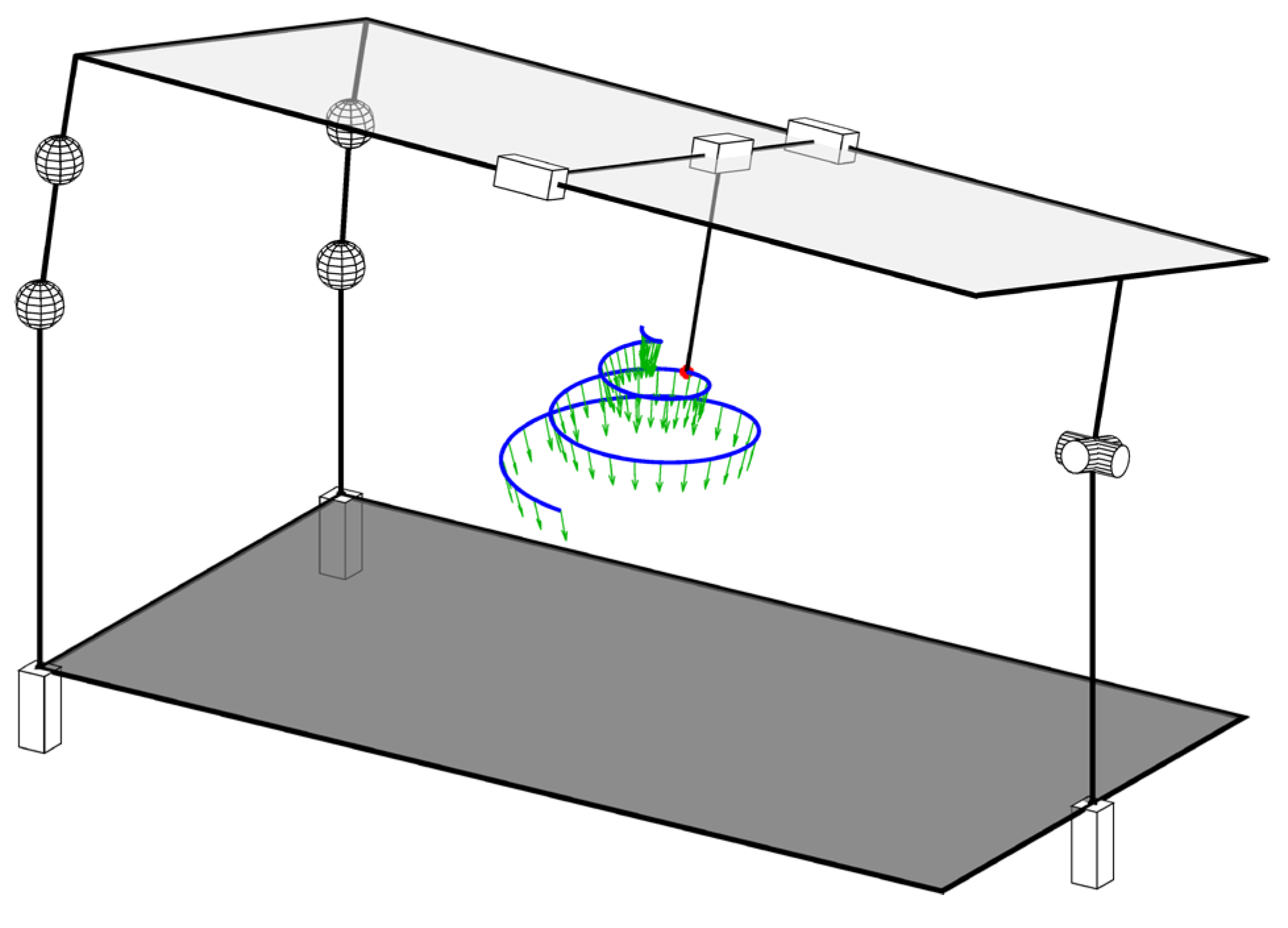
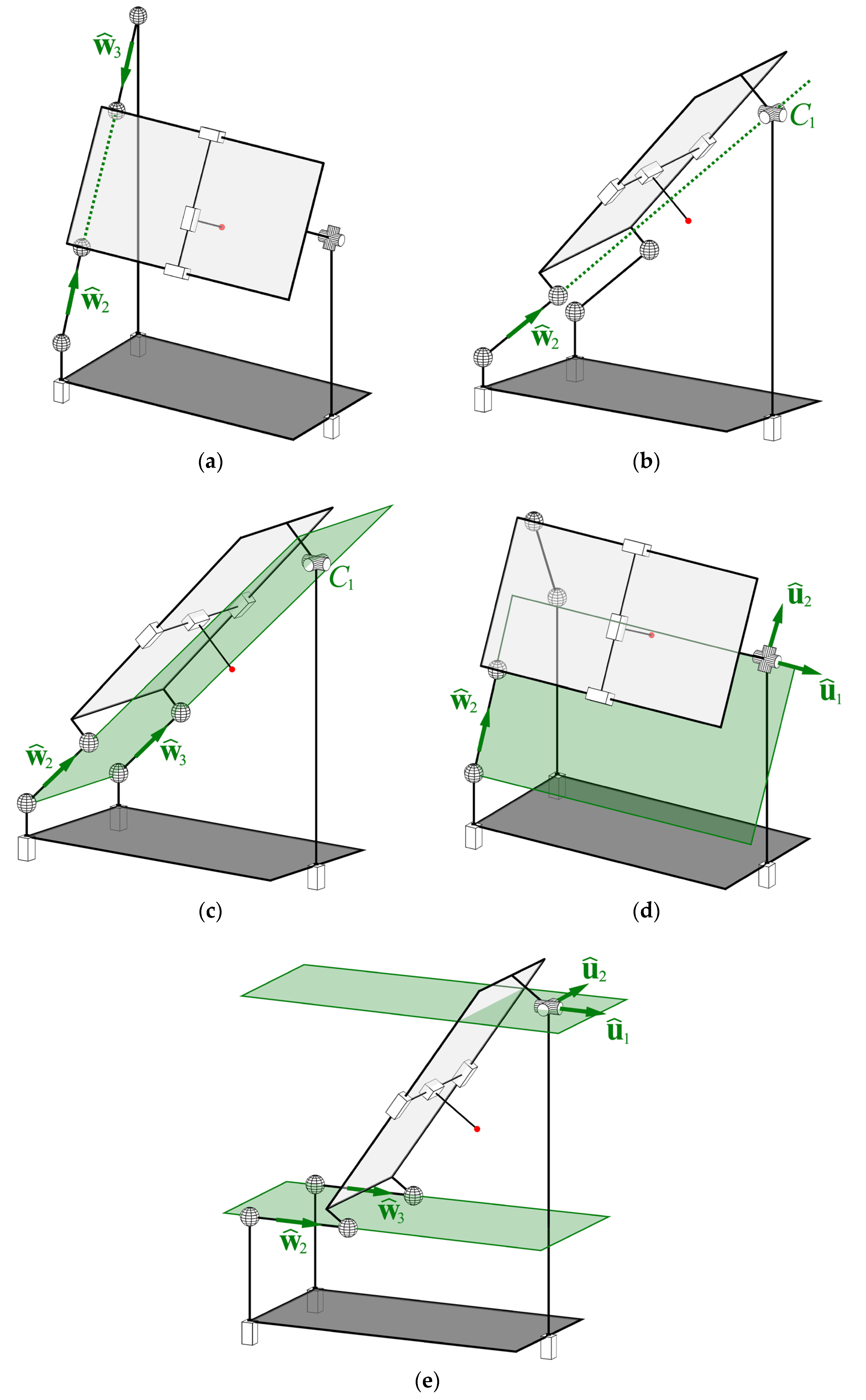
- and are collinear (Figure 8a): and are linearly dependent, and their moment parts are collinear.
- (or ) is on a line passing through point (Figure 8b): (or ) has a zero moment part.
- and lie in a plane passing through point (Figure 8c): the moment parts of and are collinear.
- (or ) lie in the spider plane, spanned by vectors and (Figure 8d): the moment part of (or ) is collinear with the axis of .
- and are parallel and lie in a plane parallel to the spider plane (Figure 8e): the moment parts of and and the axis of lie in a common plane.
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Wöhrle, H.; Fernández, J.G.; Müller, A.; Kirchner, F. A survey on modularity and distributivity in series-parallel hybrid robots. Mechatronics 2020, 68, 102367. [Google Scholar] [CrossRef]
- Wen, K.; Harton, D.; Laliberté, T.; Gosselin, C. Kinematically redundant (6+3)-dof hybrid parallel robot with large orientational workspace and remotely operated gripper. In Proceedings of the 2019 IEEE International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 1672–1678. [Google Scholar] [CrossRef]
- Liu, Q.; Huang, T. Inverse kinematics of a 5-axis hybrid robot with non-singular tool path generation. Robot. Comp.-Integr. Manuf. 2019, 56, 140–148. [Google Scholar] [CrossRef] [Green Version]
- Carbone, G.; Ceccarelli, M. A stiffness analysis for a hybrid parallel-serial manipulator. Robotica 2004, 22, 567–576. [Google Scholar] [CrossRef]
- Lai, Y.-L.; Liao, C.-C.; Chao, Z.-G. Inverse kinematics for a novel hybrid parallel–serial five-axis machine tool. Robot. Comp.-Integr. Manuf. 2018, 50, 63–79. [Google Scholar] [CrossRef]
- Oba, Y.; Kakinuma, Y. Simultaneous tool posture and polishing force control of unknown curved surface using serial-parallel mechanism polishing machine. Precis. Eng. 2017, 49, 24–32. [Google Scholar] [CrossRef]
- Tanev, T.K. Kinematics of a hybrid (parallel–serial) robot manipulator. Mech. Mach. Theory 2000, 35, 1183–1196. [Google Scholar] [CrossRef]
- Moosavian, S.A.A.; Pourreza, A.; Alipour, K. Kinematics and dynamics of a hybrid serial-parallel mobile robot. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1358–1363. [Google Scholar] [CrossRef]
- Zheng, X.Z.; Bin, H.Z.; Luo, Y.G. Kinematic analysis of a hybrid serial-parallel manipulator. Int. J. Adv. Manuf. Technol. 2004, 23, 925–930. [Google Scholar] [CrossRef]
- Nazari, A.A.; Moosavian, S.A.A.; Hasani, A. Kinematics analysis, dynamic modeling and verification of a CRRR 3-DOF spatial parallel robot. In Proceedings of the 2nd International Conference on Control, Instrumentation and Automation, Shiraz, Iran, 27–29 December 2011; pp. 1067–1073. [Google Scholar] [CrossRef]
- Kucuk, S.; Gungor, B.D. Inverse kinematics solution of a new hybrid robot manipulator proposed for medical purposes. In Proceedings of the 2016 Medical Technologies National Congress (TIPTEKNO), Antalya, Turkey, 27–29 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, D.-S.; Xu, Y.-D.; Yao, J.-T.; Zhao, Y.-S. Analysis and optimization of a spatial parallel mechanism for a new 5-DOF hybrid serial-parallel manipulator. Chin. J. Mech. Eng. 2018, 31, 54. [Google Scholar] [CrossRef] [Green Version]
- Xu, P.; Cheung, C.-F.; Li, B.; Ho, L.-T.; Zhang, J.-F. Kinematics analysis of a hybrid manipulator for computer controlled ultra-precision freeform polishing. Robot. Comp.-Integr. Manuf. 2017, 44, 44–56. [Google Scholar] [CrossRef]
- Gim, K.G.; Kim, J.; Yamane, K. Design of a serial-parallel hybrid leg for a humanoid robot. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 6076–6081. [Google Scholar] [CrossRef]
- Milutinović, M.; Slavković, N.; Milutinović, D. Kinematic modelling of hybrid parallel-serial five-axis machine tool. FME Trans. 2013, 41, 1–10. Available online: https://scholar.google.ru/scholar?cluster=10660065093727811310 (accessed on 10 April 2022).
- My, C.A.; Hoan, V.M. Kinematic and dynamic analysis of a serial manipulator with local closed loop mechanisms. Vietnam J. Mech. 2019, 41, 141–155. [Google Scholar] [CrossRef]
- Nasseri, M.A.; Eder, M.; Eberts, D.; Nair, S.; Maier, M.; Zapp, D.; Lohmann, C.P.; Knoll, A. Kinematics and dynamics analysis of a hybrid parallel-serial micromanipulator designed for biomedical applications. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 293–299. [Google Scholar] [CrossRef] [Green Version]
- Simas, H.; Di Gregorio, R. Position analysis, singularity loci and workspace of a novel 2PRPU Schoenflies-motion generator. Robotica 2019, 37, 141–160. [Google Scholar] [CrossRef]
- Rakhodaei, H.R.; Rastegarpanah, A.; Ding, C.D.; Saadat, M.S. Free singularity path planning of hybrid parallel robot. In Proceedings of the 11th International Conference on Manufacturing Research, Cranfield, UK, 19–20 September 2013; pp. 313–318. Available online: https://scholar.google.ru/scholar?cluster=4732131641093736040 (accessed on 10 April 2022).
- Amine, S.; Caro, S.; Wenger, P. Constraint and singularity analysis of the Exechon. App. Mech. Mater. 2012, 162, 141–150. [Google Scholar] [CrossRef]
- Ma, G.; Chen, Y.; Yao, Y.; Gao, J. Kinematics and singularity analysis of a four-degree-of-freedom serial-parallel hybrid manipulator. J. Robot. Mechatron. 2017, 29, 520–527. [Google Scholar] [CrossRef]
- Antonov, A.; Fomin, A.; Glazunov, V.; Kiselev, S.; Carbone, G. Inverse and forward kinematics and workspace analysis of a novel 5-DOF (3T2R) parallel–serial (hybrid) manipulator. Inter. J. Adv. Robot. Syst. 2021, 18, 1–14. [Google Scholar] [CrossRef]
- Merlet, J.-P. Parallel Robots, 2nd ed.; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Mohamed, M.G.; Duffy, J. A direct determination of the instantaneous kinematics of fully parallel robot manipulators. J. Mech. Trans. Autom. 1985, 107, 226–229. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M. Type Synthesis of Parallel Mechanisms; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Q.; Ding, H. Theory of Parallel Mechanisms; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Sun, T.; Yang, S.; Lian, B. Finite and Instantaneous Screw Theory in Robotic Mechanism; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Rodriguez-Leal, E.; Dai, J.S.; Pennock, G.R. A study of the instantaneous kinematics of the 5-RSP parallel mechanism using screw theory. In Advances in Reconfigurable Mechanisms and Robots I; Dai, J., Zoppi, M., Kong, X., Eds.; Springer: London, UK, 2012; pp. 355–369. [Google Scholar] [CrossRef]
- Guo, S.; Wang, C.; Qu, H.; Fang, Y. A novel 4-RRCR parallel mechanism based on screw theory and its kinematics analysis. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2013, 227, 2039–2048. [Google Scholar] [CrossRef]
- Lescano, S.; Zlatanov, D.; Rakotondrabe, M.; Andreff, N. Kinematic analysis of a meso-scale parallel robot for laser phonomicrosurgery. In Interdisciplinary Applications of Kinematics; Kecskeméthy, A., Geu Flores, F., Eds.; Springer: Cham, Switzerland, 2015; pp. 127–135. [Google Scholar] [CrossRef] [Green Version]
- Kang, L.; Kim, W.; Yi, B.-J. Modeling and analysis of parallel mechanisms with both kinematic and actuation redundancies via screw theory. J. Mech. Robot. 2017, 9, 061007. [Google Scholar] [CrossRef]
- Laryushkin, P.; Glazunov, V.; Erastova, K. On the maximization of joint velocities and generalized reactions in the workspace and singularity analysis of parallel mechanisms. Robotica 2019, 37, 675–690. [Google Scholar] [CrossRef]
- Bottema, O.; Roth, B. Theoretical Kinematics, reprint of 1979 ed.; Dover: New York, NY, USA, 1990; Available online: https://scholar.google.ru/scholar?cluster=7729442652911673935 (accessed on 10 April 2022).
- Gosselin, C.; Angeles, J. Singularity analysis of closed-loop kinematic chains. IEEE Trans. Robot. Autom. 1990, 6, 281–290. [Google Scholar] [CrossRef]
- Zlatanov, D.; Fenton, R.G.; Benhabib, B. Identification and classification of the singular configurations of mechanisms. Mech. Mach. Theory 1998, 33, 743–760. [Google Scholar] [CrossRef]
- Conconi, M.; Carricato, M. A new assessment of singularities of parallel kinematic chains. IEEE Trans. Robot. 2009, 25, 757–770. [Google Scholar] [CrossRef]
- Bohigas, O.; Manubens, M.; Ros, L. Singularities of Robot Mechanisms; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Chablat, D.; Wenger, P. Working modes and aspects in fully parallel manipulators. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation, Leuven, Belgium, 20–20 May 1998; pp. 1964–1969. [Google Scholar] [CrossRef] [Green Version]
- Zlatanov, D.; Bonev, I.A.; Gosselin, C.M. Constraint singularities of parallel mechanisms. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 496–502. [Google Scholar] [CrossRef]
- Liu, X.-J.; Wu, C.; Wang, J. A new approach for singularity analysis and closeness measurement to singularities of parallel manipulators. J. Mech. Robot. 2012, 4, 041001. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laryushkin, P.; Antonov, A.; Fomin, A.; Essomba, T. Velocity and Singularity Analysis of a 5-DOF (3T2R) Parallel-Serial (Hybrid) Manipulator. Machines 2022, 10, 276. https://doi.org/10.3390/machines10040276
Laryushkin P, Antonov A, Fomin A, Essomba T. Velocity and Singularity Analysis of a 5-DOF (3T2R) Parallel-Serial (Hybrid) Manipulator. Machines. 2022; 10(4):276. https://doi.org/10.3390/machines10040276
Chicago/Turabian StyleLaryushkin, Pavel, Anton Antonov, Alexey Fomin, and Terence Essomba. 2022. "Velocity and Singularity Analysis of a 5-DOF (3T2R) Parallel-Serial (Hybrid) Manipulator" Machines 10, no. 4: 276. https://doi.org/10.3390/machines10040276
APA StyleLaryushkin, P., Antonov, A., Fomin, A., & Essomba, T. (2022). Velocity and Singularity Analysis of a 5-DOF (3T2R) Parallel-Serial (Hybrid) Manipulator. Machines, 10(4), 276. https://doi.org/10.3390/machines10040276








