Abstract
This paper deals with the modeling of the thermal load and the simulation of thermal dynamic characteristics for the hydraulic system of a large airliner in a full mission profile. Firstly, the formation mechanism of the thermal load in the hydraulic system is analyzed, and thermal dynamic modeling is conducted of the hydraulic components of an hydraulic system with an immersed heat exchanger employing the lumped parameter thermal node method and oil temperature and power loss of each key node within the hydraulic system within a full mission profile. Then, a thermal dynamic simulation model based on MATLAB/Simulink is established, and the temperatures at the nodes of different components and the absorptive capacity of the fuel heat sink in the thermal management module are calculated. The simulation results show that the thermal management scheme of the heat exchanger, located in the return oil pipeline of the hydraulic piston pump housing and immersed in the central fuel tank, can dissipate the thermal load of the system. This work is of important significance for temperature analysis and thermal load dissipation of the airliner hydraulic system.
1. Introduction
The hydraulic system, as one of the airliner’s secondary power systems, commonly undertakes power transmission and control tasks such as take-off, climb, cruise flight, descent, and landing during a full-mission profile, and therefore, its performance is crucial for reliability and safety of the airliner [1,2]. During the process of a full mission, the airliner hydraulic system brings thermal loads to be mainly produced by power loss in the process of the conversion, transmitting, and regulating of the hydraulic energy, external heat radiation, or convection and friction between external air and airliner skin. In recent years, the improvement demand for maneuverability and mission payload required airliner hydraulic systems with high pressure and large power, thus inevitably leading to the increase of oil leakage, power loss, and temperature rise [3,4]. The thermal load finally results in the temperature rise of the hydraulic system. The large thermal load causes thermal expansion jam and aging of hydraulic components, thus keeping the hydraulic actuators from reaching the exact position and eventually causing safety accidents. The temperature rise also affects the viscosity of the hydraulic oil and makes the viscosity deviate from normal range, which deteriorates the working performance of the hydraulic system and even causes safety accidents. Therefore, in order to control the temperature of the hydraulic system within the allowable range, to absorb the thermal load by fuel oil as heat sink is necessary, lots of related studies have been carried out [5].
Guo et al. [6] studied the operation characteristics of the aircraft axial piston pump and pointed out that the friction power loss results from the friction pairs of the pump, and in the meantime, its compact structure and high pressure compared with other hydraulic components makes it difficult to dissipate heat. For the thermal dynamic analysis of and airliner hydraulic system, Yin [7] carried out a detailed analysis of the power loss and thermal dissipation mechanism, then established a thermal model by using AMESim, and then calculated the inlet and outlet temperature change of the aircraft axial piston pump at normal temperature working environment. Zhang et al. analyzed the churning losses of an aviation axial piston pump in a high-speed pump in the electro-hydrostatic actuator [8]. Wang et al. [9] further studied the temperature change rule of the piston pump, the hydraulic oil tank, and the hydraulic actuator at high temperature environment. Addressing the issue to decrease the power loss and the temperature rise existing in hydraulic systems during the process of conducting mission profile, Li et al. [10] carried out thermal simulations for three kinds of axial piston pump, i.e., a constant pressure variable displacement pump, a dual-stage pressure variable displacement pump, and an intelligent variable displacement pump, and the results show that the two latter kinds of pump can acquire the better energy saving effect. Jing Li et al. [11] conducted the thermal-dynamic analysis for an electro-hydraulic servo actuator of the aircraft by using the thermal node method and verified the effectiveness of the established model through the experiment. Du and Li studied the real time simulation of the aircraft hydraulic system [12]. Li et al. analyzed the power loss of the main hydraulic components of the airliner hydraulic system and proposed their calculating formula [13]. Li et al. studied the thermal dynamics modeling method for controlling volume and analyzed the existed problems of the governing equation built in Harris’s Ph. D. thesis [14] and then established new governing equation for the control volume to describe for thermal dynamic characteristics of hydraulic system [15].
Addressing the modeling issues of thermal dynamics of the heat exchanger in an aircraft hydraulic system and fuel oil system, many researchers carried out lots of studies. Jonsson [16] established the thermal dynamic model to describe hot and cold sides of heat exchanger through lumped parameter method. Dooley [17] and Glickstein [18] studied the heat dissipating mechanism and modeling of heat sink for thermal management of airborne equipment and then pointed out that fuel is a more suitable heat sink for aircraft hydraulic system. German [19] and Alyanak [20] summarized the distribution characteristics of aircraft thermal load, then proposed a general thermal management architecture applied to airborne equipment, and finally established thermal dynamic model of fuel tank by adopting lumped parameter method. In order to tackle the problem of heat accumulation and temperature rise, Doman [21,22] and Huang [23] proposed a topology architecture of dual fuel tanks and then studied the influence factors and the control strategy for temperature control. Huang [23] and Pangborn [24] researched the effectiveness of a thermal management architecture, the thermal dynamic model, and a control strategy through experiment. Focused on the low temperature rise and high power-weight ratio, Hong et al. studied the multi-objective optimal design of an electro-hydrostatic actuator [25].
At present, a great deal of commercial dynamic system simulation software such as Hopsan, Easy5, AMESim, HyPenu, and Simscape/hydraulic systems in MATLAB can be used for the analysis of the dynamic characteristics of aircraft hydraulic systems; however, thermal load analysis and models of the whole airliner hydraulic system are rarely published. Especially, there is little published on the working of the thermal load mechanism and temperature-rise issue on the airliner hydraulic components during a full mission profile.
In order to conduct the evaluation of temperature variation characteristics in the airliner hydraulic system and improve thermal load restraining and thermal management measures, this paper focuses on the thermal load and temperature-rise mechanism of key hydraulic components in the airliner hydraulic system with an immersed heat exchanger and conducts thoughtful research on temperature-rise and thermal load dissipating characteristics by means of dynamic modeling and simulation.
The rest of the paper is organized as follows. In Section 2, the paper analyzes the thermal load and thermal dissipation mechanism of airliner hydraulic system in a full flight mission profile and then establishes thermal dynamic governing equations of the principal components by using thermal node and the lumped parameter method. Section 3 calculates the temperature characteristics of the key components by using MATLAB/Simulink. Section 4 analyzes the thermal load absorptive abilities of fuel heat sink among thermal management module. Finally, the analysis of simulation results shows that immersed heat exchanger with fuel heat sink is feasible for thermal management. At the end of the paper, notations and abbreviations are provided in the nomenclature.
2. Thermal Dynamic Modeling of Hydraulic Components
2.1. The Scheme Description of Thermal Dynamic Modeling
An airliner hydraulic system commonly consists of a hydraulic power system and a hydraulic actuating system. To ensure sufficient reliability and safety, it has at least two sets of independent working systems and one set of the standby system which commonly consists of an EMDP (electric motor driven pump) based hydraulic system, or EHA (electric-hydrostatic actuator) and an EBHA (electric backup hydraulic actuator) power by electric wire system, and the primary components layout on the airliner is shown in Figure 1. Here, thermal analysis is conducted by choosing one set of primary hydraulic systems.

Figure 1.
The layout of the primary components of the airliner hydraulic system.
During the flight process of the entire mission, various power losses in the process of energy conversion, dividing, and regulation of the hydraulic system produce thermal load and result in the temperature rise of the hydraulic system. To predict the temperature rise, based on the working and thermal mechanism of the airliner hydraulic system and airliner mission profile, it is essential to establish a thermal dynamic model of key hydraulic components based on their heat-generation and heat-dissipation characteristics. Because hydraulic components spread over the wing and fuselage of the airliner, in order to facilitate subsequent analysis, we must establish thermal dynamic governing equations by dividing the airliner hydraulic system into piston pump, hydraulic oil tank, and thermal management module and then combine this into a thermal dynamic mathematical model of the whole hydraulic system. Based on the modeling scheme shown in Figure 2, thermal dynamic equations of hydraulic components are established by adopting a thermal node lumped parameter method, and then, we calculate the oil temperature of key nodes in the hydraulic system, power loss of piston pump, and heat-absorption abilities of the fuel heat sink by using MATLAB/Simulink.
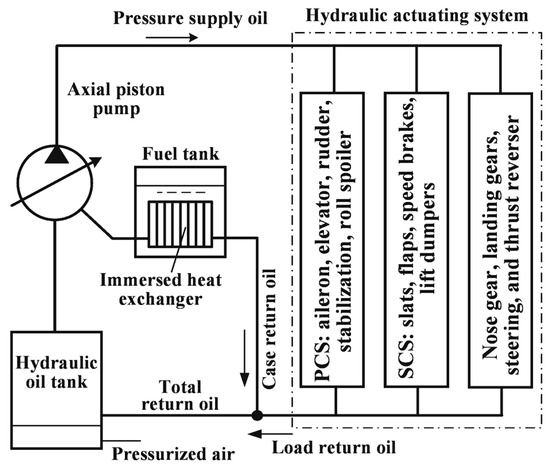
Figure 2.
Modeling scheme of hydraulic system.
Adopting the modelling method of the power losses and thermal dynamics of the hydraulic system proposed in [15], the power loss can be expressed as
where is the power loss to pass the control volume, is the input power of the control volume, and denote the flow powers of the input and the output, respectively. The governing equation of the thermal dynamics of the control volume are as follows
where and are the density, the specific heat capacity, inlet temperature, outlet temperature, inlet flowrate, and outlet flowrate of the hydraulic oil of the control volume, respectively. Equation (2) is used for the thermal analysis of the hydraulic component. It opens the coupling between hydraulic dynamic calculation and temperature dynamic calculation and clearly explains that the main heat-generation reasons of hydraulic components are the power loss of components, heat transfer rate around the control volume surface, and the mass flowrate difference to inflow and outflow the control volume.
2.2. Thermal Dynamic Modeling of Key Hydraulic Components
2.2.1. Axial Piston Pump
The structure and working mechanism of the airliner hydraulic system is shown in Figure 3. During the entire flight mission, the piston pump keeps working, and friction and leakage losses always exist. The leakage loss and friction loss are the main power losses of the pump, and the power loss also includes the mixing loss produced by the rotation of the cylinder body, pistons, and slippers for high rotational speed of the aviation pump.

Figure 3.
Structure and working mechanism of piston pump.
There are many pairs of components with relative motion in the axial piston pump. As long as the piston pump operates, the oil inside the pump body can generate heat due to the power loss of friction, leakage, and throttling, and then this heat results in the temperature rise of the hydraulic oil and components inside the pump. Meanwhile, the pump is arranged near the aero-engine, and then, it is easily affected by thermal radiation from the engine, so the high environment temperature makes the transfer of the accumulated heat in the pump to the equipment bay very difficult. Therefore, to dissipate the heat in the pump through the heat exchange between the case-returning oil and heat sink is the only effective way.
According to the above description of working and thermal mechanisms, it can be found that the piston pump includes the mechanical energy of the prime mover and continuously converts the low-pressure energy of oil at the input port into high pressure energy at the outlet, and in the meantime, part of the pressurized oil flows towards the case draining port. To make thermal dynamic modeling easy, it is necessary to divide piston pump into discharge chamber and case chamber, and then, the corresponding temperatures are respectively represented by and , while ignoring the oil leakage between absorption chamber and case chamber. The modeling mechanism is shown in Figure 4. By using (2) for two control volumes, we can write the governing equations of discharge chamber and case chamber as follows
where , , , , , , , , , , , , and denote the inlet temperature, specific heat capacity of the hydraulic oil and the material of the pump cylinder and pump case body, the equivalent mass coefficient of the heat transferring of the pump cylinder and pump case body, the mass of the pump case body and the oil in pump discharge chamber and pump case chamber, the flowrate of the pump inlet, the density of the hydraulic oil, the volume efficiency of the pump, and the mechanical power loss and volumetric power loss of the pump, respectively.
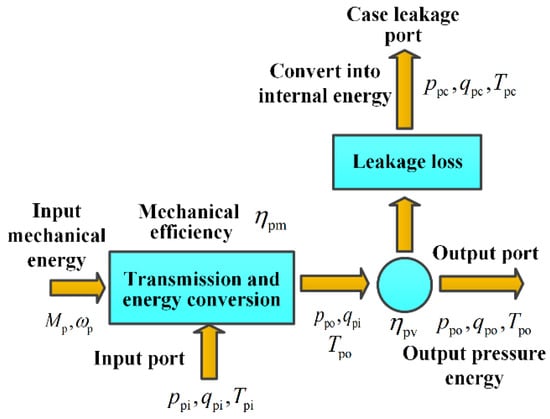
Figure 4.
Power losses of piston pump.
To solve (3) and (4) needs to determine power losses and need to be determined. Firstly, the calculating formula of the mechanical power loss of piston pump is
where , , , and are the theoretical hydraulic power, output hydraulic power, overall efficiency, and mechanical efficiency of the pump, respectively. From dimensional analysis and similarity theory, can be expressed as
where dimensionless coefficients and in (6) can be identified from the test curve of the of the pump. The terms and of the piston pump can be respectively represented by
Secondly, the volumetric power loss of piston pump. is expressed as follows
where , , , and are the pressure difference between the outlet pressure and inlet pressure, the output flowrate, theoretical flowrate, and the volumetric efficiency of the pump, respectively. The pressure difference is , and the input shaft power of the piston pump is
where , , and are the displacement, input shaft torque, and angular speed of the axial piston pump, respectively.
Considering the leakage in the pump, the output flowrate is less than theoretical flowrate , and the difference between and is the leakage flowrate to the case chamber. The , , and volumetric efficiency of the pump are expressed as
where , , , and are the dimensionless coefficient, theoretical displacement, angular speed, and inclination angle coefficient of the swash plate of the pump, respectively. can be identified from the test curve of . The expressions of and are as follows
The heat transfer rate in (3) and (4) is the heat transfer rate which takes place through pump cylinder between the discharge chamber and case chamber. Heat transfer rate in (4) is the heat transfer rate between the pump case body and the air inside the aeroengine nacelle. Their calculating formulas are as follows:
where and are the heat transfer coefficients between case body and engine nacelle air and between leakage port and outlet, respectively; and are the corresponding heat transfer areas, and is the air temperature of the engine nacelle.
2.2.2. Hydraulic Actuating Subsystem
Hydraulic actuating subsystem mainly consists of high-pressure supplying pipeline, electro-hydraulic servo actuators, and low-pressure returning pipeline. In the case of normal operation, the flowrate of the pump outlet is equal to the volume flowrate of subsystem outlet, i.e., . In the actuating subsystem, the hydraulic pressure energy of the oil converts into mechanical energy of the servo actuators. The power losses of the actuating system include the throttling loss at the valve orifice, flow loss in the supplying oil and returning oil pipelines, mechanical friction, and leakage loss in the hydraulic cylinder.
Because the hydraulic components within the subsystem are mainly located inside an airborne equipment bay, cold air from the bay can take away some thermal load, specifically, during the actuating period of the actuator. Considering the fact that this subsystem includes many components which spread over wing and fuselage, for the convenience of the follow-up research, it is necessary to regard the hydraulic actuating subsystem as a equivalent plant and then conduct thermal dynamic modeling for its outlet temperature and the inlet temperature . The modeling mechanism of the actuating subsystem is shown in Figure 5, and the thermal dynamic model of its outlet is
where is the power loss of the actuating subsystem, and is the heat flowrate exchange between subsystem and cold air from airborne equipment bay.

Figure 5.
Thermal modeling mechanism of the hydraulic actuating subsystem.
The power loss includes the leakage losses of the servo valve and cylinder and the metering loss of the servo valve. The leakage loss of the servo valve includes the leakage loss of the hydraulic preamplifier stage and the leakage loss of the slide valve power stage. This value is the largest in the zero position (standby state) area and decreases approximately to less than 20% of the zero-position leakage loss. The leakage loss of the hydraulic cylinder is very small in the standby state and is larger in the servo valve operation mode. The metering loss of the servo valve only exists in the servo valve operation state, and it can be determined by the product of pressure drop of the valve port and load flowrate, especially, when the hydraulic actuator reaches the specified position, the servo valve needs to output a certain load flowrate, which flows through the clearance and damping hole between the two working chambers of the hydraulic cylinder and produces a hydraulic force to balance the external load acting on the actuator piston rod. The calculation method of the in detail will be discussed in detail in another paper.
The heat transfer between the actuating system and the airborne equipment bay is the convective heat transfer, and the formula of the is represented by
where is the heat transfer coefficient between subsystem and cold air; is its effective heat transfer area, and is the air temperature inside airborne equipment bay.
2.2.3. Hydraulic Oil Tank
In contrast to the tank of the hydraulic system in ground mobile machinery, the aircraft hydraulic system adopts a pressurized oil tank, and the volume is very small, so its heat dissipation capacity is small. As one of heat-dissipation components in the airliner hydraulic system, it continually receives the oil which comes from the main returning oil pipeline and the case returning oil pipeline, then supplying oil to the main pump, so the volume flowrate of the pump inlet is equal to . The thermal properties of the hydraulic oil tank can affect the oil temperature change and performance of the whole hydraulic system.
As shown in Figure 6, the hydraulic oil tank is usually located inside airborne equipment bay. After the overall returning oil from case returning oil pipeline and the main returning oil pipeline passes the reservoir, the thermal load can be partly taken away through the heat exchange between the hydraulic oil and the air inside airborne equipment bay. Hydraulic oil inside the tank must ensure the demanded temperature to deliver to main pump import.

Figure 6.
Thermal modeling mechanism of hydraulic oil tank.
Through the above analysis, the thermal dynamic model of the oil temperature in hydraulic tank can be expressed as
where is the heat transfer coefficient between the hydraulic oil tank and cold air inside an airborne equipment bay; is the heat transfer area of hydraulic oil tank, and is the environment temperature of the hydraulic oil tank.
2.2.4. Thermal Management Module
The thermal management module mainly consists of a fuel heat sink, an immersed heat exchanger, and a unilateral fuel tank. It is important to note here that the layout of airliner fuel is symmetrical, so we introduced the concept of unilateral fuel tank to conduct thermal dynamic modeling to facilitate the following thermal modeling. The unilateral fuel tank consists of a unilateral wing fuel tank and half of center fuel tank. Because the power loss of the piston pump is large in the constant pressure stage and is close to nacelle, the heat accumulation of the piston pump is more serious than other hydraulic components. Although there are also power losses with the actuating system, considering the fact that the airliner does not involve large actuating maneuvers except for the taking-off and declining stages, that the actuating system has only the leakage power losses, and that the flowrate of the load returning hydraulic oil is small, we adopt the thermal management scheme in which the heat exchanger (HX) is settled in the house-draining oil line and immersed in the central wing fuel tank. Meanwhile, the central wing fuel tank of airliner has also enough space to settle HX. The fuel in the fuel tank can absorb the heat of the hydraulic system, and meanwhile, its heat can be taken away by external air outside the airliner, so the fuel temperature can be restrained.
Through the heat transfer analysis, the modeling mechanism of the thermal management module is shown in Figure 6, the outlet oil temperature of the immersed heat exchanger and the fuel temperature inside unilateral fuel tank are expressed as
where is the heat transfer coefficient between hydraulic oil and fuel, is the effective heat transfer area of immersed heat exchanger, is the inlet oil temperature of immersed heat exchanger, is the logarithmic mean temperature difference, and its formula is expressed as
Because the inlet of immersed heat exchanger is linked to the case leakage port of the axial piston pump, we can consider and . The heat transfer rate between fuel and external air outside unilateral fuel tank in (22) is calculated as follows
where is the heat transfer coefficient between fuel and boundary layer air outside wing fuel tank, is the effective heat transfer area of unilateral wing fuel tank, is the air temperature of boundary layer outside unilateral wing fuel tank, is the surface temperature of wing skin. is the heat transfer coefficient between fuel and external air outside center fuel tank, is the effective heat transfer area of half of center fuel tank, is the air temperature outside center fuel tank. For the airliner under subsonic flight, the formula of is expressed as
where is the air temperature outside airliner, is the air temperature at the stages of take-off and landing. Adiabatic coefficient is 1.4, temperature recovery factor at the boundary layer of airliner wing is 0.888. is the flight altitude of airliner, is the dimensionless number which describes the flight speed.
In order to evaluate cooling abilities of fuel heat sink inside the unilateral fuel tank, real-time cooling power and real-time residual cooling amount are defined. and directly affect the working time of the thermal management system and are the reference basis while conducting the scheduling of heat sink. means the thermal load which the fuel heat sink can absorb in units of time during the flight mission profile, and means the thermal load which real-time residual fuel inside unilateral fuel tank can absorb.
Real-time cooling power mainly depends on the difference between the given maximum temperature and the real-time temperature of the fuel heat sink inside fuel tank and the mass flowrate of the fuel sent to the combustor, and it can be expressed as
where is the given maximum temperature of the fuel heat sink inside the fuel tank. The fuel temperature at the inlet of the combustor is the highest because the fuel from the fuel tank flows through the low-pressure pump, the heat exchangers which absorb heat from lubricating oil system (airframe-mounted accessory drive, bearing and generator), the high pressure pump, and the fuel metering unit and then arrive at the combustor. The maximum temperature at the combustor is limited to the cocking temperature (generally to be 135 °C). In order to fully absorb heat, is set at 50 °C. For the case of higher ground temperature outside the airliner or less fuel left in the tank, this condition must be met, or related thermal management measures need to be taken [15]. is the mass flowrate of fuel to be used for combustion at the combustor, and its value is given by
Residual cooling amount mainly depends on the difference between the given maximum temperature and the temperature of the fuel heat sink in the fuel tank and the instantaneous mass of residual fuel inside the unilateral fuel tank, and it is calculated as
where is the real-time mass of residual fuel inside the unilateral fuel tank, and its calculation formula is expressed as
where is the initial mass of fuel inside unilateral fuel tank to be used for combustion; here, it is taken to be 5500 kg, and its value is determined according to the maximum volume of the fuel tank and the air range of the whole flight mission. Here, the two HXs of the two hydraulic systems of the airliner are respectively arranged inside the fuel tanks at the roots of the wings on both sides. Currently, B737, A350, and an airliner made in China all adopt the thermal management method to immerse the heat exchanger inside fuel tank at the wing root. The detailed instructions can be found in the Boeing company aircraft maintenance manual [26].
3. Working Condition and Simulation Model Establishment
3.1. Working Condition Used for Simulation Calculation
In order to simulate the change of hydraulic oil temperature of the airliner hydraulic system and fuel temperature of the thermal management module, thereby evaluating the thermal dissipating properties of the fuel heat sink, this paper designed a full flight missions profile, shown in Table 1, as calculation conditions according to the technical features and relevant details of the airliner. This mission profile can directly affect the air temperature of the boundary layer outside the wing fuel tank, thus affecting the fuel temperature inside the fuel tank, the cooling capacities of the fuel heat sink, and the temperature of the hydraulic system.

Table 1.
A full flight mission profile of the large airliner.
The output flowrate of the engine-driven piston pump depends on its angular speed and inclination angle coefficient of swash plate, and the values are related to outlet pressure and rotational speed of the piston pump. The values of and during the process of a full airliner mission profile are shown in Table 2.

Table 2.
Physical variables of the components and subsystems in a flight mission profile.
Considering the fact that the components of the hydraulic actuating subsystem are spread throughout the airborne equipment bay near to the wing, tail, and fuselage and that the structure of every hydraulic actuator is very complex, we set the environment temperature and the power loss of the hydraulic actuating subsystem to be shown in Table 2. Physical variables of the components and subsystems in a flight mission profile. The heat transfer coefficients of the hydraulic actuating subsystem are set in Table 3. Additionally, the heat transfer area of the hydraulic actuating subsystem can be set as 5 m2 according to the surface areas of the components and tubes of the hydraulic actuating subsystem.

Table 3.
The heat transfer coefficients of hydraulic actuating subsystem, tank, and fuel tank.
Considering the hydraulic oil tank is located inside airborne equipment bay, its environment temperature and heat transfer coefficient of hydraulic oil tank depend on the variation process of the mission profile, and the related environment temperature and parameter of the hydraulic tank in the process of the airliner mission profile are shown in Table 2 and Table 3. Additionally, the value of heat transfer area of hydraulic actuating subsystem can be set as 0.6 m2 according to the structure of the hydraulic oil tank.
The center fuel tank is next to the airborne equipment bay, and therefore, its environment temperature and heat transfer coefficient depend on the changing process of the mission profile; the related temperature and the heat-transferring coefficient are the same as in the hydraulic actuating subsystem and hydraulic oil tank and are also given in Table 2 and Table 3. Moreover, the heat transferring area of the immersed heat exchanger for thermal management is chosen as 1.8 m2, according to the sizing of the HX in the airliner.
3.2. Thermal Dynamic Simulation Model
Based on the connections of the power flow of the main components and their governing equations in Section 2, the thermal dynamic models can be established through lumped parameter-based control volume method, and then, we can get the block diagram based simulation model shown in Figure 7 through MATLAB/Simulink. Based on the established simulation model, we adopt the solver which is featured as the fourth and fifth adaptive variable step Runge–Kutta method (RK45) to conduct thermal analysis.

Figure 7.
Element-level simulation model diagram of hydraulic system.
This simulation model is used for analyzing the thermal load mechanism of an airliner hydraulic system and the thermal management module. It consists of an engine-driven piston pump, hydraulic oil tank, hydraulic actuating subsystem, and thermal management module. Among these hydraulic components, the piston pump has the most serious problem of heat accumulation. Therefore, it is necessary to manage the most important component going through the thermal management module to limit the heat accumulation of the airliner hydraulic system. The thermal management module mainly consists of heat exchanger, fuel heat sink, and unilateral fuel tank. The unilateral fuel tank consists of a unilateral wing fuel tank and half of center fuel tank, whereas the heat exchanger is immersed inside the fuel tank at the unilateral wing root and assembled at the case returning oil pipeline of the piston pump.
Through simulation by using MATLAB/Simulink, the hydraulic oil temperature at the key nodes of the airliner hydraulic system, power loss of piston pump, and cooling abilities of fuel heat sink during the process of flight mission profile can be obtained, thereby conducting in-depth research on the heat accumulation mechanism of the airliner hydraulic system and cooling performance of thermal management module and providing support for future improvement work on thermal management schemes.
4. The Analysis of Simulation Results
4.1. Temperature Characteristic Analysis at Key Nodes of Hydraulic System
Under the working condition of mission profile, the dynamic process of hydraulic oil temperature at the key nodes of airliner hydraulic system is shown in Figure 8. From Figure 8, the temperature curves of the key nodes in each task stage of the mission profile usually can clearly represent the temperature dynamic characteristics of airliner hydraulic system under a full mission profile.

Figure 8.
Temperature change at five key nodes of hydraulic system under a full mission profile. Tpc: Oil temperature at case port of piston pump, Tpo: Oil temperature at outlet of piston pump, Thao: Oil temperature at outlet of hydraulic actuating subsystem, Thto: Oil temperature at outlet of hydraulic oil tank, Thxo: Oil temperatures at outlet of heat exchanger.
In Figure 8, firstly, we can see that the temperature of hydraulic oil at pump leakage port is higher than the temperature of hydraulic oil at other key nodes for most of a full mission profile, and the temperature of hydraulic oil at outlet of heat exchanger is obviously lower than other four key nodes; secondly, among the other three nodes for most of a full mission profile, the temperature of hydraulic oil at pump outlet is the highest, the temperature of hydraulic oil at outlet of its tank is the lowest, and the temperature of hydraulic oil at outlet of hydraulic actuating subsystem is middle; thirdly, at the end of mission profile, reaches to 62.9 °C, is close to 22 °C.
Under the working condition of mission profile, except for the change trend of basically showing a slowly downward trend, the change trends of the hydraulic oil at the other four key nodes of the hydraulic system are basically equal. They show the upward trend at the stages of taxi, take-off, and landing and show the slowly downward trend at the stage of cruise. During the 1200 s process from starting a mission profile to being 450 m height off the ground, the temperature shows an upward trend, especially in the first 200 s, the temperature shows a sharply upward trend because the hydraulic system transmits power frequently towards the landing gear and flight control surface to balance airliner gravity, and in the remaining 1000 s of the 1200 s process, the upward trend is obviously weakening because the increasing flight speed makes the swing of flight control surface not very necessary. During the 1200~4800 s cruise period, the moderate swing of the flight control surface and the very low air temperature outside the airliner make the change trend of the temperature of the hydraulic system decrease slightly. During the 4800~6400 s decline period, the temperature change of the hydraulic system basically shows an obviously upward trend again because the hydraulic system transmits power frequently towards the flight control surface to balance the airliner gravity. During the 6400~6600 s approaching, landing, and taxing period, considering that the sharply decreasing flight speed leads to a sharp movement of flight control surface and landing gear to balance airliner gravity and land safely, the temperature of the hydraulic system shows a very sharp rising trend.
4.2. Power Loss Characteristic Analysis of the Axial Piston Pump
Power loss is one of the important sources of heat accumulation in the piston pump; thus, grasping its change rule is very helpful for alleviating the temperature-rise problem within the piston pump, since the power loss depends on the output volume flowrate and efficiency of the piston pump during the process of conducting mission profile.
The change process of pump efficiency is shown in Figure 9. We can see that its volumetric efficiency is always obviously larger than its mechanical efficiency, and pump efficiency at the stages of taxi, take-off, climb, decline, approach, and landing is larger than its efficiency at the stage of cruise.

Figure 9.
The volumetric and mechanical efficiency of piston pump.
The change process of volume flowrate of the piston pump is shown in Figure 10. Firstly, we can see that its volume flowrate at the stages of take-off and landing is obviously larger than its volume flowrate at the stage of cruise because under the influence of lower flight speed, the piston pump needs to supply hydraulic oil for the movement of the flight control surface and landing gear to balance airliner gravity. Secondly, because its rotational speed at the stage of take-off is larger than its rotational speed at the stage of landing, its volume flowrate at the stage of take-off is larger than its volume flowrate at the stage of land. Additionally, because the flight speed reaches to the cruise speed, the piston pump only needs to supply a small amount of hydraulic oil towards the swing of the flight control surface to adjust the flight course of the airliner, and then, its volume flowrate at the stage of cruise is obviously lower than its volume flowrate at other stages.
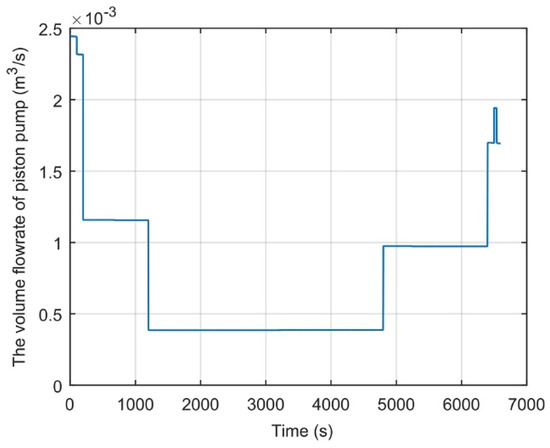
Figure 10.
The volume flowrate of piston pump.
Figure 11 shows the change of power loss of the piston pump during the full flight mission profile. Under the working condition of airliner mission profile, the change of the above working efficiency and volume flowrate of the piston pump illustrates that the mechanical power loss is always obviously larger than the volumetric power loss , and the mechanical power loss is still larger at the stage of cruise. Therefore, to assemble the heat exchanger in the case of the returning oil pipeline is very necessary.
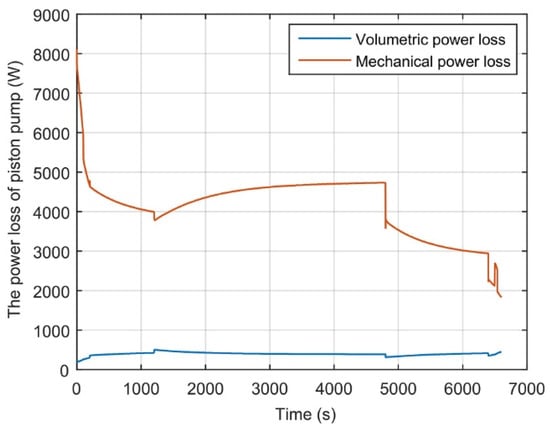
Figure 11.
Power loss of piston pump.
4.3. The Thermal Characteristic Analysis of Thermal Management Module
4.3.1. Fuel Temperature Inside the Fuel Tank
There are three kinds of heat sink used to absorb the thermal load of the airliner hydraulic system: fuel inside the fuel tank, ram air, and cooling air inside the airborne equipment system. Among these heat sinks, fuel inside the fuel tank is the most important heat sink compared with other two heat sinks because fuel inside the fuel tank is responsible for thermal management of the hydraulic system and the lubrication oil system. The heat exchanger is assembled at the case returning oil pipeline of the piston pump and is immersed inside the root of the wing fuel tank. Therefore, grasping the change process of the fuel temperature inside the fuel tank is essential for the thermal management of the airliner hydraulic system. The change process of the temperature of the fuel is shown in Figure 12.
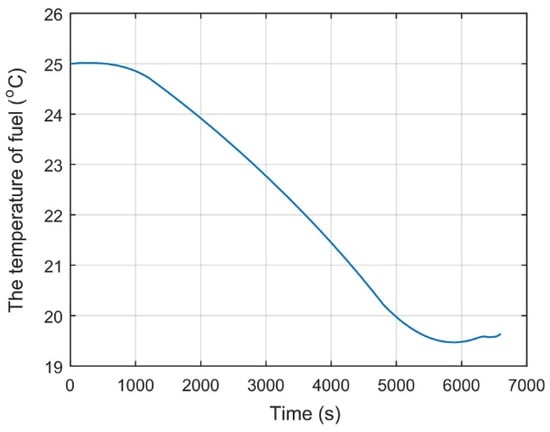
Figure 12.
Variation of fuel temperature inside wing fuel tank.
From Figure 12, we can see that the change process of fuel temperature inside its tank shows a downward trend for most of the process of conducting the mission profile. Fuel temperature inside its tank depends on heat absorption from the hydraulic system and heat exchange between fuel and external air outside its tank. During the process from starting mission profile to entering into cruise flight, the change process of fuel temperature firstly shows a mild trend and then an increasingly obvious downward trend due to the cold air outside the fuel tank and decreasingly fewer heat absorption from the hydraulic system. During the cruise flight period, the change process of fuel temperature always shows an obvious downward trend due to the cold air outside fuel tank and very few heat to absorb from hydraulic system. During the process from the end of cruise to the end of mission profile, the change process of fuel temperature firstly shows an increasingly slower downward trend and then shows a more obviously upward trend due to the increasingly higher temperature of the outside air, increasingly smaller storage inside the fuel tank and the increasing amount of heat absorption from the hydraulic system. At the end of mission profile, the fuel temperature inside its tank reaches to 21.7 °C, which is further away from 50 °C.
Considering that the thermal load of the lubrication oil system is usually much larger than the thermal load of the hydraulic system and that the maximum temperature at the combustor is generally limited to the cocking temperature of 135 °C, choosing the heat exchanger, which is assembled at the case returning oil pipeline and immersed at the wing root of the fuel tank cannot only meet the requirement for thermal management of the airliner hydraulic system but also leave enough space for thermal management of the lubrication oil system.
4.3.2. Inlet and Outlet Temperature of Heat Exchanger
The hydraulic oil inside the immersed heat exchanger conducts a heat exchange with the fuel heat sink inside the wing fuel tank to limit the temperature of airliner hydraulic system in a proper range. The change process of hydraulic oil temperature at inlet and outlet of the immersed heat exchanger is shown in Figure 13. We can see that the change process of hydraulic oil temperature at its outlet basically shows a slowly downward trend and shows an obvious gap between its inlet and outlet because the temperature of the fuel heat sink inside fuel tank is always obviously lower than the hydraulic oil temperature at the inlet of the heat exchanger. At the end of mission profile, its inlet temperature can reach to 62.9 °C, the maximum temperature during the process of conducting mission profile is obviously lower than its threshold value of 80 °C, and its outlet temperature is close to 22 °C.

Figure 13.
Inlet and outlet temperature of heat exchanger.
4.3.3. Heat Transfer Analysis of Heat Exchanger
Hot hydraulic oil inside the piston pump transfers its heat to the fuel heat sink inside the fuel tank through the immersed heat exchanger. The heat flowrate at its inlet and heat transfer rate between hydraulic oil and fuel are shown in Figure 14. We can see that there is always no significant difference between the quantity of and the quantity of . This phenomenon indicates that the fuel heat sink inside the fuel tank can always take away substantial thermal load from the hot hydraulic oil inside the piston pump during the process of conducting airliner mission profile. Then, the temperature of the hydraulic oil at its outlet is obviously lower than the temperature of the hydraulic oil at its inlet. Therefore, choosing the heat exchanger which is assembled at the case returning oil pipeline and immersed at the wing root of the fuel tank is very helpful for alleviating the heat accumulation phenomenon of airliner hydraulic system so that hydraulic system can always transfer power towards the movement of flight control surface and landing gear more safely and reliably.

Figure 14.
Heat transfer rate of heat exchanger.
4.3.4. The Cooling Ability Analysis of Fuel Heat Sink
The cooling ability is the key indicator towards measuring the performance of the fuel heat sink inside the fuel tank, and grasping its change process is very helpful for alleviating heat accumulation phenomenon of hydraulic system.
Figure 15 shows real-time cooling power of the fuel heat sink in mission profile process. It can be seen that the cooling power of fuel inside unilateral fuel tank is basically decreasing but still always very substantial Even at the end of mission profile, the cooling power of fuel inside unilateral fuel tank can still reach 3.61 × 104 W cooling power. Therefore, the fuel heat sink which is used for combustion has very strong real-time cooling abilities aimed at alleviating heat accumulation of the airliner hydraulic system.

Figure 15.
Real-time cooling power of fuel heat sink.
The developed simulation program also calculates the residual mass and residual cooling amount of fuel heat sink which is used for combustion during the entire flight mission profile. Figure 16 and Figure 17 illustrate that the residual mass and residual cooling amount that the fuel heat sink can provide decrease. Even at the end of mission profile, the residual fuel mass inside the fuel tank is about 1246.4 kg and the residual cooling amount of fuel heat sink is about 7.75 × 107 J, and the mass of remaining fuel usually needs to meet the 90 min voyage. Therefore, the fuel heat sink has a sufficient cooling amount aimed at alleviating heat accumulation in the airliner hydraulic system.

Figure 16.
The mass of residual fuel inside unilateral fuel tank.
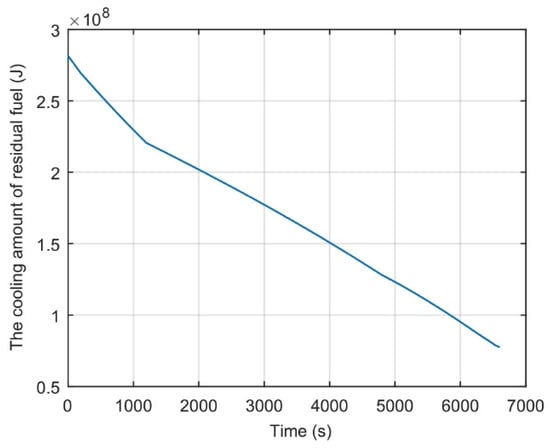
Figure 17.
Real-time cooling amount of residual fuel inside unilateral fuel tank.
Through the above thermal analysis for the calculation of results, we can see that during the process of conducting mission profile, the fuel heat sink which is used for combustion always has very strong real-time cooling abilities and sufficient cooling amount. Therefore, the scheme to set the heat exchanger at the case returning oil pipeline of the engine-driven piston pump and then to immerse the heat exchanger at the wing root of fuel tank is an effective measure to alleviate the heat accumulation of the airliner hydraulic system.
4.4. Verification of the Model of Electro-Hydraulic Servo Subsystem
The thermal dynamic model established in the paper is easily combined with the input–output characteristics of the component. The change trend of the simulation results is basically consistent with the trend reported by existing products. Here, the effectiveness of the model of the actuating subsystem is verified by simulating the temperature at the return oil port of an electro-hydraulic servo actuator in reference [11]. The comparison result is shown in Table 4; the simulation adopted the same parameters as reference [11], and the simulation result is basically consistent with the result of the test of the ground bench.

Table 4.
The comparison between test of ground bench and simulation result.
5. Conclusions
In order to analyze the temperature variation characteristics of the airliner hydraulic system and to evaluate the effectiveness of the scheme to dissipate heat loads by using an immersed heat exchanger inside fuel tank, this paper established a thermal dynamic model of key hydraulic components and a thermal management module for the airliner hydraulic system through a lumped thermal node method based on the physical parameters of the practical components and then conducted a simulation of temperature change of hydraulic oil at key nodes of the hydraulic system and temperature change and thermal load absorptive abilities of fuel inside the fuel tank during the flight mission profile based on MATLAB/Simulink. The main conclusions are as follows:
- (1)
- The established power losses model of the pump and the actuating system and the thermal dynamic model of the entire hydraulic system are effective. The temperature rise of the hydraulic system appears in stages of climbing and landing, and the maximum temperature node is at the housing port of the pump.
- (2)
- The thermal management scheme, i.e., to adopt the heat exchanger assembled at the case returning oil pipeline of the piston pump and immersed in the wing root of the fuel tank, is feasible. It can ensure the temperature rises of the hydraulic system and the fuel tank are less than the allowable values.
- (3)
- The temperature, the real-time cooling power, and the residual cooling amount of the fuel heat sink in the fuel tank meet the requirements of the full flight mission profile.
Future work prompted by this paper includes the further improvement and verification of the thermal dynamic model by combining the practical flight test data.
Author Contributions
Conceptualization, D.L., S.D., J.W. and Y.L.; methodology, D.L.; software, simulation, analysis, and investigation, D.L.; resources, D.L. and J.W.; data curation, D.L.; writing—original draft preparation, D.L.; writing—review and editing, D.L.; visualization, D.L.; supervision, J.W. and S.D.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Key Basic Research Program of China (No. 2014CB046403) and Major National Science and Technology Projects (2017-V-0015-0067).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Applicable on request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Notations | |
| Heat transfer area of pump body () | |
| Heat transfer areas of unilateral wing fuel tank and half center fuel tank () | |
| Heat transfer area of hydraulic actuating subsystem () | |
| Heat transfer areas of hydraulic oil tank and heat exchanger () | |
| Heat transfer area between pump outlet and case port () | |
| Specific heat capacity of hydraulic actuator () | |
| Specific heat capacities of fuel and specific heat capacity of hydraulic oil () | |
| Specific heat capacities of high-pressure pipeline and low-pressure pipeline () | |
| Specific heat capacities of heat exchanger and piston pump, respectively () | |
| Viscous friction coefficient, mechanical friction coefficient, and leakage flow coefficient of piston pump (-) | |
| Instantaneous displacement and maximum displacement of piston pump () | |
| Equivalent factor of product of specific heat capacity and mass of hydraulic actuating subsystem (-) | |
| Equivalent factors of products of specific heat capacity and mass of hydraulic oil tank (-) and heat exchanger (-) | |
| Equivalent factors of products of specific heat capacity and mass of the pump housing body (-) and the pump cylinder (-) | |
| Heat transfer coefficient between pump case body and nacelle air () | |
| Heat transfer coefficients, between unilateral wing fuel tank and wing surface, between half center fuel tank and cold air inside airborne equipment bay () | |
| Heat transfer coefficients, between hydraulic actuating subsystem and cold air inside airborne equipment bay, between hydraulic oil tank and equipment bay () | |
| Heat transfer coefficient between hydraulic oil and fuel of heat exchanger () | |
| Heat transfer coefficient between leakage port and outlet () | |
| Mass of hydraulic actuators () | |
| Initial fuel mass and residual fuel mass of fuel tank () | |
| Mass flow-rate which engine fuel consumes () | |
| Oil mass of hydraulic actuating subsystem () | |
| Oil mass of hydraulic oil tank and oil mass of heat exchanger, respectively () | |
| Net mass of high-pressure pipeline and net mass of hydraulic oil tank () | |
| Net mass of heat exchanger, net mass of low-pressure pipeline (kg) | |
| Net mass of piston pump (kg) | |
| Oil mass in pump discharge chamber, oil mass of pump case chamber (kg) | |
| Theoretical torque, viscous friction torque and mechanical friction torque of piston pump () | |
| Input shaft torque of piston pump (), rotational speed of piston pump (), | |
| Case port pressure, inlet pressure and of pump, outlet pressure of piston pump () | |
| Pressure difference between the outlet pressure and inlet pressure () | |
| Input shaft power and output hydraulic power of the piston pump (W) | |
| The power loss of hydraulic actuating subsystem (W) | |
| Mechanical power loss and volumetric power loss of piston pump (W) | |
| Volume flow rate at the outlet of hydraulic actuating subsystem () | |
| Volume flow rate at the outlet of heat exchanger () | |
| Input volume flowrate and output volume flowrate of piston pump () | |
| Leakage flowrate of piston pump () | |
| Theoretical volume flowrate of piston pump () | |
| Residual cooling amount which fuel heat sink can provide in current moment (J) | |
| Cooling flowrate of fuel heat sink (W) | |
| Heat flowrate of heat exchange between fuel and external air outside fuel tank (W) | |
| Heat flowrate between pump case body and nacelle air (W) | |
| Heat flowrate of heat exchange between hydraulic actuating subsystem and cold air from airborne equipment bay (W) | |
| Heat flowrate of heat exchange between fuel and hydraulic oil inside thermal management module (W) | |
| Heat flowrate between the discharge chamber and case returning chamber (W) | |
| Heat tranfer rate around the control volume surface (W) | |
| Threshold fuel temperature inside fuel tank () | |
| Fuel temperature inside fuel tank () | |
| Temperature of the cold air inside airborne equipment bay () | |
| Oil temperature at the outlet of hydraulic actuating subsystem () | |
| Environment temperature of hydraulic oil tank () | |
| Oil temperature at the outlet of hydraulic oil tank () | |
| Oil temperatures at the inlet and outlet of heat exchanger () | |
| Oil temperature at case port of piston pump () | |
| Temperature of the nacelle air () | |
| Inlet oil temperature and outlet oil temperature of piston pump () | |
| The logarithmic mean temperature difference of heat exchanger () | |
| Density of the hydraulic oil () and dynamic viscosity of hydraulic oil () | |
| Inclination angle coefficient of swash plate of piston pump (-) | |
| Rotational angular speed of piston pump (), | |
| Overall efficiency, mechanical efficiency and volumetric efficiency of the piston pump (-) | |
Abbreviations
| EBHA | Electric-Backup-Hydraulic actuator |
| EHA | Electric-hydrostatic actuator |
| EDP | Aerengine driven pump |
| EMDP | Electric motor driven pump |
| HX | Heat exchanger |
References
- Wheeler, P. Technology for the More and All Electric Aircraft of the Future. In Proceedings of the 2016 IEEE International Conference on Automatica (ICA-ACCA), Curico, Chile, 19–21 October 2016. [Google Scholar]
- Sarlioglu, B.; Morris, C.T. More Electric Aircraft: Review, Challenges, and Opportunities for Commercial Transport Aircraft. IEEE Trans. Transp. Electrif. 2015, 1, 54–64. [Google Scholar] [CrossRef]
- Fitch, E.C.; Hong, I.T. HyPneu Thermal Manual; BarDyne Inc.: Stillwater, OK, USA, 2004. [Google Scholar]
- Wang, S.P.; Tomovic, M.; Liu, H. Commercial Aircraft Hydraulic System; Shanghai Jiao Tong University Press: Shanghai, China, 2016. [Google Scholar]
- Li, D.; Hang, J.; Li, Y.; Dong, S. Fuel Flowrate Control for Aeroengine and Fuel Thermal Management for Airborne System of Aircraft-An Overview. Appl. Sci. 2022, 12, 279. [Google Scholar] [CrossRef]
- Guo, S.R.; Chen, J.H.; Lu, Y.L.; Wang, Y. Hydraulic piston pump in civil aircraft: Current status, future directions and critical technologies. Chin. J. Aeronaut. 2020, 33, 16–30. [Google Scholar] [CrossRef]
- Yin, Y.B.; Wang, Z.Y.; Li, J.; Tang, H.S. Thermal Characteristics of Aircraft Hydraulic Pump. J. Fluid Power Transm. Control. 2016, 1, 11–15. (In Chinese) [Google Scholar]
- Zhang, J.; Li, Y.; Xu, B.; Chen, X.; Pan, M. Churning losses analysis on the thermal-hydraulic model of a high-speed electro-hydrostatic actuator pump. Int. J. Heat Mass Transf. 2018, 127, 1023–1030. [Google Scholar] [CrossRef]
- Wang, K.; Huang, X.P.; Wang, H.X. Thermal-hydraulic System Modeling and Simulation of Large Aircraft Hydraulic Systems Based on AMESim. J. Fluid Power Transm. Control 2016, 3, 23–27. (In Chinese) [Google Scholar]
- Li, Y.L.; Hou, Y.Y.; Cao, K.Q.; Hu, L.M. Thermal Performance Simulation and Comparing Analysis for Aircraft Hydraulic System with Different Pumping Source Structure. J. Mech. Sci. Technol. Aerosp. Eng. 2016, 35, 1470–1476. (In Chinese) [Google Scholar]
- Li, J.; Tang, G.; Cao, J.; Shi, X. Thermodynamic Analysis and Calculations on Hydraulic Steering Units of Aircraft Hydraulic System. J. Chin. Mech. Eng. 2015, 26, 2070–2074. (In Chinese) [Google Scholar]
- Du, Z.; Li, K. Application of real-time simulation on the integrated management of aircraft hydraulic system. Aeronaut. Sci. Technol. 2016, 27, 71–74. [Google Scholar]
- Li, D.; Dong, S.J.; Wang, J.; Li, Y.H. State-of-art and some considerations on thermal load analysis and thermal management for hydraulic system in MEA. J. Eng. 2018, 13, 399–405. [Google Scholar] [CrossRef]
- Harris, R.M. The Modeling and Simulation of Temperature Effects in Hydraulic Systems. Ph.D. Thesis, School of Mechanical Engineering, University of Bath, Bath, UK, 1990. [Google Scholar]
- Li, D.; Dong, S.J.; Wang, J.; Li, Y.H. Thermal dynamics and thermal management strategy for a civil aircraft hydraulic system. Therm. Sci. 2020, 24, 2311–2318. [Google Scholar] [CrossRef]
- Jonsson, G.; Palsson, O.P. An Application of Extended Kalman Filtering to Heat Exchanger Models. J. Dyn. Sys. Meas. Control 1994, 116, 257–264. [Google Scholar] [CrossRef]
- Dooley, M.; Lui, N.; Newman, R.; Lui, C. Aircraft Thermal Management-Heat Sink Challenge. In Proceedings of the SAE 2014 Aerospace Systems and Technology Conference, Cincinnati, OH, USA, 23 September 2017; SAE Technical Paper 2014-01-2193. Available online: https://www.sae.org/publications/technical-papers/content/2014-01-2193/ (accessed on 29 March 2022).
- Glickstein, M.R.; Griethuysen, V.J.V.; Hodge, E.S. Integration of High Heat Sink Fuels in Aircraft Thermal Management Systems. In Proceedings of the ASME Turbo Expo 2003: Power for Land, Sea and Air, Atlanta, GA, USA, 16–19 June 2003; pp. 75–82. [Google Scholar]
- German, B.J. Tank heating model for aircraft fuel thermal systems with recirculation. J. Propul. Power 2012, 28, 204–210. [Google Scholar] [CrossRef]
- Alyanak, E.J.; Allison, D.L. Fuel thermal management system consideration in conceptual design sizing. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016. AIAA Paper 2016-0670. [Google Scholar]
- Doman, D.B. Fuel flow topology and control for extending aircraft thermal endurance. J. Thermophys. Heat Transf. 2018, 32, 35–50. [Google Scholar] [CrossRef]
- Doman, D.B. Fuel Flow Control for Extending Aircraft Thermal Endurance Part I: Underlying Principles. In Proceedings of the 2016 AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016. AIAA Paper 2016-1621. [Google Scholar]
- Huang, P.G.; Doman, D.B. Thermal Management of Single and Dual Tank Fuel-Flow Topologies Using an Optimal Control Strategy. J. Thermal Sci. Eng. Appl 2018, 10, 041019. [Google Scholar] [CrossRef]
- Pangborn, H.C.; Hey, J.E.; Deppen, T.O.; Alleyne, A.G.; Fisher, T.S. Hardware-in-the-Loop Validation of Advanced Fuel Thermal Management Control. J. Thermophys. Heat Transf. 2017, 32, 901–909. [Google Scholar] [CrossRef]
- Hong, G.; Wei, T.; Ding, X.F.; Duan, C.W. Multi-Objective Optimal Design of Electro-Hydrostatic Actuator Driving Motors for Low Temperature Rise and High Power Weight Ratio. Energies 2018, 11, 1173. [Google Scholar] [CrossRef] [Green Version]
- Boeing 737-600/700/800/900 Aircraft Maintenance Manual (SDS), Company, Chapter 29: Hydraulic Power, Seattle, Boeing Airplane Commercial, June 15 2016, 29-10-24.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).