Task-Level Energy Efficiency Evaluation Method Based on Aero-Engine Thrust-Specific Fuel Consumption with Application to Environment Control System
Abstract
:1. Introduction
2. Flight Profile and Engine Parameters
2.1. Flight Mission Profile
2.2. Thrust Profile
2.3. Engine Design Parameters
3. The Effect of Different Energy Extraction Methods on Engine Performance
3.1. Exergy Analysis Method
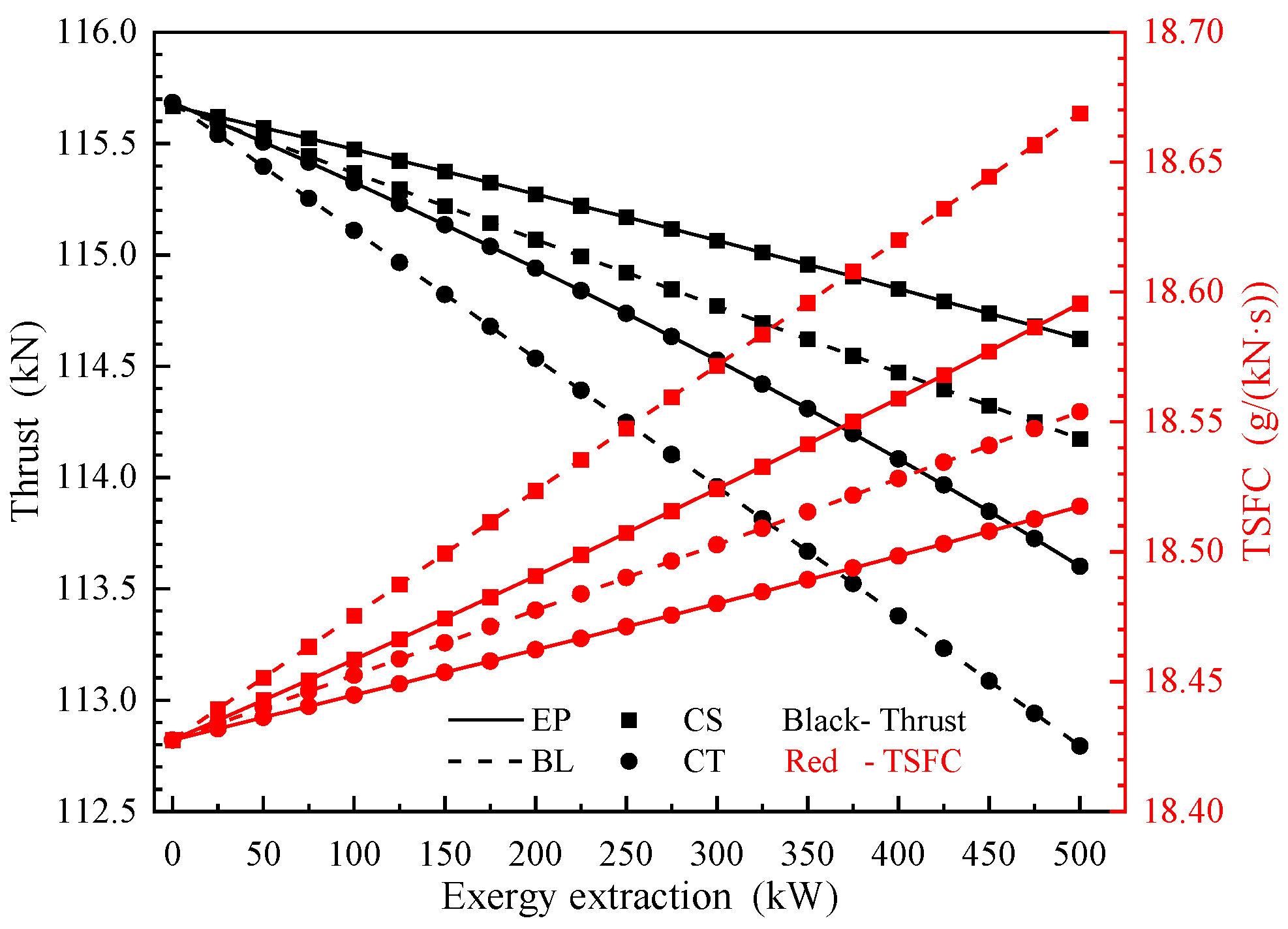
3.2. Performance Impact Analysis of Design Point
4. Construction of TSFC Surrogate Model
4.1. The First Step: Slope and Intercept Surrogate Model
4.2. The Second Step: TSFC First-Order Response Surface Model
4.3. The Two-Step TSFC Surrogate Model
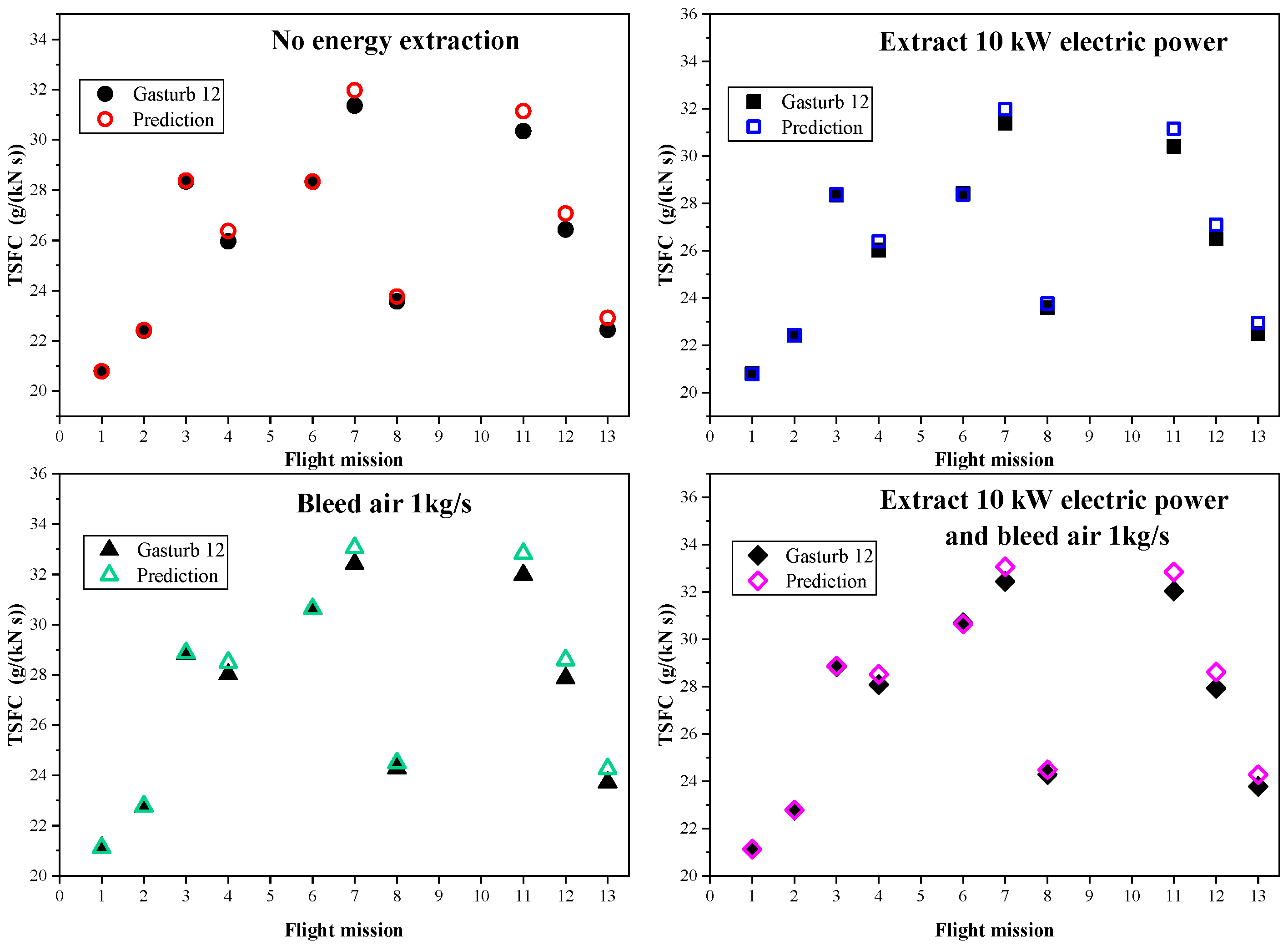
4.4. Validation of the TSFC Surrogate Model
5. Task-Level Energy Efficiency Evaluation of ECS
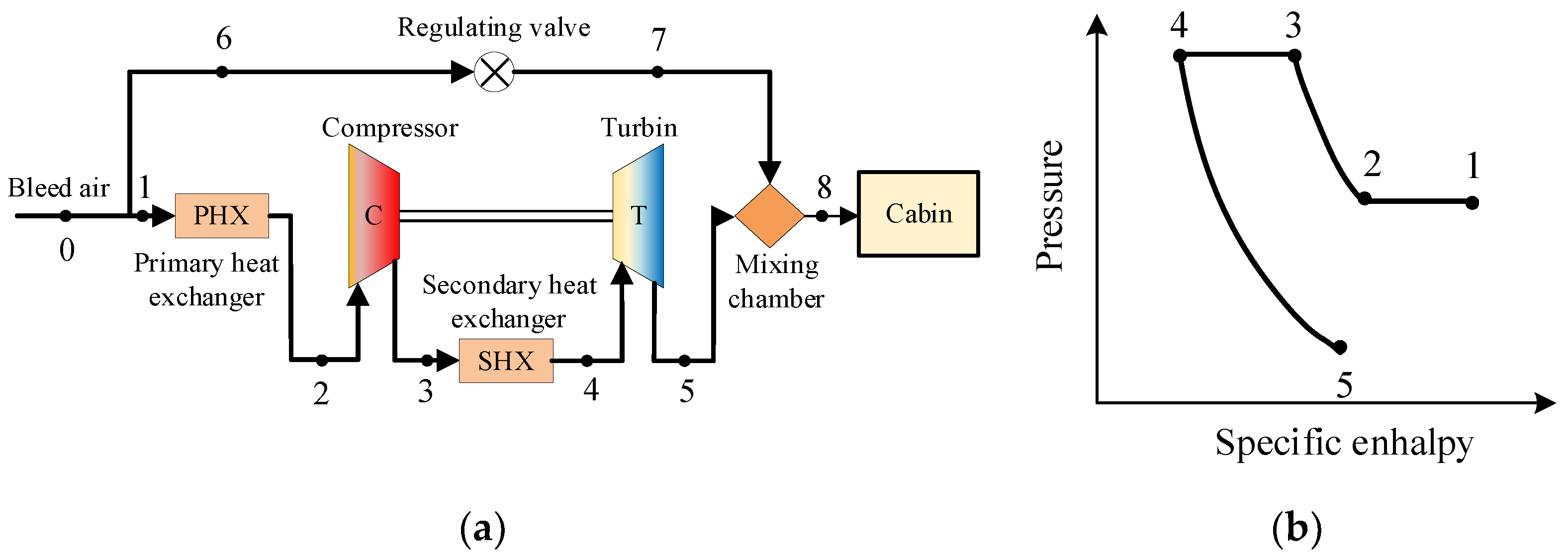
5.1. Air Cycle Refrigeration System of Aircraft
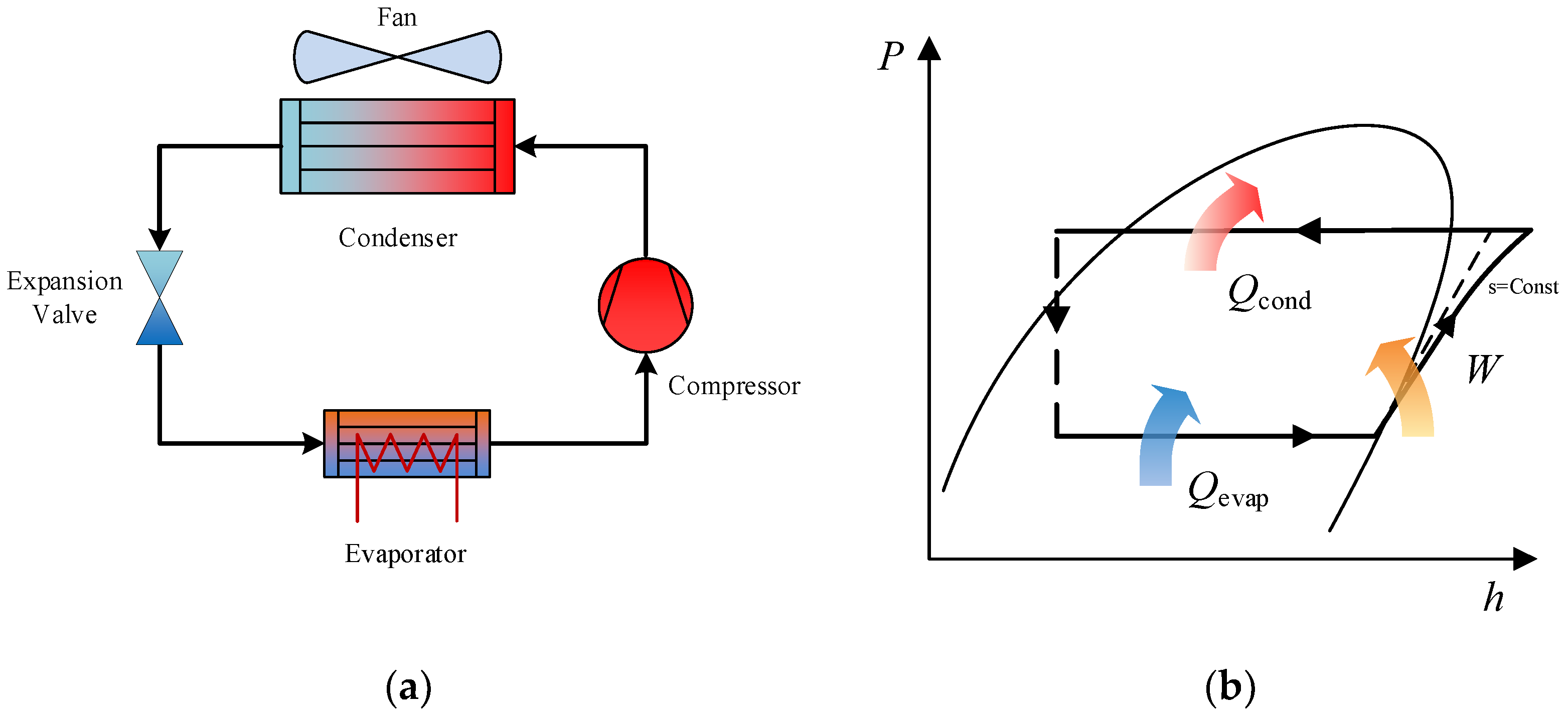
5.2. Vapor Cycle Refrigeration System of Aircraft
5.3. Bleed Air and Electric Power Extraction
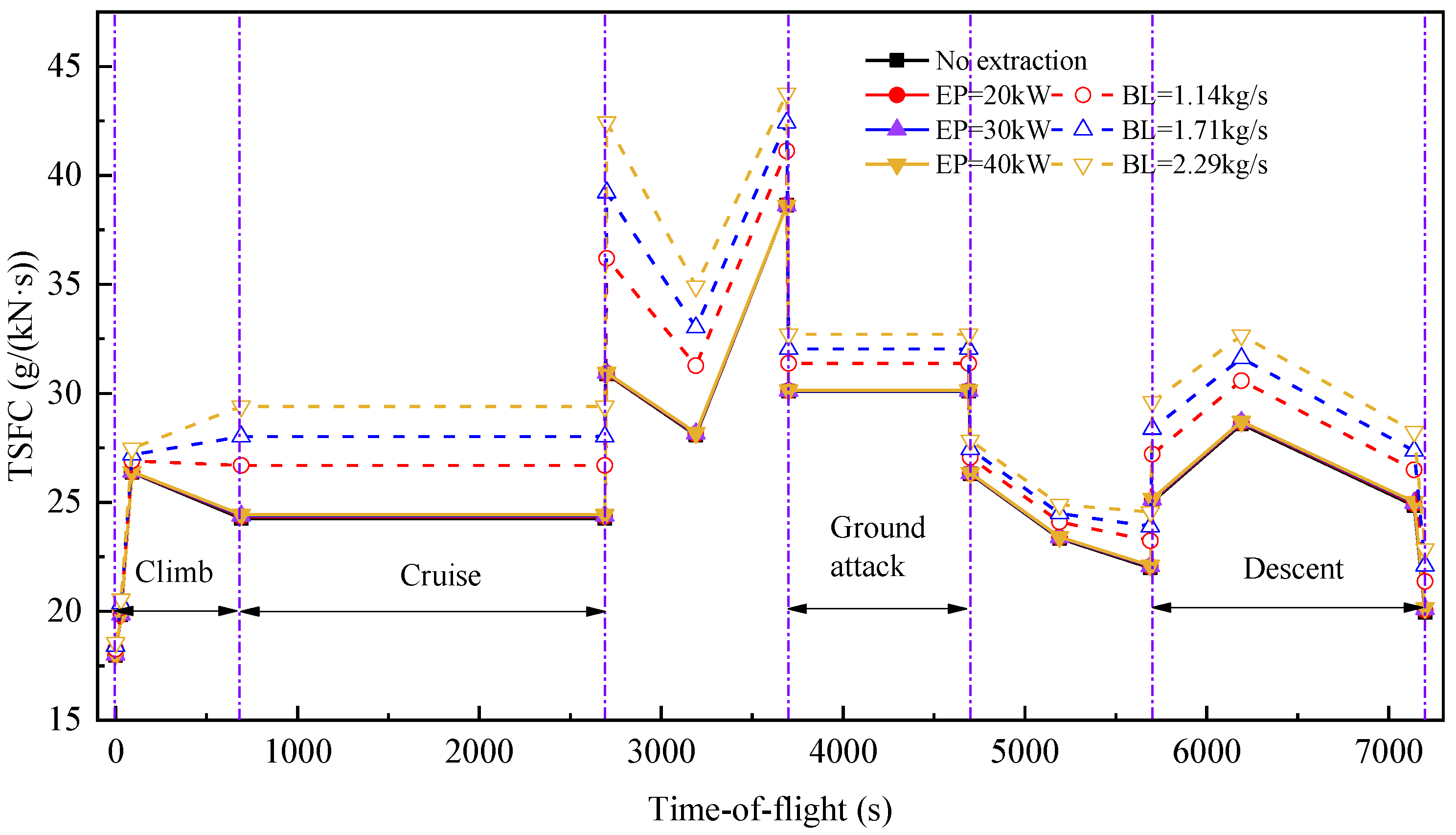
5.4. Results and Discussion
6. Conclusions
- (1)
- The error between the TSFC surrogate model and Gasturb12 is less than 5%, which means the accuracy of the TSFC surrogate model is sufficient to meet the needs of engineering.
- (2)
- According to the energy efficiency evaluation results of ECS, the vapor cycle has higher energy efficiency than the air cycle system when the cooling capacity is large. When the cooling capacity is small, the air cycle has certain advantages due to the low mass, reliable structure, and without the additional bleed air to fresh air and pressurization for the cabin.
- (3)
- The task-level energy efficiency evaluation method can provide a reference for the selection of the structure of the aircraft ECS and guide the cooling capacity distribution of coupled ECS with the air cycle and vapor cycle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Subscripts | ||
| 0 | = | no energy extraction |
| acs | = | air cycle system |
| amb | = | ambient air |
| bl | = | bleed air |
| c | = | cabin |
| e | = | end |
| ep | = | electric power extraction |
| i | = | the i-th working condition |
| s | = | start |
| Variable | ||
| CD | = | coefficient of drag (-) |
| CDmin | = | the zero-lift drag coefficient (-) |
| CL | = | coefficient of lift (-) |
| CLα | = | the derivative of the lift coefficient concerning the angle of attack (-) |
| CLα0 | = | CLα at the zero lift coefficient (-) |
| CLminD | = | the lift coefficient at CDmin (-) |
| COP | = | the refrigeration coefficient (take COP = 2.5) |
| cp | = | the specific heat capacity of air at constant pressure (J/(kg·K)) |
| Ex | = | the exergy value of bleed air (W) |
| FD | = | drag (kN) |
| FG | = | gravity (kN) |
| FL | = | lift (kN) |
| FN | = | the required thrust (kN) |
| H | = | altitude (m) |
| h | = | the specific enthalphy (J/(kg K)) |
| ∆h | = | the enthalpy difference between bleed air and ambient environment (J/kg) |
| k | = | the slopes of the linear relationship between TSFC and the amount of bleed air |
| kc | = | the induced drag coefficient (-) |
| M | = | fuel consumption (kg) |
| Mbase | fuel consumption without power extraction (kg) | |
| Ma | = | mach number (-) |
| p | = | pressure (Pa) |
| Q | = | the heat load of the electronic equipment (W) |
| qm | = | the mass flow rate of bleed air (kg/s) |
| Rg | = | the gas constant of air (J/(kg K)) |
| S | = | the wing area (m2) |
| s | = | the specific entropy (J/(kg K)) |
| ∆s | = | the entropy difference between bleed air and ambient environment (J/(kg K)) |
| T | = | temperature (take Tacs = −5 °C) |
| t | = | the mission time (s) |
| v | = | true air speed (km/s) |
| W | = | electric power extraction (kW) |
| ρ | = | the air density (kg/m3) |
| ε | = | thrust-specific fuel consumption (g/(kN s)) |
| η | = | the equivalent efficiency of aircraft power generation and transmission, which can be taken as 0.8 |
| Abbreviations | ||
| BL | = | bleed air |
| CS | = | constant engine speed |
| CT | = | constant turbine front temperature |
| ECS | = | environmental control system |
| EP | = | electric power extraction |
| TSFC | = | thrust-specific fuel consumption |
References
- Wheeler, P. Technology for the more and all electric aircraft of the future. In Proceedings of the 2016 IEEE International Conference on Automatica (ICA-ACCA), Curico, Chile, 19–21 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Robbins, D.; Bobalik, J.; De Stena, D.; Plag, K.; Rail, K.; Wall, K. F-35 Subsystems Design, Development, and Verification. In The F-35 Lightning II: From Concept to Cockpit; American Institute of Aeronautics and Astronautics, Incorporated: Reston, VA, USA, 2019; pp. 365–398. [Google Scholar] [CrossRef]
- Sarlioglu, B.; Morris, C.T. More Electric Aircraft: Review, Challenges, and Opportunities for Commercial Transport Aircraft. IEEE Trans. Transp. Electrif. 2015, 1, 54–64. [Google Scholar] [CrossRef]
- Fanxin, M.; Ruiqi, W.; Zanjun, G.; Wenyuan, Z.; Wenchao, H. Research of key technology for the more electrical aircraft electric environmental control system. Aeronaut. Sci. Technol. 2018, 29, 1–8. [Google Scholar] [CrossRef]
- Wang, J.; Yunze, L.; Liu, X.; Shen, C.; Zhang, H.; Xiong, K. Recent active thermal management technologies for the development of energy-optimized aerospace vehicles in China. Chin. J. Aeronaut. Engl. Ed. 2020, 34, 1–27. [Google Scholar] [CrossRef]
- Price, D.C. A review of selected thermal management solutions for military electronic systems. IEEE Trans. Compon. Packag. Technol. 2003, 26, 26–39. [Google Scholar] [CrossRef]
- Tu, M.; Yuan, G.; Xue, F.; Wang, X. Application of integrated thermal management in development of advanced fighter system. Acta Aeronaut. Astronaut. Sin. 2020, 41, 136–146. [Google Scholar] [CrossRef]
- Lents, C.E. Impact of Weight, Drag and Power Demand on Aircraft Energy Consumption. In AIAA Propulsion and Energy 2021 Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2021. [Google Scholar] [CrossRef]
- Zang, X.; Liu, Y.; Xu, X. Performance Simulation and Improvement of New Type Aircraft Environment Control System Base on AMESim software. Aircr. Des. 2018, 38, 56–60. [Google Scholar] [CrossRef]
- Li, X.; Chen, Q.; Hao, J.-H.; Chen, X.; He, K.-L. Heat current method for analysis and optimization of a refrigeration system for aircraft environmental control system. Int. J. Refrig. 2019, 106, 163–180. [Google Scholar] [CrossRef]
- He, H.; Hao, J. Optimum design for environmental control system of aircraft cabin. J. Beijing Univ. Aeronaut. Astronaut. 1996, 22, 563–569. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, X.; Chao, W.; Yang, C. Experimental and theoretical study on a novel energy-saving ECS for commercial airliners. Appl. Therm. Eng. 2017, 127, 1372–1381. [Google Scholar]
- Shou, R.; He, H. Aircraft Environmental Control; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2003. [Google Scholar]
- Rosales, M.A. A Preliminary Study for Selecting and Optimizing the Environmental Control System; Technical University of Madrid: Madrid, Spain, 2018. [Google Scholar]
- Jingyang, Z.; Fengying, Z.; Yeping, X. Impact Analysis of Integrated Control of Shaft Power Extraction and Air Intake on Fuel Economy of Aeroengine. Aeroengine 2019, 45, 9–14. [Google Scholar] [CrossRef]
- Slingerland, R.; Zandstra, S. Bleed Air versus Electric Power Off-takes from a Turbofan Gas Turbine over the Flight Cycle. In Proceedings of the 7th AIAA ATIO Conference, 2nd CEIAT Int’l Conf on Innov and Integr in Aero Sciences, 17th LTA Systems Tech Conference, Followed by 2nd TEOS Forum, Belfast, Northern Ireland, 18–20 September 2007; American Institute of Aeronautics and Astronautics: Belfast, Northern Ireland, 2007. [Google Scholar] [CrossRef]
- Roberts, R.A.; Eastbourn, S.M. Modeling techniques for a computational efficient dynamic turbofan engine model. Int. J. Aerosp. Eng. 2015, 2014, 283479. [Google Scholar] [CrossRef]
- Roberts, R.; Eastbourn, S. Vehicle level tip-to-tail modeling of an aircraft. Int. J. Thermodyn. 2014, 17, 107–115. [Google Scholar] [CrossRef]
- O’Connell, T.C.; Lui, C.; Walia, P.; Tschantz, J. A hybrid economy bleed, electric drive adaptive power and thermal management system for more electric aircraft. SAE Int. J. Aerosp. 2010, 3, 168–172. [Google Scholar] [CrossRef]
- Aghaei Tog, R.; Mesgarpoor Tousi, A. An empirical model for partially admitted turbine efficiency. Aircr. Eng. Aerosp. Technol. 2015, 87, 238–248. [Google Scholar] [CrossRef]
- Yu, B.; Miao, R.C.; Shu, W.J. A Rapid Method for Modeling a Variable Cycle Engine. Jove J. Vis. Exp. 2019, 150, e59151. [Google Scholar] [CrossRef] [PubMed]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. An efficient component map generation method for prediction of gas turbine performance. In ASME Turbo Expo 2014: Turbine Technical Conference and Exposition; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Kurzke, J. About simplifications in gas turbine performance calculations. In ASME Turbo Expo 2007: Power for Land, Sea, and Air; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2007; pp. 493–501. [Google Scholar] [CrossRef]
- Mack, Y.; Goel, T.; Shyy, W.; Haftka, R. Surrogate model-based optimization framework: A case study in aerospace design. In Evolutionary Computation in Dynamic and Uncertain Environments; Springer: Berlin/Heidelberg, Germany, 2007; pp. 323–342. [Google Scholar]
- Liu, W.; Sivaramakrishnan, R.; Davis, M.J.; Som, S.; Longman, D.; Lu, T. Development of a reduced biodiesel surrogate model for compression ignition engine modeling. Proc. Combust. Inst. 2013, 34, 401–409. [Google Scholar] [CrossRef]
- Drężek, P.S.; Kubacki, S.; Żółtak, J. Multi-objective surrogate model-based optimization of a small aircraft engine air-intake duct. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022. [Google Scholar] [CrossRef]
- Zhou, L.; Qiu, L. A New Method to Deal with Engine Test Data and to Build Agent Model of Engine. Helicopter Technol. 2019, 4, 32–35. [Google Scholar]
- Sha, Z. Aircraft Design Manual. Volume 4, General Design of Military Aircraft; Aviation Industry Press: Beijing, China, 2005. [Google Scholar]
- Riccardo, L. Lockheed Martin F/A-22 Raptor; Istituto Tecnico Industriale: Andria, Italy, 2012. [Google Scholar]
- Kurzke, J. GasTurb 12-Design and Off-Design Performance of Gas Turbines-Manual; GasTurb GmbH: Aachen, Germany, 2014. [Google Scholar]
- Chen, J. Development trend of military aero engine. Aeronaut. Sci. Technol. 1994, 5, 9–12. [Google Scholar]
- Jorgensen, S.E.; Svirezhev, Y.M. Towards a Thermodynamic Theory for Ecological Systems; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Gooch, J.W. Standard Atmosphere; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Müller, C.; Scholz, D. The Vapor Compression Cycle in Aircraft Air-Conditioning Systems; Aircraft Design and Systems Group (AERO), Department of Automotive and Aeronautical Engineering, Hamburg University of Applied Sciences: Berlin, Germany, 2017; p. 23. [Google Scholar]
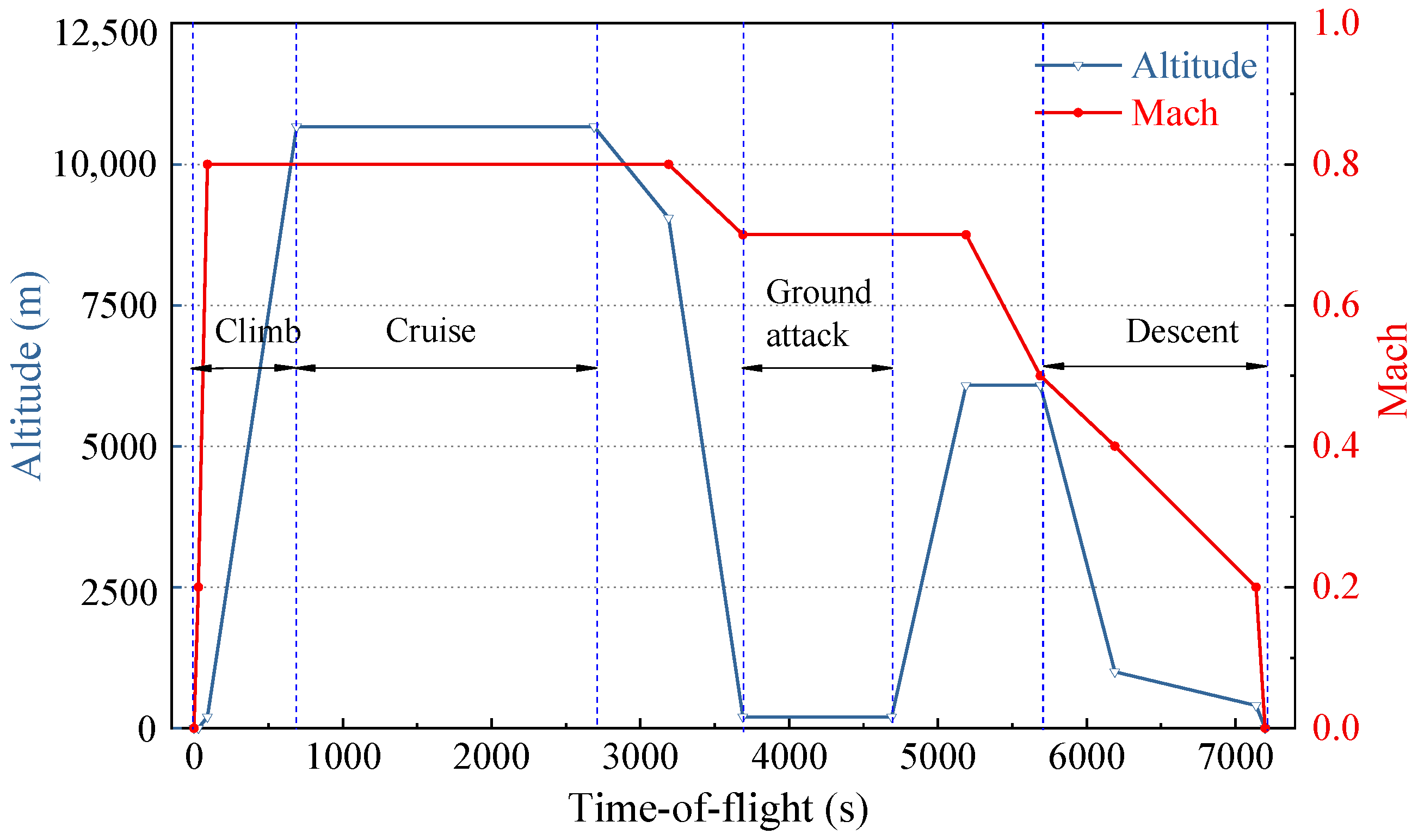
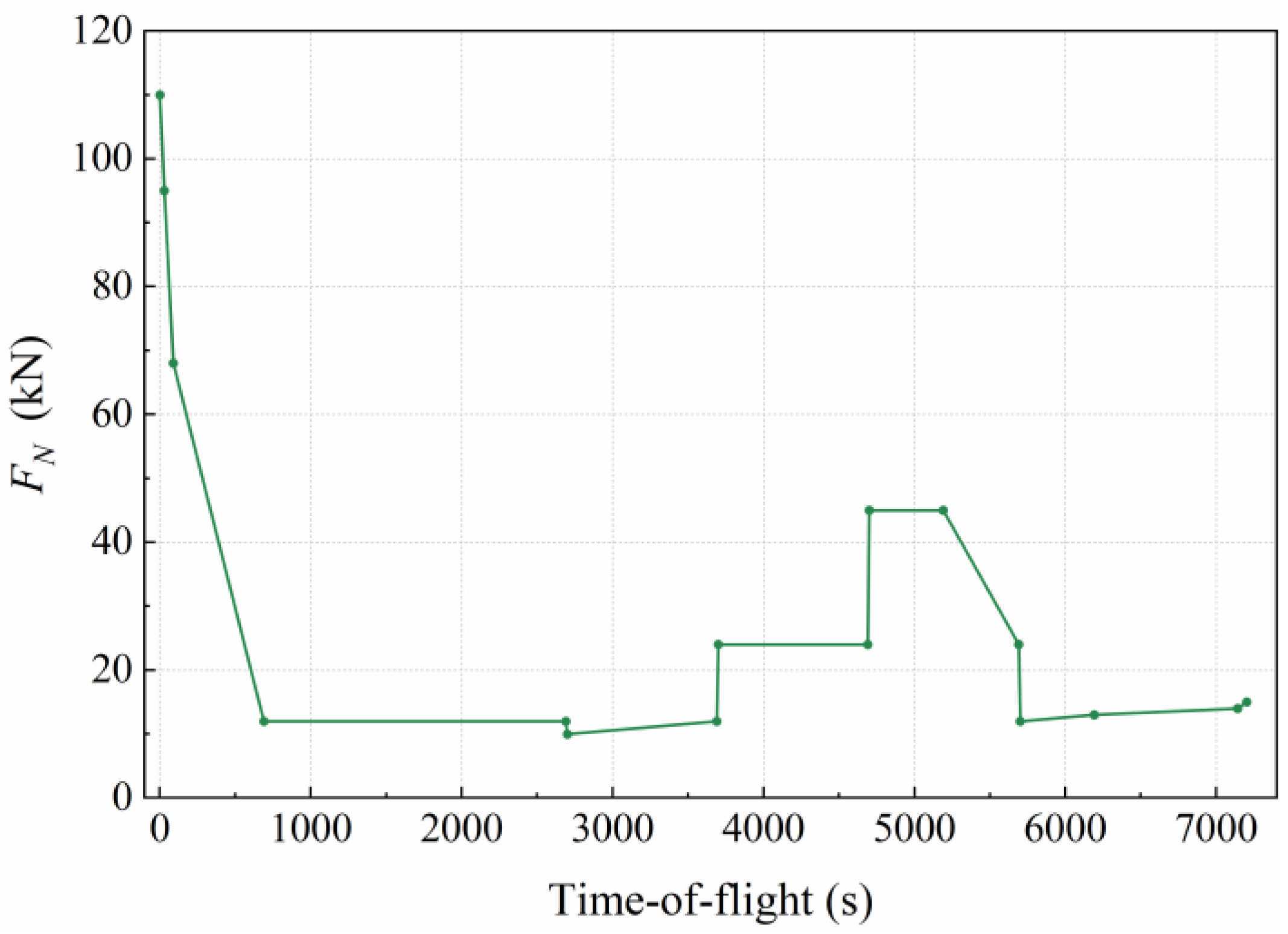
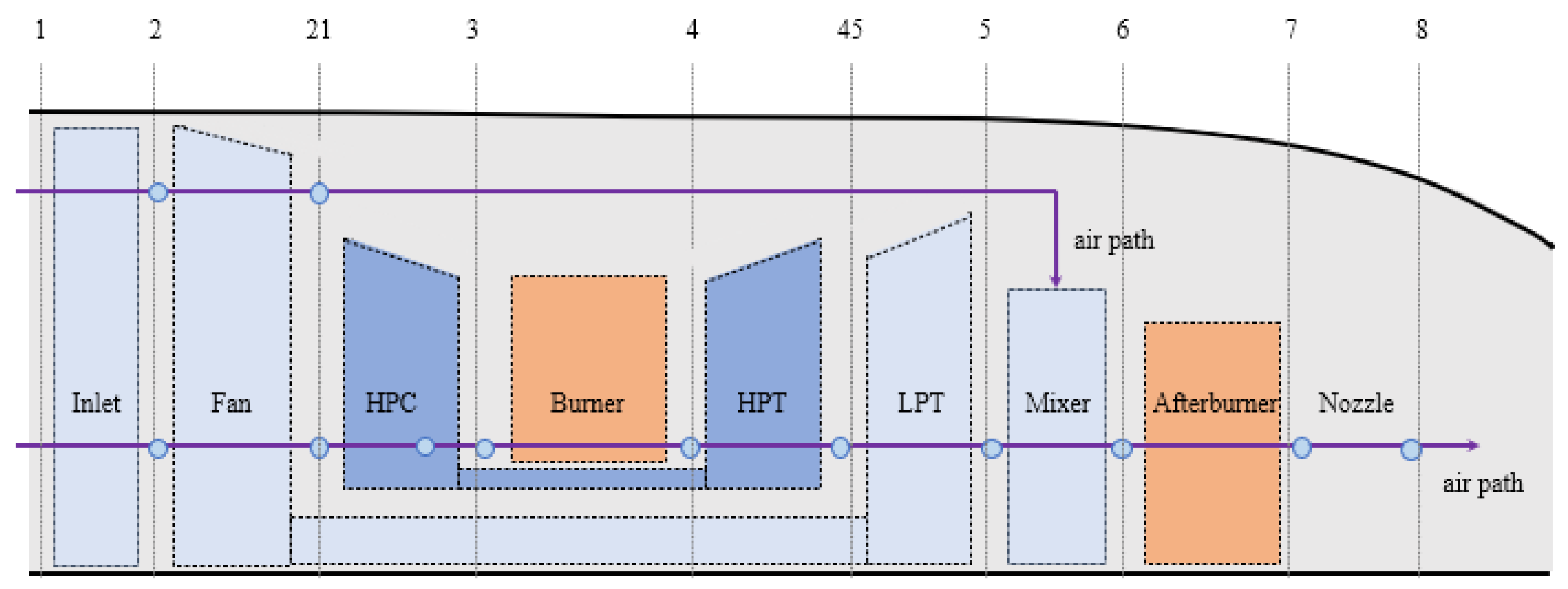
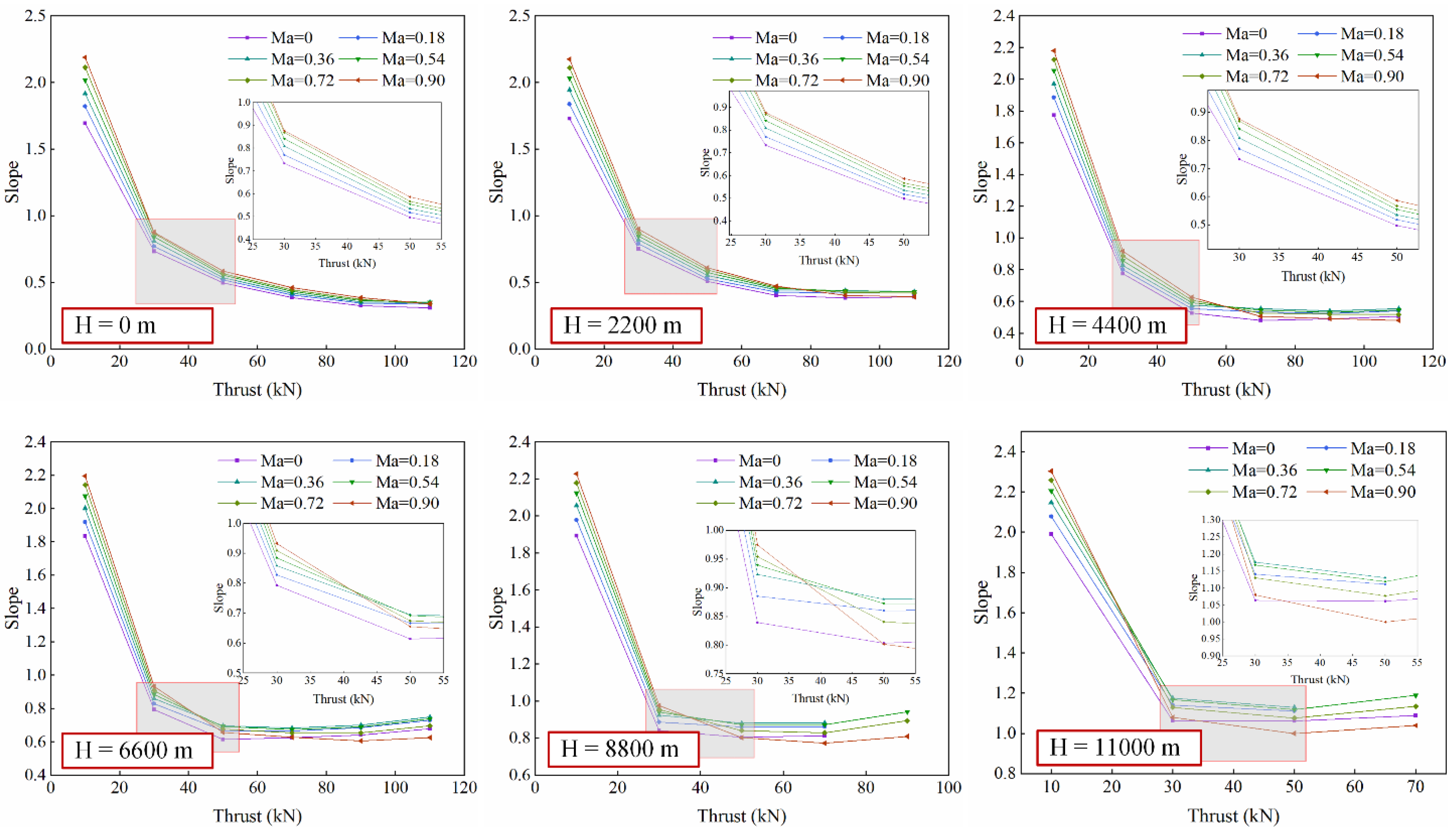
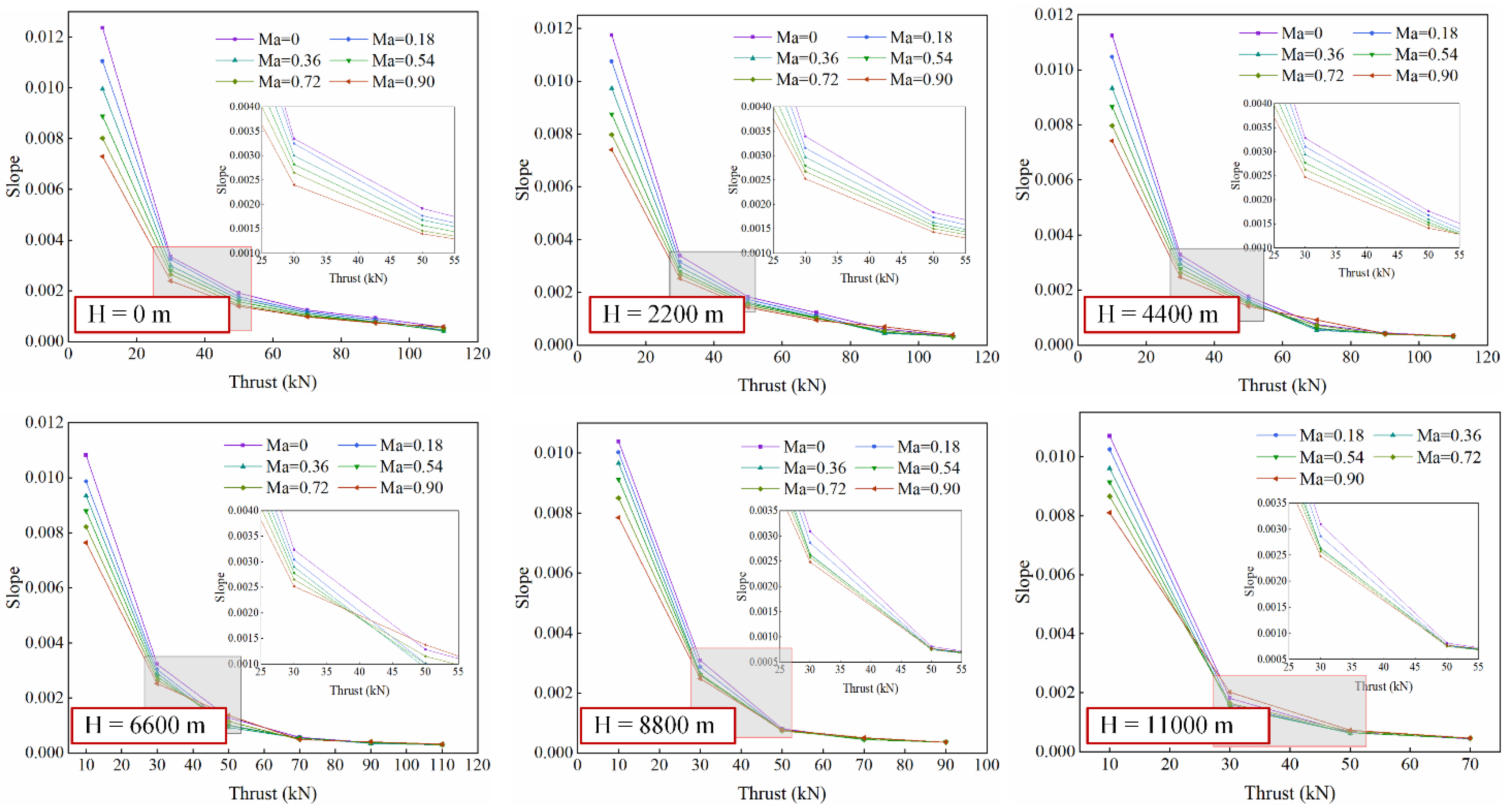
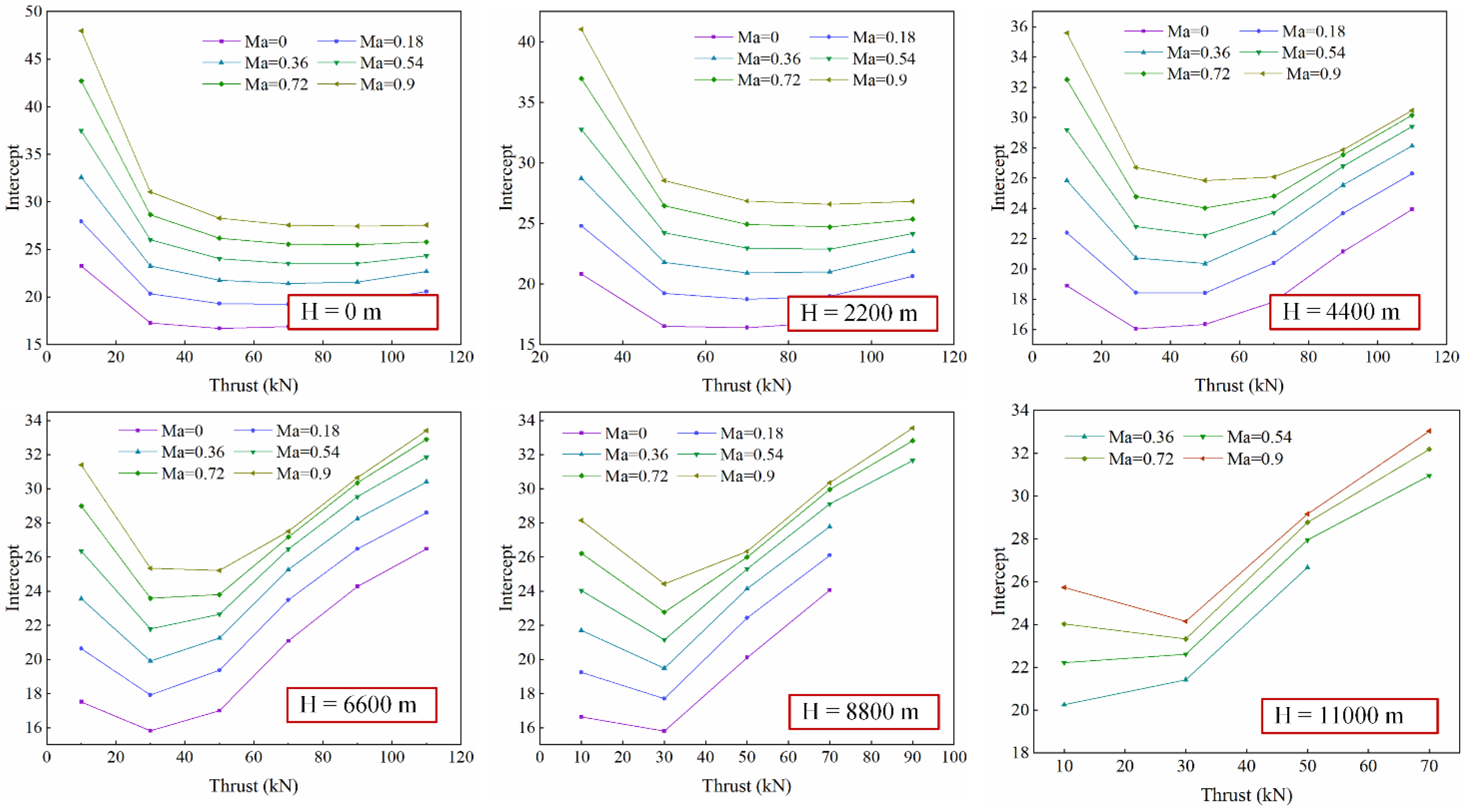
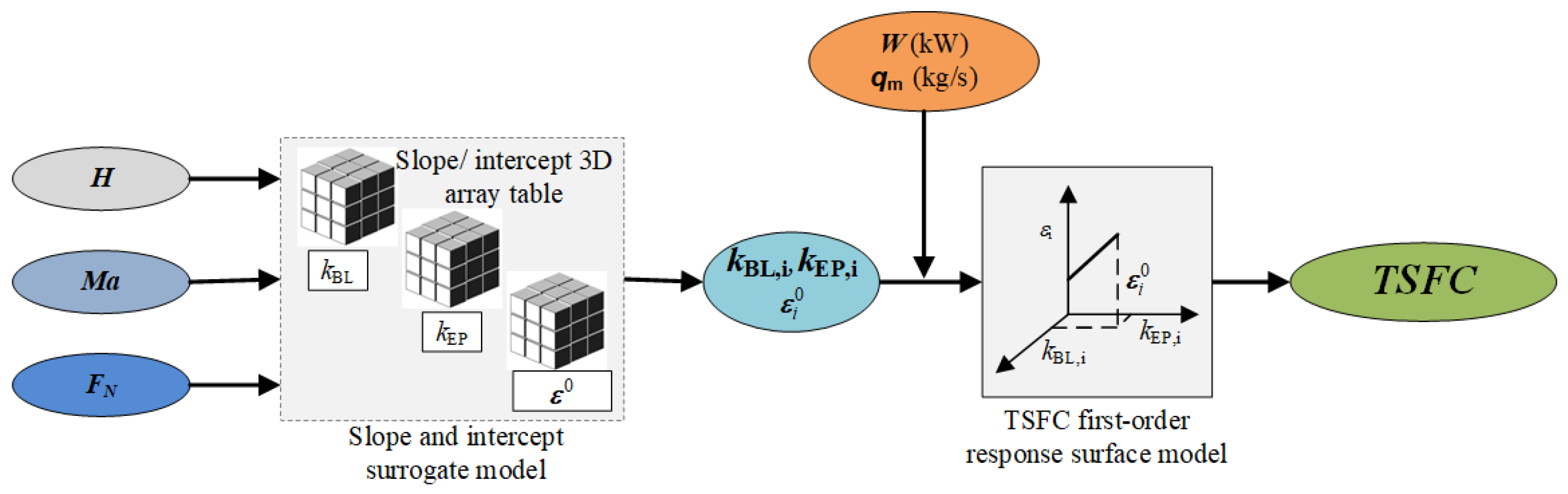
| NO. | t(s) | Altitude(m) | Mach | NO. | t(s) | Altitude(m) | Mach |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 8 | 4690 | 200 | 0.7 |
| 2 | 30 | 0 | 0.2 | 9 | 5190 | 6080 | 0.7 |
| 3 | 90 | 200 | 0.8 | 10 | 5690 | 6080 | 0.5 |
| 4 | 690 | 10,668 | 0.8 | 11 | 6190 | 1000 | 0.4 |
| 5 | 2690 | 10,668 | 0.8 | 12 | 7140 | 400 | 0.2 |
| 6 | 3190 | 9049 | 0.8 | 13 | 7200 | 0 | 0 |
| 7 | 3690 | 200 | 0.7 |
| (a) Design point parameters | ||||||
| Variable | Unit | Value | Variable | Unit | Value | |
| Intake Pressure Ratio | −0.99 | Turb. Interd. Ref. Press. Ratio | 0.98 | |||
| No (0) or Average (1) Core dP/P | 1 | Design Bypass Ratio | 0.3 | |||
| Inner Fan Pressure Ratio | 2.5 | Burner Exit Temperature | K | 1600 | ||
| Booster Map Type (0/1/2) | 0 | Burner Design Efficiency | 1 | |||
| Fan Pressure Ratio | 10 | Burner Partload Constant | 1.6 | |||
| Compr. Interduct Press. Ratio | 0.99 | Overboard Bleed | kg/s | 0 | ||
| Bypass Duct Pressure Ratio | 0.97 | Power Offtake | kW | 0 | ||
| Fuel Heating Value | MJ/kg | 43.124 | Thrust | kN | 116 | |
| (b) The result of parameter matching | ||||||
| Station | Mass Flow (kg/s) | Total Temperature (K) | Total Pressure (kPa) | Corrected Flow | ||
| amb | - | 288.15 | 101.36 | - | ||
| 1 | - | 288.15 | 101.36 | - | ||
| 2 | 156.95 | 288.15 | 100.31 | 158.54 | ||
| 21 | 120.74 | 398.36 | 250.79 | 57.36 | ||
| 3 | 117.11 | 805.65 | 2482.78 | 7.99 | ||
| 4 | 106.91 | 1600.00 | 2408.30 | 10.60 | ||
| 45 | 118.99 | 1178.25 | 643.63 | 37.88 | ||
| 5 | 122.61 | 1042.46 | 383.88 | 61.56 | ||
| 6 | 122.61 | 1042.46 | 376.20 | |||
| 8 | 158.82 | 908.39 | 323.31 | 88.38 | ||
| FN = 116 kN TSFC = 18.46 g/(kN s) | ||||||
| Factors | Sample Level |
|---|---|
| H (m) | 0, 2200, 4400, 6600, 8800, 11,000 |
| Ma | 0, 0.18, 0.36, 0.54, 0.72, 0.90 |
| FN (kN) | 10, 30, 50, 70, 90, 110 |
| qm (kg/s) | 0, 0.3, 0.6, 0.9, 1.2, 1.5, 1.8, 2.1, 2.4, 2.7, 3 |
| W (kW) | 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 |
| Refrigerating Capacity | Air Cycle Bleed Air | Vapor Cycle Electric Power |
|---|---|---|
| kW | kg/s | kW |
| 40 | 1.14 | 20 |
| 60 | 1.71 | 30 |
| 80 | 2.29 | 40 |
| Electric Power Extraction | Bleed Air | |||||
|---|---|---|---|---|---|---|
| Q | W | M | qm | M | ||
| kW | kW | kg | kg/s | kg | ||
| Base | / | 3837.63 kg | / | Base | 3837.63 kg | / |
| 40 | 20 kW | 3844.47 kg | 0.18% | 1.14 kg/s | 4060.33 kg | 5.80% |
| 60 | 30 kW | 3847.89 kg | 0.27% | 1.71 kg/s | 4178.51 kg | 8.88% |
| 80 | 40 kW | 3851.33 kg | 0.36% | 2.29 kg/s | 4301.80 kg | 12.10% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Dong, S.; Jiang, H.; Zhou, Y.; Liu, Y.; Wu, J. Task-Level Energy Efficiency Evaluation Method Based on Aero-Engine Thrust-Specific Fuel Consumption with Application to Environment Control System. Machines 2022, 10, 643. https://doi.org/10.3390/machines10080643
Liu H, Dong S, Jiang H, Zhou Y, Liu Y, Wu J. Task-Level Energy Efficiency Evaluation Method Based on Aero-Engine Thrust-Specific Fuel Consumption with Application to Environment Control System. Machines. 2022; 10(8):643. https://doi.org/10.3390/machines10080643
Chicago/Turabian StyleLiu, Haodong, Sujun Dong, Hongsheng Jiang, Yuanye Zhou, Yongji Liu, and Jianjun Wu. 2022. "Task-Level Energy Efficiency Evaluation Method Based on Aero-Engine Thrust-Specific Fuel Consumption with Application to Environment Control System" Machines 10, no. 8: 643. https://doi.org/10.3390/machines10080643
APA StyleLiu, H., Dong, S., Jiang, H., Zhou, Y., Liu, Y., & Wu, J. (2022). Task-Level Energy Efficiency Evaluation Method Based on Aero-Engine Thrust-Specific Fuel Consumption with Application to Environment Control System. Machines, 10(8), 643. https://doi.org/10.3390/machines10080643






