Experimental Study on Support Vector Machine-Based Early Detection for Sensor Faults and Operator-Based Robust Fault Tolerant Control
Abstract
:1. Introduction
2. Mathematical Preliminaries
2.1. Operator Theory
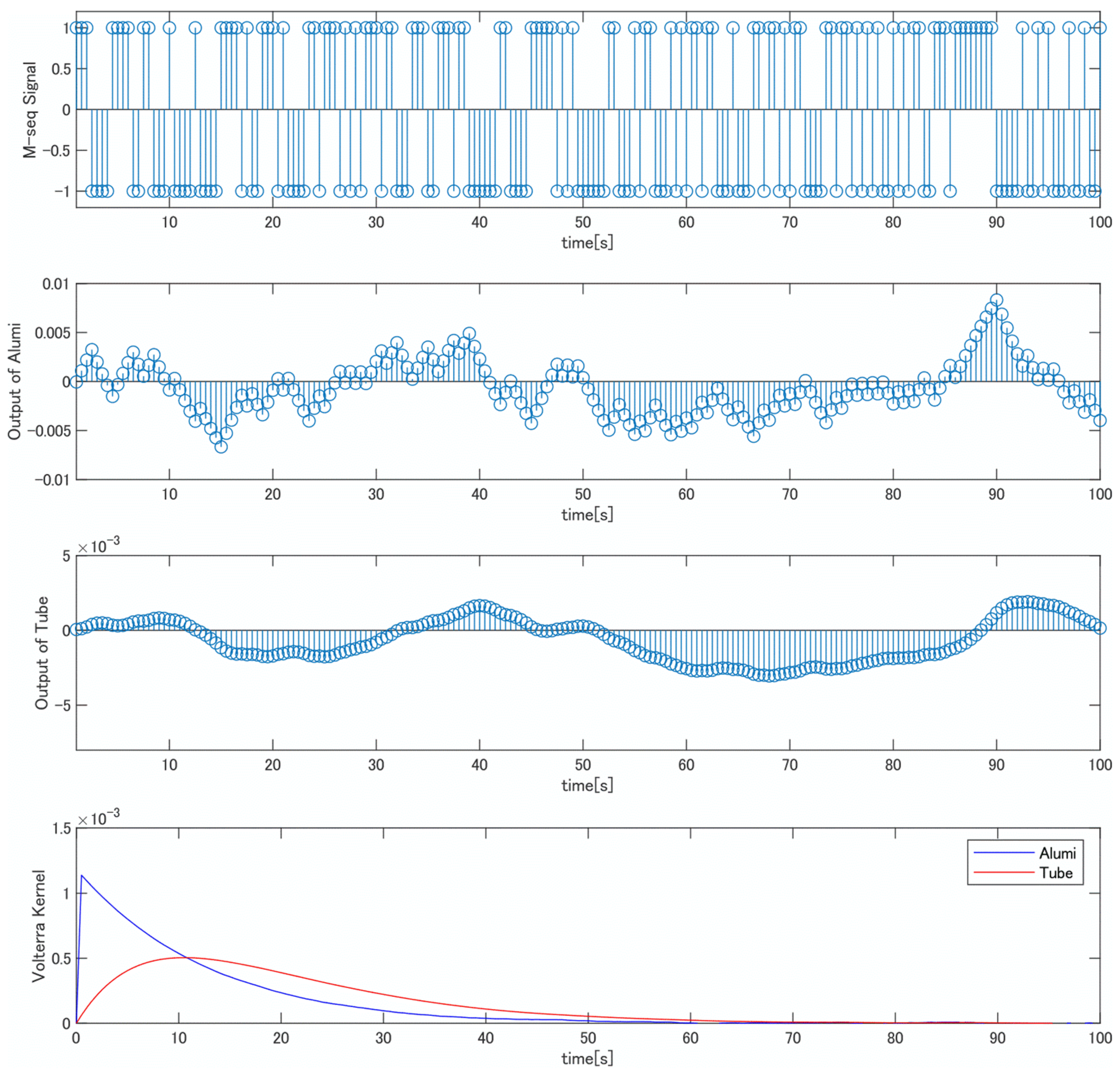
2.2. Volterra Identification
2.3. Support Vector Machine
3. Modeling of Microreactor System
3.1. Physical Model Based on Laws of Heat Transfer
3.1.1. Modeling of Peltier Device
3.1.2. Modeling of Aluminum Plate
3.1.3. Modeling of Tube
3.2. The Estimated Model by Volterra Identification
4. Control System Design
4.1. Operator-Based Robust Nonlinear Control
4.2. SVM-Based Early Fault Detection
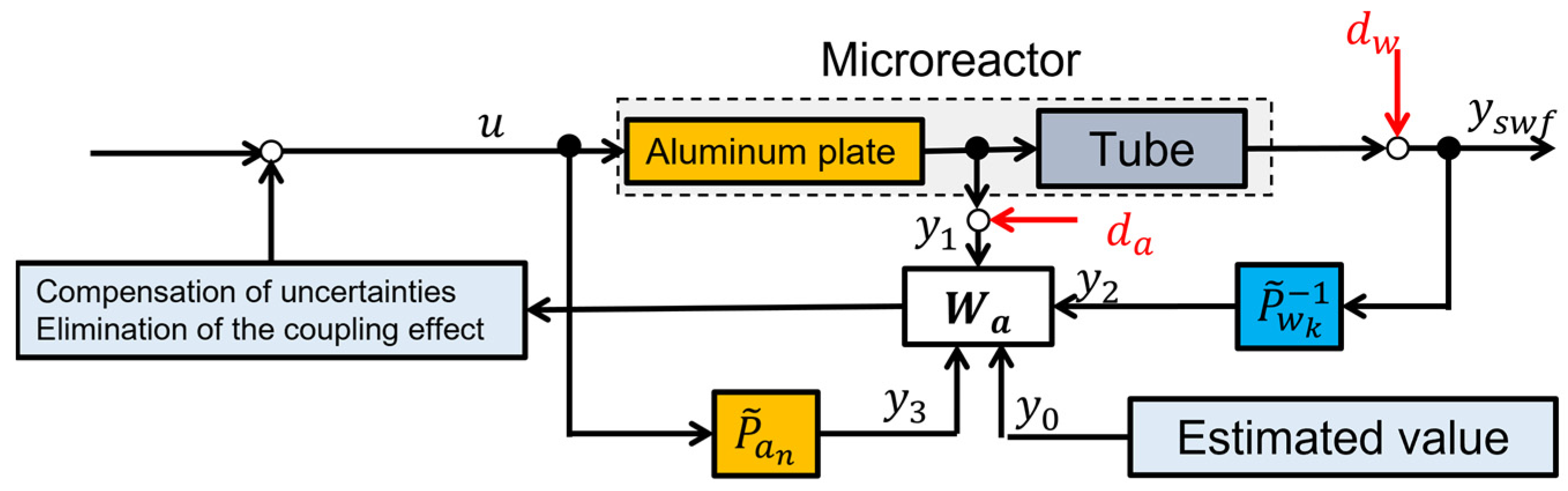
4.3. Fault Tolerant Control System
5. Simulation and Experimental Tests
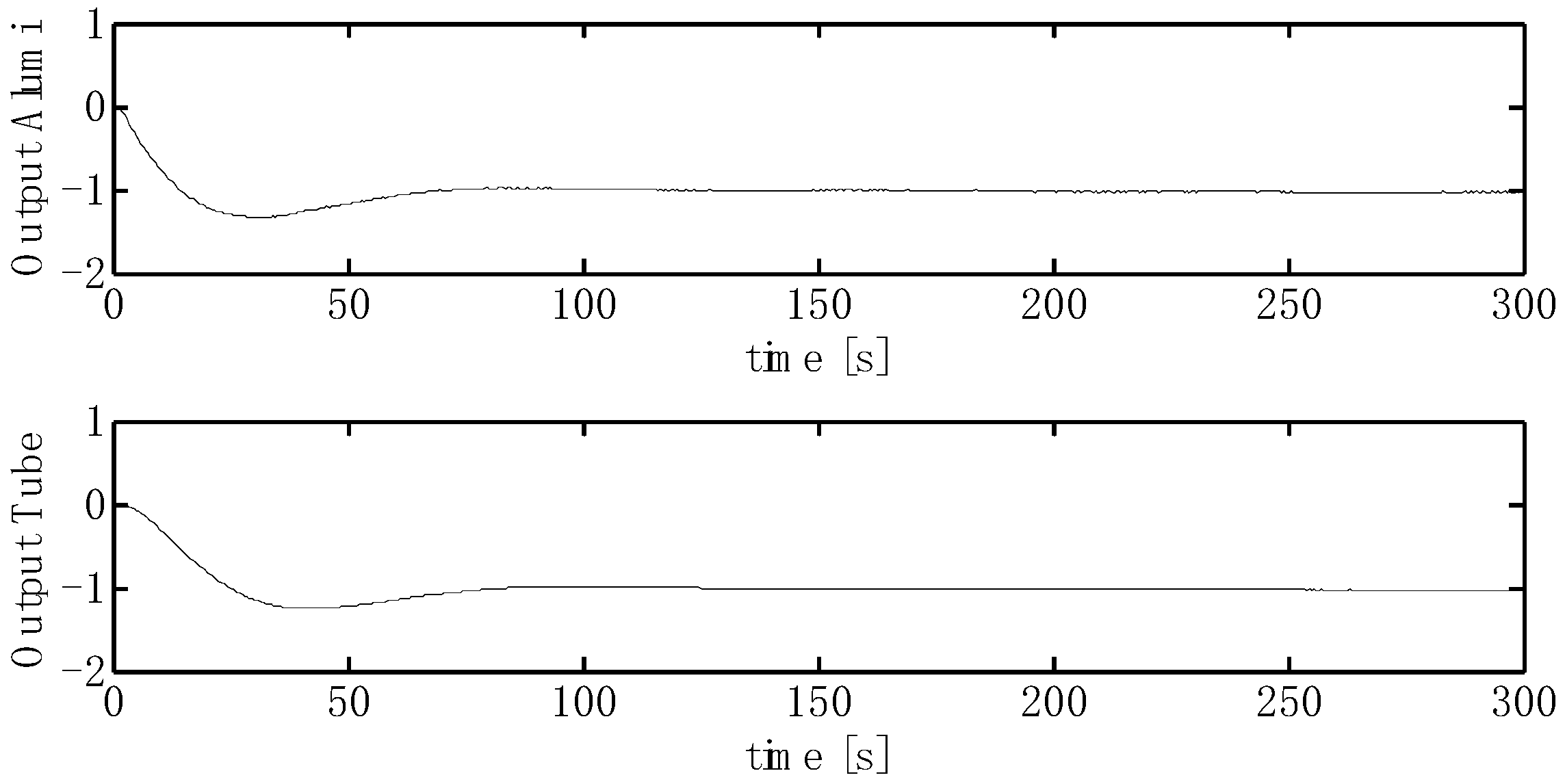
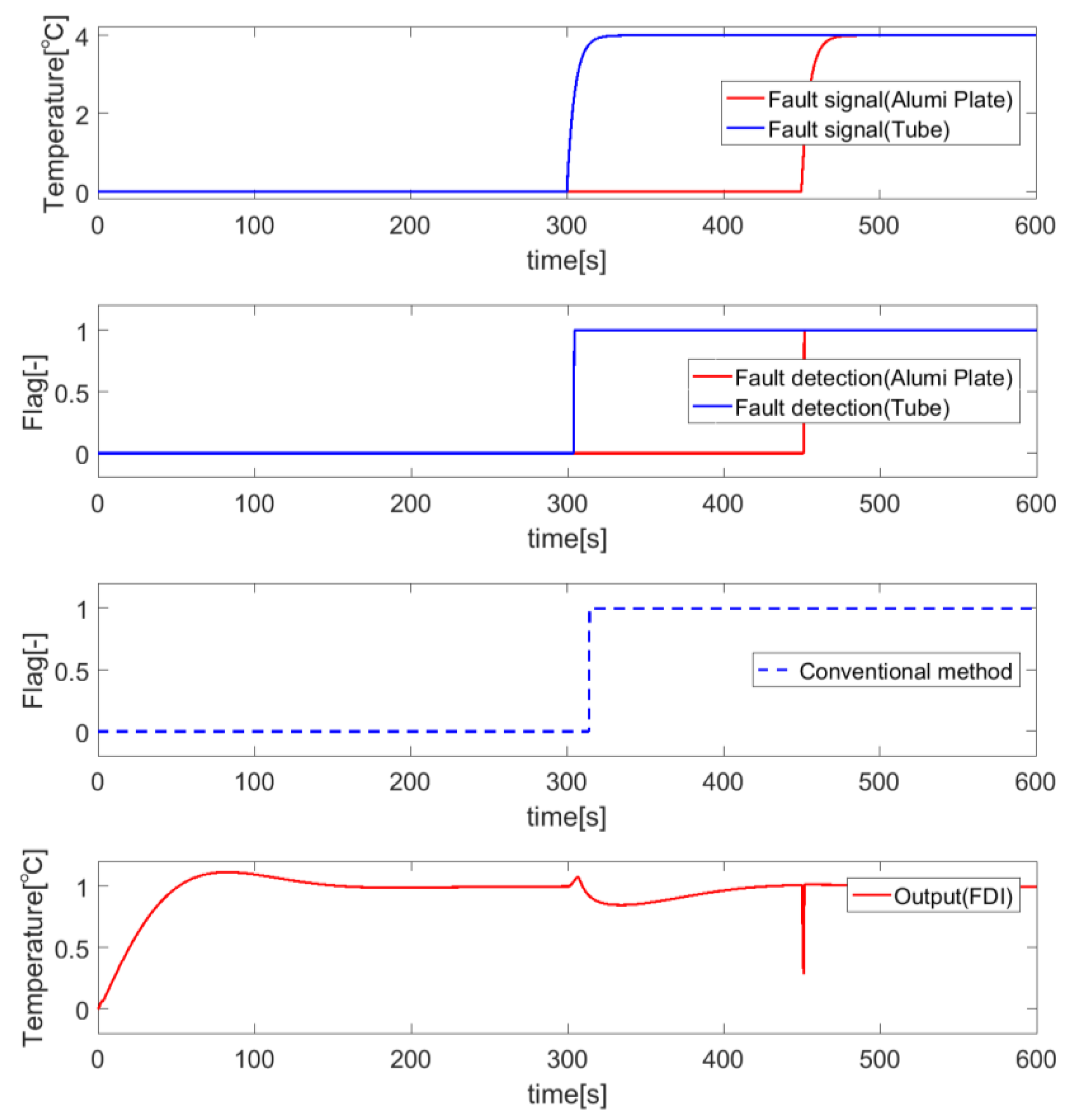
5.1. Simulation Results
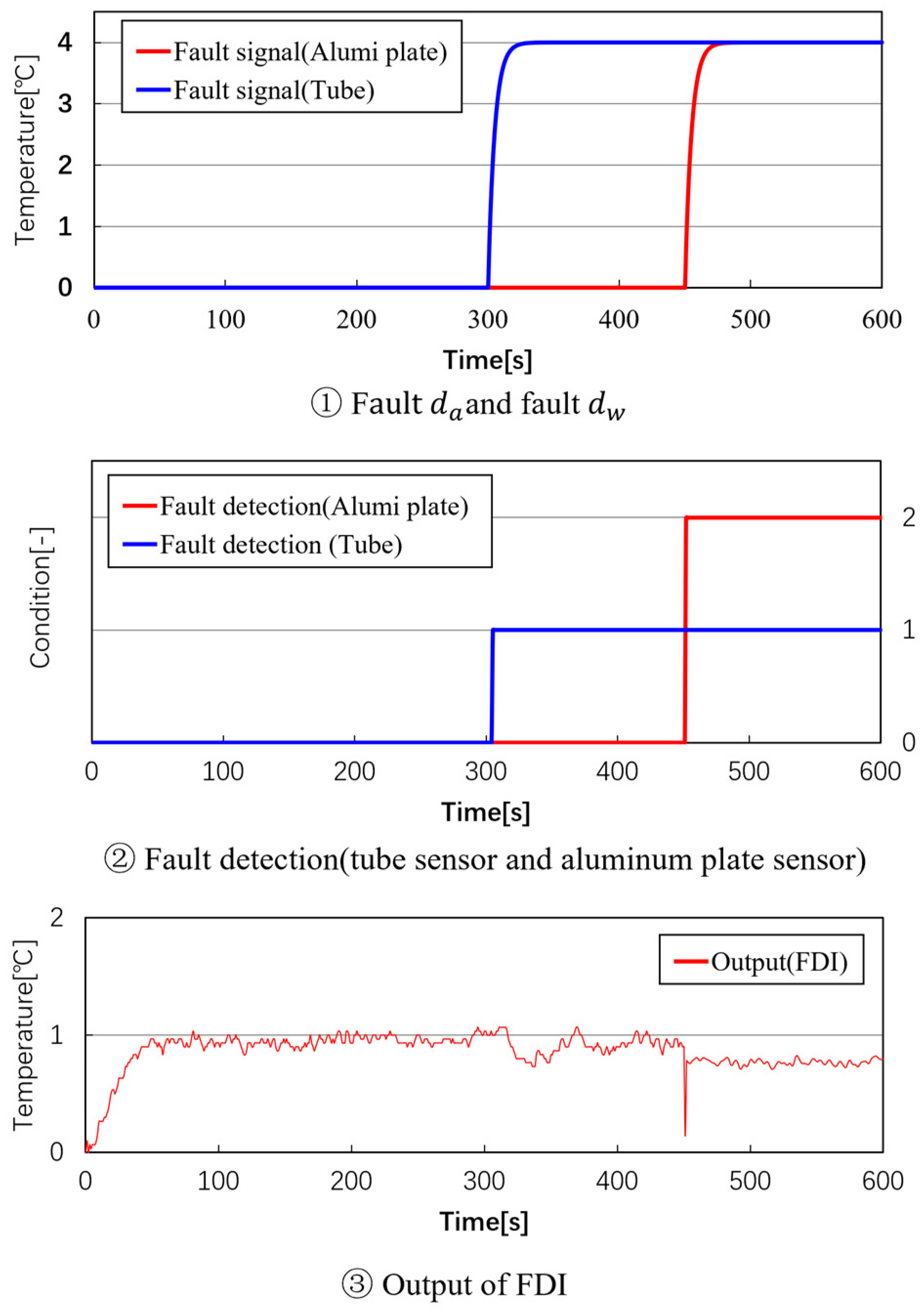
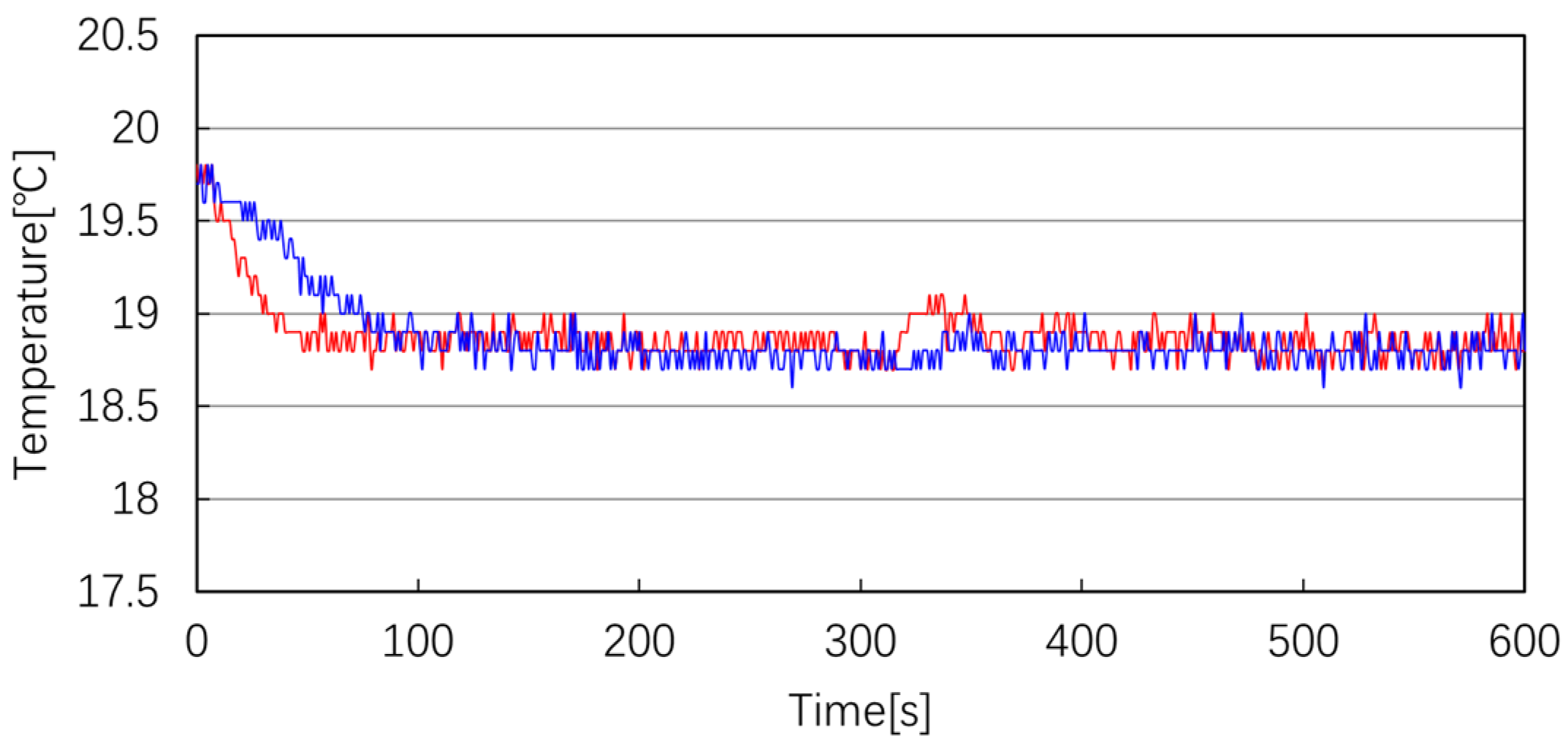
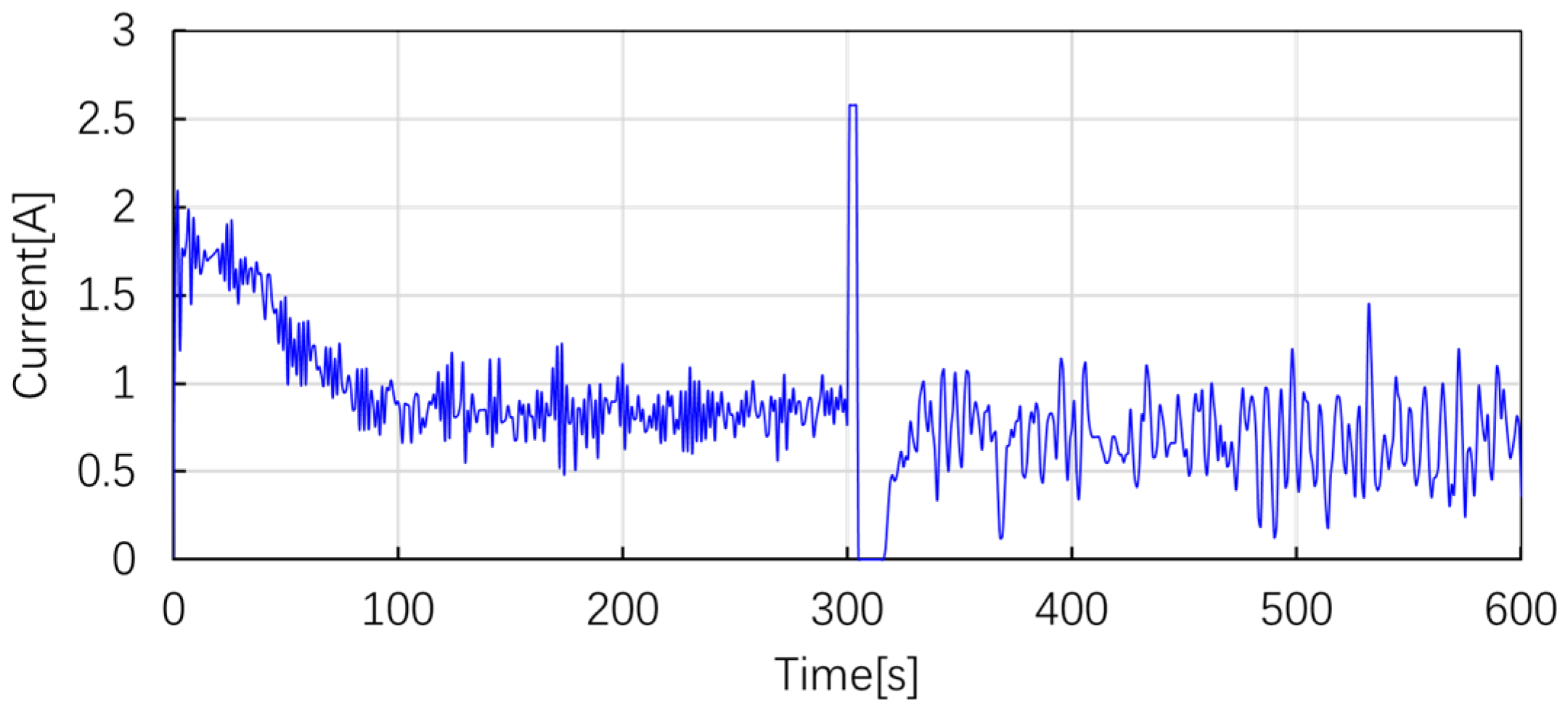
5.2. Experimental Tests
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, M.; Saijo, N.; Gomi, H.; Inoue, A. A robust real time method for estimating human multijoint arm viscoelasticity. Int. J. Innov. Comput. Inf. Control 2006, 2, 705–721. [Google Scholar]
- Deng, M.; Inoue, A.; Zhu, Q. An integrated study procedure on real time estimation of time varying multijoint human arm viscoelasticity. Trans. Inst. Meas. Control 2011, 33, 919–941. [Google Scholar] [CrossRef]
- Deng, M.; Iwai, Z.; Mizumoto, I. Robust Parallel Compensator Design for Output Feedback Stabilization of Plants with Structured Uncertainty. Syst. Control Lett. 1999, 36, 193–198. [Google Scholar] [CrossRef]
- Bi, S.; Deng, M.; Xiao, Y. Robust Stability and Tracking for Operator-Based Nonlinear Uncertain Systems. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1059–1066. [Google Scholar] [CrossRef]
- Deng, M.; Wen, S.; Inoue, A. Operator-based robust nonlinear control for a Peltier actuated process, Measurement and Control. J. Inst. Meas. Control 2011, 44, 116–120. [Google Scholar] [CrossRef]
- Deng, M.; Wang, A. Robust non-linear control design to an ionic polymer metal composite with hysteresis using operator-based approach. IET Control Theory Appl. 2012, 6, 2667–2675. [Google Scholar] [CrossRef]
- Chen, G.; Han, Z. Robust right coprime factorization and robust stabilization of nonlinear feedback control systems. IEEE Trans. Auto. Control 1998, 43, 1505–1510. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Ishikawa, K. Operator-based nonlinear feedback control design using robust right coprime factorization. IEEE Trans. Auto. Control 2006, 51, 645–648. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Zhou, M.; Wang, Y.; Cheng, J.; Yachi, H.; Wang, J. Dendritic neuron model with effective learning algorithms for classification, approximation, and prediction. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 601–614. [Google Scholar] [CrossRef] [PubMed]
- Jin, G.; Deng, M. Operator-based robust nonlinear free vibration control of a flexible plate with unknown input nonlinearity. IEEE/CAA J. Autom. Sin. 2020, 7, 442–450. [Google Scholar] [CrossRef]
- Wen, S.; Yu, J.; Guo, G.; Bi, S.; Wang, A.; Wang, D. Fractional order based robust right coprime factorization control for an inverted pendulum. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems, Melbourne, Australia, 30 November–3 December 2016; pp. 159–163. [Google Scholar]
- Jiang, C.; Chu, K.; Ueno, S. Static Analysis of a 3-link Object for Posture Maintenance Control by Nonprehensile Robot without Compensating Friction. In Proceedings of the 2020 International Conference on Advanced Mechatronic Systems, Hanoi, Vietnam, 10–13 December 2020; pp. 270–273. [Google Scholar]
- Bu, N.; Chen, W.; Jin, L.; Zhao, Y. Robust control for uncertain nonlinear feedback system using operator-based right coprime factorization. IEEE/CAA J. Autom. Sin. 2019, 6, 824–829. [Google Scholar] [CrossRef]
- Deng, M.; Jiang, J.; Inoue, A.; Su, C. Operator-based robust control for nonlinear systems with Prandtl–Ishlinskii hysteresis. Int. J. Syst. Sci. 2011, 42, 643–652. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Goto, S. Operator based thermal control of an aluminium plate with a Peltier device. In Second International Conference on Innovative Computing, Informatio and Control (ICICIC 2007); IEEE: Piscataway, NJ, USA, 2008; pp. 3219–3229. [Google Scholar]
- Wen, S.; Deng, M. Operator-based robust nonlinear control and fault detection for a Peltier actuated thermal process. Math. Comput. Model. 2013, 57, 16–29. [Google Scholar] [CrossRef]
- Kawahata, S.; Deng, M. Operator-based Nonlinear Temperature Control Experiment for Microreactor Group Actuated by Peltier Devices. Int. J. Autom. Comput. 2016, 13, 401–408. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Nguyen, X.M.; Sung, K.H. Actuator Fault Detection and Fault-tolerant Control for Hexacopter. Sensors 2019, 19, 4721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salahshoor, K.; Kordestani, M.; Khoshro, M.S. Fault detection and diagnosis of an industrial steam turbine using fusion of SVM (support vector machine) and ANFIS (adaptive neuro-fuzzy inference system) classifiers. Energy 2010, 35, 5472–5482. [Google Scholar] [CrossRef]
- Furukawa, Y.; Deng, M. Fault detection of tank-system using ChangeFinder and SVM. In Proceedings of the 2020 International Conference on Advanced Mechatronic Systems, Hanoi, Vietnam, 10–13 December 2020; pp. 260–265. [Google Scholar]
- De Figueiredo, R.; Chen, G. Nonlinear Feedback Control Systems—An Operator Theory Approach; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Jiang, L.; Deng, M.; Inoue, A. Obstacle avoidance and motion control of a two wheeled mobile robot using svr technique. Int. J. Innov. Comput. Inf. Control 2009, 5, 253–262. [Google Scholar]
- Wen, S.; Deng, M.; Inoue, A. Operator-based robust non-linear control for gantry crane system with soft measurement of swing angle. Int. J. Model. Identif. Control 2012, 16, 86–96. [Google Scholar] [CrossRef]
- Ogihara, Y.; Deng, M.; Noge, Y. Operator-based nonlinear fault detection and fault tolerance control for microreactor with generalized Gaussian function. In Proceedings of the 2019 1st International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 23–27 July 2019; pp. 1–6. [Google Scholar]
- Deng, M.; Koyama, A. Operator-based Robust Fault tolerant control for Uncertain Nonlinear Microreactors with Coupling Effects. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 3746–3751. [Google Scholar]
- Deng, M.; Tanaka, Y.; Li, X. Operator-Based Robust Fault Tolerant Control with SVM-based Early Detection for Sensor Faults. In Proceedings of the 2021 International Conference on Advanced Mechatronic Systems, Tokyo, Japan, 9–12 December 2021; pp. 37–40. [Google Scholar]
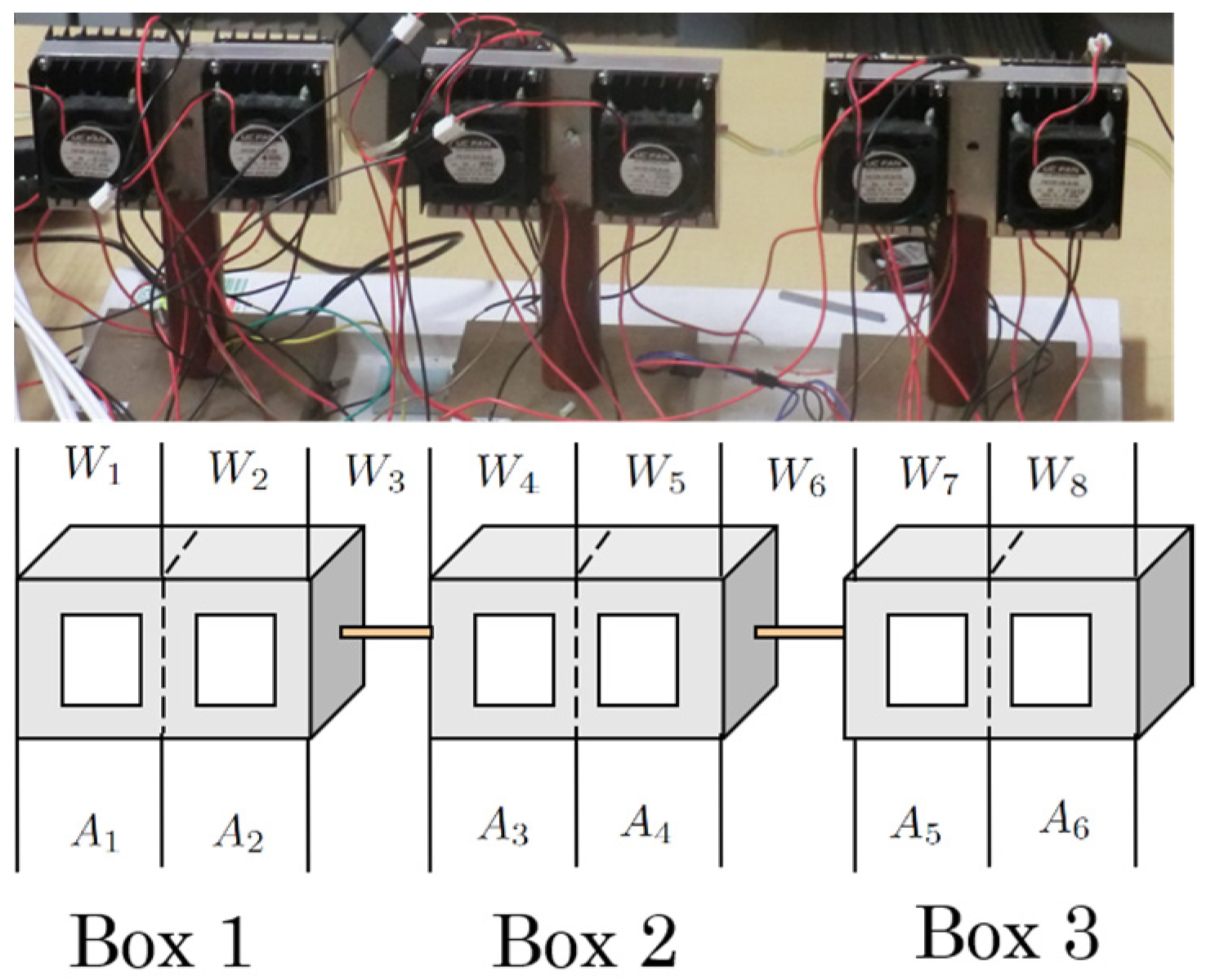

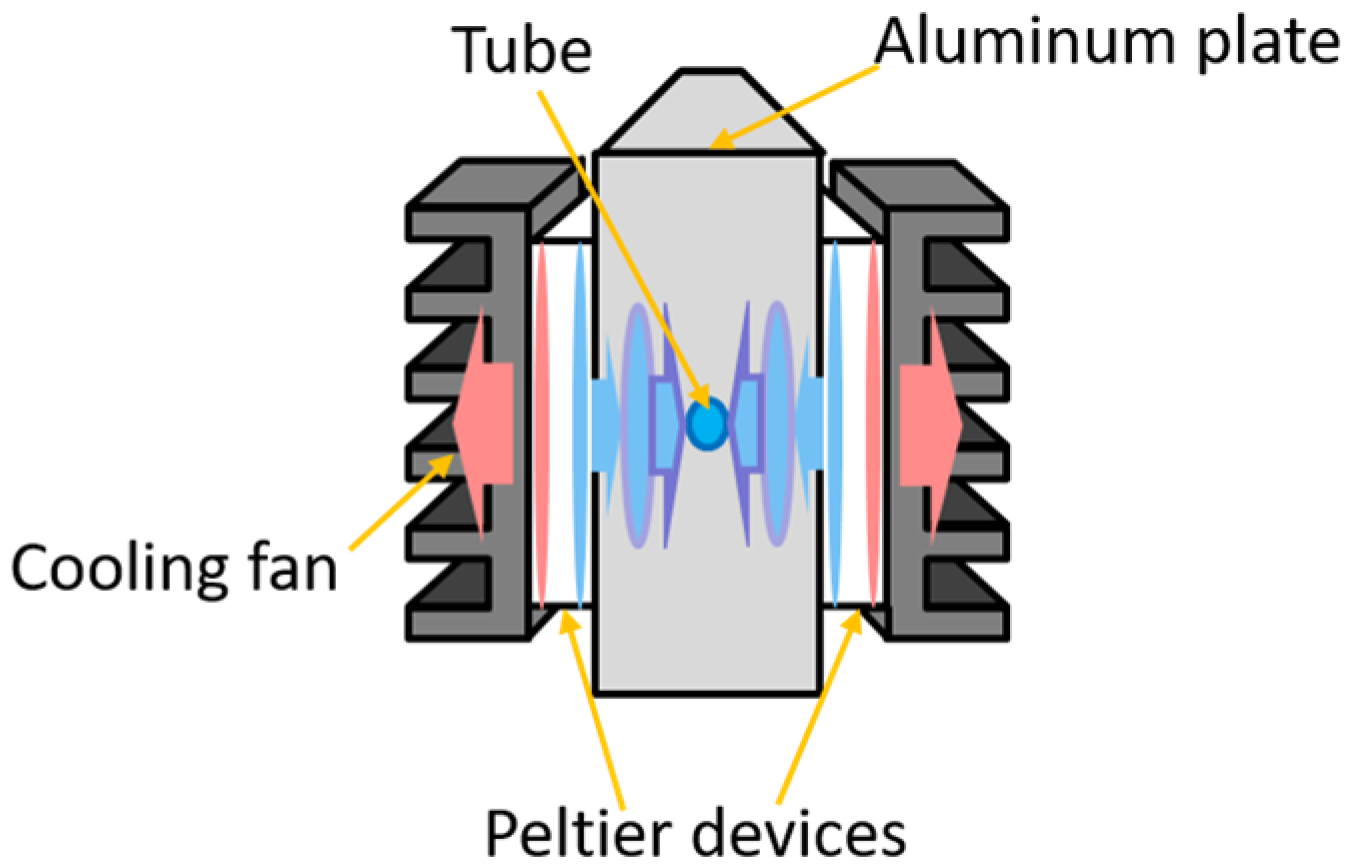



| Parameters | Value[m] | Parameters | Value[m] |
|---|---|---|---|
| d1 | 0.07 | d5 | 0.045 |
| d2 | 0.12 | d6 | 0.02 |
| d3 | 0.014 | d7 | 0.01 |
| d4 | 0.03 | d8 | 0.06 |
| Symbol | Description | Unit |
|---|---|---|
| Initial temperature | [K] | |
| Aluminum temperature of Part | [K] | |
| Water temperature of Part | [K] | |
| S | Seebeck coefficient | [V/K] |
| α | Thermal transfer rate | [W/·K] |
| λ | Thermal conductivity rate | [W/·K] |
| c | Specific heat capacity | [J/kg·K] |
| 𝝐 | Emissivity | - |
| σ | Stefan–Boltzmann constant | [W/·] |
| I | Current | [A] |
| R | Peltier’s resistance | [Ω] |
| m | mass | [kg] |
| Parameters | Value [Units] |
|---|---|
| Initial temperature | 25.0 [°C] |
| Reference input r | 1.0 [°C] |
| Sampling time | 0.5 [s] |
| Simulation time | 600 [s] |
| Gain of | 0.3 |
| Gain of | 0.008 |
| Gain of | 0.45 |
| Gain of | 0.008 |
| Designed SVM parameter C | 1 |
| Designed SVM parameter γ | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, M.; Tanaka, Y.; Li, X. Experimental Study on Support Vector Machine-Based Early Detection for Sensor Faults and Operator-Based Robust Fault Tolerant Control. Machines 2022, 10, 123. https://doi.org/10.3390/machines10020123
Deng M, Tanaka Y, Li X. Experimental Study on Support Vector Machine-Based Early Detection for Sensor Faults and Operator-Based Robust Fault Tolerant Control. Machines. 2022; 10(2):123. https://doi.org/10.3390/machines10020123
Chicago/Turabian StyleDeng, Mingcong, Yuki Tanaka, and Ximei Li. 2022. "Experimental Study on Support Vector Machine-Based Early Detection for Sensor Faults and Operator-Based Robust Fault Tolerant Control" Machines 10, no. 2: 123. https://doi.org/10.3390/machines10020123
APA StyleDeng, M., Tanaka, Y., & Li, X. (2022). Experimental Study on Support Vector Machine-Based Early Detection for Sensor Faults and Operator-Based Robust Fault Tolerant Control. Machines, 10(2), 123. https://doi.org/10.3390/machines10020123







