Fundamental Design and Modelling of the Superconducting Magnet for the High-Speed Maglev: Mechanics, Electromagnetics, and Loss Analysis during Instability
Abstract
:1. Introduction
2. HTS Magnet Design and Characterisation
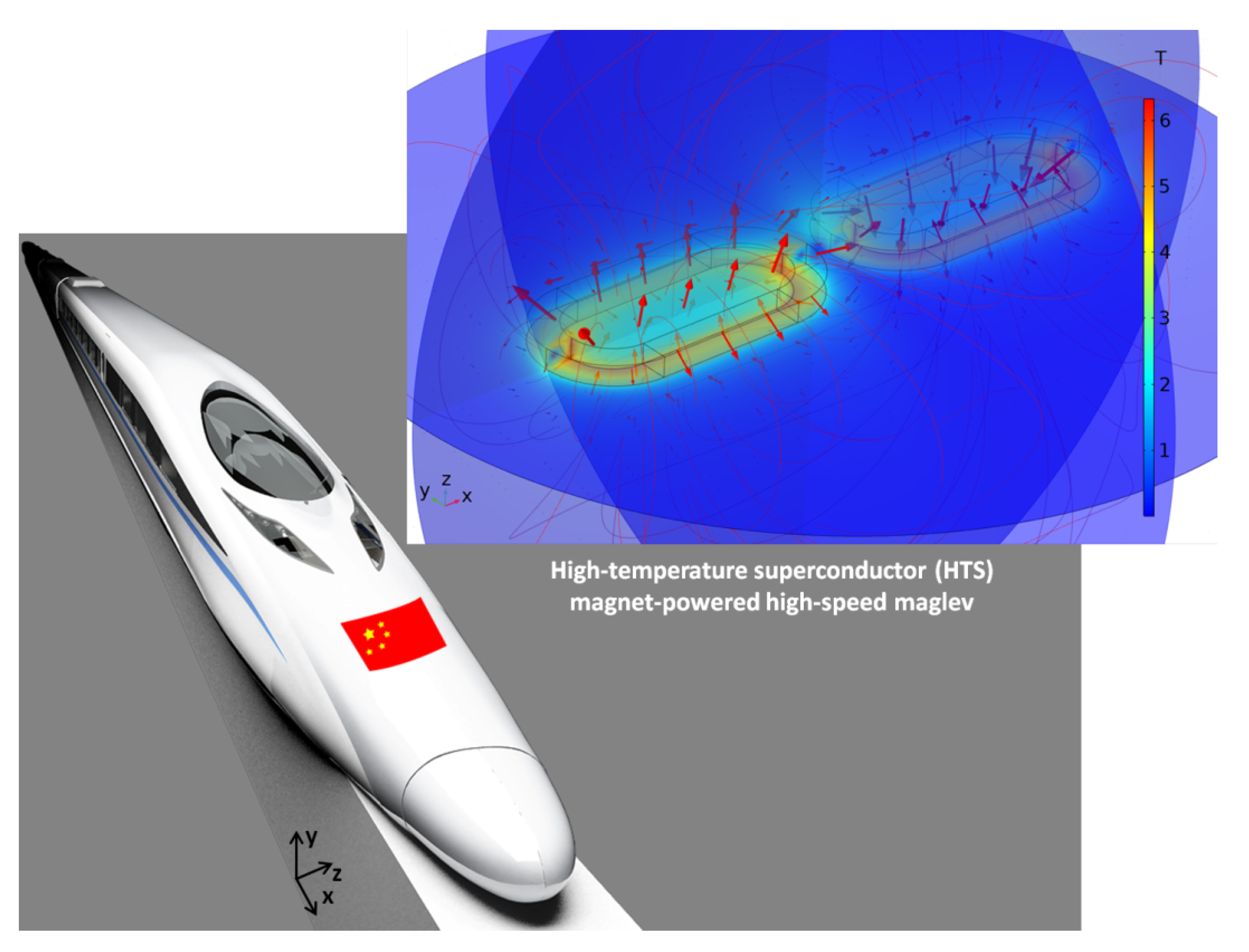
2.1. Introduction of the HTS Magnet for High-Speed Maglev
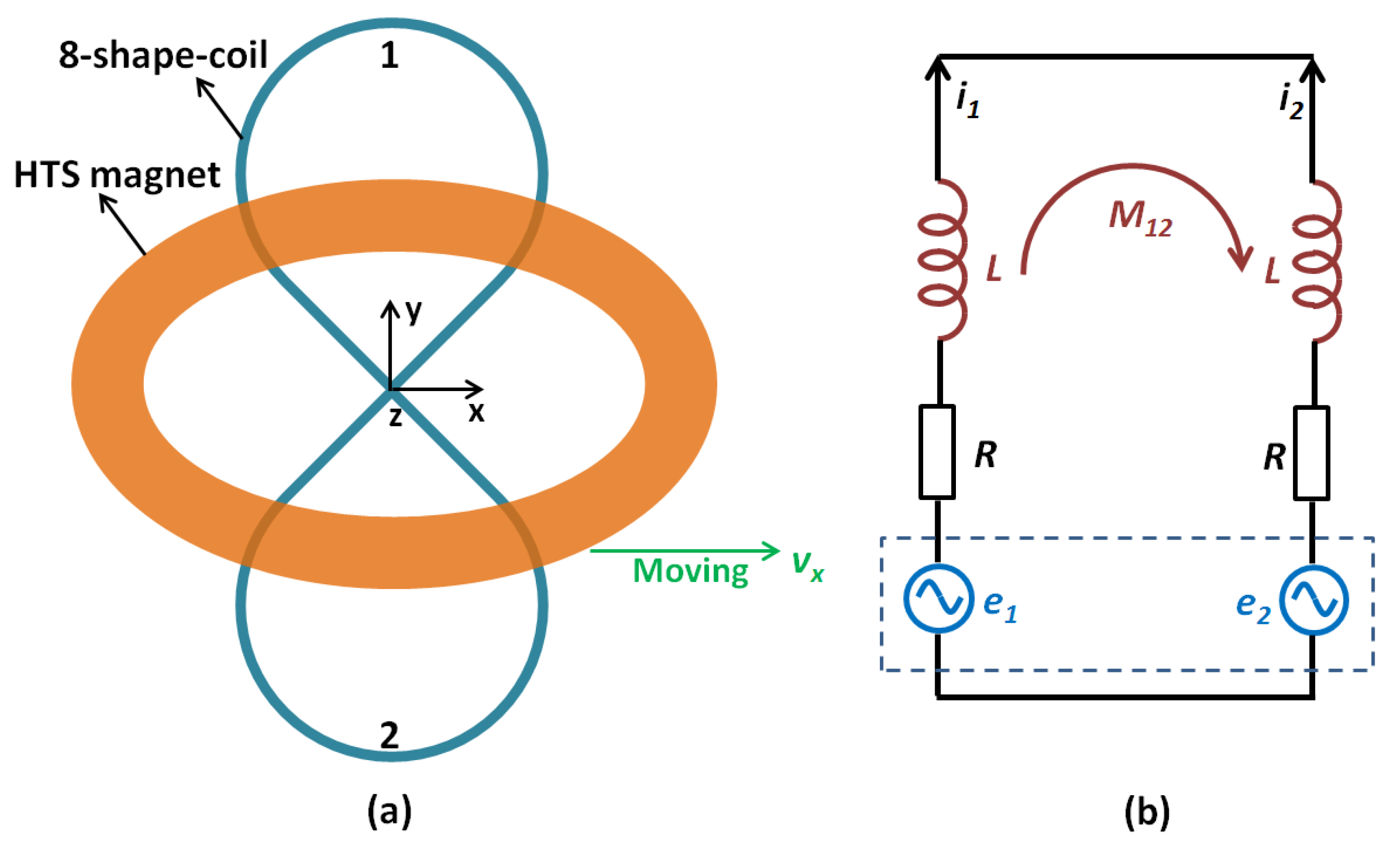
2.2. Superconducting Electrodynamic Suspension (EDS) Using the HTS Magnet
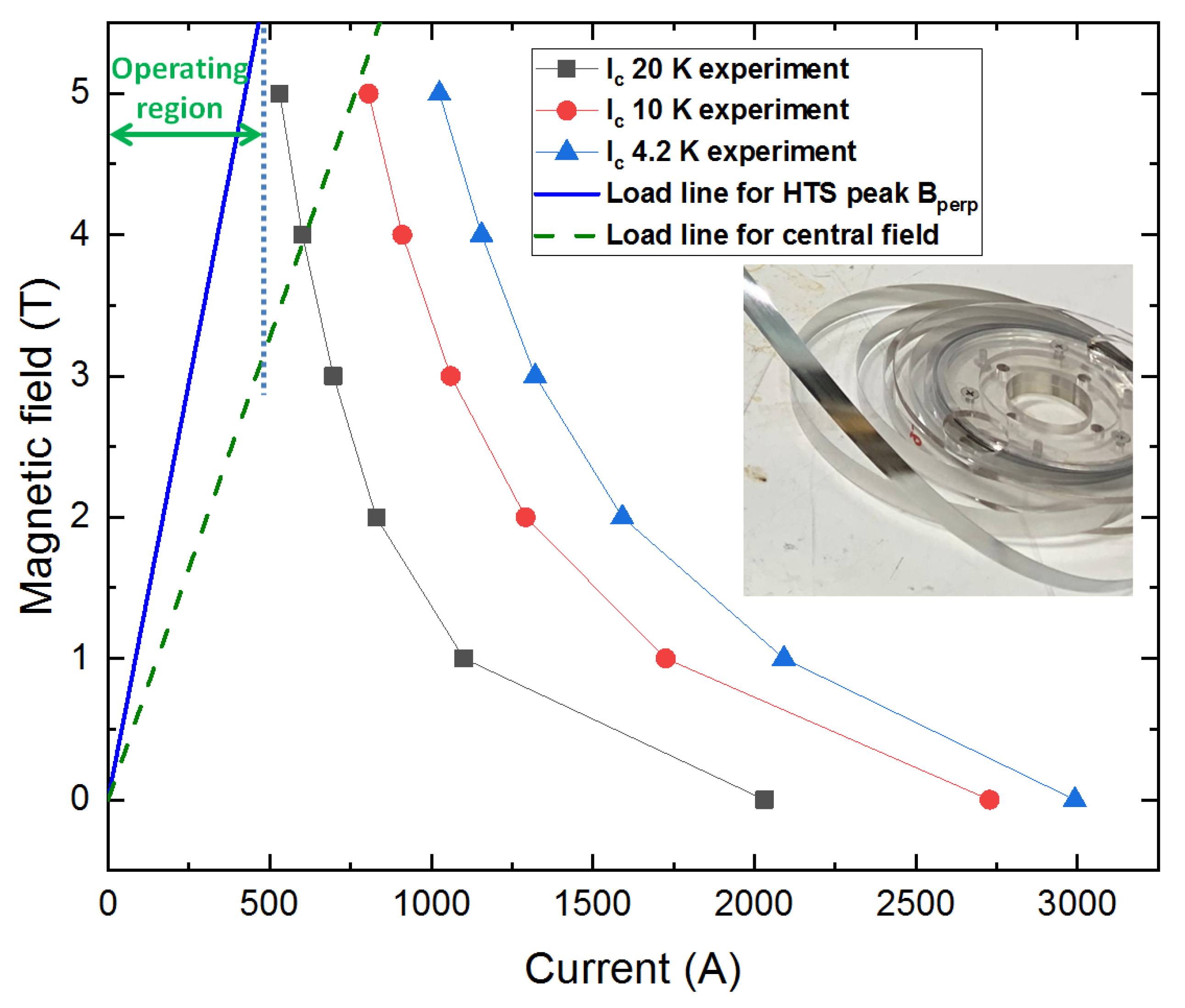
2.3. Geometry and Operating Current of the HTS Magnet
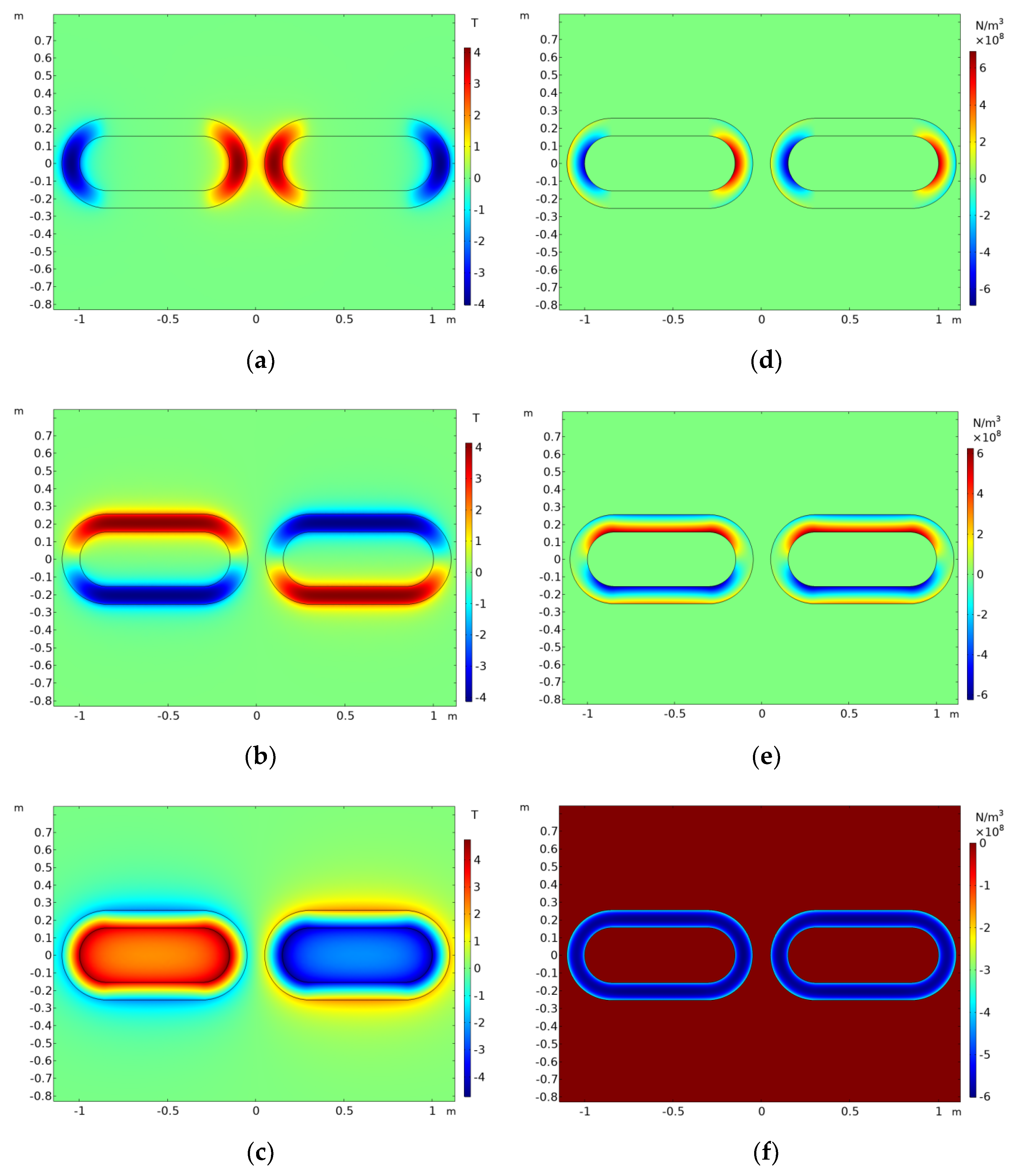
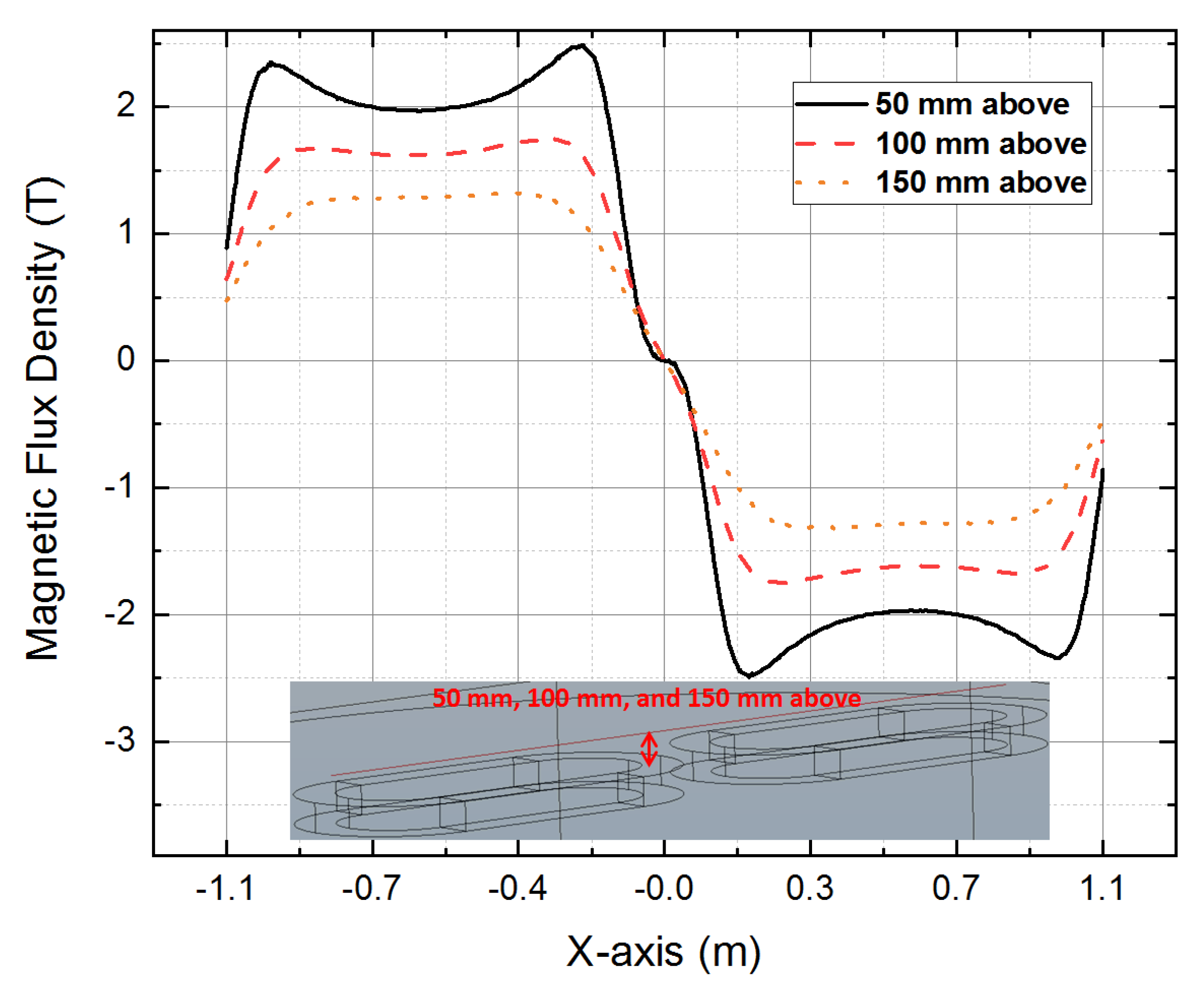
2.4. Magnetic Field and Force of the HTS Magnet
2.5. Experiment vs. Modelling
3. In-Depth Physical Phenomenon of HTS Magnet
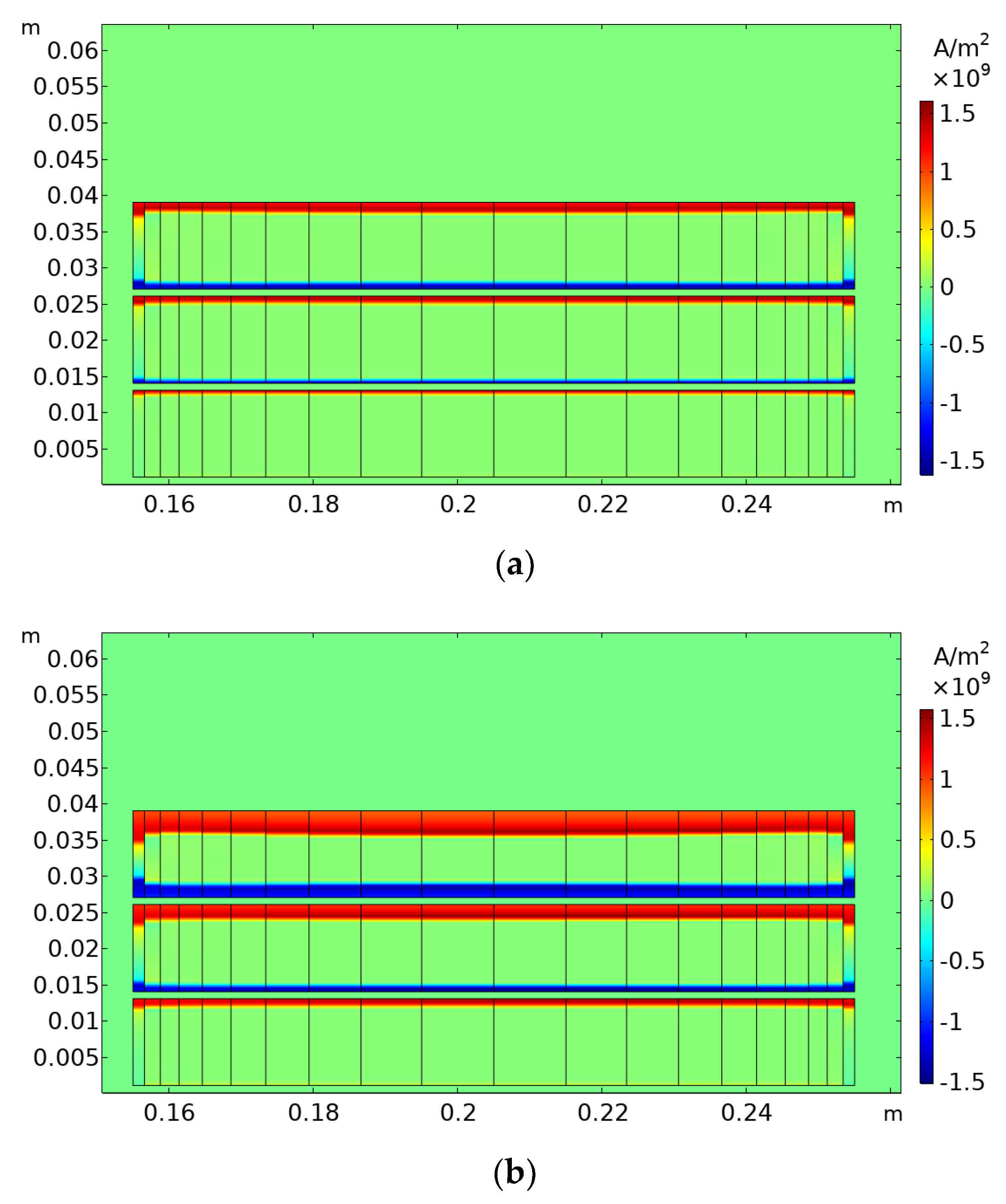
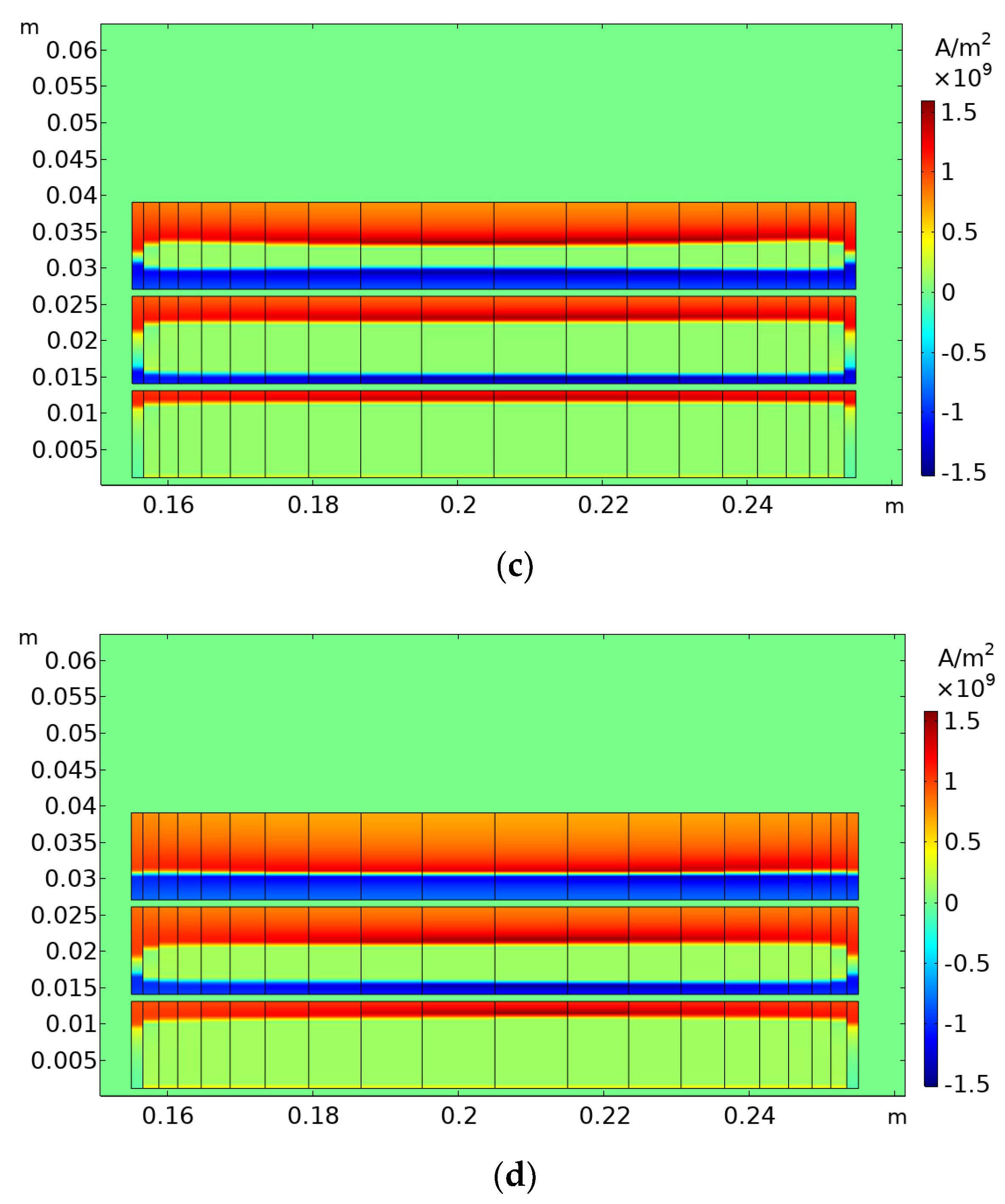
3.1. Electric Current Distribution of the HTS Magnet
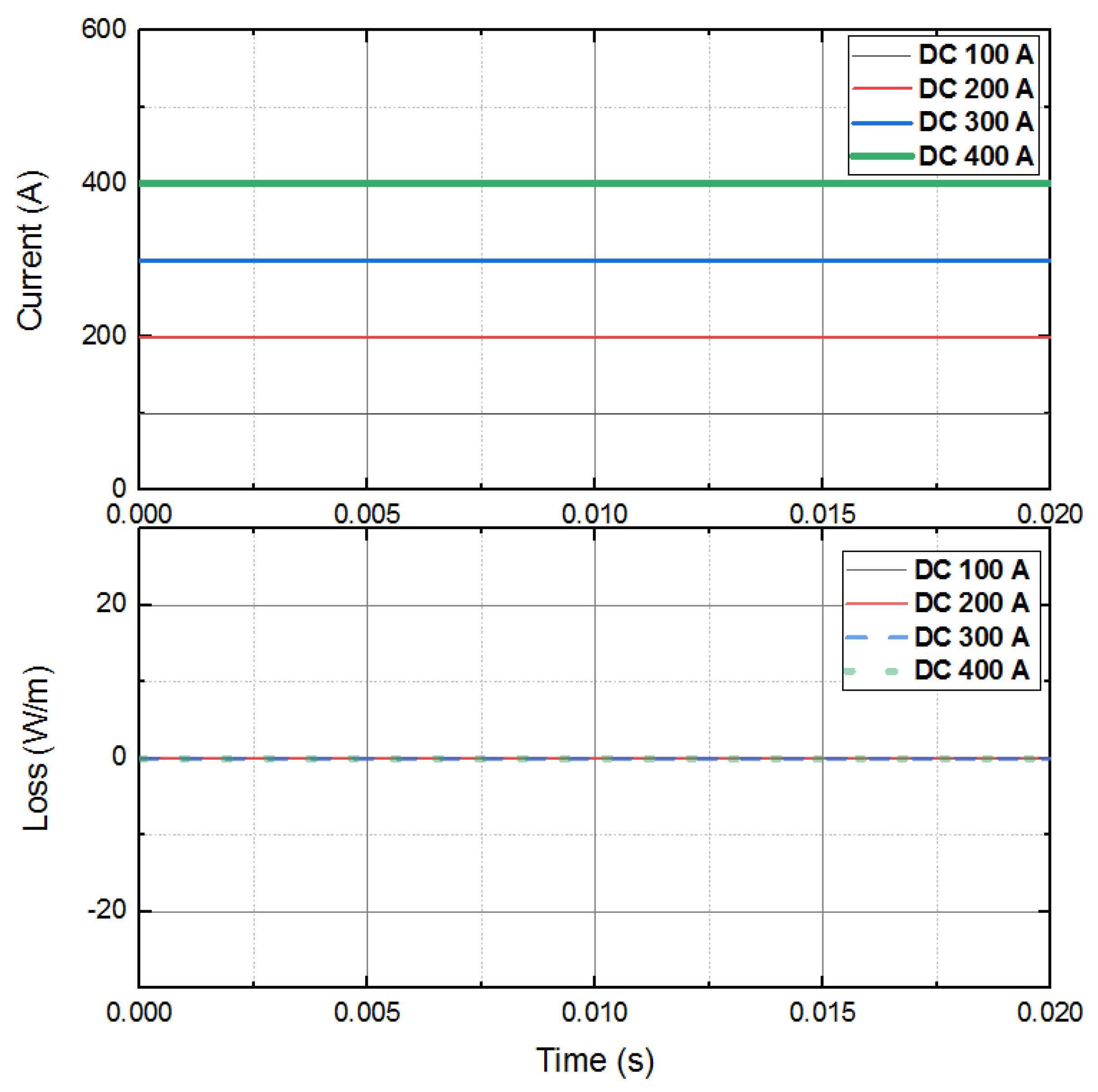
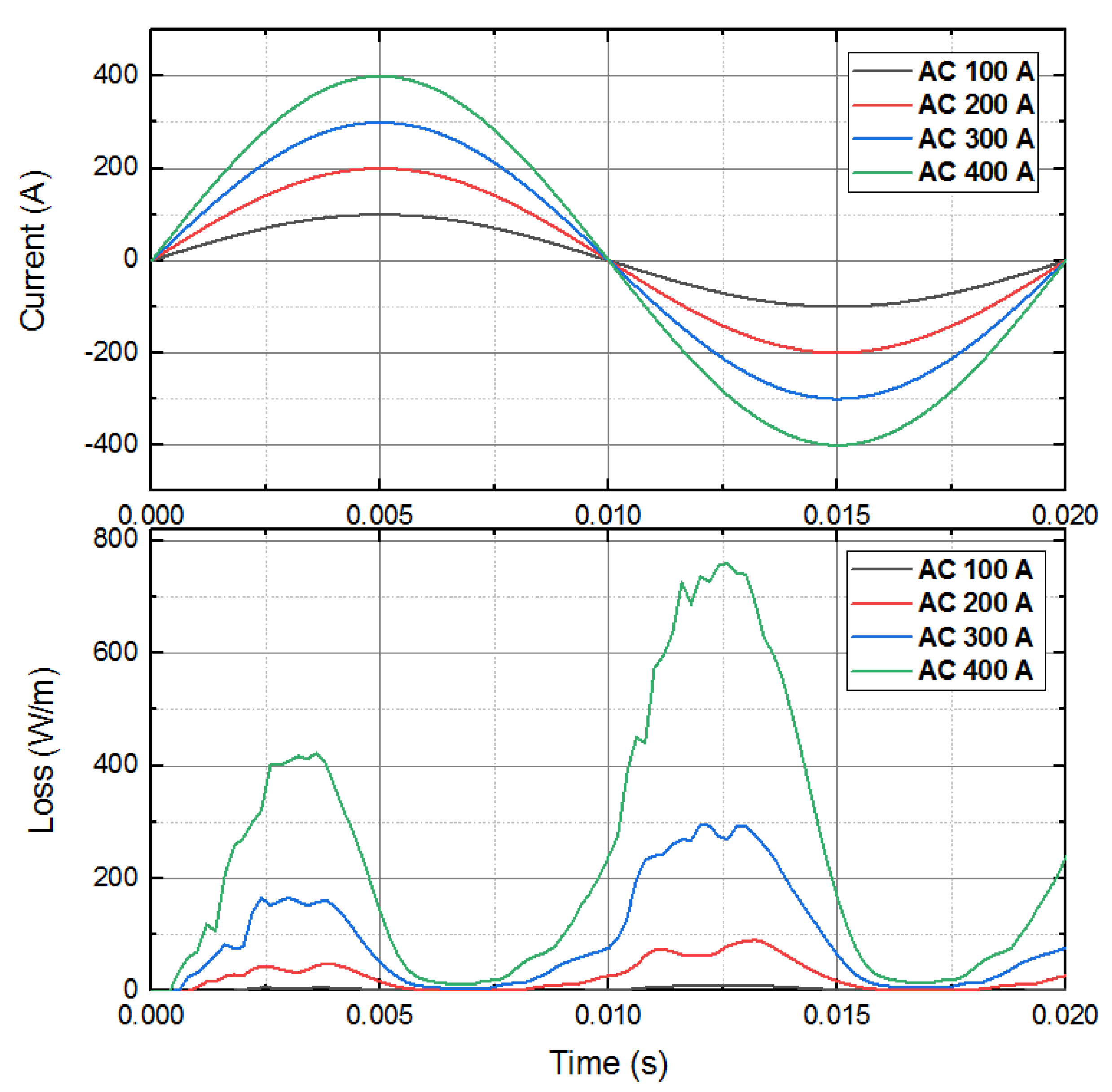
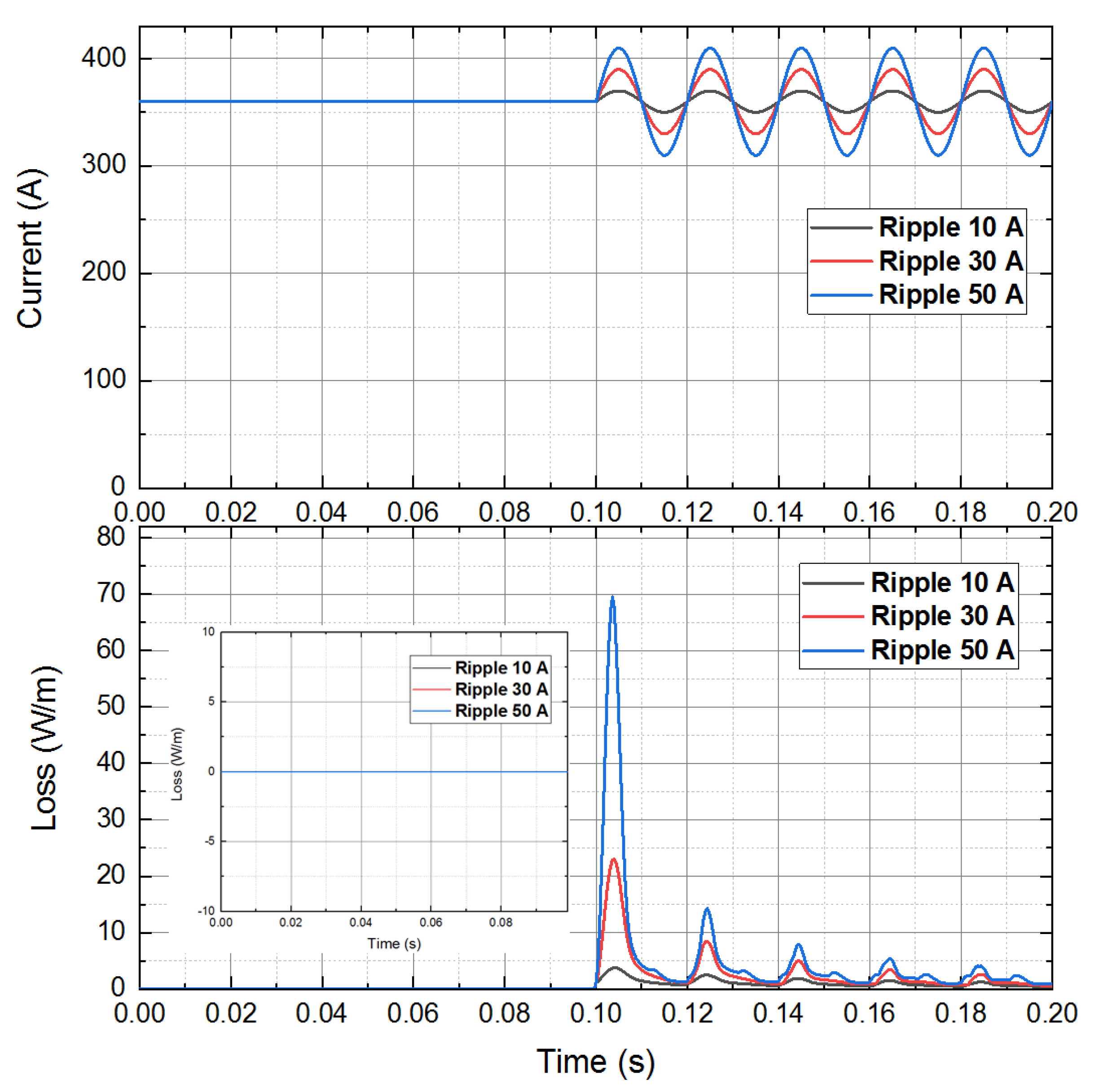
3.2. Loss in the HTS Magnet
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohajan, H. The first industrial revolution: Creation of a new global human era. J. Soc. Sci. Humanit. 2019, 5, 377–387. [Google Scholar]
- Liu, Z.; Long, Z.; Li, X. Maglev train overview. In Maglev Trains; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–28. [Google Scholar]
- Powell, J.; Danby, G. A 300-mph magnetically suspended train. Mech. Eng. 1967, 89, 30. [Google Scholar]
- Sawada, K. Outlook of the superconducting maglev. Proc. IEEE 2009, 97, 1881–1885. [Google Scholar] [CrossRef]
- Jin, J.X.; Sheng, G.; Bi, Y.F.; Song, Y.T.; Liu, X.L.; Chen, X.; Li, Q.; Deng, Z.G.; Zhang, W.H.; Zheng, J.; et al. Applied Superconductivity and Electromagnetic Devices - Principles and Current Exploration Highlights. IEEE Trans. Appl. Supercond. 2021, 31, 7000529. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Zeng, Y.; Huang, H.; Luo, F.; Xu, Z.; Tang, Q.; Lin, G.; Zhang, C.; Ren, Z. The first man-loading high temperature superconducting maglev test vehicle in the world. Phys. C Supercond. 2002, 378, 809–814. [Google Scholar] [CrossRef]
- Kovalev, K.; Koneev, S.; Poltavec, V.; Gawalek, W. Magnetically levitated high-speed carriages on the basis of bulk HTS elements. In Proceedings of the 8th Internerational Symposium Suspension Technology Technology (ISMST’8), Stanford, CA, USA, 15–17 August 2005; p. 51. [Google Scholar]
- Okano, M.; Iwamoto, T.; Furuse, M.; Fuchino, S.; Ishii, I. Running performance of a pinning-type superconducting magnetic levitation guide. J. Phys. Conf. Ser. 2006, 43, 244. [Google Scholar] [CrossRef]
- Schultz, L.; de Haas, O.; Verges, P.; Beyer, C.; Rohlig, S.; Olsen, H.; Kuhn, L.; Berger, D.; Noteboom, U.; Funk, U. Superconductively levitated transport system-the supratrans project. IEEE Trans. Appl. Supercond. 2005, 15, 2301–2305. [Google Scholar] [CrossRef]
- D’ovidio, G.; Crisi, F.; Lanzara, G. A “v” shaped superconducting levitation module for lift and guidance of a magnetic transportation system. Phys. C Supercond. 2008, 468, 1036–1040. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, W.; Zheng, J.; Wang, B.; Ren, Y.; Zheng, X.; Zhang, J. A high-temperature superconducting maglev-evacuated tube transport (hts maglev-ett) test system. IEEE Trans. Appl. Supercond. 2017, 27, 3602008. [Google Scholar] [CrossRef]
- Mattos, L.; Rodriguez, E.; Costa, F.; Sotelo, G.; De Andrade, R.; Stephan, R. Maglev-cobra operational tests. IEEE Trans. Appl. Supercond. 2016, 26, 3600704. [Google Scholar] [CrossRef]
- Kuwano, K.; Igarashi, M.; Kusada, S.; Nemoto, K.; Okutomi, T.; Hirano, S.; Tominaga, T.; Terai, M.; Kuriyama, T.; Tasaki, K. The running tests of the superconducting maglev using the hts magnet. IEEE Trans. Appl. Supercond. 2007, 17, 2125–2128. [Google Scholar] [CrossRef]
- Kusada, S.; Igarashi, M.; Nemoto, K.; Okutomi, T.; Hirano, S.; Kuwano, K.; Tominaga, T.; Terai, M.; Kuriyama, T.; Tasaki, K. The project overview of theHTS magnet for superconducting maglev. IEEE Trans. Appl. Supercond. 2007, 17, 2111–2116. [Google Scholar] [CrossRef]
- Terai, M.; Igarashi, M.; Kusada, S.; Nemoto, K.; Kuriyama, T.; Hanai, S.; Yamashita, T.; Nakao, H. The R&D project of HTS magnets for the superconducting maglev. IEEE Trans. Appl. Supercond. 2006, 16, 1124–1129. [Google Scholar]
- Zheng, J.; Huang, H.; Zhang, S.; Deng, Z. A general method to simulate the electromagnetic characteristics of HTS maglev systems by finite element software. IEEE Trans. Appl. Supercond. 2018, 28, 1–8. [Google Scholar] [CrossRef]
- Jin, J.X.; Zheng, L.H. Driving models of high temperature superconducting linear synchronous motors and characteristic analysis. Supercond. Sci. Technol. 2011, 24, 55011. [Google Scholar] [CrossRef]
- Jin, J.X.; Zheng, L.H.; Guo, Y.G.; Zhu, J.G.; Grantham, C.; Sorrell, C.C.; Xu, W. High-temperature superconducting linear synchronous motors integrated with HTS magnetic levitation components. IEEE Trans. Appl. Supercond. 2012, 22, 5202617. [Google Scholar]
- Cai, Y.; Ma, G.; Wang, Y.; Gong, T.; Liu, K.; Yao, C.; Yang, W.; Zeng, J. Semianalytical calculation of superconducting electrodynamic suspension train using figure-eight-shaped ground coil. IEEE Trans. Appl. Supercond. 2020, 30, 3602509. [Google Scholar] [CrossRef]
- Shen, B.; Grilli, F.; Coombs, T. Overview of h-formulation: A versatile tool for modelling electromagnetics in high-temperature superconductor applications. IEEE Access 2020, 8, 100403–100414. [Google Scholar] [CrossRef]
- Jin, J.X.; Zhang, R.T.; Lin, Z.W.; Guo, Y.G.; Zhu, J.G.; Chen, X.Y.; Shen, B.Y. Modelling analysis of periodically arranged high-temperature superconducting tapes. Phys. C Supercond. 2020, 578, 1353747. [Google Scholar] [CrossRef]
- Shen, B.; Grilli, F.; Coombs, T. Review of the AC loss computation for HTS using H formulation. Supercond. Sci. Technol. 2020, 33, 33002. [Google Scholar] [CrossRef] [Green Version]
- Zermeno, V.M.; Abrahamsen, A.B.; Mijatovic, N.; Jensen, B.B.; Sørensen, M.P. Calculation of alternating current losses in stacks and coils made of second generation high temperature superconducting tapes for large scale applications. J. Appl. Phys. 2013, 114, 173901. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Tang, Y.; Ren, L.; Li, J.; Xu, Y.; Liao, Y.; Deng, X. AC loss analysis of a hybrid HTS magnet for smes based on H-formulation. IEEE Trans. Appl. Supercond. 2016, 27, 4701005. [Google Scholar]
- Shen, B.; Li, C.; Geng, J.; Zhang, X.; Gawith, J.; Ma, J.; Liu, Y.; Grilli, F.; Coombs, T.A. Power dissipation in HTS coated conductor coils under the simultaneous action of ac and dc currents and fields. Supercond. Sci. Technol. 2018, 31, 075005. [Google Scholar] [CrossRef]
- Norris, W. Calculation of hysteresis losses in hard superconductors carrying ac: Isolated conductors and edges of thin sheets. J. Phys. D Appl. Phys. 1970, 3, 489–507. [Google Scholar] [CrossRef]


| Components | Specifications |
|---|---|
| Coil shape | Racetrack |
| Coil type | Double-pancake (DP) |
| Turns | 2 × 500 |
| Number of DPs for each HTS magnet | 3 |
| Size of each HTS magnet | 1050 mm × 510 mm × 72 mm |
| Operating current | 350–360 A |
| Operation temperature | 20 K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Jin, J.; Shen, B.; Hao, L.; Guo, Y.; Zhu, J. Fundamental Design and Modelling of the Superconducting Magnet for the High-Speed Maglev: Mechanics, Electromagnetics, and Loss Analysis during Instability. Machines 2022, 10, 113. https://doi.org/10.3390/machines10020113
Wu Z, Jin J, Shen B, Hao L, Guo Y, Zhu J. Fundamental Design and Modelling of the Superconducting Magnet for the High-Speed Maglev: Mechanics, Electromagnetics, and Loss Analysis during Instability. Machines. 2022; 10(2):113. https://doi.org/10.3390/machines10020113
Chicago/Turabian StyleWu, Zhihao, Jianxun Jin, Boyang Shen, Luning Hao, Youguang Guo, and Jianguo Zhu. 2022. "Fundamental Design and Modelling of the Superconducting Magnet for the High-Speed Maglev: Mechanics, Electromagnetics, and Loss Analysis during Instability" Machines 10, no. 2: 113. https://doi.org/10.3390/machines10020113
APA StyleWu, Z., Jin, J., Shen, B., Hao, L., Guo, Y., & Zhu, J. (2022). Fundamental Design and Modelling of the Superconducting Magnet for the High-Speed Maglev: Mechanics, Electromagnetics, and Loss Analysis during Instability. Machines, 10(2), 113. https://doi.org/10.3390/machines10020113









