Design and Analysis of a Spherical Robot with Rolling and Jumping Modes for Deep Space Exploration
Abstract
1. Introduction
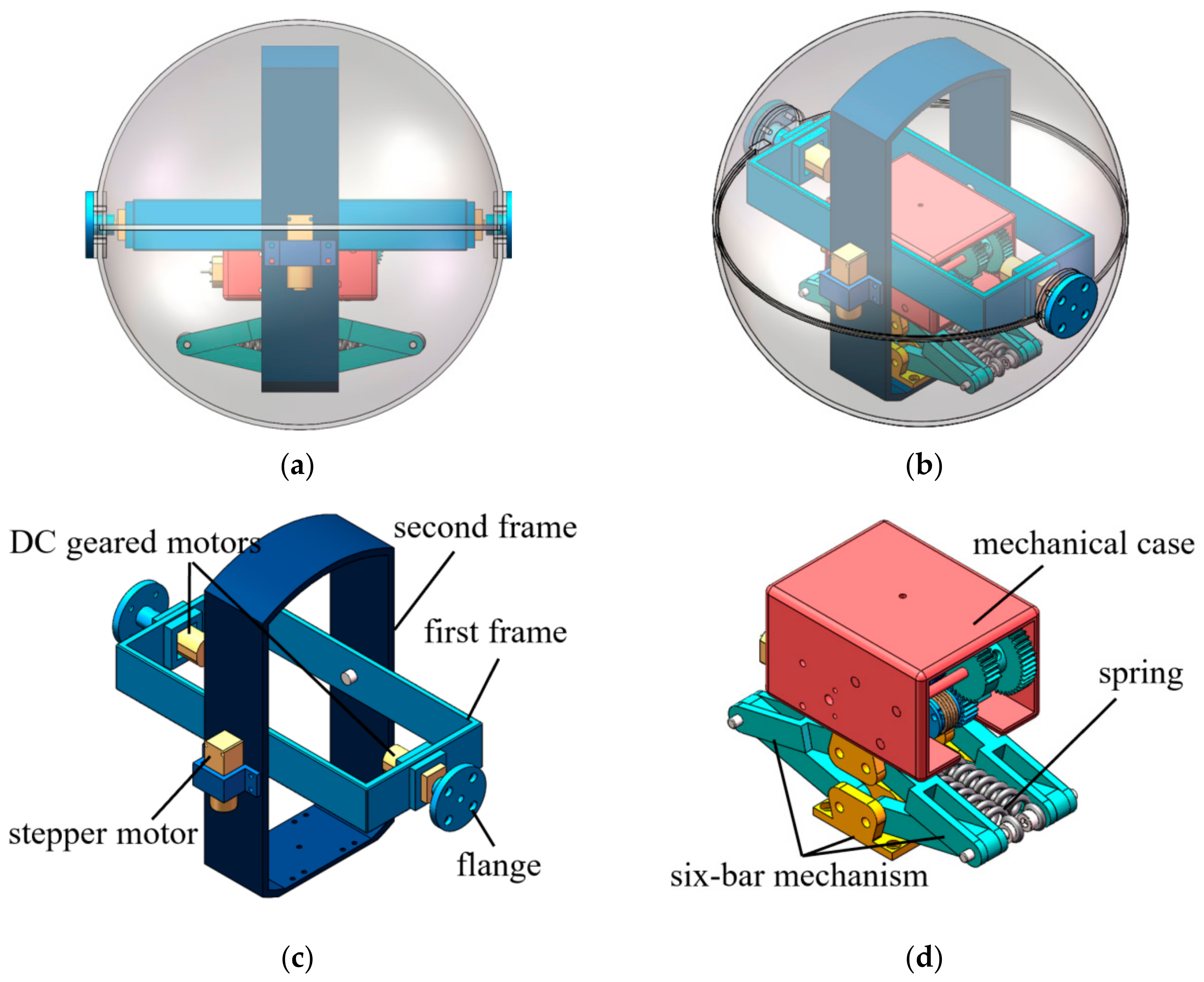
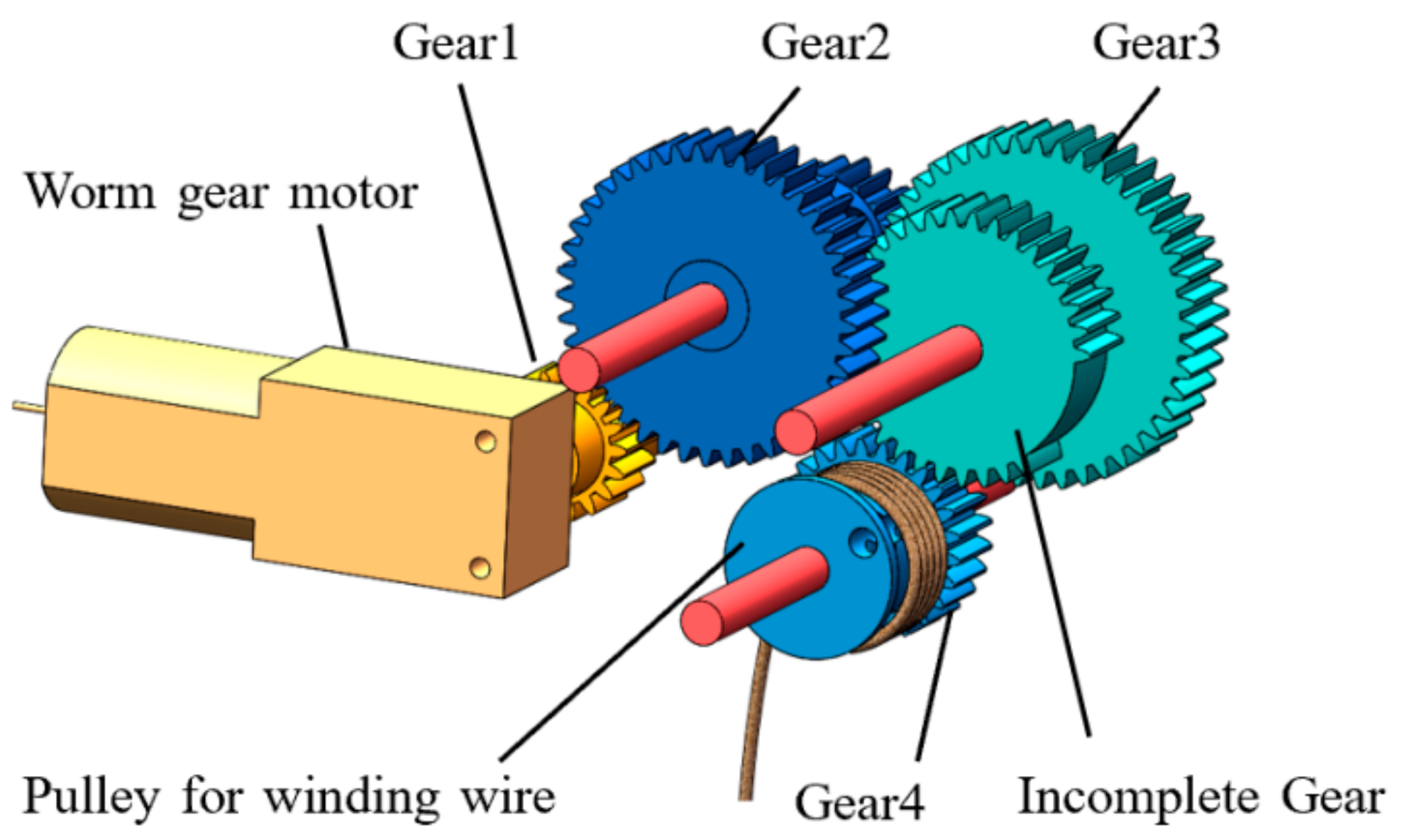
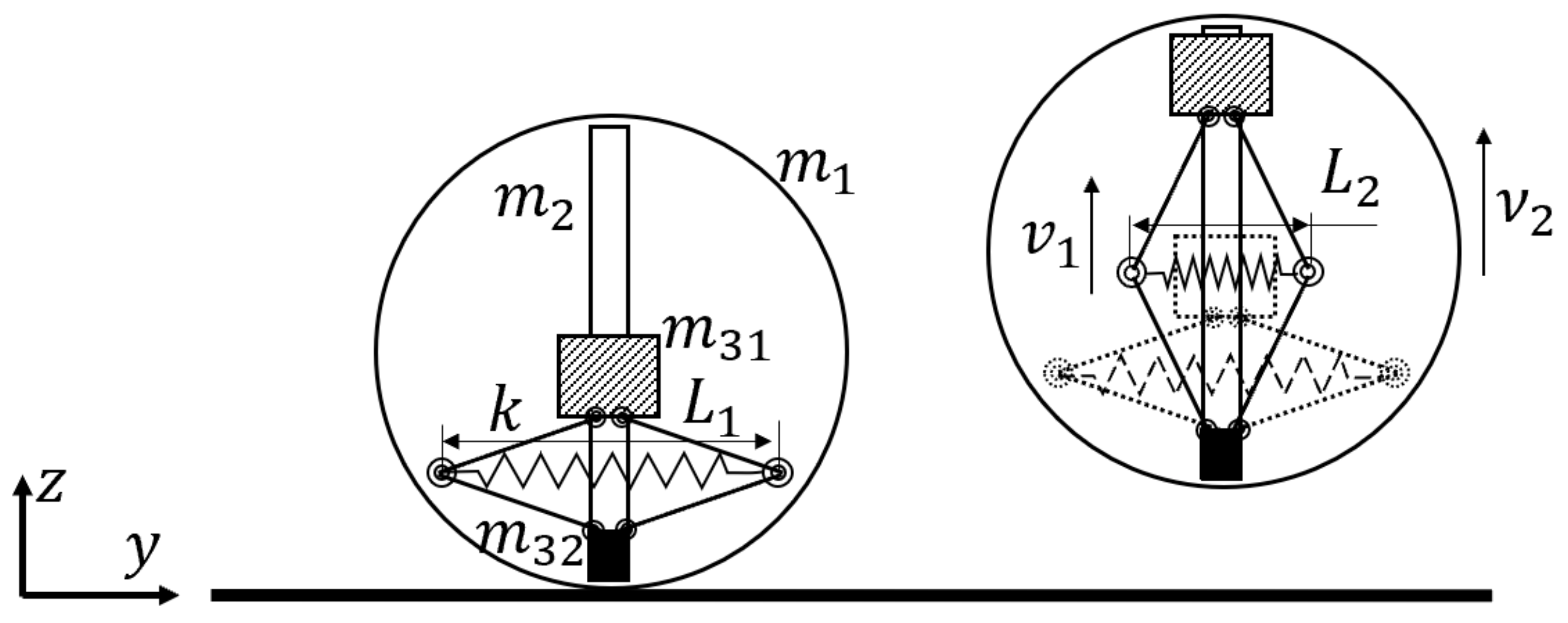
2. Structure Design
3. Dynamic Analysis
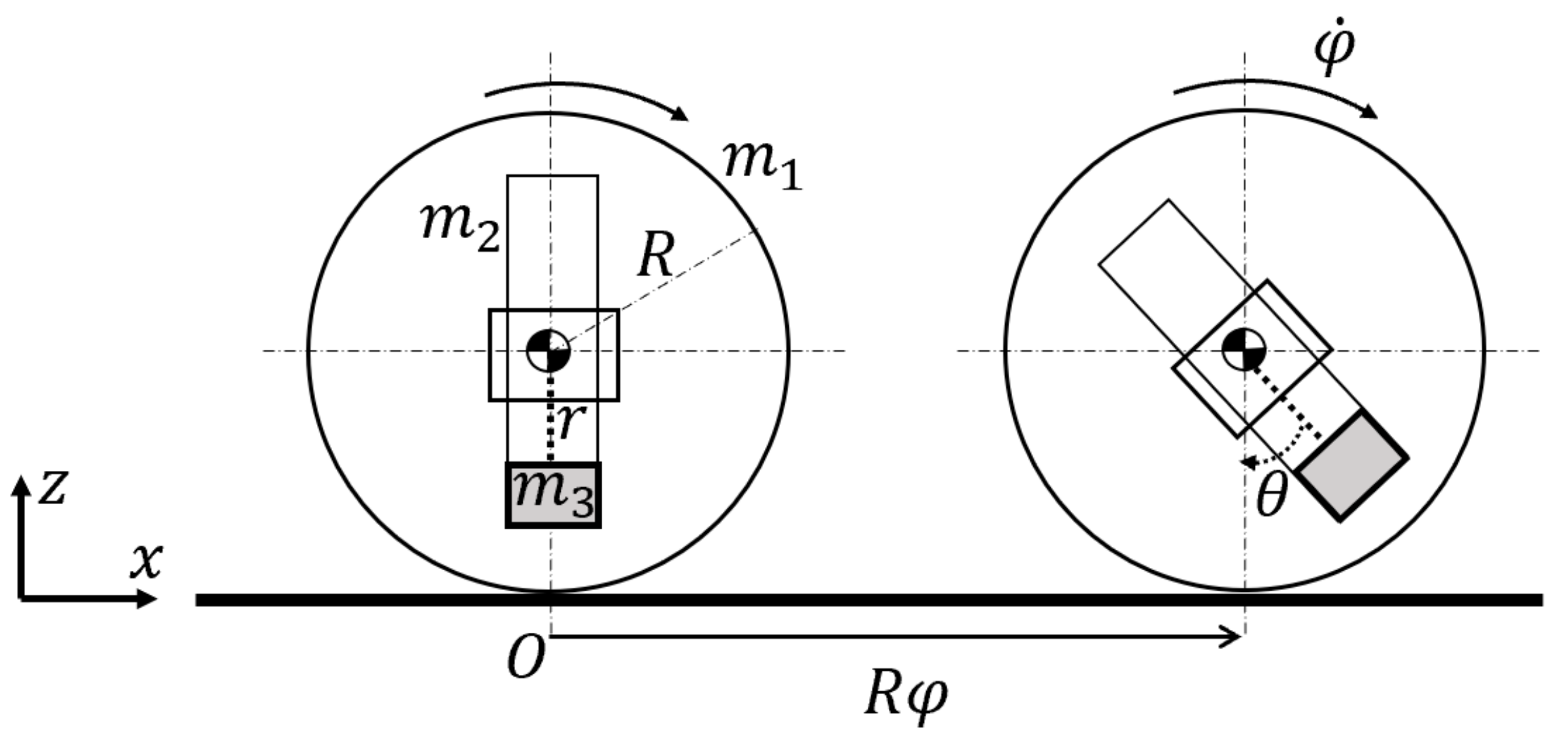
3.1. Analysis of Rolling
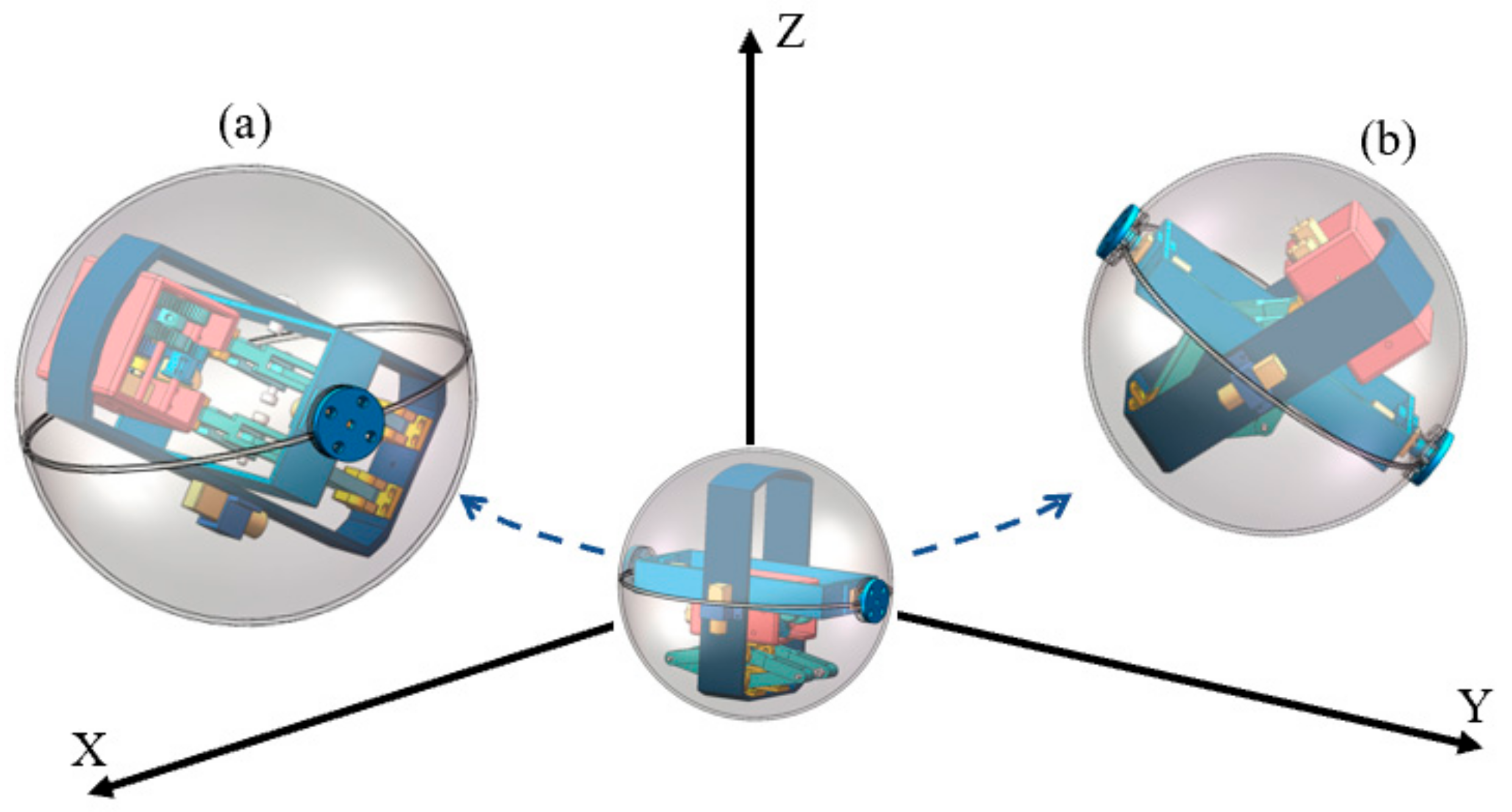
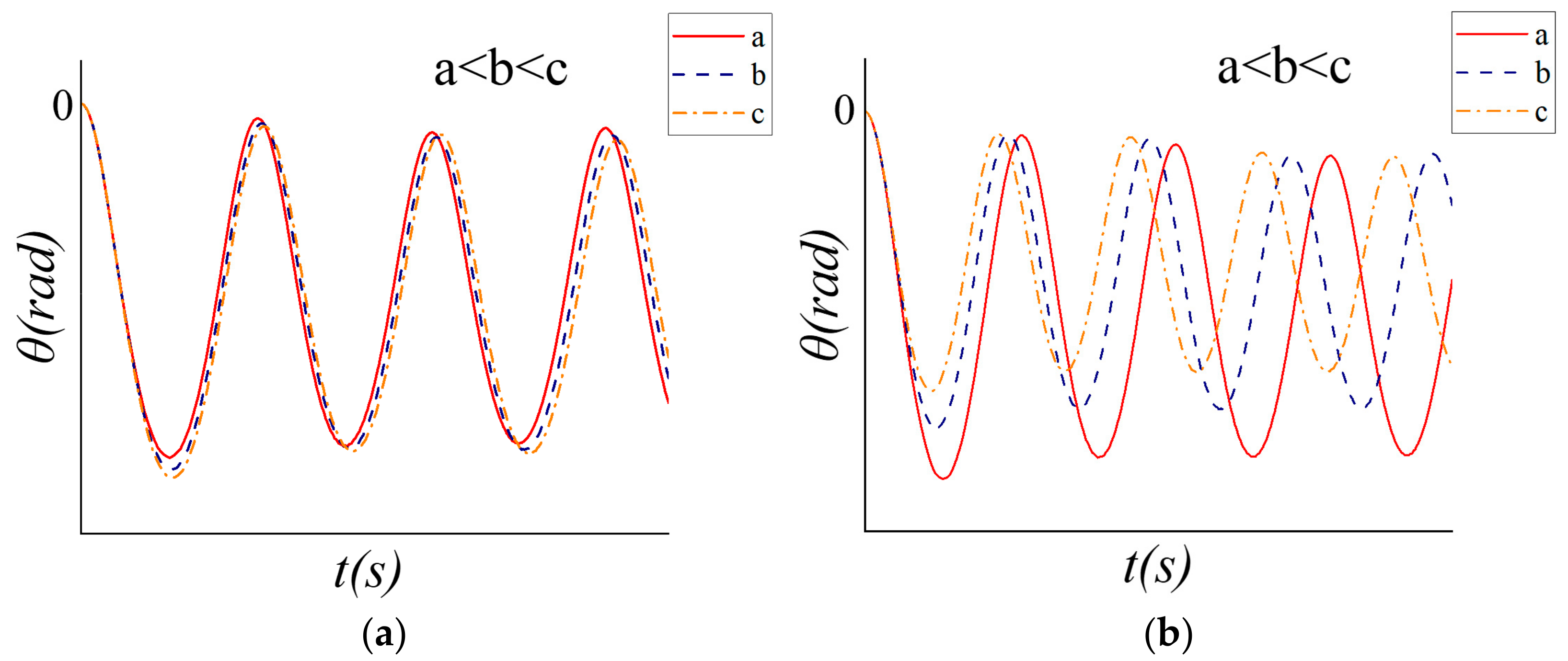
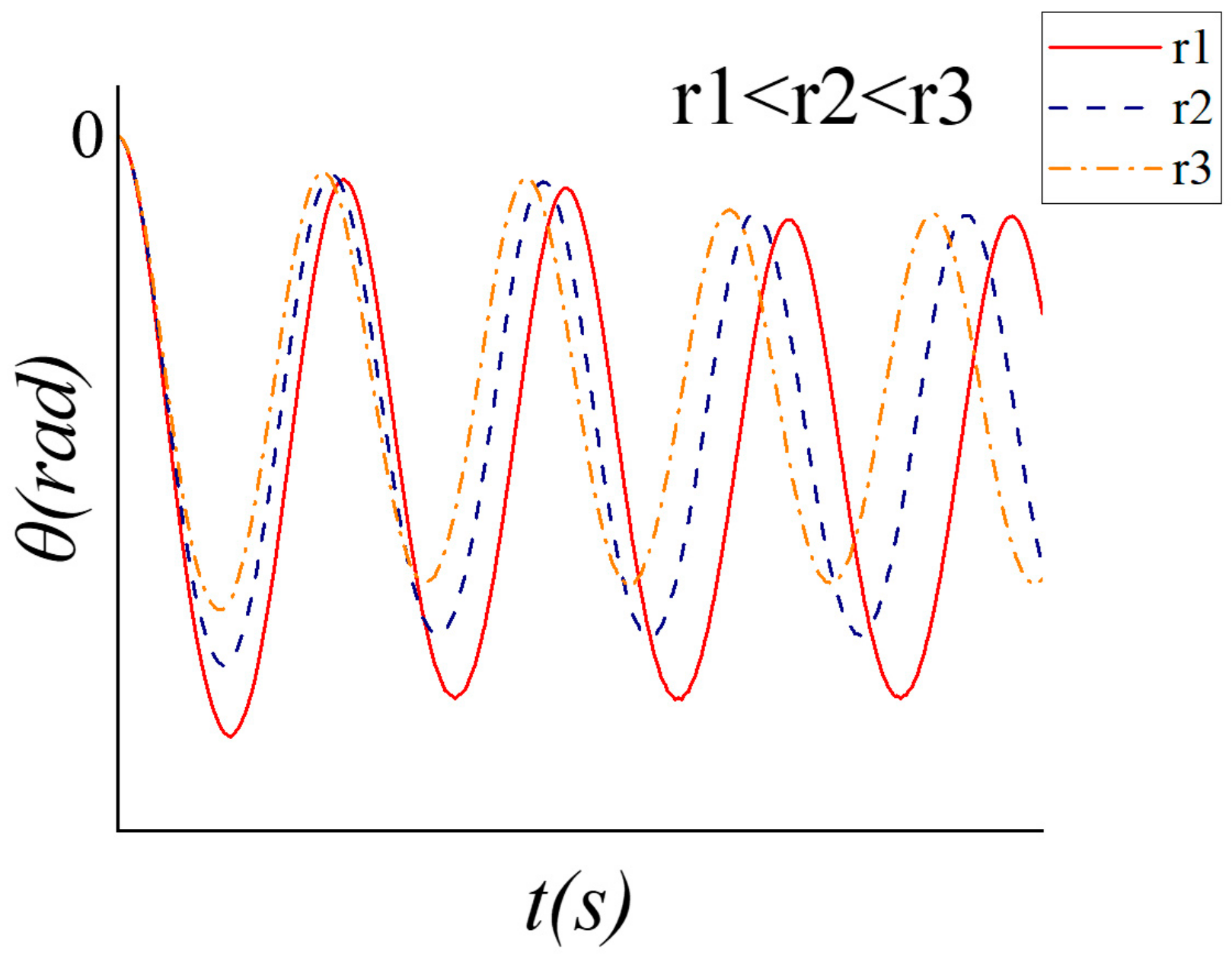
3.2. Analysis of Steering
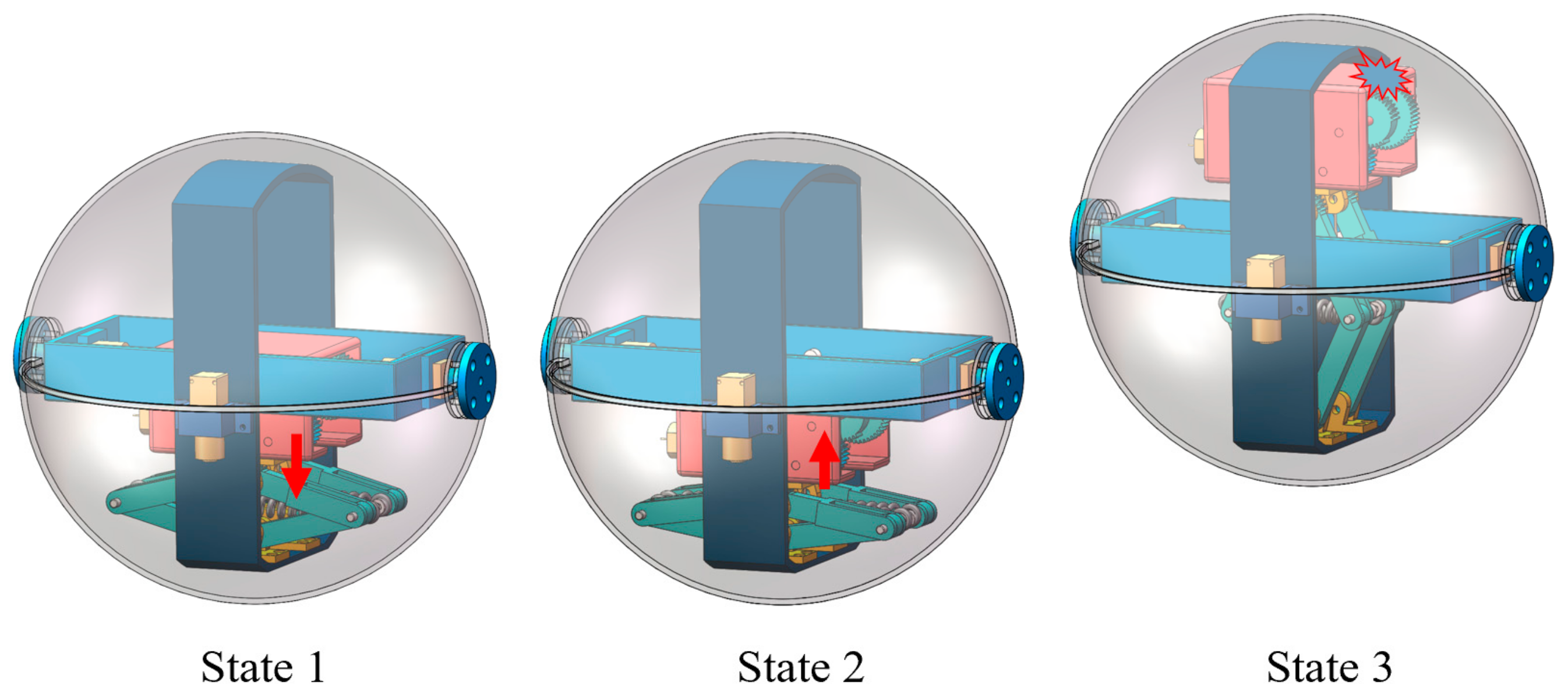
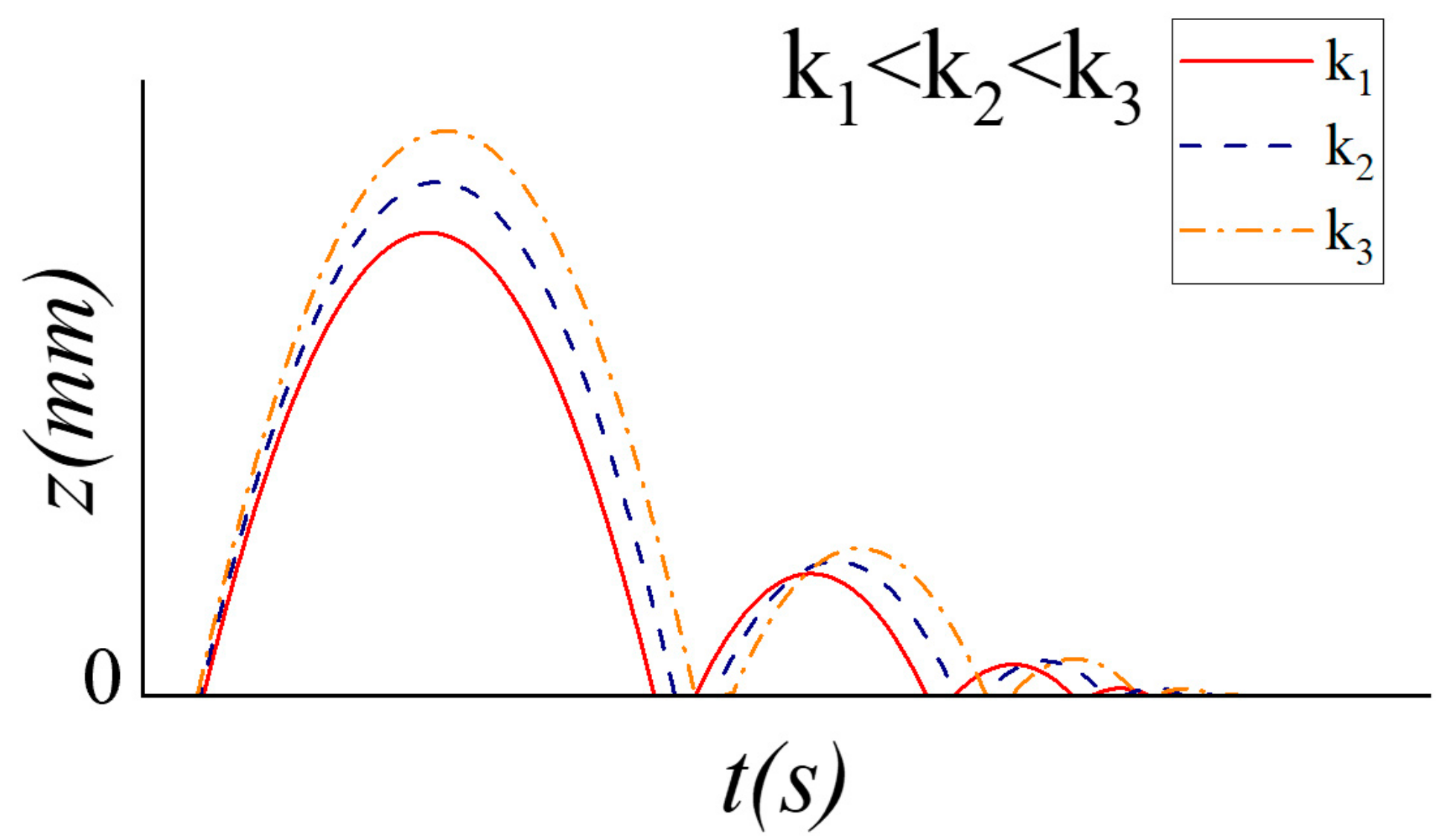
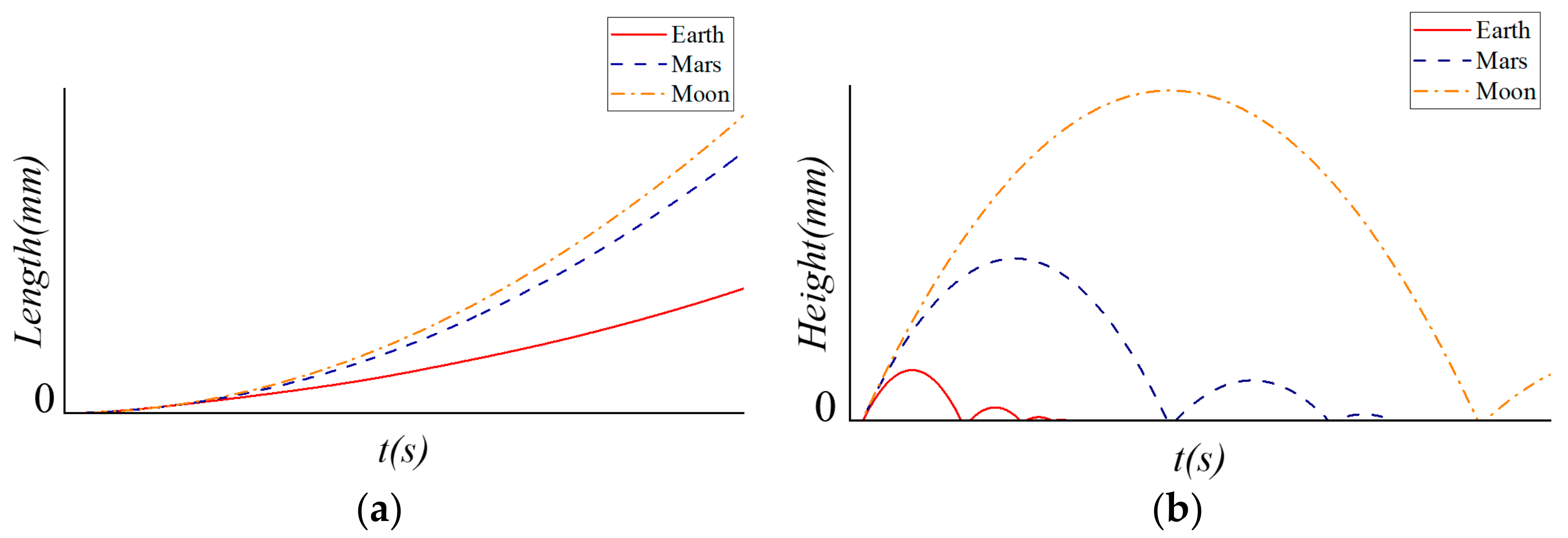
3.3. Analysis of Jumping
4. Experiments
4.1. Rolling Ability Test
4.1.1. Straight Rolling Test
4.1.2. Steering Test
4.1.3. Climbing Test
4.2. Jumping Ability Test
4.2.1. Vertical Jumping Test
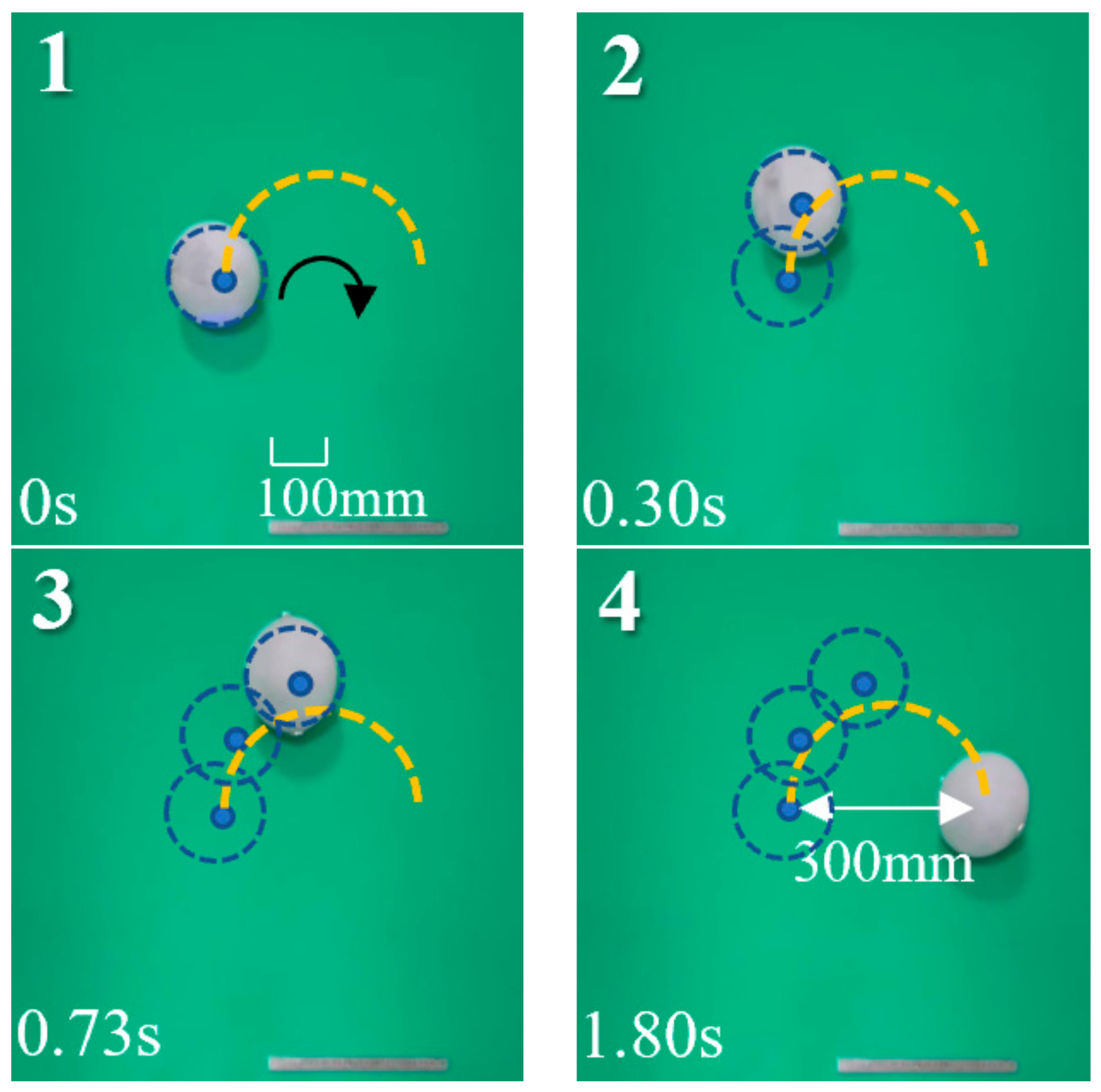
4.2.2. Multidirectional Jumping Test
4.3. Obstacle Crossing Ability Test
4.4. Comparison of Test Results with Theoretical Values
4.5. Applicability in Microgravity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Jennings Taylor, E.; Jackson, G.S. Perseverance Rover Lands on Mars. Electrochem. Soc. Interface 2021, 30, 79–80. [Google Scholar] [CrossRef]
- Binlong, Y.; Qian, Y.; Xiao, L.; Michalski, J.R.; Li, Y.; Wu, B.; Qiao, L. Geomorphologic exploration targets at the Zhurong landing site in the southern Utopia Planitia of Mars. Earth Planet. Sci. Lett. 2021, 576, 117199. [Google Scholar] [CrossRef]
- Kesner, S.B.; Plante, J.S.; Boston, P.J.; Fabian, T.; Dubowsky, S. Mobility and power feasibility of a microbot team system for extraterrestrial cave exploration. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 4893–4898. [Google Scholar] [CrossRef]
- Balaram, J.; Aung, M.M.; Golombek, M.P. The Ingenuity Helicopter on the Perseverance Rover. Space Sci. Rev. 2021, 217, 1–11. [Google Scholar] [CrossRef]
- Halme, A.; Schonberg, T.; Wang, Y. Motion control of a spherical mobile robot. In Proceedings of the International Workshop on Advanced Motion Control, AMC ’96, Mie, Japan, 18–21 March 1996; IEEE: New York, NY, USA, 1996; Volume 1, pp. 259–264. [Google Scholar]
- Mukherjee, R.; Minor, M.A.; Pukrushpan, J.T. Simple motion planning strategies for spherobot: A spherical mobile robot. In Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 7–10 December 1999; IEEE: New York, NY, USA, 1999; Volume 3, pp. 2132–2137. [Google Scholar]
- Fiorini, P.; Hayati, S.; Heverly, M.; Gensler, J. A Hopping Robot for Planetary Exploration. In Proceedings of the 1999 IEEE Aerospace Conference, Snowmass, CO, USA, 7 March 1999. [Google Scholar]
- Zhao, B.; Li, M.; Yu, H.; Hu, H.; Sun, L. Dynamics and motion control of a two pendulums driven spherical robot. In Proceedings of the IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 147–153. [Google Scholar]
- Joshi, V.A.; Banavar, R.N. Motion analysis of a spherical mobile robot. Robotica 2009, 27, 343–353. [Google Scholar] [CrossRef]
- Ferrière, L.; Campion, G.; Raucent, B. ROLLMOBS, a new drive system for omnimobile robots. Robotica 2001, 19, 1–9. [Google Scholar] [CrossRef]
- Ahn, S.S.; Lee, Y.J. Novel Spherical Robot with Hybrid Pendulum Driving Mechanism. Adv. Mech. Eng. 2014, 2014, 456727. [Google Scholar] [CrossRef]
- Ahn, S.S.; Kim, Y.M.; Lee, Y.J. A deformable spherical robot with two arms. J. Inst. Control Robot. Syst. 2010, 16, 1060–1067. [Google Scholar] [CrossRef][Green Version]
- Armour, R.; Paskins, K.; Bowyer, A.; Vincent, J.; Megill, W. Jumping robots: A biomimetic solution to locomotion across rough terrain. Bioinspiration Biomim. 2007, 2, S65. [Google Scholar] [CrossRef] [PubMed]
- Burdick, J.; Fiorini, P. Minimalist Jumping Robots for Celestial Exploration. Int. J. Rob. Res. 2003, 22, 653–674. [Google Scholar] [CrossRef]








| Outer Shell | ||
| Mass | 188 g | |
| Radius | 75 mm | |
| Moment of inertia | 6.0 × 105 g·mm2 | |
| Rolling drive module | ||
| Mass | 173 g | |
| Moment of inertia | 1.6 × 105 g·mm2 | |
| Pendulum length | 23 mm | |
| Motor rated torque | 49 mN·m | |
| Maximum deflection angle of the second frame | 30° | |
| Jumping drive module | ||
| Mass of | 390 g | |
| Mass of six-bar mechanism | 38 g | |
| Stiffness coefficient of spring | 147 g/mm | |
| The stretch length of the spring | 48 mm |
| The Theoretical Value | The Actual Value | The Relative Error | |
|---|---|---|---|
| Rolling velocity | 1005 mm/s | 800 mm/s | 20.4% |
| Steering radius | 131 mm | 150 mm | 14.5% |
| Jumping height | 212 mm | 170 mm | 19.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Li, C.; Niu, S.; Wang, P.; Wu, H.; Li, B. Design and Analysis of a Spherical Robot with Rolling and Jumping Modes for Deep Space Exploration. Machines 2022, 10, 126. https://doi.org/10.3390/machines10020126
Wang F, Li C, Niu S, Wang P, Wu H, Li B. Design and Analysis of a Spherical Robot with Rolling and Jumping Modes for Deep Space Exploration. Machines. 2022; 10(2):126. https://doi.org/10.3390/machines10020126
Chicago/Turabian StyleWang, Futao, Chaobing Li, Shaohua Niu, Pengfei Wang, Huaisong Wu, and Bingyang Li. 2022. "Design and Analysis of a Spherical Robot with Rolling and Jumping Modes for Deep Space Exploration" Machines 10, no. 2: 126. https://doi.org/10.3390/machines10020126
APA StyleWang, F., Li, C., Niu, S., Wang, P., Wu, H., & Li, B. (2022). Design and Analysis of a Spherical Robot with Rolling and Jumping Modes for Deep Space Exploration. Machines, 10(2), 126. https://doi.org/10.3390/machines10020126






