2.1. Experimental Setup
To emulate the conditions of an ICT machine, a set of experimental tests were performed in an adapted machine, presented in
Figure 1.
The machine comprised of a pneumatic cylinder and bottom and upper plates. To apply force, the upper plate moves downward and meets the bottom plate, guiding each other with the help of a guiding system.
The PCB is placed on top of support pins that imitate needles and it is guided into the experimental machine using guiding pins with tight tolerance. In the guiding pins, the PCB is restricted in the Z axis (
Figure 2).
To apply load, pressers (as shown in
Figure 3) were used. The geometry of the pressers is as it occurs in a real ICT.
For each presser, a load cell is associated to precisely quantify the force on every used presser.
To measure the strain data for each experimental test, strain gages were used. This is the most practical way to find the strains without affecting the response of the measured part [
4,
6,
7,
8,
10,
14,
17,
18]. Three uniaxial strain gages (KFGS-1-120-C1-23) were applied in strategic positions of the PCB (
Figure 4). The strain gages are connected to the signal amplifier HBM QuantumX MX1615B which, in turn, are connected to a PC where the data is displayed.
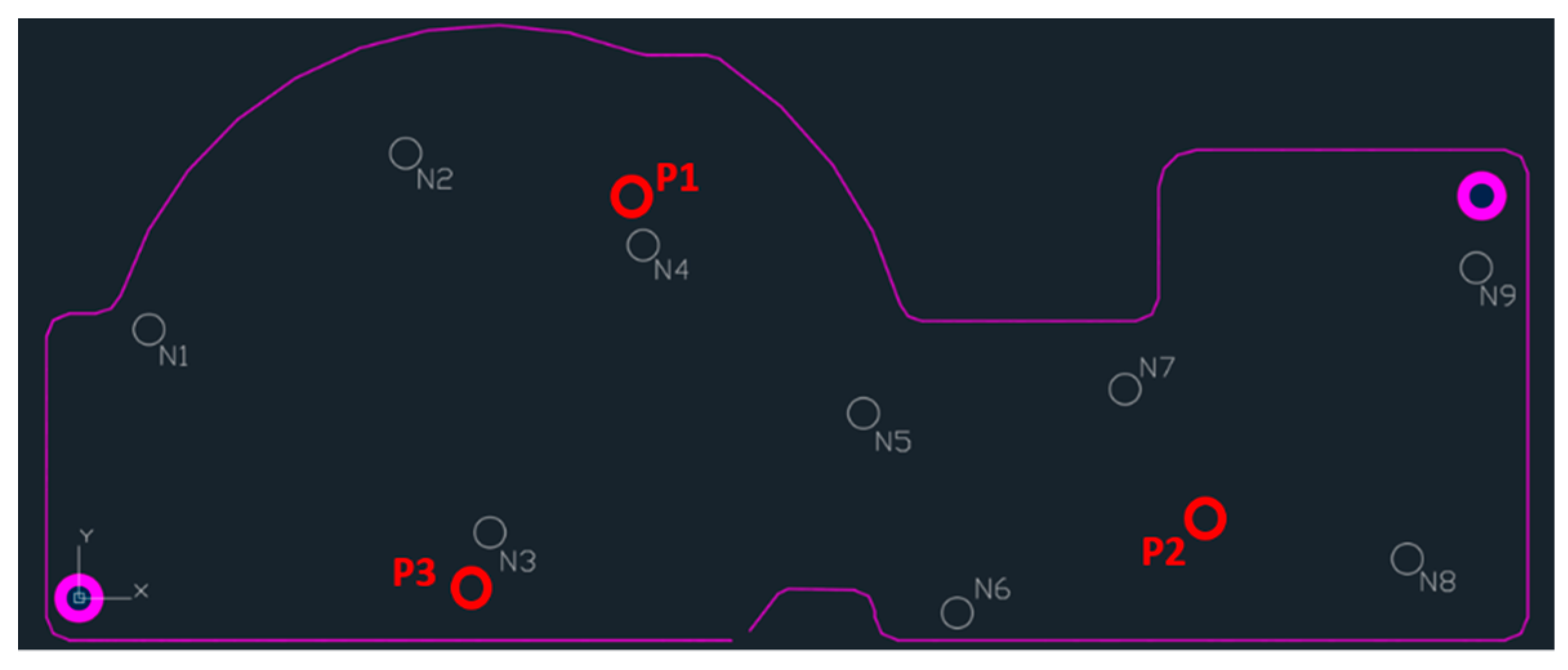
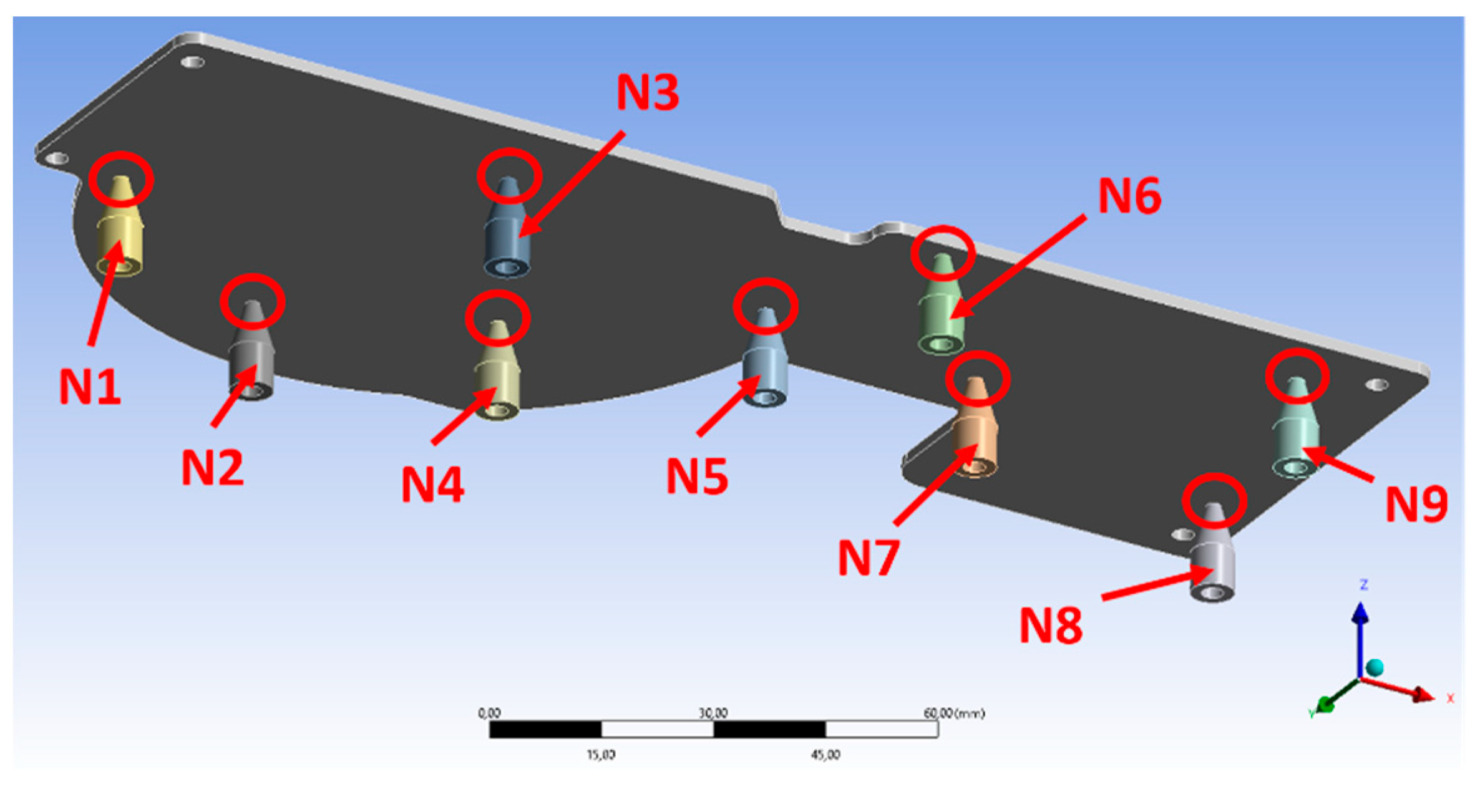
During the experimental tests, the PCB was supported by nine needles and pressed by three pressers. The relative locations of these components are shown in
Figure 5 (the letter N identifies the needles and the letter P identifies the pressers).
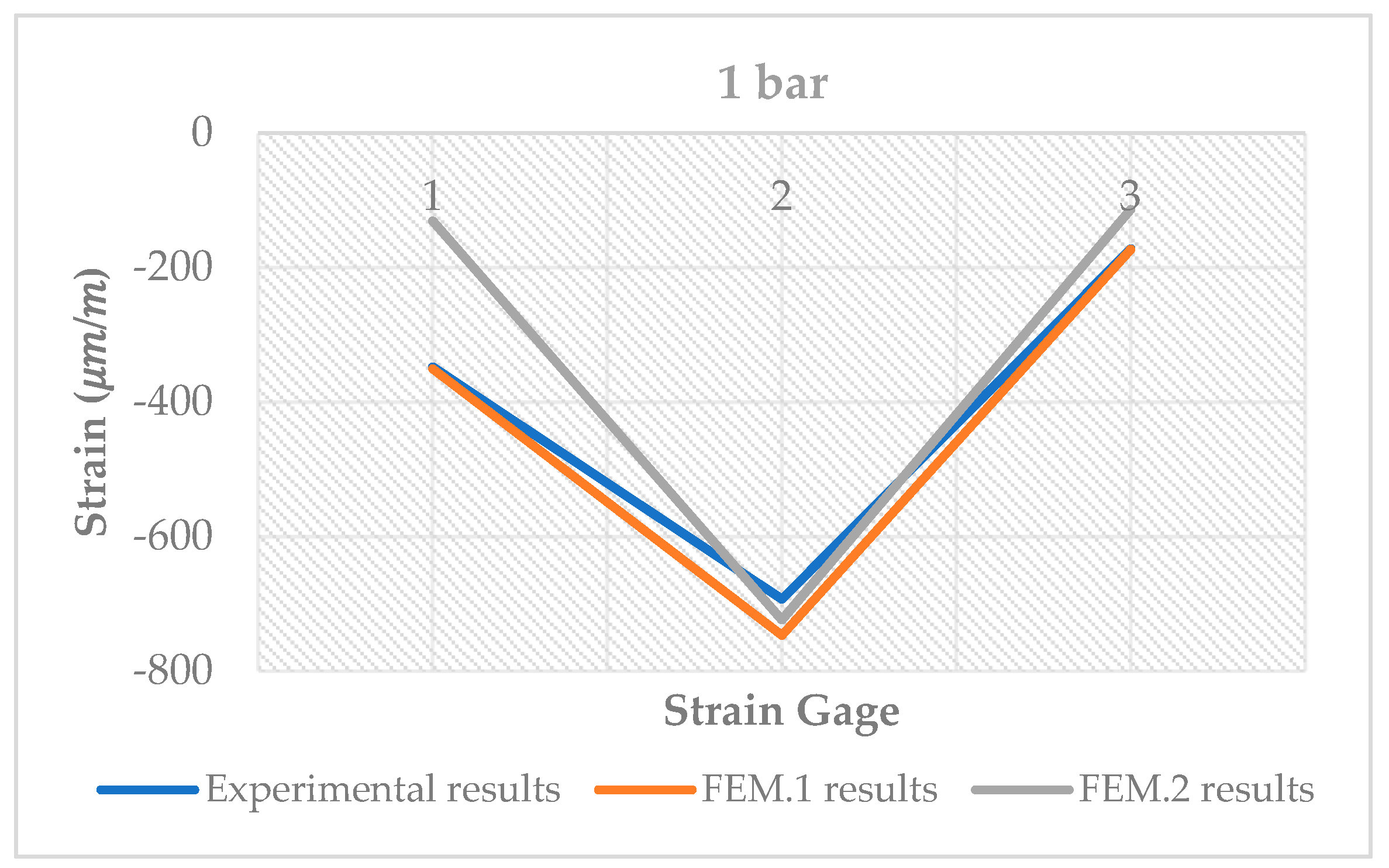
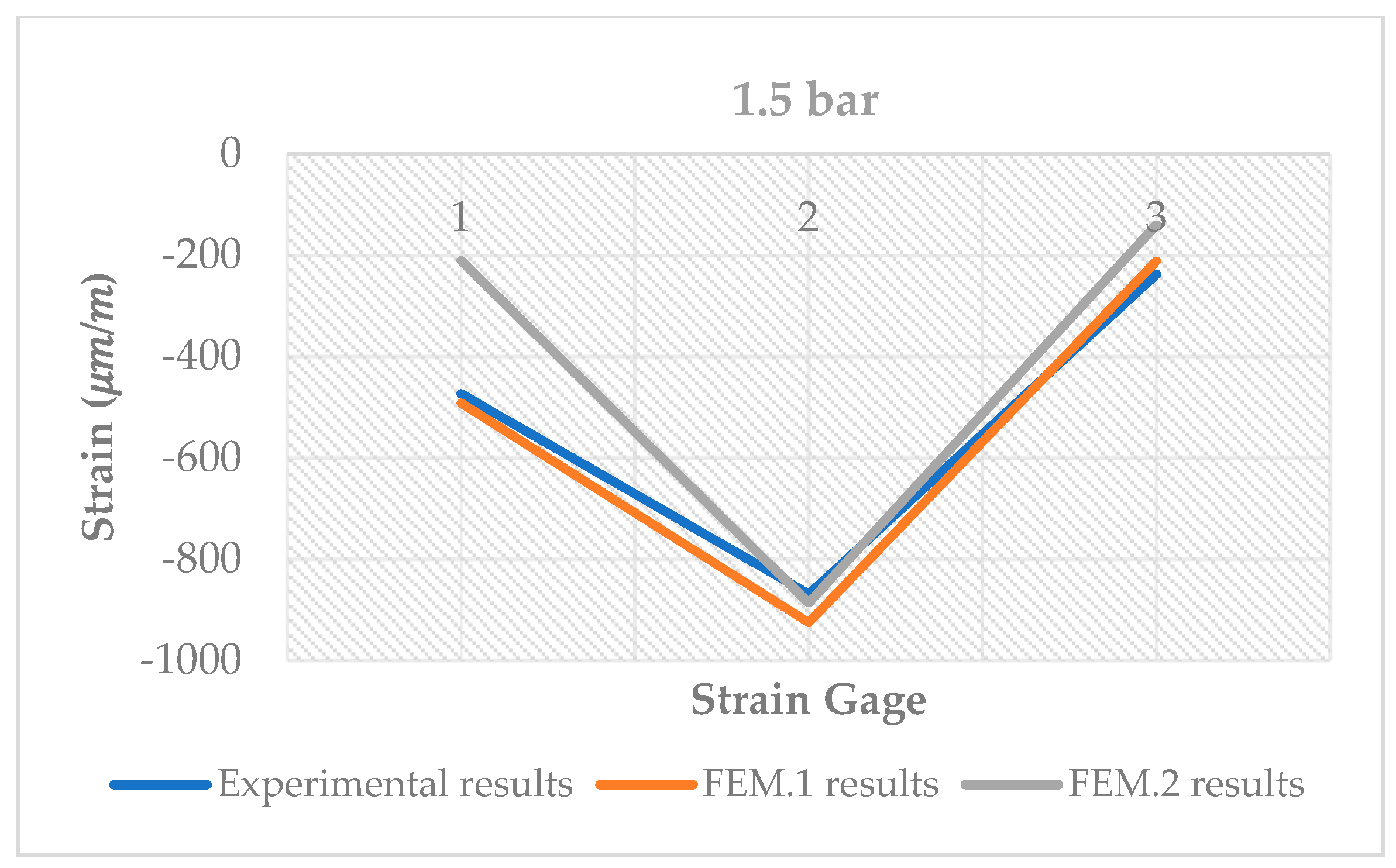
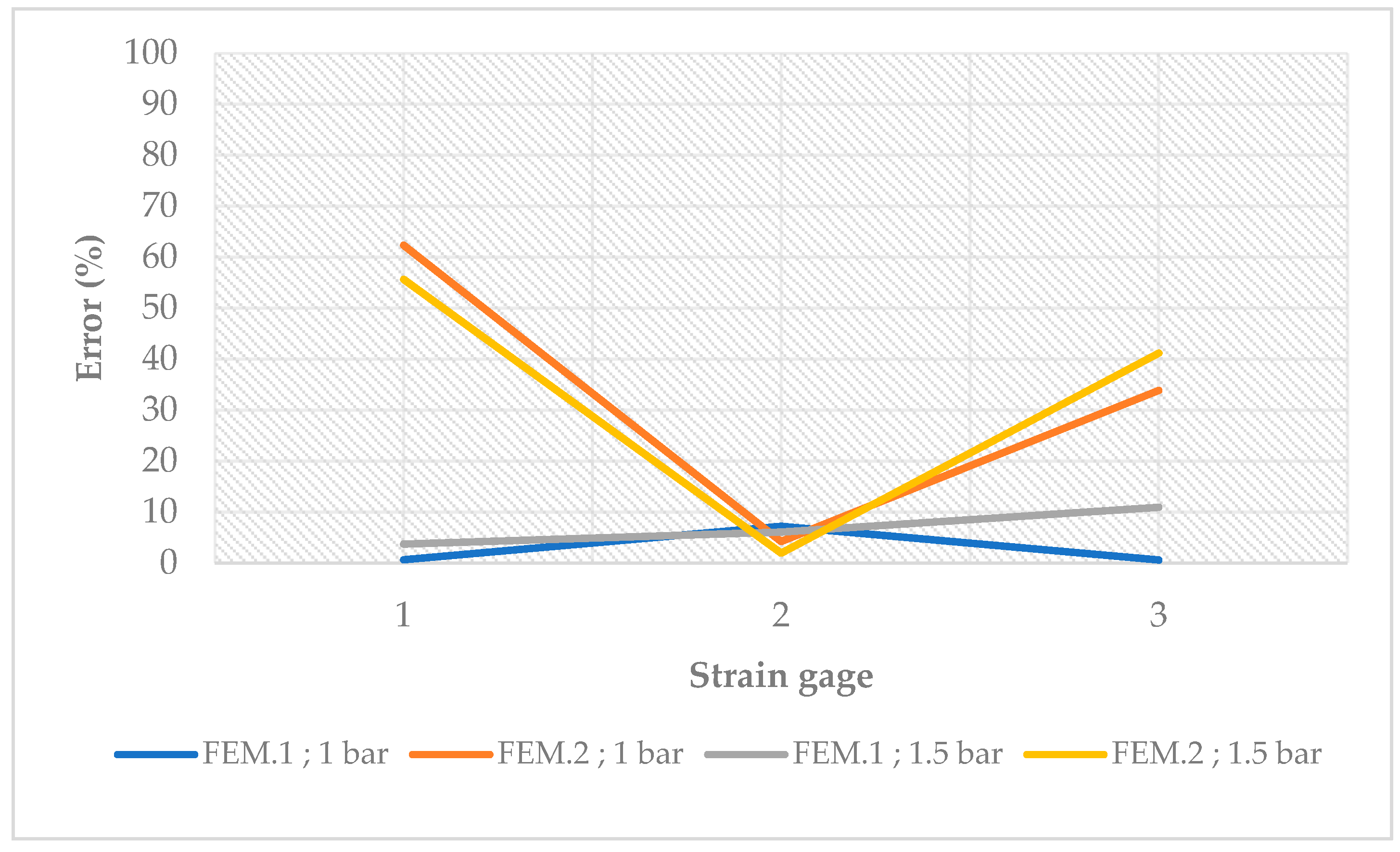
As explained, the force produced by each presser during the experimental tests were measured by load cells. Tests were performed with two different pressures, applied by a pneumatic cylinder: 1 bar and 1.5 bar. Based on the nomenclature in the
Figure 5, and arising from each pressure, the forces associated to each of the three pressers are in the
Table 1.
These positions were chosen to represent different amounts of copper in the PCB, in different directions. This way, it is possible to obtain different configurations concerning the amount of copper.
Since PCBs have different layers, it is necessary to take into account the amounts of copper on each layer.
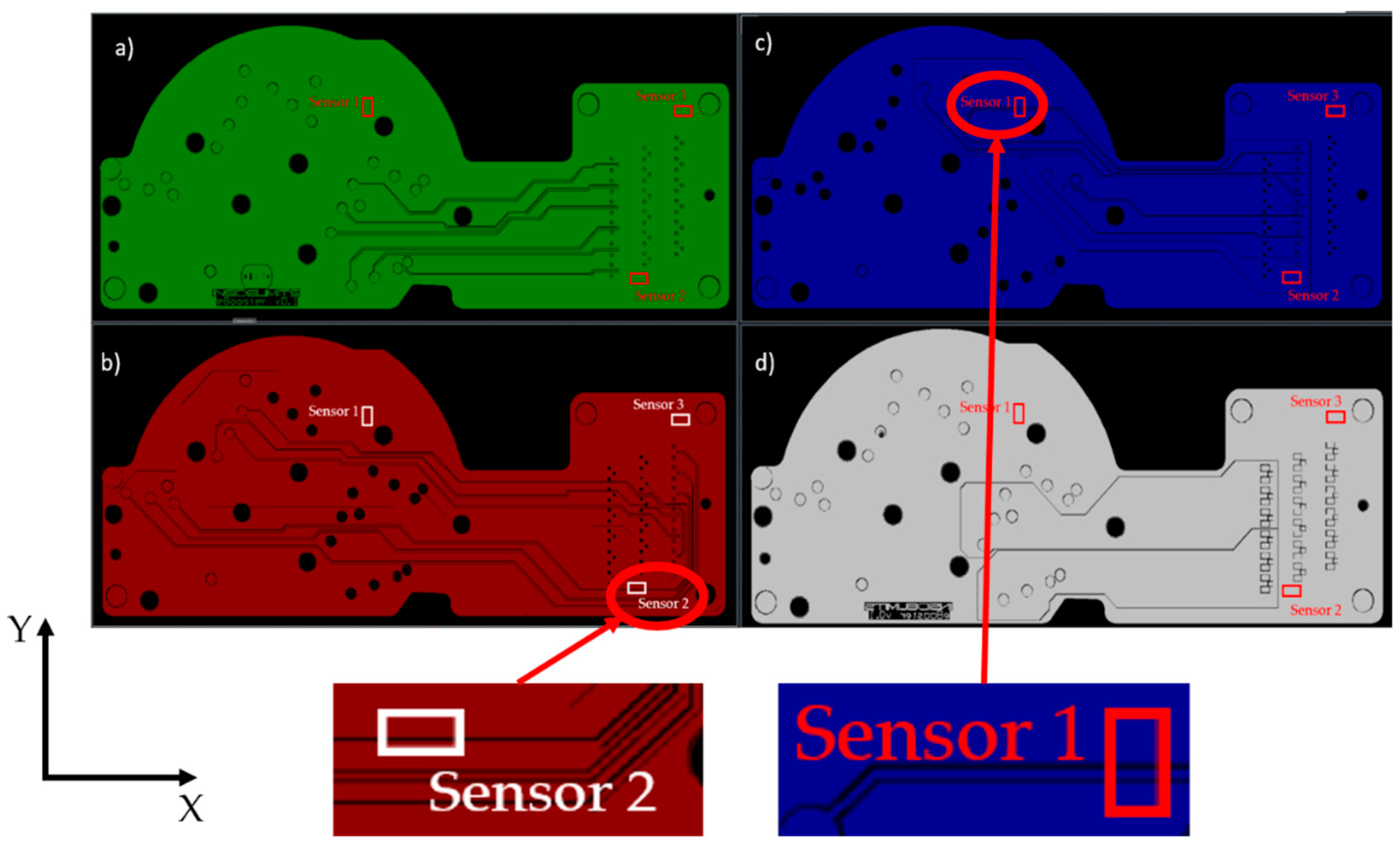
The positions of the three strain gage sensors are presented in
Figure 6: (a) 1st copper layer; (b) 2nd copper layer; (c) 3rd copper layer; (d) 4th copper layer.
According to the referential in
Figure 6, sensor 1 measures the strain in the Y direction and sensors 2 and 3 measure the strain in the X direction. It is possible to observe that sensor 1 is located above a region of the PCB where there are copper traces perpendicular to the sensor measurement direction in the third layer. Sensor 2 is in a location where it found a copper trace—in the second layer, with the same direction of the sensor measurement direction. Sensor 3 is above a region where there are no copper traces. Thus, it was possible to cover the different basic configurations of copper amounts in a PCB.
2.2. Finite Elements Analysis
A PCB is a complex device with specific and complex mechanical properties, which vary due to several factors, such as the number of layers, the thickness, the type of fiber of the composite material that attaches the copper traces, the fiber density, and the weavy-style (number of bundles in fill-and-warp directions) [
3,
19,
20]. All these variables need to be taken into account when creating an FEM of a PCB, regardless of the type of study that is being conducted. There are many authors modelling PCBs as a full single material body [
2,
5,
6,
7,
8,
10,
12,
13,
17,
18,
20,
21]; however, to obtain more accurate results, some researchers have opted to create multi-layered models considering the layers of the PCBs [
3,
11,
19,
20,
22].
When running PCB numerical simulations, when considering it as a full single material body, it is assumed that the PCBs are a whole body made of a fibrous composite (matrix phase/reinforcement phase plus fiber phase). Under these conditions, the PCB material properties could be considered either isotropic or orthotropic. In full body isotropic models, the PCBs are considered as an elastic–plastic material, defined by a stress–strain curve resultant from tensile tests, and their behaviour follows the von Mises criteria:
where
represents the Shear Modulus,
is the Young Modulus, and
represents the Poisson’s Ratio. In the full body orthotropic model, the fiber phase is neglected and this way, the PCBs are modelled as degenerated bi-phase models, acquiring an orthotropic behaviour [
20].
On the other hand, when discretizing the layers of the PCBs, there could be layers made of an electrically conductive material (copper is the most widely used), interspersed with fibrous composite layers. Similarly, fibrous composite layers might be considered either isotropic or as orthotropic. Further, a multi-layered PCB model has been also developed, which divides fibrous composite layers into two sub-layers, with each layer discretizing the fill and wrap fiber directions. The fibers are involved and impregnated in the matrix phase (FR-4 epoxy resin is most widely used for this application) [
20].
Figure 7 shows the most common ways to model a PCB.
Y. Wan et al. [
20] carried out a study on the mechanical behaviour of a PCB when subjected to a drop impact experimental test. It undoubtedly showed that the multi-layered fill-wrap model allows for the most accurate and realistic FE analysis. However, the computational requirements and the time required to run the simulations are extremely high. It also stated, as expected, that the isotropic model is the worst representation of reality if the results collected from the drop-impact experimental test are the most disparate.
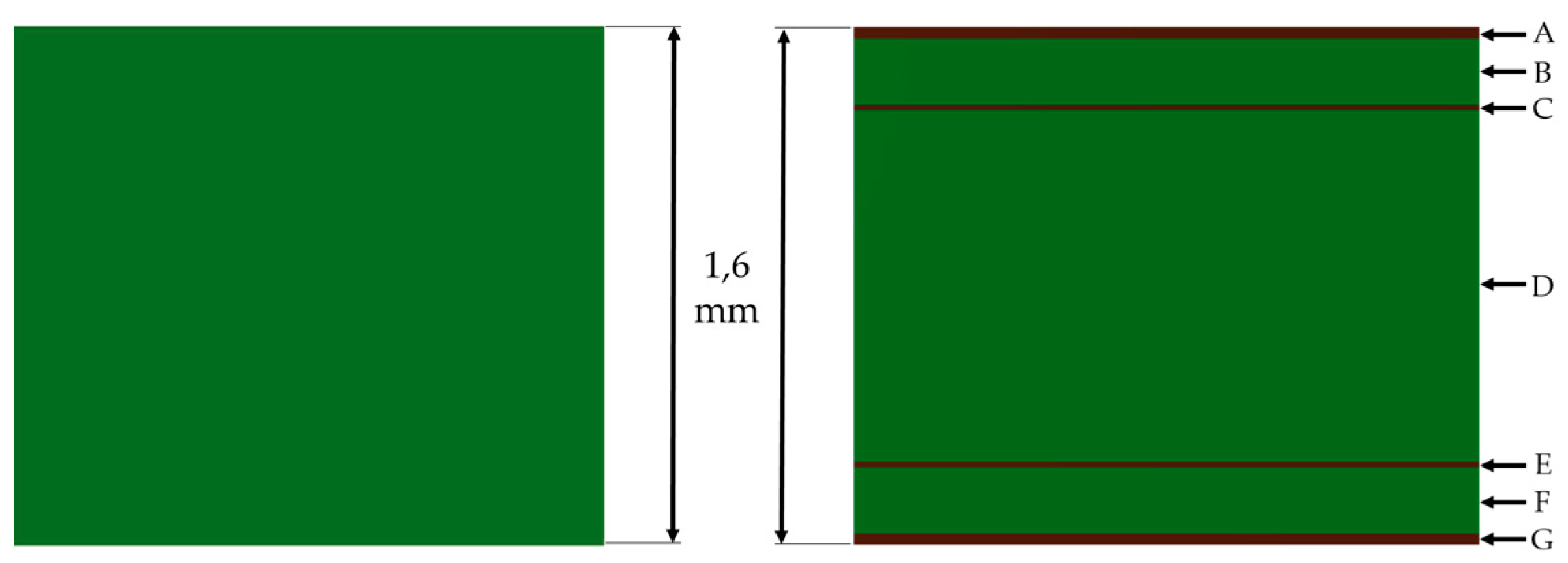
The present work tried to find out the best FEM to simulate PCB behaviour during ICTs. It used a 1.6 mm thick, multi-layered PCB (four copper layers) named eBooster.
Figure 8 shows the schematic sectional view of eBooster when considering both homogeneous and multi-layered models.
Layer thickness and materials of multi-layer PCBs models are presented in
Table 2.
Once the PCB was made using an orthotropic fibrous composite reinforcement (woven E-glass FR-4 epoxy resin), the following two FEM were created:
FEM.1: Homogenous orthotropic model with solid element meshing
FEM.2: Multi-layered orthotropic model with solid element meshing representing the fibrous composite layers and with shell element meshing representing the copper layers
The mechanical properties of each material of the PCB are tabulated in
Table 3.
In order to match the simulation approach with the experimental setup—as described in
Section 2.2—the software Ansys was used. Apart from FEM, the boundary conditions that rule all the FEA were the same. The PCB was supported by needles and loaded by pressers, and the material assigned to the needles was structural steel in order to represent the reality created in the experimental setup. The contacts between the needles and the PCB were defined as
rough with the formulation
adjust to touch. This type of contact allows gaps or penetration between the contact and target surfaces, once the FEM surfaces are mathematically approximated. In
Figure 9, the needles and their contacts with the PCB are shown. In
Figure 10, the locations where the three pressers load the PCB are represented. Naturally, those locations were based on the pressers’ locations in the experimental tests.
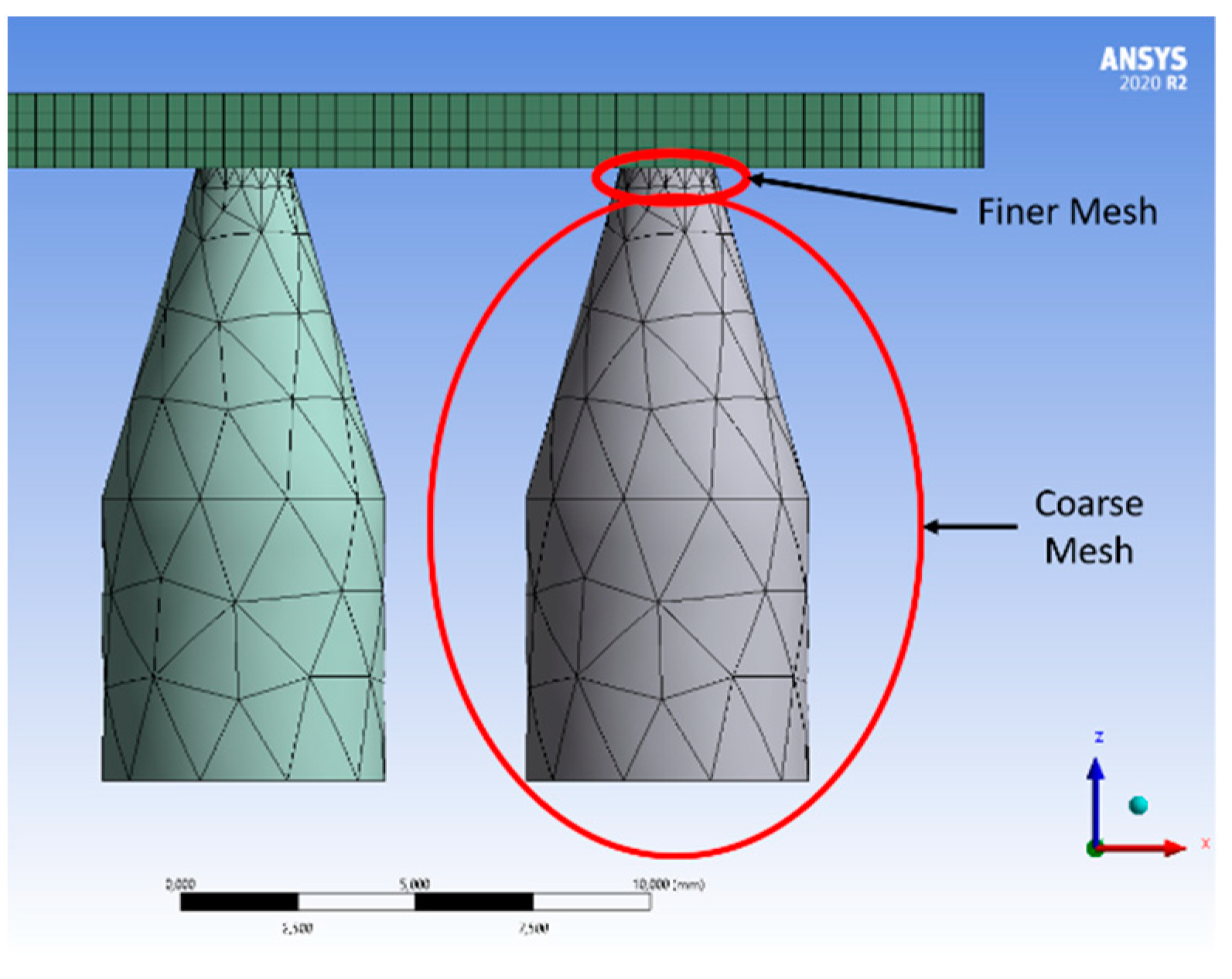
Fine mesh face sizings were applied to the needles’ faces that were in contact with the PCB. Once these contacts were defined as rough with the formulation adjust to touch, this face sizing is a crucial step, since it will prevent excessive penetration between the needles’ elements and the PCB elements.
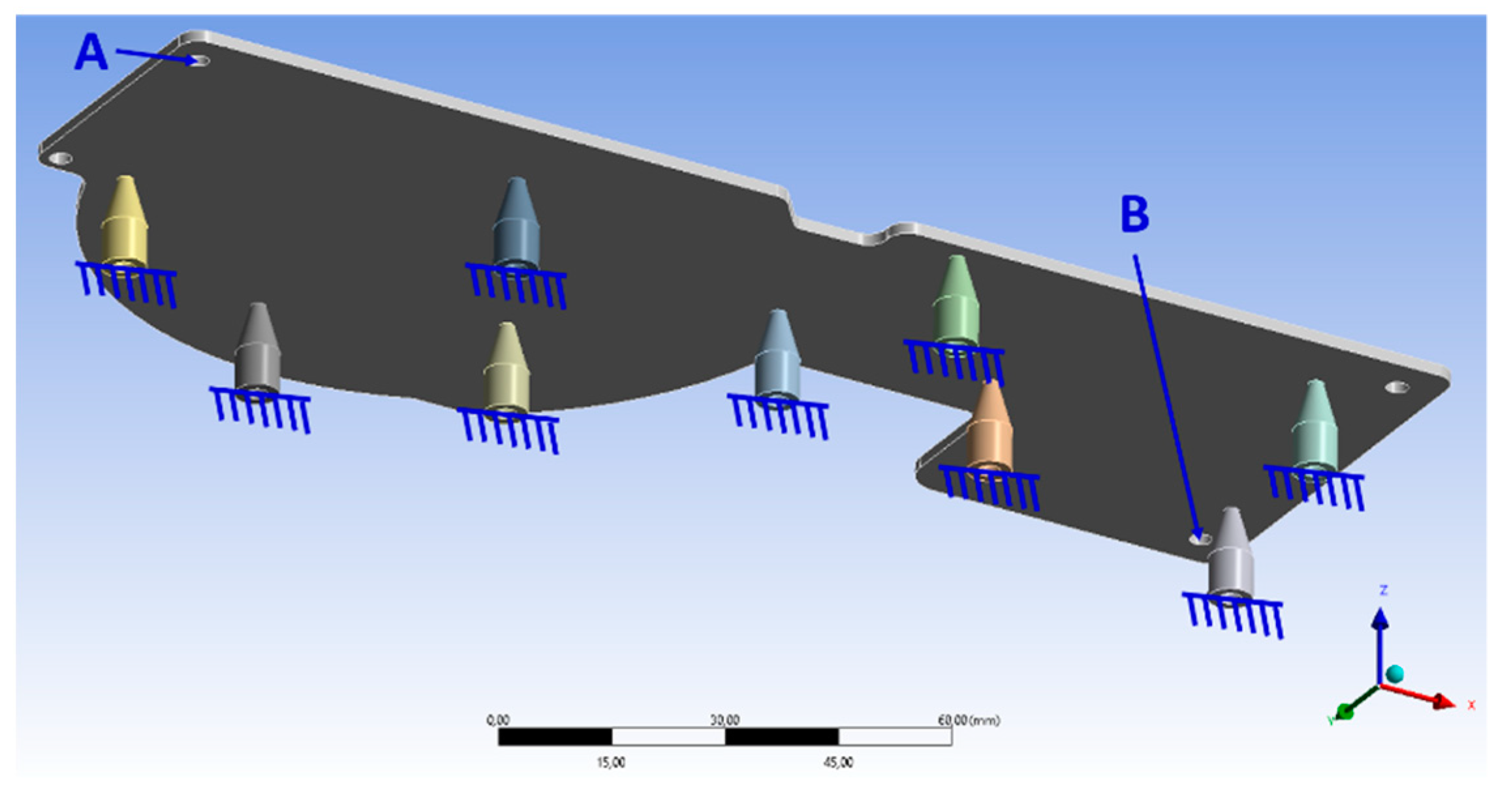
The interior walls of the guiding holes (denoted as A and B in
Figure 11), where the fixing pins are inserted to fix the PCB, were constrained as
fixed. This means the holes are prevented from any kind of motion. Further, the needles were considered as
grounded in order to restrain their movement in the Z-axis (
Figure 11).
In FEM.1, a multizone method was applied to the PCB, and it was defined with hexahedral elements which fit within the PCB geometry, allowing to obtain excellent mesh metrics properties. Once the needles are out of the interest region, they are meshed with a default coarse mesh (automatic method) to reduce computational analysis complexity. However, fine mesh face sizing was applied to the needles’ faces that were in contact with the PCB (
Figure 12). In FEM.2, the copper layers were meshed with shell elements and the fibrous composite layers were meshed with solid elements. To fit within the thinner copper layers, the quadrilateral method was used. A multizone method with hexahedral elements was used on the solid elements layers. Part of the meshes of both FEM can be seen in
Figure 13.
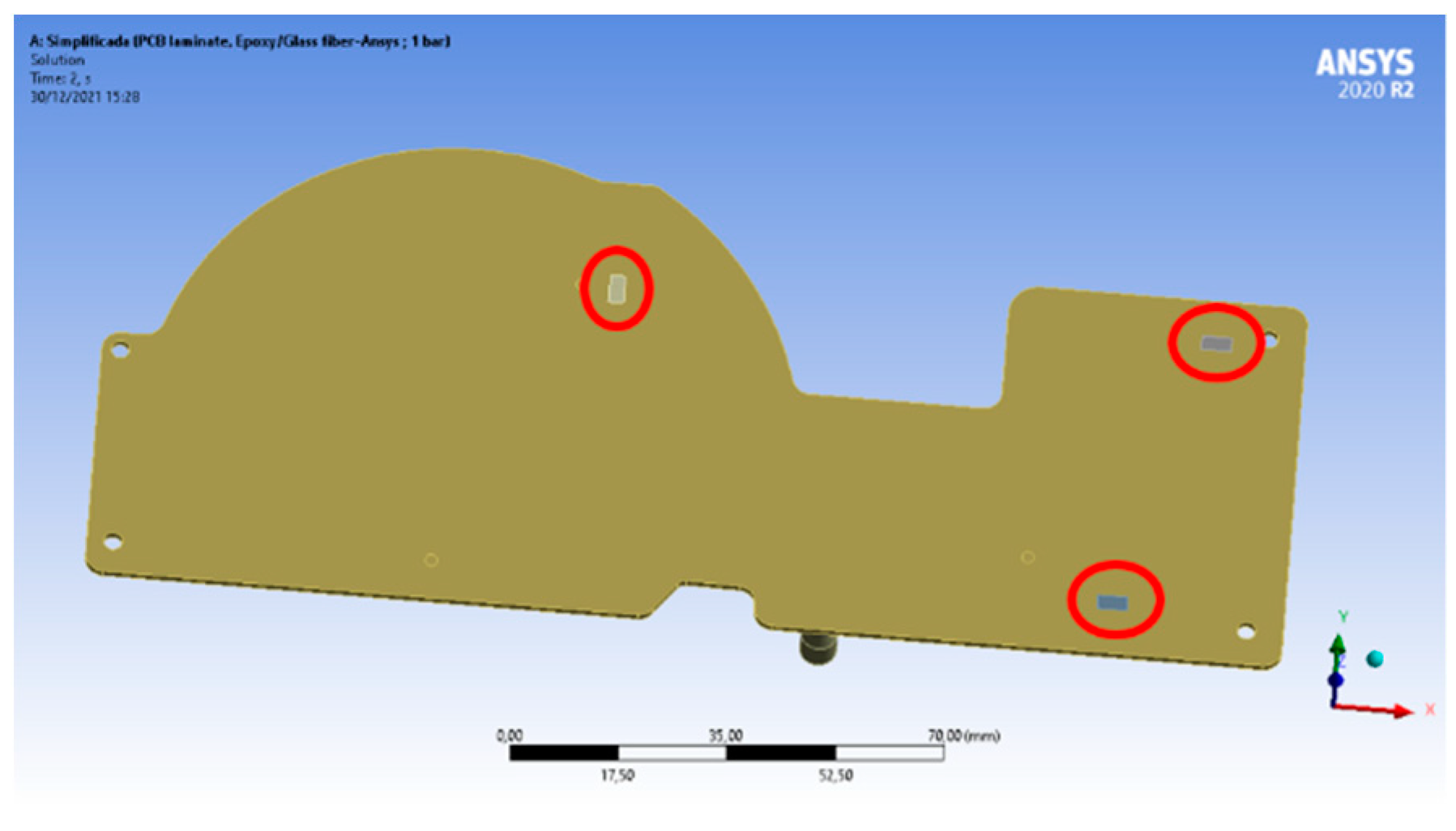
In order to match the experimental setup, the three strain gages were modelled in corresponding locations and orientations as rectangular prisms, with negligible thickness, and meshed with a single shell element (
Figure 14).
Since each strain gage is a single element, during the pre-processing phase, it was ordered to the Ansys to return the element mean strain for each of the three created strain gages. The measurement orientation of each strain gage was selected in accordance with the experimental test setup.
Thus, Finite Element Analysis for each of the two FEM was performed, applying forces performed by the three pressers. The forces measured during the experimental tests were followed, namely, those that resulted from the pneumatic pressures of 1 bar and 1.5 bar.