Investigation into the Electrohydraulic Synchronous Motion Control of a Thrust System for a Tunnel Boring Machine
Abstract
:1. Introduction
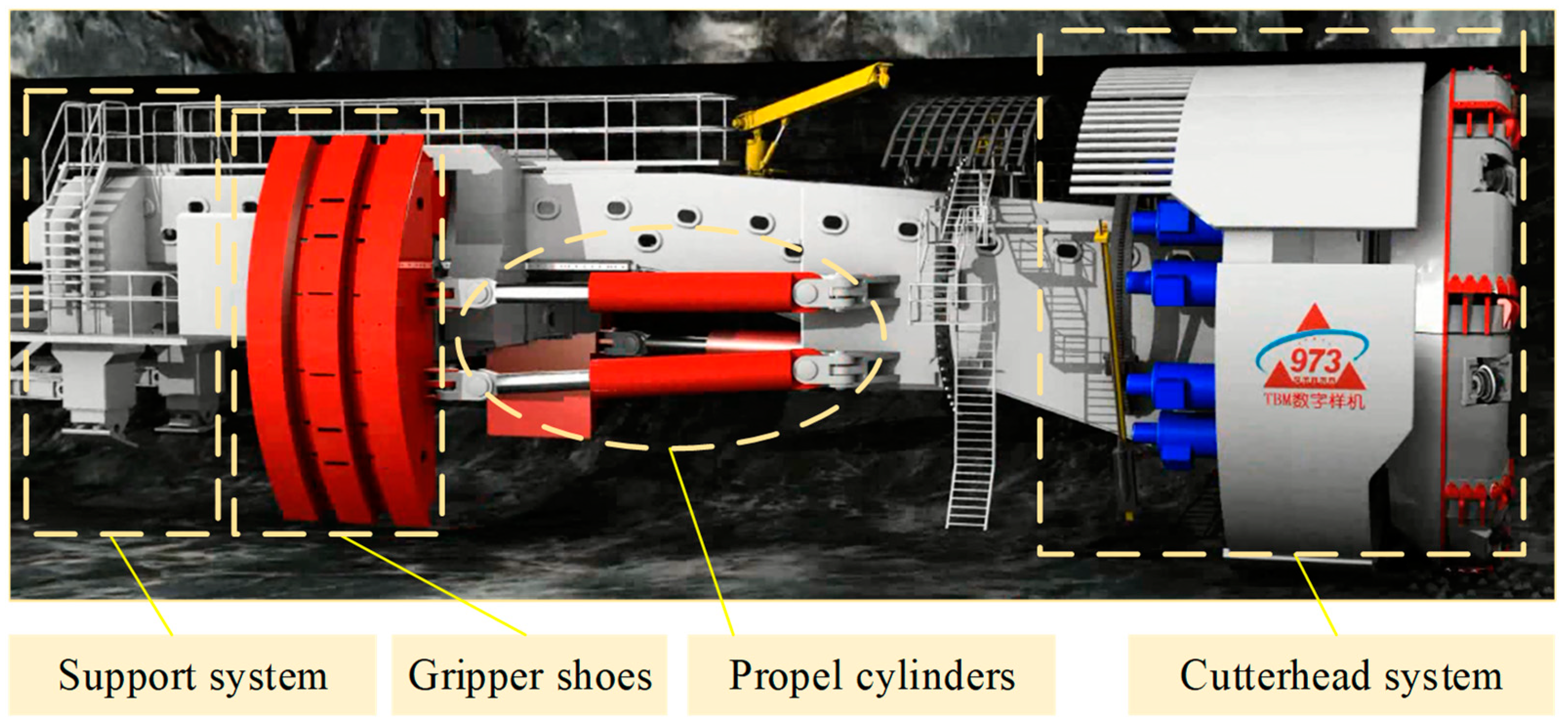
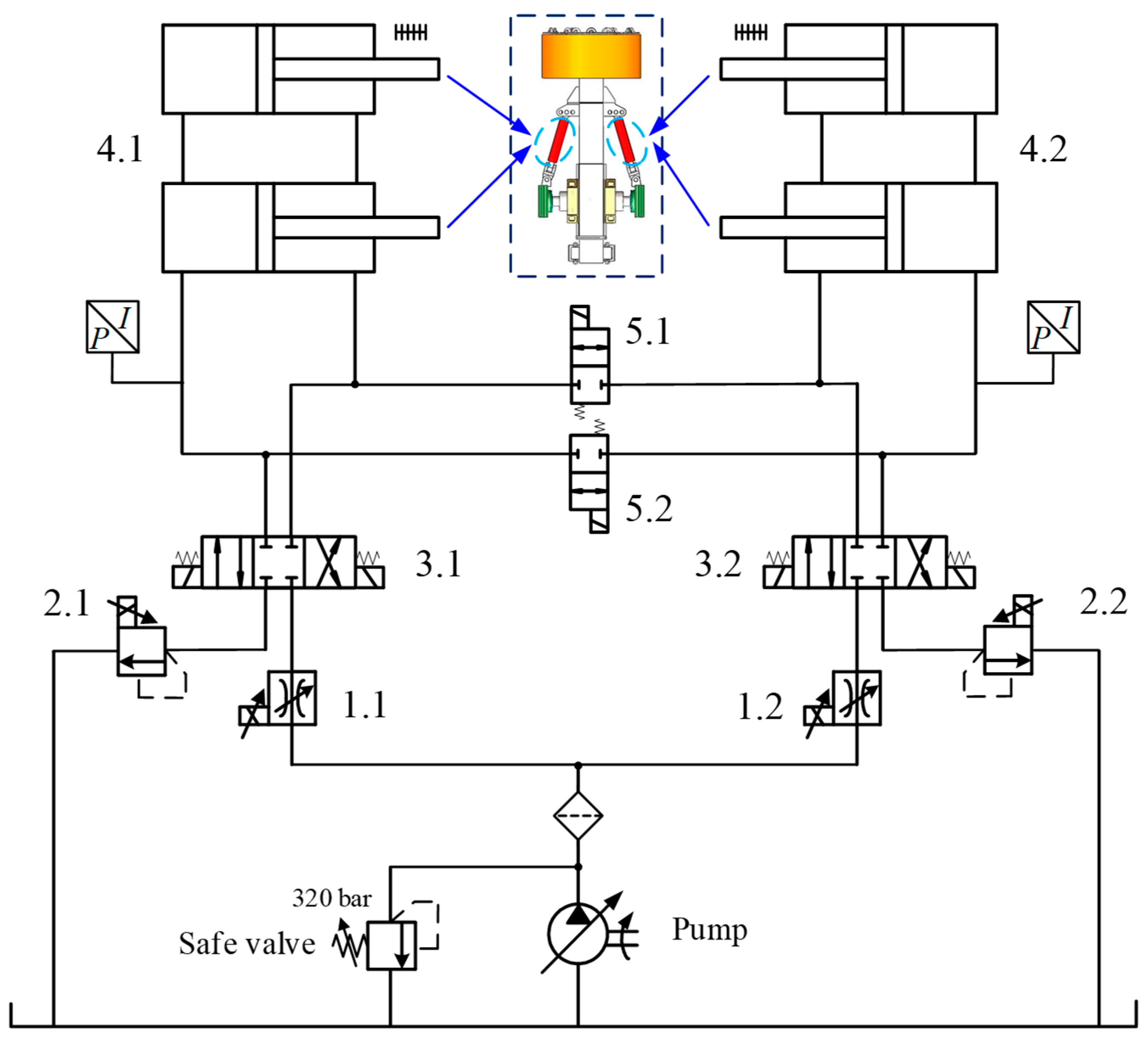
2. Description of the Thrust Hydraulic Control System
3. Electrohydraulic Control System Design
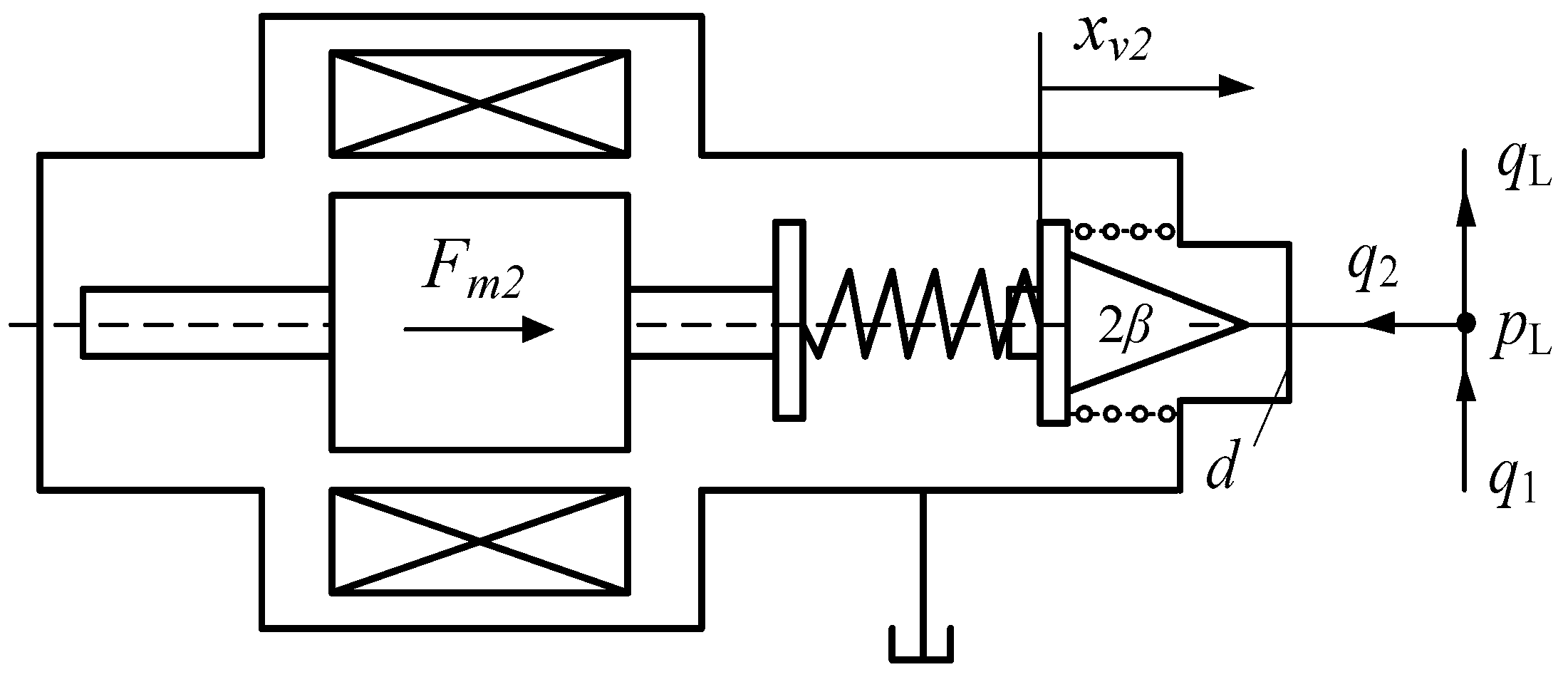
3.1. Mathematical Modeling
3.2. Control Strategy
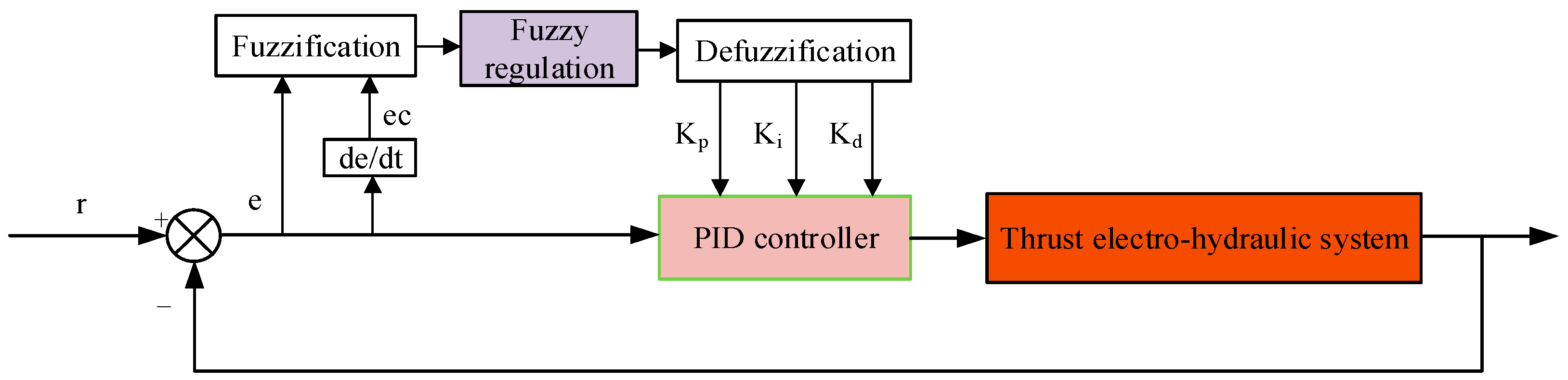
3.3. Design of the Fuzzy PID Controller
3.3.1. PID Controller Design
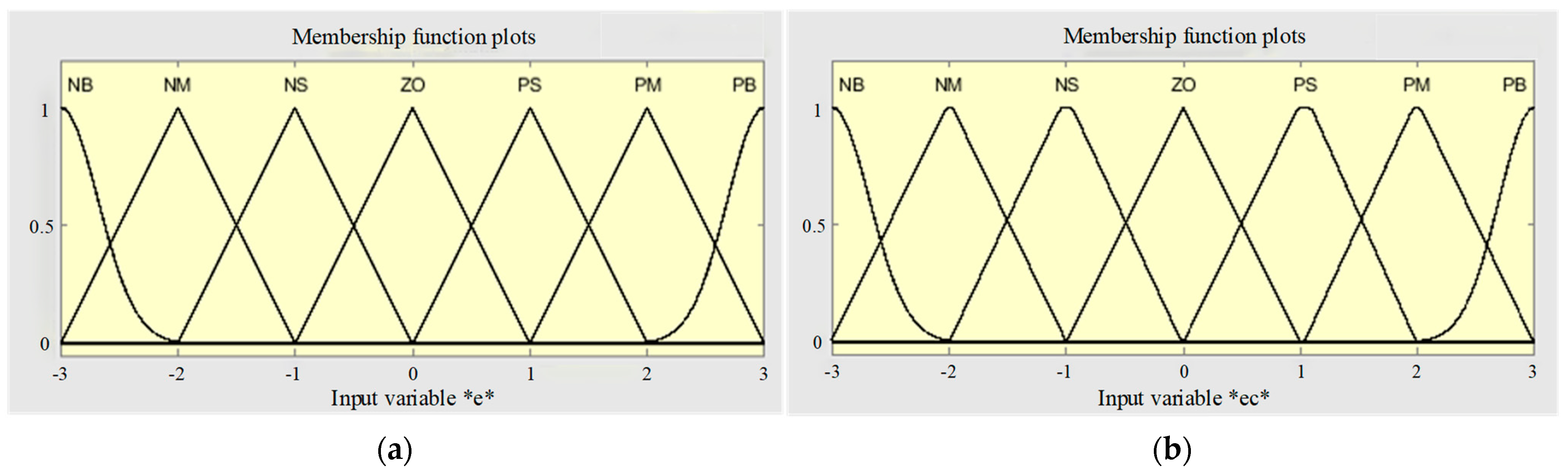
3.3.2. Definition of Domain and Membership
3.3.3. Fuzzy Control Rules
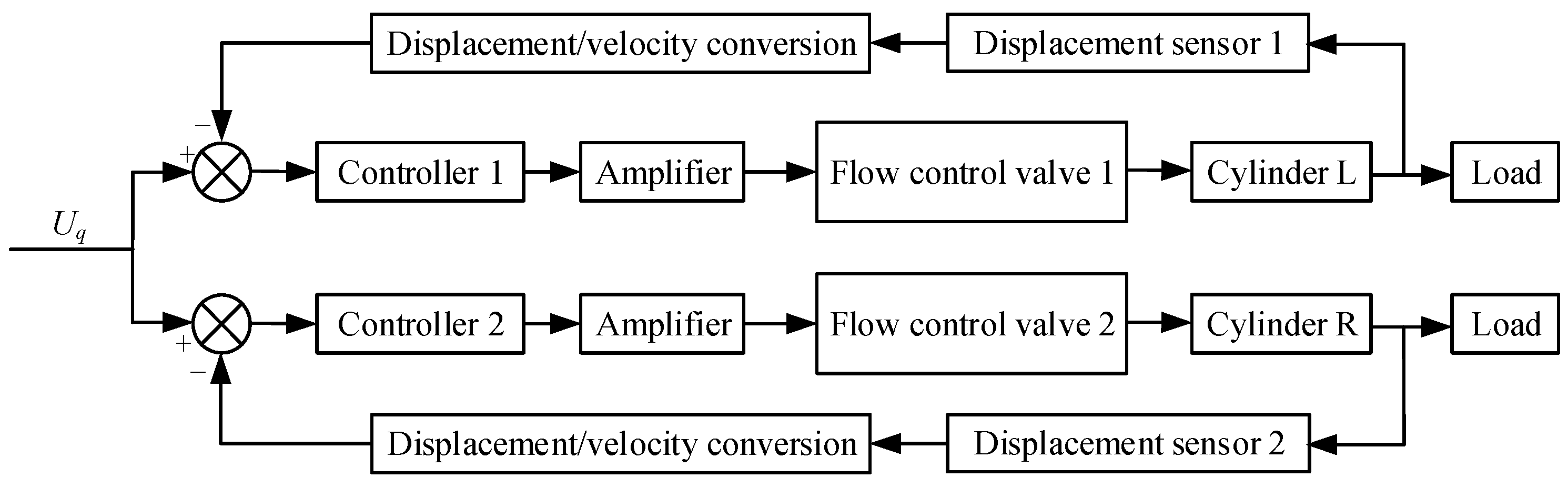
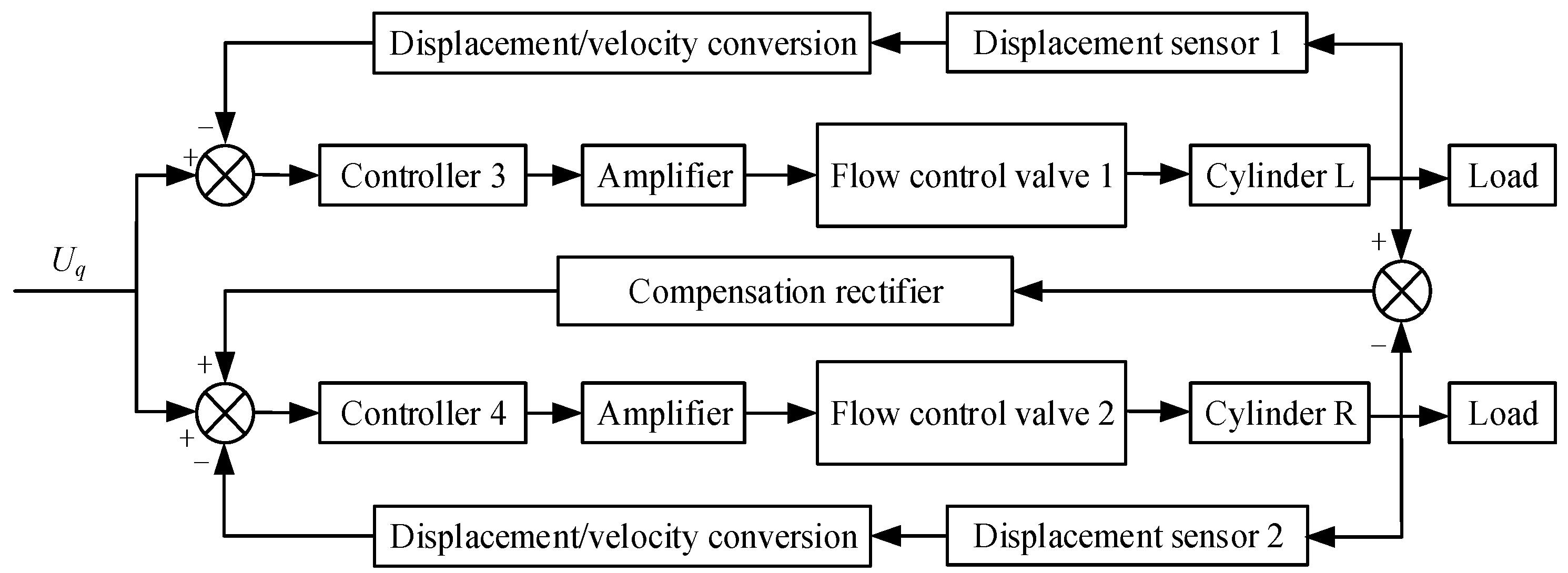
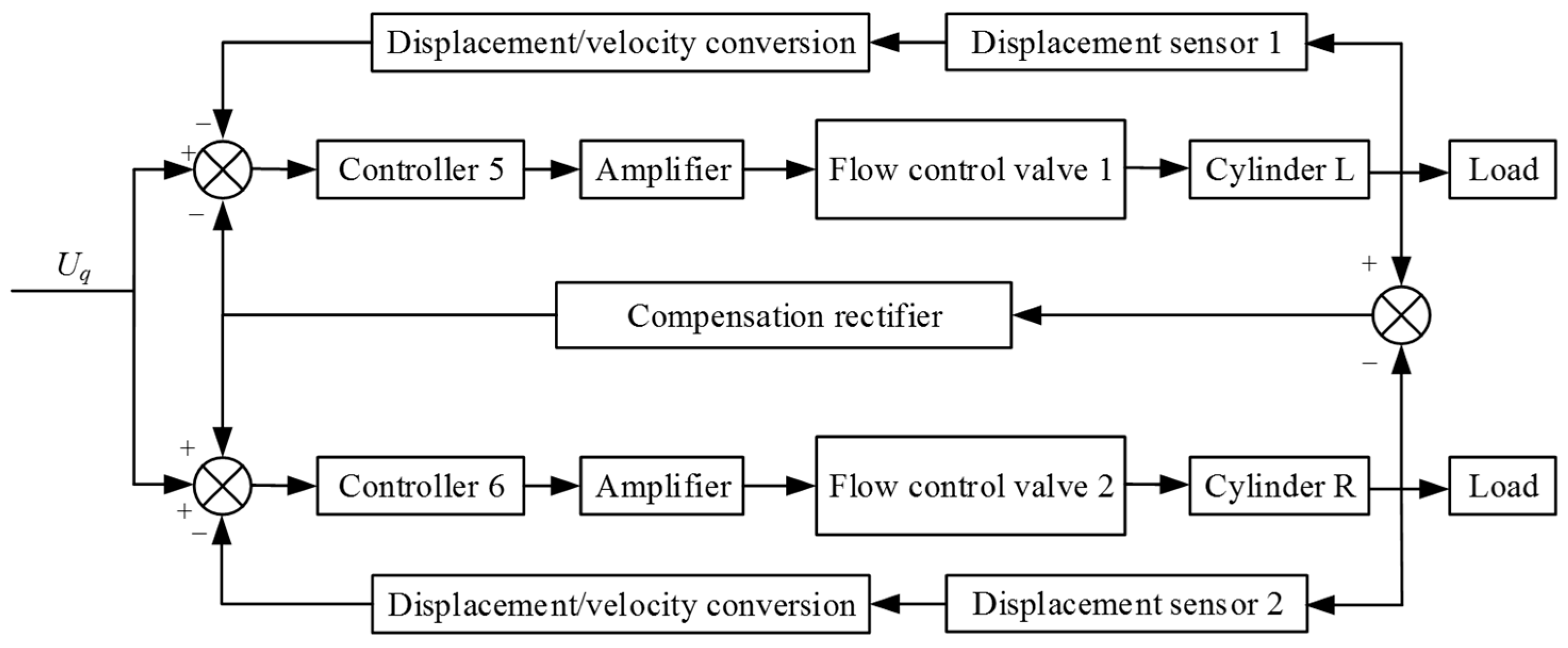
4. Synchronous Motion Control of Propel Cylinders
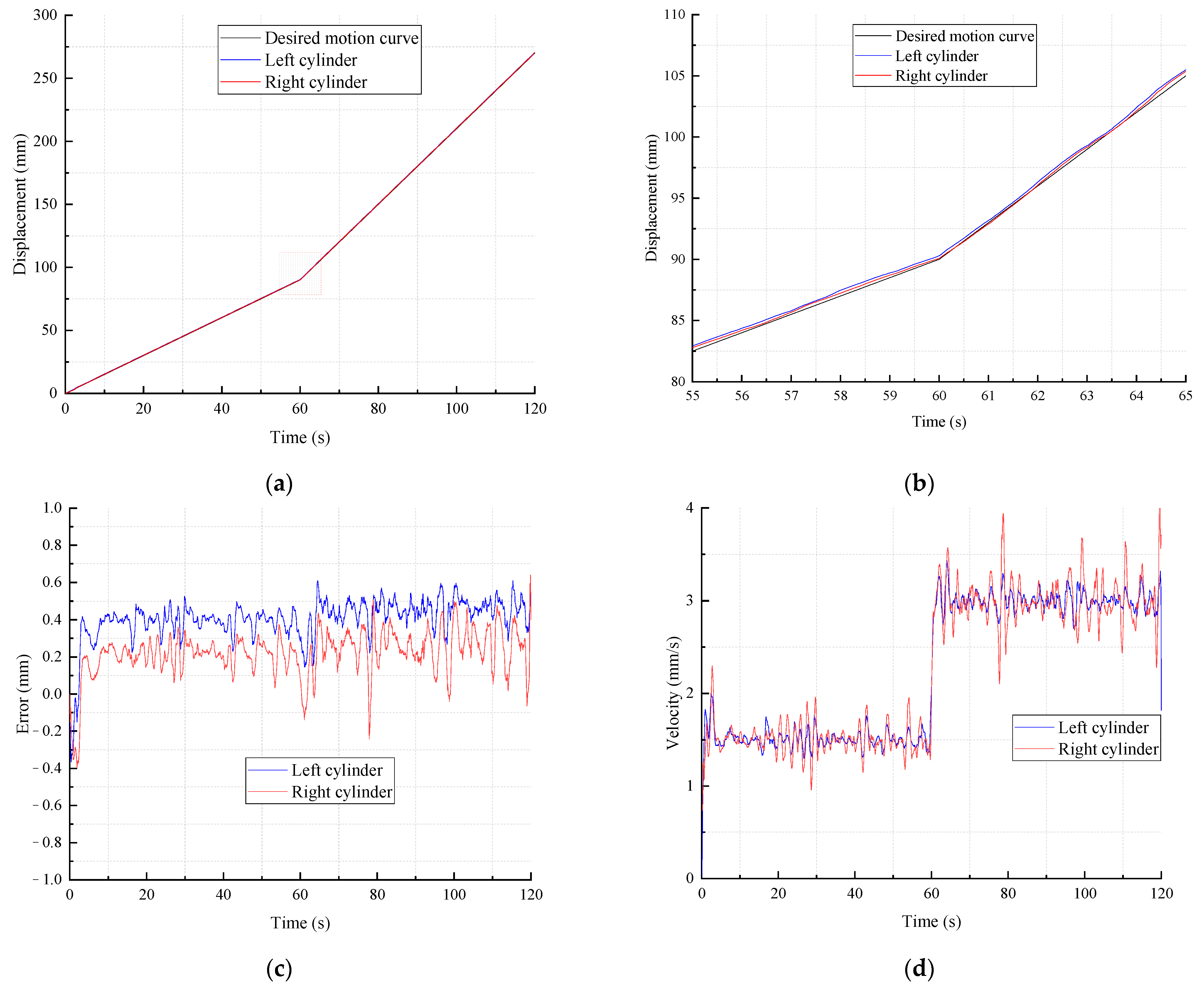
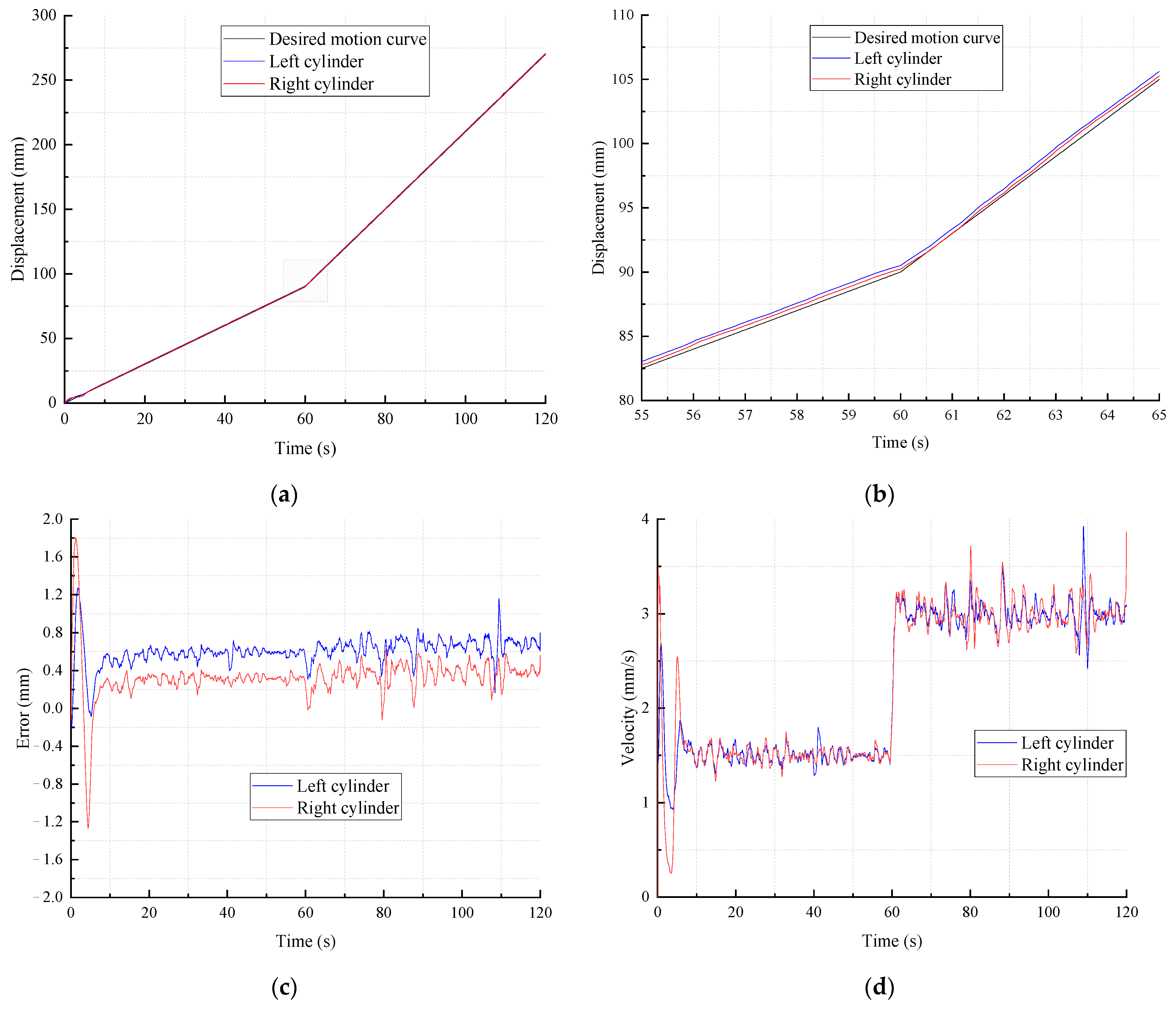
5. Experimental Results and Analysis
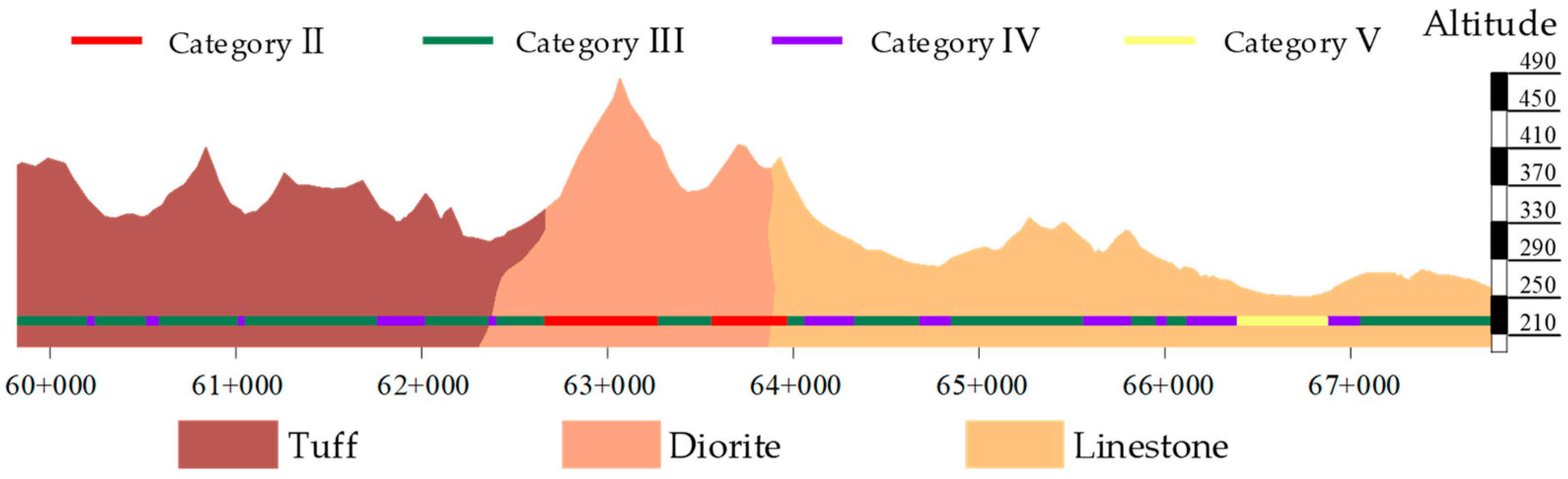
5.1. Test Rig Design
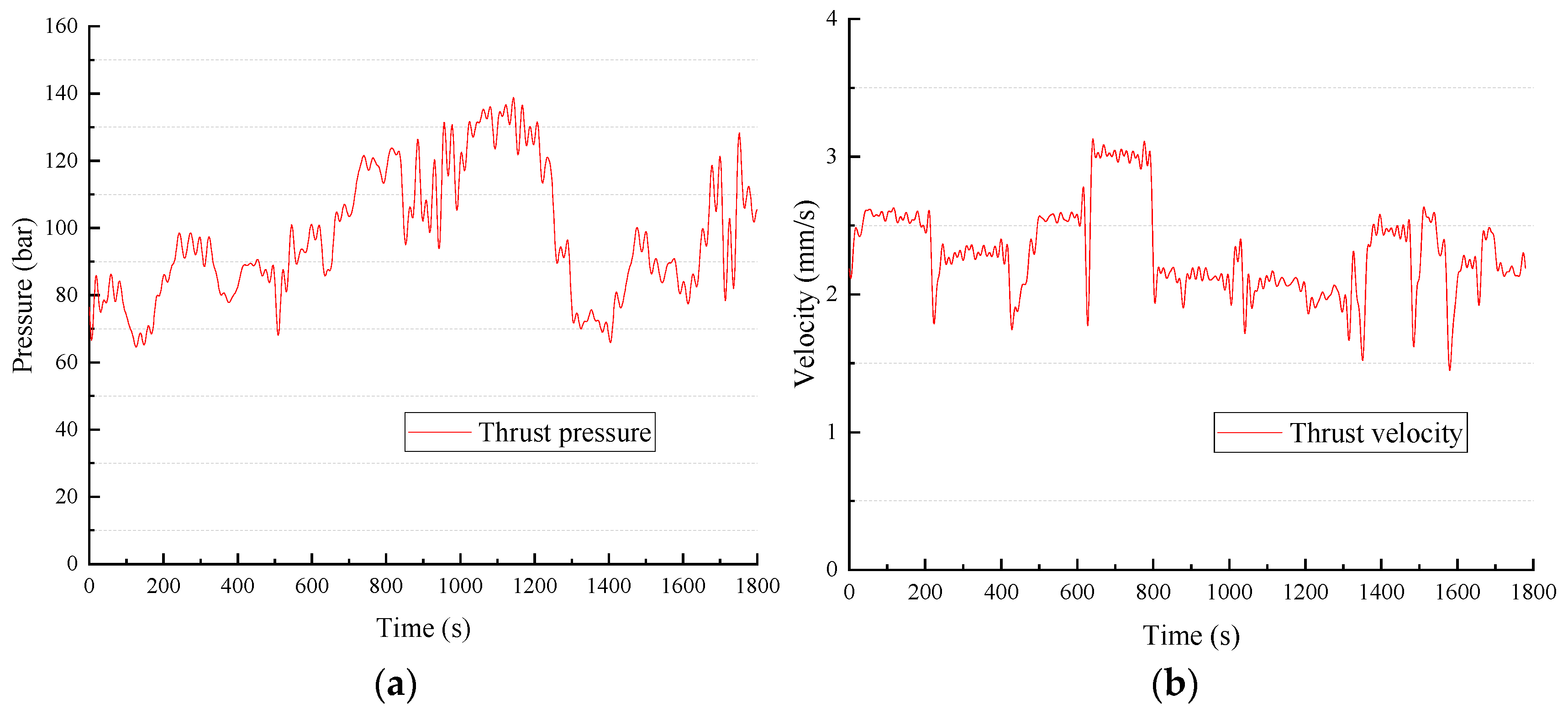
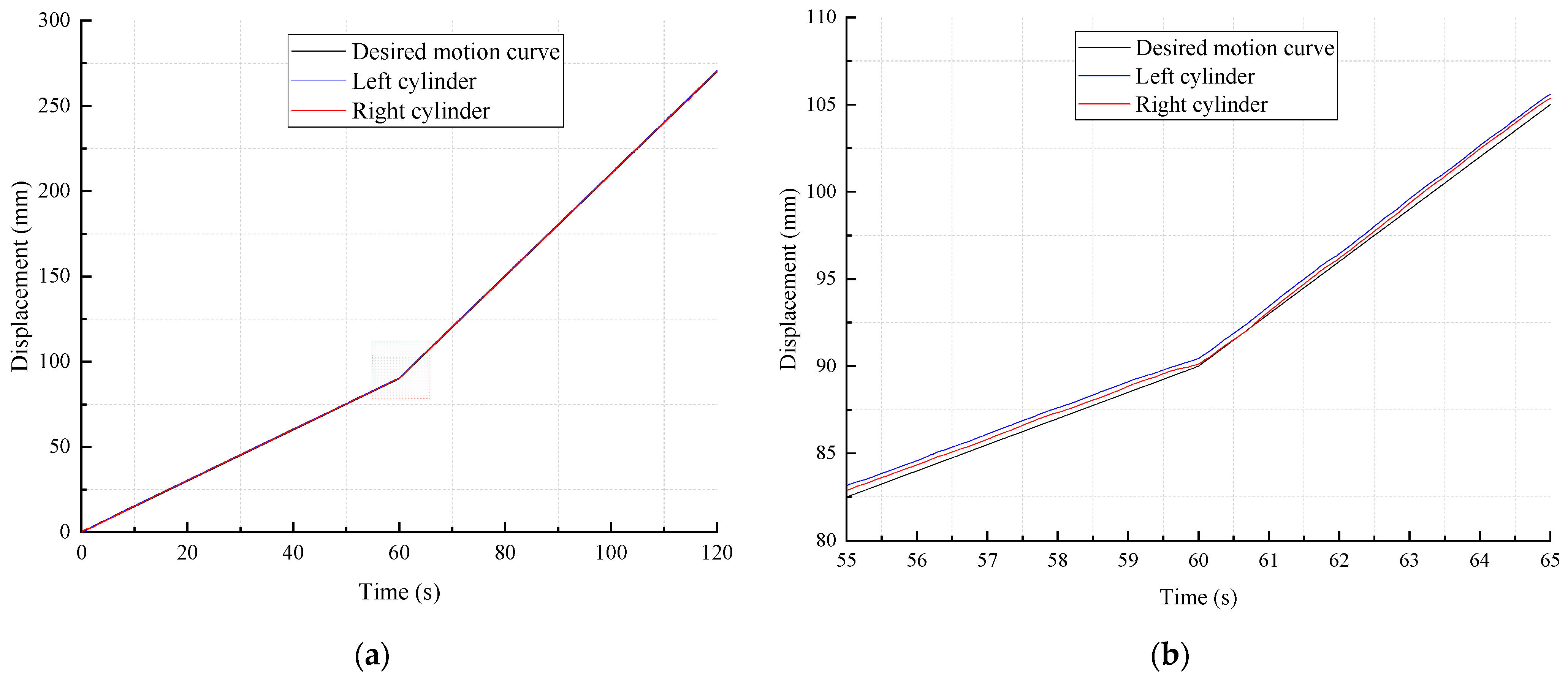
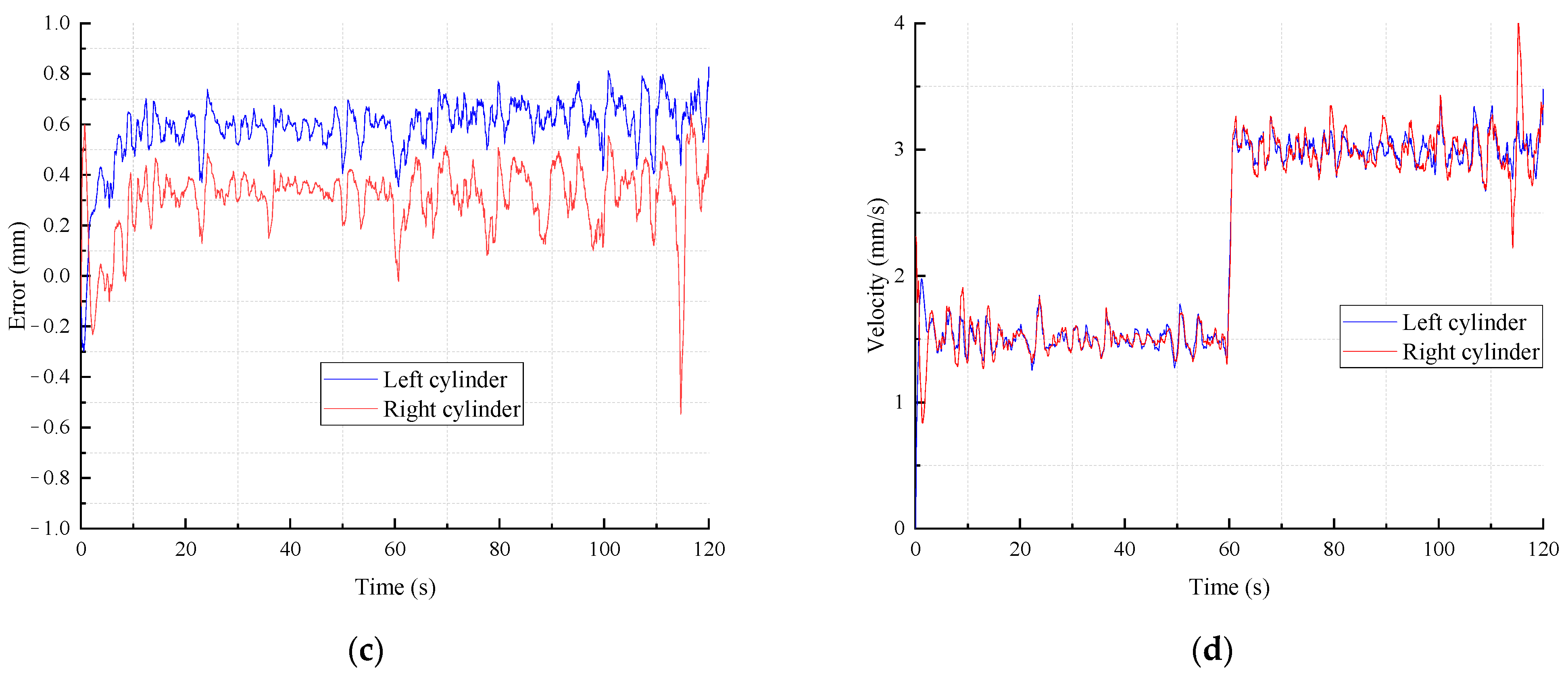
5.2. Test Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahmoodzadeh, A.; Mohammadi, M.; Ibrahim, H.H.; Abdulhamid, S.N.; Ali, H.F.H.; Hasan, A.M.; Khishe, M.; Mahmud, H. Machine learning forecasting models of disc cutters life of tunnel boring machine. Autom. Constr. 2021, 128, 103779. [Google Scholar] [CrossRef]
- Wang, F.; Gong, G.; Duan, L.; Qin, Y. XGBoost. J. Zhejiang Univ. 2020, 54, 633–641. [Google Scholar]
- Rostami, J.; Dreyer, C.; Duhme, R.; Khorshidi, B. Challenges of Designing a Tunnel Boring Machine (TBM) for Development of Under-ground Structures on the Moon; CRC Press/Balkema: Naples, Italy, 2019; pp. 4206–4217. [Google Scholar]
- Armaghani, D.J.; Azizi, A. An Overview of Field Classifications to Evaluate Tunnel Boring Machine Performance; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–16. [Google Scholar] [CrossRef]
- Grasmick, J.; Mooney, M. A Probabilistic Geostatistics-Based Approach to Tunnel Boring Machine Cutter Tool Wear and Cutterhead Clogging Prediction. J. Geotech. Geoenvironmental Eng. 2021, 147, 05021014. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Fahimifar, A.; Ghaleini, E.N.; Momenzadeh, M.; Armaghani, D.J. Development of a new hybrid ANN for solving a geotechnical problem related to tunnel boring machine performance. Eng. Comput. 2020, 36, 345–357. [Google Scholar] [CrossRef]
- Wang, L.; Sun, W.; Long, Y.; Yang, X. Reliability-Based Performance Optimization of Tunnel Boring Machine Considering Geological Uncertainties. IEEE Access 2018, 6, 19086–19098. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Faradonbeh, R.S.; Momeni, E.; Fahimifar, A.; Tahir, M.M. Performance prediction of tunnel boring machine through developing a gene expression programming equation. Eng. Comput. 2017, 34, 129–141. [Google Scholar] [CrossRef]
- Khorasani, E.; Azali, S.T.; Naghadehi, M.Z.; Jalali, S.E.; Jimenez, R.; Zare, S. Performance analysis of tunnel-boring machine by probabilistic systems approach. Proc. Inst. Civil Eng. Geotech. Eng. 2018, 171, 422–438. [Google Scholar] [CrossRef]
- Shi, H.; Yang, H.; Gong, G.; Liu, H.; Hou, D. Energy saving of cutterhead hydraulic drive system of shield tunneling machine. Autom. Constr. 2014, 37, 11–21. [Google Scholar] [CrossRef]
- Shi, H.; Yang, H.; Gong, G.; Wang, L. Key technologies of shield tunneling machine and present status and prospect of test rigs for tunneling simulation. J. Zhejiang Univ. 2013, 47, 741–749. [Google Scholar]
- Wang, L.; Gong, G.; Shi, H.; Yang, H. Modeling and analysis of thrust force for EPB shield tunneling machine. Autom. Constr. 2012, 27, 138–146. [Google Scholar] [CrossRef]
- Lee, G.-J.; Ryu, H.-H.; Kwon, T.-H.; Cho, G.-C.; Kim, K.-Y.; Hong, S. A Newly Developed State-of-the-Art Full-Scale Excavation Testing Apparatus for Tunnel Boring Machine (TBM). KSCE J. Civ. Eng. 2021, 25, 4856–4867. [Google Scholar] [CrossRef]
- Sharghi, M.; Chakeri, H.; Afshin, H.; Ozcelik, Y. An experimental study of the performance of two-component backfilling grout used be-hind the segmental lining of a tunnel-boring machine. J. Test Eval. 2018, 46, 2083–2099. [Google Scholar] [CrossRef]
- Liao, J.; Bai, K.; Xia, Y.; Li, H.; Zhao, X.; Xiao, X.; Wang, Y. Flow field characteristics of an agitator system of a large diameter slurry-water shield machine. J. Mech. Sci. Technol. 2021, 35, 1501–1513. [Google Scholar] [CrossRef]
- Men, Y.; Wang, Y.; Zhou, J.; Liao, S.; Zhang, K. Measurement and analysis on EPB shield machine tunneling efficiency in Jinan composite stratum. China Civil Eng. J. 2019, 52, 110–119. [Google Scholar]
- Huo, J.; Zhou, L.; Zhu, D.; Zhang, W.; Wang, W.; Sun, W. Cutterhead opening mode design of a composite earth pressure balance shield machine. J. Harbin Eng. Univ. 2017, 38, 433–439. [Google Scholar]
- Lyu, L.; Chen, Z.; Yao, B. Advanced Valves and Pump Coordinated Hydraulic Control Design to Simultaneously Achieve High Accuracy and High Efficiency. IEEE Trans. Control Syst. Technol. 2020, 29, 236–248. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, Z.; Yao, B. Development of Pump and Valves Combined Hydraulic System for Both High Tracking Precision and High Energy Efficiency. IEEE Trans. Ind. Electron. 2018, 66, 7189–7198. [Google Scholar] [CrossRef]
- Hou, D.; Gong, G.; Shi, H.; Wang, L. Design of new propulsion system of shield tunneling machine based on compliance characteristics. J. Zhejiang Univ. 2013, 47, 1287–1292. [Google Scholar]
- Wang, R.; Guo, X.; Li, J.; Wang, J.; Jing, L.; Liu, Z.; Xu, X. A mechanical method for predicting TBM penetration rates. Arab. J. Geosci. 2020, 13, 1–15. [Google Scholar] [CrossRef]
- Liu, B.; Wang, Y.; Zhao, G.; Yang, B.; Wang, R.; Huang, D.; Xiang, B. Intelligent decision method for main control parameters of tunnel boring machine based on multi-objective optimization of excavation efficiency and cost. Tunn. Undergr. Space Technol. 2021, 116, 104054. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y. Synchronous Control of Double Hydraulic Cylinders of Scissors Aerial Work Platform Based on Fuzzy PID. In Proceedings of the 5th International Conference on Electromechanical Control Technology and Transportation (ICECTT), Nanchang, China, 15–17 May 2020; pp. 349–354. [Google Scholar]
- Wang, L.; Zhao, D.; Liu, F.; Liu, Q.; Zhang, Z. Active Disturbance Rejection Position Synchronous Control of Dual-Hydraulic Actuators with Unknown Dead-Zones. Sensors 2020, 20, 6124. [Google Scholar] [CrossRef]
- Wanling, L.; Hongmei, W.; Huaying, Q.; Lihua, J. Research on Key Technologies of Double-cylinder Synchronous Hydraulic Machine. J. Phys. Conf. Ser. 2020, 1676, 012144. [Google Scholar] [CrossRef]
- Luo, Q.; Li, W.; Su, H.; Chen, X. Evaluating Construction Risks of Modified Shield Machine Applicable to Soft Soils Based on Fuzzy Comprehensive Evaluation Method. Math. Probl. Eng. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Do, N.A.; Dias, D.; Vu, T.T.; Dang, V.K. Impact of the shield machines performance parameters on the tunnel lining behaviour and settlements. Environ. Earth Sci. 2021, 80, 16. [Google Scholar] [CrossRef]






| e | ec | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB/NB/PS | PB/NB/NM | PM/NM/NB | PM/NM/NB | PS/NS/NB | ZO/NS/NM | ZO/ZO/PS |
| NM | PB/NB/PS | PM/NM/NM | PM/NM/NB | PS/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/PS/ZO |
| NS | PM/NM/ZO | PM/NM/NS | PS/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/PS/NS | NS/PS/ZO |
| ZO | PM/NM/ZO | PS/NS/NS | PS/NS/NS | ZO/ZO/NS | NS/PS/NS | NS/PS/NS | NM/PM/ZO |
| PS | PS/NS/ZO | PS/NS/ZO | ZO/ZO/ZO | NS/PS/ZO | NS/PS/ZO | NM/PM/ZO | NM/PM/ZO |
| PM | PS/NS/PB | ZO/ZO/NS | NS/PS/PS | NS/PS/PS | NM/PM/PS | NM/PM/PS | NB/PB/PB |
| PB | ZO/ZO/PB | NS/PS/PM | NS/PS/PM | NM/PM/PM | NM/PM/PM | NB/PB/PS | NB/PB/PB |
| Parameter | Value | Unit |
|---|---|---|
| Rod diameter of propel cylinder | 180 | mm |
| Inside bore diameter of propel cylinder | 125 | mm |
| Stroke of propel cylinder | 530 | mm |
| Max. control pressure of flow control valve | 350 | bar |
| Max. flowrate of flow control valve | 16 | L/min |
| Max. output current of solenoid of flow control valve | 680 | mA |
| Max. control pressure of pressure relief valve | 350 | bar |
| Max. flowrate of pressure relief valve | 30 | L/min |
| Max. output current of solenoid of pressure relief valve | 1600 | mA |
| Max. thrust force (4 cylinders in total) | 2000 | KN |
| Characteristics | ISCS | SRSCS | CRSCS |
|---|---|---|---|
| Overshoot | 0.69 mm | 0.43 mm | 1.27 mm |
| Settling time | 10.6 s | 8.0 s | 13.6 s |
| Steady error | 0.6 mm | 0.4 mm | 0.6 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Gong, G.; Huan, Q.; Zhou, X.; Chen, Y.; Peng, X. Investigation into the Electrohydraulic Synchronous Motion Control of a Thrust System for a Tunnel Boring Machine. Machines 2022, 10, 119. https://doi.org/10.3390/machines10020119
Wu W, Gong G, Huan Q, Zhou X, Chen Y, Peng X. Investigation into the Electrohydraulic Synchronous Motion Control of a Thrust System for a Tunnel Boring Machine. Machines. 2022; 10(2):119. https://doi.org/10.3390/machines10020119
Chicago/Turabian StyleWu, Weiqiang, Guofang Gong, Quan Huan, Xinghai Zhou, Yuxi Chen, and Xiongbin Peng. 2022. "Investigation into the Electrohydraulic Synchronous Motion Control of a Thrust System for a Tunnel Boring Machine" Machines 10, no. 2: 119. https://doi.org/10.3390/machines10020119
APA StyleWu, W., Gong, G., Huan, Q., Zhou, X., Chen, Y., & Peng, X. (2022). Investigation into the Electrohydraulic Synchronous Motion Control of a Thrust System for a Tunnel Boring Machine. Machines, 10(2), 119. https://doi.org/10.3390/machines10020119





