A Novel Learning Based Non-Lambertian Photometric Stereo Method for Pixel-Level Normal Reconstruction of Polished Surfaces
Abstract
:1. Introduction
2. Materials and Methods
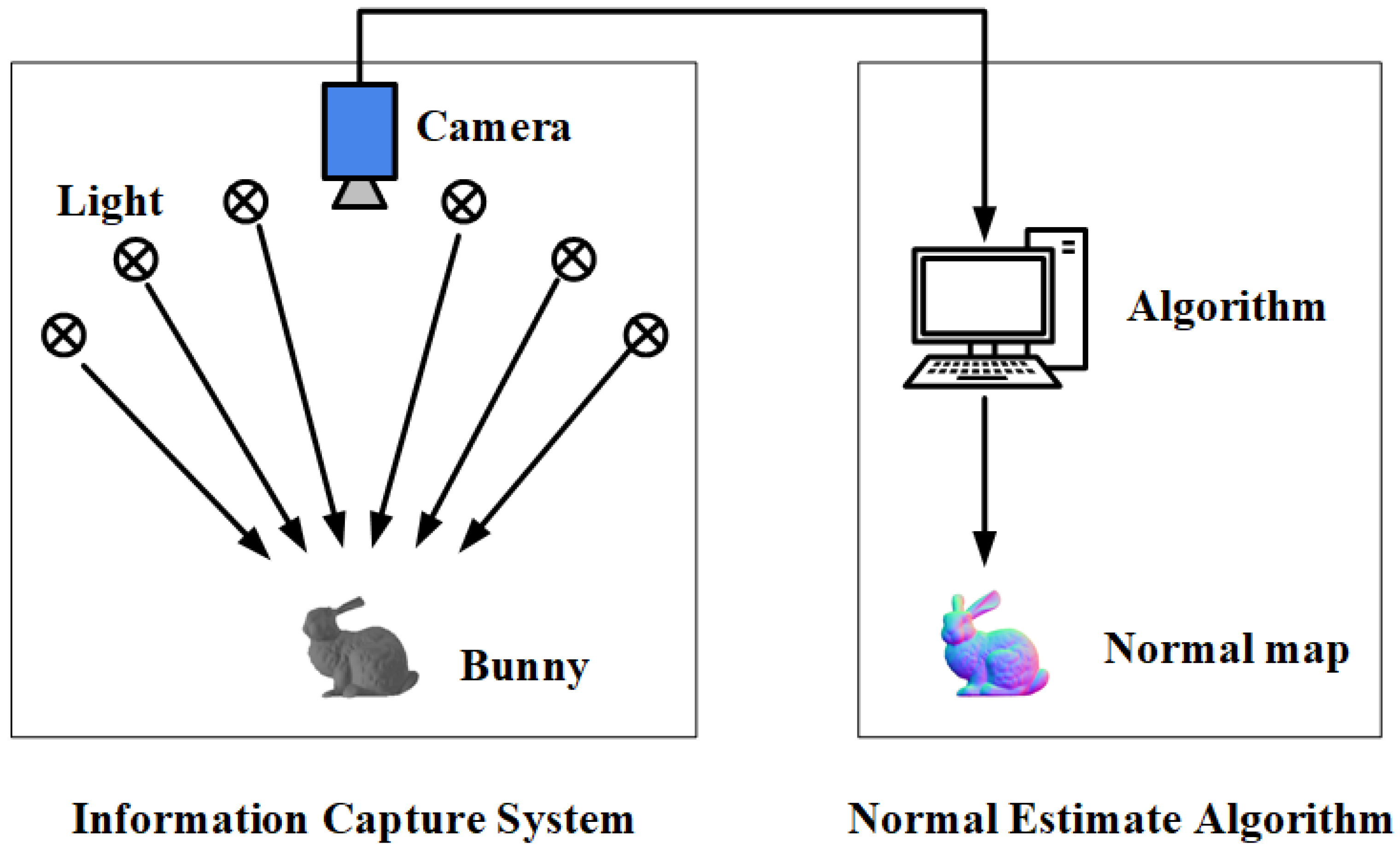
2.1. Principle of Photometric Stereo
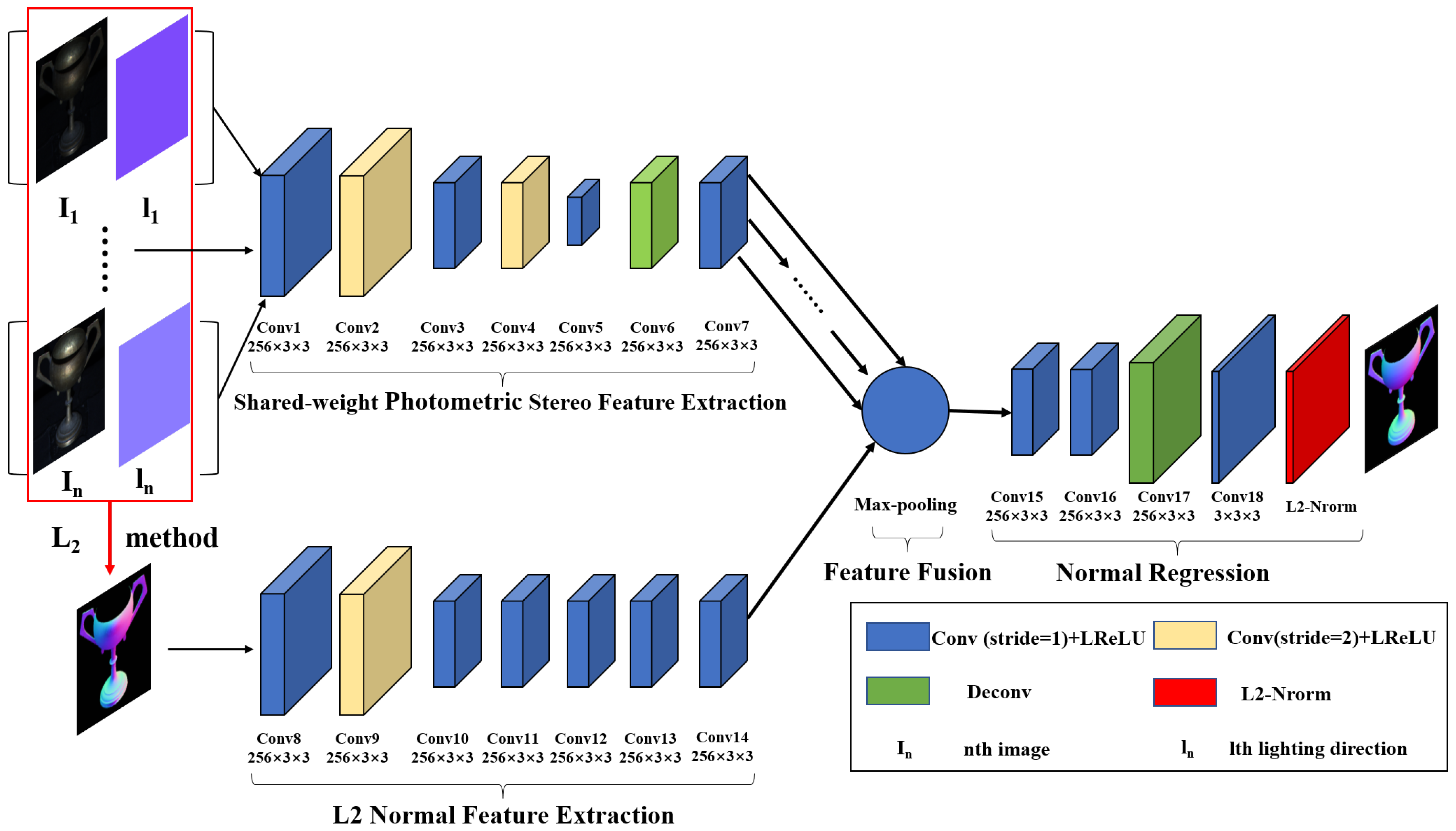
2.2. Learning Based Photometric Stereo: FFCNN
3. Dataset and Implementation Details
3.1. Dataset
3.2. Training Details
3.3. Testing Details
4. Experiments and Results
4.1. Network Analysis
4.1.1. Effects of Kernel Size
4.1.2. Effects of Input Number
4.1.3. Effects of Feature Fusion
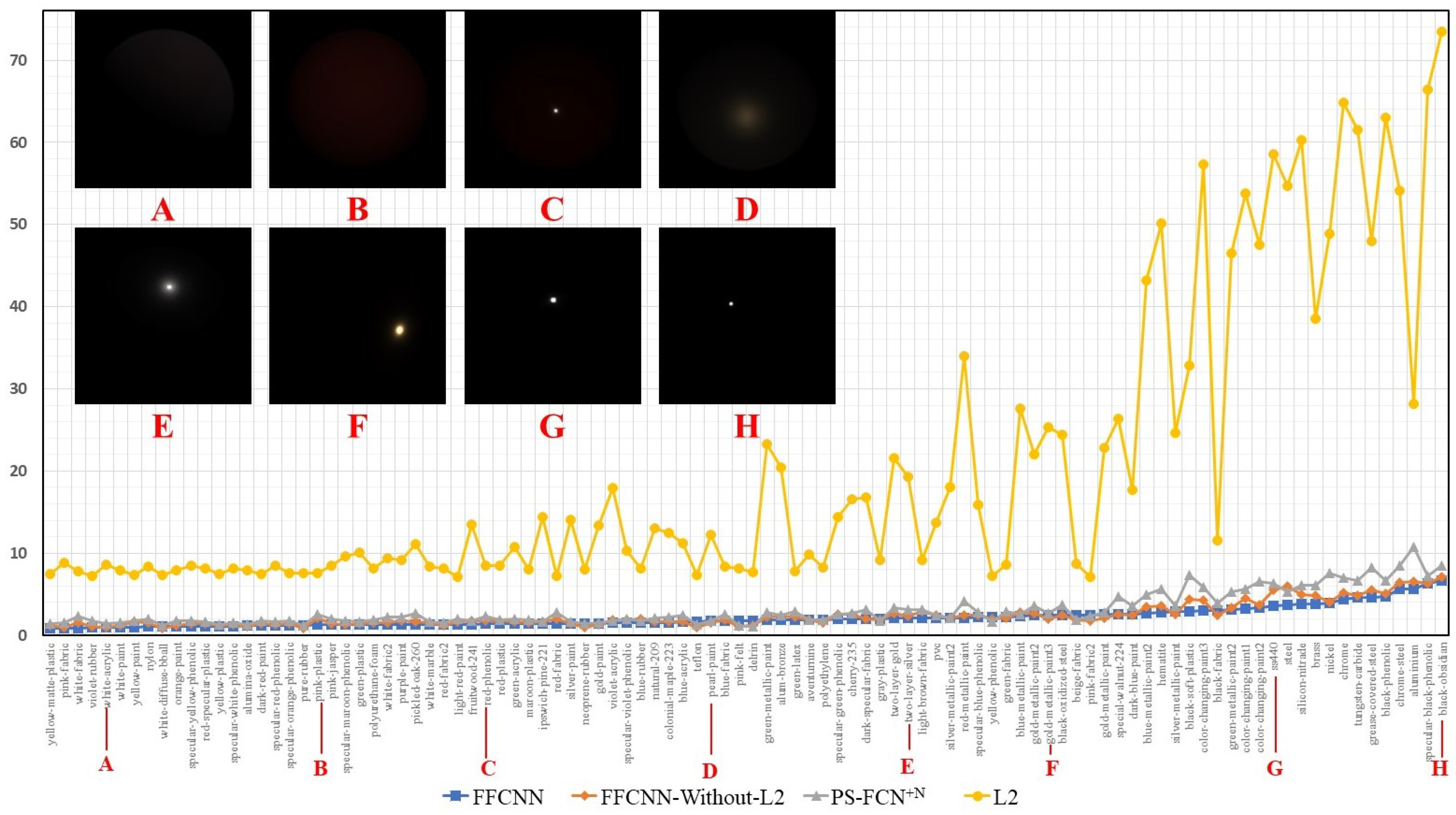
4.1.4. Results on Different Materials
4.2. Benchmark Comparisons
4.2.1. Quantitative Comparison
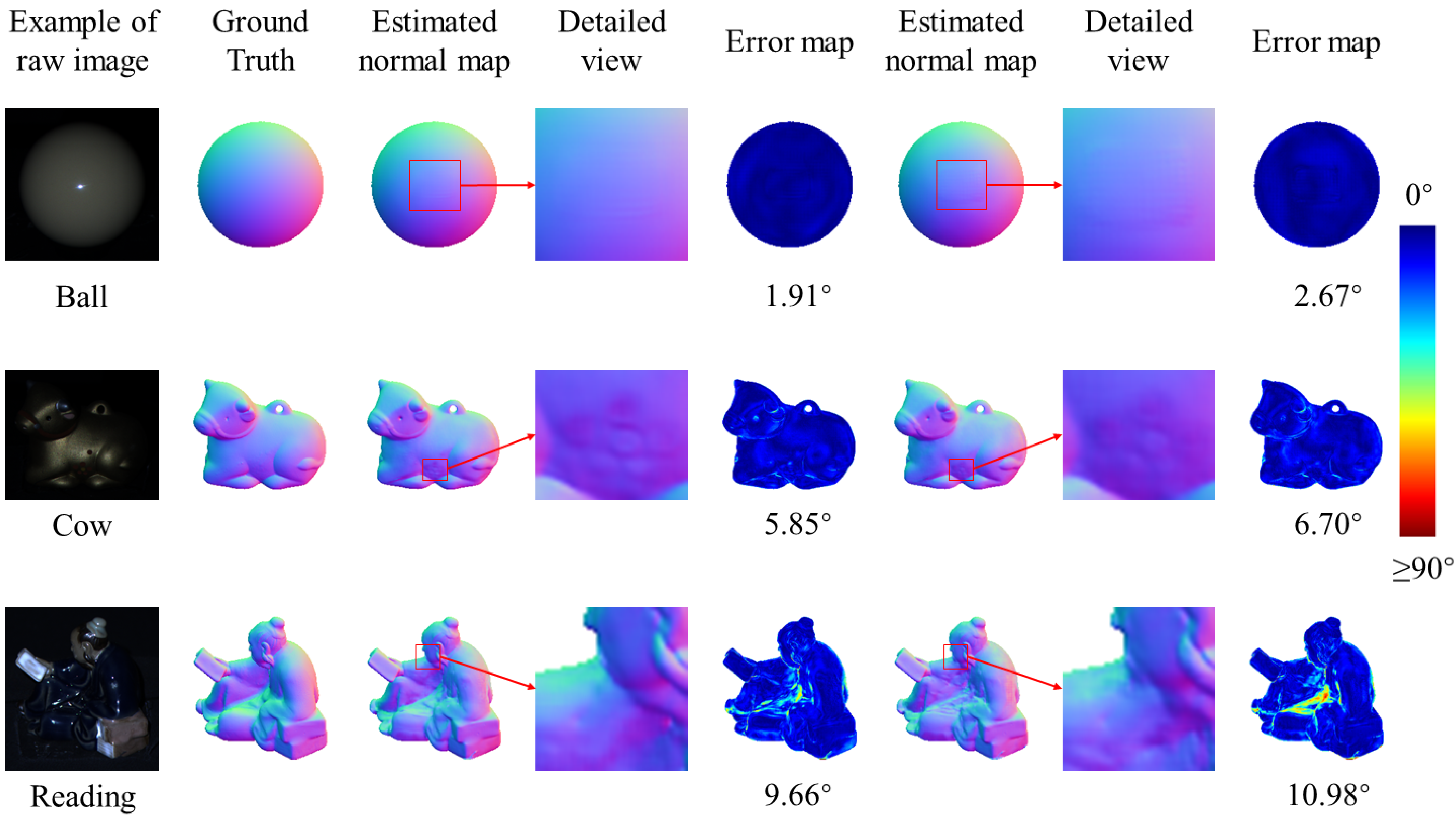
4.2.2. Qualitative Comparison
4.3. Application in Industrial Field
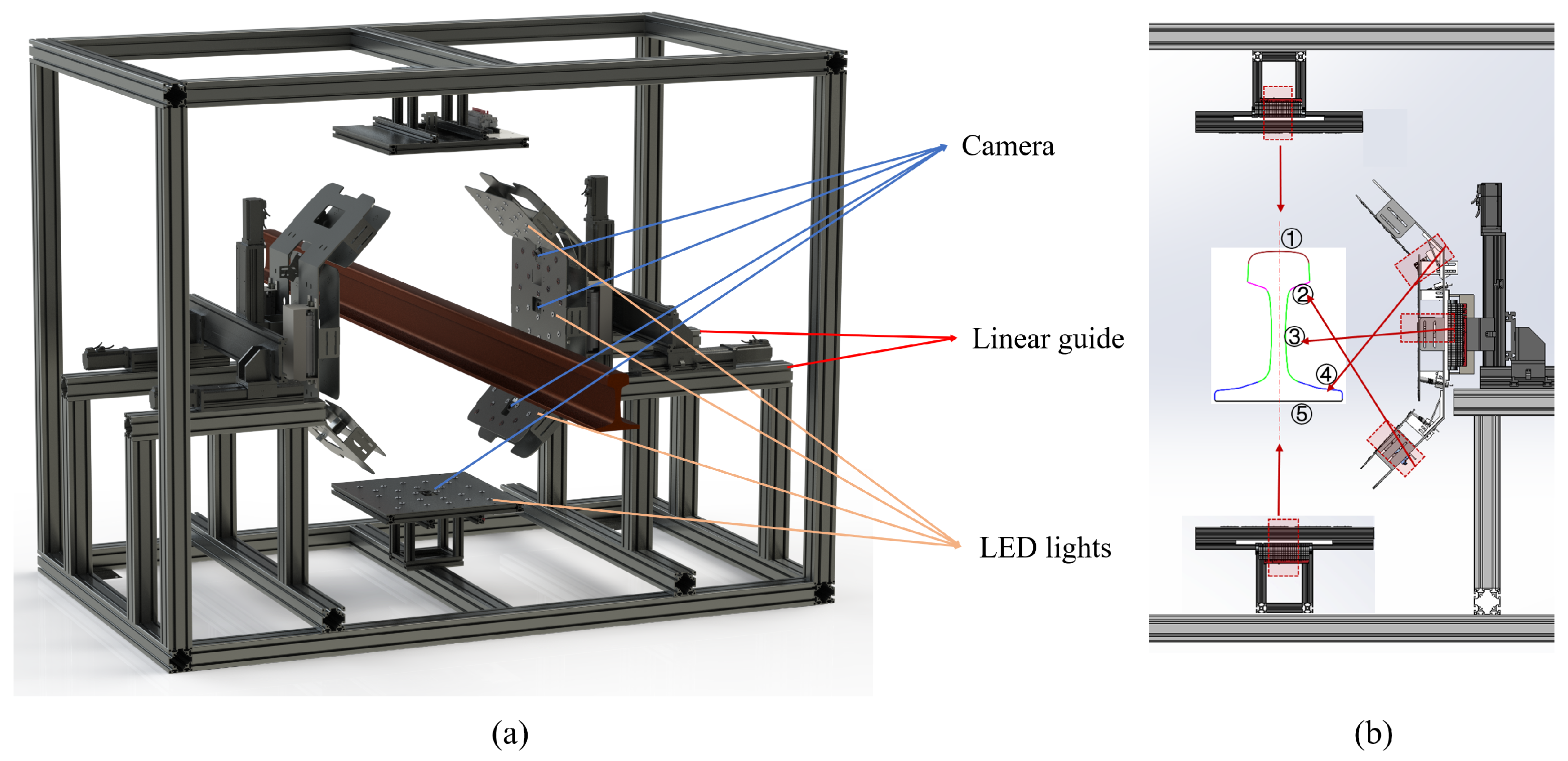
4.3.1. The Setup of Photometric Stereo System
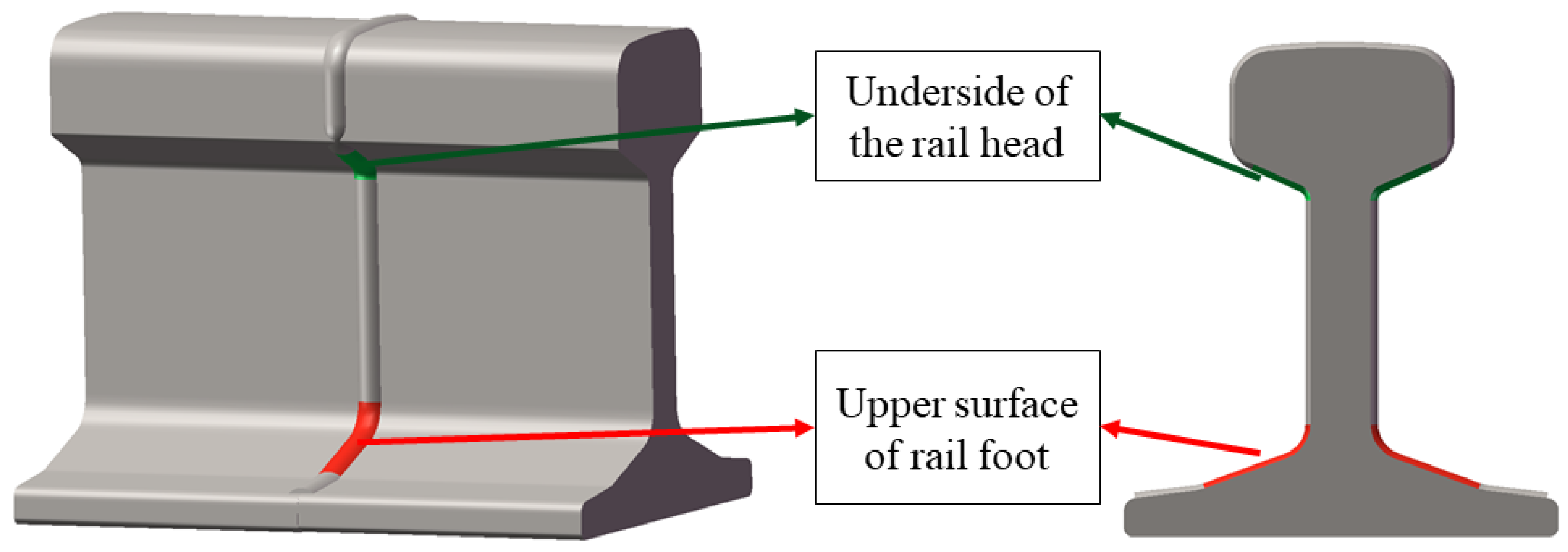
4.3.2. Result on Polished Rail Welding Surface
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cui, Z.; Lu, W.; Liu, J. Real-time industrial vision system for automatic product surface inspection. In Proceedings of the 2016 8th International Conference on Information Management and Engineering, Istanbul, Turkey, 2–5 November 2016; pp. 93–97. [Google Scholar]
- Zheng, X.; Zheng, S.; Kong, Y.; Chen, J. Recent advances in surface defect inspection of industrial products using deep learning techniques. Int. J. Adv. Manuf. Technol. 2021, 113, 35–58. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, Y.; Zhao, F.; Zhang, E.; Wu, Z.; Shao, L. Surface Defect Detection Methods for Industrial Products: A Review. Appl. Sci. 2021, 11, 7657. [Google Scholar] [CrossRef]
- Kowal, J.; Sioma, A. Surface defects detection using a 3D vision system. In Proceedings of the 13th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 28–31 May 2012; pp. 382–387. [Google Scholar]
- Yan, Z.; Shi, B.; Sun, L.; Xiao, J. Surface defect detection of aluminum alloy welds with 3D depth image and 2D gray image. Int. J. Adv. Manuf. Technol. 2020, 110, 741–752. [Google Scholar] [CrossRef]
- Rosati, G.; Boschetti, G.; Biondi, A.; Rossi, A. Real-time defect detection on highly reflective curved surfaces. Opt. Lasers Eng. 2009, 47, 379–384. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Q.; Wang, H.; Li, J.; Ke, Y. A novel 3D laser scanning defect detection and measurement approach for automated fibre placement. Meas. Sci. Technol. 2021, 32, 075201. [Google Scholar] [CrossRef]
- Cao, X.; Xie, W.; Ahmed, S.M.; Li, C.R. Defect detection method for rail surface based on line-structured light. Measurement 2020, 159, 107771. [Google Scholar] [CrossRef]
- Zhang, S. High-speed 3D shape measurement with structured light methods: A review. Opt. Lasers Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Lee, J.H.; Oh, H.M.; Kim, M.Y. Deep learning based 3D defect detection system using photometric stereo illumination. In Proceedings of the 2019 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Okinawa, Japan, 11–13 February 2019; pp. 484–487. [Google Scholar]
- Kang, D.; Jang, Y.J.; Won, S. Development of an inspection system for planar steel surface using multispectral photometric stereo. Opt. Eng. 2013, 52, 039701. [Google Scholar] [CrossRef] [Green Version]
- Woodham, R.J. Photometric method for determining surface orientation from multiple images. Opt. Eng. 1980, 19, 191139. [Google Scholar] [CrossRef]
- Wu, L.; Ganesh, A.; Shi, B.; Matsushita, Y.; Wang, Y.; Ma, Y. Robust photometric stereo via low-rank matrix completion and recovery. In Proceedings of the Asian Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 703–717. [Google Scholar]
- Mukaigawa, Y.; Ishii, Y.; Shakunaga, T. Analysis of photometric factors based on photometric linearization. JOSA A 2007, 24, 3326–3334. [Google Scholar] [CrossRef]
- Miyazaki, D.; Hara, K.; Ikeuchi, K. Median photometric stereo as applied to the segonko tumulus and museum objects. Int. J. Comput. Vis. 2010, 86, 229. [Google Scholar] [CrossRef]
- Wu, T.P.; Tang, C.K. Photometric stereo via expectation maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 546–560. [Google Scholar]
- Ikehata, S.; Wipf, D.; Matsushita, Y.; Aizawa, K. Robust photometric stereo using sparse regression. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 318–325. [Google Scholar]
- Tozza, S.; Mecca, R.; Duocastella, M.; Del Bue, A. Direct differential photometric stereo shape recovery of diffuse and specular surfaces. J. Math. Imaging Vis. 2016, 56, 57–76. [Google Scholar] [CrossRef] [Green Version]
- Georghiades, A.S. Incorporating the torrance and sparrow model of reflectance in uncalibrated photometric stereo. In Proceedings of the IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 3, p. 816. [Google Scholar]
- Chung, H.S.; Jia, J. Efficient photometric stereo on glossy surfaces with wide specular lobes. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Ruiters, R.; Klein, R. Heightfield and spatially varying BRDF reconstruction for materials with interreflections. Comput. Graph. Forum 2009, 28, 513–522. [Google Scholar] [CrossRef]
- Shi, B.; Tan, P.; Matsushita, Y.; Ikeuchi, K. Bi-Polynomial Modeling of Low-Frequency Reflectances. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1078–1091. [Google Scholar] [CrossRef]
- Ikehata, S.; Aizawa, K. Photometric stereo using constrained bivariate regression for general isotropic surfaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2179–2186. [Google Scholar]
- Holroyd, M.; Lawrence, J.; Humphreys, G.; Zickler, T. A photometric approach for estimating normals and tangents. ACM Trans. Graph. 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Hertzmann, A.; Seitz, S.M. Example-based photometric stereo: Shape reconstruction with general, varying brdfs. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1254–1264. [Google Scholar] [CrossRef]
- Hui, Z.; Sankaranarayanan, A.C. A dictionary-based approach for estimating shape and spatially-varying reflectance. In Proceedings of the 2015 IEEE International Conference on Computational Photography (ICCP), Houston, TX, USA, 24–26 April 2015; pp. 1–9. [Google Scholar]
- Santo, H.; Samejima, M.; Sugano, Y.; Shi, B.; Matsushita, Y. Deep photometric stereo network. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 501–509. [Google Scholar]
- Ikehata, S. CNN-PS: CNN-based photometric stereo for general non-convex surfaces. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–18. [Google Scholar]
- Chen, G.; Han, K.; Wong, K.Y.K. PS-FCN: A flexible learning framework for photometric stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–18. [Google Scholar]
- Cao, Y.; Ding, B.; He, Z.; Yang, J.; Chen, J.; Cao, Y.; Li, X. Learning inter-and intraframe representations for non-Lambertian photometric stereo. Opt. Lasers Eng. 2022, 150, 106838. [Google Scholar] [CrossRef]
- Chen, G.; Han, K.; Shi, B.; Matsushita, Y.; Wong, K.Y.K. Deep photometric stereo for non-Lambertian surfaces. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 129–142. [Google Scholar] [CrossRef]
- Miyazaki, D.; Onishi, Y.; Hiura, S. Color photometric stereo using multi-band camera constrained by median filter and occluding boundary. J. Imaging 2019, 5, 64. [Google Scholar] [CrossRef] [Green Version]
- Chandraker, M.; Ramamoorthi, R. What an image reveals about material reflectance. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 1076–1083. [Google Scholar]
- Matusik, W.; Pfister, H.; Brand, M.; McMillan, L. A Data-Driven Reflectance Model. ACM Trans. Graph. 2003, 22, 759–769. [Google Scholar] [CrossRef]
- Johnson, M.K.; Adelson, E.H. Shape estimation in natural illumination. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2553–2560. [Google Scholar]
- Zisserman, A.; Wiles, O. SilNet: Single-and Multi-View Reconstruction by Learning from Silhouettes; Oxford University: Oxford, UK, 2017. [Google Scholar]
- Shi, B.; Wu, Z.; Mo, Z.; Duan, D.; Yeung, S.K.; Tan, P. A benchmark dataset and evaluation for non-lambertian and uncalibrated photometric stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3707–3716. [Google Scholar]
- Taniai, T.; Maehara, T. Neural inverse rendering for general reflectance photometric stereo. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 4857–4866. [Google Scholar]






| (a) Performance on bunny (MAE) | |||||||
| Variants | Test with # images | ||||||
| Train with # images | 4 | 8 | 16 | 32 | 48 | 64 | 100 |
| 4 | 19.88 | 14.33 | 10.1 | 8.19 | 7.99 | 8.09 | 8.38 |
| 8 | 16.95 | 10.93 | 6.79 | 5.08 | 4.82 | 4.82 | 4.93 |
| 16 | 17.40 | 9.59 | 5.36 | 3.77 | 3.49 | 3.44 | 3.50 |
| 32 | 20.54 | 9.31 | 4.93 | 3.34 | 2.98 | 2.9 | 2.86 |
| 48 | 22.01 | 9.54 | 5.02 | 3.44 | 3.01 | 2.9 | 2.86 |
| (b) Performance on sphere (MAE) | |||||||
| Variants | Test with # images | ||||||
| Train with # images | 4 | 8 | 16 | 32 | 48 | 64 | 100 |
| 4 | 14.16 | 10.76 | 7.59 | 5.7 | 5.44 | 5.38 | 5.56 |
| 8 | 13.81 | 9.20 | 5.11 | 3.65 | 3.47 | 3.51 | 3.82 |
| 16 | 15.15 | 8.24 | 4.21 | 2.78 | 2.55 | 2.55 | 2.73 |
| 32 | 17.70 | 8.25 | 3.84 | 2.39 | 2.13 | 2.07 | 2.14 |
| 48 | 19.17 | 8.62 | 4.11 | 2.55 | 2.23 | 2.15 | 2.17 |
| (a) Performance on the PS Sphere Bunny dataset | |||||||||||
| model | bunny | sphere | average | ||||||||
| FFCNN-Without-L2 | 3.23 | 2.40 | 2.81 | ||||||||
| FFCNN | 2.86 | 2.14 | 2.5 | ||||||||
| (b) Performance on the DiLiGenT benchmark dataset | |||||||||||
| Method | ball | cat | pot1 | bear | pot2 | buddha | goblet | reading | cow | harvest | average |
| FFCNN-Without-L2 | 2.09 | 4.66 | 5.66 | 6.73 | 7.42 | 7.34 | 7.75 | 11.2 | 6.46 | 12.48 | 7.18 |
| FFCNN | 1.91 | 4.87 | 5.41 | 6.5 | 6.62 | 7.5 | 7.79 | 9.66 | 5.85 | 12.22 | 6.83 |
| Method | Ball | Cat | pot1 | Bear | pot2 | Buddha | Goblet | Reading | Cow | Harvest | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| proposed | 1.91 | 4.87 | 5.41 | 6.50 | 6.62 | 7.50 | 7.79 | 9.66 | 5.85 | 12.22 | 6.83 |
| CH-20 [31] | 2.67 | 4.74 | 6.16 | 7.72 | 7.15 | 7.56 | 7.88 | 10.98 | 6.70 | 12.42 | 7.40 |
| CA-21 [30] | 2.29 | 5.87 | 6.92 | 5.79 | 6.89 | 6.85 | 7.88 | 11.94 | 7.48 | 13.71 | 7.56 |
| SI-18 * [28] | 2.20 | 4.60 | 5.40 | 12.30 | 6.00 | 7.90 | 7.30 | 12.60 | 7.90 | 13.90 | 8.01 |
| CH-18 [29] | 2.82 | 6.16 | 7.13 | 7.55 | 7.25 | 7.91 | 8.60 | 13.33 | 7.33 | 15.85 | 8.39 |
| TM-18 [38] | 1.47 | 5.44 | 6.09 | 5.79 | 7.76 | 10.36 | 11.47 | 11.03 | 6.32 | 22.59 | 8.83 |
| HI-17 [27] | 2.02 | 6.54 | 7.05 | 6.31 | 7.86 | 12.68 | 11.28 | 15.51 | 8.01 | 16.86 | 9.41 |
| ST-14 [22] | 1.74 | 6.12 | 6.51 | 6.12 | 8.78 | 10.60 | 10.09 | 13.63 | 13.93 | 25.44 | 10.30 |
| IA-14 [23] | 3.34 | 6.74 | 6.64 | 7.11 | 8.77 | 10.47 | 9.71 | 14.19 | 13.05 | 25.95 | 10.60 |
| L2 Baseline [12] | 4.10 | 8.41 | 8.89 | 8.39 | 14.65 | 14.92 | 18.50 | 19.80 | 25.60 | 30.62 | 15.39 |
| Method | Ball | Cat | pot1 | Bear | pot2 | Buddha | Goblet | Reading | Cow | Harvest | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| proposed | 1.91 | 4.87 | 5.41 | 4.52 | 6.62 | 7.50 | 7.79 | 9.66 | 5.85 | 12.22 | 6.64 |
| SI-18 [28] | 2.20 | 4.60 | 5.40 | 4.10 | 6.00 | 7.90 | 7.30 | 12.60 | 7.90 | 13.90 | 7.19 |
| Method | Running Time (s) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ball | Cat | pot1 | Bear | pot2 | Buddha | Goblet | Reading | Cow | Harvest | Avg. | |
| proposed | 1.199 | 0.508 | 0.545 | 0.357 | 0.383 | 0.378 | 0.492 | 0.294 | 0.268 | 0.485 | 0.491 |
| SI-18 [28] | 9.858 | 25.608 | 32.555 | 23.631 | 14.070 | 25.414 | 10.430 | 11.087 | 10.563 | 32.263 | 19.548 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Wei, X.; Liu, W.; Ding, B.; Yang, J.; Cao, Y. A Novel Learning Based Non-Lambertian Photometric Stereo Method for Pixel-Level Normal Reconstruction of Polished Surfaces. Machines 2022, 10, 120. https://doi.org/10.3390/machines10020120
Cao Y, Wei X, Liu W, Ding B, Yang J, Cao Y. A Novel Learning Based Non-Lambertian Photometric Stereo Method for Pixel-Level Normal Reconstruction of Polished Surfaces. Machines. 2022; 10(2):120. https://doi.org/10.3390/machines10020120
Chicago/Turabian StyleCao, Yanlong, Xiaoyao Wei, Wenyuan Liu, Binjie Ding, Jiangxin Yang, and Yanpeng Cao. 2022. "A Novel Learning Based Non-Lambertian Photometric Stereo Method for Pixel-Level Normal Reconstruction of Polished Surfaces" Machines 10, no. 2: 120. https://doi.org/10.3390/machines10020120
APA StyleCao, Y., Wei, X., Liu, W., Ding, B., Yang, J., & Cao, Y. (2022). A Novel Learning Based Non-Lambertian Photometric Stereo Method for Pixel-Level Normal Reconstruction of Polished Surfaces. Machines, 10(2), 120. https://doi.org/10.3390/machines10020120








