Uncertainty Quantification for Full-Flight Data Based Engine Fault Detection with Neural Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Artificial Neural Networks with Uncertainty Quantification
2.1.1. Approximating the Aleatoric Uncertainty
2.1.2. Approximating the Epistemic Uncertainty
2.2. Fault Detection
- Identification of Regions with High Epistemic Uncertainty: Timestamps with high modeling uncertainty are identified and removed to ensure that only data points with high modeling accuracy are used for fault detection. Regions with high epistemic uncertainty are identified by defining a threshold on the confidence score .
- Outlier Detection: The detection of outliers indicating unusual system performance is based on the Mahalanobis Distance . The corresponding data points are considered outliers if the Mahalanobis Distance exceeds a predefined threshold .
- Fault Detection: The total number of outliers is computed in the last step. Since there will always be a certain number of statistical outliers, a threshold on the total number of outliers is introduced. If the number of outliers detected exceeds this predefined threshold , the outliers are no longer considered statistical but systematic, indicating a fault.
2.3. Description of the Database
3. Results
3.1. Assessment of the Articifical Neural Network
3.2. Detection Rates
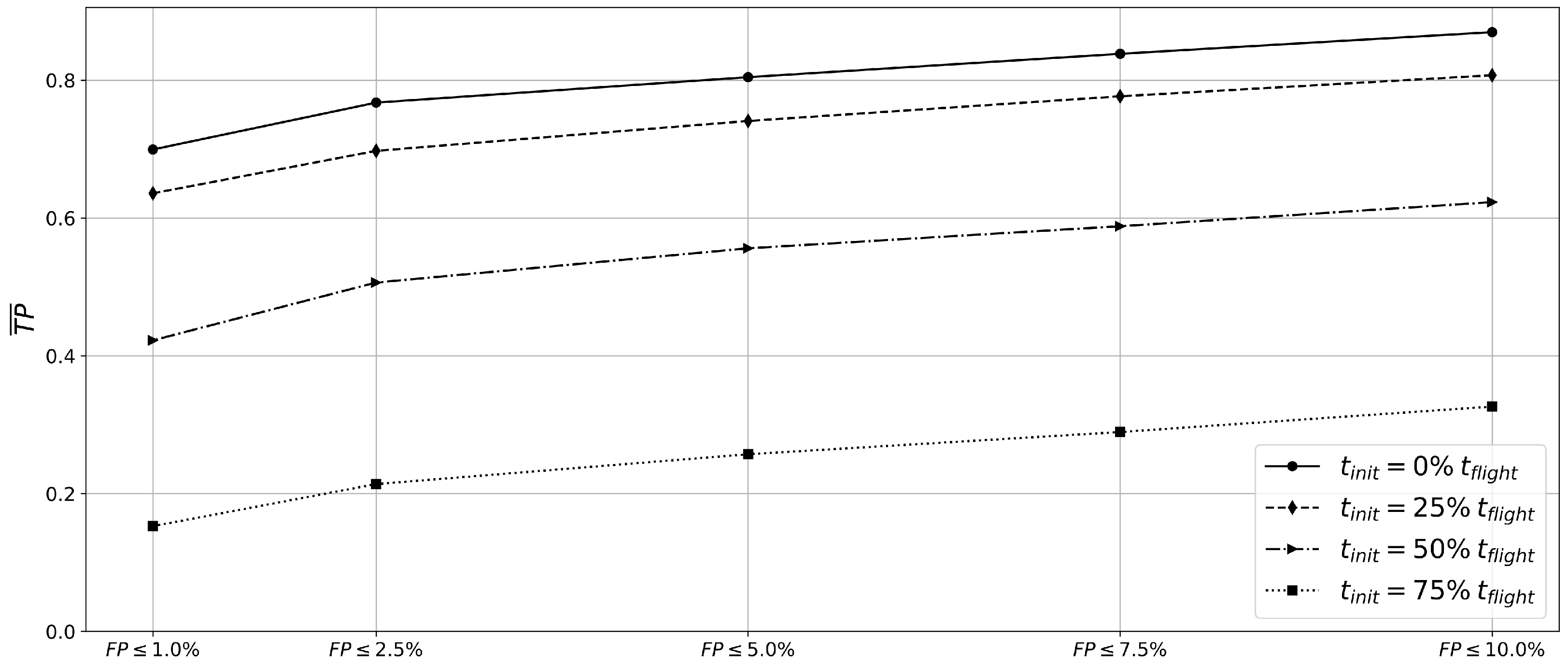
3.3. Sensitivity Study: Fault Initiation
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature and Abbreviations
Nomenclature
| Symbols | |
| Altitude | |
| Bleed Setting | |
| Mahalanobis Distance | |
| Threshold for the Mahalanobis Distance | |
| Exhaust Gas Temperature | |
| Engine Anti-Icing | |
| False Positive Detection Rate | |
| l | Flight Length |
| Learning Rate | |
| Mach-Number | |
| Mean Squared Error | |
| Threshold for the Confidence Score | |
| Confidence Score | |
| Threshold for the Number of Outliers Tolerated | |
| Shaft Speed Fan | |
| Shaft Speed Core | |
| Negative Log-Likelihood | |
| p | Pressure |
| Airflow towards the Cabin | |
| Flight Phase | |
| Q | Capacity |
| T | Temperature |
| t | Time |
| Time Until Fault Initiation | |
| Tail Anti-Icing | |
| True Positive Detection Rate | |
| Wing Anti-Icing | |
| Fuel Flow | |
| x | Input-Parameter |
| y | Measurement |
| Deviation | |
| Correction Factor Pressure | |
| Correlation Matrix | |
| Standard Deviation | |
| Mean Value | |
| Efficiency | |
| Parameter Set | |
| Correction Factor Temperature | |
| Superscripts and Subscripts | |
| Averaged Value | |
| c | ISA-Corrected Value |
| ISA Reference Value | |
| Acronyms | |
| CC | Combustion Chamber |
| HPC | High Pressure Compressor |
| HPT | High Pressure Turbine |
| LPC | Low Pressure Compressor |
| LPT | Low Pressure Turbine |
References
- IATA. Airline Maintenance Cost Executive Commentary; Technical Report; IATA: Montreal, QC, Canada, 2016. [Google Scholar]
- Fentaye, A.; Baheta, A.T.; Gilani, S.I.; Kyprianidis, K.G. A Review on Gas Turbine Gas-Path Diagnostics: State-of-the-Art Methods, Challenges and Opportunities. Aerospace 2019, 6, 83. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Zaccaria, V.; Kyprianidis, K. Aircraft Engine Performance Monitoring and Diagnostics Based on Deep Convolutional Neural Networks. Machines 2021, 9, 337. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Ul-Haq Gilani, S.I.; Baheta, A.T.; Li, Y.G. Performance-based fault diagnosis of a gas turbine engine using an integrated support vector machine and artificial neural network method. Proc. Inst. Mech. Eng. Part J. Power Energy 2019, 233, 786–802. [Google Scholar] [CrossRef]
- Pérez-Ruiz, J.L.; Tang, Y.; Loboda, I. Aircraft Engine Gas-Path Monitoring and Diagnostics Framework Based on a Hybrid Fault Recognition Approach. Aerospace 2021, 8, 232. [Google Scholar] [CrossRef]
- Lipowsky, H.; Staudacher, S.; Bauer, M.; Schmidt, K.J. Application of Bayesian Forecasting to Change Detection and Prognosis of Gas Turbine Performance. J. Eng. Gas Turbines Power 2010, 132, 1–8. [Google Scholar] [CrossRef]
- Koskoletos, O.A.; Aretakis, N.; Alexiou, A.; Romesis, C.; Mathioudakis, K. Evaluation of Aircraft Engine Diagnostic Methods Through ProDiMES. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition (GT2018), Oslo, Norway, 11–15 June 2018; ASME: New York, NY, USA, 2018; p. V006T05A023. [Google Scholar] [CrossRef]
- Loboda, I.; Pérez-Ruiz, J.L.; Yepifanov, S. A Benchmarking Analysis of a Data-Driven Gas Turbine Diagnostic Approach. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition (GT2018), Oslo, Norway, 11–15 June 2018; ASME: New York, NY, USA, 2018; p. V006T05A027. [Google Scholar] [CrossRef]
- Badea, V.E.; Zamfiroiu, A.; Boncea, R. Big Data in the Aerospace Industry. Inform. Econ. 2018, 22, 17–24. [Google Scholar] [CrossRef]
- Volponi, A.J.; Tang, L. Improved Engine Health Monitoring Using Full Flight Data and Companion Engine Information. SAE Int. J. Aerosp. 2016, 9, 91–102. [Google Scholar] [CrossRef]
- Tang, L.; Volponi, A.J.; Prihar, E. Extending engine gas path analysis using full flight data. Proc. ASME Turbo Expo 2019, 6, 1–11. [Google Scholar] [CrossRef]
- Weiss, M.; Staudacher, S.; Becchio, D.; Keller, C.; Mathes, J. Steady-State Fault Detection with Full-Flight Data. Machines 2022, 10, 140. [Google Scholar] [CrossRef]
- Dai, X.; Gao, Z. From model, signal to knowledge: A data-driven perspective of fault detection and diagnosis. IEEE Trans. Ind. Inform. 2013, 9, 2226–2238. [Google Scholar] [CrossRef]
- Zhao, F.; Dasgupta, A.; Yuan, C.; Chakraborty, A. Multi-Level Neural Network Based Gas Turbine Modeling. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition (GT2018), Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Bai, M.; Liu, J.; Ma, Y.; Zhao, X.; Long, Z.; Yu, D. Long Short-Term Memory Network-Based Normal Pattern Group for Fault Detection of Three-Shaft Marine Gas Turbine. Energies 2020, 14, 13. [Google Scholar] [CrossRef]
- Pogorelov, G.; Kulikov, G.; Abdulnagimov, A.; Badamshin, B. Application of Neural Network Technology and High-performance Computing for Identification and Real-time Hardware-in-the-loop Simulation of Gas Turbine Engines. Procedia Eng. 2017, 176, 402–408. [Google Scholar] [CrossRef]
- Goyal, V.; Xu, M.; Kapat, J.; Vesely, L. Prediction of gas turbine performance using machine learning methods. Proc. ASME Turbo Expo 2020, 6, 1–11. [Google Scholar] [CrossRef]
- Castillo, I.G.; Loboda, I.; Pérez Ruiz, J.L. Data-Driven Models for Gas Turbine Online Diagnosis. Machines 2021, 9, 372. [Google Scholar] [CrossRef]
- Loboda, I.; Feldshteyn, Y. Polynomials and neural networks for gas turbine monitoring: A comparative study. Int. J. Turbo Jet Engines 2011, 28, 227–236. [Google Scholar] [CrossRef]
- Goyal, V.; Xu, M.; Kapat, J. Statistical modeling in failure detection in gas turbines. In Proceedings of the AIAA Propulsion and Energy Forum and Exposition, Indianopolis, IN, USA, 19–22 August 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, N. Aero-Engine Condition Monitoring Based on Support Vector Machine. Phys. Procedia 2012, 24, 1546–1552. [Google Scholar] [CrossRef][Green Version]
- Michelmore, R.; Wicker, M.; Laurenti, L.; Cardelli, L.; Gal, Y.; Kwiatkowska, M. Uncertainty Quantification with Statistical Guarantees in End-to-End Autonomous Driving Control. In Proceedings of the IEEE International Conference on Robotics and Automation, Paris, France, 31 May–31 August 2020; pp. 7344–7350. [Google Scholar] [CrossRef]
- Kompa, B.; Snoek, J.; Beam, A.L. Second opinion needed: Communicating uncertainty in medical machine learning. NPJ Digit. Med. 2021, 4, 1–6. [Google Scholar] [CrossRef]
- Hüllermeier, E.; Waegeman, W. Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods. Mach. Learn. 2021, 110, 457–506. [Google Scholar] [CrossRef]
- Haley, P.; Soloway, D. Extrapolation limitations of multilayer feedforward neural networks. In Proceedings of the IJCNN International Joint Conference on Neural Networks, Baltimore, MD, USA, 7–11 June 1992; Volume 4, pp. 25–30. [Google Scholar] [CrossRef]
- McCartney, M.; Haeringer, M.; Polifke, W. Comparison of Machine Learning Algorithms in the Interpolation and Extrapolation of Flame Describing Functions. J. Eng. Gas Turbines Power 2020, 142, 061009. [Google Scholar] [CrossRef]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. Adv. Neural Inf. Process. Syst. 2016, 2017, 6403–6414. [Google Scholar]
- Bishop, C. Novelty detection and neural network validation. IEE Proc. Vision Image Signal Process. 1994, 141, 217. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning, ICML 2016, New York, NY, USA, 20–22 June 2016; Volume 3, pp. 1651–1660. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight Uncertainty in Neural Networks. In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6–11 July 2015; Volume 2, pp. 1613–1622. [Google Scholar] [CrossRef]
- Likas, A. Probability density estimation using artificial neural networks. Comput. Phys. Commun. 2001, 135, 167–175. [Google Scholar] [CrossRef]
- Hartwell, A.; Montana, F.; Jacobs, W.; Kadirkamanathan, V.; Mills, A.R.; Clark, T. In-flight Novelty Detection with Convolutional Neural Networks. arXiv 2021, arXiv:2112.03765. [Google Scholar]
- Putz, A.; Staudacher, S.; Koch, C.; Brandes, T. Jet Engine Gas Path Analysis Based on Takeoff Performance Snapshots. J. Eng. Gas Turbines Power 2017, 139, 111201. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Volponi, A.J. Gas Turbine Parameter Corrections. J. Eng. Gas Turbines Power 1999, 121, 613–621. [Google Scholar] [CrossRef]
- Walsh, P.P.; Fletcher, P. Gas Turbine Performance, 2nd ed.; Wiley Blackwell: Oxford, UK, 2004. [Google Scholar] [CrossRef]
- Mahalanobis, P. On the generalized distance in statistics. In National Institute of Science of India; National Institute of Science of India: Calcutta, India, 1936; pp. 49–55. [Google Scholar]
- Butterworth, S. On the theory of filter amplifiers. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Matthews, B.; Oza, N. NASA—Sample Flight Data. 2012. Available online: https://c3.ndc.nasa.gov/dashlink/projects/85/ (accessed on 25 May 2020).
- Köhli, R. Untersuchungen zum Einfluss der Modellbildung auf das Trend Monitoring von Fluggasturbinen. Ph.D Thesis, Universität Stuttgart, Stuttgart, Germany, 2016. [Google Scholar]
- Spieler, S.; Staudacher, S.; Fiola, R.; Sahm, P.; Weißschuh, M. Probabilistic engine performance scatter and deterioration modeling. J. Eng. Gas Turbines Power 2008, 130, 042507. [Google Scholar] [CrossRef]
- Babbar, A.; Ortiz, E.M.; Syrmos, V.L.; Arita, M.M. Advanced diagnostics and prognostics for engine health monitoring. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MN, USA, 7–14 March 2009; pp. 1–10. [Google Scholar] [CrossRef]
- Sheridan, K.; Puranik, T.G.; Mangortey, E.; Pinon-Fischer, O.J.; Kirby, M.; Mavris, D.N. An Application of DBSCAN Clustering for Flight Anomaly Detection During the Approach Phase. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute of Aeronautics and Astronautics: Reston, VI, USA, 2020. [Google Scholar] [CrossRef]
- Da Silva, I.N.; Hernane Spatti, D.; Andrade Flauzino, R.; Liboni, L.H.B.; dos Reis Alves, S.F. Artificial Neural Networks; Springer International Publishing: Cham, Switzerland, 2017; p. 307. [Google Scholar] [CrossRef]
- Curnock, B. Obidicote Project—Work Package 4: Steady-State Test Cases; Technical Report DNS62433; Rolls-Royce Plc: Manchester, UK, 2000. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015-Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Simon, D.L.; Bird, J.; Davison, C.; Volponi, A.; Iverson, R.E. Benchmarking Gas Path Diagnostic Methods: A Public Approach. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; Volume 2, pp. 325–336. [Google Scholar] [CrossRef]








| Input Parameter | |
|---|---|
| Parameter | Description |
| Correction factor temperature | |
| Correction factor pressure | |
| Corrected spool speed of the fan | |
| Mach-Number | |
| Setting bleed extraction | |
| Airflow towards the cabin | |
| Setting engine-anti-icing | |
| Setting tail-anti-icing | |
| Setting wing-anti-icing | |
| Flight phase | |
| Output Parameter | |
| Parameter | Description |
| Corrected spool speed of the core | |
| Corrected exhaust gas temperature | |
| Corrected fuel flow |
| Label | Fault Description | |
|---|---|---|
| a | ||
| b | − | |
| c | ||
| d | − | |
| e | − | |
| f | − | |
| g | ||
| h | − | |
| i | − | |
| j | ||
| k | − | |
| l | ||
| Climb | Cruise | Descent | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Training | 3.22 K | 0.13% | 0.64% | 3.20 K | 0.19% | 0.74% | 8.37 K | 0.77% | 2.36% |
| Validation | 3.50 K | 0.13% | 0.69% | 3.75 K | 0.20% | 0.82% | 8.76 K | 0.78% | 2.44% |
| Testing | 3.76 K | 0.16% | 0.78% | 5.06 K | 0.23% | 0.98% | 9.57 K | 0.80% | 2.55% |
| Climb | Cruise | Descent | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Training | 3.03 K | 0.13% | 0.66% | 2.80 K | 0.15% | 0.73% | 6.30 K | 0.67% | 2.63% |
| Validation | 3.01 K | 0.13% | 0.66% | 2.80 K | 0.15% | 0.73% | 6.23 K | 0.66% | 2.60% |
| Testing | 3.11 K | 0.14% | 0.68% | 2.91 K | 0.15% | 0.74% | 6.50 K | 0.70% | 2.71% |
| TP | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e | f | g | h | i | j | k | l | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weiss, M.; Staudacher, S.; Mathes, J.; Becchio, D.; Keller, C. Uncertainty Quantification for Full-Flight Data Based Engine Fault Detection with Neural Networks. Machines 2022, 10, 846. https://doi.org/10.3390/machines10100846
Weiss M, Staudacher S, Mathes J, Becchio D, Keller C. Uncertainty Quantification for Full-Flight Data Based Engine Fault Detection with Neural Networks. Machines. 2022; 10(10):846. https://doi.org/10.3390/machines10100846
Chicago/Turabian StyleWeiss, Matthias, Stephan Staudacher, Jürgen Mathes, Duilio Becchio, and Christian Keller. 2022. "Uncertainty Quantification for Full-Flight Data Based Engine Fault Detection with Neural Networks" Machines 10, no. 10: 846. https://doi.org/10.3390/machines10100846
APA StyleWeiss, M., Staudacher, S., Mathes, J., Becchio, D., & Keller, C. (2022). Uncertainty Quantification for Full-Flight Data Based Engine Fault Detection with Neural Networks. Machines, 10(10), 846. https://doi.org/10.3390/machines10100846








