Optimal Classifier to Detect Unit of Measure Inconsistency in Gas Turbine Sensors

Abstract

Label noise is a harmful issue that arises when data are erroneously labeled. Several label noise issues can occur but, among them, unit of measure inconsistencies (UMIs) are inexplicably neglected in the literature. Despite its relevance, a general and automated approach for UMI detection suitable to gas turbines (GTs) has not been developed yet; as a result, GT diagnosis, prognosis, and control may be challenged since collected data may not reflect the actual operation. To fill this gap, this paper investigates the capability of three supervised machine learning classifiers, i.e., Support Vector Machine, Naïve Bayes, and K-Nearest Neighbors, that are tested by means of challenging analyses to infer general guidelines for UMI detection. Classification accuracy and posterior probability of each classifier is evaluated by means of an experimental dataset derived from a large fleet of Siemens gas turbines in operation. Results reveal that Naïve Bayes is the optimal classifier for UMI detection, since 88.5% of data are correctly labeled with 84% of posterior probability when experimental UMIs affect the dataset. In addition, Naïve Bayes proved to be the most robust classifier also if the rate of UMIs increases.

1. Introduction

1.1. Problem Statement and Literature Survey

Monitoring, diagnostics, and prognostics are fundamental tasks that can be efficiently performed only if data reflect the actual operating condition of the unit under analysis. However, data may be corrupted by means of both feature and label noise, whose rate may be even equal to 5% in real-word installations [1]. Faulty sensors and transmission errors generally cause feature noise [1]. Instead, label noise, which is also known in the literature as class noise, occurs when data are incorrectly labeled [2] because of erroneous labelling processes [3] and process anomalies [4]. In the literature, some studies, e.g., [3], claimed that label noise issue is usually more harmful than feature noise.

Thus, several studies have recently developed data-cleaning approaches, e.g., the study [5], as well as tolerant and robust methodologies (e.g., [3,6,7]), for identifying noisy labels and smoothing the negative effect of incorrectly labeled data.

However, Pu and Li [6] and Liu et al. [7] have recently stated that label noise is an urgent and neglected issue in industry. So far, only Pu and Li [6], Liu et al. [7], and Zhang et al. [8] have dealt with the removal of label noise in industrial applications.

In general, data are stored in databases in which data are marked by means of several labels. As demonstrated by Wang et al. [9], the identification of the actual label can be performed by means of data-based models. To this purpose, supervised machine learning (ML) techniques can be efficiently exploited, since data are classified within different classes, e.g., fault and normal operation. For example, Chen et al. [10] have recently developed a novel hierarchical ML model for the detection and identification of faults affecting rotary machines. Instead, Si et al. [11] exploited an SVM-based classifier for classifying the shear cutting state into eight classes.

Though some authors addressed the label noise issue affecting a unit health state, e.g., a wind turbine gearbox in [8], no studies tuned and tested proper methodologies for the detection of unit of measure inconsistencies (UMIs), which occur because of the availability of several systems of measurements. As a result, unit of measure (UOM) may be incorrectly assumed. Such event is not infrequent since GTs are currently equipped with hundreds of sensors and manufacturer diagnostic centers monitor large fleets of machines. Moreover, it should be noted that UMI detection is a highly challenging task, since UMIs and sensor anomalies sometime exhibit a similar behavior, especially in field datasets.

Unit of measure inconsistencies also affect data acquired from GTs, because their acquisition systems do not usually include automated and general procedures for detecting UMIs. In fact, UMIs are identified by means of visual and manual checks that require an in-depth insight about GT operation [4,12]. Such analyses are usually inefficient since they are time consuming and wrong units may persist even after manual verification.

Alternatively, UMIs can be detected by considering the expected range of variation of the physical quantity under analysis. Based on engineering practice, minimum and maximum acceptability thresholds are identified; if the physical quantity exceeds such a range, a UMI is identified. Such a practice clearly requires a fine tuning of the acceptability thresholds, otherwise UMIs may not be detected.

As a consequence, the diagnosis of GT sensors may be compromised, by leading to several false positives and eventually wrong recommendation to customers.

To the authors’ knowledge, so far only Manservigi et al. [4,12] have focused on the detection of UMIs in GT sensors. These two papers exploited the Support Vector Machine (SVM) classifier, which proved to be a general and automated data-cleaning approach to both detect UMIs and provide the actual label, i.e., UOM. Four SVM approaches were investigated, by coupling two kernel functions, i.e., linear and Radial Basis Function (RBF), to two decomposition strategies, i.e., One-Vs-One (OVO) and One-Vs-All (OVA). The SVM classifier was significantly challenged by using up to 12 classes and training the ML models also by means of noisy data. The comprehensive analyses pointed out that the SVM classifier coupled to the RBF OVO approach (SVM RO) outperformed the other alternatives, since it was more robust and accurate.

Despite the encouraging results documented in [4,12], further attempts are required to identify the optimal approach for UMI detection. To this purpose, the capability of alternative supervised classifiers, e.g., Naïve Bayes (NB) and K-Nearest Neighbors (K-NNs), is worth investigation. In fact, as demonstrated by recent studies, e.g., [13], accuracy of these classifiers may also be close to 100%.

In the literature, both NB and K-NN classifiers broadly proved their reliability and versatility in real-world applications.

For example, the NB classifier is usually exploited for spam filtering and document classification, as well as for diagnostic purposes. Aralikatti et al. [14] exploited the NB classifier to classify the faulty condition of a carbide tool, while it detected hotspots in solar photovoltaic modules in Niazi et al. [15]. Recently, the NB classifier has also been applied for detecting and classifying faults occurring in transmission lines [16,17]. In a study developed by da Silva et al. [16], the NB accuracy was equal to 95%, while an NB-based classifier outperformed alternative classifiers, e.g., Multi-Layer Perceptron Neural Network, in Aker et al. [17].

In the literature, several studies exploited the K-NN classifier to diagnostic purposes. For example, Shi et al. [18] applied the K-NN classifier to detect different fault types affecting rotors. The authors compared the K-NN accuracy to other classifiers, e.g., linear SVM, by stating that K-NN exhibited the highest fault diagnosis accuracy. Aslinezhad and Hejazi [19] used the K-NN classifier for assessing the deformation of turbine blade tip. The authors varied the K number, by achieving acceptable results in terms of accuracy.

1.2. Contribution and Outline of This Paper

This study contributes to state-of-the-art-literature in the field of artificial intelligence by focusing on UMIs occurring in GTs. The novelty of the paper is acknowledged by recent studies [6,7], even in industrial applications. To fill this gap, the current paper identifies the optimal supervised classifier for UMI detection. To this purpose, the capability of three supervised classifiers is compared by means of comprehensive and challenging analyses. The goal of this paper is in fact the comparison of the classifiers aimed at investigating the benefits and drawbacks of each methodology with respect to UMI detection to extract general guidelines for field application.

First, SVM RO is accounted for thanks to the classification capability demonstrated in Manservigi et al. [4,12]. In addition, the NB and K-NN classifiers are also investigated, since they are usually more accurate than more interpretable methods, e.g., decision trees, [20].

Finally, with respect to Manservigi et al. [4,12], the current study also evaluates the robustness of each classifier by varying the rate of UMI.

As a result, the optimal classifier may be exploited as a general data-cleaning approach that filters out or correctly labels noisy data before the evaluation of GT health state. Thus, the methodologies and results of this paper can be used to improve the reliability of GT monitoring, diagnostics, and prognostics.

The paper is structured as follows. First, characteristics, basics, benefits, and drawbacks of the three supervised classifiers are described. Then, the paper outlines the general procedure to identify data used for training and testing the considered classifiers. Furthermore, field data are shown, and results are broadly discussed. Robustness of each classifier is evaluated by means of a sensitivity analysis to provide general rules of thumb for UMI detection.

2. Supervised Machine Learning Classifiers

2.1. Overview

Machine learning techniques are useful approaches that are currently exploited in several research fields. Their effectiveness strongly depends on theoretical rules, as well as characteristics of data used for training and testing the methodology.

In artificial intelligence, two different learning strategies exist, namely eager and lazy learners. Eager learners exploit labeled data to construct a generalization model [21], which is built throughout the training phase. The general validity of the model is subsequently tested during the test phase. Conversely, lazy learners do not construct a model, but labeled data are only stored [21]. Thus, an appropriate training phase is not performed [22].

As stated in Kumar and Sahoo [23], supervised classifiers can be divided into two classes, i.e., density-based and geometric-based classifiers. Most classifiers belong to the density-based class, which further discriminates between parametric and non-parametric classifiers.

In the following, the classification procedure adopted by SVM, Naïve Bayes, and K-NN classifiers is described, by also highlighting their benefits and drawbacks.

2.2. Basics of Support Vector Machine

Support Vector Machine is one of the most popular eager classifiers exploited for both binary and multi-class problems.

Data classification can be performed by means of linear or non-linear kernel functions that identify the optimal separating hyperplane that separates different classes [24]. The former is exploited when data are linearly separable. Conversely, non-linear kernel functions, such as Radial Basis Function (RBF), are recommended.

Support Vector Machine exploits the divide-and-conquer paradigm for dividing a multi-class problem into binary subproblems. To this purpose, two different strategies, namely One-vs-One (OVO) and One-vs-All (OVA) decompositions, can be exploited. In OVO decomposition, each learner is trained by means of a pair of UOMs, whereas in OVA decomposition the learner is trained by using one class vs. all the others.

In a binary classification problem that exploits a linear kernel function, the SVM classifier uses labeled data, i.e., y, and their labels, i.e., l, to identify a linear decision hyperplane. To this aim, a constrained optimization problem is solved by setting the derivative of the Lagrangian equal to zero [12,25]. Thus, the linear decision hyperplane is obtained by maximizing Equation (1)

$$\max \left({\displaystyle \sum }_{\mathrm{i}=1}^{{\mathit{N}}_{\mathrm{tr}}}{\mathsf{\alpha }}_{\mathrm{i}}-\frac{1}{2}{\displaystyle \sum }_{\mathrm{i}=1}^{{\mathit{N}}_{\mathrm{tr}}}{\displaystyle \sum }_{\mathrm{j}=1}^{{\mathit{N}}_{\mathrm{tr}}}{\mathsf{\alpha }}_{\mathrm{i}}{\mathsf{\alpha }}_{\mathrm{j}}{\mathit{l}}_{\mathrm{i}}{\mathit{l}}_{\mathrm{j}}\langle {\mathit{y}}_{\mathrm{i}}{, \mathit{y}}_{\mathrm{j}}\rangle \right)$$

(1)

where α is the Lagrangian multiple and N_tr is the number of training data. Data for testing, i.e., x, are labeled as the sign provided by Equation (2), where b is the intercept of decision hyperplane:

$$\mathrm{g}\left(\mathit{x}\right)=\mathrm{sign}\left({\displaystyle \sum }_{\mathrm{i}=1}^{{\mathit{N}}_{\mathrm{tr}}}{\mathit{l}}_{\mathrm{i}}{\mathsf{\alpha }}_{\mathrm{i}}\langle {\mathit{x},\mathit{y}}_{\mathrm{i}}\rangle +\mathit{b}\right)$$

(2)

Equations (1) and (2) can be generalized by using the non-linear kernel function k (Equation (3)):

$$\mathrm{k}\left({\mathit{y}}_{\mathrm{i}}{, \mathit{y}}_{\mathrm{j}}\right)=\langle \mathsf{\Phi }\left({\mathit{y}}_{\mathrm{i}}\right), \mathsf{\Phi }\left({\mathit{y}}_{\mathrm{j}}\right)\rangle$$

(3)

where Φ is the mapping function [25]. According to Equation (3), Equations (1) and (2) can be written in the form reported in Equations (4) and (5):

$$\max \left({\displaystyle \sum }_{\mathrm{i}=1}^{{\mathit{N}}_{\mathrm{tr}}}{\mathsf{\alpha }}_{\mathrm{i}}-\frac{1}{2}{\displaystyle \sum }_{\mathrm{i}=1}^{{\mathit{N}}_{\mathrm{tr}}}{\displaystyle \sum }_{\mathrm{j}=1}^{{\mathit{N}}_{\mathrm{tr}}}{\mathsf{\alpha }}_{\mathrm{i}}{\mathsf{\alpha }}_{\mathrm{j}}{\mathit{l}}_{\mathrm{i}}{\mathit{l}}_{\mathrm{j}}\mathrm{k}\left({\mathit{y}}_{\mathrm{i}}{, \mathit{y}}_{\mathrm{j}}\right)\right)$$

(4)

$$\mathrm{g}\left(\mathit{x}\right)=\mathrm{sign}\left({\displaystyle \sum }_{\mathrm{i}=1}^{{\mathit{N}}_{\mathrm{tr}}}{\mathit{l}}_{\mathrm{i}}{\mathsf{\alpha }}_{\mathrm{i}}\mathrm{k}\left({\mathit{x}, \mathit{y}}_{\mathrm{i}}\right)+\mathit{b}\right)$$

(5)

Based on the results reported in [4,12], the current paper exploits the RBF kernel function, which is defined as in Equation (6):

$$\mathrm{k}\left({\mathit{y}}_{\mathrm{i}}{, \mathit{y}}_{\mathrm{j}}\right){=\mathrm{e}}^{-\mathsf{\gamma }{\left({\mathit{y}}_{\mathrm{i}}{ - \mathit{y}}_{\mathrm{j}}\right)}^2}$$

(6)

where γ = 1/2σ² is the distance between data and the decision hyperplane.

2.3. Benefits and Drawbacks of Support Vector Machine

In the literature, several studies stated that SVM usually outperforms other supervised classifiers [26,27,28]. This benefit is generally clearer when the training dataset comprises a limited amount of data. In addition, SVM is slightly affected by overfitting problems [29], so that an excellent generalization can be achieved [30].

Benefits and drawbacks of the SVM classifier are strictly correlated to both kernel functions and decomposition strategies. As demonstrated in Manservigi et al. [4,12] and Krawczyk et al. [31], OVO decomposition usually achieves higher classification accuracy than the OVA decomposition, though non-competent classifiers are trained and computational time may be high.

2.4. Basics of Naïve Bayes

Naïve Bayes classifier is a parametric classifier whose classification response is provided by means of an eager learning [23]. It is based on the Bayes’ theorem and assumes that f features are mutually independent. In practice, the independency assumption may be violated, but it significantly simplifies the classification task, without a dramatic reduction of prediction accuracy and robustness [16,32].

Naïve Bayes classifier assigns each unlabeled data, i.e., x_i, to the most probable class C, i.e., the one that accounts for the highest posterior probability (or conditional probability), calculated as in Equation (7):

$$\mathrm{P}\left({\mathit{C}}_{\mathrm{k}}{|\mathit{x}}_{\mathrm{i}}\right)=\frac{\mathrm{P}\left({\mathit{x}}_{\mathrm{i}}{|\mathit{C}}_{\mathrm{k}}\right)\mathrm{P}\left({\mathit{C}}_{\mathrm{k}}\right)}{\mathrm{P}\left({\mathit{x}}_{\mathrm{i}}\right)}$$

(7)

According to Equation (7), the conditional probability that data x_i belongs to class C_k depends on the class prior probability P(C_k) and the likelihood P(x_i|C_k). Based on the conditional independency assumption, likelihood P(x_i|C_k) can be calculated separately for each variable, by reducing a multidimensional problem to a one-dimensional problem, as in Equation (8):

$$\mathrm{P}\left({\mathit{C}}_{\mathrm{k}}{|\mathit{x}}_{\mathrm{i}}\right)=\frac{\mathrm{P}\left({\mathit{C}}_{\mathrm{k}}\right){{\displaystyle \prod }}_{\mathrm{i}=1}^{\mathit{f}}\mathrm{P}\left({\mathit{x}}_{\mathrm{i}}{|\mathit{C}}_{\mathrm{k}}\right)}{\mathrm{P}\left({\mathit{x}}_{\mathrm{i}}\right)}$$

(8)

The predicted label is the one that maximizes the numerator of Equation (8), since the prior probability is constant [32].

Several Naïve Bayes classifiers exist, which differ from the likelihood distribution assumption. In the literature, the Gaussian Naïve Bayes, Bernoulli Naïve Bayes and Multinomial Naïve Bayes are popular Naïve Bayes classifiers [33].

2.5. Benefits and Drawbacks of Naïve Bayes

The Naïve Bayes classifier is effective at handling both limited and very large datasets. In fact, the classification model is easily built and its parameters are not estimated by means of complex iterations [23].

Despite its simplicity, the Naïve Bayes classifier can be efficiently exploited for complex real-world problems, even though an explicit model for its deployment cannot be provided [23].

2.6. Basics of K-Nearest Neighbors

K-Nearest Neighbors is a popular lazy learner and non-parametric classifier [22], [34] exploited in different research fields.

The K-NN learner classifies each unlabeled data as the most frequent label among its K nearest labeled neighbors [35], which are identified by means of the Minkowski distance, reported in Equation (9):

$$\mathit{d}={\left({\displaystyle \sum }_{i=1}^{\mathit{f}}{\left|{\mathit{x}}_{\mathrm{i}}-{ \mathit{y}}_{\mathrm{i}}\right|}^{\mathit{z}}\right)}^{\frac{1}{\mathit{z}}}$$

(9)

where f are the considered features and x_i and y_i are the coordinates of each unlabeled and labeled data in the f-dimensional space, respectively. If z is set equal to 1, d is named Manhattan distance, whereas Equation (9) calculates the Euclidean distance if z is equal to 2.

2.7. Benefits and Drawbacks of K-Nearest Neighbors

The K-NN classifier is broadly exploited thanks to its conceptual straightforwardness, which makes it also suitable for handling multi-classification problems [34,35,36]. However, despite its simplicity, the accuracy of the K-NN classifier can be equal or even higher than that of more complex classifiers [37]. In addition, since lazy learners do not account for an explicit training phase, the computational time is usually very low.

However, the K-NN classifier is affected by two main drawbacks: (i) the tuning of the K value and (ii) the negative effect of outliers.

Several studies were addressed to identify the optimal K value for accuracy maximization. In general, 1-NN (i.e., K = 1) is considered a promising classifier, which has been considered hard to be beaten for classification purposes [38]; however, misleading results can be achieved since the label is assigned only by the nearest neighbor. Thus, the reliability of the 1-NN classifier may be compromised if outliers are included within the dataset.

Instead, given that N_tr is the number of available labeled data, Cheng et al. [22] suggested setting K equal to N_tr^0.5 if the dataset is larger than 100 samples. However, the same authors also stated that this rule of thumb has not been proved suitable for all datasets. Thus, the optimal setting of the K value is still an ongoing research topic.

Finally, the K-NN classifier may be significantly challenged if the number of features is higher than the number of labeled data [34] or when unbalanced datasets are used [36].

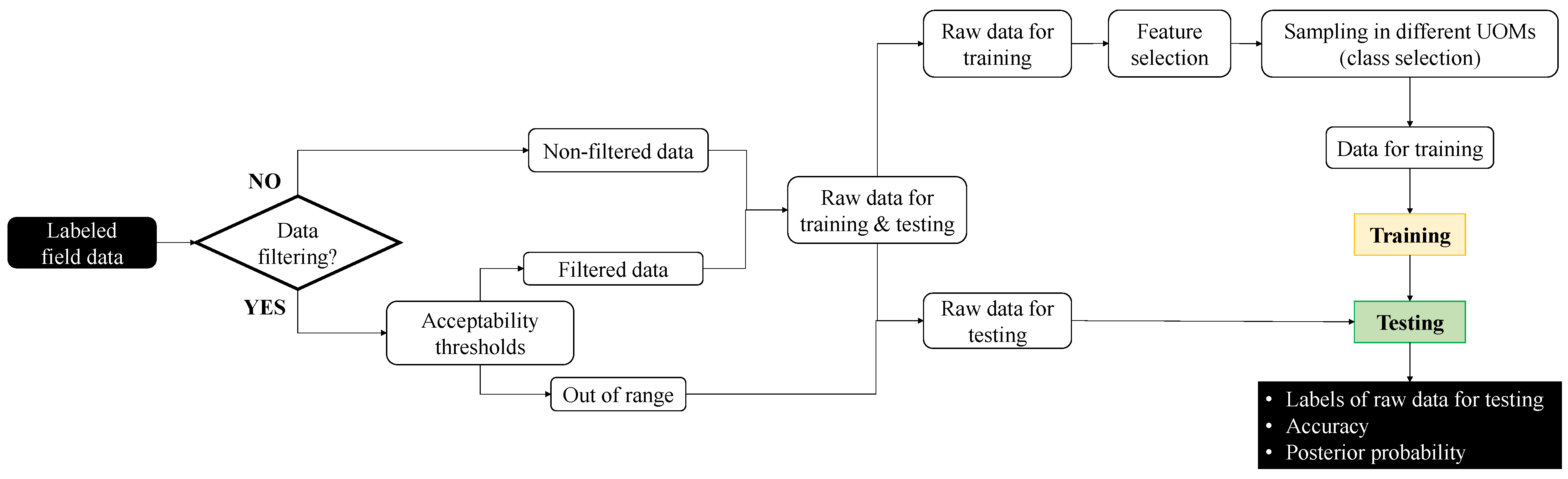
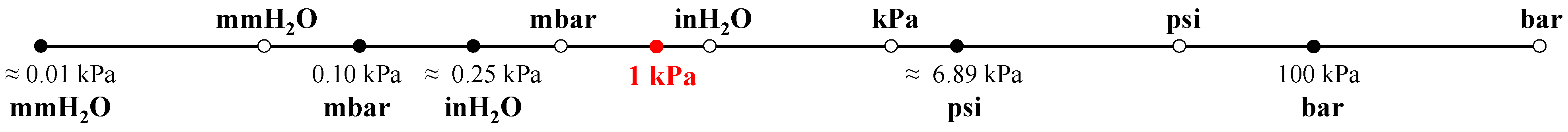3. Training and Testing

The general procedure for identifying the data used to train and test the classifiers is sketched in Figure 1, where it has to be observed that the word “training” does not rigorously apply to the K-NN classifier because there is no training phase.

First, each piece of field data is labelled with the supposed label.

After that, rough acceptability thresholds can be used to filter the labeled field data. This step relies on the fact that, in the GT field, UMIs are currently detected by using physics-based acceptability thresholds: if a given piece of data exceeds such thresholds, it is labeled as a UMI. In practice, such assumption may lead to misleading results, since anomalous observations may be caused by feature noise, e.g., sensor faults. Thus, in the current paper, the out-of-range values, i.e., the ones that exceed the acceptability thresholds, are tested because they are candidate UMIs.

Conversely, data that lie within the minimum and maximum acceptability thresholds are used to both train and test the supervised classifiers. Such data are named “filtered data” in Figure 1.

Alternatively, if the acceptability thresholds are not used to preliminary filter the candidate UMIs, all labeled field data, namely non-filtered data in Figure 1, are used to both train and test the classifiers.

A fraction of filtered or non-filtered data is identified to train each classifier, while the remaining data are used for testing. Then, the features are selected and the “Raw data for training” (see Figure 1) are sampled in different UOMs, by defining the number of classes c. Thus, the dataset of training data comprises both field and scaled data, by making all classes inherently balanced. Once the classifiers have been trained, raw data for testing are used to test the capability of the learner. For each piece of testing data, its label is provided, as well as the accuracy and the posterior probability of prediction.

Each classifier was trained and tested by means of the tools available in the Matlab^® environment.

4. Field Data

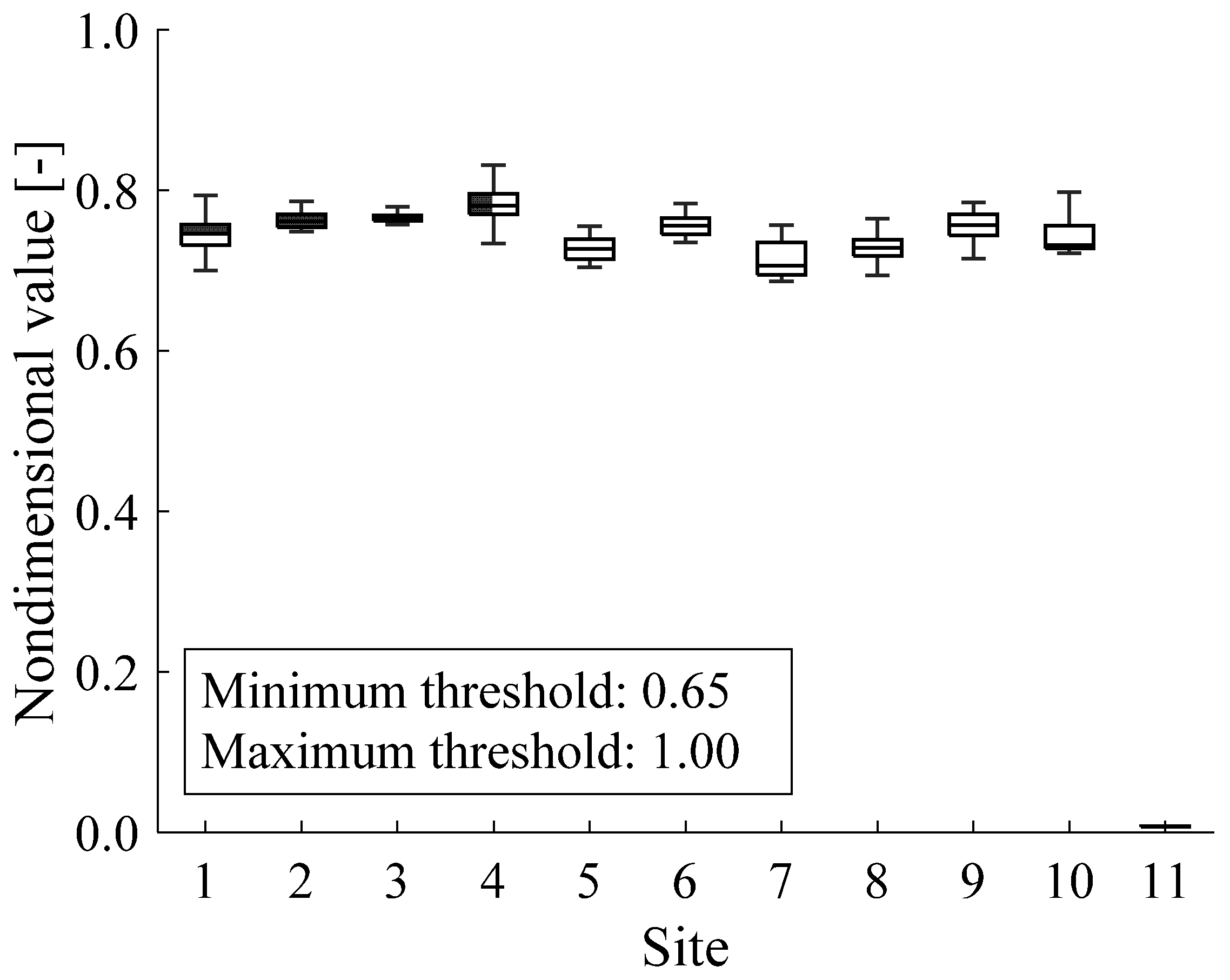
In the current paper, each ML classifier is tested by using one experimental dataset collected by a pressure sensor (see Figure 2).

The field dataset comprises a fleet of thirty Siemens GTs of the same type, installed in eleven sites worldwide. Thus, coherent comparisons can be performed among the considered GTs. Each site comprises a different number of GTs, which varies from one to ten; the amount of data acquired from each site is in the range from 0.7% (i.e., Site 6) to 24.2% (i.e., Site 8), with respect to the total amount of available data (

Table 1. Dataset characteristics.

Site	Number of GTs	Share	True UOM
1	10	21.1%	kPa absolute
2	1	6.1%
3	1	2.7%
4	2	12.1%
5	1	6.1%
6	1	0.7%
7	1	2.8%
8	7	24.2%
9	2	7.9%
10	1	2.9%
11	3	13.4%	bar absolute
TOTAL	30	100.0 %

).

In order to distinguish UMIs from sensor faults [12], field data were elaborated to extract two features, i.e., mean value and standard deviation, which are exploited to train and test the classifiers. For feature extraction, only steady state operations were considered. Each piece of data of the dataset was obtained by considering the mean value and standard deviation over sixty consecutive field time points. As a result, 2721 measurements in total were obtained.

The characteristics of the dataset are shown in Figure 2; for each site, box plots report the median, the lower and upper quartiles, as well as the minimum and maximum values of data. All measurements were normalized with respect to the maximum acceptability threshold for confidentiality reasons. The values of skewness and kurtosis of the two considered features are reported in

Table 2. Skewness and kurtosis of the field data.

Site	Feature #1 (Mean Value)		Feature #2 (Standard Deviation)
	Skewness	Kurtosis	Skewness	Kurtosis
#1	−0.11	2.60	1.32	3.78
#2	0.41	1.98	1.33	5.29
#3	1.19	3.67	3.81	21.55
#4	−0.08	2.97	5.52	34.27
#5	1.06	3.35	1.88	7.06
#6	0.15	2.22	−0.18	1.69
#7	0.61	1.88	3.55	16.81
#8	−0.23	2.58	0.90	3.20
#9	−0.29	2.21	1.74	5.87
#10	1.15	2.87	4.50	24.75
#11	1.18	3.14	6.81	65.48

. Based on the analysis of such indices, Site #11 is characterized by the highest values of the skewness and kurtosis, thus revealing that its data distribution is heavy-tailed.

Based on engineering practice and an in-depth knowledge of the GT type, the nondimensional pressure is expected to lie between 0.65 (i.e., minimum acceptability threshold) and 1.00 (i.e., maximum acceptability threshold).

All data were originally labeled as kPa absolute. However, all data acquired from Site #11 are approximately two orders of magnitude lower than the minimum acceptability threshold; such data represent 13.4% of the entire dataset. Thus, data acquired from Site #11 may be incorrectly classified as out of range values [12], whose anomalous behavior may be caused by sensor faults [39]. However, sensor faults generally affect a limited amount of data. Thus, based on the general procedure outlined in Figure 1, all data acquired from Site #11 are candidate UMIs.

Subsequently, an inspection made by Siemens confirmed that all data collected from Site #11 were affected by UMIs and, based on the scale factor between such piece of data and the ones acquired from the other sites, the bar absolute label was subsequently assigned.

It has to be mentioned that the use of an experimental dataset strengthens the outcomes of this paper. In fact, experimental noisy labels are included within the dataset, while the common practice is to artificially introduce misleading labels [5].

5. Analysis of Classification Performance

Performance of ML classifiers strictly depends on the characteristics of training data, such as data quality and quantity [40], which can negatively affect the capability of supervised learners. To provide a general classifier able to efficiently detect UMIs, several analyses are documented and discussed for testing each classifier in challenging scenarios. Such analyses evaluate the influence of (i) data quality, (ii) data quantity and (iii) number of classes on the performance of each classifier.

Data quality. In the current paper, the influence of data quality is evaluated by means of different analyses. First, each classifier is trained by means of correctly labeled data only, i.e., filtered data (Figure 1). Then, each classifier is trained by means of non-filtered data (Figure 1), in which all data acquired from Site #11 (approximately 13% of the dataset) are experimentally affected by label noise issue. The effect of UMIs on classification capability is further investigated by means of a sensitivity analysis in which the rate of UMI is progressively increased, as outlined in

Table 3. Scheme of the sensitivity analysis.

Rate of UMIs	Sites Affected by UMIs
0%	/
13.4%	Site #11
20.2%	Site #2, Site 6, Site #11
30.8%	Site #2, Site #3, Site 6, Site #9, Site #11
39.8%	Site #2, Site #3, Site #5, Site 6, Site #9, Site #10, Site #11
51.9%	Site #2, Site #3, Site #4, Site #5, Site 6, Site #9, Site #10, Site #11
60.9%	Site #1, Site #2, Site #3, Site #5, Site #6, Site #9, Site #10, Site #11
73.0%	From Site #1 to #6 and from Site #9 to Site #11
97.2%	Site #1 through #6 and Site #8 through #11
100.0%	All sites

. At each step, the rate of UMIs is increased by roughly 10%, so that the label noise experimentally affects all data acquired from Site #11, as well as all data collected from additional sites, in which noisy labels were implanted. As in Site #11, implanted UMIs were originally labeled as kPa absolute, though bar absolute was the correct label. Such analyses are aimed at assessing the robustness of each classifier by varying data quality.

Data quantity. The amount of data used for training a classifier usually affects its classification capability. In this paper, the influence of data quantity is assessed by means of two analyses.

In the first analysis, each classifier is trained by using 10% of filtered or non-filtered data of each site. This choice is in line with the outcomes documented in Manservigi et al. [12], which reports a detailed sensitivity analysis on the amount of data used for training the SVM classifier. In Manservigi et al. [12], the amount of data used for training the classifier was equal to 10%, 25%, 50%, 75%, and 90% of both filtered and non-filtered data. Based on results, in most cases the SVM classifier was slightly affected by the amount of training data. Thus, in the current paper, each classifier is trained by means of the lowest rate of data, i.e., 10%.

The second analysis, namely site cross-validation, mimics the practical condition in which all data acquired from a novel site have to be labeled. In line with the case study reported in Section 4, if filtered data train the classifier, all data acquired from two sites, i.e., Site #11 and one additional site in turn, are tested. Instead, if non-filtered data are used, all data acquired from only one site in turn are tested. Since each site accounts for a different number of data, each training combination is performed by means of a different amount of data, which varies from 62.4% to 99.3% of the data included in the dataset. As a result, the site cross-validation further strengthens the classifier reliability vs. amount of training data.

Number of classes. The classification capability of the classifiers is tested by means of twelve classes. The selected UOMs were identified by means of engineering practice. In fact, since all field data were originally labeled as kPa absolute, five additional UOMs, i.e., mmH₂O, mbar, inH₂O, psi, and bar, are accounted for in absolute terms. As a result, six absolute UOMs in total are considered, whose scale factors with respect to the kPa absolute are highlighted in Figure 3 (full circles). Such scale factors are independent from the dataset under analysis.

Moreover, the six absolute UOMs are converted in gauge terms, by obtaining twelve UOMs in total. It has to be mentioned that the relationship between absolute and gauge UOMs is strictly correlated to the dataset under analysis. The position of the gauge UOMs (empty circles) with respect to the absolute UOMs is reported in Figure 3 for the considered case study.

It can be observed that, in the current paper, the identification of the true UOM is significantly challenged. In fact, the conversion factor between kPa absolute and inH₂O gauge is equal to just 1.2. In addition, regardless of the number of classes, when non-filtered data are used, each classifier is also trained by means of incorrectly labeled data.

6. Indices of Classification Performance

The performance of each classifier is evaluated by means of two indices, i.e., classification accuracy and posterior probability.

Classification accuracy. In the field of ML, confusion matrix is usually exploited to evaluate the effectiveness of supervised classifiers. Based on the classifier prediction, four metrics can be calculated, i.e., the rate of true positives (TPs), false positives (FPs), true negatives (TNs) and false negatives (FNs), which can be used to calculate classification accuracy, precision, recall, and specificity.

In the current paper, accuracy (Equation (10)) meaningfully quantifies the performance of the classifiers.

$$\mathit{A}=\frac{\mathit{TP}+\mathit{TN}}{\mathit{TP}+\mathit{TN}+\mathit{FP}+\mathit{FN}}$$

(10)

In fact, based on the training and testing procedure outlined in Section 3, for each site, the true label (i.e., the positive class) of all data used for testing is unique. Thus, true negative and false positive rates are inherently null. As a result, precision is equal to 100%, while specificity cannot be calculated and accuracy corresponds to recall.

Since classification accuracy represents the rate of correctly labeled data, the higher the classification accuracy the better is the classification performance.

Posterior probability. The posterior probability represents the confidence that a given data belongs to a given class. By considering all classes, for each data the sum of the c posterior probabilities is equal to 100%.

The procedure employed to calculate the posterior probability depends the considered ML classifier.

In the SVM RO classifier, the score-matrix P is calculated for each pair of classes; each element p_ij (p_ij ∈ [0,1]) is the confidence that a given data belongs to the class i. Consequently, p_ji = 1 − p_ij. The comprehensive procedure to calculate the score-matrix P is described in Platt [41].

In the NB classifier, the posterior probability is calculated as in Equation (8).

Finally, in the K-NN classifier, the posterior probability of a given class is the ratio between the number of the K neighbors that belong to that class and the K value.

The optimal supervised classifier is the one that correctly classifies the “Raw data for testing” (see Figure 1) and that maximizes both classification accuracy and posterior probability. In addition, for the sake of industrial attractiveness, classification results have to be obtained with the lowest computational effort.

Receiver Operating Characteristic curve. The capability of each ML classifier is also assessed by means of the receiver operating characteristic (ROC) curve, which displays the false positive rate (FPR) vs. the true positive rate (TPR). Thus, the ROC curve shows the trade-off between the probability of detecting false positives or true positives. For an accurate ML classifier, the ROC curve should climb steeply [42].

Area Under the Curve. The area under the curve (AUC) is the area under the ROC curve, which is in the range from 0 to 1. The higher the AUC value, the better the performance of the ML classifier [26].

7. Results and Discussion

This section compares classification accuracy, posterior probability, and computational time of the supervised classifiers.

Support Vector Machine, NB, and K-NN classifiers can classify data by means of several approaches. For the sake of brevity, for each classifier, only the most promising approach is hereafter reported. In the current paper, the identification of the optimal ML classifier is focused on three alternatives, i.e., SVM RO, NB, and K-NN by using K = N_tr^0.5.

In fact, Manservigi et al. [12] demonstrated that SVM RO is the most suitable approach for UMI detection. As in Subasi et al. [42], the σ value (defined in Equation (6)) is equal to 1. In addition, a specific analysis on the influence of the σ parameter revealed that its value slightly affected SVM performance [12].

Regarding the NB classifier, as made in Petschke and Staab [32] a Gaussian Naïve Bayes classifier is assumed.

Finally, Manservigi [43] has recently examined the effect of the K value on the capability of the K-NN classifier. By assuming that N_tr is the number of training data (Figure 1), three analyses were carried out, in which: (i) K = 1, (ii) K = (N_tr/c)^0.5, and (iii) K = N_tr^0.5. In these analyses, the ratio N_tr/c corresponds to the number of “Raw data for training” (Figure 1). Among the three K value settings, the best results were obtained when K = N_tr^0.5, especially when non-filtered data were accounted for. This outcome confirms the analysis reported in Cheng et al. [22], which suggested setting K = N_tr^0.5.

For the K-NN classifier, neighbors are identified by means of the Euclidean distance.

The results are split into four sections. Section 7.1 describes in detail the case in which data are filtered by means of acceptability thresholds, which were previously set thanks to domain knowledge about the considered GT type. For each classifier, Section 7.2 documents the classification performance when raw data are not filtered out. This analysis mimics the situation in which acceptability thresholds cannot be employed (e.g., their boundaries are not known). Thus, the effect of the experimental noise label can be evaluated.

For all sites characterized by the same true UOM, the mean classification accuracy and posterior probability is calculated; posterior probabilities of absolute and gauge UOMs are highlighted by means of full and dotted bars, respectively.

Then, a sensitivity analysis on the rate of UMIs is reported in Section 7.3. For the sake of clarity, the sensitivity analysis is separately discussed since implanted UMIs are also accounted for.

Section 7.1, Section 7.2, Section 7.3, Section 7.4, Section 7.5 are aimed at identifying the optimal supervised classifier.

7.1. Training with Filtered Data

When 10% of filtered data train the classifiers, the label selection of the kPa absolute sites is mainly focused on two out of twelve classes, i.e., kPa absolute and inH₂O gauge.

SVM RO and NB achieve approximately the same classification accuracy. In fact, the rate of correctly labeled data slightly varies from 95% (i.e., SVM RO) to 97% (i.e., NB). The K-NN classifier achieves the poorest classification accuracy, since 77% of data were correctly labeled.

The inH₂O gauge label slightly challenges the classifiers. In fact, for SVM RO and NB a limited fraction of data (between 3% and 9%) is classified as inH₂O gauge; this rate increases up to 23% in the K-NN classifier.

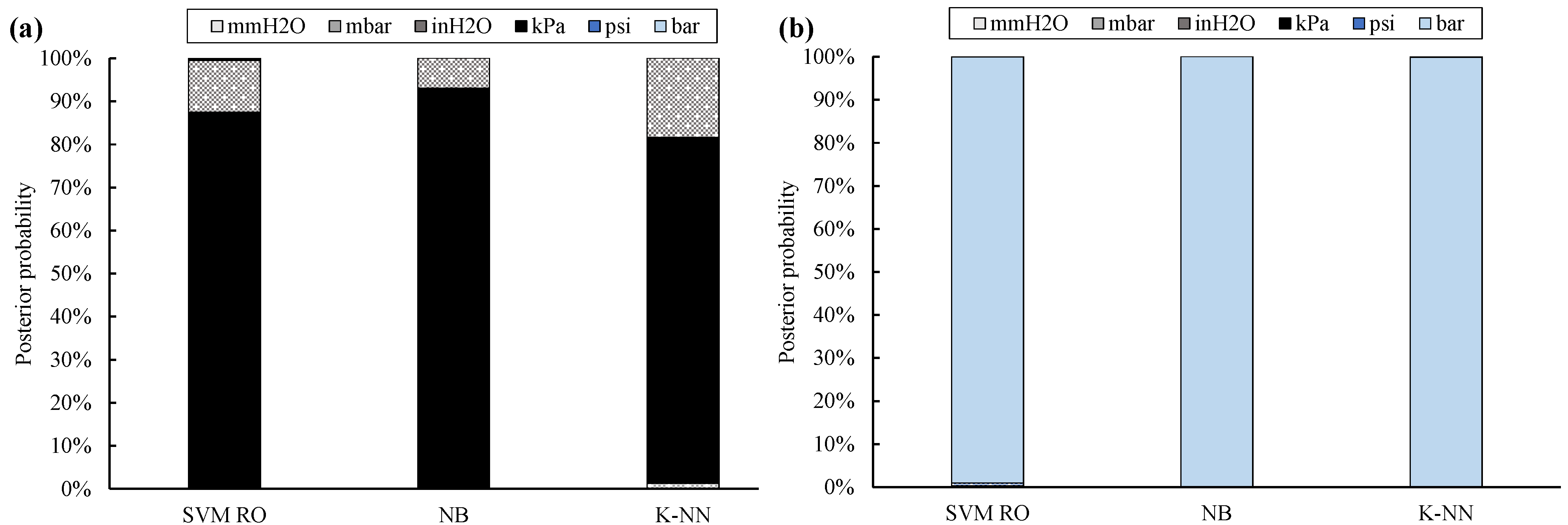
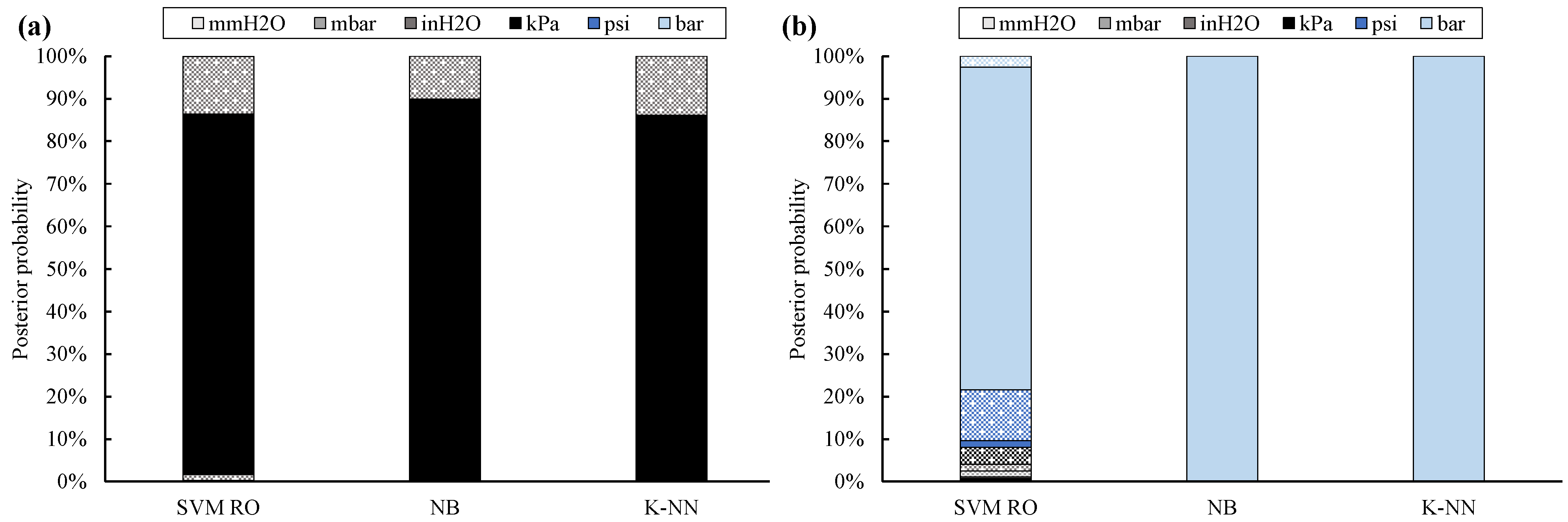
Posterior probability values (Figure 4) confirm these positive results. In fact, the correct UOM is provided by the NB classifier by means of the highest posterior probability, which is on average equal to 93%, followed by the SVM RO (i.e., 87%) and K-NN (i.e., 80%).

Instead, all data of Site #11 are always univocally classified; in addition, posterior probability is always equal to 100%.

Both classification accuracy and posterior probability of kPa absolute sites are usually lower than the ones obtained for Site #11. This is due to the scale factor between the true label of the site under analysis and its nearest UOM. In fact, the conversion factor between kPa absolute and inH₂O gauge is only equal to 1.2, while the scale factor between bar absolute and bar gauge is roughly equal to 5. As a result, the assignment of the correct UOM is more challenging for Site #1 through #10 than for Site #11.

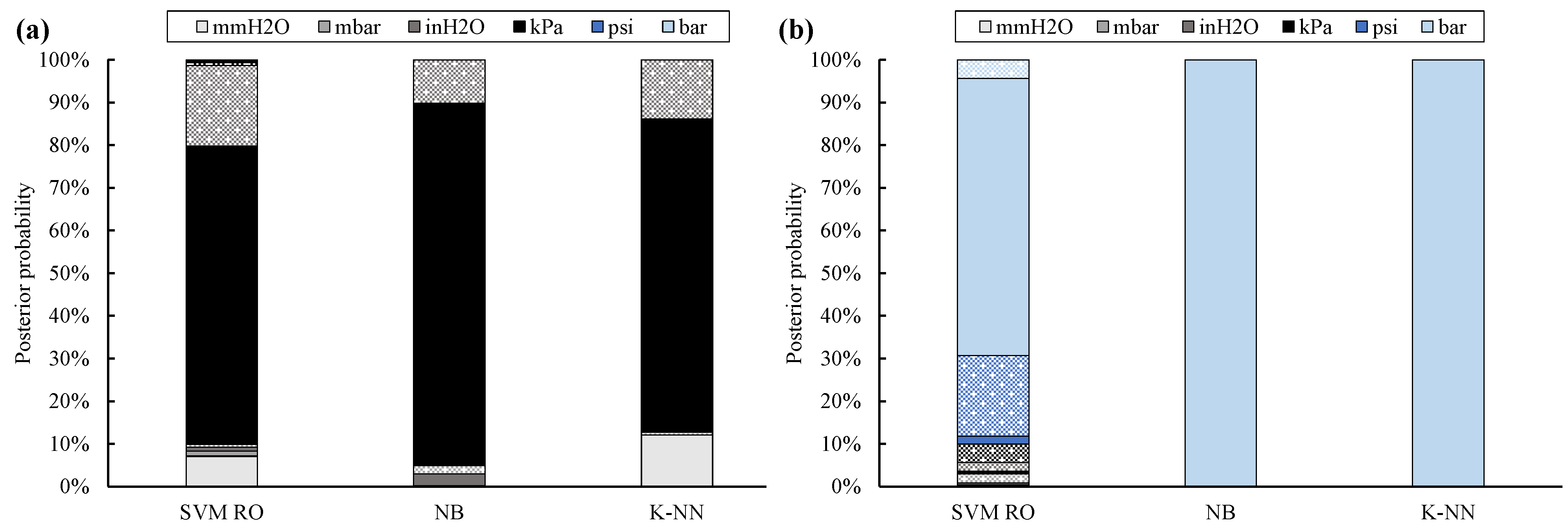
Site cross-validation generally confirms the results achieved by using 10% of filtered data for training the classifiers. In fact, classification accuracy and posterior probability (Figure 5) are always higher than 89% and 75%, respectively.

7.2. Training with Non-Filtered Data

The comparison between the exploitation of filtered and non-filtered data for training the classifiers reveals that all ML approaches are only slightly affected by data reliability. In fact, the reduction in terms of classification accuracy is lower than 3%, thus proving the robustness of all classifiers.

As a general comment, the highest and homogeneous classification accuracy is provided by SVM RO, i.e., 97% and 99% for the kPa absolute and bar absolute sites, respectively. Instead, NB correctly classifies 94% of data acquired from Site #1 through #10 and 99% of data acquired from Site #11. The K-NN classifier confirms the poorest classification capability, since 76% of data acquired from Site #1 through #10 are correctly labeled.

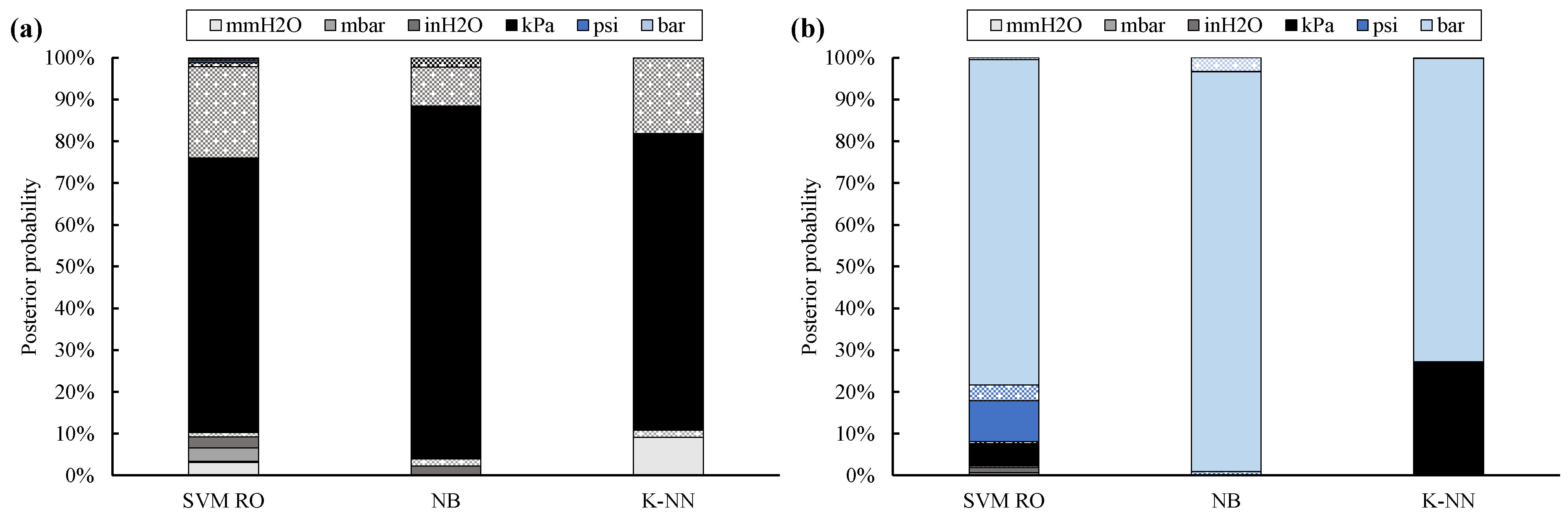
Though the classification accuracy is generally confirmed, posterior probability (Figure 6) proves to be more affected by data reliability. Therefore, the label is correctly provided, but classifier confidence decreases. This outcome is clearer for the SVM RO and K-NN classifiers, whose posterior probability decrease up to 24% (Site #1 through #10) and 27% (Site #11), respectively. As a result, SVM RO provides the true UOM with 66% (kPa absolute sites) and 78% (bar absolute sites) of confidence, while such rates are equal to 71% (kPa absolute sites) and 73% (bar absolute sites) for the K-NN classifier.

Instead, posterior probability of the Naïve Bayes classifier only slightly decreases; in fact, it is equal to 84% for the kPa absolute sites and 96% for the bar absolute site.

A further interesting result, which highlights the theoretical differences among the classifiers, can be inferred by comparing the posterior probability of the twelve UOMs. As a general comment, posterior probability of SVM RO is significantly scattered. For Site #1 through #10, UOMs at the left-hand side of kPa absolute (Figure 3) usually achieve higher posterior probability values than UOMs placed at the right-hand side; this rule of thumb holds with the exception of the inH₂O gauge label, which is the second-most probable label because of the challenging scale factor.

This result may rely on the fact that the wrongly assumed mmH₂O absolute data of Site #11 slightly overlap the kPa absolute data acquired from the other sites. Thus, the area that identifies the mmH₂O absolute label is shifted toward the kPa absolute label.

As a consequence, the posterior probability of all UOMs located between mmH₂O absolute and kPa absolute is higher than that of the other UOMs. However, this outcome cannot be clearly grasped from Figure 6 because few outliers are included within the dataset.

Similarly, psi absolute and kPa absolute are the second and third-most probable labels, respectively, for Site #11.

Instead, for the NB classifier, posterior probability of each class strictly depends on its proximity to the true UOM. In fact, for Site #1 through #10, posterior probability of inH₂O absolute, mbar absolute, inH₂O gauge, and kPa gauge is higher than the one of the other UOMs. Similarly, for Site #11, posterior probability of all UOMs is null, with the exception of bar gauge and psi gauge.

The K-NN classifier identifies the correct UOM among a limited number of labels. In fact, for Site #1 through #10, posterior probability of four classes only is not null, i.e., mmH₂O absolute, inH₂O gauge, mbar gauge, and kPa absolute (the true UOM). This outcome can be explained by considering that wrongly assumed mmH₂O absolute data approximately overlap data that are correctly labeled as kPa absolute. In addition, the inH₂O gauge and mbar gauge labels are the classes that are nearest and second-nearest to the true UOM (see Figure 3). A similar result is confirmed for Site #11, in which the kPa absolute label is the only incorrect UOM whose posterior probability is not null. In fact, wrongly assumed kPa absolute data numerically overlap data correctly labeled as bar absolute.

The site cross-validation carried out by means of non-filtered data (Figure 7) generally confirms the results provided by training the classifiers with 10% of non-filtered data. In fact, the classification accuracy for Site #1 through #10 is in the range from 86% (i.e., K-NN) to 93% (i.e., SVM RO). However, the true label is assigned by SVM RO by means of the lowest posterior probability, i.e., 70%.

As previously demonstrated, the true UOM of Site #11 is usually better detected in terms of both classification accuracy and posterior probability. In addition, the site cross-validation further proves that quality of data for training slightly affects the classification accuracy, while posterior probability may significantly decrease, even by 19%, as in SVM RO. In addition, SVM RO confirms the most scattered results in terms of posterior probability, whereas only a few classes are more probable for the K-NN classifier.

7.3. ROC Curve and AUC

The results reported in Figure 4, Figure 5, Figure 6 and Figure 7 are confirmed by analyzing the ROC curves reported in Figure 8 and the AUC values shown in

Table 4. AUC of the SVM RO, NB, and K-NN classifiers.

	SVM RO	NB	K-NNs
kPa absolute sites	0.992	0.993	0.990
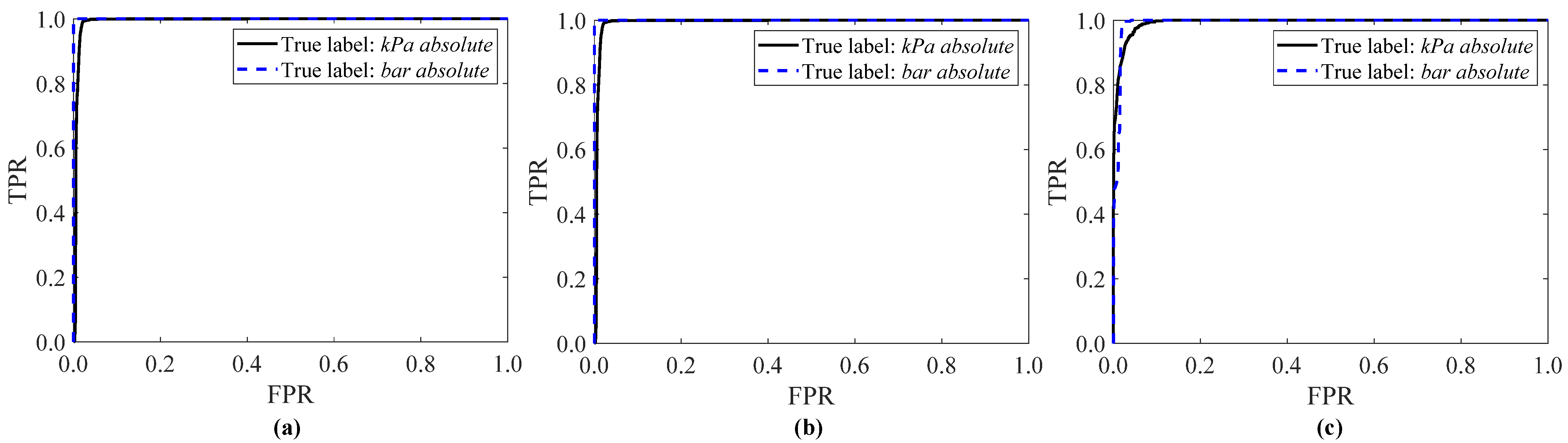
bar absolute site	1.000	1.000	0.992

for the three ML classifiers. For the Naïve Bayes classifier, the ROC curve of both the kPa absolute sites and the bar absolute site exhibit a stepwise behavior (Figure 8b) and the AUC is always higher than 0.993 (Table 4). The SVM RO classifier is the second-best ML approach, since the AUC is at least 0.992. Finally, the ROC curve of the K-NN classifier is characterized by a smoother trend than the NB and SVM RO classifiers, by achieving a lower AUC value, accordingly. Thus, such results point out that the NB classifier is the optimal ML classifier because it minimizes the false positive rate and simultaneously maximizes the true positive rate.

7.4. Sensitivity Analysis

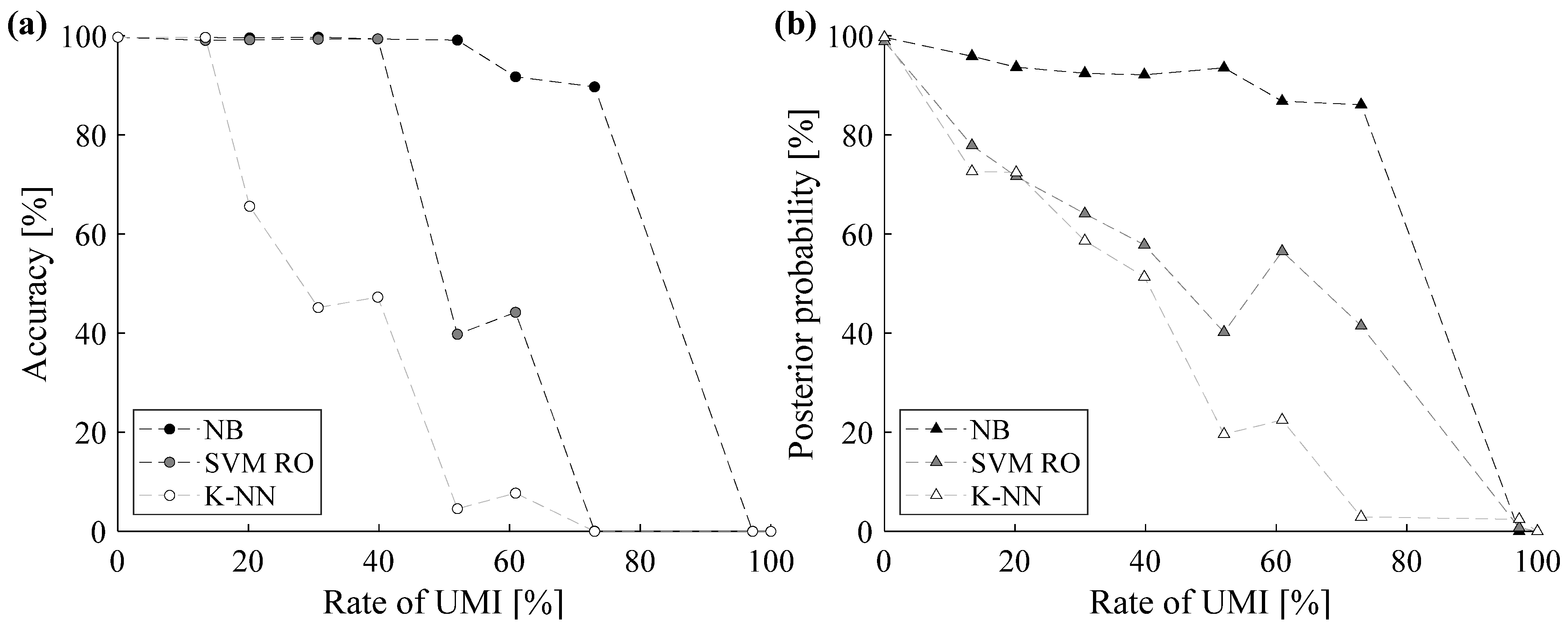
The effect of UMIs on classification capability is further investigated by means of a sensitivity analysis in which the rate of UMIs varies from 0% to 100%. This analysis is performed by considering 12 UOMs and by training the classifier by means of 10% of data.

The sensitivity analysis comprises ten scenarios. In the first scenario, the rate of UMI is equal to 0% and the corresponding classification results have already been thoroughly analyzed in Section 7.1, i.e., “Training with filtered data”. In the second scenario, the classifiers are trained by also using the experimentally noisy labels of Site #11, i.e., Section 7.2 “Training with non-filtered data”. The remaining scenarios account for both experimental and implanted UMIs. Accuracy and posterior probability of incorrectly labeled data obtained by varying the rate of UMI are reported in Figure 9.

As can be grasped from Figure 9, the sensitivity analysis confirms that the NB is the most robust classifier for UMI detection. In fact, both accuracy (Figure 9a) and posterior probability (Figure 9b) slightly decrease by increasing the rate of UMI and are always higher than the values provided by the other two methodologies, especially when the rate of UMIs is high.

Slightly poorer results are achieved by using SVM RO. In particular, the rate of UMI mainly affects the posterior probability, which exhibits an almost linear trend by increasing the noise rate. However, the classifier proves to be reliable up to a rate of UMI roughly equal to 40%.

Finally, the sensitivity analysis further proves that the K-NN classifier can be exploited only when a limited amount of data is incorrectly labeled or in the case that a limited number of outliers is included within the dataset [44]. In fact, both accuracy and posterior probability of the K-NN classifier significantly decrease when the rate of UMI is approximately equal to 20%, so that only 66% of data are correctly labeled.

These results can be explained by considering the theoretical differences among the considered classifiers. In fact, as stated in Section 7.2, the posterior probability of each class provided by the NB classifier strictly depends on its proximity to the true UOM. Thus, the NB classifier proves to be more robust than SVM RO and K-NNs. In fact, the SVM RO classifier tends to scatter the posterior probabilities, while the K-NN classifier labels the testing data as outliers.

7.5. Discussion and Guidelines

The capability of SVM RO, NB, and K-NNs is directly compared in

Table 5. Product of accuracy and posterior probability for each training approach.

Site	Data Quality	Training	SVM RO	NB	K-NNs
Site #1–#10	Filtered	10% of data	83%	90%	62%
		Site cross-validation	81%	85%	77%
	Non-filtered	10% of data	64%	79%	54%
		Site cross-validation	65%	76%	63%
Site #11	Filtered	10% of data	99%	100%	99%
		Site cross-validation	75%	100%	100%
	Non-filtered	10% of data	77%	95%	72%
		Site cross-validation	65%	100%	100%

and

Table 6. Comparison of classifier performance.

	SVM RO	NB	K-NNs
Robustness in the presence of UMIs	✓	✓✓	✕
Computational time	✕	✓	✓✓

. In Table 6, robustness in the presence of UMIs and computational time are qualitatively described as extremely positive (✓✓), positive (✓), or not acceptable (✕).

As demonstrated in Section 7.1, Section 7.2, Section 7.3, the accuracy of SVM RO is generally slightly higher than that of the NB classifier. However, NB provides the correct label by means of a higher posterior probability. Thus, since the optimal classifier is the one that maximize both accuracy and posterior probability, their product is calculated. As can be grasped by means of Table 5, the NB classifier always provides the highest product of accuracy and posterior probability, which is always higher than 76%.

Furthermore, the computational of both training and testing is low, by taking less than 1 s for the considered dataset (Table 6). In addition, NB is a robust classifier even when increasing the rate of UMI (Table 6). For these reasons, NB proved to be the optimal classifier for UMI detection.

The SVM RO may represent an effective alternative to the NB classifier, despite the fact that the computational time for both training and testing the classifier may be up to 30 times higher than that the optimal methodology. In addition, the robustness of the SVM technique may be significantly compromised in terms of posterior probability when noisy labels are used to train the model.

Finally, despite the promising results achieved in this paper and the low computational time, the exploitation of the K-NN classifier is discouraged for detecting UMIs, since its classification capability is strongly correlated to the K value and dataset composition. Thus, K-NN may not be a general approach suitable for detecting heterogeneous data, because it may require a fine tuning based on its application. In addition, a limited rate of UMIs, e.g., 20%, may significantly decrease the classifier capability.

As a final comment, it has to be mentioned that the experimental noisy labels of the dataset challenge all classifiers in realistic GT applications; thus, the inferred rules of thumb can be considered of general validity.

8. Conclusions

This paper dealt with the detection of the unit of measure inconsistency, a challenging label noise issue that makes a physical quantity inconsistent with the assigned unit of measure. To this purpose, the capability of three supervised classifiers was compared with the final aim to provide general guidelines for detecting unit of measure inconsistencies in gas turbines. Three well-known classifiers, i.e., Support Vector Machine, Naïve Bayes, and K-Nearest Neighbors, were tested by considering a test case composed of an experimental dataset collected on a large fleet of Siemens gas turbines in operation.

The effectiveness and robustness of each classifier were thoroughly assessed by varying field data reliability for training each classifier.

The analyses revealed that the Naïve Bayes classifier provided the most reliable results, both in terms of classification accuracy and posterior probability. In fact, when experimental label noise issues affected the dataset, accuracy and posterior probability were equal to 94.4% and 84.0%, respectively. In addition, a sensitivity analysis on the rate of incorrectly labeled data revealed that the NB classifier was only slightly affected by noisy data. The superior capability of the Naïve Bayes classifier was also demonstrated by means of the receiver operating characteristic curve and the related area under the curve, which provide a trade-off between the probability of detecting false positives or true positives.

Despite the promising results obtained by means of the Support Vector Machine classifier (with Radial Basis Function and One-vs-One decomposition strategy), its classification capability was usually lower than that of NB. In addition, computational time for both training and testing the classifier was higher than that of the other methodologies.

Finally, the exploitation of the K-Nearest Neighbors was discouraged, since its effectiveness may be strongly correlated to the selected K value and dataset composition.

Future works are planned to further test the Naïve Bayes by means of additional experimental datasets.