An Accelerated Extragradient Method for Solving Pseudomonotone Equilibrium Problems with Applications
Abstract
1. Introduction
2. Preliminaries
- (1)
- strongly monotone if:
- (2)
- monotone if:
- (3)
- strongly pseudomonotone if:
- (4)
- pseudomonotone if:
- (i)
- For every exists;
- (ii)
- each sequentially weak cluster limit point of belongs to set
- (1)
- for all , and f is pseudomonotone on
- (2)
- f satisfies the Lipschitz-type condition on through and
- (3)
- for each and satisfy ;
- (4)
- is subdifferentiable and convex on for each
3. An Accelerated Method for Pseudomonotone Equilibrium Problems and Its Convergence Analysis
| Algorithm 1 (Accelerated method for pseudomonotone equilibrium problems) |
|
4. Applications of the Main Results
- (i)
- L-Lipschitz continuous on if:
- (ii)
- pseudomonotone on if:
- (G1)
- G is pseudomonotone on with solution set ;
- (G2)
- G is L-Lipschitz continuous on with ;
- (G3)
- and satisfy
- (i)
- Choose , and a sequence such that:
- (ii)
- Let satisfy such that:
- (iii)
- Set , and compute:where
- (iv)
- Next, stepsize is obtained as follows:
- (i)
- (ii)
- sequentially weakly continuous on if:
- (i)
- Choose , and a sequence such that:
- (ii)
- Let satisfy such that:
- (iii)
- Set , and compute:where
- (iv)
- Next, stepsize is obtained as follows:
5. Numerical Experiments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blum, E. From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63, 123–145. [Google Scholar]
- Muu, L.D.; Oettli, W. Convergence of an adaptive penalty scheme for finding constrained equilibria. Nonlinear Anal. Theory Methods Appl. 1992, 18, 1159–1166. [Google Scholar] [CrossRef]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Konnov, I. Equilibrium Models and Variational Inequalities; Elsevier: Amsterdam, The Netherlands, 2007; Volume 210. [Google Scholar]
- Quoc Tran, D.; Le Dung, M.N.V.H. Extragradient algorithms extended to equilibrium problems. Optimization 2008, 57, 749–776. [Google Scholar] [CrossRef]
- Quoc, T.D.; Anh, P.N.; Muu, L.D. Dual extragradient algorithms extended to equilibrium problems. J. Glob. Optim. 2011, 52, 139–159. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Cho, Y.J.; Yordsorn, P. Weak convergence of explicit extragradient algorithms for solving equilibirum problems. J. Inequal. Appl. 2019, 2019. [Google Scholar] [CrossRef]
- Lyashko, S.I.; Semenov, V.V. A New Two-Step Proximal Algorithm of Solving the Problem of Equilibrium Programming. In Optimization and Its Applications in Control and Data Sciences; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 315–325. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Je Cho, Y.; Suleiman, Y.I.; Kumam, W. Modified Popov’s explicit iterative algorithms for solving pseudomonotone equilibrium problems. Optim. Methods Softw. 2020, 1–32. [Google Scholar] [CrossRef]
- Takahashi, S.; Takahashi, W. Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. J. Math. Anal. Appl. 2007, 331, 506–515. [Google Scholar] [CrossRef]
- Anh, P.N.; Hai, T.N.; Tuan, P.M. On ergodic algorithms for equilibrium problems. J. Glob. Optim. 2015, 64, 179–195. [Google Scholar] [CrossRef]
- Hieu, D.V.; Quy, P.K.; Vy, L.V. Explicit iterative algorithms for solving equilibrium problems. Calcolo 2019, 56. [Google Scholar] [CrossRef]
- Hieu, D.V. New extragradient method for a class of equilibrium problems in Hilbert spaces. Appl. Anal. 2017, 97, 811–824. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Abubakar, A.B.; Cho, Y.J. The extragradient algorithm with inertial effects extended to equilibrium problems. Comput. Appl. Math. 2020, 39. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Kumam, W.; Shutaywi, M.; Jirakitpuwapat, W. The Inertial Sub-Gradient Extra-Gradient Method for a Class of Pseudo-Monotone Equilibrium Problems. Symmetry 2020, 12, 463. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Argyros, I.K.; Deebani, W.; Kumam, W. Inertial Extra-Gradient Method for Solving a Family of Strongly Pseudomonotone Equilibrium Problems in Real Hilbert Spaces with Application in Variational Inequality Problem. Symmetry 2020, 12, 503. [Google Scholar] [CrossRef]
- Hieu, D.V.; Cho, Y.J.; Xiao, Y.B. Modified extragradient algorithms for solving equilibrium problems. Optimization 2018, 67, 2003–2029. [Google Scholar] [CrossRef]
- Yordsorn, P.; Kumam, P.; ur Rehman, H.; Ibrahim, A.H. A Weak Convergence Self-Adaptive Method for Solving Pseudomonotone Equilibrium Problems in a Real Hilbert Space. Mathematics 2020, 8, 1165. [Google Scholar] [CrossRef]
- Vinh, N.T.; Muu, L.D. Inertial Extragradient Algorithms for Solving Equilibrium Problems. Acta Math. Vietnam. 2019, 44, 639–663. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Argyros, I.K.; Alreshidi, N.A.; Kumam, W.; Jirakitpuwapat, W. A Self-Adaptive Extra-Gradient Methods for a Family of Pseudomonotone Equilibrium Programming with Application in Different Classes of Variational Inequality Problems. Symmetry 2020, 12, 523. [Google Scholar] [CrossRef]
- ur Rehman, H.; Gopal, D.; Kumam, P. Generalizations of Darbo’s fixed point theorem for new condensing operators with application to a functional integral equation. Demonstr. Math. 2019, 52, 166–182. [Google Scholar] [CrossRef]
- Gibali, A.; Hieu, D.V. A new inertial double-projection method for solving variational inequalities. J. Fixed Point Theory Appl. 2019, 21. [Google Scholar] [CrossRef]
- Censor, Y.; Gibali, A.; Reich, S. Extensions of Korpelevich’s extragradient method for the variational inequality problem in Euclidean space. Optimization 2012, 61, 1119–1132. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Dhompongsa, S. Existence of tripled fixed points and solution of functional integral equations through a measure of noncompactness. Carpath. J. Math. 2019, 35, 193–208. [Google Scholar]
- Dong, Q.L.; Jiang, D.; Gibali, A. A modified subgradient extragradient method for solving the variational inequality problem. Numer. Algorithms 2018, 79, 927–940. [Google Scholar] [CrossRef]
- Abubakar, J.; Kumam, P.; ur Rehman, H.; Ibrahim, A.H. Inertial Iterative Schemes with Variable Step Sizes for Variational Inequality Problem Involving Pseudomonotone Operator. Mathematics 2020, 8, 609. [Google Scholar] [CrossRef]
- Abubakar, J.; Sombut, K.; ur Rehman, H.; Ibrahim, A.H. An Accelerated Subgradient Extragradient Algorithm for Strongly Pseudomonotone Variational Inequality Problems. Thai J. Math. 2019, 18, 166–187. [Google Scholar]
- Hammad, H.A.; ur Rehman, H.; la Sen, M.D. Advanced Algorithms and Common Solutions to Variational Inequalities. Symmetry 2020, 12, 1198. [Google Scholar] [CrossRef]
- Santos, P.; Scheimberg, S. An inexact subgradient algorithm for equilibrium problems. Comput. Appl. Math. 2011, 30, 91–107. [Google Scholar]
- ur Rehman, H.; Kumam, P.; Argyros, I.K.; Shutaywi, M.; Shah, Z. Optimization Based Methods for Solving the Equilibrium Problems with Applications in Variational Inequality Problems and Solution of Nash Equilibrium Models. Mathematics 2020, 8, 822. [Google Scholar] [CrossRef]
- Hieu, D.V. Halpern subgradient extragradient method extended to equilibrium problems. Rev. Real Acad. Cienc. Exactas Físicas Nat. Ser. Matemáticas 2016, 111, 823–840. [Google Scholar] [CrossRef]
- Yordsorn, P.; Kumam, P.; Rehman, H.U. Modified two-step extragradient method for solving the pseudomonotone equilibrium programming in a real Hilbert space. Carpath. J. Math. 2020, 36, 313–330. [Google Scholar]
- Anh, P.N.; An, L.T.H. The subgradient extragradient method extended to equilibrium problems. Optimization 2012, 64, 225–248. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Shutaywi, M.; Alreshidi, N.A.; Kumam, W. Inertial Optimization Based Two-Step Methods for Solving Equilibrium Problems with Applications in Variational Inequality Problems and Growth Control Equilibrium Models. Energies 2020, 13, 3292. [Google Scholar] [CrossRef]
- Muu, L.D.; Quoc, T.D. Regularization Algorithms for Solving Monotone Ky Fan Inequalities with Application to a Nash-Cournot Equilibrium Model. J. Optim. Theory Appl. 2009, 142, 185–204. [Google Scholar] [CrossRef]
- Argyros, I.K.; Magreñán, Á. Iterative Methods and Their Dynamics with Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Argyros, I.K.; d Hilout, S. Computational Methods in Nonlinear Analysis: Efficient Algorithms, Fixed Point Theory and Applications; World Scientific: Singapore, 2013. [Google Scholar]
- Flåm, S.D.; Antipin, A.S. Equilibrium programming using proximal-like algorithms. Math. Program. 1996, 78, 29–41. [Google Scholar] [CrossRef]
- Korpelevich, G. The extragradient method for finding saddle points and other problems. Matecon 1976, 12, 747–756. [Google Scholar]
- Dadashi, V.; Iyiola, O.S.; Shehu, Y. The subgradient extragradient method for pseudomonotone equilibrium problems. Optimization 2019, 1–23. [Google Scholar] [CrossRef]
- Bianchi, M.; Schaible, S. Generalized monotone bifunctions and equilibrium problems. J. Optim. Theory Appl. 1996, 90, 31–43. [Google Scholar] [CrossRef]
- Mastroeni, G. On Auxiliary Principle for Equilibrium Problems. In Nonconvex Optimization and Its Applications; Springer US: New York, NY, USA, 2003; pp. 289–298. [Google Scholar] [CrossRef]
- Tiel, J.V. Convex Analysis: An Introductory Text, 1st ed.; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 1967, 73, 591–598. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: Berlin/Heidelberg, Germany, 2011; Volume 408. [Google Scholar]
- Tan, K.; Xu, H. Approximating Fixed Points of Nonexpansive Mappings by the Ishikawa Iteration Process. J. Math. Anal. Appl. 1993, 178, 301–308. [Google Scholar] [CrossRef]
- Browder, F.; Petryshyn, W. Construction of fixed points of nonlinear mappings in Hilbert space. J. Math. Anal. Appl. 1967, 20, 197–228. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Ping, P.; Cho, Y.; Guo, H. New extragradient methods with non-convex combination for pseudomonotone equilibrium problems with applications in Hilbert spaces. Filomat 2019, 33, 1677–1693. [Google Scholar] [CrossRef]
- ur Rehman, H.; Pakkaranang, N.; Hussain, A.; Wairojjana, N. A modified extra-gradient method for a family of strongly pseudomonotone equilibrium problems in real Hilbert spaces. J. Math. Comput. Sci. 2020, 22, 38–48. [Google Scholar] [CrossRef]
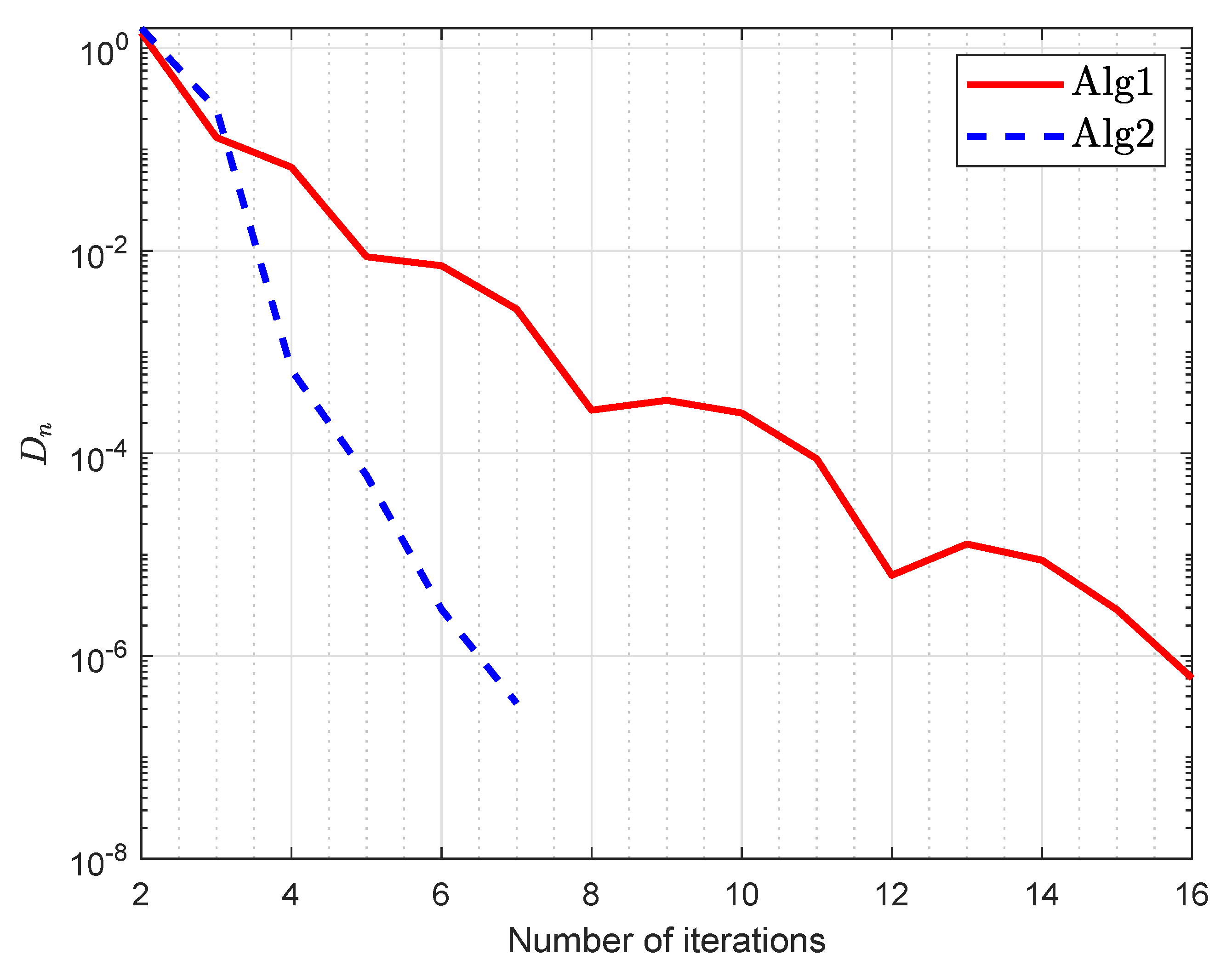

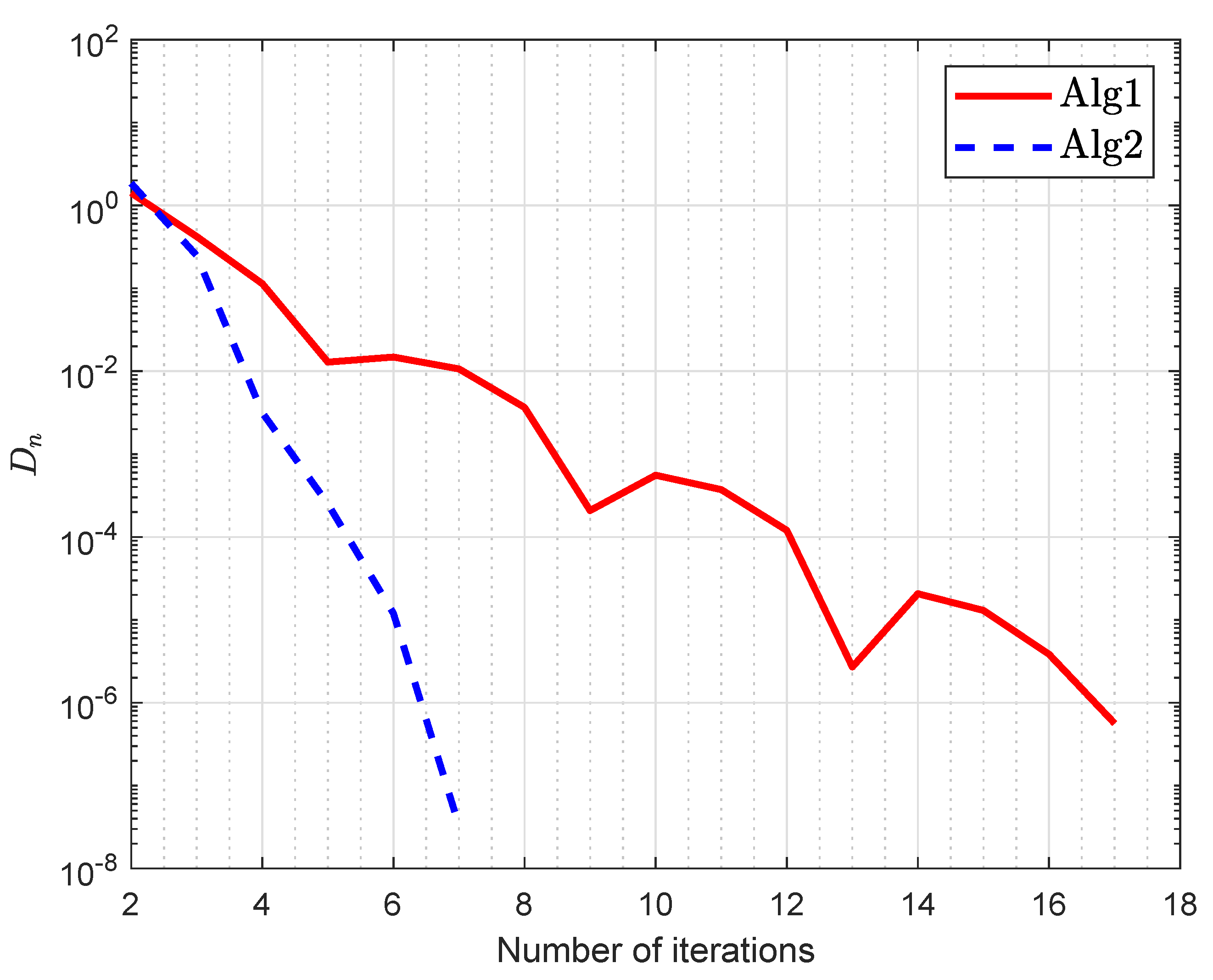
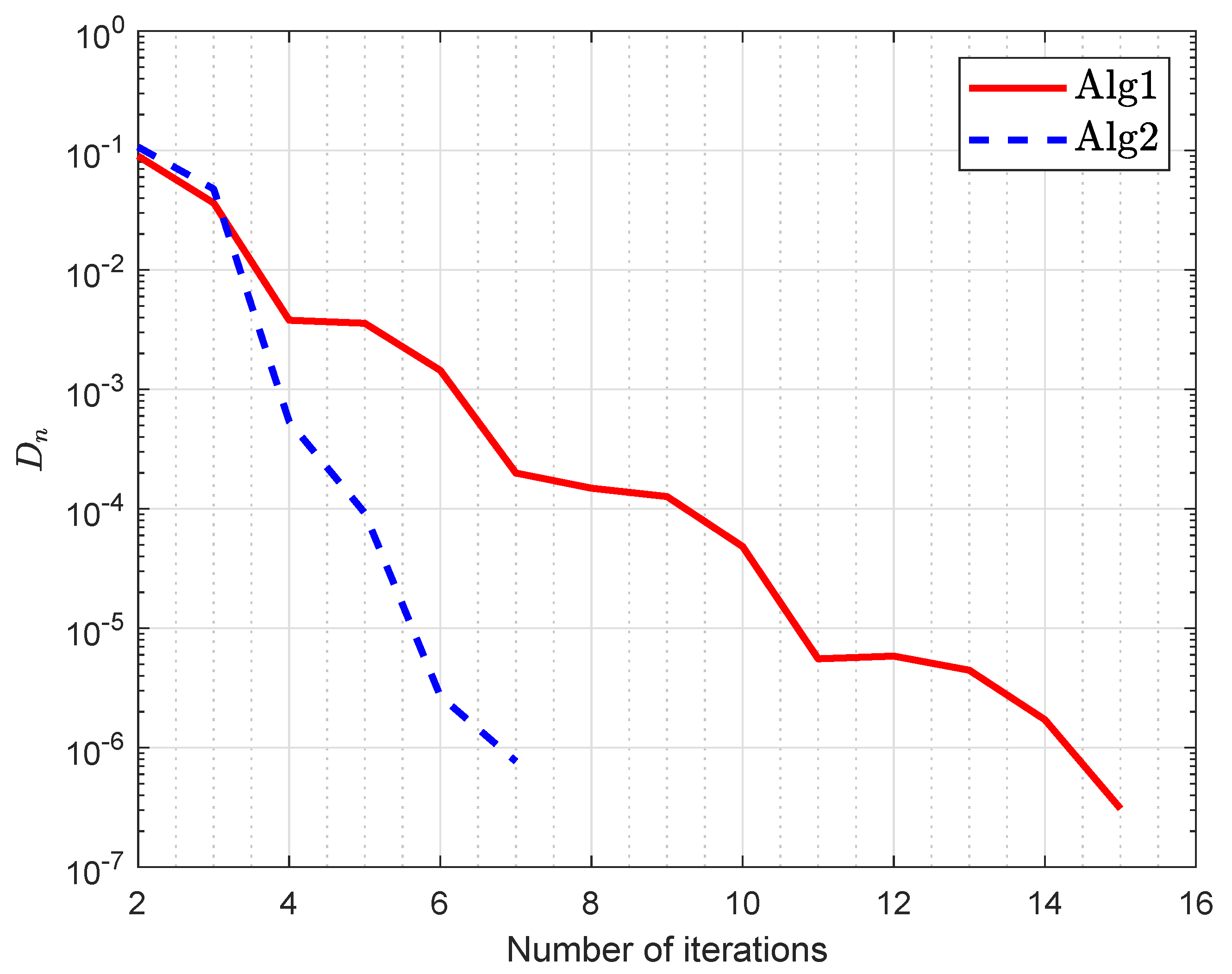
| Number of Iterations | CPU Time in Seconds | |||||
|---|---|---|---|---|---|---|
| Alg1 | Alg2 | Alg1 | Alg2 | |||
| 0.40 | 0.22 | 0.45 | 14 | 2 | 0.9134 | 0.5424 |
| 0.40 | 0.17 | 0.35 | 18 | 2 | 0.8615 | 0.5223 |
| 0.40 | 0.12 | 0.32 | 20 | 2 | 1.0815 | 0.5112 |
| 0.40 | 0.07 | 0.25 | 22 | 2 | 1.4219 | 0.5367 |
| 0.40 | 0.02 | 0.05 | 26 | 2 | 1.7329 | 0.5181 |
| Number of Iterations | CPU Time in Seconds | |||||
|---|---|---|---|---|---|---|
| Alg1 | Alg2 | Alg1 | Alg2 | |||
| 0.80 | 0.22 | 0.16 | 21 | 2 | 1.0482 | 0.0811 |
| 0.60 | 0.22 | 0.16 | 15 | 2 | 0.8676 | 0.0626 |
| 0.40 | 0.22 | 0.16 | 12 | 2 | 1.0545 | 0.0791 |
| 0.20 | 0.22 | 0.16 | 11 | 2 | 0.09923 | 0.0892 |
| 0.05 | 0.22 | 0.16 | 19 | 2 | 1.09151 | 0.0788 |
| Number of Iterations | CPU Time in Seconds | |||
|---|---|---|---|---|
| Alg1 | Alg2 | Alg1 | Alg2 | |
| 0.10 | 42 | 8 | 1.5851 | 0.2822 |
| 0.15 | 29 | 8 | 1.3148 | 0.2433 |
| 0.40 | 28 | 7 | 1.1278 | 0.2662 |
| 0.55 | 37 | 8 | 1.2211 | 0.2745 |
| 0.70 | 47 | 8 | 1.7188 | 0.2279 |
| 0.85 | 49 | 8 | 1.6188 | 0.2179 |
| Number of Iterations | CPU Time in Seconds | |||
|---|---|---|---|---|
| Alg1 | Alg2 | Alg1 | Alg2 | |
| 22 | 7 | 1.0321 | 0.1634 | |
| 24 | 7 | 1.0945 | 0.1858 | |
| 25 | 7 | 1.0328 | 0.2012 | |
| 30 | 7 | 1.0517 | 0.2020 | |
| 35 | 8 | 1.0919 | 0.1428 | |
| Number of Iterations | CPU Time in Seconds | |||
|---|---|---|---|---|
| Alg1 | Alg2 | Alg1 | Alg2 | |
| 37 | 4 | 4.9566 | 0.5460 | |
| 41 | 2 | 5.2378 | 0.4331 | |
| 48 | 3 | 6.4556 | 0.3945 | |
| 51 | 6 | 6.6756 | 0.4945 | |
| 56 | 6 | 6.8713 | 0.5108 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wairojjana, N.; Rehman, H.u.; Argyros, I.K.; Pakkaranang, N. An Accelerated Extragradient Method for Solving Pseudomonotone Equilibrium Problems with Applications. Axioms 2020, 9, 99. https://doi.org/10.3390/axioms9030099
Wairojjana N, Rehman Hu, Argyros IK, Pakkaranang N. An Accelerated Extragradient Method for Solving Pseudomonotone Equilibrium Problems with Applications. Axioms. 2020; 9(3):99. https://doi.org/10.3390/axioms9030099
Chicago/Turabian StyleWairojjana, Nopparat, Habib ur Rehman, Ioannis K. Argyros, and Nuttapol Pakkaranang. 2020. "An Accelerated Extragradient Method for Solving Pseudomonotone Equilibrium Problems with Applications" Axioms 9, no. 3: 99. https://doi.org/10.3390/axioms9030099
APA StyleWairojjana, N., Rehman, H. u., Argyros, I. K., & Pakkaranang, N. (2020). An Accelerated Extragradient Method for Solving Pseudomonotone Equilibrium Problems with Applications. Axioms, 9(3), 99. https://doi.org/10.3390/axioms9030099







