Heat-Assisted Batch Settling of Mineral Suspensions in Inclined Containers
Abstract
1. Introduction
2. Governing Equations
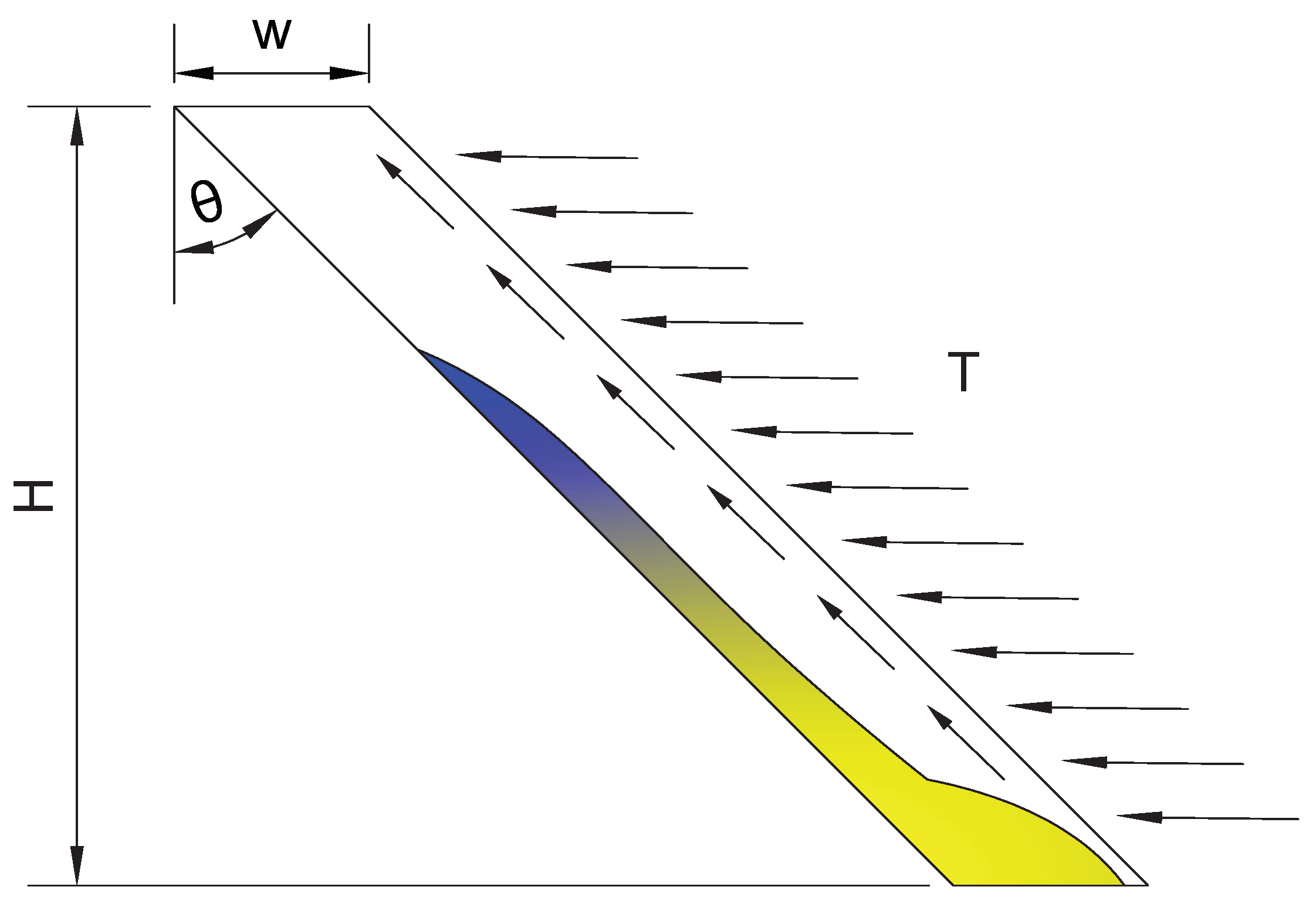
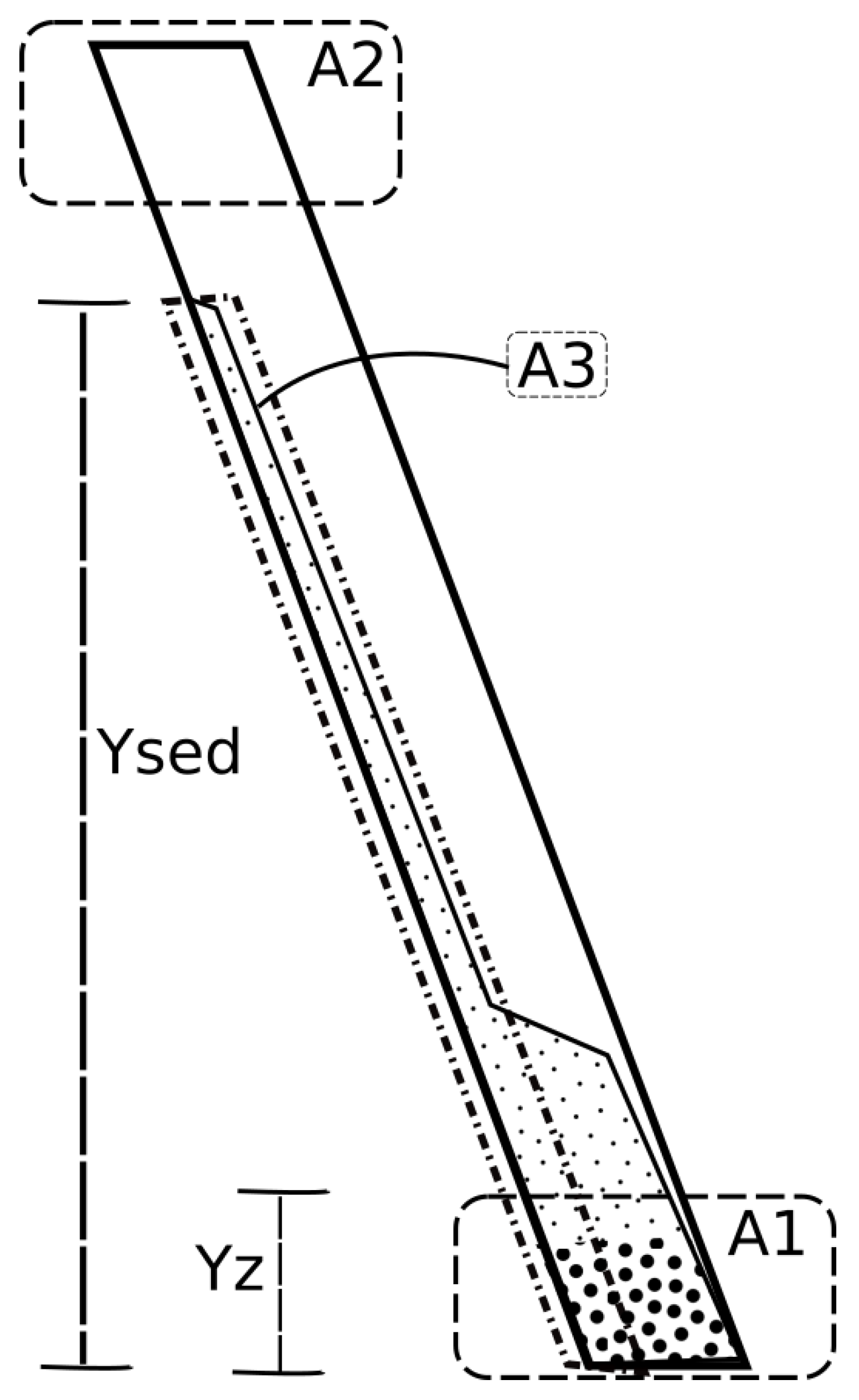
3. Simulation Cases and Boundary Conditions
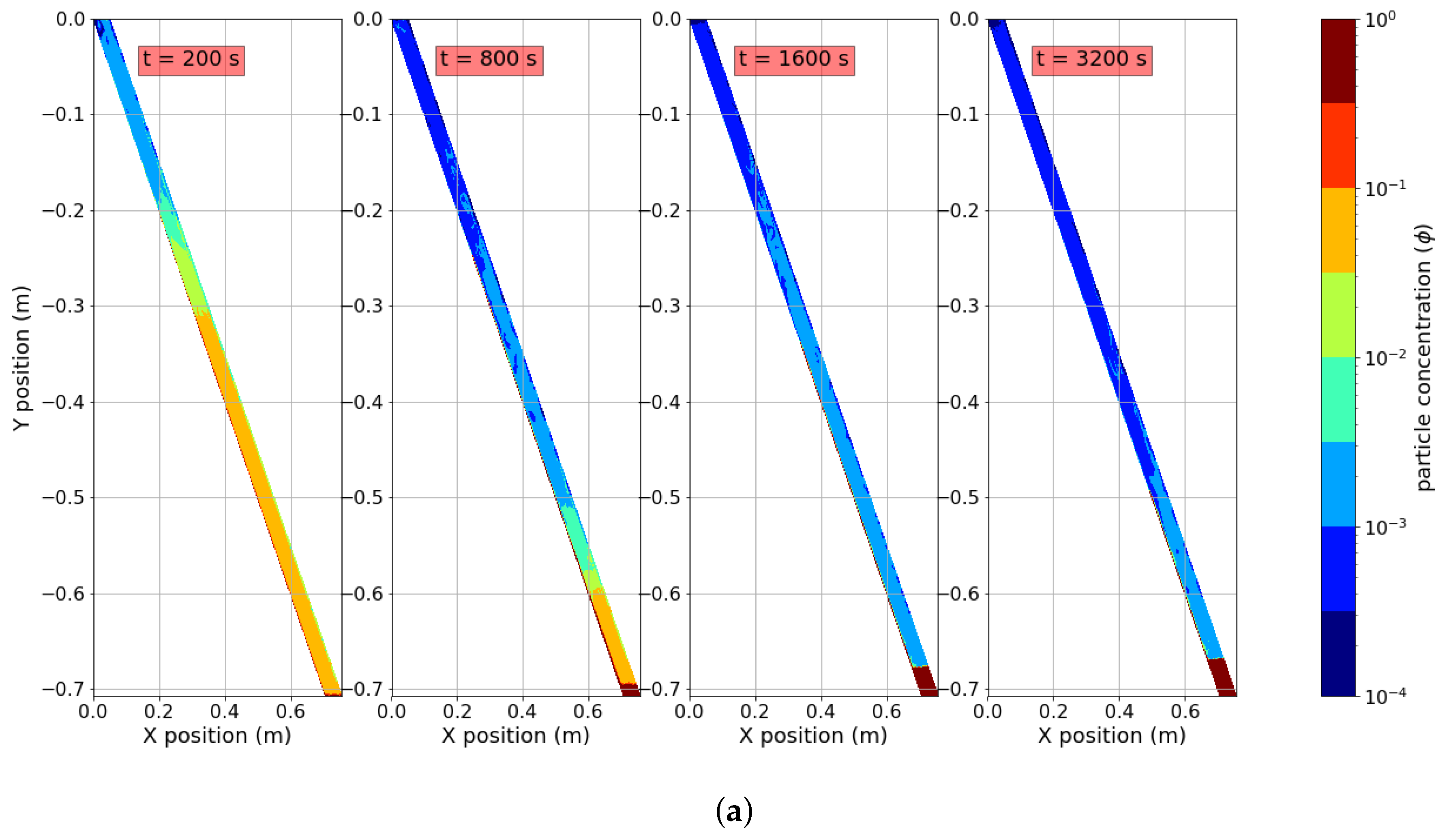
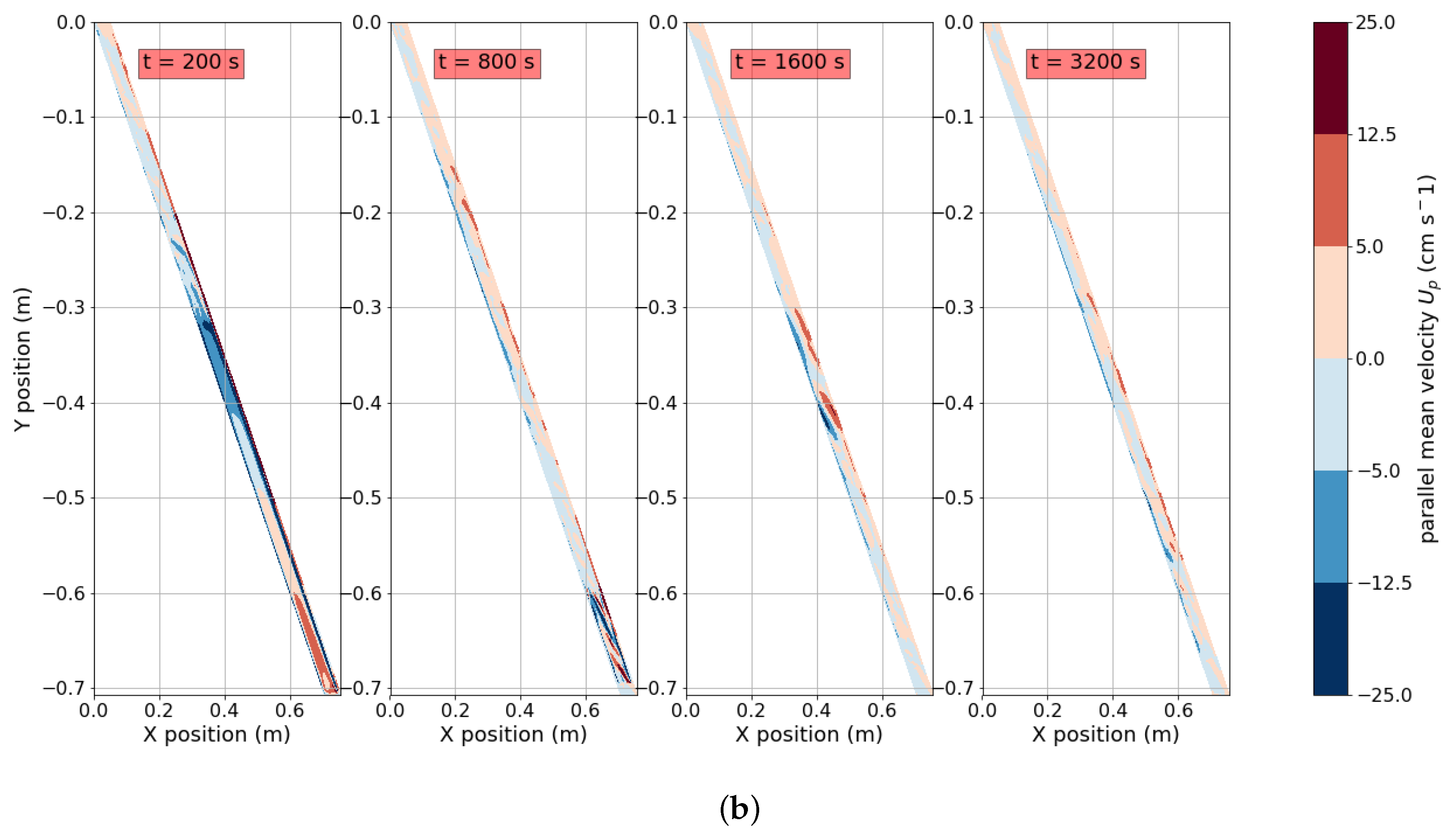
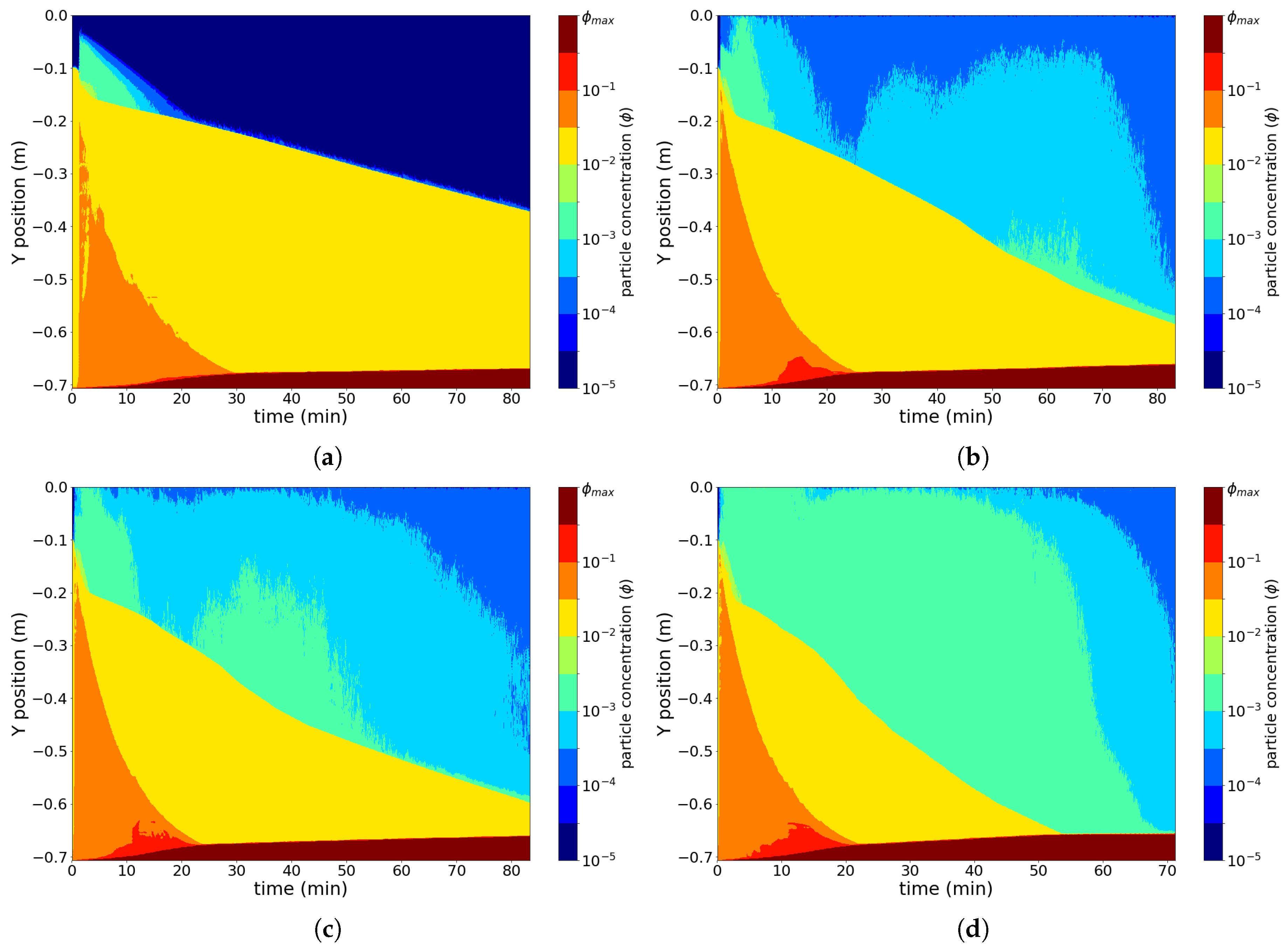
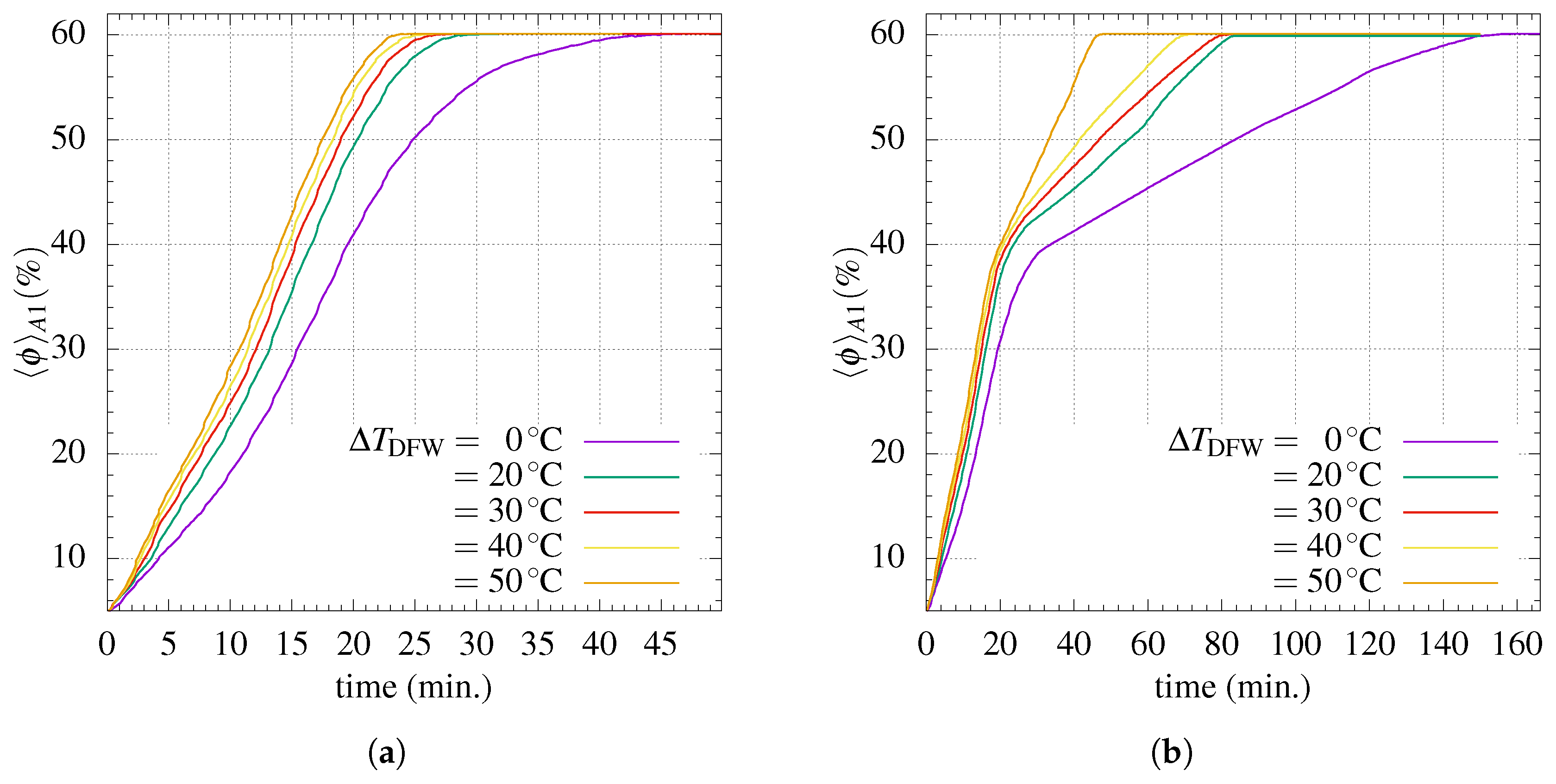
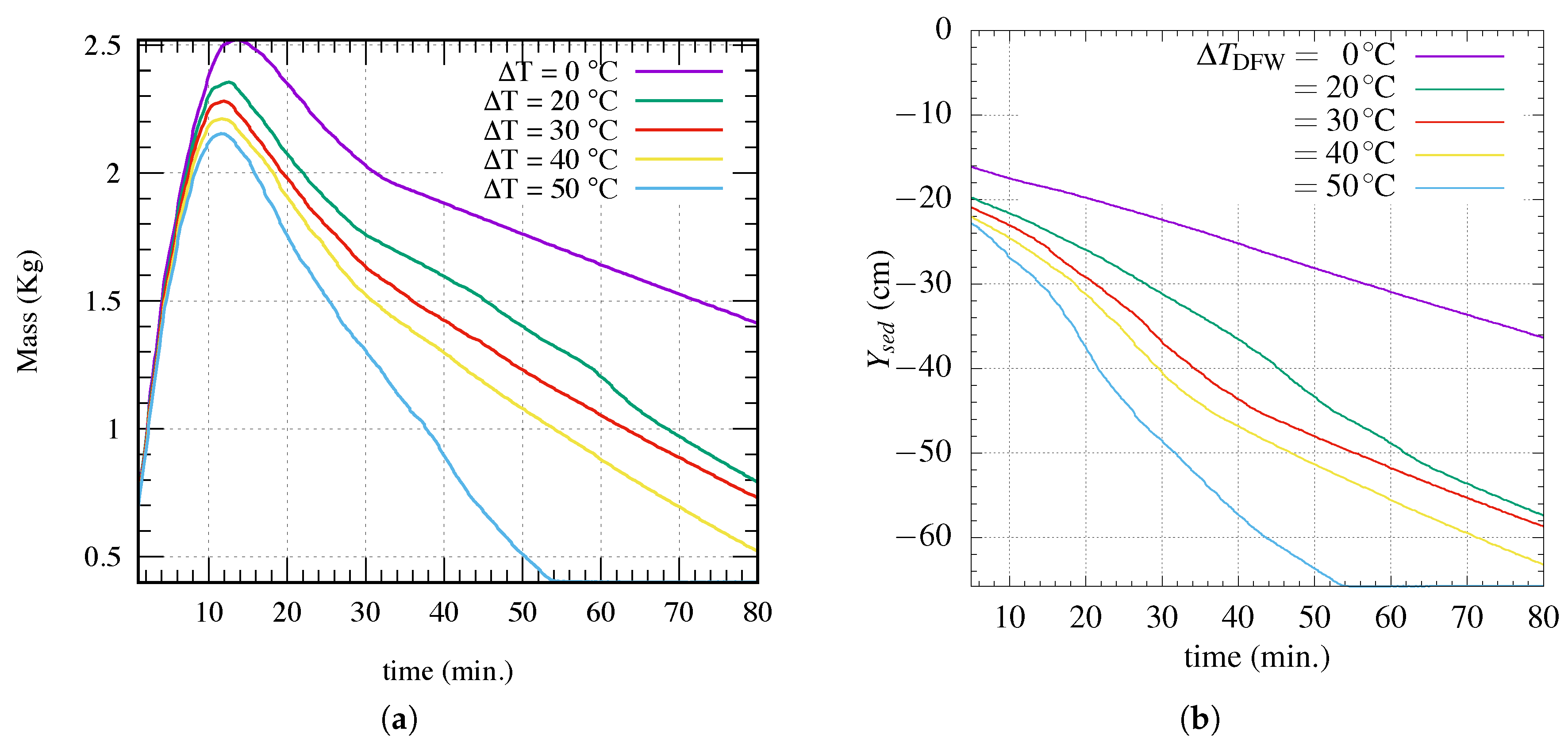
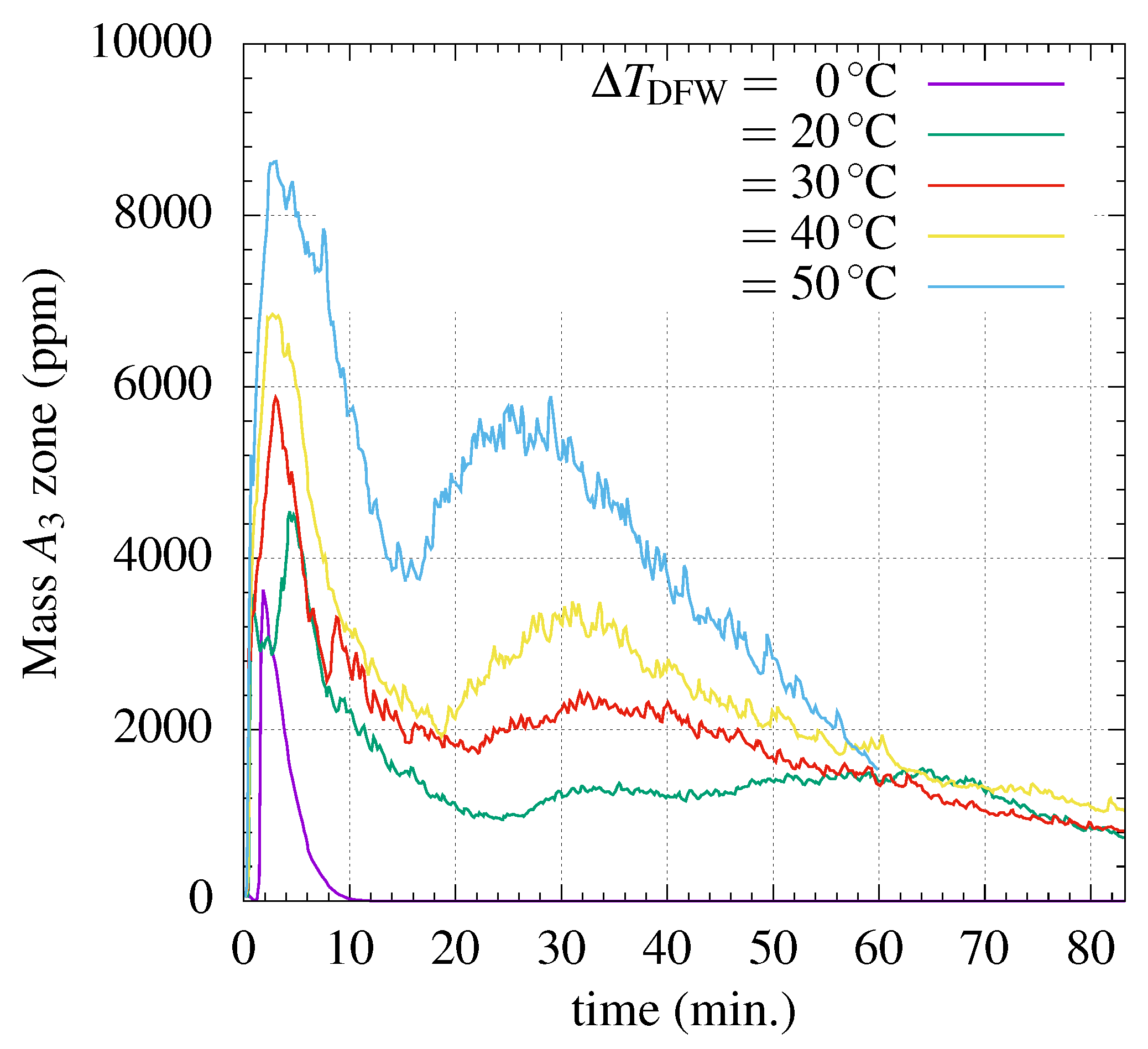
4. Results and Discussion
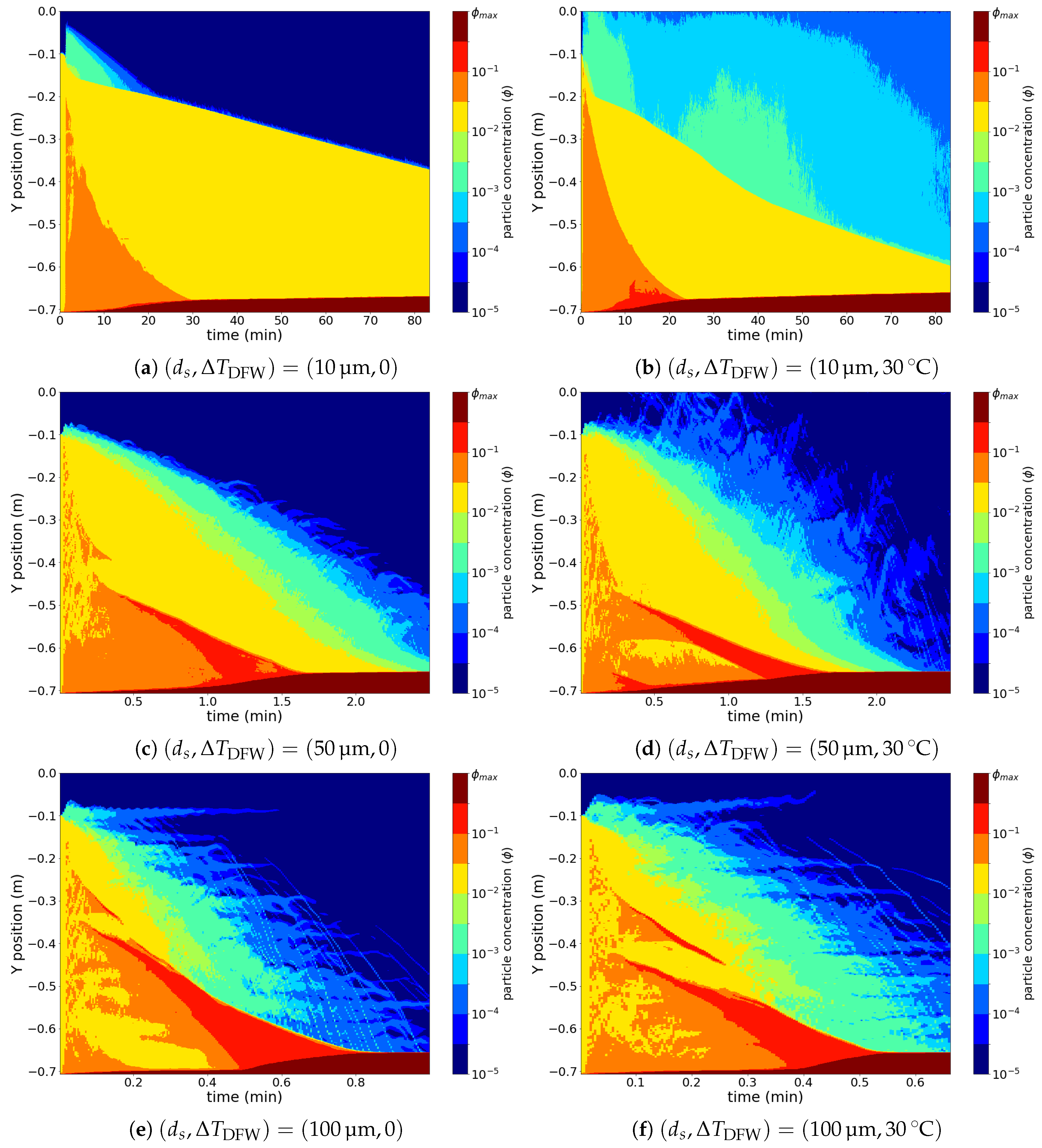
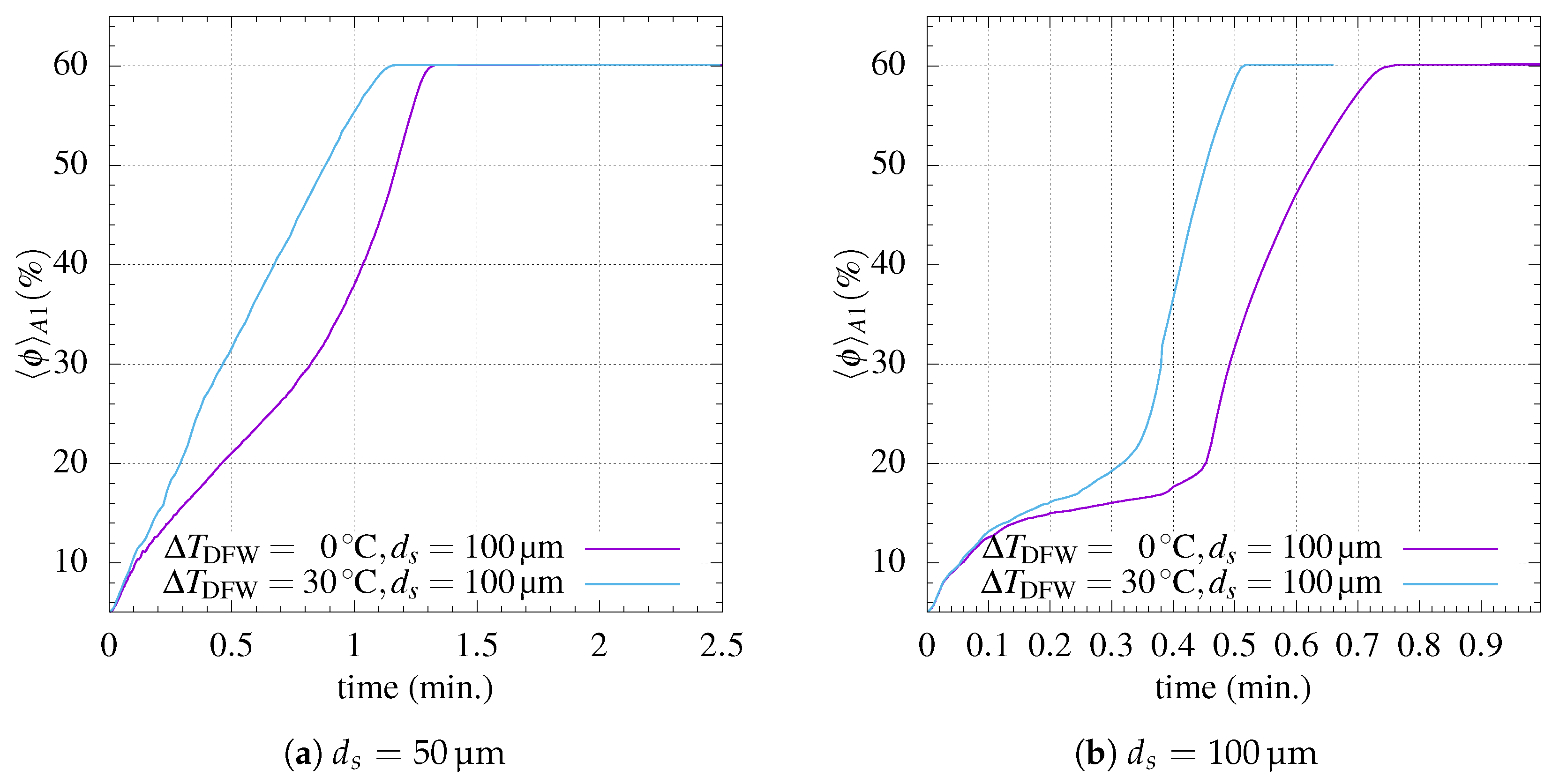
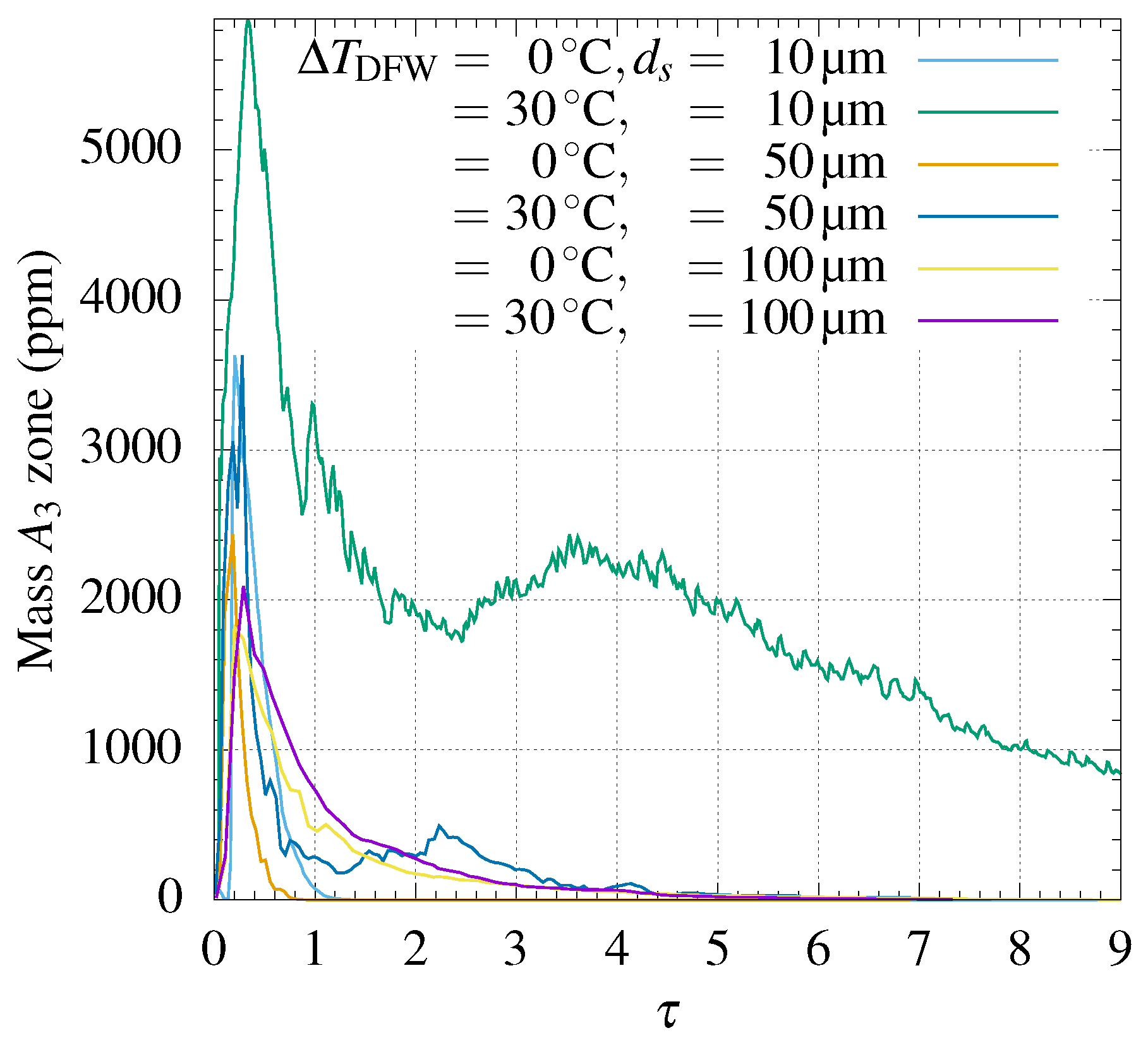
4.1. Effect of Temperature
4.2. Effect of Particle Diameter
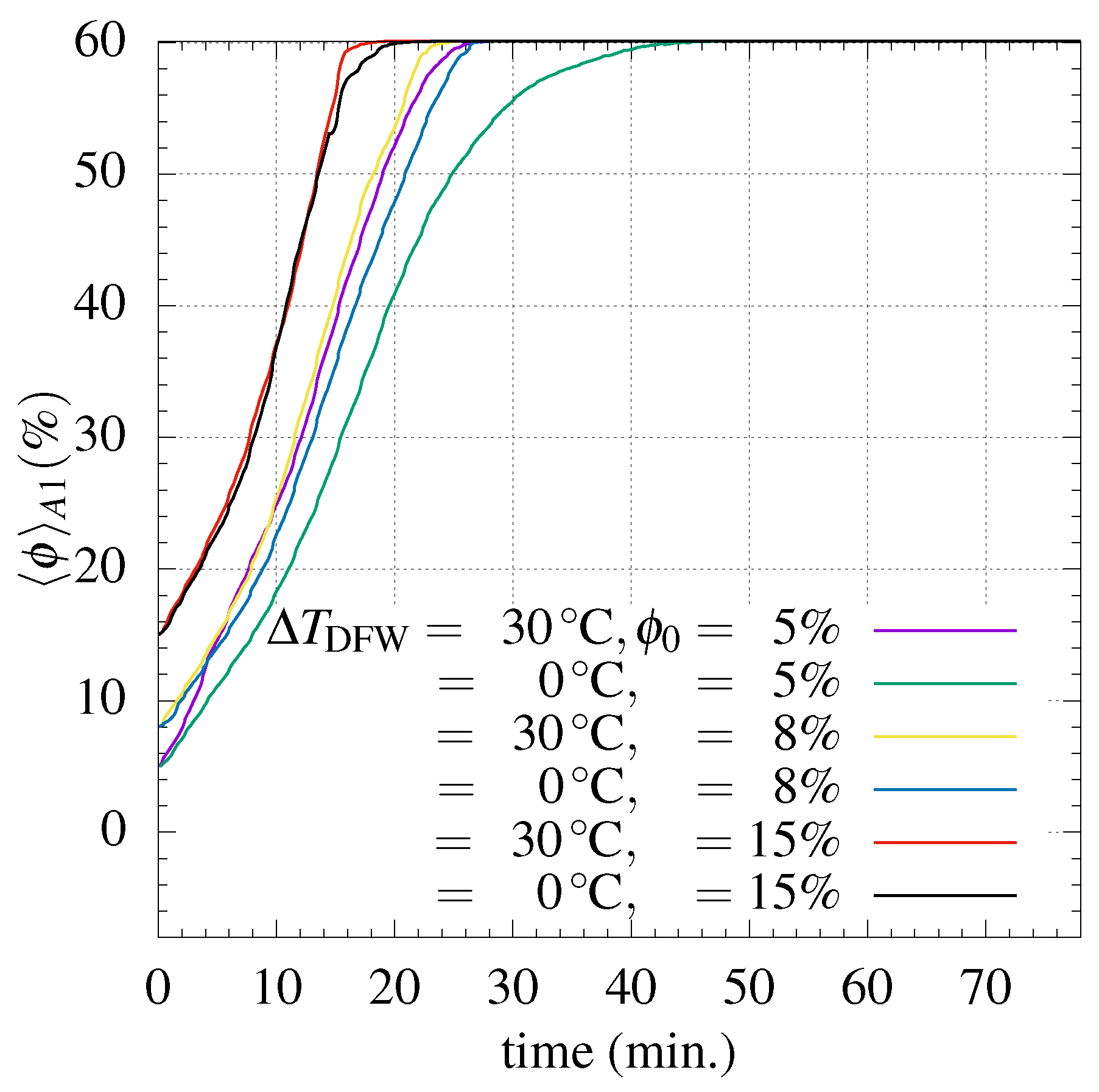
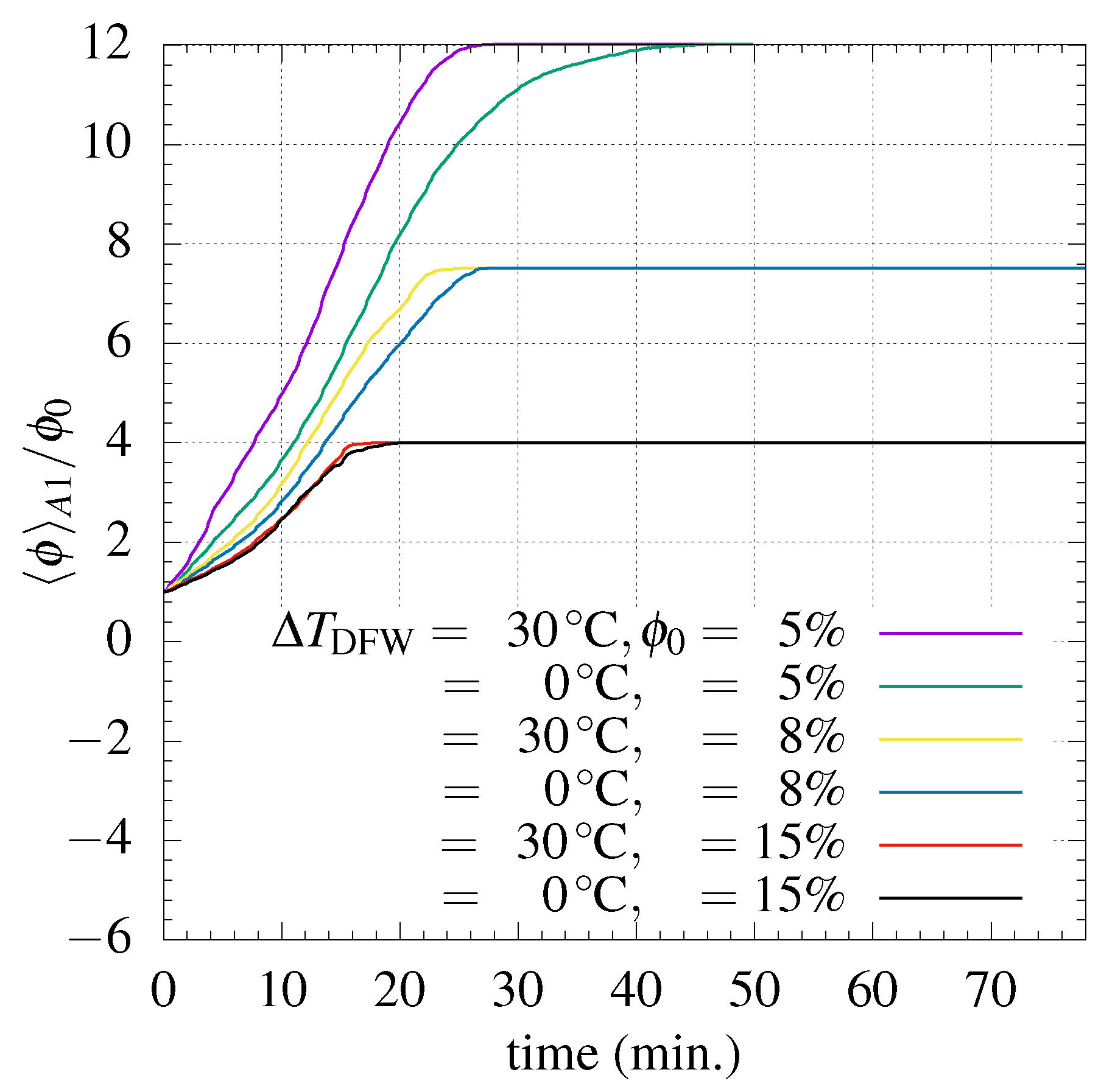
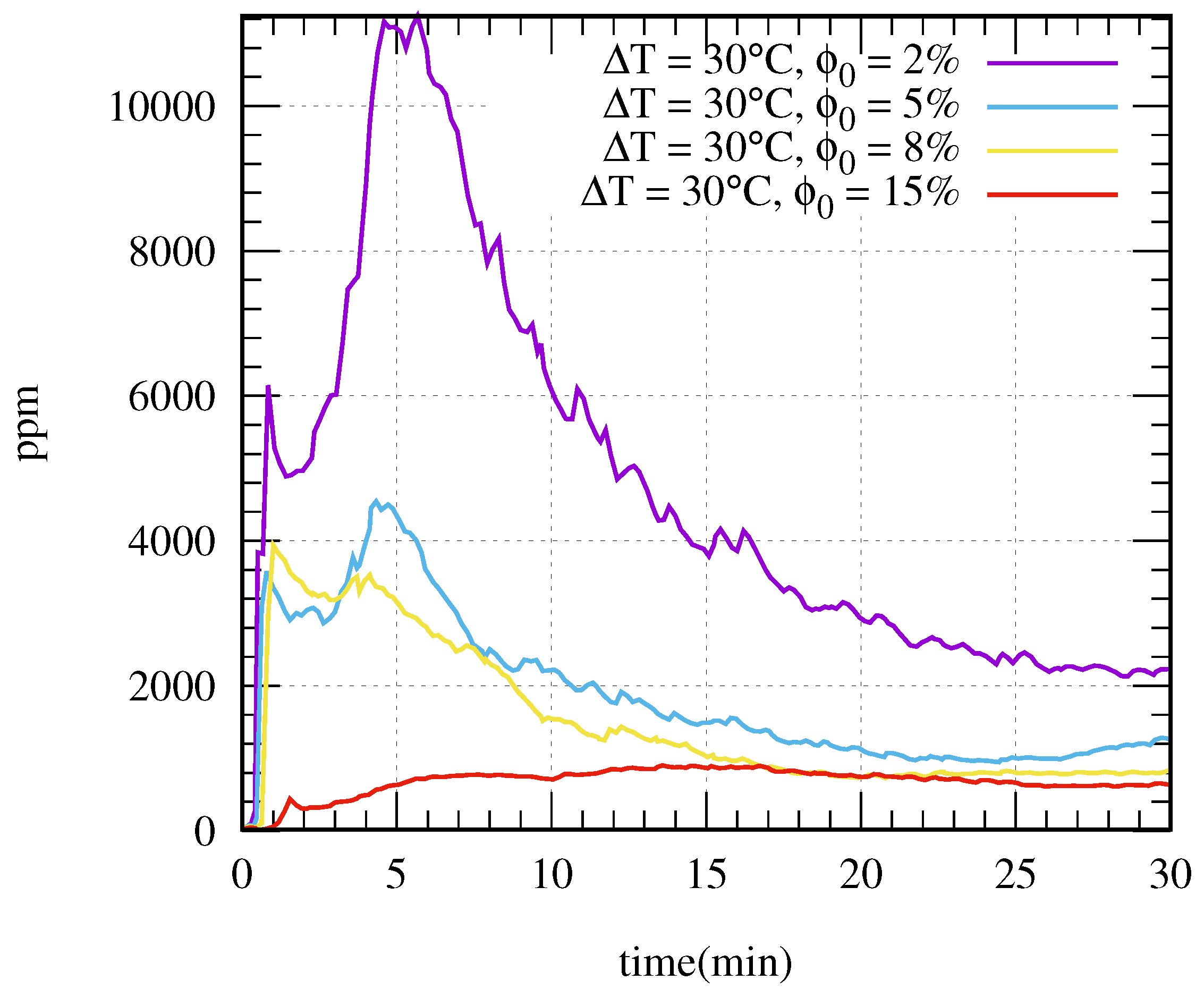
4.3. Effect of Particle Concentration
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ihle, C.; Tamburrino, A. Variables affecting energy efficiency in turbulent ore concentrate pipeline transport. Miner. Eng. 2012, 39, 62–70. [Google Scholar] [CrossRef]
- Ihle, C.F.; Kracht, W. The relevance of water recirculation in large scale mineral processing plants with a remote water supply. J. Clean. Prod. 2018, 177, 34–51. [Google Scholar] [CrossRef]
- Herrera-León, S.; Lucay, F.A.; Cisternas, L.A.; Kraslawski, A. Applying a multi-objective optimization approach in designing water supply systems for mining industries. The case of Chile. J. Clean. Prod. 2019, 210, 994–1004. [Google Scholar] [CrossRef]
- Wang, C.; Harbottle, D.; Liu, Q.; Xu, Z. Current state of fine mineral tailings treatment: A critical review on theory and practice. Miner. Eng. 2014, 58, 113–131. [Google Scholar] [CrossRef]
- Tankosić, L.; Tančić, P.; Sredić, S.; Nedić, Z. Comparative Study of the Mineral Composition and Its Connection with Some Properties Important for the Sludge Flocculation Process-Examples from Omarska Mine. Minerals 2018, 8, 119. [Google Scholar] [CrossRef]
- Ma, X.; Fan, Y.; Dong, X.; Chen, R.; Li, H.; Sun, D.; Yao, S. Impact of Clay Minerals on the Dewatering of Coal Slurry: An Experimental and Molecular-Simulation Study. Minerals 2018, 8, 400. [Google Scholar] [CrossRef]
- Falconer, A. Gravity separation: Old technique/new methods. Phys. Sep. Sci. Eng. 2003, 12, 31–48. [Google Scholar] [CrossRef]
- Concha, F. Solid-Liquid Separation in the Mining Industry; Springer: Berlin, Germany, 2014. [Google Scholar]
- Chen, G.; Xiong, Q.; Morris, P.J.; Paterson, E.G.; Sergeev, A.; Wang, Y. OpenFOAM for computational fluid dynamics. Not. AMS 2014, 61, 354–363. [Google Scholar] [CrossRef]
- Leung, W.F.; Probstein, R.F. Lamella and tube settlers. 1. Model and operation. Ind. Eng. Chem. Process Des. Dev. 1983, 22, 58–67. [Google Scholar] [CrossRef]
- Boycott, A.E. Sedimentation of blood corpuscles. Nature 1920, 104, 532. [Google Scholar] [CrossRef]
- Davis, R.H.; Zhang, X.; Agarwala, J.P. Particle classification for dilute suspensions using an inclined settler. Ind. Eng. Chem. Res. 1989, 28, 785–793. [Google Scholar] [CrossRef]
- Acrivos, A.; Herbolzheimer, E. Enhanced sedimentation in settling tanks with inclined walls. J. Fluid Mech. 1979, 92, 435. [Google Scholar] [CrossRef]
- Ortega, A.; Escobar, R.; Colle, S.; De Abreu, S.L. The state of solar energy resource assessment in Chile. Renew. Energy 2010, 35, 2514–2524. [Google Scholar] [CrossRef]
- Solangi, K.H.; Islam, M.R.; Saidur, R.; Rahim, N.A.; Fayaz, H. A review on global solar energy policy. Renew. Sustain. Energy Rev. 2011, 15, 2149–2163. [Google Scholar] [CrossRef]
- Kaviany, M. Essentials of Heat Transfer: Principles, Materials, And Applications; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Fujii, T.; Imura, H. Natural-convection heat transfer from a plate with arbitrary inclination. Int. J. Heat Mass Transf. 1972, 15, 755–767. [Google Scholar] [CrossRef]
- Palma, S.; Ihle, C.F.; Tamburrino, A.; Dalziel, S.B. Particle organization after viscous sedimentation in tilted containers. Phys. Fluids 2016, 28. [Google Scholar] [CrossRef]
- Reyes, C.; Ihle, C.F. Numerical simulation of cation exchange in fine-coarse seawater slurry pipeline flow. Miner. Eng. 2018, 117, 14–23. [Google Scholar] [CrossRef]
- Maidment, D.R. Handbook of Hydrology; McGraw-HillL: New York, NY, USA, 1993; Volume 1. [Google Scholar]
- Enwald, H.; Peirano, E.; Almstedt, A.E. Eulerian two-phase flow theory applied to fluidization. Int. J. Multiph. Flow 1996, 22, 21–66. [Google Scholar] [CrossRef]
- Al-Shemmeri, T. Engineering Fluid Mechanics; Bookboon: London, UK, 2012. [Google Scholar]
- Boyer, F.; Guazzelli, É.; Pouliquen, O. Unifying suspension and granular rheology. Phys. Rev. Lett. 2011, 107, 188301. [Google Scholar] [CrossRef] [PubMed]
- Baumgarten, A.S.; Kamrin, K. A general fluid–sediment mixture model and constitutive theory validated in many flow regimes. J. Fluid Mech. 2019, 861, 721–764. [Google Scholar] [CrossRef]
- Hanley, E.J.; Dewitt, D.P.; Roy, R.F. The thermal diffusivity of eight well-characterized rocks for the temperature range 300–1000 K. Eng. Geol. 1978, 12, 31–47. [Google Scholar] [CrossRef]
- MacIntyre, S.; Romero, J.R.; Kling, G.W. Spatial-temporal variability in surface layer deepening and lateral advection in an embayment of Lake Victoria, East Africa. Limnol. Oceanogr. 2002, 47, 656–671. [Google Scholar] [CrossRef]
- Herbolzheimer, E.; Acrivos, A. Enhanced sedimentation in narrow tilted channels. J. Fluid Mech. 1981, 108, 485. [Google Scholar] [CrossRef]
- Hill, W.D.; Rothfus, R.; Li, K. Boundary-enhanced sedimentation due to settling convection. Int. J. Multiph. Flow 1977, 3, 561–583. [Google Scholar] [CrossRef]
- Herbolzheimer, E. Stability of the flow during sedimentation in inclined channels. Phys. Fluids 1983, 26, 2043–2054. [Google Scholar] [CrossRef]
- Dobashi, T.; Idonuma, A.; Toyama, Y.; Sakanishi, A. Effect of concentration on enhanced sedimentation rate of erythrocytes in an inclined vessel. Biorheology 1994, 31, 383–393. [Google Scholar] [CrossRef]
- Davis, R.H.; Acrivos, A. Sedimentation of noncolloidal particles at low Reynolds numbers. Annu. Rev. Fluid Mech. 1985, 17, 91–118. [Google Scholar] [CrossRef]
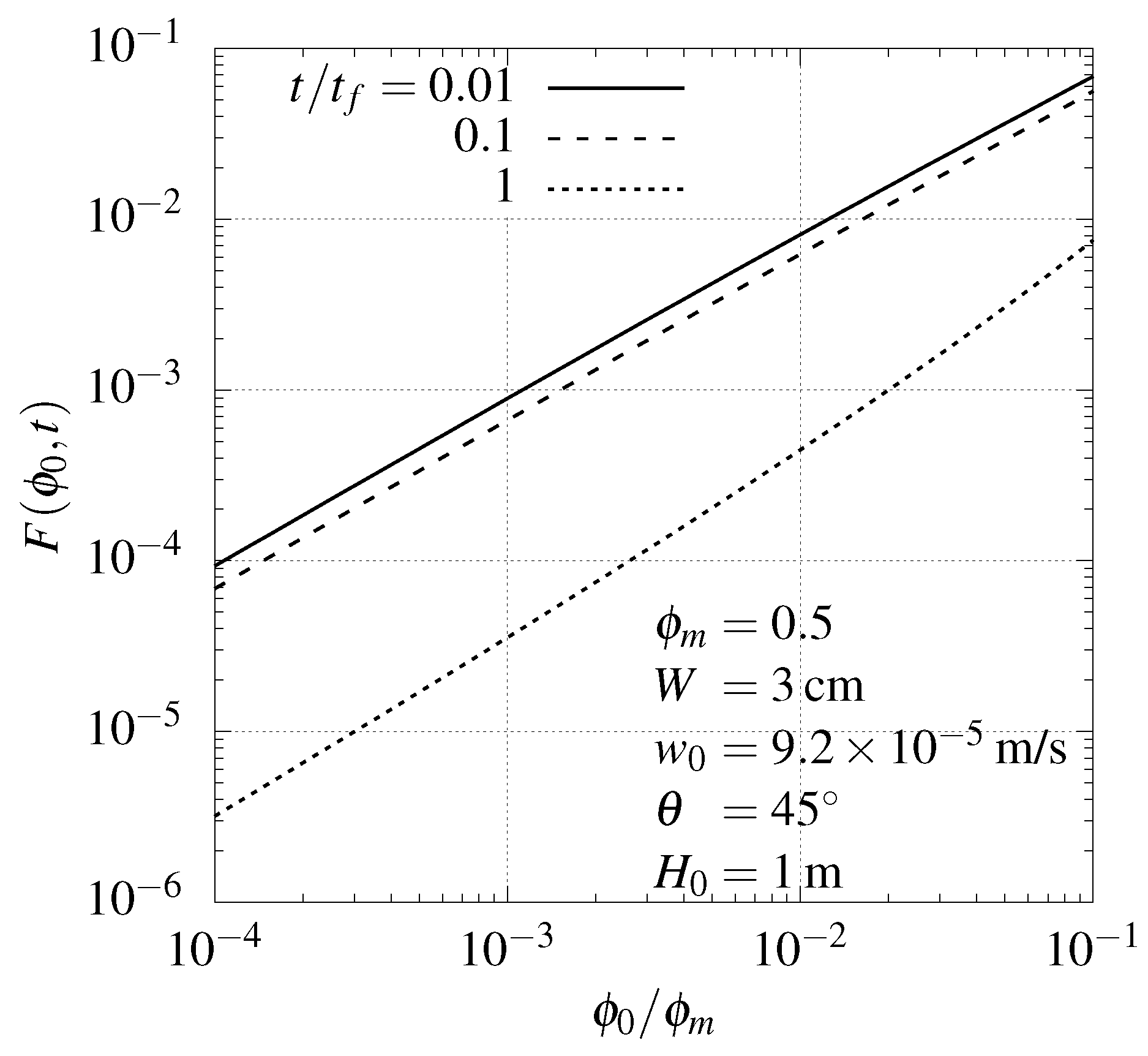
| Variable | Cases Considered |
|---|---|
| 20, 30, 40, and 50 | |
| 5, 10, and 50 | |
| 2%, 5%, 8%, and 15% | |
| 45 | |
| W | 5 |
| (K) | ||
|---|---|---|
| 20 | 0.62 | 0.54 |
| 30 | 0.58 | 0.53 |
| 40 | 0.53 | 0.43 |
| 50 | 0.51 | 0.29 |
| (m) | |
|---|---|
| 10 | 0.94 |
| 50 | 0.94 |
| 100 | 0.70 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reyes, C.; Ihle, C.F.; Apaz, F.; Cisternas, L.A. Heat-Assisted Batch Settling of Mineral Suspensions in Inclined Containers. Minerals 2019, 9, 228. https://doi.org/10.3390/min9040228
Reyes C, Ihle CF, Apaz F, Cisternas LA. Heat-Assisted Batch Settling of Mineral Suspensions in Inclined Containers. Minerals. 2019; 9(4):228. https://doi.org/10.3390/min9040228
Chicago/Turabian StyleReyes, Cristian, Christian F. Ihle, Fernando Apaz, and Luis A. Cisternas. 2019. "Heat-Assisted Batch Settling of Mineral Suspensions in Inclined Containers" Minerals 9, no. 4: 228. https://doi.org/10.3390/min9040228
APA StyleReyes, C., Ihle, C. F., Apaz, F., & Cisternas, L. A. (2019). Heat-Assisted Batch Settling of Mineral Suspensions in Inclined Containers. Minerals, 9(4), 228. https://doi.org/10.3390/min9040228







