Abstract
The design of a flotation circuit based on optimization techniques requires a superstructure for representing a set of alternatives, a mathematical model for modeling the alternatives, and an optimization technique for solving the problem. The optimization techniques are classified into exact and approximate methods. The first has been widely used. However, the probability of finding an optimal solution decreases when the problem size increases. Genetic algorithms have been the approximate method used for designing flotation circuits when the studied problems were small. The Tabu-search algorithm (TSA) is an approximate method used for solving combinatorial optimization problems. This algorithm is an adaptive procedure that has the ability to employ many other methods. The TSA uses short-term memory to prevent the algorithm from being trapped in cycles. The TSA has many practical advantages but has not been used for designing flotation circuits. We propose using the TSA for solving the flotation circuit design problem. The TSA implemented in this work applies diversification and intensification strategies: diversification is used for exploring new regions, and intensification for exploring regions close to a good solution. Four cases were analyzed to demonstrate the applicability of the algorithm: different objective function, different mathematical models, and a benchmarking between TSA and Baron solver. The results indicate that the developed algorithm presents the ability to converge to a solution optimal or near optimal for a complex combination of requirements and constraints, whereas other methods do not. TSA and the Baron solver provide similar designs, but TSA is faster. We conclude that the developed TSA could be useful in the design of full-scale concentration circuits.
1. Introduction
Froth flotation is a process used in mining, based on the different surface properties of ore, for separating the valuable mineral from gangue. This process is performed in an aerated tank where the ore is mixed with water and reagents to render the valuable mineral hydrophobic [1]. Due to the complexity of the process in practice, multiple interconnected stages are used to form a flotation circuit.
The design of flotation circuits using optimization techniques has been widely studied in the literature [2,3]. The design requires three elements: (1) defining superstructures for representing a set of alternatives for design; (2) a mathematical model for modeling the different alternatives of the design, here considered goals and constraints, and determining the objectives to be optimized; and (3) an optimization technique for solving the problem.
The optimization techniques can be broadly classified into exact and approximate methods [4]. Exact methods obtain optimal solutions and guarantee their optimality. These methods use the analytical properties of the problem for generating a sequence of points converging to a global optimal solution [5]. This category includes methods such as the branch and bound algorithm, branch and cut algorithm, dynamic programming, Bayesian search algorithms, and successive approximation methods. Approximate methods are aimed at providing a good quality solution in a reasonable amount of time, but finding a global optimal solution is not guaranteed. Approximate methods can be classified into approximation algorithms and heuristic methods. The latter may be divided into two families: specific heuristics and metaheuristics. Specific heuristics are tailored and designed for solving a specific problem. Metaheuristics are general-purpose algorithms that can be applied to solve almost any optimization problem [4].
The term metaheuristics was introduced in 1986 by Glover [6], and is defined as an iterative generation process guiding a subordinate heuristic by combining intelligently different concepts for exploring and exploiting the search space; learning strategies are used to structure information in order to efficiently find the near-optimal solution [7]. Some of the proposed metaheuristics algorithms in the literature are: differential evolution [8], genetic algorithm (GA) [9], memetics algorithm [10], artificial immune system [11], simulated annealing [12], ant colony optimisation [13], particle swarm optimisation [14], and Tabu-search [15].
The Tabu-search algorithm (TSA) is a local search methodology used for solving combinatorial optimization problems [6]. The TSA is an adaptive procedure with the ability to apply other methods, such as linear and nonlinear programming algorithms [16]. The TSA uses the information gathered during the iterations to create a more efficient search process. TSA uses short-term memory to prevent previously visited solutions from being accepted. This memory prevents the algorithm from being trapped in cycles.
The literature shows that TSA has been used and compared to other optimization techniques in different disciplines. Han et al. [17] used TSA for training neural networks for wind power prediction. They reported that, compared with the backpropagation algorithm, TSA can improve prediction precision as well as convergence rate. Ting et al. [18] hybridized TSA and GA; this strategy was called the Tabu genetic algorithm (TGA). TGA integrates TSA into GA’s selection. GA and TSA structures are not modified in these approaches. The classic traveling salesman problem was used for validating the proposed algorithm. Along this line, Soto et al. [19] hybridized TSA with multiple neighborhood searches for addressing multi-depot open vehicle routing. The proposed hybrid system provided good results, which was attributed to the successful exploration of neighborhoods. This allowed the search to achieve a good balance between intensification and diversification. Lin and Miller [20] applied TSA to chemical engineering problems. When TSA was compared with simulated annealing, TSA provided superior performance; this was attributed to the use of short-term memory, which enables it to escape from local optima [20]. Konak et al. [21] demonstrated that TSA is more efficient than GA because TSA does not require objective function gradient information. Kis [22] solved job-shop scheduling problems using TSA and GA. Kis reported that TSA was superior to GA both in terms of solution quality and computation time. Pan et al. [23] proposed a particle swarm optimization (PSO) algorithm for a no-wait flow shop scheduling problem. They compared PSO and TSA. The results indicated that the TSA and their hybrids generate better results than PSO. Mandami and Camarda [24] proposed a multi-objective optimization technique for plant design using TSA. They used a bounding technique for increasing the efficacy of the algorithm. They evaluated the effectiveness of the algorithm using a nonlinear model of 10 variables. The authors concluded that it is feasible to generate a Pareto-optimality curve for plant design problems using multi-objectives.
As stated by Cisternas et al. [2], the exact methods only guarantee finding the global solution when the design problem is small. This observation was corroborated by the works of Mehrotra and Kapur [25], Reuter et al. [26,27], Schena et al. [28,29], Mendez et al. [3], Maldonado et al. [30], Cisternas et al. [31,32], Calisaya et al. [33], and Acosta-Flores et al. [34]. Similar to exact methods, the probability of finding the global solution using approximate methods decreases as the problem size increases [5]. In this context, according to Acosta-Flores et al. [34] and Cisternas et al. [2], the genetic algorithms are the only metaheuristic algorithms that have been used for designing flotation circuits [1,35,36,37,38]. However, GA has been used only for small problems because its convergence is slow.
The methodologies proposed in the literature considered different assumptions for simplifying the design problem. For example, many of these methodologies considered a maximum of six flotation banks and a maximum of eight cells; however, these studies usually considered only two species in the fed ore to the flotation circuit. The exceptions are the works of Calisaya et al. [33] and Acosta-Flores et al. [34]. These authors examined several species in the fed ore, but their works were based on the fact that there are few structures that are optimal for a given problem [39]. These few structures were identified before applying the optimization search, which reduces the size of the optimization problem. Therefore, the studied problem is complex and difficult to solve when obtaining a global solution.
In this study, we propose using the TSA for designing flotation circuits. The developed algorithm incorporates diversification and intensification, the first of which is used for exploring new regions, and the second, for exploring regions close to a good solution. The algorithm was implemented for designing circuits that process several species. The superstructure implemented involves five flotation banks and each bank could use 3–15 cells, and the objective functions are economical. Four case studies were developed for illustrating the applicability of the algorithm.
2. Background
2.1. Superstructure
The proposed superstructures in the literature usually correspond to an equipment superstructure, which allows the streams of concentrate and tail of one equipment to be sent to any other equipment. The superstructures are important because they define the alternatives and the size of the problem [2]. According to Sepúlveda et al. [40], the circuits generally use between three and five flotation stages. Then, the equipment superstructure (Figure 1) used in this work considers the following stages: rougher stage (R), cleaner stage (C1), re-cleaner stage (C2), scavenger stage (S1), and re-scavenger stage (S2).
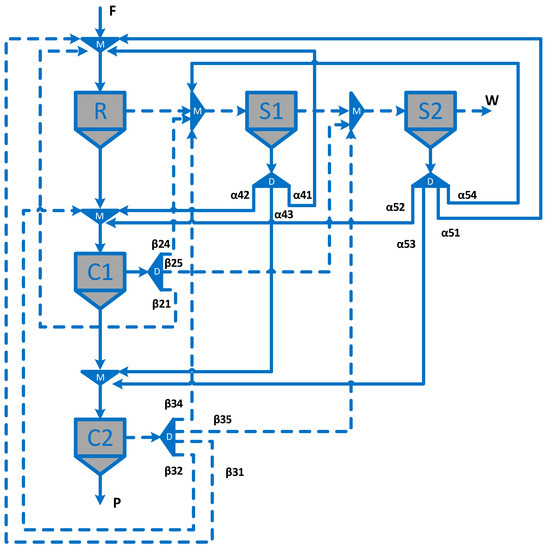
Figure 1.
Equipment superstructure. R: rougher stage, C1: cleaner stage, C2: re-cleaner stage, S1: scavenger stage, S2: re-scavenger stage, M: stream mixer, D: stream splitter, decision variables indicating the destination of the concentrate stream from stage , decision variables indicating the destination of the tail stream from stage .
Many of the proposed superstructures in the literature considered nonsensical alternatives and/or presented degeneracy, i.e., alternatives that are equivalent [2]. All the design alternatives shown in Figure 1 have sense and do not present degeneracy. In Figure 1, the triangles with label M represent mixers of the feed that arrive at stage , where . Note that the numbers 1, 2, 3, 4, and 5 are related to and , respectively. The triangles with label represent splitters that allow sending the concentrate and tail streams from stage to the other stages of the superstructure.
2.2. Mathematical Model
The model includes mass balances in flotation stages, splitters, and mixers, and goals, constraints, and objective function are considered. The mass balance in flotation stages is determined with:
where is the mass flow of the species fed to the flotation stage , is the mass flow of the species in the concentrate stream of the flotation stage , is the mass flow of the species in the tail stream of the flotation stage , and is the recovery of the species in the flotation stage , where , , and is the number of species. The flotation model used for representing the recovery in the flotation stages was proposed by Yianatos and Henríquez [41]:
where is the recovery of the species in the flotation stage , is the maximum rate constant of the species in the flotation stage , is the cell residence time in the flotation stage , is the number of flotation cells used in the flotation stage , and is the maximum recovery at the infinite time of the species in the flotation stage .
In practice, the flotation circuits do not use stream branching because a large number of pumps and junction boxes are necessary for carrying out the concentration process [37]. Then, the mass balances in the splitters of the concentrate streams are expressed as:
where are decision variables indicating the destination of the concentrate stream (Figure 1), is the mass flow of species in the concentrate stream from stage to stage , and is the mass flow of species in the concentrate stream of stage . Similarly, for the tail streams:
where are decision variables indicating the destination of the tail stream (Figure 1), is the mass flow of species in the tail stream from stage to stage , and is the mass flow of species in the tail stream of stage . The mass balances in mixers are expressed as:
where is the mass flow of the species fed to the flotation circuit. Note that mass balance for each species processed in the circuit can be rewritten as a matrix system. These systems are solved numerically for and using a linear programming algorithm. The TSA has the ability to make use of this type of algorithm.
The market for copper concentrate establishes a minimum grade (); then, the following equation is included in the mathematical model:
where is the copper grade of the species , and is the copper grade in the final concentrate of flotation circuit. In this work, the value of is 0.25.
Several objective functions have been used in the literature. Mehrotra and Kapur [25], Green [42], and Pirouzan et al. [38] implemented technical expressions for designing flotation circuits. The technical functions are difficult to define. For example, if the recovery is maximized, it is necessary to restrict the concentration grade to a value that is not known a priori. This difficulty was overcome by some authors using a multi-objective function; however, it is difficult to define the relative weight of each objective. Schena et al. [29] and Cisternas et al. [32,39,43] implemented economic expressions for designing circuits. These expressions highlight the maximization of revenues, maximization of profits, and the maximization of the net present worth. These last two expressions require estimating both the equipment costs and the operating costs. Cisternas et al. [43] found that the objective function has a significant effect on both the solution and circuit structure obtained. In this work, we used the maximization of revenues and maximization of the net present worth as the objective functions.
The revenue can be calculated using different models depending on the type of product and its market. In the case of copper concentrate, the net-smelter-return formula can be used [32,43]:
where is the fraction of metal paid, is the grade deduction, is the treatment charge, is the metal price, is the refinery charge, is the mass flow of the species in the final concentrate, and is the copper grade of the species
For determining net present worth, the capital costs and total costs of the process must first be estimated. The capital cost considers the fixed capital and working capital. The first is estimated with the following equation:
where [44]:
with
where is the cell volume (m3) of flotation stage , is the feed stream to stage , is the gas factor, is the pulp density, is the fixed capital cost to stage , is the fixed capital cost of circuit, and is the Lang factor [45]. Equation (10) is valid for volume between 5 m3 and 200 m3. The working capital costs are estimated with the following equation:
where is the Lang factor for working capital and is assumed to be 0.9. The total costs of the process are estimated with the following equation:
with
where is the operating cost of flotation stage , is the kilowatt-hours cost, is the gas factor, and are the costs of mine-crushing-grinding per ton of fed ore to the flotation plant. The profits generated by the project are estimated with:
The annual cash flows are estimated using the following expression:
with
where are the profits before taxes, is the tax rate, is the annual depreciation, and is the life time of the project (the value of used here is 15). The net present worth is calculated using:
where is the net present worth, , and is the discount rate. It is assumed that cash flows are equal in all years of the project, so Equation (19) is simplified:
with
where γ denotes the penalty parameter [46]. For each violation of the constraints of the mathematical model, a value is considered, defined by the user. This penalty parameter must also be considered when the objective function is the maximization of revenues.
2.3. Optimization Technique: Tabu-Search Algorithm
TSA is a local search methodology that was proposed by Glover and Laguna in 1998 [15]. TSA is a strategy for solving combinatorial optimization problems ranging from graph theory to mixed integer programming problems. It is an adaptive procedure with the ability to making use of other methods, such as linear programming algorithms, which help to overcome the limitations of local optimality [16]. Gogna and Tayal [47] stated that the TSA uses the information gathered during the iterations to produce a more efficient search process. Here, the search space is simply the space of all possible solutions that can be considered during the search. For example, in vehicle routing problems, the search space considers both binary and continuous variables [48]. The TSA accepts non-improving solutions to the global solution to move out of local optima. The distinguishing feature of the TSA is the use of memory structures.
The main memory structure used by the TSA is the Tabu list () short-term memory, which has a record of previously visited solutions. This key idea can be linked to artificial intelligence concepts [48]. The should be carefully formulated for an effective search while minimizing the computation time and the memory requirements. Medium- and long-term memories can be used for improving the intensification and diversification of the TSA [4].
Usually, the TSA starts with an initial solution, randomly selected, which is entered to . Then the algorithm uses a local search procedure or neighborhoods to move iteratively from a potential solution to an improved solution , also called the best neighbor, in the neighborhood of (). Local search procedures often become stuck in local optima. In order to avoid these pitfalls and to explore regions of search space that would be left unexplored by other local search procedures, TSA carefully explores the neighborhood of each solution as the search progresses [47]. The solutions admitted to the new neighborhood are determined through the use of memory structures. The best neighbor of is accepted as a global solution if and if it maximizes the objective function. If the best neighbor , then the next best neighbor of is the new postulant to enter into . This procedure is repeated until is entered into . Next, the new neighborhood of the best neighbor is generated, and the procedure described earlier is repeated until some stopping criterion is satisfied [49].
The search space of the design problem studied in this work considers binary, discrete, and continuous variables, which are related to circuit structure, the number of cells in flotation stages, and the operating conditions in flotation stages, respectively. The developed TSA implements short-term and long-term memories: the and the frequency matrix (), respectively. The latter was proposed by De los Cobos [50], which allows the exploration of new regions of the search space.
In our case, the algorithm starts with an initial solution , which is entered into . Here, the variables are associated with the circuit structure, and are associated with number of equipment and operating conditions of circuit. Then, the neighborhood of the initial solution is generated to create natural permutations of the structural variables, i.e., a set of structures is generated. Subsequently, the operating conditions and equipment number are assigned to each structure through a uniform distribution function. The uniform distribution function is defined using the operating conditions and the equipment number of the initial solution. This method of generating neighborhoods is based on the structure being more influential on the objective function than the operating conditions and equipment number [43]. Subsequently, the equipment size, copper grade of the concentrate, and profitability parameters of each flotation circuit, neighbor of are determined via mass balances. If the constraints of the mathematical model are violated for some neighbor of then its objective function is penalized . Then, the best neighbor of is determined, i.e., the neighbor maximizing the objective function. The best solution () is accepted as a global solution if and . If , the next best neighbor of is taken as . This step is repeated until is entered to . The structural variables of are entered into . Subsequently, the neighborhood of is generated and the search procedure described earlier is repeated times. Notably, has a determined number of rows (), i.e., once is full, the update of its information is carried out at each iteration of the algorithm. Next, we explain how diversification and intensification strategies are included in the search procedure. Each time that does not improve before iterations of algorithm, then the diversification in the search procedure is incorporated. The diversification allows the generation of a new best neighbor, whose structural variables are obtained from the gathered information in , and operating conditions and equipment number are assigned through a uniform distribution function. Note that records all the structural variables of from the first iteration of algorithm. This information allows us to determine the structures more often visited (high frequency in FM) by the algorithm. A structure not visited, or rarely visited (low frequency in ), is assigned to the new best neighbor. The intensification is incorporated in the search procedure each time passing iterations of the algorithm. The intensification allows the exploration of regions close to a good solution. In this work, this is carried out using the gathered information in . The new best neighbor is aleatorily selected among the better neighbors recorded in . The full procedure is shown in Figure 2.
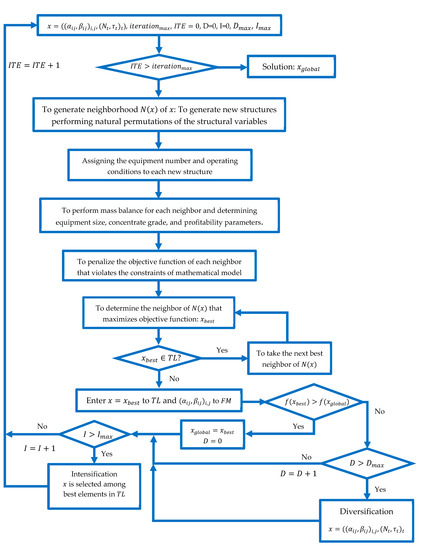
Figure 2.
Block diagram of Tabu-search algorithm. ITE: iteration of algorithm, TL: Tabu list, FM: frequency matrix, D: iteration related to diversification, I: iteration related to intensification, : circuit structure, : number of equipment and operating conditions of circuit, : neighborhood of the solution , : best neighbor of , : objective function, number of iteration related to the implementation of diversification, number of iteration related to the implementation of intensification.
3. Applications
Four case studies were developed for illustrating the proposed algorithm. The first and second cases involve designing a copper ore concentrator plant considering the maximization of revenues and maximization of the net present worth as the objective function, respectively. The third case analyses a benchmarking between the Tabu-search algorithm and the Baron solver. Finally, the fourth case provides the comparison between our approach and the methodology proposed by Acosta-Flores et al. [34].
The feed is composed of seven species: (chalcopyrite fast), (chalcopyrite slow), (chalcocite fast), (chalcocite slow), (pyrite), (silica), and (gangue). The mass flows of the fed species are shown in Table 1. The values of the constants in Equation (3) are shown in Table 2. The values for the constants in Equation (8) are: , , US$/ton, US$/ton, US$/ton, and h/year. The TSA could assign between 3 and 15 cells, and between three and five minutes of residence time to flotation stages.

Table 1.
Species in feed to process.

Table 2.
Values of and for each stage and species in Equation (3).
3.1. Maximization of Revenues
The equipment superstructure, the mathematical model, included maximization of revenues as the objective function, and the TSA were used for solving the design problem. The developed algorithm was capable of solving the design problem despite the number of species processed, and the requirements and constraints established in the design procedure. The obtained structure is shown in Figure 3, and the revenue, the net present worth, profit before taxes, total capital investment, and total costs of the circuit were USD $130,960,079/year, USD $595,475,455, USD $91,716,855/year, USD $53,265,087, and USD $36,358,032/year, respectively. The , , , , , , , , and were 5 min, 3 min, 3 min, 5 min, 5 min, 15 cells, 3 cells, 3 cells, 15 cells, 15 cells, 197.60 m3, 22.63 m3, 9.98 m3, 167.59 m3, and 155.91 m3, respectively. The final concentrate of the circuit was 14.962 ton/h of chalcopyrite fast, 7.916 ton/h of chalcopyrite slow, 4.938 ton/h of chalcocite fast, 2.633 ton/h of chalcocite slow, 0.008 ton/h of pyrite, 0.017 ton/h of silica, and 0.001 ton/hr of gangue, and its copper grade was 25.70%.
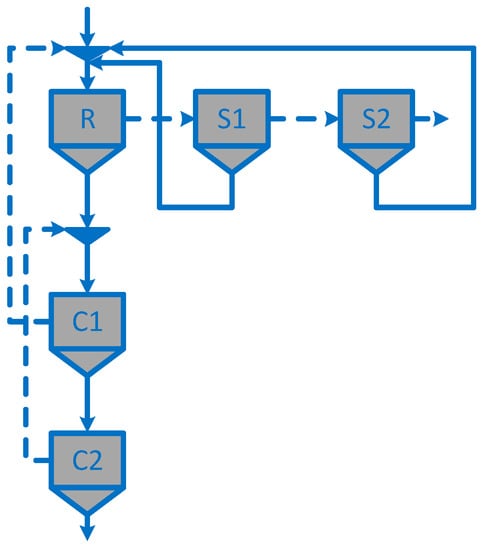
Figure 3.
Structure obtained by maximizing the revenues.
The number of cells and residence time in rougher, scavenger, and re-scavenger are the maxima available. These results are logical because the metallurgical aim of these stages is increasing the recovery of the valuable ore. Also, the objective function does not consider either the equipment costs or the operating costs. The number of cells and residence time in the cleaner and recleaner stages are the minima available. Again, these results are logical because the aim of these stages is increasing the copper grade in the concentrate. These results were obtained by previously evaluating different combinations of the algorithm parameters. In this case, the TSA used 170 neighbors in each neighborhood, 2000 iterations, diversification was applied each time the global solution did not improve after 30 iterations, the intensification was applied each time passing 50 iterations of the algorithm, and the number of rows of the TL was 50. The runtime of the TSA was 601.63 s.
3.2. Maximization of the Net Present Worth
The equipment superstructure and mathematical model included maximization of the net present worth as the objective function, and the TSA was used for solving the design problem. Again, the developed algorithm was capable of solving the design problem despite the number of species processed, and the requirements and constraints established in the design procedure. The obtained structure is shown in Figure 4, and the net present worth, revenue, profit before taxes, total capital investment, and total costs of the circuit were USD $724,828,320, USD $129,830,340/year, USD $107,977,400/year, USD $ 8,386,189, and USD $21,398,690/year, respectively. The values of , , , , , , , , and were 3 min, 3 min, 3 min, 3 min, 3 min, 3 cells, 4 cells, 3 cells, 3 cells, 3 cells, 106.84 m3, 19.84 m3, 9.60 m3, 95.72 m3, and 91.41 m3, respectively. The final concentrate of circuit contained 14.846 ton/h of chalcopyrite fast, 7.757 ton/h of chalcopyrite slow, 4.739 ton/h of chalcocite fast, 2.164 ton/h of chalcocite slow, 0.009 ton/h of pyrite, 0.019 ton/h of silica, and 0.001 ton/h of gangue, with a copper grade of 26.07%.
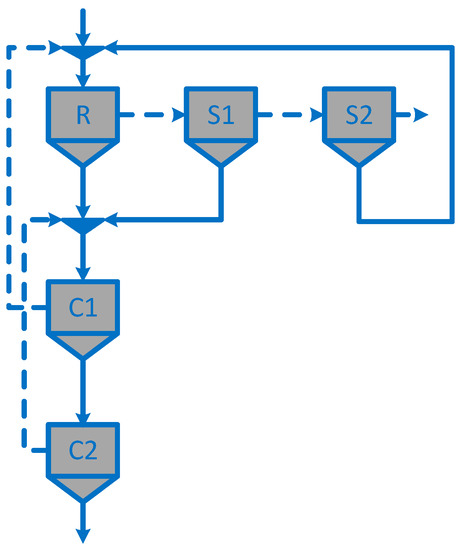
Figure 4.
Structure obtained by maximizing the net present worth.
The number of cells and residence time used in the circuit and shown in Figure 4 are lower compared with the obtained in the case outlined in Section 3.1. These results are logical because the net present worth considers both the equipment costs and the operating costs. The obtained designs in the cases in Section 3.1 and Section 3.2 are different, corroborating the results reported by Cisternas et al. [43], i.e., the objective function affects the design of concentration plants. The TSA used 170 neighbors at each neighborhood, 2000 iterations, the diversification was applied each time that the global solution was not improved after 30 iterations, the intensification was applied each time passing 50 iterations of the algorithm, and the number of rows of the TL was 50. The runtime of the algorithm was 527.61 s.
3.3. Benchmarking between the Tabu-Search Algorithm and the Baron Solver
Many authors have used the Baron solver to solve design problems. As such, we completed benchmarking between the TSA and the Baron solver. The mathematical model for the Baron solver appears in Appendix A. Note that the Baron solver is based on the branch and cut algorithm, i.e., belongs to the family of exact methods.
Initially, we completed benchmarking using the maximization of the revenues as the objective function; the results are shown in Table 3 and Figure 3, Figure 4 and Figure 5. Then, we performed benchmarking using the maximization of the net present worth as the objective function, and the results are shown in Table 4 and Figure 3, Figure 4 and Figure 5. Many authors only used the revenues for designing the circuit, i.e., they included neither equipment design nor operational costs in the mathematical model [1,31,32,34,51]. Thus, we performed benchmarking using a simplified mathematical model, and the results are shown in Table 5 and Figure 3, Figure 4 and Figure 5. Note that the superstructure of Figure 1 represents a total of 144 flotation circuit configurations and that only 11 configurations were selected in all the analyzed cases. These structures correspond to 4 for the case maximization of the revenues as the objective function, 4 for the case the maximization of the net present worth as the objective, and 3 when a simplified mathematical model is used. The structures of Figure 3 and Figure 4 were the most frequently selected circuits.

Table 3.
Benchmarking between the Tabu-search algorithm and the Baron Solver (revenues, Bof = bornite fast).
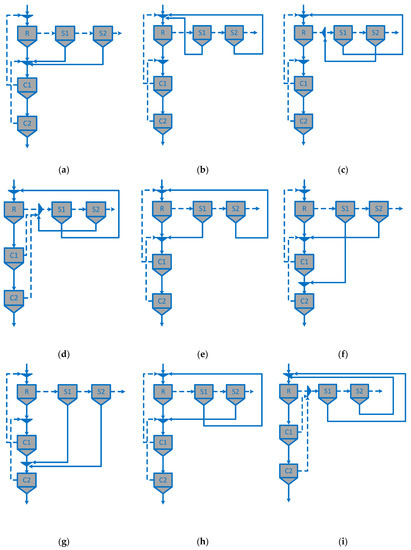
Figure 5.
Structures of circuits obtained by maximization of net present worth (a,c) or revenues (c,d,i) in the case 3.3. Structures (a,b,e–h) are obtained by maximization revenues in the case 3.4.

Table 4.
Benchmarking between the Tabu-search algorithm and the Baron solver (net present worth; Bof = bornite fast, Bos = bornite slow).

Table 5.
Benchmarking between the Tabu algorithm and the Baron solver (revenues; reduced mathematical model; Pf = pyrite fast, Ps = pyrite slow).
Table 3 shows the benchmarking between the TSA and the Baron solver when the maximization of revenues was the objective function. This table depicts five cases. The first considered the species Cpf, Cps, S, and G; the second considered the species Cpf, Cps, P, S, and G; the third considered the species Cpf, Cps, Cf, P, S, and G; the fourth considered the species Cpf, Cps, Cf, Cs, P, S, and G; and the fifth considered the species Cpf, Cps, Cf, Cs, Bof (bornite fast), P, S, and G. In each case, the following output variables were considered: the revenues, net present worth, profit before taxes, total capital investment, total annual cost, equipment size, operating conditions, number of equipment, copper grade in concentrate, circuit structure, runtime of algorithm, number of iterations of TSA, neighborhood size, number of iterations of each diversification, number of iterations of each intensification, and number of rows of . Table 3 shows that TSA is capable to converge independently of the number of species processed in the flotation circuit. The results provided by the TSA and the Baron solver were similar in all analysed cases, except in the fifth case. In this last case, both optimization techniques provided similar revenue; however, the other output variables were different. This result could be related to the simultaneous imposition of all goals and constraints of the mathematical model. Perhaps a relaxation of constraints could help with the exploration of regions, offering a better quality solution. The runtime of TLA in the first, second, third, fourth, and fifth cases was 21.3, 183.4, 287.7, 344.7, and 386.2 s, respectively. The runtime for the Baron solver in the first, second, third, fourth, and fifth cases was 233.0, 423.0, 9026.2, 14,640.0, and 10,257.0 s, respectively. The TSA provided results faster than the Baron solver, but only provides a good quality solution.
Table 4 shows the benchmarking between TSA and the Baron solver when the maximization of the net present worth was the objective function. This table demonstrates six cases. The first considered the species Cpf, Cps, S, and G; the second considered the species Cpf, Cps, P, S, and G; the third considered the species Cpf, Cps, Cf, P, S, and G; the fourth considered the species Cpf, Cps, Cf, Cs, P, S, and G; the fifth considered the species Cpf, Cps, Cf, Cs, Bof, P, S, and G; and the sixth considered the species Cpf, Cps, Cf, Cs, Bof, Bos (bornite slow), P, S, and G. In each case, the following output variables were considered: net present worth, revenues, profit before taxes, total capital investment, total annual cost, equipment size, operating conditions, number of equipment, copper grade in concentrate, circuit structure, runtime of algorithm, number of iterations of TSA, neighborhood size, number of iterations of each diversification, number of iterations of each intensification, and number of rows of . Table 4 shows that TSA is capable to converge independently of the number of species processed in the flotation circuit and objective function used. The results provided by both optimization techniques were similar in all analysed cases. The runtime of TLA in the first, second, third, fourth, fifth, and sixth cases was 106.260 secs, 424.72, 464.99, 527.61, 710.04, and 875.98 s, respectively. The runtime for the Baron solver in the first, second, third, fourth, fifth, and sixth cases was 94.2, 294.92, 533.40, 355.20, 1082.64, and 4299.86 s, respectively. In the first, second, and fourth cases, the Baron solver provided results before the TSA. In the third, fifth, and sixth cases, the TSA provided results before the Baron solver.
Table 5 shows the benchmarking between the TSA and the Baron solver when the mathematical model is simplified. This table demonstrates six cases. The first considered the species Cpf, S and G; the second considered the species Cpf, Cps, S, and G; the third considered the species Cpf, Cps, Pf (pyrite fast), S, and G; the fourth considered the species Cpf, Cps, Pf, Ps (pyrite slow), S, and G; the fifth considered the species Cpf, Cps, Cf, Pf, Ps, S, and G; and the sixth considered the species Cpf, Cps, Cf, Cs, Pf, Ps, S, and G. In each case, are the following output variables were considered: revenue, operating conditions, number of equipment, copper grade in concentrate, circuit structure, runtime of algorithm, number of iterations of TSA, neighborhood size, number of iterations of each diversification, number of iterations of each intensification, and number of rows of . The runtime of TLA in the first, second, third, fourth, and fifth cases was 162.36, 344.06, 368.83, 480.36, and 1098.57 s, respectively. The runtime for the Baron solver in the first case was 1961.8 s, and in the second to fifth cases, the Baron solver did not converge after five days. Both optimization techniques do not provide a solution for the sixth case because the minimal copper grade constraint in the final concentrate cannot be satisfied. Note, the results provided by the TSA could be used for reducing the runtime of the Baron solver. When we delimited the search space of the Baron solver in the fifth case in Table 5, based on the TSA results, runtime of the Baron solver was 101.22 s, and the output variables of mathematical model were similar to those provided by the TSA.
3.4. Comparison with Another Approach
Section 3.3 showed that the Baron solver could converge after a long time period depending on the mathematical model and number of species used in the design procedure. Maybe, due to these results, Acosta-Flores et al. [34] proposed a design methodology based on two phases. In the first phase, they identified a set of optimal structures using discrete values for the flotation stages, then, in the second phase, they determined the optimal design of each structure obtained in the previous phase. Note that they used a superstructure of six flotation stages. However, the optimal structures only used five stages (R, C1, C2, S1, and S2). These authors modeled the flotation stages using the expressions proposed by Yianatos et al. [41]. When all parameters used by Acosta-Flores et al. [34] were included in the proposed methodology, the design shown in Table 6 was obtained. Considering that versions of the Baron solver in the General Algebraic Modeling System (GAMS) environment improve over time, we determined the final design of the structures proposed by Acosta-Flores et al. [34] using our version of GAMS. The results are shown in Table 6.

Table 6.
Comparison between approaches.
Table 6 shows that TSA is capable of converging despite changing the parameters in the methodology proposed. The best design provided by both approaches was similar. However, our method required fewer computational resources. The TSA used 320 neighbors at each neighborhood, 1500 iterations, the diversification was applied each time that the global solution was not improved after 20 iterations; the intensification was applied each time passing 40 iterations of the algorithm, and the number of rows of the TL was 70. Note that the TSA provided secondary designs (Table 7). However, neither approach guarantees finding a global solution.

Table 7.
Best design and secondary designs provided by the Tabu-search algorithm.
In general, Table 3, Table 4, Table 5 and Table 6 show that the TSA converges faster than the Baron solver, and, the TSA always provided a solution in a reasonable amount of time when the mathematical model was well-defined. Notably, the TSA parameters must be adjusted. Evidently, this procedure took time. For example, Lin et al. [52] proposed determining the neighborhood size using the number of free variables of a mathematical model. A similar strategy was applied in this work; however, in general, the TSA did not provide good results. This behavior could be related to the considered multispecies in the design procedure. Then, the neighborhood size was tuned by trial and error.
Cisternas et al. [2] and Lin et al. [5] mentioned that both exact and approximate methods have a low probability of finding the global solution in a reasonable amount of time for large. However, our results contradict these observations. Table 3 and Table 4 show that both optimization techniques converge and provided similar designs despite the design procedure considering several species, operating costs, capital costs, size of equipment, number of equipment, and metallurgical parameters, among other variables. In the case of the TSA, these results could be explained by a minimally dynamic and noncomplex superstructure, which did reduce the number of alternatives to 144. In the case of the Baron solver, these results could be explained by the delimitation of the search space due to large number of equations used by the mathematical model, which helped the solver to converge in a reasonable amount of time. This finding is corroborated by the results shown in Table 5. In this case, the mathematical model included neither equipment design nor operational cost, and generally, the solver did not converge.
The results indicate that the diversification and neighborhood have a strong influence on the results of TSA. When the diversification was not incorporated into the search procedure, the results of the TSA were distinct compared to the results provided by the Baron solver. Although a large neighborhood did not help with obtaining good solutions, better solutions were obtained using small neighborhoods and many iterations of the TSA, i.e., achieving a gradual improvement in the best neighbor.
The TSA developed in this work is flexible, i.e., would allow including into the design procedure grinding models, cell models, or the geological uncertainty (non-linear algorithm). The latter is related to the variation of copper grade that occurs during real operation of the circuit. Initially, the consideration of geological uncertainty or degree of liberation of valuable minerals (grinding) drives optimization under uncertainty. There are several approaches for addressing this type of problem such as stochastic optimization [53]. A possible strategy for solving the stochastic optimization problem is scenario trees based on stochastic parameters of the model. The solution of each scenario would be determined via TSA. A summary of the advantages and disadvantages of the optimization techniques used in this work is shown in Table 8.

Table 8.
Comparison between the Tabu-search algorithm and the Baron solver.
4. Discussion and Conclusions
An algorithm based on Tabu-search was developed and used for designing flotation circuits for several species. The algorithm incorporates diversification for exploring new regions and intensification for exploring regions close to a good solution. The circuits designed using the Tabu-search algorithm were logical and allowed incorporating the influence of the objective function into the design of concentration plants. A comparison between the Tabu-search algorithm and the Baron solver in the GAMS environment was performed. In general, the solutions provided by both optimization techniques were similar. The Tabu-search algorithm always quickly provided a solution when the mathematical model was well-defined, whereas the Baron solver, in some cases, converged slowly or did not converge at all. Finally, we compared our approach and the methodology proposed by Acosta-Flores et al. [34]. The results indicated the best design provided by both proposals was similar. Both approaches provided secondary designs, but our proposal required fewer computational resources. Thus, the developed algorithm can converge to an optimal solution or near optimal for a complex combination of requirements and constraints in a design problem, whereas other methods do not. The developed algorithm represents progress in the design of flotation circuits, which could be useful in the design of full-scale mineral concentration circuits.
In future work, we will seek to include geological uncertainty, operating uncertainty, and grinding in the design procedure. Furthermore, we will analyze the hybridization between TSA and genetic algorithms.
Author Contributions
F.A.L. developed the ideas and objectives of the work. F.A.L. developed the algorithms, simulations and prepared the original draft manuscript. L.A.C. and E.D.G. were responsible for supervision and project administration. E.D.G. and L.A.C. reviewed the final manuscript. L.A.C. analyzed the results.
Acknowledgments
The financial support from CONICYT (Fondecyt 1171341 and 1180826) is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Cleaner stage | |
| Re-cleaner stage | |
| Concentrate stream of the flotation stage | |
| Mass flow of species in concentrate | |
| Mass flow of species in the concentrate stream from stage to stage | |
| Operating cost of flotation stage | |
| Annual depreciation | |
| Gas factor | |
| Annual cash flows | |
| Lang factor | |
| Lang factor for working capital | |
| Frequency matrix | |
| Grade | |
| Number of hours per year of plant operation | |
| Capital cost | |
| Fixed capital cost | |
| Working capital cost | |
| Mass flow of species in feed streams of stage | |
| Maximum rate constant of the species in flotation stage | |
| Mass flow of species fed to the flotation circuit | |
| Number of flotation cell in stage | |
| Neighborhood of | |
| Life time of the project | |
| Number of rows of Tabu list | |
| Final concentrate | |
| Profits before taxes | |
| Kilowatt-hours cost | |
| Fraction of metal paid | |
| Rougher stage | |
| Recovery of stage for species | |
| Maximum recovery at infinite time of stage for species | |
| Refinery charge | |
| Tax rate | |
| Scavenger stage | |
| Re-scavenger stage | |
| Tail stream of the flotation stage | |
| Mass flow of the species in tail | |
| Mass flow of species in the tail stream from stage to stage | |
| Tabu list | |
| Treatment charge | |
| Cell volumen in stage | |
| Final tail | |
| Net present worth | |
| Best neighbor of | |
| Greek symbols | |
| Decision variables | |
| Decision variables | |
| Penalty parameter | |
| Pulp density | |
| Grade deduction | |
| Cell residence time in stage |
Appendix A
Mathematical model in the GAMS environment.
Note that GAMS implements sets for defining the mathematical model. The main sets are:
For the mass balance in splitters, the following equations are considered:
where is the concentrate flows of species in the stream from to , is tail flow of species from to , and are the mass flow of species in the concentrate and tail streams of stage , respectively. Stream branching is not allowed, so the following equations are included:
where and are binary variables indicating the choice of the destination of the concentrate and tail streams, respectively; and correspond to the lower and upper bounds of mass flow of species in the concentrate and tail, respectively. For the mass balance in the mixer, the following equations are considered:
where is the mass flow of species in feed streams to stage . The final concentrate of the flotation circuits is calculated using:
where is the mass flow of species in final concentrate. The mass balance in the flotation stages is determined using:
where is the flotation model proposed by Yianatos and Henríquez [41]. The objective function is defined using the Equations (8)–(20), without considering the penalty parameter.
References
- Hu, W.; Hadler, K.; Neethling, S.J.; Cilliers, J.J. Determining flotation circuit layout using genetic algorithms with pulp and froth models. Chem. Eng. Sci. 2013, 102, 32–41. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Lucay, F.A.; Acosta-Flores, R.; Gálvez, E.D. A quasi-review of conceptual flotation design methods based on computational optimization. Miner. Eng. 2018, 117, 24–33. [Google Scholar] [CrossRef]
- Mendez, D.A.; Gálvez, E.D.; Cisternas, L.A. State of the art in the conceptual design of flotation circuits. Int. J. Miner. Process. 2009, 90, 1–15. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 9780470278581. [Google Scholar]
- Lin, M.H.; Tsai, J.F.; Yu, C.S. A review of deterministic optimization methods in engineering and management. Math. Probl. Eng. 2012, 2012, 756023. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Osman, I.H.; Laporte, G. Metaheuristics: A bibliography. Ann. Oper. Res. 1996, 63, 511–623. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization (Natural Computing Series); Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems. MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Moscato, P. On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms. Caltech Concurrent Computation Program; C3P Report. 1989. Available online: http://citeseer.ist.psu.edu/viewdoc/download?doi=10.1.1.27.9474&rep=rep1&type=pdf (accessed on 31 January 2019).
- Farmer, J.D.; Packard, N.H.; Perelson, A.S. The immune system, adaptation, and machine learning. Phys. D Nonlinear Phenom. 1986, 22, 187–204. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Dipartimento di Elettronica, Politecnico di Milano, Milan, Italy, 1992. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume IV, pp. 1942–1948. [Google Scholar]
- Glover, F.; Laguna, M. Tabu Search. In Handbook of Combinatorial Optimization; Du, D.Z., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 1998; pp. 2093–2229. ISBN 978-1-4613-0303-9. [Google Scholar]
- Glover, F. Tabu Search-Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Han, S.; Li, J.; Liu, Y. Tabu search algorithm optimized ANN model for wind power prediction with NWP. Energy Procedia 2011, 12, 733–740. [Google Scholar] [CrossRef]
- Ting, C.K.; Li, S.T.; Lee, C. On the harmonious mating strategy through tabu search. Inf. Sci. 2003, 156, 189–214. [Google Scholar] [CrossRef]
- Soto, M.; Sevaux, M.; Rossi, A.; Reinholz, A. Multiple neighborhood search, tabu search and ejection chains for the multi-depot open vehicle routing problem. Comput. Ind. Eng. 2017, 107, 211–222. [Google Scholar] [CrossRef]
- Lin, B.; Miller, D.C. Application of tabu search to model indentification. In Proceedings of the AIChE Annual Meeting, Los Angeles, CA, USA, 12–17 November 2000. [Google Scholar]
- Kulturel-Konak, S.; Smith, A.E.; Coit, D.W. Efficiently solving the redundancy allocation problem using tabu search. IIE Trans. (Inst. Ind. Eng.) 2003, 35, 515–526. [Google Scholar] [CrossRef]
- Kis, T. Job-shop scheduling with processing alternatives. Eur. J. Oper. Res. 2003, 151, 307–332. [Google Scholar] [CrossRef]
- Pan, Q.K.; Fatih Tasgetiren, M.; Liang, Y.C. A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem. Comput. Oper. Res. 2008, 35, 2807–2839. [Google Scholar] [CrossRef]
- Mandani, F.; Camarda, K. Multi-objective Optimization for Plant Design via Tabu Search. Comput. Aided Chem. Eng. 2018, 43, 543–548. [Google Scholar]
- Mehrotra, S.P.; Kapur, P.C. Optimal-Suboptimal Synthesis and Design of Flotation Circuits. Sep. Sci. 1974, 9, 167–184. [Google Scholar] [CrossRef]
- Reuter, M.A.; van Deventer, J.S.J.; Green, J.C.A.; Sinclair, M. Optimal design of mineral separation circuits by use of linear programming. Chem. Eng. Sci. 1988, 43, 1039–1049. [Google Scholar] [CrossRef]
- Reuter, M.A.; Van Deventer, J.S.J. The use of linear programming in the optimal design of flotation circuits incorporating regrind mills. Int. J. Miner. Process. 1990, 28, 15–43. [Google Scholar] [CrossRef]
- Schena, G.; Villeneuve, J.; Noël, Y. A method for a financially efficient design of cell-based flotation circuits. Int. J. Miner. Process. 1996, 46, 1–20. [Google Scholar] [CrossRef]
- Schena, G.D.; Zanin, M.; Chiarandini, A. Procedures for the automatic design of flotation networks. Int. J. Miner. Process. 1997, 52, 137–160. [Google Scholar] [CrossRef]
- Maldonado, M.; Araya, R.; Finch, J. Optimizing flotation bank performance by recovery profiling. Miner. Eng. 2011, 24, 939–943. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Méndez, D.A.; Gálvez, E.D.; Jorquera, R.E. A MILP model for design of flotation circuits with bank/column and regrind/no regrind selection. Int. J. Miner. Process. 2006, 79, 253–263. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Gálvez, E.D.; Zavala, M.F.; Magna, J. A MILP model for the design of mineral flotation circuits. Int. J. Miner. Process. 2004, 74, 121–131. [Google Scholar] [CrossRef]
- Calisaya, D.A.; López-Valdivieso, A.; de la Cruz, M.H.; Gálvez, E.E.; Cisternas, L.A. A strategy for the identification of optimal flotation circuits. Miner. Eng. 2016, 96–97, 157–167. [Google Scholar] [CrossRef]
- Acosta-Flores, R.; Lucay, F.A.; Cisternas, L.A.; Galvez, E.D. Two-phase optimization methodology for the design of mineral flotation plants, including multispecies and bank or cell models. Miner. Metall. Process. 2018, 35, 24–34. [Google Scholar] [CrossRef]
- Guria, C.; Verma, M.; Mehrotra, S.P.; Gupta, S.K. Multi-objective optimal synthesis and design of froth flotation circuits for mineral processing, using the jumping gene adaptation of genetic algorithm. Ind. Eng. Chem. Res. 2005, 44, 2621–2633. [Google Scholar] [CrossRef]
- Guria, C.; Verma, M.; Gupta, S.K.; Mehrotra, S.P. Simultaneous optimization of the performance of flotation circuits and their simplification using the jumping gene adaptations of genetic algorithm. Int. J. Miner. Process. 2005, 77, 165–185. [Google Scholar] [CrossRef]
- Ghobadi, P.; Yahyaei, M.; Banisi, S. Optimization of the performance of flotation circuits using a genetic algorithm oriented by process-based rules. Int. J. Miner. Process. 2011, 98, 174–181. [Google Scholar] [CrossRef]
- Pirouzan, D.; Yahyaei, M.; Banisi, S. Pareto based optimization of flotation cells configuration using an oriented genetic algorithm. Int. J. Miner. Process. 2014, 126, 107–116. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Jamett, N.; Gálvez, E.D. Approximate recovery values for each stage are sufficient to select the concentration circuit structures. Miner. Eng. 2015, 83, 175–184. [Google Scholar] [CrossRef]
- Sepúlveda, F.D.; Lucay, F.; González, J.F.; Cisternas, L.A.; Gálvez, E.D. A methodology for the conceptual design of flotation circuits by combining group contribution, local/global sensitivity analysis, and reverse simulation. Int. J. Miner. Process. 2017, 164, 56–66. [Google Scholar] [CrossRef]
- Yianatos, J.B.; Henríquez, F.D. Short-cut method for flotation rates modelling of industrial flotation banks. Miner. Eng. 2006, 19, 1336–1340. [Google Scholar] [CrossRef]
- Green, J.C.A. The optimisation of flotation networks. Int. J. Miner. Process. 1984, 13, 83–103. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Lucay, F.; Gálvez, E.D. Effect of the objective function in the design of concentration plants. Miner. Eng. 2014, 63, 16–24. [Google Scholar] [CrossRef]
- Ruhmer, W. Handbook on the Estimation of Metallurgical Process Cost, 2nd ed.; Mintek: Randburg, South Africa, 1991. [Google Scholar]
- Peters, M.S.; Timmerhaus, K.D.; West, R.E. Plant Design and Economics for Chemical Engineers, 4th ed.; McGraw-Hill Publishing Company: New York, NY, USA, 1991; ISBN 0070496137. [Google Scholar]
- Masuda, K.; Kurihara, K.; Aiyoshi, E. A penalty approach to handle inequality constraints in particle swarm optimization. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Istanbul, Turkey, 10–13 October 2010. [Google Scholar]
- Gogna, A.; Tayal, A. Metaheuristics: Review and application. J. Exp. Theor. Artif. Intell. 2013, 25, 503–526. [Google Scholar] [CrossRef]
- Gendreau, M.; Potvin, J.-Y. Variable Nneighborhood search (chapter). In Handbook of Metaheuristics; Springer: Berlin, Germany, 2010. [Google Scholar] [CrossRef]
- López, E.; Salas, Ó.; Murillo, Á. A deterministic algorithm using tabu search. Revista de Matemática Teoría y Aplicaciones 2014, 21, 127–144. [Google Scholar] [CrossRef]
- De los cobos, S.G.; Goddard, J.; Gutiérrez, M.; Martínez, A. Búsqueda y Exploración Estocástica, 1st ed.; Universidad Autonoma Metropolitana: Mexico City, Mexico, 2010; ISBN 9786074772395. [Google Scholar]
- Jamett, N.; Cisternas, L.A.; Vielma, J.P. Solution strategies to the stochastic design of mineral flotation plants. Chem. Eng. Sci. 2015, 134, 850–860. [Google Scholar] [CrossRef]
- Lin, B.; Chavali, S.; Camarda, K.; Miller, D.C. Using Tabu search to solve MINLP problems for PSE. Comput. Aided Chem. Eng. 2003, 15, 541–546. [Google Scholar] [CrossRef]
- Fouskakis, D.; Draper, D. Stochastic optimization: A review. Int. Stat. Rev. 2002, 70, 315–349. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).